Biophysical Characterization of (Silica-coated) Cobalt Ferrite Nanoparticles for Hyperthermia Treatment
Abstract
:1. Introduction
2. Materials and Methods
3. Results
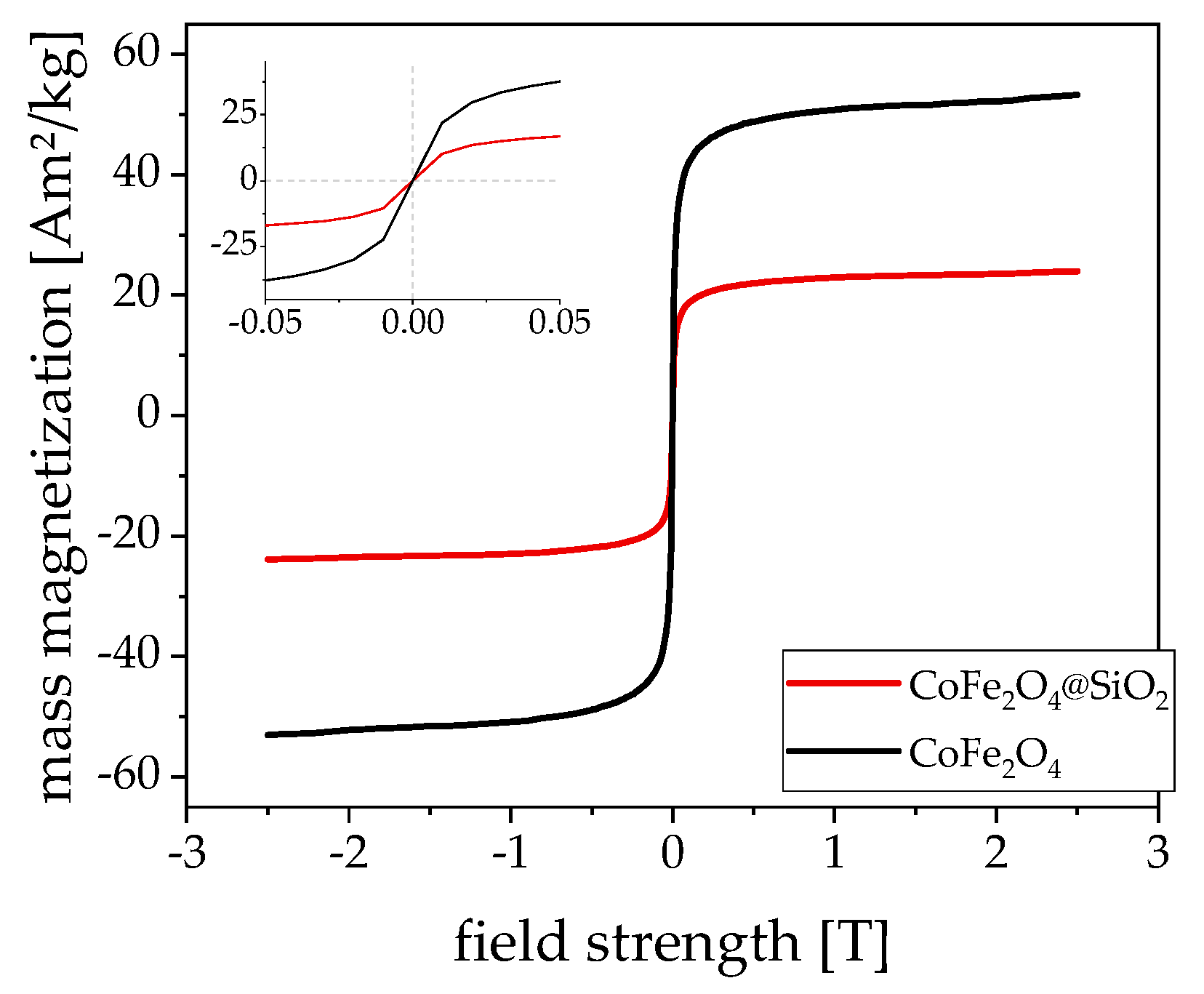
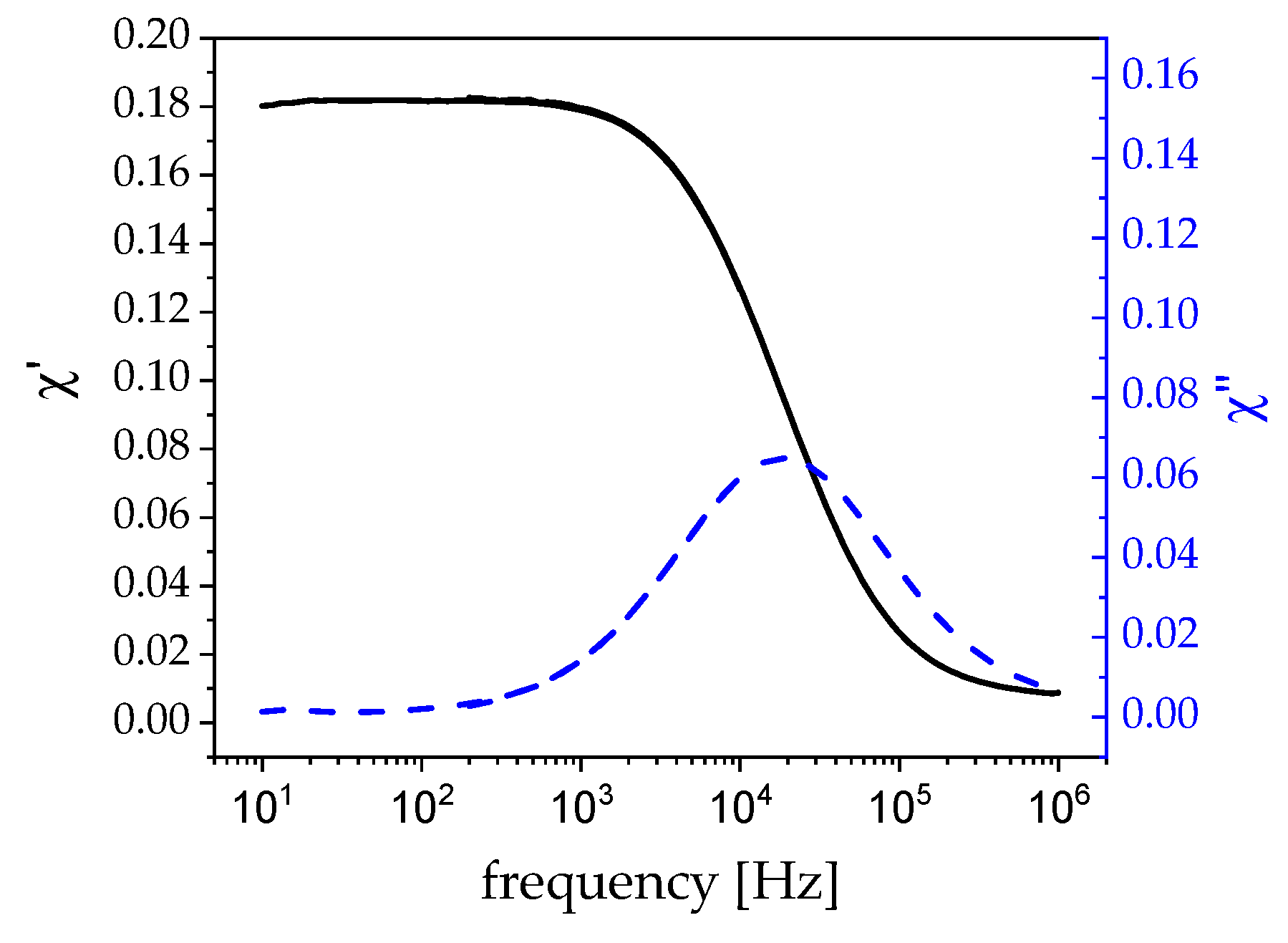
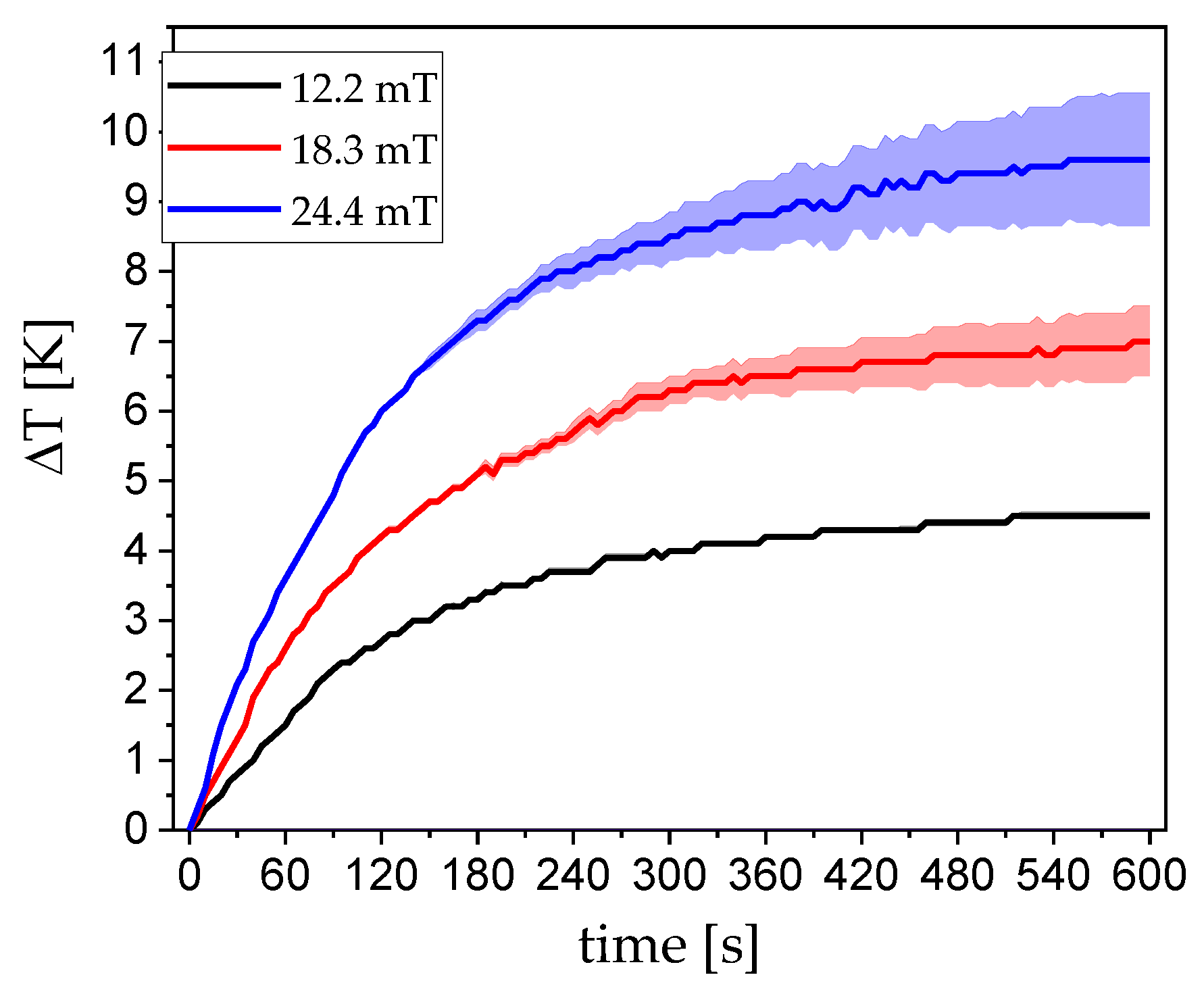
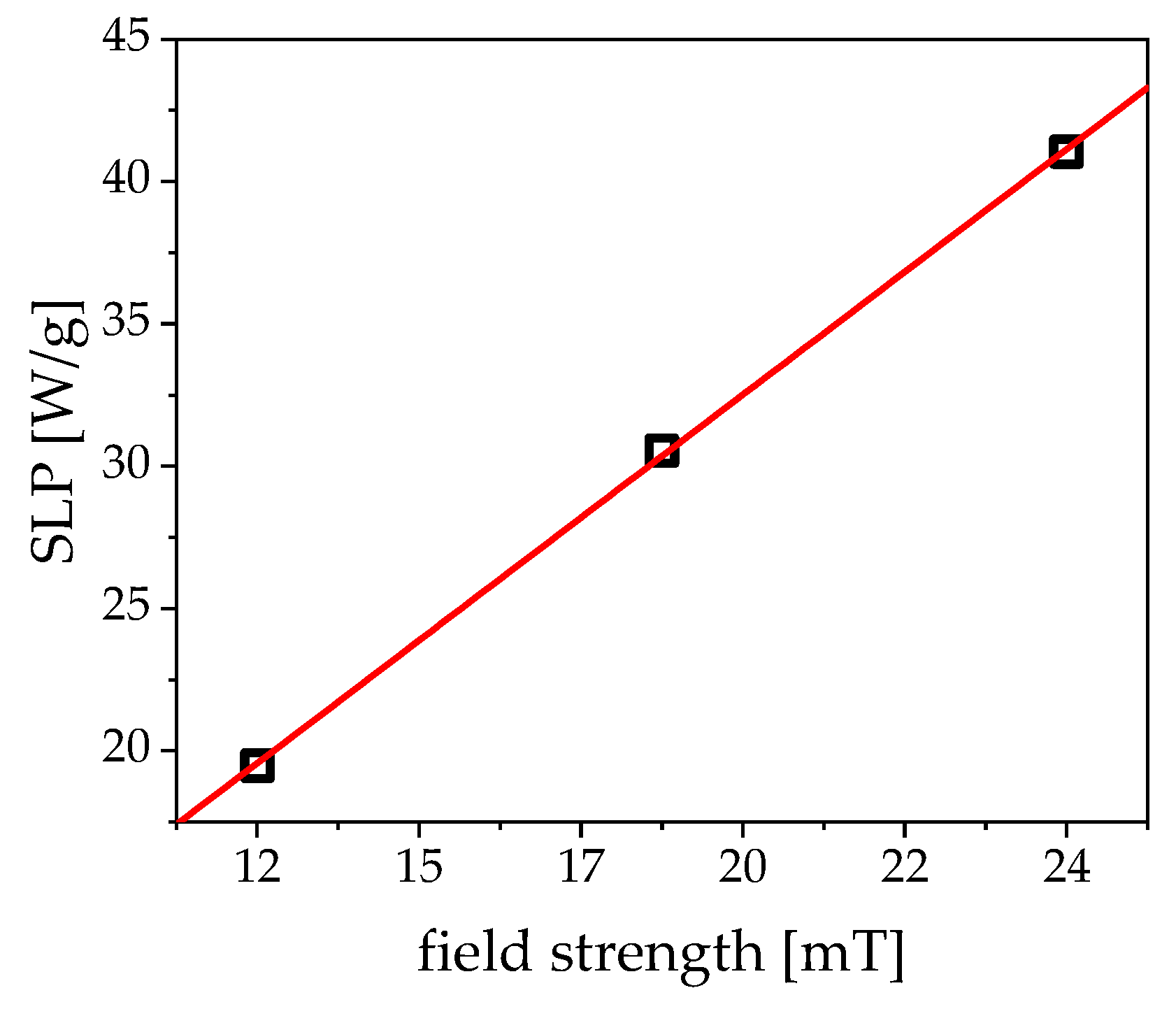
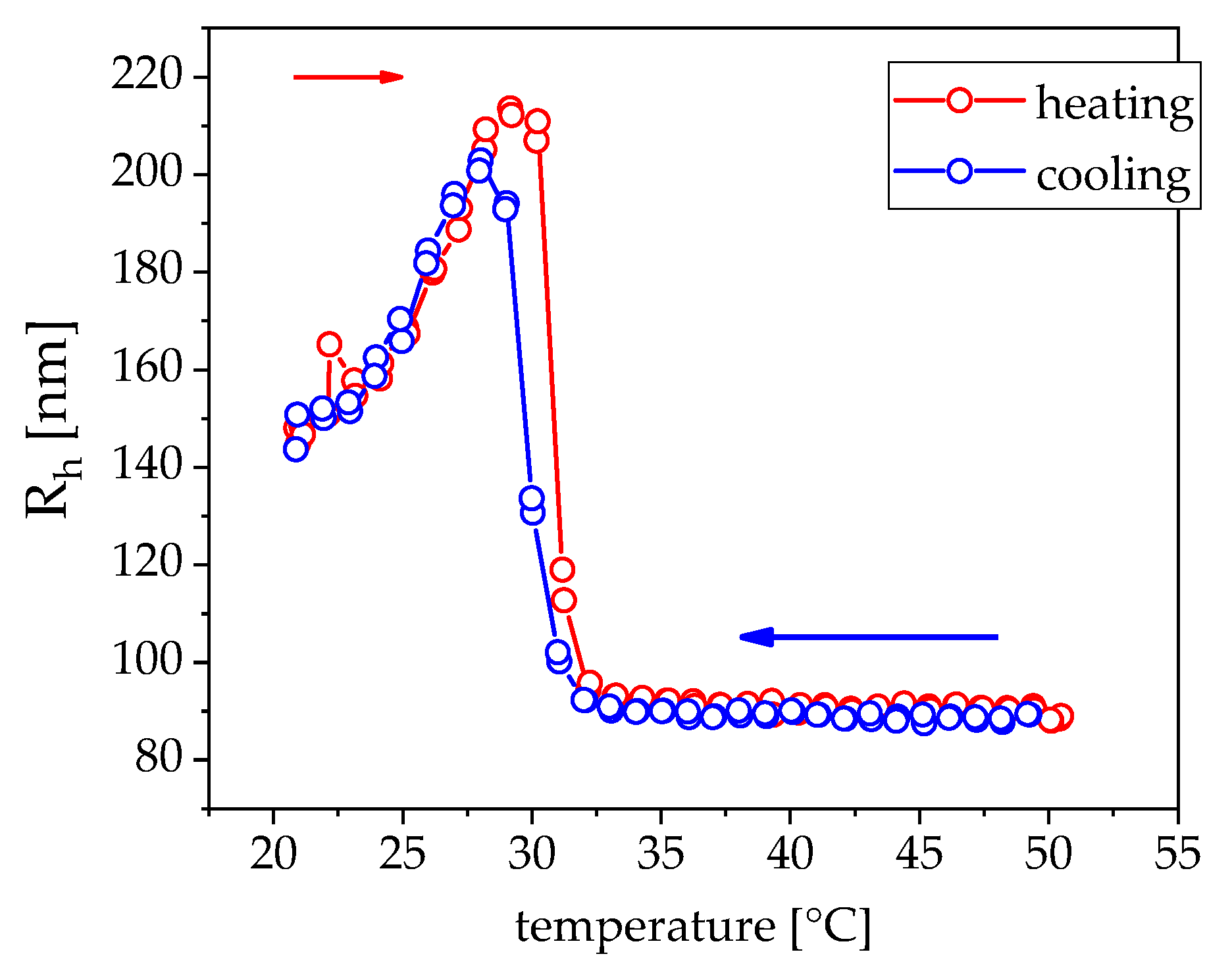
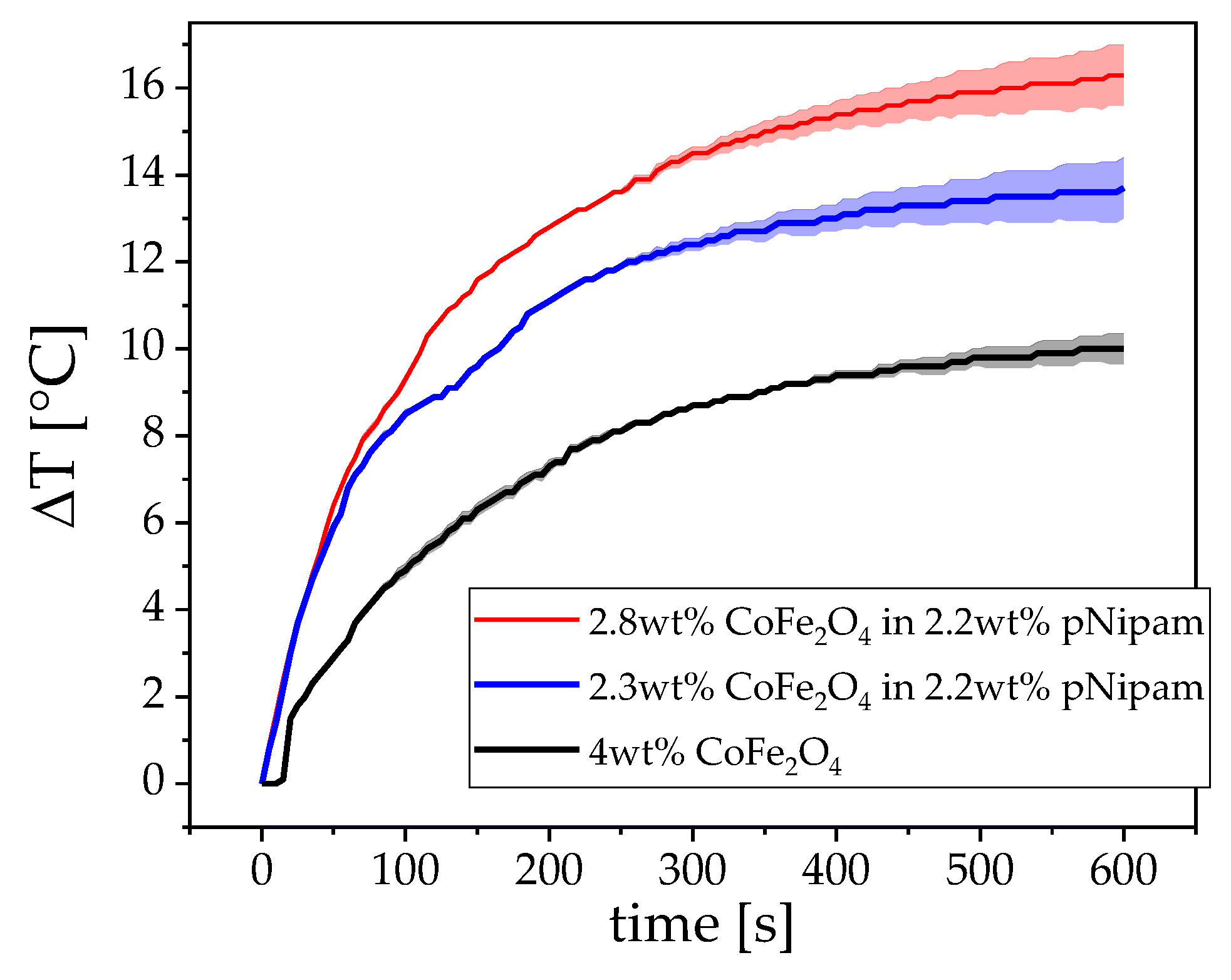
3.1. Magnetism
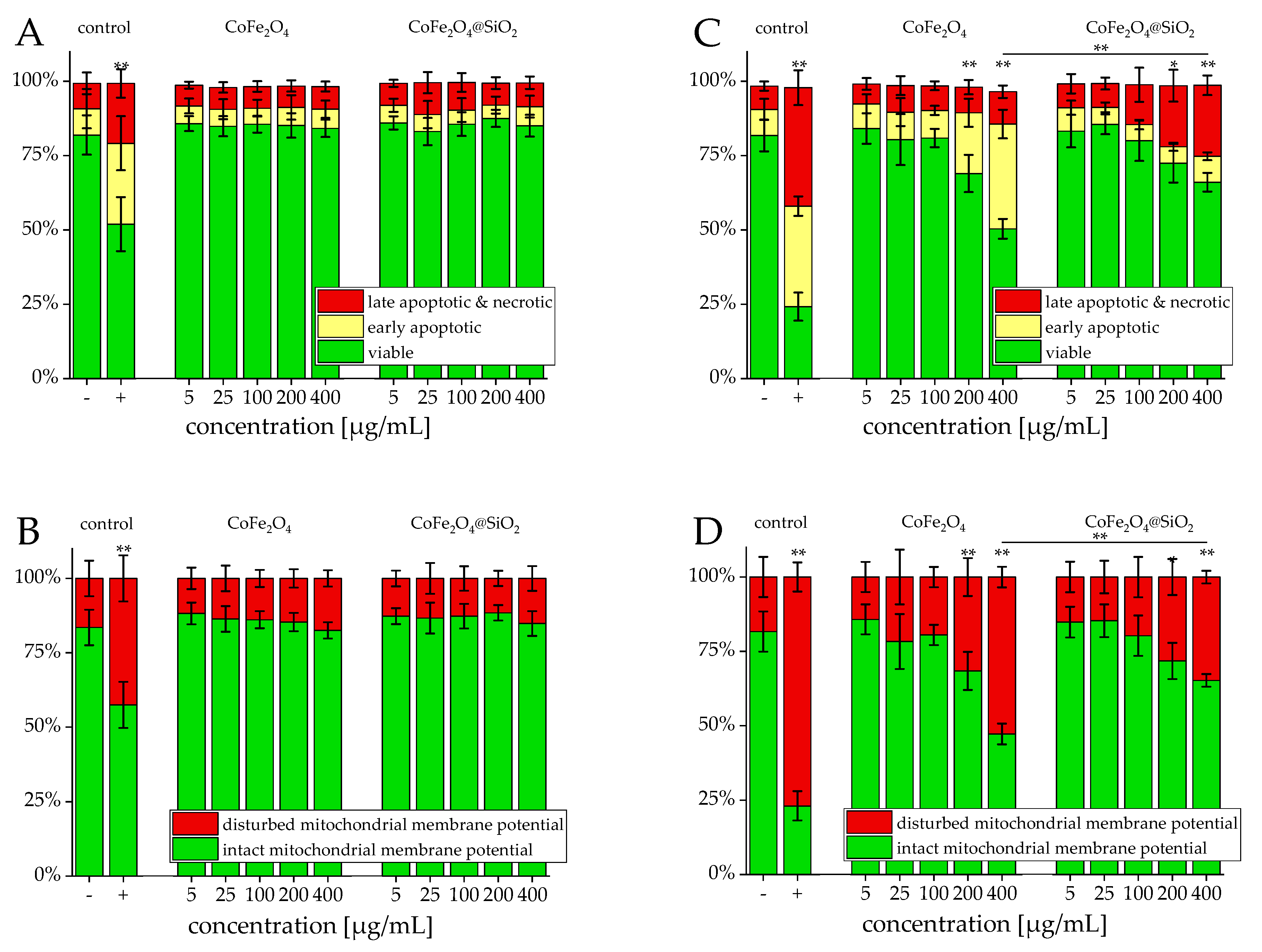
3.2. Viability
4. Discussion
4.1. Viability
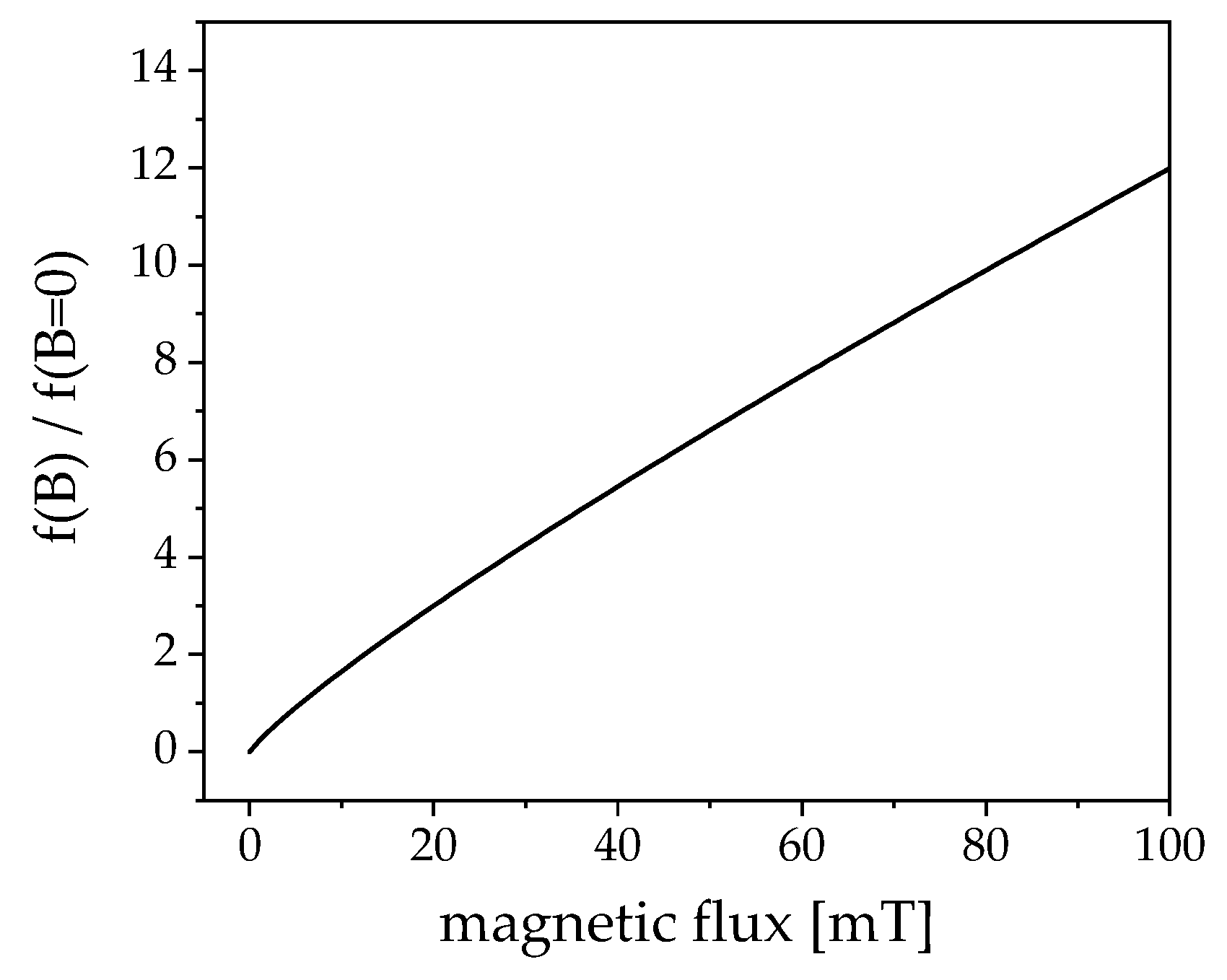
4.2. Hyperthermia:
4.3. Outlook
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gao, R.; Lu, D.F.; Cheng, J.; Jiang, Y.; Jiang, L.; Ye, J.S.; Qi, Z.M. Magnetic Fluid-Infiltrated Anti-Resonant Reflecting Optical Waveguide for Magnetic Field Sensing Based on Leaky Modes. J. Lightwave Technol. 2016, 34, 3490–3495. [Google Scholar] [CrossRef]
- Kurian, M.; Thankachan, S.; Nair, D.S.; Aswathy, E.K.; Babu, A.; Thomas, A.; Krishna, K.T.B. Structural, magnetic, and acidic properties of cobalt ferrite nanoparticles synthesised by wet chemical methods. J. Adv. Ceram. 2015, 4, 199–205. [Google Scholar] [CrossRef]
- Habash, R.W.Y. Therapeutic hyperthermia. Hand Clin. 2018, 157, 853–868. [Google Scholar]
- Tang, J.D.; Qiao, Y.C.; Chu, Y.H.; Tong, Z.F.; Zhou, Y.F.; Zhang, W.L.; Xie, S.J.; Hu, J.; Wang, T.J. Magnetic double-network hydrogels for tissue hyperthermia and drug release. J. Mater. Chem. B 2019, 7, 1311–1321. [Google Scholar] [CrossRef]
- Brown, D.M.; Johnston, H.J.; Gaiser, B.; Pinna, N.; Caputo, G.; Culha, M.; Kelestemur, S.; Altunbek, M.; Stone, V.; Roy, J.C.; et al. A cross-species and model comparison of the acute toxicity of nanoparticles used in the pigment and ink industries. Nanoimpact 2018, 11, 20–32. [Google Scholar] [CrossRef]
- Susan-Resiga, D.; Vekas, L. From High Magnetization Ferrofluids to Nano-Micro Composite Magnetorheological Fluids: Properties and Applications. Rom. Rep. Phys. 2018, 70, 134–143. [Google Scholar]
- George, T.; Sunny, A.T.; Varghese, T. Magnetic properties of cobalt ferrite nanoparticles synthesized by sol-gel method. IOP Conf. Ser. Mater. Sci. Eng. 2015, 73, 012050. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Heating magnetic fluid with alternating magnetic field. J. Magn. Magn. Mater. 2002, 252, 370–374. [Google Scholar] [CrossRef]
- Tabish, T.A.; Ashiq, M.N.; Ullah, M.A.; Iqbal, S.; Latif, M.; Ali, M.; Ehsan, M.F.; Iqbal, F. Biocompatibility of cobalt iron oxide magnetic nanoparticles in male rabbits. Korean J. Chem. Eng. 2016, 33, 2222–2227. [Google Scholar] [CrossRef]
- Lima-Tenorio, M.K.; Tenorio-Neto, E.T.; Hechenleitner, A.A.W.; Fessi, H.; Pineda, E.A.G. CoFe2O4 and ZnFe2O4 Nanoparticles: An Overview About Structure, Properties, Synthesis and Biomedical Applications. J. Colloid Sci. Biotechnol. 2016, 5, 45–54. [Google Scholar] [CrossRef]
- Nappini, S.; Magnano, E.; Bondino, F.; Pis, I.; Barla, A.; Fantechi, E.; Pineider, F.; Sangregorio, C.; Vaccari, L.; Venturelli, L.; et al. Surface Charge and Coating of CoFe2O4 Nanoparticles: Evidence of Preserved Magnetic and Electronic Properties. J. Phys. Chem. C 2015, 119, 25529–25541. [Google Scholar] [CrossRef]
- Zou, J.; Peng, Y.G.; Tang, Y.Y. A facile bi-phase synthesis of Fe3O4@SiO2 core-shell nanoparticles with tunable film thicknesses. RSC Adv. 2014, 4, 9693–9700. [Google Scholar] [CrossRef]
- Wu, X.; Pelton, R.H.; Hamielec, A.E.; Woods, D.R.; Mcphee, W. The Kinetics of Poly (N-Isopropylacrylamide) Microgel Latex Formation. Colloid Polym. Sci. 1994, 272, 467–477. [Google Scholar] [CrossRef]
- Nack, A. Particle-Matrix Interactions in Ferrogels Containing Shape-Anisotropic, Magnetic Nanoparticles. Ph.D. Thesis, University of Rostock, Rostock, Germany, 24 May 2017. [Google Scholar]
- Ludwig, F.; Guillaume, A.; Schilling, M.; Frickel, N.; Schmidt, A.M. Determination of core and hydrodynamic size distributions of CoFe2O4 nanoparticle suspensions using ac susceptibility measurements. J. Appl. Phys. 2010, 108. [Google Scholar] [CrossRef]
- Ludwig, F.; Balceris, C.; Jonasson, C.; Johansson, C. Analysis of AC Susceptibility Spectra for the Characterization of Magnetic Nanoparticles. IEEE Trans. Magn. 2017, 53, 6100904. [Google Scholar] [CrossRef]
- Janko, C.; Munoz, L.; Chaurio, R.; Maueröder, C.; Berens, C.; Lauber, K.; Herrmann, M. Navigation to the Graveyard-Induction of Various Pathways of Necrosis and Their Classification by Flow Cytometry, 1st ed.; Humana Press: Totowa, NJ, USA, 2013; pp. 3–15. [Google Scholar]
- Allaedini, G.; Tasirin, S.M.; Aminayi, P. Magnetic properties of cobalt ferrite synthesized by hydrothermal method. Int. Nano Lett. 2015, 5, 183–186. [Google Scholar] [CrossRef]
- Al Lehyani, S.H.A.; Hassan, R.A.; Alharbi, A.A.; Alomayri, T. Magnetic Hyperthermia using Cobalt Ferrite Nanoparticles: The Influence of Particle Size. Int. J. Adv. Technol. 2017, 8, 1000196–1000201. [Google Scholar]
- Darwish, M.S.A.; Kim, H.; Lee, H.; Ryu, C.; Lee, J.Y.; Yoon, J. Synthesis of Magnetic Ferrite Nanoparticles with High Hyperthermia Performance via a Controlled Co-Precipitation Method. Nanomaterials 2019, 9, 1176. [Google Scholar] [CrossRef]
- Phong, P.T.; Phuc, N.X.; Nam, P.H.; Chien, N.V.; Dung, D.D.; Linh, P.H. Size-controlled heating ability of CoFe2O4 nanoparticles for hyperthermia applications. Phys. B Condens. Matter 2018, 531, 30–34. [Google Scholar] [CrossRef]
- Draack, S.; Lucht, N.; Remmer, H.; Martens, M.; Fischer, B.; Schilling, M.; Ludwig, F.; Viereck, T. Multiparametric Magnetic Particle Spectroscopy of CoFe2O4 Nanoparticles in Viscous Media. J. Phys. Chem. C 2019, 123, 6787–6801. [Google Scholar] [CrossRef]
- Torres, T.E.; Lima, E.; Calatayud, M.P.; Sanz, B.; Ibarra, A.; Fernandez-Pacheco, R.; Mayoral, A.; Marquina, C.; Ibarra, M.R.; Goya, G.F. The relevance of Brownian relaxation as power absorption mechanism in Magnetic Hyperthermia. Sci. Rep. 2019, 9, 3392. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, T.; Enpuku, K. Simulation and Quantitative Clarification of AC Susceptibility of Magnetic Fluid in Nonlinear Brownian Relaxation Region. Jpn. J. Appl. Phys. 2009, 48. [Google Scholar] [CrossRef]
- Zhong, J.; Dieckhoff, J.; Schilling, M.; Ludwig, F. Influence of static magnetic field strength on the temperature resolution of a magnetic nanoparticle thermometer. J. Appl. Phys. 2016, 120, 143902. [Google Scholar] [CrossRef]
- Remmer, H.; Gratz, M.; Tschope, A.; Ludwig, F. Magnetic Field Dependence of Ni Nanorod Brownian Relaxation. IEEE Trans. Magn. 2017, 53. [Google Scholar] [CrossRef]
- Ansari, A.A.; Hasan, T.N.; Syed, N.A.; Labis, J.P.; Alshatwi, A.A. In-vitro cytotoxicity and cellular uptake studies of luminescent functionalized core-shell nanospheres. Saudi J. Biol. Sci. 2017, 24, 1392–1403. [Google Scholar] [CrossRef] [PubMed]
- Bossi, E.; Zanella, D.; Gornati, R.; Bernardini, G. Cobalt oxide nanoparticles can enter inside the cells by crossing plasma membranes. Sci. Rep. 2016, 6, 22254. [Google Scholar] [CrossRef] [PubMed]
- Abudayyak, M.; Gurkaynak, T.A.; Ozhan, G. In Vitro Evaluation of the Toxicity of Cobalt Ferrite Nanoparticles in Kidney Cell. Turk. J. Pharm. Sci. 2017, 14, 169–173. [Google Scholar] [CrossRef]
- Han, Q.L.; Liu, F. Low doses of Co nanoparticles induce death and regulate osteogenic differentiation in MG-63 cells. Mol. Med. Rep. 2017, 16, 7591–7596. [Google Scholar] [CrossRef]
- Pasukoniene, V.; Mlynska, A.; Steponkiene, S.; Poderys, V.; Matulionyte, M.; Karabanovas, V.; Statkute, U.; Purviniene, R.; Krasko, J.A.; Jagminas, A.; et al. Accumulation and biological effects of cobalt ferrite nanoparticles in human pancreatic and ovarian cancer cells. Medicina 2014, 50, 237–244. [Google Scholar] [CrossRef]
- Mariani, V.; Ponti, J.; Giudetti, G.; Broggi, F.; Marmorato, P.; Gioria, S.; Franchini, F.; Rauscher, H.; Rossi, F. Online monitoring of cell metabolism to assess the toxicity of nanoparticles: The case of cobalt ferrite. Nanotoxicology 2012, 6, 272–287. [Google Scholar] [CrossRef]
- Wang, H.G.; Ren, T.T.; Zhu, N.L.; Yu, Q.L.; Li, M.C. Co3O4 nanoparticles at sublethal concentrations inhibit cell growth by impairing mitochondrial function. Biochem. Biophys. Res. Commun. 2018, 505, 775–780. [Google Scholar] [CrossRef] [PubMed]
- Deatsch, A.E.; Evans, B.A. Heating efficiency in magnetic nanoparticle hyperthermia. J. Magn. Magn. Mater. 2014, 354, 163–172. [Google Scholar] [CrossRef]
- Andreu, I.; Natividad, E.; Ravagli, C.; Castro, M.; Baldi, G. Heating ability of cobalt ferrite nanoparticles showing dynamic and interaction effects. RSC Adv. 2014, 4, 28968–28977. [Google Scholar] [CrossRef]
- Khalid, W.; Jafar, F.; Iqbal, N.; Ali, Z.; Humayon, A.; Akhtar, J.; Atif, M. Synthesis of gold-coated CoFe2O4 and their potential in magnetic hyperthermia. Appl. Phys. A 2018, 124, 501. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lucht, N.; Friedrich, R.P.; Draack, S.; Alexiou, C.; Viereck, T.; Ludwig, F.; Hankiewicz, B. Biophysical Characterization of (Silica-coated) Cobalt Ferrite Nanoparticles for Hyperthermia Treatment. Nanomaterials 2019, 9, 1713. https://doi.org/10.3390/nano9121713
Lucht N, Friedrich RP, Draack S, Alexiou C, Viereck T, Ludwig F, Hankiewicz B. Biophysical Characterization of (Silica-coated) Cobalt Ferrite Nanoparticles for Hyperthermia Treatment. Nanomaterials. 2019; 9(12):1713. https://doi.org/10.3390/nano9121713
Chicago/Turabian StyleLucht, Niklas, Ralf P. Friedrich, Sebastian Draack, Christoph Alexiou, Thilo Viereck, Frank Ludwig, and Birgit Hankiewicz. 2019. "Biophysical Characterization of (Silica-coated) Cobalt Ferrite Nanoparticles for Hyperthermia Treatment" Nanomaterials 9, no. 12: 1713. https://doi.org/10.3390/nano9121713
APA StyleLucht, N., Friedrich, R. P., Draack, S., Alexiou, C., Viereck, T., Ludwig, F., & Hankiewicz, B. (2019). Biophysical Characterization of (Silica-coated) Cobalt Ferrite Nanoparticles for Hyperthermia Treatment. Nanomaterials, 9(12), 1713. https://doi.org/10.3390/nano9121713




