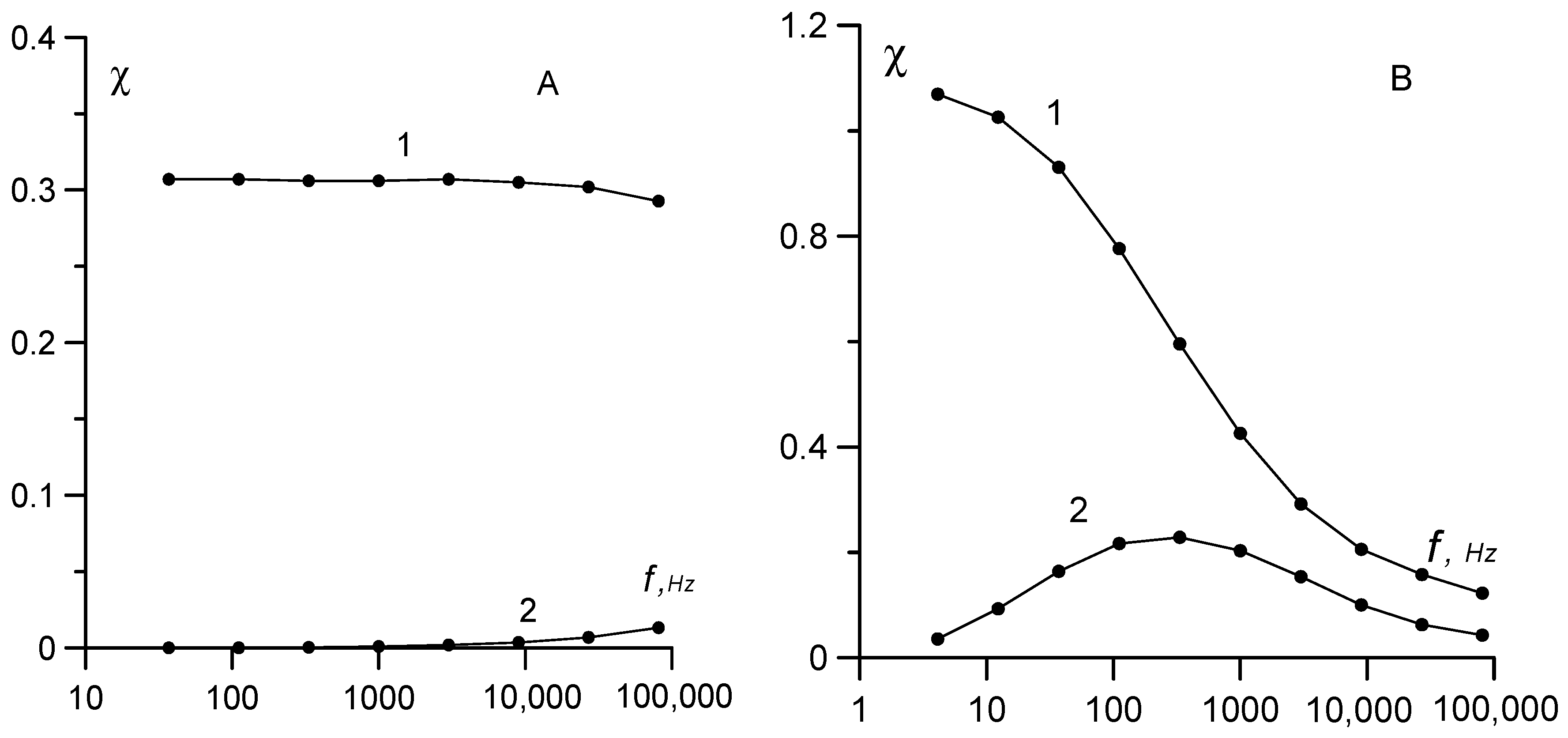3.1. Relaxation Processes
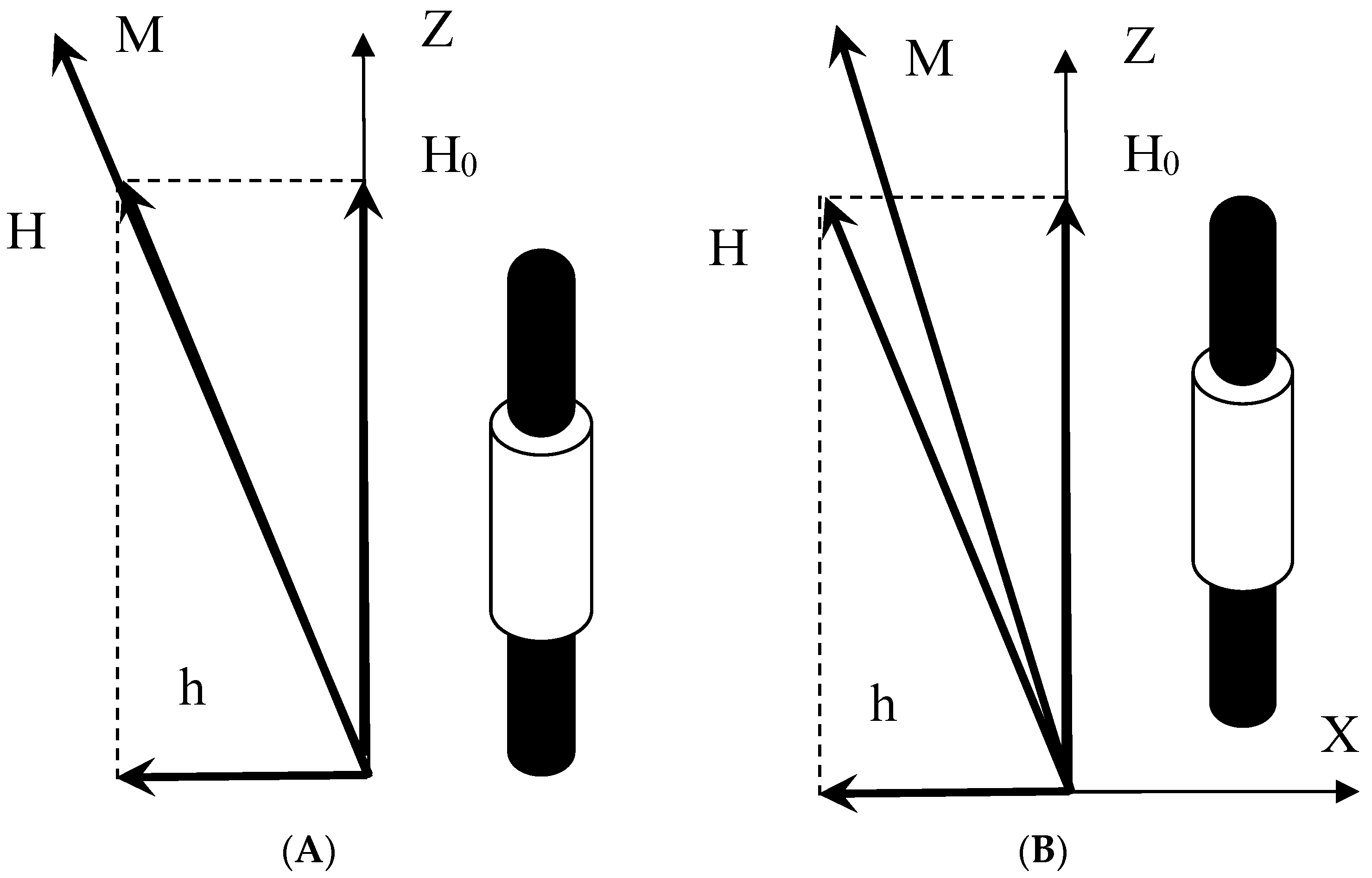
We determined the output signal at an arbitrary frequency of the probe field. In this case, the magnetization of the sample differed from the equilibrium value, the co-linearity of the vectors
M and
H was violated (
Figure 1B), and Equation (2) became inapplicable. To determine the components of magnetization, it was necessary to solve the relaxation equation, which contains the characteristic relaxation times
τ of the magnetic moment taken as parameters. Real magnetic fluids, as a rule, have broad particle-size distributions and wide ranges of magnetization relaxation times. Considering the polydispersity of particles in the dynamic problem makes it unnecessarily cumbersome. Therefore, in this section, we restrict our discussion to the monodisperse ferrofluids, in which all particles are identical.
Since, according to the experimental conditions, the AC field component was small, we used the linearized relaxation equation [
20,
21]
where
is the equilibrium magnetization corresponding to the instantaneous value of the field strength in the sample. The relaxation times
τII and
for the longitudinal and transverse components of magnetization, respectively, depend on the field strength; in the dilute solution they are described by [
20,
21]:
where
τB is the Brownian time of rotational diffusion of particles in zero magnetic field,
η is the ferrofluid viscosity, and
V is the volume of the particle covered with a protective shell. In weak fields (
ξ << 1), both relaxation times coincide with the Brownian time
τB and monotonically decrease with the growth of the magnetic field.
Expanding the equilibrium magnetization,
in Equation (11) in a power series of the weak ac field
h, and retaining only the terms of the lowest power, we obtain:
Then, substituting the explicit expression for the internal field
h =
a cos
ωt in Equation (13), we find:
Using Equation (14) and the relationship between the applied and internal probe fields given as:
we find the amplitude of the probe field inside the sample:
Substituting Equations (15) and (16) into Equation (1) yields the required expression for the output signal:
Equation (17) determines the field and frequency dependences of output signal. It is valid for an arbitrary magnetic fluid with a rather narrow particle size distribution and negligible spread of particles in the relaxation time.
To analyze the experimental data, we introduced the normalized output signal
E* by dividing Equation (17) into a coefficient that included the parameters of the measuring coil, the frequency, and square of the probing field amplitude. The normalized signal thus describes only the effect of the bias field and relaxation processes:
We theoretically analyzed Equation (18), considering the steric and magneto dipole–interparticle interactions. For this purpose, we used the modified effective field model [
6], which adequately describes the equilibrium magnetization of concentrated ferrofluids. Samples studied in the experiment (
Table 2) had relatively low concentrations of particles; therefore, when calculating the effective field, we considered only the correction, which was linear in concentration (i.e., proportional to Langevin susceptibility):
where
is the Langevin parameter, which is determined in terms of the bias field strength. Substituting Equation (19) into (18) leads to the expression:
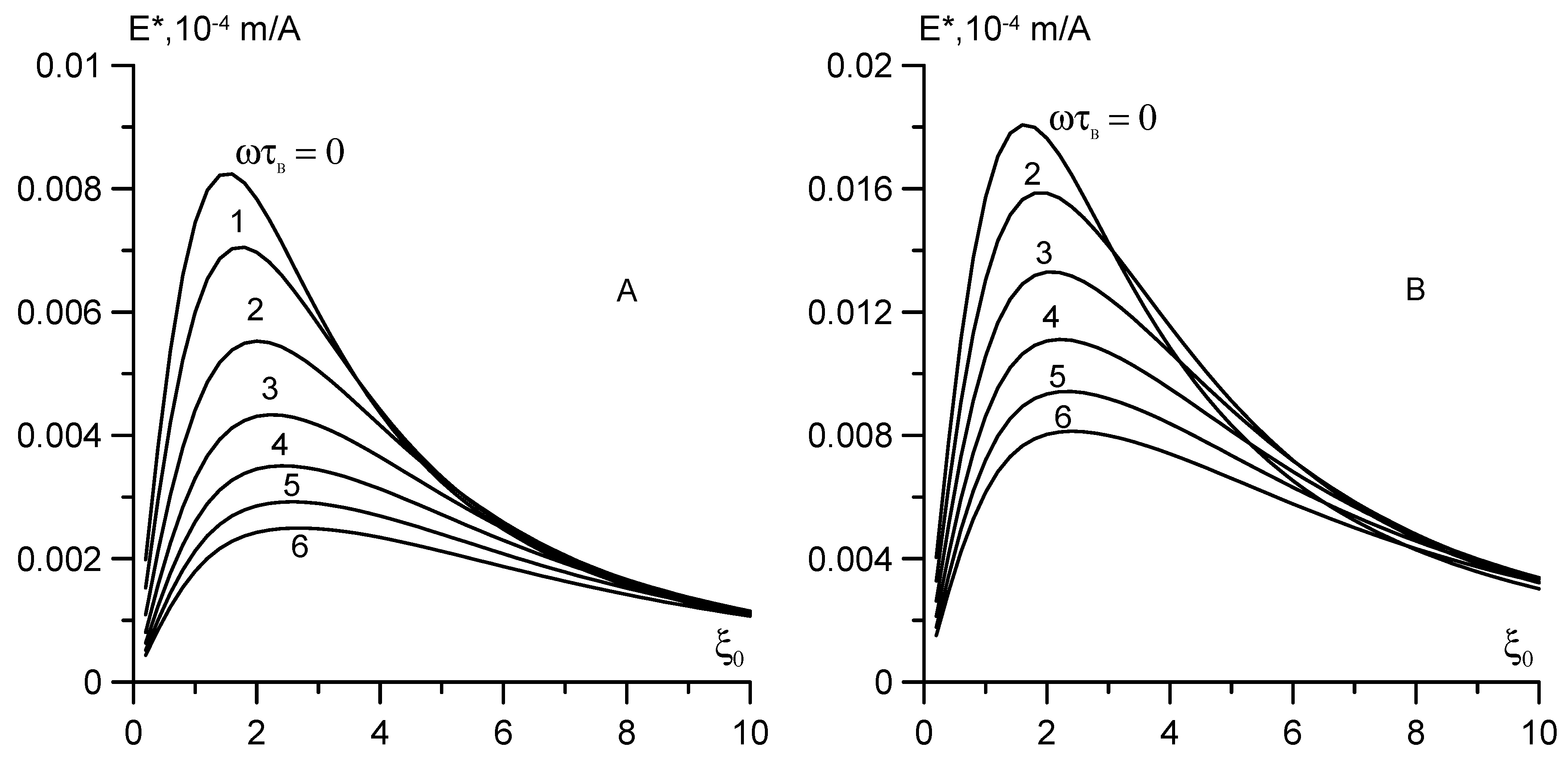
The field dependence of the output signal calculated by Equation (20) is shown in
Figure 3A,B. To compare the experimental results, the magnetic moments
m of the particles and the Langevin susceptibility
χL of the model fluids were considered identical to those of samples No. 1 and 2 in
Table 1 and
Table 2. Since Equations (19) and (20) do not consider the polydispersity of particles, one good quantitative agreement between the calculated and experimental data in the case of the broad size distribution of particles should not be expected. The main advantage of Equations (18) and (20) is that they consider the dynamic effects, magneto dipole–interparticle interactions, and the demagnetizing field. The last two factors compete with each other. The magneto dipole interactions increase ferrofluid magnetization, whereas the demagnetizing field causes its decrease. Their total effect remains appreciable even for moderately concentrated solutions, such as samples No. 1 and 2. In
Figure 3A,B this effect is manifested in the shift of the maximum of the function
E* =
f(
ξ) toward weak fields. For dilute magnetic fluids in which the interparticle interactions and demagnetizing fields are negligible, the Langevin parameter, corresponding to the maximum of the function
E* =
f(
ξ), is equal to
ξ* = 1.93 [
2,
3]. Equation (2) supports the correctness of this value in the case when the fluid magnetization is calculated in the Langevin approximation. However, the curves in
Figure 3 constructed with regard for the interparticle interactions demonstrate markedly lower values of
ξ*:
ξ* ≈ 1.53 for sample No. 1 and
ξ* ≈ 1.65 for sample No. 2.
The shapes of the
E* =
f(
ξ,ω) curves in
Figure 3A,B for two model monodisperse fluids are qualitatively identical. With increasing frequency of the probe field (
ωτB ≥ 1), the output signal decreased and the maximum was smeared. In the strong bias field (
ξ0 ≥ 10), relaxation times decreased, as predicted by Equation (12), therefore, the dynamic contributions to Equations (18) and (20) decreased by almost two orders of magnitude. The process of magnetization reversal became quasi-static and the output signal was no longer dependent on the frequency, at least at
ωτB ≤ 6.
3.2. Results of Dynamic Susceptibility Experiment
The real ferrofluids have a wide spectrum of relaxation times due to the polydispersity of single-domain particles, the formation of the clusters, and two independent relaxation mechanisms (Brownian and Néel). The Brownian mechanism of magnetization relaxation is associated with the rotation of particles in a viscous medium, and the characteristic relaxation time is determined by Equation (12). The Néel mechanism of magnetization relaxation is associated with the rotation of the magnetic moment of the particle relative to the crystallographic axes [
22,
23,
24]. For the uniaxial single-domain particle the most energetically favorable orientations of the magnetic moment are the two opposite directions along the easy axis. These two states are separated by the energy barrier
KVm, where
K is the magnetic anisotropy constant and
Vm is the volume of the particle magnetic core. In the weak field, this barrier can be overcome due to thermal fluctuations within the particle itself, which corresponds to the Néel relaxation mechanism.
The Néel time
τN required to overcome the barrier grows exponentially with decreasing temperature, i.e.,
τN ~
τ0 exp
σ, where
τ0 ~ 10
−9 s is the damping time of the Larmor precession, and
σ is the reduced barrier height (anisotropy parameter):
The magnetization dynamics in the weak applied field are determined by that of two relaxation mechanisms, which ensures the shortest relaxation time. The Brownian and Néel relaxation times depend differently on the particle volume [
23]. The condition
τN =
τB provides the characteristic magnetic core diameter
x*, which corresponds to “switching” off the relaxation mechanism. If
x <
x*, then the Néel relaxation mechanism prevails, and if
x >
x*, then the Brownian mechanism is predominant. Generally,
x* does not coincide with the limiting size of superparamagnetic particles: the Brownian fraction includes both magnetically hard particles and some superparamagnetic particles with
τN >
τB. According to estimates [
25], for low-viscous magnetite ferrofluids
x* ≈ 16−18 nm,
τN = 10
−10 −10
−5 s, and
τB = 10
−5 −10
−3 s. Thus, at frequencies up to 10
4 Hz, the dispersion of the dynamic susceptibility is specified by the particles with Brownian relaxation mechanism and at frequencies above 10
5 Hz by the particles with the Néel magnetic moment relaxation mechanism.
The frequency dependence of the initial susceptibility for samples No. 1 and 2 with the lowest and highest concentrations of large particles is shown in
Figure 4. The
χ(
ω) curves differ drastically. For sample No. 1, a weak susceptibility dispersion was observed only at frequencies of the order of 10
5 Hz; for sample No. 2, the maximum dispersion was observed at frequencies of 300–400 Hz. Such difference in the dynamics of magnetization is the direct result of differences in the particle size distributions.
Sample No. 1 had a relatively narrow particle size distribution. The main contribution to the dynamic susceptibility was from superparamagnetic particles with magnetic core diameter
x < x* ≈ 16 nm and rather short relaxation times (
τN < 10
−5 s). In the examined frequency range, this sample showed a quasi-static behavior, and the region of susceptibility dispersion was beyond the upper boundary of this range. Conversely, sample No. 2 had a broad particle-size distribution (
Table 1) with a long tail, so the main contribution to the dynamic susceptibility was due to the Brownian particles with a magnetic core diameter
x > x* and long relaxation times. Notably, the contribution of large particles to the initial susceptibility was disproportionately high; it grew as the squared magnetic moment or as the sixth power of the diameter. The hydrodynamic diameter
d of the particles, which contributed the most to the susceptibility dispersion, could be estimated from the condition 2π
f*τB = 1, where
f* is the frequency corresponding to the maximum on the
χ″(
ω) curve. Substituting
f* ≈ 330 Hz into this condition and the Brownian relaxation time from Equation (12) yielded
d ≈ 100 nm. This hydrodynamic diameter value is approximately three or four times greater than the maximum possible diameter of the individual particles, which in magnetite ferrofluids is determined with an electron microscope. The existence of the surfactant protective shell with a characteristic thickness slightly higher than 2 nm cannot account for such a large difference in size. This led us to conclude that the multi-particle aggregates (clusters) rather than single particles acted as independent kinetic units, which generated the spectrum of dynamic susceptibility of sample No. 2. This conclusion agrees well with the data, which we obtained earlier in similar experiments [
25] and in experiments on the diffusion and magnetophoresis of particles in magnetic fluids containing coarse particles [
8,
26]. The same results were reported [
9] using the dynamic light scattering method.
3.3. Crossed Field Experiment
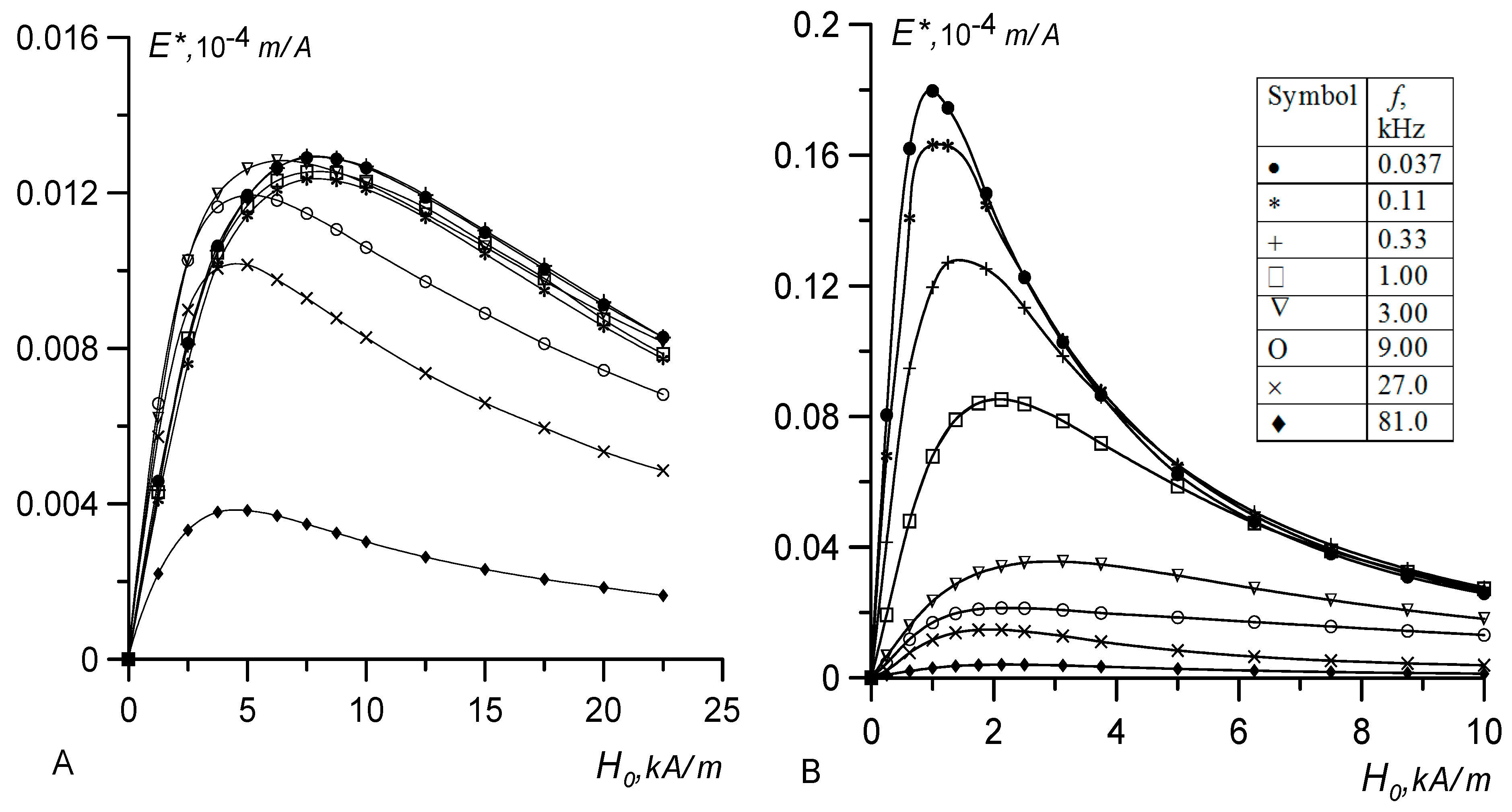
The results of the crossed fields experiments are shown in
Figure 5A,B in the dimensional coordinates. For both samples, we used the same set of frequencies at which measurements were made. The experimental
E*(
H) curves for different samples differ significantly. First, at the low-frequency limit, there is an eight-fold difference in the H* positions of maxima of the
E*(
H) functions (8.0 kA/m and 1.0 kA/m for No. 1 and No. 2, respectively), and the corresponding signal amplitudes differ approximately by a factor of 14. Second, the frequency dependence of the signal for sample No. 1 became distinguishable at frequencies of about 6 kHz, and for sample No. 2 at 60 Hz. Third, with an increase in the frequency of the probe field, the maximum of the function
E*(
H) for sample No. 1 shifted toward weak fields, and for sample No. 2, it shifted toward strong fields. The curves plotted in
Figure 2 predict a discrepancy an order of magnitude weaker between the samples. Since Equation (20) considers all significant factors except for the polydispersity of particles, we can assume that a broad particle size distribution (most pronounced in sample No. 2) was the main cause of the observed discrepancies. The coarse particle fractions existing in magnetic fluids disproportionately contributed to the output signal; therefore, the substitution of the mean value of the magnetic moment from
Table 2 into Equation (21) led to a systematic error, which increased with the width of the particle size distribution.
Let us consider the problem of particle size distribution in magnetic fluids in more detail. This deserves special attention, since the size distribution of particles often plays an important role in the comparison of experimental and theoretical results. Thus, for example, when constructing an equilibrium magnetization curve, the third- and sixth order-moments should be used, i.e., <
x3> and <
x6> [
17]. It may be necessary to use the moments of the ninth order <
x9> when processing experimental data on birefringence in magnetic fluids, because in weak magnetic fields the output signal grows in proportion to the ninth power of the diameter [
27,
28].
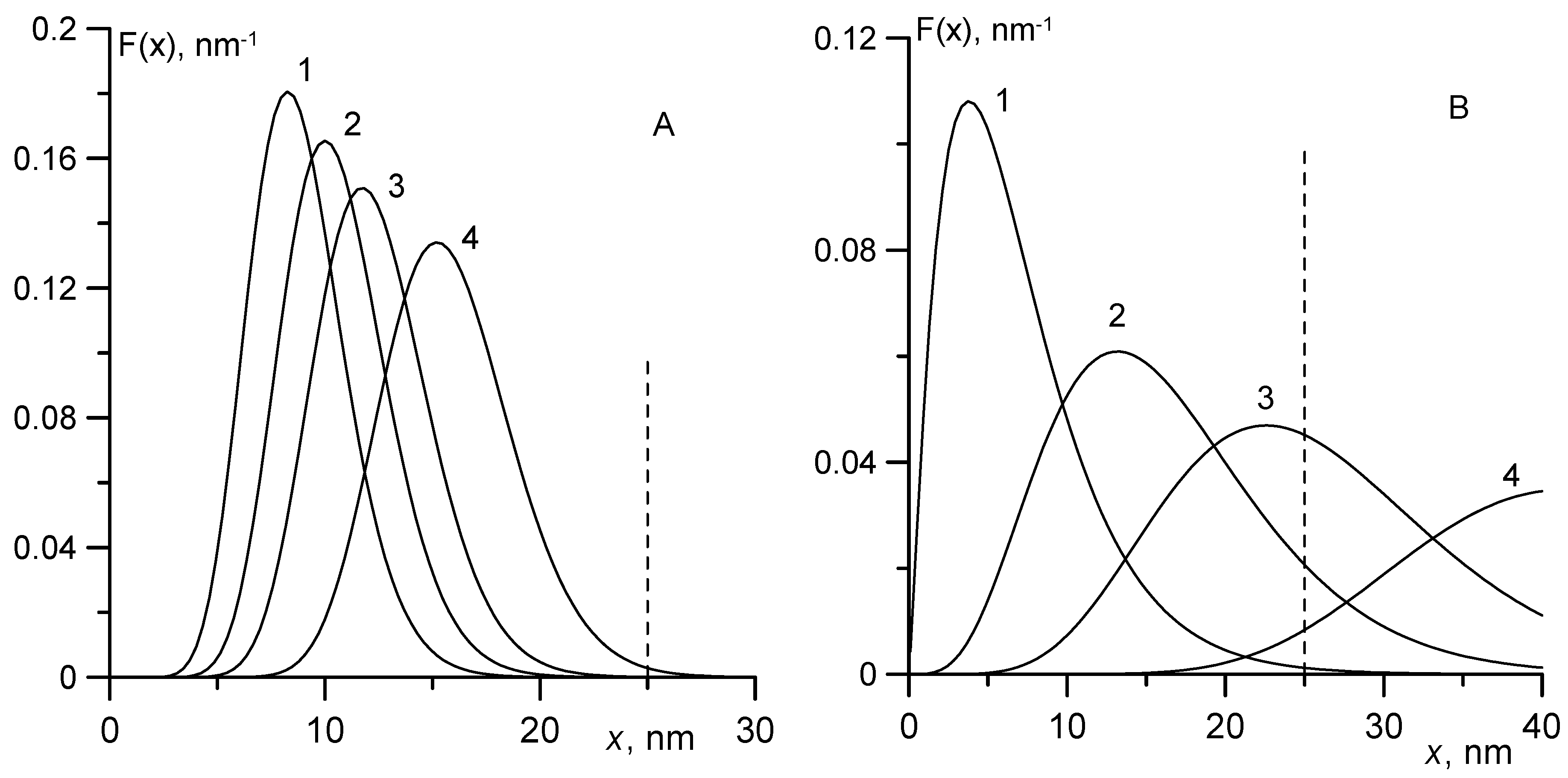
Figure 6A,B presents curves illustrating the contribution of separate fractions to the saturation magnetization of the ferrofluid proportional to <
x3>, Langevin susceptibility (<
x6>), and output signal in the crossed field experiment (<
x12>). The density of the particle size distribution (curve 1) was calculated by Equation (7) for the Γ-distribution. All curves were normalized to unity. The parameters used in calculations were taken from
Table 1 and
Table 2. The parameters associated with sample No. 1 can be considered typical of magnetite ferrocolloids, including commercial ferrofluids. Sample No. 2 was specifically chosen to demonstrate the effects associated with polydispersity, and had a very broad particle size distribution.
In
Figure 6, the vertical dashed line is used to denote the maximum diameter
xmax ≈ 20–25 nm of magnetite particles, which were still observable in an electron microscope in highly stable magnetic fluids and powders obtained by the chemical precipitation method [
9,
10,
29,
30,
31,
32]. In real solutions, particles with magnetic cores of large diameter are absent, since the concentration of iron salts in solutions and the duration of the chemical reaction are limited. Strictly, the Γ-distribution in Equation (7), which suggests the existence of particles with arbitrary large diameters, contradicts the experimental data on the existence of
xmax. However, Equation (7) is often used to approximate the size distribution of particles, since the systematic error associated with the tail of the distribution is inessential when calculating the moments of
x of low orders, for example, <
x>.
Figure 6 shows that the Γ-distribution correctly describes the size distribution of the particles in both samples. Only a negligible fraction of particles had magnetic cores with diameter exceeding
xmax.
The evaluation of high-order moments of
x did not pose serious difficulties in the case when the width of the particle size distribution was rather small (sample No. 1,
Figure 6A). A qualitative change in the situation was observed when calculating the high-order moments of
x for a large width of the particle size distribution (
δx > 0.4).
Figure 6B shows that even when calculating <
x6>, the systematic error associated with the long tail of the distribution reached 40% and became unacceptably large. The results of calculation of <
x12> (curve 4,
Figure 6B) are unreliable due to uncertainty about the concentration of large particles (with diameters
x ≈ 25 nm and higher). Notably, replacing the Γ-distribution with the lognormal distribution, which is often used to analyze experimental data [
27,
28], does not resolve the issue. The lognormal distribution has a longer tail than the Γ-distribution and the systematic error in calculating high-order moments will be even higher.
We used the
E*(
H) calculated curves for the model monodisperse liquids plotted in
Figure 3 and the experimental curves from
Figure 5 to estimate the magnetic moments
me of particles in the coarse fraction, responsible for the appearance of the maximum on the
E*(
H) curve and contributing the most to the normalized signal. To this end, we equated the Langevin parameter
ξ*, corresponding to the maximum of the signal in
Figure 3, to the Langevin parameter determined in terms of the effective magnetic moment
me and the value of the bias field
H* in
Figure 5:
where
Ms = 480 kA/m is the saturation magnetization of the magnetite. For sample No. 1 we obtained
ξ* = 1.53 and
me = 6.2 × 10
−19 A·m
2, which is a value three times higher than the average magnetic moment <m> = 2.08 × 10
−19 A·m
2 in
Table 1. The maximum diameter of the magnetic core of particles was
xmax = 13.5 nm, and the hydrodynamic diameter of the particles was
d = 18 nm. The corresponding Brownian relaxation time was
. This implies that the dynamic effects in weak fields should be observed at frequencies higher than 80 kHz, which is substantiated by the experimental data on the dynamic susceptibility in
Figure 4A. The dispersion of dynamic susceptibility at frequencies up to 80 kHz is rather weak, since particles with the diameter of magnetic cores close to the average value contribute the most to the susceptibility, at which the quasi-static condition
ωτB << 1 is fulfilled.
In general, the dynamics of sample No. 1 in the weak bias field (up to 2 kA/m) were consistent with the above statements. In this case, the
E*(
H) curves had approximately the same slope for all frequencies except for the highest frequency of 80 kHz. The signal dispersion was insignificant due to the absence of large particles in the solution and the short Brownian relaxation time (
ωτB << 1). With increasing bias field strength, the relaxation times decrease, according to Equation (12), and the signal dispersion should decrease additionally, as shown in
Figure 3A. However, in the experiment, we observed an opposite effect. With the growth of the bias field, the signal dispersion also increased. For
H0 ≥ 5 kA/m the frequency dependence was observed at a frequency of 9 kHz, which implies a three- to four-fold increase in the Brownian relaxation time. In our opinion, this paradoxical behavior of sample No. 1 can only be explained by the formation of short chains in the magnetic fluid at the cost of anisotropic dipole–dipole interparticle interactions and bias field.
As is known [
23,
33], the probability of the formation of chains in magnetic fluids is determined by the value of the dipolar coupling constant
λ, which is the ratio of dipole–dipole interaction energy to thermal energy. At
λ < 1, the effect of aggregates on the properties of magnetic fluids is insignificant, but at
λ ≥ 2, the number of aggregates increases exponentially. For polydisperse fluid, the value of
λ can be estimated in terms of the Langevin susceptibility
χL and the hydrodynamic concentration
φ of particles, which were determined from the results of independent experiments:
[
6,
19]. The values of the dipolar coupling constant for the examined samples calculated by this formula are provided in
Table 2. For sample No. 1,
λ = 0.6, and in the weak bias field, the influence of aggregates can be neglected. The application of the stronger field corresponding to the Langevin parameter
ξ ≥ 1 stimulated the growth of chains and increased the relaxation time of the magnetization due to an increase in the volume of the chain and its form-factor. So, the dispersion of the signal observed in
Figure 5A at frequencies higher than 9 kHz is the consequence of the change in the internal structure of the magnetic fluid.
A different situation was observed when analyzing the data for sample No. 2 with the broad particle size distribution in
Figure 5B. For this sample, the coupling constant
λ = 2.1 and the majority of large particles were combined into chains or quasi-spherical clusters already in a zero-bias field. As in the case of linear susceptibility, the strong signal dispersion was already observed at frequencies of 100–300 Hz, which is one more indication of the presence of aggregates with a characteristic size of the order of 100 nm. According to Rosensweig [
15], for typical magnetic fluids that are stabilized by oleic acid, the height of the energy barrier associated with the steric repulsion is close to 20
kT. This barrier ensures the negligible rate of irreversible particle aggregation and high stability of the magnetic fluid for many years. Experiments devoted to studying the rheology and diffusion of particles in magnetic fluids [
26], dynamic magnetic susceptibility [
19], and dynamic light scattering method [
9] suggest that in the presence of large-sized particles, quasi-spherical aggregates with a characteristic size up to 100 nm have a high probability of occurrence. Our results confirm this inference.
Magneto dipole interactions are not the only reason for the aggregation of particles in ferrofluids. Van der Waals attractive forces and defects in the protective shells [
26] can play an important or even a key role in this process. In this case, the application of the bias field did not change the structure of the colloidal solution. The nanoscale aggregates with the uncompensated magnetic moment behaved like single particles. This is why the experimental curves in
Figure 5B do not qualitatively differ from the model curves for monodisperse liquid in
Figure 2B.
The quantitative discrepancies between the families of curves representing different samples are large and related to the width of the particle size distribution. First, from the maximum condition in Equation (22) for sample No. 2 (
ξ* = 1.65), we obtained an estimate for the effective moment of particles, which contribute the most to the normalized output signal:
me = 54 × 10
−19 A m
2. This value exceeds the average magnetic moment <
m> = 2.31 × 10
−19 A m
2 already by a factor of 23. The diameter of the magnetic core of such particles should be close to the maximum possible value of
xmax. An estimate using Equation (22) provided
xmax ≈ 28 nm, which is only slightly higher than the maximum possible value corresponding to the dashed line in
Figure 6, but is significantly smaller than the diameter
xmax ≈ 41 nm obtained with the use of the standard Γ-distribution in Equation (7). This result demonstrates once again the need to replace the Γ-distribution by another distribution characterized by the absence of a long tail.
The easiest way to replace the Γ-distribution is to cut the tail. The distribution in Equation (7) is replaced by the equation:
in which the normalization constant
A differs from the unit by less than 1%. The truncated Γ- distribution in Equation (23) was used previously [
28] for processing the birefringence results and by Aref’ev et al. [
34], for calculating high-order moments describing the nonlinear susceptibility of magnetic fluids. In both cases, the use of the truncated Γ-distribution enabled a significant reduction of the discrepancy between the experimental and calculated results. The results reported by Aref’ev et al. [
34] revealed a correlation between the numerical value
xmax and the Γ-distribution parameters, which was valid, at least for the magnetite colloids obtained by the chemical precipitation method. According to Aref’ev et al. [
34]:
For sample No. 2, the calculations using Equation (30) resulted in xmax = 29 nm, which practically coincides with the estimate xmax = 28 nm found by Equation (22). Estimates for sample No. 1 were xmax = 13.6 and 13.5 nm for Equations (30) and (22), respectively. Thus, the two methods for evaluating the maximum size of particles existing in magnetite colloids agree well for both samples, despite these methods being based on different experimental techniques.