Bending and Elastic Vibration of a Novel Functionally Graded Polymer Nanocomposite Beam Reinforced by Graphene Nanoplatelets
Abstract
:1. Introduction
2. A Novel GPL-Reinforced Nanocomposite
2.1. Evaluation of Effective Mechanical Properties
2.2. A New GPL Distribution
- The total weight fraction of GPLs remains constant with the r variations.
- The GPLs symmetrically disperse in the matrix about the mid-plane of the beam.
- When r increases, many GPLs are increasingly dispersed to the upper and lower surfaces of the beam.
- This GPL graded distribution is continuous along the thickness and makes the mechanical properties of the FG-GPLRCs continuously vary.
3. Theory and Formulations
3.1. An Improved Third Order Shear Deformation Theory
3.2. Chebyshev–Ritz Method
- (1)
- Hinged-Hinged (H-H)x = 0: u0 = 0; w = 0; φx ≠ 0x = L: u0 = 0; w = 0; φx ≠ 0
- (2)
- Clamped-Clamped (C-C)x = 0: u0 = 0; w = 0; ; φx ≠ 0x = L: u0 = 0; w = 0; ; φx ≠ 0
- (3)
- Clamped-Hinged (C-H)x = 0: u0 = 0; w = 0; ; φx = 0x = L: u0 = 0; w = 0; φx = 0
4. Convergence and Validation Studies
5. Results and Discussion
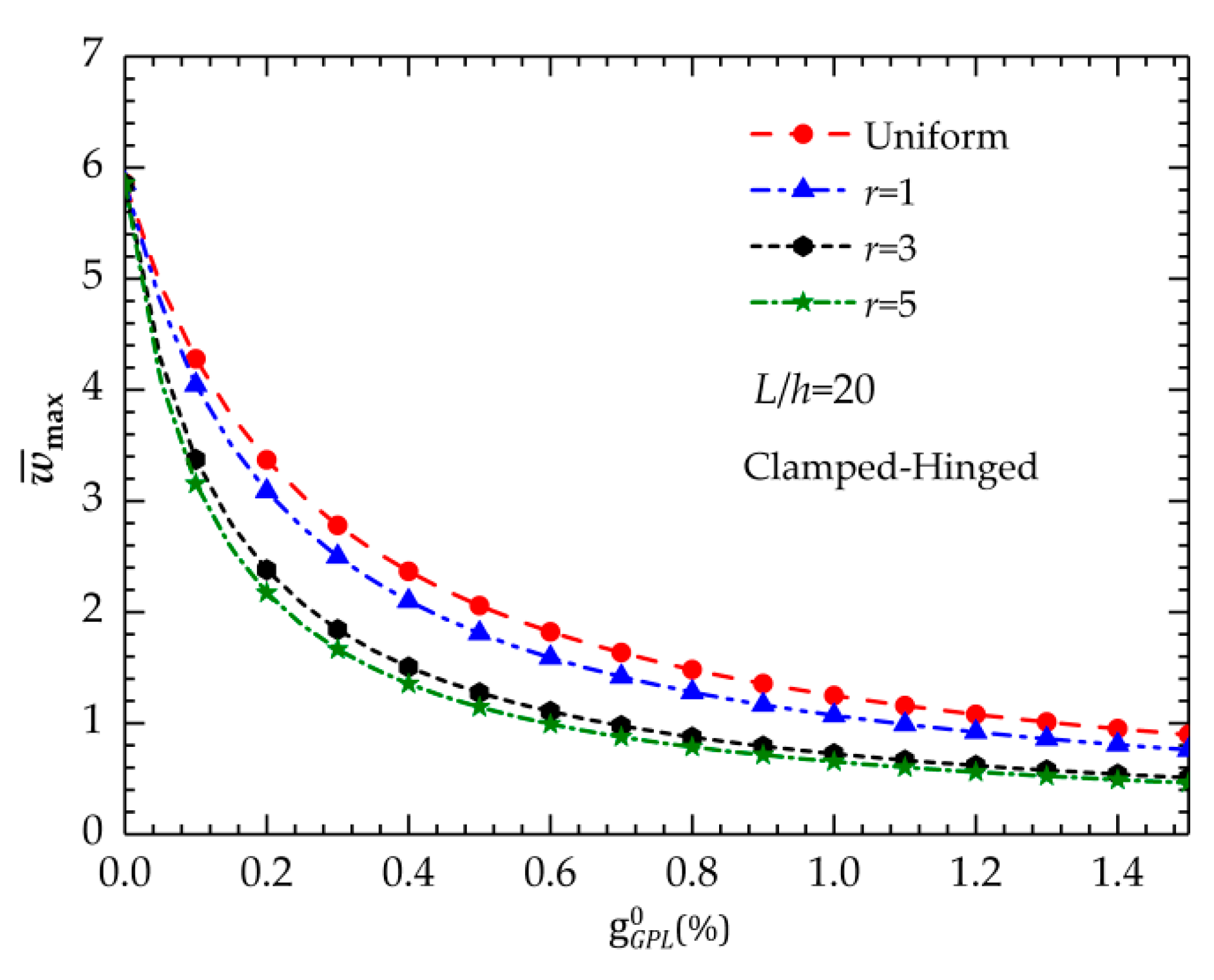
5.1. Bending Analysis
5.1.1. Bending Deflection
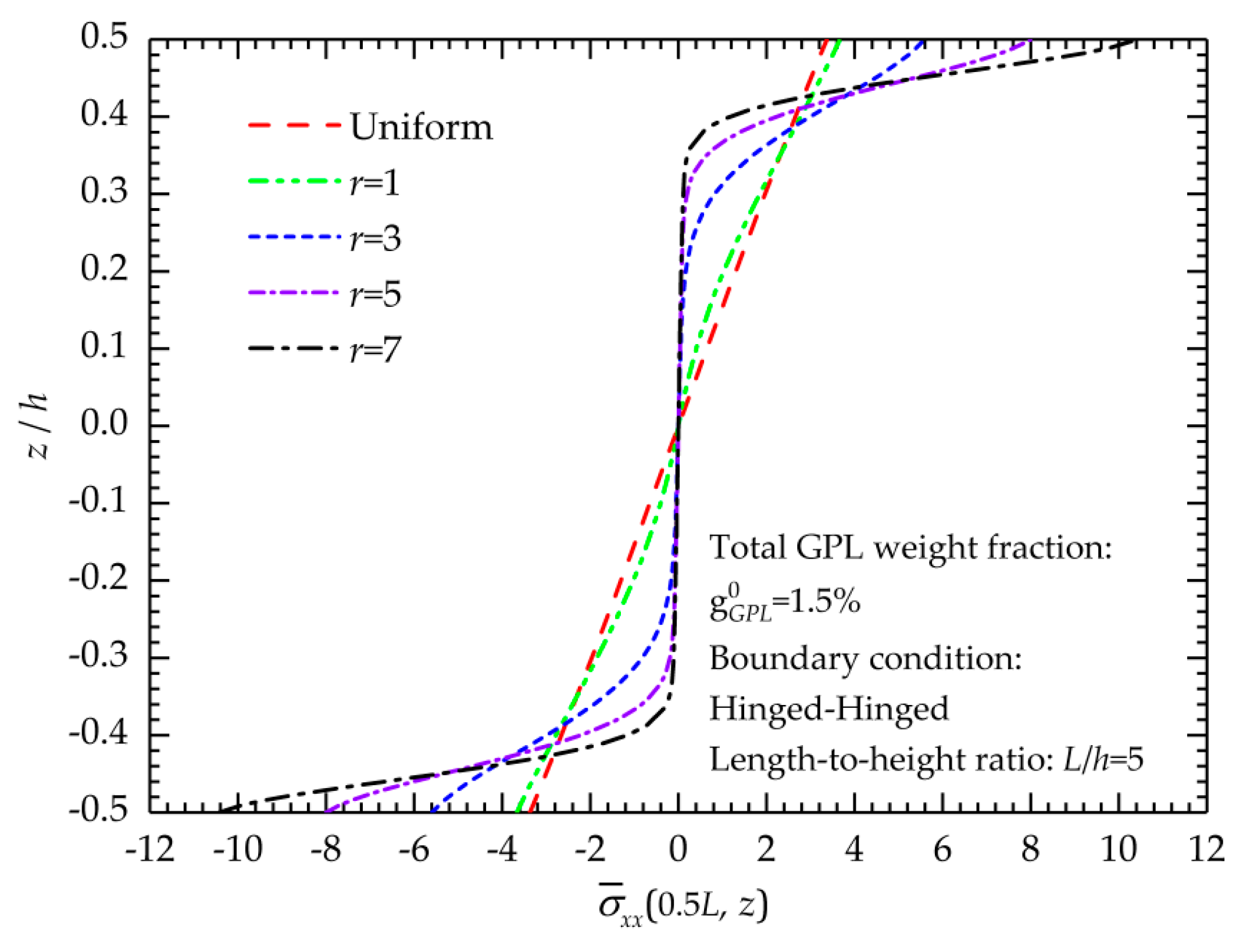
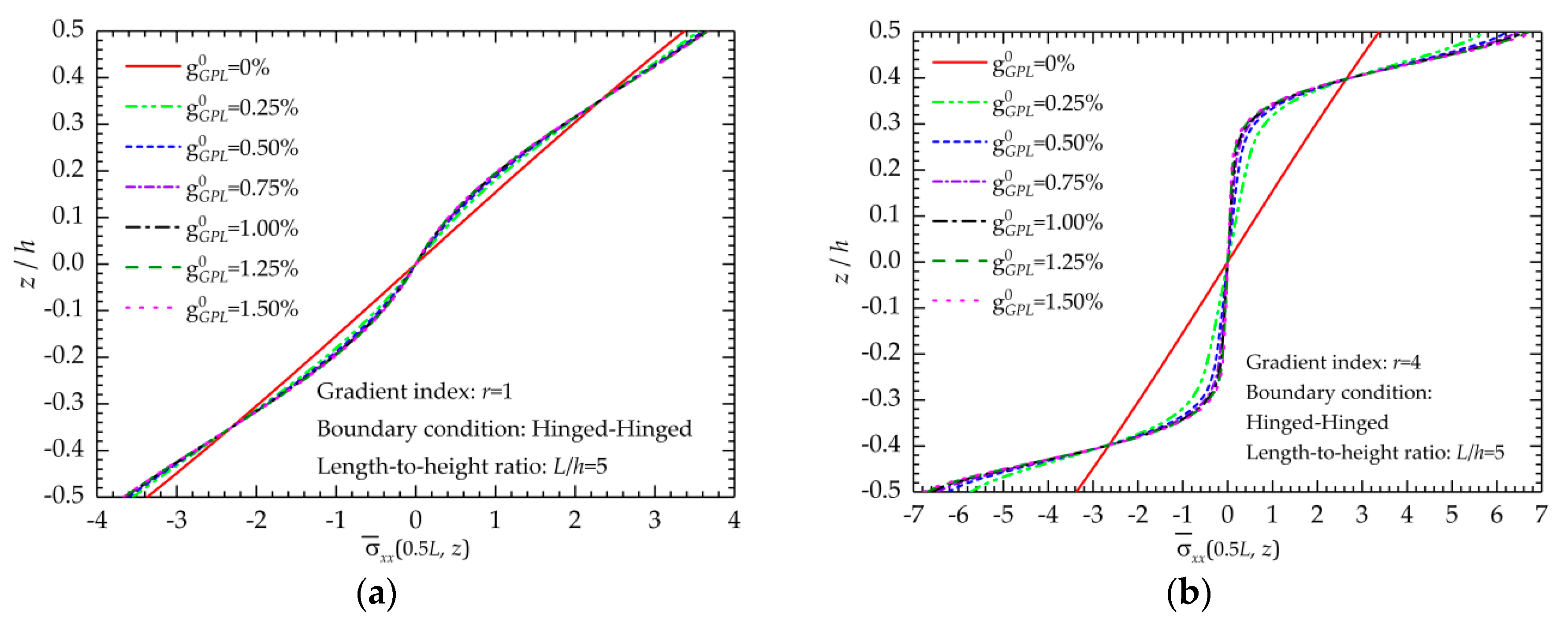
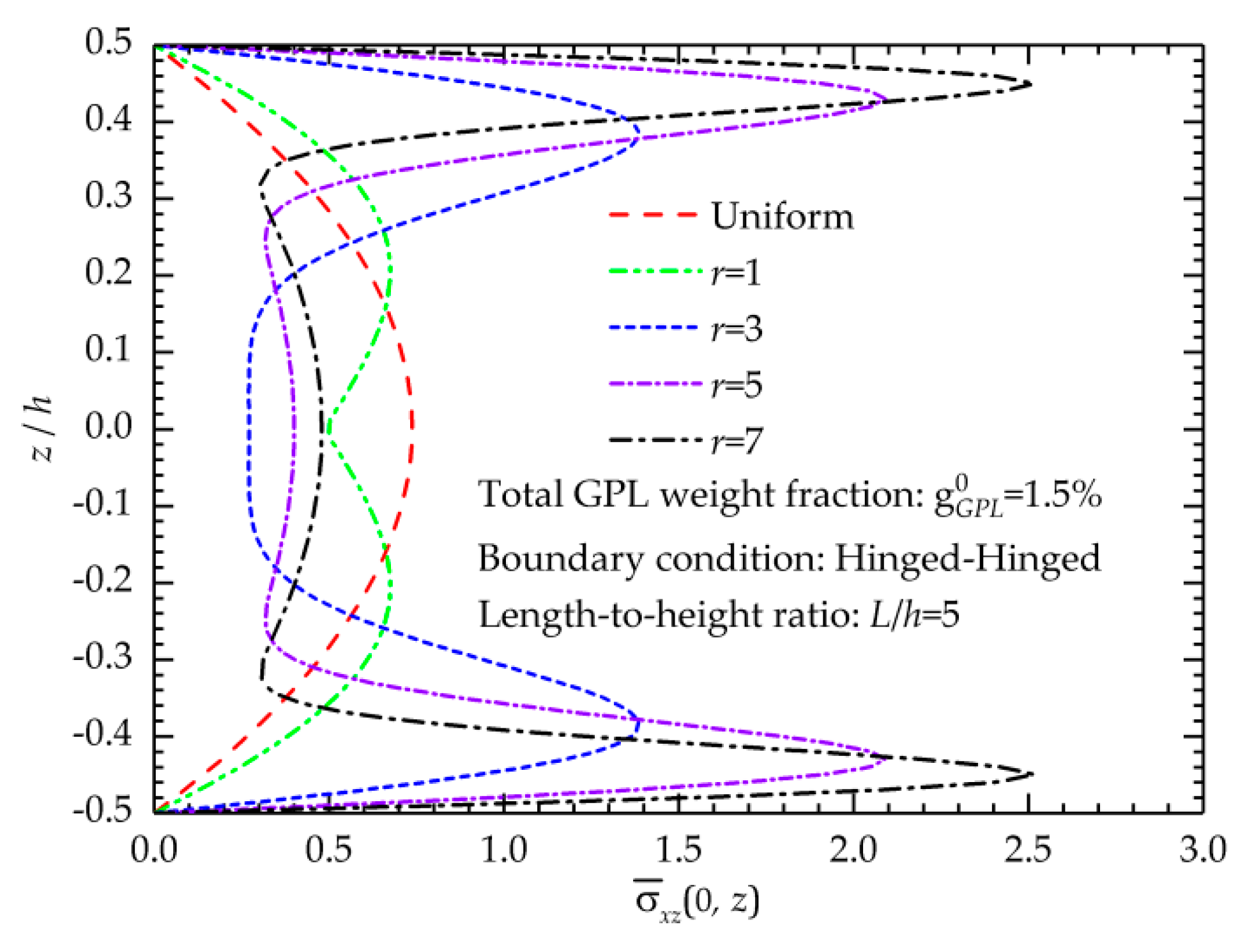
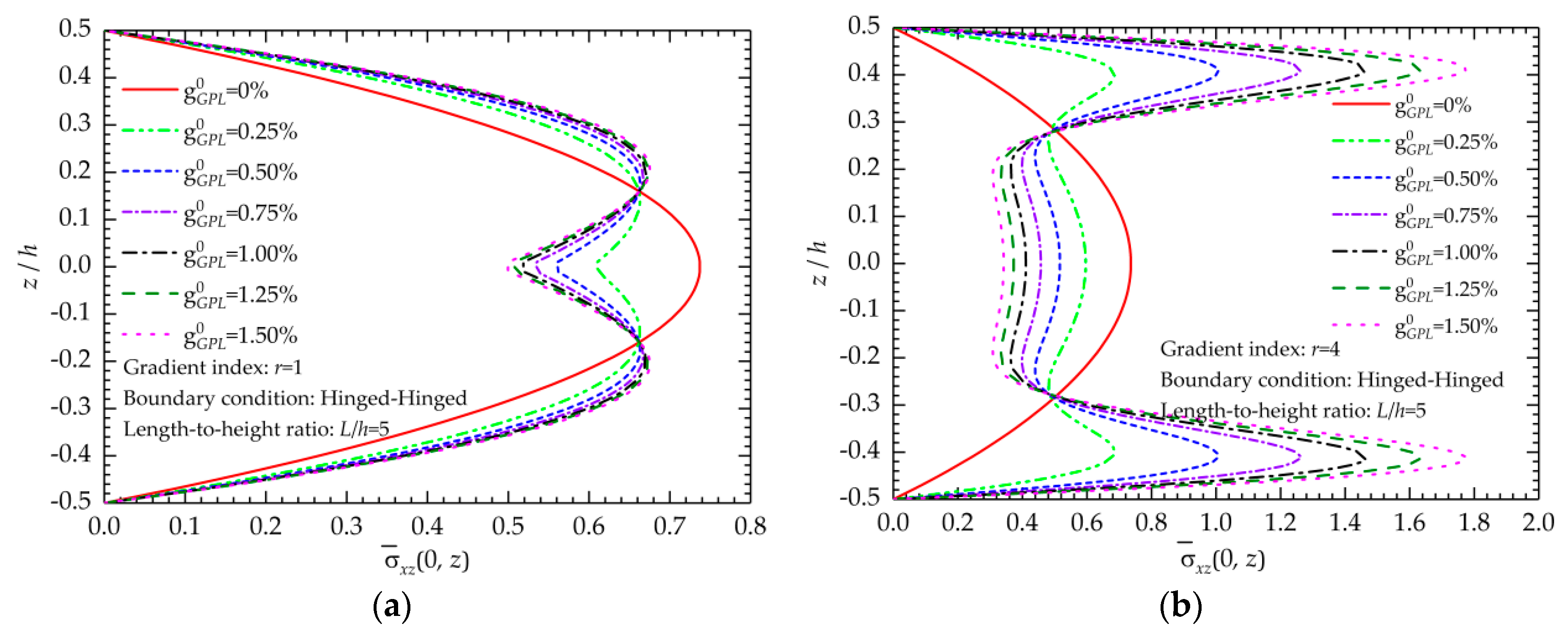
5.1.2. Stress State
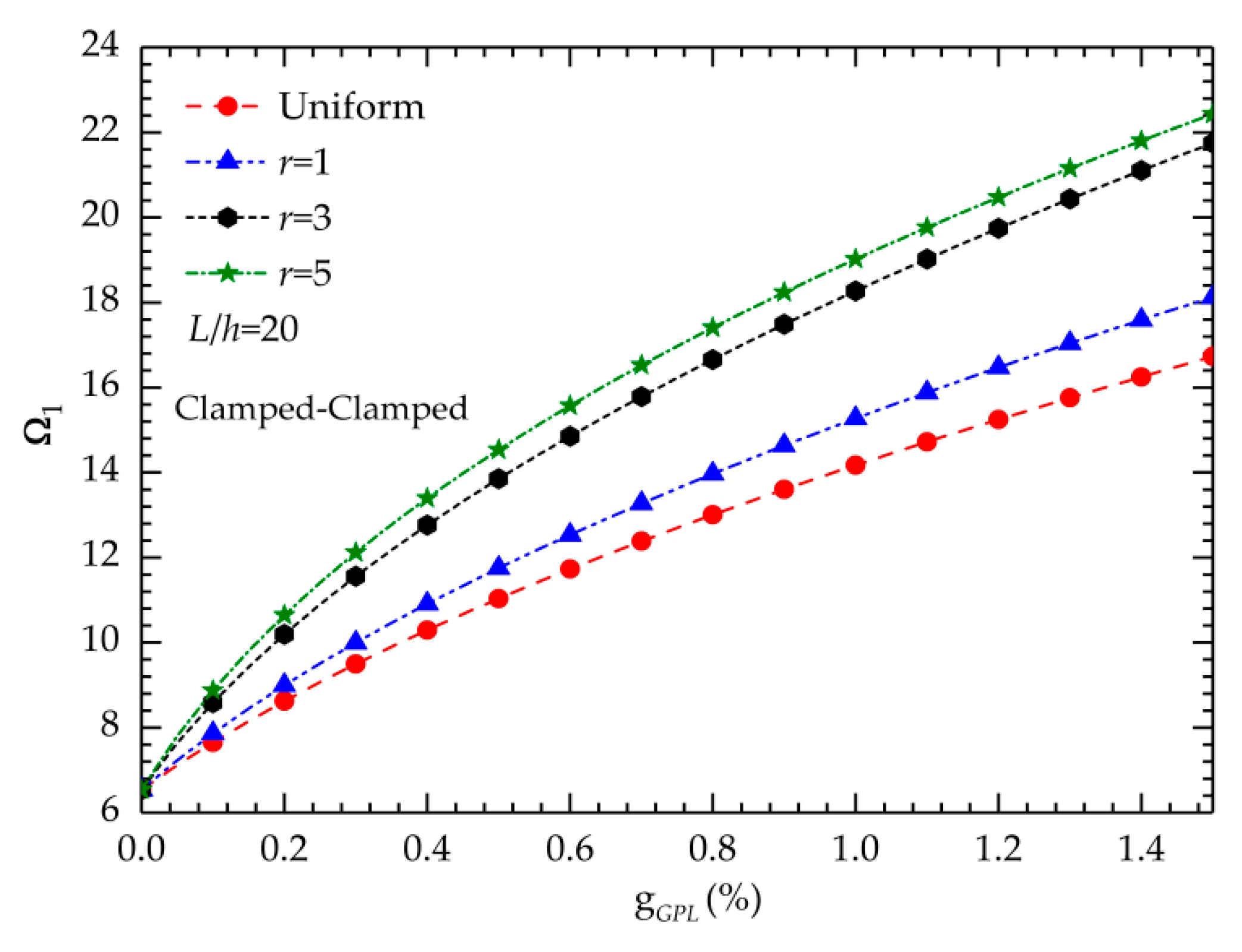
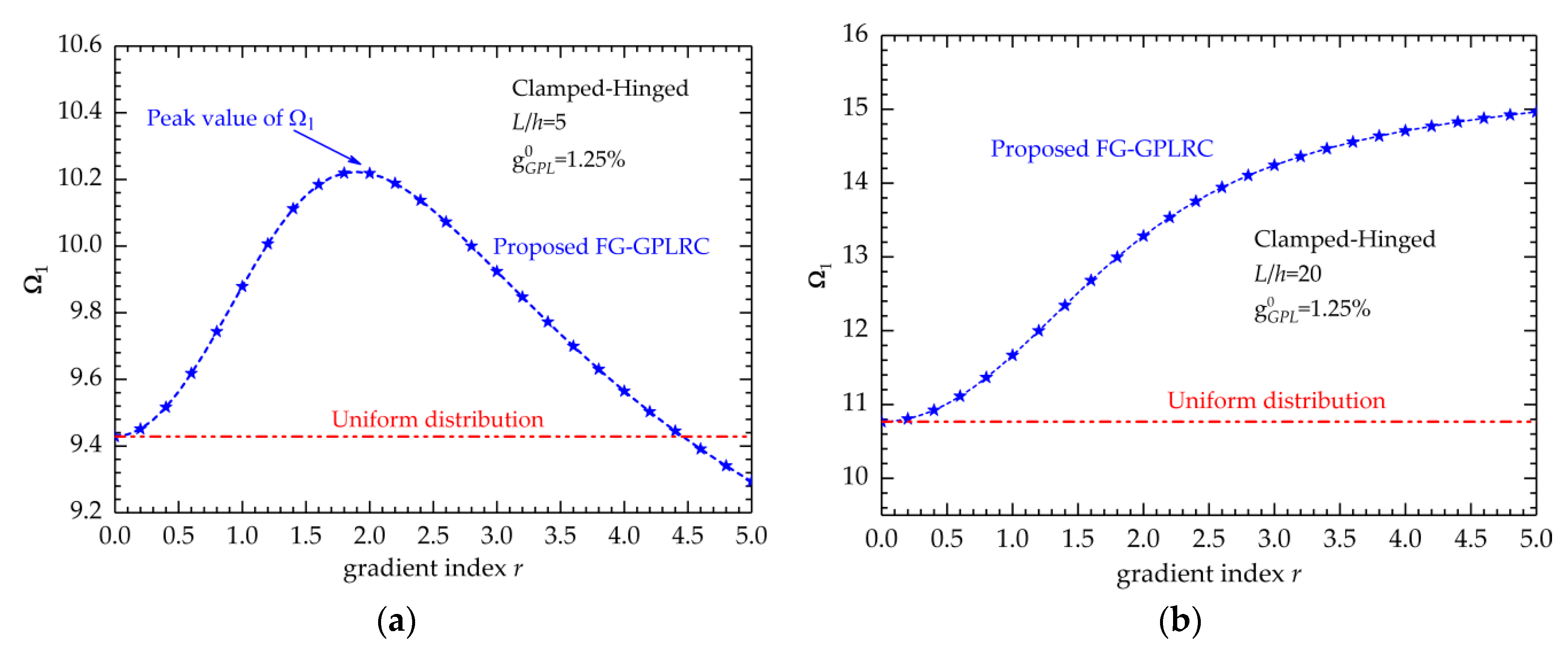
5.2. Elastic Vibration Behavior
6. Conclusions
- (1)
- With respect to the GPL distribution patterns, low-content GPL additions can significantly improve the stiffness and bending resistance of the beam.
- (2)
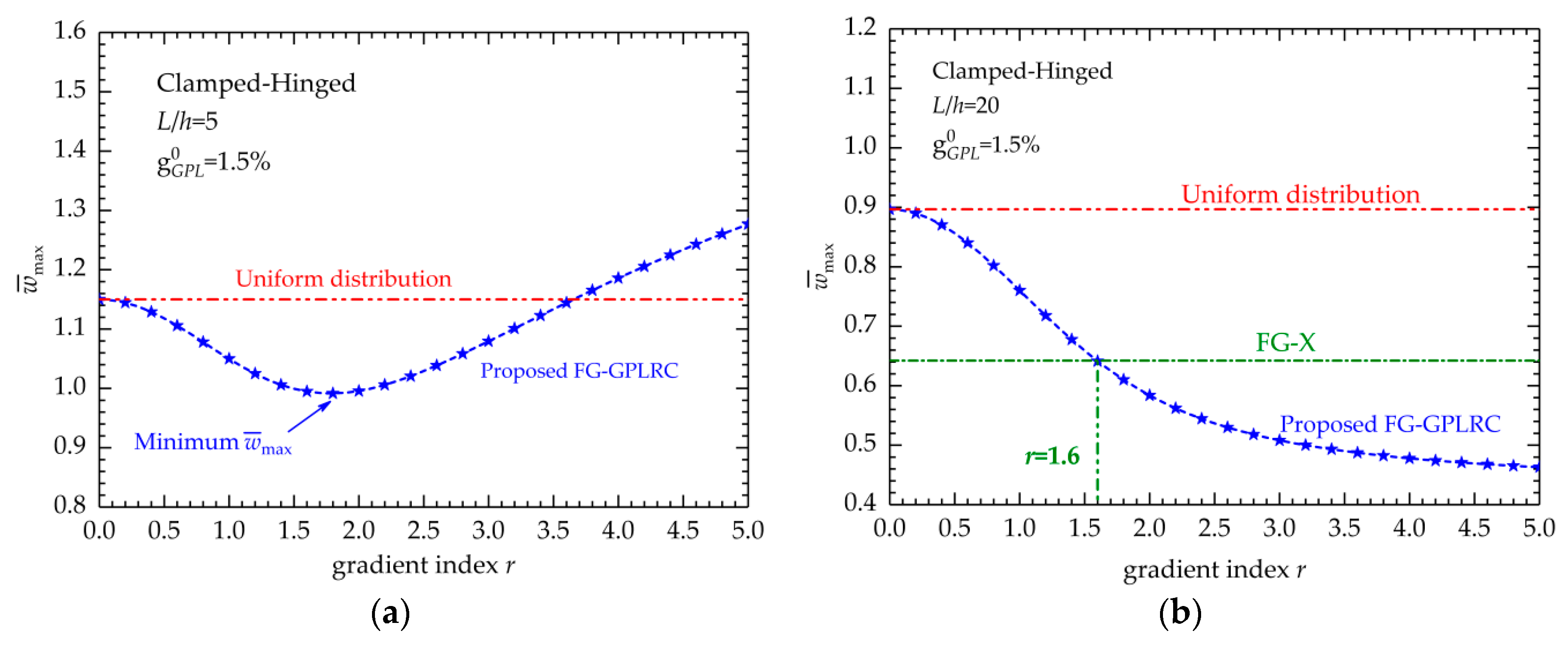
- For the thick FG-GPLRC beam, the new distribution law can produce the stiffest FG-GPLRC beams with the lowest bending displacements and highest fundamental frequencies. In other words, by adjusting the gradient index, the most optimized distribution law for the new FG-GPLRCs can be found, which results in an FG-GPLRC beam with the greatest bending resistance and vibration stiffness.
- (3)
- For the thin FG-GPLRC beam, the increase in gradient index reduces the bending displacements and increases the fundamental frequencies. In addition, if the gradient index is beyond 1.6, the new FG-GPLRCs exhibit better capabilities in the static and vibration analysis than the common FG-X ones.
- (4)
- A multilayer GPLRC beam with 12 or more layers is an ideal alternative structure for fabricating the new FG-GPLRC structures.
Author Contributions
Funding
Conflicts of Interest
References
- García-Macías, E.; Rodríguez-Tembleque, L.; Sáez, A. Bending and free vibration analysis of functionally graded graphene vs. carbon nanotube reinforced composite plates. Compos. Struct. 2018, 186, 123–138. [Google Scholar] [CrossRef]
- Coleman, J.N.; Khan, U.; Blau, W.J.; Yurii, K.G. Small but strong: A review of the mechanical properties of carbon nanotube–polymer composites. Carbon 2006, 44, 1624–1652. [Google Scholar] [CrossRef]
- Viculis, L.M. Intercalation and exfoliation routes to graphite nanoplatelets. J. Mater. Chem. 2005, 15, 974–978. [Google Scholar] [CrossRef]
- Lu, W.; Lin, H.; Wu, D.; Chen, G. Unsaturated polyester resin/graphite nanosheet conducting composites with a low percolation threshold. Polymer 2006, 47, 4440–4444. [Google Scholar] [CrossRef]
- Si, Y.; Samulski, E.T. Synthesis of water soluble graphene. Nano Lett. 2008, 8, 1679–1682. [Google Scholar] [CrossRef] [PubMed]
- Spitalsky, Z.; Tasis, D.; Papagelis, K.; Galiotis, C. Carbon nanotube—Polymer composites: Chemistry, processing, mechanical and electrical properties. Prog. Polym. Sci. 2010, 35, 357–401. [Google Scholar] [CrossRef]
- Dang, Z.M.; Yuan, J.K.; Zha, J.W.; Zhou, T.; Li, S.T.; Hu, G.H. Fundamentals, processes and applications of high-permittivity polymer–matrix composites. Prog. Mater. Sci. 2012, 57, 660–723. [Google Scholar] [CrossRef]
- Ramanathan, T.; Abdala, A.A.; Stankovich, S.; Dikin, D.A.; Herrera-Alonso, M.; Piner, R.D.; Adamson, D.H.; Schniepp, H.C.; Chen, X.R.R.S.; Ruoff, R.S.; et al. Functionalized graphene sheets for polymer nanocomposites. Nat. Nanotechnol. 2008, 3, 327–331. [Google Scholar] [CrossRef]
- Formica, G.; Milicchio, F.; Lacarbonara, W. Hysteretic damping optimization in carbon nanotube nanocomposites. Compos. Struct. 2018, 194, 633–642. [Google Scholar] [CrossRef]
- Sengupta, R.; Bhattacharya, M.; Bandyopadhyay, S.; Bhowmick, A.K. A review on the mechanical and electrical properties of graphite and modified graphite reinforced polymer composites. Prog. Polym. Sci. 2011, 36, 638–670. [Google Scholar] [CrossRef]
- Koizumi, M. FGM Activities in Japan. Compos. Part B Eng. 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, D. Thermal effect on the dynamic response of axially functionally graded beam subjected to a moving harmonic load. Acta Astronaut. 2016, 127, 171–181. [Google Scholar] [CrossRef]
- Gupta, A.; Talha, M. Recent development in modeling and analysis of functionally graded materials and structures. Prog. Aerosp. Sci. 2015, 79, 1–14. [Google Scholar] [CrossRef]
- Sahmania, S.; Safaei, B. Nonlinear free vibrations of bi-directional functionally graded micro/nano-beams including nonlocal stress and microstructural strain gradient size effects. Thin Walled Struct. 2019, 140, 342–356. [Google Scholar] [CrossRef]
- Mohammadi, M.; Arefi, M.; Dimitri, R.; Tornabene, F. Higher-Order Thermo-Elastic Analysis of FG-CNTRC Cylindrical Vessels Surrounded by a Pasternak Foundation. Nanomaterials 2019, 9, 79. [Google Scholar] [CrossRef]
- Liew, K.M.; Lei, Z.X.; Yu, J.L.; Zhang, L.W. Postbuckling of carbon nanotube-reinforced functionally graded cylindrical panels under axial compression using a meshless approach. Comput. Methods Appl. Mech. Eng. 2014, 268, 1–17. [Google Scholar] [CrossRef]
- Frikha, A.; Zghal, S.; Dammak, F. Dynamic analysis of functionally graded carbon nanotubes-reinforced plate and shell structures using a double directors finite shell element. Aerosp. Sci. Technol. 2018, 78, 438–451. [Google Scholar] [CrossRef]
- Song, M.; Kitipornchai, S.; Yang, J. Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Struct. 2016, 159, 579–588. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, K.; Shi, C.; Fu, T. Nonlinear bending of axially functionally graded microbeams reinforced by graphene nanoplatelets in thermal environments. Mater. Res. Express 2019, 6, 085615. [Google Scholar] [CrossRef]
- Mao, J.J.; Zhang, W. Buckling and post-buckling analyses of functionally graded graphene reinforced piezoelectric plate subjected to electric potential and axial forces. Compos. Struct. 2019, 216, 392–405. [Google Scholar] [CrossRef]
- Arefi, M.; Bidgoli, E.M.R.; Dimitri, R.; Tornabene, F. Free vibrations of functionally graded polymer composite nanoplates reinforced with graphene nanoplatelets. Aerosp. Sci. Technol. 2018, 81, 108–117. [Google Scholar] [CrossRef]
- Ke, L.L.; Yang, J.; Kitipornchai, S. Nonlinear free vibration of functionally graded carbon nanotube-reinforced composite beams. Compos. Struct. 2010, 92, 676–683. [Google Scholar] [CrossRef]
- Tam, M.; Yang, Z.; Zhao, S.; Yang, J. Vibration and Buckling Characteristics of Functionally Graded Graphene Nanoplatelets Reinforced Composite Beams with Open Edge Cracks. Materials 2019, 12, 1412. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Zhang, Y.; Yao, G.; Zhou, Y. Nonlinear primary and super-harmonic resonances of functionally graded carbon nanotube reinforced composite beams. Int. J. Mech. Sci. 2019, 153–154, 321–340. [Google Scholar] [CrossRef]
- Bahaadini, R.; Saidi, A.R. Aeroelastic analysis of functionally graded rotating blades reinforced with graphene nanoplatelets in supersonic flow. Aerosp. Sci. Technol. 2018, 80, 381–391. [Google Scholar] [CrossRef]
- Banić, D.; Bacciocchi, M.; Tornabene, F.; Ferreira, A.J.M. Influence of Winkler-Pasternak Foundation on the Vibrational Behavior of Plates and Shells Reinforced by Agglomerated Carbon Nanotubes. Appl. Sci. 2017, 7, 1228. [Google Scholar] [CrossRef]
- Yang, B.; Mei, J.; Chen, D.; Yu, F.; Yang, J. 3D thermo-mechanical solution of transversely isotropic and functionally graded graphene reinforced elliptical plates. Compos. Struct. 2018, 184, 1040–1048. [Google Scholar] [CrossRef]
- Yang, B.; Kitipornchai, S.; Yang, Y.F.; Yang, J. 3D thermo-mechanical bending solution of functionally graded graphene reinforced circular and annular plates. Appl. Math. Model. 2017, 49, 69–86. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, K.; Fu, T.; Shi, C. Vibration response of a functionally graded graphene nanoplatelet reinforced composite beam under two successive moving masses. Compos. Struct. 2019, 209, 928–939. [Google Scholar] [CrossRef]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear free vibration of functionally graded polymer composite beams reinforced with graphene nanoplatelets (GPLs). Eng. Struct. 2017, 140, 110–119. [Google Scholar] [CrossRef]
- Wu, H.; Yang, J.; Kitipornchai, S. Dynamic instability of functionally graded multilayer graphene nanocomposite beams in thermal environment. Compos. Struct. 2017, 162, 244–254. [Google Scholar] [CrossRef] [Green Version]
- Song, M.; Yang, J.; Kitipornchai, S.; Zhu, W. Buckling and postbuckling of biaxially compressed functionally graded multilayer graphene nanoplatelet-reinforced polymer composite plates. Int. J. Mech. Sci. 2017, 131, 345–355. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.S.; Xiang, Y.; Lin, F. Thermal buckling and postbuckling of functionally graded graphene-reinforced composite laminated plates resting on elastic foundations. Thin Walled Struct. 2017, 118, 229–237. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y.; Fan, Y. Nonlinear vibration of functionally graded graphenereinforced composite laminated cylindrical shells in thermal environments. Compos. Struct. 2017, 182, 447–456. [Google Scholar] [CrossRef]
- Mao, J.J.; Zhang, W. Linear and nonlinear free and forced vibrations of graphene reinforced piezoelectric composite plate under external voltage excitation. Compos. Struct. 2018, 201, 551–565. [Google Scholar] [CrossRef]
- Wang, A.; Chen, H.; Hao, Y.; Zhang, W. Vibration and bending behavior of functionally graded nanocomposite doubly-curved shallow shells reinforced by graphene nanoplatelets. Results Phys. 2018, 9, 550–559. [Google Scholar] [CrossRef]
- Gholami, R.; Ansari, R. Nonlinear harmonically excited vibration of third-order shear deformable functionally graded graphene platelet-reinforced composite rectangular plates. Eng. Struct. 2017, 156, 197–209. [Google Scholar] [CrossRef]
- Lezgy-Nazargah, M.; Salahshuran, S. A new mixed-field theory for bending and vibration analysis of multi-layered composite plate. Arch. Civ. Mech. Eng. 2018, 18, 818–832. [Google Scholar] [CrossRef]
- Wattanasakulpong, N.; Ungbhakorn, V. Analytical solutions for bending, buckling and vibration responses of carbon nanotube-reinforced composite beams resting on elastic foundation. Comput. Mater. Sci. 2013, 71, 201–208. [Google Scholar] [CrossRef]
- Ghannadpour, S.A.M.; Mohammadi, B.; Fazilati, J. Bending, buckling and vibration problems of nonlocal Euler beams using Ritz method. Compos. Struct. 2013, 96, 584–589. [Google Scholar] [CrossRef]
- Zhao, Z.; Feng, C.; Wang, Y.; Yang, J. Bending and vibration analysis of functionally graded trapezoidal nanocomposite plates reinforced with graphene nanoplatelets (GPLs). Compos. Struct. 2017, 180, 799–808. [Google Scholar] [CrossRef]
- Formica, G.; Lacarbonara, W.; Alessi, R. Vibrations of carbon nanotube-reinforced composite. J. Sound Vib. 2010, 329, 1875–1889. [Google Scholar] [CrossRef]
- Formica, G.; Talò, M.; Lacarbonara, W. Nonlinear modeling of carbon nanotube composites dissipation due to interfacial stick–slip. Int. J. Plast. 2014, 53, 148–163. [Google Scholar] [CrossRef]
- Odegard, G.M.; Gates, T.S.; Wise, K.E.; Park, C.; Siochi, E.J. Constitutive modeling of nanotube–reinforced polymer composites. Compos. Sci. Technol. 2003, 63, 1671–1687. [Google Scholar] [CrossRef]
- Talò, M.; Krause, B.; Pionteck, J.; Lanzara, G.; Lacarbonara, W. An updated micromechanical model based on morphological characterization of carbon nanotube nanocomposites. Compos. Part B Eng. 2017, 115, 70–78. [Google Scholar] [CrossRef]
- Formica, G.; Talò, M.; Lanzara, G.; Lacarbonara, W. Parametric identification of carbon nanotube nanocomposites constitutive response. J. Appl. Mech. 2019, 86, 041007. [Google Scholar] [CrossRef]
- Rafiee, A.M.; Rafiee, J.; Wang, Z.; Song, H.; Yu, Z.Z.; Koratkar, N. Enhanced mechanical properties of nanocomposites at low graphene content. ACS Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef]
- Shokrieh, M.; Esmkhani, M.; Shokrieh, Z.; Zhao, Z. Stiffness prediction of graphene nanoplatelet/epoxy nanocomposites by a combined molecular dynamics—Micromechanics method. Comput. Mater. Sci. 2014, 92, 444–450. [Google Scholar] [CrossRef]
- Tha, H.C.; Ferreira, A.J.M.; Tran, T.D.; Phung-Van, P. Free vibration, buckling and bending analyses of multilayer functionally graded graphene nanoplatelets reinforced composite plates using the NURBS formulation. Compos. Struct. 2019, 220, 749–759. [Google Scholar] [CrossRef]
- Gholami, R.; Ansari, R. Large deflection geometrically nonlinear analysis of functionally graded multilayer graphene platelet-reinforced polymer composite rectangular plates. Compos. Struct. 2017, 180, 760–771. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; Wu, H.; Zhang, H.; Wu, H.; Jiang, S.; Chai, G. Mechanical analysis of functionally graded graphene oxide-reinforced composite beams based on the first-order shear deformation theory. Mech. Adv. Mater. Struct. 2018. [Google Scholar] [CrossRef]
- Shi, G. A new simple third-order shear deformation theory of plates. Int. J. Solids Struct. 2007, 44, 4399–4417. [Google Scholar] [CrossRef] [Green Version]
- Nuttawit, W.; Gangadhara, B.P.; Donald, W.K. Thermal buckling and elastic vibration of third-order shear deformable functionally graded beams. Int. J. Mech. Sci. 2011, 53, 734–743. [Google Scholar]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Application, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Wang, L.; Liu, Y.; Liu, Y. An inverse method for distributed dynamic load identification of structures with interval uncertainties. Adv. Eng. Softw. 2019, 131, 77–89. [Google Scholar] [CrossRef]
- Liang, K.; Sun, Q.; Liu, X.R. Investigation on imperfection sensitivity of composite cylindrical shells using the nonlinearity reduction technique and the polynomial chaos method. Acta Astronaut. 2018, 146, 349–358. [Google Scholar] [CrossRef]
- Fox, L.; Parker, I.B. Chebyshev Polynomials in Numerical Analysis; Oxford University Press: London, UK, 1968. [Google Scholar]
- Zhou, D.; Lo, S.H.; Au, F.T.K.; Cheung, Y.K.; Liu, W.Q. 3-D vibration analysis of skew thick plates using Chebyshev–Ritz method. Int. J. Mech. Sci. 2006, 48, 1481–1493. [Google Scholar] [CrossRef]
- Nguyen, T.K.; Nguyen, B.D. A new higher-order shear deformation theory for static, buckling and free vibration analysis of functionally graded sandwich beams. J. Sandw. Struct. Mater. 2015, 17, 613–631. [Google Scholar] [CrossRef]
- Vo, T.P.; Thai, H.T.; Nguyen, T.K.; Inam, F.; Lee, J. Static behaviour of functionally graded sandwich beams using a quasi-3D theory. Compos. Part B Eng. 2015, 68, 59–74. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.K.; Vo, T.P.; Nguyen, B.D.; Lee, J. An analytical solution for buckling and vibration analysis of functionally graded sandwich beams using a quasi-3D shear deformation theory. Compos. Struct. 2016, 156, 238–252. [Google Scholar] [CrossRef] [Green Version]


| Boundary Conditions | Lu | Lϕ | Lw | Ru | Rϕ | Rw |
|---|---|---|---|---|---|---|
| H-H | 1 | 0 | 1 | 1 | 0 | 1 |
| C-C | 1 | 1 | 2 | 1 | 1 | 2 |
| C-H | 1 | 1 | 2 | 1 | 0 | 1 |
| N | ω1 | ω2 | ω3 | |||
|---|---|---|---|---|---|---|
| 2 | 0.2665 | 0.7793 | 0.8495 | 4.6677 | 28.1358 | 35.2954 |
| 3 | 0.2664 | 0.7783 | 0.9104 | 4.6672 | 18.2622 | 27.9520 |
| 4 | 0.3281 | 1.1625 | 0.8476 | 4.2363 | 18.1846 | 27.9520 |
| 5 | 0.3281 | 1.1624 | 0.8448 | 4.2363 | 15.1507 | 27.9518 |
| 6 | 0.3281 | 1.1624 | 0.8416 | 4.2351 | 15.0990 | 27.9518 |
| 7 | 0.3281 | 1.1624 | 0.8416 | 4.2351 | 15.0990 | 27.9518 |
| 8 | 0.3281 | 1.1624 | 0.8416 | 4.2351 | 15.0990 | 29.5854 |
| Ref. [59] | 0.3282 | 1.1632 | 0.8371 | 4.3052 |
| Source | H-H | C-C | ||||
|---|---|---|---|---|---|---|
| p = 1 | p = 5 | p = 10 | p = 1 | p = 5 | p = 10 | |
| FSDT [60] | 5.4408 | 8.1409 | 9.0232 | 1.3770 | 2.0635 | 2.2614 |
| TSDT [60] | 5.4122 | 8.5762 | 9.4800 | 1.3372 | 1.9896 | 2.1747 |
| Qusi-3D [60] | 5.3612 | 8.5137 | 9.4050 | 1.3077 | 1.9416 | 2.1211 |
| Present | 5.3822 | 8.5140 | 9.4049 | 1.3126 | 1.9637 | 2.1487 |
| Source | H-H | C-C | ||||
|---|---|---|---|---|---|---|
| p = 1 | p = 2 | p = 5 | p = 1 | p = 2 | p = 5 | |
| HSDT [61] | 4.1105 | 3.7334 | 3.3771 | 8.3747 | 7.7149 | 7.0723 |
| TSDT [61] | 4.1105 | 3.7334 | 3.3771 | 8.3705 | 7.7114 | 7.0691 |
| Qusi-3D [61] | 4.1185 | 3.7410 | 3.3840 | 8.4653 | 7.8008 | 7.1550 |
| Present | 4.1146 | 3.7374 | 3.3791 | 8.4163 | 7.7731 | 7.1265 |
| L/h | Gradient Index | 0% | 0.25% | 0.5% | 0.75% | 1.0% | 1.25% | 1.5% |
|---|---|---|---|---|---|---|---|---|
| 5 | uniform | 15.4247 | 8.0196 | 5.4191 | 4.0927 | 3.2882 | 2.7483 | 2.3609 |
| r = 2 | 15.4247 | 6.4531 | 4.1506 | 3.0742 | 2.4460 | 2.0329 | 1.7402 | |
| r = 4 | 15.4247 | 5.7356 | 3.7519 | 2.8576 | 2.3350 | 1.9865 | 1.7351 | |
| r = 6 | 15.4247 | 5.4902 | 3.6468 | 2.8394 | 2.3727 | 2.0618 | 1.8364 | |
| r = 8 | 15.4247 | 5.3602 | 3.5876 | 2.8274 | 2.3940 | 2.1081 | 1.9019 | |
| r = 10 | 15.4247 | 5.2786 | 3.5469 | 2.8146 | 2.4019 | 2.1323 | 1.9394 | |
| 20 | uniform | 13.9187 | 7.2366 | 4.8901 | 3.6931 | 2.9672 | 2.4800 | 2.1304 |
| r = 2 | 13.9187 | 5.4633 | 3.4046 | 2.4744 | 1.9442 | 1.6015 | 1.3618 | |
| r = 4 | 13.9187 | 4.5728 | 2.7528 | 1.9752 | 1.5429 | 1.2673 | 1.0760 | |
| r = 6 | 13.9187 | 4.2864 | 2.5560 | 1.8303 | 1.4302 | 1.1764 | 1.0007 | |
| r = 8 | 13.9187 | 4.1479 | 2.4628 | 1.7627 | 1.3785 | 1.1355 | 0.9676 | |
| r = 10 | 13.9187 | 4.0666 | 2.4087 | 1.7238 | 1.3490 | 1.1124 | 0.9492 |
| L/h | Gradient Index | 0% | 0.25% | 0.5% | 0.75% | 1.0% | 1.25% | 1.5% |
|---|---|---|---|---|---|---|---|---|
| 5 | uniform | 4.2718 | 2.2210 | 1.5008 | 1.1335 | 0.9107 | 0.7611 | 0.6538 |
| r = 2 | 4.2718 | 2.0630 | 1.4099 | 1.0798 | 0.8776 | 0.7402 | 0.6404 | |
| r = 4 | 4.2718 | 2.0489 | 1.5206 | 1.2491 | 1.0734 | 0.9466 | 0.8494 | |
| r = 6 | 4.2718 | 2.0297 | 1.5695 | 1.3427 | 1.1963 | 1.0891 | 1.0048 | |
| r = 8 | 4.2718 | 2.0089 | 1.5836 | 1.3834 | 1.2575 | 1.1663 | 1.0947 | |
| r = 10 | 4.2718 | 1.9912 | 1.5853 | 1.4011 | 1.2884 | 1.2083 | 1.1461 | |
| 20 | uniform | 2.8595 | 1.4867 | 1.0046 | 0.7587 | 0.6096 | 0.5095 | 0.4377 |
| r = 2 | 2.8595 | 1.1424 | 0.7184 | 0.5250 | 0.4140 | 0.3419 | 0.2913 | |
| r = 4 | 2.8595 | 0.9728 | 0.6006 | 0.4392 | 0.3482 | 0.2894 | 0.2482 | |
| r = 6 | 2.8595 | 0.9175 | 0.5657 | 0.4165 | 0.3332 | 0.2795 | 0.2419 | |
| r = 8 | 2.8595 | 0.8902 | 0.5488 | 0.4057 | 0.3264 | 0.2757 | 0.2402 | |
| r = 10 | 2.8595 | 0.8739 | 0.5386 | 0.3992 | 0.3224 | 0.2734 | 0.2393 |
| L/h | Gradient Index | 0% | 0.25% | 0.5% | 0.75% | 1.0% | 1.25% | 1.5% |
|---|---|---|---|---|---|---|---|---|
| 5 | uniform | 7.5135 | 3.9064 | 2.6397 | 1.9936 | 1.6017 | 1.3387 | 1.1500 |
| r = 2 | 7.5135 | 3.4008 | 2.2651 | 1.7109 | 1.3784 | 1.1557 | 0.9956 | |
| r = 4 | 7.5135 | 3.2236 | 2.2761 | 1.8171 | 1.5328 | 1.3344 | 1.1859 | |
| r = 6 | 7.5135 | 3.1492 | 2.2960 | 1.8972 | 1.6517 | 1.4789 | 1.3474 | |
| r = 8 | 7.5135 | 3.1002 | 2.2946 | 1.9303 | 1.7105 | 1.5572 | 1.4409 | |
| r = 10 | 7.5135 | 3.0651 | 2.2863 | 1.9427 | 1.7390 | 1.5990 | 1.4938 | |
| 20 | uniform | 5.8586 | 3.0460 | 2.0583 | 1.5545 | 1.2489 | 1.0439 | 0.8967 |
| r = 2 | 5.8586 | 2.3178 | 1.4503 | 1.0567 | 0.8317 | 0.6859 | 0.5837 | |
| r = 4 | 5.8586 | 1.9552 | 1.1908 | 0.8621 | 0.6781 | 0.5602 | 0.4779 | |
| r = 6 | 5.8586 | 1.8379 | 1.1131 | 0.8076 | 0.6382 | 0.5300 | 0.4546 | |
| r = 8 | 5.8586 | 1.7807 | 1.0759 | 0.7820 | 0.6200 | 0.5170 | 0.4454 | |
| r = 10 | 5.8586 | 1.7468 | 1.0541 | 0.7670 | 0.6095 | 0.5095 | 0.4403 |
| L/h | Gradient Index | 0% | 0.25% | 0.5% | 0.75% | 1.0% | 1.25% | 1.5% |
|---|---|---|---|---|---|---|---|---|
| 5 | uniform | 2.7510 | 3.8158 | 4.6427 | 5.3432 | 5.9621 | 6.5225 | 7.0386 |
| r = 2 | 2.7510 | 4.2651 | 5.3256 | 6.1935 | 6.9478 | 7.6247 | 8.2444 | |
| r = 4 | 2.7510 | 4.5350 | 5.6241 | 6.4572 | 7.1538 | 7.7643 | 8.3151 | |
| r = 6 | 2.7510 | 4.6392 | 5.7135 | 6.4913 | 7.1141 | 7.6421 | 8.1065 | |
| r = 8 | 2.7510 | 4.6969 | 5.7644 | 6.5112 | 7.0902 | 7.5672 | 7.9764 | |
| r = 10 | 2.7510 | 4.7340 | 5.7995 | 6.5292 | 7.0827 | 7.5291 | 7.9046 | |
| 20 | uniform | 2.9268 | 4.0597 | 4.9394 | 5.6846 | 6.3430 | 6.9393 | 7.4884 |
| r = 2 | 2.9268 | 4.6725 | 5.9202 | 6.9457 | 7.8372 | 8.6366 | 9.3677 | |
| r = 4 | 2.9268 | 5.1077 | 6.5850 | 7.7759 | 8.8002 | 9.7123 | 10.5423 | |
| r = 6 | 2.9268 | 5.2758 | 6.8343 | 8.0789 | 9.1418 | 10.0828 | 10.9349 | |
| r = 8 | 2.9268 | 5.3632 | 6.9627 | 8.2328 | 9.3125 | 10.2640 | 11.1221 | |
| r = 10 | 2.9268 | 5.4166 | 7.0405 | 8.3256 | 9.4143 | 10.3708 | 11.2306 |
| L/h | Gradient Index | 0% | 0.25% | 0.5% | 0.75% | 1.0% | 1.25% | 1.5% |
|---|---|---|---|---|---|---|---|---|
| 5 | uniform | 5.3197 | 7.3788 | 8.9778 | 10.3324 | 11.5291 | 12.6129 | 13.6109 |
| r = 2 | 5.3197 | 7.6810 | 9.3025 | 10.6367 | 11.8043 | 12.8582 | 13.8276 | |
| r = 4 | 5.3197 | 7.7226 | 8.9804 | 9.9178 | 10.7058 | 11.4055 | 12.0454 | |
| r = 6 | 5.3197 | 7.7644 | 8.8480 | 9.5769 | 10.1536 | 10.6478 | 11.0904 | |
| r = 8 | 5.3197 | 7.8076 | 8.8135 | 9.4412 | 9.9106 | 10.2972 | 10.6339 | |
| r = 10 | 5.3197 | 7.8441 | 8.8118 | 9.3854 | 9.7956 | 10.1215 | 10.3976 | |
| 20 | uniform | 6.5386 | 9.0696 | 11.0349 | 12.6999 | 14.1709 | 15.5030 | 16.7297 |
| r = 2 | 6.5386 | 10.3472 | 13.0511 | 15.2697 | 17.1980 | 18.9272 | 20.5089 | |
| r = 4 | 6.5386 | 11.2140 | 14.2769 | 16.6999 | 18.7603 | 20.5820 | 22.2321 | |
| r = 6 | 6.5386 | 11.5474 | 14.7112 | 17.1514 | 19.1832 | 20.9484 | 22.5245 | |
| r = 8 | 6.5386 | 11.7233 | 14.9375 | 17.3787 | 19.3812 | 21.0964 | 22.6079 | |
| r = 10 | 6.5386 | 11.8322 | 15.0780 | 17.5201 | 19.5036 | 21.1854 | 22.6525 |
| L/h | Gradient Index | 0% | 0.25% | 0.5% | 0.75% | 1.0% | 1.25% | 1.5% |
|---|---|---|---|---|---|---|---|---|
| 5 | uniform | 3.9767 | 5.5159 | 6.7112 | 7.7238 | 8.6184 | 9.4286 | 10.1746 |
| r = 2 | 3.9767 | 5.9341 | 7.2835 | 8.3886 | 9.3517 | 10.2182 | 11.0134 | |
| r = 4 | 3.9767 | 6.1126 | 7.2968 | 8.1804 | 8.9168 | 9.5648 | 10.1527 | |
| r = 6 | 3.9767 | 6.1901 | 7.2756 | 8.0200 | 8.6064 | 9.1038 | 9.5442 | |
| r = 8 | 3.9767 | 6.2417 | 7.2826 | 7.9571 | 8.4646 | 8.8798 | 9.2376 | |
| r = 10 | 3.9767 | 6.2788 | 7.2983 | 7.9352 | 8.3986 | 8.7669 | 9.0768 | |
| 20 | uniform | 4.5406 | 6.2982 | 7.6630 | 8.8192 | 9.8407 | 10.7658 | 11.6176 |
| r = 2 | 4.5406 | 7.2203 | 9.1296 | 10.6976 | 12.0606 | 13.2829 | 14.4007 | |
| r = 4 | 4.5406 | 7.8622 | 10.0781 | 11.8488 | 13.3635 | 14.7076 | 15.9278 | |
| r = 6 | 4.5406 | 8.1096 | 10.4252 | 12.2445 | 13.7795 | 15.1260 | 16.3366 | |
| r = 8 | 4.5406 | 8.2391 | 10.6045 | 12.4444 | 13.9819 | 15.3181 | 16.5093 | |
| r = 10 | 4.5406 | 8.3185 | 10.7144 | 12.5662 | 14.1037 | 15.4314 | 16.6070 |
| Total Layer Number | Ω1 | |||||
|---|---|---|---|---|---|---|
| r = 1 | r = 3 | r = 5 | r = 1 | r = 3 | r = 5 | |
| 2 | 0.8810 | 1.8431 | 4.1067 | 11.9650 | 8.2686 | 5.5381 |
| 4 | 0.8633 | 0.9409 | 1.3221 | 12.0850 | 11.5581 | 9.7511 |
| 8 | 0.8639 | 0.9674 | 1.1190 | 12.0809 | 11.3910 | 10.5805 |
| 12 | 0.8643 | 0.9720 | 1.1323 | 12.0778 | 11.3637 | 10.5198 |
| 16 | 0.8645 | 0.9743 | 1.1368 | 12.0764 | 11.3504 | 10.4995 |
| 20 | 0.8646 | 0.9775 | 1.1425 | 12.0748 | 11.3324 | 10.4871 |
| 50 | 0.8648 | 0.9777 | 1.1442 | 12.0746 | 11.3304 | 10.4656 |
| Monolithic | 0.8648 | 0.9777 | 1.1452 | 12.0746 | 11.3302 | 10.4610 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xie, K.; Fu, T.; Shi, C. Bending and Elastic Vibration of a Novel Functionally Graded Polymer Nanocomposite Beam Reinforced by Graphene Nanoplatelets. Nanomaterials 2019, 9, 1690. https://doi.org/10.3390/nano9121690
Wang Y, Xie K, Fu T, Shi C. Bending and Elastic Vibration of a Novel Functionally Graded Polymer Nanocomposite Beam Reinforced by Graphene Nanoplatelets. Nanomaterials. 2019; 9(12):1690. https://doi.org/10.3390/nano9121690
Chicago/Turabian StyleWang, Yuewu, Ke Xie, Tairan Fu, and Congling Shi. 2019. "Bending and Elastic Vibration of a Novel Functionally Graded Polymer Nanocomposite Beam Reinforced by Graphene Nanoplatelets" Nanomaterials 9, no. 12: 1690. https://doi.org/10.3390/nano9121690
APA StyleWang, Y., Xie, K., Fu, T., & Shi, C. (2019). Bending and Elastic Vibration of a Novel Functionally Graded Polymer Nanocomposite Beam Reinforced by Graphene Nanoplatelets. Nanomaterials, 9(12), 1690. https://doi.org/10.3390/nano9121690







