Preheating Modeling of Forming Region and Design of Electrode Structure During Integral Electric Hot Incremental Forming
Abstract
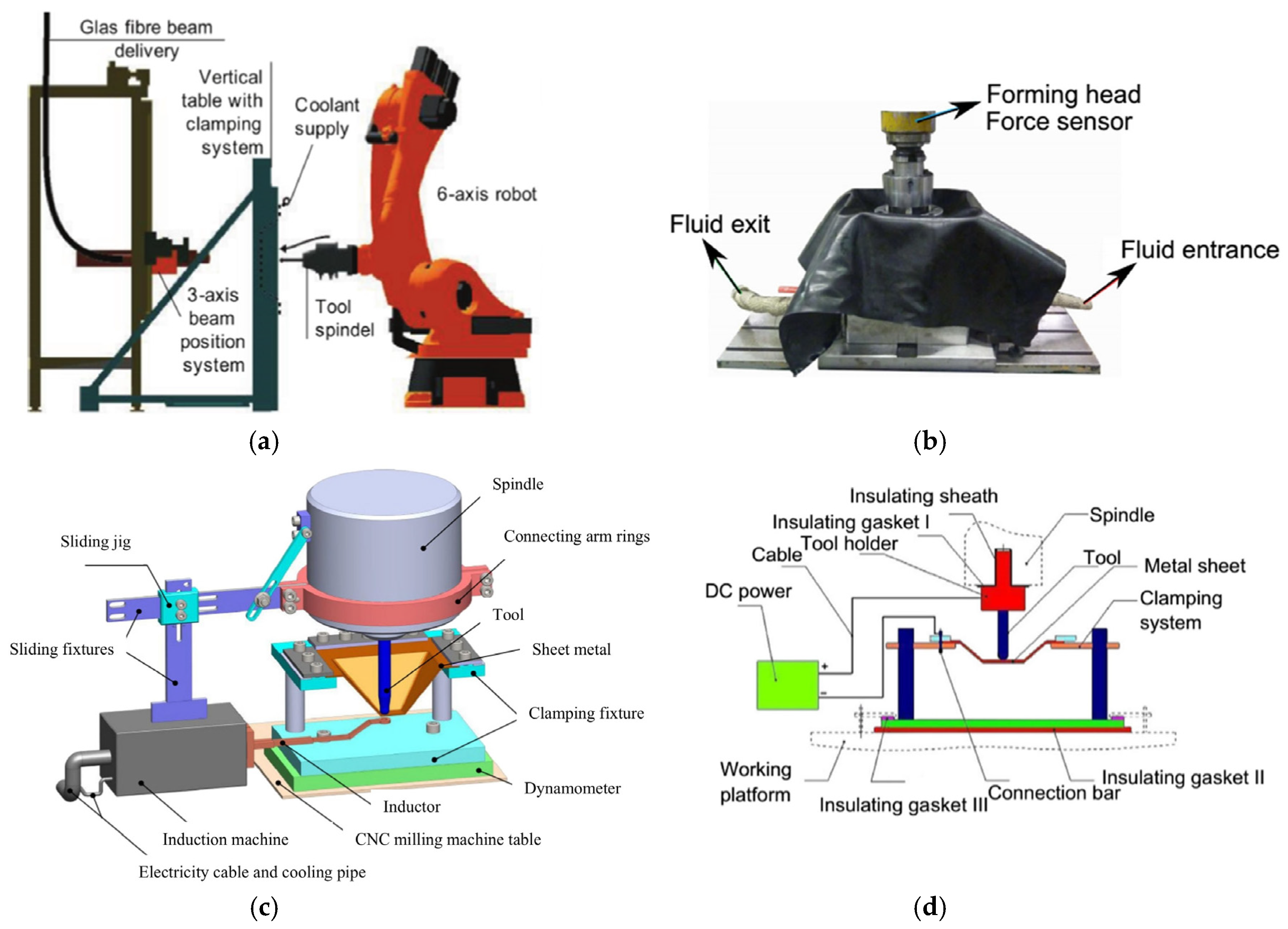
1. Introduction
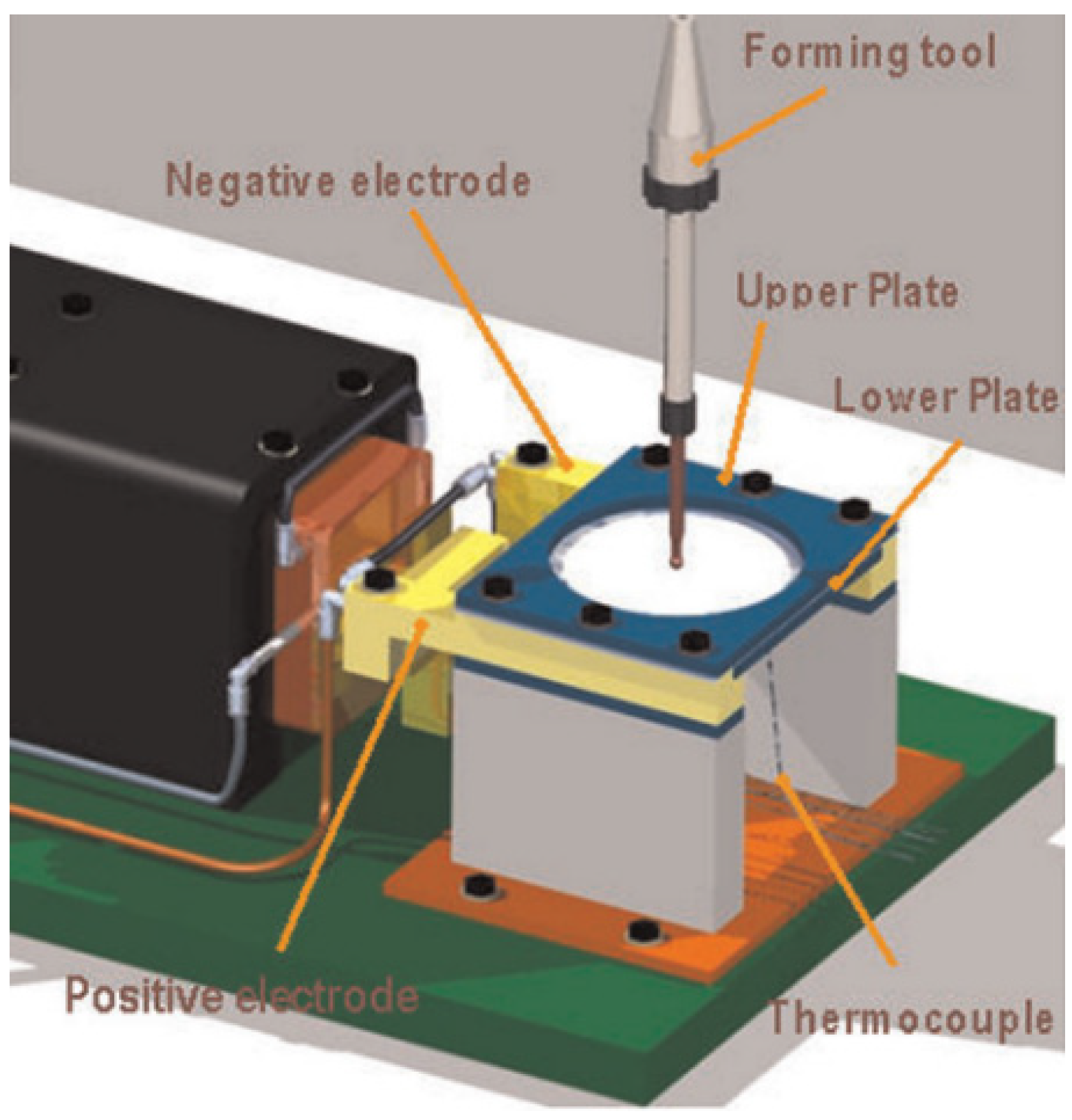
2. Materials and Methods
2.1. Heat Flux Models
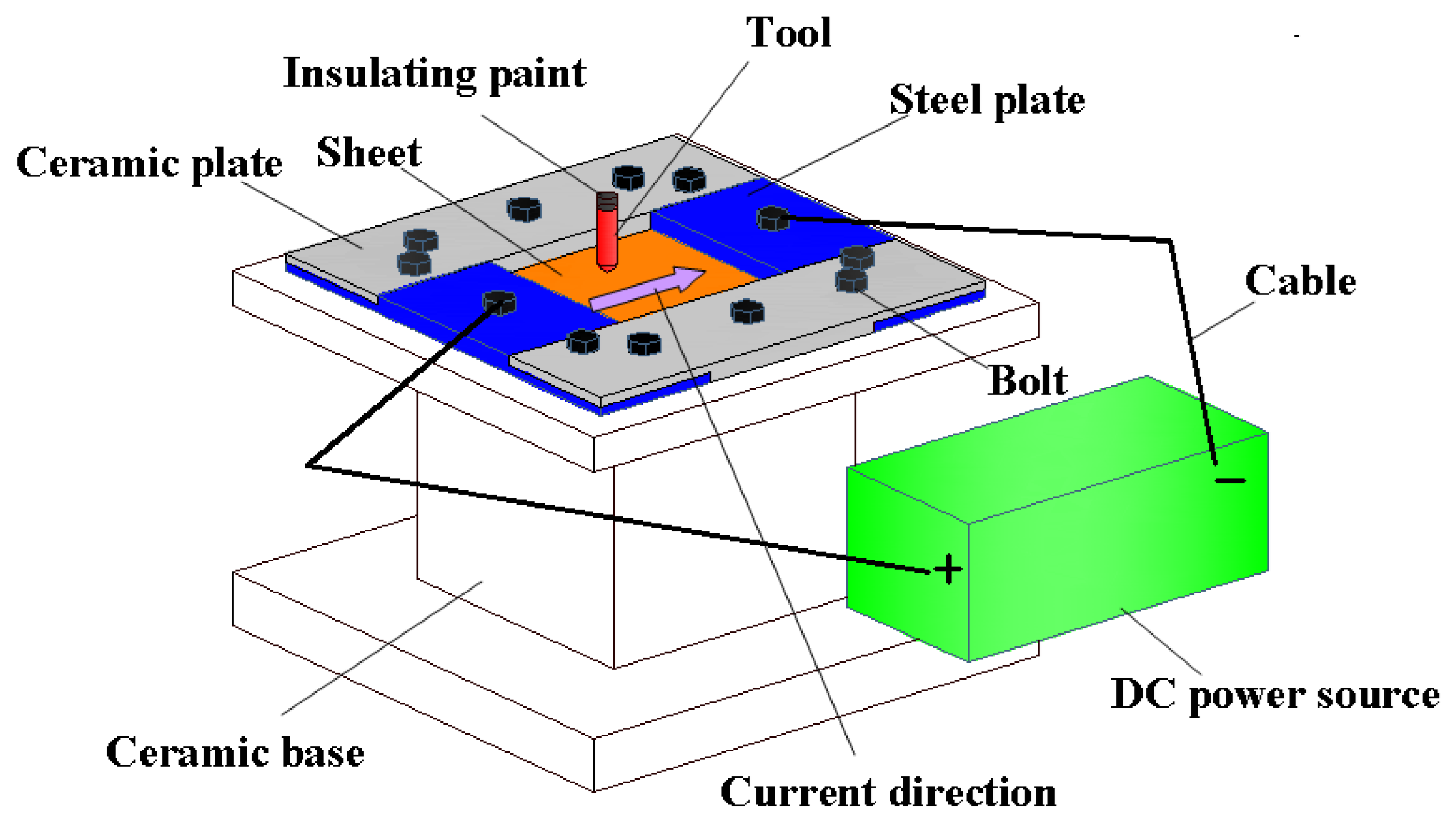
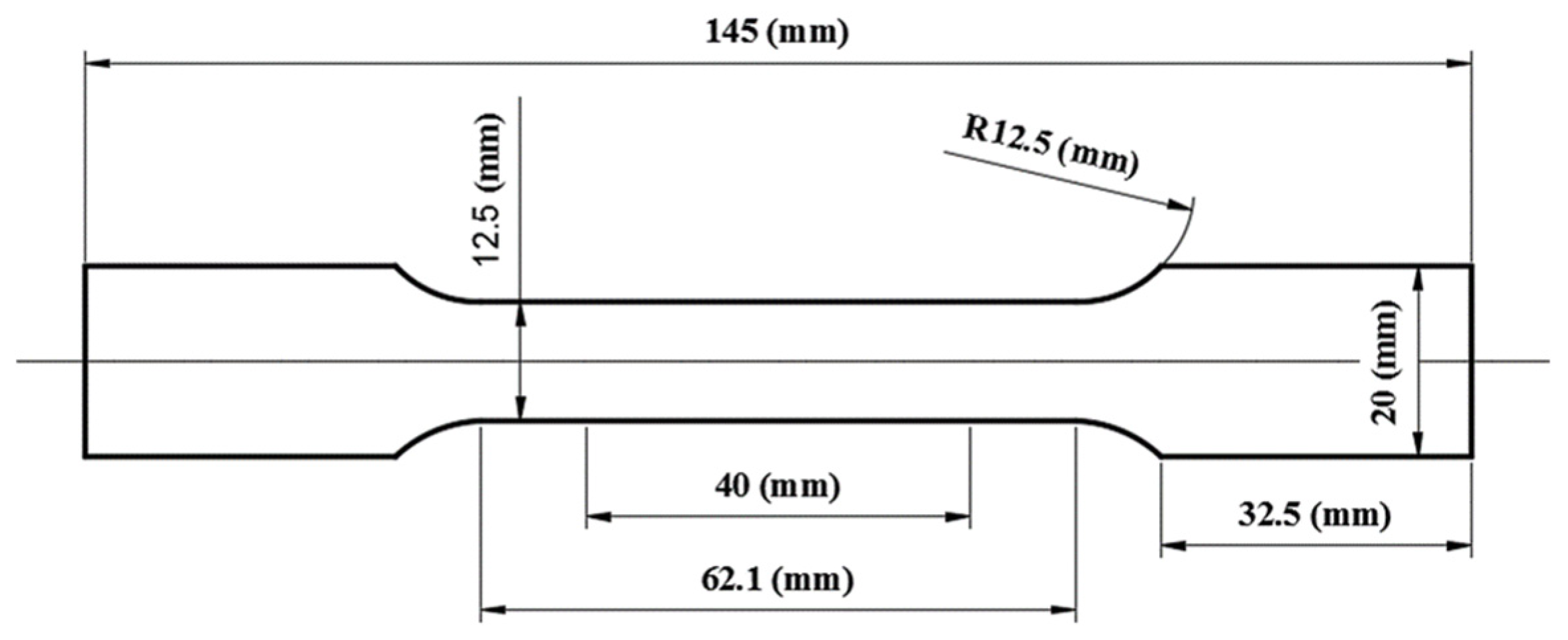
2.2. Design of Electrode Structure
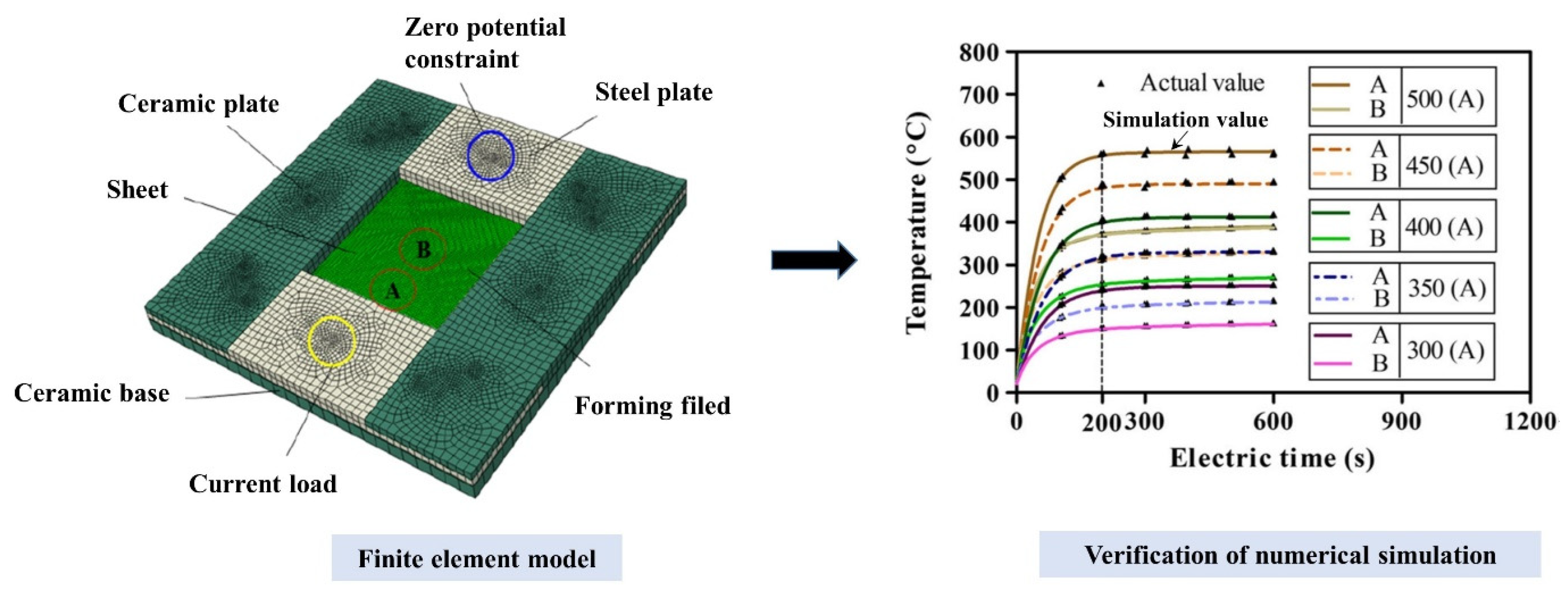
2.3. Finite Element Modeling
3. Results and Discussion
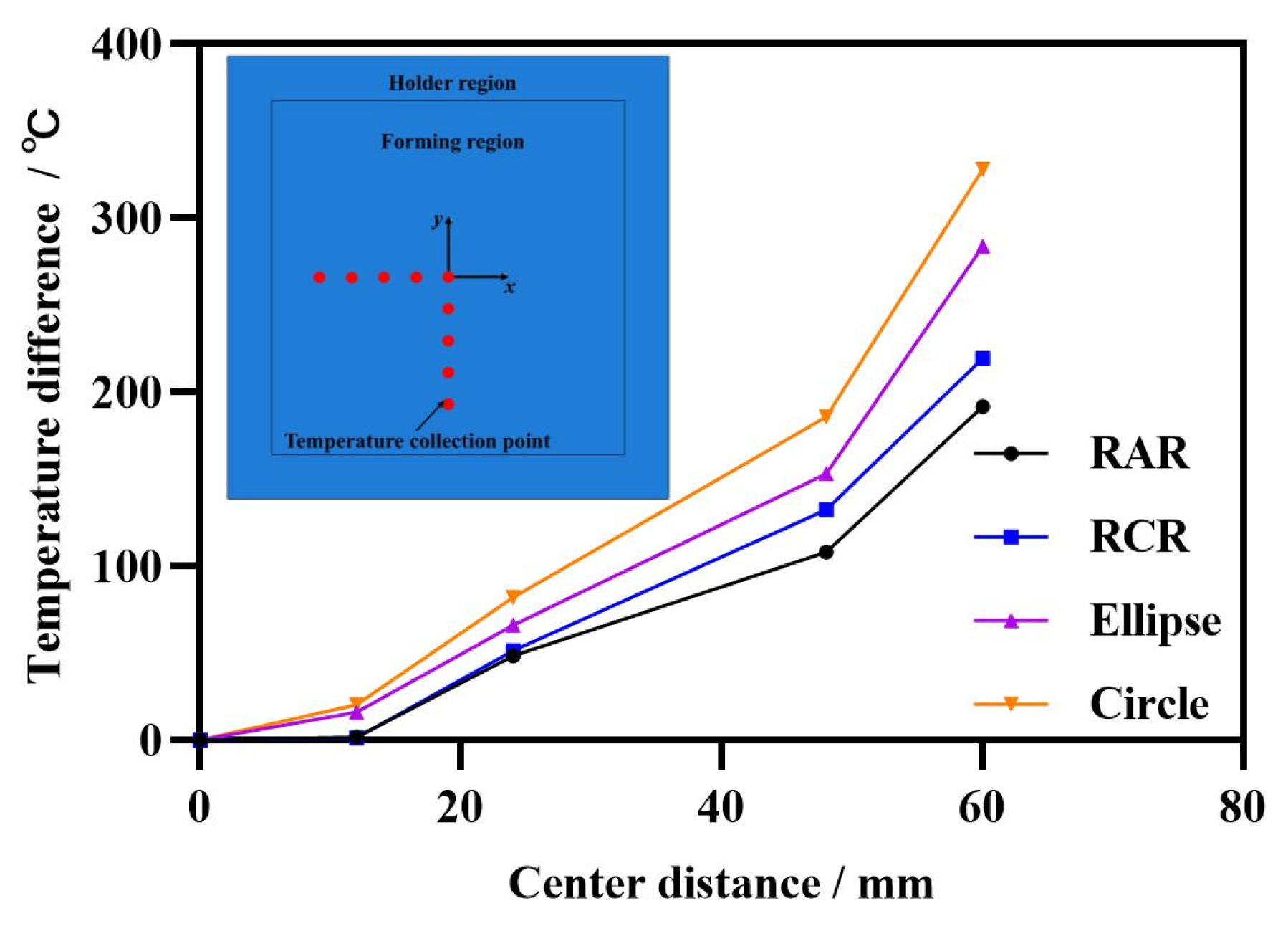
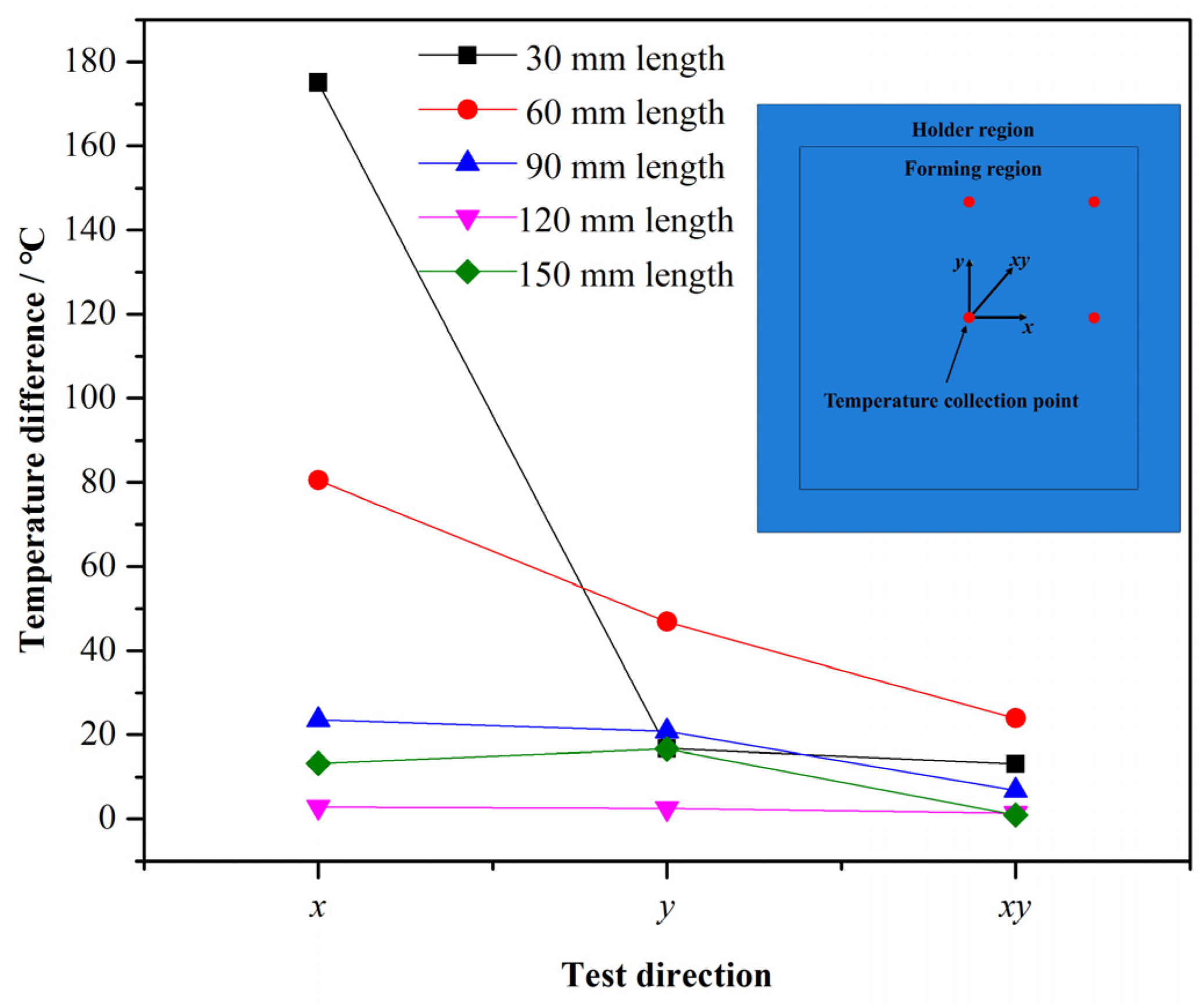
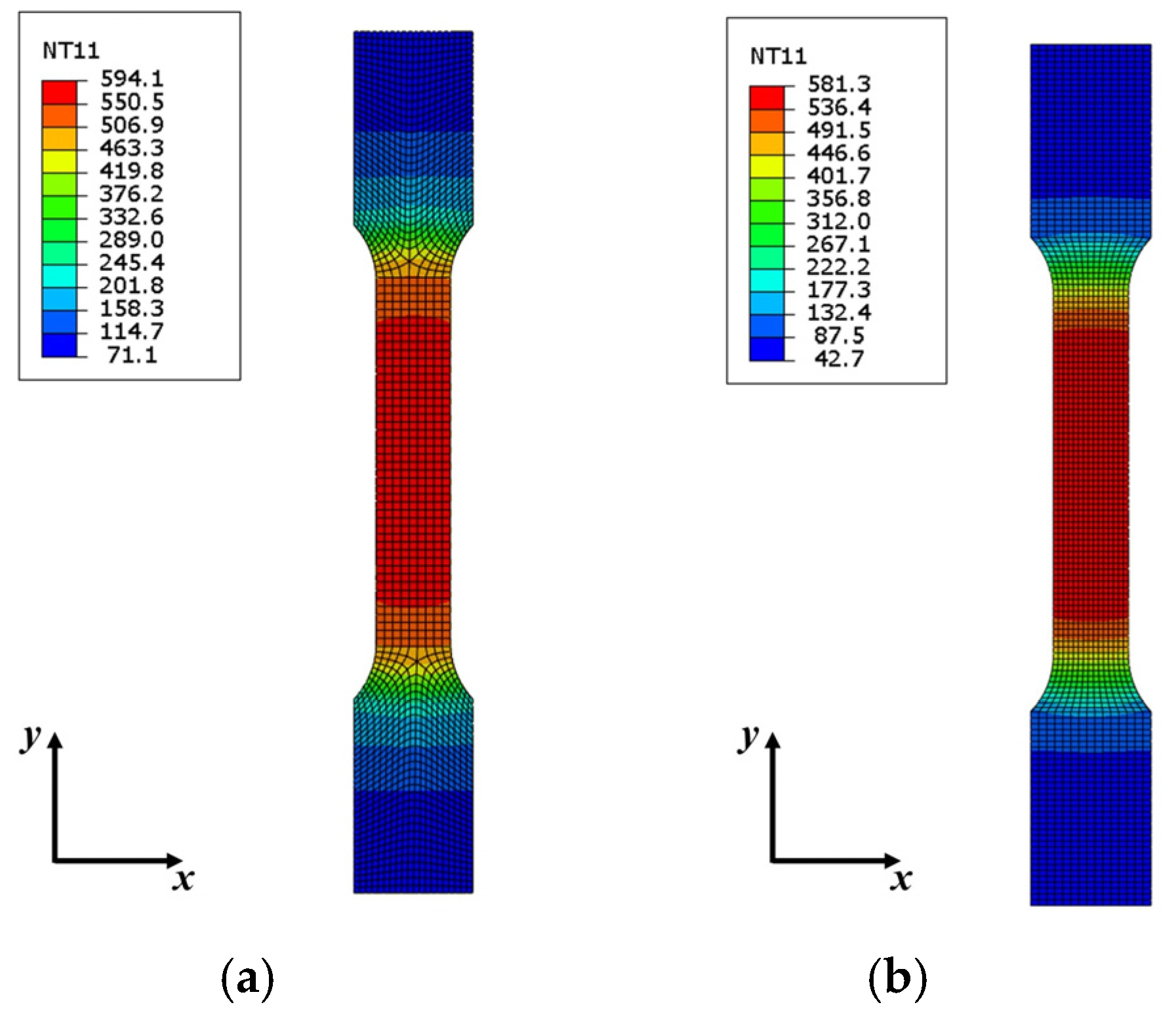
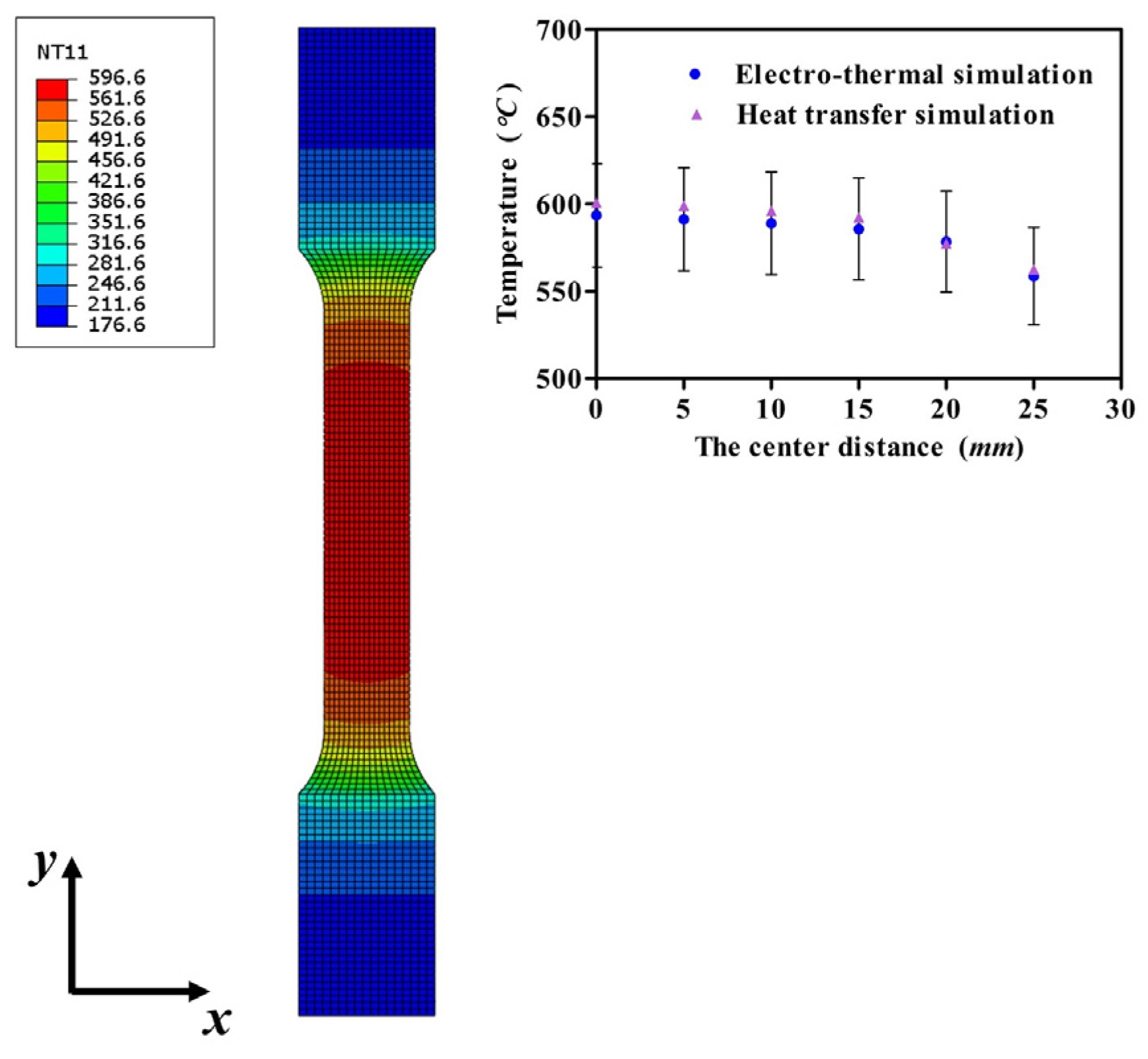
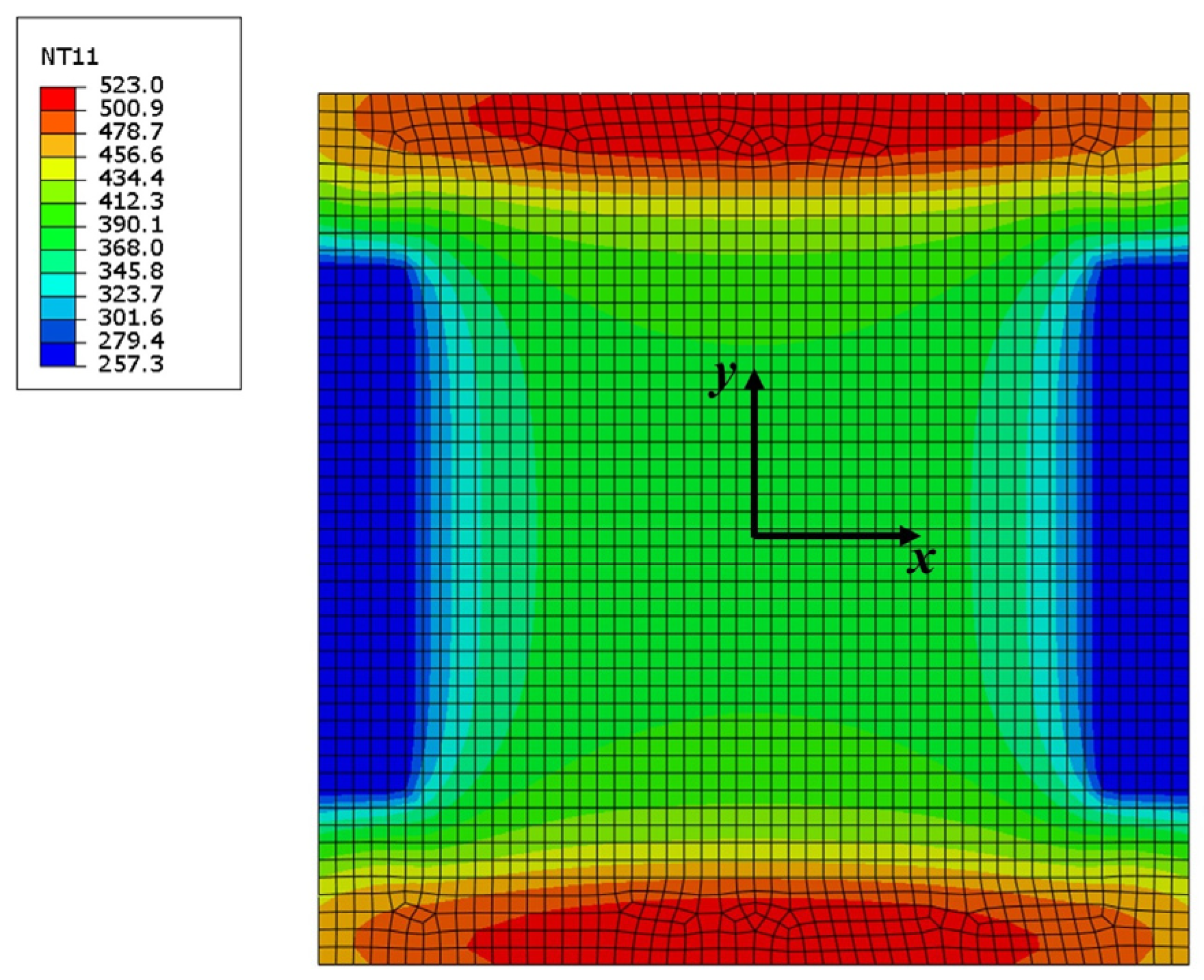
3.1. Analysis of Electrode Structures
3.2. Electrical Resistivity and Hardness
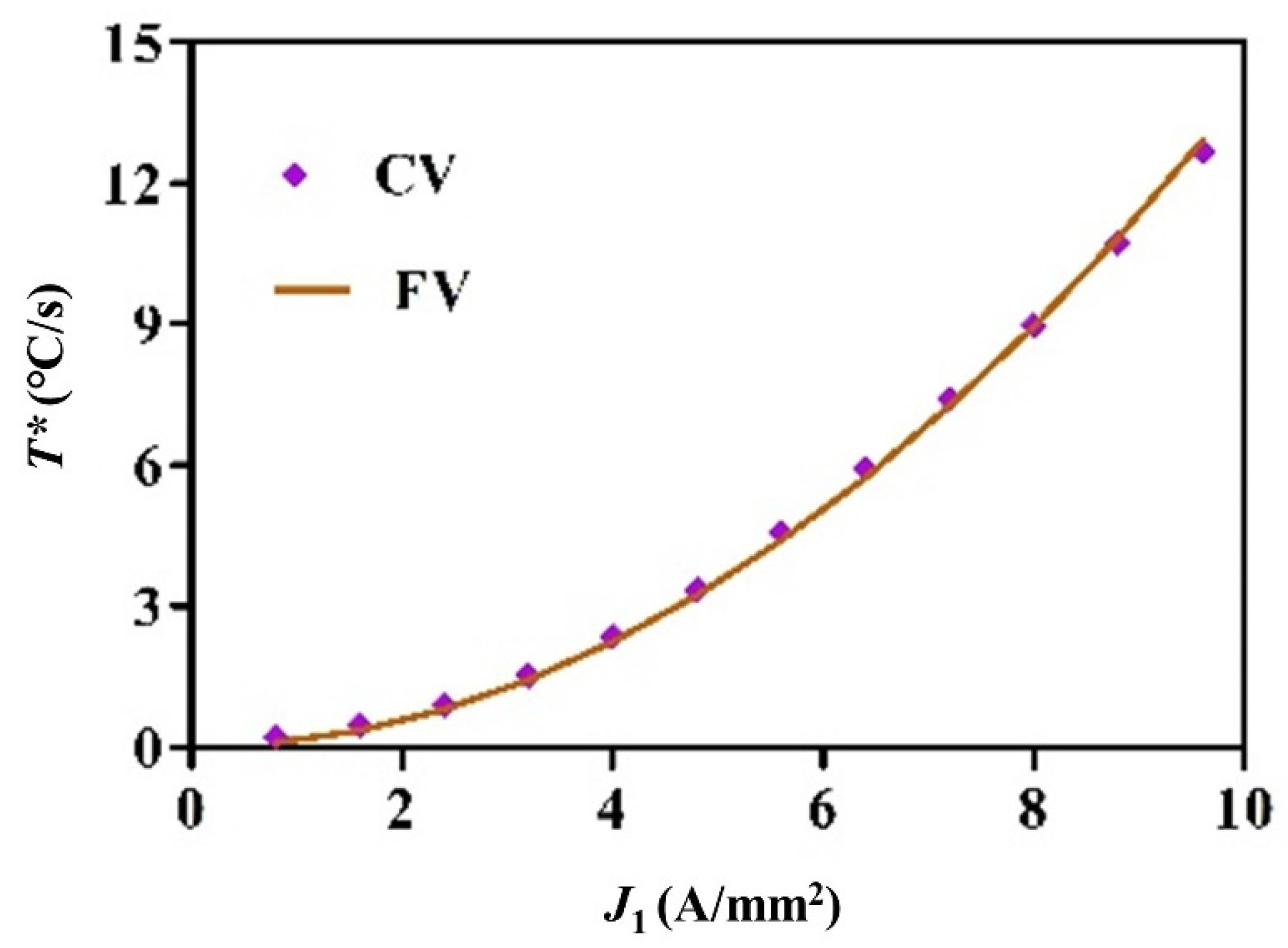
3.3. Analysis of Heat Flux Models
4. Conclusions
- (1)
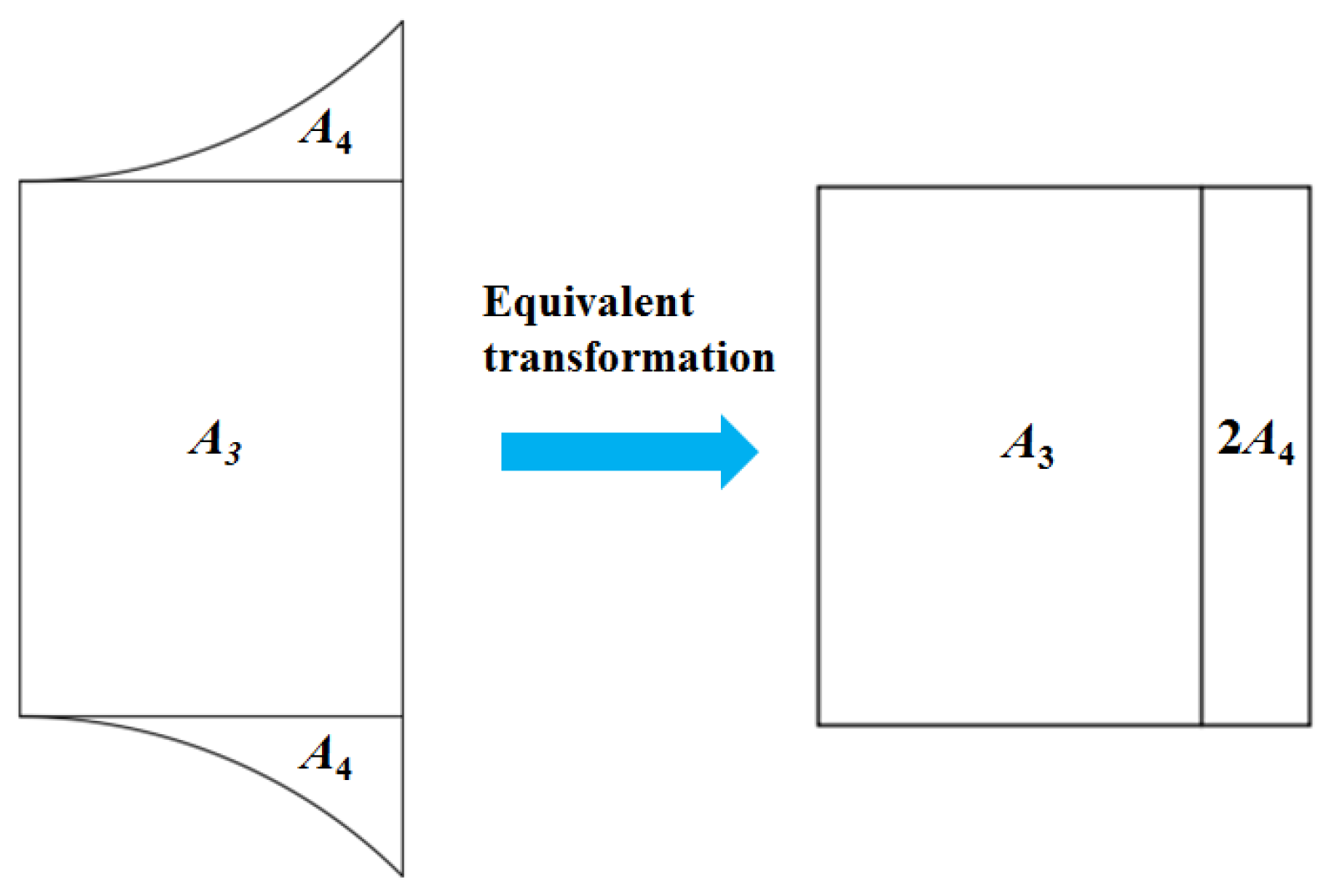
- The design of the electrode structure is exerted to analyze the temperature distribution of the sheet with Ti-6Al-4V titanium alloy in IEHIF, and the use of RAR could obtain a more homogeneous temperature distribution compared with the other sections.
- (2)
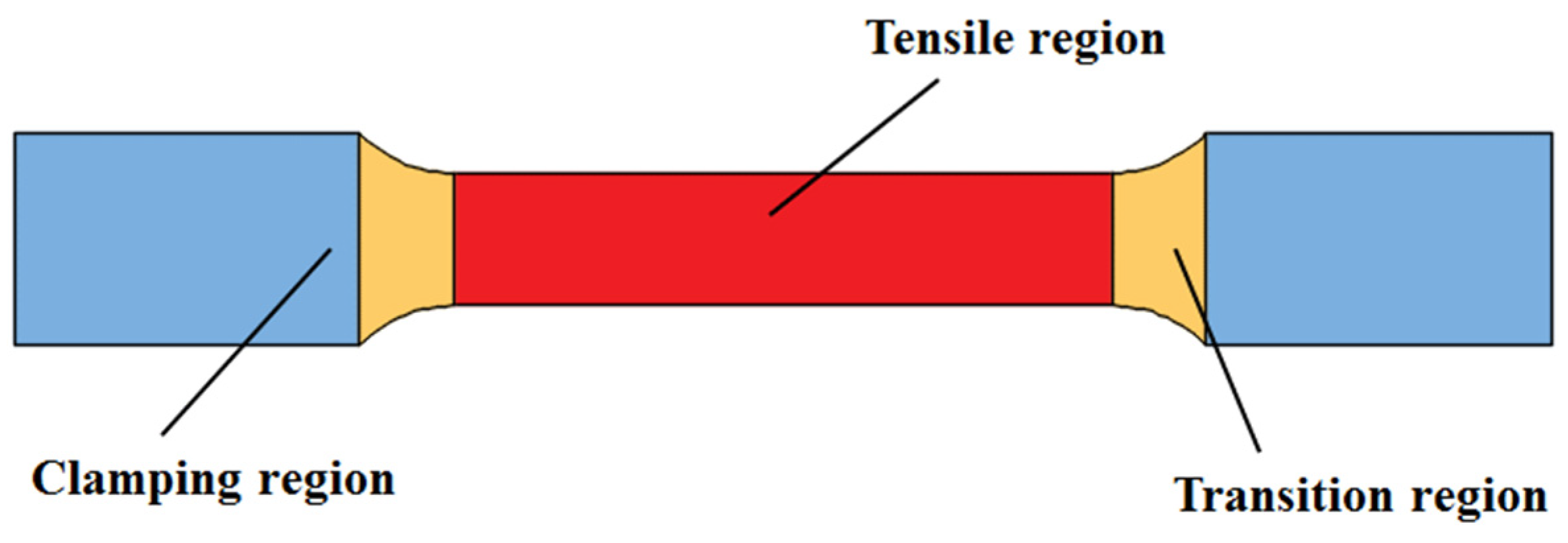
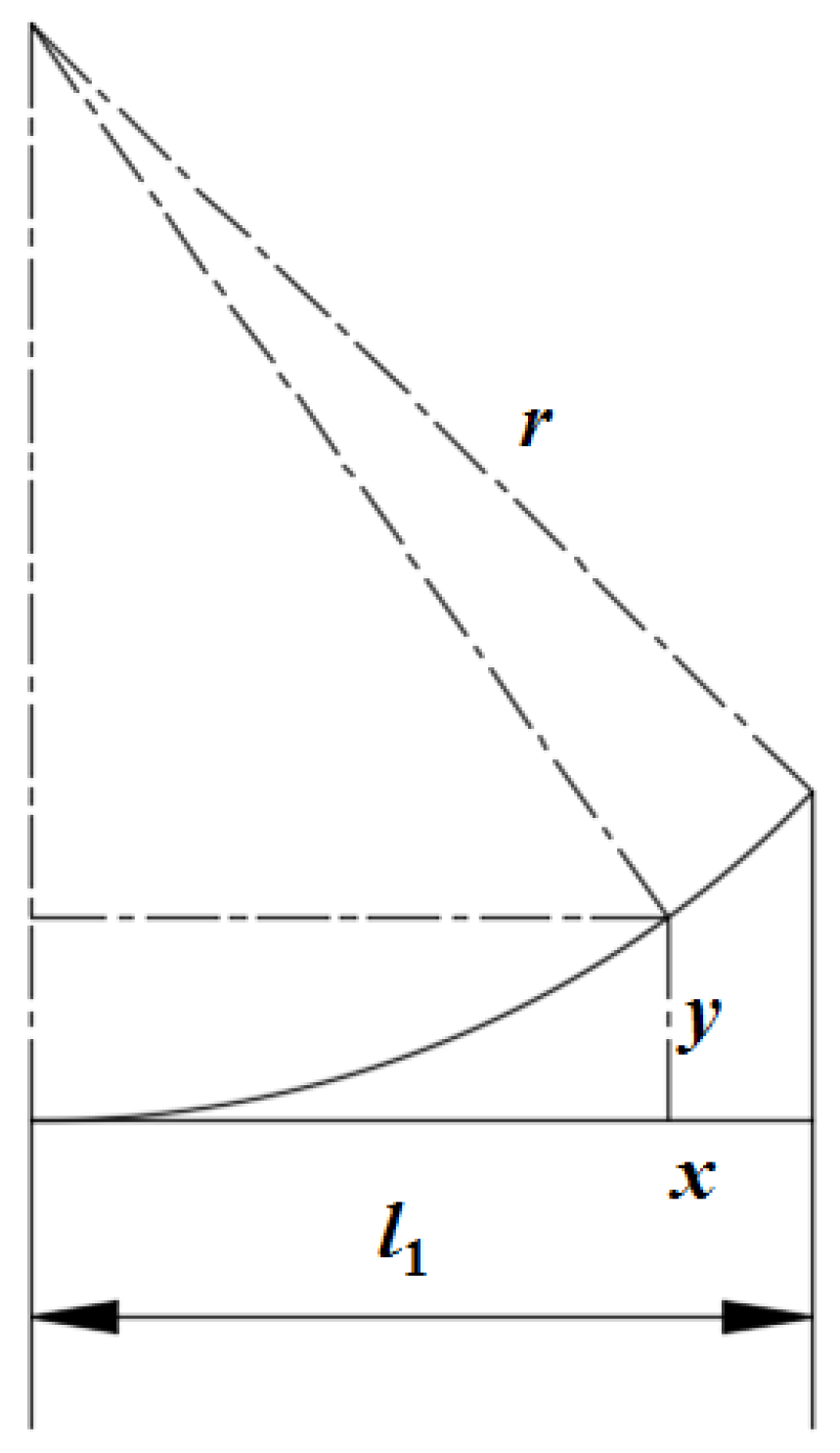
- The hourglass distribution of the forming region could be eliminated when the electrode length is 0.75 times the length of the forming region. Heat flux models for electric hot tension and IEHIF are separately established based on the effect of Joule heat.
- (3)
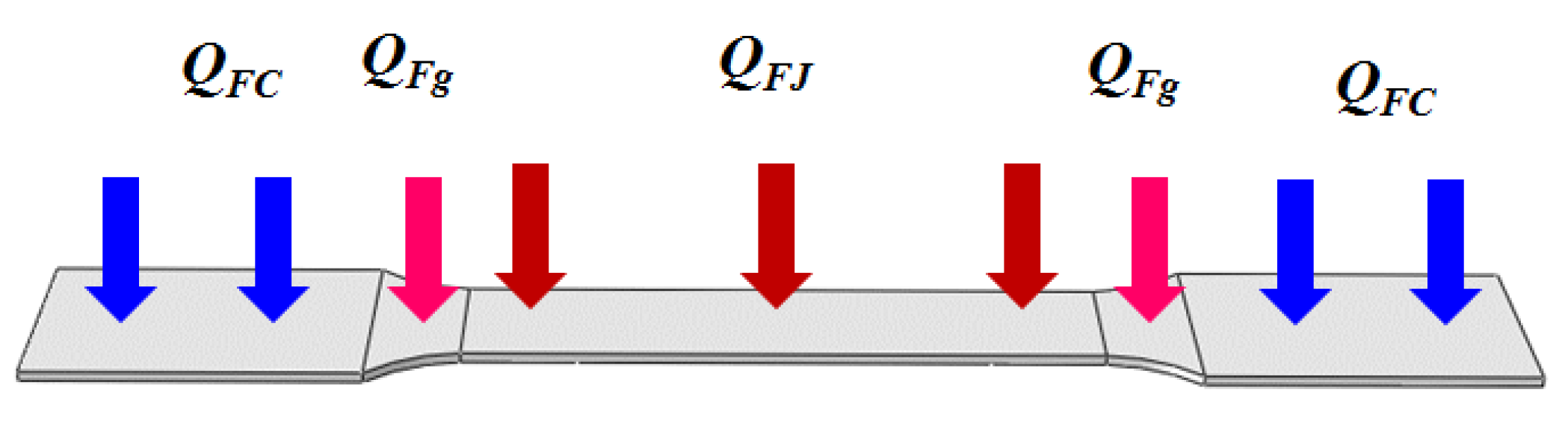
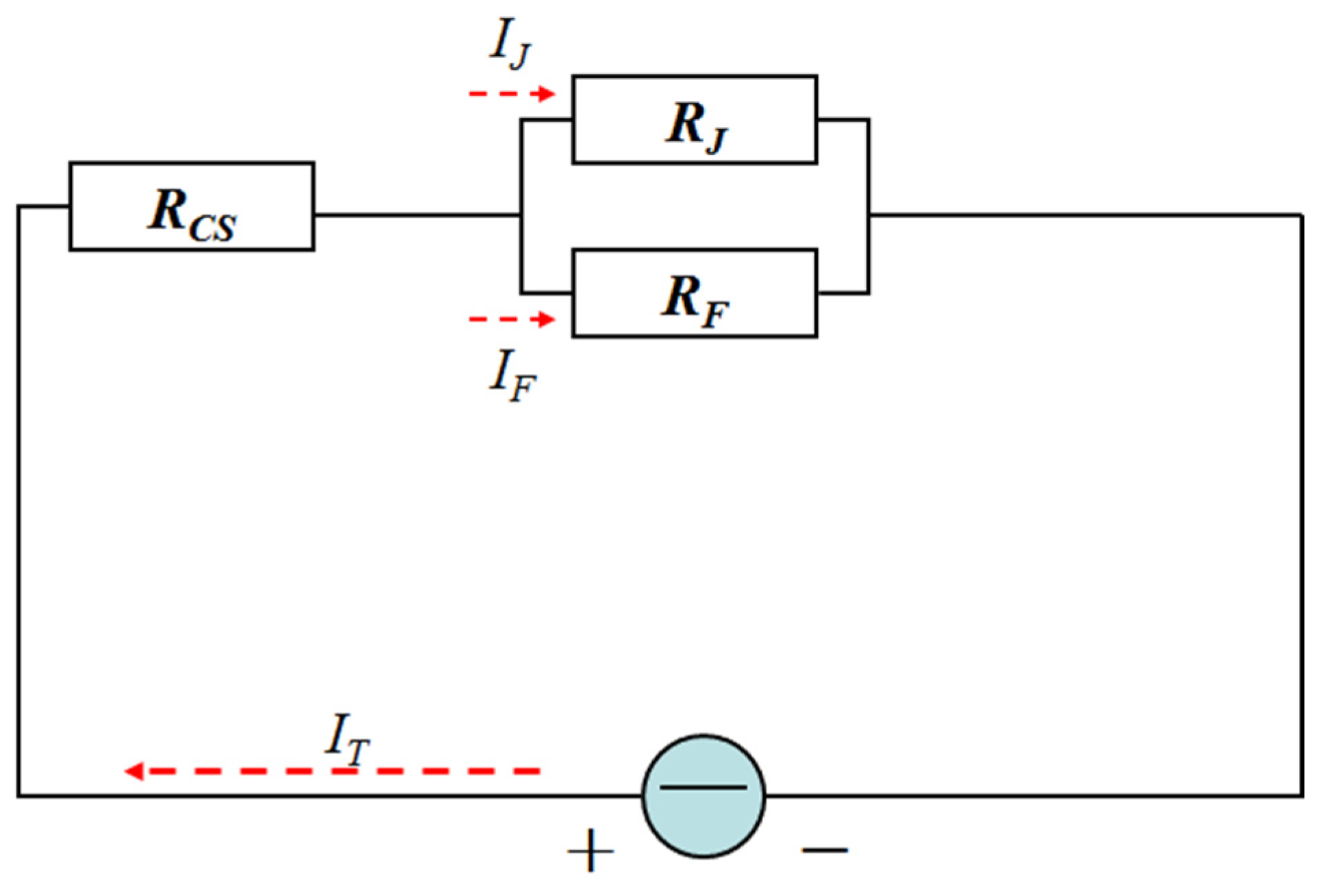
- Two scale factors, p and q, are proposed to correct the heat flux models of the tensile region and the transition region in electric hot tension and to improve heat flux models of FR and IHR in IEHIF, where p is a scaling factor and q is a compensation factor.
- (4)
- The sum between p and q is 2 according to the energy conservation principle, and p is obtained considering the power loss and the ratio of current surfaces to heat flux surfaces.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Matteo, B.; Vigilio, F.; Bernardo, M. Single-point incremental forming of sheet metals: Experimental study and numerical simulation. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2017, 231, 301–312. [Google Scholar]
- Suresh, K.; Bagade, S.D.; Regalla, S.P. Deformation Behavior of extra deep drawing steel in single-point incremental forming. Mater. Manuf. Process. 2015, 30, 1202–1209. [Google Scholar] [CrossRef]
- Küçüktürk, G.; Akıllılar, H. Investigating the Effect of Electron Beam Melting Parameters on the Ti6Al4V Alloy: A Simulation Study. Trans. Famena 2022, 46, 45–58. [Google Scholar] [CrossRef]
- Gao, H.; Fan, Q.; Chu, Z. Simulation Research on the Forming Process of Large Axles Rolled by Cross-Wedge Rolling. Trans. Famena 2022, 46, 63–80. [Google Scholar] [CrossRef]
- Küçüktürk, G.; Tahta, M.; Gürün, H.; Karaağaç, I. Evaluation of the Effects of Local Heating on Springback Behaviour for AHSS Docol 1400 Sheet Metal. Trans. Famena 2022, 46, 51–62. [Google Scholar] [CrossRef]
- Najafabady, S.A.; Ghaei, A. An experimental study on dimensional accuracy, surface quality, and hardness of Ti-6Al-4 V titanium alloy sheet in hot incremental forming. Int. J. Adv. Manuf. Technol. 2016, 87, 3579–3588. [Google Scholar] [CrossRef]
- Cao, X.D.; Kim, B.H.; Chu, C.N. Hybrid Micromachining of Glass Using ECDM and Micro Grinding. Int. J. Precis. Eng. Manuf. 2013, 14, 5–10. [Google Scholar] [CrossRef]
- Galdos, L.; Argandona, E.S.D.; Ulacia, I.; Arruebarrena, G. Warm incremental forming of magnesium alloys using hot fluid as heating media. Key Eng. Mater. 2012, 504, 815–820. [Google Scholar] [CrossRef]
- Zhu, Z.; Dhokia, V.G.; Nassehi, A.; Newman, S.T. A Review of Hybrid Manufacturing Processes—State of the Art and Future Perspectives. Int. J. Comput. Integr. Manuf. 2013, 26, 596–615. [Google Scholar] [CrossRef]
- Hinoa, R.; Kawabatab, K.; Yoshida, F. Incremental Forming with Local Heating by Laser Irradiation for Magnesium Alloy Sheet, 11th International Conference on Technology of Plasticity. Procedia Eng. 2014, 81, 2330–2335. [Google Scholar] [CrossRef]
- Lehtinena, P.; Väisänenb, T.; Salmi, M. The Effect of Local Heating by Laser Irradiation for Aluminum, Deep Drawing Steel and Copper Sheets in Incremental Sheet Forming. Phys. Procedia 2015, 78, 312–319. [Google Scholar] [CrossRef]
- Li, W.; Attallah, M.M.; Essa, K. Experimental and numerical investigations on the process quality and microstructure during induction heating assisted incremental forming of Ti-6Al-4V sheet. J. Mater. Process. Technol. 2022, 299, 117323. [Google Scholar] [CrossRef]
- Duflou, J.; Callebaut, B.; Verbert, J.; De Baerdemaeker, H. Laser Assisted Incremental Forming: Formability and Accuracy Improvement. CIRP Ann. Manuf. Technol. 2007, 56, 273–276. [Google Scholar] [CrossRef]
- Chu, W.S.; Kim, C.S.; Lee, H.T. Hybrid Manufacturing in Micro/Nano Scale: A Review. Int. J. Precis. Eng. Manuf.-Green Technol. 2014, 1, 75–92. [Google Scholar] [CrossRef]
- Kim, J.H.; Choi, J.Y.; Lee, C.M. A Study on the Effect of Laser Preheating on Laser Assisted Turn-Mill for Machining Square and Spline Members. Int. J. Precis. Eng. Manuf. 2014, 15, 275–282. [Google Scholar] [CrossRef]
- Ahn, S.H.; Chun, D.M.; Kim, C.S. Nanoscale Hybrid Manufacturing Process by Nano Particle Deposition System (NPDS) and Focused Ion Beam (FIB). CIRP Ann. Manuf. Technol. 2011, 60, 583–586. [Google Scholar] [CrossRef]
- Park, C.; Shin, B.S.; Kang, M.S. Experimental Study on Micro-Porous Patterning Using UV Pulse Laser Hybrid Process with Chemical Foaming Agent. Int. J. Precis. Eng. Manuf. 2015, 16, 1385–1390. [Google Scholar] [CrossRef]
- Fan, G.Q.; Gao, L.; Hussain, G. Electric Hot Incremental Forming: A Novel Technique. Int. J. Mach. Tools Manuf. 2008, 48, 1688–1692. [Google Scholar] [CrossRef]
- Fan, G.Q.; Gao, L. Mechanical Property of Ti-6Al-4V Sheet in One-sided Electric Hot Incremental Forming. Int. J. Adv. Manuf. Technol. 2014, 72, 989–994. [Google Scholar] [CrossRef]
- Fan, G.Q.; Gao, L. Numerical Simulation and Experimental Investigation to Improve the Dimensional Accuracy in Electric Hot Incremental Forming of Ti-6Al-4V Titanium Sheet. Int. J. Adv. Manuf. Technol. 2014, 72, 1133–1141. [Google Scholar] [CrossRef]
- Honarpisheh, M.; Abdolhoseini, M.J.; Amini, S. Experimental and Numerical Investigation of The Hot Incremental Forming of Ti-6Al-4V Sheet Using Electrical Current. Int. J. Adv. Manuf. Technol. 2016, 83, 2027–2037. [Google Scholar] [CrossRef]
- Li, Z.; Gao, Z.; An, Z.; Sun, Y.; Wu, B.; Zhai, Y. A Novel Temperature Model of Rregions Formed during the Preheating Stage of Belt Heating in Incremental Sheet Forming. Trans. Famena 2023, 47, 1–12. [Google Scholar] [CrossRef]
- Van Sy, L.; Nam, N.T. Hot incremental forming of magnesium and aluminum alloy sheets by using direct heating system. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2013, 227, 1099–1110. [Google Scholar] [CrossRef]
- Li, Z.; Lu, S.; Zhang, T.; Zhang, C.; Mao, Z. Electric assistance hot incremental sheet forming: An integral heating design. Int. J. Adv. Manuf. Technol. 2018, 96, 3209–3215. [Google Scholar] [CrossRef]
- Tslaf, A. A Thermophysical Criterion for the Weldability of Electric Contact Material in a Steady-State Regime. IEEE Trans. Compon. Hybrids Manuf. Technol. 2003, 5, 147–152. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, S.; Li, Z.; Mao, Z.; Xiang, L. Temperature control system of integral self-resistive electric heating incremental forming. Forg. Stamp. Technol. 2019, 44, 119–125. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Liu, L.; Song, J.; Wu, S.; Liu, L.; Zhai, X. Preheating Modeling of Forming Region and Design of Electrode Structure During Integral Electric Hot Incremental Forming. Nanomaterials 2025, 15, 698. https://doi.org/10.3390/nano15090698
Li Z, Liu L, Song J, Wu S, Liu L, Zhai X. Preheating Modeling of Forming Region and Design of Electrode Structure During Integral Electric Hot Incremental Forming. Nanomaterials. 2025; 15(9):698. https://doi.org/10.3390/nano15090698
Chicago/Turabian StyleLi, Zhengfang, Lijia Liu, Jiangpeng Song, Shuang Wu, Li Liu, and Xinhao Zhai. 2025. "Preheating Modeling of Forming Region and Design of Electrode Structure During Integral Electric Hot Incremental Forming" Nanomaterials 15, no. 9: 698. https://doi.org/10.3390/nano15090698
APA StyleLi, Z., Liu, L., Song, J., Wu, S., Liu, L., & Zhai, X. (2025). Preheating Modeling of Forming Region and Design of Electrode Structure During Integral Electric Hot Incremental Forming. Nanomaterials, 15(9), 698. https://doi.org/10.3390/nano15090698




