Characterization of the Second Harmonic Generation of Boron Nitride Nanotube Macroscopic Assemblies
Abstract
1. Introduction
2. Experimental Results and Discussion
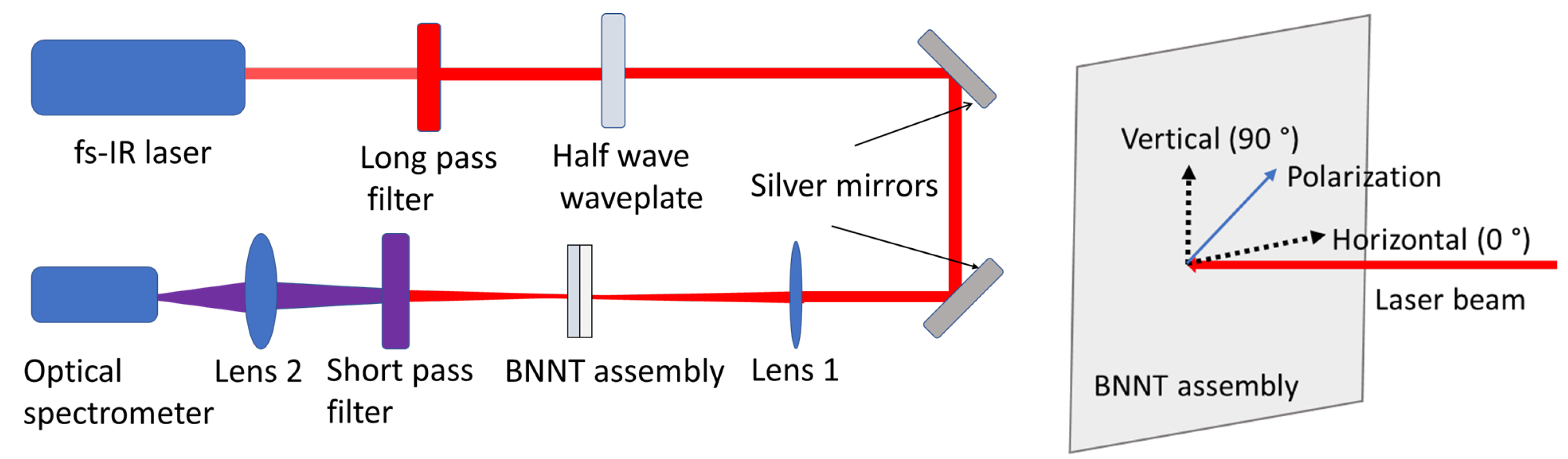
2.1. Experiment Setup
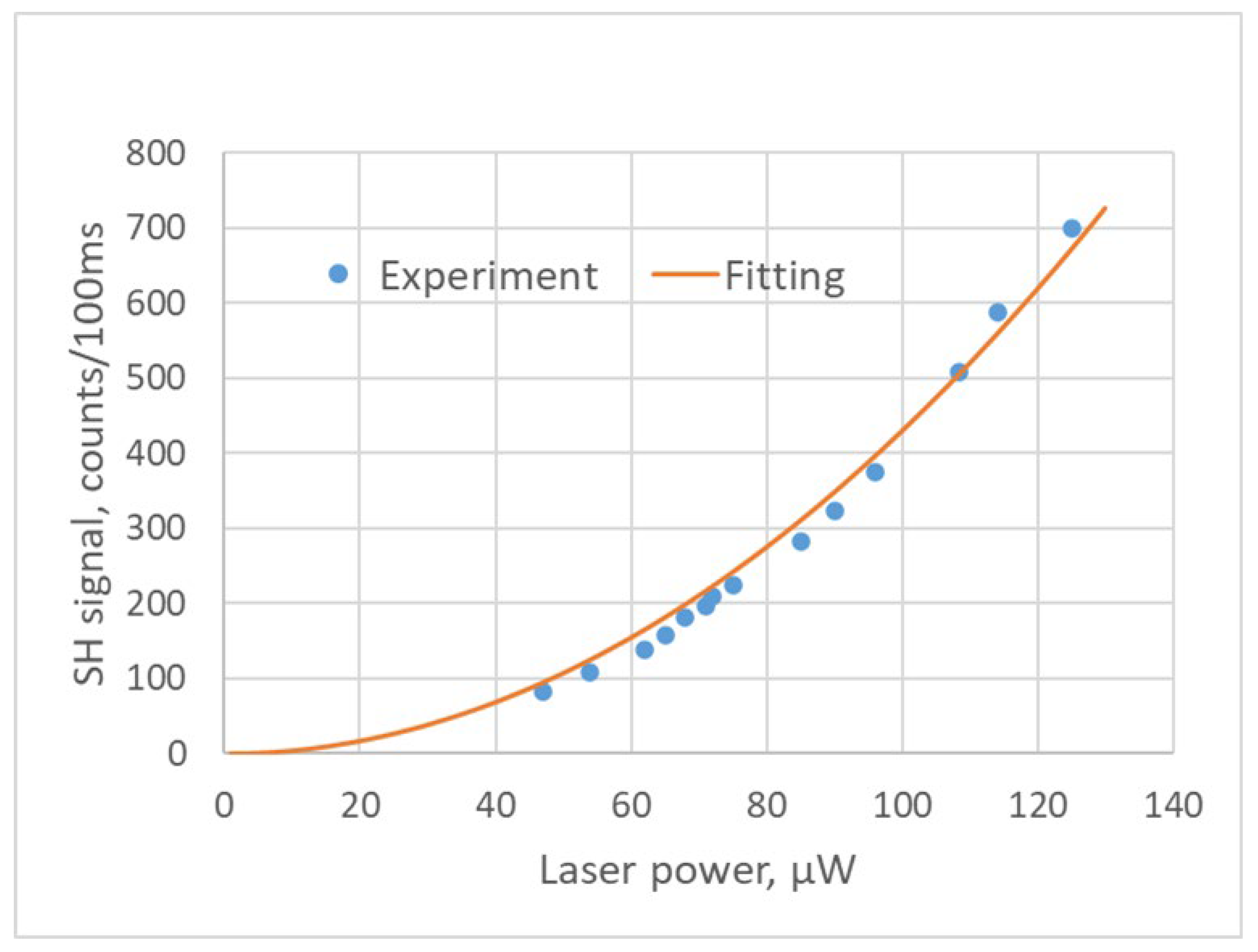
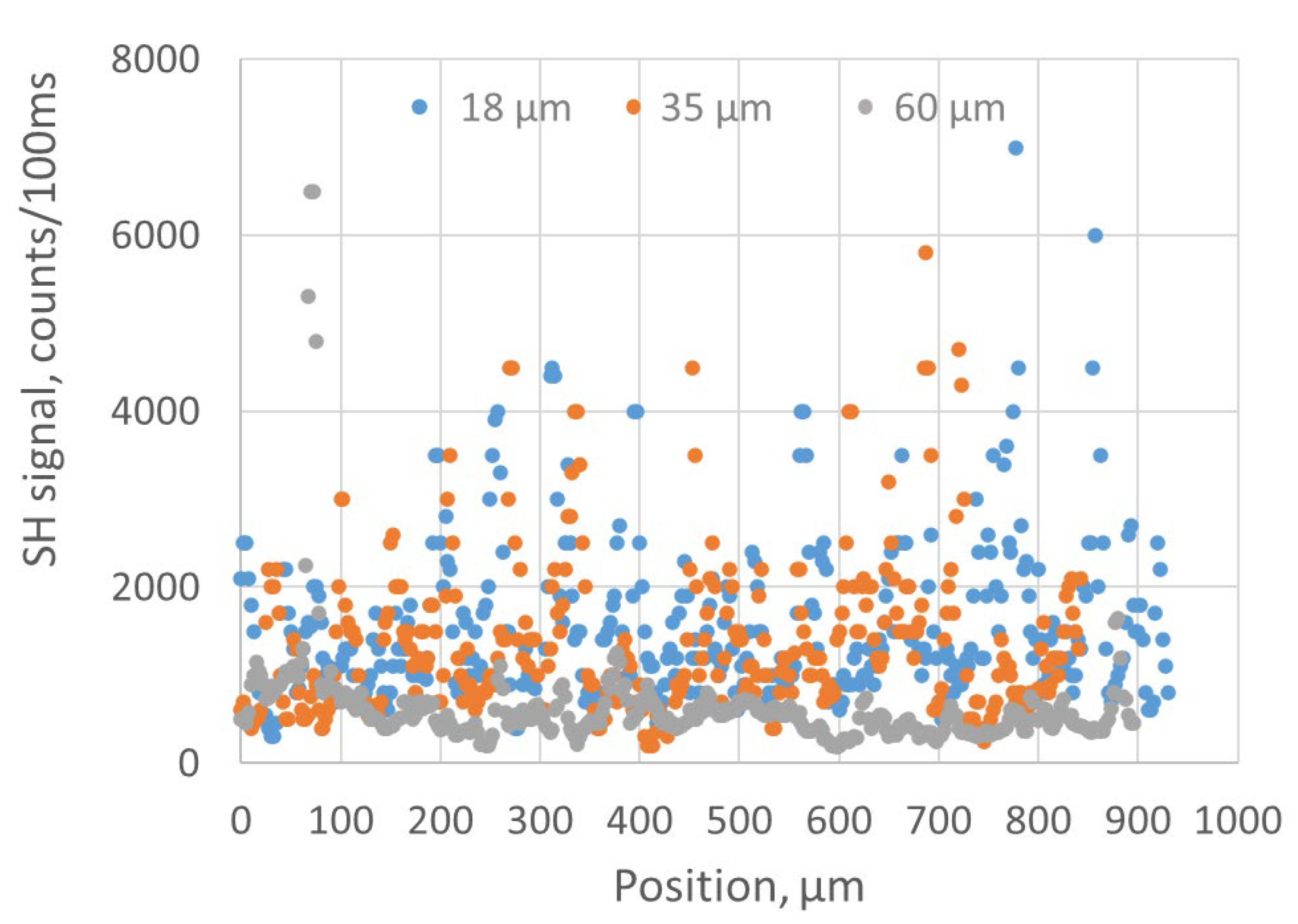
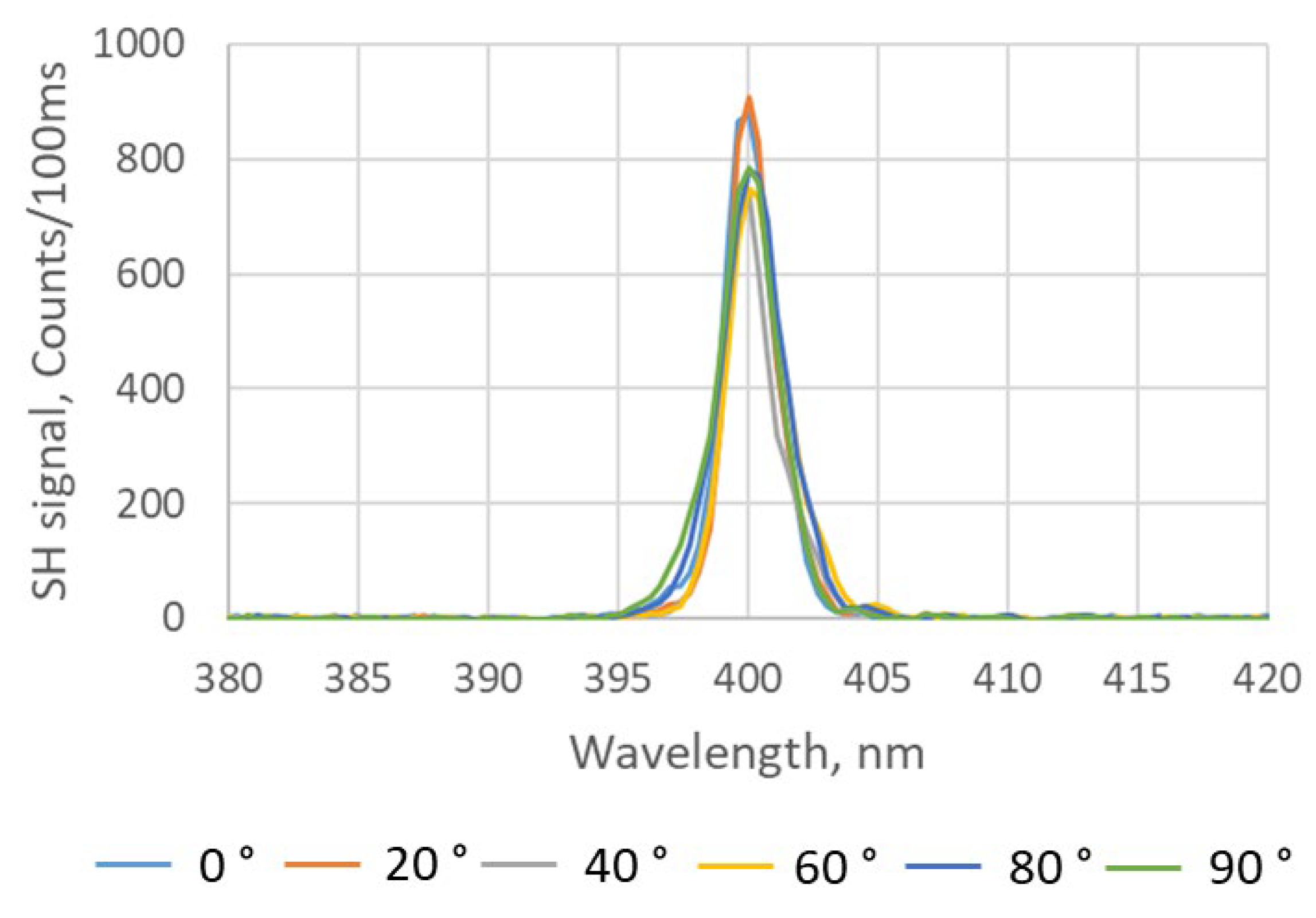
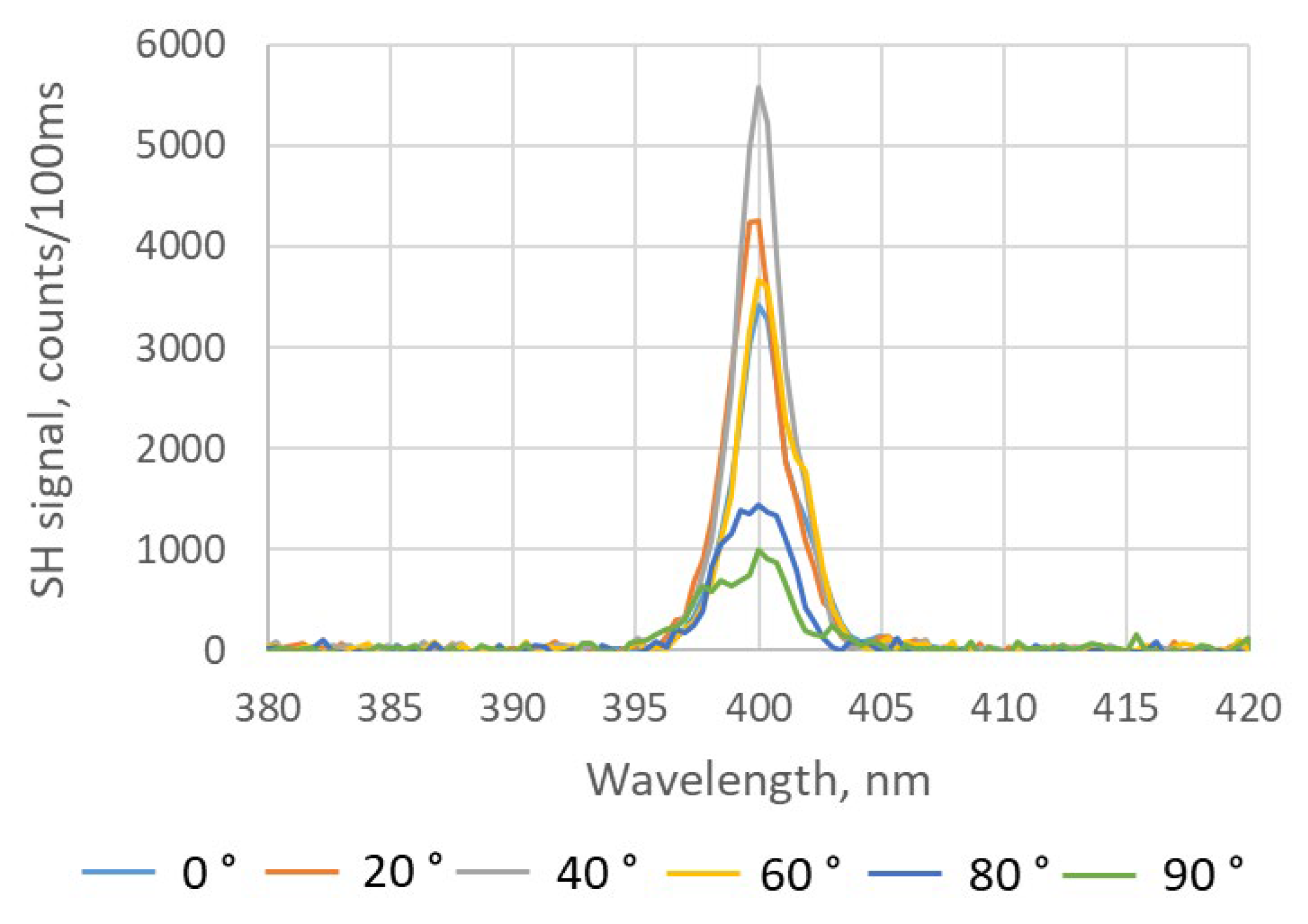
2.2. SHG in Free-Standing BNNT Sheets
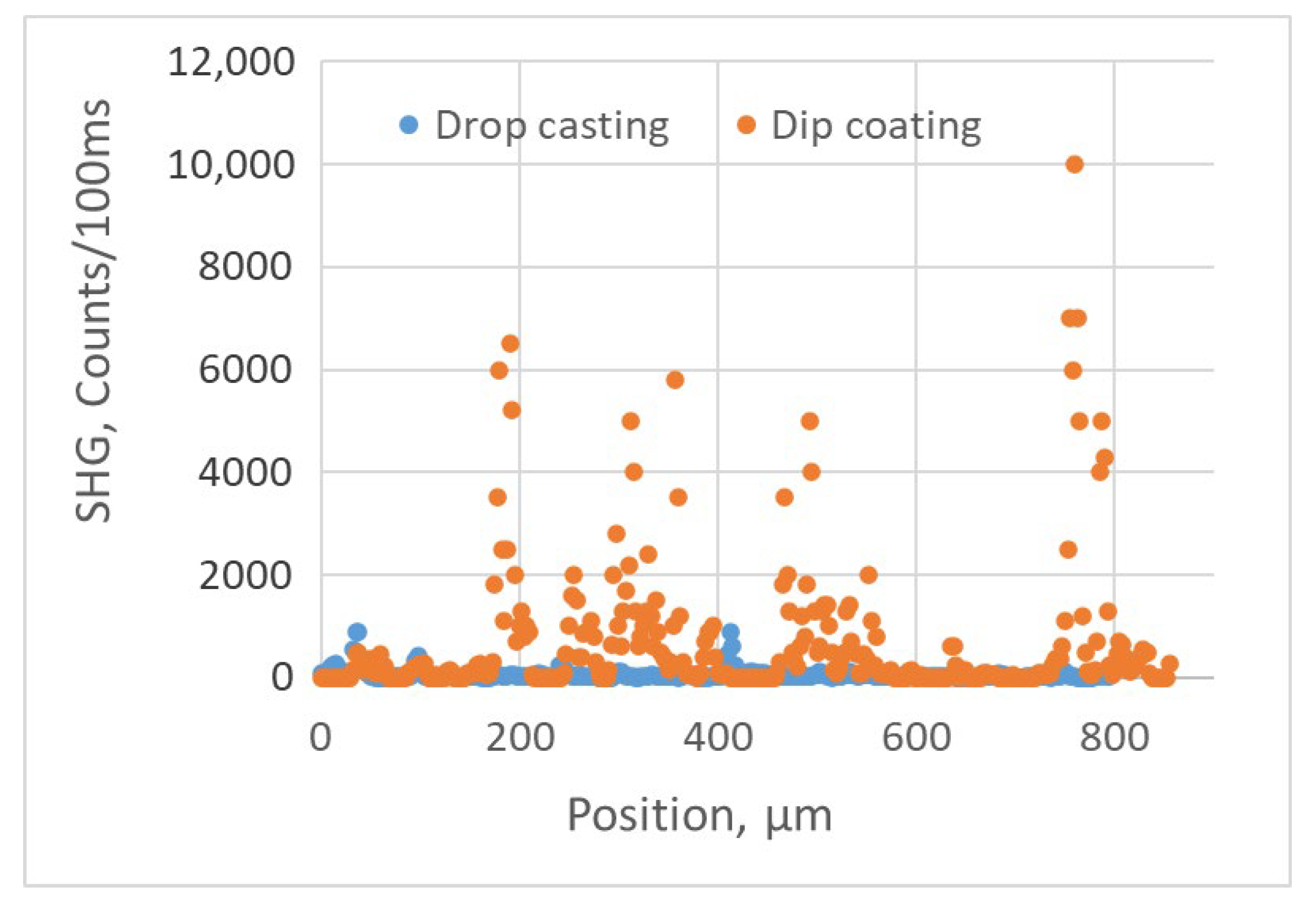
2.3. SHG in BNNT Coatings on Silica Substrates
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BNNT | Boron nitride nanotube |
| SHG | Second harmonic generation |
| SH | Second harmonic |
| Fs-IR | Femtosecond infrared |
| h-BN | Hexagonal boron nitride |
| CNT | Carbon nanotube |
References
- Chopra, N.G.; Luyken, R.J.; Cherrey, K.; Crespi, V.H.; Cohen, M.L.; Louie, S.G.; Zettl, A. Boron Nitride Nanotubes. Science 1995, 269, 966–967. [Google Scholar] [CrossRef] [PubMed]
- Boron Nitride Nanotubes. Available online: https://www.tekna.com/boron-nitride-nanotubes (accessed on 20 March 2025).
- Mamak, M.; Choi, S.Y.; Stadler, U.; Dolbec, R.; Boulos, M.; Petrov, S. Thermal plasma synthesis of tungsten bronze nanoparticles for near infra-red absorption applications. J. Mater. Chem. 2010, 20, 9855–9857. [Google Scholar] [CrossRef]
- Guo, J.; Fan, X.; Richard, D.; Xue, S.; Jerzy, J.; Maher, B. Development of Nanopowder Synthesis Using Induction Plasma. Plasma Sci. Technol. 2010, 12, 188–199. [Google Scholar]
- Kim, K.S.; Kingston, C.T.; Ruth, D.; Barnes, M.; Simard, B. Synthesis of high quality single-walled carbon nanotubes with purity enhancement and diameter control by liquid precursor Ar–H2 plasma spraying. Chem. Eng. J. 2014, 250, 331–341. [Google Scholar] [CrossRef]
- Meunier, J.L.; Mendoza-Gonzalez, N.Y.; Pristavita, R.; Binny, D.; Berk, D. Two-Dimensional Geometry Control of Graphene Nanoflakes Produced by Thermal Plasma for Catalyst Applications. Plasma Chem. Plasma Process. 2014, 34, 505–521. [Google Scholar] [CrossRef]
- Thompson, D.; Leparoux, M.; Jaeggi, C.; Buha, J.; Pui, D.Y.; Wang, J. Aerosol emission monitoring in the production of silicon carbide nanoparticles by induction plasma synthesis. J. Nanopart. Res. 2013, 15, 1–13. [Google Scholar] [CrossRef][Green Version]
- Aktekin, B.; Çakmak, G.; Öztürk, T. Induction thermal plasma synthesis of Mg2Ni nanoparticles. Int. J. Hydrogen Energy 2014, 39, 9859–9864. [Google Scholar] [CrossRef]
- So, K.S.; Lee, H.; Kim, T.H.; Choi, S.; Park, D.W. Synthesis of silicon nanopowder from silane gas by RF thermal plasma. Phys. Status Solidi (a) 2014, 211, 310–315. [Google Scholar] [CrossRef]
- Son, S.; Taheri, M.; Carpenter, E.; Harris, V.G.; McHenry, M.E. Synthesis of ferrite and nickel ferrite nanoparticles using radio-frequency thermal plasma torch. J. Appl. Phys. 2002, 91, 7589. [Google Scholar] [CrossRef]
- Kim, K.; Kingston, C.; Hrdina, A.; Jakubinek, M.; Guan, J.; Plunkett, M.; Simard, B. Hydrogen-Catalyzed, Pilot-Scale Production of Small-Diameter Boron Nitride Nano-tubes and Their Macroscopic Assemblies. ACS Nano 2014, 8, 6211–6220. [Google Scholar] [CrossRef]
- Kim, K.; Kim, M.; Park, C.; Fay, C.; Chu, S.; Kingston, C.; Simard, B. Scalable manufacturing of boron nitride nanotubes and their assemblies: A review. Semicond. Sci. Technol. 2017, 32, 013003. [Google Scholar] [CrossRef]
- Weng, Q.; Wang, X.; Wang, X.; Bando, Y.; Golberg, D. Functionalized hexagonal boron nitride nanomaterials: Emerging properties and applications. Chem. Soc. Rev. 2016, 45, 3989–4012. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.; Guan, J.; Zgierski, M.Z.; Kim, K.S.; Kingston, C.T.; Simard, B. Covalent functionalization of boron nitride nanotubes via reduction chemistry. ACS Nano 2015, 9, 12573–12582. [Google Scholar] [CrossRef] [PubMed]
- Cassabois, G.; Valvin, P.; Gil, B. Hexagonal boron nitride is an indirect bandgap semiconductor. Nat. Photonics 2016, 10, 262–266. [Google Scholar] [CrossRef]
- Blase, X.; Rubio, A.; Louie, S.G.; Cohen, M.L. Stability and band gap constancy of boron nitride nanotubes. Europhys. Lett. 1994, 28, 335. [Google Scholar] [CrossRef]
- Baierle, R.J.; Schmidt, T.M.; Fazzio, A. Adsorption of CO and NO molecules on carbon doped boron nitride nanotubes. Solid State Commun. 2007, 142, 49–53. [Google Scholar] [CrossRef]
- Wang, R.; Zhu, R.; Zhang, D. Adsorption of formaldehyde molecule on the pristine and silicon-doped boron nitride nanotubes. Chem. Phys. Lett. 2008, 467, 131–135. [Google Scholar] [CrossRef]
- Wu, X.; Yang, J.; Zeng, X. Adsorption of hydrogen molecules on the platinum-doped boron nitride nanotubes. J. Chem. Phys. 2006, 125, 044704. [Google Scholar] [CrossRef]
- Xiang, H.J.; Yang, J.; Hou, J.G.; Zhu, Q. Are fluorinated boron nitride nanotubes n-type semiconductors? Appl. Phys. Lett. 2005, 87, 243113. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Z.; Zhao, J. Functionalization of BN nanotubes with dichlorocarbenes. Nanotechnology 2008, 19, 015202. [Google Scholar] [CrossRef]
- Zhi, C.; Bando, Y.; Tang, C.; Golberg, D. Engineering of electronic structure of boron-nitride nanotubes by covalent functionalization. Phys. Rev. B Condens. Matter Mater. Phys. 2006, 74, 153413. [Google Scholar] [CrossRef]
- Chen, X.; Dmuchowski, C.; Park, C.; Fay, C.C.; Ke, C. Quantitative Characterization of Structural and Mechanical Proper-ties of Boron Nitride Nanotubes in High Temperature Environments. Sci. Rep. 2017, 7, 11388. [Google Scholar]
- Jakubinek, M.; Kim, K.; Kim, M.; Martí, A.A.; Pasquali, M. Recent advances and perspective on boron nitride nanotubes: From synthesis to applications. J. Mater. Res. 2022, 37, 4403–4418. [Google Scholar] [CrossRef]
- Golberg, D.; Bando, Y.; Kurashima, K.; Sato, T. Synthesis and characterization of ropes made of bn multiwalled nanotubes. Scr. Mater. 2001, 44, 1561–1565. [Google Scholar] [CrossRef]
- Darwish, A.; Hassan, M.; Mandour, M.A.; Maarouf, A. Mechanical properties of defective double-walled boron nitride nanotubes for radiation shielding applications: A computational study. Comput. Mater. Sci. 2019, 156, 142–147. [Google Scholar] [CrossRef]
- Chen, Y.; Zou, J.; Campbell, S.; Caer, G. Boron nitride nanotubes: Pronounced resistance to oxidation. Appl. Phys. Lett. 2004, 84, 2430–2432. [Google Scholar] [CrossRef]
- Mierzwa, G.; Gordon, A.; Berski, S. The nature of multiple boron-nitrogen bonds studied using electron localization function (ELF), electron density (AIM), and natural bond orbital (NBO) methods. J. Mol. Model. 2020, 26, 136. [Google Scholar] [CrossRef]
- Grüning, M.; Attaccalite, C. Second harmonic generation in ℎ-BN and MoS2 monolayers: Role of electron-hole interaction. Phys. Rev. B 2014, 89, 081102. [Google Scholar] [CrossRef]
- Li, Y.; Rao, Y.; Mak, K.; You, Y.; Wang, S.; Dean, C.R.; Heinz, T.F. Probing Symmetry Properties of Few-Layer MoS2 and h-BN by Optical Second-Harmonic Generation. Nano Lett. 2013, 13, 3329–3333. [Google Scholar] [CrossRef]
- Kim, S.; Fröch, J.E.; Gardner, A.; Li, C.; Aharonovich, I.; Solntsev, A.S. Second-harmonic generation in multilayer hexagonal boron nitride flakes. Opt. Lett. 2019, 44, 5792–5795. [Google Scholar] [CrossRef]
- Guo, G.; Lin, C. Second-harmonic generation and linear electro-optical coefficients of BN nanotubes. Phys. Rev. B Condens. Matter Mater. Phys. 2005, 72, 075416. [Google Scholar] [CrossRef]
- Margulis, V.; Muryumin, E.; Gaiduk, E. Second-order nonlinear optical response of zigzag single-walled nanotubes. Phys. Rev. B Condens. Matter Mater. Phys. 2010, 82, 235326. [Google Scholar] [CrossRef]
- Ma, C.; Ma, C.; Liu, C.; Guo, Q.; Huang, C.; Yao, G.; Li, M.; Qi, J.; Qin, B.; Sui, X.; et al. Strong chiroptical nonlinearity in coherently stacked boron nitride nanotubes. Nat. Nanotechnol. 2024, 19, 1299–1305. [Google Scholar] [CrossRef] [PubMed]
- Lu, P.; Guan, J.; Ding, H.; De Silva, K.; Kingston, C.; Mihailov, S.J. Refractive Index Determination and Air-Void Characterization of BNNT Assembly Using Optical Fiber Bragg Grating Sensors. IEEE Sens. J. 2024, 24, 23886–23891. [Google Scholar] [CrossRef]
- Ding, H.; Guan, J.; Lu, P.; Mihailov, S.J.; Kingston, C.T.; Simard, B. Boron Nitride Nanotubes for Optical Fiber Chemical Sensing Applications. IEEE Sens. Lett. 2020, 4, 500804. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, P.; Guan, J.; Hnatovsky, C.; Ding, H.; Silva, K.D.; Gaburici, L.; Kingston, C.; Mihailov, S.J. Characterization of the Second Harmonic Generation of Boron Nitride Nanotube Macroscopic Assemblies. Nanomaterials 2025, 15, 861. https://doi.org/10.3390/nano15110861
Lu P, Guan J, Hnatovsky C, Ding H, Silva KD, Gaburici L, Kingston C, Mihailov SJ. Characterization of the Second Harmonic Generation of Boron Nitride Nanotube Macroscopic Assemblies. Nanomaterials. 2025; 15(11):861. https://doi.org/10.3390/nano15110861
Chicago/Turabian StyleLu, Ping, Jingwen Guan, Cyril Hnatovsky, Huimin Ding, Kasthuri De Silva, Liliana Gaburici, Christopher Kingston, and Stephen J. Mihailov. 2025. "Characterization of the Second Harmonic Generation of Boron Nitride Nanotube Macroscopic Assemblies" Nanomaterials 15, no. 11: 861. https://doi.org/10.3390/nano15110861
APA StyleLu, P., Guan, J., Hnatovsky, C., Ding, H., Silva, K. D., Gaburici, L., Kingston, C., & Mihailov, S. J. (2025). Characterization of the Second Harmonic Generation of Boron Nitride Nanotube Macroscopic Assemblies. Nanomaterials, 15(11), 861. https://doi.org/10.3390/nano15110861







