Abstract
A numerical investigation of three-dimensional hybrid nanomaterial micropolar fluid flow across an exponentially stretched sheet is performed. Recognized similarity transformations are adopted to convert governing equations from PDEs into the set ODEs. The dimensionless system is settled by the operating numerical approach bvp4c. The impacts of the nanoparticle volume fraction, dimensionless viscosity ratio, stretching ratio parameter, and dimensionless constant on fluid velocity, micropolar angular velocity, fluid temperature, and skin friction coefficient in both x-direction and y-direction are inspected. Graphical outcomes are shown to predict the features of the concerned parameters into the current problem. These results are vital in the future in the branches of technology and industry. The micropolar function increases for higher values of the micropolar parameter and nanoparticle concentration. Micropolar function declines for higher values of the micropolar parameter and nanoparticle concentration. Temperature function is enhanced for higher values of solid nanoparticle concentration. Temperature function declines for higher values of the micropolar parameter. The range of the physical parameters are presented as: .
1. Introduction
The micropolar theory was inspected as a theoretical model, but currently, it is animated with several applications. Micropolar fluids, in particular, have found a niche in the field of modeling liquid crystals with magnetic fluids, stiff molecules, muddy liquids, and biological fluids [1]. The classical Navier–Stokes model is utilized to analyze the micropolar fluid, and the microrotation vector is extensively used to define microphenomena. In mathematics, the micropolar fluid model is studied in two opposite directions: one examines incompressible flow, and the other investigates compressible flows. Micropolar sap has been extensively studied for incompressible flow [2], but there are still several issues. The micropolar fluid for compressible flow has been deliberated in a few years (see [3,4,5,6]).
Hybrid nanofluids are a novel type of nanofluid that contains a finite range of metallic nanoparticles and nonmetallic nanoparticles. Using hydrogen reduction technique, Jeena et al. [7] organized a composite of alumina–copper from CuO and Al2O3 mixture. Suresh et al. [8] described a symbolic expansion in viscosity which increase in thermal conductivity was lower than the variation in thickness. Senthilraja et al. [9] observed the thermal conductivity of nanomaterial and hybrid nanomaterial experimentally with base fluid. For the hybrid nanofluids, natural convection causes a change in heat transfer as see in Refs. [10,11,12]. Suresh et al. [13] obtained a maximum Nusselt number augmentation of 13.56% for hybrid nanofluid. Hemmat et al. [14] used silver and magnesium with water-based hybrid nanofluid in the presence of the nanoparticle volume fraction, which lies between 0% and 2%. Moghadassi et al. [15] investigated the effects of and with base fluid water hybrid nanofluid with 0.1% volume fraction on laminar-driven convective heat transmission. In a porous medium, the natural convection of the hybrid nanofluids was examined by Mehryan et al. [16]. Ismael et al. [17] investigated the viscous dissipation and mixed convection of hybrid nanoparticles in a lid-driven cavity. Nadeem et al. [18] studied the effects of MHD with carbon nanofluid over curved surfaces. Nadeem and Abbas [19] highlighted the effects of a modified nanofluid model under time-dependent properties at porous surfaces. Nadeem et al. [20] discussed hybrid nanofluid over a curved surface. Awan et al. [21] worked at an unsteady oblique stagnation point for nanofluid. Awan et al. [22] highlighted the effects of an MHD unsteady oblique stagnation point for second-grade fluid at an oscillatory stretching surface. The micropolar fluid flow over a Riga surface was analyzed by Nadeem et al. [23]. Many researchers have conducted a lot of work on stretching surfaces; interested readers can see [24,25,26,27,28].
The current discussion talks about an steady, incompressible, three-dimensional boundary layer flow of micropolar hybrid nanofluid passing through an exponentially stretching sheet. Recognized similarity transformations are adopted to convert modeled equations from PDEs into a set of ODEs. The reconstructed equations are then solved by the operating numerical approach BVP4C. The impacts of the nanoparticle volume fraction, dimensionless viscosity ratio, stretching ratio parameter, and dimensionless constant on fluid velocity, micropolar angular speed, temperature gradient, and skin friction index in both and have been inspected through tables and graphs.
2. Mathematical Formulation
Here, a steady, incompressible, 3-D boundary layer flow of micropolar hybrid nanomaterial over an exponentially expanding sheet is taken into account, as revealed in Figure 1.
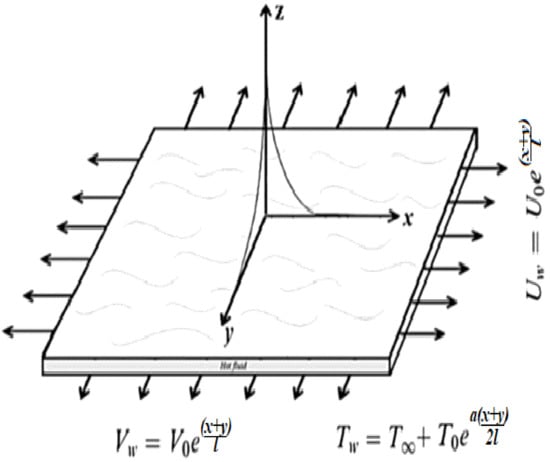
Figure 1.
Flow pattern of micropolar hybrid nanofluid.
We assumed that the temperature at the wall of the stretching sheet is , whereas and are velocities at the wall of the stretching sheet along -axis and -axis, respectively. Assumptions of the problem are as follows:
- Three-dimensional flow;
- Micropolar fluid;
- Two-phase model (nanofluid model);
- Exponential stretching sheet;
- Thermal slip.
The mathematical equations for three-dimensional flow are derived using boundary layer assumptions as (see [23,24,25]):
Associated boundary conditions for three-dimensional flow are:
Here,, and are the velocity components along and -axes, respectively. and are the constants, and is the reference length. and are the density and variable viscosity of hybrid nanomaterial, respectively; is the vortex viscosity; and are the microangular speeds; is the microinertia, which is defined as ; is the coefficient of kinematic viscosity; and is the hybrid nanofluids’ thermal conductivity, whereas is the specific heat capacity, and is a constant that belongs to the interval (0, 1). In the current work, we use m = 1/2. The rotational gradient viscosity of a hybrid nanofluid, indicated by is defined as:
Some physical properties such as viscosity, density, heat capacity and thermal conductivity for the hybrid nanofluid are expressed in the following Table 1.

Table 1.
Physical properties of hybrid nanofluid.
3. Similarity Variables
Suitable similarity transformations for three-dimensional flow are defined as (see [23,24,26]):
Making use of suitable transformations, which are defined in Equation (10), our original governing Equations (2)–(6) are transformed into a system of nonlinear ODEs as follows:
Related nondimensional boundary conditions for three-dimensional flow are defined as:
where all the derivatives are taken concerning and denoted by , is the dimensionless parameter, is the micropolar parameter, is the ratio of the stretching rate along the y-direction to the x-direction, is the Prandtl number, and and are two nanoparticles whose values are 0.1 and 0.01, respectively, constant in all scenarios. Now the coefficients of skin friction in -direction and -direction are defined as:
where and are defined as:
Making use of nondimensional variables, the physical parameters have the form
where the Reynolds number is .
4. Numerical Procedure
In this analysis, the steady, incompressible, 3-D boundary layer flow of the micropolar hybrid nanomaterial over the exponentially expanding sheet is taken into account. To solve the developing mathematical model and to solve the differential equations by using the bvp4c method after converting differential equations into first-order differential equations, thus the reduced higher-order differential system in the initial value problem. The procedure of the numerical technique is defined below:
Related nondimensional boundary conditions for three-dimensional flow are defined as:
5. Graphical Results and Discussion
Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 demonstrated the effects of different parameters, such as the nanoparticle volume fraction , dimensionless viscosity ratio , nondimensional constant , stretching ratio parameter on and . Figure 2a–d presented the effects of solid nanoparticle concentrations on the velocity functions () and micropolar functions (), respectively. It is noted that the velocity function increases for both profiles () due to higher values of solid nanoparticle concentrations. The momentum thickness enhances with increasing solid nanoparticles concentrations. The micropolar function increases for higher values of solid nanoparticle concentrations but declines the micropolar function because of higher values of solid nanoparticle concentrations, which are presented in Figure 2c,d. The variation of the micropolar parameter and velocity functions () and micropolar functions (), respectively, are presented in Figure 3a–d. It is noted that the velocity functions () increased due to higher values of the micropolar parameter, which is revealed in Figure 3a,b. As the vertex velocity was enhanced, the movement of the fluid was enhanced. The micropolar function is enhanced due to increasing values of the micropolar parameter. The micropolar function declines for higher values of the micropolar parameter. The variation of the stretching parameter and velocity functions () and micropolar functions (), respectively, is presented in Figure 4a–d. It is noted that the velocity functions () declined due to higher values of the stretching parameter, which is revealed in Figure 4a,b. The micropolar function declines due to increasing values of the stretching parameter, which is revealed in Figure 4c. The micropolar function enhances for higher values of the micropolar parameter, which is revealed in Figure 4d. The impacts of the nanoparticle volume fraction on temperature profile are demonstrated in Figure 5a. We noticed that for large values of , temperature function increases. Figure 5b shows the influence of on temperature function . It is examined that augmentation in decreases . Figure 6 signifies the influence of the stretching ratio factor on temperature function . It is observed that the nature of the stretching ratio parameter is the same as the nature of temperature function .
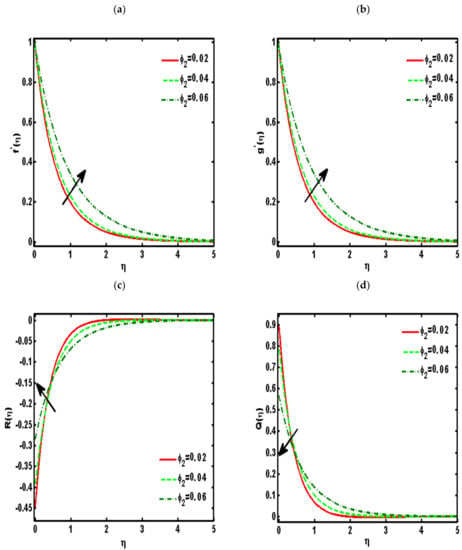
Figure 2.
Effects of the nanoparticle volume fraction on (a) (b) (c) (d) ().
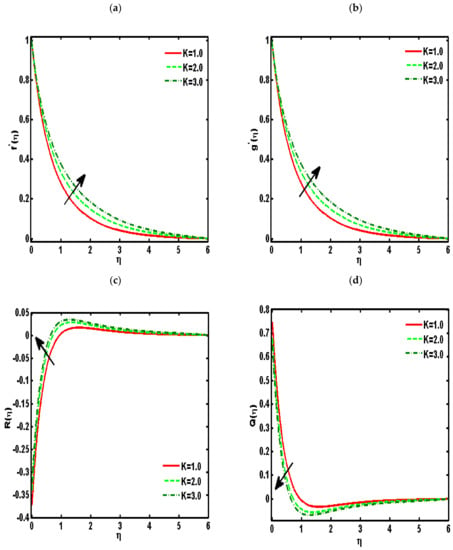
Figure 3.
Effects of the dimensionless viscosity ratio on (a) (b) (c) (d) . ().
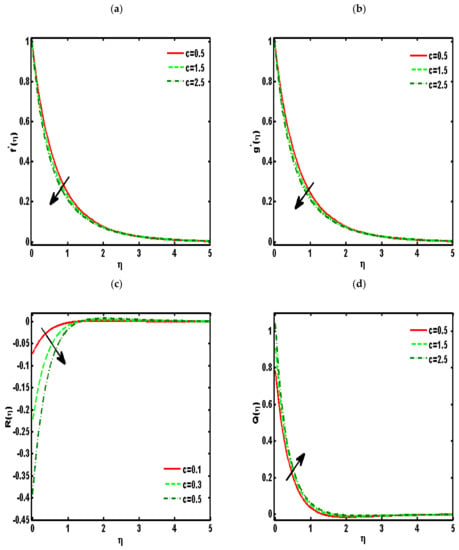
Figure 4.
Effects of the stretching ratio parameter on (a) (b) (c) (d) . ().
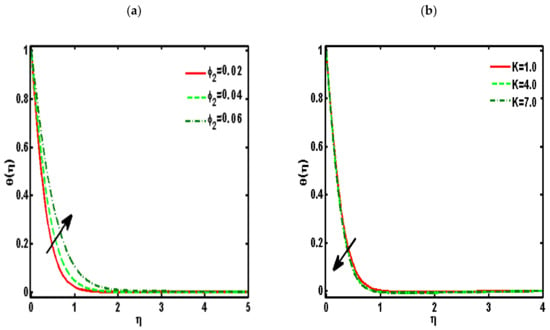
Figure 5.
Effects of the (a) nanoparticle volume fraction and (b) dimensionless viscosity ratio on temperature profile . ().
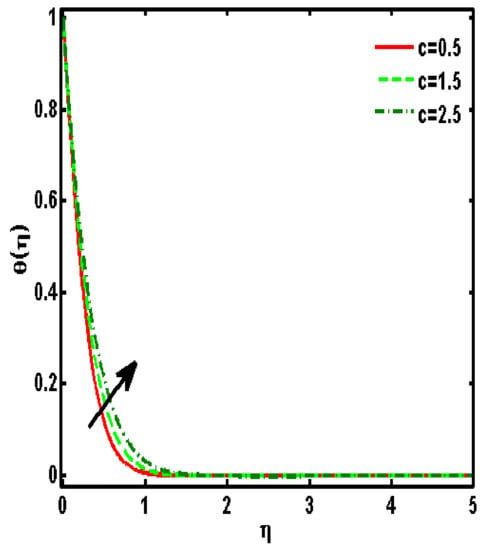
Figure 6.
Effects of the stretching ratio parameter on temperature profile . ().
In Table 2, the influences of various physical parameters, such as the nanoparticle volume concentration , micropolar parameter , nondimensional constant , and stretching ratio parameter , on the coefficient of skin friction along -direction and -direction are illustrated. In Table 2, it is analyzed that for large values of the nanoparticle volume fraction , the skin friction coefficient in both - and -directions declines. The effects of the dimensionless viscosity ratio on and are presented in Table 2. It is realized that increasing (K) decreases the skin friction coefficient in both - and - directions. The impacts of the stretching ratio parameter on and are demonstrated in Table 2. It is recognized that for large values of the stretching ratio parameter , the skin friction coefficient in both directions such that and shows a decaying nature. The effects of the nondimensional constant on the skin friction constant in both and are highlighted in Table 2. It is detected that with an increase in the nondimensional constant , there is no effect of on and such that and remains constant. In Table 3, our present work with Elbashbeshy et al. [29] and Sandeep et al. [30] is found to be in good agreement.

Table 2.
Numerical values of and for )/Water.

Table 3.
Comparison of the present work with Elbashbeshy et al. [29] and Sandeep et al. [30] when the rest of the physical parameters are zero.
6. Conclusions
In the current article, a numerical investigation of three-dimensional hybrid nanomaterial micropolar fluid flow across an exponentially stretched sheet is conducted. By utilizing some appropriate transformations, the system of PDEs is transfigured into the design of ODEs and then solved via the bvp4c technique. The influences of different parameters are demonstrated through tables and graphs. However, some conclusions can be drawn from the current study.
- The velocity function is enhanced due to higher values of the solid nanoparticle concentration.
- The velocity function is enhanced due larger values of the micropolar parameter.
- The micropolar function increases for higher values of the micropolar parameter and nanoparticle concentration.
- The micropolar function declines for higher values of the micropolar parameter and nanoparticle concentration.
- The temperature function is enhanced for higher values of the solid nanoparticle concentration.
- Temperature function declines for higher values of the micropolar parameter.
- A comparison of the present work with those of Elbashbeshy et al. [29] and Sandeep et al. [30] when the rest of the physical parameters to be considered are zero are shown in Table 3.
Author Contributions
Conceptualization, A.U.A. and N.A.; Methodology, P.L. and A.U.A.; Resources, P.L., A.A.-Z. and D.A.; Software, A.U.A. and A.A.-Z.; Validation, N.A., F.Z.D. and D.A.; Funding acquisition, A.A.-Z., F.Z.D. and D.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used to support the findings of this study are included within the article.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through research groups program under Grant No. R.G.P2/172/43.
Conflicts of Interest
Authors declared that they have no conflict of interest about this manuscript.
References
- Eringen, A.C. Microcontinuum Field Theories: II. Fluent Media; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; Volume 2. [Google Scholar]
- Lukaszewicz, G. Micropolar Fluids: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Qin, Y.; Liu, X.; Wang, T. The Cauchy Problem for a 1D Compressible Viscous Micropolar Fluid Model. In Global Existence and Uniqueness of Nonlinear Evolutionary Fluid Equations; Birkhäuser: Basel, Switzerland, 2015; pp. 113–141. [Google Scholar]
- Chen, M.; Xu, X.; Zhang, J. Global weak solutions of 3D compressible micropolar fluids with discontinuous initial data and vacuum. Commun. Math. Sci. 2015, 13, 225–247. [Google Scholar] [CrossRef]
- Su, J. Incompressible limit of a compressible micropolar fluid model with general initial data. Nonlinear Anal. Theory Methods Appl. 2016, 132, 1–24. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, P. Optimal time decay of the compressible micropolar fluids. J. Differ. Equ. 2016, 260, 7634–7661. [Google Scholar] [CrossRef]
- Jena, P.; Brocchi, E.; Motta, M. In-situ formation of Cu–Al2O3 nano-scale composites by chemical routes and studies on their microstructures. Mater. Sci. Eng. A 2001, 313, 180–186. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P.; Chandrasekar, M. Synthesis of Al2O3–Cu/water hybrid nanofluids using two step method and its thermo physical properties. Colloid. Surf. A Physicochem. Eng. Asp. 2011, 388, 41–48. [Google Scholar] [CrossRef]
- Senthilraja, S.; Vijayakumar, K.; Gangadevi, R. A comparative study on thermal conductivity of Al2O3/water, CuO/water and Al2O3–CuO/water nanofluids. Dig. J. Nanomater. Biostruct. 2015, 10, 1449–1458. [Google Scholar]
- Chamkha, A.; Doostanidezfuli, A.; Izadpanahi, E.; Ghalambaz, M. Phase-change heat transfer of single/hybrid nanoparticles-enhanced phase-change materials over a heated horizontal cylinder confined in a square cavity. Adv. Powder Technol. 2017, 28, 385–397. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Doostani, A.; Chamkha, A.J.; Ismael, M. Melting of nanoparticles-enhanced phase-change materials in an enclosure: Effect of hybrid nanoparticles. Int. J. Mech. Sci. 2017, 134, 85–97. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Doostani, A.; Izadpanahi, E.; Chamkha, A. Phase-change heat transfer in a cavity heated from below: The effect of utilizing single or hybrid nanoparticles as additives. J. Taiwan Inst. Chem. Eng. 2017, 72, 104–115. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P.; Chandrasekar, M. Effect of Al2O3–Cu/water hybrid nanofluid in heat transfer. Exp. Therm. Fluid Sci. 2012, 38, 54–60. [Google Scholar] [CrossRef]
- Esfe, M.H.; Arani, A.A.A.; Rezaie, M.; Yan, W.-M.; Karimipour, A. Experimental determination of thermal conductivity and dynamic viscosity of Ag–MgO/water hybrid nanofluid. Int. Commun. Heat Mass Transf. 2015, 66, 189–195. [Google Scholar] [CrossRef]
- Moghadassi, A.; Ghomi, E.; Parvizian, F. A numerical study of water based Al2O3 and Al2O3–Cu hybrid nanofluid effect on forced convective heat transfer. Int. J. Therm. Sci. 2015, 92, 50–57. [Google Scholar] [CrossRef]
- Mehryan, S.; Kashkooli, F.M.; Ghalambaz, M.; Chamkha, A.J. Free convection of hybrid Al2O3-Cu water nanofluid in a differentially heated porous cavity. Adv. Powder Technol. 2017, 28, 2295–2305. [Google Scholar] [CrossRef]
- Ismael, M.; Armaghani, T.; Chamkha, A.J. Mixed convection and entropy generation in a lid-driven cavity filled with a hybrid nanofluid and heated by a triangular solid. Heat Transf. Res. 2018, 49, 1645–1665. [Google Scholar] [CrossRef]
- Nadeem, S.; Ahmed, Z.; Saleem, S. Carbon nanotubes effects in magneto nanofluid flow over a curved stretching surface with variable viscosity. Microsyst. Technol. 2018, 25, 2881–2888. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N. Effects of MHD on Modified Nanofluid Model with Variable Viscosity in a Porous Medium. Nanofluid Flow Porous Media 2019, 69, 109–117. [Google Scholar]
- Nadeem, S.; Abbas, N.; Malik, M. Inspection of hybrid based nanofluid flow over a curved surface. Comput. Methods Programs Biomed. 2020, 189, 105193. [Google Scholar] [CrossRef]
- Awan, A.U.; Abid, S.; Abbas, N. Theoretical study of unsteady oblique stagnation point based Jeffrey nanofluid flow over an oscillatory stretching sheet. Adv. Mech. Eng. 2020, 12, 1687814020971881. [Google Scholar] [CrossRef]
- Awan, A.U.; Abid, S.; Ullah, N.; Nadeem, S. Magnetohydrodynamic oblique stagnation point flow of second grade fluid over an oscillatory stretching surface. Results Phys. 2020, 18, 103233. [Google Scholar] [CrossRef]
- Nadeem, S.; Malik, M.Y.; Abbas, N. Heat transfer of three-dimensional micropolar fluid on a Riga plate. Can. J. Phys. 2020, 98, 32–38. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F.; Abu-Hamdeh, N. Mixed convection due to rotating cylinder in an internally heated and flexible walled cavity filled with SiO2 –water nanofluids: Effect of nanoparticle shape. Int. Commun. Heat Mass Transf. 2016, 71, 9–19. [Google Scholar] [CrossRef]
- Gireesha, B.; Sowmya, G.; Khan, M.I.; Öztop, H.F. Flow of hybrid nanofluid across a permeable longitudinal moving fin along with thermal radiation and natural convection. Comput. Methods Programs Biomed. 2020, 185, 105166. [Google Scholar] [CrossRef] [PubMed]
- Gopal, D.; Saleem, S.; Jagadha, S.; Ahmad, A.; Almatroud, A.O.; Kishan, N. Numerical analysis of higher order chemical reaction on electrically MHD nanofluid under influence of viscous dissipation. Alex. Eng. J. 2021, 60, 1861–1871. [Google Scholar] [CrossRef]
- Xie, Y.; Meng, X.; Chang, Y.; Mao, D.; Yang, Y.; Xu, Y.; Wan, L.; Huang, Y. Ameliorating strength-ductility efficiency of graphene nanoplatelet-reinforced aluminum composites via deformation-driven metallurgy. Compos. Sci. Technol. 2021, 219, 109225. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, Y.; Zhang, F.; Lee, C.-S. A Novel Aluminum-Graphite Dual-Ion Battery. Adv. Energy Mater. 2016, 6, 1502588. [Google Scholar] [CrossRef] [Green Version]
- Elbashbeshy, E.M.; Emam, T.; Abdelgaber, K. Effects of thermal radiation and magnetic field on unsteady mixed convection flow and heat transfer over an exponentially stretching surface with suction in the presence of internal heat generation/absorption. J. Egypt. Math. Soc. 2012, 20, 215–222. [Google Scholar] [CrossRef] [Green Version]
- Sandeep, N.; Sulochana, C.; Kumar, B.R. Unsteady MHD radiative flow and heat transfer of a dusty nanofluid over an exponentially stretching surface. Eng. Sci. Technol. Int. J. 2016, 19, 227–240. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).