Effects of Hall Current and Viscous Dissipation on Bioconvection Transport of Nanofluid over a Rotating Disk with Motile Microorganisms
Abstract
1. Introduction
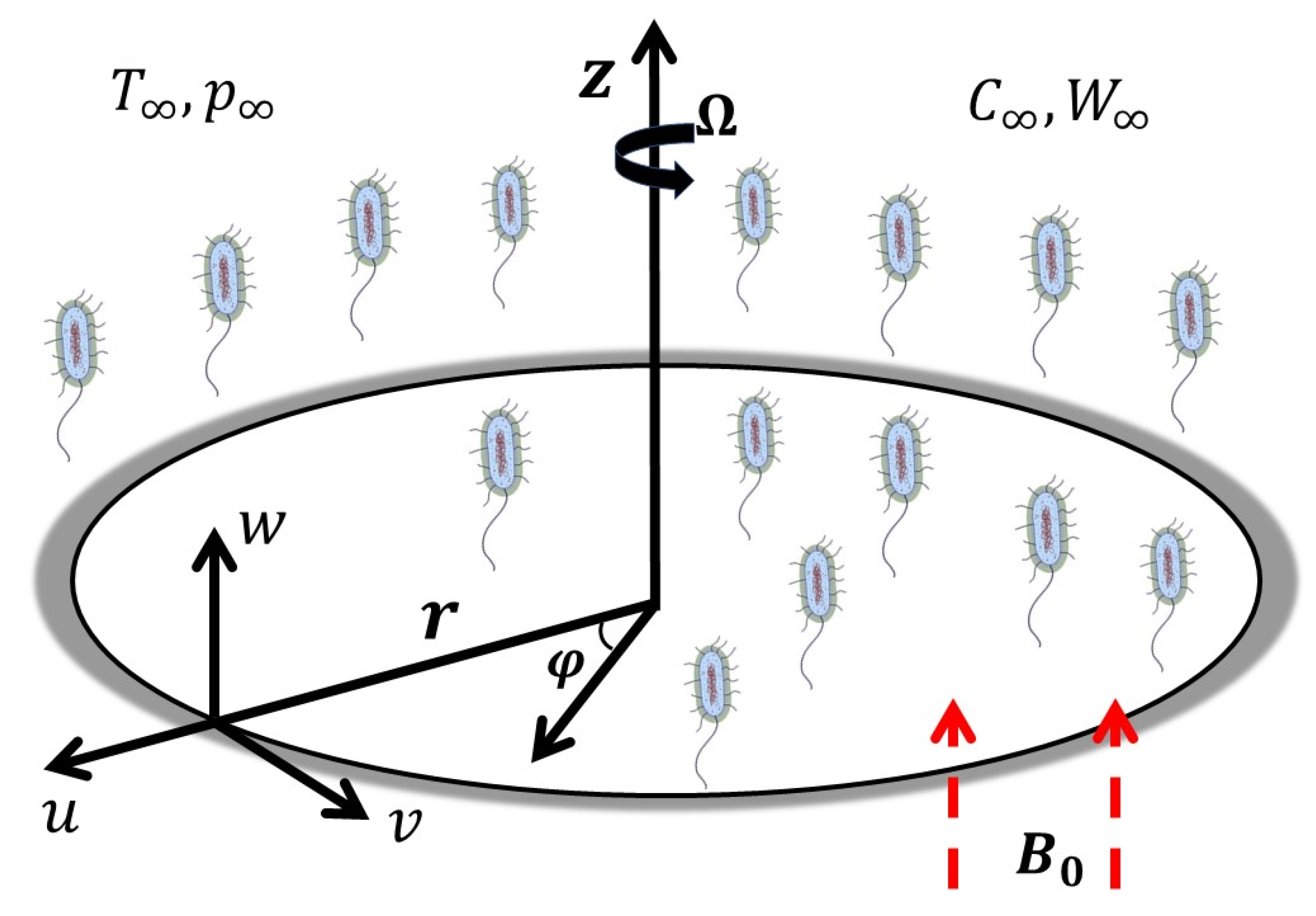
2. Formulation of the Problem
3. Numerical Approach
4. Results and Discussion
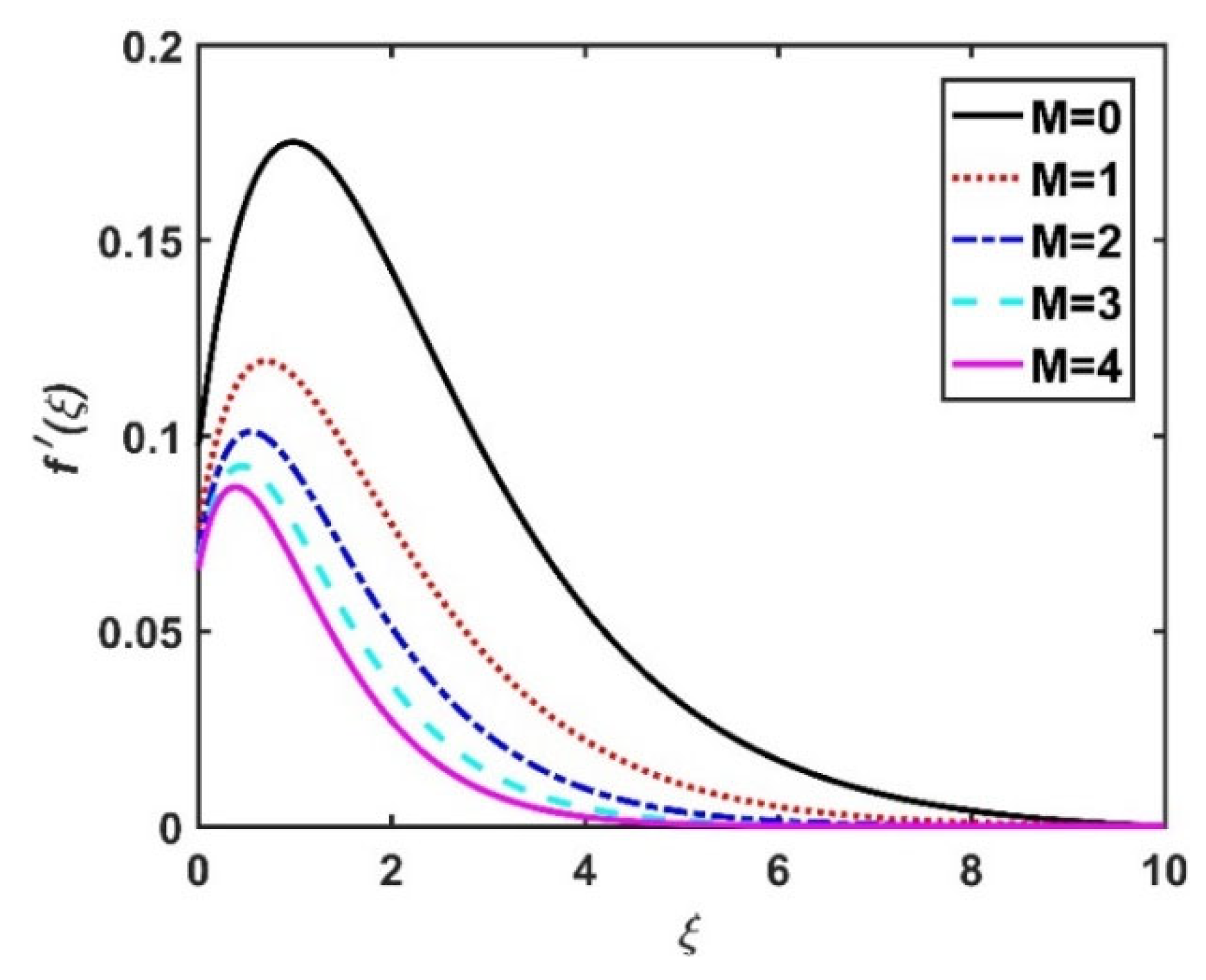
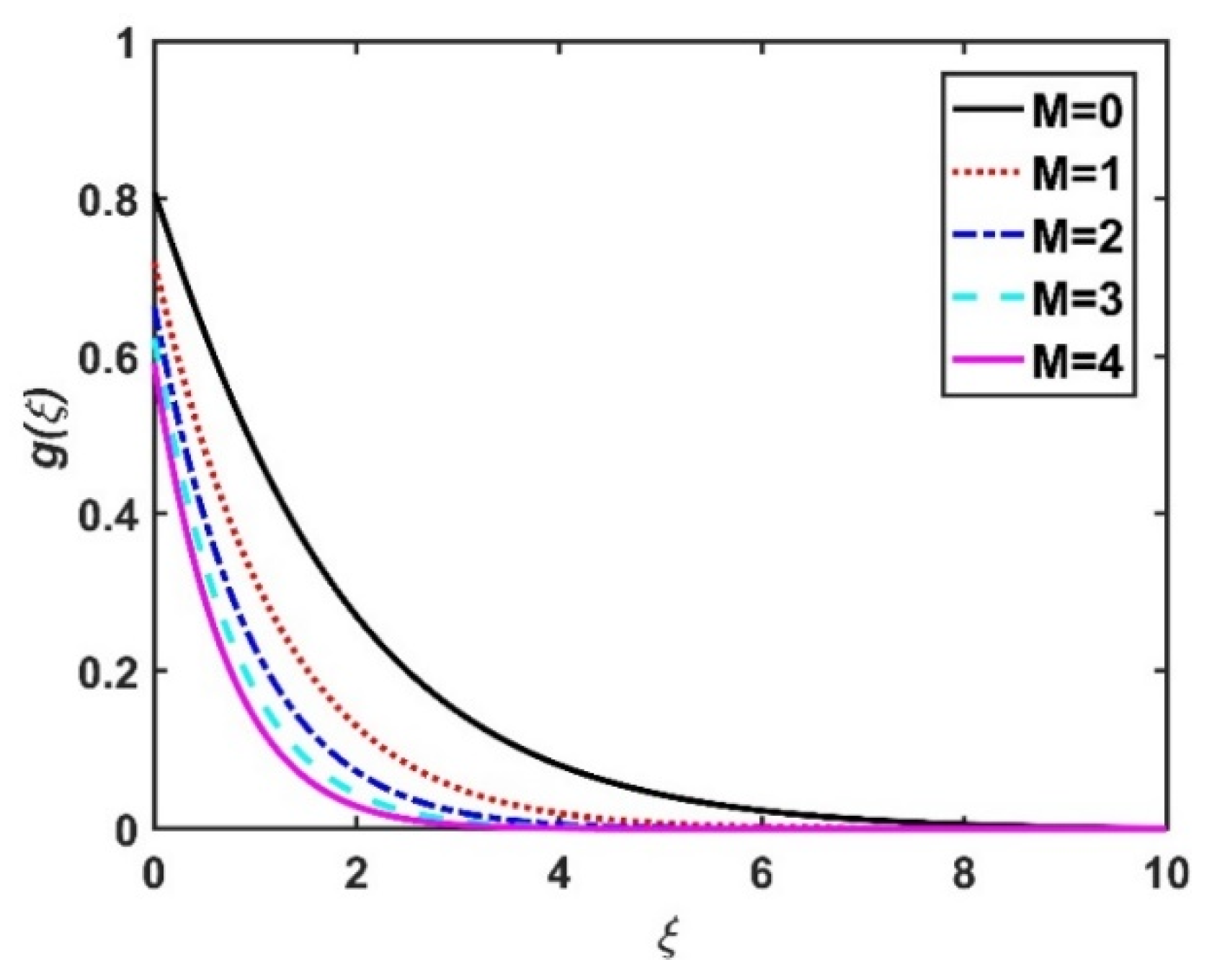
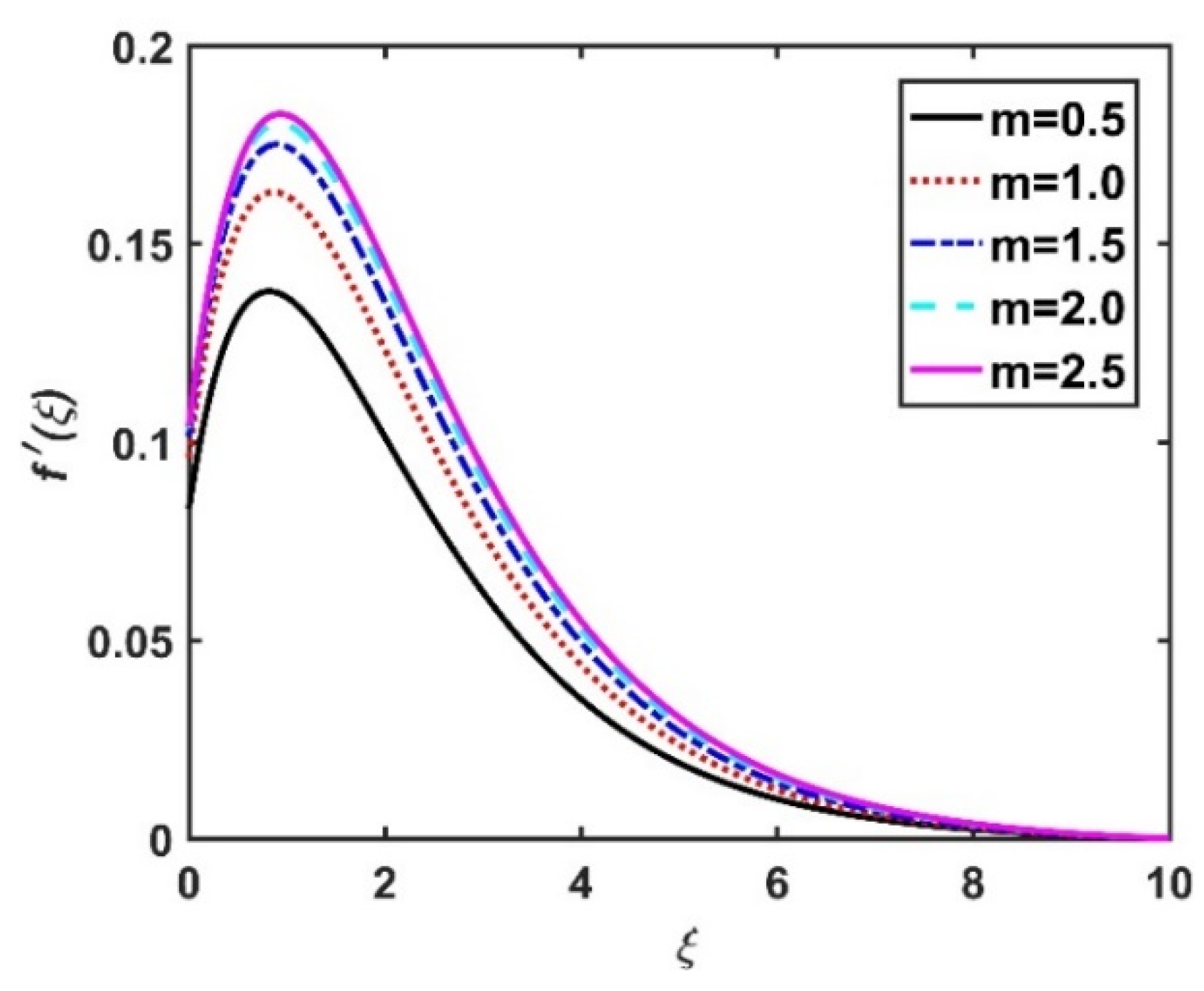
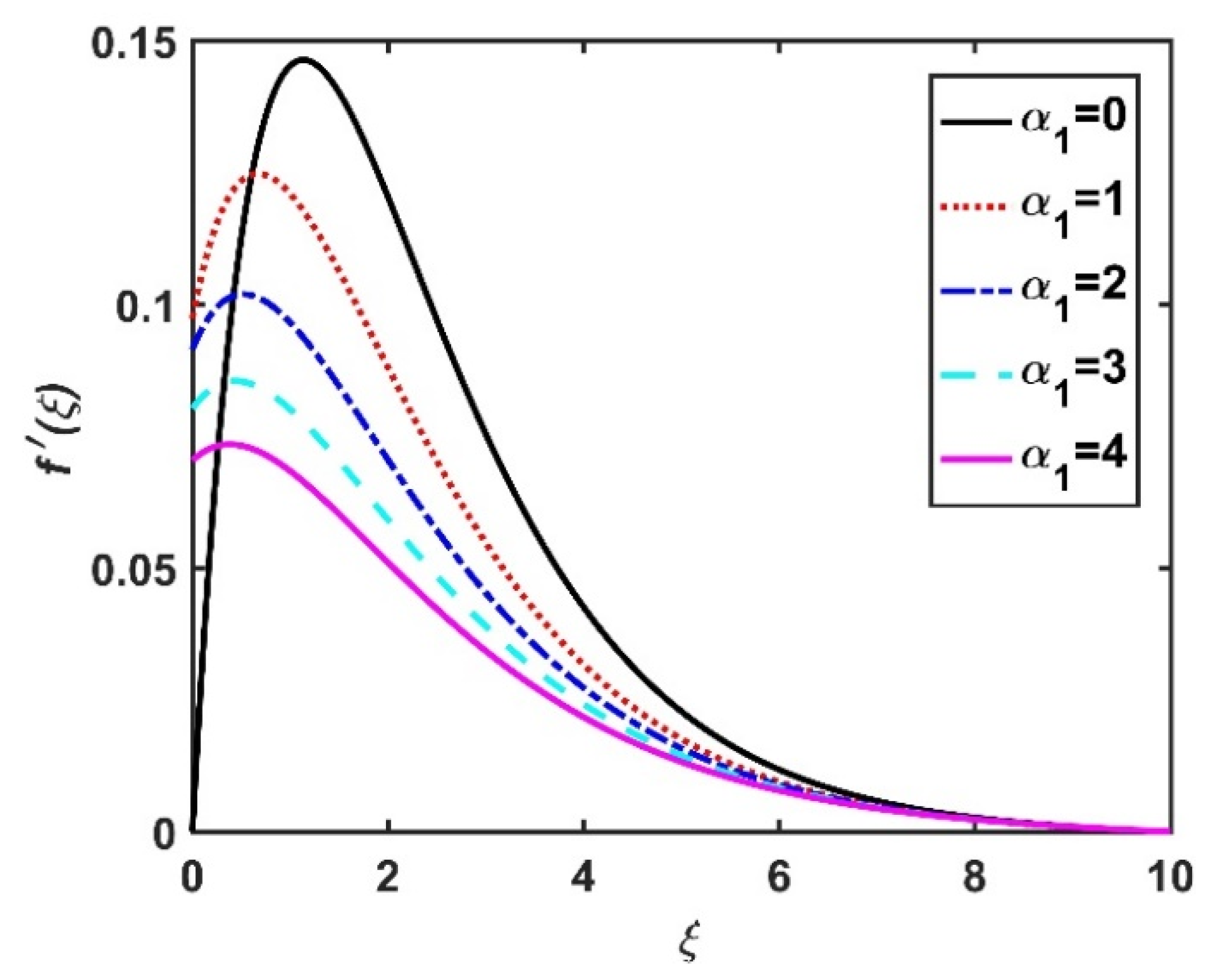
4.1. Velocity Profiles ()
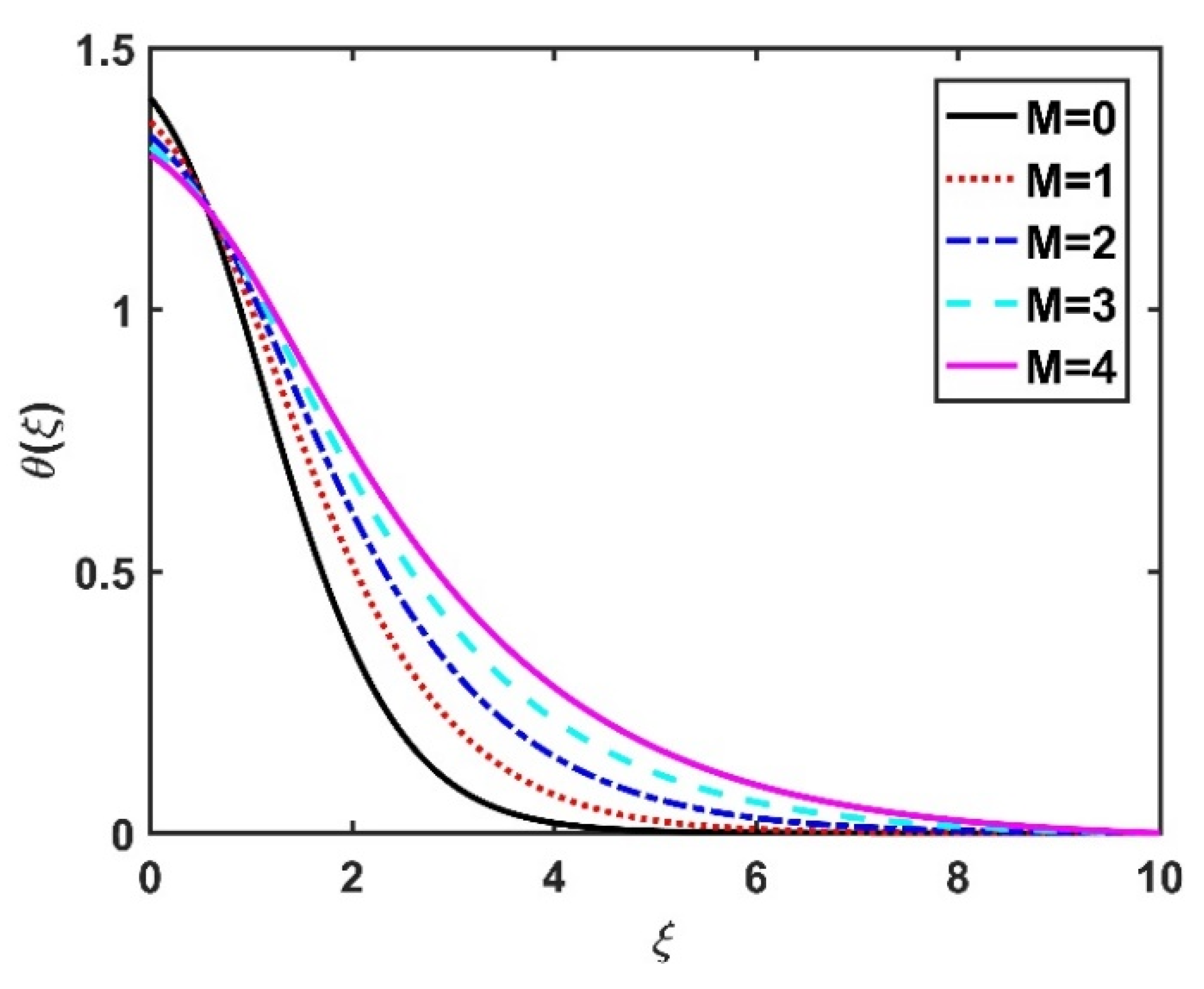
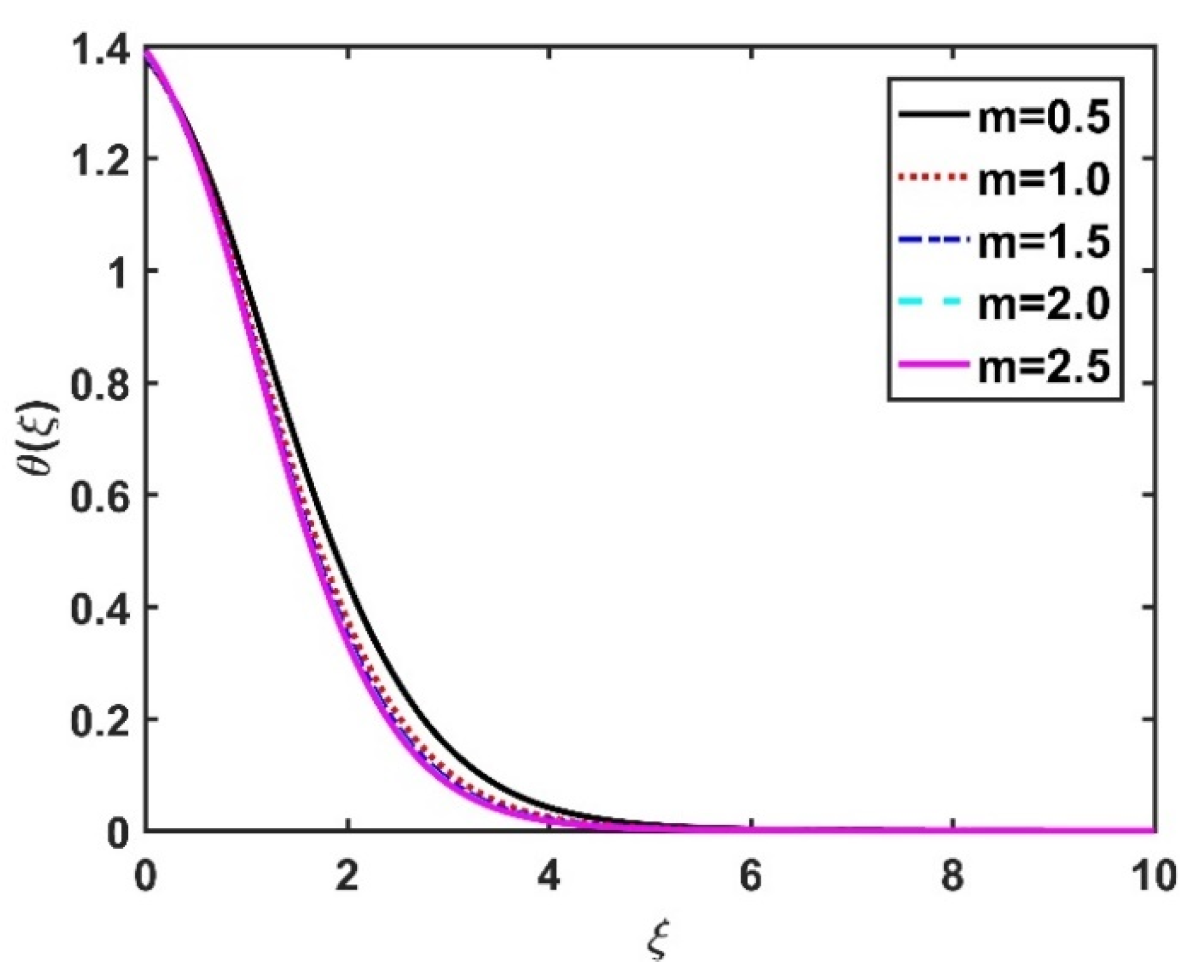
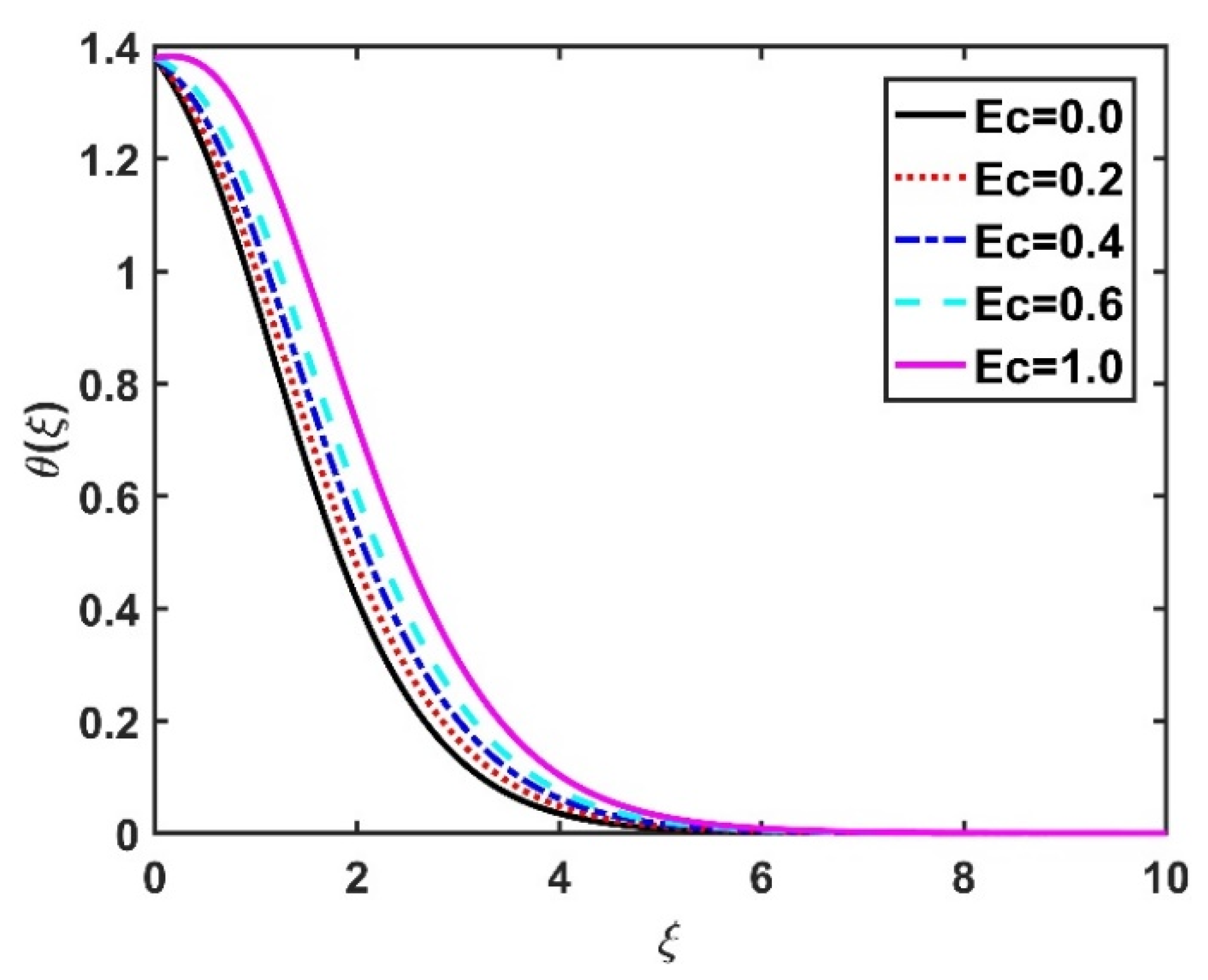
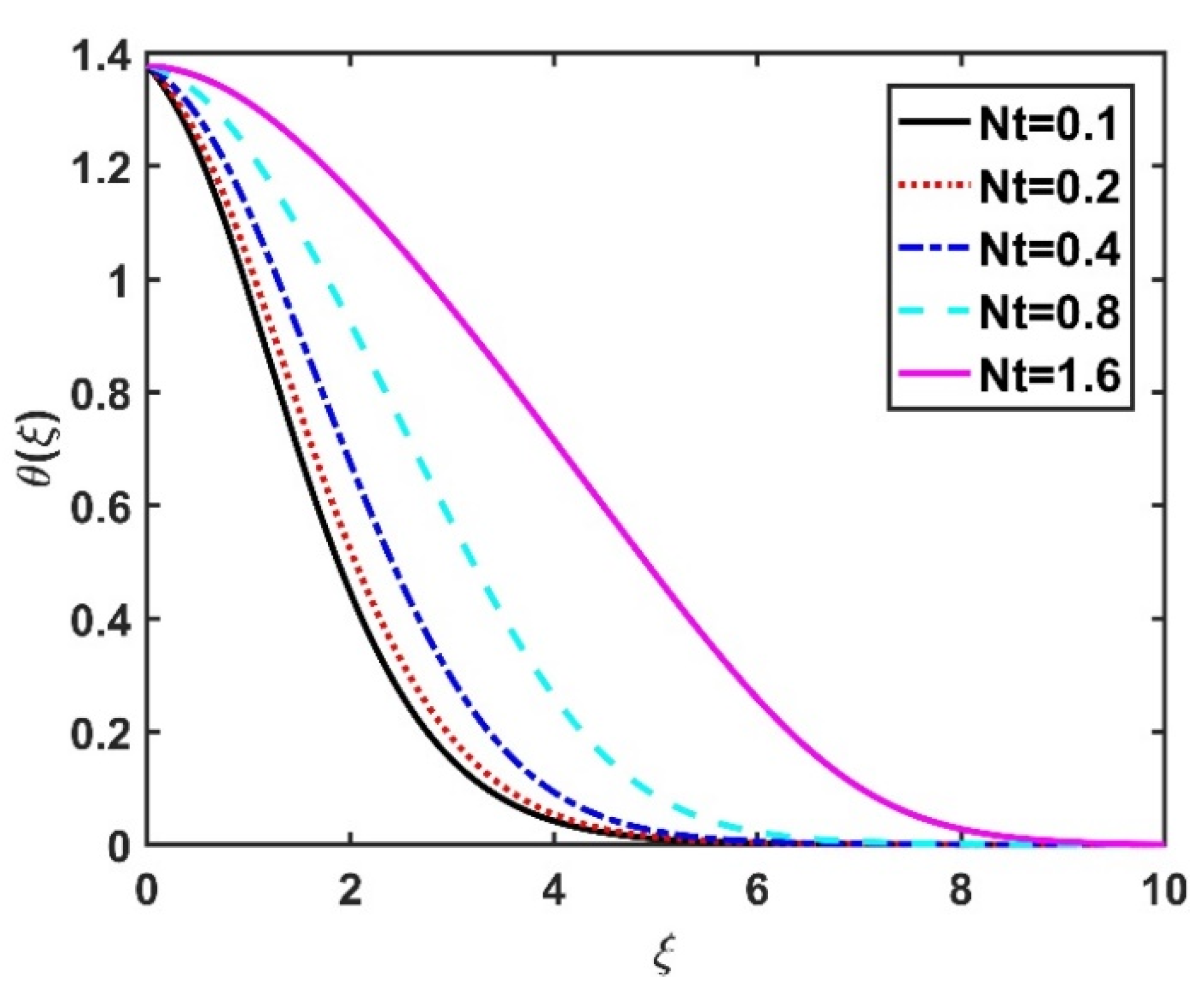
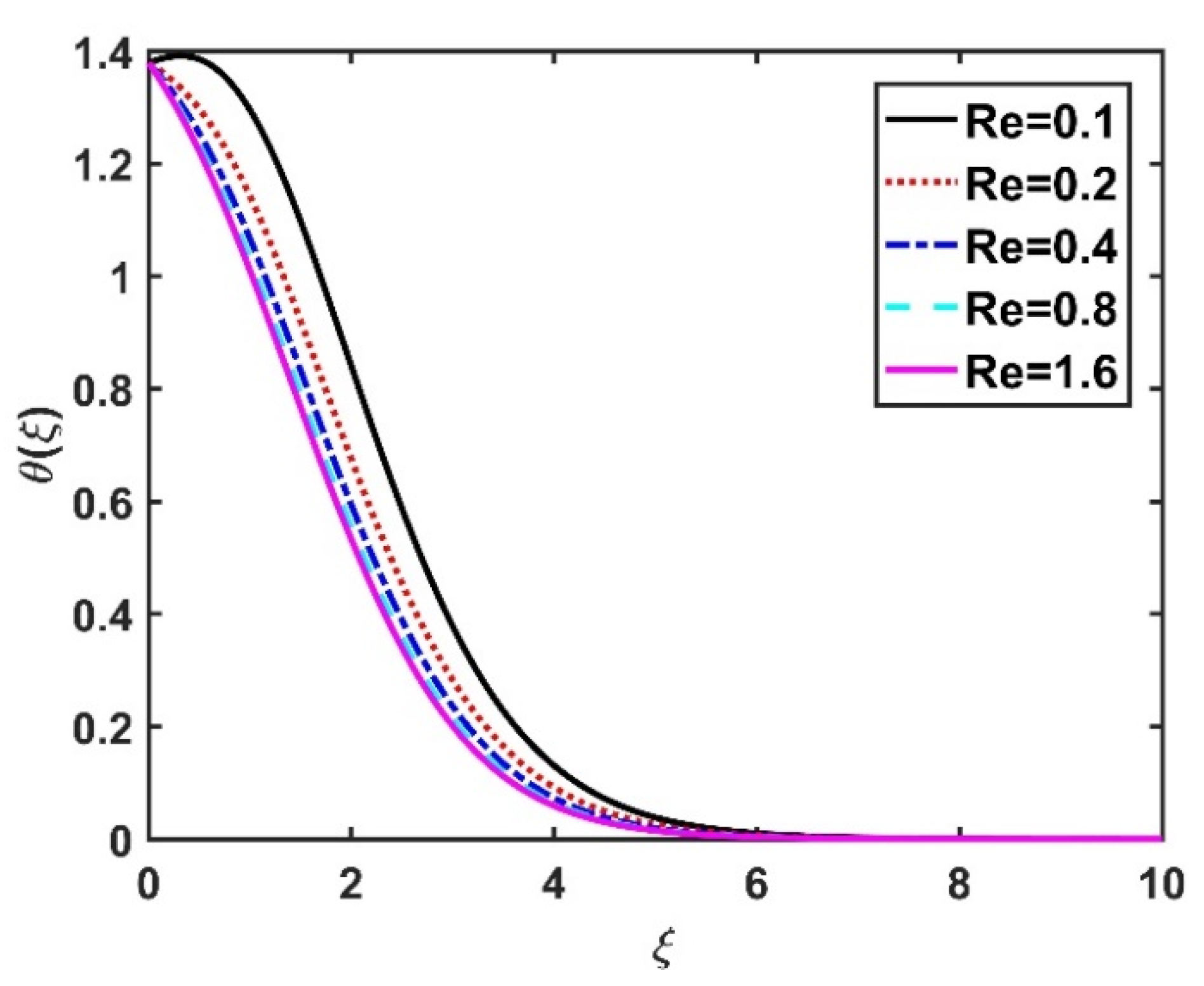
4.2. Temperature Profile ()
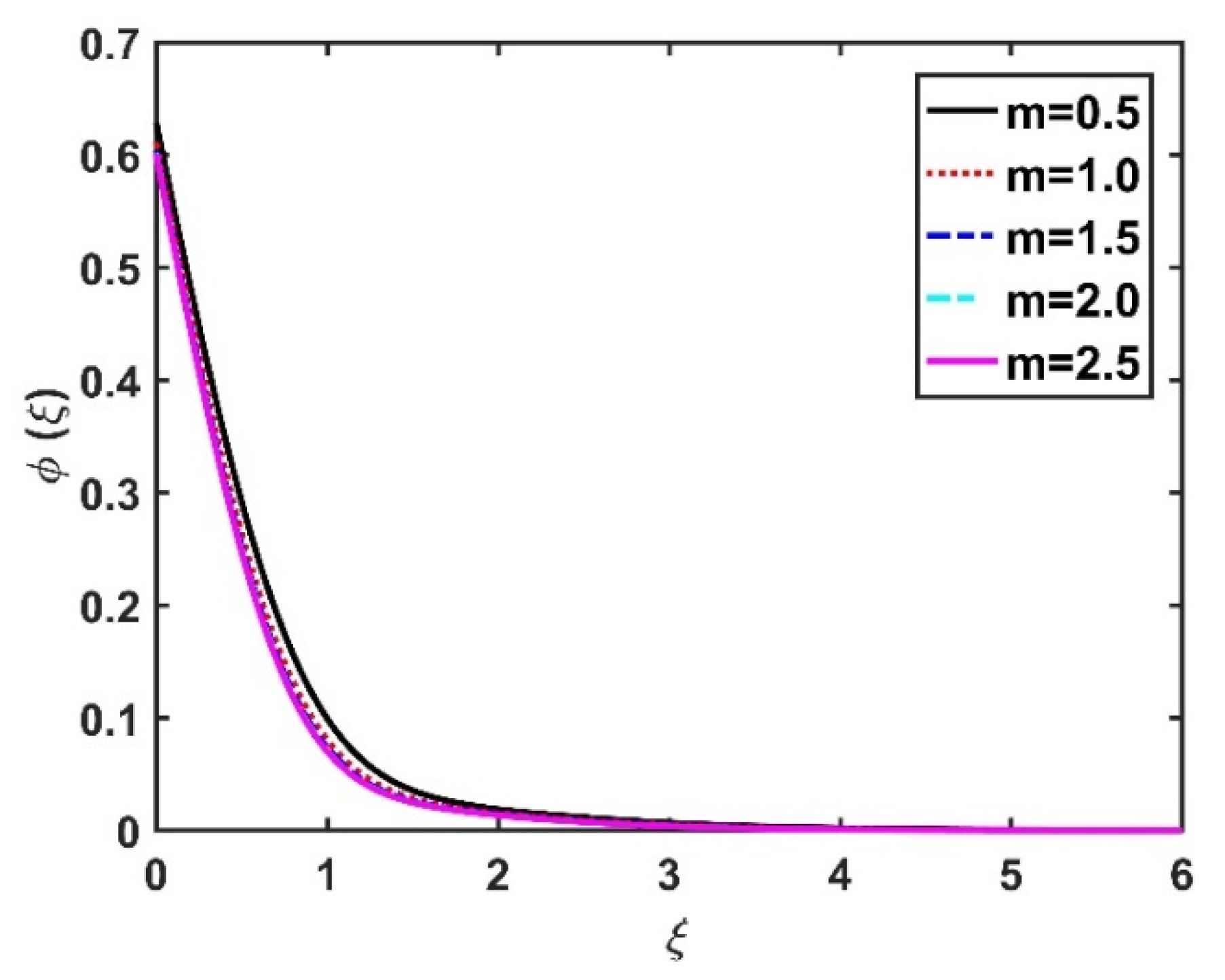
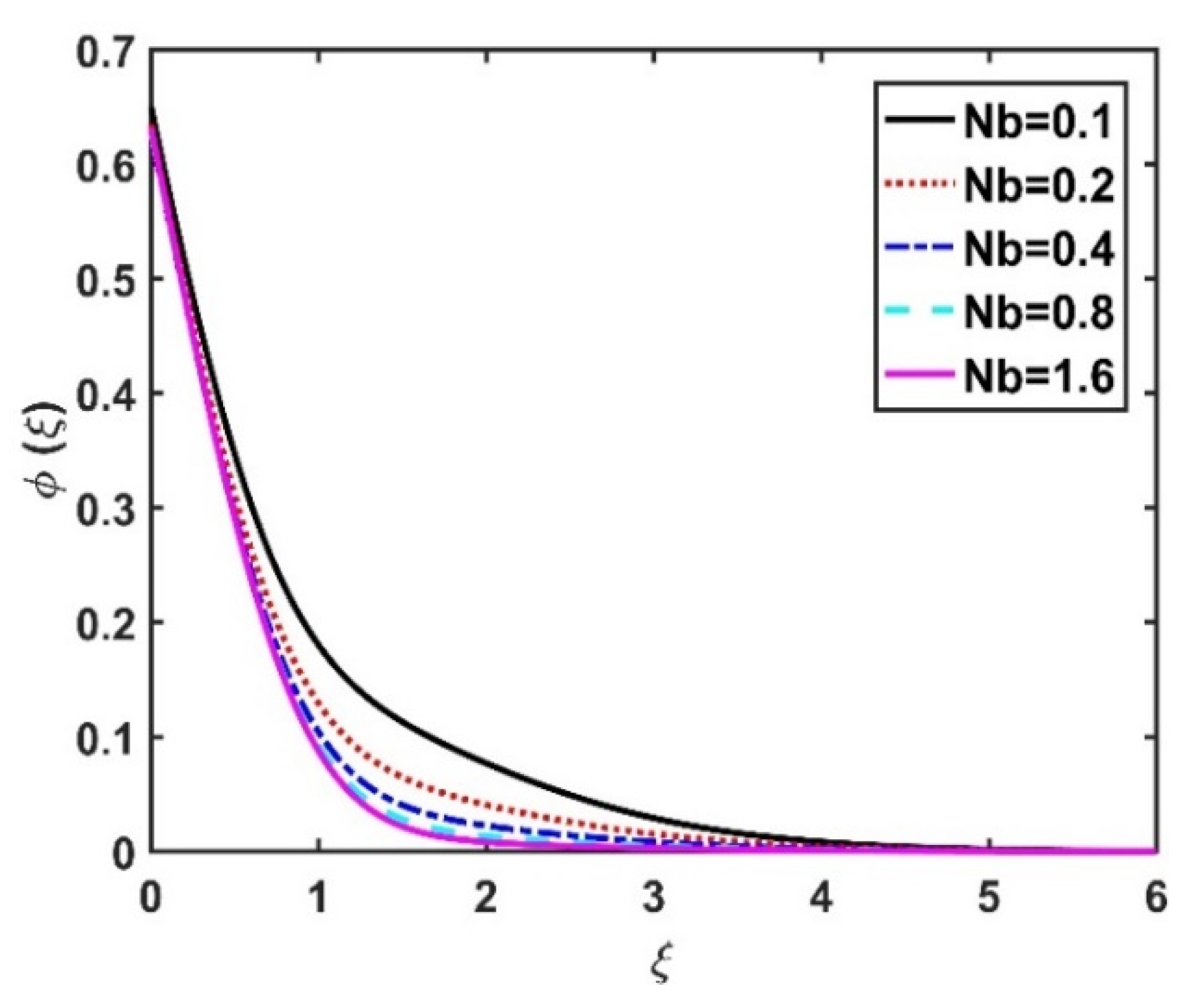
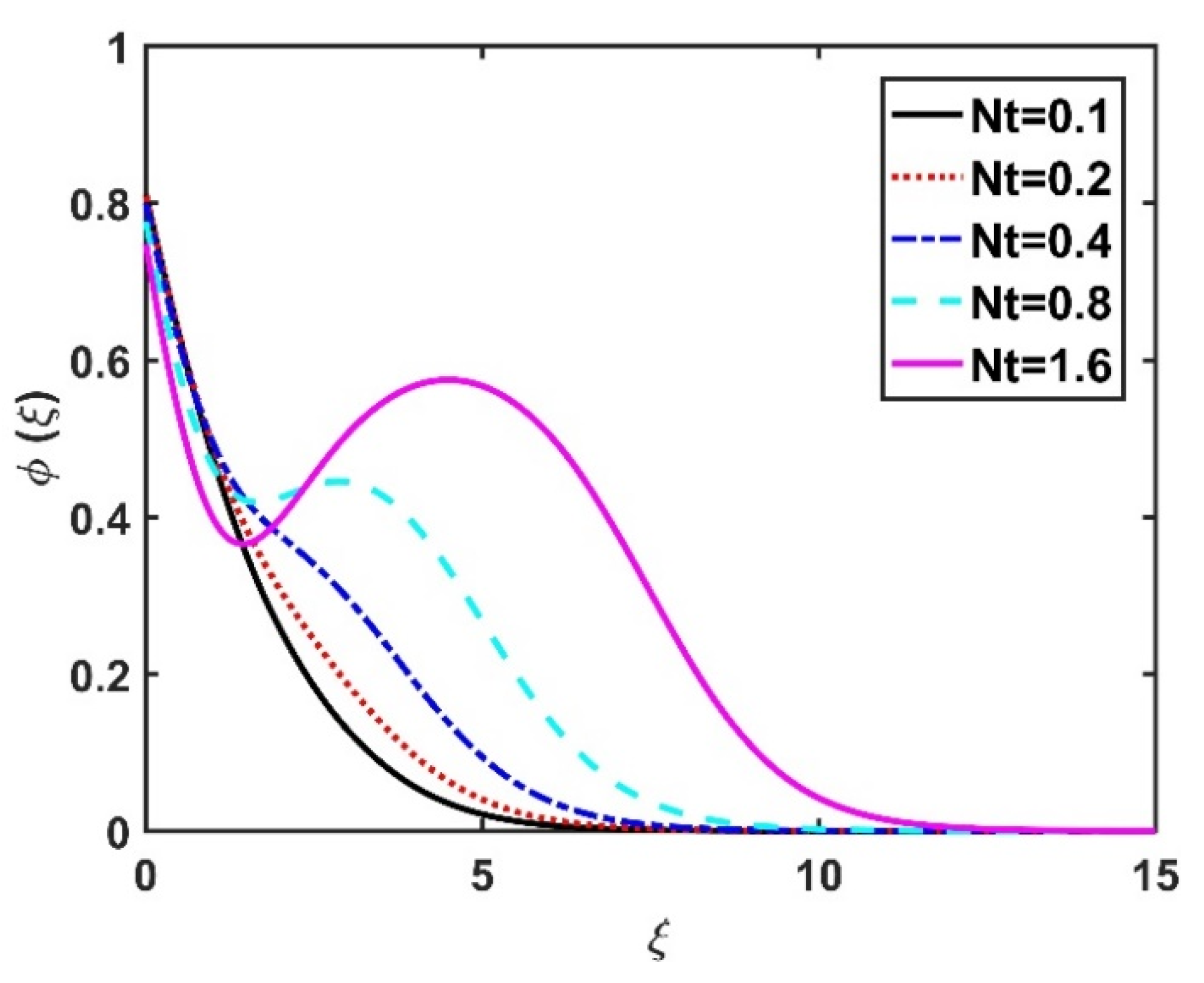
4.3. Nanoparticle Concentration Profile ()
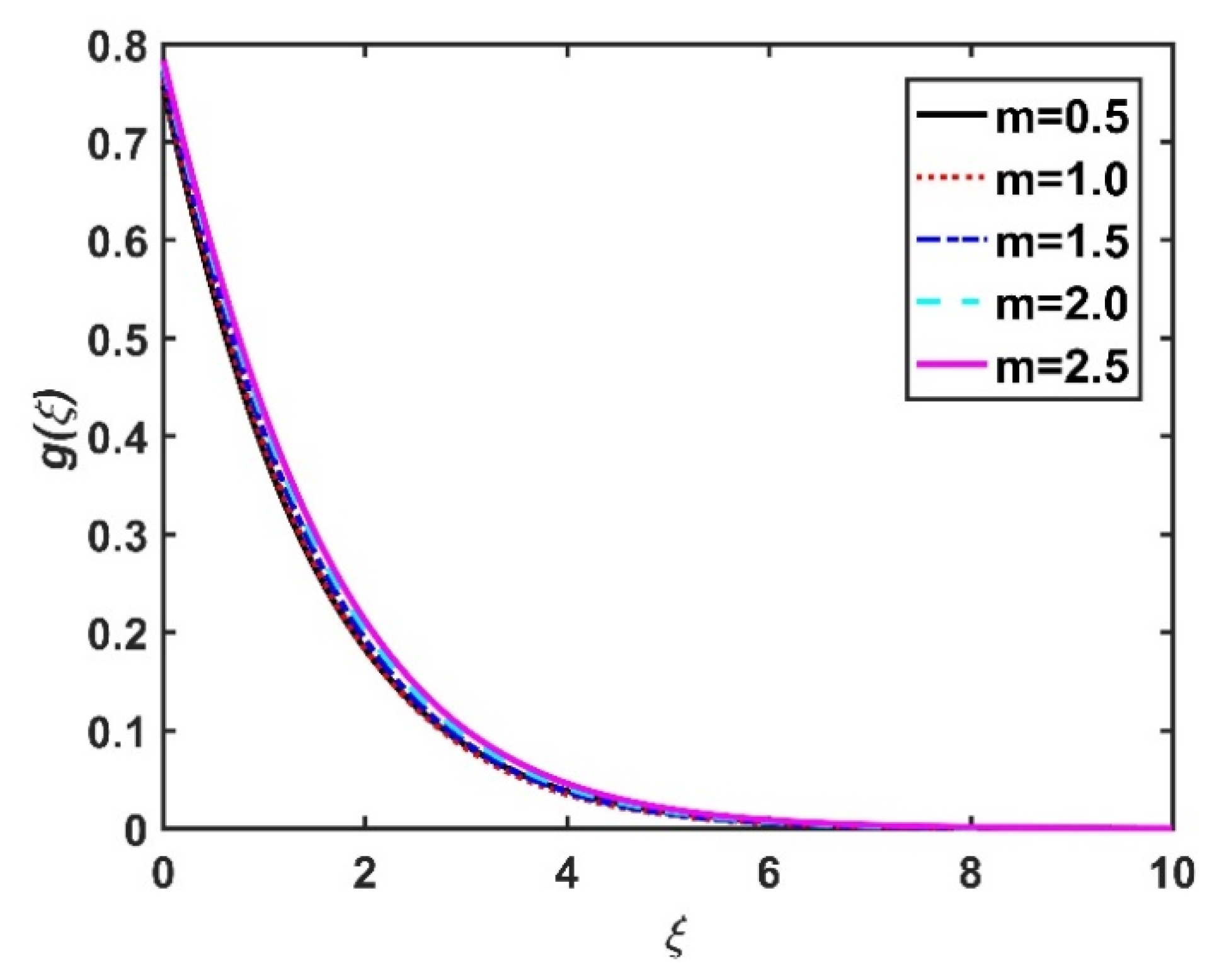
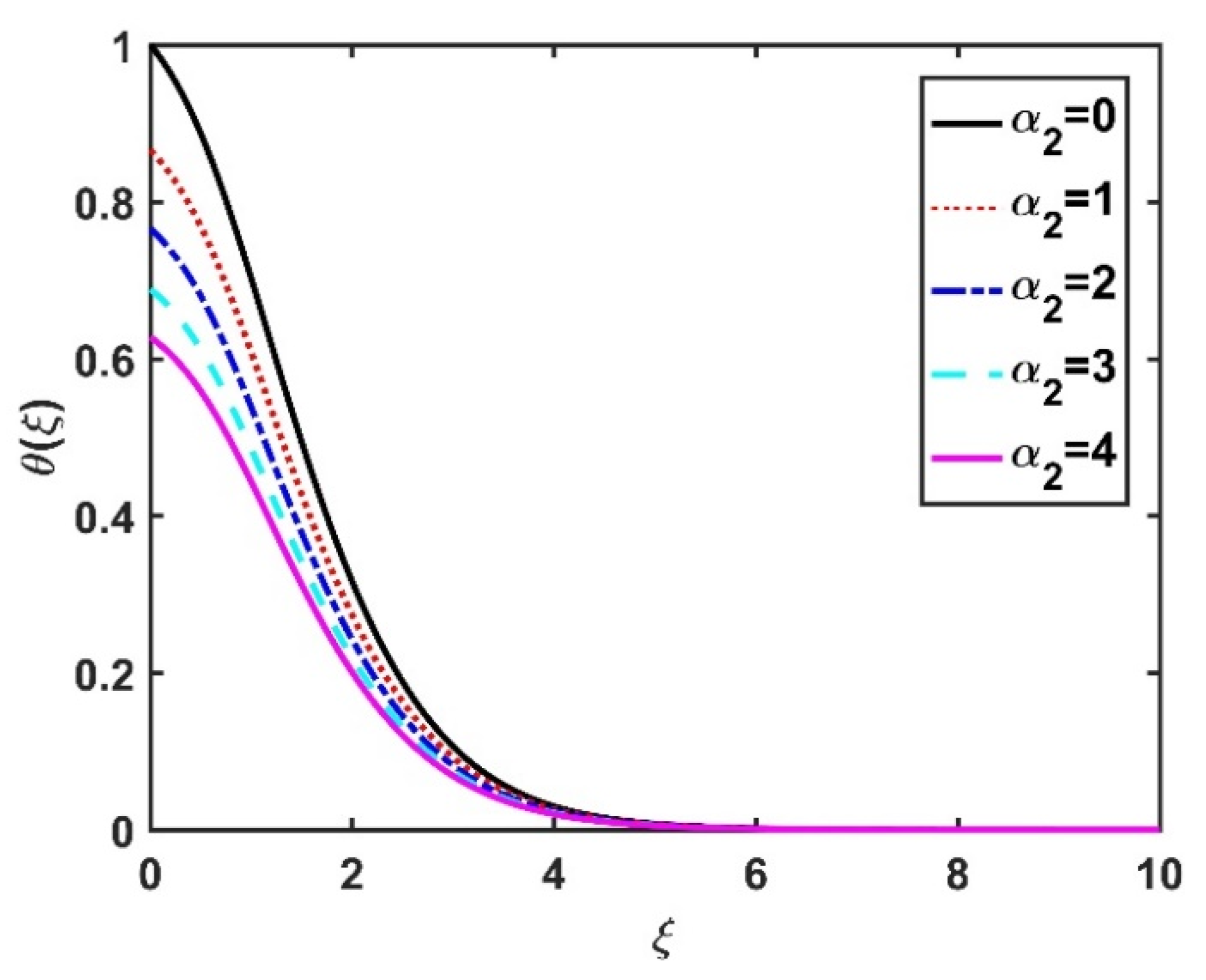
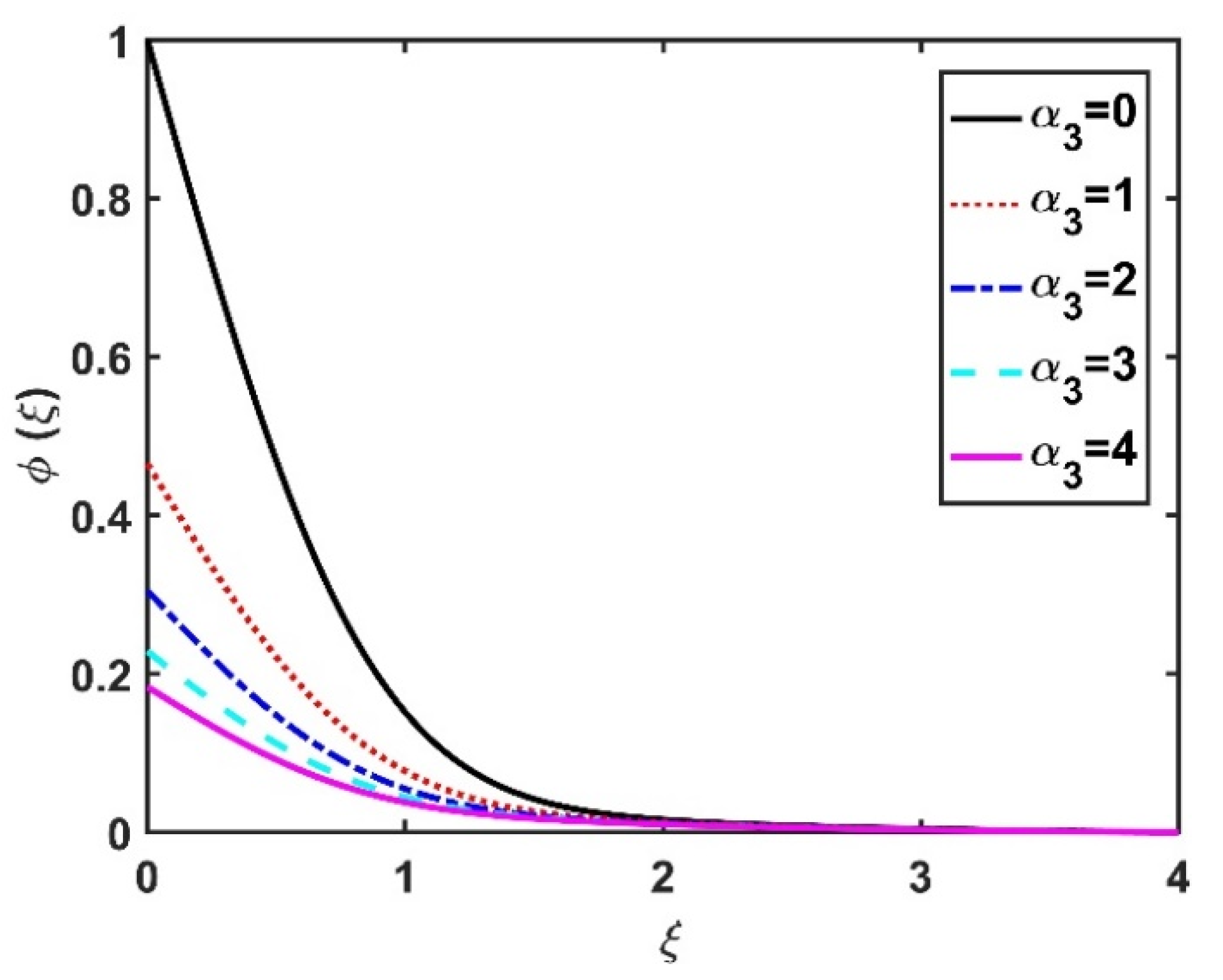
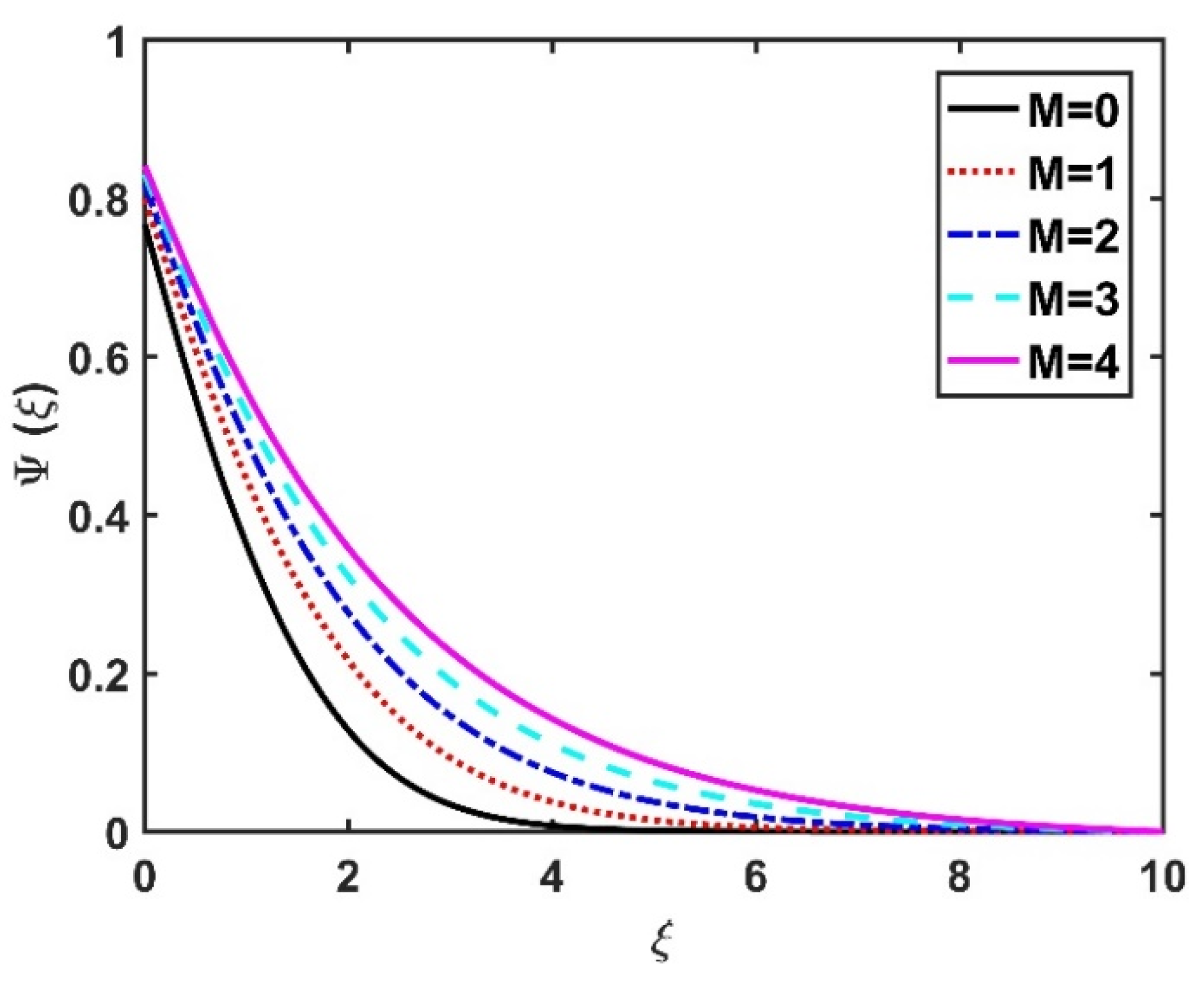
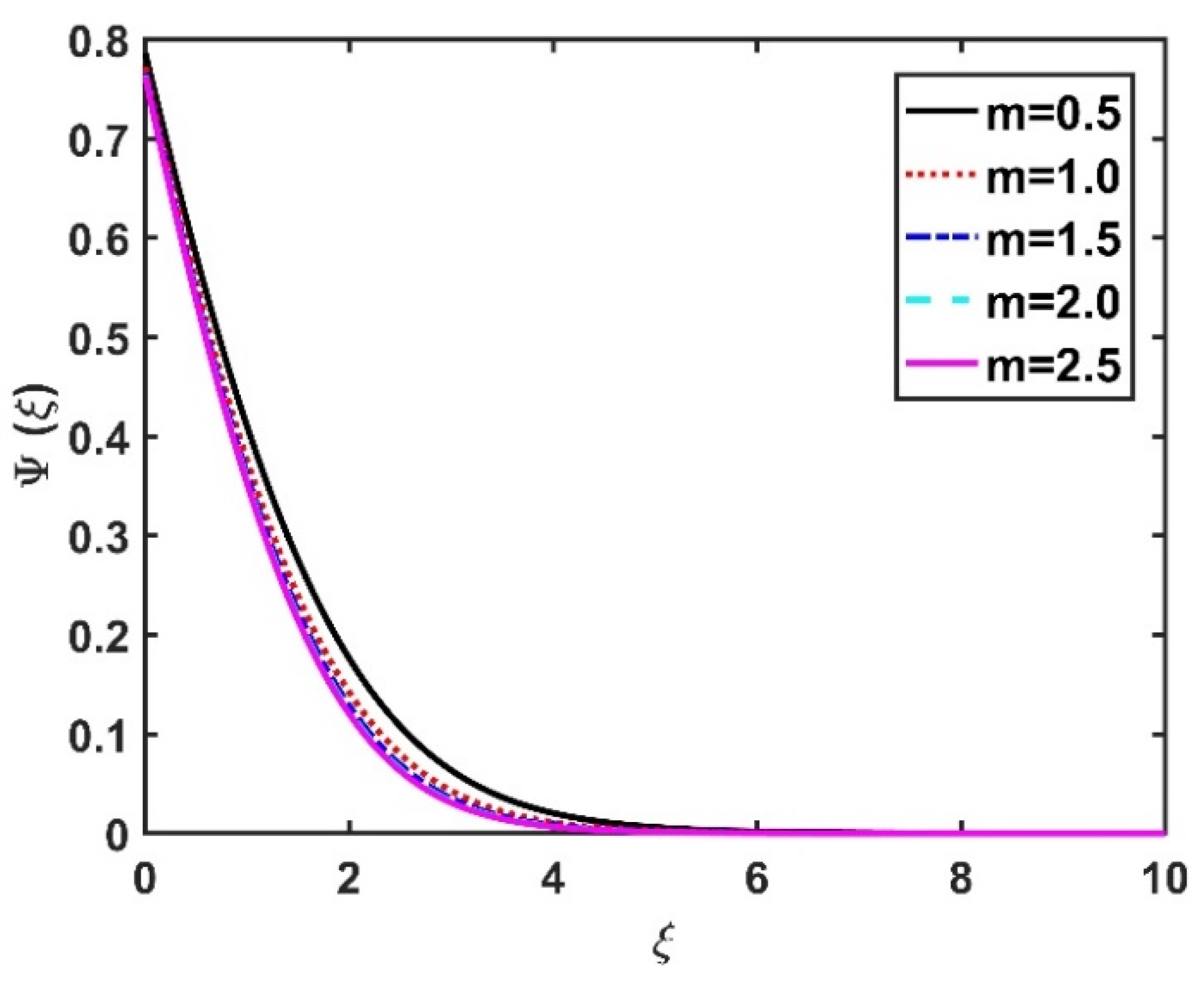
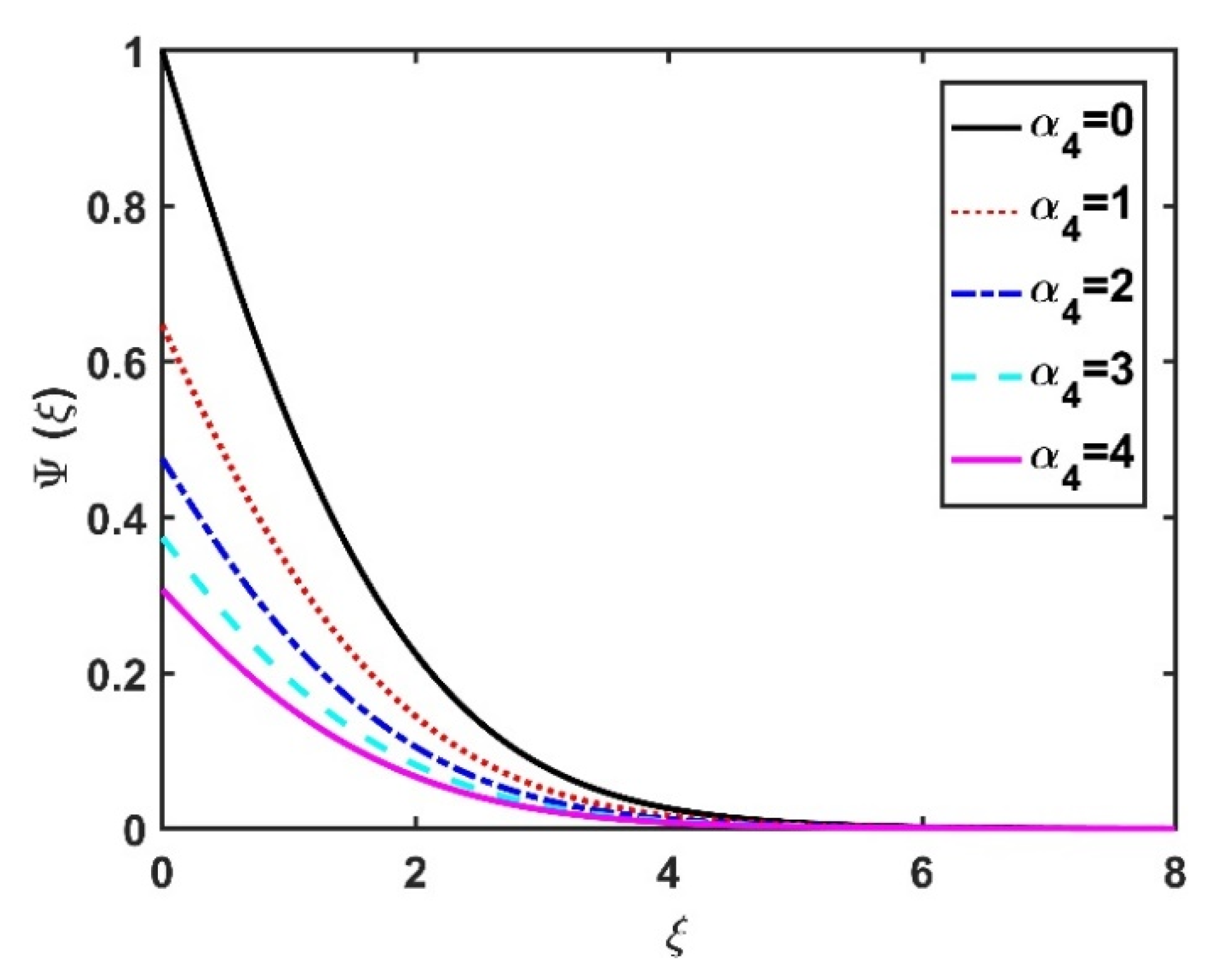
4.4. Motile Microorganism Profile ()
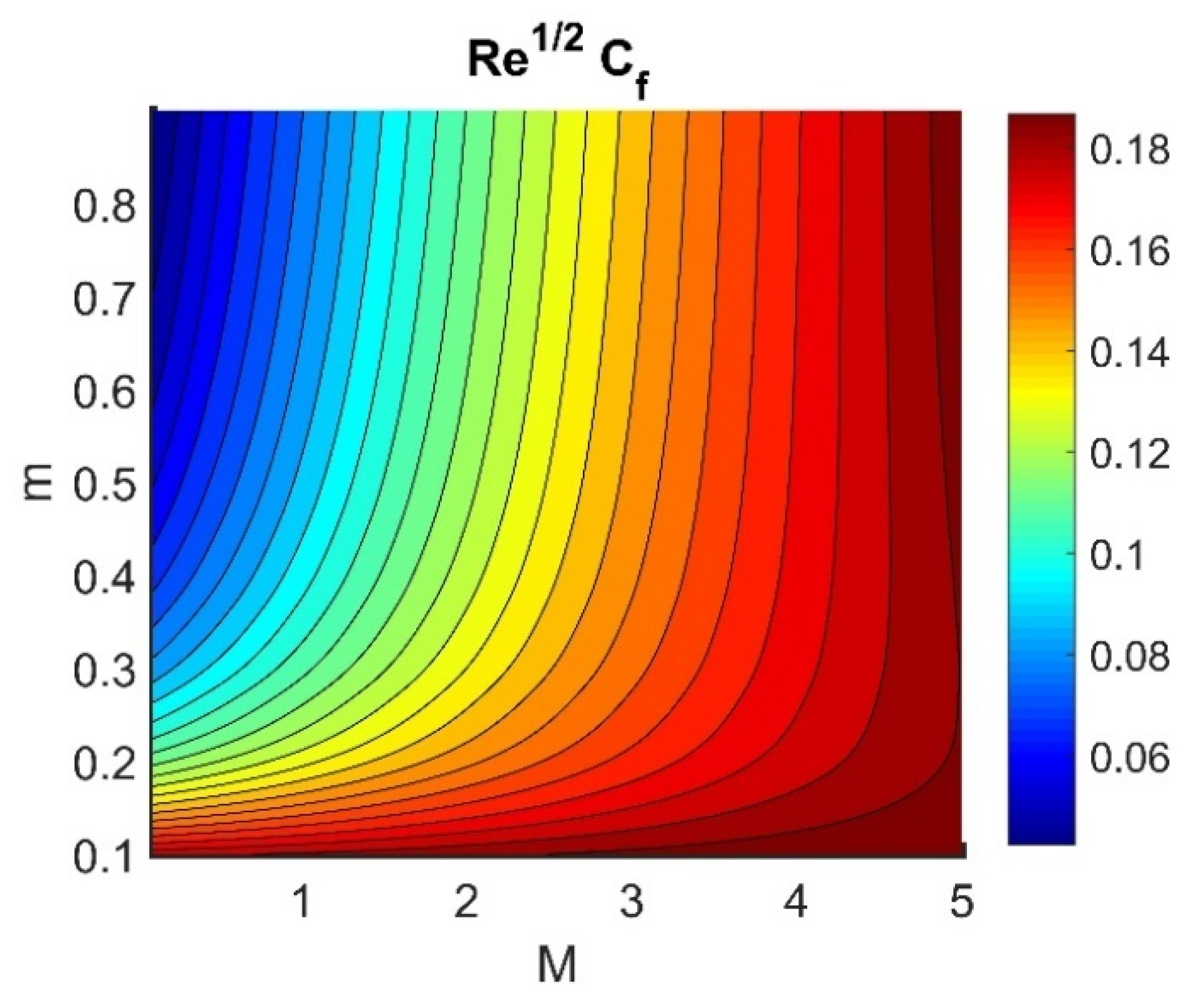
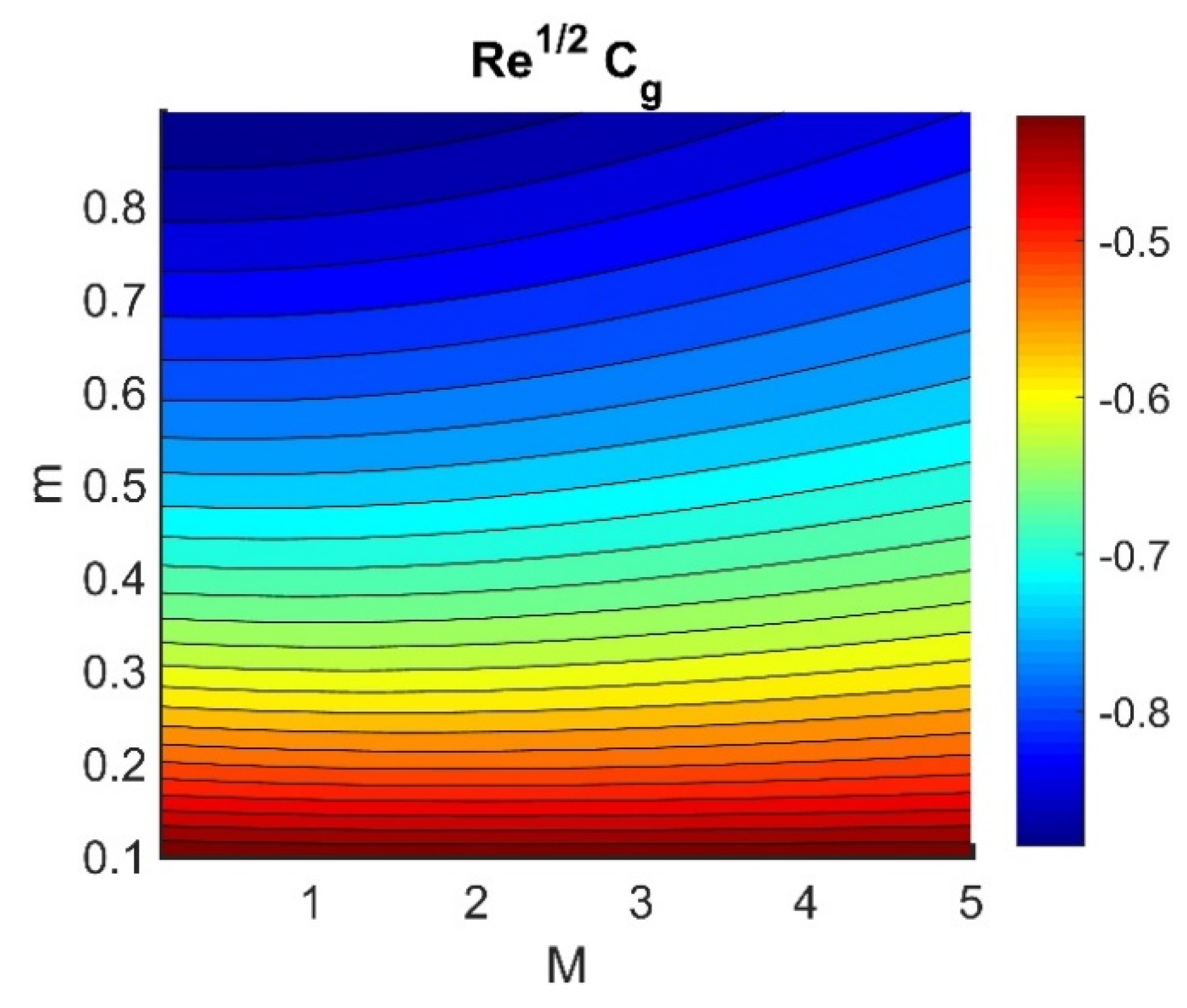
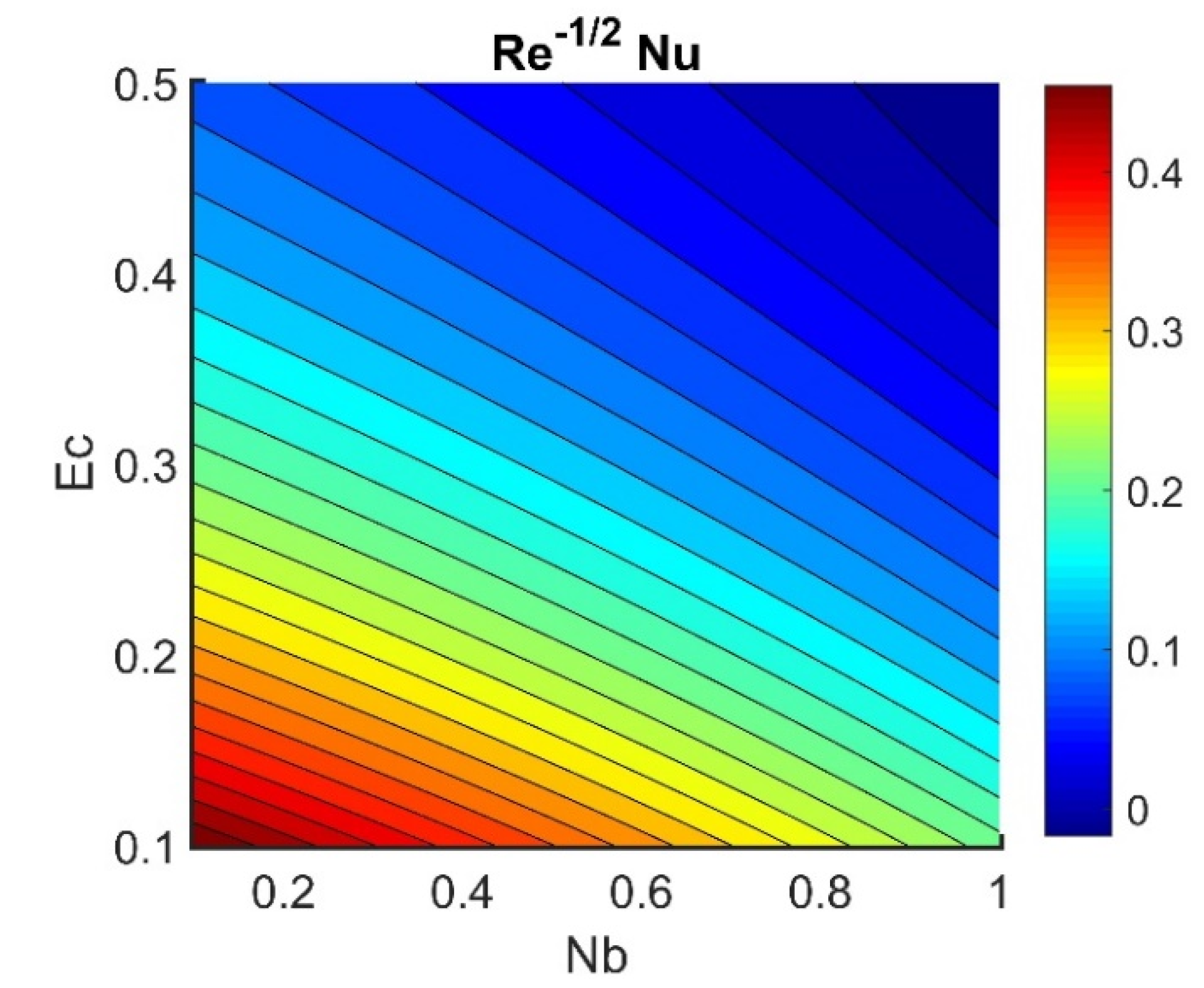
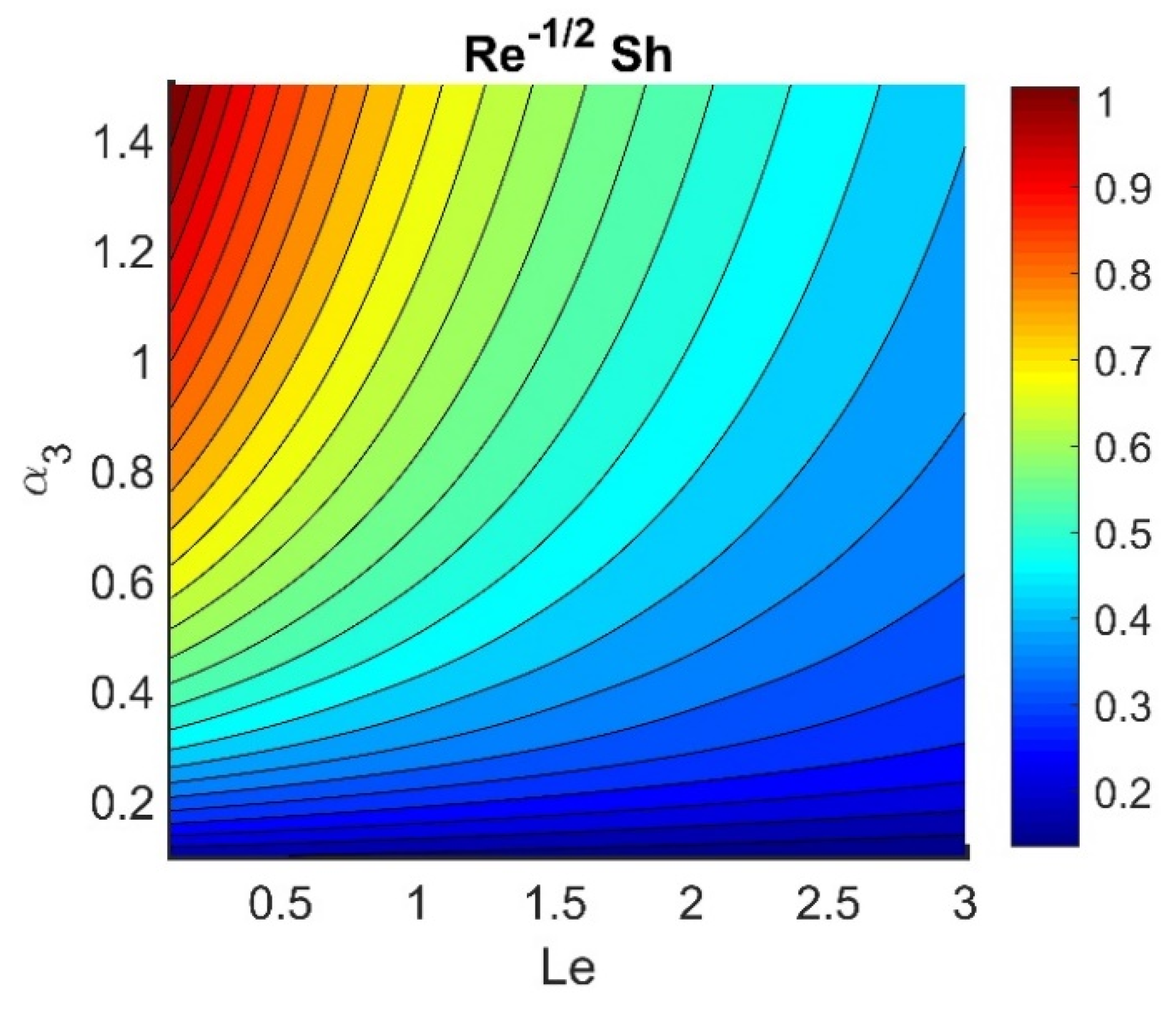
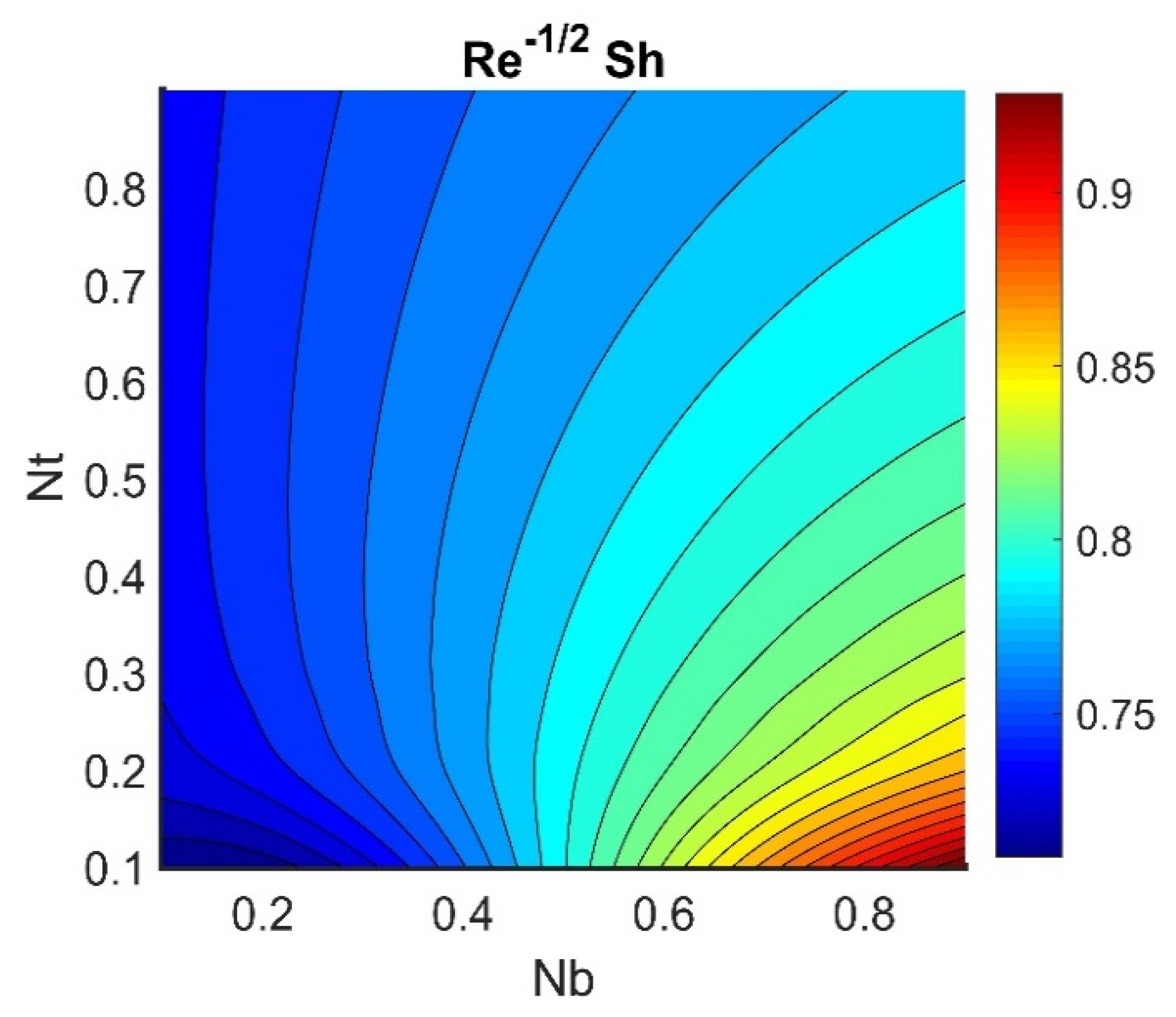
4.5. Physical Quantities (, , , , and )
5. Concluding Remarks
- The radial velocity diminished with an increase in the magnetic field and rose with an increase in the Hall current.
- The velocities declined as a result of higher velocity slip parameters.
- The temperature field was improved under higher magnetic number, Eckert number, and radiation parameter values.
- The thermophoresis number had a greater impact on the heat field compared to the Brownian number.
- Multiple slip conditions reduced the transport fields.
- The frictional coefficient of the wall in the radial direction was reduced by an increase the Hall current.
- The heat transfer rate was reduced by an increase in the Brownian motion number, while an increase in thermal radiation elevated the heat transfer rate.
- An increase in Brownian motion and thermophoresis reduced the rate of heat transfer.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| u, v, w | Velocity components |
| Magnetic field strength | |
| Nanoparticle specific heat | |
| Velocity slip parameter | |
| Temperature slip parameter | |
| Concentration slip parameter | |
| Microorganism slip parameter | |
| Prandtl parameter | |
| Bioconvection Lewis number | |
| R | Radiation parameter |
| Lewis number | |
| Peclet parameter | |
| Magnetic parameter | |
| Nusselt number | |
| Friction coefficients | |
| Sherwood number | |
| Motile number | |
| b | Chemotaxis constant |
| Ambient microorganisms | |
| Ambient temperature | |
| Ambient concentration | |
| Brownian diffusivity | |
| Microorganism diffusivity | |
| Kinematic viscosity | |
| Eckert number | |
| Electrical conductivity | |
| Speed of cell swimming | |
| Thermophoresis diffusivity | |
| Fluid density | |
| Concentration at wall | |
| Microorganisms at wall | |
| Temperature at wall | |
| Thermophoresis parameter | |
| Brownian motion parameter |
References
- Abu-Nada, E. Application of nanofluids for heat transfer enhancement of separated flows encountered in a backward facing step. Int. J. Heat Fluid Flow 2008, 29, 242–249. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; (No. ANL/MSD/CP-84938; CONF-951135-29); Argonne National Lab. (ANL): Argonne, IL, USA, 1995. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 28, 240–250. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Nield, D.A. Natural convective boundary-layer flow of a nanofluid past a vertical plate. Int. J. Therm. Sci. 2010, 49, 243–247. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The Cheng–Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. Int. J. Heat Mass Transf. 2009, 52, 5792–5795. [Google Scholar] [CrossRef]
- Wakif, A.; Zaydan, M.; Alshomrani, A.S.; Muhammad, T.; Sehaqui, R. New insights into the dynamics of alumina-(60% ethylene glycol+ 40% water) over an isothermal stretching sheet using a renovated Buongiorno’s approach: A numerical GDQLLM analysis. Int. Commun. Heat Mass Transf. 2022, 133, 105937. [Google Scholar] [CrossRef]
- Rasheed, H.U.; Khan, W.; Khan, I.; Alshammari, N.; Hamadneh, N. Numerical computation of 3D Brownian motion of thin film nanofluid flow of convective heat transfer over a stretchable rotating surface. Sci. Rep. 2022, 12, 1–14. [Google Scholar]
- Gumber, P.; Yaseen, M.; Rawat, S.K.; Kumar, M. Heat transfer in micropolar hybrid nanofluid flow past a vertical plate in the presence of thermal radiation and suction/injection effects. Partial Differ. Equ. Appl. Math. 2022, 5, 100240. [Google Scholar] [CrossRef]
- Mahanthesh, B. Flow and heat transport of nanomaterial with quadratic radiative heat flux and aggregation kinematics of nanoparticles. Int. Commun. Heat Mass Transf. 2021, 127, 105521. [Google Scholar] [CrossRef]
- Areekara, S.; Mackolil, J.; Mahanthesh, B.; Mathew, A.; Rana, P. A study on nanoliquid flow with irregular heat source and realistic boundary conditions: A modified Buongiorno model for biomedical applications. ZAMM-J. Appl. Math. Mech./Z. Für Angew. Math. Und Mech. 2022, 102, e202100167. [Google Scholar] [CrossRef]
- Farooq, U.; Waqas, H.; Imran, M.; Albakri, A.; Muhammad, T. Numerical investigation for melting heat transport of nanofluids due to stretching surface with Cattaneo-Christov thermal model. Alex. Eng. J. 2022, 61, 6635–6644. [Google Scholar] [CrossRef]
- Dawar, A.; Wakif, A.; Saeed, A.; Shah, Z.; Muhammad, T.; Kumam, P. Significance of Lorentz forces on Jeffrey nanofluid flows over a convectively heated flat surface featured by multiple velocity slips and dual stretching constraint: A homotopy analysis approach. J. Comput. Des. Eng. 2022, 9, 564–582. [Google Scholar] [CrossRef]
- Nazeer, M.; Khan, M.I.; Khan, S.U.; Saleem, A.; Muhammad, T.; Shah, S.I. Assessment of heat and mass transfer characteristics in Poiseuille flow of non-Newtonian nanofluid in a porous channel with convectively heated lower wall. Chin. J. Phys. 2022, 77, 1065–1079. [Google Scholar] [CrossRef]
- Mishra, S.R.; Sun, T.C.; Rout, B.C.; Khan, M.I.; Alaoui, M.K.; Khan, S.U. Control of dusty nanofluid due to the interaction on dust particles in a conducting medium: Numerical investigation. Alex. Eng. J. 2022, 61, 3341–3349. [Google Scholar] [CrossRef]
- Li, P.; Abbasi, A.; El-Zahar, E.R.; Farooq, W.; Hussain, Z.; Khan, S.U.; Khan, M.I.; Farooq, S.; Malik, M.; Wang, F. Hall effects and viscous dissipation applications in peristaltic transport of Jeffrey nanofluid due to wave frame. Colloid Interface Sci. Commun. 2022, 47, 100593. [Google Scholar] [CrossRef]
- Kuznetsov, A.V. Nanofluid bioconvection in water-based suspensions containing nanoparticles and oxytactic microorganisms: Oscillatory instability. Nanoscale Res. Lett. 2011, 6, 1–13. [Google Scholar] [CrossRef]
- Sampath Kumar, P.B.; Gireesha, B.J.; Mahanthesh, B.; Chamkha, A.J. Thermal analysis of nanofluid flow containing gyrotactic microorganisms in bioconvection and second-order slip with convective condition. J. Therm. Anal. Calorim. 2019, 136, 1947–1957. [Google Scholar] [CrossRef]
- Chu, Y.M.; Shankaralingappa, B.M.; Gireesha, B.J.; Alzahrani, F.; Khan, M.I.; Khan, S.U. Combined impact of Cattaneo-Christov double diffusion and radiative heat flux on bio-convective flow of Maxwell liquid configured by a stretched nano-material surface. Appl. Math. Comput. 2022, 419, 126883. [Google Scholar] [CrossRef]
- Ayodeji, F.; Tope, A.; Pele, O. Magneto-hydrodynamics (MHD) Bioconvection nanofluid slip flow over a stretching sheet with thermophoresis, viscous dissipation and brownian motion. Mach. Learn. Res. 2020, 4, 51. [Google Scholar] [CrossRef]
- Khan, M.; Salahuddin, T.; Malik, M.Y.; Alqarni, M.S.; Alqahtani, A.M. Numerical modeling and analysis of bioconvection on MHD flow due to an upper paraboloid surface of revolution. Phys. A Stat. Mech. Its Appl. 2020, 553, 124231. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Mushtaq, T.; Abbas, Z.; Rauf, A.; Khan, S.U.; Tlili, I. Dynamics of bioconvection flow of micropolar nanoparticles with Cattaneo-Christov expressions. Appl. Math. Mech. 2020, 41, 1333–1344. [Google Scholar] [CrossRef]
- Khan, M.I.; Haq, F.; Khan, S.A.; Hayat, T.; Khan, M.I. Development of thixotropic nanomaterial in fluid flow with gyrotactic microorganisms, activation energy, mixed convection. Comput. Methods Programs Biomed. 2020, 187, 105186. [Google Scholar] [CrossRef] [PubMed]
- Ferdows, M.; Zaimi, K.; Rashad, A.M.; Nabwey, H.A. MHD bioconvection flow and heat transfer of nanofluid through an exponentially stretchable sheet. Symmetry 2020, 12, 692. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.U.; Bhatti, M.M.; Imran, M. Significance of bioconvection in chemical reactive flow of magnetized Carreau–Yasuda nanofluid with thermal radiation and second-order slip. J. Therm. Anal. Calorim. 2020, 140, 1293–1306. [Google Scholar] [CrossRef]
- Muhammad, T.; Waqas, H.; Mahanthesh, B. Computational analysis of bioconvection in magnetized flow of thixotropic nanofluid with gyrotactic microorganisms. Math. Fluid Mech. Adv. Convect. Instab. Incompressible Fluid Flow 2021, 7, 75. [Google Scholar]
- Von Karman, T. Classical problem of rotating disk. Transfer ASME 1939, 61, 705. [Google Scholar]
- Benton, E.R. On the flow due to a rotating disk. J. Fluid Mech. 1966, 24, 781–800. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Heat and mass transfer on the MHD fluid flow due to a porous rotating disk with hall current and variable properties. J. Heat Transf. 2011, 133, 021701. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Hatami, M.; Ganji, D.D. Nanofluid flow and heat transfer in a rotating system in the presence of a magnetic field. J. Mol. Liq. 2014, 190, 112–120. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Nanofluid flow and heat transfer due to a rotating disk. Comput. Fluids 2014, 94, 139–146. [Google Scholar] [CrossRef]
- Hayat, T.; Rashid, M.; Imtiaz, M.; Alsaedi, A. Magnetohydrodynamic (MHD) flow of Cu-water nanofluid due to a rotating disk with partial slip. AIP Adv. 2015, 5, 067169. [Google Scholar] [CrossRef]
- Abdel-Wahed, M.; Akl, M. Effect of hall current on MHD flow of a nanofluid with variable properties due to a rotating disk with viscous dissipation and nonlinear thermal radiation. AIP Adv. 2016, 6, 095308. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Shehzad, S.A.; Alsaedi, A. On magnetohydrodynamic flow of nanofluid due to a rotating disk with slip effect: A numerical study. Comput. Methods Appl. Mech. Eng. 2017, 315, 467–477. [Google Scholar] [CrossRef]
- Rehman, K.U.; Malik, M.Y.; Zahri, M.; Tahir, M. Numerical analysis of MHD Casson Navier’s slip nanofluid flow yield by rigid rotating disk. Results Phys. 2018, 8, 744–751. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Reddy, M.G.; Rauf, A.; Abbas, Z. Bioconvection of Maxwell nanofluid under the influence of double diffusive Cattaneo–Christov theories over isolated rotating disk. Phys. Scr. 2020, 95, 045207. [Google Scholar] [CrossRef]
- Waqas, H.; Naseem, R.; Muhammad, T.; Farooq, U. Bioconvection flow of Casson nanofluid by rotating disk with motile microorganisms. J. Mater. Res. Technol. 2021, 13, 2392–2407. [Google Scholar] [CrossRef]
- Jawad, M.; Saeed, A.; Khan, A.; Islam, S. MHD bioconvection Darcy-Forchheimer flow of Casson nanofluid over a rotating disk with entropy optimization. Heat Transf. 2021, 50, 2168–2196. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Abbas, Z.; Rauf, A.; Mushtaq, T. Effectiveness of Hall current and thermophysical properties in compressible flow of viscous fluid thorough spinning oscillatory disk. Int. Commun. Heat Mass Transf. 2020, 116, 104678. [Google Scholar] [CrossRef]
- Khan, M.; Ali, W.; Ahmed, J. A hybrid approach to study the influence of Hall current in radiative nanofluid flow over a rotating disk. Appl. Nanosci. 2020, 10, 5167–5177. [Google Scholar] [CrossRef]
- Bég, O.A.; Kabir, M.N.; Uddin, M.J.; Izani Md Ismail, A.; Alginahi, Y.M. Numerical investigation of Von Karman swirling bioconvective nanofluid transport from a rotating disk in a porous medium with Stefan blowing and anisotropic slip effects. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 3933–3951. [Google Scholar] [CrossRef]
- Rana, P.; Mackolil, J.; Mahanthesh, B.; Muhammad, T. Cattaneo-Christov Theory to model heat flux effect on nanoliquid slip flow over a spinning disk with nanoparticle aggregation and Hall current. Waves Random Complex Media 2022, 1–23. [Google Scholar] [CrossRef]
- Rana, P.; Mahanthesh, B.; Thriveni, K.; Muhammad, T. Significance of aggregation of nanoparticles, activation energy, and Hall current to enhance the heat transfer phenomena in a nanofluid: A sensitivity analysis. Waves Random Complex Media 2022, 1–23. [Google Scholar] [CrossRef]
- Ha, S.N. A nonlinear shooting method for two-point boundary value problems. Comput. Math. Appl. 2001, 42, 1411–1420. [Google Scholar] [CrossRef]
- Mathews, J.H.; Fink, K.D. Numerical Methods Using MATLAB; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2004; Volume 4. [Google Scholar]
- Beers, K.J.; Beers, K.J. Numerical Methods for Chemical Engineering: Applications in Matlab; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Pal, D.; Mandal, G. Effects of Hall current on magnetohydrodynamic heat transfer of nanofluids over a non-linear stretching/shrinking sheet. Int. J. Appl. Comput. Math. 2017, 3, 1103–1120. [Google Scholar] [CrossRef]
- Pal, D.; Mandal, G. Magnetohydrodynamic heat and mass transfer of Sisko nanofluid past a stretching sheet with nonlinear thermal radiation and convective boundary condition. J. Nanofluids 2019, 8, 852–860. [Google Scholar] [CrossRef]
- Mandal, G.; Pal, D. Entropy generation analysis of radiated magnetohydrodynamic flow of carbon nanotubes nanofluids with variable conductivity and diffusivity subjected to chemical reaction. J. Nanofluids 2021, 10, 491–505. [Google Scholar] [CrossRef]
- Pal, D.; Mandal, G. Magnetohydrodynamic nonlinear thermal radiative heat transfer of nanofluids over a flat plate in a porous medium in existence of variable thermal conductivity and chemical reaction. Int. J. Ambient Energy 2021, 42, 1167–1177. [Google Scholar] [CrossRef]
- Mandal, G.; Pal, D. Entropy generation analysis of magnetohydrodynamic Darcy-Forchheimer Williamson hybrid nanofluid flow through porous medium with nonlinear thermal radiation. Spec. Top. Rev. Porous Media Int. J. 2022, 13, 57–79. [Google Scholar] [CrossRef]







| Hayat et al. [33] | Rehman et al. [34] | Our Results | ||
|---|---|---|---|---|
| 0 | 0.7 | 0.30494 | 0.3050 | 0.304948 |
| 0.7 | 0.7 | 0.24421 | 0.2443 | 0.244214 |
| 1.4 | 0.7 | 0.17566 | 0.1757 | 0.175661 |
| 0.3 | 0.2 | 0.32655 | 0.3266 | 0.326552 |
| 0.3 | 0.5 | 0.30360 | 0.3036 | 0.303607 |
| 0.3 | 0.8 | 0.28715 | 0.2872 | 0.287155 |
| 0 | 0 | 0.5 | 0.27223285 | −0.60016174 | 0.18411756 | 0.61217292 | 0.35891396 |
| 0.5 | 0.34804091 | −0.60760591 | 0.20678466 | 0.66211221 | 0.40193257 | ||
| 1 | 0.38657686 | −0.57472358 | 0.21535335 | 0.68590441 | 0.42344578 | ||
| 0.5 | 0 | 0.36000722 | −0.43512123 | 0.21557962 | 0.68362256 | 0.42656590 | |
| 1 | 0.35017124 | −0.75136693 | 0.19808066 | 0.64951373 | 0.38490344 | ||
| 2 | 0.34939527 | −0.98614427 | 0.18346595 | 0.63623923 | 0.36227622 | ||
| 1 | 0 | 0.5 | 0.06907399 | −0.37685871 | 0.19043449 | 0.65499791 | 0.35472070 |
| 0.5 | 0.09729511 | −0.38822687 | 0.23499319 | 0.73620866 | 0.41653888 | ||
| 1 | 0.11529524 | −0.38145137 | 0.25654230 | 0.77752075 | 0.44911090 | ||
| 0.5 | 0 | 0.12206753 | −0.31990335 | 0.26542362 | 0.79444265 | 0.46550481 | |
| 1 | 0.08479902 | −0.43742667 | 0.21112374 | 0.69834925 | 0.38281983 | ||
| 2 | 0.07294442 | −0.50408669 | 0.17797708 | 0.65135755 | 0.33905929 |
| 0 | 0.5 | 0.5 | 0.5 | 0.09536398 | 0.74735703 | 0.42765668 |
| 1 | 0.37593681 | 0.73549955 | 0.42662967 | |||
| 2 | 0.61025676 | 0.73202599 | 0.42630997 | |||
| 0.5 | 0 | 0.5 | 0.5 | 0.25909380 | 0.74013993 | 0.42704913 |
| 1 | 0.22314167 | 0.73889796 | 0.42692132 | |||
| 2 | 0.19518753 | 0.73798530 | 0.42682639 | |||
| 0.5 | 0.5 | 0 | 0.5 | 0.13514058 | 1.17259288 | 0.45258266 |
| 1 | 0.30584709 | 0.53909050 | 0.41493130 | |||
| 2 | 0.37956428 | 0.34920648 | 0.40338675 | |||
| 0.5 | 0.5 | 0.5 | 0 | 0.23995186 | 0.73946890 | 0.53998522 |
| 1 | 0.23995170 | 0.73946891 | 0.35308806 | |||
| 2 | 0.23995170 | 0.73946888 | 0.26230148 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alzahrani, A.K. Effects of Hall Current and Viscous Dissipation on Bioconvection Transport of Nanofluid over a Rotating Disk with Motile Microorganisms. Nanomaterials 2022, 12, 4027. https://doi.org/10.3390/nano12224027
Alzahrani AK. Effects of Hall Current and Viscous Dissipation on Bioconvection Transport of Nanofluid over a Rotating Disk with Motile Microorganisms. Nanomaterials. 2022; 12(22):4027. https://doi.org/10.3390/nano12224027
Chicago/Turabian StyleAlzahrani, Abdullah K. 2022. "Effects of Hall Current and Viscous Dissipation on Bioconvection Transport of Nanofluid over a Rotating Disk with Motile Microorganisms" Nanomaterials 12, no. 22: 4027. https://doi.org/10.3390/nano12224027
APA StyleAlzahrani, A. K. (2022). Effects of Hall Current and Viscous Dissipation on Bioconvection Transport of Nanofluid over a Rotating Disk with Motile Microorganisms. Nanomaterials, 12(22), 4027. https://doi.org/10.3390/nano12224027






