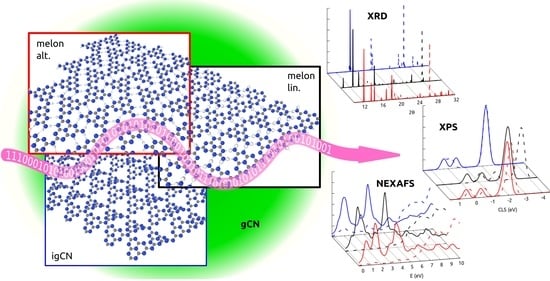
Ab-Initio Spectroscopic Characterization of Melem-Based Graphitic Carbon Nitride Polymorphs
Abstract
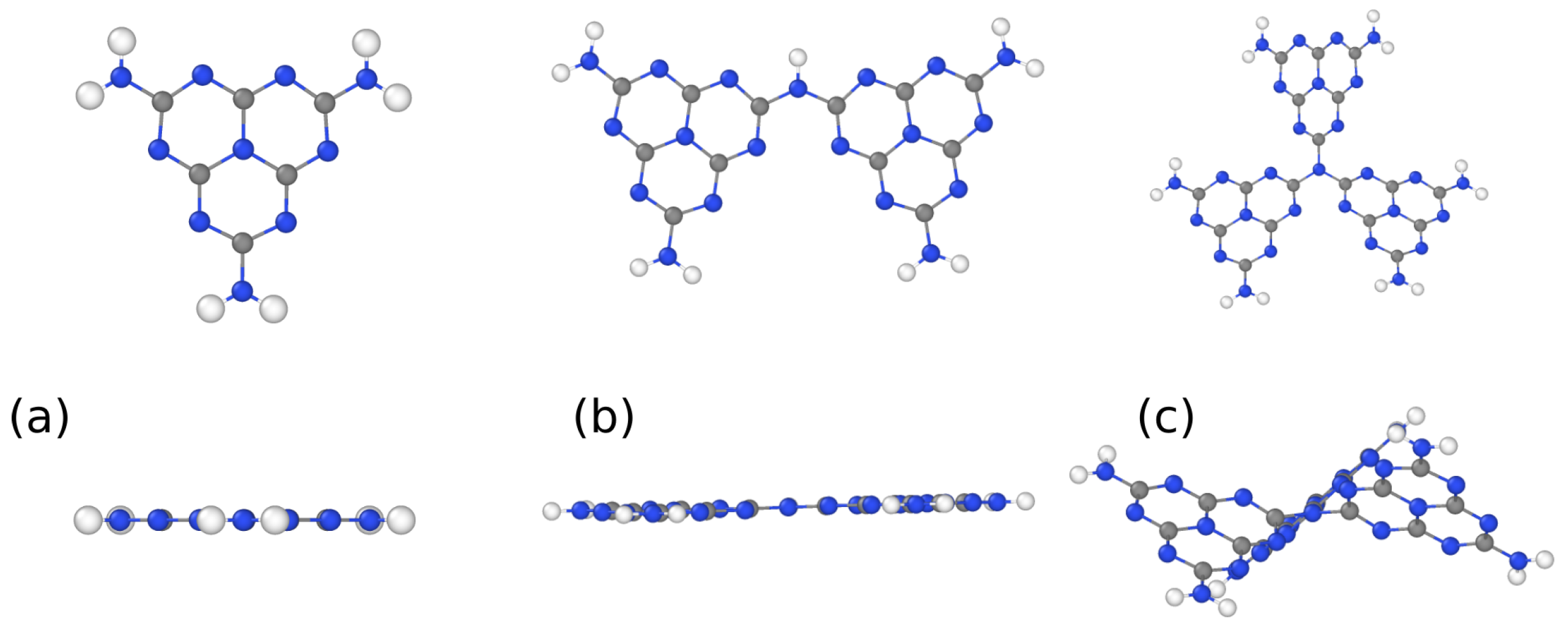
:1. Introduction
2. Computational Methods
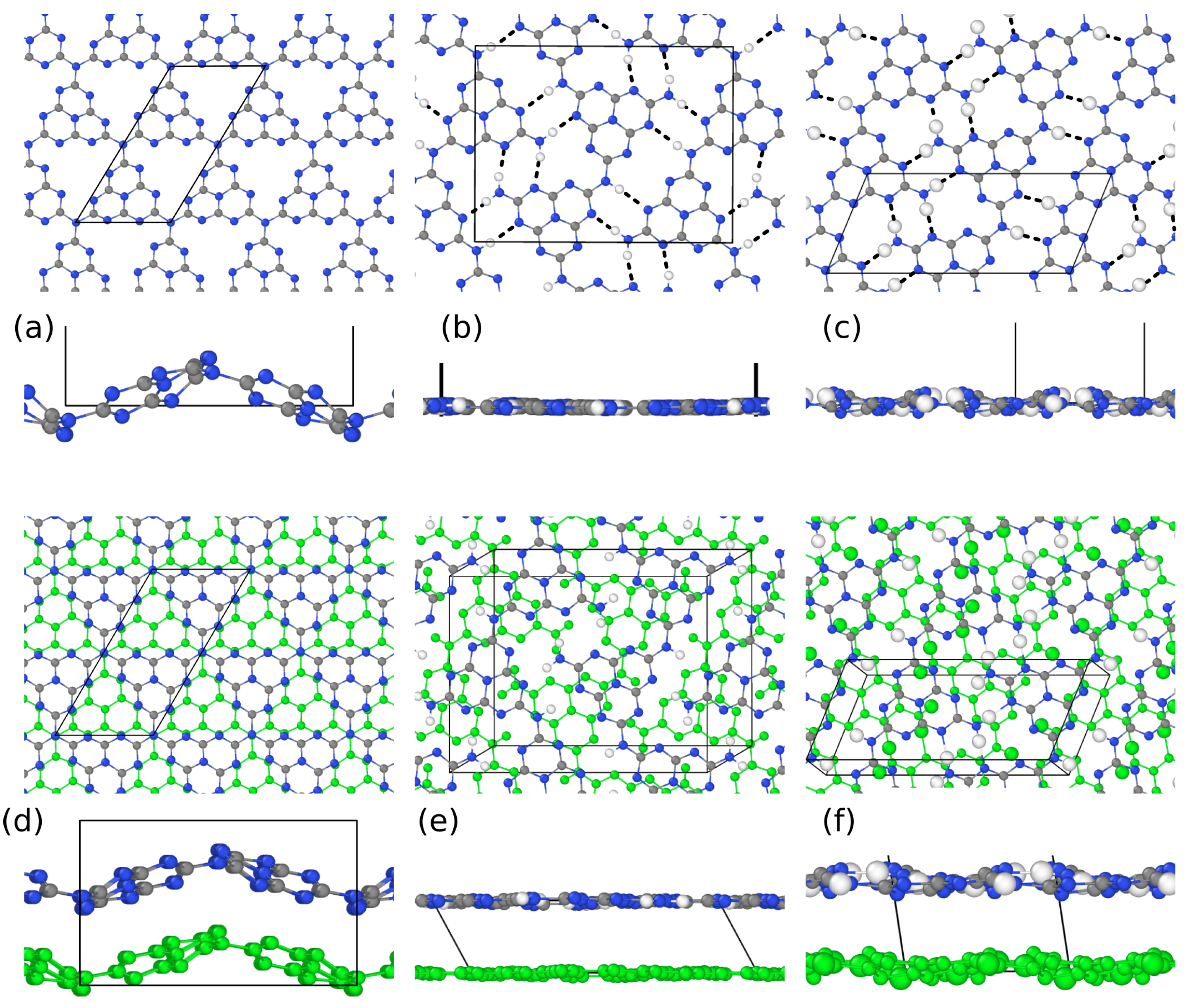
3. Results and Discussion
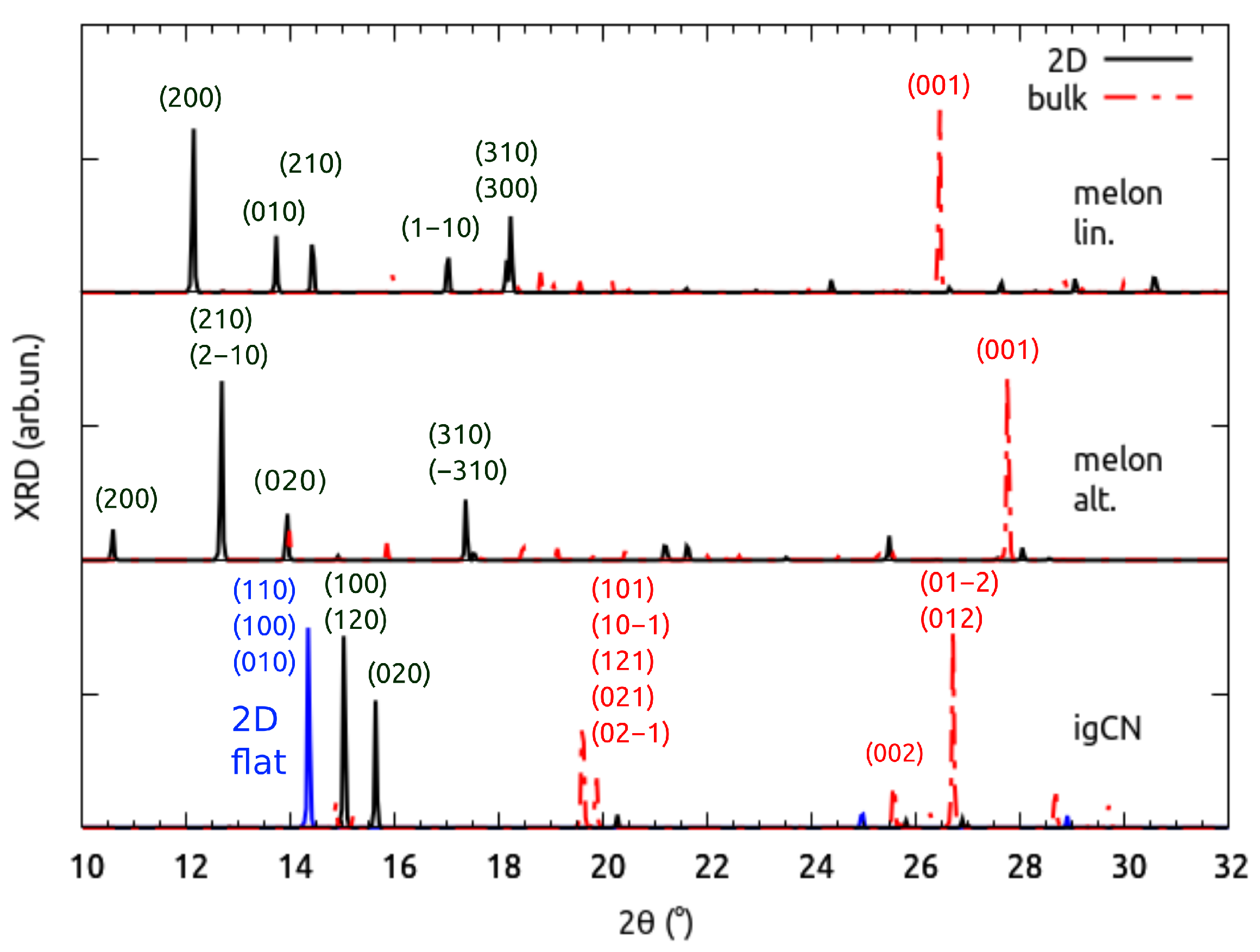
3.1. Structural Properties by Simulated XRD Characterization
3.2. Electronic Properties by Simulated X-ray Spectroscopies
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Thomas, A.; Fischer, A.; Goettmann, F.; Antonietti, M.; Müller, J.O.; Schlögl, R.; Carlsson, J.M. Graphitic carbon nitride materials: Variation of structure and morphology and their use as metal-free catalysts. J. Mater. Chem. 2008, 18, 4893–4908. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Liu, J.; Liang, J.; Jaroniec, M.; Qiao, S.Z. Graphitic carbon nitride materials: Controllable synthesis and applications in fuel cells and photocatalysis. Energy Environ. Sci. 2012, 5, 6717. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, L.; Shi, R.; Zhu, Y. Chemical exfoliation of graphitic carbon nitride for efficient heterogeneous photocatalysis. J. Mater. Chem. A 2013, 1, 14766. [Google Scholar] [CrossRef]
- Zheng, Y.; Lin, L.; Wang, B.; Wang, X. Graphitic Carbon Nitride Polymers toward Sustainable Photoredox Catalysis. Angew. Chem. Int. Ed. 2015, 54, 12868. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Sun, Y.; Dong, F. Graphitic carbon nitride based nanocomposites: A review. Nanoscale 2015, 7, 15. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Wang, H.; Antonietti, M. Graphitic carbon nitride ‘‘reloaded’’: Emerging applications beyond (photo)catalysis. Chem. Soc. Rev. 2016, 45, 2308. [Google Scholar] [CrossRef] [Green Version]
- Wen, J.; Xie, J.; Chen, X.; Li, X. A review on g-C3N4-based photocatalysts. Appl. Surf. Sci. 2017, 391, 72. [Google Scholar] [CrossRef]
- Kumar, P.; Boukherroub, R.; Shankar, K. Sunlight-driven water-splitting using two-dimensional carbon based semiconductors. J. Mater. Chem. A 2018, 6, 12876. [Google Scholar] [CrossRef]
- Vidyasagar, D.; Bhoyar, T.; Singh, G.; Vinu, A. Recent progress in polymorphs of carbon nitride: Synthesis, properties, and their applications. Macrom. Rapid Commun. 2021, 2000676. [Google Scholar] [CrossRef]
- Wang, X.; Maeda, K.; Thomas, A.; Takanabe, K.; Gang, X.; Carlsson, J.; Domen, K.; Antonietti, M. A metal-free polymeric photocatalyst for hydrogen production from water under visible light. Nat. Mater. 2009, 8, 76. [Google Scholar] [CrossRef]
- Wang, X.; Blechert, S.; Antonietti, M. Polymeric Graphitic Carbon Nitride for Heterogeneous Photocatalysis. ACS Catal. 2012, 2, 1596. [Google Scholar] [CrossRef]
- Shalom, M.; Gimenez, S.; Schipper, F.; Herraiz-Cardona, I.; Bisquert, J.; Antonietti, M. Controlled Carbon Nitride Growth on Surfaces for Hydrogen Evolution Electrodes. Angew. Chem. Int. Ed. 2014, 53, 3654. [Google Scholar] [CrossRef]
- Wirth, J.; Neumann, R.; Antonietti, M.; Saalfrank, P. Adsorption and photocatalytic splitting of water on graphitic carbon nitride: A combined first principles and semiempirical study. Phys. Chem. Chem. Phys. 2014, 16, 15917. [Google Scholar] [CrossRef] [Green Version]
- Lai, L.; Potts, J.R.; Zhan, D.; Wang, L.; Poh, C.K.; Tang, C.; Gong, H.; Shen, Z.; Lin, J.; Ruoff, R.S. Exploration of the active center structure of nitrogen-doped graphene-based catalysts for oxygen reduction reaction. Energy Environ. Sci. 2012, 5, 7936. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Zhang, L.; Xie, F.; Vasileff, A.; Qiao, S.Z. Graphitic Carbon Nitride (g-C3N4 )-Derived N-Rich Graphene with Tuneable Interlayer Distance as a High-Rate Anode for Sodium-Ion Batteries. Adv. Mater. 2019, 31, 1901261. [Google Scholar] [CrossRef]
- Perilli, D.; Fiori, S.; Panighel, M.; Liu, H.; Cepek, C.; Peressi, M.; Comelli, G.; Africh, C.; Di Valentin, C. Mechanism of CO Intercalation through the Graphene/Ni(111) Interface and Effect of Doping. J. Phys. Chem. Lett. 2021, 171, 704. [Google Scholar] [CrossRef] [PubMed]
- Brothers, P.J.; Collman, J.P. The organometallic chemistry of transition-metal porphyrin complexes. Acc. Chem. Res. 1986, 19, 209. [Google Scholar] [CrossRef]
- Sessler, J.L.; Tomat, E. Transition-Metal Complexes of Expanded Porphyrins. Acc. Chem. Res. 2007, 40, 371. [Google Scholar] [CrossRef] [PubMed]
- Kojima, Y.; Ohfuji, H. Structure and stability of carbon nitride under high pressure and high temperature up to 125 GPa and 3000 K. Diam. Relat. Mater. 2013, 39, 1. [Google Scholar] [CrossRef]
- Lee, H.L.; Sofer, Z.; Mazánek, V.; Luxa, J.; Chua, C.K.; Pumera, M. Graphitic carbon nitride: Effects of various precursors on the structural, morphological and electrochemical sensing properties. Appl. Mater. Today 2017, 8, 150–162. [Google Scholar] [CrossRef]
- Verma, S.; Baig, R.; Changseok, H.; Nadagouda, M.; Varma, R. Magnetic graphitic carbon nitride: Its application in the C–H activation of amines. Chem. Commun. 2015, 51, 15554. [Google Scholar] [CrossRef]
- Jiao, Y.; Zheng, Y.; Chen, P.; Jaroniec, M.; Qiao, S.Z. Molecular Scaffolding Strategy with Synergistic Active Centers To Facilitate Electrocatalytic CO2 Reduction to Hydrocarbon/Alcohol. J. Am. Chem. Soc. 2017, 139, 18093. [Google Scholar] [CrossRef]
- Cometto, C.; Ugolotti, A.; Grazietti, E.; Moretto, A.; Bottario, G.; Armelao, L.; Di Valentin, C.; Calvillo, L.; Granozzi, G. Copper single-atoms embedded in 2D graphitic carbon nitride for the CO2 reduction. npj 2D Mater. Appl. 2021, 5, 63. [Google Scholar] [CrossRef]
- Pieta, I.S.; Rathi, A.; Pieta, P.; Nowakowski, R.; Holdynski, M.; Pisarek, M.; Kaminska, A.; Gawande, M.B.; Zboril, R. Electrocatalytic methanol oxidation over Cu, Ni and bimetallic Cu-Ni nanoparticles supported on graphitic carbon nitride. Appl. Cat. B Environ. 2019, 244, 272. [Google Scholar] [CrossRef]
- Lanzilotto, V.; Silva, J.L.; Zhang, T.; Stredansky, M.; Grazioli, C.; Simonov, K.; Giangrisostomi, E.; Ovsyannikov, R.; De Simone, M.; Coreno, M.; et al. Spectroscopic Fingerprints of Intermolecular H-Bonding Interactions in Carbon Nitride Model Compounds. Chem. A Eur. J. 2018, 24, 14198–14206. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wei, W.; Jacob, T. Strong excitonic effects in the optical properties of graphitic carbon nitride g-C3N4 from first principles. Phys. Rev. B 2013, 87, 085202. [Google Scholar] [CrossRef]
- Fina, F.; Callear, S.; Carins, G.; Irvine, J.T. Structural investigation of graphitic carbon nitride via XRD and neutron diffraction. Chem. Mater. 2015, 27, 2612. [Google Scholar] [CrossRef] [Green Version]
- Akaike, K.; Aoyama, K.; Dekubo, S.; Onishi, A.; Kanai, K. Characterizing electronic structure near the energy gap of graphitic carbon nitride based on rational interpretation of chemical analysis. Chem. Mater. 2018, 30, 2341. [Google Scholar] [CrossRef]
- Deifallah, M.; McMillan, P.; Corà, F. Electronic and structural properties of two-dimensional carbon nitride graphenes. J. Phys. Chem. C 2008, 112, 5447. [Google Scholar] [CrossRef]
- Azofra, L.; MacFarlane, D.; Sun, C. A DFT study of planar vs. corrugated graphenelike carbon nitride (g-C3N4) and its rola in the catalytic performance of CO2 covertion. Phys. Chem. Chem. Phys. 2016, 18, 18507. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [Green Version]
- Giannozzi, P.; Baseggio, O.; Bonfà, P.; Brunato, D.; Car, R.; Carnimeo, I.; Cavazzoni, C.; de Gironcoli, S.; Delugas, P.; Ferrari Ruffino, F.; et al. Quantum ESPRESSO toward the exascale. J. Chem. Phys. 2020, 152, 154105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dal Corso, A. Pseudopotentials periodic table: From H to Pu. Comput. Mater. Sci. 2014, 95, 337–350. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Becke, A. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648. [Google Scholar] [CrossRef] [Green Version]
- Schlipf, M.; Gygi, F. Optimization algorithm for the generation of ONCV pseudopotentials. Comput. Phys. Commun. 2015, 196, 36–44. [Google Scholar] [CrossRef] [Green Version]
- Hamann, D.R. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 2013, 88, 085117. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B Condens. Matter Mater. Phys. 1976, 13, 5188. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Izumi, F.; Momma, K. Three-Dimensional Visualization in Powder Diffraction. Solid State Phenom. 2007, 130, 15. [Google Scholar] [CrossRef]
- García-Gil, S.; García, A.; Ordejón, P. Alculation of core level shifts within DFT using pseudopotentials and localized basis sets. Eur. Phys. J. 2012, 85, 239. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1994, 50, 17953. [Google Scholar] [CrossRef] [Green Version]
- Fiori, S.; Perilli, D.; Panighel, M.; Cepek, C.; Ugolotti, A.; Sala, A.; Liu, H.; Comelli, G.; Di Valentin, C.; Africh, C. “Inside out” growth method for high-quality nitrogen-doped graphene. Carbon 2021, 171, 704–710. [Google Scholar] [CrossRef]
- Slater, J.C.; Johnson, K.H. Self-consistent-field Xα cluster method for polyatomic molecules and solids. Phys. Rev. B 1972, 5, 844. [Google Scholar] [CrossRef]
- Gougoussis, C.; Calandra, M.; Seitsonen, A.P.; Mauri, F. First-principles calculations of X-ray absorption in a scheme based on ultrasoft pseudopotentials: From α-quartz to high-Tc compounds. Phys. Rev. B Condens. Matter Mater. Phys. 2009, 80, 075102. [Google Scholar] [CrossRef]
- Liu, X.; Kang, W.; Zeng, W.; Zhang, Y.; Qi, L.; Ling, F.; Fang, L.; Chen, Q.; Zhou, M. Structural, electronic and photocatalytic properties of g-C3N4 with intrinsic defects: A first-principles hybrid functional investigation. Appl. Surf. Sci. 2020, 499, 143994. [Google Scholar] [CrossRef]
- Tyborski, T.; Merschjann, C.; Orthmann, S.; Yang, F.; Lux-Steiner, M.C.; Schedel-Niedrig, T. Crystal structure of polymeric carbon nitride and the determination of its process-temperature-induced modifications. J. Phys. Condens. Matter 2013, 25, 395402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thonhauser, T.; Zuluaga, S.; Arter, C.A.; Berland, K.; Schröder, E.; Hyldgaard, P. Spin Signature of Nonlocal Correlation Binding in Metal-Organic Frameworks. Phys. Rev. Lett. 2015, 115, 136402. [Google Scholar] [CrossRef] [Green Version]
- Thonhauser, T.; Cooper, V.R.; Li, S.; Puzder, A.; Hyldgaard, P.; Langreth, D.C. Van der Waals density functional: Self-consistent potential and the nature of the van der Waals bond. Phys. Rev. B 2007, 76, 125112. [Google Scholar] [CrossRef] [Green Version]
- Berland, K.; Cooper, V.R.; Lee, K.; Schröder, E.; Thonhauser, T.; Hyldgaard, P.; Lundqvist, B.I. Van der Waals forces in density functional theory: A review of the vdW-DF method. Rep. Prog. Phys. 2015, 78, 066501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Langreth, D.C.; Lundqvist, B.I.; Chakarova-Käck, S.D.; Cooper, V.R.; Dion, M.; Hyldgaard, P.; Kelkkanen, A.; Kleis, J.; Kong, L.; Li, S.; et al. A density functional for sparse matter. J. Phys. Condens. Matter 2009, 21, 084203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dai, Y.; Gu, Y.; Bu, Y. Modulation of the photocatalytic performance of g-C3N4 by two-sites co-doping using variable valence metal. Appl. Surf. Sci. 2020, 500, 144036. [Google Scholar] [CrossRef]
- Jorge, A.B.; Martin, D.J.; Dhanoa, M.T.S.; Rahman, A.S.; Makwana, N.; Tang, J.; Sella, A.; Corà, F.; Firth, S.; Darr, J.A.; et al. H2 and O2 Evolution from Water Half-Splitting Reactions by Graphitic Carbon Nitride Materials. J. Phys. Chem. C 2013, 117, 7178–7185. [Google Scholar] [CrossRef]
- Mane, P.; Talapaneni, S.; Lakhi, K.; Ilbeygi, H.; Ravon, U.; Al-bahily, K.; Mori, T.; Park, D.H.; Vinu, A. Highly ordered nitrogen-rich mesoporous carbon nitrides and their superior performance for sensing and photocatalytic hydrogen generation. Angew. Chem. Int. Ed. 2017, 56, 8481. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Zuo, X.; Tang, H.; Li, G.; Zhou, Z. Origin of photoactivity in graphitic carbon nitride and strategies for enhancement of photocatalytic efficiency: Insights from first-principles computations. Phys. Chem. Chem. Phys. 2015, 17, 6280–6288. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, W.-D. Modification of TiO2 nanorod arrays by graphite-like C3N4 with high visible light photoelectrochemical activity. Electrochim. Acta 2012, 71, 10. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, J.; Yuan, Q.; Dong, B. Intercalated graphitic carbon nitride: A fascinating two-dimensional nanomaterial for an ultra-sensitive humidity nanosensor. Nanoscale 2014, 6, 9250. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Wang, J.; Yang, P. Preparation of luminescent graphitic C3N4 NS and their composites with RGO for property controlling. RSC Adv. 2016, 6, 112581. [Google Scholar] [CrossRef]
- Zeng, Z.; Quan, X.; Yu, H.; Chen, S.; Zhang, Y.; Zhao, H.; Zhang, S. Carbon nitride with electron storage property: Enhanced exciton dissociation for high-efficiency photocatalysis. Appl. Catal. B Environ. 2018, 236, 9. [Google Scholar] [CrossRef]
- Xue, J.; Fujitsuka, M.; Majima, T. The role of nitrogen defects in graphitic carbon nitride for visible-light-driven hydrogen evolution. Phys. Chem. Chem. Phys. 2019, 21, 2318. [Google Scholar] [CrossRef] [PubMed]
- Hellgren, N.; Guo, J.; Luo, Y.; Sathe, C.; Agui, A.; Kashtanov, S.; Nordgren, J.; Agren, H.; Sundgren, J. Electronic structure of carbon nitride thin films studied by X-ray spectroscopy techniques. Thin Solid Films 2005, 471, 19. [Google Scholar] [CrossRef]
- Zheng, Y.; Jiao, Y.; Zhu, Y.; Li, L.H.; Han, Y.; Chen, Y.; Aijun, D.; Mietek, J.; Qiao, S.Z. Hydrogen evolution by a metal-free electrocatalyst. Nat. Commun. 2014, 5, 3783. [Google Scholar] [CrossRef] [PubMed] [Green Version]
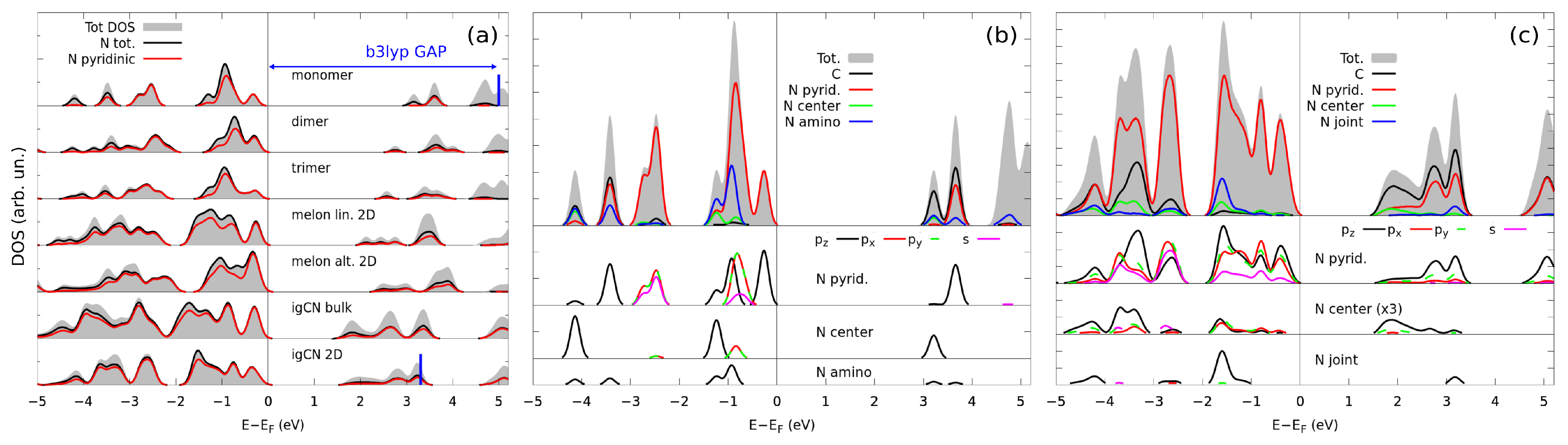
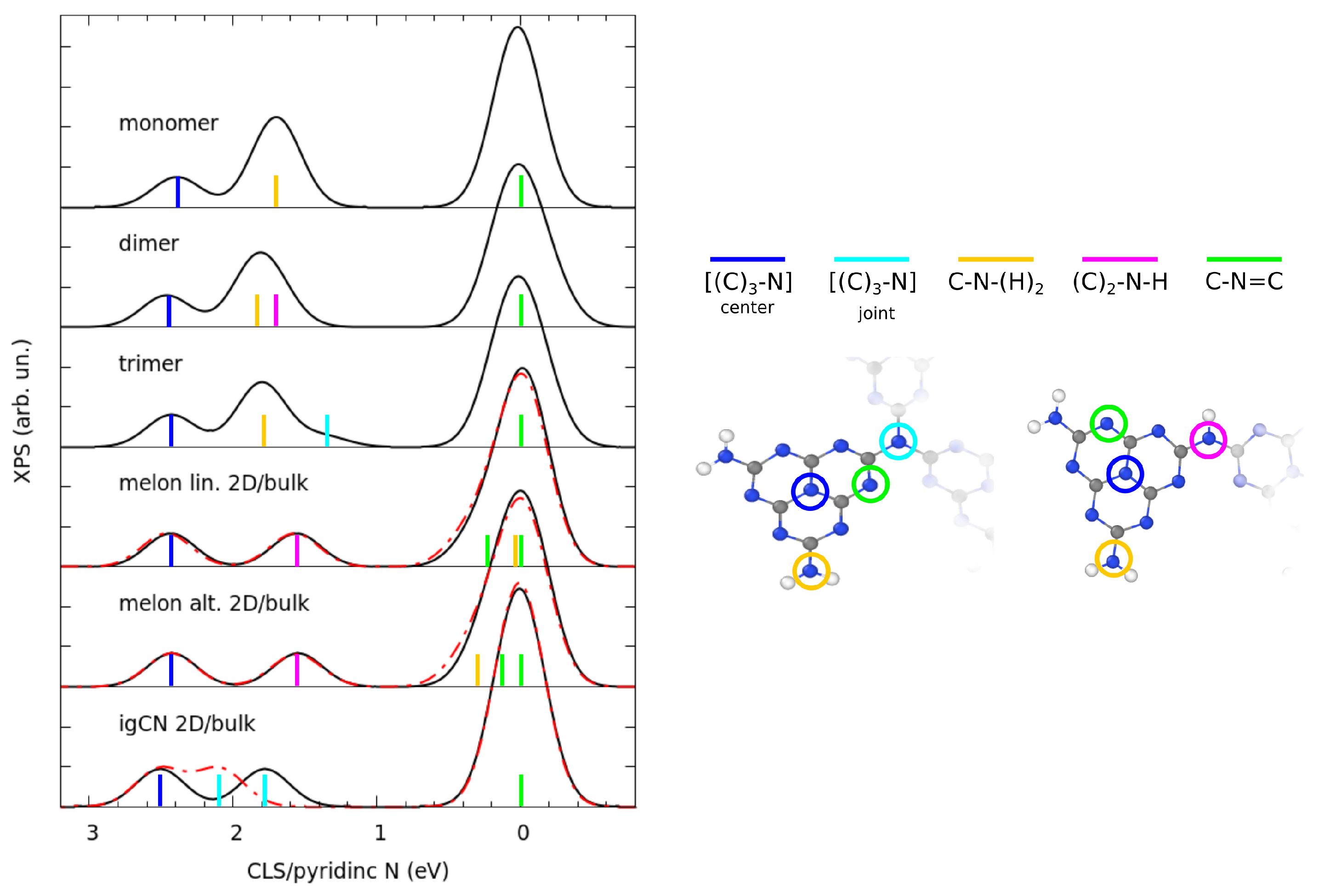
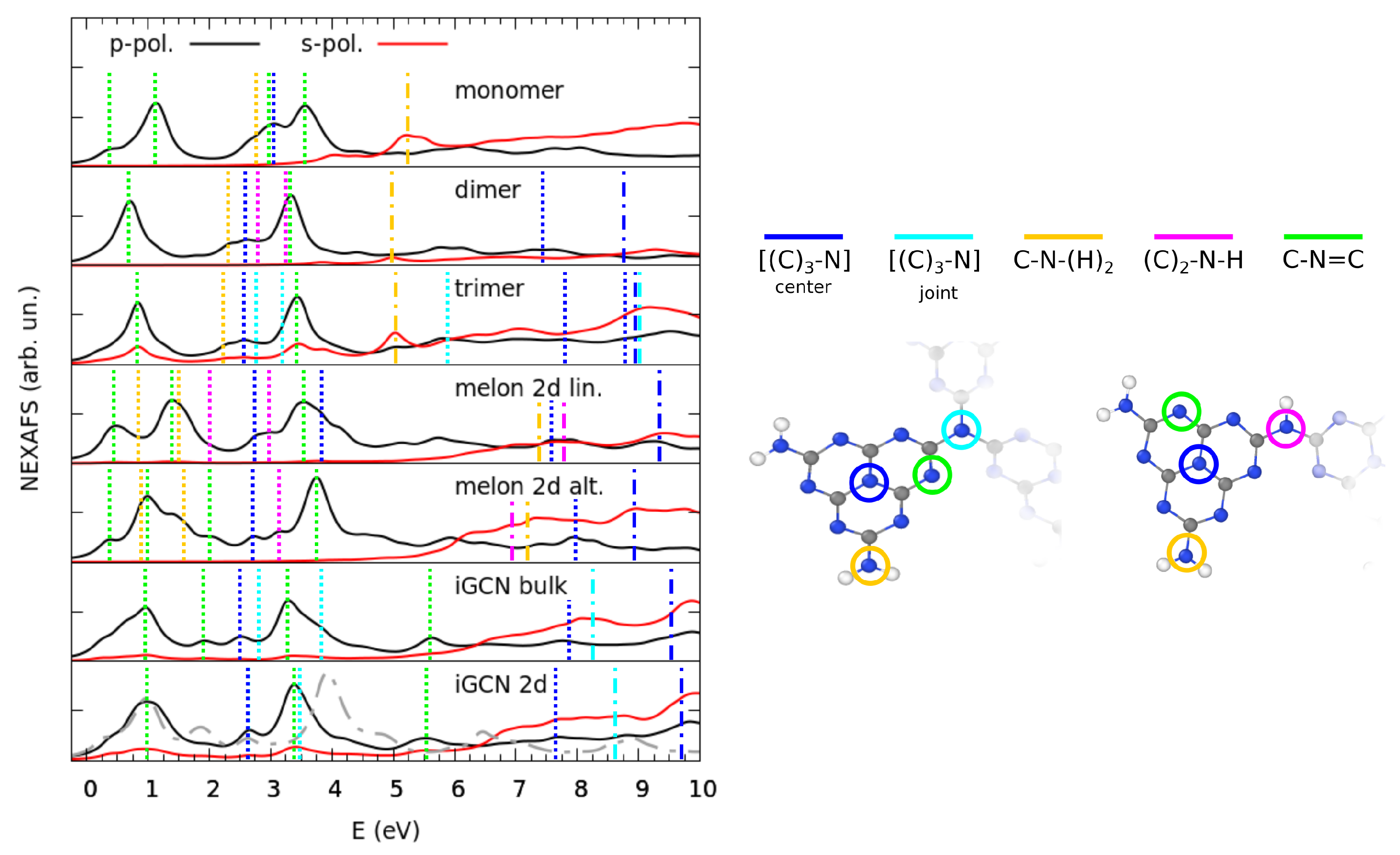
| Model | Isolated | 2D | Bulk |
|---|---|---|---|
| Monomer | −2.6 | - | - |
| Dimer | −2.6 | - | - |
| Trimer | −2.5 | - | - |
| Melon linear | - | −1.4 | −1.6 |
| Melon alternated | - | −2.3 | −3.1 |
| igCN | - | −1.7 | −1.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ugolotti, A.; Di Valentin, C. Ab-Initio Spectroscopic Characterization of Melem-Based Graphitic Carbon Nitride Polymorphs. Nanomaterials 2021, 11, 1863. https://doi.org/10.3390/nano11071863
Ugolotti A, Di Valentin C. Ab-Initio Spectroscopic Characterization of Melem-Based Graphitic Carbon Nitride Polymorphs. Nanomaterials. 2021; 11(7):1863. https://doi.org/10.3390/nano11071863
Chicago/Turabian StyleUgolotti, Aldo, and Cristiana Di Valentin. 2021. "Ab-Initio Spectroscopic Characterization of Melem-Based Graphitic Carbon Nitride Polymorphs" Nanomaterials 11, no. 7: 1863. https://doi.org/10.3390/nano11071863
APA StyleUgolotti, A., & Di Valentin, C. (2021). Ab-Initio Spectroscopic Characterization of Melem-Based Graphitic Carbon Nitride Polymorphs. Nanomaterials, 11(7), 1863. https://doi.org/10.3390/nano11071863