Beam Theory of Thermal–Electro-Mechanical Coupling for Single-Wall Carbon Nanotubes
Abstract
1. Introduction
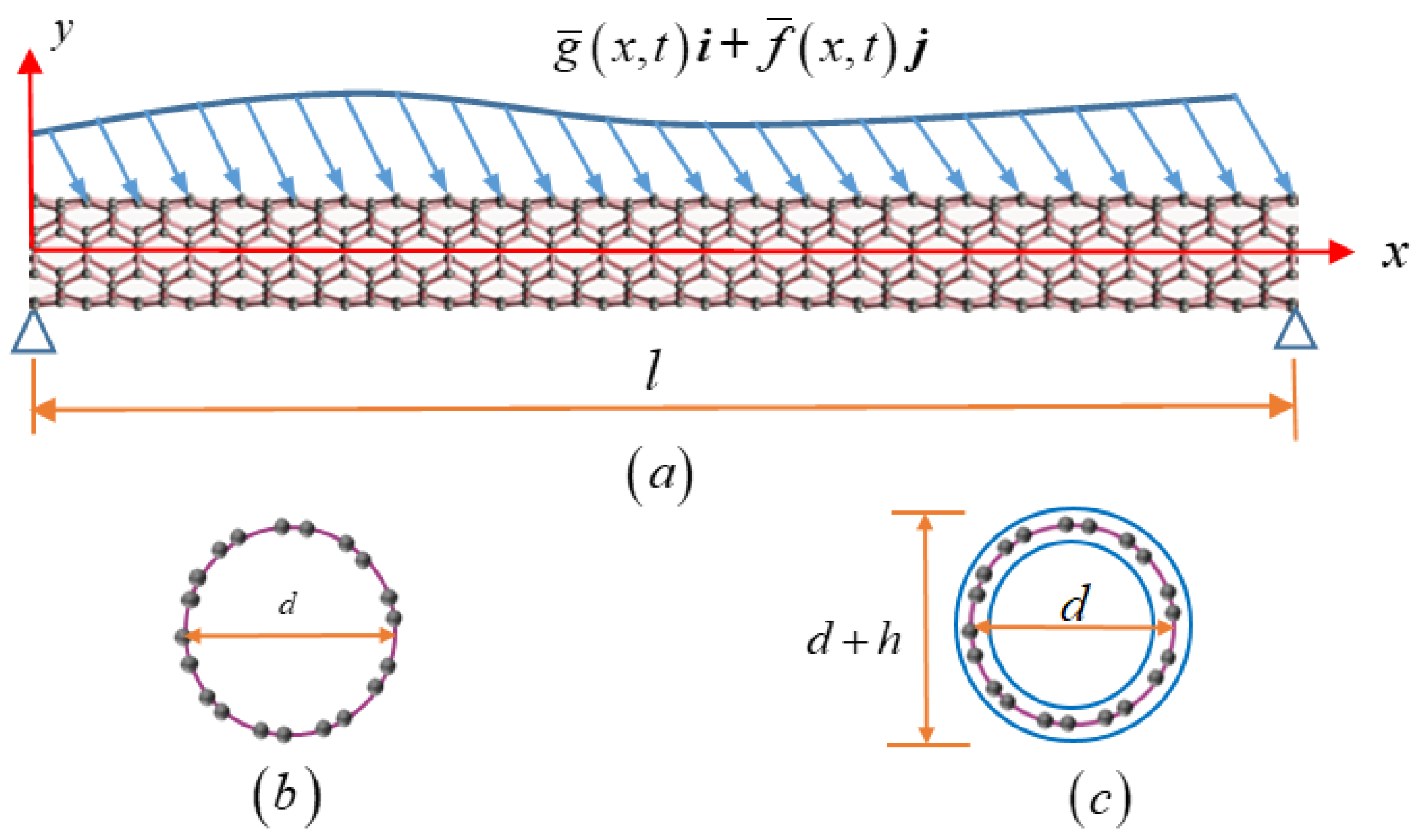
2. Thermal–Electro-Mechanical Coupling Beam Model with Two Independent Stiffnesses
3. Example and Discussion
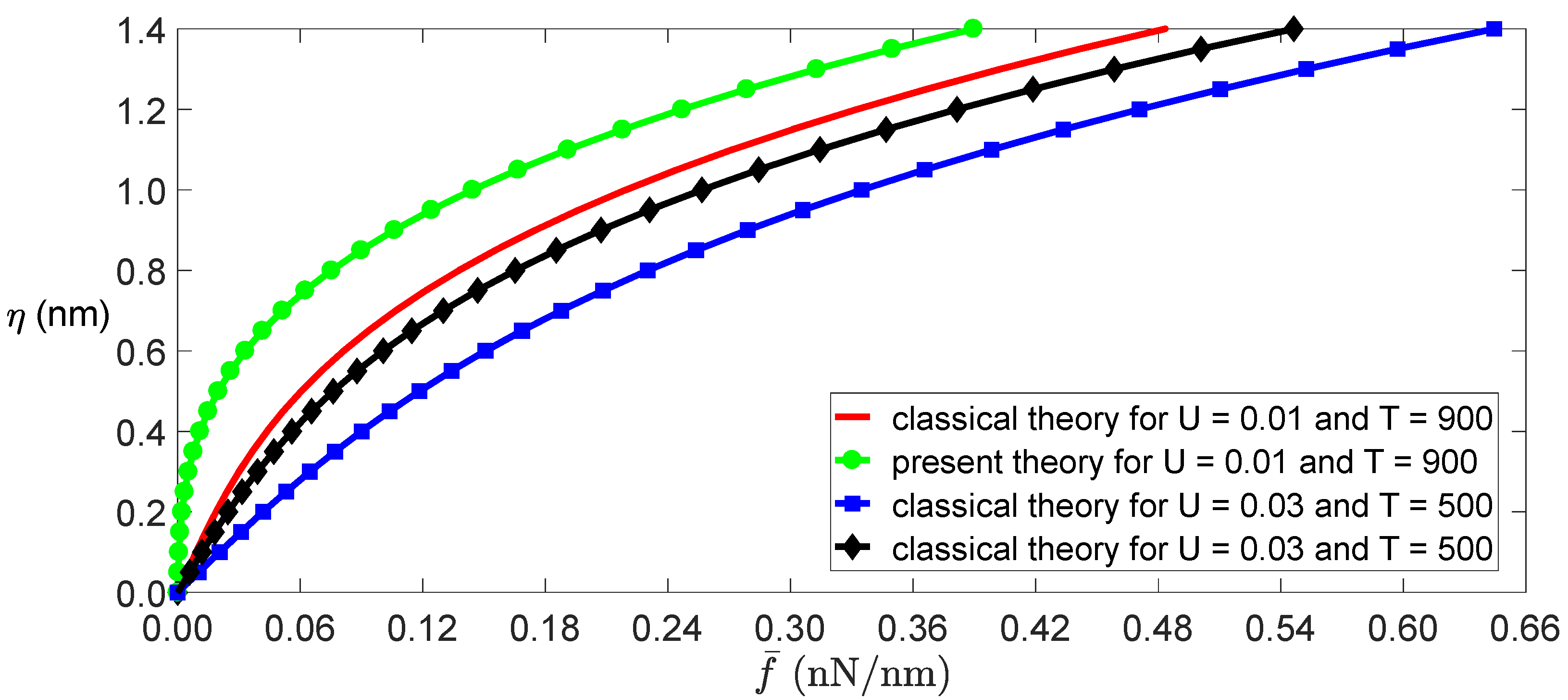
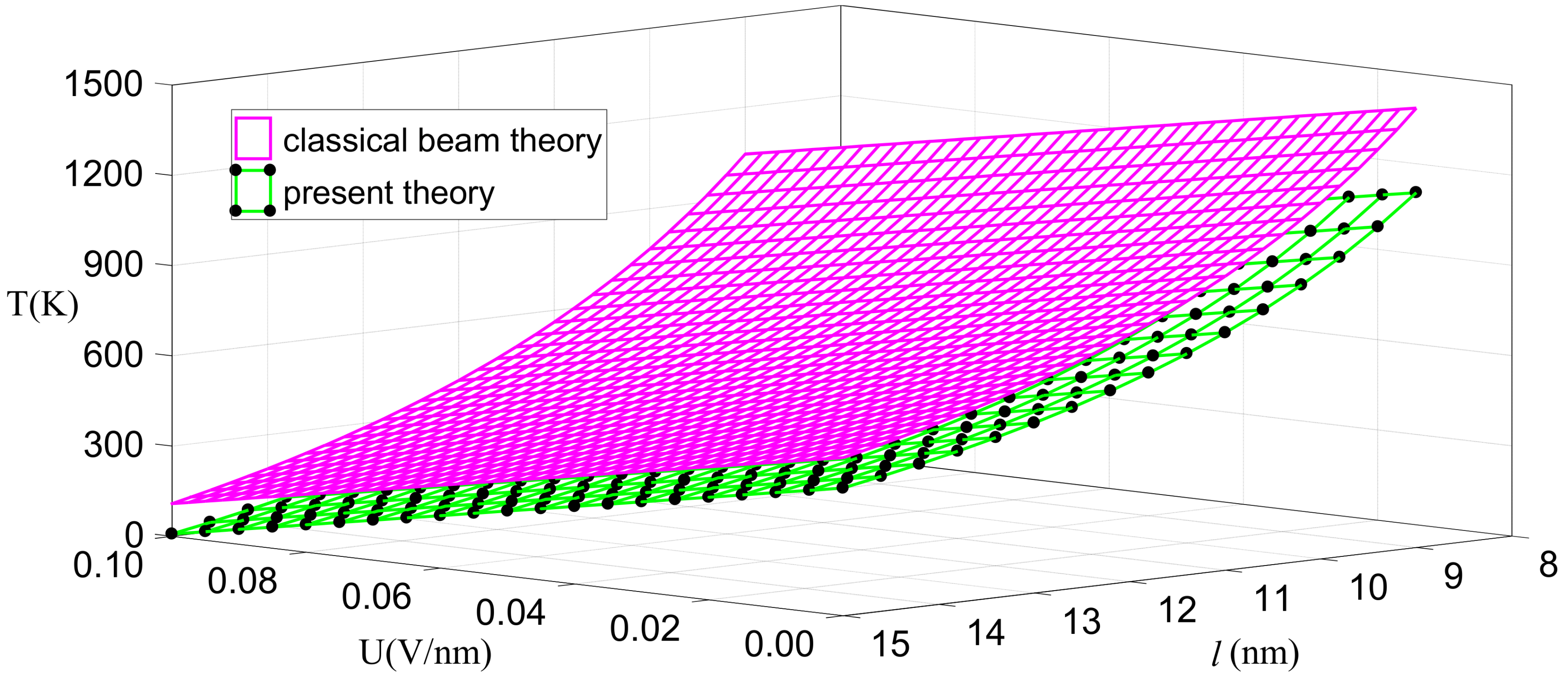
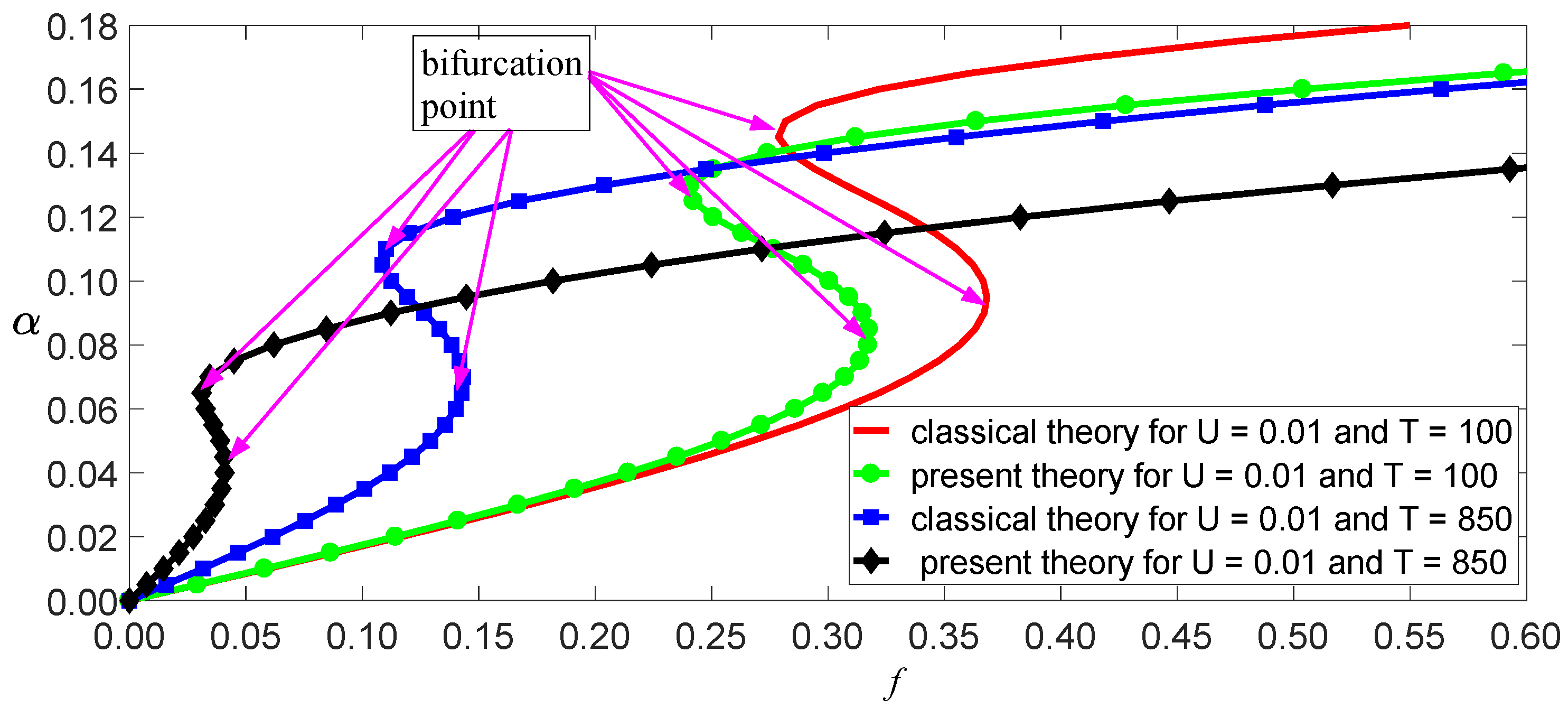
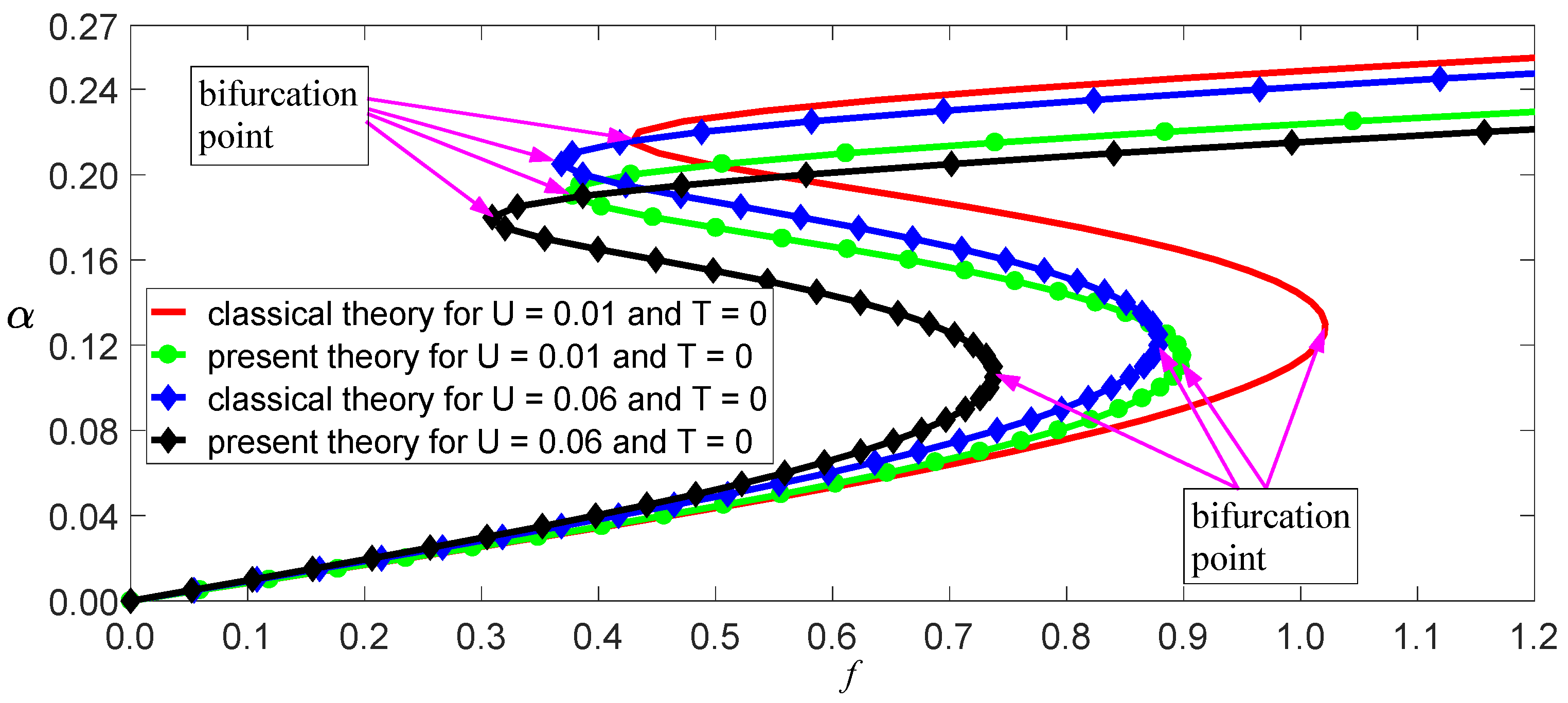
3.1. Static Bending Deformation and Buckling
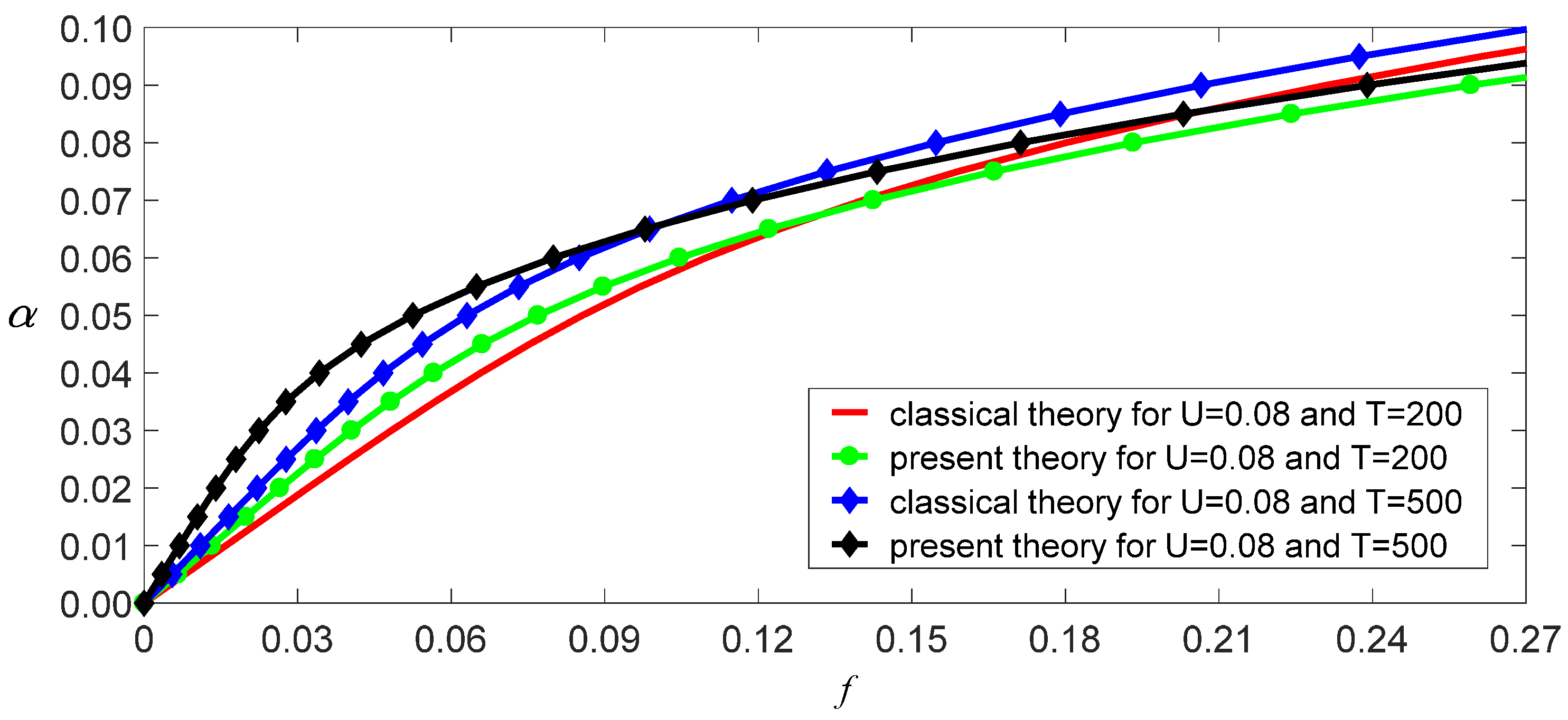
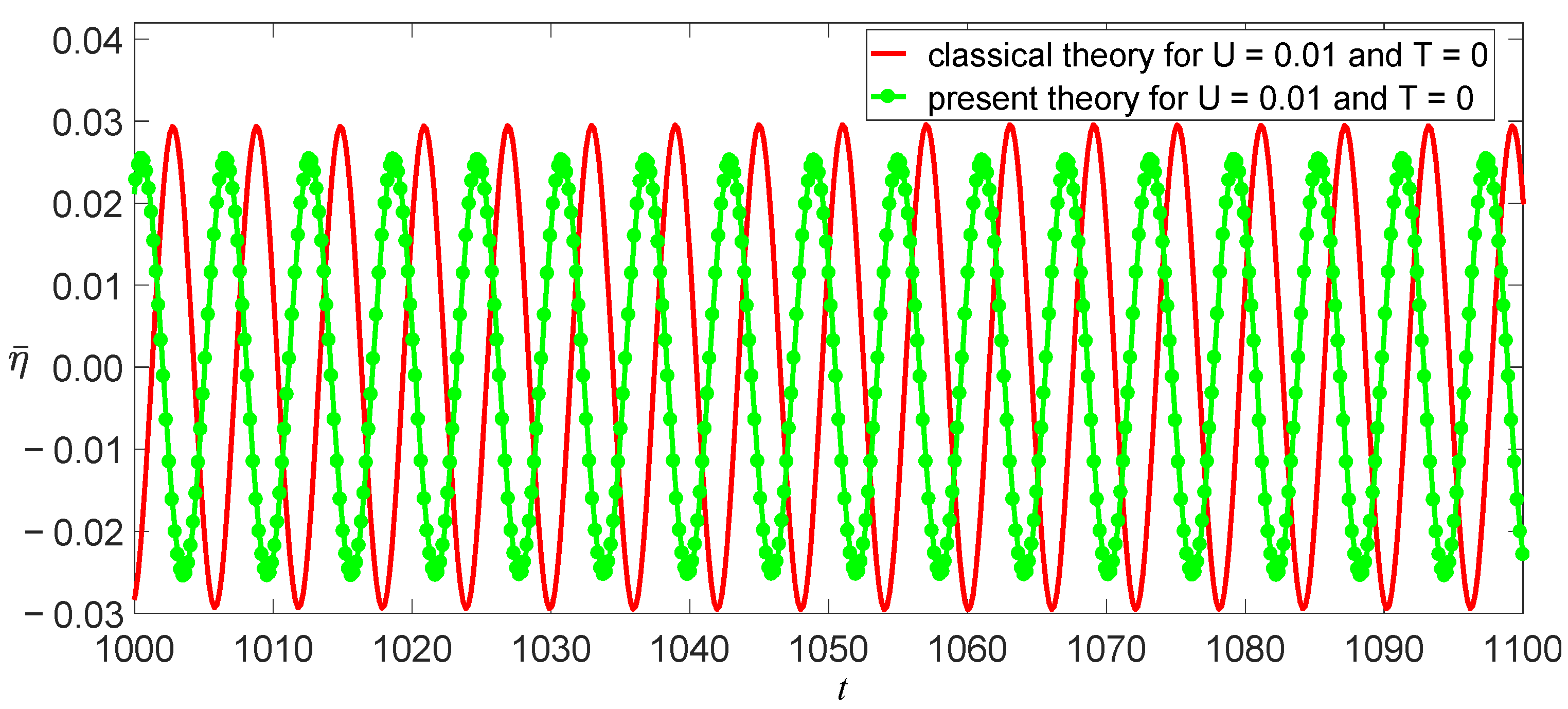
3.2. Nonlinear Bending Vibrations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kis, A.; Zettl, A. Nanomechanics of carbon nanotubes. Philos. Trans. 2008, 366, 1591–1611. [Google Scholar] [CrossRef]
- Stevens, K.; Tran-Duc, T.; Thamwattana, N.; Hill, J.M. Continuum modeling for interacting coronene molecules with a carbon nanotube. Nanomaterials 2020, 10, 152. [Google Scholar] [CrossRef]
- Sakharova, N.A.; Pereira, A.F.G.; Antunes, J.M.; Brett, C.M.A.; Fernandes, J.V. Mechanical characterization of single-walled carbon nanotubes: Numerical simulation study. Comp. Part B Eng. 2015, 75, 73–85. [Google Scholar] [CrossRef]
- Rafii-Tabar, H.; Ghavanloo, E.; Fazelzadeh, S.A. Nonlocal continuum-based modeling of mechanical characteristics of nanoscopic structures. Phys. Rep. 2016, 638, 1–97. [Google Scholar] [CrossRef]
- Zhu, T.; Chen, D. Nanomechanics of Materials: Overview. In Handbook of Materials Modeling; Andreoni, W., Yip, S., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Tanaka, K.; Iijima, S. (Eds.) Carbon Nanotubes and Graphene, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Shoukat, R.; Khan, M.I. Carbon nanotubes: A review on properties, synthesis methods and applications in micro and nanotechnology. Microsyst. Technol. 2021, 1–10. [Google Scholar] [CrossRef]
- Akinwande, D.; Brennan, C.J.; Bunch, J.S.; Egberts, P.; Felts, J.R.; Gao, H.; Huang, R.; Kim, J.-S.; Li, T.; Li, Y.; et al. A review on mechanics and mechanical properties of 2D materials—Graphene and beyond. Extrem. Mech. Lett. 2017, 13, 42–77. [Google Scholar] [CrossRef]
- Izadi, R.; Tuna, M.; Trovalusci, P.; Ghavanloo, E. Torsional Characteristics of Carbon Nanotubes: Micropolar Elasticity Models and Molecular Dynamics Simulation. Nanomaterials 2021, 11, 453. [Google Scholar] [CrossRef]
- Duan, W.H.; Wang, C.M.; Zhang, Y.Y. Calibration of nonlocal scaling effect parameter for free vibration of carbon nanotubes by molecular dynamics. J. Appl. Phys. 2007, 101, 024305. [Google Scholar] [CrossRef]
- Papanikos, P.; Nikolopoulos, D.D.; Tserpes, K.I. Equivalent beams for carbon nanotubes. Comput. Mater. Sci. 2008, 43, 345e52. [Google Scholar] [CrossRef]
- Huang, K.; Cai, X.; Wang, M. Bernoulli-Euler beam theory of single-walled carbon nanotubes based on nonlinear stress-strain relationship. Mater. Res. Express 2020, 7, 125003. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, S.; Li, J.; Li, Z. Nonlocal nonlinear model of Bernoulli–Euler nanobeam with small initial curvature and its application to single-walled carbon nanotubes. Microsyst. Technol. 2019, 25, 4303–4310. [Google Scholar] [CrossRef]
- Chandel, V.S.; Wang, G.; Talha, M. Advances in modelling and analysis of nano structures: A review. Nanotechnol. Rev. 2020, 9, 230–258. [Google Scholar] [CrossRef]
- Askes, H.; Aifantis, E.C. Gradient elasticity in statics and dynamics: An overview of formulations, length scale identification procedures, finite element implementations and new results. Int. J. Solids Struct. 2011, 48, 1962–1990. [Google Scholar] [CrossRef]
- Zhang, D.B.; Akatyeva, E.; Dumitrică, T. Bending ultrathin graphene at the margins of continuum mechanics. Phys. Rev. Lett. 2011, 106, 255503. [Google Scholar] [CrossRef]
- Wei, Y.; Yang, R. Nanomechanics of graphene. Natl. Sci. Rev. 2019, 6, 148–172. [Google Scholar]
- Jiang, J.W.; Wang, B.S.; Wang, J.S.; Park, H.S. A review on the flexural mode of graphene: Lattice dynamics, thermal conduction, thermal expansion, elasticity and nanomechanical resonance. J. Phys. Condens. Matter 2015, 27, 083001. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, B.; Huang, Y.; Hwang, K.C. Thermal expansion of single wall carbon nanotubes. J. Eng. Mater. Technol. 2004, 126, 265–270. [Google Scholar] [CrossRef]
- Jiang, J.W.; Wang, J.S.; Li, B. Thermal expansion in single-walled carbon nanotubes and graphene: Nonequilibrium Green’s function approach. Phys. Rev. B 2009, 80, 205429. [Google Scholar] [CrossRef]
- Deng, L.; Young, R.J.; Kinloch, I.A.; Sun, R.; Zhang, G.; Noé, L.; Monthioux, M. Coefficient of thermal expansion of carbon nanotubes measured by Raman spectroscopy. Appl. Phys. Lett. 2014, 104, 051907. [Google Scholar] [CrossRef]
- Guo, W.; Guo, Y. Giant axial electrostrictive deformation in carbon nanotubes. Phys. Rev. Lett. 2003, 91, 115501. [Google Scholar] [CrossRef]
- Li, J.; Shen, H. The mechanical property of single-walled carbon nanotube under combined electromechanical loading. Mol. Phys. 2016, 114, 2144–2156. [Google Scholar] [CrossRef]
- Liang, H.; Upmanyu, M. Axial-strain-induced torsion in single-walled carbon nanotubes. Phys. Rev. Lett. 2006, 96, 165501. [Google Scholar] [CrossRef]
- Singh, R.; Kumar, S.; Kumar, A. Effect of intrinsic twist and orthotropy on extension–twist–inflation coupling in compressible circular tubes. J. Elast. 2017, 128, 175–201. [Google Scholar] [CrossRef]
- Kumar, A.; Mukherjee, S.; Paci, J.T.; Chandraseker, K.; Schatz, G.C. A rod model for three dimensional deformations of single-walled carbon nanotubes. Int. J. Solids Struct. 2011, 48, 2849–2858. [Google Scholar] [CrossRef]
- Chandraseker, K.; Mukherjee, S.; Paci, J.T.; Schatz, G.C. An atomistic-continuum Cosserat rod model of carbon nanotubes. J. Mech. Phys. Solids 2009, 57, 932–958. [Google Scholar] [CrossRef]
- Plischke, M.; Bergersen, B. Equilibrium Statistical Physics; World Scientific Publishing Company: Singapore, 2006. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity; Pergamon: New York, NY, USA, 1986. [Google Scholar]
- Zhang, C.L.; Shen, H.S. Temperature-dependent elastic properties of single-walled carbon nanotubes: Prediction from molecular dynamics simulation. Appl. Phys. Lett. 2006, 89, 081904. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Pai, P.F. Linear and Nonlinear Structural Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Washizu, K. Variational Methods in Elasticity and Plasticity; Pergamon Press: Oxford, UK, 1968. [Google Scholar]
- Lacarbonara, W. Nonlinear Structural Mechanics: Theory, Dynamical Phenomena and Modeling; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Luongo, A.; Di Egidio, A. Bifurcation equations through multiple-scales analysis for a continuous model of a planar beam. Nonlinear Dyn. 2005, 41, 171–190. [Google Scholar] [CrossRef]
- Emam, S.A.; Nayfeh, A.H. Nonlinear responses of buckled beams to subharmonic-resonance excitations. Nonlinear Dyn. 2004, 35, 105–122. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; Wiley: New York, NY, USA, 1980. [Google Scholar]



| Classical model | ||||
| Independent stiffness model |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, K.; Yao, J. Beam Theory of Thermal–Electro-Mechanical Coupling for Single-Wall Carbon Nanotubes. Nanomaterials 2021, 11, 923. https://doi.org/10.3390/nano11040923
Huang K, Yao J. Beam Theory of Thermal–Electro-Mechanical Coupling for Single-Wall Carbon Nanotubes. Nanomaterials. 2021; 11(4):923. https://doi.org/10.3390/nano11040923
Chicago/Turabian StyleHuang, Kun, and Ji Yao. 2021. "Beam Theory of Thermal–Electro-Mechanical Coupling for Single-Wall Carbon Nanotubes" Nanomaterials 11, no. 4: 923. https://doi.org/10.3390/nano11040923
APA StyleHuang, K., & Yao, J. (2021). Beam Theory of Thermal–Electro-Mechanical Coupling for Single-Wall Carbon Nanotubes. Nanomaterials, 11(4), 923. https://doi.org/10.3390/nano11040923





