Influence of Sulphur Content on Structuring Dynamics during Nanosecond Pulsed Direct Laser Interference Patterning
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
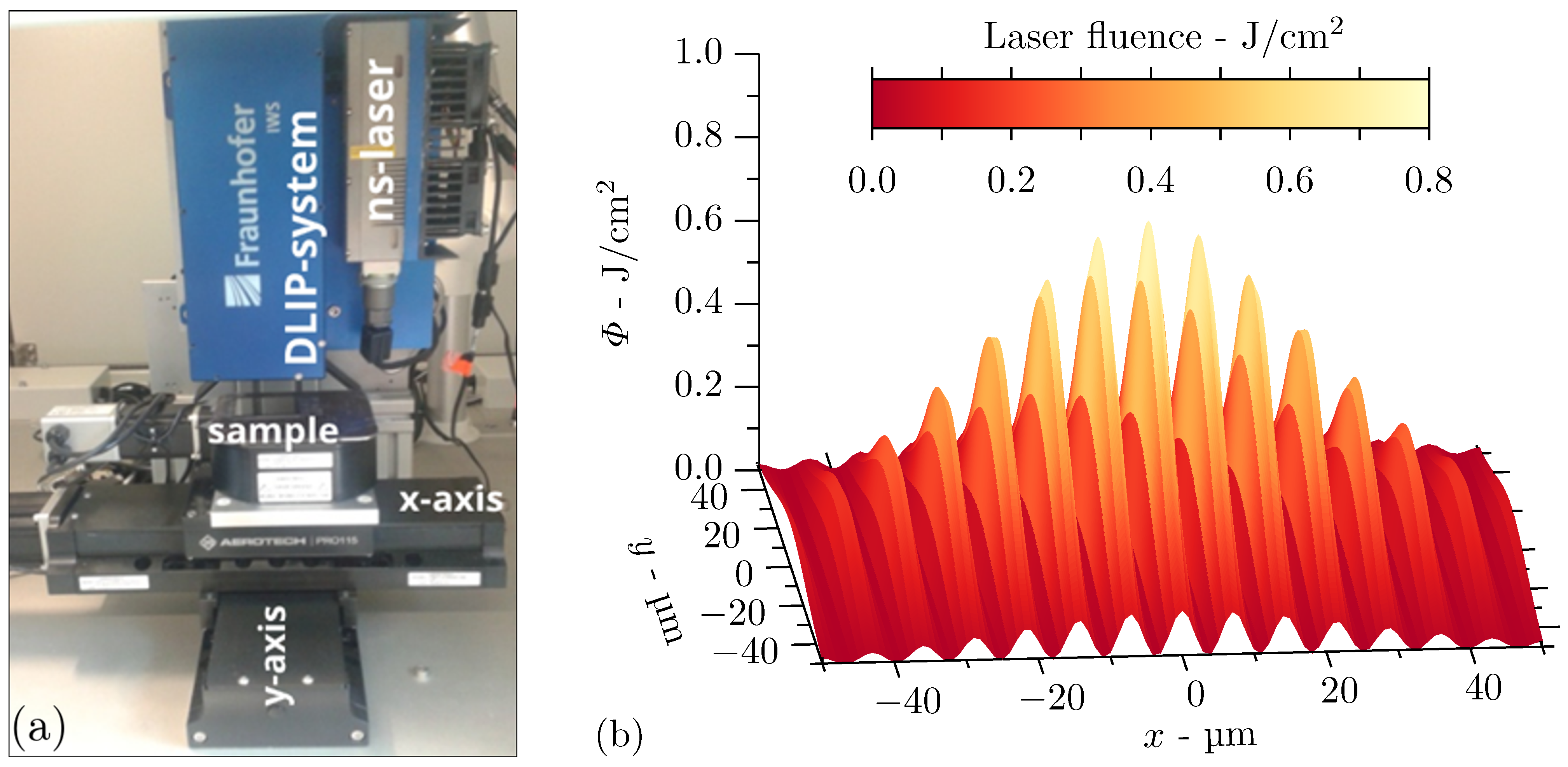
2.2. Nanosecond Direct Laser Interference Patterning
2.3. Surface Characterisation
2.4. Mathematical Model
2.5. Numerical Simulation
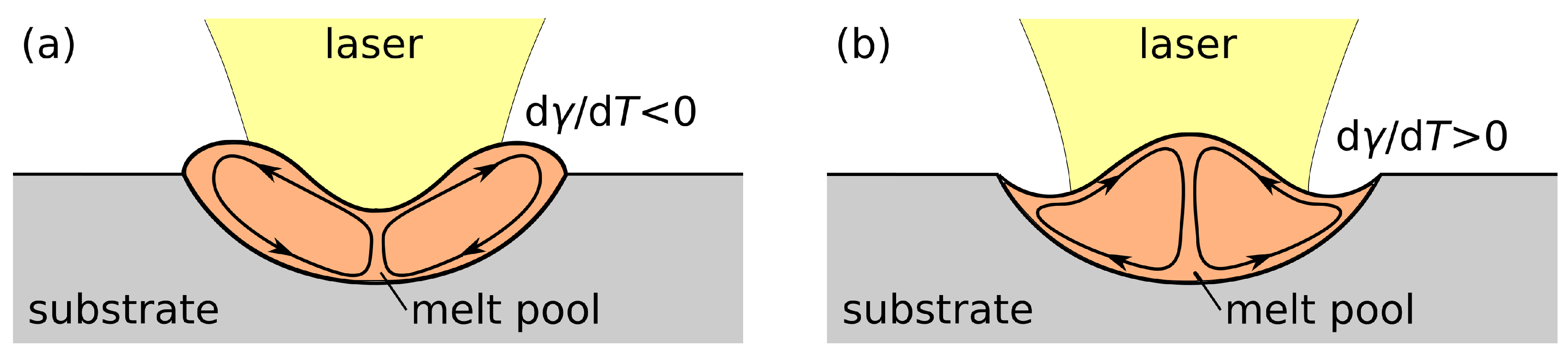
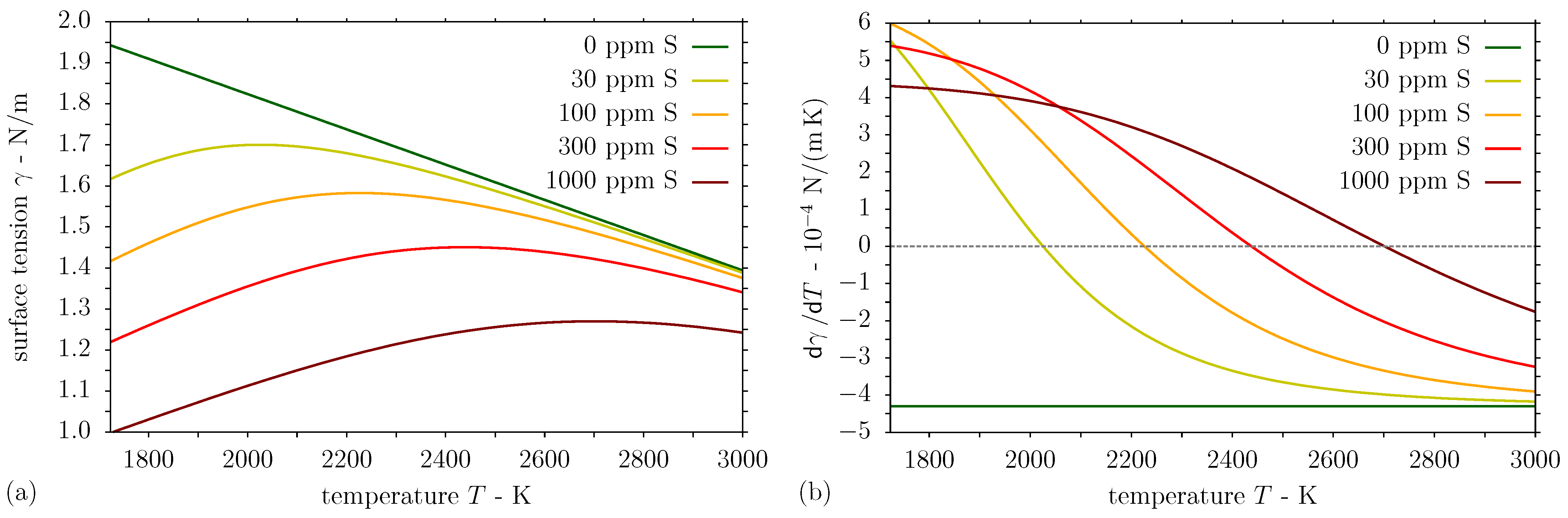
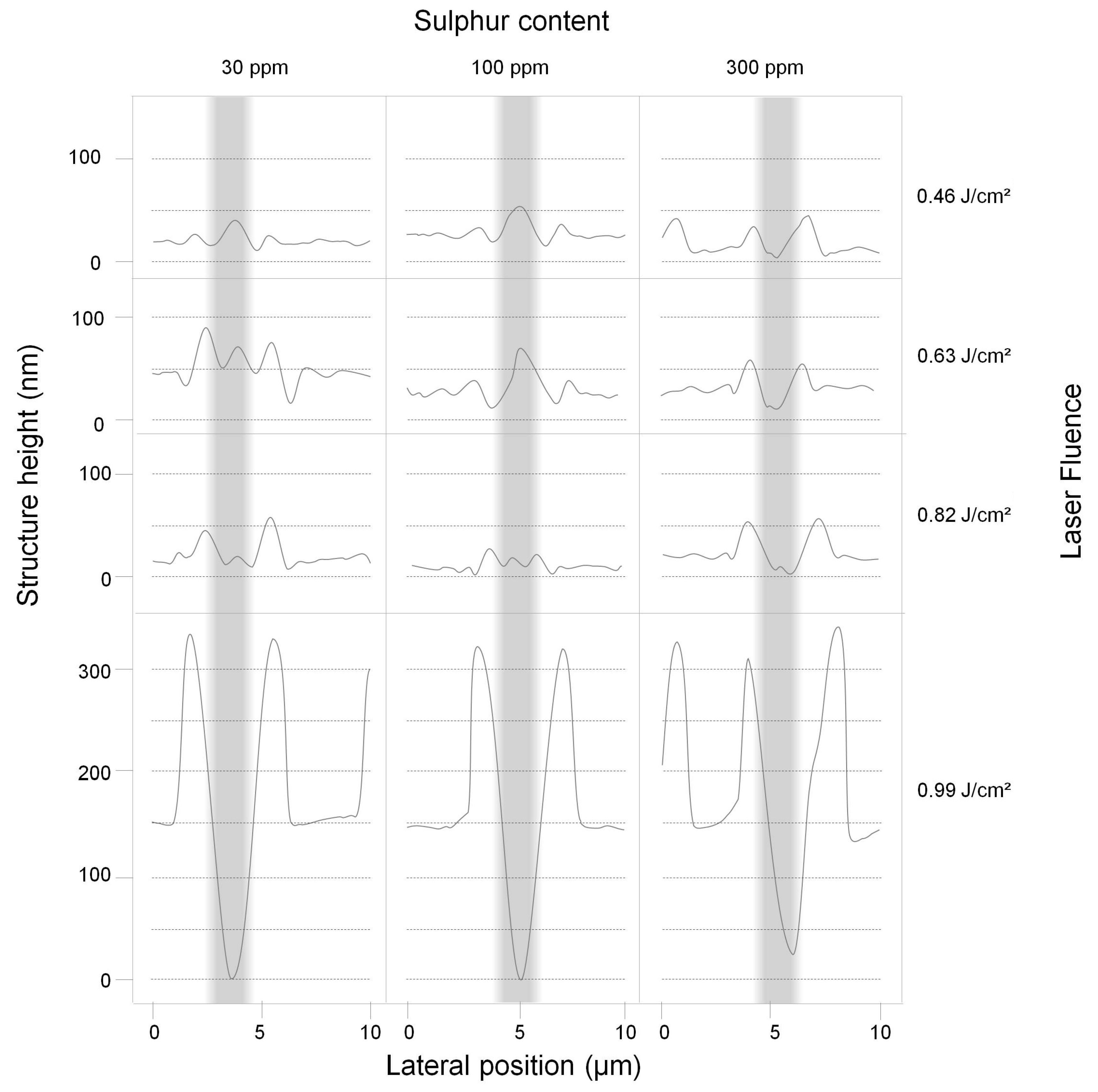
3. Results and Discussion
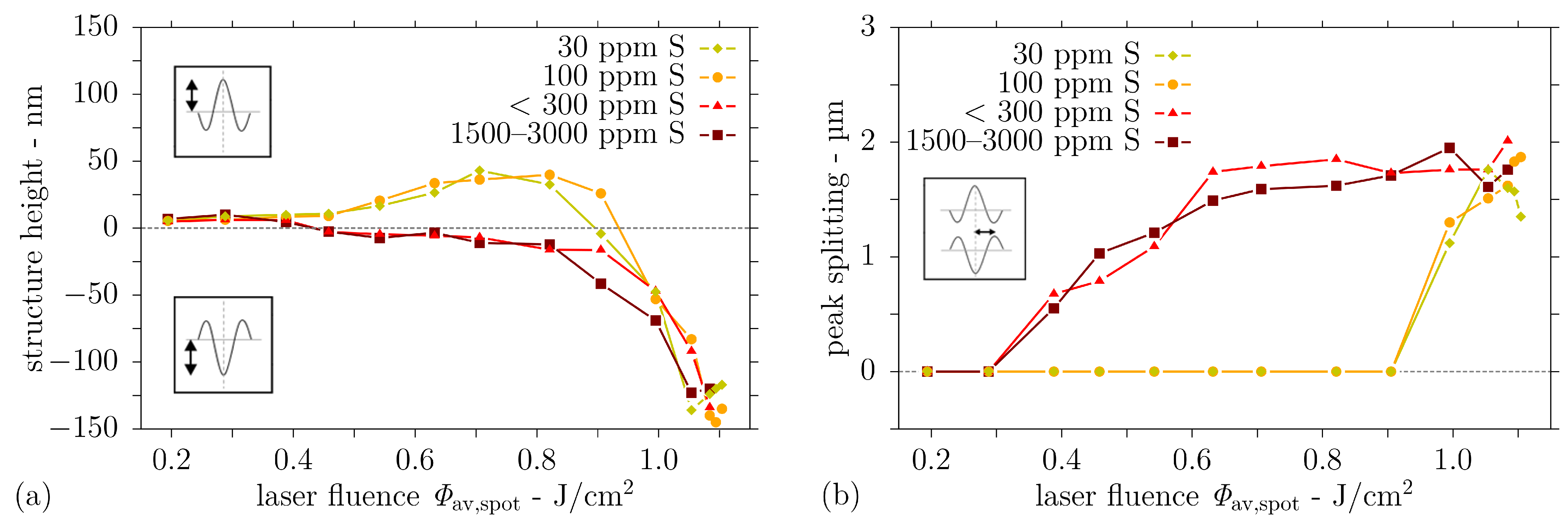
3.1. Experimental Results
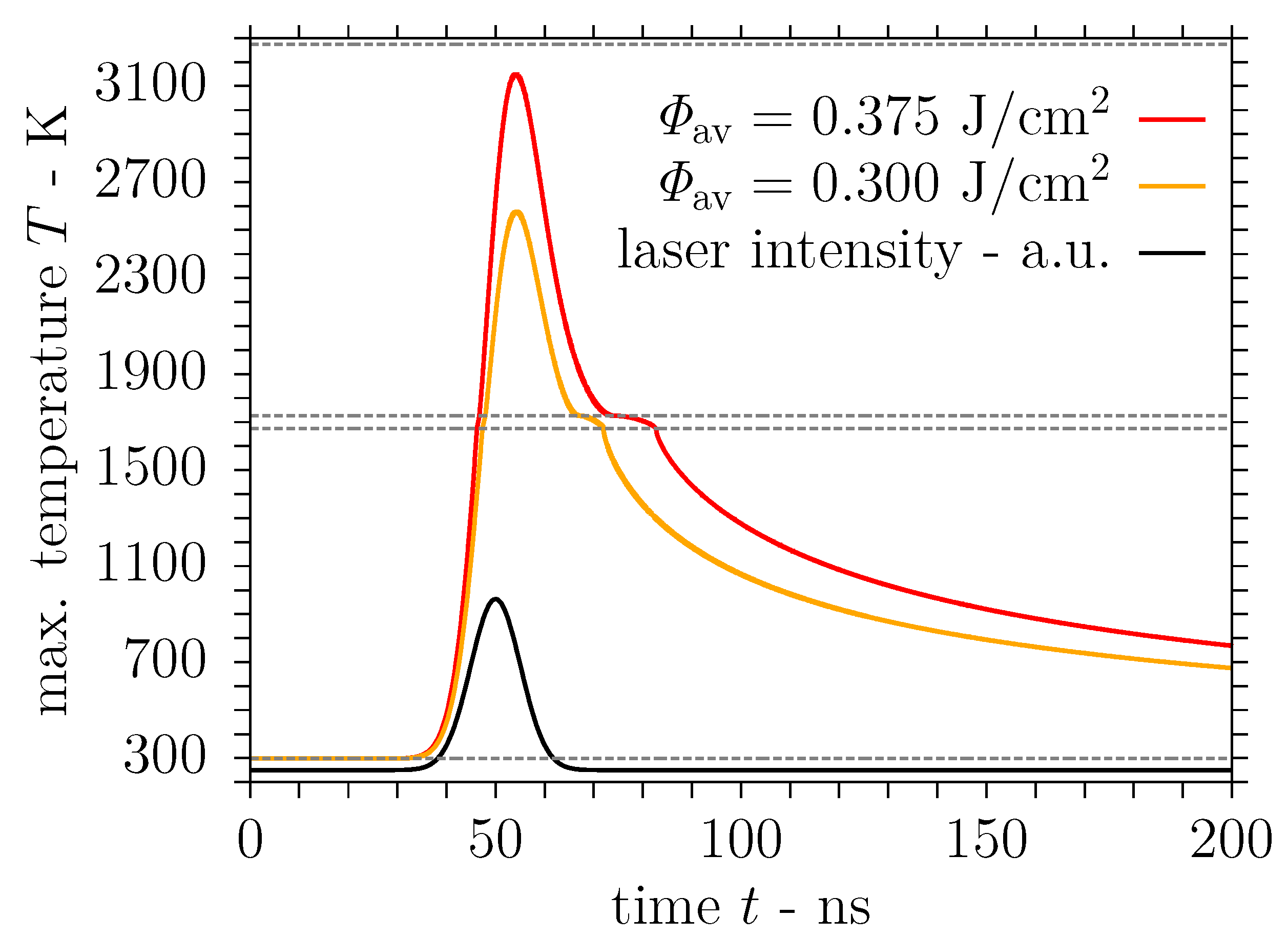
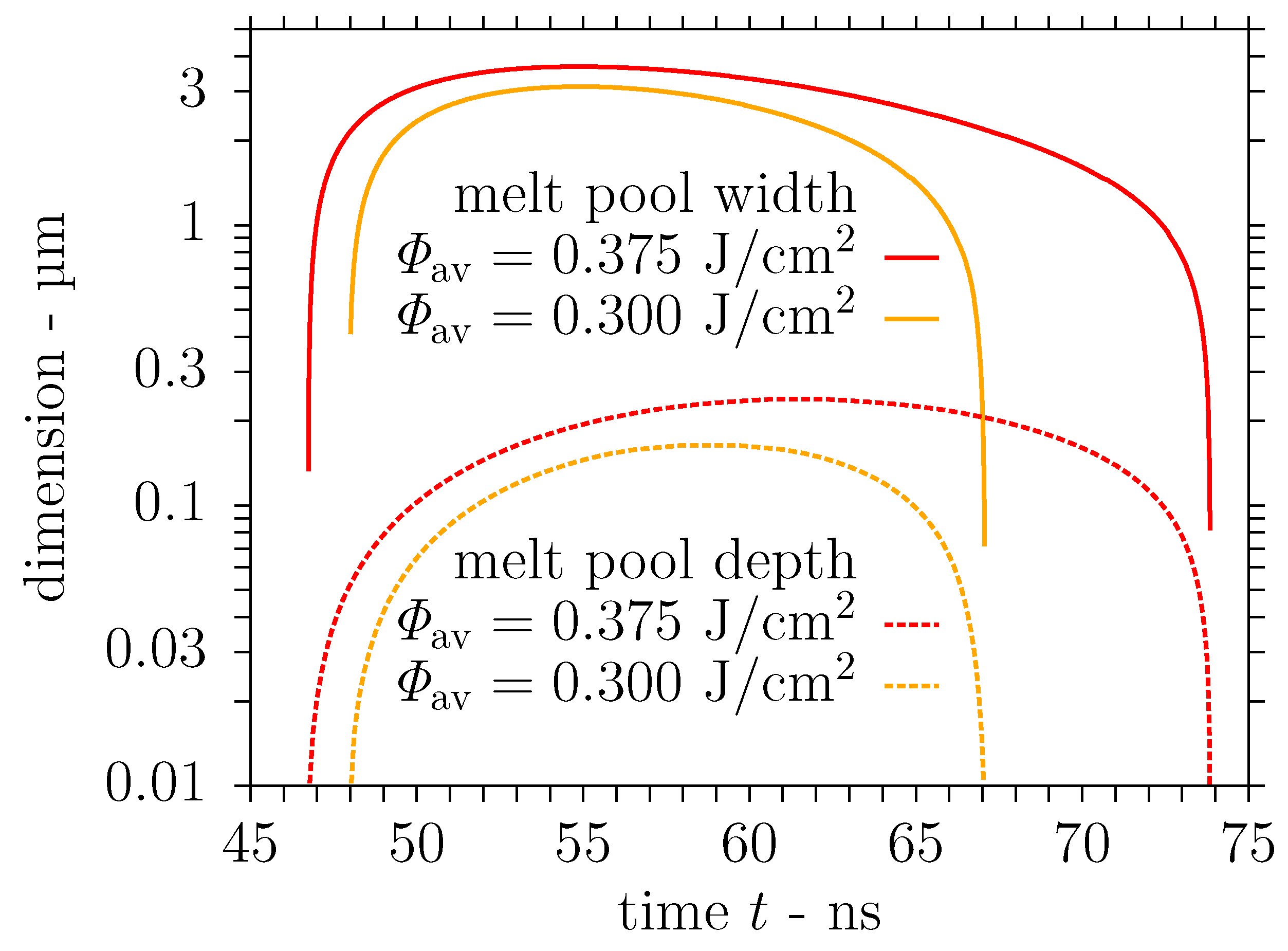
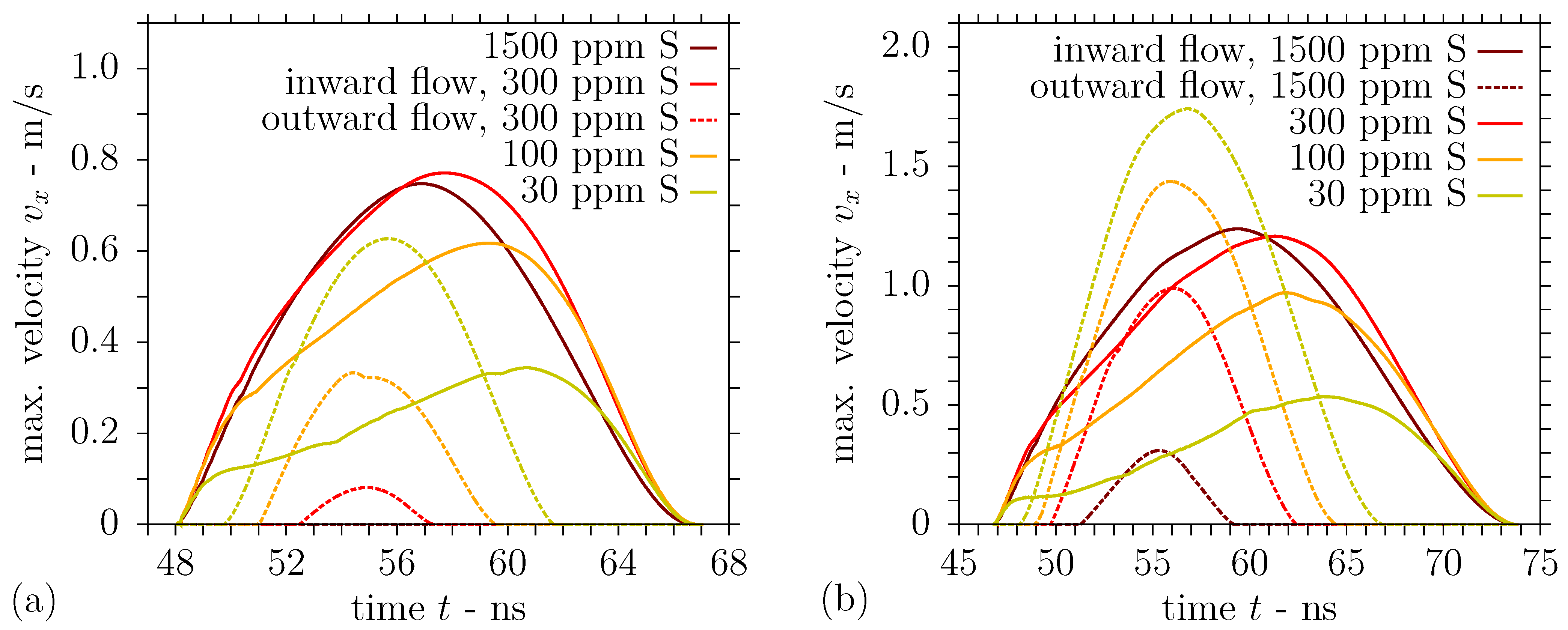
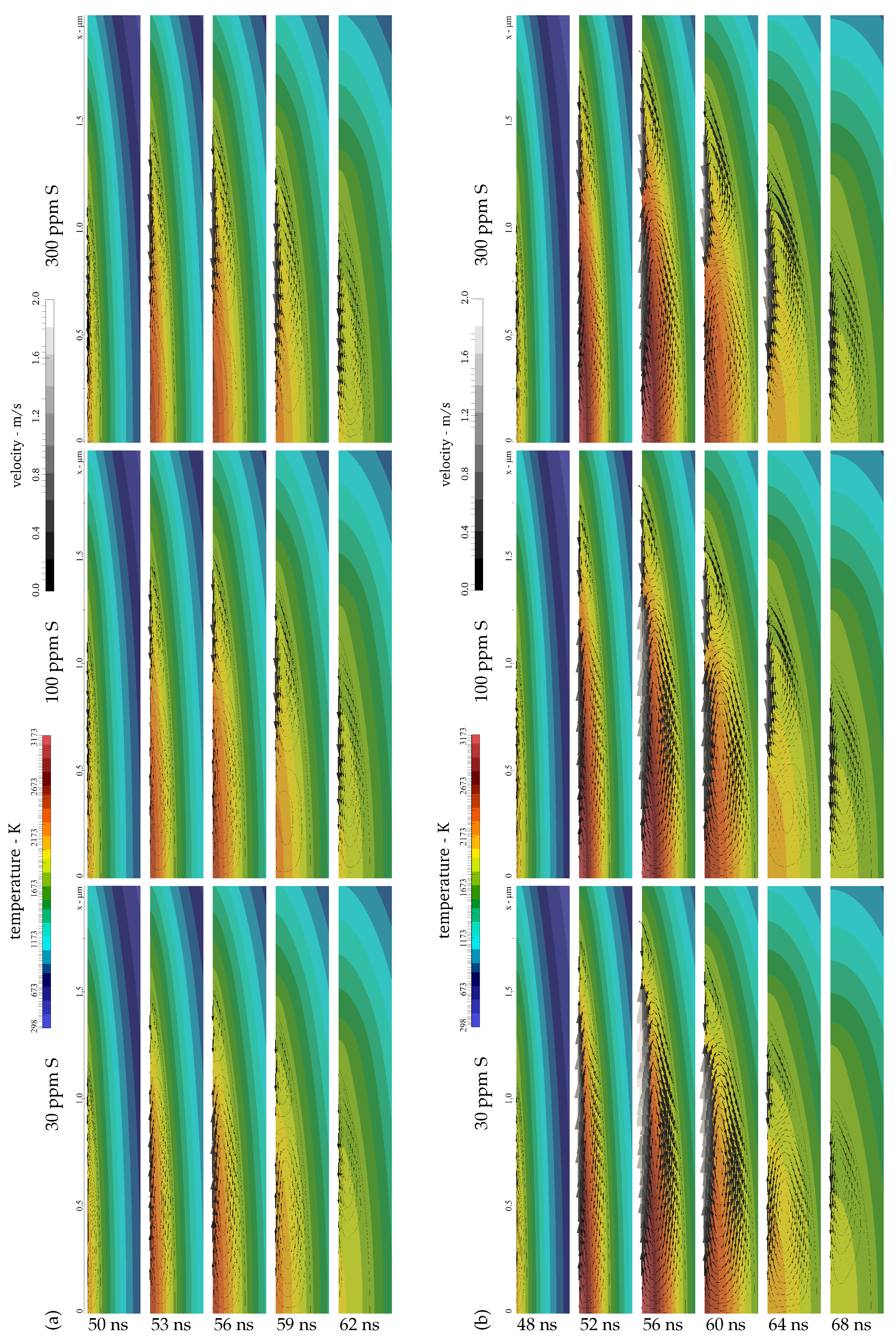
3.2. Simulation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AISI | American Iron and Steel Institute |
| DLIP | direct laser interference patterning |
| DOE | diffractive optical element |
| FOV | field of view |
| FWHM | full width at half maximum |
| LASER | light amplification by stimulated emission of radiation |
| Nd:YLF | neodymium-doped yttrium lithium fluoride |
| ppm | parts per million |
| SEM | scanning electron microscope |
| SPH | smoothed particle hydrodynamics |
| TEM | fundamental transverse electromagnetic mode |
Appendix A. Governing Equations and Boundary Conditions
References
- Ball, P. Shark skin and other solutions. Nature 1999, 400, 507–509. [Google Scholar] [CrossRef]
- Dusser, B.; Sagan, Z.; Soder, H.; Faure, N.; Colombier, J.P.; Jourlin, M.; Audouard, E. Controlled nanostructures formation by ultra fast laser pulses for color marking. Opt. Express 2010, 18, 2913–2924. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.G.; Lim, H.S.; Lee, D.Y.; Kwak, D.; Cho, K. Tunable anisotropic wettability of rice leaf-like wavy surfaces. Adv. Funct. Mater. 2013, 23, 547–553. [Google Scholar] [CrossRef]
- Ahsan, M.S.; Ahmed, F.; Kim, Y.G.; Lee, M.S.; Jun, M.B.G. Colorizing stainless steel surface by femtosecond laser induced micro/nano-structures. Appl. Surf. Sci. 2011, 257, 7771–7777. [Google Scholar] [CrossRef]
- Verma, L.K.; Sakhuja, M.; Son, J.; Danner, A.J.; Yang, H.; Zeng, H.C.; Bhatia, C.S. Self-cleaning and antireflective packaging glass for solar modules. Renew. Energy 2011, 36, 2489–2493. [Google Scholar] [CrossRef]
- Madou, M.J. Manufacturing Techniques for Microfabrication and Nanotechnology, 3rd ed.; Fundamentals of microfabrication and nanotechnology; CRC Press: Boca Raton, FL, USA, 2011; Volume II. [Google Scholar]
- Matsui, S. Three-dimensional nanostructure fabrication by focused ion beam chemical vapor deposition. In Springer Handbook of Nanotechnology, 2nd ed.; Bhushan, B., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; Chapter 6; pp. 179–195. [Google Scholar] [CrossRef]
- Etsion, I. State of the Art in Laser Surface Texturing. J. Tribol. 2005, 127, 248–253. [Google Scholar] [CrossRef]
- Bonse, J.; Kirner, S.V.; Griepentrog, M.; Spaltmann, D.; Krüger, J. Femtosecond Laser Texturing of Surfaces for Tribological Applications. Materials 2018, 11, 801. [Google Scholar] [CrossRef]
- Tripathy, A.; Sen, P.; Su, B.; Briscoe, W.H. Natural and bioinspired nanostructured bactericidal surfaces. Adv. Colloid Interface Sci. 2017, 248, 85–104. [Google Scholar] [CrossRef]
- Alamri, S.; Aguilar-Morales, A.I.; Lasagni, A.F. Controlling the wettability of polycarbonate substrates by producing hierarchical structures using direct laser interference patterning. Eur. Polym. J. 2018, 99, 27–37. [Google Scholar] [CrossRef]
- Roch, T.; Benke, D.; Milles, S.; Roch, A.; Kunze, T.; Lasagni, A. Dependence between friction of laser interference patterned carbon and the thin film morphology. Diamond Relat. Mater. 2015, 55, 16–21. [Google Scholar] [CrossRef]
- Baharin, A.F.S.; Ghazali, M.J.; Wahab, J.A. Laser surface texturing and its contribution to friction and wear reduction: A brief review. Ind. Lubr. Tribol. 2016, 68, 57–66. [Google Scholar] [CrossRef]
- Bremus-Koebberling, E.A.; Beckemper, S.; Koch, B.; Gillner, A. Nano structures via laser interference patterning for guided cell growth of neuronal cells. J. Laser Appl. 2012, 24, 042013. [Google Scholar] [CrossRef]
- Langheinrich, D.; Yslas, E.; Broglia, M.; Rivarola, V.; Acevedo, D.; Lasagni, A. Control of cell growth direction by direct fabrication of periodic micro- and submicrometer arrays on polymers. J. Polym. Sci. Part B Polym. Phys. 2012, 50, 415–422. [Google Scholar] [CrossRef]
- Rößler, F.; Kunze, T.; Lasagni, A.F. Fabrication of diffraction based security elements using direct laser interference patterning. Opt. Express 2017, 25, 22959–22970. [Google Scholar] [CrossRef]
- Bieda, M.; Schmädicke, C.; Roch, T.; Lasagni, A. Ultra-low friction on 100Cr6-steel surfaces after direct laser interference patterning. Adv. Eng. Mater. 2015, 17, 102–108. [Google Scholar] [CrossRef]
- Lasagni, A.F.; Beyer, E. Fabrication of periodic submicrometer and micrometer arrays using laser interference-based methods. In Laser Surface Engineering: Processes and Applications, 1st ed.; Lawrence, J., Waugh, D.G., Eds.; Woodhead Publishing Series in Electronic and Optical Materials; Woodhead Publishing: Cambridge, UK, 2015; Chapter 17; Volume 65, pp. 423–439. [Google Scholar] [CrossRef]
- Bieda, M.; Siebold, M.; Lasagni, A.F. Fabrication of sub-micron surface structures on copper, stainless steel and titanium using picosecond laser interference patterning. Appl. Surf. Sci. 2016, 387, 175–182. [Google Scholar] [CrossRef]
- Nebel, C.; Dahlheimer, B.; Schöniger, S.; Stutzmann, M. Sub-micron silicon structures for thin film solar cells. Phys. Status Solidi B 1996, 194, 55–67. [Google Scholar] [CrossRef]
- Lasagni, A.; Holzapfel, C.; Mücklich, F. Periodic pattern formation of intermetallic phases with long range order by laser interference metallurgy. Adv. Eng. Mater. 2005, 7, 487–492. [Google Scholar] [CrossRef]
- Chichkov, B.N.; Momma, C.; Nolte, S.; von Alvensleben, F.; Tünnermann, A. Femtosecond, picosecond and nanosecond laser ablation of solids. Appl. Phys. A: Mater. Sci. Process. 1996, 63, 109–115. [Google Scholar] [CrossRef]
- Semerok, A.; Chaléard, C.; Detalle, V.; Lacour, J.L.; Mauchien, P.; Meynadier, P.; Nouvellon, C.; Sallé, B.; Palianov, P.; Perdrix, M. Experimental investigations of laser ablation efficiency of pure metals with femto, pico and nanosecond pulses. Appl. Surf. Sci. 1999, 138–139, 311–314. [Google Scholar] [CrossRef]
- D’Alessandria, M.; Lasagni, A.; Mücklich, F. Direct micropatterning of aluminum substrates via laser interference metallurgy. Appl. Surf. Sci. 2008, 255, 3210–3216. [Google Scholar] [CrossRef]
- Rosenthal, D. Mathematical theory of heat distribution during welding and cutting. Weld. J. 1941, 20, 220–234. [Google Scholar]
- Ishizaki, K.; Murai, K.; Kanbe, Y. Penetration in Arc Welding and Convection in Molten Metal; Technical Report, Study Group 212, Document 212-77-66; International Institute of Welding: Genoa, Italy, 1966. [Google Scholar]
- Kou, S.; Wang, Y.H. Weld pool convection and its effect. Weld. J. Res. Suppl. 1986, 65, 63–70. [Google Scholar]
- Mundra, K.; Debroy, T.; Zacharia, T.; David, S.A. Role of thermophysical properties in weld pool modeling. Weld. J. Res. Suppl. 1992, 71, 313–320. [Google Scholar]
- Heiple, C.R.; Roper, J.R. Mechanism for minor element effect on GTA fusion zone geometry. Weld. J. Res. Suppl. 1982, 61, 97–102. [Google Scholar]
- Atthey, D.R. A mathematical model for fluid flow in a weld pool at high currents. J. Fluid Mech. 1980, 98, 787–801. [Google Scholar] [CrossRef]
- Aidun, D.K.; Martin, S.A. Effect of sulfur and oxygen on weld penetration of high-purity austenitic stainless steels. J. Mater. Eng. Perform. 1997, 6, 496–502. [Google Scholar] [CrossRef]
- Mills, K.C.; Keene, B.J.; Brooks, R.F.; Shirali, A. Marangoni effects in welding. Phil. Trans. R. Soc. Lond. A 1998, 356, 911–925. [Google Scholar] [CrossRef]
- Oreper, G.M.; Eagar, T.W.; Szekely, J. Convection in arc weld pools. Weld. J. Res. Suppl. 1983, 62, 307–312. [Google Scholar]
- Oreper, G.M.; Szekely, J. Heat- and fluid-flow phenomena in weld pools. J. Fluid Mech. 1984, 147, 53–79. [Google Scholar] [CrossRef]
- Chan, C.; Mazumder, J.; Chen, M.M. A two-dimensional transient model for convection in laser melted pool. Metall. Trans. A 1984, 15, 2175–2184. [Google Scholar] [CrossRef]
- Kou, S.; Sun, D.K. Fluid flow and weld penetration in stationary arc welds. Metall. Trans. A 1985, 16, 203–213. [Google Scholar] [CrossRef]
- Kou, S.; Wang, Y.H. Three-dimensional convection in laser melted pools. Metall. Trans. A 1986, 17, 2265–2270. [Google Scholar] [CrossRef]
- Zacharia, T.; David, S.A.; Vitek, J.M.; Debroy, T. Weld pool development during GTA and laser beam welding of type 304 stainless steel, Part I—Theoretical analysis and Part II—Experimental correlation. Weld. J. Res. Suppl. 1989, 68, 499–509; 510–519. [Google Scholar]
- Zacharia, T.; David, S.A.; Vitek, J.M.; Kraus, H.G. Computational modeling of stationary gas-tungsten-arc weld pools and comparison to stainless steel 304 experimental results. Metall. Trans. B 1991, 22, 243–257. [Google Scholar] [CrossRef]
- Choo, R.T.C.; Szekely, J. Vaporization kinetics and surface temperature in a mutually coupled spot gas tungsten arc weld and weld pool. Weld. J. Res. Suppl. 1992, 71, 77–93. [Google Scholar]
- Choo, R.T.C.; Szekely, J.; David, S.A. On the calculation of the free surface temperature of gas-tungsten-arc weld pools from first principles: Part II. Modeling the weld pool and comparison with experiments. Metall. Trans. B 1992, 23, 371–384. [Google Scholar] [CrossRef]
- Lei, Y.; Shi, Y.; Murakawa, H.; Ueda, Y. Numerical analysis of the effect of sulfur content upon fluid flow and weld pool geometry for type 304 stainless steel. Trans. JWRI 1997, 26, 1–8. [Google Scholar]
- Bäuerle, D. Laser Processing and Chemistry, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Demuth, C.; Lasagni, A.F. An incompressible smoothed particle hydrodynamics (ISPH) model of direct laser interference patterning. Computation 2020, 8, 9. [Google Scholar] [CrossRef]
- Sahoo, P.; Debroy, T.; McNallan, M.J. Surface tension of binary metal—surface active solute systems under conditions relevant to welding metallurgy. Metall. Trans. B 1988, 19, 483–491. [Google Scholar] [CrossRef]
- McNallan, M.J.; Debroy, T. Effect of temperature and composition on surface tension in Fe-Ni-Cr alloys containing sulfur. Metall. Trans. B 1991, 22, 557–560. [Google Scholar] [CrossRef]
- Wang, Y.; Tsai, H.L. Effects of surface active elements on weld pool fluid flow and weld penetration in gas metal arc welding. Metall. Mater. Trans. B 2001, 32, 501–515. [Google Scholar] [CrossRef]
- Nepomnyashchy, A.; Simanovskii, I.; Legros, J.C. Interfacial Convection in Multilayer Systems; Springer Monographs in Mathematics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Demuth, C.; Bieda, M.; Lasagni, A.F.; Mahrle, A.; Wetzig, A.; Beyer, E. Thermal simulation of pulsed direct laser interference patterning of metallic substrates using the smoothed particle hydrodynamics approach. J. Mater. Process. Technol. 2012, 212, 689–699. [Google Scholar] [CrossRef]
- Mills, K.C. Recommended Values of Thermophysical Properties for Selected Commercial Alloys; Woodhead Publishing: Cambridge, UK, 2002. [Google Scholar]
- Steen, W.M.; Mazumder, J. Laser Material Processing, 4th ed.; Springer: London, UK, 2010. [Google Scholar]
- Valencia, J.J.; Quested, P.N. Thermophysical properties. In Casting, ASM Handbook; ASM International: Materials Park, OH, USA, 2008; Volume 15, pp. 468–481. [Google Scholar]
- Kaptay, G. A unified model for the cohesive enthalpy, critical temperature, surface tension and volumetric thermal expansion coefficient of liquid metals of bcc, fcc and hcp crystals. Mater. Sci. Eng. A 2008, 495, 19–26. [Google Scholar] [CrossRef]
- Nasch, P.M.; Steinemann, S.G. Density and thermal expansion of molten manganese, iron, nickel, copper, aluminum and tin by means of the gamma-ray attenuation technique. Phys. Chem. Liq. 1995, 29, 43–58. [Google Scholar] [CrossRef]
- Lide, D.R. (Ed.) Handbook of Chemistry and Physics, 85th ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Semak, V.; Matsunawa, A. The role of recoil pressure in energy balance during laser materials processing. J. Phys. D Appl. Phys. 1997, 30, 2541–2552. [Google Scholar] [CrossRef]
- Abbaschian, R.; Abbaschian, L.; Reed-Hill, R.E. Physical Metallurgy Principles, 4th ed.; The Hardening of Steel, Section 19.11 Dimensional Changes Associated with Transformation of Martensite; Cengage Learning: Stamford, CT, USA, 2010; Chapter 19; p. 631. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics; Course of Theoretical Physics; Pergamon Press: London, UK, 1959; Volume 6. [Google Scholar]



| Process Parameter | Symbol | Value |
|---|---|---|
| wavelength | 1053 nm | |
| intersection angle between beams | 0.1464 rad | |
| periodicity of interference pattern | 7.2 µm | |
| average fluence in interference spot | 0.300 J/cm2 | |
| fluence of interference pattern | 0.532 J/cm2 | |
| pulse duration (FWHM) | 12 ns | |
| pulse time | 50 ns | |
| simulation duration | 200 ns | |
| initial substrate temperature | 298.15 K | |
| gravitational acceleration | g | 9.81 m/s2 |
| Fourier number |
| Material Property | Symbol | AISI 304 Steel | Unit | References |
|---|---|---|---|---|
| solidus temperature | 1673 | K | [50] | |
| liquidus temperature | 1727 | K | [50] | |
| vapourisation temperature | 3273 | K | [51] | |
| density | 7262 | kg/m3 | [50] | |
| specific heat | 704 | J/(kg K) | [50,52] | |
| thermal conductivity | 26.8 | W/(m K) | [50] | |
| thermal diffusivity | a | m2/s | ||
| enthalpy of fusion | 251 | kJ/kg | [50,51] | |
| enthalpy of vapourisation | 6500 | kJ/kg | [51] | |
| dynamic viscosity (at ) | Pa s | [50] | ||
| kinematic viscosity (at ) | m2/s | |||
| volumetric thermal expansion coefficient | 1/K | [53,54] | ||
| temperature coefficient of surface tension | N/(m K) | [45] | ||
| absorption coefficient (at 1053 nm) | 1/m | [55] | ||
| reflectivity (at 1053 nm) | R | 1 | [55] |
| Quantity | Symbol | AISI 304 Steel |
|---|---|---|
| thermal diffusion length | L | 501.5 nm |
| laser number | 18.0241 | |
| solid–liquid phase change number | 0.119849 | |
| liquid–vapour phase change number | 3.10367 | |
| Prandtl number | 0.1947 | |
| Rayleigh number | ||
| Marangoni number | 9.08939 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jähnig, T.; Demuth, C.; Lasagni, A.F. Influence of Sulphur Content on Structuring Dynamics during Nanosecond Pulsed Direct Laser Interference Patterning. Nanomaterials 2021, 11, 855. https://doi.org/10.3390/nano11040855
Jähnig T, Demuth C, Lasagni AF. Influence of Sulphur Content on Structuring Dynamics during Nanosecond Pulsed Direct Laser Interference Patterning. Nanomaterials. 2021; 11(4):855. https://doi.org/10.3390/nano11040855
Chicago/Turabian StyleJähnig, Theresa, Cornelius Demuth, and Andrés Fabián Lasagni. 2021. "Influence of Sulphur Content on Structuring Dynamics during Nanosecond Pulsed Direct Laser Interference Patterning" Nanomaterials 11, no. 4: 855. https://doi.org/10.3390/nano11040855
APA StyleJähnig, T., Demuth, C., & Lasagni, A. F. (2021). Influence of Sulphur Content on Structuring Dynamics during Nanosecond Pulsed Direct Laser Interference Patterning. Nanomaterials, 11(4), 855. https://doi.org/10.3390/nano11040855







