Self-Organization Regimes Induced by Ultrafast Laser on Surfaces in the Tens of Nanometer Scales
Abstract
1. Introduction
2. Materials and Methods
2.1. Material Preparation
2.2. Laser Setup
2.3. Characterization
3. Results
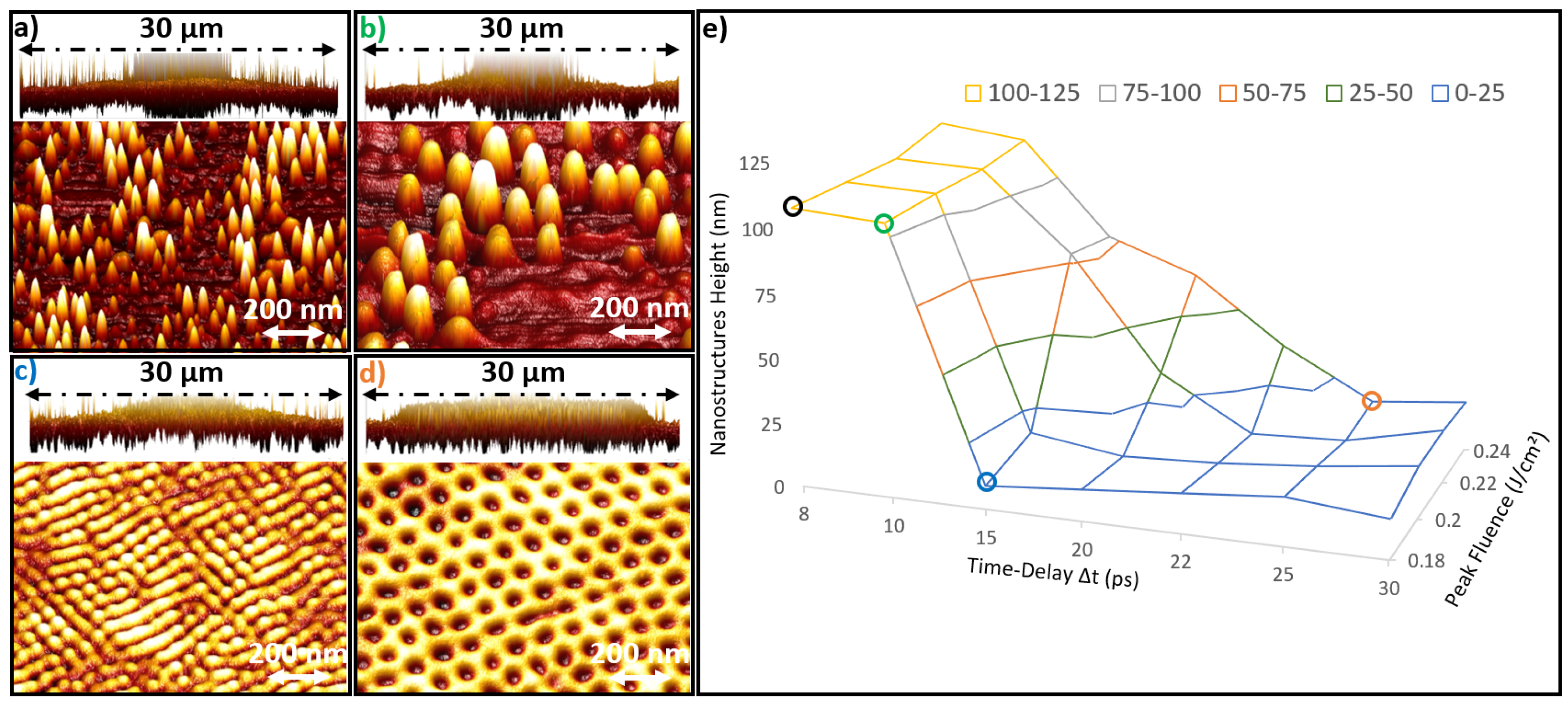
3.1. Advanced Surface Topography Control as a Function of Time Delay and Laser Fluence
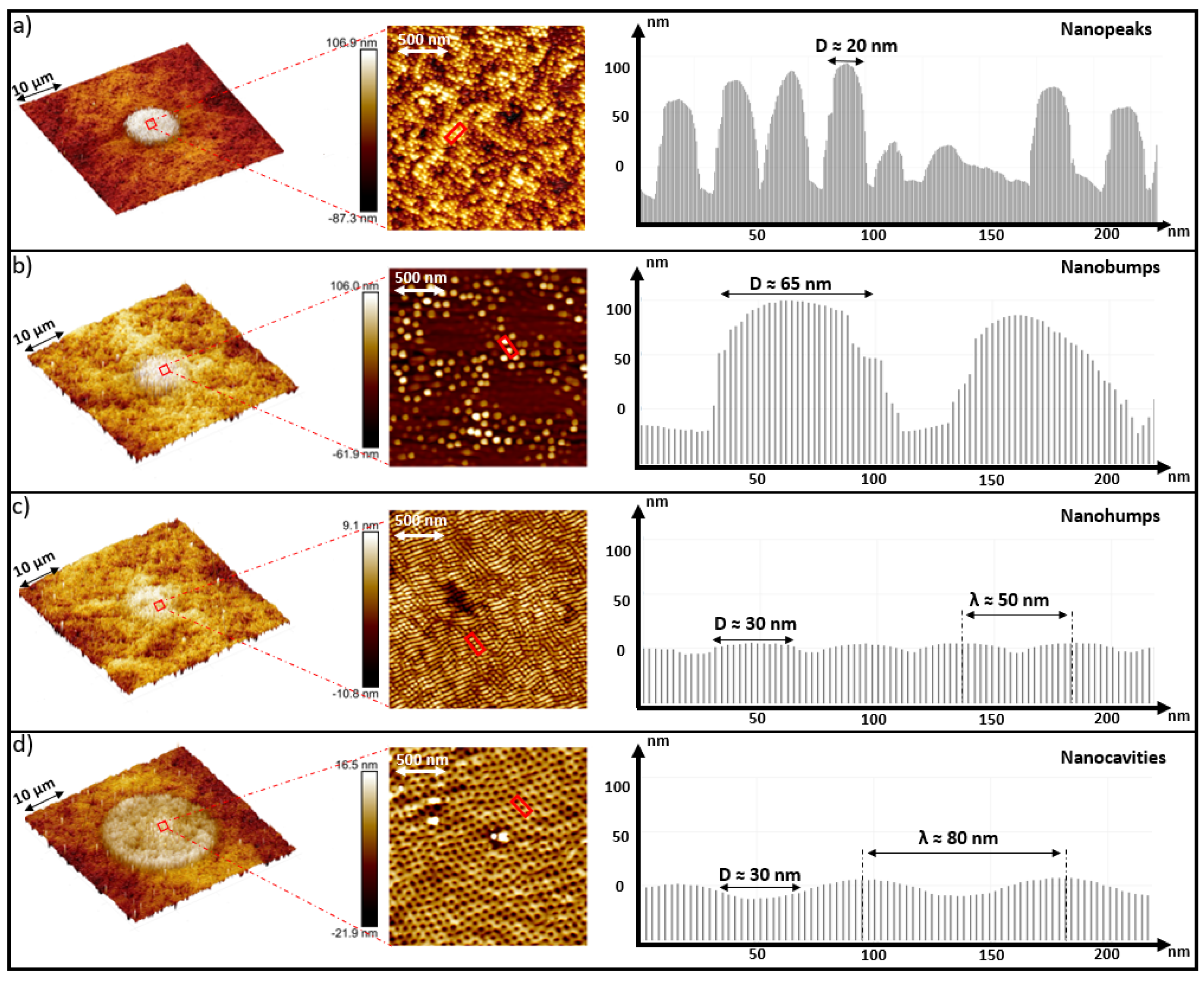
3.2. Wide Variety of Nanostructure Regimes
3.3. Wide Variety Nanopatterns Morphologies
3.4. Nanopatterns Control by Laser Dose
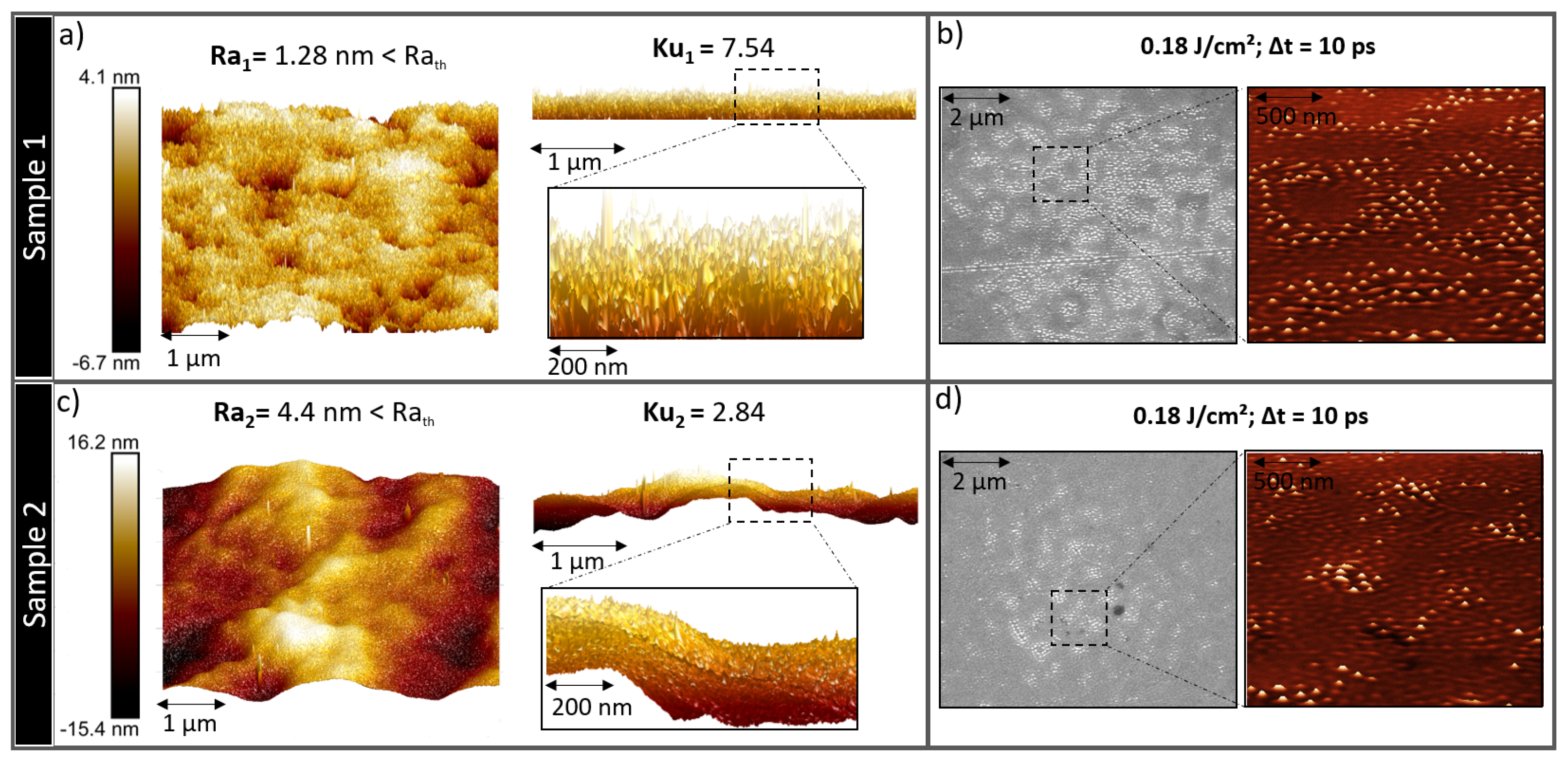
3.5. Initial Roughness Effect on Nanostructures Formation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LIPSS | Laser-Induced Periodic Surface Structures |
| HSFL | High Spatial Frequency LIPSS |
| SEM | Scanning Electron Microscopy |
| AFM | Atomic Force Microscopy |
| Ra | Arithmetic Roughness |
| Rath | Arithmetic Roughness Threshold |
| Ku | Kurtosis |
| Prandtl Number | |
| Critical Prandtl Number | |
| Number of Double-Pulses Sequences | |
| Time-Delay Between the Double-Pulses |
References
- Echeverría-Alar, S.; Clerc, M.G. Labyrinthine patterns transitions. Phys. Rev. Res. 2020, 2, 042036. [Google Scholar] [CrossRef]
- Sedao, X.; Maurice, C.; Garrelie, F.; Colombier, J.-P.; Reynaud, S.; Quey, R.; Pigeon, F. Influence of crystal orientation on the formation of femtosecond laser-induced periodic surface structures and lattice defects accumulation. Appl. Phys. Lett. 2014, 104, 171605. [Google Scholar] [CrossRef]
- Abou-Saleh, A.; Colombier, J.-P.; Garrelie, F. Relation Entre Auto-Organisation et Création/Résorption de Défauts Microsturaux Sous Irradiation Laser Ultrabrèves. Ph.D. Thesis, Université de Lyon, Lyon, France, 2019. Available online: http://theses.fr/2019LYSES001 (accessed on 27 January 2020).
- Bonse, J.; Krüger, J.; Höhm, S.; Rosenfeld, A. Femtosecond Laser-Induced Periodic Surface Structures. J. Laser Appl. 2012, 24, 042006. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, L.; Han, W.; Liu, W.; Hu, J.; Wang, S.; Lu, Y. Controllable formation of laser-induced periodic surface structures on ZnO film by temporally shaped femtosecond laser scanning. Opt. Lett. 2020, 45, 2411–2414. [Google Scholar] [CrossRef]
- Zhang, H.; Colombier, J.-P.; Li, C.; Faure, N.; Cheng, G.; Stoian, R. Coherence in Ultrafast Laser-Induced Periodic Surface Structures. Phys. Rev. B 2015, 92, 174109. [Google Scholar] [CrossRef]
- Déziel, J.-L.; Dumont, J.; Gagnon, D.; Dubé, L.J.; Messaddeq, S.H.; Messaddeq, Y. Constructive feedback for the growth of laser-induced periodic surface structures. Phys. Status Solidi C 2016, 13, 121–124. [Google Scholar] [CrossRef]
- Skolski, J.Z.P.; Römer, G.R.B.E.; Vincenc Obona, J.; Huis in’t Veld, A.J. Modeling laser-induced periodic surface structures: Finite-difference time-domain feedback simulations. J. Appl. Phys. 2014, 115, 103102. [Google Scholar] [CrossRef]
- Rudenko, A.; Mauclair, C.; Garrelie, F.; Stoian, R.; Colombier, J.P. Light absorption by surface nanoholes and nanobumps. Appl. Surf. Sci. 2019, 470, 228–233. [Google Scholar] [CrossRef]
- Rudenko, A.; Colombier, J.-P.; Höhm, S.; Rosenfeld, A.; Krüger, J.; Bonse, J.; Itina, T.E. Spontaneous Periodic Ordering on the Surface and in the Bulk of Dielectrics Irradiated by Ultrafast Laser: A Shared Electromagnetic Origin. Sci Rep. 2017, 7, 12306. [Google Scholar] [CrossRef] [PubMed]
- Skolski, J.Z.P.; Römer, G.R.B.E.; Obona, J.V.; Ocelik, V.; Huis in’t Veld, A.J.; De Hosson, J.T.M. Laser-Induced Periodic Surface Structures: Fingerprints of Light Localization. Phys. Rev. B 2012, 85, 075320. [Google Scholar] [CrossRef]
- Sedao, X.; Abou Saleh, A.; Rudenko, A.; Douillard, T.; Esnouf, C.; Reynaud, S.; Maurice, C.; Pigeon, F.; Garrelie, F.; Colombier, J.-P. Self-Arranged Periodic Nanovoids by Ultrafast Laser-Induced Near-Field Enhancement. ACS Photonics 2018, 5, 1418–1426. [Google Scholar] [CrossRef]
- Rudenko, A.; Saleh, A.A.; Pigeon, F.; Mauclair, C.; Garrelie, F.; Stoian, R.; Colombier, J.-P. High-frequency periodic patterns driven by non-radiative fields coupled with Marangoni convection instabilities on laser-excited surfaces. ACS Photonics 2020, 194, 93–105. [Google Scholar] [CrossRef]
- Abou-Saleh, A.; Karim, E.T.; Maurice, C.; Reynaud, S.; Pigeon, F.; Garrelie, F.; Zhigilei, L.V.; Colombier, J.P. Spallation-Induced Roughness Promoting High Spatial Frequency Nanostructure Formation on Cr. Appl. Phys. 2018, 124, 308. [Google Scholar] [CrossRef]
- Jalil, S.A.; Yang, J.; ElKabbash, M.; Cong, C.; Guo, C. Formation of controllable 1D and 2D periodic surface structures on cobalt by femtosecond double pulse laser irradiation. Appl. Phys. Lett. 2019, 115, 031601. [Google Scholar] [CrossRef]
- Fraggelakis, F.; Mincuzzi, G.; Lopez, J.; Manek-Hönninger, I.; Kling, R. Controlling 2D Laser Nano Structuring over Large Area with Double Femtosecond Pulses. Appl. Surf. Sci. 2019, 470, 677–686. [Google Scholar] [CrossRef]
- Fraggelakis, F.; Giannuzzi, G.; Gaudiuso, C.; Manek-Hönninger, I.; Mincuzzi, G.; Ancona, A.; Kling, R. Double- and Multi-Femtosecond Pulses Produced by Birefringent Crystals for the Generation of 2D Laser-Induced Structures on a Stainless Steel Surface. Materials 2019, 12, 1257. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Yin, K.; Wu, J.; Zhu, Z.; Duan, J.-A.; He, J. Recent advances in femtosecond laser-structured Janus membranes with asymmetric surface wettability. Nanoscale 2021, 13, 2209–2226. [Google Scholar] [CrossRef] [PubMed]
- Bonse, J. Quo Vadis LIPSS?—Recent and Future Trends on Laser-Induced Periodic Surface Structures. Nanomaterials 2020, 10, 1950. [Google Scholar] [CrossRef]
- Zorba, V.; Stratakis, E.; Barberoglou, M.; Spanakis, E.; Tzanetakis, P.; Anastasiadis, S.H.; Fotakis, C. Biomimetic Artificial Surfaces Quantitatively Reproduce the Water Repellency of a Lotus Leaf. Adv. Mater. 2008, 20, 4049–4054. [Google Scholar] [CrossRef]
- Elbourne, A.; Crawford, R.J.; Ivanova, E.P. Nano-structured antimicrobial surfaces: From nature to synthetic analogues. J. Colloid Interface Sci. 2017, 508, 603–616. [Google Scholar] [CrossRef] [PubMed]
- Vorobyev, A.Y.; Guo, C. Colorizing Metals with Femtosecond Laser Pulses. Appl. Phys. 2008, 4. [Google Scholar] [CrossRef]
- Guay, J.-M.; Calà Lesina, A.; Côté, G.; Charron, M.; Poitras, D.; Ramunno, L.; Berini, P.; Weck, A. Laser-Induced Plasmonic Colours on Metals. Nat Commun. 2017, 8, 16095. [Google Scholar] [CrossRef] [PubMed]
- Bonse, J.; Koter, R.; Hartelt, M.; Spaltmann, D.; Pentzien, S.; Höhm, S.; Rosenfeld, A.; Krüger, J. Tribological Performance of Femtosecond Laser-Induced Periodic Surface Structures on Titanium and a High Toughness Bearing Steel. Appl. Surf. Sci. 2015, 336, 21–27. [Google Scholar] [CrossRef]
- Abou Saleh, A.; Rudenko, A.; Reynaud, S.; Pigeon, F.; Garrelie, F.; Colombier, J.-P. Sub-100 Nm 2D Nanopatterning on a Large Scale by Ultrafast Laser Energy Regulation. Nanoscale 2020, 12, 6609–6616. [Google Scholar] [CrossRef]
- Liu, J.M. Simple technique for measurements of pulsed Gaussian-beam spot sizes. Opt. Lett. 1982, 7, 196–198. [Google Scholar] [CrossRef] [PubMed]
- Bévillon, E.; Stoian, R.; Colombier, J.P. Nonequilibrium optical properties of transition metals upon ultrafast electron heating. J. Phys. Condens. Matter. 2018, 30, 385401. [Google Scholar] [CrossRef]
- Korte, F.; Koch, J.; Chichkov, B.N. Formation of microbumps and nanojets on gold targets by femtosecond laser pulses. Appl. Phys. A 2004, 79, 879–881. [Google Scholar] [CrossRef]
- Savolainen, J.M.; Christensen, M.S.; Balling, P. Material swelling as the first step in the ablation of metals by ultrashort laser pulses. Phys. Rev. B 2011, 84, 193410. [Google Scholar] [CrossRef]
- Baset, F.; Popov, K.; Villafranca, A.; Alshehri, A.M.; Guay, J.M.; Ramunno, L.; Bhardwaj, V.R. Nanopillar formation from two-shot femtosecond laser ablation of poly-methyl methacrylate. Appl. Surf. Sci. 2015, 357, 273–281. [Google Scholar] [CrossRef]
- Vitral, E.; Mukherjee, S.; Leo, P.H.; Viñals, J.; Paul, M.R.; Huang, Z.F. Spiral defect chaos in Rayleigh-Bénard convection: Asymptotic and numerical studies of azimuthal flows induced by rotating spirals. Phys. Rev. Fluids 2020, 5, 093501. [Google Scholar] [CrossRef]
- Bodenschatz, E.; Pesch, W.; Ahlers, G. Recent Developments in Rayleigh-Bénard Convection. Phys. Rev. Fluids Annu. Rev. Fluid Mech. 2000, 32, 709–778. [Google Scholar] [CrossRef]
- Thess, A.; Bestehorn, M. Planform selection in Bénard-Marangoni convection: L hexagons versus g hexagons. Phys. Rev. E 1995, 52, 6358–6367. [Google Scholar] [CrossRef] [PubMed]
- Pearson, J. On convection cells induced by surface tension. J. Fluid Mech. 1958, 4, 489–500. [Google Scholar] [CrossRef]
- Sharp, D.H. An overview of rayleigh-taylor instability. Presented at the International Conference on “Fronts, Interfaces and Patterns”, Los Alamos, NM, USA, 2–6 May 1983. [Google Scholar]
- Morgan, R.V.; Cabot, W.H.; Greenough, J.A.; Jacobs, J.W. Rarefaction-driven Rayleigh–Taylor instability. Part 2. Experiments and simulations in the nonlinear regime. J. Fluid Mech. 2018, 838, 320–355. [Google Scholar] [CrossRef]
- Smith, M.K.; Davis, S.H. Instabilities of dynamic thermocapillary liquid layers. Part 1. Convective instabilities. J. Fluid Mech. 1983, 132, 119–144. [Google Scholar] [CrossRef]
- Smith, M. Instability mechanisms in dynamic thermocapillary liquid layers. Phys. Fluids 1986, 29, 3182–3186. [Google Scholar] [CrossRef]
- Tsibidis, G.D.; Fotakis, C.; Stratakis, E. From ripples to spikes: A hydrodynamical mechanism to interpret femtosecond laser-induced self-assembled structures. Phys. Rev. B 2015, 92, 041405. [Google Scholar] [CrossRef]
- Busse, F.H. Remarks on the critical value Pc = 0.25 of the Prandtl number for internally heated convection found by Tveitereid and Palm. Eur. J. Mech. B/Fluids 2014, 47, 32–34. [Google Scholar] [CrossRef]
- Boeck, T.; Thess, A. Bénard–Marangoni convection at low Prandtl number. J. Fluid Mech. 1999, 399, 251–275. [Google Scholar] [CrossRef]
- Bragard, J.; Velarde, M.G. Bénard–Marangoni convection: Planforms and related theoretical predictions. J. Fluid Mech. 1998, 368, 165–194. [Google Scholar] [CrossRef]
- Starikov, S.V.; Pisarev, V.V. Atomistic simulation of laser-pulse surface modification: Predictions of models with various length and time scales. J. Appl. Phys. 2015, 117, 135901. [Google Scholar] [CrossRef]
- Bonse, J.; Kirner, S.V.; Krüger, J. Laser-Induced Periodic Surface Structures (LIPSS). In Handbook of Laser Micro- and Nano-Engineering; Springer International Publishing: Cham, Switzerland, 2020; pp. 1–59. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakhoul, A.; Maurice, C.; Agoyan, M.; Rudenko, A.; Garrelie, F.; Pigeon, F.; Colombier, J.-P. Self-Organization Regimes Induced by Ultrafast Laser on Surfaces in the Tens of Nanometer Scales. Nanomaterials 2021, 11, 1020. https://doi.org/10.3390/nano11041020
Nakhoul A, Maurice C, Agoyan M, Rudenko A, Garrelie F, Pigeon F, Colombier J-P. Self-Organization Regimes Induced by Ultrafast Laser on Surfaces in the Tens of Nanometer Scales. Nanomaterials. 2021; 11(4):1020. https://doi.org/10.3390/nano11041020
Chicago/Turabian StyleNakhoul, Anthony, Claire Maurice, Marion Agoyan, Anton Rudenko, Florence Garrelie, Florent Pigeon, and Jean-Philippe Colombier. 2021. "Self-Organization Regimes Induced by Ultrafast Laser on Surfaces in the Tens of Nanometer Scales" Nanomaterials 11, no. 4: 1020. https://doi.org/10.3390/nano11041020
APA StyleNakhoul, A., Maurice, C., Agoyan, M., Rudenko, A., Garrelie, F., Pigeon, F., & Colombier, J.-P. (2021). Self-Organization Regimes Induced by Ultrafast Laser on Surfaces in the Tens of Nanometer Scales. Nanomaterials, 11(4), 1020. https://doi.org/10.3390/nano11041020







