3. Results and Discussion
The goal of this work is the analysis of light emission from a layer of semiconductor nanoparticles. As there is reciprocity between absorption and emission, we first investigate the absorption of light in a monolayer of spherical SNPs with diameter
dSNP arranged in a regular square or triangular grid. There can be a distance
dgap between two particles and the grid side is given by the sum
d = dSNP + dgap << λο, where
λο is a free-space wavelength of light. Typically, SNPs have a dielectric constant
εp that is much larger than that of the embedding medium
εm = εo · nm2. When the layer of SNPs is placed in a static homogeneous external field
Ee, the field inside the SNPs is typically reduced in amplitude due to dielectric depolarization and the internal field is determined by the position-dependent tensor
β:
. When the incident light has a wavelength much longer than the grid side
d, the static field approximation can be used to estimate the optical absorption. The absorption is proportional to |
Ei(
r)|
2 when the dielectric constant of the nanoparticles has a small complex component [
6]. When, for example, an external field is applied along the z-axis, perpendicular to the particle layer, then the ratio of the internal squared field |
Ei(
r)|
2 over the external squared field |
Ee|
2 is given by
This quantity, which depends on the ratio of dielectric constants and on the interparticle distance, is proportional to the local absorption in the nanoparticle layer.
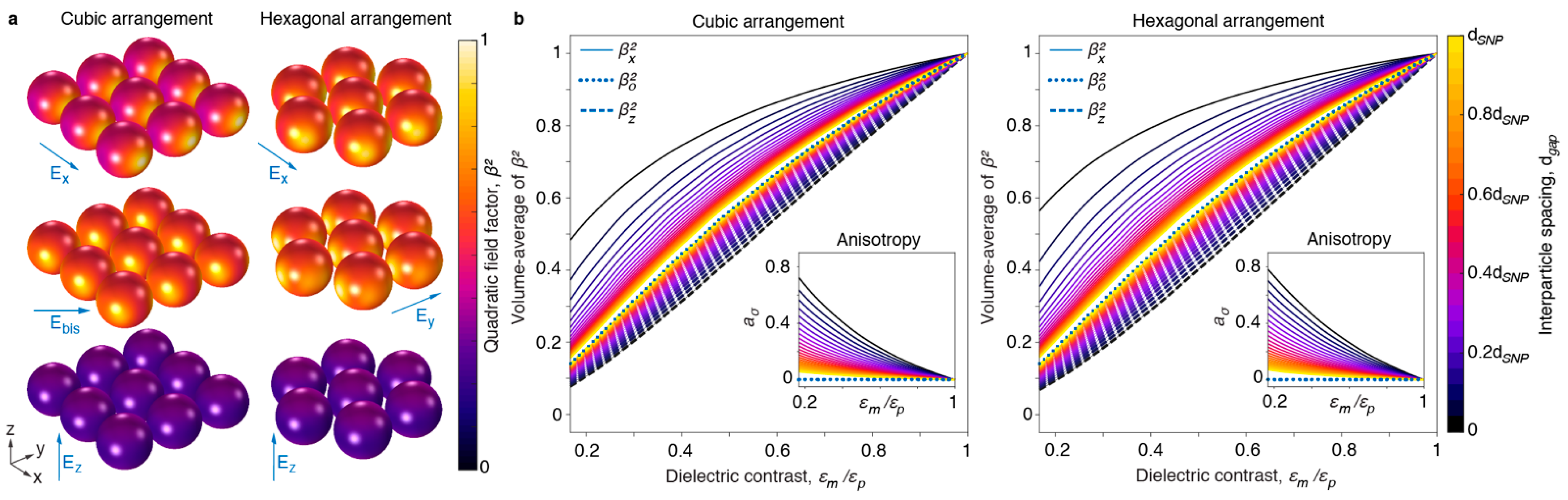
Figure 3a illustrates the spatial dependency of the factor
β2 in the layer of spherical nanoparticles for different directions of the electric field vector of the external incident light. In the closely packed square lattice the incident field is
Ez,
Ex or along the bisector
Ebis. For the triangular grid, the incident field is along
Ez,
Ex or
Ey. In the example shown, the dielectric constants of the embedding medium and the SNPs are 2.25 ×
εo and 6 ×
εo, respectively, which yields
εm/εp = 0.375. The simulations show that, similar to a planar layer, the field in the nanoparticles is smaller when the external field is perpendicular to the layer. To determine the average absorption in the particle, the quantity
β2 is averaged over the volume of the particle, for the different directions of the incident field. The result in
Figure 3b shows the average
<β2> as a function of the ratio of the dielectric constants and the interparticle distance
dgap. When
dgap is much larger than
dSNP, the particles are isolated and the total absorption is similar to that of an isolated SNP, with corresponding factor
. The ratio between
and
can be considered as the enhancement factor due to incorporation in a layer and has also been studied elsewhere [
20], for materials in which the dielectric constant has a significant imaginary part. Note that for in-plane fields, the absorption is independent of the azimuthal angle, due to the four-fold or six-fold symmetry axis of rotation for the structure. Absorption is larger for fields parallel to the layer and smaller for fields perpendicular to the layer. In the following we use the quantities
for in-plane fields and
for perpendicular fields. The anisotropy in the absorption [
6] for
versus ⊥ polarized light is defined as
aσ:
The anisotropy in absorption is larger when the layer is more densely packed and for larger dielectric contrasts (
Figure 3b, insets).
To estimate the light emission from a nanoparticle, we assume that each nanoparticle is well described by an elementary electrical dipole oscillator. Since the particle diameter
dSNP and the gap
dgap are much smaller than the wavelength of the emitted light, quasistatic electric field calculations can be used to estimate the field in the neighborhood of the layer. When the dipole moment of the emitter inside the nanoparticle is
pi, then the field well above or below the layer is described by an equivalent electrical dipole moment
pe present in the medium with dielectric constant
εm. According to the reciprocity theorem [
21], the external dipole moment
pe and the internal dipole moment
pi at position
r are linked by the transposed tensor
β:
The equivalent electrical dipole moment in the embedding medium is typically not parallel to the dipole in the internal medium, because the tensor components are different, for example for a layer of SNPs the coefficient βzz is typically smaller than βxx.
The radiation of an oscillating dipole
pi in an SNP in a given structure is equal to the radiation of the equivalent oscillating dipole
pe in medium
εm according to Equation (3). The excited state in the layer of SNPs can return to the ground state by an electrical dipole transition. In ref. [
6] it was shown that the assumption of a random orientation of the dipole orientation seems appropriate. In this work we assume that the excitation can happen from any location in the layer. This means that the power emitted from the oscillating electrical dipole
pi should be averaged over all possible orientations and over all positions in the layer
r. The emission from oscillating dipoles in the SNP layer has three contributions: emission towards the upper medium, emission towards the lower medium and emission that is waveguided by the layer. The emission can have TM and TE contributions. As we assume that the layer is very thin, phase delays can be neglected and the emissions of the dipole
pe towards the upper and lower medium are equal. In the following we investigate the influence of the SNP arrangement on the different contributions.
The power emitted per unit solid angle in the embedding medium
m for a layer of SNPs that is excited is obtained after averaging the emission of the oscillating dipole
pi over orientations and locations. The TM and TE contributions are, respectively, given by:
In these formulas the
β2 factors are the same as defined previously. As the parallel factor is larger than the perpendicular factor (
Figure 3), the TM emission is not isotropic but has a maximum in the direction perpendicular to the layer plane.
A layer consisting of SNPs is strictly speaking a lossy waveguide, because light propagating along the layer is scattered by the nanoparticles. Here we consider particles with a diameter much smaller than the wavelength of light, such that scattering is limited and we can approximate the layer as a lossless waveguide [
11]. When the layer of SNPs is embedded in a medium with a lower refractive index, the
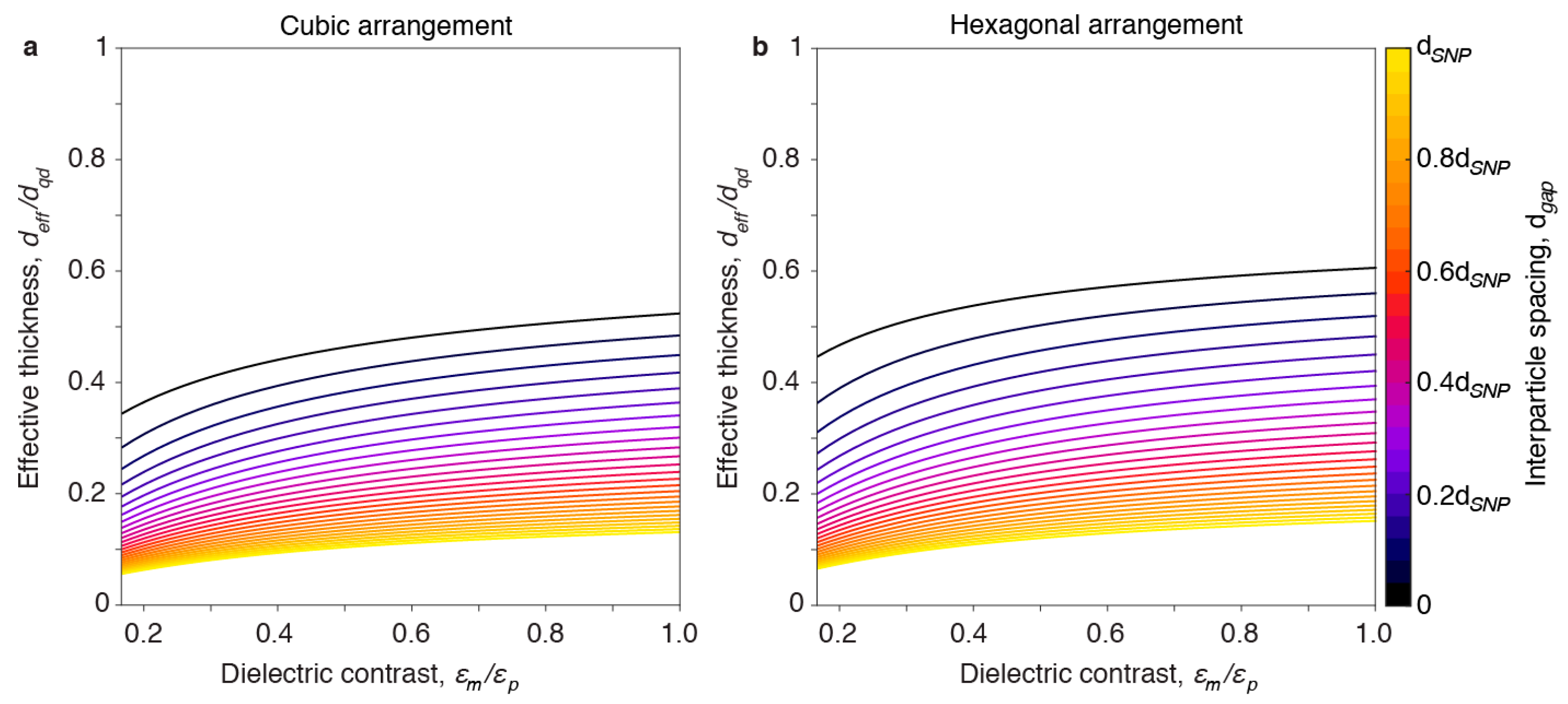
TE0 waveguided mode with an electric field vector parallel to the layer is the most important mode. For a homogeneous slab waveguide with a thickness much smaller than the wavelength of the light, the waveguided
TE0 mode is determined by the difference in dielectric constant and the film thickness (
Supplementary Materials). For an inhomogeneous thin film, we assume that the waveguided mode
TE0 is determined by the excess polarization in the layer when a field is applied parallel to the layer. For the case of a
TE0 waveguided mode propagating in the
y-direction within an inhomogeneous layer consisting of nanoparticles, and with the field mainly polarized in the
x-direction, the penetration depth in the embedding medium is determined by the effective thickness (
Figure 4), which takes into account the excess polarization due to the SNP layer (
Supplementary Materials):
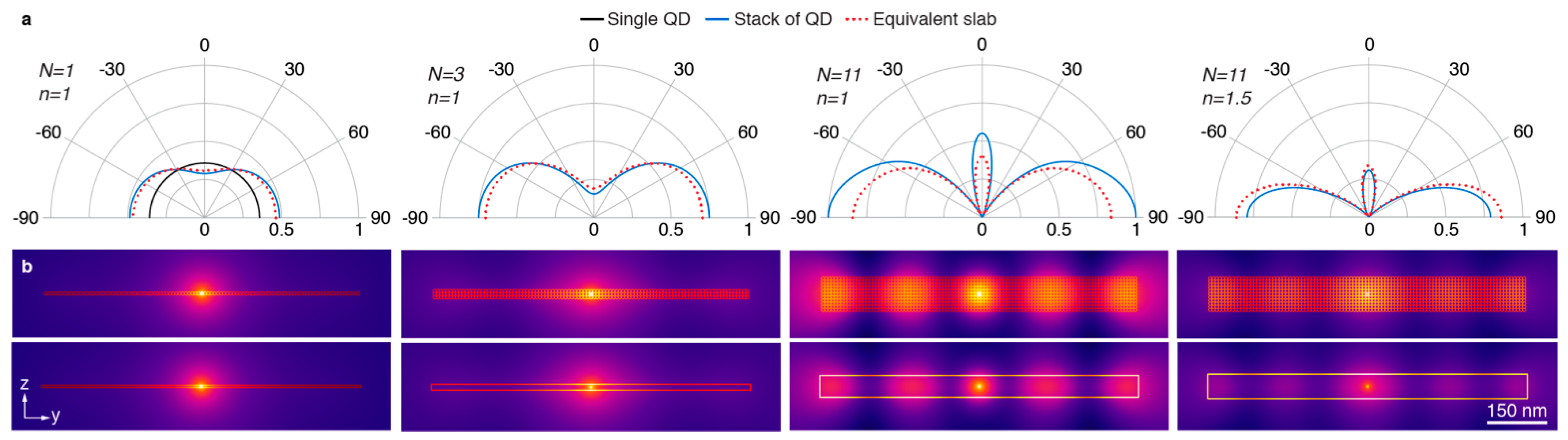
To verify the validity of the approximation for the waveguided mode and the corresponding effective thickness, we calculated the emission by an oscillating 1D electrical dipole in the
x-direction, in the center of a layer of cylinders with diameter 8 nm, with infinite extension in the
x-direction and 101 cylinders in each layer (
Figure 5). The 2D simulations were carried out in COMSOL Multiphysics for the nanoparticle layer and for a homogeneous thin film with the same dielectric constant and the same effective thickness (
Figure S2). The results of the simulations are shown in
Figure 5, for a monolayer of cylinders, and for stacks of three and eleven layers of cylinders. It can be seen that the far-field patterns (
Figure 5a) and the near-field intensities (
Figure 5b) for the nanoparticle layer and for the thin film are very similar, which validates the approximations. The simulations show that for the thicker layers, there is an important waveguiding effect. Due to reflections at the left and right edges of the SNP layer, there are standing waves formed in the layer.
The power coupled to the waveguided mode for an electrical dipole with random orientation and random position, for a homogeneous thin layer and for a layer of SNPs is, respectively, given by:
Note that the β factor is smaller than one, which means that for a layer of SNPs the coupling with the waveguide mode is less than for a continuous layer with the same effective thickness.
In many applications the embedding medium that surrounds the SNP layer is a polymer substrate (or another material) and above and below this substrate there is air. We are therefore particularly interested in the fraction of the light that is emitted from the layer into air. Usually the interface between the embedding medium
m and air is parallel to the SNP layer. In LEDs or in photoluminescent layers, the fraction of light emitted into air should be as high as possible. In solar concentrators on the other hand, the aim is to trap light in a plate with a higher refractive index by total internal reflection (TIR). TIR in a medium with refractive index
nm in contact with air takes place when the wave vector lies within a cone with half angle
θTIR = arcsin(1/
nm). For randomly oriented dipoles that are homogeneously distributed over the SNP layer, the fraction of light that is emitted into air can be calculated from previous results (
Supplementary Materials):
The third term in
F represents the contribution due to waveguiding, and becomes negligible when the effective thickness is sufficiently small. Thin layers have a relatively high outcoupling fraction into air, as we take into account that
is typically larger than
(
Figure 3). When the layer is thicker, waveguiding becomes more prominent and less light is outcoupled to air (this is visible in
Figure 5b).
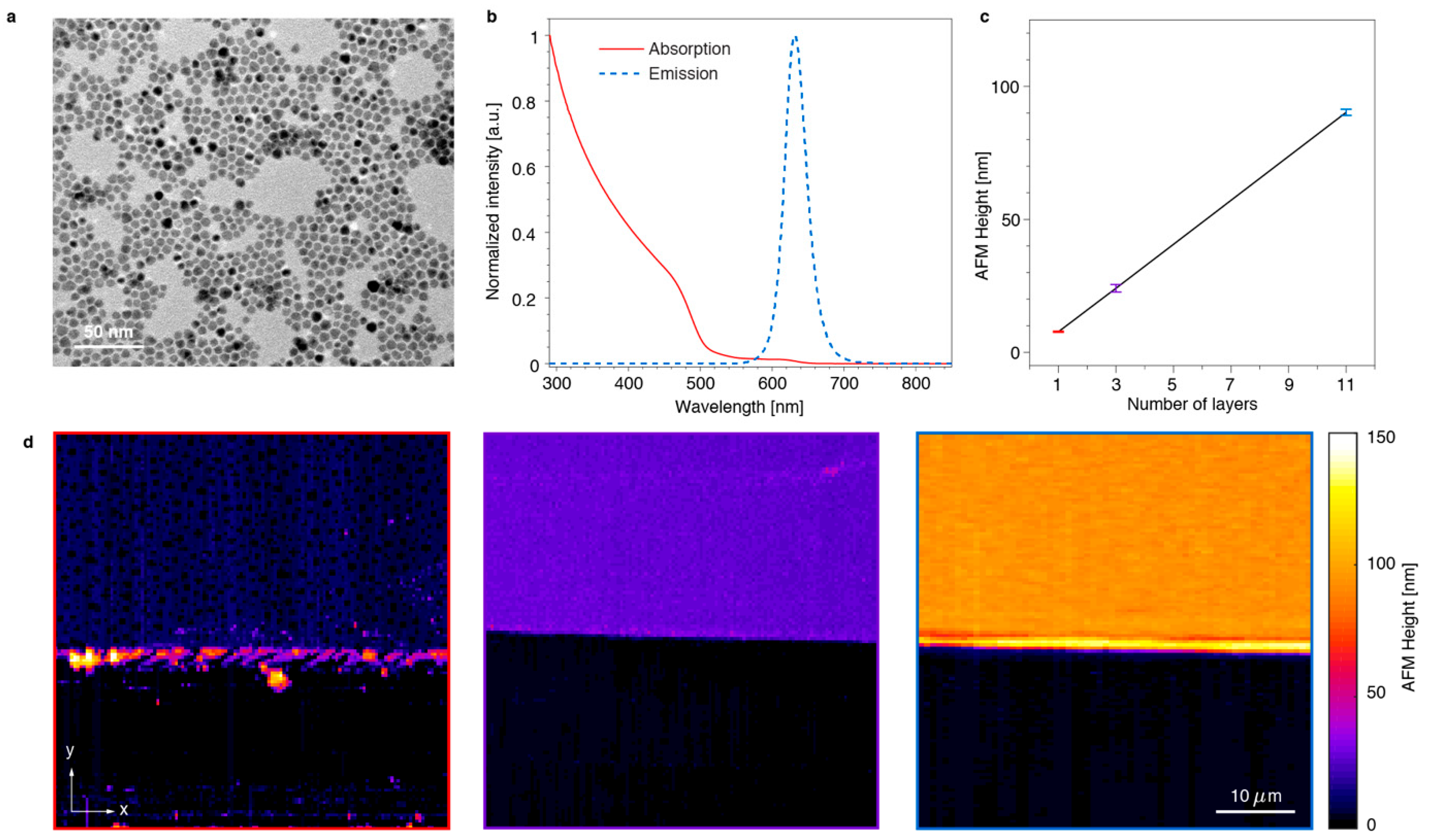
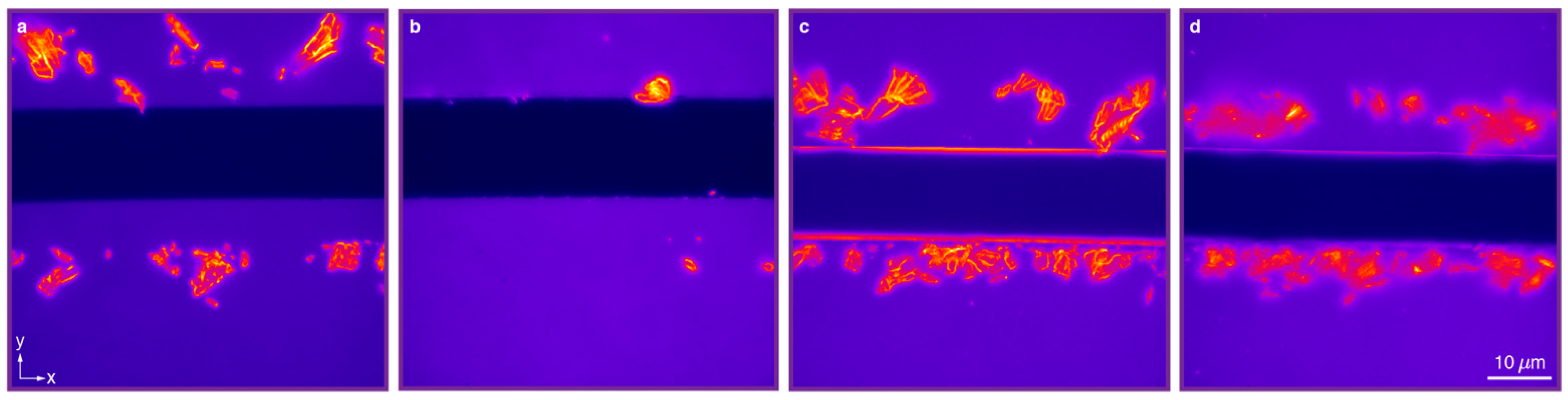
In order to verify the dependency of outcoupling and waveguiding on the thickness of the SNP layer, we set up a series of experiments. First, we spin-coated layers of spherical core/shell CdSe/CdS quantum dots (
dSNP = 8 nm) on glass substrates. The fabricated samples had film thicknesses of 8, 25 and 90 nm (
Figure 1c,d), which correspond to one, three and eleven layers, respectively. The SNP films were scratched with a lancet to remove the quantum dots along a stripe, and to create a sharp edge of the deposited nanoparticle film as shown in
Figure 6 (with bright field images in
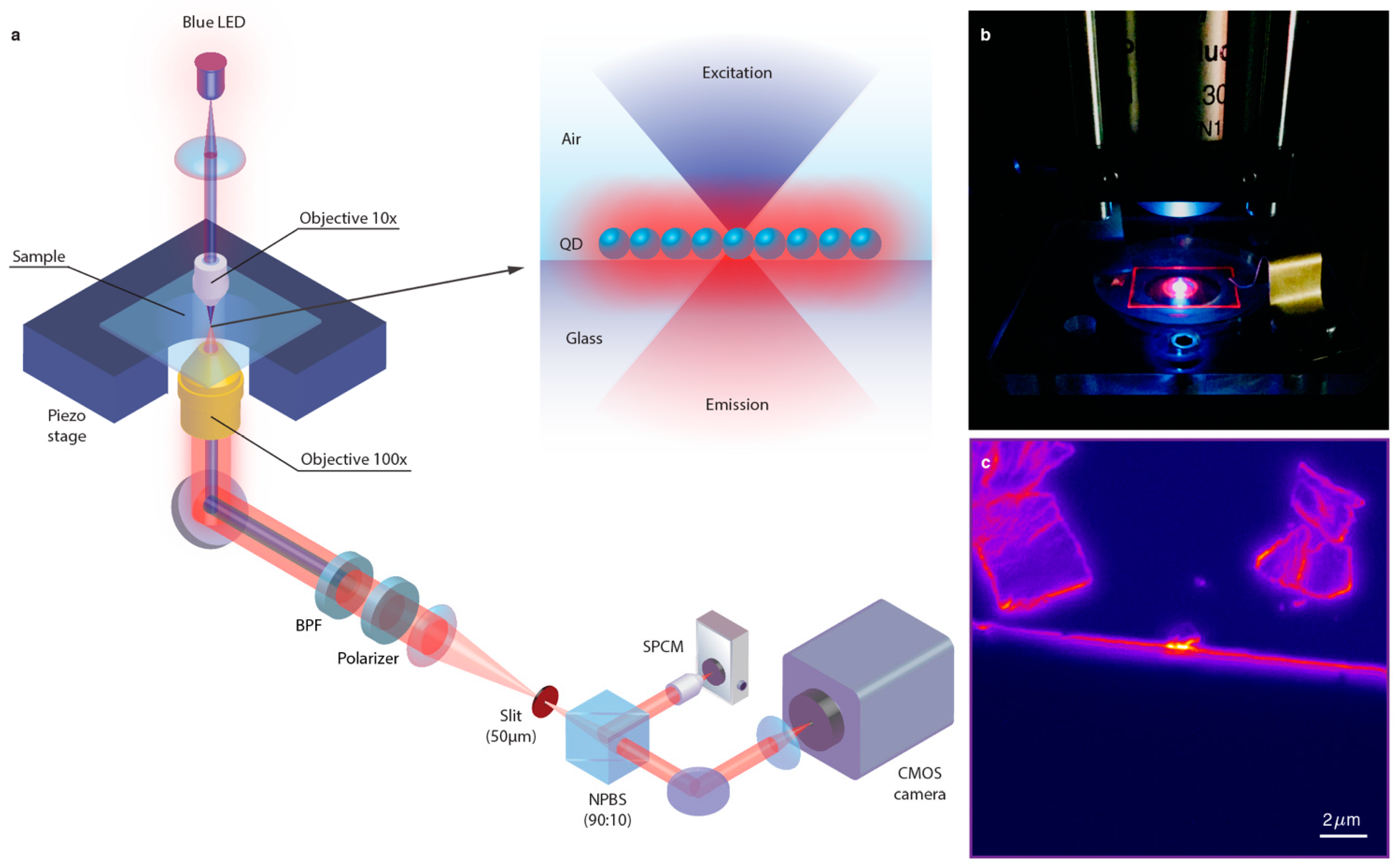
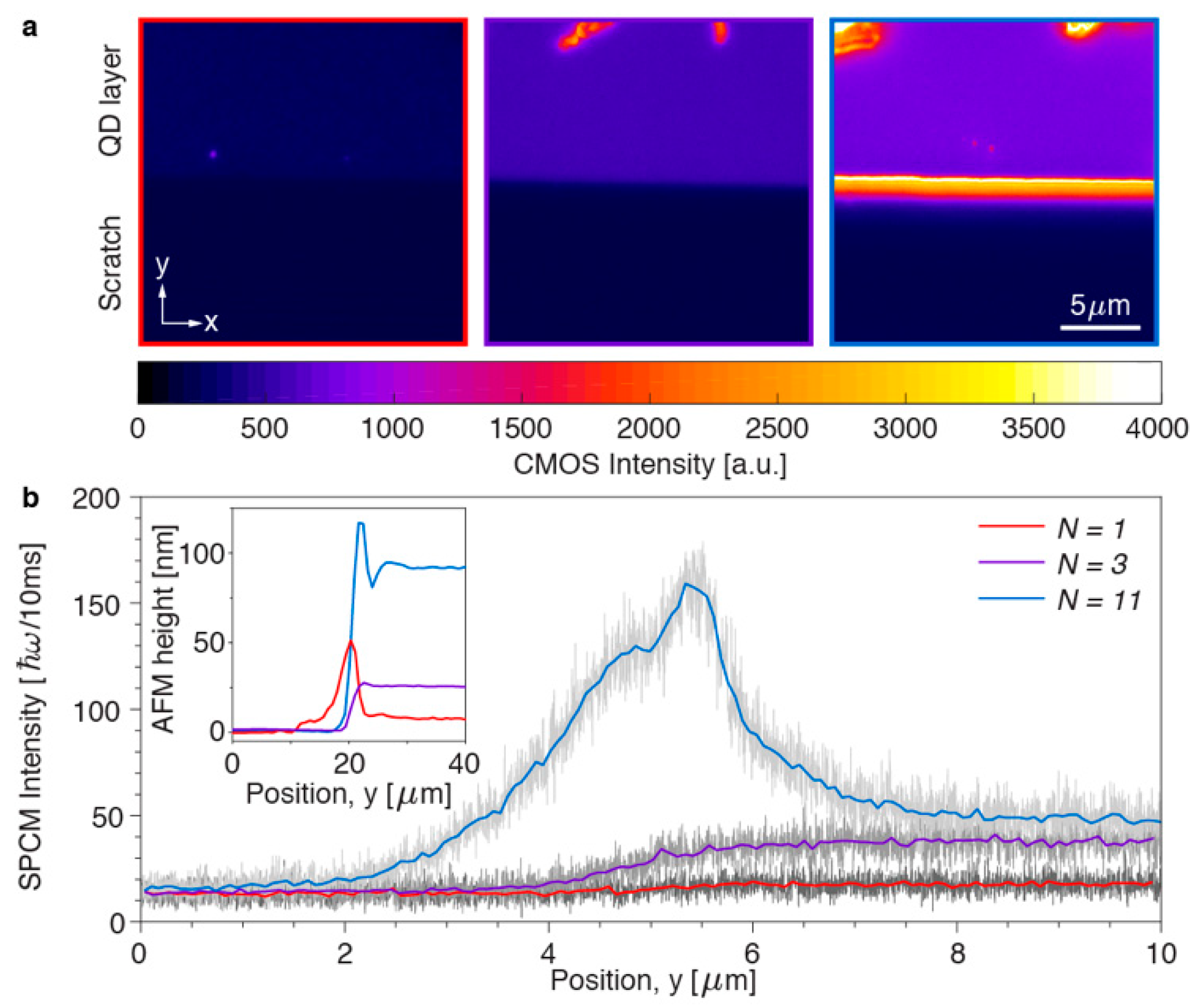
Figure S3). It can be seen that some aggregates of SNPs were deposited on the film along the scratch, during the removal process. The nanostructures were visualized by a microscope setup, in which the SNPs were excited with a blue LED and the photoluminescent emission was collected with a high-numerical aperture objective lens (NA 1.3, 100×). Spectral measurements show that only 15% of the LED light was absorbed in the 90 nm thick SNP layer, indicating that the excitation level is more or less the same for all SNPs. Some selected areas of interest are shown in
Figure 7a, which depict the boundary of the SNP film with a minimal number of SNP clusters near the scratch. By averaging the pixel intensity over a horizontal line, we obtained a low-noise intensity profile of the emission near the edge of the SNP layer (
Figure S4), where the SNPs have been removed in the region
y < 5 μm. In addition, we also integrated the number of the emitted photons with a single-photon counting module (SPCM) through the slit aligned parallel to the scratch (
Figure S5). This setup allows integration of the emitted photons for the same
y coordinate during the slow movement of the sample in the
y-direction with a nanometer-precision piezostage (
Figure 7b).
The experimental results summarized in
Figure 7 allow evaluation of the importance of photoluminescence outcoupling and waveguiding in SNP films with different thicknesses. In general, microscopy-based observation of waveguiding inside a planar structure is problematic, unless the waveguide is strongly scattering. Our approach enables direct detection of waveguided light at the edge of the nanostructure, where part of the light is scattered into the observation cone of the high NA objective. For a monolayer and for a film of three SNP layers, mainly light outcoupled from the plane of the structure (
Figure 7b) is observed, with intensity at most 50 photons per 10 ms. In contrast to the thinner films, the 11-layer SNP film waveguides a lot of the emission towards the edges leading to a peak of 160 photons per 10 ms (
Figure 7b). This peak is asymmetric, with different features on both sides of the edge: the left side (
y < 5 μm) originates mainly from waveguided light and the right side is related to the peak of SNPs clustered at the boundary according to the AFM measurements in the inset of
Figure 7b. Overall, the obtained experimental results are in agreement with our theoretical predictions (Equation (9),
Figure 5a,b), revealing a strong dependence of photoluminescence waveguiding on the thickness of the SNP layer.
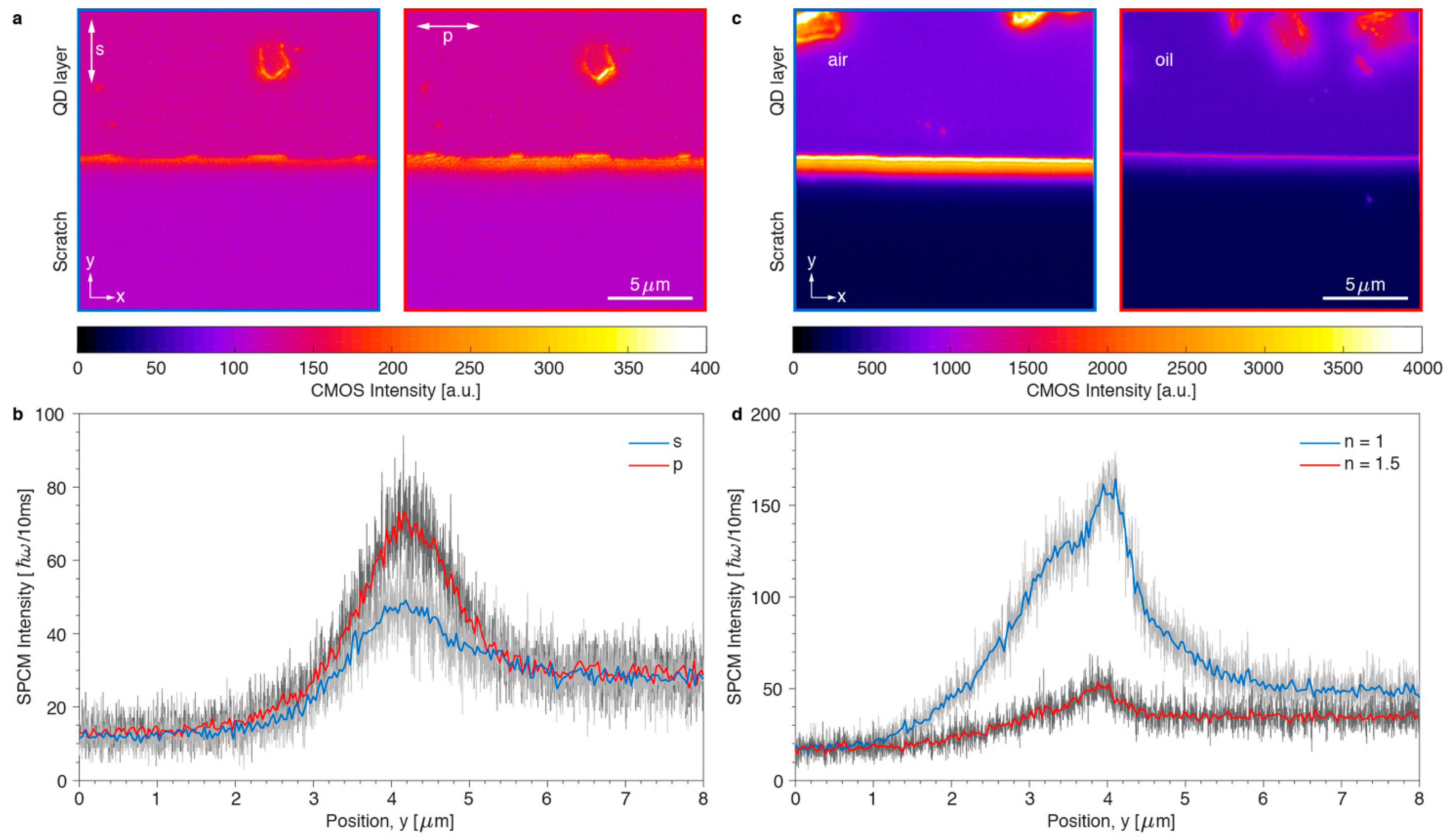
Next, we characterized the properties of the photoluminescent light waveguided within the thick (
N = 11) film of SNPs. By using a polarizer in the imaging path of the microscope, we found that the waveguided emission was mainly polarized with the electric field parallel to the edge of the film (
Figure 8a). The dominance of p-polarized photons over s-polarization (
Figure 8b) confirms that waveguiding is related to the
TE0 polarized mode. Another important parameter for the waveguiding is the dielectric contrast between the SNP film and the surrounding medium. All measurements up to now were performed with SNPs deposited on glass substrates with air on top, leading to an asymmetric slab waveguide. To obtain a symmetric waveguide, we added a drop of oil immersion on top of the SNP film (
Figure 8c), which had the same refractive index as the supporting glass (
nm = 1.5). Due to the weaker dielectric contrast between the film (
εp = 6) and the overlaying medium at the edge of the waveguide (
εm = 2.25 instead of 1), scattering from the edge of the film into the observation cone of the objective lens was reduced (
Figure 8d), as predicted by the simulations in
Figure 8b. The observed properties of waveguided photoluminescence, polarization anisotropy and dielectric contrast-dependence, make thicker SNP films highly suitable for diverse waveguiding applications.
The presented theoretical and experimental results are important for the smart design of photonic devices based on SNPs. According to Equation (9), the estimated fraction of light outcoupled into air is 27% for a SNP monolayer immersed in a polymer, because waveguiding can be neglected. This factor decreases for increasing layer thickness, because more light is subjected to waveguiding in the SNP layer (the outcoupling factor reduces to 15.5% for
N = 10 according to Equation (9)). This effect plays a crucial role for QD-based LEDs and organic light-emitting diodes (OLEDs), where the maximum outcoupling of photons into air is highly desired [
1]. Indeed, recent reports show that LEDs attain the best emission characteristics when the thickness of the emitting layer does not exceed three layers of colloidal nanoparticles [
22,
23,
24,
25]. On the other hand, looking through the literature did not lead us to any other experimental evidence for waveguiding of light within the multilayer of SNP that is acting as the emitter itself. The thickness of the SNP layer may, apart from the optical properties, also affect the electrical properties (for example the efficiency of electron–hole recombination in the semiconductor [
26]) and, hence, one should carefully tune and adjust the device architecture to find the optimal operating conditions. Based on the results obtained in this work, we claim that the effect of waveguiding in SNP layers should be taken into account in the design of SNP-based LEDs. The stronger waveguiding properties for thicker QD films, on the other hand, make them highly attractive for solar concentrators [
27,
28]. The amount of photoluminescence waveguided under TIR already reaches 74% for isotropically emitting spherical QDs that are suspended in a planar polymer slab [
6]. The fraction of the waveguided light can be further increased to 84.5% (according to Equation (9),
ηair,RND decreases to 15.5%) by using a thick film with ten SNP layers embedded in a polymer medium (
nm = 1.5). In this configuration, an important part of the light is waveguided in the SNP layer itself and this may lead to an increase of reabsorption events [
4], which is an important loss mechanism in solar concentrators. A possible strategy to minimize reabsorption, while maintaining a large amount of total internal reflection in the polymer substrate, is to deposit the QD film onto a structured substrate with two height levels and a lateral dimension of, for example, 10 μm (smaller than the typical length related to reabsorption in the SNP waveguide). With this geometry an important amount of light is initially waveguided by the SNP film, and when it reaches the edge of a structure element, it is scattered into the substrate, in a direction that is still large enough to maintain total internal reflection in the substrate.