Figure 1.
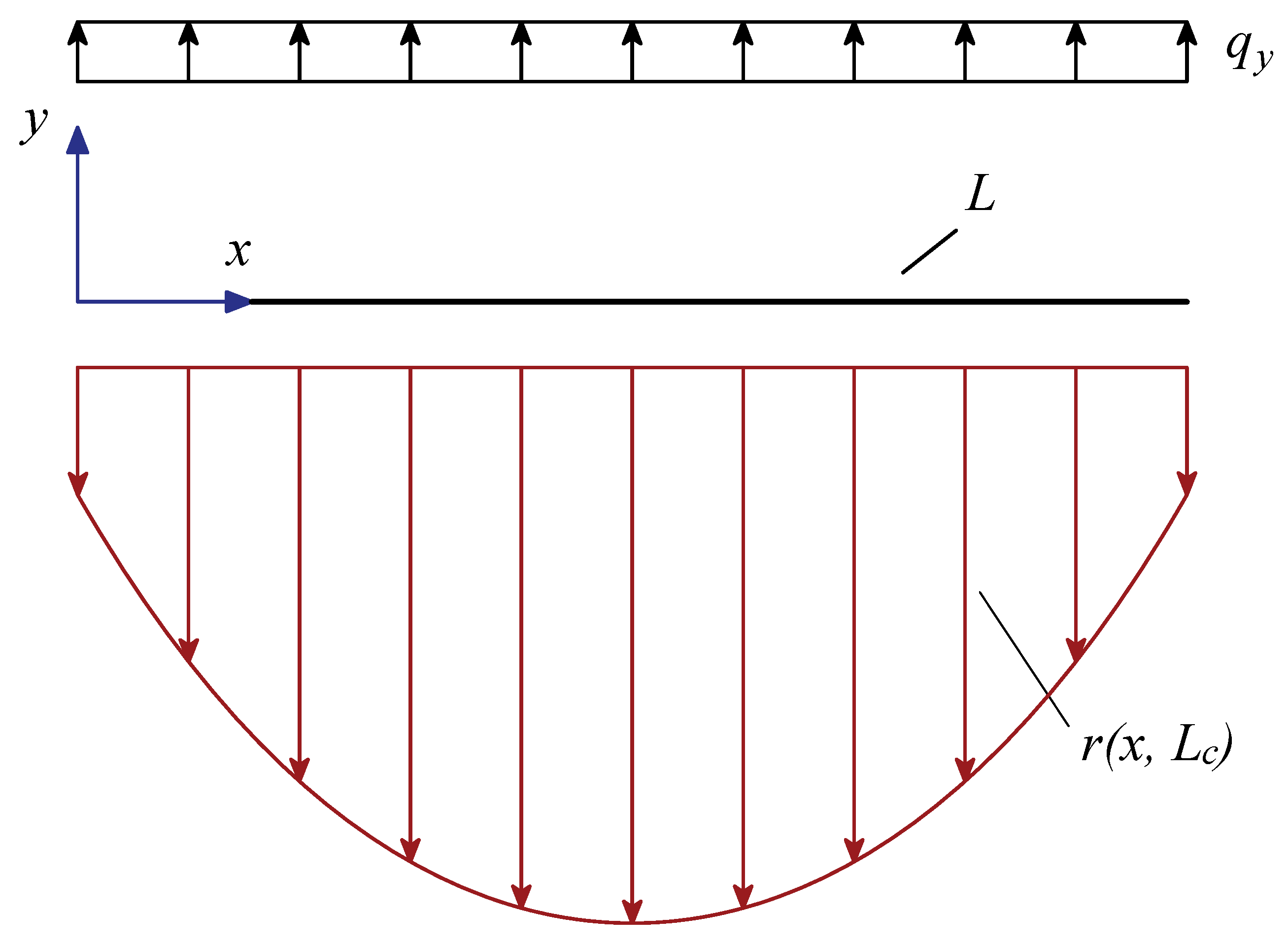
Geometric sketch of a free-beam on displacement-driven nonlocal foundation.
Figure 1.
Geometric sketch of a free-beam on displacement-driven nonlocal foundation.
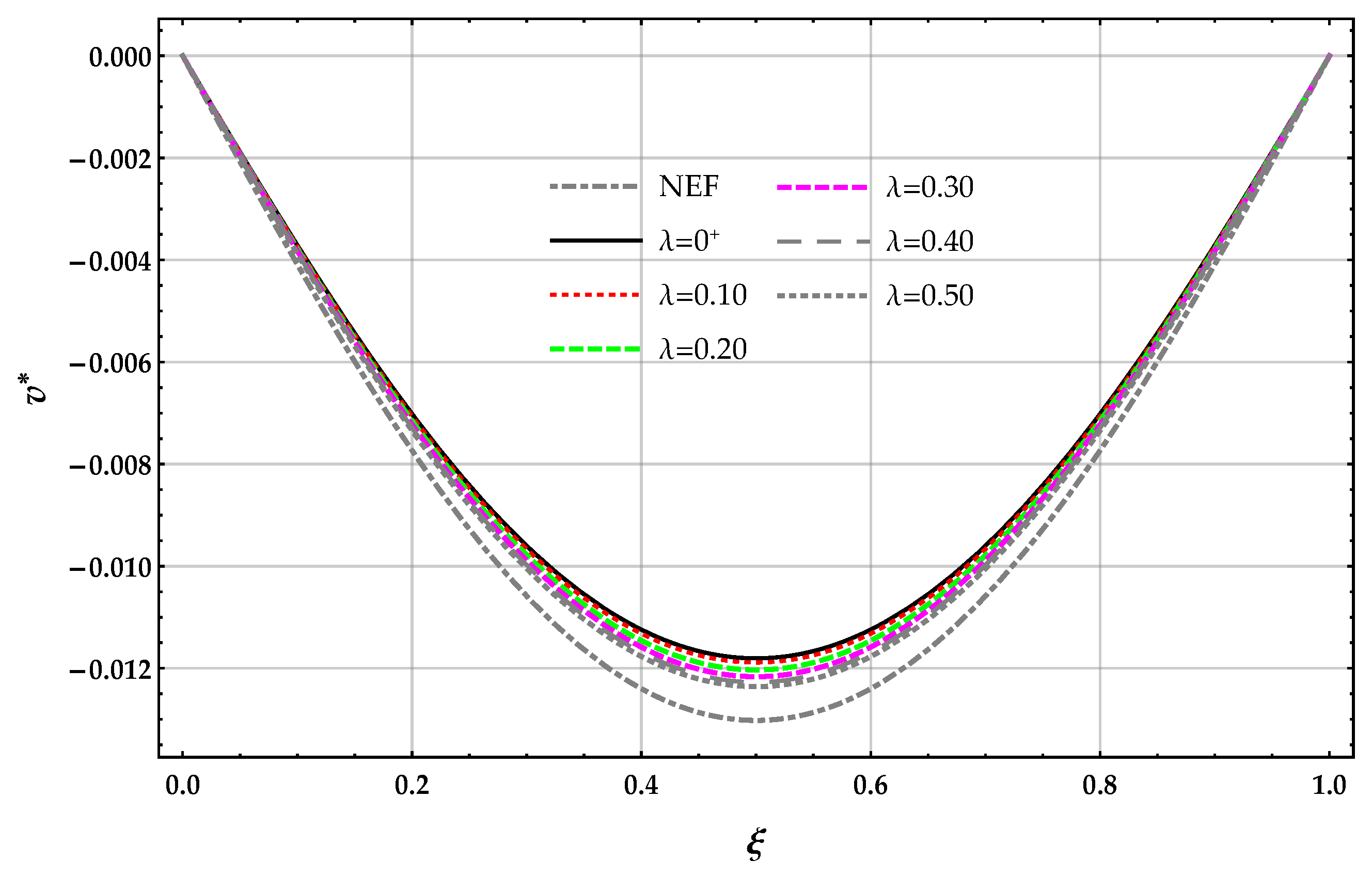
Figure 2.
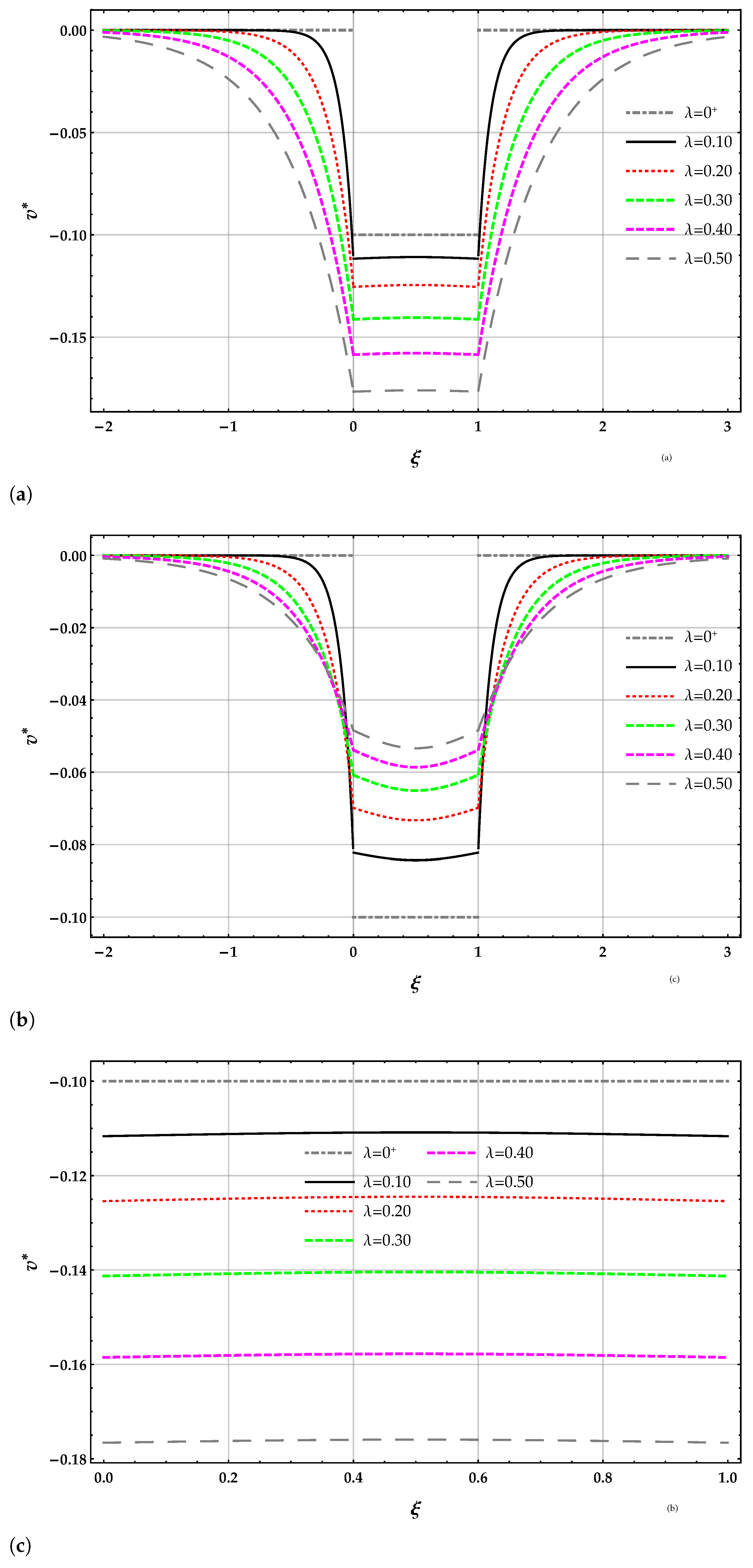
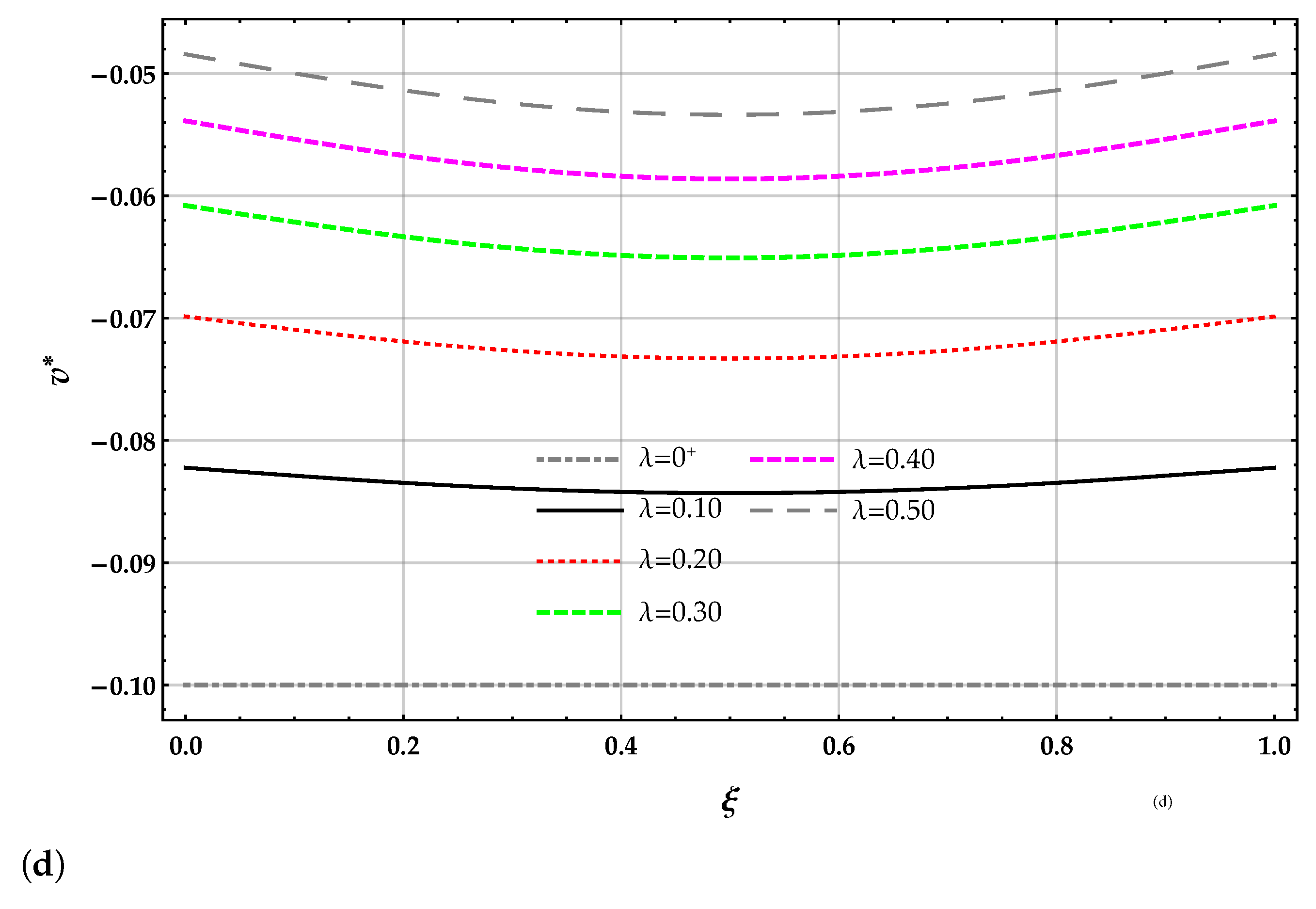
beam. Plots of the non-dimensional transverse displacement of the surface of the elastic foundation for increasing values of the non-dimensional non-local parameter in the set with : (a) DD method, (b) MRD method, (c) zoom of the beam deflection using the DD method, (d) zoom of the beam deflection using the MRD method.
Figure 2.
beam. Plots of the non-dimensional transverse displacement of the surface of the elastic foundation for increasing values of the non-dimensional non-local parameter in the set with : (a) DD method, (b) MRD method, (c) zoom of the beam deflection using the DD method, (d) zoom of the beam deflection using the MRD method.
Figure 3.
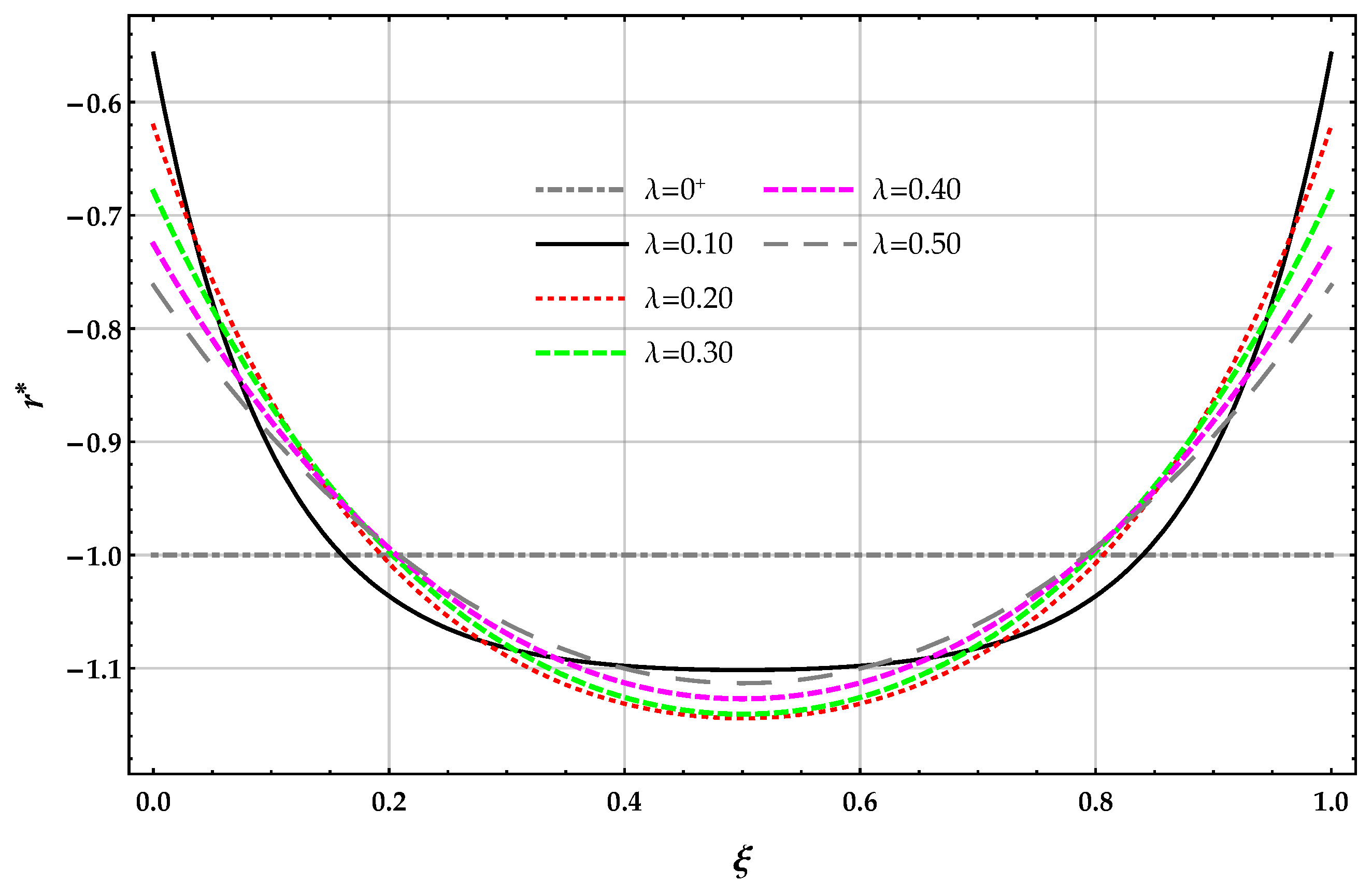
beam. DD method: plots of the non-dimensional reaction of the elastic foundation for increasing values of the non-dimensional non-local parameter in the set with .
Figure 3.
beam. DD method: plots of the non-dimensional reaction of the elastic foundation for increasing values of the non-dimensional non-local parameter in the set with .
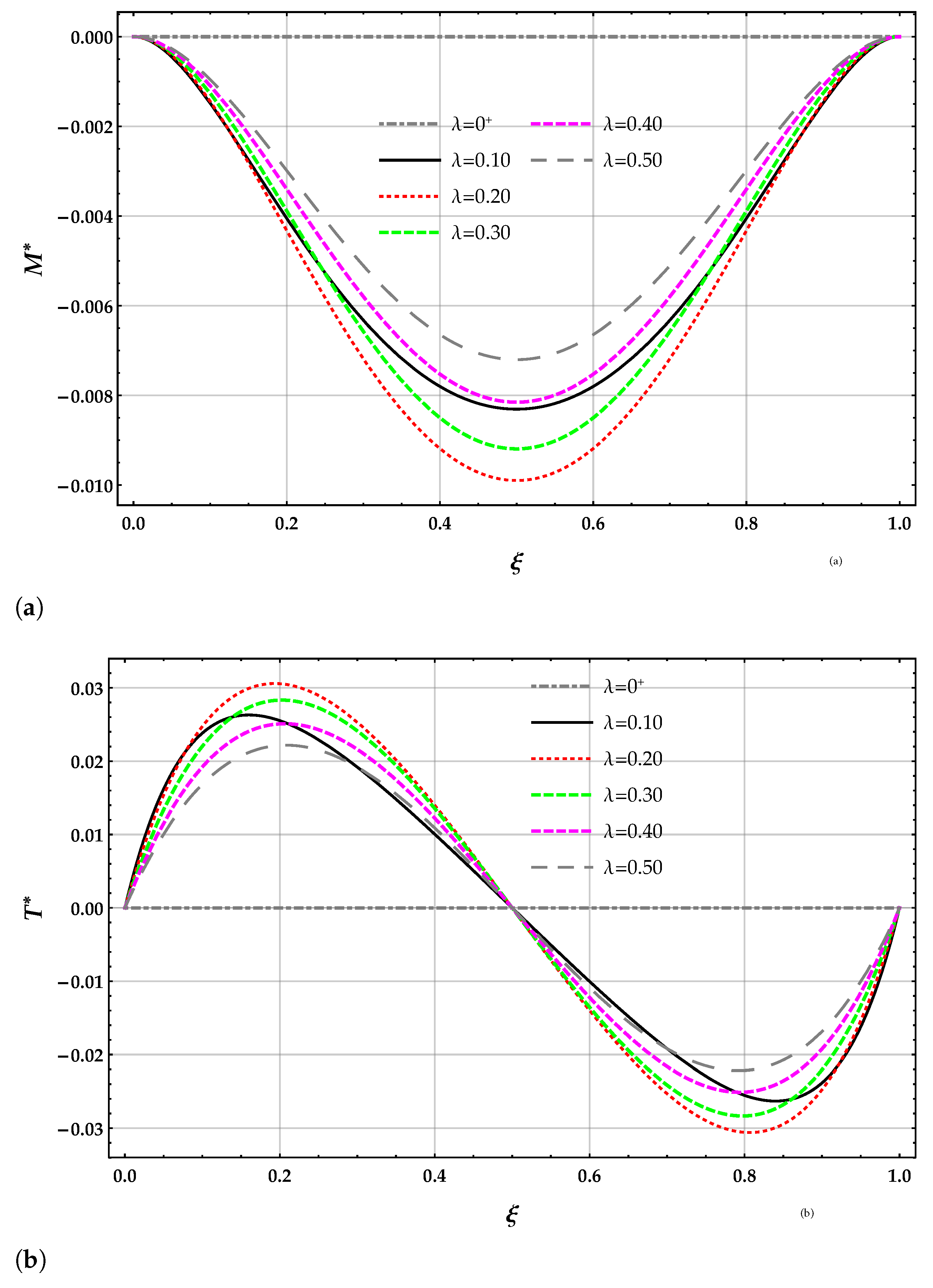
Figure 4.
beam. Plots for increasing values of the non-dimensional non-local parameter in the set with of (a) non-dimensional bending moment using the DD method and (b) non-dimensional shear force using the DD method.
Figure 4.
beam. Plots for increasing values of the non-dimensional non-local parameter in the set with of (a) non-dimensional bending moment using the DD method and (b) non-dimensional shear force using the DD method.
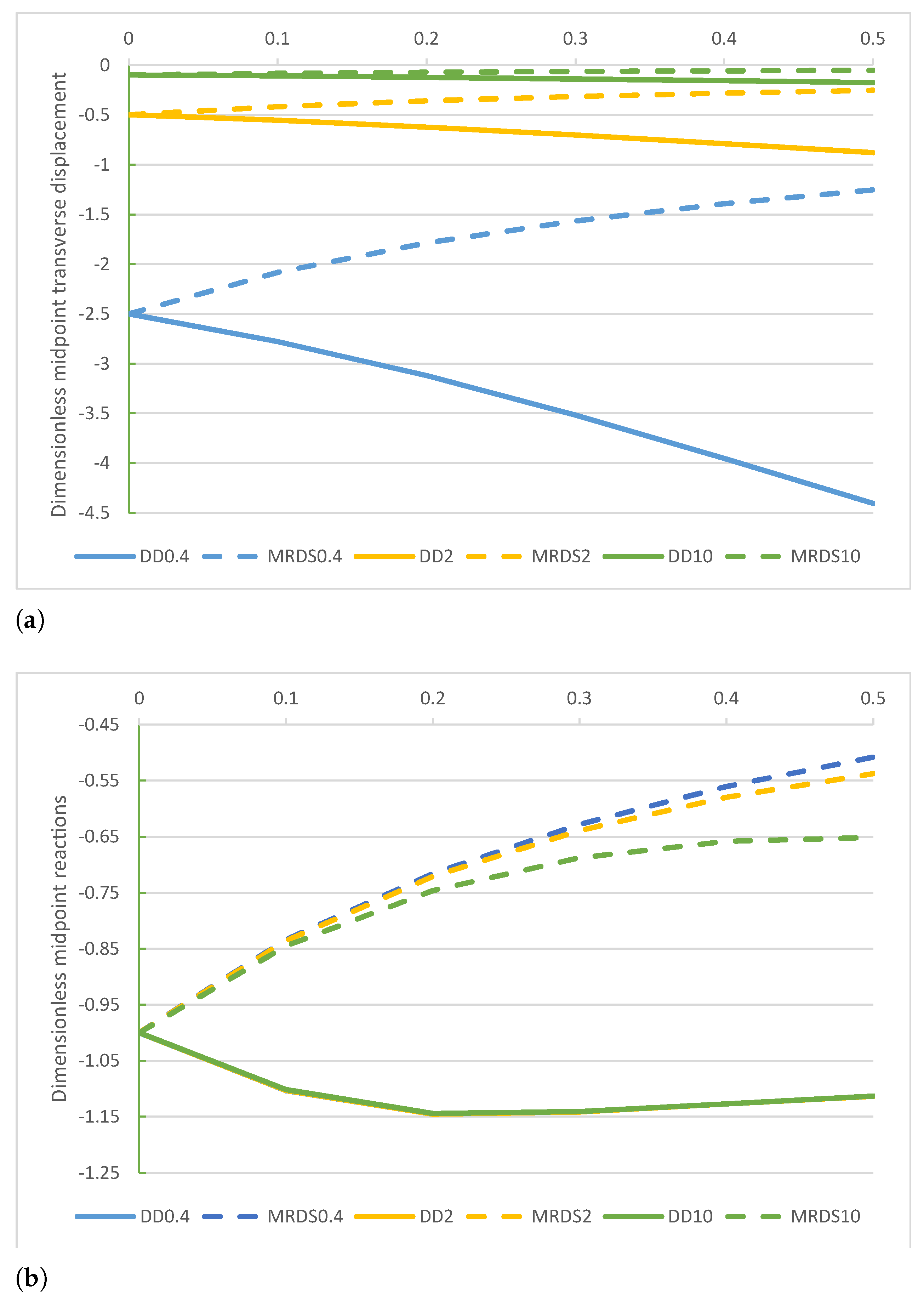
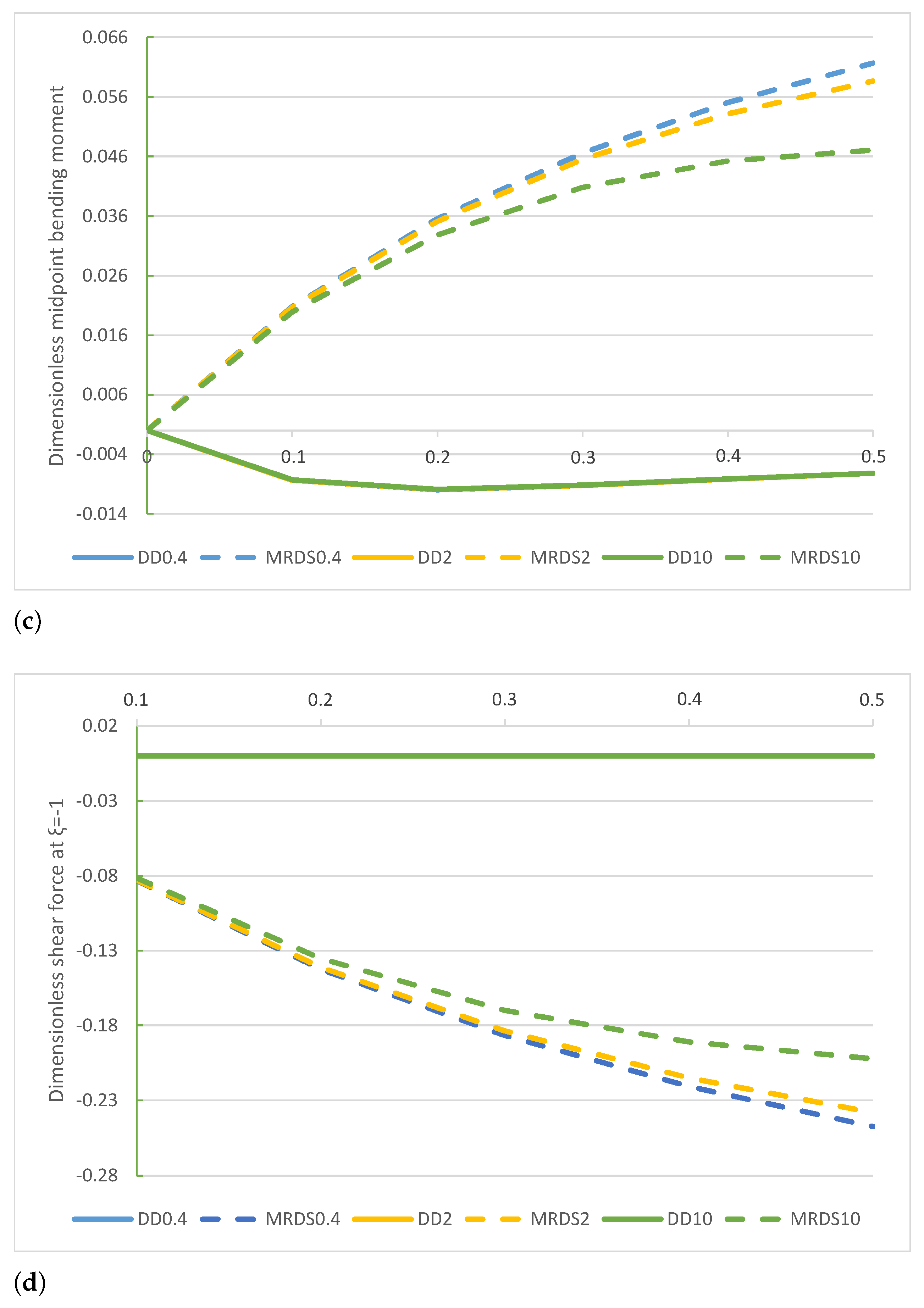
Figure 5.
beam. Comparison of the DD and MRD methods for increasing values of the non-dimensional non-local parameter in the set with : (a) non-dimensional transverse midpoint displacement , (b) dimensionless reaction , (c) non-dimensional bending moment , and (d) non-dimensional shear force .
Figure 5.
beam. Comparison of the DD and MRD methods for increasing values of the non-dimensional non-local parameter in the set with : (a) non-dimensional transverse midpoint displacement , (b) dimensionless reaction , (c) non-dimensional bending moment , and (d) non-dimensional shear force .
Figure 6.
beam. DD method: plots of the non-dimensional transverse displacement of the surface of the elastic foundation for increasing values of the non-dimensional non-local parameter in the set with .
Figure 6.
beam. DD method: plots of the non-dimensional transverse displacement of the surface of the elastic foundation for increasing values of the non-dimensional non-local parameter in the set with .
Figure 7.
beam. DD method: plots of the non-dimensional reaction of the elastic foundation for increasing values of the non-dimensional non-local parameter in the set with .
Figure 7.
beam. DD method: plots of the non-dimensional reaction of the elastic foundation for increasing values of the non-dimensional non-local parameter in the set with .
Figure 8.
beam. Plots for increasing values of the non-dimensional non-local parameter in the set with of (a) non-dimensional bending moment using the DD method and (b) non-dimensional shear force using the DD method.
Figure 8.
beam. Plots for increasing values of the non-dimensional non-local parameter in the set with of (a) non-dimensional bending moment using the DD method and (b) non-dimensional shear force using the DD method.
Figure 9.
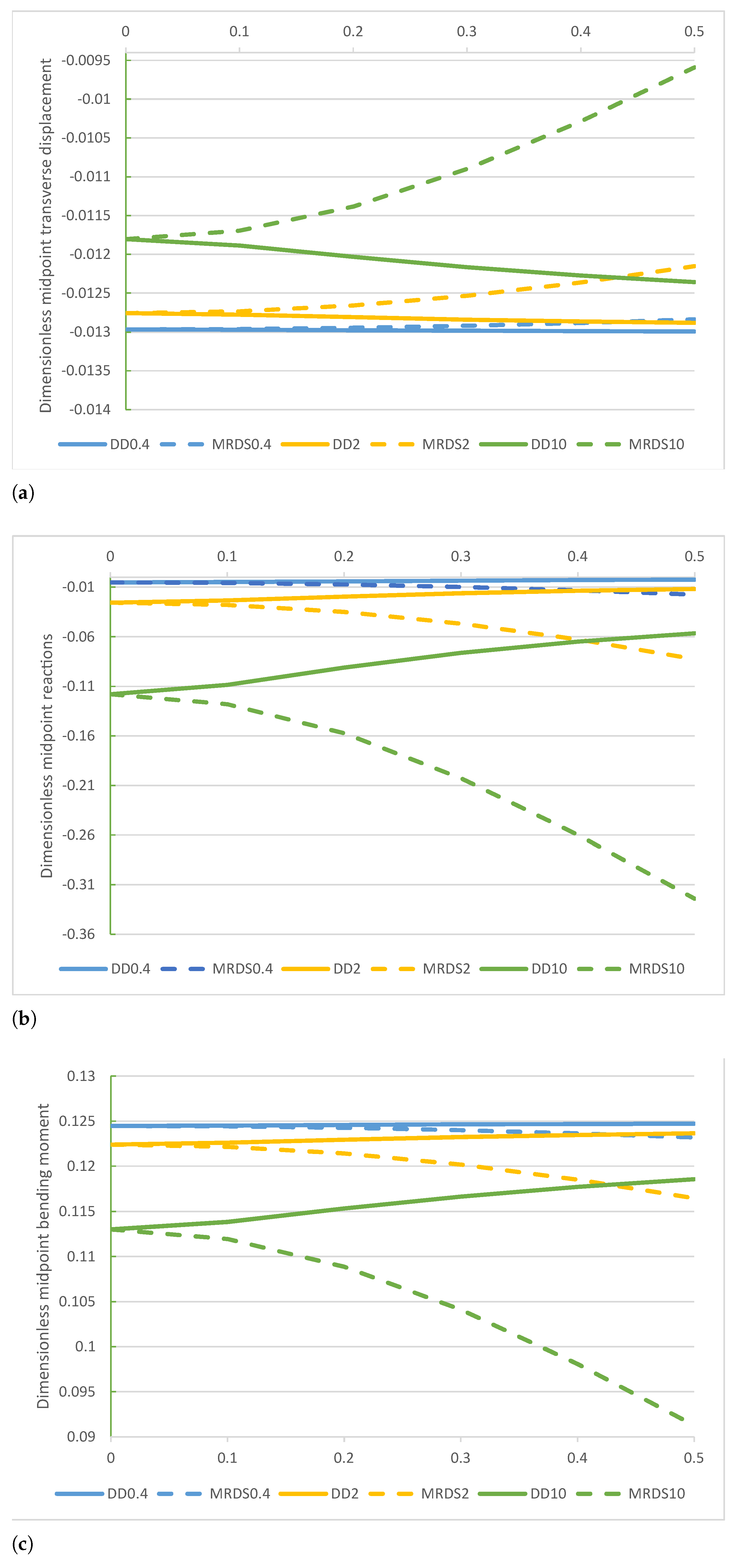
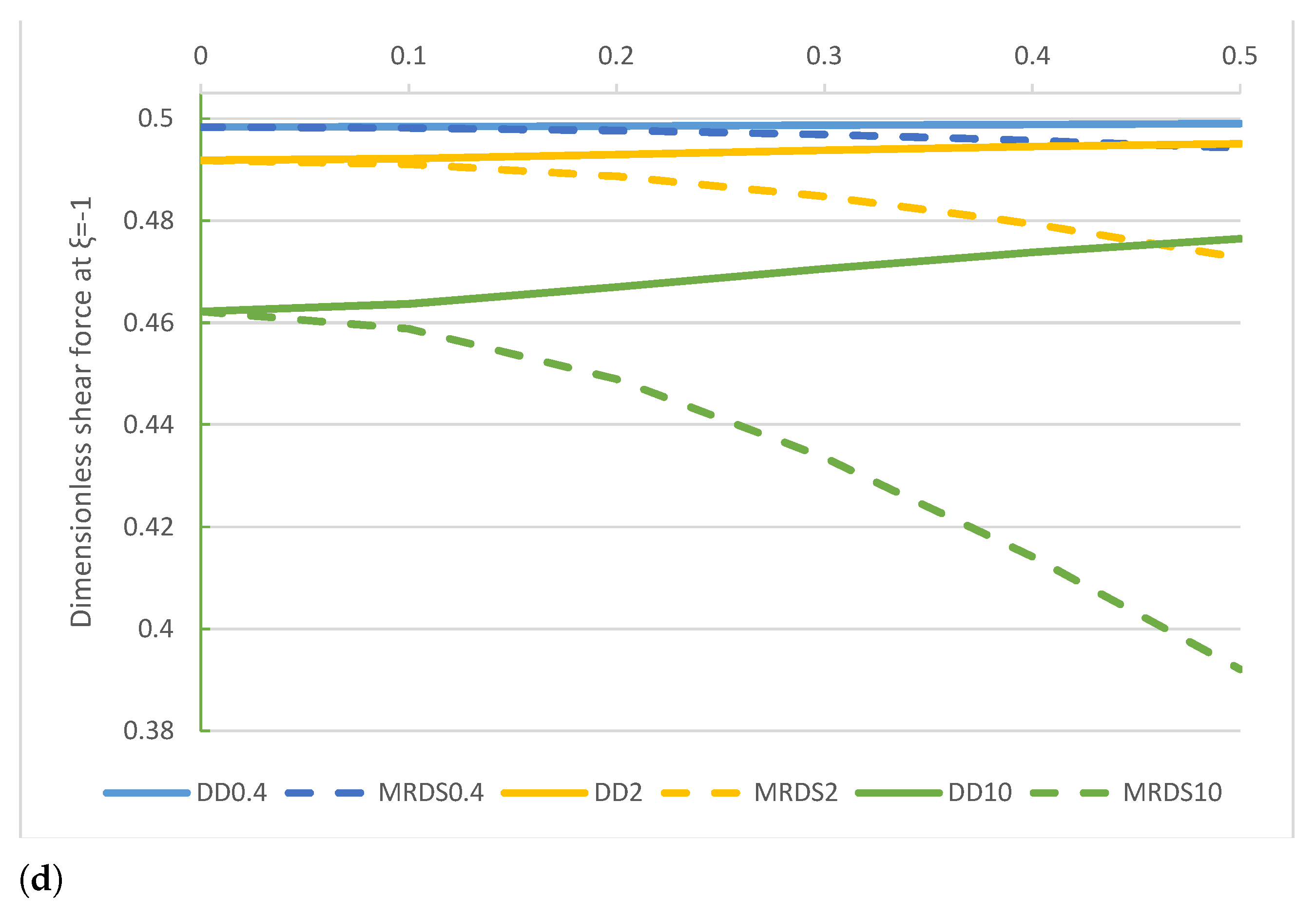
beam. Comparison of the DD and MRD methods for increasing values of the non-dimensional non-local parameter in the set with : (a) non-dimensional transverse midpoint displacement , (b) dimensionless reaction , (c) non-dimensional bending moment , and (d) non-dimensional shear force .
Figure 9.
beam. Comparison of the DD and MRD methods for increasing values of the non-dimensional non-local parameter in the set with : (a) non-dimensional transverse midpoint displacement , (b) dimensionless reaction , (c) non-dimensional bending moment , and (d) non-dimensional shear force .
Table 1.
Free beam subjected to a non-dimensional uniform load . Non-dimensional maximum displacement versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the DD and MRD models.
Table 1.
Free beam subjected to a non-dimensional uniform load . Non-dimensional maximum displacement versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the DD and MRD models.
| v (1/2) |
|---|
| DD | | MRD |
| k = 0.4 | k = 2 | k = 10 | k = 20 | | k = 0.4 | k = 2 | k = 10 | k = 20 |
| −2.5 | −0.5 | −0.1 | −0.05 | | −2.5 | −0.5 | −0.1 | −0.05 |
| 0.1 | −2.7775 | −0.555285 | −0.110845 | −0.0552931 | | −2.08434 | −0.41767 | −0.0843029 | −0.0425966 |
| 0.2 | −3.11944 | −0.623643 | −0.124485 | −0.0620923 | | −1.78773 | −0.359129 | −0.0732901 | −0.0374405 |
| 0.3 | −3.51736 | −0.703245 | −0.140422 | −0.0700698 | | −1.56541 | −0.315348 | −0.0650625 | −0.0335266 |
| 0.4 | −3.95023 | −0.789841 | −0.157764 | −0.0787552 | | −1.39259 | −0.28135 | −0.0586113 | −0.030365 |
| 0.5 | −4.40376 | −0.880569 | −0.175931 | −0.0878521 | | −1.25437 | −0.254164 | −0.0533617 | −0.0277079 |
Table 2.
Free beam subjected to a non-dimensional uniform load . Non-dimensional midpoint foundation reaction versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the DD and MRD models.
Table 2.
Free beam subjected to a non-dimensional uniform load . Non-dimensional midpoint foundation reaction versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the DD and MRD models.
| r (1/2) |
|---|
| DD | | MRD |
| k = 0.4 | k = 2 | k = 10 | k = 20 | | k = 0.4 | k = 2 | k = 10 | k = 20 |
| −1.0 | −1.0 | −1.0 | −1.0 | | −1.0 | −1.0 | −1.0 | −1.0 |
| 0.1 | −1.10354 | −1.10322 | −1.10166 | −1.09974 | | −0.833821 | −0.835754 | −0.845019 | −0.85574 |
| 0.2 | −1.14542 | −1.14522 | −1.14425 | −1.14305 | | −0.71566 | −0.721065 | −0.746027 | −0.773076 |
| 0.3 | −1.14127 | −1.14117 | −1.14065 | −1.14001 | | −0.627843 | −0.638892 | −0.687364 | −0.735528 |
| 0.4 | −1.12745 | −1.12739 | −1.1271 | −1.12673 | | −0.560558 | −0.579707 | −0.658509 | −0.729175 |
| 0.5 | −1.11353 | −1.1135 | −1.11332 | −1.1131 | | −0.507919 | −0.537668 | −0.651312 | −0.742323 |
Table 3.
Free beam subjected to a non-dimensional uniform load . Non-dimensional midpoint bending moment versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the Displacement-Driven (DD) and Modified Reaction-Driven (MRD) models.
Table 3.
Free beam subjected to a non-dimensional uniform load . Non-dimensional midpoint bending moment versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the Displacement-Driven (DD) and Modified Reaction-Driven (MRD) models.
| M (1/2) |
|---|
| DD | | MRD |
| k = 0.4 | k = 2 | k = 10 | k = 20 | | k = 0.4 | k = 2 | k = 10 | k = 20 |
| 0 | 0 | 0 | 0 | | 0 | 0 | 0 | 0 |
| 0.1 | −0.00840319 | −0.00838687 | −0.00830616 | −0.00820727 | | 0.0207943 | 0.0206397 | 0.0198977 | 0.0190375 |
| 0.2 | −0.00995599 | −0.00994611 | −0.00989699 | −0.00983623 | | 0.0355889 | 0.0350958 | 0.0328139 | 0.0303315 |
| 0.3 | −0.00922294 | −0.00921768 | −0.00919144 | −0.00915884 | | 0.0465999 | 0.0455298 | 0.0408201 | 0.0361086 |
| 0.4 | −0.00816841 | −0.00816543 | −0.00815058 | −0.00813209 | | 0.0550571 | 0.0531471 | 0.0452469 | 0.038086 |
| 0.5 | −0.00721239 | −0.00721058 | −0.00720154 | −0.00719027 | | 0.0616985 | 0.0586827 | 0.0470779 | 0.037633 |
Table 4.
Free beam subjected to a non-dimensional uniform load . Non-dimensional parameters versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the MRD model.
Table 4.
Free beam subjected to a non-dimensional uniform load . Non-dimensional parameters versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the MRD model.
|
|---|
| MRD |
| k = 0.4 | k = 2 | k = 10 | k = 20 |
| −0.0832594 | −0.0829661 | −0.0815572 | −0.0799202 |
| −0.142532 | −0.141251 | −0.135315 | −0.128836 |
| −0.186708 | −0.183624 | −0.170018 | −0.156337 |
| −0.220721 | −0.214963 | −0.191062 | −0.169231 |
| −0.247531 | −0.23823 | −0.202257 | −0.172651 |
Table 5.
Free beam subjected to a non-dimensional uniform load with the non-dimensional length-scale parameter . Non-dimensional displacement evaluated by the non-dimensional Winkler parameter in the DD and MRD models.
Table 5.
Free beam subjected to a non-dimensional uniform load with the non-dimensional length-scale parameter . Non-dimensional displacement evaluated by the non-dimensional Winkler parameter in the DD and MRD models.
| with |
|---|
| DD | | MRD |
| k = 0.4 | k = 2 | k = 10 | k = 20 | | k = 0.4 | k = 2 | k = 10 | k = 20 |
| 0.5 | −4.40376 | −0.880569 | −0.175931 | −0.0878521 | | −1.25437 | −0.254164 | −0.0533617 | −0.0277079 |
| 0.6 | −4.40379 | −0.880604 | −0.175967 | −0.0878876 | | −1.25407 | −0.253872 | −0.0531278 | −0.0275208 |
| 0.7 | −4.40389 | −0.880706 | −0.176068 | −0.0879886 | | −1.25317 | −0.253021 | −0.0524435 | −0.0269726 |
| 0.8 | −4.40405 | −0.880858 | −0.17622 | −0.0881401 | | −1.25176 | −0.251679 | −0.0513622 | −0.0261034 |
| 0.9 | −4.40423 | −0.88104 | −0.176402 | −0.0883215 | | −1.24996 | −0.249964 | −0.049975 | −0.0249838 |
| 1.0 | −4.40442 | −0.881232 | −0.176594 | −0.0885133 | | −1.24794 | −0.24804 | −0.0484141 | −0.0237196 |
| 1.2 | −2.95237 | −0.590707 | −0.118374 | −0.0593323 | | −0.836521 | −0.166266 | −0.032453 | −0.0158997 |
| 1.4 | −1.97903 | −0.395963 | −0.0793487 | −0.0397716 | | −0.560737 | −0.111451 | −0.021753 | −0.0106579 |
| 1.6 | −1.32659 | −0.265422 | −0.053189 | −0.0266597 | | −0.375873 | −0.0747081 | −0.0145821 | −0.0071442 |
| 1.8 | −0.889237 | −0.177918 | −0.0356536 | −0.0178705 | | −0.251955 | −0.0500784 | −0.00977464 | −0.0047889 |
| 2.0 | −0.596073 | −0.119262 | −0.0238994 | −0.011979 | | −0.168891 | −0.0335685 | −0.00655214 | −0.00321009 |
| 2.2 | −0.39956 | −0.0799436 | −0.0160202 | −0.00802975 | | −0.113211 | −0.0225017 | −0.0043920 | −0.00215179 |
| 2.4 | −0.267833 | −0.0535878 | −0.0107387 | −0.0053825 | | −0.0758875 | −0.0150833 | −0.00294407 | −0.00144239 |
| 2.6 | −0.179534 | −0.035921 | −0.00719835 | −0.003608 | | −0.0508689 | −0.0101106 | −0.00197347 | −0.000966862 |
| 2.8 | −0.120345 | −0.0240785 | −0.0048252 | −0.00241851 | | −0.0340984 | −0.00677737 | −0.00132285 | −0.00064810 |
| 3.0 | −0.0806698 | −0.0161403 | −0.00323443 | −0.00162118 | | −0.0228569 | −0.00454301 | −0.000886735 | −0.000434439 |
Table 6.
Simply supported beam subjected to a non-dimensional uniform load . Non-dimensional maximum displacement versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the DD and MRD models.
Table 6.
Simply supported beam subjected to a non-dimensional uniform load . Non-dimensional maximum displacement versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the DD and MRD models.
| v (1/2) |
|---|
| DD | | MRD |
| k = 0.4 | k = 2 | k = 10 | k = 20 | | k = 0.4 | k = 2 | k = 10 | k = 20 |
| −0.0129674 | −0.0127579 | −0.011804 | −0.0107944 | | −0.0129674 | −0.0127579 | −0.011804 | −0.0107944 |
| 0.1 | −0.0129713 | −0.0127769 | −0.0118858 | −0.0109322 | | −0.0129621 | −0.0127325 | −0.0116961 | −0.0106152 |
| 0.2 | −0.0129781 | −0.0128101 | −0.012031 | −0.0111806 | | −0.0129464 | −0.012657 | −0.0113839 | −0.0101115 |
| 0.3 | −0.0129842 | −0.0128399 | −0.0121636 | −0.0114121 | | −0.0129203 | −0.0125331 | −0.010899 | −0.00937019 |
| 0.4 | −0.0129891 | −0.0128637 | −0.0122715 | −0.0116035 | | −0.0128839 | −0.0123637 | −0.0102855 | −0.00849743 |
| 0.5 | −0.0129929 | −0.0128826 | −0.0123577 | −0.0117587 | | −0.0128374 | −0.0121524 | −0.00959096 | −0.00758798 |
Table 7.
Simply supported beam subjected to a non-dimensional uniform load . Non-dimensional midpoint foundation reaction versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the DD and MRD models.
Table 7.
Simply supported beam subjected to a non-dimensional uniform load . Non-dimensional midpoint foundation reaction versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the DD and MRD models.
| r (1/2) |
|---|
| DD | | MRD |
| k = 0.4 | k = 2 | k = 10 | k = 20 | | k = 0.4 | k = 2 | k = 10 | k = 20 |
| −0.00518695 | −0.0255157 | −0.11804 | −0.215888 | | −0.00518695 | −0.0255157 | −0.11804 | −0.215888 |
| 0.1 | −0.00473987 | −0.0233446 | −0.108595 | −0.199791 | | −0.00568254 | −0.0279081 | −0.128154 | −0.232559 |
| 0.2 | −0.00392519 | −0.0193724 | −0.0909833 | −0.169134 | | −0.00716682 | −0.0350271 | −0.157386 | −0.279296 |
| 0.3 | −0.00325168 | −0.016078 | −0.0761649 | −0.142938 | | −0.00963245 | −0.0467014 | −0.202683 | −0.347708 |
| 0.4 | −0.00275059 | −0.0136205 | −0.0649725 | −0.122886 | | −0.0130672 | −0.0626567 | −0.259779 | −0.427556 |
| 0.5 | −0.00237493 | −0.011774 | −0.0564754 | −0.107486 | | −0.0174544 | −0.082531 | −0.324063 | −0.509754 |
Table 8.
Simply supported beam subjected to a non-dimensional uniform load . Non-dimensional midpoint bending moment versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the DD and MRD models.
Table 8.
Simply supported beam subjected to a non-dimensional uniform load . Non-dimensional midpoint bending moment versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the DD and MRD models.
| M (1/2) |
|---|
| DD | | MRD |
| k = 0.4 | k = 2 | k = 10 | k = 20 | | k = 0.4 | k = 2 | k = 10 | k = 20 |
| 0.124473 | 0.122406 | 0.112995 | 0.103036 | | 0.124473 | 0.122406 | 0.112995 | 0.103036 |
| 0.1 | 0.124512 | 0.122598 | 0.113826 | 0.104439 | | 0.124421 | 0.122156 | 0.111935 | 0.101277 |
| 0.2 | 0.124582 | 0.122936 | 0.115305 | 0.106976 | | 0.124266 | 0.121414 | 0.108867 | 0.0963317 |
| 0.3 | 0.124643 | 0.123235 | 0.116638 | 0.109306 | | 0.124009 | 0.120195 | 0.104103 | 0.0890578 |
| 0.4 | 0.124691 | 0.123472 | 0.11771 | 0.111212 | | 0.123651 | 0.118529 | 0.0980778 | 0.0805024 |
| 0.5 | 0.124729 | 0.123658 | 0.118562 | 0.112747 | | 0.123194 | 0.116452 | 0.0912613 | 0.0715989 |
Table 9.
Simply supported beam subjected to a non-dimensional uniform load . Non-dimensional shear force versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the DD and MRD models.
Table 9.
Simply supported beam subjected to a non-dimensional uniform load . Non-dimensional shear force versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the DD and MRD models.
| T (1) |
|---|
| DD | | MRD |
| k = 0.4 | k = 2 | k = 10 | k = 20 | | k = 0.4 | k = 2 | k = 10 | k = 20 |
| 0.49834 | 0.491834 | 0.462207 | 0.430842 | | 0.49834 | 0.491834 | 0.462207 | 0.430842 |
| 0.1 | 0.498415 | 0.492192 | 0.463669 | 0.433139 | | 0.498175 | 0.491035 | 0.4588 | 0.425162 |
| 0.2 | 0.498576 | 0.492972 | 0.466991 | 0.43863 | | 0.49768 | 0.488657 | 0.448937 | 0.409178 |
| 0.3 | 0.498743 | 0.493787 | 0.470565 | 0.444756 | | 0.496858 | 0.484753 | 0.433596 | 0.385589 |
| 0.4 | 0.498889 | 0.494496 | 0.473746 | 0.450343 | | 0.495712 | 0.479413 | 0.414148 | 0.357704 |
| 0.5 | 0.499009 | 0.495087 | 0.476435 | 0.45515 | | 0.494248 | 0.472753 | 0.392079 | 0.328478 |
Table 10.
Simply supported beam subjected to a non-dimensional uniform load . Non-dimensional parameters versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the MRD model.
Table 10.
Simply supported beam subjected to a non-dimensional uniform load . Non-dimensional parameters versus the non-dimensional length-scale parameter evaluated by the non-dimensional Winkler parameter in the MRD model.
|
|---|
| MRD |
| k = 0.4 | k = 2 | k = 10 | k = 20 |
| 0.000165929 | 0.00081521 | 0.00375032 | 0.00682117 |
| 0.000662923 | 0.00324183 | 0.0146081 | 0.0260151 |
| 0.00148862 | 0.00722391 | 0.0314937 | 0.0543281 |
| 0.0026391 | 0.0126718 | 0.0528961 | 0.087776 |
| 0.00410896 | 0.0194672 | 0.0771786 | 0.1228 |