Influences of Elastic Foundations and Material Gradient on the Dynamic Response of Polymer Cylindrical Pipes Patterned by Carbon Nanotube Subjected to Moving Pressures
Abstract
:1. Introduction
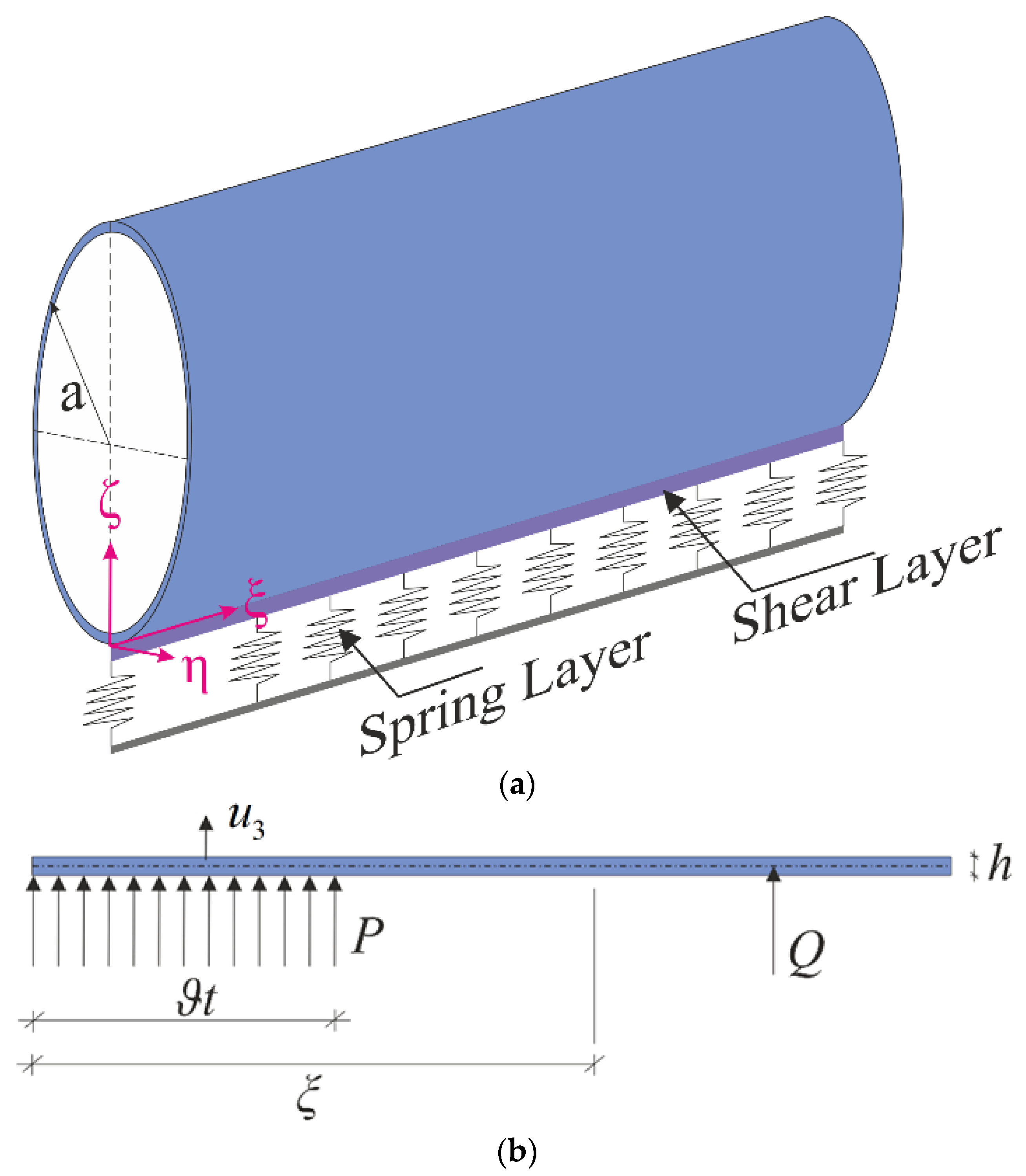
2. Problem Description
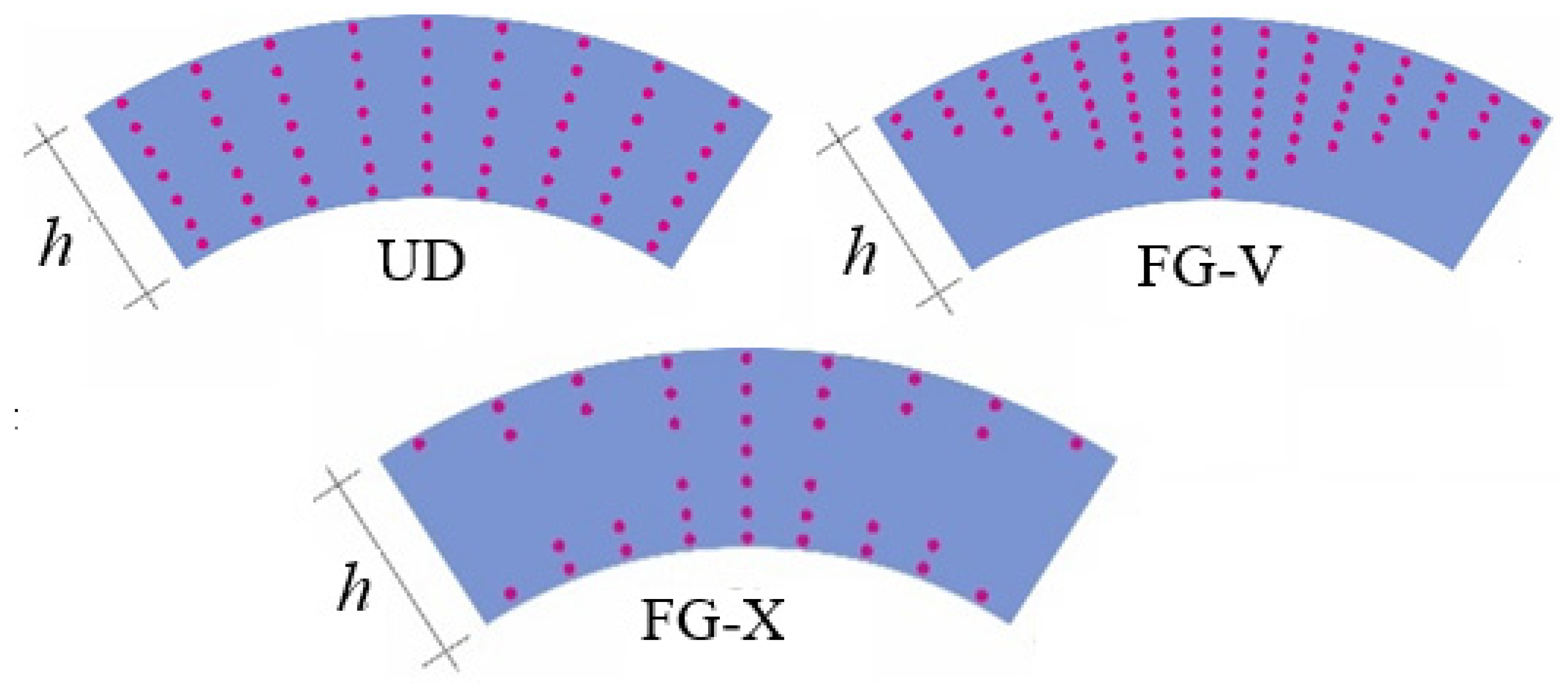
Modeling of Material Properties
3. Basic Assumptions and Equations
4. Solution Procedure
5. Numerical Examples
5.1. Comparisons
5.2. Specific Numerical Results for the Dynamic Response of CNT-Based Cylindrical Pipes
6. Conclusions
- (a)
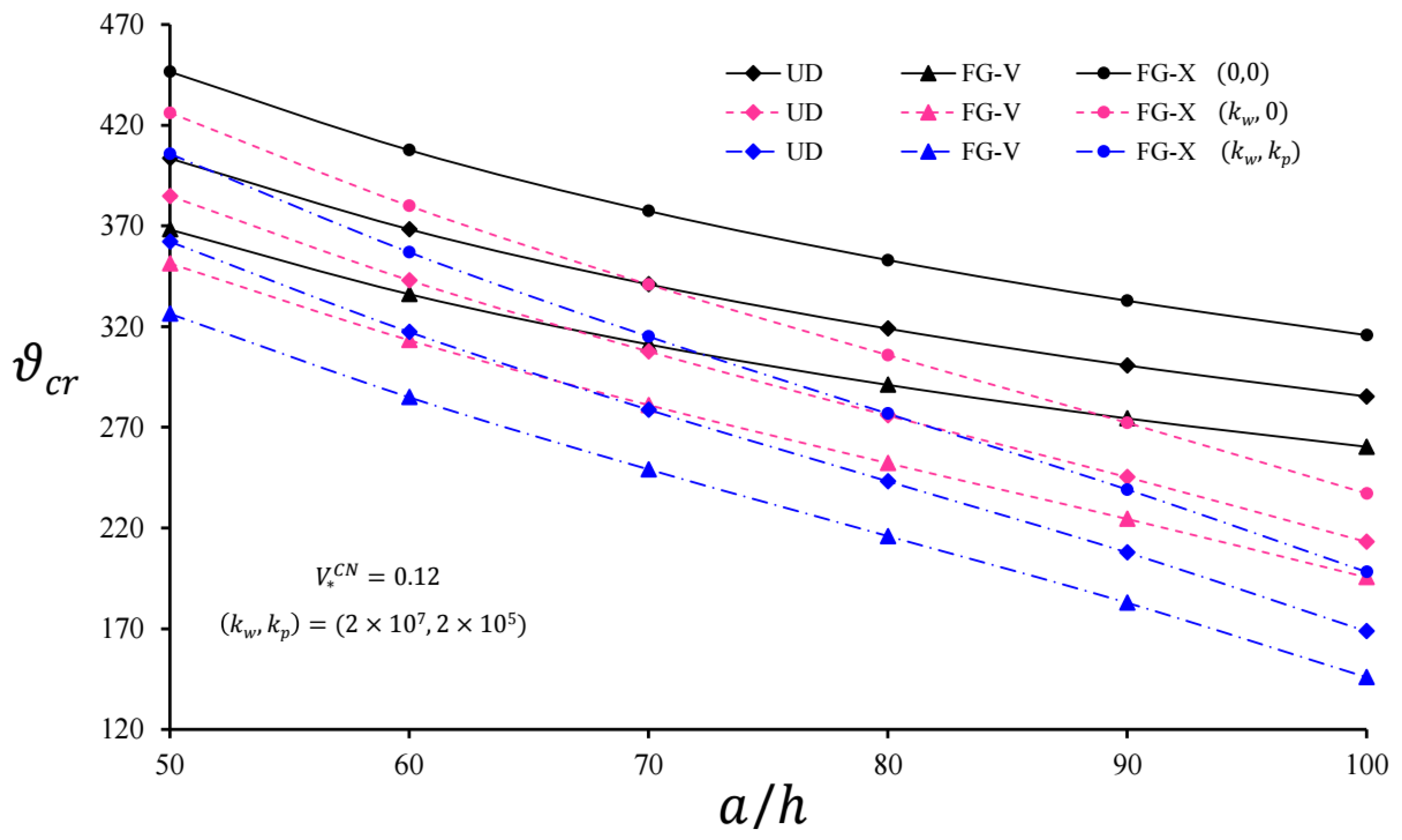
- In the presence of the WEF and the PEF, the critical velocity values of endless length pipes reinforced with UD, FG-V, and FG-X type CNTs were significantly reduced;
- (b)
- Considering the effect of soils, the influences of functionally graded distributions of CNTs over the cylinder thickness on the critical velocity were more pronounced than the foundationless condition;
- (c)
- When the coefficients of the EFs increased, the influence of soils on the critical velocity became apparent, while the increase in significantly reduced this effect;
- (d)
- Since infinitely long FG-V and FG-X cylindrical pipes with and without EFs were compared with the infinitely long UD-cylinder with and without EFs, respectively, the influence on the critical speed was more noticeable for the FG-X cylinder;
- (e)
- The critical velocity of moving pressure affecting the cylindrical pipes originating from CNTs on the WEF and the PEF decreased faster than the unconstrained cylinders with an increase in ;
- (f)
- Although the effect of heterogeneity did not depend on the in the unconstrained CNT-based cylindrical pipes, the effect of heterogeneity on the critical speed of the CNT-based polymer pipes on the PEF became more pronounced as the increased;
- (g)
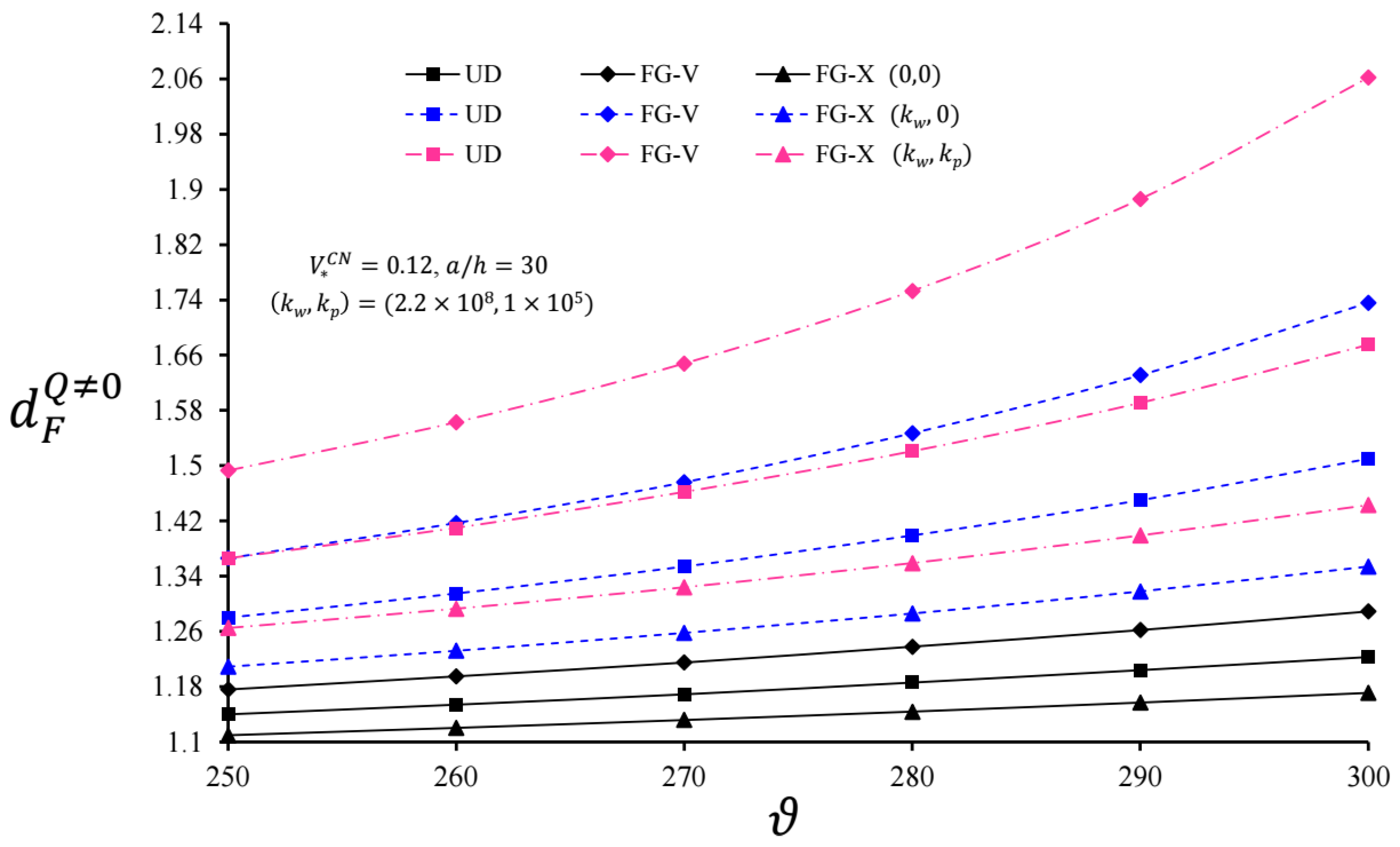
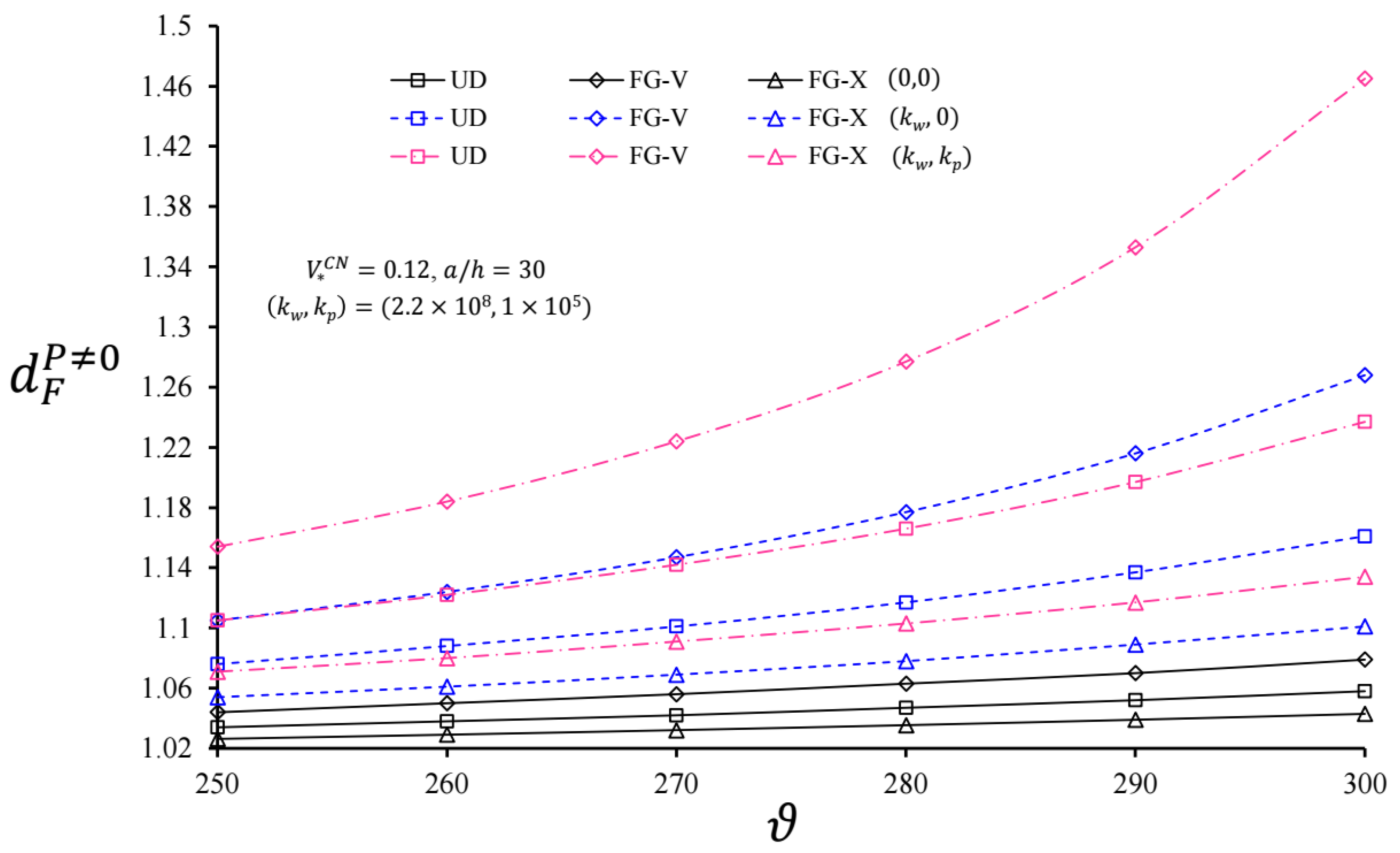
- The dynamic coefficients of the infinite length CNT-based cylindrical pipes with UD, FG-V, and FG-X types on the WEF and PEF increased with the increasing coefficients of shear and spring layers together and separately;
- (h)
- The dynamic coefficient of the CNT-based polymer pipes with the shape FG-V on the EFs was higher than that of the pipe originating from CNTs of the shape UD on the EFs, while the dynamic coefficient of the CNT-based polymer pipes with the shape FG-X on the EFs was lower;
- (i)
- The use of EFs was one of the remarkable points and made the heterogeneous distribution of CNTs on the influence of the dynamic coefficients more obvious;
- (j)
- An increase in significantly reduced the influence of the inhomogeneous distribution of CNTs on the dynamic coefficient of polymer cylinders, since both types of EFs were taken into account;
- (k)
- As the influences of the linear variation in carbon nanotubes on and were compared with each other, the influence of heterogeneity on was approximately twice that on ;
- (l)
- With the increase in , although the dynamic coefficients increased for pipes with and without EFs, the foundation effect accelerated the increase of and ;
- (m)
- The heterogeneity effect was more prominent for cylindrical pipes originating from CNTs on the EFs and increased with the increment of in comparison with UD-cylinders.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNT | Carbon nanotube |
| EFs | Elastic foundations |
| FG-V | V-type functionally graded distribution |
| FG-X | X-type functionally graded distribution |
| PEF | Pasternak elastic foundation |
| WEF | Winkler elastic foundation |
| UD | Uniform distribution |
Appendix A
References
- Ogibalov, P.M.; Koltunov, M.A. Shells and Plates; Izd Moscow Univ: Moscow, Russia, 1969. (in Russian) [Google Scholar]
- Fryba, L. Vibration of Solids and Structures under Moving Loads; Thomas Telford: London, UK, 1999. [Google Scholar]
- Forrestal, M.J.; Alzheimer, W.E. Response of a circular elastic shell to moving and simultaneous loads. AIAA J. 1970, 8, 970–971. [Google Scholar] [CrossRef]
- Huang, C.-C. Moving loads on elastic cylindrical shells. J. Sound Vib. 1976, 49, 215–220. [Google Scholar] [CrossRef]
- Singh, V.; Upadhyay, P.; Kishor, B. On the dynamic response of buried orthotropic cylindrical shells under moving load. Int. J. Mech. Sci. 1988, 30, 397–406. [Google Scholar] [CrossRef]
- Panneton, R.; Berry, A.; Laville, F. Vibration and sound radiation of a cylindrical shell under a circumferentially moving load. J. Acoust. Soc. Am. 1995, 98, 2165–2173. [Google Scholar] [CrossRef]
- Ruzzene, M.; Baz, A. Dynamic stability of periodic shells with moving loads. J. Sound Vib. 2006, 296, 830–844. [Google Scholar] [CrossRef]
- Karttunen, A.T.; von Hertzen, R. Dynamic response of a cylinder cover under a moving load. Int. J. Mech. Sci. 2014, 82, 170–178. [Google Scholar] [CrossRef] [Green Version]
- Eipakchi, H.; Nasrekani, F.M. Vibrational behavior of composite cylindrical shells with auxetic honeycombs core layer subjected to a moving pressure. Compos. Struct. 2020, 254, 112847. [Google Scholar] [CrossRef]
- Eipakchi, H.; Nasrekani, F.M.; Ahmadi, S. An analytical approach for the vibration behavior of viscoelastic cylindrical shells under internal moving pressure. Acta Mech. 2020, 231, 3405–3418. [Google Scholar] [CrossRef]
- Sheng, G.G.; Wang, X. Studies on dynamic behavior of functionally graded cylindrical shells with PZT layers under moving loads. J. Sound Vib. 2009, 323, 772–789. [Google Scholar] [CrossRef]
- Sheng, G.; Wang, X. Response and control of functionally graded laminated piezoelectric shells under thermal shock and moving loadings. Compos. Struct. 2010, 93, 132–141. [Google Scholar] [CrossRef]
- Sofiyev, A. Dynamic response of an FGM cylindrical shell under moving loads. Compos. Struct. 2010, 93, 58–66. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Halilov, H.M.; Kuruoglu, N. Analytical solution of the dynamic behavior of non-homogenous orthotropic cylindrical shells on elastic foundations under moving loads. J. Eng. Math. 2011, 69, 359–371. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Heydarpour, Y. Response of functionally graded cylindrical shells under moving thermo-mechanical loads. Thin-Walled Struct. 2012, 58, 51–66. [Google Scholar] [CrossRef]
- Arazm, M.; Eipakchi, H.; Ghannad, M. Vibrational behavior investigation of axially functionally graded cylindrical shells under moving pressure. Acta Mech. 2019, 230, 3221–3234. [Google Scholar] [CrossRef]
- Ramezani, H.; Mirzaei, M. Transient elastodynamic behavior of cylindrical tubes under moving pressures and different boundary conditions. Appl. Math. Model. 2020, 77, 934–949. [Google Scholar] [CrossRef]
- Zhen, B.; Xu, J.; Sun, J. Analytical solutions for steady state responses of an infinite Euler-Bernoulli beam on a nonlinear viscoelastic foundation subjected to a harmonic moving load. J. Sound Vib. 2020, 476, 115271. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Thostenson, E.; Ren, Z.; Chou, T. Advances in the science and technology of carbon nanotubes and their composites: A review. Compos. Sci. Technol. 2001, 61, 1899–1912. [Google Scholar] [CrossRef] [Green Version]
- Kiani, K. Nanoparticle delivery via stocky single-walled carbon nanotubes: A nonlinear-nonlocal continuum-based scrutiny. Compos. Struct. 2014, 116, 254–272. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Bacciocchi, M.; Agnelli, J.; Benedetti, D. Three-phase homogenization procedure for woven fabric composites reinforced by carbon nanotubes in thermal environment. Compos. Struct. 2020, 254, 112840. [Google Scholar] [CrossRef]
- Chandel, V.S.; Wang, G.; Talha, M. Advances in modelling and analysis of nano structures: A review. Nanotechnol. Rev. 2020, 9, 230–258. [Google Scholar] [CrossRef]
- Shen, H.-S.; Xiang, Y. Nonlinear vibration of nanotube-reinforced composite cylindrical shells in thermal environments. Comput. Methods Appl. Mech. Eng. 2012, 213-216, 196–205. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Free vibrations of free-form doubly-curved shells made of functionally graded materials using higher-order equivalent single layer theories. Compos. Part B Eng. 2014, 67, 490–509. [Google Scholar] [CrossRef]
- Liew, K.M.; Lei, Z.; Yu, J.; Zhang, L. Postbuckling of carbon nanotube-reinforced functionally graded cylindrical panels under axial compression using a meshless approach. Comput. Methods Appl. Mech. Eng. 2014, 268, 1–17. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Linear static response of nanocomposite plates and shells reinforced by agglomerated carbon nanotubes. Compos. Part B Eng. 2017, 115, 449–476. [Google Scholar] [CrossRef]
- Sofiyev, A.; Turkaslan, B.E.; Bayramov, R.; Salamci, M. Analytical solution of stability of FG-CNTRC conical shells under external pressures. Thin-Walled Struct. 2019, 144, 1–12. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Tornabene, F.; Dimitri, R.; Kuruoglu, N. Buckling Behavior of FG-CNT Reinforced Composite Conical Shells Subjected to a Combined Loading. Nanomaterials 2020, 10, 419. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bacciocchi, M.; Tarantino, A.M. Time-dependent behavior of viscoelastic three-phase composite plates reinforced by Carbon nanotubes. Compos. Struct. 2019, 216, 20–31. [Google Scholar] [CrossRef]
- Bacciocchi, M. Buckling analysis of three-phase CNT/polymer/fiber functionally graded orthotropic plates: Influence of the nonuniform distribution of the oriented fibers on the critical load. Eng. Struct. 2020, 223, 111176. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Tarantino, A.M. Critical buckling load of honeycomb sandwich panels reinforced by three-phase orthotropic skins enhanced by carbon nanotubes. Compos. Struct. 2020, 237, 111904. [Google Scholar] [CrossRef]
- Daikh, A.A.; Houari, M.S.A.; Karami, B.; Eltaher, M.A.; Dimitri, R.; Tornabene, F. Buckling analysis of CNTRC curved sandwich nanobeams in thermal environment. Appl. Sci. 2021, 11, 3250. [Google Scholar] [CrossRef]
- Karami, B.; Janghorban, M.; Shahsavari, D.; Dimitri, R.; Tornabene, F. Nonlocal Buckling Analysis of Composite Curved Beams Reinforced with Functionally Graded Carbon Nanotubes. Molecules 2019, 24, 2750. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, Y.; Karami, B.; Shahsavari, D.; Tounsi, A. Static stability analysis of carbon nanotube reinforced polymeric composite doubly curved microshell panels. Archiv. Civil Mech. Eng. 2021, 21, 139. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Tarantino, A.M. Modeling and numerical investigation of the viscoelastic behavior of laminated concrete beams strengthened by CFRP strips and carbon nanotubes. Constr. Build. Mater. 2020, 233, 117311. [Google Scholar] [CrossRef]
- Eyvazian, A.; Sebaey, T.A.; Żur, K.K.; Khan, A.; Zhang, H.; Wong, S.H. On the dynamics of FG-GPLRC sandwich cylinders based on an unconstrained higher-order theory. Compos. Struct. 2021, 267, 113879. [Google Scholar] [CrossRef]
- Avey, M.; Fantuzzı, N.; Sofıyev, A.H.; Kuruoglu, N. Nonlinear vibration of multilayer shell-type structural elements with double curvature consisting of CNT patterned layers within different theories. Compos. Struct. 2021, 2751, 114401. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Avey, M.; Kuruoglu, N. An approach to the solution of nonlinear forced vibration problem of structural systems reinforced with advanced materials in the presence of viscous damping. Mech. Sys. Signal Process. 2021, 161, 107991. [Google Scholar] [CrossRef]
- Avey, M.; Sofiyev, A.H.; Fantuzzi, N.; Kuruoglu, N. Primary resonance of double-curved nanocomposite systems using improved nonlinear theory and multi-scales method: Modeling and analytical solution. Int. J. Nonlin. Mech. 2021, 137, 103816. [Google Scholar]
- Deniz, A.; Fantuzzi, N.; Sofiyev, A.H.; Kuruoglu, N. Modeling and solution of large amplitude vibration problem of construction elements made of nanocomposites using shear deformation theory. Materials 2021, 14, 3843. [Google Scholar] [CrossRef]
- Mahmure, A.; Tornabene, F.; Dimitri, R.; Kuruoglu, N. Free Vibration of Thin-Walled Composite Shell Structures Reinforced with Uniform and Linear Carbon Nanotubes: Effect of the Elastic Foundation and Nonlinearity. Nanomaterials 2021, 11, 2090. [Google Scholar] [CrossRef]
- Izadi, R.; Tuna, M.; Trovalusci, P.; Ghavanloo, E. Torsional Characteristics of Carbon Nanotubes: Micropolar Elasticity Models and Molecular Dynamics Simulation. Nanomaterials 2021, 11, 453. [Google Scholar] [CrossRef] [PubMed]
- Pasternak, P.L. On a New Method of Analysis of an Elastic Foundation by Means of Two Foundation Constants; State Publishing House Building and Architecture Literature: Moscow, Russia, 1954; pp. 1–56. (in Russian) [Google Scholar]
- Kerr, A.D. Elastic and Viscoelastic Foundation Models. J. Appl. Mech. 1964, 31, 491–498. [Google Scholar] [CrossRef]
- Gorbunov-Possadov, M.I.; Malikova, T.A.; Solomin, V.I. Design of Structures on Elastic Foundation; State Publishing House Building and Architecture Literature: Moscow, Russia, 1984. (in Russian) [Google Scholar]
- Bazhenov, V.A. The Bending of the Cylindrical Shells in Elastic Medium; Visha Shkola: Kiev, Ukraine, 1975. (in Russian) [Google Scholar]
- Shen, H.S.; Xiang, Y. Nonlinear vibration of nanotube-reinforced composite cylindrical panels resting on elastic foundations in thermal environments. Compos. Struct. 2014, 111, 291–300. [Google Scholar] [CrossRef]
- Banić, D.; Bacciocchi, M.; Tornabene, F.; Ferreira, A.J.M. Influence of Winkler-Pasternak Foundation on the Vibrational Behavior of Plates and Shells Reinforced by Agglomerated Carbon Nanotubes. Appl. Sci. 2017, 7, 1228. [Google Scholar] [CrossRef] [Green Version]
- Bidgoli, M.R.; Karimi, M.S.; Arani, A.G. Nonlinear vibration and instability analysis of functionally graded CNT-reinforced cylindrical shells conveying viscous fluid resting on orthotropic Pasternak medium. Mech. Adv. Mater. Struct. 2016, 23, 819–831. [Google Scholar] [CrossRef]
- Mohammadi, M.; Arefi, M.; Dimitri, R.; Tornabene, F. Higher-order thermo-elastic analysis of FG-CNTRC cylindrical vessels surrounded by a Pasternak foundation. Nanomaterials 2019, 9, 79. [Google Scholar] [CrossRef] [Green Version]
- Van Thanh, N.; Quang, V.D.; Khoa, N.D.; Seung-Eock, K.; Duc, N.D. Nonlinear dynamic response and vibration of FG CNTRC shear deformable circular cylindrical shell with temperature-dependent material properties and surrounded on elastic foundations. J. Sandw. Struct. Mater. 2018, 21, 2456–2483. [Google Scholar] [CrossRef]
- Froio, D.; Rizzi, E.; Simões, F.M.; Da Costa, A.P. Universal analytical solution of the steady-state response of an infinite beam on a Pasternak elastic foundation under moving load. Int. J. Solids Struct. 2018, 132-133, 245–263. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Pirmamedov, I.T.; Kuruoglu, N. Influence of elastic foundations and carbon nanotube reinforcement on the hydrostatic buckling pressure of truncated conical shells. Appl. Math. Mech. 2020, 41, 1011–1026. [Google Scholar] [CrossRef]
- Kiani, Y. Dynamics of FG-CNT reinforced composite cylindrical panel subjected to moving load. Thin-Walled Struct. 2017, 111, 48–57. [Google Scholar] [CrossRef]
- Kiani, Y. Analysis of FG-CNT reinforced composite conical panel subjected to moving load using Ritz method. Thin-Walled Struct. 2017, 119, 47–57. [Google Scholar] [CrossRef]
- Sofiyev, A.; Bayramov, R.P.O.; Heydarov, S.H.O. The forced vibration of infinitely long cylinders reinforced by carbon nanotubes subjected to combined internal and ring-shaped compressive pressures. Math. Methods Appl. Sci. 2020, 1–12. [Google Scholar] [CrossRef]
- Kiani, K.; Wang, Q. On the interaction of a single-walled carbon nanotube with a moving nanoparticle using nonlocal Rayleigh, Timoshenko, and higher-order beam theories. Eur. J. Mech.-A/Solids 2012, 31, 179–202. [Google Scholar] [CrossRef]
- Kiani, K. Nonlinear vibrations of a single-walled carbon nanotube for delivering of nanoparticles. Nonlinear Dyn. 2014, 76, 1885–1903. [Google Scholar] [CrossRef]
- Nikkhoo, A.; Zolfaghari, S.; Kiani, K. A simplified-nonlocal model for transverse vibration of nanotubes acted upon by a moving nanoparticle. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 4929–4941. [Google Scholar] [CrossRef]
| 0.12 | 0.17 | 0.28 | |
| 0.137 | 0.142 | 0.141 | |
| 1.022 | 1.626 | 1.585 | |
| 0.715 | 1.138 | 1.109 |
| UD | FG-V | FG-X | ||
|---|---|---|---|---|
| = 0.12 | ||||
| 0 | 0 | 902.208 | 823.248 | 998.503 |
| 0 | 811.820 | 741.751 | 899.657 | |
| 785.289 | 712.616 | 875.791 | ||
| 1.5 × 106 | 729.337 | 650.443 | 825.992 | |
| 2 × 109 | 0 | 673.812 | 618.249 | 749.863 |
| 0.5 × 106 | 641.600 | 582.974 | 721.055 | |
| 1.5 × 106 | 571.755 | 505.087 | 659.678 | |
| = 0.17 | ||||
| 0 | 0 | 1123.632 | 1025.740 | 1247.171 |
| 0 | 1061.269 | 969.987 | 1179.382 | |
| 1041.327 | 948.128 | 1161.470 | ||
| 1000.253 | 902.823 | 1124.791 | ||
| 0 | 985.445 | 902.522 | 1097.353 | |
| 963.936 | 878.987 | 1078.079 | ||
| 919.411 | 829.916 | 1038.459 | ||
| = 0.28 | ||||
| 0 | 0 | 1290.708 | 1187.119 | 1447.294 |
| 0 | 1227.587 | 1132.531 | 1380.741 | |
| 1210.779 | 1114.290 | 1365.820 | ||
| 1.5 × 106 | 1176.444 | 1076.882 | 1335.476 | |
| 0 | 1152.882 | 1068.665 | 1302.878 | |
| 1134.969 | 1049.314 | 1287.054 | ||
| 1098.265 | 1009.502 | 1254.807 | ||
| UD | FG-V | FG-X | |||||
| (N/m3) | (N/m) | ||||||
| 0 | 0 | 1.223 | 1.058 | 1.289 | 1.079 | 1.171 | 1.043 |
| 0 | 1.337 | 1.095 | 1.455 | 1.139 | 1.249 | 1.066 | |
| 1.401 | 1.118 | 1.556 | 1.181 | 1.290 | 1.079 | ||
| 1.437 | 1.132 | 1.616 | 1.208 | 1.312 | 1.087 | ||
| 0 | 1.413 | 1.123 | 1.572 | 1.188 | 1.296 | 1.081 | |
| 1.2 × 105 | 1.500 | 1.157 | 1.722 | 1.261 | 1.349 | 1.099 | |
| 1.8 × 105 | 1.549 | 1.178 | 1.815 | 1.311 | 1.378 | 1.110 | |
| = 0.17 | |||||||
| 0 | 0 | 1.128 | 1.031 | 1.160 | 1.040 | 1.100 | 1.024 |
| 0 | 1.153 | 1.038 | 1.193 | 1.049 | 1.119 | 1.029 | |
| 1.175 | 1.044 | 1.222 | 1.058 | 1.135 | 1.033 | ||
| 1.8 × 105 | 1.187 | 1.047 | 1.237 | 1.062 | 1.143 | 1.035 | |
| 0 | 1.164 | 1.041 | 1.206 | 1.053 | 1.126 | 1.031 | |
| 1.187 | 1.048 | 1.238 | 1.063 | 1.143 | 1.035 | ||
| 1.200 | 1.051 | 1.255 | 1.068 | 1.152 | 1.038 | ||
| = 0.28 | |||||||
| 0 | 0 | 1.092 | 1.022 | 1.112 | 1.027 | 1.071 | 1.017 |
| 0 | 1.107 | 1.026 | 1.130 | 1.032 | 1.082 | 1.019 | |
| 1.121 | 1.029 | 1.147 | 1.036 | 1.092 | 1.022 | ||
| 1.129 | 1.031 | 1.156 | 1.039 | 1.097 | 1.023 | ||
| 0 | 1.113 | 1.027 | 1.136 | 1.033 | 1.086 | 1.020 | |
| 1.128 | 1.031 | 1.155 | 1.038 | 1.097 | 1.023 | ||
| 1.136 | 1.033 | 1.164 | 1.041 | 1.102 | 1.024 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deniz, A.; Avey, M.; Fantuzzi, N.; Sofiyev, A.; Esencan Turkaslan, B.; Yuce, S.; Schnack, E. Influences of Elastic Foundations and Material Gradient on the Dynamic Response of Polymer Cylindrical Pipes Patterned by Carbon Nanotube Subjected to Moving Pressures. Nanomaterials 2021, 11, 3075. https://doi.org/10.3390/nano11113075
Deniz A, Avey M, Fantuzzi N, Sofiyev A, Esencan Turkaslan B, Yuce S, Schnack E. Influences of Elastic Foundations and Material Gradient on the Dynamic Response of Polymer Cylindrical Pipes Patterned by Carbon Nanotube Subjected to Moving Pressures. Nanomaterials. 2021; 11(11):3075. https://doi.org/10.3390/nano11113075
Chicago/Turabian StyleDeniz, Ali, Mahmure Avey, Nicholas Fantuzzi, Abdullah Sofiyev, Banu Esencan Turkaslan, Salim Yuce, and Eckart Schnack. 2021. "Influences of Elastic Foundations and Material Gradient on the Dynamic Response of Polymer Cylindrical Pipes Patterned by Carbon Nanotube Subjected to Moving Pressures" Nanomaterials 11, no. 11: 3075. https://doi.org/10.3390/nano11113075
APA StyleDeniz, A., Avey, M., Fantuzzi, N., Sofiyev, A., Esencan Turkaslan, B., Yuce, S., & Schnack, E. (2021). Influences of Elastic Foundations and Material Gradient on the Dynamic Response of Polymer Cylindrical Pipes Patterned by Carbon Nanotube Subjected to Moving Pressures. Nanomaterials, 11(11), 3075. https://doi.org/10.3390/nano11113075







