Ultrawide Bandgap and High Sensitivity of a Plasmonic Metal-Insulator-Metal Waveguide Filter with Cavity and Baffles
Abstract
:1. Introduction
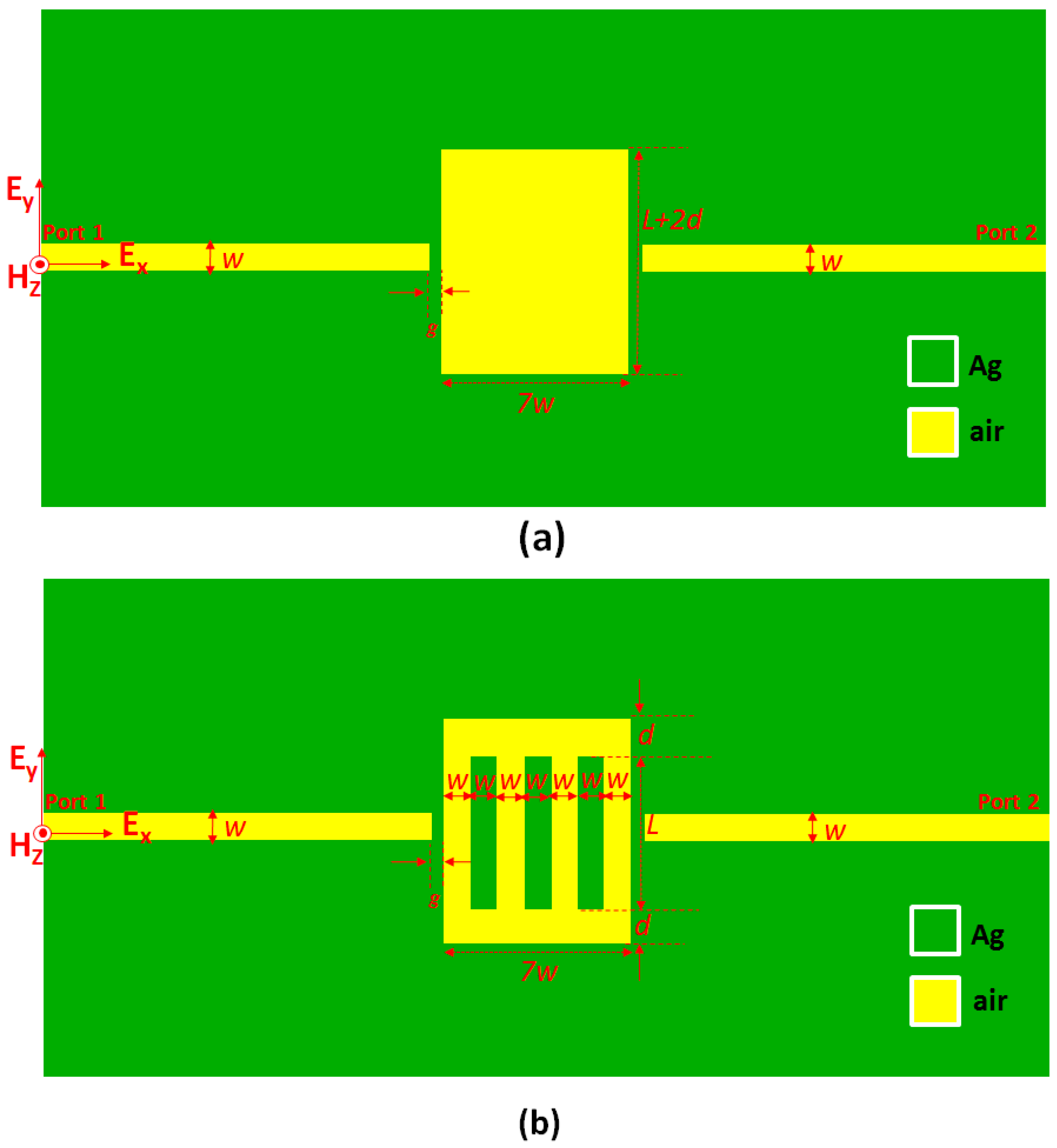
2. Structure Design and Simulation Method
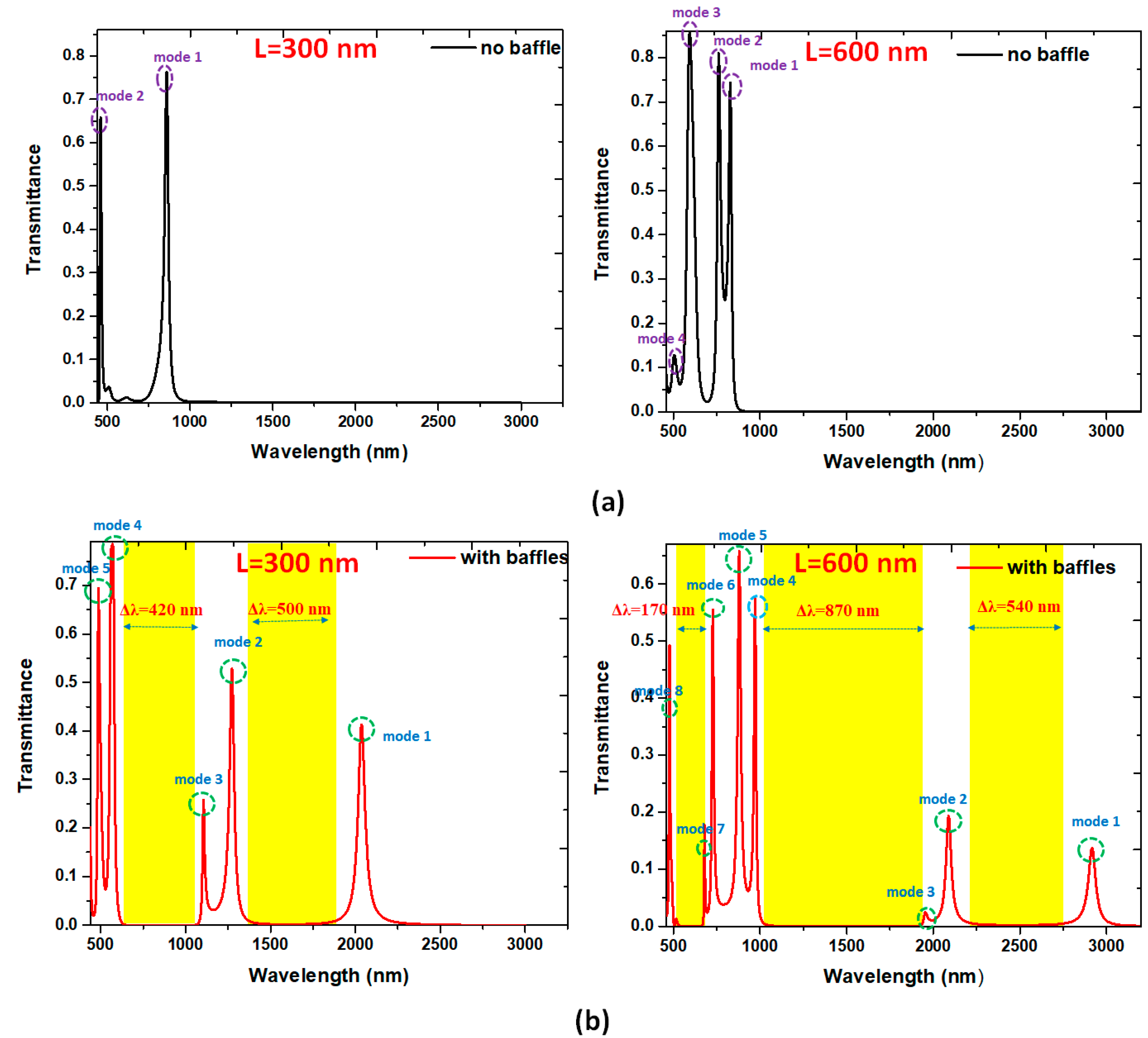
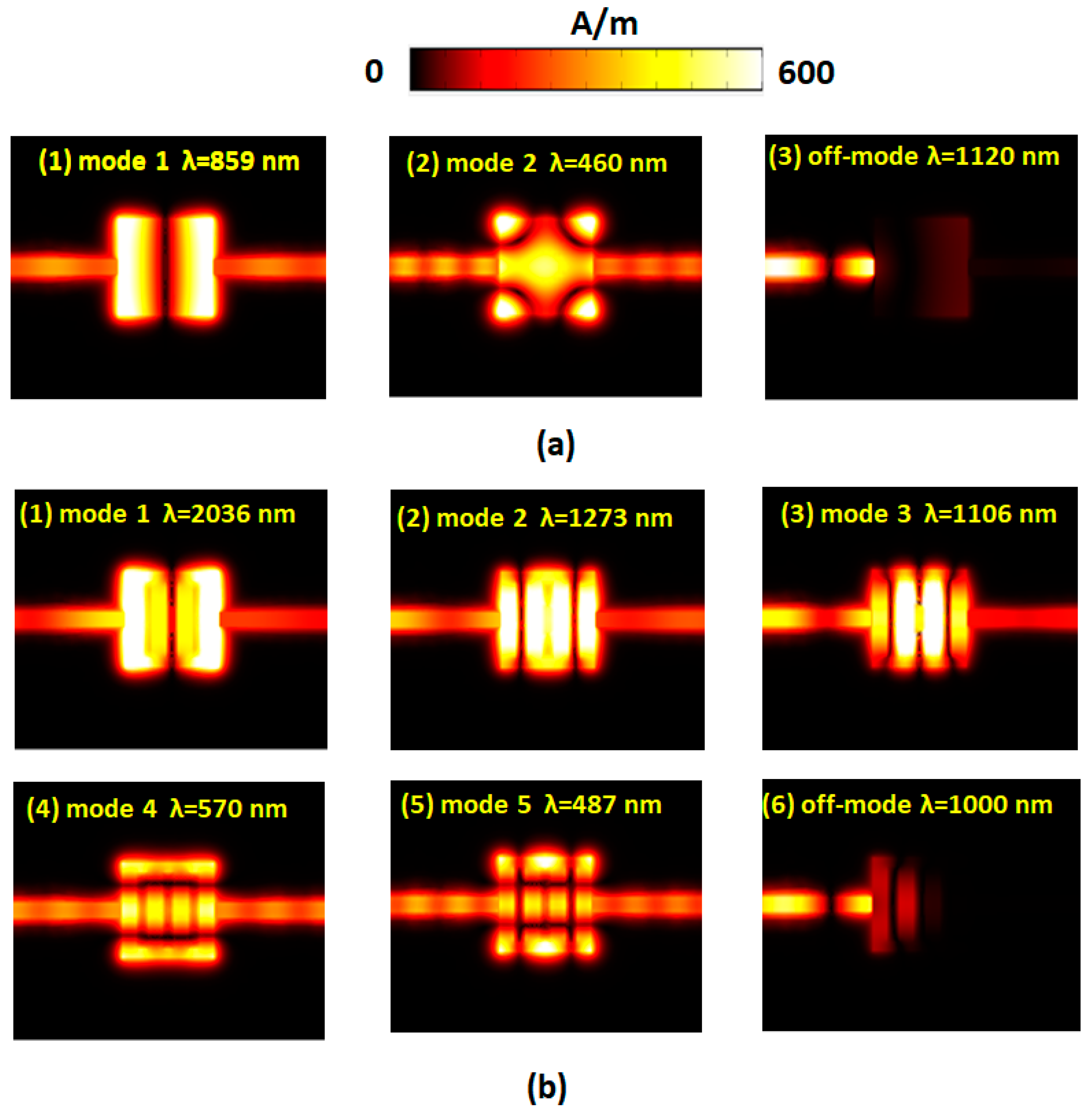
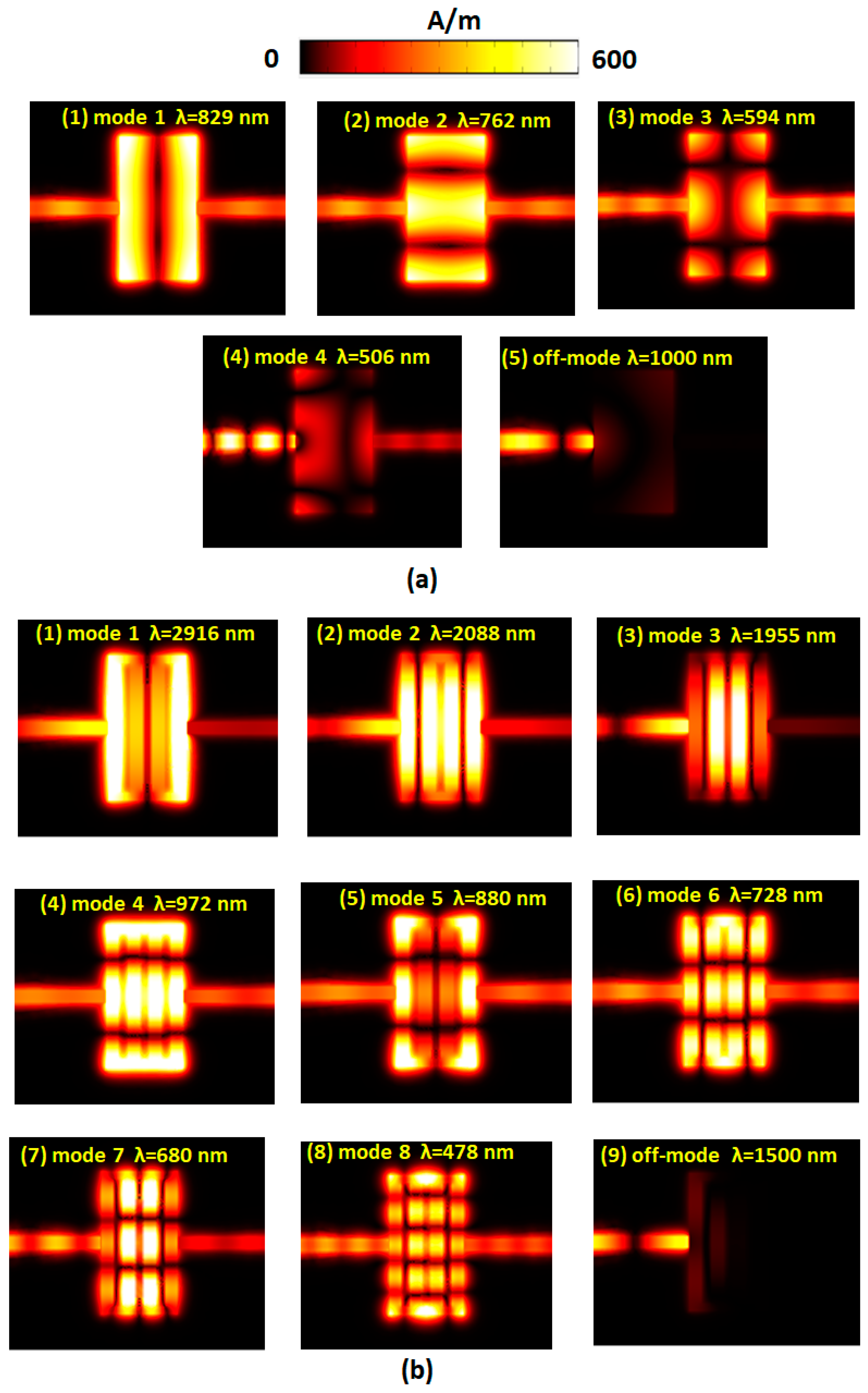
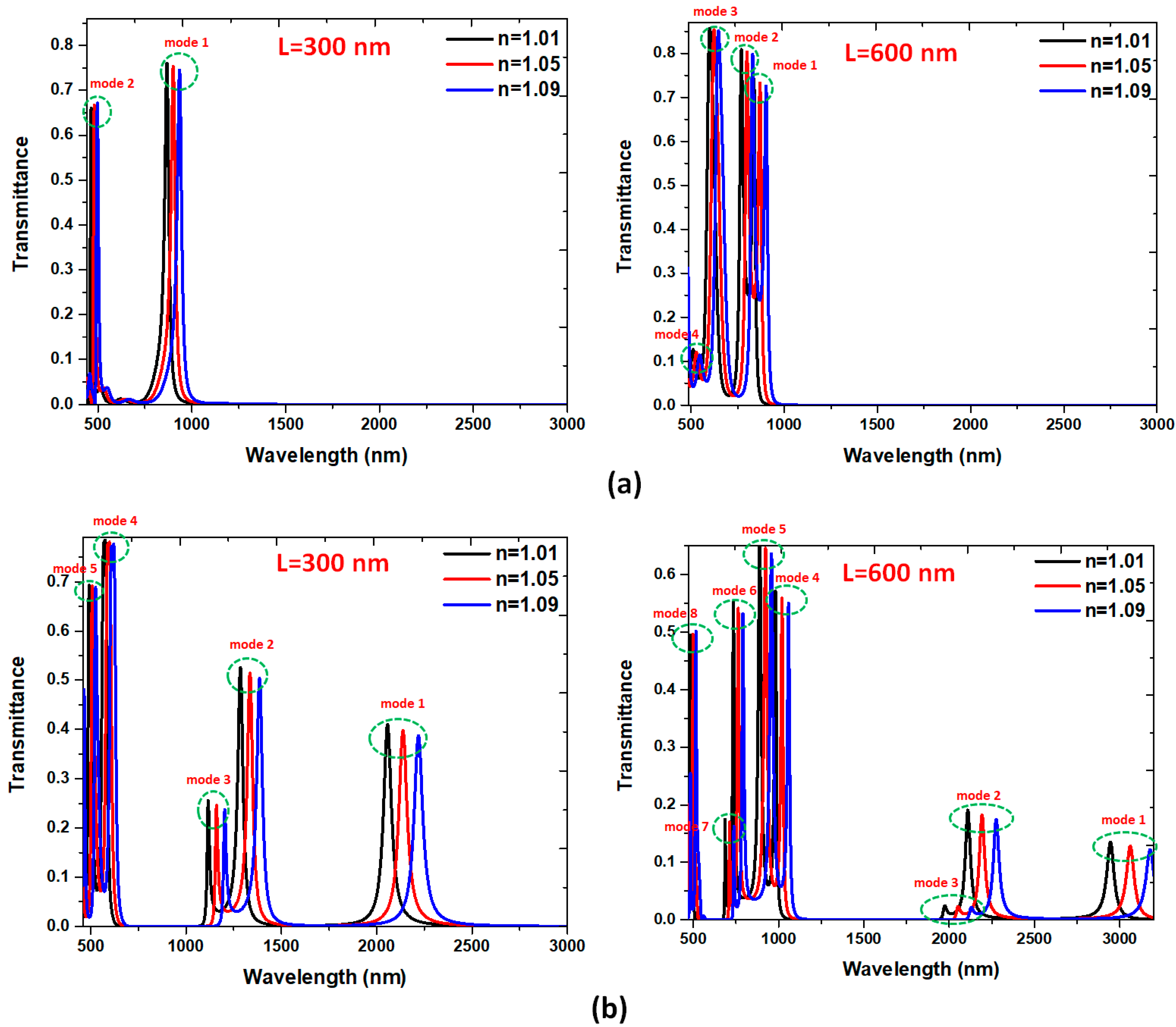
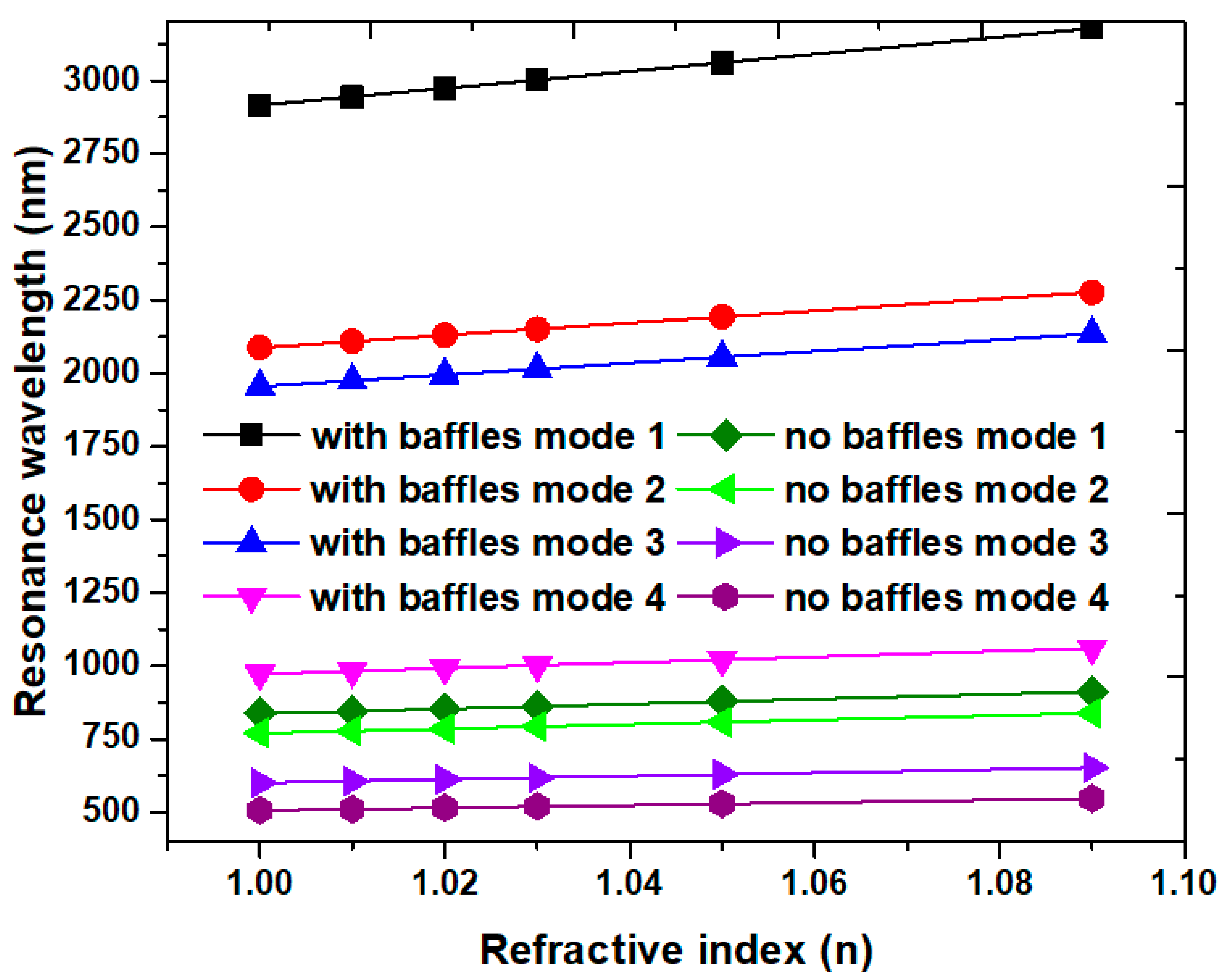
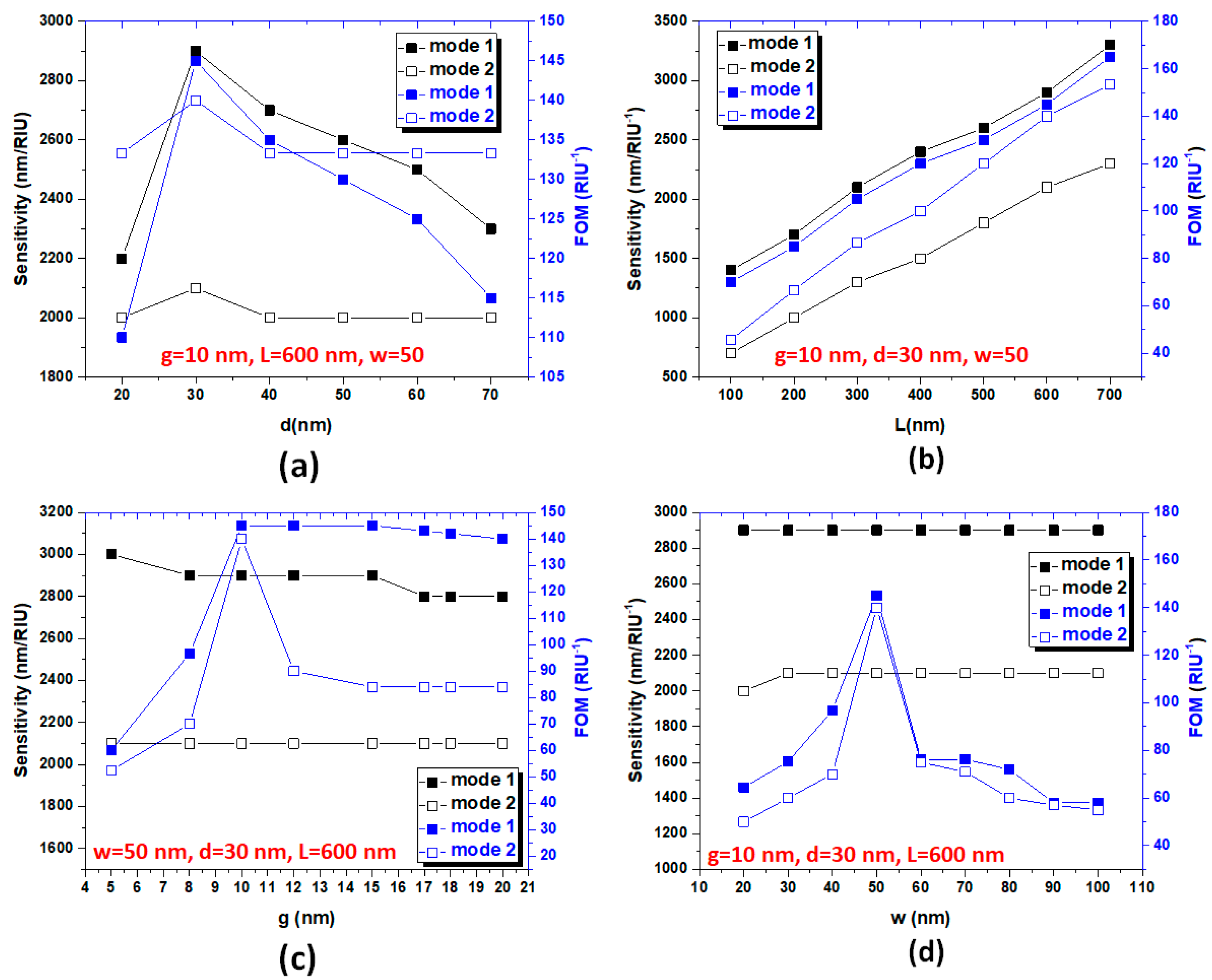
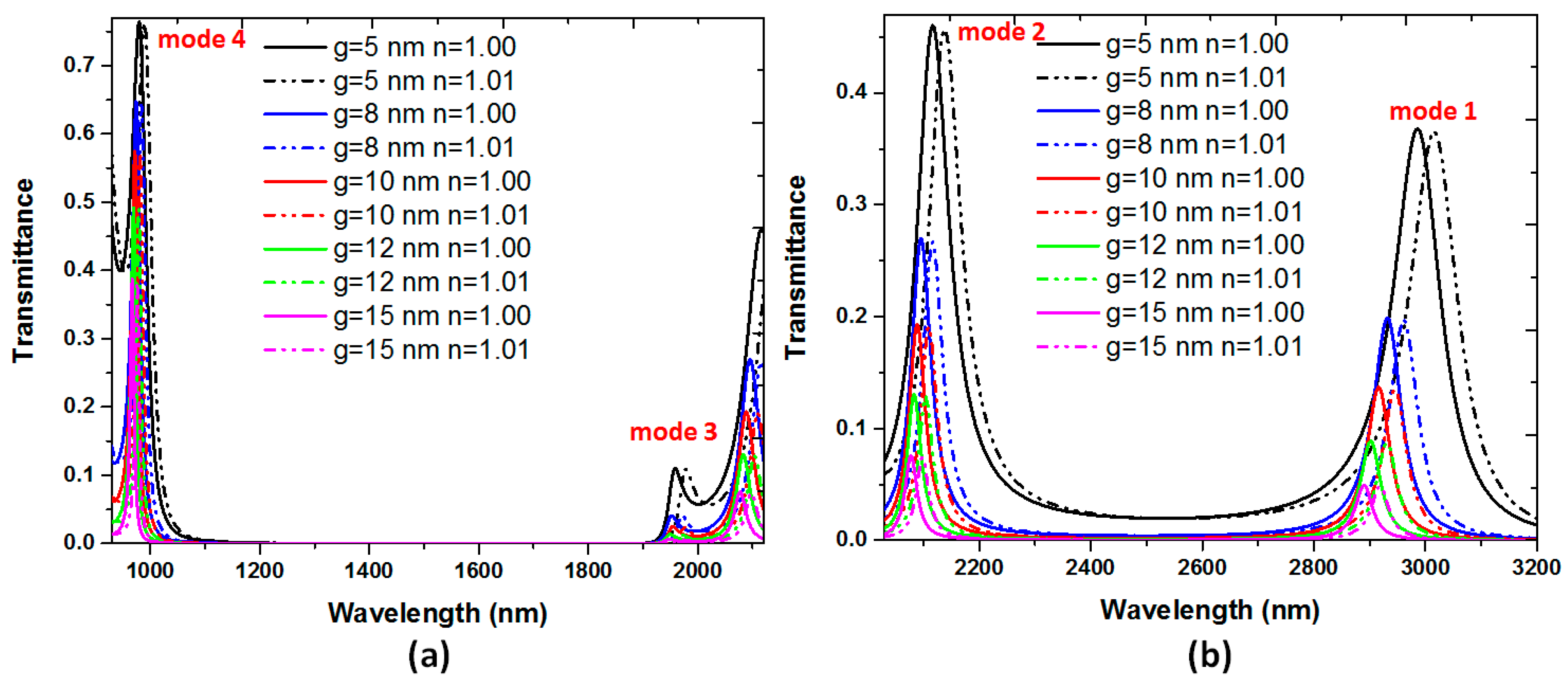
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, W.T.; Wu, P.C.; Chen, C.J.; Chung, H.Y.; Chau, Y.; Kuan, C.H.; Tsai, D.P. Electromagnetic energy vortex associated with sub-wavelength plasmonic Taiji marks. Opt. Express 2010, 18, 19665–19671. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Wen, K.; Hu, Q.; Lai, W.; Lin, J.; Fang, Y. Plasmonic multichannel refractive index sensor based on subwavelength tangent-ring metal–insulator–metal waveguide. Sensors 2018, 18, 1348. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chau, Y.; Tsai, D.P. Three-dimensional analysis of silver nano-particles doping effects on super resolution near-field structure. Opt. Commun. 2007, 269, 389–394. [Google Scholar] [CrossRef]
- Hsieh, L.-Z.; Chau, Y.; Lim, C.; Lin, M.-H.; Huang, H.J.; Lin, C.-T.; Syafi’Ie, I.M.N. Metal nano-particles sizing by thermal annealing for the enhancement of surface plasmon effects in thin-film solar cells application. Opt. Commun. 2016, 370, 85–90. [Google Scholar] [CrossRef]
- Sung, M.J.; Ma, Y.F.; Chau, Y.; Huang, D.W. Plasmon field enhancement in silver core-protruded silicon shell nanocylinder illuminated with light at 633 nm. Appl. Opt. 2010, 49, 6295–6301. [Google Scholar] [CrossRef] [PubMed]
- Chou, Y.; Yeh, H.-H.; Tsai, D.P. Surface plasmon effects excitation from three-pair arrays of silver-shell nanocylinders. Phys. Plasmas 2009, 16, 22303. [Google Scholar] [CrossRef]
- Hayashi, S.; Nesterenko, D.V.; Sekkat, Z. Waveguide-coupled surface plasmon resonance sensor structures: Fano lineshape engineering for ultrahigh-resolution sensing. J. Phys. D Appl. Phys. 2015, 48, 325303. [Google Scholar] [CrossRef]
- Najafabadi, M.M.; Vahidi, S.; Ghafoorifard, H.; Valizadeh, M. Single-channel high-transmission optical band-pass filter based on plasmonic nanocavities. J. Opt. Soc. Am. B 2020, 37, 2329–2337. [Google Scholar] [CrossRef]
- Ho, Y.Z.; Chen, W.T.; Huang, Y.-W.; Wu, P.C.; Tseng, M.L.; Wang, Y.T.; Chau, Y.-F.C.; Tsai, D.P. Tunable plasmonic resonance arising from broken-symmetric silver nanobeads with dielectric cores. J. Opt. 2012, 14, 114010. [Google Scholar] [CrossRef]
- Hu, C.; Yang, W.; Tsai, Y.T.; Chau, Y.F. Gap enhancement and transmittance spectra of a periodic bowtie nanoantenna array buried in a silica substrate. Opt. Commun. 2014, 324, 227–233. [Google Scholar] [CrossRef]
- Lin, C.-T.; Chang, M.-N.; Huang, H.J.; Chen, C.-H.; Sun, R.-J.; Liao, B.-H.; Chau, Y.; Hsiao, C.-N.; Shiao, M.-H.; Tseng, F.-G. Rapid fabrication of three-dimensional gold dendritic nanoforests for visible light-enhanced methanol oxidation. Electrochim. Acta 2016, 192, 15–21. [Google Scholar] [CrossRef]
- Shen, L.; Yang, T.J.; Chau, Y. Effect of internal period on the optical dispersion of indefinite-medium materials. Phys Rev. B 2008, 77, 205124. [Google Scholar] [CrossRef] [Green Version]
- Jankovic, N.; Cselyuszka, N. Multiple Fano-Like MIM Plasmonic Structure Based on Triangular Resonator for Refractive Index Sensing. Sensors 2018, 18, 287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, M.; Cushing, S.K.; Wu, N. Plasmon-enhanced optical sensors: A review. Analyst. 2015, 140, 386–406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, C.-C.; Tsai, Y.-T.; Yang, W.; Chau, Y. Effective Coupling of Incident Light Through an Air Region into an S-Shape Plasmonic Ag Nanowire Waveguide with Relatively Long Propagation Length. Plasmonics 2014, 9, 573–579. [Google Scholar] [CrossRef]
- Chau, Y.; Yang, T.J.; Lee, W.D. Coupling technique for efficient interfacing between silica waveguides and planar photonic crystal circuits. Appl. Opt. 2004, 43, 6656–6663. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fang, Y.; Sun, M. Nanoplasmonic waveguides: Towards applications in integrated nanophotonic circuits. Light. Sci. Appl. 2015, 4, e294. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.J.; Sun, C.W.; Hu, X.Y. Nanoscale all-optical devices based on surface plasmon polaritons. Chinese Sci. Bull. 2014, 59, 2661–2665. [Google Scholar] [CrossRef]
- Kim, N.C.; Ko, M.C.; Wang, Q.Q. Single plasmon switching with n quantum dots system coupled to one-dimensional waveguide. Plasmonics 2015, 10, 611–615. [Google Scholar] [CrossRef] [Green Version]
- Chou Chao, C.-T.; Chou Chau, Y.; Huang, H.J.; Kumara, N.T.R.N.; Kooh, M.R.R.; Lim, C.M.; Chiang, H.-P. Highly Sensitive and Tunable Plasmonic Sensor Based on a Nanoring Resonator with Silver Nanorods. Nanomaterials 2020, 10, 1399. [Google Scholar] [CrossRef]
- Chou Chau, Y.F. Mid-infrared sensing properties of a plasmonic metal–insulator–metal waveguide with a single stub including defects. J. Phys. D Appl. Phys. 2020, 53, 115401. [Google Scholar] [CrossRef]
- Zhao, H.; Huang, X.; Huang, J. Surface plasmon polaritons based optical directional coupler. Sci. China Ser. G Phys. Mech. Astron. 2008, 51, 1877–1882. [Google Scholar] [CrossRef]
- Matsubara, K.; Kawata, S.; Minami, S. Optical chemical sensor based on surface plasmon measurement. Appl. Opt. 1988, 27, 1160–1163. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Luo, L.; Xue, C.; Zhang, W.; Yan, S. Fano Resonance Based on Metal-Insulator-Metal Waveguide-Coupled Double Rectangular Cavities for Plasmonic Nanosensors. Sensors. 2016, 16, 642. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, F.; Yi, H.; Zhou, Z. Wavelength demultiplexing structure based on arrayed plasmonic slot cavities. Opt. Lett. 2011, 36, 1500–1502. [Google Scholar] [CrossRef]
- Drezet, A.; Hohenau, A.; Stepanov, A.L.; Ditlbacher, H.; Steinberger, B.; Aussenegg, F.R.; Leitner, A.; Krenn, J.R. Surface plasmon polariton Mach–Zehnder interferometer and oscillation fringes. Plasmonics 2006, 1, 141–145. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Zhao, Y.; Lu, D.; Xiong, Z. Numerical investigation of a branch-shaped filter based on metal-insulator-metal waveguide. Plasmonics 2011, 6, 773–778. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Khonina, S.N.; Butt, M.A. Plasmonic sensors based on Metal-insulator-metal waveguides for refractive index sensing applications: A brief review. Physica E 2020, 117, 113798. [Google Scholar] [CrossRef]
- Tong, L.M.; Wei, H.; Zhang, S.P.; Xu, H.X. Recent advances in plasmonic sensors. Sensors 2014, 14, 7959–7973. [Google Scholar] [CrossRef] [Green Version]
- Qi, J.; Chen, Z.; Chen, J.; Li, Y.; Qiang, W.; Xu, J.; Sun, Q. Independently tunable double Fano resonances in asymmetric MIM waveguide structure. Opt. Express 2014, 22, 14688–14695. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, H.; Zhang, Z.; Tang, J.; Cui, J.; Xue, C.; Yan, S. Transmission and refractive index sensing based on Fano resonance in MIM waveguide-coupled trapezoid cavity. AIP Adv. 2017, 7, 015020. [Google Scholar] [CrossRef] [Green Version]
- Chou Chau, Y.-F.; Chou Chao, C.-T.; Huang, H.J.; Kumara, N.T.R.N.; Lim, C.M.; Chiang, H.-P. Ultra-High Refractive Index Sensing Structure Based on a Metal-Insulator-Metal Waveguide-Coupled T-Shape Cavity with Metal Nanorod Defects. Nanomaterials 2019, 9, 1433. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Z.; Yang, J.; He, X.; Zhang, J.; Huang, J.; Chen, D.; Han, Y. Plasmonic Refractive Index Sensor with High Figure of Merit Based on Concentric-Rings Resonator. Sensors 2018, 18, 116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, T.; Liu, Y.; Yu, Z.; Ye, H.; Peng, Y.; Shu, S.; Yang, C.; Zhang, W.; He, H. A nanometeric temperature sensor based on plasmonic waveguide with an ethanol-sealed rectangular cavity. Opt. Commun. 2015, 339, 1–6. [Google Scholar] [CrossRef]
- Chau, Y.-F.C.; Chao, C.T.C.; Huang, H.J.; Wang, Y.-C.; Chiang, H.-P.; Idris, M.N.S.M.; Masri, Z.; Lim, C.M. Strong and tunable plasmonic field coupling and enhancement generating from the protruded metal nanorods and dielectric cores. Results Phys. 2019, 13, 102290. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Y.; Yu, Z.; Wu, D.; Ma, R.; Zhang, Y.; Ye, H. Numerical analysis of a near-infrared plasmonic refractive index sensor with high figure of merit based on a fillet cavity. Opt. Express 2016, 24, 9975–9983. [Google Scholar] [CrossRef]
- Chau, Y.-F.C.; Chao, C.T.C.; Chiang, H.-P. Ultra-broad bandgap metal-insulator-metal waveguide filter with symmetrical stubs and defects. Results Phys. 2020, 17, 103116. [Google Scholar] [CrossRef]
- Chen, J.; Sun, C.; Gong, Q. Fano resonances in a single defect nanocavity coupled with a plasmonic waveguide. Opt. Lett. 2014, 39, 52–55. [Google Scholar] [CrossRef]
- Chou Chau, Y.-F.; Chou Chao, C.-T.; Huang, H.J.; Kooh, M.R.R.; Kumara, N.T.R.N.; Lim, C.M.; Chiang, H.-P. Perfect Dual-Band Absorber Based on Plasmonic Effect with the Cross-Hair/Nanorod Combination. Nanomaterials 2020, 10, 493. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Li, Z.; Zou, Y.; Deng, Z.; Xiao, J.; Gong, Q. Coupled-resonator-induced Fano resonances for plasmonic sensing with ultra-high figure of merits. Plasmonics. 2013, 8, 1627–1631. [Google Scholar] [CrossRef]
- Huang, H.J.; Liu, B.H.; Su, J.; Chen, P.J.; Lin, C.T.; Chiang, H.P.; Kao, T.S.; Chou Chau, Y.F.; Kei, C.C.; Hwang, C.H. Light energy transformation over a few nanometers. J. Phys. D Appl. Phys. 2017, 50, 375601. [Google Scholar] [CrossRef]
- Ameling, R.; Langguth, L.; Hentschel, M.; Mesch, M.; Braun, P.V.; Giessen, H. Cavity-enhanced localized plasmon resonance sensing. Appl. Phys. Lett. 2010, 97, 253116. [Google Scholar] [CrossRef]
- Tsigaridas, G.N. A study on refractive index sensors based on optical micro-ring resonators. Photonic Sens. 2017, 7, 217–225. [Google Scholar] [CrossRef]
- Cai, Y.; Li, Y.; Nordlander, P.; Cremer, P.S. Fabrication of elliptical nanorings with highly tunable and multiple plasmonic resonances. Nano Lett. 2012, 12, 4881–4888. [Google Scholar] [CrossRef] [PubMed]
- Tian, M.; Lu, P.; Chen, L.; Lv, C.; Liu, D.M. A subwavelength MIM waveguide resonator with an outer portion smooth bend structure. Opt. Commun. 2011, 284, 4078–4081. [Google Scholar] [CrossRef]
- Vesseur, E.J.R.; De Waele, R.; Lezec, H.J.; Atwater, H.A.; Garcia de Abajo, F.J.; Ploman, A. Surface plasmon polaritons modes in a single crystal Au nanoresonator fabricated using focused-ion-beam milling. Appl. Phys. Lett. 2008, 92, 083110-1–083110-3. [Google Scholar] [CrossRef] [Green Version]
- Yun, B.; Hu, G.; Zhang, R.; Cui, Y. Fano resonances in a plasmonic waveguide system composed of stub coupled with a square cavity resonator. J. Opt. 2016, 18, 055002. [Google Scholar]
- Yun, B.; Zhang, R.; Hu, G.; Cui, Y. Ultra sharp Fano Resonances Induced by Coupling between Plasmonic Stub and Circular Cavity Resonators. Plasmonics 2016, 11, 1157–1162. [Google Scholar]
- El Haffar, R.; Farkhsi, A.; Mahboub, O. Optical properties of MIM plasmonic waveguide with an elliptical cavity resonator. Appl. Phys. A 2020, 126, 486. [Google Scholar] [CrossRef]
- Wang, Q.; Meng, H.; Huang, B.; Wang, H.; Zhang, X.; Yu, W.; Tan, C.; Huang, X.; Li, S. Dual coupled-resonator system for plasmoninduced transparency and slow light effect. Opt. Commun. 2016, 380, 95–100. [Google Scholar] [CrossRef]
- Yang, X.; Hua, E.; Wang, M.; Wang, Y.; Wen, F.; Yan, S. Fano resonance in a MIM waveguide with two triangle stubs coupled with a split-ring nanocavity for sensing application. Sensors 2019, 19, 4972. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, Z.; He, S. Two-dimensional model for three-dimensional index-guided multimode plasmonic waveguides and the design of ultrasmall multimode interference splitters. Appl. Opt. 2007, 46, 6223–6227. [Google Scholar] [CrossRef] [PubMed]
- Chau, Y.-F.C.; Lim, C.; Lee, C.; Huang, H.J.; Lin, C.-T.; Kumara, N.; Yoong, V.N.; Chiang, H.-P. Tailoring surface plasmon resonance and dipole cavity plasmon modes of scattering cross section spectra on the single solid-gold/gold-shell nanorod. J. Appl. Phys. 2016, 120, 093110. [Google Scholar] [CrossRef]
- Yang, J.; Song, X.; Chen, Z.; Cui, L.; Yang, S.; Yu, L. Tunable Multi-Fano Resonances in MDM-Based Side-Coupled Resonator System and its Application in Nanosensor. Plasmonics 2017, 12, 1665–1672. [Google Scholar] [CrossRef]
- Wen, K.; Hu, Y.; Chen, L.; Zhou, J.; He, M.; Lei, L.; Meng, Z.; Wu, Y.; Li, J. Fano Resonance Based on End-Coupled Cascaded-Ring MIM Waveguides Structure. Plasmonics 2017, 12, 1875–1880. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Zhang, Y.; Yu, L. Independently Formed Multiple Fano Resonances for Ultra-High Sensitivity Plasmonic Nanosensor. Plasmonics 2016, 11, 1–7. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Chen, Z.; Jiang, P.; Jiao, R.; Zhang, Y.; Wang, L.; Yu, L. Ultra-high Sensitivity Plasmonic Nanosensor Based on Multiple Fano Resonance in the MDM Side-Coupled Cavities. Plasmonics 2017, 12, 1099–1105. [Google Scholar] [CrossRef]
- Li, H.-J.; Wang, L.-L.; Zhai, X. Fano response induced by the interference between localized plasmons and interface reflections in metal-insulator-metal waveguide structure. J. Appl. Phys. 2016, 119, 243101. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Y.; Song, X.; Wang, Y.; Yu, L. Tunable triple Fano resonances based on multimode interference in coupled plasmonic resonator system. Opt. Express 2016, 24, 15351–15361. [Google Scholar] [CrossRef]
- COMSOL Multiphysics Reference Manual. Available online: http://www.comsol.com (accessed on 3 October 2018).
- Wen, K.; Hu, Y.; Chen, L.; Zhou, J.; Lei, L.; Guo, Z. Fano Resonance with Ultra-High Figure of Merits Based on Plasmonic Metal-Insulator-Metal Waveguide. Plasmonics 2014, 10, 27–32. [Google Scholar] [CrossRef]
- Akhavan, A.; Fard, H.G.; Abdolhosseini, S.; Habibiyan, H.; Ghafoorifard, H. Metal–insulator–metal waveguide-coupled asymmetric resonators for sensing and slow light applications. IET Optoelectron. 2018, 12, 220–227. [Google Scholar] [CrossRef]
- Bahramipanah, M.; Abrishamian, M.S.; Mirtaheri, S.A.; Liu, J.M. Ultracompact plasmonic loop–stub notch filter and sensor. Sens. Actuators B 2014, 194, 311–318. [Google Scholar] [CrossRef]
- Chu, Y.; Schonbrun, E.; Yang, T.; Crozier, K.B. Experimental observation of narrow surface plasmon resonances in gold nanoparticle arrays. Appl. Phys. Lett. 2008, 93, 181108-1–181108-3. [Google Scholar] [CrossRef]
- Shibayama, J.; Kawai, H.; Yamauchi, J.; Nakano, H.; Shibayama, J.; Kawai, H.; Yamauchi, J.; Nakano, H. Analysis of a 3D MIM waveguide-based plasmonic demultiplexer using the TRC-FDTD method. Opt. Commun. 2019, 452, 360–365. [Google Scholar] [CrossRef]
- Butt, M.A.; Kazanskiy, N.L.; Khonina, S.N. Highly integrated plasmonic sensor design for the simultaneous detection of multiple analytes. Curr. Appl. Phys. 2020, 20, 1274–1280. [Google Scholar] [CrossRef]
- Kekatpure, R.D.; Hryciw, A.C.; Barnard, E.S.; Brongersma, M.L. Solving dielectric and plasmonic waveguide dispersion relations on a pocket calculator. Opt. Express 2009, 17, 24112–24129. [Google Scholar] [CrossRef] [Green Version]
- Wu, T.; Liu, Y.; Yu, Z.; Peng, Y.; Shu, C.; Ye, H. The sensing characteristics of plasmonic waveguide with a ring resonator. Opt. Express 2014, 22, 7669–7677. [Google Scholar] [CrossRef]
- He, Z.H.; Zhou, Z.P. Theoretically Analyze the Tunable Wide Band-Stop Filtering in Plasmonic Waveguide Coupled With Fixed Height to Length Stubs. IEEE Photonics J. 2018, 10, 1–8. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, L.; Gao, F. Plasmonically induced reflection in metal-insulator-metal waveguides with two silver baffles coupled square ring resonator. Chin. Phys. B. 2017, 26, 312–316. [Google Scholar] [CrossRef]
- Tao, J.; Wang, Q.; Huang, X. All-Optical plasmonic switches based on coupled nano-disk cavity structures containing nonlinear material. Plasmonics 2011, 6, 753–759. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Xu, Q.; Li, S. A MIM Filter Based on a side-coupled crossbeam square-ring resonator. Plasmonics 2016, 11, 1291–1296. [Google Scholar] [CrossRef]
- Giurlani, W.; Zangari, G.; Gambinossi, F.; Passaponti, M.; Salvietti, E.; Di Benedetto, F.; Caporali, S.; Innocenti, M. Electroplating for decorative applications: Recent trends in research and development. Coatings 2018, 8, 260. [Google Scholar] [CrossRef] [Green Version]
- Kannegulla, A.; Cheng, L.-J. Metal assisted focused-ion beam nanopatterning. Nanotechnology 2016, 27, 36TL01. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hindmarch, A.T.; Parkes, D.E.; Rushforth, A.W. Fabrication of metallic magnetic nanostructures by argon ion milling using a reversed-polarity planar magnetron ion source. Vacuum 2012, 86, 1600–1604. [Google Scholar] [CrossRef] [Green Version]
- Masson, J.-F.; Murray-Methot, M.-P.; Live, L.S. Nanohole arrays in chemical analysis: Manufacturing methods and applications. Analyst 2010, 135, 1483–1489. [Google Scholar] [CrossRef]
- Cao, J.; Sun, T.; Grattan, K.T.V. Gold nanorod-based localized surface plasmon resonance biosensors: A review. Sens. Actuators B Chem. 2014, 195, 332–351. [Google Scholar] [CrossRef]
- Wei, H.X.; Qin, Q.H.; Ma, M.; Sharif, R.; Han, X.F. 80% tunneling magnetoresistance at room temperature for thin Al–O barrier magnetic tunnel junction with CoFeB as free and reference layers. J. Appl. Phys. 2007, 101, 09B501. [Google Scholar] [CrossRef]
- Kamada, S.; Okamoto, T.; El-Zohary, S.E.; Haraguchi, M. Design optimization and fabrication of Mach- Zehnder interferometer based on MIM plasmonic waveguides. Opt. Express 2016, 24, 16224–16231. [Google Scholar] [CrossRef]
- Kuttge, M.; De Abajo, F.J.G.; Polman, A. Ultrasmall Mode Volume Plasmonic Nanodisk Resonators. Nano Lett. 2010, 10, 1537–1541. [Google Scholar] [CrossRef]
- Walther, C.; Scalari, G.; Amanti, M.I.; Beck, M.; Faist, J. Microcavity Laser Oscillating in a Circuit-Based Resonator. Science 2010, 327, 1495–1497. [Google Scholar] [CrossRef]
- Lin, B.; Wang, X.; Lv, J.; Cao, Y.; Yang, Y.; Zhang, Y.; Zhang, A.; Yi, Y.; Wang, F.; Zhang, D. Low-power-consumption polymer Mach–Zehnder interferometer thermo-optic switch at 532 nm based on a triangular waveguide. Opt. Lett. 2020, 45, 4448–4451. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Li, H.; Li, B.; He, Z.; Xu, H.; Zheng, M.; Zhao, M. Tunable ultra-wide band-stop filter based on single-stub plasmonic-waveguide system. Appl. Phys. Express 2016, 9, 102002. [Google Scholar] [CrossRef]
- Yu, S.; Wang, S.; Zhao, T.; Yu, J. Tunable ultra-width bandgap U-shaped band-stop filters of chip scale based on periodic staggered double-side trapezoidal resonators in a metallic nanowaveguide. Opt. Commun. 2020, 463, 125439. [Google Scholar] [CrossRef]
- Sun, R.J.; Huang, H.J.; Hsiao, C.N.; Lin, Y.W.; Liao, B.H.; Chau, Y.F.C.; Chiang, H.P. Reusable TiN Substrate for Surface Plasmon Resonance Heterodyne Phase Interrogation Sensor. Nanomaterials. 2020, 10, 1325. [Google Scholar] [CrossRef] [PubMed]
- Chau, Y.-F.C.; Syu, J.-Y.; Chao, C.-T.C.; Chiang, H.-P.; Lim, C. Design of crossing metallic metasurface arrays based on high sensitivity of gap enhancement and transmittance shift for plasmonic sensing applications. J. Phys. D Appl. Phys. 2017, 50, 045105. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, Y.; Wang, Z. A refractive index sensor based on an analogy T shaped metal–insulator–metal waveguide. Optik 2018, 172, 1199–1204. [Google Scholar] [CrossRef]
- Chau, Y.; Chao, C.; Huang, H. Plasmonic perfect absorber based on metal nanorod arrays connected with veins. Result Phys. 2019, 15, 102567. [Google Scholar] [CrossRef]
- Li, S.; Wang, Y.; Jiao, R.; Wang, L.; Duan, G.; Yu, L. Fano resonances based on multimode and degenerate mode interference in plasmonic resonator system. Opt. Express 2017, 25, 3525–3533. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L.; Xu, W. Surface plasmon polaritons: Physics and applications. J. Phys. D Appl. Phys. 2012, 45, 113001. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Qi, J.W.; Chen, J.; Li, Y.D.; Hao, Z.Q.; Lu, W.Q.; Xu, J.J.; Sun, Q. Fano Resonance Based on Multimode Interference in Symmetric Plasmonic Structures and Its Applications in Plasmonic Nanosensors. Chin. Phys. Lett. 2013, 30, 057301. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, G.; Wang, Z.; Fan, G.; Yan, Y. Study on the Fano resonance of coupling M-type cavity based on surface plasmon polaritons. Opt. Commun. 2019, 433, 144–149. [Google Scholar] [CrossRef]
- Zand, I.; Abrishamian, M.S.; Pakizeh, T. Nanoplasmonic loaded slot cavities for wavelength filtering and demultiplexing. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 4600505. [Google Scholar] [CrossRef]
- Veronis, G.; Fan, S. Bends and splitters in metal-dielectric-metal subwavelength plasmonic waveguides. Appl. Phys. Lett. 2005, 87, 131102. [Google Scholar] [CrossRef]
- Chen, P.; Liang, R.; Huang, Q. Plasmonic filters and optical directional couplers based on wide metal-insulator-metal structure. Opt. Express. 2011, 19, 7633–7639. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Lu, H.; Liu, X.; Gong, Y.; Wang, L. Optical bistability in metal-insulator-metal plasmonic waveguide with nanodisk resonator containing Kerr nonlinear medium. Appl. Opt. 2011, 50, 5287–5290. [Google Scholar] [CrossRef]
- Hocini, A.; Hocine, B.; Khedrouche, D.; Melouki, N. A high-sensitive sensor and band-stop filter based on intersected double ring resonators in metal–insulator–metal structure. Opt. Quantum. Electron. 2020, 52, 336. [Google Scholar] [CrossRef]
- Wu, T.; Liu, Y.; Yu, Z.; Peng, Y.; Shu, C.; He, H. The sensing characteristics of plasmonic waveguide with a single defect. Opt. Commun. 2014, 323, 44–48. [Google Scholar] [CrossRef]
- Xiang, D.; Li, W. MIM plasmonic waveguide splitter with tooth-shaped structures. J. Mod. Opt. 2014, 61, 222–226. [Google Scholar] [CrossRef]
- Qi, Y.; Zhou, P.; Zhang, T.; Zhanga, X.; Wang, Y.; Liu, C.; Bai, Y.; Wang, X. Theoretical study of a multichannel plasmonic waveguide notch filter with double-sided nanodisk and two slot cavities. Results Phys. 2019, 14, 102506. [Google Scholar] [CrossRef]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Hybrid plasmonic waveguide-assisted Metal–Insulator–Metal ring resonator for refractive index sensing. J. Mod. Opt. 2018, 65, 1135–1140. [Google Scholar] [CrossRef]
- Su, W.; Ding, Y.; Luo, Y.; Liu, Y. A high figure of merit refractive index sensor based on Fano resonance in all-dielectric metasurface. Results Phys. 2020, 16, 102833. [Google Scholar] [CrossRef]
- Mejía-Salazar, J.R.; Camacho, S.A.; Constantino, C.J.L.; Oliveira, O.N. New trends in plasmonic (bio) sensing. An. Acad. Bras. Cienc. 2018, 90, 779–801. [Google Scholar]
- Peng, T.C.; Lin, W.C.; Chen, C.W.; Tsai, D.P.; Chiang, H.P. Enhanced Sensitivity of Surface Plasmon Resonance Phase-Interrogation Biosensor by Using Silver Nanoparticles. Plasmonics 2011, 6, 29–34. [Google Scholar] [CrossRef]
- Tseng, M.L.; Chang, C.M.; Cheng, B.H.; Wu, P.C.; Chung, K.S.; Hsiao, M.K.; Huang, H.W.; Huang, D.W.; Chiang, H.P.; Leung, P.K.; et al. Multi-level surface enhanced Raman scattering using AgOx thin film. Opt. Express 2013, 21, 24460–24467. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, T.B.; Wen, X.W.; Yin, C.P.; Wang, H.Z. The transmission characteristics of surface plasmon polaritons in ring resonator. Opt. Express 2009, 17, 24096–24101. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chou Chau, Y.-F.; Chou Chao, C.-T.; Huang, H.J.; Kooh, M.R.R.; Kumara, N.T.R.N.; Lim, C.M.; Chiang, H.-P. Ultrawide Bandgap and High Sensitivity of a Plasmonic Metal-Insulator-Metal Waveguide Filter with Cavity and Baffles. Nanomaterials 2020, 10, 2030. https://doi.org/10.3390/nano10102030
Chou Chau Y-F, Chou Chao C-T, Huang HJ, Kooh MRR, Kumara NTRN, Lim CM, Chiang H-P. Ultrawide Bandgap and High Sensitivity of a Plasmonic Metal-Insulator-Metal Waveguide Filter with Cavity and Baffles. Nanomaterials. 2020; 10(10):2030. https://doi.org/10.3390/nano10102030
Chicago/Turabian StyleChou Chau, Yuan-Fong, Chung-Ting Chou Chao, Hung Ji Huang, Muhammad Raziq Rahimi Kooh, Narayana Thotagamuge Roshan Nilantha Kumara, Chee Ming Lim, and Hai-Pang Chiang. 2020. "Ultrawide Bandgap and High Sensitivity of a Plasmonic Metal-Insulator-Metal Waveguide Filter with Cavity and Baffles" Nanomaterials 10, no. 10: 2030. https://doi.org/10.3390/nano10102030
APA StyleChou Chau, Y.-F., Chou Chao, C.-T., Huang, H. J., Kooh, M. R. R., Kumara, N. T. R. N., Lim, C. M., & Chiang, H.-P. (2020). Ultrawide Bandgap and High Sensitivity of a Plasmonic Metal-Insulator-Metal Waveguide Filter with Cavity and Baffles. Nanomaterials, 10(10), 2030. https://doi.org/10.3390/nano10102030









