Characterisation of the PS-PMMA Interfaces in Microphase Separated Block Copolymer Thin Films by Analytical (S)TEM
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Sample Preparation
2.2. Characterisation Techniques
2.3. Calculation of Expected Interfacial Widths and Interface Position Fluctuation
3. Results
3.1. Polymer Domain Morphology and Line Edge Roughness Investigated by STEM-ADF
3.2. Spatially Resolved Investigation of the Composition of the Polymer Film Using (S)TEM-EELS
3.3. EFTEM Spectroscopic Imaging of PS and PMMA Lamellae
- 0 eV. EFTEM zero loss imaging is known to increase contrasts in copolymers by removing inelastically scattered electrons from the image. This technique was introduced by Kunz et al. [69] and applied to copolymer blends [44]. Compared to conventional bright-field TEM images as shown in Figure 1h, the contrast in this image is increased and the resolution is high allowing for imaging of the internal structure of the polymer domains. This is also clearly visible in the zero loss images of both cylinder-forming BCPs (Figures S2 and S3). It is to note that an inversion of the contrasts between PS and PMMA in this zero-loss region occurs: PMMA appears brighter in TEM bright-field and zero-loss filtered EFTEM images than PS. In energy filtered images with the energy window centred at values between 10 and 110 eV PS rich domains appear brighter than their PMMA rich surroundings. This contrast inversion most likely results from a comparatively large plasmon excitation in PS compared to PMMA, since the low-loss region between 10 and 110 eV is dominated by the plasmon peak as visible in Figure 3a.
- 20–60 eV. This energy region around and above the plasmon resonances of PS and PMMA [66,67,68] gives the best material contrasts. The internal structure of polymer domains with grains of inverse contrast, as discussed on the STEM-ADF images in Figure 2, become particularly visible in images obtained at 25–44 eV. The presence of ‘bright’ grains in a darker PS surrounding can be interpreted as the presence of PMMA inclusions leading to a locally enhanced plasmonic energy loss. Vice versa, the presence of ‘darker’ grains in an environment of bright PMMA rich surrounding would indicate a lack of PMMA material due to the inclusion of small PS grains. However, it is not possible to exclude that such ‘inclusions’ are actually located at the surface and are residuals of the random copolymer brush layer. In any case, it is likely that these grains contain the opposite polymer species.
3.4. Determination of Material Density Distributions by EFTEM Thickness Mapping
3.5. Fraction of Non-Separated Polymers
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bates, C.M.; Bates, F.S. 50th anniversary perspective: Block polymers-pure potential. Macromolecules 2016, 50, 3–22. [Google Scholar] [CrossRef]
- Luo, M.; Epps, T.H. Directed block copolymer thin film self-assembly: Emerging trends in nanopattern fabrication. Macromolecules 2013, 46, 7567–7579. [Google Scholar] [CrossRef]
- Darling, S.B. Directing the self-assembly of block copolymers. Prog. Polym. Sci. 2007, 32, 1152–1204. [Google Scholar] [CrossRef]
- Ferrarese Lupi, F.; Giammaria, T.J.; Miti, A.; Zuccheri, G.; Carignano, S.; Sparnacci, K.; Seguini, G.; De Leo, N.; Boarino, L.; Perego, M.; et al. Hierarchical order in dewetted block copolymer thin films on chemically patterned surfaces. ACS Nano 2018, 12, 7076–7085. [Google Scholar] [CrossRef]
- Brassat, K.; Kool, D.; Bürger, J.; Lindner, J.K.N. Hierarchical nanopores by block copolymer lithography on surfaces of different materials pre-patterned by nanosphere lithography. Nanoscale 2018, 10, 10005–10017. [Google Scholar] [CrossRef]
- Bates, F.S.; Fredrickson, G.H. Block copolymer thermodynamics: Theory and experiment. Annu. Rev. Phys. Chem. 1990, 41, 525–557. [Google Scholar] [CrossRef]
- Leibler, L. Theory of microphase separation in block copolymers. Macromolecules 1980, 13, 1602–1617. [Google Scholar] [CrossRef]
- Hu, H.; Gopinadhan, M.; Osuji, C.O. Directed self-assembly of block copolymers: A tutorial review of strategies for enabling nanotechnology with soft matter. Soft Matter 2014, 10, 3867–3889. [Google Scholar] [CrossRef]
- Brassat, K.; Lindner, J.K.N. Nanoscale block copolymer self-assembly and microscale polymer film dewetting: Progress in understanding the role of interfacial energies in the formation of hierarchical nanostructures. Adv. Mater. Interfaces 2019, 1901565. [Google Scholar] [CrossRef]
- Brassat, K.; Kool, D.; Nallet, C.G.A.; Lindner, J.K.N. Understanding film thickness-dependent block copolymer self-assembly by controlled polymer dewetting on pre-patterned surfaces. Adv. Mater. Interfaces 2019, 190165. (In press) [CrossRef]
- Brassat, K.; Kool, D.; Lindner, J.K.N. Modification of block copolymer lithography mask by O2/Ar plasma treatment: Insights from lift off experiments, nanopore etching and free membranes. Nanotechnology 2019, 30, 225302. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Sargent, J.L.; Boudouris, B.W.; Phillip, W.A. Nanoporous membranes generated from self-assembled block polymer precursors: Quo vadis? J. Appl. Polym. Sci. 2015, 132, 41683. [Google Scholar]
- Yu, H.; Qiu, X.; Moreno, N.; Ma, Z.; Calo, V.M.; Nunes, S.P.; Peinemann, K.V. Self-assembled asymmetric block copolymer membranes: Bridging the gap from ultra-to nanofiltration. Angew. Chem. Int. Ed. 2015, 54, 13937–13941. [Google Scholar] [CrossRef] [PubMed]
- Takashi, I.; Ghimire, G. Electrochemical applications of microphase-separated block copolymer thin films. ChemElectroChem 2018, 5, 2937–2953. [Google Scholar]
- Steinhaus, A.; Srivastva, D.; Nikoubashman, A.; Gröschel, A.H. Janus Nanostructures from ABC/B Triblock Terpolymer Blends. Polymers 2019, 11, 1107. [Google Scholar] [CrossRef] [PubMed]
- Majewski, P.W.; Gopinadhan, M.; Osuji, C.O. The effects of magnetic field alignment on lithium ion transport in a polymer electrolyte membrane with lamellar morphology. Polymers 2019, 11, 887. [Google Scholar] [CrossRef]
- Young, W.S.; Kuan, W.F.; Epps, T.H., III. Block copolymer electrolytes for rechargeable lithium batteries. J. Polym. Sci. B Polym. Phys. 2014, 52, 1–16. [Google Scholar] [CrossRef]
- Kuang, H.; Janik, M.J.; Gomez, E.D. Quantifying the role of interfacial width on intermolecular charge recombination in block copolymer photovoltaics. J. Polym. Sci. B Polym. Phys. 2015, 53, 1224–1230. [Google Scholar] [CrossRef]
- Cianci, E.; Nazzari, D.; Seguini, G.; Perego, M. Trimethylaluminum Diffusion in PMMA Thin Films during Sequential Infiltration Synthesis: In Situ Dynamic Spectroscopic Ellipsometric Investigation. Adv. Mater. Interfaces 2018, 5, 1801016. [Google Scholar] [CrossRef]
- Peng, Q.; Tseng, Y.C.; Mane, A.U.; DiDona, S.; Darling, S.B.; Elam, J.W. Effect of nanostructured domains in self-assembled block copolymer films on sequential infiltration synthesis. Langmuir 2017, 33, 13214–13223. [Google Scholar] [CrossRef]
- Sunday, D.F.; Maher, M.J.; Hannon, A.F.; Liman, C.D.; Tein, S.; Blachut, G.; Asano, Y.; Ellison, C.J.; Willson, C.G.; Kline, R.J. Characterizing the interface scaling of high X block copolymers near the order-disorder transition. Macromolecules 2017, 51, 173–180. [Google Scholar] [CrossRef] [PubMed]
- Longanecker, M.; Modi, A.; Dobrynin, A.; Kim, S.; Yuan, G.; Jones, R.; Satija, S.; Bang, J.; Karim, A. Reduced Domain Size and interfacial width in fast ordering nanofilled block copolmyer films by direct immersion annealing. Macromolecules 2016, 49, 8563–8571. [Google Scholar] [CrossRef]
- Sunday, D.F.; Kline, R.J. Reducing block copolymer interfacial width through polymer additives. Macromolecules 2015, 48, 679–686. [Google Scholar] [CrossRef]
- Kim, J.M.; Hur, Y.H.; Jeong, J.W.; Nam, T.W.; Lee, J.H.; Jeon, K.; Kim, Y.; Jung, Y.S. Block copolymer with am extremely high block-to-block interaction for a significant reduction of line-edge fluctuations in self-assembled patterns. Chem. Mater. 2016, 28, 5680–5688. [Google Scholar] [CrossRef]
- Helfand, E.; Tagami, Y. Theory of the interface between immiscible polymers. II. J. Chem. Phys. 1972, 56, 3592–3601. [Google Scholar] [CrossRef]
- Broseta, D.; Fredrickson, G.H.; Helfand, E.; Leibler, L. Molecular weight and polydispersity effects at polymer-polymer interfaces. Macromolecules 1990, 23, 132–139. [Google Scholar] [CrossRef]
- Helfand, E.; Tagami, Y. Theory of the interface between immiscible polymers. J. Chem. Phys. 1972, 57, 1812–1813. [Google Scholar] [CrossRef]
- Helfand, E.; Wasserman, Z.R. Block copolymer theory. 4. Narrow interphase approximation. Macromolecules 1976, 9, 879–888. [Google Scholar] [CrossRef]
- Shull, K.R. Mean-field theory of block copolymers: Bulk melts, surfaces, and thin films. Macromolecules 1992, 25, 2122–2133. [Google Scholar] [CrossRef]
- Shull, K.R.; Mayes, A.M.; Russell, T.P. Segment distributions in lamellar diblock copolymers. Macromolecules 1993, 26, 3929–3936. [Google Scholar] [CrossRef]
- Ermoshkin, A.V.; Semenov, A.N. Interfacial tension in binary polymer mixtures. Macromolecules 1996, 29, 6294–6300. [Google Scholar] [CrossRef]
- Tang, H.; Freed, K.F. Interfacial studies of incompressible binary blends. J. Chem. Phys. 1991, 94, 6307–6322. [Google Scholar] [CrossRef]
- Semenov, A.N. Theory of block copolymer interfaces in the strong segregation limit. Macromolecules 1993, 26, 6617–6621. [Google Scholar] [CrossRef]
- Black, C.T.; Ruiz, R.; Breyta, G.; Cheng, J.Y.; Colburn, M.E.; Guarini, K.W.; Kim, H.-C.; Zhang, Y. Polymer self assembly in semiconductor microelectronics. IBM J. Res. Dev. 2007, 51, 605–633. [Google Scholar] [CrossRef]
- Mocan, M.; Kamperman, M.; Leermakers, F.A.M. Microphase segregation of diblock copolymers studies by the self-consistent field theory of Scheutjens and Fleer. Polymers 2018, 10, 78. [Google Scholar] [CrossRef]
- Foster, M.D.; Sikka, M.; Singh, N.; Bates, F.S.; Satija, S.K.; Majkrzak, C.F. Structure of symmetric polyolefin block copolymer thin films. J. Chem. Phys. 1992, 96, 8605–8615. [Google Scholar] [CrossRef]
- Winey, K.L.; Thomas, E.L.; Fetters, L.J. Ordered morphologies in binary blends of diblock copolymer and homopolymer and characterization of their intermaterial dividing surfaces. J. Chem. Phys. 1991, 95, 9367–9375. [Google Scholar] [CrossRef]
- Scherble, J.; Stark, B.; Stühn, B.; Kressler, J.; Budde, H.; Höring, S.; Schubert, D.W.; Simon, P.; Stamm, M. Comparison of interfacial width of block copolymers of d8-poly(methylmethacrylate) with various poly(n-alkylmethacrylate)s and the respective homopolymer pairs as measured by neutron reflection. Macromolecules 1999, 32, 1859–1864. [Google Scholar] [CrossRef]
- Melekevitz, J.; Muthukumar, M. Density functional theory of lamellar ordering in diblock copolymers. Macromolecules 1991, 24, 4199–4205. [Google Scholar] [CrossRef]
- Russell, T.P. On the reflectivity of polymers: Neutrons and X-rays. Phys. B 1996, 221, 267–283. [Google Scholar] [CrossRef]
- Hannon, A.F.; Sunday, D.F.; Bowen, A.; Khaira, G.; Ren, J.; Nealey, P.F.; de Pablo, J.J.; Kline, R.J. Optimizing self-consistent field theory block copolymer models with X-ray metrology. Mol. Syst. Des. Eng. 2018, 3, 376–389. [Google Scholar] [CrossRef] [PubMed]
- Anastasiadis, S.H.; Retsos, H.; Toprakcioglu, C.; Menelle, A.; Hadziioannou, G. On the interfacial width in triblock versus diblock copolymers: A neutron reflectivity investigation. Macromolecules 1998, 31, 6600–6604. [Google Scholar] [CrossRef]
- Bates, F.S.; Schulz, M.F.; Khandpur, A.K.; Förster, S.; Rosedale, J.H.; Almdal, K.; Mortensen, K. Fluctuations, conformational asymmetry and block copolymer phase behaviour. Faraday Discuss. 1994, 98, 7–18. [Google Scholar] [CrossRef]
- Gomez, E.D.; Ruegg, M.L.; Minor, A.M.; Kisielowski, C.; Downing, K.H.; Glaeser, R.M.; Balsara, N.P. Interfacial concentration profiles of rubbery polyolefin lamellae determined by quantitative electron microscopy. Macromolecules 2008, 41, 156–162. [Google Scholar] [CrossRef]
- Majewski, P.W.; Yager, K.G. Rapid ordering of block copolymer thin films. J. Phys. Condens. Matter 2016, 28, 403002. [Google Scholar] [CrossRef]
- Anastasiadis, S.H.; Russell, T.P.; Satija, S.K.; Majkrzak, C.F. The morphology of symmetric diblock copolymers as revealed by neutron reflectivity. J. Chem. Phys. 1990, 92, 5677–5691. [Google Scholar] [CrossRef]
- Green, P.F.; Christensen, T.M.; Russell, T.P.; Jerome, R. Equilibrium surface composition of diblock copolymers. J. Chem. Phys. 1990, 92, 1478–1482. [Google Scholar] [CrossRef]
- Russell, T.P.; Menelle, A.; Hamilton, W.A.; Smith, G.S.; Satija, S.K.; Majkrzak, C.F. Width of homopolymer interfaces in the presence of symmetric diblock copolymers. Macromolecules 1991, 24, 5721–5726. [Google Scholar] [CrossRef]
- Anastasiadia, S.H.; Russell, T.P.; Satija, S.K.; Majkrzak, C.F. Neutron reflectivity studies of the surface-induced ordering of diblock copolymer films. Phys. Rev. Lett. 1989, 62, 1852. [Google Scholar] [CrossRef]
- Stamm, M. Investigation of the interface between polymers: A comparison of scattering and reflectivity techniques. J. Appl. Crystallogr. 1991, 24, 651–658. [Google Scholar] [CrossRef]
- Lee, J.; Kang, M.H.; Lim, W.C.; Shin, K.; Lee, Y. Characterization of microphase-separated diblock copolymer films by TOF-SIMS. Surf. Interface Anal. 2013, 45, 498–502. [Google Scholar] [CrossRef]
- Wang, C.; Araki, T.; Ade, H. Soft X-ray resonant reflectivity of low-z material thin films. Appl. Phys. Lett. 2005, 87, 214109. [Google Scholar] [CrossRef]
- Ade, H.; Wang, C.; Garcia, A.; Yan, H.; Sohn, K.E.; Hexemer, A.; Bazan, G.C.; Nguyen, T.Q.; Kramer, E.J. Characterization of multicomponent polymer trilayers with resonant soft X-ray reflectivity. J. Polym. Sci. Part B Polym. Phys. 2009, 47, 1291–1299. [Google Scholar] [CrossRef]
- Yan, H.; Wang, C.; Garica, A.; Swaraj, S.; Gu, Z.; McNeill, C.R.; Schuettfort, T.; Sohn, K.E.; Kramer, E.J.; Bazan, G.C.; et al. Interfaces in organic devices studied with resonant soft X-ray reflectivity. J. Appl. Phys. 2011, 110, 102220. [Google Scholar] [CrossRef]
- Jinnai, H.; Higuchi, T.; Zhuge, X.; Kumamoto, A.; Batenburg, K.J.; Ikuhara, Y. Three-dimensional visualization and characterization of polymeric self-assemblies by transmission electron microtomography. Acc. Chem. Res. 2017, 50, 1293–1302. [Google Scholar] [CrossRef]
- Lohse, D.J.; Hadjichristidis, N. Microphase separation in block copolymers. Curr. Opin. Colloid Interface Sci. 1997, 2, 171–176. [Google Scholar] [CrossRef]
- Kunz, M.; Shull, K. Improved technique for cross-sectional imaging of thin polymer films by transmission electron microscopy. Polymer 1993, 34, 2427–2430. [Google Scholar] [CrossRef]
- Segal-Peretz, T.; Winterstein, J.; Doxastakis, M.; Ramirez-Hernandez, A.; Biswas, M.; Ren, J.; Suh, H.S.; Darling, S.B.; Liddle, J.A.; Elam, J.W.; et al. Characterizing the three-dimensional structure of block copolymers via sequential infiltration synthesis and scanning transmission electron tomography. ACS Nano 2015, 9, 5333–5347. [Google Scholar] [CrossRef]
- Segal-Peretz, T.; Ren, J.; Xiong, S.; Khaira, G.; Bowen, A.; Ocola, L.E.; Divan, R.; Doxastakis, M.; Ferrier, N.J.; de Pablo, J.J.; et al. Quantitative three-dimensional characterization of block copolymer directed self-assembly on combined chemical and topographical prepatterned templates. ACS Nano 2017, 11, 1307–1319. [Google Scholar] [CrossRef]
- Handlin, D.L.; Thomas, E.L. Phase contrast imaging of styrene-isoprene and styrene-butadiene block copolymers. Macromolecules 1983, 16, 1514–1525. [Google Scholar] [CrossRef]
- Iakoubovskii, K.; Mitsuishi, K.; Nakayama, Y.; Furuya, K. Thickness measurements with electron energy loss spectroscopy. Microsc. Res. Tech. 2008, 71, 626–631. [Google Scholar] [CrossRef] [PubMed]
- Russell, T.P.; Hjelm, R.P.; Seeger, P.A. Temperature dependence of the interaction parameter of polystyrene and poly (methyl methacrylate). Macromolecules 1990, 23, 890–893. [Google Scholar] [CrossRef]
- Puglisi, R.A. Towards ordered silicon nanostructures through self-assembling mechanisms and processes. J. Nanomater. 2015, 16, 229. [Google Scholar] [CrossRef]
- Lee, K.S.; Lee, J.; Kwak, J.; Moon, H.C.; Kim, J.K. Reduction of line edge roughness of polystyrene-block-polymethylmethacrylate copolymer nanopatterns by introducing hydrogen bonding at the junction point of two block chains. ACS Appl. Mater. Interfaces 2017, 9, 31245–31251. [Google Scholar] [CrossRef]
- Yakovlev, S.; Libera, M. Dose-limited spectroscopic imaging of soft materials by low-loss EELS in the scanning transmission electron microscope. Micron 2008, 39, 734–740. [Google Scholar] [CrossRef]
- Varlot, K.; Martin, J.M.; Quet, C. Physical and chemical changes in polystyrene during electron irradiation using EELS in the TEM: Contribution of the dielectric function. J. Microsc. 1998, 191, 187–194. [Google Scholar] [CrossRef]
- Ritsko, J.J.; Brillson, L.J.; Bigelow, R.W.; Fabish, T.J. Electron energy loss spectroscopy and the optical properties of polymethylmethacrylate from 1 to 300 eV. J. Chem. Phys. 1978, 69, 3931–3939. [Google Scholar] [CrossRef]
- Varlot, K.; Martin, J.M.; Quet, C. EELS analysis of PMMA at high spatial resolution. Micron 2001, 32, 371–378. [Google Scholar] [CrossRef]
- Kunz, M.; Moller, M.; Cantow, H.J. The net distribution of elements by element specific electron microscopy-ESI, Morphological studies of polystyrene-block-poly (2-vinylpyridine). Macromol. Chem. Rapid Commun. 1987, 8, 401–410. [Google Scholar] [CrossRef]
- Malis, T.; Cheng, S.C.; Egerton, R.F. EELS log ratio technique for specimen-thickness measurement in the TEM. J. Electron Microsc. Tech. 1988, 8, 193–200. [Google Scholar] [CrossRef]
- Polymer Properties Database. Available online: http://polymerdatabase.com/polymer%20physics/Polymer%20Density.html (accessed on 29 November 2019).
- Lorenzoni, M.; Evangelio, L.; Nicolet, C.; Navarro, C.; San Paulo, A.; Pérez-Murano, F. Nanomechanical properties of solvent cast PS and PMMA polymer blends and block copolymers. In Proceedings of the SPIE, San Jose, CA, USA, 27 March 2015; Volume 9423, p. 942325. [Google Scholar]
- Egerton, R.F. Electron Energy-Loss Spectroscopy in the Transmission Electron Micoscope; Plenum Press: New York, NY, USA, 1996. [Google Scholar]
- Sparnacci, K.; Antonioli, D.; Gianotti, V.; Laus, M.; Ferrarese Lupi, F.; Giammaria, T.J.; Seguini, G.; Perego, M. Ultrathin random copolymer-grafted layers for block copolymer self-assembly. ACS Appl. Mater. Interfaces 2015, 7, 1094–10951. [Google Scholar] [CrossRef] [PubMed]

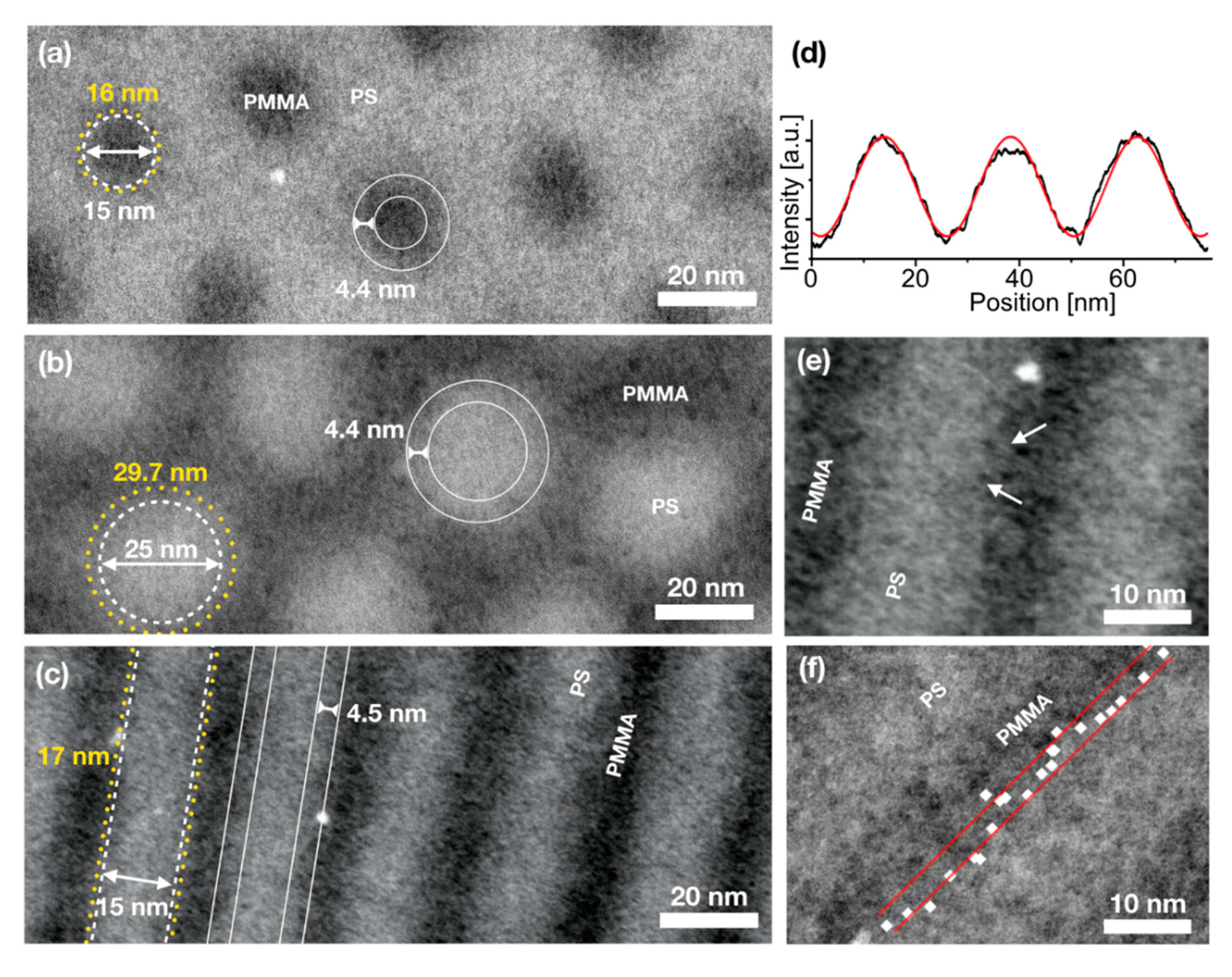
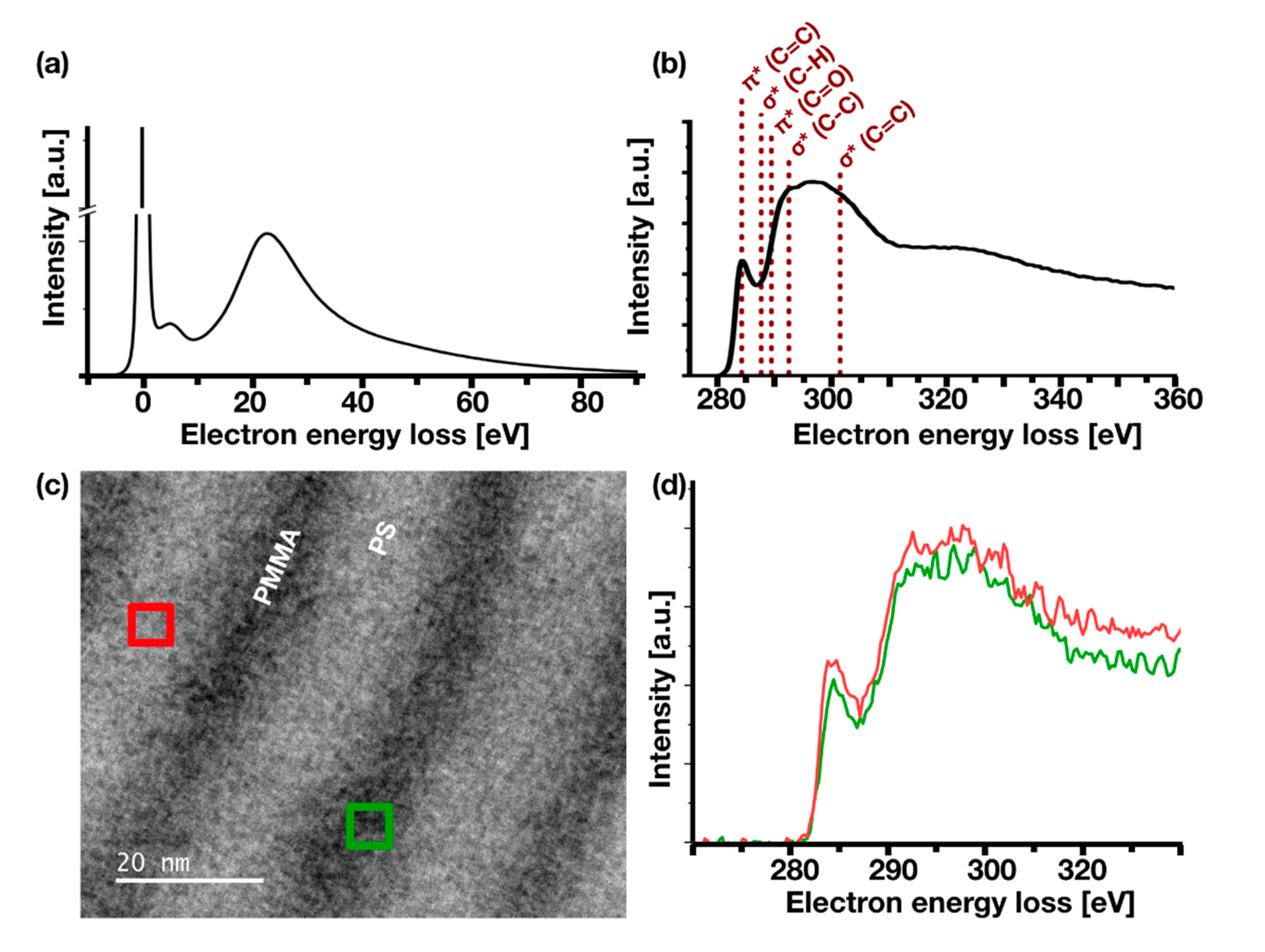

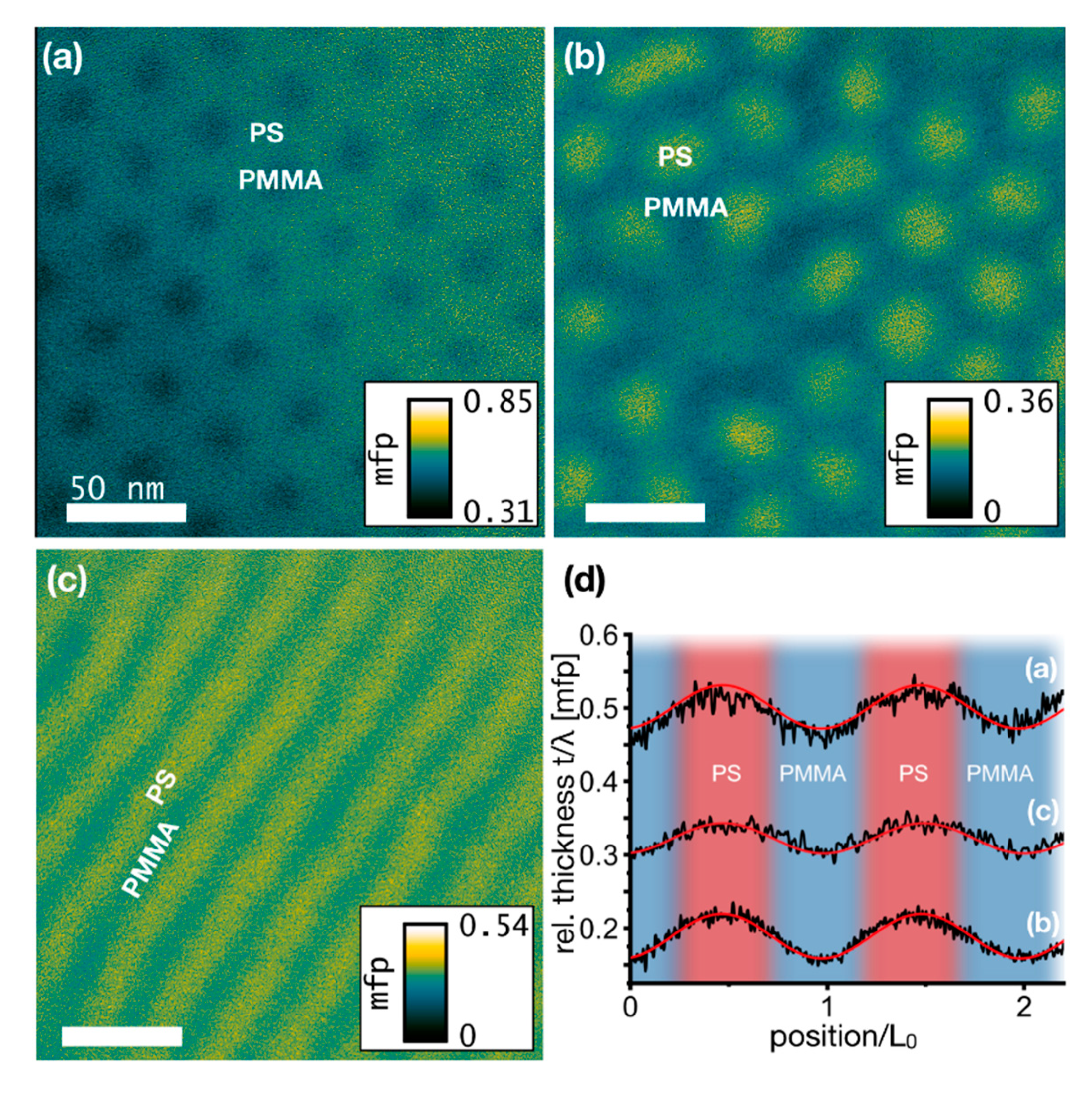
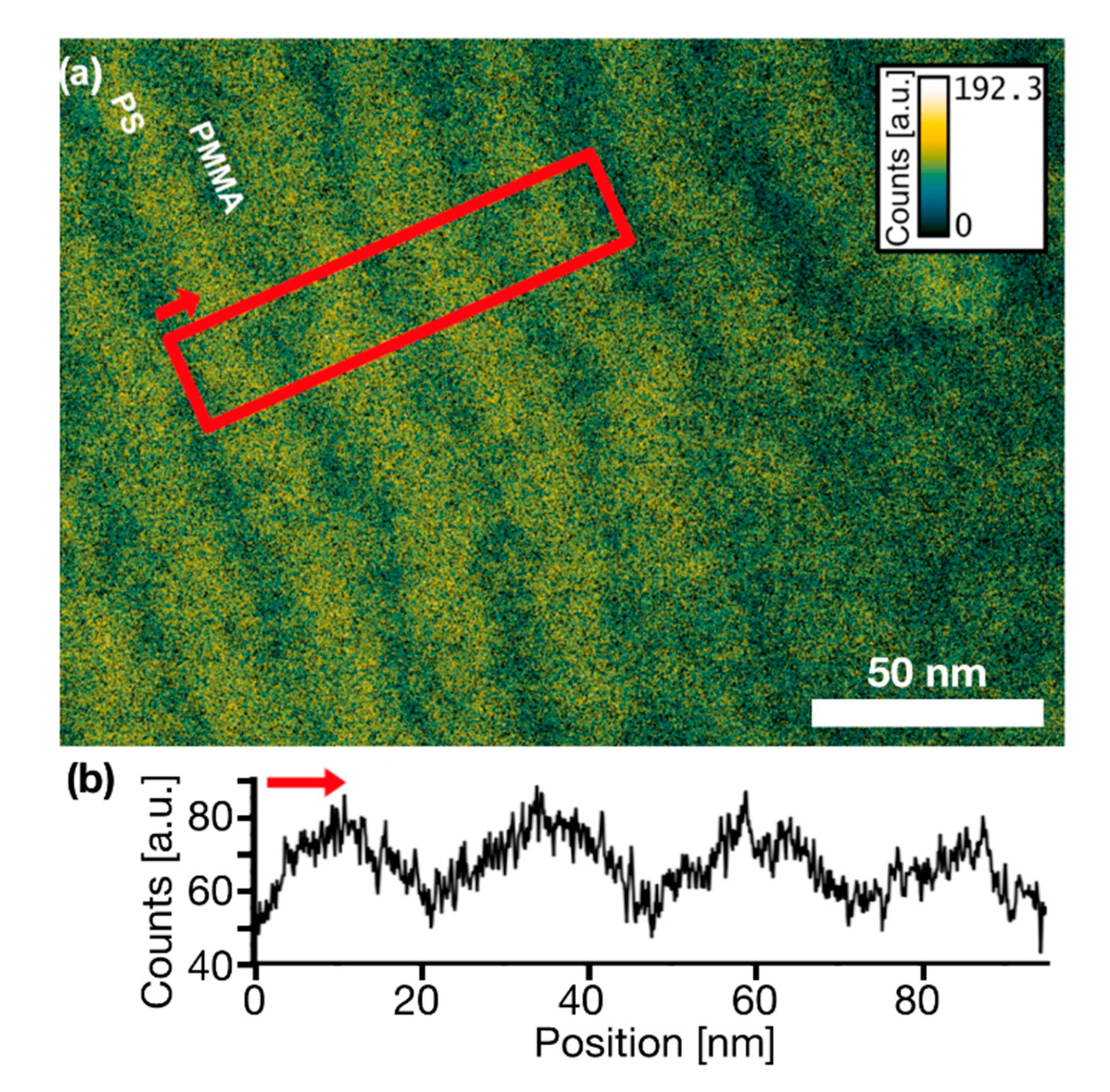
| Polymer | Mn (PS-PMMA) [kg/mol] | NPS-NPMMA | χN | dSEM [nm] | L0,SEM [nm] | dTEM [nm] | hAFM [nm] | ∆x [nm] | σ [nm] |
|---|---|---|---|---|---|---|---|---|---|
| PS:PMMA 70:30 | 46.1–21.0 | 443–210 | 23.9 | 15.0± 2.6 a | 35.0 ± 4.4 | 16.0 ± 0.9 a | 1.12 ± 0.30 | 4.39 | 1.04 |
| PS:PMMA 30:70 | 20.2–50.5 | 194–505 | 25.6 | 24.6± 4.5 b | 35.6 ± 6.0 | 29.7 ± 0.6 b | 1.15 ± 0.27 | 4.36 | 1.04 |
| PS:PMMA 50:50 | 25.0–26.0 | 240–257 | 18.2 | 14.7 ± 2.4 c | 24.3 ± 1.2 | 9.2 c | 1.28 ± 0.28 | 4.53 | 0.93 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bürger, J.; Kunnathully, V.S.; Kool, D.; Lindner, J.K.N.; Brassat, K. Characterisation of the PS-PMMA Interfaces in Microphase Separated Block Copolymer Thin Films by Analytical (S)TEM. Nanomaterials 2020, 10, 141. https://doi.org/10.3390/nano10010141
Bürger J, Kunnathully VS, Kool D, Lindner JKN, Brassat K. Characterisation of the PS-PMMA Interfaces in Microphase Separated Block Copolymer Thin Films by Analytical (S)TEM. Nanomaterials. 2020; 10(1):141. https://doi.org/10.3390/nano10010141
Chicago/Turabian StyleBürger, Julius, Vinay S. Kunnathully, Daniel Kool, Jörg K. N. Lindner, and Katharina Brassat. 2020. "Characterisation of the PS-PMMA Interfaces in Microphase Separated Block Copolymer Thin Films by Analytical (S)TEM" Nanomaterials 10, no. 1: 141. https://doi.org/10.3390/nano10010141
APA StyleBürger, J., Kunnathully, V. S., Kool, D., Lindner, J. K. N., & Brassat, K. (2020). Characterisation of the PS-PMMA Interfaces in Microphase Separated Block Copolymer Thin Films by Analytical (S)TEM. Nanomaterials, 10(1), 141. https://doi.org/10.3390/nano10010141








