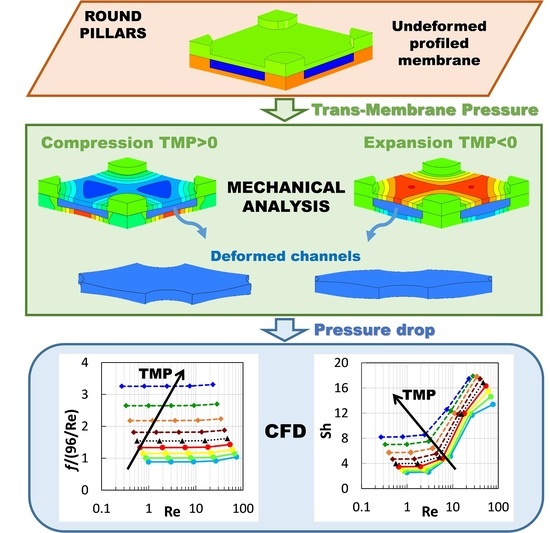
Pressure-Induced Deformation of Pillar-Type Profiled Membranes and Its Effects on Flow and Mass Transfer
Abstract
1. Introduction
2. Materials and Methods
2.1. Computational Strategy
2.2. Mechanical Model
- The four external vertical edges of the domain were clamped, i.e., zero displacement and zero rotation were imposed.
- The four side faces of the domain were imposed zero normal displacement so that the computational domain was representative of a periodic array of repetitive units.
- The transmembrane pressure relative to that of the internal fluid channel (and thus >0 for compression and <0 for expansion) was applied to the whole outer surface of the domain.
2.3. CFD Model
3. Results and Discussion
3.1. Mechanical Simulations
3.1.1. Influence of Pitch to Height ratio (P/H) and Limiting Value
3.1.2. Membrane and Channel Deformation for the Selected Geometry (P/H = 10)
3.2. CFD Simulations for the Selected Geometry (P/H = 10)
3.2.1. Local Quantities
3.2.2. Global Quantities
3.2.3. Comparison with OCF Profiled Membranes
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Campione, A.; Gurreri, L.; Ciofalo, M.; Micale, G.; Tamburini, A.; Cipollina, A. Electrodialysis for water desalination: A critical assessment of recent developments on process fundamentals, models and applications. Desalination 2018, 434, 121–160. [Google Scholar] [CrossRef]
- Cipollina, A.; Micale, G.; Tamburini, A.; Tedesco, M.; Gurreri, L.; Veerman, J.; Grasman, S. Reverse electrodialysis: Applications. In Sustainable Energy from Salinity Gradients; Cipollina, A., Micale, G., Eds.; Woodhead Publishing, Elsevier: Amsterdam, The Netherlands, 2016; pp. 135–180. [Google Scholar]
- Pawlowski, S.; Geraldes, V.; Crespo, J.G.; Velizarov, S. Computational fluid dynamics (CFD) assisted analysis of profiled membranes performance in reverse electrodialysis. J. Membr. Sci. 2016, 502, 179–190. [Google Scholar] [CrossRef]
- Gurreri, L.; Battaglia, G.; Tamburini, A.; Cipollina, A.; Micale, G.; Ciofalo, M. Multi-physical modelling of reverse electrodialysis. Desalination 2017, 423, 52–64. [Google Scholar] [CrossRef]
- La Cerva, M.L.; Di Liberto, M.; Gurreri, L.; Tamburini, A.; Cipollina, A.; Micale, G.; Ciofalo, M. Coupling CFD with a one-dimensional model to predict the performance of reverse electrodialysis stacks. J. Membr. Sci. 2017, 541, 595–610. [Google Scholar] [CrossRef]
- Lian, B.; Blandin, G.; Leslie, G.; Le-Clech, P. Impact of module design in forward osmosis and pressure assisted osmosis: An experimental and numerical study. Desalination 2017, 426, 108–117. [Google Scholar] [CrossRef]
- She, Q.; Hou, D.; Liu, J.; Tan, K.H.; Tang, C.Y. Effect of feed spacer induced membrane deformation on the performance of pressure retarded osmosis (PRO): Implications for PRO process operation. J. Membr. Sci. 2013, 445, 170–182. [Google Scholar] [CrossRef]
- Karabelas, A.J.; Koutsou, C.P.; Sioutopoulos, D.C. Comprehensive performance assessment of spacers in spiral-wound membrane modules accounting for compressibility effects. J. Membr. Sci. 2018, 549, 602–615. [Google Scholar] [CrossRef]
- Huang, S.M. Laminar flow and heat transfer in plate membrane channels: Effects of the deformation heights. Int. J. Therm. Sci. 2016, 109, 44–53. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, X. A numerical study of flow crossover between adjacent flow channels in a proton exchange membrane fuel cell with serpentine flow field. J. Power Sour. 2008, 185, 985–992. [Google Scholar] [CrossRef]
- Zhou, Y.; Jiao, K.; Du, Q.; Yin, Y.; Li, X. Gas diffusion layer deformation and its effect on the transport characteristics and performance of proton exchange membrane fuel cell. Int. J. Hydrog. Energy 2013, 38, 12891–12903. [Google Scholar] [CrossRef]
- Hereijgers, J.; Ottevaere, H.; Breugelmans, T.; De Malsche, W. Membrane deflection in a flat membrane microcontactor: Experimental study of spacer features. J. Membr. Sci. 2016, 504, 153–161. [Google Scholar] [CrossRef]
- Moreno, J.; Slouwerhof, E.; Vermaas, D.A.; Saakes, M.; Nijmeijer, K. The breathing cell: Cyclic intermembrane distance variation in reverse electrodialysis. Environ. Sci. Technol. 2016, 50, 11386–11393. [Google Scholar] [CrossRef] [PubMed]
- Tadimeti, J.G.D.; Kurian, V.; Chandra, A.; Chattopadhyay, S. Corrugated membrane surfaces for effective ion transport in electrodialysis. J. Membr. Sci. 2016, 499, 418–428. [Google Scholar] [CrossRef]
- Vermaas, D.A.; Saakes, M.; Nijmeijer, K. Power generation using profiled membranes in reverse electrodialysis. J. Membr. Sci. 2011, 385, 234–242. [Google Scholar] [CrossRef]
- Vermaas, D.A.; Saakes, M.; Nijmeijer, K. Enhanced mixing in the diffusive boundary layer for energy generation in reverse electrodialysis. J. Membr. Sci. 2014, 453, 312–319. [Google Scholar] [CrossRef]
- Güler, E.; Elizen, R.; Saakes, M.; Nijmeijer, K. Micro-structured membranes for electricity generation by reverse electrodialysis. J. Membr. Sci. 2014, 458, 136–148. [Google Scholar] [CrossRef]
- Pawlowski, S.; Rijnaarts, T.; Saakes, M.; Nijmeijer, K.; Crespo, J.G.; Velizarov, S. Improved fluid mixing and power density in reverse electrodialysis stacks with chevron-profiled membranes. J. Membr. Sci. 2017, 531, 111–121. [Google Scholar] [CrossRef]
- Larchet, C.; Zabolotsky, V.I.; Pismenskaya, N.; Nikonenko, V.V.; Tskhay, A.; Tastanov, K.; Pourcelly, G. Comparison of different ED stack conceptions when applied for drinking water production from brackish waters. Desalination 2008, 222, 489–496. [Google Scholar] [CrossRef]
- Battaglia, G.; Gurreri, L.; Airò Farulla, G.; Cipollina, A.; Pirrotta, A.; Micale, G.; Ciofalo, M. Membrane deformation and its effects on flow and mass transfer in the electromembrane processes. Int. J. Mol. Sci. 2019, 20, 1840. [Google Scholar] [CrossRef] [PubMed]
- Bdiri, M.; Dammak, L.; Larchet, C.; Hellal, F.; Porozhnyy, M.; Nevakshenova, E.; Pismenskaya, N.; Nikonenko, V. Characterization and cleaning of anion-exchange membranes used in electrodialysis of polyphenol-containing food industry solutions; comparison with cation-exchange membranes. Sep. Purif. Technol. 2019, 210, 636–650. [Google Scholar] [CrossRef]
- Garcia-Vasquez, W.; Dammak, L.; Larchet, C.; Nikonenko, V.; Grande, D. Effects of acid-base cleaning procedure on structure and properties of anion-exchange membranes used in electrodialysis. J. Membr. Sci. 2016, 507, 12–23. [Google Scholar] [CrossRef]
- Safronova, E.Y.; Golubenko, D.V.; Shevlyakova, N.V.; D’yakova, M.G.; Tverskoi, V.A.; Dammak, L.; Grande, D.; Yaroslavtsev, A.B. New cation-exchange membranes based on cross-linked sulfonated polystyrene and polyethylene for power generation systems. J. Membr. Sci. 2016, 515, 196–203. [Google Scholar] [CrossRef]
- Vandiver, M.A.; Caire, B.R.; Carver, J.R.; Waldrop, K.; Hibbs, M.R.; Varcoe, J.R.; Herring, A.M.; Liberatore, M.W. Mechanical characterization of anion exchange membranes by extensional rheology under controlled hydration. J. Electrochem. Soc. 2014, 161, H677–H683. [Google Scholar] [CrossRef]
- Solasi, R.; Zou, Y.; Huang, X.; Reifsnider, K. A time and hydration dependent viscoplastic model for polyelectrolyte membranes in fuel cells. Mech. Time Depend. Mater. 2008, 12, 15–30. [Google Scholar] [CrossRef]
- Kusoglu, A.; Karlsson, A.M.; Santare, M.H.; Cleghorn, S.; Johnson, W.B. Mechanical behavior of fuel cell membranes under humidity cycles and effect of swelling anisotropy on the fatigue stresses. J. Power Sour. 2007, 170, 345–358. [Google Scholar] [CrossRef]
- Pawlowski, S.; Crespo, J.; Velizarov, S. Profiled ion exchange membranes: A comprehensible review. Int. J. Mol. Sci. 2019, 20, 165. [Google Scholar] [CrossRef] [PubMed]
- Tufa, R.A.; Pawlowski, S.; Veerman, J.; Bouzek, K.; Fontananova, E.; di Profio, G.; Velizarov, S.; Goulão Crespo, J.; Nijmeijer, K.; Curcio, E. Progress and prospects in reverse electrodialysis for salinity gradient energy conversion and storage. Appl. Energy 2018, 225, 290–331. [Google Scholar] [CrossRef]
- La Cerva, M.; Gurreri, L.; Tedesco, M.; Cipollina, A.; Ciofalo, M.; Tamburini, A.; Micale, G. Determination of limiting current density and current efficiency in electrodialysis units. Desalination 2018, 445, 138–148. [Google Scholar] [CrossRef]
- Campione, A.; Cipollina, A.; Bogle, I.D.L.; Gurreri, L.; Tamburini, A.; Tedesco, M.; Micale, G. A hierarchical model for novel schemes of electrodialysis desalination. Desalination 2019, 465, 79–93. [Google Scholar] [CrossRef]
- Doornbusch, G.J.; Tedesco, M.; Post, J.W.; Borneman, Z.; Nijmeijer, K. Experimental investigation of multistage electrodialysis for seawater desalination. Desalination 2019, 464, 105–114. [Google Scholar] [CrossRef]
- Iyengar, K.T.S.R.; Naqvi, M.M. Large deflections of rectangular plates. Int. J. Non Linear Mech. 1966, 1, 109–122. [Google Scholar] [CrossRef]
- Gurreri, L.; Ciofalo, M.; Cipollina, A.; Tamburini, A.; Van Baak, W.; Micale, G. CFD modelling of profiled-membrane channels for reverse electrodialysis. Desalin. Water Treat. 2015, 55, 3404–3423. [Google Scholar] [CrossRef]










| Quantity | Value | Units |
|---|---|---|
| Membrane Young modulus, E | 150 | MPa |
| Membrane Poisson ratio, ν | 0.4 | - |
| Channel thickness, H | 200 | μm |
| Membrane thickness, δ | 120 | μm |
| Pitch-to-height ratio, P/H | 9–11 | - |
| Pillar diameter, d | 1 | mm |
| Intrinsic angle of pillar lattice, α | 60 | deg |
| FE Mesh | No. Elements | Maximum Displacement (μm) |
|---|---|---|
| RP-I | 21 × 103 | 67.69 |
| RP-II | 60 × 103 | 67.97 |
| RP-III | 180 × 103 | 68.06 |
| Property | Value | Units |
|---|---|---|
| Density, ρ | 1017 | kg m−3 |
| Viscosity, µ | 0.931 × 10−3 | N s m−2 |
| Salt diffusivity, D | 1.47 × 10−9 | m2 s−1 |
| Schmidt number, Sc = µ/(ρD) | 622 | - |
| FV Mesh | No. Elements | f | Sh |
|---|---|---|---|
| RP-A | 2.576 × 106 | 6.941 | 13.769 |
| RP-B | 4.142 × 106 | 6.965 | 13.719 |
| RP-C | 6.091 × 106 | 6.976 | 13.689 |
| Quantities | Compressed +0.4 Bar | Undeformed | Expanded −0.4 Bar | |||
|---|---|---|---|---|---|---|
| RP | OCF | RP | OCF | RP | OCF | |
| U (cm/s) | 0.5 | 0.4 | 1.1 | 1.0 | 2.0 | 2.0 |
| F | 129.0 | 260.5 | 28.9 | 43.2 | 9.5 | 10.3 |
| k (m/s), upper wall | 3.2 × 10−5 | 2.6 × 10−5 | 1.9 × 10−5 | 1.9 × 10−5 | 1.9 × 10−5 | 2.2 × 10−5 |
| k (m/s), lower wall | 3.2 × 10−5 | 2.6 × 10−5 | 1.9 × 10−5 | 1.4 × 10−5 | 1.9 × 10−5 | 1.1 × 10−5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Battaglia, G.; Gurreri, L.; Airò Farulla, G.; Cipollina, A.; Pirrotta, A.; Micale, G.; Ciofalo, M. Pressure-Induced Deformation of Pillar-Type Profiled Membranes and Its Effects on Flow and Mass Transfer. Computation 2019, 7, 32. https://doi.org/10.3390/computation7020032
Battaglia G, Gurreri L, Airò Farulla G, Cipollina A, Pirrotta A, Micale G, Ciofalo M. Pressure-Induced Deformation of Pillar-Type Profiled Membranes and Its Effects on Flow and Mass Transfer. Computation. 2019; 7(2):32. https://doi.org/10.3390/computation7020032
Chicago/Turabian StyleBattaglia, Giuseppe, Luigi Gurreri, Girolama Airò Farulla, Andrea Cipollina, Antonina Pirrotta, Giorgio Micale, and Michele Ciofalo. 2019. "Pressure-Induced Deformation of Pillar-Type Profiled Membranes and Its Effects on Flow and Mass Transfer" Computation 7, no. 2: 32. https://doi.org/10.3390/computation7020032
APA StyleBattaglia, G., Gurreri, L., Airò Farulla, G., Cipollina, A., Pirrotta, A., Micale, G., & Ciofalo, M. (2019). Pressure-Induced Deformation of Pillar-Type Profiled Membranes and Its Effects on Flow and Mass Transfer. Computation, 7(2), 32. https://doi.org/10.3390/computation7020032