Binary Competitive Swarm Optimizer Approaches for Feature Selection

Abstract

Feature selection is known as an NP-hard combinatorial problem in which the possible feature subsets increase exponentially with the number of features. Due to the increment of the feature size, the exhaustive search has become impractical. In addition, a feature set normally includes irrelevant, redundant, and relevant information. Therefore, in this paper, binary variants of a competitive swarm optimizer are proposed for wrapper feature selection. The proposed approaches are used to select a subset of significant features for classification purposes. The binary version introduced here is performed by employing the S-shaped and V-shaped transfer functions, which allows the search agents to move on the binary search space. The proposed approaches are tested by using 15 benchmark datasets collected from the UCI machine learning repository, and the results are compared with other conventional feature selection methods. Our results prove the capability of the proposed binary version of the competitive swarm optimizer not only in terms of high classification performance, but also low computational cost.

1. Introduction

In recent days, many applications involve the role of extracting useful information for data collection. The extracted information is known as feature, and it is useful in describing the target concept [1]. However, an increment in the number of features will cause the “curse of dimensionality” in which the performance of the system is degraded and becomes complex. This is mainly due to the existence of irrelevant and redundant information, which badly affects the performance of the classification model [2]. To resolve the issue above, a proper selection of extracted features is critically important. Hence, the feature selection problem has become one of the major concerns in most of the research areas [3].

Feature selection is the pre-processing step to determine a subset of significant features that can strongly improve the performance of the system. It not only eliminates the redundant information, but also reduces the temporal and spatial complexity of the classification model [4]. Generally, feature selection can be classified into two approaches: filter and wrapper. The former identifies the relevant features by using the proxy measure, mutual information, and data characteristics, while the later utilizes a predictive model to train the feature set for evaluating the nearly optimal feature subset [5,6]. As compared to the wrapper, filter feature selection is independent of the learning algorithm, and it is computationally less expensive. However, wrapper feature selection can usually offer better performance [7].

As for the wrapper approach, the feature selection is considered as a combinatorial optimization problem, which can be solved by using metaheuristic algorithms [8,9]. The most common wrapper feature selection methods are the genetic algorithm (GA) and binary particle swarm optimization (BPSO). The GA is an evolutionary algorithm that generates the population of solutions called chromosomes. For each generation, the solutions are evolved based on the selection, crossover, and mutation operations [10]. Several studies have shown that GA is good for the high dimensional feature selection problem [10,11]. However, the GA suffers from time consumption and parameter setting. Thus, Ghareb et al. [12] performed the hybridization between an enhanced genetic algorithm (EGA) and a filter approach for text categorization. The authors first employed the filter approach to identify the potential initial solutions, and the solutions are then evaluated by the EGA. Ma and Xia [13] introduced a novel tribe competition-based genetic algorithm (TCbGA) to tackle the feature selection problem in pattern classification. Another study proposed the adaptive multi-parent crossover GA for epileptic seizure identification [14].

BPSO is a binary variant of particle swarm optimization (PSO). Unlike GA, BPSO is a swarm-based algorithm that generates the population of solutions called particles. The particles adjust their positions by changing their velocities according to their own experience, as well as the experience of their neighbors [15]. BPSO is a useful tool and it has been widely applied for feature selection. However, BPSO has the disadvantages of premature convergence and stagnation, thus leading to ineffective solutions [15,16]. Therefore, Chuang et al. [17] proposed a chaotic binary particle swarm optimization (CBPSO) for feature selection in which the chaotic maps were implemented for identifying the inertia weight in each iteration. Jain et al. [18] developed an improved binary particle swarm optimization (iBPSO) for gene selection and cancer classification. The authors first applied the correlation-based feature selection (CFS) to reduce the dimensions, and then evaluated the relevant features using iBPSO. Another study introduced the BPSO with the personal best (pbest) guide strategy to tackle the feature selection problem in electromyography signals classification [19].

Competitive swarm optimizer (CSO) is a newly introduced variant of PSO [20]. In comparison with other metaheuristic algorithms, CSO has shown superior performance in several benchmark tests. Generally, CSO employs the competition strategy that partitioned the solutions into winners and losers in which the winners are directly moved to the next iteration. In this way, CSO is computationally less expensive since only half of the population is used in the evaluations. In this paper, we propose the binary version of CSO to solve the feature selection problem in classification tasks. The binary version introduced here is performed by implementing the transfer functions. In this approach, the transfer functions from S-shaped and V-shaped families are used to allow the search agents to move around the binary search space. The proposed approaches are validated with 15 benchmark datasets, and the results are compared with other conventional methods.

The organization of this paper as the following: Section 2 details the background of the competitive swarm optimizer (CSO). Section 3 presents the proposed binary version of the competitive swarm optimizer (BCSO) and Section 4 describes the application of BCSO in feature selection. The experimental results are discussed in Section 5. Finally, conclusions are offered in Section 6.

2. The Competitive Swarm Optimizer

The competitive swarm optimizer (CSO) is a recent metaheuristic optimization algorithm proposed by Cheng and Jin in 2015 [20]. The CSO is a new variant of particle swarm optimization (PSO), and it has been proven to work more effectively on large-scale optimization. In addition, the CSO is able to find the global optimum in a very short period, which leads to fast computational speed. In the CSO, the population of particles is randomly partitioned into two groups with equal size. The competition is then made between the particles from each group. From the competition, the particle that scores a better fitness value is known as the winner and it is directly moved to the new iteration. On the contrary, the loser updates its velocity and position by learning from the winner. Mathematically, the velocity and position of loser is updated as follows:

$$v_{l,d}\left(t+1\right)=r_1{v}_{l,d}\left(t\right)+r_2\left(x_{w,d}\left(t\right)-x_{l,d}\left(t\right)\right)+\varphi r_3\left({\overline{x}}_d\left(t\right)-x_{l,d}\left(t\right)\right)$$

(1)

$$x_{l,d}\left(t+1\right)=x_{l,d}\left(t\right)+v_{l,d}\left(t+1\right)$$

(2)

where v_l is the velocity of loser particle, x_w is the position of the winner particle, x_l is the position of the loser particle, $\overline{x}$ is the mean position of the current swarm, r₁, r₂, and r₃ are three independent random vectors in [0, 1], $\varphi$ is the social factor, d is the dimension of search space, and t is the iteration number. The pseudocode of the CSO is presented in Algorithm 1.

Algorithm 1. Competitive swarm optimizer

Input parameter:N, Tmax and $\varphi$

(1) Initialize a population of particles, x

(2) Calculate the fitness of particles, F(x)

(3) Define the best particle as gbest

(4) for t = 1 to maximum number of iterations, Tmax

// Competition Strategy //

(5)  for i = 1 to half of population, N/2

(6)   Random select two particles, xk and xm

(7)   if F(xk) better than F(xm)

(8)    xw = xk, xl = xm

(9)   else

(10)    xw = xm, xl = xk

(11)   end if

(12)   Add xw into new population

(13)   Remove xk and xm from the population

(14)  next i

//Velocity and Position Update //

(15)  for i = 1 to half of population, N/2

(16)   for d = 1 to the dimension of search space, D

(17)    Update velocity of loser using Equation (1)

(18)    Update position of loser as shown in Equation (2)

(19)   next d

(20)   Calculate the fitness of new loser, F(xl)

(21)   Move new loser into new population

(22)   Update gbest if there is better solution

(23)  next i

(24)  Pass new population to next iteration

(25) next t

Output: Global best solution

3. Binary Version of the Competitive Swarm Optimizer

The CSO is a swarm intelligent method that mimics the concept of competition between particles in the population. As mentioned in [20], the CSO has been tested on several benchmark functions, and it showed superior performance against other conventional optimization algorithms. The CSO algorithm utilizes the competition strategy and new velocity updating rule, which is beneficial in improving the exploration and convergence rate [20]. This motivates us to model the CSO so that it can be useful for wrapper-based feature selection.

Generally speaking, wrapper feature selection is considered as a binary optimization problem. In wrapper feature selection, the solution is represented as either 0 or 1 [8]. In the traditional CSO, the particles are moved around the search space by updating their positions within the continuous real domain. However, the real continuous value is not suitable for binary optimization since the solution should be represented in binary form. For such a reason, the CSO is modeled into the binary version.

One of the effective ways to convert the continuous optimization into a binary version is the utilization of a transfer function. In binary optimization, a transfer function is a mathematical function that determines the probability of changing a position vector’s dimension from 0 to 1, and vice versa [21]. More importantly, a transfer function is an extremely cheap operator, and it can improve the exploitation and exploration of the CSO in feature selection [22]. Hence, the transfer function has become our main focus in this work. In this paper, we propose eight versions of binary competitive swarm optimizers for feature selection.

3.1. S-Shaped Family

In general, the transfer function can be categorized into S-shaped and V-shaped families. In this sub-section, the implementation of the S-shaped transfer function is described. The S-shaped transfer function forces the search agents to move around the binary search space [8]. Previously, S-shaped transfer functions have been successfully applied in binary particle swarm optimization (BPSO), binary antlion optimizer (BALO) and binary salp swarm algorithm (BSSA) [8,21,23]. The four commonly used S-shaped transfer functions (S1–S4) are expressed as follows:

$$S1\left(v_{l,d}\left(t+1\right)\right)=\frac{1}{1+\exp \left(-2v_{l,d}\left(t+1\right)\right)}$$

(3)

$$S2\left(v_{l,d}\left(t+1\right)\right)=\frac{1}{1+\exp \left(-v_{l,d}\left(t+1\right)\right)}$$

(4)

$$S3\left(v_{l,d}\left(t+1\right)\right)=\frac{1}{1+\exp \left(-v_{l,d}\left(t+1\right)/2\right)}$$

(5)

$$S4\left(v_{l,d}\left(t+1\right)\right)=\frac{1}{1+\exp \left(-v_{l,d}\left(t+1\right)/3\right)}$$

(6)

where v_l is the velocity of loser particle, d is the dimension, and t is the iteration number. The illustrations of the S-shaped transfer functions are presented in Figure 1. In these approaches, the velocity of the loser is first calculated as shown in Equation (1). The transfer function is then used to convert the velocity into a probability value between [0, 1]. After that, the position of the loser is updated as:

$$x_{l,d}\left(t+1\right)=\{\begin{array}{l}1 , \mathrm{if} S\left(v_{l,d}\left(t+1\right)\right) > r_4\\ 0 , \mathrm{otherwise}\end{array}$$

(7)

where S can be S1, S2, S3, or S4 and r₄ is a random vector distributed in [0, 1].

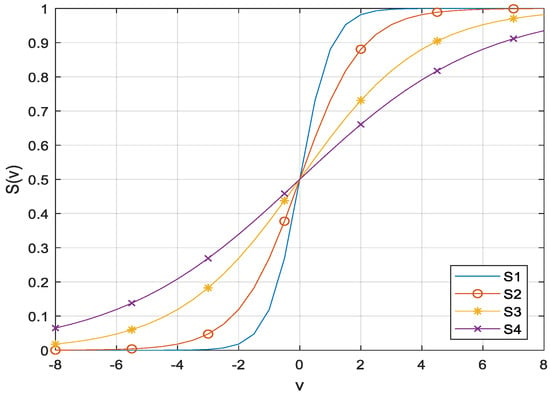
Figure 1. S-shaped transfer functions (S1–S4).

3.2. V-Shaped Family

In this sub-section, the implementation of the V-shaped transfer function is presented. The V-shaped transfer function allows the search agents to perform the search within the binary search space. Many studies employ the V-shaped transfer function to convert the metaheuristic algorithms into a binary version [23,24,25]. The four frequently used V-shaped transfer functions (V1–V4) are defined as follows:

$$V1\left(v_{l,d}\left(t+1\right)\right)=\left|\mathrm{erf}\left(\frac{\sqrt{\pi }}{2}{v}_{l,d}\left(t+1\right)\right)\right|$$

(8)

$$V2\left(v_{l,d}\left(t+1\right)\right)=\left|\tanh \left(v_{l,d}\left(t+1\right)\right)\right|$$

(9)

$$V3\left(v_{l,d}\left(t+1\right)\right)=\left|\frac{v_{l,d}\left(t+1\right)}{\sqrt{1+{\left(v_{l,d}\left(t+1\right)\right)}^2}}\right|$$

(10)

$$V4\left(v_{l,d}\left(t+1\right)\right)=\left|\frac{2}{\pi }\mathrm{arc}\tan \left(\frac{\pi }{2}{v}_{l,d}\left(t+1\right)\right)\right|$$

(11)

where v_l is the velocity of loser particle, d is the dimension, and t is the iteration number. The illustrations of the V-shaped transfer functions are shown in Figure 2. Unlike the S-shaped transfer function, the V-shaped transfer function does not force the search agents to move on the binary search space. In this approach, the position of loser particle is updated as:

$$x_{l,d}\left(t+1\right)=\{\begin{array}{ll}1 -x_{l,d}\left(t\right)& , \mathrm{if} V\left(v_{l,d}\left(t+1\right)\right) \ge r_5\\ x_{l,d}\left(t\right)& , \mathrm{otherwise}\end{array}$$

(12)

where V can be V1, V2, V3, or V4 and r₅ is a random vector distributed in [0, 1].

Figure 2. V-shaped transfer functions (V1–V4).

The pseudocode of the binary competitive swarm optimizer (BCSO) is shown in Algorithm 2. N and T_max are the number of particles and the maximum number of iterations. In the first step, a population of N particles is randomly initialized, and the velocity of each particle is initialized as zero. Then, the fitness of each particle is evaluated. The best particle is defined as the global best, gbest. For each iteration, the particles are randomly divided into two groups, and the competition is made between two coupled particles. From the competition, the winners are directly passed into the new population. On the other hand, the losers update their velocity using Equation (1). Then, the velocity is converted into a probability value by employing S-shaped or V-shaped transfer functions. Afterward, the position of the loser particle is updated using Equation (7) or Equation (12). Next, the fitness of each new loser is evaluated, and the new losers are moved into the new population for the next iteration. At the end of each iteration, the global best solution gbest is updated. The procedure is repeated iteratively until the maximum number of iterations is reached. Finally, the global best solution is achieved.

Algorithm 2. Binary competitive swarm optimizer.

Input parameter:N, Tmax and $\varphi$

(1) Initialize a population of particles, x

(2) Calculate the fitness of particles, F(x)

(3) Define the best particle as gbest

(4) for t = 1 to maximum number of iterations, Tmax

// Competition Strategy //

(5)  for i = 1 to half of population, N/2

(6)   Random select two particles, xk and xm

(7)   if F(xk) better than F(xm)

(8)    xw = xk, xl = xm

(9)   else

(10)    xw = xm, xl = xk

(11)   end if

(12)   Add xw into new population

(13)   Remove xk and xm from the population

(14)  next i

//Velocity and Position Update //

(15)  for i = 1 to half of population, N/2

(16)   for d = 1 to the dimension of search space, D

(17)    Update velocity of loser using Equation (1)

(18)    Convert velocity into probability using S-shaped or V-shaped transfer function

(19)    Update position of loser as shown in Equation (7) or Equation (12)

(20)   next d

(21)   Calculate the fitness of new loser, F(xl)

(22)   Move new loser into new population

(23)   Update gbest if there is better solution

(24)  next i

(25)  Pass new population to next iteration

(26) next t

Output: Global best solution

4. Application of the Binary Competitive Swarm Optimizer for Feature Selection

In this section, the proposed binary competitive swarm optimization approaches are applied to solve the feature selection problem in classification tasks. In wrapper feature selection, the solution is represented in binary form. Bit 1 indicates that the feature is selected, while bit 0 denotes the unselected feature [23]. For example, let solution X = {0, 1, 0, 0, 1, 0, 0, 0, 1, 1}. As can be seen, solution X consists of 10 dimensions (features). Among them, only four features (2nd, 5th, 9th, and 10th) are selected.

Feature selection is an NP-hard combinatorial problem. For a dataset with feature size D, the possible combination of feature subsets will be 2^D – 1, which is impractical for searching exhaustively. Therefore, the proposed approaches are used to evaluate the best feature subset. In this paper, the fitness function that considers both classification error rate and number of features is applied. Mathematically, the fitness function can be expressed as:

$$\downarrow Fitness=\alpha ER\left(K\right)+\left(1-\alpha \right)\frac{\left|S\right|}{\left|C\right|}$$

(13)

where ER(K) is the classification error rate computed by a classifier relative to selection decision K of the features, |C| is the total number of features in the dataset, |S| is the length of selected feature subset, and α is the parameter in [0, 1] that controls the influence of the classification error rate. According to [8,23,26], the a is set at 0.99 since classification performance is the most important measure in this framework.

5. Experimental Results and Discussions

5.1. Experiment Setup

In this sub-section, the performances of the proposed binary competitive swarm optimizer approaches are investigated. The proposed approaches are validated with fifteen benchmark datasets acquired from the UCI machine learning repository [27]. Table 1 outlines the detail of the datasets in terms of the number of instances, number of features, and number of classes. Note that the features in the LSVT Voice Rehabilitation dataset are normalized in order to prevent numerical problems.

Table 1. List of the used datasets.

No.	Dataset	Number of Instances	Number of Features	Number of Classes
1	Arrhythmia	452	279	16
2	Breast Cancer Wisconsin	699	9	2
3	Dermatology	366	34	6
4	Diabetic Retinopathy Debrecen	1151	19	2
5	Hepatitis	155	19	2
6	Ionosphere	351	34	2
7	Libras Movement	360	90	15
8	LSVT Voice Rehabilitation	126	309	2
9	SCADI	70	205	7
10	Wine	178	13	3
11	Breast Cancer Coimbra	116	9	2
12	Iris	150	4	3
13	Lung Cancer	32	56	2
14	Musk 1	476	167	2
15	Seeds	210	7	3

As for wrapper feature selection, the classification error rate in the fitness function is computed by using the k-nearest neighbor (KNN) classifier with Euclidean distance metric and k = 5. The KNN is chosen due to its promising performance and fast computation speed in previous work [10]. In this paper, we use a hold-out strategy in which each dataset is partitioned into 80% for training and 20% for testing.

5.2. Comparison Algorithms and Evaluation Metrics

To examine the efficiency and efficacy of the proposed approaches, four state-of-the-art feature selection methods, including binary particle swarm optimization (BPSO), genetic algorithm (GA), binary differential evolution (BDE) [28], and binary salp swarm algorithm (BSSA) [23], are used for the comparison of performance. To ensure a fair comparison, the population size (N) and maximum number of iterations (T_max) are fixed at 10 and 100, respectively [23]. On one hand, the dimension of the search space (D) is equal to the total number of features in each dataset. Table 2 exhibits the parameter settings for the utilized approaches. Note that there is no additional parameter setting for BSSA.

Table 2. Parameter settings of the utilized approaches.

Algorithm	Parameter	Value
BPSO	Inertia weight, w	[0.9–0.4]
	Acceleration coefficient, c1 and c2	2
	Maximum velocity, Vmax	6
GA	Crossover rate, CR	0.8
	Mutation rate, MR	0.01
BDE	Crossover rate, CR	0.9
BCSO	Social factor, $\varphi$	0.2
	Maximum velocity, Vmax	6

In the experiment, six evaluation metrics, including the best fitness, worst fitness, mean fitness, standard deviation of fitness (STD), feature size (number of selected features), and accuracy, are recorded. The details of the evaluation metrics can be found in [9,29,30]. To achieve statistically meaningful results, each approach is repeated for 30 independent runs. Thereafter, the average statistical measurements obtained throughout 30 independent runs are displayed as the experimental results. All the evaluations are conducted with MATLAB 2017 software (MathWorks, Natick, MA, USA) by using a computer with 2.90 GHz Intel Core i5-9400 CPU and 16 GB RAM.

5.3. Assessments of the BCSO in Feature Selection

In the first part of the experiment, the BCSO with the best transfer function is determined. There are eight transfer functions (from both S-shaped and V-shaped families) utilized in this work. Table 3 displays the experimental results of the best fitness, worst fitness, mean fitness, STD of fitness, and feature size of BCSOs on 15 datasets. Note that the best results among eight BCSOs are highlighted with bold text. In this table, the smaller the best, worst, mean, and STD of fitness values are, the better the performances are. As for the feature size, a lower value indicates that fewer features are selected by the algorithm. In other words, a smaller number of the feature size means more irrelevant and redundant features have been eliminated. From Table 3, it is observed that BCSO-V2 offered the smallest best fitness value on five datasets (6, 7, 9, 13, and 14), which overwhelmed other transfer functions in feature selection tasks. On the other hand, BCSO-S4 perceived the optimal STD value in most cases, in which a high consistency result can be ensured. In terms of feature size, BCSO-V3 contributed the lowest number of selected features for most of the datasets.

Table 3. The experimental results of BCSO with eight different transfer functions.

Dataset	Metrics	Binary Version of Competitive Swarm Optimizer (BCSO)
		S1	S2	S3	S4	V1	V2	V3	V4
1	Best fitness	0.3927	0.3947	0.4008	0.4015	0.3656	0.3645	0.3641	0.3656
	Worst fitness	0.4030	0.4041	0.4052	0.4045	0.4035	0.4031	0.4034	0.4023
	Mean fitness	0.3945	0.3974	0.4013	0.4020	0.3717	0.3709	0.3703	0.3726
	STD	0.0027	0.0031	0.0009	0.0006	0.0096	0.0095	0.0096	0.0094
	Feature size	133.00	138.07	134.57	134.17	134.03	132.70	132.17	133.57
2	Best fitness	0.0286	0.0301	0.0316	0.0316	0.0215	0.0221	0.0219	0.0201
	Worst fitness	0.0314	0.0308	0.0319	0.0320	0.0302	0.0304	0.0304	0.0306
	Mean fitness	0.0291	0.0301	0.0316	0.0316	0.0223	0.0231	0.0228	0.0213
	STD	0.0007	0.0001	0.0001	0.0001	0.0019	0.0020	0.0020	0.0026
	Feature size	3.50	3.33	4.43	4.47	3.47	3.57	3.57	3.63
3	Best fitness	0.0064	0.0067	0.0069	0.0069	0.0173	0.0182	0.0201	0.0214
	Worst fitness	0.0295	0.0261	0.0224	0.0197	0.0437	0.0437	0.0437	0.0437
	Mean fitness	0.0080	0.0074	0.0073	0.0072	0.0209	0.0217	0.0240	0.0259
	STD	0.0046	0.0030	0.0022	0.0018	0.0058	0.0057	0.0057	0.0067
	Feature size	21.63	22.83	23.47	23.53	15.90	15.83	16.17	15.73
4	Best fitness	0.2976	0.3033	0.3056	0.3056	0.2874	0.2885	0.2828	0.2863
	Worst fitness	0.3047	0.3057	0.3056	0.3056	0.3094	0.3092	0.3101	0.3101
	Mean fitness	0.2979	0.3034	0.3056	0.3056	0.2897	0.2904	0.2858	0.2891
	STD	0.0013	0.0006	0.0000	0.0000	0.0046	0.0038	0.0064	0.0055
	Feature size	8.70	10.80	11.23	11.23	7.87	7.63	7.33	7.20
5	Best fitness	0.1300	0.1443	0.1464	0.1464	0.1222	0.1263	0.1276	0.1245
	Worst fitness	0.1355	0.1465	0.1465	0.1465	0.1433	0.1434	0.1434	0.1434
	Mean fitness	0.1306	0.1444	0.1464	0.1464	0.1256	0.1289	0.1294	0.1274
	STD	0.0015	0.0004	0.0000	0.0000	0.0063	0.0047	0.0041	0.0049
	Feature size	6.37	7.17	7.10	7.13	5.73	5.37	5.77	5.93
6	Best fitness	0.1207	0.1393	0.1423	0.1432	0.0886	0.0868	0.0894	0.0890
	Worst fitness	0.1423	0.1429	0.1437	0.1437	0.1423	0.1423	0.1419	0.1428
	Mean fitness	0.1252	0.1400	0.1425	0.1435	0.1005	0.0980	0.1016	0.1035
	STD	0.0056	0.0010	0.0005	0.0003	0.0139	0.0152	0.0152	0.0146
	Feature size	11.30	13.47	14.03	14.00	11.03	11.33	10.77	11.03
7	Best fitness	0.2321	0.2356	0.2428	0.2410	0.2004	0.1991	0.2060	0.2107
	Worst fitness	0.2643	0.2666	0.2702	0.2698	0.2696	0.2683	0.2683	0.2683
	Mean fitness	0.2386	0.2401	0.2471	0.2463	0.2190	0.2181	0.2219	0.2266
	STD	0.0083	0.0069	0.0071	0.0080	0.0192	0.0194	0.0158	0.0153
	Feature size	46.67	49.63	48.47	48.93	38.47	38.57	38.63	39.67
8	Best fitness	0.0935	0.1146	0.1449	0.1595	0.1049	0.1114	0.1022	0.1062
	Worst fitness	0.1648	0.1701	0.1622	0.1701	0.1871	0.1857	0.1857	0.1844
	Mean fitness	0.1033	0.1193	0.1483	0.1596	0.1261	0.1272	0.1215	0.1273
	STD	0.0162	0.0107	0.0045	0.0012	0.0205	0.0193	0.0237	0.0218
	Feature size	156.60	155.57	155.80	156.37	140.60	140.27	141.00	142.63
9	Best fitness	0.2169	0.2217	0.2287	0.2288	0.2086	0.2040	0.2063	0.2063
	Worst fitness	0.2358	0.2358	0.2358	0.2288	0.2403	0.2404	0.2427	0.2427
	Mean fitness	0.2181	0.2234	0.2295	0.2288	0.2126	0.2097	0.2132	0.2138
	STD	0.0043	0.0045	0.0022	0.0000	0.0073	0.0094	0.0091	0.0088
	Feature size	97.57	98.77	98.50	99.07	73.17	74.17	74.33	73.90
10	Best fitness	0.0741	0.0799	0.0878	0.0878	0.0524	0.0514	0.0497	0.0472
	Worst fitness	0.0863	0.0845	0.0880	0.0880	0.0848	0.0848	0.0904	0.0906
	Mean fitness	0.0742	0.0799	0.0878	0.0878	0.0550	0.0549	0.0533	0.0502
	STD	0.0014	0.0005	0.0000	0.0000	0.0068	0.0069	0.0079	0.0079
	Feature size	5.73	4.90	4.47	4.53	4.90	4.87	5.07	5.30
11	Best fitness	0.1352	0.1352	0.1357	0.1358	0.1467	0.1455	0.1495	0.1456
	Worst fitness	0.1537	0.1425	0.1385	0.1358	0.2101	0.2101	0.2101	0.2100
	Mean fitness	0.1355	0.1353	0.1357	0.1358	0.1499	0.1501	0.1529	0.1491
	STD	0.0021	0.0009	0.0003	0.0000	0.0120	0.0135	0.0114	0.0118
	Feature size	5.47	5.47	5.90	6.00	4.17	4.37	4.10	4.47
12	Best fitness	0.0025	0.0025	0.0025	0.0025	0.0037	0.0037	0.0039	0.0038
	Worst fitness	0.0091	0.0066	0.0061	0.0061	0.0099	0.0099	0.0099	0.0099
	Mean fitness	0.0026	0.0025	0.0025	0.0025	0.0039	0.0039	0.0040	0.0040
	STD	0.0007	0.0004	0.0004	0.0004	0.0009	0.0009	0.0009	0.0009
	Feature size	1.00	1.00	1.00	1.00	1.03	1.03	1.10	1.07
13	Best fitness	0.0321	0.2409	0.2077	0.2685	0.0031	0.0031	0.0032	0.0088
	Worst fitness	0.2577	0.2632	0.2631	0.2741	0.2740	0.2740	0.2684	0.2631
	Mean fitness	0.0868	0.2471	0.2136	0.2689	0.0282	0.0346	0.0326	0.0422
	STD	0.0781	0.0082	0.0158	0.0014	0.0638	0.0655	0.0644	0.0648
	Feature size	25.57	24.77	23.67	25.10	17.53	17.60	17.93	18.60
14	Best fitness	0.0742	0.0824	0.0924	0.0969	0.0667	0.0622	0.0645	0.0674
	Worst fitness	0.1043	0.1078	0.1055	0.1048	0.1071	0.1074	0.1077	0.1067
	Mean fitness	0.0812	0.0882	0.0942	0.0983	0.0767	0.0737	0.0747	0.0779
	STD	0.0078	0.0063	0.0035	0.0021	0.0106	0.0124	0.0107	0.0103
	Feature size	84.87	82.6	81.03	81.70	82.07	82.10	79.40	81.97
15	Best fitness	0.0517	0.0517	0.0517	0.0517	0.0504	0.0504	0.0503	0.0504
	Worst fitness	0.0556	0.0517	0.0517	0.0517	0.0652	0.0652	0.0652	0.0660
	Mean fitness	0.0517	0.0517	0.0517	0.0517	0.0509	0.0510	0.0509	0.0510
	STD	0.0004	0.0000	0.0000	0.0000	0.0023	0.0024	0.0025	0.0026
	Feature size	3.17	3.20	3.20	3.20	2.30	2.30	2.20	2.27

Another important measurement is the accuracy obtained from the features selected by each approach. Figure 3 demonstrates the boxplot of BCSO with eight different transfer functions across 15 datasets. As can be seen, BCSOs with V-shaped transfer functions can usually achieve better results as compared to S-shaped transfer functions. This is because the V-shaped transfer function does not force the search agent to take the bits 1 or 0, thus resulting in excellent performance. Across 15 datasets, it is seen that the optimal classification performance is achieved by BCSO-V1 and BCSO-V2. Based on the results obtained from Table 3 and Figure 3, it can conclude that the BCSO with transfer function V2 yielded superior performance in evaluating the relevant features, which overtakes other transfer functions in the current work.

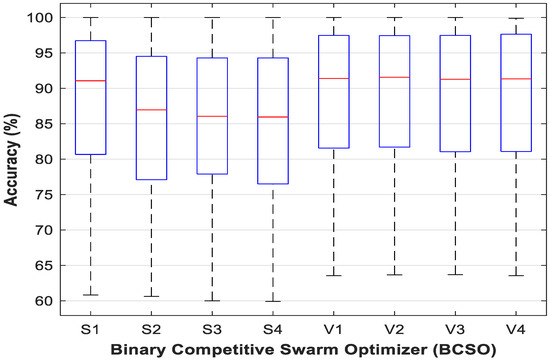
Figure 3. Boxplot of the BCSO with eight different transfer functions across 15 datasets.

5.4. Comparison with Other Algorithms

Table 4 presents the comparison of the results of the BCSO with BDE, BPSO, BSSA, and GA. In Table 4, the best result on each metric is bolded. Through observation from the result in Table 4, it is seen that BCSO showed competitive performance in feature selection tasks. In comparison with BDE, BPSO, BSSA, and GA, the BCSO achieved the optimal best fitness value on 11 datasets. This result implies that the performance of the BCSO was superior, which overtakes other algorithms in identifying the significant features.

Table 4. Comparison of the results of BCSO with BDE, BPSO, BSSA, and GA.

Dataset	Metrics	Feature Selection Method
		BDE	BPSO	BSSA	GA	BCSO
1	Best fitness	0.3965	0.3604	0.3854	0.3806	0.3645
	Worst fitness	0.4034	0.3994	0.4071	0.4013	0.4031
	Mean fitness	0.3966	0.3631	0.3862	0.3811	0.3709
	STD	0.0009	0.0073	0.0032	0.0027	0.0095
	Feature size	156.97	131.73	102.43	132.67	132.70
2	Best fitness	0.0279	0.0259	0.0260	0.0228	0.0221
	Worst fitness	0.0297	0.0262	0.0320	0.0254	0.0304
	Mean fitness	0.0279	0.0259	0.0264	0.0228	0.0231
	STD	0.0002	0.0000	0.0011	0.0003	0.0020
	Feature size	4.53	4.43	3.87	3.77	3.57
3	Best fitness	0.0291	0.028	0.0358	0.0203	0.0182
	Worst fitness	0.0365	0.042	0.0445	0.0346	0.0437
	Mean fitness	0.0292	0.0289	0.0366	0.0206	0.0217
	STD	0.0009	0.0021	0.0019	0.0017	0.0057
	Feature size	19.10	15.13	14.30	15.33	15.83
4	Best fitness	0.306	0.2986	0.2945	0.3043	0.2885
	Worst fitness	0.3103	0.3151	0.3151	0.3118	0.3092
	Mean fitness	0.3061	0.3004	0.2967	0.3044	0.2904
	STD	0.0006	0.0039	0.0049	0.0009	0.0038
	Feature size	10.80	8.13	6.77	8.97	7.63
5	Best fitness	0.1425	0.1296	0.1216	0.1343	0.1263
	Worst fitness	0.1446	0.1466	0.1466	0.1411	0.1434
	Mean fitness	0.1426	0.1304	0.1223	0.1344	0.1289
	STD	0.0003	0.0030	0.0032	0.0008	0.0047
	Feature size	7.90	5.47	4.47	6.40	5.37
6	Best fitness	0.1359	0.1016	0.1095	0.1184	0.0868
	Worst fitness	0.1402	0.1398	0.1438	0.1341	0.1423
	Mean fitness	0.1360	0.1045	0.1103	0.1186	0.0980
	STD	0.0006	0.0078	0.0044	0.0020	0.0152
	Feature size	16.47	15.23	8.60	12.90	11.33
7	Best fitness	0.2611	0.2269	0.2433	0.2430	0.1991
	Worst fitness	0.2669	0.2708	0.2733	0.2628	0.2683
	Mean fitness	0.2612	0.2313	0.2450	0.2433	0.2181
	STD	0.0008	0.0091	0.0049	0.0025	0.0194
	Feature size	48.03	45.93	28.23	41.60	38.57
8	Best fitness	0.1653	0.1065	0.1418	0.1379	0.1114
	Worst fitness	0.1809	0.1806	0.1923	0.1830	0.1857
	Mean fitness	0.1656	0.1187	0.1473	0.1393	0.1272
	STD	0.0021	0.0184	0.0120	0.0069	0.0193
	Feature size	171.73	151.27	99.73	141.50	140.27
9	Best fitness	0.2335	0.2256	0.2170	0.2142	0.2040
	Worst fitness	0.2382	0.2451	0.2451	0.2332	0.2404
	Mean fitness	0.2336	0.2286	0.2175	0.2146	0.2097
	STD	0.0007	0.0055	0.0032	0.0024	0.0094
	Feature size	99.07	81.7	51.23	91.47	74.17
10	Best fitness	0.0752	0.0531	0.0613	0.0511	0.0514
	Worst fitness	0.0835	0.0980	0.0980	0.0678	0.0848
	Mean fitness	0.0754	0.0574	0.0628	0.0514	0.0549
	STD	0.0012	0.0103	0.0054	0.0022	0.0069
	Feature size	6.03	4.63	4.67	5.60	4.87
11	Best fitness	0.1739	0.1812	0.1710	0.1556	0.1455
	Worst fitness	0.1993	0.2259	0.2259	0.1831	0.2101
	Mean fitness	0.1744	0.1840	0.1724	0.1561	0.1501
	STD	0.0035	0.0089	0.0068	0.0035	0.0135
	Feature size	5.40	4.27	4.10	4.47	4.37
12	Best fitness	0.0114	0.0059	0.0073	0.0051	0.0037
	Worst fitness	0.0115	0.0126	0.0126	0.0064	0.0099
	Mean fitness	0.0114	0.0069	0.0074	0.0051	0.0039
	STD	0.0000	0.0021	0.0006	0.0001	0.0009
	Feature size	1.47	1.03	1.17	1.17	1.03
13	Best fitness	0.1647	0.0918	0.1241	0.1419	0.0031
	Worst fitness	0.2196	0.0975	0.2742	0.2026	0.2740
	Mean fitness	0.1661	0.0951	0.1326	0.1429	0.0346
	STD	0.0079	0.0027	0.0252	0.0071	0.0655
	Feature size	29.23	21.47	17.53	24.43	17.60
14	Best fitness	0.0878	0.0692	0.0899	0.0816	0.0622
	Worst fitness	0.1015	0.1005	0.1099	0.1012	0.1074
	Mean fitness	0.0881	0.0742	0.0911	0.0822	0.0737
	STD	0.0018	0.0074	0.0033	0.0029	0.0124
	Feature size	108.63	82.43	63.23	80.80	82.10
15	Best fitness	0.0599	0.0624	0.0554	0.0520	0.0504
	Worst fitness	0.0611	0.0667	0.0667	0.0602	0.0652
	Mean fitness	0.0600	0.0625	0.0556	0.0521	0.0510
	STD	0.0002	0.0006	0.0013	0.0010	0.0024
	Feature size	2.90	3.00	2.47	2.83	2.30

On the other hand, one can see that BSSA perceived the smallest feature size (number of selected features) in this work. This finding indicates that BSSA can usually select a subset of minimal features while maintaining high performance. In terms of robustness, the most consistent results are provided by BDE due to the smallest standard deviation value.

Figure 4 demonstrates the accuracy of BDE, BPSO, GA, BSSA, and BCSO on 15 datasets. From Figure 4, the best classification performance was perceived by the BCSO. As compared to other methods, the BCSO showed superior accuracy on 11 datasets. It is obvious that the BCSO is a useful feature selection tool, which provides better classification performance in this work. As for datasets 1 and 8, the best accuracy was achieved by the BPSO. On one hand, BSSA and GA obtained the best accuracy on datasets 5 and 10, respectively. Inspecting the result, the worst performance was found to be BDE. The result obtained implies that BDE did not work very well in this study.

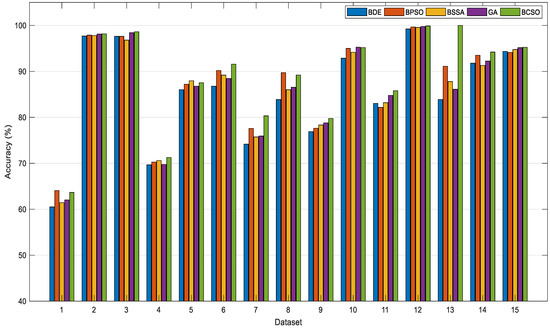
Figure 4. Accuracy of BDE, BPSO, BSSA, GA, and BCSO on 15 datasets.

Figure 5 and Figure 6 illustrate the convergence curves of BDE, BPSO, BSSA, GA, and BCSO for 15 datasets. Note that the fitness is the average fitness value obtained from 30 runs. In these figures, it is observed that BCSO provided competitive performance against BPSO, GA, BSSA, and BDE. Among the rivals, the worst performance was achieved by BDE. Unfortunately, BDE did not find the global optimum efficiently, thus resulting in ineffective resolution. On one hand, the BCSO keeps tracking the global optimum, which leads to good exploitation and exploration capability. As a result, the BCSO offers very good diversity, perceived as the best performance on most of the datasets.

Figure 5. Convergence curves of BDE, BPSO, BSSA, GA, and BCSO on datasets 1–8.

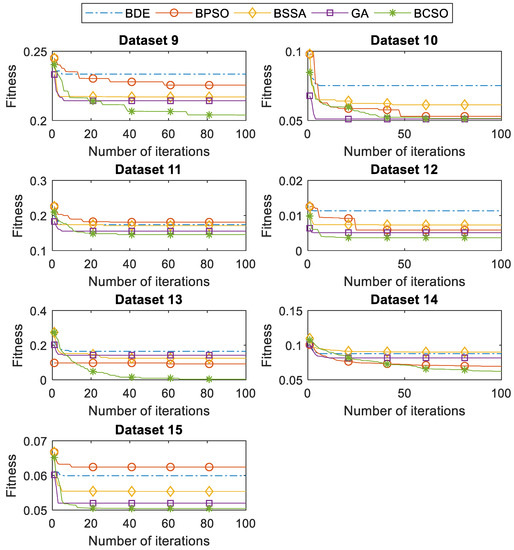
Figure 6. Convergence curves of BDE, BPSO, BSSA, GA, and BCSO on datasets 9–15.

Furthermore, the Wilcoxon rank sum test with 95% confidence level is applied to examine whether the classification performance achieved by the BCSO is significantly better than other methods. The BCSO is selected as the reference algorithm since it offers better classification results in this work. The results of the Wilcoxon test with p-values is presented in Table 5. For the ease of understanding, the symbols “w/t/l” indicate the BCSO is superior to (win), equal to (tie), and inferior to (lose) other algorithms. As can be seen, the classification performance of the BCSO was significantly better than BPSO, BSSA, GA, and BDE (p-value < 0.05) in most cases. For example, the performance of the BCSO was significantly better than the BPSO on nine datasets. Additionally, the analysis of variance (ANOVA) with post-hoc test is applied to investigate whether there is a significant difference between the BCSO and other algorithms across 15 datasets. Successively, the performance of our BCSO was significantly better (p-value < 0.05) when compared to BDE, BPSO, BSSA, and GA. The results obtained evidently show the superiority of the BCSO with respect to the feature selection problem.

Table 5. p-values of the Wilcoxon rank sum test of the BCSO accuracy results versus other algorithms.

Dataset	P-Value
	BDE	BPSO	BSSA	GA
1	0.000000	0.380188	6.00 × 10−6	0.000434
2	3.70 × 10−5	0.000532	0.001921	0.630455
3	0.001156	0.017644	2.60 × 10−5	0.107494
4	0.000000	0.016211	0.012478	1.38 × 10−4
5	0.016281	0.587798	0.546144	0.214683
6	0.000000	0.001541	4.00 × 10−6	0.000000
7	0.000000	0.000000	0.000000	0.000000
8	0.000000	0.356995	5.70 × 10−5	0.001066
9	0.000591	0.003016	0.013394	0.090513
10	0.033928	0.919999	0.151188	0.797191
11	0.004939	0.000866	3.20 × 10−5	0.319416
12	0.024637	0.312817	0.169401	0.570163
13	0.000000	4.00 × 10−6	2.00 × 10−6	0.000000
14	0.000000	0.170318	0.000000	3.00 × 10−6
15	0.005555	5.80 × 10−5	0.021498	0.333711
w/t/l	15/0/0	9/6/0	12/3/0	7/8/0

Table 6 outlines the results of the computational cost of BDE, BPSO, BSSA, GA, and BCSO on 15 datasets. Judging from Table 6, the lowest computation time is perceived by the BCSO. This is expected since the proposed approaches only update the velocity and position of losers (half of the population) in the process of evaluations. In this way, the proposed approaches compute faster than other conventional methods in feature selection. On the contrary, the slowest processing speed is found to be the GA, followed by the BPSO. Based on the results obtained, the BCSO not only achieves the best classification performance, but is also computationally less expensive. Evidently, the BCSO is a powerful feature selection tool and it can be applied to other engineering applications.

Table 6. Computational cost of BDE, BPSO, GA, BSSA and BCSO on 15 datasets.

Dataset	Average Computational Time (s)
	BDE	BPSO	BSSA	GA	BCSO
1	1.9970	2.2986	1.8710	3.4647	1.4204
2	2.6003	2.5338	2.3849	4.3947	1.2760
3	1.5281	1.4024	1.3335	2.4316	0.7592
4	7.3024	7.0196	6.6112	12.305	3.6870
5	0.8450	0.7938	0.7571	0.9028	0.4451
6	1.3588	1.3879	1.2595	2.2471	0.7262
7	1.4888	1.5563	1.3818	2.4323	0.8689
8	0.8920	1.1479	0.9308	1.4286	0.9336
9	0.6814	0.8616	0.7186	1.2021	0.6763
10	0.8608	0.8524	0.8020	1.2649	0.4529
11	0.6864	0.6677	0.6298	1.2466	0.3558
12	0.7488	0.7489	0.7048	1.0054	0.3944
13	0.5667	0.6357	0.5720	0.8743	0.3884
14	2.0475	2.0989	1.8085	3.6051	1.2123
15	0.9156	0.8726	0.8549	1.5100	0.4702

6. Conclusions

In this paper, binary variants of the CSO are proposed and applied for feature selection tasks. The continuous CSO is converted into the binary version by using transfer functions. Eight different transfer functions from S-shaped and V-shaped families are implemented in the BCSO. The S-shaped transfer functions force the search agents to move on the binary search space. On one hand, the V-shaped transfer functions allow the search agents to perform the search around the binary search space. The proposed BCSO is validated using 15 benchmark datasets. Firstly, the BCSO with the optimal transfer function is investigated. In comparison with other transfer functions, we found that the BCSO with the V2 transfer function was the most suitable, which perceived the optimal performance in current work. Secondly, the performance of the BCSO is verified with four other conventional feature selection methods. Based on the results obtained, the BCSO outperformed other methods (BDE, BSSA, BPSO, and GA) when finding the significant features, in which a high searching capability can be ensured. In addition, BCSO can often select a smaller number of significant features that contributed a high accuracy. Moreover, the processing speed of the BCSO is extremely fast, which is more appropriate in real-world applications. All in all, it can be inferred that the BCSO is a valuable feature selection tool. In the future, the BCSO can be applied to other binary optimization tasks, such as unit commitment issues, optimized neural networks, and the knapsack problem.