A Review on Computational Modeling Tools for MOF-Based Mixed Matrix Membranes
Abstract
1. Introduction
2. Trade-Off between Permeability and Selectivity
3. Fundamental Approaches Employed to Describe Permeability and Perm-Selectivity Trade-Off
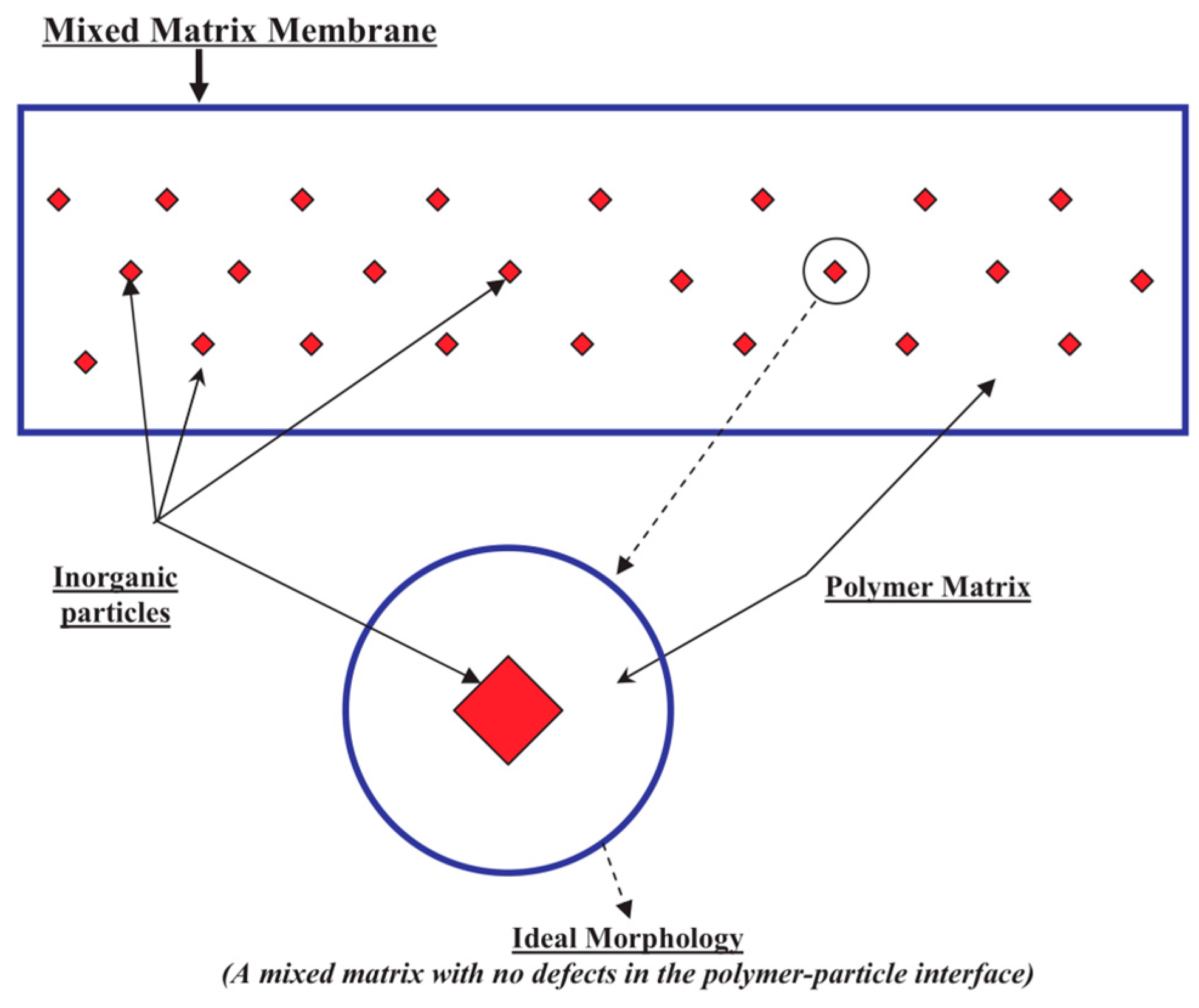
4. Mixed Matrix Membranes
4.1. Types of Fillers Used
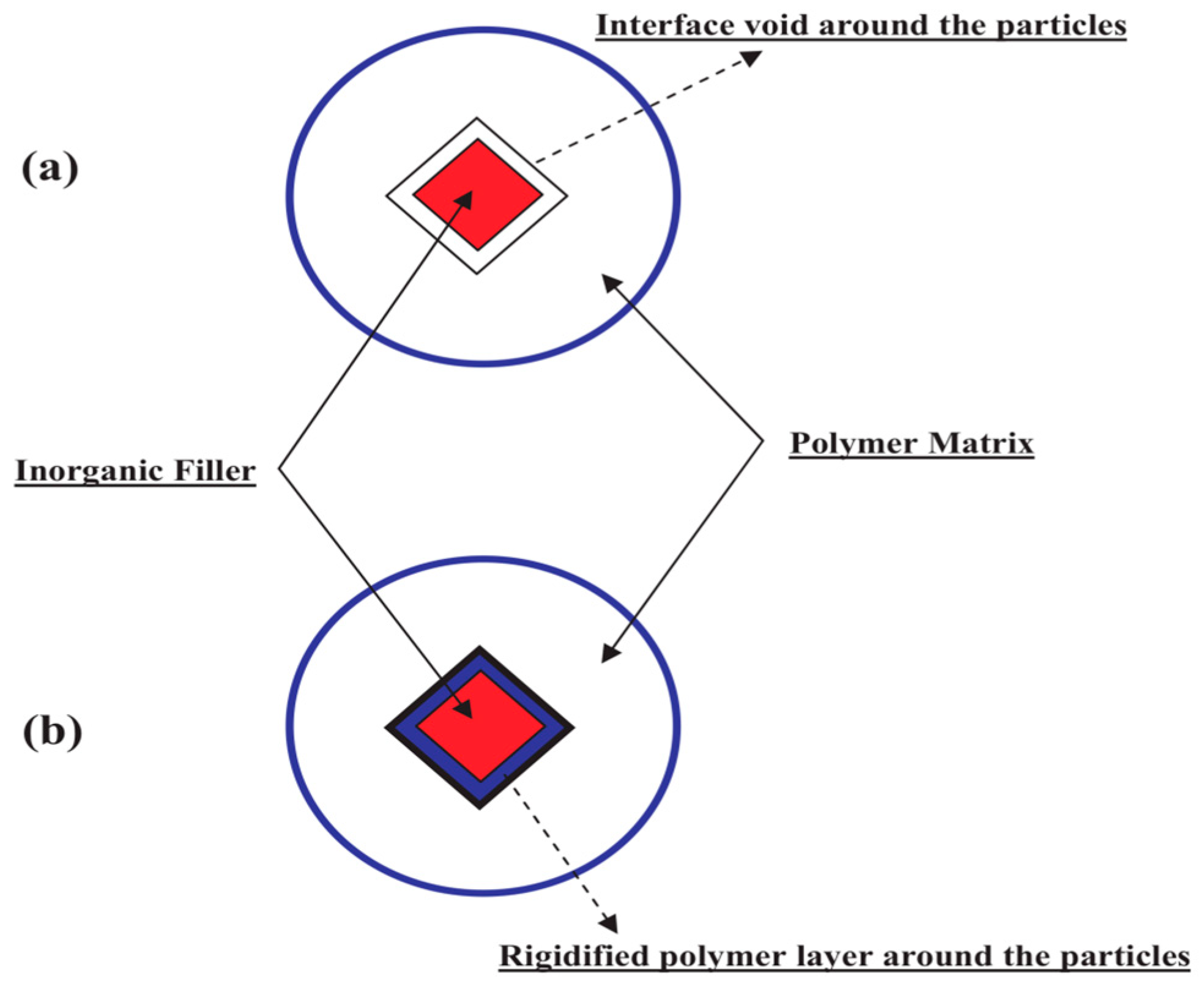
4.2. Fundamental Approaches for Predicting Permeation through MMMs
5. Recent Advances in Metal Organic Framework (MOF)-Based MMMs for Gas Separations
6. Computational Tools in High-Throughput Screening of MOF for MMM Applications
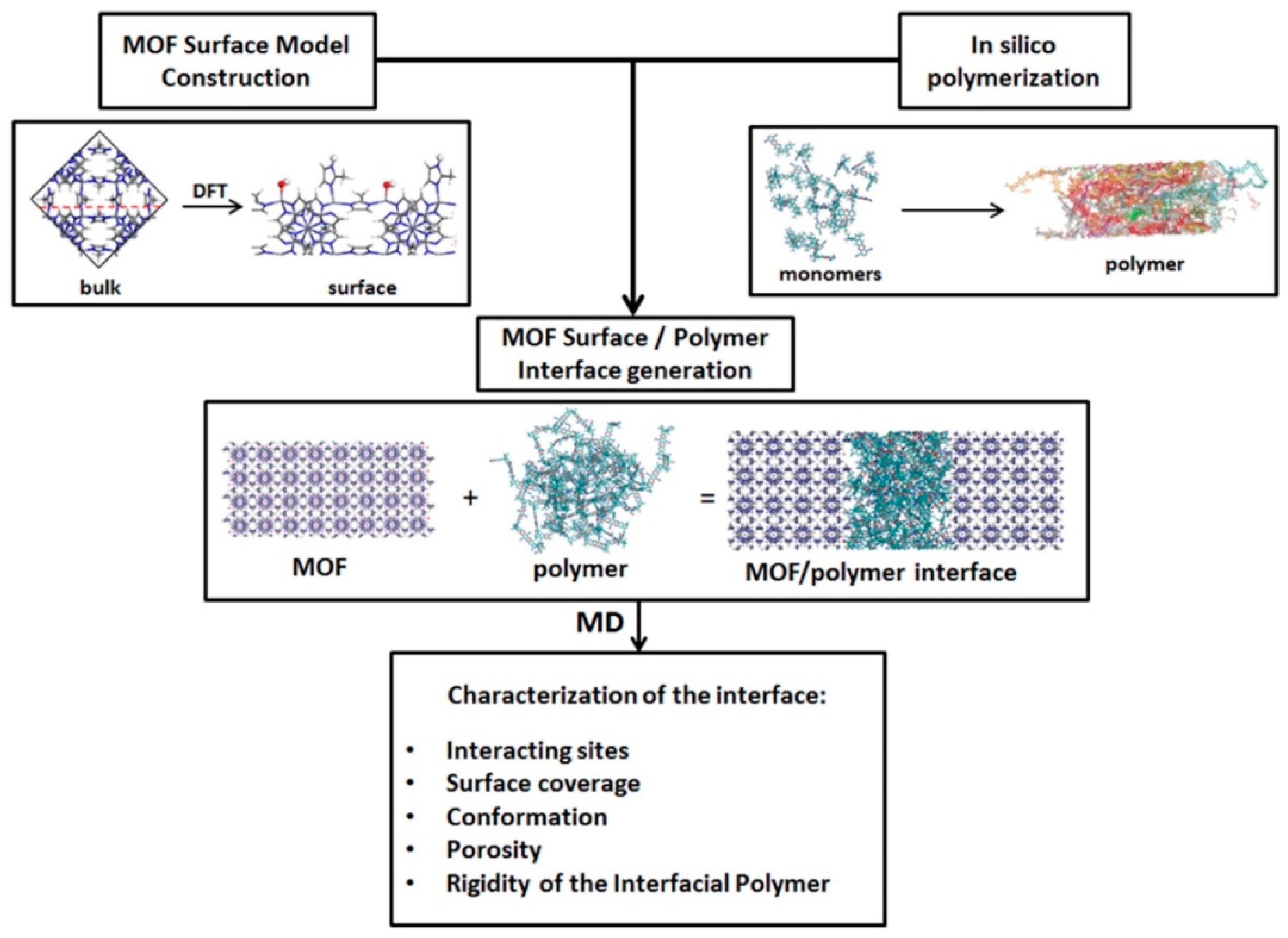
7. Understanding the MOF/Polymer Compatibility: The Role of Computational Tools
8. The Role of Computational Studies in Analyzing the Barriers That Must Be Overcome to Advance MOF-Based Membranes Beyond Fundamental Characterizations
9. Concluding Remarks and Future Directions
Funding
Conflicts of Interest
References
- Robeson, L.J. Correlation of Separation Factor Versus Permeability for Polymeric Membranes. J. Membr. Sci. 1991, 62, 165–185. [Google Scholar] [CrossRef]
- Freeman, B.D. Basis of permeability/selectivity tradeoff relations in polymeric gas separation membranes. Macromolecules 1999, 32, 375–380. [Google Scholar] [CrossRef]
- Burns, R.L.; Koros, W.J. Defining the challenges for C3H6/C3H8 separation using polymeric membranes. J. Membr. Sci. 2003, 211, 299–309. [Google Scholar] [CrossRef]
- Rungta, M.; Zhang, C.; Koros, W.J.; Xu, L.R. Membrane-based ethylene/ethane separation: The upper bound and beyond. AIChE J. 2013, 59, 3475–3489. [Google Scholar] [CrossRef]
- Rowe, B.W.; Robeson, L.M.; Freeman, B.D.; Paul, D.R. Influence of temperature on the upper bound: Theoretical considerations and comparison with experimental results. J. Membr. Sci. 2010, 360, 58–69. [Google Scholar] [CrossRef]
- Alentiev, A.Y.; Yampolskii, Y.P. Correlation of gas permeability and diffusivity with selectivity: Orientations of the clouds of the data points and the effects of temperature. Ind. Eng. Chem. Res. 2013, 52, 8864–8874. [Google Scholar] [CrossRef]
- Alentiev, A.Y.; Yampolskii, Y.P. Free volume model and tradeoff relations of gas permeability and selectivity in glassy polymers. J. Membr. Sci. 2000, 165, 201–216. [Google Scholar] [CrossRef]
- Alentiev, A.Y.; Yampolskii, Y.P. Meares equation and the role of cohesion energy density in diffusion in polymers. J. Membr. Sci. 2002, 206, 291–306. [Google Scholar] [CrossRef]
- Lou, Y.C.; Hao, P.J.; Lipscomb, G. NELF predictions of a solubility–solubility selectivity upper bound. J. Membr. Sci. 2014, 455, 247–253. [Google Scholar] [CrossRef]
- Lin, H.; Yavari, M. Upper bound of polymeric membranes for mixed-gas CO2/CH4 separations. J. Membr. Sci. 2015, 475, 101–109. [Google Scholar] [CrossRef]
- Budd, P.M.; McKeown, N.B. Highly permeable polymers for gas separation membranes. Polym. Chem. 2010, 1, 63–68. [Google Scholar] [CrossRef]
- Wiegand, J.R.; Smith, Z.P.; Liu, Q.; Patterson, C.T.; Freeman, B.D.; Guo, R.L. Synthesis and characterization of triptycene-based polyimides with tunable high fractional free volume for gas separation membranes. J. Mater. Chem. A 2014, 2, 13309–13320. [Google Scholar] [CrossRef]
- Singh, A.; Koros, W.J. Significance of entropic selectivity for advanced gas sep-aration membranes. Ind. Eng. Chem. Res. 1996, 35, 1231–1234. [Google Scholar] [CrossRef]
- Goh, P.S.; Ismail, A.F.; Sanip, S.M.; Ng, B.C.; Aziz, M. Recent advances of inorganic fillers in mixed matrix membrane for gas separation. Sep. Purif. Technol. 2011, 81, 243–264. [Google Scholar] [CrossRef]
- Park, H.B.; Kamcev, J.; Robeson, L.M.; Elimelech, M.; Freeman, B.D. Maximizing the right stuff: The trade-off between membrane permeability and selectivity. Science 2017, 356, eaab0530. [Google Scholar] [CrossRef] [PubMed]
- Sen, D.; Kalipcilar, H.; Yilmaz, L. Development of polycarbonate based zeolite 4A filled mixed matrix gas separation membranes. J. Membr. Sci. 2007, 303, 194–203. [Google Scholar] [CrossRef]
- Sen, D.; Kalipcilar, H.; Yilmaz, L. Development of zeolite filled polycarbonate mixed matrix gas separation membranes. Desalination 2006, 200, 222–224. [Google Scholar] [CrossRef]
- Tantekin-Ersolmaz, S.B.; Atalay-Oral, C.; Tather, M.; Erdem-Senatalar, A.; Schoeman, B.; Sterte, J. Effect of zeolite particle size on the performance of polymer-zeolite mixed matrix membranes. J. Membr. Sci. 2000, 175, 285–288. [Google Scholar] [CrossRef]
- Pechar, T.W.; Kim, S.; Vaughan, B.; Marand, E.; Tsapatsis, M.; Jeong, H.K.; Cornelius, C.J. Fabrication and characterization of polyimide-zeolite L mixed matrix membranes for gas separations. J. Membr. Sci. 2006, 277, 195–202. [Google Scholar] [CrossRef]
- Husain, S.; Koros, W.J. Mixed matrix hollow fiber membranes made with modified HSSZ-13 zeolite in polyetherimide polymer matrix for gas separation. J. Membr. Sci. 2007, 288, 195–207. [Google Scholar] [CrossRef]
- Gorgojo, P.; Zornoza, B.; Uriel, S.; Telelz, C.; Coronas, J. Mixed Matrix Membranes from Nanostructured Materials for Gas Separation. Stud. Surf. Sci. Catal. 2008, 174, 653–656. [Google Scholar]
- Pechar, T.W.; Kim, S.; Vaughan, B.; Marand, E.; Baranauskas, V.; Riffle, J.; Jeong, H.K.; Tsapatsis, M. Preparation and characterization of a poly(imide siloxane) and zeolite L mixed matrix membrane. J. Membr. Sci. 2006, 277, 210–218. [Google Scholar] [CrossRef]
- Zeng, C.; Zhang, L.; Cheng, X.; Wang, H.; Xu, N. Preparation and gas permeation of nano-sized zeolite NaA-filled carbon membranes. Sep. Purif. Technol. 2008, 63, 628–633. [Google Scholar] [CrossRef]
- Li, Y.; Chung, T.-S.; Cao, C.; Kulprathipanja, S. The effects of polymer chain rigidification, zeolite pore size and pore blockage on polyethersulfone (PES)-zeolite A mixed matrix membranes. J. Membr. Sci. 2005, 260, 45–55. [Google Scholar] [CrossRef]
- Clarizia, G.; Algieri, C.; Regina, A.; Drioli, E. Zeolite-based composite PEEK-WC membranes: Gas transport and surface properties. Microporous Mesoporous Mater. 2008, 115, 67–74. [Google Scholar] [CrossRef]
- Vu, D.Q.; Koros, W.J.; Miller, S.J. Mixed matrix membranes using carbon molecular sieves—I. Preparation and experimental results. J. Membr. Sci. 2003, 211, 311–334. [Google Scholar] [CrossRef]
- Moore, T.T.; Mahajan, R.; Vu, D.Q.; Koros, W.J. Hybrid membrane materials comprising organic polymers with rigid dispersed phases. AIChE J. 2004, 50, 311–321. [Google Scholar] [CrossRef]
- Vu, D.Q.; Koros, W.J.; Miller, S.J. Effect of condensable impurity in CO2/CH4 gas feeds on performance of mixed matrix membranes using carbon molecular sieves. J. Membr. Sci. 2003, 221, 233–239. [Google Scholar] [CrossRef]
- Das, M.; Perry, J.D.; Koros, W.J. Gas-Transport-Property Performance of Hybrid Carbon Molecular Sieve-Polymer Materials. Ind. Eng. Chem. Res. 2010, 49, 9310–9321. [Google Scholar] [CrossRef]
- Vu, D.Q.; Koros, W.J.; Miller, S.J. Mixed matrix membranes using carbon molecular sieves—II. Modeling permeation behavior. J. Membr. Sci. 2003, 211, 335–348. [Google Scholar] [CrossRef]
- Shimekit, B.; Muktar, H.; Maitra, S. Comparison of Predictive Models for Relative Permeability of CO2 in Matrimid-Carbon Molecular Sieve Mixed Matrix Membrane. J. Appl. Sci. 2010, 10, 1204–1211. [Google Scholar] [CrossRef]
- Kusakabe, K.; Ichiki, K.; Hayashi, J.-I.; Maeda, H.; Morroka, S. Preparation and characterization of silica-polyimide composite membranes coated on porous tubes for CO2 separation. J. Membr. Sci. 1996, 115, 65–75. [Google Scholar] [CrossRef]
- Moadded, M.; Koros, W.J. Effects of colloidal silica incorporation on oxygen nitrogen separation properties of ceramic-supported 6FDA-IPDA thin films. J. Membr. Sci. 1996, 111, 283–290. [Google Scholar] [CrossRef]
- Zornoza, B.; Tellex, C.; Coronas, J. Mixed matrix membranes comprising glassy polymers and dispersed mesoporous silica spheres for gas separation. J. Membr. Sci. 2011, 368, 100–109. [Google Scholar] [CrossRef]
- Merkel, T.C.; He, Z.; Pinnau, I. Effect of nanoparticles on gas sorption and transport in poly(1-trimethylsilyl-1-propyne). Macromolecules 2003, 36, 6844–6855. [Google Scholar] [CrossRef]
- Merkel, T.C.; Freeman, B.D.; Spontak, R.J.; He, Z.; Pinnau, I.; Meakin, P.; Hill, A.J. Sorption, transport, and structural evidence for enhanced free volume in poly(4-methyl-2-pentyne)/fumed silica nanocomposite membranes. Chem. Mater. 2003, 15, 109–123. [Google Scholar] [CrossRef]
- Hosseini, S.S.; Li, Y.; Chung, T.-S.; Liu, Y. Enhanced gas separation performance of nanocomposite membranes using MgO nanoparticles. J. Membr. Sci. 2007, 302, 207–217. [Google Scholar] [CrossRef]
- Matteucci, S.; Raharjo, R.D.; Kusuma, V.A.; Swinnea, S.; Freeman, B.D. Gas Permeability, Solubility, and Diffusion Coefficients in 1,2-Polybutadiene Containing Magnesium Oxide. Macromolecules 2008, 41, 2144–2156. [Google Scholar] [CrossRef]
- Chen, H.; Sholl, D.S. Predictions of selectivity and flux for CH4/H-2 separations using single walled carbon nanotubes as membranes. J. Membr. Sci. 2006, 269, 152–160. [Google Scholar] [CrossRef]
- Skoulidas, A.I.; Sholl, D.S.; Johnson, J.K. Adsorption and diffusion of carbon dioxide and nitrogen through single-walled carbon nanotube membranes. J. Chem. Phys. 2004, 124, 054708. [Google Scholar] [CrossRef]
- Cong, H.; Zhang, J.; Radosx, M.; Shen, Y. Carbon nanotube composite membranes of brominated poly(2,6-diphenyl-1,4-phenylene oxide) for gas separation. J. Membr. Sci. 2007, 294, 178–185. [Google Scholar] [CrossRef]
- Ge, L.; Zhu, Z.; Rudolph, V. Enhanced gas permeability by fabricating functionalized multi-walled carbon nanotubes and polyethersulfone nanocomposite membrane. Sep. Purif. Technol. 2011, 78, 76–82. [Google Scholar] [CrossRef]
- Ge, L.; Zhu, Z.; Li, F.; Liu, S.; Wang, L.; Tang, X.; Rudolph, V. Investigation of Gas Permeability in Carbon Nanotube (CNT)-Polymer Matrix Membranes via Modifying CNTs with Functional Groups/Metals and Controlling Modification Location. J. Phys. Chem. C 2011, 115, 6661–6670. [Google Scholar] [CrossRef]
- Goh, P.S.; Ng, B.C.; Ismail, A.F.; Sanip, S.M.; Aziz, M.; Kassim, M.A. Effect of Dispersed Multi-Walled Carbon Nanotubes on Mixed Matrix Membrane for O2/N2 Separation. Sep. Sci. Technol. 2011, 46, 1250–1261. [Google Scholar] [CrossRef]
- Aroon, M.A.; Ismail, A.F.; Montazer-Rahmati, M.M.; Matsuura, T. Effect of chitosan as a functionalization agent on the performance and separation properties of polyimide/multi-walled carbon nanotubes mixed matrix flat sheet membranes. J. Membr. Sci. 2010, 364, 309–317. [Google Scholar] [CrossRef]
- Weng, T.-H.; Tseng, H.-H.; Wey, M.-Y. Preparation and characterization of multi-walled carbon nanotube/PBNPI nanocomposite membrane for H-2/CH4 separation. Int. J. Hydrog. Energy 2009, 34, 8707–8715. [Google Scholar] [CrossRef]
- Kim, S.; Chen, L.; Johnson, J.K.; Marand, E. Polysulfone and functionalized carbon nanotube mixed matrix membranes for gas separation: Theory and experiment. J. Membr. Sci. 2007, 294, 147–158. [Google Scholar] [CrossRef]
- Kim, S.; Pechar, T.W.; Marand, E. Poly(imide siloxane) and carbon nanotube mixed matrix membranes for gas separation. Desalination 2006, 192, 330–339. [Google Scholar] [CrossRef]
- Leszczynska, A.; Njuguna, J.; Pielichowski, K.; Banerjee, J.R. Polymer/montmorillonite nanocomposites with improved thermal properties. Part II. Thermal stability of montmorillonite nanocomposites based on different polymeric matrixes. Thermochim. Acta 2007, 454, 1–22. [Google Scholar] [CrossRef]
- Defontaine, G.; Barichard, A.; Letaief, S.; Feng, C.; Matsuura, T.; Detellier, C. Nanoporous polymer—Clay hybrid membranes for gas separation. Colloid. Interface Sci. 2010, 343, 622–627. [Google Scholar] [CrossRef]
- Wu, Y.; Jia, P.; Xu, L.L.; Chen, Z.Y.; Xiao, L.H.; Sun, J.H.; Zhang, J.; Huang, Y.; Bielawski, C.W.; Geng, J.X. Tuning the surface properties of graphene oxide by surface-initiated polymerization of epoxides: An efficient method for enhancing gas separation. ACS Appl. Mater. Interfaces 2017, 9, 4998–5005. [Google Scholar] [CrossRef] [PubMed]
- Karunakaran, M.; Shevate, R.; Kumar, M.; Peinemann, K.V. CO2-selective PEO-PBT (PolyActive)/graphene oxide composite membranes. Chem. Commun. 2015, 51, 14187–14190. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Hou, J.; Wang, Y.Q.; Ou, R.W.; Simon, G.P.; Seong, J.G.; Lee, Y.M.; Wang, H.T. Highly permeable thermally rearranged polymer composite membranes with a graphene oxide scaffold for gas separation. J. Mater. Chem. A. 2018, 6, 7668–7674. [Google Scholar] [CrossRef]
- Dong, G.; Hou, J.; Wang, J.; Zhang, Y.; Chen, V.; Liu, J. Enhanced CO2/N2 separation by porous reduced graphene oxide/Pebax mixed matrix membranes. J. Membr. Sci. 2016, 520, 860–868. [Google Scholar] [CrossRef]
- Berean, K.J.; Ou, J.Z.; Nour, M.; Field, M.R.; Alsaif, M.M.Y.A.; Wang, Y.; Ramanathan, R.; Bansal, V.; Kentish, S.; Doherty, C.M.; et al. Enhanced gas permeation through graphene nanocomposites. J. Phys. Chem. C 2015, 119, 13700–13712. [Google Scholar] [CrossRef]
- Zimmerman, C.M.; Singh, A.; Koros, W.J. Tailoring mixed matrix composite membranes for gas separations. J. Membr. Sci. 1997, 137, 145–154. [Google Scholar] [CrossRef]
- Te Hennepe, H.J.C.; Smolders, C.A.; Bargeman, D.; Mulder, M.H.V. Exclusion and Tortuosity Effects for Alcohol/Water Separation by Zeolite-Filled PDMS Membranes. Sep. Sci. Technol. 1991, 26, 585–596. [Google Scholar] [CrossRef]
- Cussler, E.L. Membranes containing selective flakes. J. Membr. Sci. 1990, 52, 275–288. [Google Scholar] [CrossRef]
- Ebneyamini, A.; Azimi, H.; Tezel, F.H.; Thibault, J. Mixed matrix membranes applications: Development of a resistance-based model. J. Membr. Sci. 2017, 543, 351–360. [Google Scholar] [CrossRef]
- Kang, D.-Y.; Jones, C.W.; Nair, S. Modeling molecular transport in composite membranes with tubular fillers. J. Membr. Sci. 2011, 381, 50–63. [Google Scholar] [CrossRef]
- Cosenza, P.; Ghorbani, A.; Camerlynck, C.; Rejiba, F.; Guerin, R.; Tabbagh, A. Effective medium theories for modelling the relationships between electromagnetic properties and hydrological variables in geomaterials: A review. Near Surf. Geophys. 2009, 7, 563–578. [Google Scholar] [CrossRef]
- Pal, R. Newmodels for thermal conductivity of particulate composites. J. Reinf. Plast. Compos. 2007, 26, 643–651. [Google Scholar] [CrossRef]
- Chiew, Y.C.; Glandt, E.D. The effect of structure on the conductivity of a dispersion. J. Colloid Interface Sci. 1983, 94, 90–104. [Google Scholar] [CrossRef]
- Jeffrey, D.J. Conduction through a Random Suspension of Spheres. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1973, 335, 355–367. [Google Scholar] [CrossRef]
- Landauer, R.; Garland, J.C.; Tanner, D.B. Electrical Conductivity in inhomogeneous media. AIP Conf. Proc. 1978, 40, 2–45. [Google Scholar]
- Higuchi, W.I. A New Relationship for the Dielectric Properties of Two Phase Mixtures. J. Phys. Chem. 1958, 62, 649–653. [Google Scholar] [CrossRef]
- Te Hennepe, H.J.C.; Boswerger, W.B.F.; Bargeman, D.; Mulder, M.H.V.; Smolders, C.A. Zeolite-filled silicone rubber membranes experimental determination of concentration profiles. J. Membr. Sci. 1994, 89, 185–196. [Google Scholar] [CrossRef]
- Falla, W.R.; Mulski, M.; Cussler, E.L. Estimating diffusion through flake-filled membranes. J. Membr. Sci. 1996, 119, 129–138. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism; Clarendon Press: Oxford, UK, 1873. [Google Scholar]
- Bouma, R.H.B.; Checchetti, A.; Chidichimo, G.; Drioli, E. Permeation through a heterogeneous membrane: The effect of the dispersed phase. J. Membr. Sci. 1997, 128, 141–149. [Google Scholar] [CrossRef]
- Lewis, T.B.; Nielsen, L.E. Dynamic mechanical properties of particulate-filled Composites. J. Appl. Polym. Sci. 1970, 14, 1449–1471. [Google Scholar] [CrossRef]
- Felske, J.D. Effective thermal conductivity of composite spheres in a continuous medium with contact resistance. Int. J. Heat Mass Transf. 2004, 47, 3453–3461. [Google Scholar] [CrossRef]
- Shimekit, B.; Mukhtar, H.; Murugesan, T. Prediction of the relative permeability of gases in mixed matrix membranes. J. Membr. Sci. 2011, 373, 152–159. [Google Scholar] [CrossRef]
- Mahajan, R.; Koros, W.J. Mixed matrix membrane materials with glassy polymers. Part 1. Polym. Eng. Sci. 2002, 42, 1420–1431. [Google Scholar] [CrossRef]
- Fang, M.; Wu, C.; Yang, Z.; Wang, T.; Xia, Y.; Li, J. ZIF-8/PDMS mixed matrix membranes for propane/nitrogen mixtureseparation: Experimental result and permeation model validation. J. Membr. Sci. 2015, 474, 103–113. [Google Scholar] [CrossRef]
- Shariati, A.; Omidkhah, M.; Pedram, M.Z. New permeation models for nanocomposite polymeric membranes filled with nonporous particles. Chem. Eng. Res. Des. 2012, 90, 563–575. [Google Scholar] [CrossRef]
- Aroon, M.A.; Ismail, A.F.; Matsuura, T.; Montazer-Rahmati, M.M. Performance studies of mixed matrix membranes for gas separation: A review. Sep. Purif. Technol. 2010, 75, 229–242. [Google Scholar] [CrossRef]
- Monsalve-Bravo, G.M.; Bhatia, S.K. Modeling Permeation through Mixed-Matrix Membranes: A Review. Processes 2018, 6, 172. [Google Scholar] [CrossRef]
- Monsalve-Bravo, G.M.; Bhatia, S.K. Concentration-dependent transport in finite sized composites: Modified effective medium theory. J. Membr. Sci. 2018, 550, 110–125. [Google Scholar] [CrossRef]
- Lin, R.; Hernandez, B.V.; Ge, L.; Zhu, Z. Metal organic framework based mixed matrix membranes: An overview on filler/polymer interfaces. J. Mater. Chem. A 2018, 6, 293–312. [Google Scholar] [CrossRef]
- Dai, L.; Yu, S.; Shan, Y.; He, M. Novel room temperature inorganic ionic liquids. Eur. J. Inorg. Chem. 2004, 2004, 237–241. [Google Scholar] [CrossRef]
- Marsh, K.; Boxall, J.; Lichtenthaler, R. Room temperature ionic liquids and their mixtures—A review. Fluid Phase Equilib. 2004, 219, 93–98. [Google Scholar] [CrossRef]
- Hao, L.; Liao, K.-S.; Chung, T.-S. Photo-oxidative PIM-1 based mixed matrix membranes with superior gas separation performance. J. Mater. Chem. A 2015, 3, 17273–17281. [Google Scholar] [CrossRef]
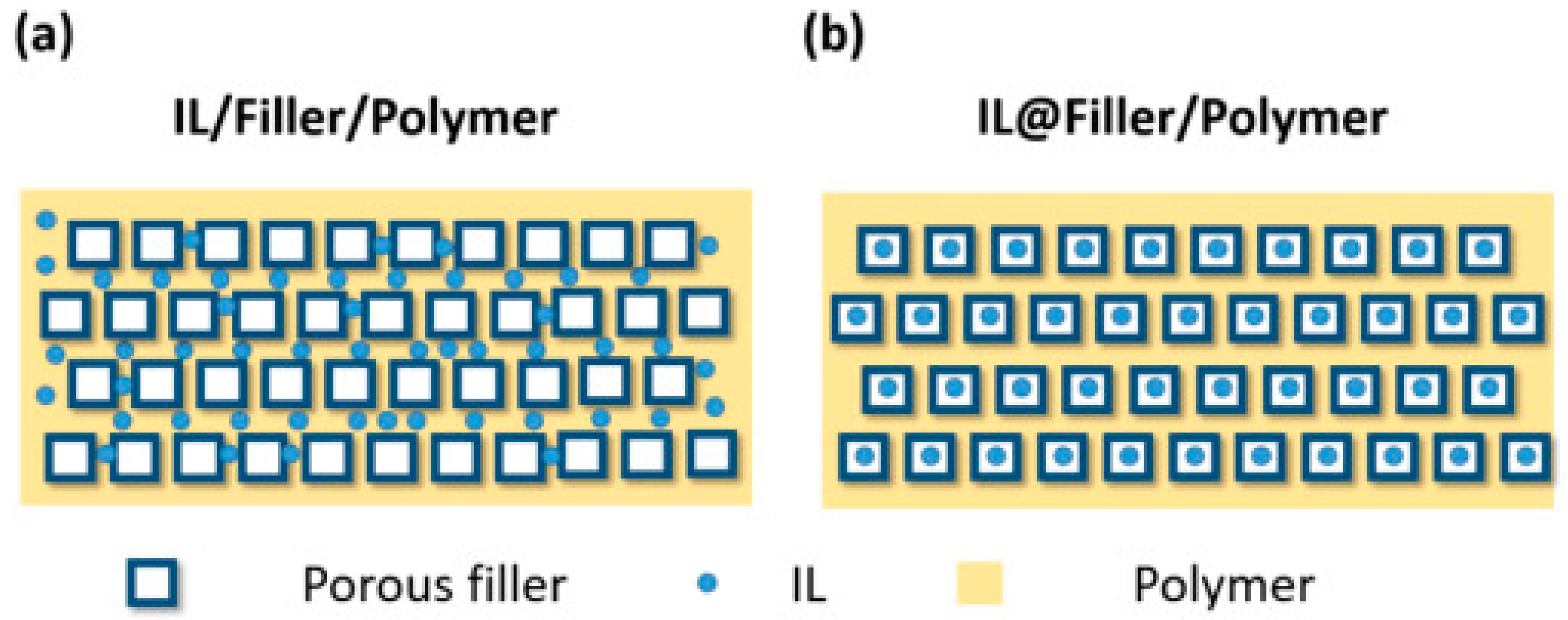
- Li, H.; Tuo, L.; Yang, K.; Jeong, H.-K.; Dai, Y.; He, G.; Zhao, W. Simultaneous enhancement of mechanical properties and CO2 selectivity of ZIF-8 mixed matrix membranes: Interfacial toughening effect of ionic liquid. J. Membr. Sci. 2016, 511, 130–142. [Google Scholar] [CrossRef]
- Ban, Y.; Li, Z.; Li, Y.; Peng, Y.; Jin, H.; Jiao, W.; Guo, A.; Wang, P.; Yang, Q.; Zhong, C. Confinement of ionic liquids in nanocages: Tailoring the molecular sieving properties of ZIF-8 for membrane-based CO2 capture. Angew. Chem. Int. Ed. 2015, 54, 15483–15487. [Google Scholar] [CrossRef] [PubMed]
- Lin, R.; Ge, L.; Diao, H.; Rudolph, V.; Zhu, Z. Ionic liquids as the MOFs/polymer interfacial binder for efficient membrane separation. ACS Appl. Mater. Interfaces 2016, 8, 32041–32049. [Google Scholar] [CrossRef] [PubMed]
- Erucar, I.; Yilmaz, G.; Keskin, S. Recent advances in metal–organic framework-based mixed matrix membranes. Chem. Asian J. 2013, 8, 1692–1704. [Google Scholar] [CrossRef] [PubMed]
- Erucar, I.; Keskin, S. Molecular modeling of MOF-based mixed matrix membranes. Curr. Org. Chem. 2014, 18, 2364–2380. [Google Scholar] [CrossRef]
- Adatoz, E.; Avci, A.K.; Keskin, S. Opportunities and challenges of MOF-based membranes in gas separations. Sep. Purif. Technol. 2015, 152, 207–237. [Google Scholar] [CrossRef]
- Erucar, I.; Keskin, S. Computational methods for MOF/polymer membranes. Chem. Rec. 2016, 16, 703–718. [Google Scholar] [CrossRef]
- Pal, R. Permeation models for mixed matrix membranes. J. Colloid Interface Sci. 2008, 317, 191–198. [Google Scholar] [CrossRef]
- Zornoza, B.; Tellez, C.; Coronas, J.; Gascon, J.; Kapteijn, F. Metal organic framework based mixed matrix membranes: An increasingly important field of research with a large application potential. Microporous Mesoporous Mater. 2013, 166, 67–78. [Google Scholar] [CrossRef]
- Erucar, I.; Keskin, S. Separation of CO2 mixtures using Zn(bdc)(ted)0.5 membranes and composites: A molecular simulation study. J. Phys. Chem. C 2011, 115, 13637–13644. [Google Scholar] [CrossRef]
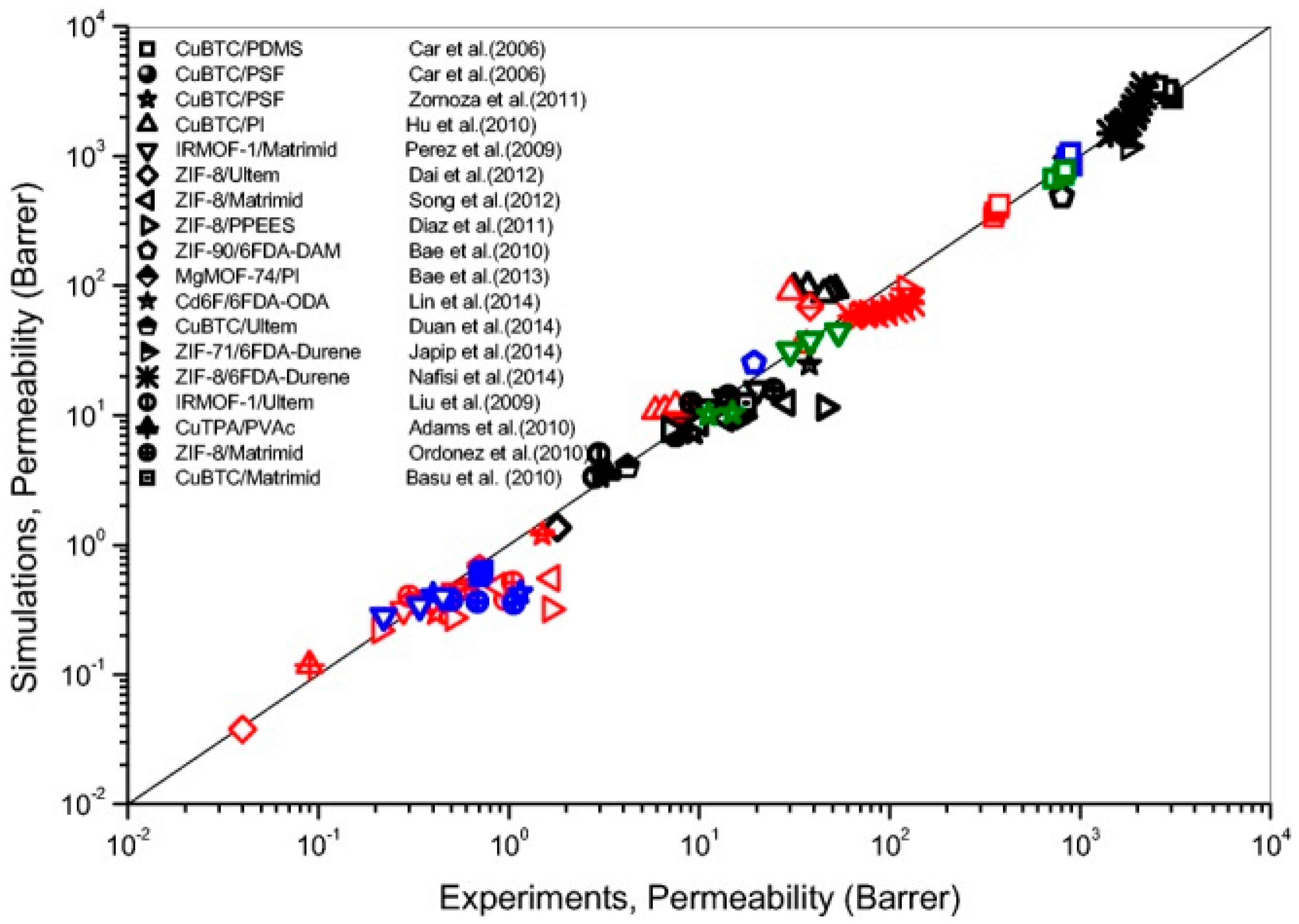
- Erucar, I.; Keskin, S. Screening metal–organic framework-based mixed-matrix membranes for CO2/CH4 separations. Ind. Eng. Chem. Res. 2011, 50, 12606–12616. [Google Scholar] [CrossRef]
- Erucar, I.; Keskin, S. Computational screening of metal organic frameworks for mixed matrix membrane applications. J. Membr. Sci. 2012, 407, 221–230. [Google Scholar] [CrossRef]
- Yilmaz, G.; Keskin, S. Predicting the performance of zeolite imidazolate framework/polymer mixed matrix membranes for CO2, CH4, and H2 separations using molecular simulations. Ind. Eng. Chem. Res. 2012, 51, 14218–14228. [Google Scholar] [CrossRef]
- Yilmaz, G.; Keskin, S. Molecular modeling of MOF and ZIF-filled MMMs for CO2/N2 separations. J. Membr. Sci. 2014, 454, 407–417. [Google Scholar] [CrossRef]
- Altintas, C.; Keskin, S. Molecular simulations of porous coordination network-based mixed matrix membranes for CO2/N2 separations. Mol. Sim. 2015, 41, 1396–1408. [Google Scholar] [CrossRef]
- Sumer, Z.; Keskin, S. Computational screening of MOF-based mixed matrix membranes for CO2/N2 separations. J. Nanomater. 2016, 2016, 12. [Google Scholar] [CrossRef]
- Altintas, C.; Keskin, S. Molecular simulations of MOF membranes and performance predictions of MOF/polymer mixed matrix membranes for CO2/CH4 Separations. ACS Sustain. Chem. Eng. 2018, 7, 2739–2750. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, Z.; Jiang, J. Metal–organic framework/polymer mixed-matrix membranes for H2/CO2 separation: A fully atomistic simulation study. J. Phys. Chem. C 2012, 116, 19268–19277. [Google Scholar] [CrossRef]
- Budhathoki, S.; Ajayi, O.; Steckel, J.A.; Wilmer, C.E. High-throughput computational prediction of the cost of carbon capture using mixed matrix membranes. Energy Environ. Sci. 2019, 12, 1255–1264. [Google Scholar] [CrossRef]
- Semino, R.; Ramsahye, N.A.; Ghoufi, A.; Maurin, G. Microscopic model of the metal–organic framework/polymer interface: A first step toward understanding the compatibility in mixed matrix membranes. ACS Appl. Mater. Interfaces 2016, 8, 809–819. [Google Scholar] [CrossRef] [PubMed]
- Benzaqui, M.; Semino, R.; Menguy, N.; Carn, F.; Kundu, T.; Guigner, J.-M.; McKeown, N.B.; Msayib, K.J.; Carta, M.; Malpass-Evans, R.; et al. Toward an understanding of the microstructure and interfacial properties of PIMs/ZIF-8 mixed matrix membranes. ACS Appl. Mater. Interfaces 2016, 8, 27311–27321. [Google Scholar] [CrossRef] [PubMed]
- Semino, R.; Moreton, J.C.; Ramsahye, N.A.; Cohen, S.M.; Maurin, G. Understanding the origins of metal–organic framework/polymer compatibility. Chem. Sci. 2018, 9, 315–324. [Google Scholar] [CrossRef] [PubMed]
- St. Petkov, P.; Vayssilov, G.N.; Liu, J.; Shekhah, O.; Wang, Y.; Wöll, C.; Heine, T. Defects in MOFs: A thorough characterization. ChemPhysChem 2012, 13, 2025–2029. [Google Scholar] [CrossRef] [PubMed]
- Yuan, L.; Tian, M.; Lan, J.; Cao, X.; Wang, X.; Chai, Z.; Gibson, J.K.; Shi, W. Defect engineering in metal–organic frameworks: A new strategy to develop applicable actinide sorbents. Chem. Commun. 2018, 54, 370–373. [Google Scholar] [CrossRef] [PubMed]
- Semino, R.; Ramsahye, N.A.; Ghoufi, A.; Maurin, G. Role of MOF surface defects on the microscopic structure of MOF/polymer interfaces: A computational study of the ZIF-8/PIMs systems. Microporous Mesoporous Mater. 2017, 254, 184–191. [Google Scholar] [CrossRef]
- Semino, R.; Dürholt, J.P.; Schmid, R.; Maurin, G. Multiscale modeling of the HKUST-1/Poly(vinyl alcohol) interface: From an atomistic to a coarse graining approach. J. Phys. Chem. C 2017, 121, 21491–21496. [Google Scholar] [CrossRef]
- Hwang, S.; Semino, R.; Seoane, B.; Zahan, M.; Chmelik, C.; Valiullin, R.; Bertmer, M.; Haase, J.; Kapteijn, F.; Gascon, J.; et al. Revealing the transient concentration of CO2 in a mixed-matrix membrane by IR microimaging and molecular modeling. Angew. Chem. Int. Ed. 2018, 57, 5156–5160. [Google Scholar] [CrossRef]
- Ahmad, M.Z.; Navarro, M.; Lhotka, M.; Zornoza, B.; Téllez, C.; de Vos, W.M.; Benes, N.E.; Konnertz, N.M.; Visser, T.; Semino, R.; et al. Enhanced gas separation performance of 6FDA-DAM based mixed matrix membranes by incorporating MOF UiO-66 and its derivatives. J. Membr. Sci. 2018, 558, 64–77. [Google Scholar] [CrossRef]
- Cheng, Y.; Tavares, S.R.; Doherty, C.M.; Ying, Y.; Sarnello, E.; Maurin, G.; Hill, M.R.; Li, T.; Zhao, D. Enhanced polymer crystallinity in mixed-matrix membranes induced by metal–organic framework nanosheets for efficient CO2 Capture. ACS Appl. Mater. Interfaces 2018, 10, 43095–43103. [Google Scholar] [CrossRef] [PubMed]
- Bachman, J.E.; Smith, Z.P.; Li, T.; Xu, T.; Long, J.R. Enhanced ethylene separation and plasticization resistance in polymer membranes incorporating metal–organic framework nanocrystals. Nat. Mater. 2016, 15, 845. [Google Scholar] [CrossRef] [PubMed]



| Reference | Key Assumptions | Permeability | Resistance Circuit |
|---|---|---|---|
| Zimmerman et al. [56] | Two resistances: Matrix and filler |  | |
| Zimmerman et al. [56] | Two resistances: Matrix and filler |  | |
| Te Hennepe et al. [57] | One-dimensional transport, idealized MMM as a lamella containing composite layers. Polymer region is assumed in series with parallel resistances of the second mixed region. Polymer, filler and diffusional resistance to account for tortuosity effects in the permeant diffusion path are considered. |  | |
| Cussler [58] | Idealize membrane as lamella. Each lamella contains two layers. Pure polymer and polymer and filler. Resistance of pure polymer is connected in series with the parallel resistances due to filler and tortuosity in the second mixed lamella layer. Two-dimensional transport in the mixed region is assumed to be in the permeation direction through filler and perpendicular to the permeation direction through polymer. | 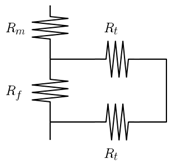 | |
| Ebneyamini et al. [59] | Suggested for ideal MMM containing cubic fillers. MMM four: (1) The continuous phase above the filler, (2) the cubical filler particle located in the centre of the unit element, (3) the continuous phase below the filler and (4) the continuous phase, which surrounds Regions 1, 2 and 3. The model is based on thee resistances of these four regions. | 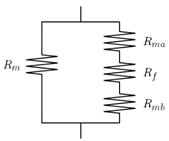 | |
| Kang et al. [60] * | Developed for MMM containing a nano-sized tubular filler. Matrix and filler resistances are assumed to be serially connected. The effect of orientation of the filler with respect to the permeation direction was considered through an arbitrary filler orientation distribution function. |  |
| Reference | Key Assumptions | Permeability | Applicable Range of the Model (Volume Fraction of Filler) |
|---|---|---|---|
| Maxwell theory [69] | Dispersion in the matrix is spherical. No interaction between the particles | <0.2 | |
| Maxwell-Wagner–Sillars model [70] | Dispersion in the matrix is ellipsoid. No interaction between the particles | <0.2 | |
| Chiew and Glandt [63] | Dispersion of spherical particles in the matrix is modeled using pair-correlation functions of hard-sphere fluid simulations. | <0.645 | |
| Lewis-Nielsen [71] | Dispersion in the matrix is spherical. Loose or random close packing of spheres and morphology of particles are considered with the maximum achievable volume fraction () of filler. | < : 059 (Loose random packing) : 0.64 (Close random packing : 0.86 (Binary packing of spherical particles) | |
| Felske model [72] | Accounts for non-ideal polymer–particle morphologies. Core-shell particles are assumed to be non-interactive. | <0.2 | |
| Modified Felske model [73] | Accounts for the morphology and packing intensity of particles. | <0.2 | |
| Two-Phase Maxwell model [74] | Three-phase composite can be idealized as pseudo two-phase composite (Phase 1: Polymer matrix, Phase 2: Combined filler-interface) | <0.2 | |
| Four-Phase Maxwell model [75] | The model considers chain rigidification, pore blockage effect and particle aggregation. Permeability is modeled using four phases: Phase 1: Polymer matrix, Phase 2: Chain rigidification region, Phase 3: Nanoparticles and particle blockage layer, Phase 4: Particle aggregate layer | <0.2 | |
| Bruggeman [61] | Composite is formed by incrementally adding new dispersed phase to an existing composite. Newly added particles do not interact with each other, they only interact with those previously added to the composite. | <0.35 | |
| Pal [62] | Composite with a high filler loading is obtained by successively adding small differential quantities of particles to the system until the desired loading is achieved. | < | |
| Pseudo-two phase Bruggeman model [76] | The model considers voids creation in the interface layer of MMM. The MMM is assumed to consist of the pseudo two-phase region: The matrix and the filler + void volume region. | <0.35 | |
| Pseudo-two phase Pal model [73] | Polymer matrix and Interfacial rigidified matrix chains are considered in predicting the permeability. | < |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keskin, S.; Alsoy Altinkaya, S. A Review on Computational Modeling Tools for MOF-Based Mixed Matrix Membranes. Computation 2019, 7, 36. https://doi.org/10.3390/computation7030036
Keskin S, Alsoy Altinkaya S. A Review on Computational Modeling Tools for MOF-Based Mixed Matrix Membranes. Computation. 2019; 7(3):36. https://doi.org/10.3390/computation7030036
Chicago/Turabian StyleKeskin, Seda, and Sacide Alsoy Altinkaya. 2019. "A Review on Computational Modeling Tools for MOF-Based Mixed Matrix Membranes" Computation 7, no. 3: 36. https://doi.org/10.3390/computation7030036
APA StyleKeskin, S., & Alsoy Altinkaya, S. (2019). A Review on Computational Modeling Tools for MOF-Based Mixed Matrix Membranes. Computation, 7(3), 36. https://doi.org/10.3390/computation7030036




