Abstract
To enable net zero sustainable thermal building energy, this study develops an open-source thermal house model to couple solar photovoltaic (PV) and heat pumps (HPs) for grid-connected residential housing. The calculation of both space heating and cooling thermal loads and the selection of HP is accomplished with a validated Python model for air-source heat pumps. The capacity of PV required to supply the HPs is calculated using a System Advisor Model integrated Python model. Self-sufficiency and self-consumption of PV and the energy imported/exported to the grid for a case study are provided, which shows that simulations based on the monthly load profile have a significant reduction of 43% for energy sent to/from the grid compared to the detailed hourly simulation and an increase from 30% to 60% for self-consumption and self-sufficiency. These results show the importance of more granular modeling and also indicate mismatches of PV generation and HP load based on hourly simulation datasets. The back-calculation PV sizing algorithm combined with HP and thermal loads presented in this study exhibited robust performance. The results indicate this approach can be used to accelerate the solar electrification of heating and cooling to offset the use of fossil fuels in northern climates.
1. Introduction
Access to energy is crucial in determining social-economic development and reducing poverty [1] as modern societies depend on abundant and low-cost energy [2]. Unfortunately, the energy sector is also the largest emitter of greenhouse gases (GHGs) [3], which are driving climate change and the concomitant negative externalities for humanity and nature [4]. For example, in Canada, the energy sector emitted 80% of the total GHG emissions [5] and Canadian per capita emissions are some of the highest in the world [6]. To rectify this, Canada has made a commitment to aggressively reduce GHG emissions by passing the Net-Zero Emission Accountability Act, with the mandate to reach net zero emissions by 2050 [7]. To reach zero emissions, the residential sector is of particular interest because building energy use is responsible for 17% of the GHG emissions in Canada [5] and residential buildings are under the control of consumers/citizens [8,9]. For the energy use in residential buildings space, heating, and domestic hot water demand account for 63.6% and 17.2% of energy consumption in average Canadian homes, respectively [10]. Thermal energy demands also drive energy use in the residential sector outside of Canada, as about 27% of the world’s total energy consumption is used by residential structures [11].
One of the solutions to the energy/emissions challenge is the deployment of renewable energy sources, which can meet rising energy demands without harming the environment by replacing scarce and unsustainable fossil fuels [12,13]. Among renewable energy sources, solar photovoltaic (PV) systems have gained prominence due to their environmentally friendly, clean and safe operations [14]. Since its commercial development a few decades ago, the growth of power generation utilizing PV technology has been sustained and increased [15]. PV accounted for 2.6% of the world’s electricity generation in 2019 and is projected to provide 25% of the energy required by 2050 [16]. Additionally, it is anticipated that integrated PV buildings will provide 40% of this energy [16]. In recent years, solar energy has radically dropped in price [15] and been employed at accelerating rates [17], making it one of the most rapidly growing sources of energy supply globally [18]. PV systems can be deployed for stand-alone operation in residential homes economically [19,20,21]; sizing such systems can be complicated because of the need for battery storage [22,23,24,25,26]. Recent work has even used artificial neural networks (ANNs) and metaheuristic methods [27], which are computationally demanding [28] but reliable techniques that provide a techno-economic solution to determine appropriate sizing [29]. Stand-alone PV systems, however, are the minority as most residential PV systems are grid-tied [30].
Although the value of solar electricity is often higher than the net metered rate [31], residential solar customers may be credited far lower than the net metered rate [32]. In such instances, it is economically optimal for the residential solar customer to self-consume, that is, to use their higher-value solar energy rather than feed it back to the grid. Nicoletti et al. [33], have shown it is challenging to guarantee high self-consumption with just the installation of the PV system alone. PV coupled with electric storage increases the ability for self-consumption but is generally costly [34]. Another approach, which has recently gained economic viability in North America is to use PV-powered heat pumps (HPs) [35,36,37]. PV coupled with HPs can also increase the self-sufficiency and self-consumption rates of households, becoming a source of local flexibility [38,39]. Electrically powered HPs efficiently serve both space/water heating and cooling, making them superior to conventional heaters as they also function as air conditioners during the summer [40]. Due to the great thermodynamic efficiency of HPs and the potential to use renewable electricity as a source of energy, they are currently the most promising technology for reducing the carbon footprint of the heat supply while fostering the integration of renewable energy in buildings [41]. For example, solar PV technology with HPs can reduce residential building GHG emissions by up to 50% immediately [36]. Several studies perform sizing of HPs for different objectives [42,43,44] along with numerous heat pump designs that consider the available heat source (such as air, earth, or water) and the way the heat is delivered to the building. (e.g., ducted air, ductless air, hydronic) [45].
HPs can be broadly categorized into two groups: ground-source heat pumps (GSHP), often known as geothermal heat pumps, and air-source heat pumps (ASHP). GSHPs are generally more efficient and have more installation cost than ASHPs [46]. In GSHP, with a coefficient of performance (COP) equal to 2.94 at −17.7 °C [47], the ground heat exchanger’s (GHE) design is frequently the most important factor in determining performance and economics [48,49,50]. The drilling prices of GSHPs are also an added cost that makes the capital expense much higher than the ASHP [51]. One of the ways to reduce the cost of GSHPs is to use horizontal GHE; however, this approach requires more land area and thus is not suitable for all residential applications. According to Lim et al. [52], only 61% of residences in the U.S. can install GSHPs; of those that can, 8% must utilize the more expensive vertical GHE. Beyond installation costs, it is challenging to make a single HP design proposal for an entire region [53], due to the significant relationships between climate, geology, energy prices, fuel prices, and inflation rates [54].
By eliminating the requirement for GHE, ASHPs offer a stronger economic proposition than GSHPs, and in recent years the technology has advanced to be a competitive alternative in cold areas [55]. Lowering the minimum operating temperatures and reducing auxiliary heat have been accomplished using new refrigerants, ejectors, and dual-stage compression [56]. The COP of air-to-air heat pumps normally ranges between 2 and 5.4 at 8 °C [57] and can fall to a meager 1.04 at −21 °C [58]; testing on commercial models has shown that it can reach 1.5 [59]. Thus, the economic competitiveness of ASHP varies by geography and application, just as GSHP. The economics, however, have recently shifted in favor of HPs. According to the latest International Energy Agency (IEA) analysis, global sales of HPs grew by 11% in 2022, with Europe’s HP sales growing by nearly 40%, whereas in 2023 in the U.S. HP sales exceeded gas furnaces for the first time [60]. Dated studies of only a few years on Canadian buildings [61,62] showed that ASHPs are more expensive than natural gas in most places, with milder climates being the most promising. More recent results, however, have shown that PV-powered ASHPs are economical in Canada [35]. Similarly, in the northern U.S. Padovani et al. [36] showed that the electrification of the heating system by combining PV and HPs can be economical at the residential level for replacing propane and other studies have shown the same for natural gas [35,37]. HPs achieve up to 66% secondary energy savings and up to 84% in GHG reductions [63].
If PV systems are to also cover thermal loads, these have a great influence on the sizing of the PV [64]. Determining the amount of energy needed to provide thermal loads in buildings today is challenging as it depends on a variety of factors like the kind of construction materials and their coefficients of heat transfer, outside and indoor temperatures, humidity, the number of occupants, lightning and human behavior [65,66]. In addition, the optimal sizing of the PV+HP system depends on various other parameters i.e., solar radiation, and variable solar electricity costs that are sensitive to initial costs of every component of the system. Although much work has been done on sizing PV systems to meet non-thermal electric loads, comparatively less work has focused on the use of solar-powering heat pumps for heating and cooling thermal loads.
This study aims to develop an open-source thermal house model to be coupled to solar PV and HP models for grid-connected residential housing. This model provides hourly and monthly thermal load profiles that are used to observe how the import and export of electricity to/from the grid changes based on different load profiles for optimally sized solar PV systems used to run optimally sized HPs. After briefly reviewing the literature, the calculation of the thermal loads (i.e., both space heating and cooling) is made to provide the selection of HPs. This is done using the black box model developed in Python for an air-source heat pump to meet thermal loads for a one-story grid-connected residential building model for both space heating and cooling and validated by using the Hourly Analysis Program 5.11 (HAP) [67]. Finally, the capacity of PV required to supply the HP is calculated using the System Advisor Model (SAM) integrated Python model [68]. The novelty of this approach is a PV model which has been introduced to select the system developed for an optimal power supply considering both heating and cooling load requirements of the HP. This model provides details about the import/export of electricity to/from the grid, self-consumption, and self-sufficiency, and how they change based on hourly and monthly load profiles. A case study is presented for Ontario Canada, but the model can be used for other geographical regions globally. The results are presented and discussed in the context of accelerating the solar electrification of heating and cooling to offset the use of fossil fuels.
2. Background
For all PV system-sizing calculations, input data (system specifications, meteorological data, load demand data), system models, simulation techniques and formulated objective functions are typically the four key components of numerical techniques [69]. Analytical techniques [70] generate a simple formula that specifies the size of PV systems to achieve desired system reliabilities. This method’s main advantage is its simple computations, while its main drawback is the difficulty of predicting the coefficients of mathematical models and the dependence of these models on location [21,71]. With purely electrical residential PV systems, there are a wide variety of PV simulation tools to match simple electric loads [72] which includes ESP-r [73], SolarGIS (PV Planner) [74], SolarDesignTool [75], Aurora Solar Software [76], PVSYST [77], SolarPro [78] and others. To solve the general issue of PV sizing for more complex systems involving thermal loads, various software programs, including TRNSYS [79], RETScreen [80], SAM [68], HOMER [81], IHOGA [82] and HYBRID2 [83], have been developed to determine the PV system’s optimal size [84,85]. The most well-known software for PV scaling of complex systems is RETscreen and HOMER [86,87] although many authors write MATLAB code for the optimization of PV size [26,88]. The vast majority of these tools are adequate for net metered systems, but as many utilities do not net meter [89] and there is a trend away from net metering [32,90] more complex calculations are necessary to optimize the economic return of a PV system.
For PV+HP systems, the dimensioning of all the components is carried out considering economic criteria [91] and therefore it is necessary to analyze the whole system together, as the size chosen for one of these components inevitably affects the size of the others. For example, Angenendt et al. [92] used different operating strategies to perform optimization of PV+HP+battery system component size and the results showed a great economic impact on the cost associated with the operation. Beck et al. [93] analyzed the combined size of PV and heat pumps under different scenarios and found that the size of the PV field and the electrical storage are significantly influenced by the electrical load profiles, while the choice of heat pump is almost completely independent of scenario assumptions. These articles do not consider the impact on summer behavior and thus space cooling loads. Other studies have also analyzed the dimensioning of the heat pump coupled with PV systems [93,94,95]. Lyden et al. [95] designed the heat pump size based on the different tariffs and assumed predictive control. These articles, however, did not focus on the sizing of the PV system. Energy simulations were carried out by Dongellini et al. [96] using an air–water heat pump (AWHP) that only provides a portion of the building’s thermal demand while the remaining portion is delivered by the boiler. The study highlights the significance of appropriate design by showing that the performance is highly related to HP sizing.
Air–water HPs are systems that are frequently utilized to offer space heating and cooling in the Mediterranean region. The optimal dimensioning of components for cold climate locations, where cooling is not necessary, is the subject of the research works listed so far. Space cooling is a crucial factor to take into account in areas with temperate climates [97]. The quantity of electrical energy needed by the HP during the summer must be considered while choosing the best dimensions. Nicoletti et al. [33] used EnergyPlus to carry out energy simulations for obtaining data for the combined sizing of PV-battery and air–water HP systems considering both heating and cooling demand. Baghoolizadeh et al. [2] simulated a building model in cities with different climatic conditions using EnergyPlus to optimize the energy loads and their costs for both heating and cooling loads. In the literature, combined optimal dimensioning is only used for cold areas with low cooling demand. In warm climate sites where it is necessary to consider both the winter and summer building–plant behavior, there is a gap in the literature about the joint dimensioning of these systems. Therefore, in this study, the sizing of PV is done conducted on both the HP specification and all the thermal loads (both heating and cooling).
3. Methodology
A one-story residential house located in London, Ontario, Canada, is first modeled to calculate the energy required for space heating and cooling load for the house to select the desired system. To have precise and hourly data, the considered system is validated at each step. The validation of the house model is done by using HAP V 5.11. (Hourly Analysis Program) software, whereas the PV system is modeled by a SAM-integrated Python model, which is used in the calculation of the PV size required to run the HP loads and supply the house heating/cooling loads. Since the PV system depends on the meteorological data from [98], the system model can be implemented in different locations. The flowchart for the methodology is shown in Figure 1.
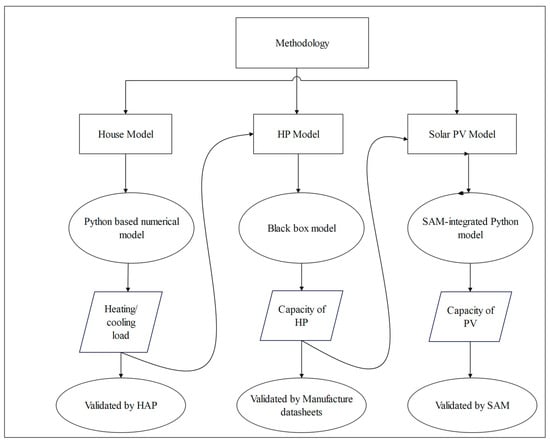
Figure 1.
Flowchart showing the proposed methodology.
3.1. Calculation of Heating/Cooling Loads
The walls, ceiling, floor, people, lighting system, electrical equipment, air infiltration, doors, and windows all contribute to energy losses in the house that affect the cooling and heating loads. The calculation for thermal loads is first done using the heat transfer principles provided in the book Heating, Ventilating, and Air Conditioning: Analysis and Design (HVAC) [99] and then validated using HAP V 5.11. (Hourly Analysis Program). Only the waste heat produced by the most energy-demanding electrical applications, i.e., oven, microwave, and refrigerator, are considered in the model. Moreover, cooling loads of people, lighting as well as infiltration are also included. The detailed calculation for the heating/cooling loads can be found in the OSF depository [100]. The load calculation is done for a one-bed one-bath one-story house without a basement considering the effect of thermal losses from the roof and floor. Figure 2 illustrates the schematic of the House+HP+PV system.

Figure 2.
Schematic of the house+HP+PV system.
3.1.1. Heating Load Calculations
The heating calculation model is developed for the whole house. The first step is to determine the areas for walls, windows, doors, and floors that are exposed to the outside—these are the surfaces where heat transfer will take place and hence affect the heating load. The area for each space is determined by measuring the distance of walls and selecting a suitable scale based on the dimensions provided in the floor plans (scale: 1 cm = 1.5 m). The plan view and dimensions of the main level of the house are shown in Figure 3. Further, the calculation of the surface areas of heat transfer walls for each space of the main level is shown in Table 1.
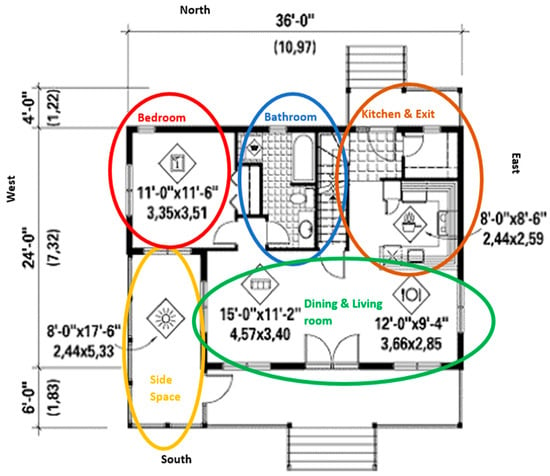
Figure 3.
Floor plan of the house.

Table 1.
Calculated surface areas and perimeter of the house plan.
Once the areas of walls, windows, doors, perimeter of floors, etc., contributing to heat transfer are determined for each space, the overall heat transfer coefficient (U) for walls, windows, doors, roofs and floors in each space is then calculated. The block diagram in Figure 4 shows the further heating-calculation process and all the formulas required are given in Table 2.

Figure 4.
Block diagram for heating load calculations.

Table 2.
Required heat transfer equations for heating load calculations [99].
The following assumptions are made about the structure of house, materials used and design conditions:
- Walls: The value of unit thermal resistances is provided in Table 5-4a (construction 2) of the HVAC book [99]. This value can be determined by using thermal conductivity () for each material.
- ○
- Construction 2 is taken for the project with a slight change. Aluminum siding backed with a 0.375 in (9.5 mm) insulating board is incorporated in place of the brick whose conductance is taken as 3.123 W/m2°C. These are installed in the space of reflective air space and constitute 20% of the space.
- ○
- Two resistances are calculated, one considering reflective air space and one considering vertical furring instead of reflective air space. Since vertical furring only corresponded with 20%, the U value determined from resistances is multiplied by 0.2, while other resistance is multiplied by 0.8.
- ○
- Utot for walls = 0.6814 W/m2-°C.
- ○
- Utot for roof = 0.2839 W/m2-°C (Example 5-2 from HVAC book [99]).
- ○
- For a 0.15 m concrete floor with an average thermal conductivity of 1.7 W/mK, fully covered by an insulation material with a thermal resistance of 0.88 m2K/W on the ground with thermal conductivity of 0.1152 W/mK (London, Ontario) [67], the edge heat loss coefficient (HLCedge) for the floor slab is 0.8304 W/m°C [99,101].
- The height of north and west facing windows are 0.914 m and 1.829 m. While the height of the door is considered 2.134 m.
- For doors and windows
- ○
- All windows and doors are assumed to be double glazed with 0.0127 m air space (wood/vinyl).
- Inside temperature, i.e., space temperature, which is to be maintained inside the house, is assumed to be 22.22 °C; i.e., the set point temperature and outside temperature (to) is taken as −14.2 °C.
- For infiltration:
- ○
- To determine the latent heat transfer, the humidity ratio for inside conditions (Wi) and humidity ratio for outside conditions (Wo) are ascertained. These are determined through a psychrometric chart [102] at an inside temperature of 22.22 °C and assuming a 30% relative humidity and meteorological data for ambient conditions. The relative humidity might change for indoors which will change the humidity ratio accordingly.
- ○
- For our calculations, Wi is taken as 0.005 kg(w)/kg(a), hg is found to be 2,541,150 J/kg and hf is found to be 93,040 J/kg.
- ○
- The amount of infiltration for space of the residential building air is considered as 0.5 air change per hour (ACH).
Further, the value of sensible heating load from the heat transfer surfaces and infiltration are added to ascertain the total sensible heating loads for individual spaces.
3.1.2. Cooling Load Calculations
The cooling load calculation block diagram is shown in Figure 5 and the formulas are presented in Table 3 following the Radiant Time Series Method (RTSM) [99]. The first step is to determine the sol-air temperature, which is an equivalent temperature that eliminates the requirement to model convection for the outdoor air, radiation to the ground and sky, and solar radiation separately. This simplifies the calculations as a single heat transfer between an equivalent (sol-air) temperature and the surface temperature then can be calculated. Solar intensities are required as input to calculate sol-air temperature. Next, heat gains are ascertained for windows (using solar intensities—referred to as solar heat gain) and for exterior surfaces of the space (using sol-air temperature—referred to as conduction heat gain). Conduction heat gain is calculated for windows as well. Lighting, equipment, people, and infiltration heat gains are then estimated. All the calculations performed are on an hourly basis. The cooling loads are then segregated into radiative and convective components. The radiative components are processed further through an appropriate radiant time series before being added into convective components to come up with the final cooling loads. Figure 5 shows the process of cooling load calculations.
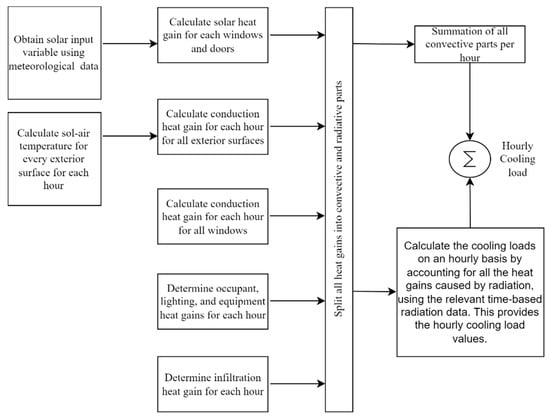
Figure 5.
Block diagram for cooling load calculations.

Table 3.
Required heat transfer equations for cooling load calculations.
The following assumptions are made about the structure of the house, materials used and design conditions:
- All the required data mentioned below are taken from the HVAC handbook [99].
- ○
- The design dry bulb temperature for the day (T) and daily range (DR) (which is the difference between the average maximum and average minimum for the hottest month of a location) are, respectively, taken from National Renewable Energy Laboratories (NREL) [98] and HVAC book [99]. The daily range is taken as 18.5 °F. The design temperatures and daily ranges are also provided in Appendix B (Table B-1) of HVAC handbook [99].
- ○
- The hourly incident solar radiation is ascertained from NREL [98].
- ○
- For determining the solar heat gain constant for diffuse (d) and direct radiation (D), Table 7-3 from the HVAC handbook [99] is used.
- ○
- The periodic response factors are available in Table 8-18 in the HVAC book [99]. Wall 1 and Roof 1 are considered for calculations, while radiant time factors from Table 8-28 are assumed. The radiant time factors for low-weight, medium-weight, and heavy-weight buildings are available in Table 8-21 in the HVAC Book [99].
- ○
- Heat transfer through the floor for cooling load calculations is neglected.
- From Table 8-2 in the HVAC book [99], the sensible and latent heat gain for occupants can be estimated. However, the sensible and latent heat gain for occupants is taken as 73.27 W and 58.61 W, respectively, from the HVAC Book [99] (Table 8-2 moderately active office work or standing, light work, walking).
- is a constant in Table 3 [99] and is normally selected as −13.8 °C for horizontal surfaces and −17.7 °C for vertical surfaces.
- The heat gain from lighting is considered as 21.5 W/m2 [99].
- The heat gain from equipment (refrigerator, microwave, and oven) is taken as 4.8 kW [99].
- The sensible and latent load associated with infiltration is determined in a similar manner as for heating load calculations. For the calculations, the specific volume of outdoor air is considered as 0.89 m3/Kg. Humidity ratio values are taken as 85 °F outdoor temperature and 72 °F indoor temperature, which is the set point temperature for cooling load calculations.
- The cooling load essentially represents the incumbent energy removal rate to maintain the desired temperature and humidity in a space. It typically differs from heat gain because radiation from interior surfaces and direct solar radiation entering through openings does not immediately warm the air inside. Instead, this radiant energy is absorbed by floors, walls, and furniture, primarily cooled through convection as they reach temperatures higher than the room air. Only when this energy is transferred to the air by convection does it contribute to the cooling load. The thermal inertia of the building resists changes in temperature, maintaining a stable internal climate by absorbing and slowly releasing heat energy over time. The thermal properties of the structure and interior objects determine the thermal lag, influencing the relationship between heat gain and the cooling load. The heat emitted by people and equipment operates similarly. The radiant energy portion generated by lights, equipment, or individuals is temporarily stored in the surroundings. Energy directly transferred into the air by lights and people, eventually transferred by the surroundings, becomes part of the cooling load. As the RTSM employs a radiant time series for the radiative segments of heat gain, designers need to categorize all heat gains into radiative and convective components. The radiative-convective splits for the heat gain are shown in Table 4.
 Table 4. Radiative-convective heat gain.
Table 4. Radiative-convective heat gain.
3.2. Black Box Heat Pump (BBHP) Model
The black box heat pump model is developed using the datasheet of the Goodman Air-Air heat pump for both heating and cooling operation modes [103]; a supervised regression learning model was developed in Python to export the mathematical functions for COP of heat pumps with a nominal capacity range of 18,000–60,000 BTU/h. As Li et al. [104] have proposed correlations for load demand and COP of an air-conditioning heat pump, it is expected that the regressions of COP would be a second-degree polynomial as a function of indoor and ambient temperatures.
3.2.1. Heating Mode
The correlation of COP is dependent on ambient temperature (T) in (°C) as Equation (1):
The coefficients b0–b2 are extracted using the polynomial curve fitting technique and are shown for all rated capacities of GSZ16 Goodman Heat Pumps in Table 5 for heating mode. The fitting curve of heating COP for an 18,000 BTU/h heat pump is shown in Figure 6a.

Table 5.
Coefficients of polynomial correlations of COP in heating mode.

Figure 6.
Fitting curves of COP for 18,000 BTU/h heat pump: (a) heating mode, (b) cooling mode.
3.2.2. Cooling Mode
The manufacturer’s datasheets for cooling mode were prepared based on the variations of ambient temperature and indoor dry bulb and wet bulb temperatures [103]. To be able to illustrate the fitting surfaces in 3D plots, the cooling capacity and COP correlations were developed as a function of ambient temperature and another second-degree polynomial, as shown in Table 6 which is itself is a function of indoor temperatures. Figure 6b presents the fitting surface for COP of an 18,000 BTU/h heat pump in cooling mode. The COP of the cooling mode is obtained using Equation (2).

Table 6.
Coefficients of polynomial correlations of COP in cooling mode.
When the maximum heating (cooling) demand of a house on the coldest (warmest) day of the year is calculated, the size of the HP can be determined. After selecting the heat pump, its COP correlation is used to calculate the power consumption. The same correlations of the selected heat pump on the other days of the year will be used to calculate the power consumption as well.
3.3. Solar PV Sizing
The solar PV system sizing is performed using a new design approach proposed in a recent study [40] to calculate the optimal size of PV for supplying the residential thermal load. This new approach relies on the strength of SAM [68] developed by NREL [68] and uses the flexibility of a Python implementation of SAM [105,106] to design and evaluate the performance of a PV system coupled with a load.
SAM is generally capable of evaluating the generation potential of a PV system with a known DC power rating. In this research, however, the energy consumption (electricity load of HP in kW) and operating hours are known, and the PV DC power rating needs to be calculated. To achieve this, a reverse calculation approach is applied. This approach involves calculating the actual PV system size by considering the total load demand (in this context, the power demanded by HP), local weather data, and system losses. The back-calculation code is integrated with the Python version of SAM, which extracts all the necessary data for simulation. The details of this method along with the required inputs are provided in [40].
Based on solar irradiation data and the hourly power consumption of the HP, the PV capacity is estimated using Equation (3). It is important to note that this estimation relies on approximations, as the average irradiation and certain losses are variable and dependent on ambient and operating conditions. Equation (4) is then used to calculate the number of PV modules required.
In these equations, Pestimated represents the estimated total PV power in kW, is the hourly average HP consumption in kW, is the daily average solar irradiation in kWh/m2day, n and η are, respectively, the number of hours in a day (24) and the combined efficiency factor (between 0 and 1, both excluded) of all the PV system components (assumed as 0.5 in this study), and N denotes the number of PV modules, while represents the individual module power in W. Once the estimated number of modules is determined, the annual AC energy estimate is obtained by running the Python implementation of SAM. This estimated annual AC energy is then compared to the actual AC energy required, which is calculated using Equation (5):
In this equation, Eact.needed is the actual annual AC energy required in kWh, and n‘ represents the number of days (365 in this study). The results obtained from the back-calculation algorithm are used to design a realistic PV system for residential houses in London, Ontario, Canada. The PV modules and inverters are selected to match the lifetime energy demand of the house to the lifetime energy production of the PV. The loss values used in this study were taken from SAM and the PV was considered fixed tilt with an optimal inclination angle of 34° for annual production. The 34°-tilt angle has been shown in past studies to be the optimal inclination for non-tracking PV systems in London, ON [107]. The total energy produced by the PV, the energy sent to and taken from the grid, and the system’s self-consumption and self-sufficiency are the metrics used to assess the performance of the residential PV system.
A distributed energy system’s energy performance can be assessed locally using two metrics: self-consumption (SC(%)) and self-sufficiency (SS(%)) [108]. Self-consumption measures the proportion of locally consumed energy that is generated on-site relative to the total energy generated locally. In this research, self-consumption is determined as the discrepancy between the energy produced by the PV system and the energy exported to the grid, divided by the total energy generated by the PV, as expressed in Equation (6) [108]. Likewise, self-sufficiency is computed by dividing the difference between the energy generated by the PV system and the energy sent to the grid by the total load consumption, as demonstrated in Equation (7) [108].
3.4. Limited Data PV System Sizing
The main challenge for sizing PV and conducting energy performance analysis is data availability [109]. Therefore, a specific case was investigated by considering a limited data scenario to further the analysis in this study. In this scenario, it was considered that only monthly data were available for the user, which are usually the data provided to the users by utilities. To reproduce the monthly energy-consumption data, the hourly data generated in this study was aggregated monthly. Starting from the monthly energy value, the following procedure was adopted to generate hourly values.
The data-disaggregation process used here relied on a previous study that examined the statistical distribution of HVAC energy loads in residential buildings. According to the study’s findings, the energy-consumption model of a house is on average a Gaussian [110]. This concept was applied here by generating Gaussian hourly data from the monthly energy. First, the monthly energy is averaged to find the average daily energy for each month. Then, average daily energy is distributed on a Gaussian curve centered on the middle of the day (noon) as shown in Equation (8) to obtain hourly values.
where Ehourly (kWh) is the hourly energy of the system, σ is the standard deviation of the distribution, hod (h) is the hour of the day (0 to 23) for which the calculation is performed, μ (h) is the time of the day around which the gaussian is centered (12 pm or noon in this study) and k is a constant scale factor that is applied to the distribution to ensure the sum of the hourly energy equals the average daily energy. The standard deviation and the mean value can be adjusted to suit the most common load profile in a specific geographical area. In this study, the standard deviation was set at 2. For each month, all days are considered to have the same load profile. The generated Gaussian hourly data are then used to size the PV system as described in the section above.
4. Results
4.1. Validation
By contrasting the simulation results obtained from HAP software V 5.11. for the same residential house and the mathematically modelled ones, the performance of the house model was validated for the heating load. For the same input meteorological data, the comparative results are exported for heating load on the coldest day of the year. The total sensible heating load is found to be 8499 W, while the total latent heating load is found to be 367 W. The values of sensible and latent heating load from HAP are found to be 7890 W and 368 W, respectively. The difference between the sensible loads is approximately 7.16%, whereas for latent heating loads it is 0.3%. The present model, however, provides a more conservative estimate. The maximum cooling load (sensible) for an hour is 10,741 W. For the same hour, the maximum latent cooling load is determined as 956 W. The model is validated using data from McQuiston et al. [99].
Similarly, the validation of the BB HP model is done using the manufacture datasheet of the GSZ16 series Goodman Air-Air heat pump. The average deviation of the correlated results for heating COP with the datasheet of the manufacturer is found to be 2.5%, whereas the average deviation of the correlated results for cooling COP is 1.3%.
4.2. Heating/Cooling Load Demand
The total heating load requirement for the house on the coldest day is obtained at 7695 W from the simulation. Similarly, the maximum cooling load for an hour is ascertained at 11,277 W. In this study, the heating and cooling load for the proposed house model on a monthly, daily, and hourly basis is also obtained from the simulation results.
4.2.1. Monthly Load Demand
The average monthly heating and cooling load demand for the house in London, Ontario, Canada, was calculated and is shown in Figure 7. The load calculations are performed on an hourly basis.

Figure 7.
Comparison of average monthly load demand profile for heating and cooling.
4.2.2. Daily Load Demand
Figure 8 shows the average daily heating and cooling load demand of the house throughout the year. The total heating load requirement for the house on the coldest day occurs on the 48th day of the year, i.e., 17 February. Similarly, the maximum total cooling load occurs on the 212th day of the year, i.e., 31 July. Here, the daily average cooling demand is less than the daily average heating demand. The daily load can be one of the parameters for the system modelling giving more precise data than the monthly average.

Figure 8.
Comparison of average daily load demand profile for heating and cooling.
4.2.3. Hourly Load Demand
The hourly load data are also obtained and used for further modelling of the system. Figure 9 shows the hourly heating and cooling demand of the house throughout the year. The maximum heating load is 7695 W, which occurs on 17 February at 4 am while the maximum cooling load comes out to be 11,277 W on 31 July at 5 pm. The BBHP and PV sizing models rely on hourly data and predominantly employ the BTU/h capacity parameter, which is widely recognized for its common usage and precision. Figure 10 shows the hourly–monthly heating loads, of the proposed house to have a detailed analysis of the pattern and variation of load with time. The average air temperature used for calculation is shown in Figure 11 whereas Figure 12 shows the hourly-monthly cooling loads for the proposed system

Figure 9.
Comparison of average hourly load demand profile for heating and cooling.

Figure 10.
Hourly–monthly load profile for net heating load.

Figure 11.
Hourly–monthly average air temperature for heating load.

Figure 12.
Hourly–monthly load profile for net cooling load.
4.3. Sizing of Heat Pump
Based on the hourly heating/cooling load of the proposed model, the sizing (capacity) of the heat pump is found separately for heating and cooling loads, and the COP of the heat pump is calculated. It is found that based on the maximum heating and cooling load at the coldest and hottest day, the HP required from the manufacture datasheet of the Goodman HP model is 0301B series with a capacity of 30,000 BTU/h and 0421B with a capacity of 42,000 BTU/h, respectively. The COP for the heating load in the manufacturing datasheet for 0301B ranges from 4.73 to 1.01; however, the COP calculated on the worst day, i.e., the coldest day using Equation (1) is 2.05. Similarly, for the cooling load, the manufacturing datasheet for 0421B ranges from 6.09 to 2.52; however, the EER calculated on the worst day, i.e., the hottest day using Equation (2) is 4.42. The seasonal COP/EER for heating and cooling mode is shown in Table 7, whereas the seasonal EER (SEER) is obtained by dividing cooling energy output in BTU with the electrical energy input in Wh obtained over a season. The detailed calculations for calculating EER and SEER are available in the OSF depository [100].

Table 7.
COP and EER of the proposed heat pumps on the worst day of the year and seasonal, respectively.
4.4. Sizing of Solar PV
The back-calculation algorithm yielded a PV capacity necessary to support the proposed residential house model of 6.88 kW. Using this theoretical PV capacity, a real PV system made up of specific modules with a rated power of 6.85kW was designed in SAM using the parameters in Table 8, resulting in a negligible deviation of 0.44%. The simulation results, as presented in Table 9, show that the energy fed into the grid and the energy drawn from the grid are closely aligned. The design aims to keep these values as similar as possible to minimize grid electricity costs, especially in areas with net-metering or value of solar quantification for grid-connected PV systems [31]. According to Table 9, the system’s self-consumption is 30.02%, meaning that 30.02% of the energy generated by the PV system is utilized on-site by the heat pump during its lifetime. Additionally, the self-sufficiency of the system is 30.06%, indicating that 30.06% of the energy required by the heat pump is met by the PV system over its lifetime. Here, the electric load of the house in addition to the HP is not considered.

Table 8.
Parameters of the designed PV system in SAM.

Table 9.
Lifetime simulation results of the PV-ASHP in SAM showing the energy performance of the PV system using the thermal model data in this study and the Gaussian distribution data for limited load data scenarios.
Figure 13 illustrates the annual energy performance over the lifetime of the air-source HP model and PV generation. The PV system generates surplus energy compared to the load demand during the initial 14 years, but less energy in the last 9 years. The decline in PV energy generation is attributed to an annual PV degradation rate of 0.5% [31], while the HP load is considered constant over the lifetime of the system. This difference is offset by the simultaneous increase in self-consumption and decrease in self-sufficiency as the system matures.

Figure 13.
Twenty-five-year lifetime annual energy performance results of the proposed residential house with air-source heat pump.
In Figure 14, the PV generation and HP load for the initial year of the residential house equipped with ASHP are shown. In Figure 14a, the data reveal the daily fluctuations in PV generation in relation to the HP load. The peak load and peak PV generation do not consistently coincide, underscoring the need for grid connectivity in the system. Figure 14b illustrates a noteworthy inverse relationship between self-consumption and self-sufficiency. Self-consumption reaches its peak during the winter months, particularly in January and December (68% and 48%, respectively), while self-sufficiency is notably higher during the summer (50% in July). Figure 14c depicts the monthly patterns in PV energy generation and monthly load requirements. Additionally, it shows the energy supplied to and drawn from the grid. Energy drawn from the grid is highest in the winter, moderately high in summer, and lower during the transitional seasons of spring and autumn. Conversely, energy sent to the grid is less during the winter and highest in the summer.

Figure 14.
Year 1 energy performance results of proposed residential house with ASHP: (a) Daily PV energy generation and load demand. (b) Monthly PV generation, load demand, self-consumption, and self-sufficiency. (c) Monthly PV generation, load demand, energy to the grid, and energy from the grid.
To verify the opposite trend operation of the PV system observed in the summer and winter, the result for the warmest day (a, b) and the coldest day of the year (c, d) is shown in Figure 15. The warmest day was July 31, while the coldest day was February 17. As depicted in Figure 15a, PV self-consumption and self-sufficiency both reach 100%, but at different time intervals. On the warmest day, PV generation peaks in the middle of the day, while the heat pump load reaches its peak at 5 pm, as shown in Figure 15b. This leads to a mismatch in peak load timings between the PV system generation and the heat pump load during the summer. In contrast, on February 17, the heat pump load was elevated during the nighttime due to a significant drop in winter temperatures, resulting in increased heating demands. The PV generation, however, reaches its peak in the middle of the day, causing a peak load timing discrepancy between the PV system generation and the heat pump load during the winter as well. The plots in Figure 15c confirm these findings, showing the opposite behavior of self-sufficiency and self-consumption during the morning and nighttime hours.
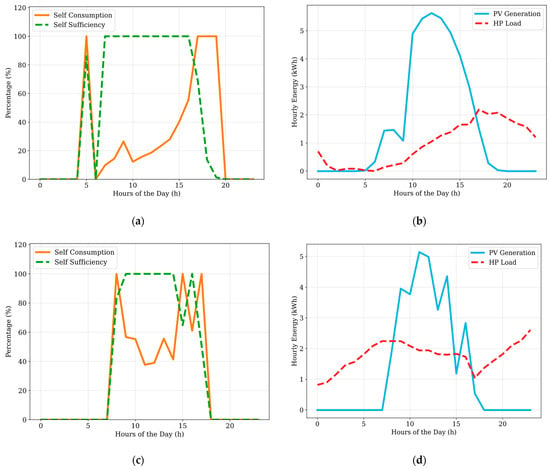
Figure 15.
Energy performance results of the warmest day (July 31) and the coldest day (February 17) of the study period: (a) Self-sufficiency and self-consumption on the warmest day. (b) PV generation and HP load for the warmest day. (c) Self-sufficiency and self-consumption on the coldest day. (d) PV generation and HP load for the coldest day.
Similarly, for the spring and fall equinoxes which occur on 21 March and 22 September, respectively, energy performance results are shown in Figure 16. Figure 16a,c shows the self-sufficiency and self-consumption on the spring and fall equinoxes, which is 100% during slightly different time intervals. Figure 16b,d shows the variation in PV system generation and HP load during the day and night. It can be seen that HP load demand is comparatively less than PV generation, which shows energy supplied to the grid is greater during spring and fall in Figure 14b,c.

Figure 16.
Energy performance results of the spring equinox (March 21) and the fall equinox (September 22) of the study period: (a) Self-sufficiency and self-consumption on the spring equinox. (b) PV generation and HP load for the spring equinox. (c) Self-sufficiency and self-consumption on the fall equinox. (d) PV generation and HP load for the fall equinox.
4.5. Impacts of the Limited Data Model on PV Sizing
When the PV system is designed using the Gaussian data model, the estimated PV rating, the real PV rating, the load demand, and the PV energy generation remain unchanged over the system’s lifetime compared to the hourly data model, as shown in Table 9. These results are expected because the PV size is designed to ensure the overall annual PV energy generation matches the total annual heat pump load. There is, however, a significant change in the other parameters in Table 9. A significant reduction is observed in the energy sent to the grid (from 154.7 to 88.7 MWh) and the energy taken from the grid (from 152.2 to 86.2 MWh), representing close to a 43% decrease. On the other hand, the self-consumption and self-sufficiency values have increased significantly. More specifically, self-consumption and self-sufficiency both doubled in value (from 30% to 60%).
Figure 17 compares the monthly energy sent and taken from the grid for the hourly data model and the Gaussian data model. The comparison between the hourly data model and the Gaussian data model emphasizes the importance of collecting accurate data for heat pumps in residential buildings. Even though the limited model data predicts the same PV size as the hourly data, it may skew the economic analysis by underestimating the amount of electricity taken and sent to the grid.

Figure 17.
Comparison of the energy sent to the grid and the energy received from the grid using two different load data models. (a) hourly data model proposed in this study. (b) Gaussian model generated from unique monthly data.
5. Discussion
The size of the PV system plays a crucial role in determining the economic viability, feasibility, and extent of adoption [69]. Thus, designing optimal systems sizing is essential for achieving reliability and the highest degree of cost-effectiveness [19,20,112]. Existing studies provide combined sizing of PV+HP systems in cold climates [64,92,93,113,114], by only considering the heating load of the house neglecting the cooling load. Similarly, other studies focus on sizing PV and battery systems without including the HP sizing [115,116,117], or only focus on the sizing of HP systems [94,95,96,118]. In contrast, this study presents a mathematical model for heat pump sizing as well as a straightforward PV sizing method, shedding light on the potential of PV-powered heat pumps for residential housing based on both heating and cooling loads with stepwise sizing of the system, providing the basis for the economic analysis of the system based on the load profile and importance of coupling thermal energy storage to the PV+HP system. The house model is validated with HAP and the HP model with the manufactural datasheets and presents the reliability of these models for future techno-economic optimizations under the circumstances of any possible locations. The heating and cooling load demand for the house is obtained by developing an open-source Python model of the house as it gives more flexibility in terms of customization to the users as compared to HAP software. HAP has limitations in terms of customization, and users are typically bound to the offered features i.e., it takes default values for certain parameters whereas the proposed model parameters can be modified as required giving an advantage for unique or specialized simulations.
The open-source house model, including the heating/cooling loads that can be regulated by the users, is developed and well-defined. The simulation results are obtained on an hourly, daily, and monthly basis. Although monthly data provides seasonal variations and trends with an understanding of monthly energy consumption, it may not provide short-term variations within the month. Daily load data simulations, however, provide more details than monthly load data but still lack the granularity of hourly load simulations. Hourly load data simulation is also useful for understanding the impact of diurnal and seasonal change; however, it requires more computational time and detailed input data. Since the sizing of one component can affect the other it is therefore necessary to analyze the mutual influence to appropriately size the whole system and this is achieved in this study by hourly simulation data. The system sizing based on hourly simulations provides more precise results compared to monthly for understanding energy consumption and PV self-consumption and self-sufficiency on specific days which is used for import/export of electricity to/from the grid providing especially for economic studies and evaluating peak loads which are shown in this study. Furthermore, the open-source black box air-air heat pump model is developed based on the Goodman manufacturers’ datasheet and hourly load of the house. The COP and EER of the proposed HP model 0301B series on the coldest and for 0421B on the warmest day are 2.06 and 4.42 respectively. This underscores the need to correctly select the situation that the optimization is run for in the system.
The maximum size of PV required to provide the power to run the heat pump to supply the residential thermal loads is estimated as 6.88 kW. The PV system is designed in SAM with an aim to minimize the grid electricity costs and the emissions from the residential sectors, aligning with the overarching goal of achieving net zero energy consumption. Therefore, in this study, PV power generated over the year, monthly, and on the coldest/warmest day as well as on the spring/fall equinox is also presented with self-consumption and self-sufficiency of PV as well as energy sent to/from the grid to provide clarity. By integrating these analyses, the study not only addresses immediate energy needs but also contributes to the larger objective of sustainable energy practices and achieving a net zero energy footprint for the residential sector. Residential sectors account for energy use amounting to 20% of energy consumption in Ontario [119], where 40% of emissions come from space and water heating [120], i.e., an average home in London emits 10.5 tons of carbon emission each year [120]. To reduce these emissions and achieve Canada’s net zero energy goal [7], the data obtained for energy sent to/from the grid will give us a reference to fulfill our missing targets. It also highlights the change in energy sent to/from the grid based on the hourly and monthly load profile, which is an important consideration when it comes to an economic analysis of the system model.
It is also shown in this study referring to the coldest, warmest, spring and fall equinox day of the year that there is a peak time mismatch for maximum PV generation and peak-time HP load as shown in Figure 15b; PV generation peaks in the middle of the day, while the heat pump load reaches its peak at 5 pm for summer. Similarly, on February 17, the heat pump load is elevated during the nighttime due to a significant drop in winter temperatures, resulting in increased heating demands. The PV generation, however, reaches its peak in the middle of the day, causing a peak load timing discrepancy during the winter as well, as shown in Figure 15d. Similar trends are also seen on the spring and fall equinoxes as shown in Figure 16b,d. Thus, maintaining the reliability on the grid during these periods is critical. This, however, opens future opportunities to store the excess PV energy generated during these mismatch periods in thermal energy-storage systems (i.e., thermal batteries) to increase the reliability of system models and decrease the dependence on the grid.
One of the limitations of this study pertains to the use of only the Gaussian model to generate the hourly data from the monthly energy. The main argument for using another model was to show the importance of generating accurate hourly data on PV system sizing in residential buildings’ heat pump applications. The results have, expectedly, revealed the importance of hourly data for PV-HP energy performance and economic analysis. Future work is required to investigate the impact of changing the mean and standard deviation of the normal distribution on the PV performance. This could result in proposing an optimal distribution model that matches the hourly data generated in this study. Further studies are also required to investigate other types of statistical distributions for the heat pump load [121]. These results can be further improved by incorporating non-HP electric loads into the full system with sizing. Future work can also include the optimization of this model based on the other constraints, i.e., space and specific economic limitations. These results can also be used further to size the backup system for the model, for example, integration of a thermal storage system; i.e., developing an optimal thermal battery (TB) model that can store the excess energy from the solar PV during the generation in the off-peak time period and use it during the peak time period so the need for electricity from the grid can be minimized. Thermal batteries can allow the storing of this excess energy which can be used when necessary, thus minimizing the energy supply–demand mismatch occurring due to the integration of renewable resources [122]. Moreover, this thermal battery model should also be sized accordingly based on the economics and size of the whole system, which again raises the need for economic analysis of the PV+HP+TB system. The technical, economical, and environmental benefits of integrating PV+HP with thermal energy storage have been identified by many researchers, including peak shaving, enhancing system overall efficiency, economic and energy savings, demand-side management, and emission mitigation [123]. Further studies are required to obtain the performance analysis, different system configurations and control strategies of the PV+HP+TB system as presented in [124] for the PV+HP system with integration of thermal and electrical energy storage. Along with this, the strategy needs to store energy in the TB system to be developed with a detailed thermodynamic model of the heat pump to optimize the size of TB and obtain its charging and discharging capability. Further, the study can also include electrical loads and domestic hot water demand throughout the year and optimize the system together making it more sustainable, leading to the net zero energy goal. This also opens the scope of carrying out economic efficiency and environmental impact studies to calculate yearly carbon tax/reduction compared to conventional fossil fuel systems.
6. Conclusions
This study outlines the sizing of the solar PV and HP based on the hourly and monthly heating and cooling loads of the residential house. The code written for each system model is open source and is available for other residential PV+HP models for different locations. Here, the heat pump model developed selects the heat pump based on the heating and cooling load of the house, giving an optimal HP size for the required house. The sizing of the PV system is such that the power generated is used to supply HP on an annual basis based on heating and cooling loads, the weather, and location data. Self-sufficiency and self-consumption of PV and the energy taken and fed to the grid are provided, which shows that the simulation based on the monthly load profile has a significant reduction of 43% for energy sent to/from the grid compared to the detailed hourly simulation and an increase from 30% to 60% for self-consumption and self-sufficiency. It also highlights the mismatch of PV system generation and HP load based on hourly simulation datasets for specific days in each season, i.e., the warmest and coldest day as well as spring and fall equinox. In future work, these datasets can be used to further economic analysis and design backup systems and/or reduce dependence on the grid with the help of optimal load management. The back-calculation PV-sizing algorithm combined with HP and thermal loads presented in this study exhibited robust performance and can be seamlessly used alongside other PV performance-analysis software tools like SAM. In the case study, the algorithm precisely determined the required PV size to meet the demands of the proposed residential house, which roughly doubles the size of a PV system targeted at meeting conventional plug loads. These results are easily integrated into the SAM to provide PV system designs for the combined house and heat pump. The algorithm’s flexibility positions it as a valuable tool for enabling solar electrification of both space heating and cooling.
Author Contributions
Conceptualization, J.M.P.; methodology, S.R., U.J., N.A., K.S.H., J.G. and J.M.P.; software, S.R., U.J., N.A., K.S.H. and J.G.; validation, S.R., U.J., N.A., K.S.H., J.G. and J.M.P.; formal analysis, S.R., U.J., N.A., K.S.H., J.G. and J.M.P.; investigation, S.R., U.J., N.A., K.S.H., J.G. and J.M.P.; resources, J.M.P.; data curation, S.R., U.J., N.A., K.S.H. and J.G.; writing—original draft preparation, S.R., U.J., N.A., K.S.H., J.G. and J.M.P.; writing—review and editing, S.R., U.J., N.A., K.S.H., J.G. and J.M.P.; visualization, S.R., U.J., N.A. and K.S.H.; supervision, J.M.P.; funding acquisition, J.M.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Western University Carbon Solutions Grant, the Natural Sciences and Engineering Research Council of Canada, and the Thompson Endowment.
Data Availability Statement
All data is available on the Open Science Framework https://osf.io/msrgk/.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analysis or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Nomenclature
| Abbreviations | |
| ACH | Air Change per Hour |
| ANN | Artificial Neural Network |
| ASHP | Air Source Heat Pump |
| AWHP | Air–Water Heat Pump |
| COP | Coefficient of Performance |
| E | Energy |
| EER | Energy Efficiency Ratio |
| HAP | Hourly Analysis Program |
| HP | Heat pump |
| HVAC | Heating, Ventilation and Air Conditioning |
| GHE | Ground Heat Exchanger |
| GHG | Greenhouse Gas |
| GSHP | Ground Source Heat Pump |
| NREL | National Renewable Energy Laboratories |
| PV | Photovoltaics |
| SAM | System Advisor Model |
| SC | Self-consumption |
| SS | Self-sufficiency |
| SHG | Solar Heat Gain |
| SHGC | Solar Heat Gain Constant |
| Latin symbols | |
| dt/dx | Temperature gradient across the heat transfer surface |
| Area normal to the direction of heat transfer (m2) | |
| Area of floor (m2) | |
| Area of frame (m2) | |
| Projected surface area of frame (m2) | |
| Area of glazing (m2) | |
| Actual surface area of the frame incorporating the depth at which the glass is placed inside the frame (m2) | |
| Absorptivity | |
| Solar absorptivity of exterior frame surface (W/m2) | |
| Conductance (W/(m2K)) | |
| Specific heat of infiltrated air (kJ/(kg-K)) | |
| Daily range | |
| Direct irradiance (W/m2) | |
| Incident solar radiation (W/m2) | |
| Convective heat transfer coefficient (W/(m2°C)) | |
| Overall exterior surface conductance (1/(Ohmm)) | |
| Combined convection and conduction coefficient (W/(m2C)) | |
| Height of ceiling (m) | |
| Latent heat of vaporization (J/Kg) | |
| Infiltration (m3/s) | |
| Thermal conductivity (W/(m°C)) | |
| Mass flow rate (kg/s) | |
| Heat transfer rate (W) | |
| Conduction heat flux (W/m2) | |
| Latent heat transfer (W) | |
| Sensible heat transfer (W) | |
| Thermal unit resistance ((m2 °C)/W) | |
| Resistance (°C/W) | |
| Hourly temperature (°C) | |
| Hourly Sol-air temperature (°C) | |
| Temperature of fluid in contact with heat transfer surface (°C) | |
| Temperature of heat transfer surface (°C) | |
| : (to−ti) | Difference between indoor and outdoor dry bulb temperature (°C) |
| Ambient temperature (°C) | |
| Overall heat transfer coefficient | |
| Space volume (m3) | |
| Specific Volume (m3/kg) | |
| Humidity ratio | |
| Percentage (%) | |
| Subscripts and superscripts | |
| Conduction | |
| Convection | |
| Direct radiation | |
| Diffuse radiation | |
| Frame | |
| Glazing | |
| Inside | |
| Inside wet bulb | |
| Infiltration | |
| Outside | |
| Original | |
| Load | |
| Sunlit area | |
| Total |
References
- Dincer, I.; Rosen, M.A.; Ahmadi, P. Optimization of Energy Systems; John Wiley & Sons: Hoboken, NJ, USA, 2017; ISBN 1-118-89443-X. [Google Scholar]
- Baghoolizadeh, M.; Rostamzadeh-Renani, R.; Rostamzadeh-Renani, M.; Toghraie, D. A Multi-Objective Optimization of a Building’s Total Heating and Cooling Loads and Total Costs in Various Climatic Situations Using Response Surface Methodology. Energy Rep. 2021, 7, 7520–7538. [Google Scholar] [CrossRef]
- USEPA. O Sources of Greenhouse Gas Emissions. Available online: https://www.epa.gov/ghgemissions/sources-greenhouse-gas-emissions (accessed on 20 September 2023).
- IPCC. The Evidence Is Clear: The Time for Action Is Now. We Can Halve Emissions by 2030; IPCC: Geneva, Switzerland, 2022. [Google Scholar]
- Environment and Climate Change Canada. Greenhouse Gas Sources and Sinks in Canada: Executive Summary. 2022. Available online: https://www.canada.ca/en/environment-climate-change/services/climate-change/greenhouse-gas-emissions/sources-sinks-executive-summary-2022.html (accessed on 4 July 2023).
- Canada: CO2 Emissions per Capita 1970–2022. Available online: https://www.statista.com/statistics/1290653/per-capita-emissions-in-canada/ (accessed on 20 September 2023).
- Canada, S. Net-Zero Emissions by 2050. Available online: https://www.canada.ca/en/services/environment/weather/climatechange/climate-plan/net-zero-emissions-2050.html (accessed on 11 July 2023).
- Dubois, G.; Sovacool, B.; Aall, C.; Nilsson, M.; Barbier, C.; Herrmann, A.; Bruyère, S.; Andersson, C.; Skold, B.; Nadaud, F.; et al. It Starts at Home? Climate Policies Targeting Household Consumption and Behavioral Decisions Are Key to Low-Carbon Futures. Energy Res. Soc. Sci. 2019, 52, 144–158. [Google Scholar] [CrossRef]
- Gandzeichuk, I. Council Post: Smart Homes: Reducing Carbon Footprint and Expenses. Available online: https://www.forbes.com/sites/forbestechcouncil/2021/12/10/smart-homes-reducing-carbon-footprint-and-expenses/ (accessed on 11 July 2023).
- Canada.ca. Heating Equipment for Residential Use. Available online: https://natural-resources.canada.ca/energy-efficiency/products/heating-equipment-for-residential-use/13740 (accessed on 25 February 2023).
- Zhang, C.; Nielsen, E.; Fan, J.; Furbo, S.; Li, Q. Experimental Investigation on a Combined Solar and Ground Source Heat Pump System for a Single-Family House: Energy Flow Analysis and Performance Assessment. Energy Build. 2021, 241, 110958. [Google Scholar] [CrossRef]
- El Hannach, M.; Ahmadi, P.; Guzman, L.; Pickup, S.; Kjeang, E. Life Cycle Assessment of Hydrogen and Diesel Dual-Fuel Class 8 Heavy Duty Trucks. Int. J. Hydrogen Energy 2019, 44, 8575–8584. [Google Scholar] [CrossRef]
- Mahjoob, A.; Ahmadi, P.; Afsaneh, H.; Vojdani, M.; Mortazavi, M. System Sizing and Transient Simulation of a Solar Photovoltaic Off-Grid Energy System in Various Climates with Air Heat Pumps. Sustain. Energy Technol. Assess. 2022, 54, 102788. [Google Scholar] [CrossRef]
- Karayel, G.K.; Javani, N.; Dincer, I. Green Hydrogen Production Potential for Turkey with Solar Energy. Int. J. Hydrogen Energy 2022, 47, 19354–19364. [Google Scholar] [CrossRef]
- Matasci, S. How Solar Panel Cost & Efficiency Change Over Time; EnergySage: Boston, MA, USA, 2022. [Google Scholar]
- Masson, G. 2018 Snapshot of Global Photovoltaic Markets. Report IEA PVPS T1-33: 2018. 2018. Available online: https://apvi.org.au/wp-content/uploads/2018/04/IEA_PVPS-A_Snapshot_of_Global_PV-1992-2017.pdf (accessed on 20 September 2023).
- Ahmadi, P.; Khoshnevisan, A. Dynamic Simulation and Lifecycle Assessment of Hydrogen Fuel Cell Electric Vehicles Considering Various Hydrogen Production Methods. Int. J. Hydrogen Energy 2022, 47, 26758–26769. [Google Scholar] [CrossRef]
- Mertens, K. Photovoltaics: Fundamentals, Technology, and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2018; ISBN 1-119-40104-6. [Google Scholar]
- Al-Falahi, M.D.; Jayasinghe, S.D.G.; Enshaei, H. A Review on Recent Size Optimization Methodologies for Standalone Solar and Wind Hybrid Renewable Energy System. Energy Convers. Manag. 2017, 143, 252–274. [Google Scholar] [CrossRef]
- Goel, S.; Sharma, R. Performance Evaluation of Stand Alone, Grid Connected and Hybrid Renewable Energy Systems for Rural Application: A Comparative Review. Renew. Sustain. Energy Rev. 2017, 78, 1378–1389. [Google Scholar] [CrossRef]
- Okoye, C.O.; Solyalı, O. Optimal Sizing of Stand-Alone Photovoltaic Systems in Residential Buildings. Energy 2017, 126, 573–584. [Google Scholar] [CrossRef]
- Shukla, A.K.; Sudhakar, K.; Baredar, P. Design, Simulation and Economic Analysis of Standalone Roof Top Solar PV System in India. Sol. Energy 2016, 136, 437–449. [Google Scholar] [CrossRef]
- Al-Salaymeh, A.; Al-Hamamre, Z.; Sharaf, F.; Abdelkader, M.R. Technical and Economical Assessment of the Utilization of Photovoltaic Systems in Residential Buildings: The Case of Jordan. Energy Convers. Manag. 2010, 51, 1719–1726. [Google Scholar] [CrossRef]
- Khatib, T.; Mohamed, A.; Sopian, K. A Review of Photovoltaic Systems Size Optimization Techniques. Renew. Sustain. Energy Rev. 2013, 22, 454–465. [Google Scholar] [CrossRef]
- Sidrach-de-Cardona, M.; Lopez, L.M. A Simple Model for Sizing Stand Alone Photovoltaic Systems. Sol. Energy Mater. Sol. Cells 1998, 55, 199–214. [Google Scholar] [CrossRef]
- Kazem, H.A.; Khatib, T.; Sopian, K. Sizing of a Standalone Photovoltaic/Battery System at Minimum Cost for Remote Housing Electrification in Sohar, Oman. Energy Build. 2013, 61, 108–115. [Google Scholar] [CrossRef]
- Muhsen, D.H.; Nabil, M.; Haider, H.T.; Khatib, T. A Novel Method for Sizing of Standalone Photovoltaic System Using Multi-Objective Differential Evolution Algorithm and Hybrid Multi-Criteria Decision Making Methods. Energy 2019, 174, 1158–1175. [Google Scholar] [CrossRef]
- Ridha, H.M.; Gomes, C.; Hizam, H.; Ahmadipour, M.; Heidari, A.A.; Chen, H. Multi-Objective Optimization and Multi-Criteria Decision-Making Methods for Optimal Design of Standalone Photovoltaic System: A Comprehensive Review. Renew. Sustain. Energy Rev. 2021, 135, 110202. [Google Scholar] [CrossRef]
- Amara, S.; Toumi, S.; Salah, C.B.; Saidi, A.S. Improvement of Techno-Economic Optimal Sizing of a Hybrid off-Grid Micro-Grid System. Energy 2021, 233, 121166. [Google Scholar] [CrossRef]
- Do Grid-Tied Photovoltaic Systems Really Have an Advantage? Available online: https://www.greenbuildingadvisor.com/article/do-grid-tied-photovoltaic-systems-really-have-an-advantage (accessed on 11 October 2023).
- Hayibo, K.S.; Pearce, J.M. A Review of the Value of Solar Methodology with a Case Study of the U.S. VOS. Renew. Sustain. Energy Rev. 2021, 137, 110599. [Google Scholar] [CrossRef]
- The Role of Net Metering in the Evolving Electricity System|National Academies. Available online: https://www.nationalacademies.org/our-work/the-role-of-net-metering-in-the-evolving-electricity-system (accessed on 19 July 2023).
- Nicoletti, F.; Cucumo, M.A.; Arcuri, N. Cost Optimal Sizing of Photovoltaic-Battery System and Air–Water Heat Pump in the Mediterranean Area. Energy Convers. Manag. 2022, 270, 116274. [Google Scholar] [CrossRef]
- O’Shaughnessy, E.; Cutler, D.; Ardani, K.; Margolis, R. Solar plus: A Review of the End-User Economics of Solar PV Integration with Storage and Load Control in Residential Buildings. Appl. Energy 2018, 228, 2165–2175. [Google Scholar] [CrossRef]
- Pearce, J.M.; Sommerfeldt, N. Economics of Grid-Tied Solar Photovoltaic Systems Coupled to Heat Pumps: The Case of Northern Climates of the U.S. and Canada. Energies 2021, 14, 834. [Google Scholar] [CrossRef]
- Padovani, F.; Sommerfeldt, N.; Longobardi, F.; Pearce, J.M. Decarbonizing Rural Residential Buildings in Cold Climates: A Techno-Economic Analysis of Heating Electrification. Energy Build. 2021, 250, 111284. [Google Scholar] [CrossRef]
- Sommerfeldt, N.; Pearce, J.M. Can Grid-Tied Solar Photovoltaics Lead to Residential Heating Electrification? A Techno-Economic Case Study in the Midwestern U.S. Appl. Energy 2023, 336, 120838. [Google Scholar] [CrossRef]
- Pena-Bello, A.; Schuetz, P.; Berger, M.; Worlitschek, J.; Patel, M.K.; Parra, D. Decarbonizing Heat with PV-Coupled Heat Pumps Supported by Electricity and Heat Storage: Impacts and Trade-Offs for Prosumers and the Grid. Energy Convers. Manag. 2021, 240, 114220. [Google Scholar] [CrossRef]
- Battaglia, M.; Haberl, R.; Bamberger, E.; Haller, M. Increased Self-Consumption and Grid Flexibility of PV and Heat Pump Systems with Thermal and Electrical Storage. Energy Procedia 2017, 135, 358–366. [Google Scholar] [CrossRef]
- Asgari, N.; Hayibo, K.S.; Groza, J.; Rana, S.; Pearce, J.M. Greenhouse Applications of Solar Photovoltaic Driven Heat Pumps in Northern Environments; Western University: London, ON, Canada, 2024; under review. [Google Scholar]
- Bloess, A.; Schill, W.-P.; Zerrahn, A. Power-to-Heat for Renewable Energy Integration: A Review of Technologies, Modeling Approaches, and Flexibility Potentials. Appl. Energy 2018, 212, 1611–1626. [Google Scholar] [CrossRef]
- Rana, S.; Sommerfeldt, N.; Pearce, J.M. Best Practices of Techno-Economic Methods for Solar Photovoltaic Coupled Heat Pump Analysis in Cold Climates; Western University: London, ON, Canada, 2024; under review. [Google Scholar]
- Heidarinejad, M.; Mattise, N.; Dahlhausen, M.; Sharma, K.; Benne, K.; Macumber, D.; Brackney, L.; Srebric, J. Demonstration of Reduced-Order Urban Scale Building Energy Models. Energy Build. 2017, 156, 17–28. [Google Scholar] [CrossRef]
- Jin, H.; Spitler, J.D. A Parameter Estimation Based Model of Water-to-Water Heat Pumps for Use in Energy Calculation Programs. ASHRAE Trans. 2002, 108, 3. [Google Scholar]
- Staffell, I.; Brett, D.; Brandon, N.; Hawkes, A. A Review of Domestic Heat Pumps. Energy Environ. Sci. 2012, 5, 9291–9306. [Google Scholar] [CrossRef]
- Emily Air Source vs Ground Source Heat Pumps (GSHPs). Available online: https://www.boreholesolutions.co.uk/blog/air-source-vs-ground-source-heat-pumps-gshps/ (accessed on 21 May 2024).
- Ground-Source versus Air-Source Heat Pumps. Dandelion Energy. Available online: https://dandelionenergy.com/ground-source-vs-air-source-heat-pumps (accessed on 7 July 2023).
- Casasso, A.; Sethi, R. Efficiency of Closed Loop Geothermal Heat Pumps: A Sensitivity Analysis. Renew. Energy 2014, 62, 737–746. [Google Scholar] [CrossRef]
- Cho, H.; Choi, J.M. The Quantitative Evaluation of Design Parameter’s Effects on a Ground Source Heat Pump System. Renew. Energy 2014, 65, 2–6. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, G.; Zhou, J.; Wu, J.; Shen, W. A Techno-Economic Comparison of a Direct Expansion Ground-Source and a Secondary Loop Ground-Coupled Heat Pump System for Cooling in a Residential Building. Appl. Therm. Eng. 2012, 35, 29–39. [Google Scholar] [CrossRef]
- Lazzarin, R. Heat Pumps and Solar Energy: A Review with Some Insights in the Future. Int. J. Refrig. 2020, 116, 146–160. [Google Scholar] [CrossRef]
- Lim, T.H.; De Kleine, R.D.; Keoleian, G.A. Energy Use and Carbon Reduction Potentials from Residential Ground Source Heat Pumps Considering Spatial and Economic Barriers. Energy Build. 2016, 128, 287–304. [Google Scholar] [CrossRef]
- Aditya, G.R.; Mikhaylova, O.; Narsilio, G.A.; Johnston, I.W. Comparative Costs of Ground Source Heat Pump Systems against Other Forms of Heating and Cooling for Different Climatic Conditions. Sustain. Energy Technol. Assess. 2020, 42, 100824. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Law, Y.L.E.; Alavy, M.; Walsh, P.R.; Leong, W.H.; Dworkin, S.B. An Analysis of the Factors Affecting Hybrid Ground-Source Heat Pump Installation Potential in North America. Appl. Energy 2014, 125, 28–38. [Google Scholar] [CrossRef]
- Baxter, V.D.; Groll, E.; Sikes, K. IEA HPT Annex 41 Cold Climate Heat Pumps—Final Report (HPT-AN41-1); IEA Heat Pump Centre: London, UK, 2017. [Google Scholar]
- Zhang, L.; Jiang, Y.; Dong, J.; Yao, Y. Advances in Vapor Compression Air Source Heat Pump System in Cold Regions: A Review. Renew. Sustain. Energy Rev. 2018, 81, 353–365. [Google Scholar] [CrossRef]
- Natural Resources Canada. Heating and Cooling with a Heat Pump. Available online: https://natural-resources.canada.ca/energy-efficiency/energy-star-canada/about/energy-star-announcements/publications/heating-and-cooling-heat-pump/6817 (accessed on 7 July 2023).
- Zhang, Y.; Ma, Q.; Li, B.; Fan, X.; Fu, Z. Application of an Air Source Heat Pump (ASHP) for Heating in Harbin, the Coldest Provincial Capital of China. Energy Build. 2017, 138, 96–103. [Google Scholar] [CrossRef]
- Kegel, M.; Sager, J.; Thomas, M.; Giguere, D.; Sunye, R. Performance Testing of Cold Climate Air Source Heat Pumps. In Proceedings of the 12th IEA Heat Pump Conference 2017, Rotterdam, The Netherlands, 15–18 May 2017; pp. 15–18. [Google Scholar]
- Global Heat Pump Sales Continue Double-Digit Growth—Analysis. Available online: https://www.iea.org/commentaries/global-heat-pump-sales-continue-double-digit-growth (accessed on 7 July 2023).
- Asaee, S.R.; Ugursal, V.I.; Beausoleil-Morrison, I. Techno-Economic Feasibility Evaluation of Air to Water Heat Pump Retrofit in the Canadian Housing Stock. Appl. Therm. Eng. 2017, 111, 936–949. [Google Scholar] [CrossRef]
- Udovichenko, A.; Zhong, L. Techno-Economic Analysis of Air-Source Heat Pump (ASHP) Technology for Single-Detached Home Heating Applications in Canada. Sci. Technol. Built Environ. 2020, 26, 1352–1370. [Google Scholar] [CrossRef]
- Kegel, M.; Tamasauskas, J.; Sunye, R.; Giguère, D. Heat Pumps in the Canadian Residential Sector. In Proceedings of the 11th IEA Heat Pump Conference, Montreal, QC, Canada, 12–16 May 2014. [Google Scholar]
- Fischer, D.; Lindberg, K.B.; Madani, H.; Wittwer, C. Impact of PV and Variable Prices on Optimal System Sizing for Heat Pumps and Thermal Storage. Energy Build. 2016, 128, 723–733. [Google Scholar] [CrossRef]
- Zaya, N.E.; Hassan, L.H.; Bilgil, H. Mathematical Modeling for Prediction of Heating and Air-Conditioning Energies of Multistory Buildings in Duhok City. Acad. J. Nawroz Univ. 2018, 7, 153–167. [Google Scholar] [CrossRef]
- Ashrae, A.H.F.; Atlanta, G. American Society of Heating. Refrig. Air-Cond. Eng. 2009, 1, 17.1–17.32. [Google Scholar]
- Hourly Analysis Program|Carrier Carrier Commercial North America. Available online: https://www.carrier.com/commercial/en/us/software/hvac-system-design/hourly-analysis-program/ (accessed on 7 June 2023).
- Freeman, J.M.; DiOrio, N.A.; Blair, N.J.; Neises, T.W.; Wagner, M.J.; Gilman, P.; Janzou, S. System Advisor Model (SAM) General Description (Version 2017.9.5); NREL/TP--6A20-70414; National Renewable Energy Laboratory: Golden, CO, USA, 2018; p. 1440404.
- Ibrahim, I.A.; Khatib, T.; Mohamed, A. Optimal Sizing of a Standalone Photovoltaic System for Remote Housing Electrification Using Numerical Algorithm and Improved System Models. Energy 2017, 126, 392–403. [Google Scholar] [CrossRef]
- Ibrahim, H.; Anani, N. Evaluation of Analytical Methods for Parameter Extraction of PV Modules. Energy Procedia 2017, 134, 69–78. [Google Scholar] [CrossRef]
- Egido, M.; Lorenzo, E. The Sizing of Stand Alone PV-System: A Review and a Proposed New Method. Sol. Energy Mater. Sol. Cells 1992, 26, 51–69. [Google Scholar] [CrossRef]
- Solar Photovoltaic Software—Appropedia, the Sustainability Wiki. Available online: https://www.appropedia.org/Solar_photovoltaic_software (accessed on 11 July 2023).
- ESP-r. Available online: https://web.archive.org/web/20200202174513/http://www.esru.strath.ac.uk:80/Programs/ESP-r.htm (accessed on 20 September 2023).
- s.r.o, © Solargis Solargis: pvPlanner. Available online: https://solargis.info/pvplanner/#tl=Google:hybrid&bm=satellite (accessed on 20 September 2023).
- Solar, L. Generate Solar Permit Packages in Minutes|Lyra Solar. Available online: https://get.solardesigntool.com/ (accessed on 20 September 2023).
- Aurora Solar: The World’s #1 Solar Design Software. Available online: https://aurorasolar.com/ (accessed on 20 September 2023).
- PVsyst—Logiciel Photovoltaïque. Available online: https://www.pvsyst.com/ (accessed on 20 September 2023).
- Laplace Systems Co., Ltd. Available online: https://www.lapsys.co.jp/english/products/pro.html (accessed on 20 September 2023).
- Welcome|TRNSYS: Transient System Simulation Tool. Available online: https://www.trnsys.com/ (accessed on 11 April 2023).
- RETScreen. Available online: https://www.deassociation.ca/retscreen (accessed on 26 May 2023).
- HOMER—Hybrid Renewable and Distributed Generation System Design Software. Available online: https://www.homerenergy.com/ (accessed on 20 September 2023).
- iHOGA/MHOGA—Simulation and Optimization of Stand-Alone and Grid-Connected Hybrid Renewable Systems. Available online: https://ihoga.unizar.es/en/ (accessed on 20 September 2023).
- Hybrid2|Wind Energy Center. Available online: https://www.umass.edu/windenergy/research/topics/tools/software/hybrid2 (accessed on 20 September 2023).
- Connolly, D.; Lund, H.; Mathiesen, B.V.; Leahy, M. A Review of Computer Tools for Analysing the Integration of Renewable Energy into Various Energy Systems. Appl. Energy 2010, 87, 1059–1082. [Google Scholar] [CrossRef]
- Bajpai, P.; Dash, V. Hybrid Renewable Energy Systems for Power Generation in Stand-Alone Applications: A Review. Renew. Sustain. Energy Rev. 2012, 16, 2926–2939. [Google Scholar] [CrossRef]
- Cui, W.; Li, X.; Li, X.; Si, T.; Lu, L.; Ma, T.; Wang, Q. Thermal Performance of Modified Melamine Foam/Graphene/Paraffin Wax Composite Phase Change Materials for Solar-Thermal Energy Conversion and Storage. J. Clean. Prod. 2022, 367, 133031. [Google Scholar] [CrossRef]
- Ani, V.A. Feasibility and Optimal Design of a Stand-Alone Photovoltaic Energy System for the Orphanage. J. Renew. Energy 2014, 2014, 379729. [Google Scholar] [CrossRef]
- Li, H.; Hou, K.; Xu, X.; Jia, H.; Zhu, L.; Mu, Y. Probabilistic Energy Flow Calculation for Regional Integrated Energy System Considering Cross-System Failures. Appl. Energy 2022, 308, 118326. [Google Scholar] [CrossRef]
- Schelly, C.; Louie, E.P.; Pearce, J.M. Examining Interconnection and Net Metering Policy for Distributed Generation in the United States. Renew. Energy Focus 2017, 22–23, 10–19. [Google Scholar] [CrossRef]
- Revesz, R.L.; Unel, B. The Future of Distributed Generation: Moving Past Net Metering. Envtl. L. Rep. News Anal. 2018, 48, 10719–10725. [Google Scholar]
- Bruno, R.; Bevilacqua, P.; Carpino, C.; Arcuri, N. The Cost-Optimal Analysis of a Multistory Building in the Mediterranean Area: Financial and Macroeconomic Projections. Energies 2020, 13, 1243. [Google Scholar] [CrossRef]
- Angenendt, G.; Zurmühlen, S.; Rücker, F.; Axelsen, H.; Sauer, D.U. Optimization and Operation of Integrated Homes with Photovoltaic Battery Energy Storage Systems and Power-to-Heat Coupling. Energy Convers. Manag. X 2019, 1, 100005. [Google Scholar] [CrossRef]
- Beck, T.; Kondziella, H.; Huard, G.; Bruckner, T. Optimal Operation, Configuration and Sizing of Generation and Storage Technologies for Residential Heat Pump Systems in the Spotlight of Self-Consumption of Photovoltaic Electricity. Appl. Energy 2017, 188, 604–619. [Google Scholar] [CrossRef]
- Lindberg, K.B.; Doorman, G.; Fischer, D.; Korpås, M.; Ånestad, A.; Sartori, I. Methodology for Optimal Energy System Design of Zero Energy Buildings Using Mixed-Integer Linear Programming. Energy Build. 2016, 127, 194–205. [Google Scholar] [CrossRef]
- Lyden, A.; Tuohy, P.G. Planning Level Sizing of Heat Pumps and Hot Water Tanks Incorporating Model Predictive Control and Future Electricity Tariffs. Energy 2022, 238, 121731. [Google Scholar] [CrossRef]
- Dongellini, M.; Naldi, C.; Morini, G.L. Influence of Sizing Strategy and Control Rules on the Energy Saving Potential of Heat Pump Hybrid Systems in a Residential Building. Energy Convers. Manag. 2021, 235, 114022. [Google Scholar] [CrossRef]
- Bruno, R.; Bevilacqua, P.; Arcuri, N. Assessing Cooling Energy Demands with the EN ISO 52016-1 Quasi-Steady Approach in the Mediterranean Area. J. Build. Eng. 2019, 24, 100740. [Google Scholar] [CrossRef]
- NSRDB. Available online: https://nsrdb.nrel.gov/ (accessed on 6 November 2023).
- McQuiston, F.C.; Parker, J.D.; Spitler, J.D.; Taherian, H. Heating, Ventilating, and Air Conditioning: Analysis and Design; John Wiley & Sons: Hoboken, NJ, USA, 2023; ISBN 978-1-119-89416-2. [Google Scholar]
- Rana, S.; Jamil, U.; Asgari, N.; Hayibo, K.S.; Groza, J.; Pearce, J.M. Residential Sizing of Solar Photovoltaic Systems and Heat Pumps to Provide Net Zero Sustainable Electrical and Thermal Building Energy. Open Sci. Framew. 2023. Available online: https://osf.io/msrgk, (accessed on 19 July 2023).
- Knapstein, K. Below-Grade Insulation—Part 2: Preventing Heat Transfer. Available online: https://framebuildingnews.com/below-grade-insulation-part-2-preventing-heat-transfer/ (accessed on 12 February 2024).
- Horan, P.; Luther, M.B. Using the Psychrometric Chart in Building Measurements. In Proceedings of the 44th Annual Conference of the Architectural Science Association, Auckland, New Zealand, 24 November 2010; pp. 1–8. [Google Scholar]
- Heat Pump|GSZ16|up to 16 SEER|9.0 HSPF|Goodman. Available online: https://www.goodmanmfg.com/products/heat-pumps/16-seer-gsz16 (accessed on 8 January 2023).
- Li, S.; Gong, G.; Peng, J. Dynamic Coupling Method between Air-Source Heat Pumps and Buildings in China’s Hot-Summer/Cold-Winter Zone. Appl. Energy 2019, 254, 113664. [Google Scholar] [CrossRef]
- Hayibo, K.S.; Pearce, J.M. Vertical Free-Swinging Photovoltaic Racking Energy Modeling: A Novel Approach to Agrivoltaics. Renew. Energy 2023, 218, 119343. [Google Scholar] [CrossRef]
- Hayibo, K.S.; Pearce, J.M. Vertical Free-Swinging Photovoltaic Racking Energy Modelling—Data and Performance Code. Open Sci. Framew. 2023. Available online: https://osf.io/jhx4b/ (accessed on 27 July 2023).
- Vandewetering, N.; Hayibo, K.S.; Pearce, J.M. Impacts of Location on Designs and Economics of DIY Low-Cost Fixed-Tilt Open Source Wood Solar Photovoltaic Racking. Designs 2022, 6, 41. [Google Scholar] [CrossRef]
- Ciocia, A.; Amato, A.; Di Leo, P.; Fichera, S.; Malgaroli, G.; Spertino, F.; Tzanova, S. Self-Consumption and Self-Sufficiency in Photovoltaic Systems: Effect of Grid Limitation and Storage Installation. Energies 2021, 14, 1591. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhuang, Z.; Lian, Z.; Yu, Y. Study on Building Energy Load Prediction Based on Monitoring Data. Procedia Eng. 2017, 205, 716–723. [Google Scholar] [CrossRef]
- An, J.; Yan, D.; Hong, T. Clustering and Statistical Analyses of Air-Conditioning Intensity and Use Patterns in Residential Buildings. Energy Build. 2018, 174, 214–227. [Google Scholar] [CrossRef]
- SunPower M Series SPR-M430-H-AC|EnergySage. Available online: https://www.energysage.com/solar-panels/sunpower/2730/SPR-M430-H-AC/ (accessed on 28 May 2024).
- Abbes, D.; Martinez, A.; Champenois, G. Life Cycle Cost, Embodied Energy and Loss of Power Supply Probability for the Optimal Design of Hybrid Power Systems. Math. Comput. Simul. 2014, 98, 46–62. [Google Scholar] [CrossRef]
- Coppitters, D.; De Paepe, W.; Contino, F. Robust Design Optimization of a Photovoltaic-Battery-Heat Pump System with Thermal Storage under Aleatory and Epistemic Uncertainty. Energy 2021, 229, 120692. [Google Scholar] [CrossRef]
- Wolisz, H.; Schütz, T.; Blanke, T.; Hagenkamp, M.; Kohrn, M.; Wesseling, M.; Müller, D. Cost Optimal Sizing of Smart Buildings’ Energy System Components Considering Changing End-Consumer Electricity Markets. Energy 2017, 137, 715–728. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, P.; Pimm, A.; Feng, D.; Zheng, M. Optimal Design and Operation of PV-Battery Systems Considering the Interdependency of Heat Pumps. J. Energy Storage 2019, 23, 526–536. [Google Scholar] [CrossRef]
- Duman, A.C.; Erden, H.S.; Gönül, Ö.; Güler, Ö. Optimal Sizing of PV-BESS Units for Home Energy Management System-Equipped Households Considering Day-Ahead Load Scheduling for Demand Response and Self-Consumption. Energy Build. 2022, 267, 112164. [Google Scholar] [CrossRef]
- Fioriti, D.; Pellegrino, L.; Lutzemberger, G.; Micolano, E.; Poli, D. Optimal Sizing of Residential Battery Systems with Multi-Year Dynamics and a Novel Rainflow-Based Model of Storage Degradation: An Extensive Italian Case Study. Electr. Power Syst. Res. 2022, 203, 107675. [Google Scholar] [CrossRef]
- Cruz-Peragón, F.; Gómez-de La Cruz, F.J.; Palomar-Carnicero, J.M.; López-García, R. Optimal Design of a Hybrid Ground Source Heat Pump for an Official Building with Thermal Load Imbalance and Limited Space for the Ground Heat Exchanger. Renew. Energy 2022, 195, 381–394. [Google Scholar] [CrossRef]
- Government of Canada, Canada Energy Regulator. CER—Provincial and Territorial Energy Profiles—Ontario. Available online: https://www.cer-rec.gc.ca/en/data-analysis/energy-markets/provincial-territorial-energy-profiles/provincial-territorial-energy-profiles-ontario.html (accessed on 28 November 2023).
- Household Energy Use and Greenhouse Gas Emissions. Available online: https://caroliniancanada.ca/article/household-energy-use-and-greenhouse-gas-emissions-20201125 (accessed on 28 November 2023).
- Melo, F.C.; Carrilho da Graça, G.; Oliveira Panão, M.J.N. A Review of Annual, Monthly, and Hourly Electricity Use in Buildings. Energy Build. 2023, 293, 113201. [Google Scholar] [CrossRef]
- Ermel, C.; Bianchi, M.V.A.; Cardoso, A.P.; Schneider, P.S. Thermal Storage Integrated into Air-Source Heat Pumps to Leverage Building Electrification: A Systematic Literature Review. Appl. Therm. Eng. 2022, 215, 118975. [Google Scholar] [CrossRef]
- Li, Y.; Rosengarten, G.; Stanley, C.; Mojiri, A. Electrification of Residential Heating, Cooling and Hot Water: Load Smoothing Using Onsite Photovoltaics, Heat Pump and Thermal Batteries. J. Energy Storage 2022, 56, 105873. [Google Scholar] [CrossRef]
- Aneli, S.; Arena, R.; Marco Tina, G.; Gagliano, A. Improvement of Energy Self-Sufficiency in Residential Buildings by Using Solar-Assisted Heat Pumps and Thermal and Electrical Storage. Sustain. Energy Technol. Assess. 2023, 60, 103446. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).