Implications of Using Scalar Forcing to Sustain Reactant Mixture Stratification in Direct Numerical Simulations of Turbulent Combustion

Abstract

A recently proposed scalar forcing scheme that maintains the mixture fraction mean, root-mean-square and probability density function in the unburned gas can lead to a statistically quasi-stationary state in direct numerical simulations of turbulent stratified combustion when combined with velocity forcing. Scalar forcing alongside turbulence forcing leads to greater values of turbulent burning velocity and flame surface area in comparison to unforced simulations for globally fuel-lean mixtures. The sustained unburned gas mixture inhomogeneity changes the percentage shares of back- and front-supported flame elements in comparison to unforced simulations, and this effect is particularly apparent for high turbulence intensities. Scalar forcing does not significantly affect the heat release rates due to different modes of combustion and the micro-mixing rate within the flame characterised by scalar dissipation rate of the reaction progress variable. Thus, scalar forcing has a significant potential for enabling detailed parametric studies as well as providing well-converged time-averaged statistics for stratified-mixture combustion using Direct Numerical Simulations in canonical configurations.

1. Introduction

Forcing the turbulent velocity field enables Direct Numerical Simulations (DNS) of turbulent fluid motion to reach a quasi-stationary state in canonical configurations where no other mechanism is available for turbulence generation. This enables the extraction of converged statistics from DNS data by time averaging, even for a limited domain size. Time-averaged statistics from statistically stationary DNS databases have assisted numerous studies in the field of turbulent non-reacting and reacting flow analyses. Until recently, the benefits of achieving statistical stationarity in DNS of turbulent combustion in canonical configurations with forced turbulence have been limited to premixed combustion simulations, since mixture inhomogeneity in the unburned gas decays under sustained turbulence conditions in the case of partially premixed mixtures. Without any external scalar fluctuation generating mechanism, a statistically quasi-stationary state can only be achieved once the reactants have become perfectly mixed (i.e., premixed combustion). As such, many DNS studies of turbulent stratified-mixture combustion have relied on unsteady decaying turbulence conditions (e.g., [1,2,3,4,5,6,7,8,9,10,11,12,13]). However, mixture inhomogeneity in the unburned gas can be sustained with scalar forcing by including an additional term in the species conservation equations, which can be utilised to reach a quasi-steady state for stratified-mixture combustion. An appropriate scalar forcing term offers additional advantages aside from converged statistics, such as enabling precise control over the probability density function (PDF) of the species mass fractions (and the corresponding mixture fraction) in the unburned gas, enabling comprehensive parametric analyses on the effects of the mixture fraction distribution.

Stratified-mixture combustion offers some benefits compared to premixed combustion, such as allowing for leaner combustion conditions, manipulating the flammability limits, flame propagation rate and pollutant emission rates [14]. Moreover, stratified-mixture combustion can also take place as a result of unintentional inadequate mixing. Lipatnikov [14] and Domingo et al. [15] provided an extensive review of experimental and numerical findings of stratified-mixture combustion. High-performance computing has enabled DNS of stratified-mixture combustion [1,2,3,4,5,6,7,8,9,10,11,12,13,16,17,18,19], and the vast majority of these studies have been conducted for statistically planar flames in canonical ‘flame-in-a-box’ configuration [1,2,3,4,5,6,7,8,9,10,11,12,13]. Richardson and Chen [16] and Brearley et al. [19] analysed turbulent stratified-mixture combustion using three-dimensional DNS to analyse the effects of the relative alignments of equivalence ratio and reaction progress variable gradients on the global behaviours of burning, flame propagation rate and flame surface area and their modelling implications. Proch et al. [17] and Inanc et al. [18] carried out flame-resolved three-dimensional high-fidelity simulations of turbulent stratified-mixture combustion of a laboratory-scale configuration used in experiments by Barlow et al. [20] and Sweeney et al. [21,22]. The aforementioned DNS analyses on turbulent stratified-mixture combustion offered fundamental physical information on the stratified flame structure [1,2,3,5,8,13,16,18,19] and flame propagation rate [4,12,16,18]. This information was subsequently utilised to develop closure methodologies for scalar variances and co-variances [3,5,11], turbulent scalar flux [9], flame surface density [10,19], and scalar dissipation and cross-scalar dissipation rates [7,8,13].

The development of a scalar forcing methodology that accurately captures characteristics of turbulent stratified combustion has been the subject of recent research efforts [23,24] where the effectiveness of the methodology was demonstrated mainly for passive scalar mixing. The sensitivity of the method to different turbulence and scalar conditions, including decaying turbulence and different turbulence forcing schemes (Lundgren forcing [25] and Modified Bandwidth forcing [26]) along with different scalar length scales, has been performed in the earlier work by Brearley et al. [24]. It was found that the length scale of the scalar distribution at the end of simulation time is independent of the initial value specified for the scalar length scale and was only dependent on the nature of the velocity forcing scheme. Ideally, the scalar forcing should only influence the root-mean-square (rms) scalar value and the underlying scalar distribution, but should not interfere with other flow properties. Therefore, the evolution of the scalar-to-turbulence integral length scale ratio should be determined by turbulent mixing in the unburned mixture. The mean values of the normalised scalar dissipation rate were shown to change from its initial value for scalar forcing irrespective of the nature of turbulent flow forcing. Furthermore, it has also been shown by Brearley et al. [24] that the PDF shape can be maintained for all turbulence conditions, i.e., decaying turbulence, Lundgren forcing and Modified Bandwidth forcing, without any modifications needed to the scalar forcing method. Brearley et al. [24] also showed that the root-mean-square value of scalar fluctuation is faithfully maintained by the scalar forcing technique for different PDF shapes (i.e., bimodal or Gaussian). However, the influence of sustained mixture stratification on the structure and dynamics of turbulent planar flames is yet to be analysed in detail. Therefore, the main objectives of this paper are (i) to understand the capabilities and limitations of the scalar forcing methodology by simulating a varied DNS database, and (ii) to analyse the statistical behaviours of turbulent burning velocity, flame surface area and reaction zone structure (e.g., the fractional share of front- and back-supported combustion, and the contributions of heat release originating from different modes of combustion) extracted from DNS of turbulent stratified flame simulations where (a) both the scalar field and the turbulence field are forced, (b) only the scalar field is forced and (c) where neither fields are subject to external forcing.

The following section provides the mathematical description of the scalar forcing methodology and Section 3 describes the DNS database. The results and corresponding discussion are presented in Section 4, which is followed by the conclusions of the work in Section 5.

2. Forcing Methodology

The scalar forcing methodology proposed by Daniel et al. [23] and further developed by Brearley et al. [24] has been adopted for this study as it can maintain a prescribed distribution (i.e., probability density function (PDF)) of a scalar field (e.g., bimodal, uniform, or bell-shaped). Consequently, the mean, root-mean-square (rms) and scalar bounds are also maintained.

A detailed description and derivation of the scalar forcing scheme used here are provided by Daniel et al. [23] for the original scalar forcing scheme and details on the modified scalar forcing scheme to account for the feedback on the scalar dissipation rate to maintain the prescribed rms value of the scalar fluctuations are available in Brearley et al. [24]. It should be recognised here that Daniel et al. [23] originally proposed the scalar forcing methodology based on a reaction analogy to describe mixing. According to this analogy, hypothetical chemical species have reactions which constitute a demixing processes that transform a partially mixed state into the excess pure component. In terms of a scalar field, the reactions transform the regions with below-average scalar values into the lower bound values and regions with above-average scalar values into the upper bound values. Thus, the reactions counteract the effects of diffusion and turbulent mixing. A complete derivation for this is already provided in the work by Daniel et al. [23] and is not presented in the current paper to avoid repetition and to maintain brevity as the main focus of the paper is the application of the scalar forcing methodology to reacting flow simulations of stratified mixtures.

The transport equation of a species mass fraction $Y_i$ under scalar forcing is

$$\frac{\partial \left(\rho Y_i\right)}{\partial t}+\frac{\partial \left(\rho u_k{Y}_i\right)}{\partial x_k}=\frac{\partial }{\partial x_k}\left(\rho D\frac{\partial Y_i}{\partial x_k}\right)+{\dot{\omega }}_i+\rho f_{Y_i}$$

(1)

where $Y_i$ represents the reactant species in the unburned gas (i.e., $Y_F$ and $Y_O$), ${\dot{\omega }}_i$ is its reaction rate (negligible in the unburned gas where the scalar forcing is applied) and $f_{Y_i}$ is the scalar forcing term (i.e., $f_{Y_F}$ and $f_{Y_O}$). Daniel et al. [23] developed a forcing scheme capable of satisfying characteristics of fuel-air stratification by considering a hypothetical chemical reaction that converts mixed fluid into its unmixed states, and proposed a forcing term for a generic scalar $\psi$ (the scalar being forced) which is given as [23]:

$$f_{\psi }=\left\{\begin{array}{cc}-\left({\psi }_u-{\psi }_l\right)jK{\left(\frac{{\psi }_u+{\psi }_l-2\psi }{{\psi }_u-{\psi }_l}\right)}^g{\left(\frac{\psi -{\psi }_l}{{\psi }_u-{\psi }_l}\right)}^j\hfill & \mathrm{when}\psi \le {\psi }_{\mathrm{m}}\hfill \\ +\left({\psi }_u-{\psi }_l\right)jK{\left(\frac{2\psi -{\psi }_u-{\psi }_l}{{\psi }_u-{\psi }_l}\right)}^g{\left(\frac{{\psi }_u-\psi }{{\psi }_u-{\psi }_l}\right)}^j\hfill & \mathrm{when}\psi >{\psi }_{\mathrm{m}}\hfill \end{array}\right.$$

(2)

where ${\psi }_l$ and ${\psi }_u$ are the chosen lower and upper bounds of $\psi$ respectively with a target mean ${\psi }_{\mathrm{m}}=({\psi }_u+{\psi }_l)/2$ assuming a symmetrical scalar distribution. The reaction rate constant of the hypothetical chemical reaction is K, with j and g being the stoichiometric coefficients. The hypothetical chemical reaction is given by:

$$\begin{array}{cc}\hfill jM+g{E}_l& \to \left(2j+g\right)E_l\mathrm{when}\psi \le {\psi }_{\mathrm{m}}\hfill \end{array}$$

(3a)

$$\begin{array}{cc}\hfill jM+g{E}_u& \to \left(2j+g\right)E_u\mathrm{when}\psi >{\psi }_{\mathrm{m}}\hfill \end{array}$$

(3b)

where M is a hypothetical chemical species representing the mixed fluid state, $E_l$ and $E_u$ are hypothetical chemical species representing the extra concentrations of unmixed fluid towards the lower or upper bounds of the scalar respectively. Brearley et al. [24] made modifications to Equation (2) to make it more robust for a chemically reacting flow. According to Daniel et al. [23] K value should be chosen such that it corresponds to the desired steady state scalar dissipation rate, which controls the scalar PDF distribution. As in the case of reacting flow simulations the prescribed rms value of scalar fluctuation ${\psi }_0^{\prime }$ needs to be maintained, a rms error signal term $\left({\psi }_0^{\prime }-{\psi }^{\prime }\right)$ to Equation (2) was introduced [24]. Then, K is considered as the constant in the proportional control system to maintain ${\psi }^{\prime }$. The forcing term with these modifications therefore takes the following form:

$$f_{\psi }=\left\{\begin{array}{cc}-\left({\psi }_0^{\prime }-{\psi }^{\prime }\right)\left({\psi }_u-{\psi }_l\right)jK{\left(\frac{{\psi }_u+{\psi }_l-2\psi }{{\psi }_u-{\psi }_l}\right)}^g{\left(\frac{\psi -{\psi }_l}{{\psi }_u-{\psi }_l}\right)}^j\hfill & \mathrm{when}\psi \le {\psi }_{\mathrm{m}}\hfill \\ +\left({\psi }_0^{\prime }-{\psi }^{\prime }\right)\left({\psi }_u-{\psi }_l\right)jK{\left(\frac{2\psi -{\psi }_u-{\psi }_l}{{\psi }_u-{\psi }_l}\right)}^g{\left(\frac{{\psi }_u-\psi }{{\psi }_u-{\psi }_l}\right)}^j\hfill & \mathrm{when}\psi >{\psi }_{\mathrm{m}}\hfill \end{array}\right.$$

(4)

In the case when the scalar field is subject to asymmetries, the above forcing scheme would eventually convert all the fluid into a uniform field of either $\psi ={\psi }_u$ or $\psi ={\psi }_l$. Such asymmetries could be introduced in the initial conditions, or due to the flame preferentially propagating through certain mixture compositions. In order to avoid this issue, the expression given by Equation (4) was modified by Brearley et al. [24] to allow for a self-correction mechanism. According to this modification, the instantaneous mean scalar $〈\psi 〉$, not to be confused with the target mean ${\psi }_{\mathrm{m}}$, is calculated and fed back to the forcing equation which allows for self-regulation of the PDF of $\psi$. The updated ${\psi }_{\mathrm{m}}$ when used in the forcing equation yields:

$${\psi }_{\mathrm{m}}^{*}=K^{*}\left(〈\psi 〉-{\psi }_{\mathrm{m}}\right)+{\psi }_{\mathrm{m}}$$

(5)

where $K^{*}$ is the proportional control constant to maintain ${\psi }_{\mathrm{m}}$. In addition, hypothetical lower and upper limits ${\psi }_l^{*}$ and ${\psi }_u^{*}$ corresponding to ${\psi }_{\mathrm{m}}^{*}$ should be evaluated in the following manner:

$$\begin{array}{cc}\hfill {\psi }_l^{*}& ={\psi }_u-2\left({\psi }_u-{\psi }_{\mathrm{m}}^{*}\right)\hfill \end{array}$$

(6a)

$$\begin{array}{cc}\hfill {\psi }_u^{*}& ={\psi }_l+2\left({\psi }_{\mathrm{m}}^{*}-{\psi }_l\right)\hfill \end{array}$$

(6b)

Note that these limits do not influence the location of the specified upper and lower bounds ${\psi }_u$ and ${\psi }_l$. In this case ${\psi }_u^{*}$ is only used in the calculation of the forcing term for $\psi \le {\psi }_{\mathrm{m}}^{*}$, and ${\psi }_l^{*}$ is only used in the calculation for $\psi >{\psi }_{\mathrm{m}}^{*}$. This yields the modified forcing term as [24]:

$$f_{\psi }=\left\{\begin{array}{cc}-\left({\psi }_0^{\prime }-{\psi }^{\prime }\right)\left({\psi }_u^{*}-{\psi }_l\right)jK{\left(\frac{{\psi }_u^{*}+{\psi }_l-2\psi }{{\psi }_u^{*}-{\psi }_l}\right)}^g{\left(\frac{\psi -{\psi }_l}{{\psi }_u^{*}-{\psi }_l}\right)}^j\hfill & \mathrm{when}\psi \le {\psi }_{\mathrm{m}}^{*}\hfill \\ +\left({\psi }_0^{\prime }-{\psi }^{\prime }\right)\left({\psi }_u-{\psi }_l^{*}\right)jK{\left(\frac{2\psi -{\psi }_u-{\psi }_l^{*}}{{\psi }_u-{\psi }_l^{*}}\right)}^g{\left(\frac{{\psi }_u-\psi }{{\psi }_u-{\psi }_l^{*}}\right)}^j\hfill & \mathrm{when}\psi >{\psi }_{\mathrm{m}}^{*}\hfill \end{array}\right.$$

(7)

It should be recognised here that when different instantaneous values of global mean $〈\psi 〉$ with ${\psi }_l=0$ and ${\psi }_u=1$ are used, the forcing term naturally reduces to zero at the specified bounds under all conditions. The effects of modifying the stoichiometric coefficients (j and g) change the shape of the forcing term and consequently, the resulting scalar PDF. Following Brearley et al. [24] $j=g=1$ is considered and a detailed account of the sensitivity to these parameters is provided by Daniel et al. [23]. It has been demonstrated in [24] that the forcing term tends to maintain the required mean values of the scalar, when $〈\psi 〉<{\psi }_{\mathrm{m}}$ and $〈\psi 〉>{\psi }_{\mathrm{m}}$, by using the self-correction control system.

For the transport equations of the species mass fractions as shown in Equation (1), the following source terms are used:

$$\begin{array}{c}\hfill f_{Y_F}=\left\{\begin{array}{cc}-\left(Y_{F0}^{\prime }-Y_F^{\prime }\right)\left(Y_{Fu}^{*}-Y_{Fl}\right)K\left(\frac{Y_{Fu}^{*}+Y_{Fl}-2Y_F}{Y_{Fu}^{*}-Y_{Fl}}\right)\left(\frac{Y_F-Y_{Fl}}{Y_{Fu}^{*}-Y_{Fl}}\right)\hfill & \mathrm{when}{Y}_F\le Y_{Fm}^{*}\hfill \\ +\left(Y_{F0}^{\prime }-Y_F^{\prime }\right)\left(Y_{Fu}-Y_{Fl}^{*}\right)K\left(\frac{2Y_F-Y_{Fu}-Y_{Fl}^{*}}{Y_{Fu}-Y_{Fl}^{*}}\right)\left(\frac{Y_{Fu}-Y_F}{Y_{Fu}-Y_{Fl}^{*}}\right)\hfill & \mathrm{when}{Y}_F>Y_{Fm}^{*}\hfill \end{array}\right.\\ \hfill f_{Y_O}=\left\{\begin{array}{cc}+\left(Y_{O0}^{\prime }-Y_O^{\prime }\right)\left(Y_{Ou}^{*}-Y_{Ol}\right)K\left(\frac{Y_{Ou}^{*}+Y_{Ol}-2Y_O}{Y_{Ou}^{*}-Y_{Ol}}\right)\left(\frac{Y_O-Y_{Ol}}{Y_{Ou}^{*}-Y_{Ol}}\right)\hfill & \mathrm{when}{Y}_O\le Y_{Om}^{*}\hfill \\ -\left(Y_{O0}^{\prime }-Y_O^{\prime }\right)\left(Y_{Ou}-Y_{Ol}^{*}\right)K\left(\frac{2Y_O-Y_{Ou}-Y_{Ol}^{*}}{Y_{Ou}-Y_{Ol}^{*}}\right)\left(\frac{Y_{Ou}-Y_O}{Y_{Ou}-Y_{Ol}^{*}}\right)\hfill & \mathrm{when}{Y}_O>Y_{Om}^{*}\hfill \end{array}\right.\end{array}$$

(8)

where subscripts l and u indicate the chosen lower and upper bounds of the scalar, a subscript m gives the mean value, and a subscript 0 denotes the target value. These quantities can be derived from the target mixture fraction $\xi =(Y_F-Y_O/s+Y_{O\infty }/s)/(Y_{F\infty }+Y_{O\infty }/s)$ values in the unburned gas, i.e., $Y_F=Y_{F\infty }\xi$ and $Y_O=Y_{O\infty }(1-\xi )$ where $Y_{F\infty }=1.0$ and $Y_{O\infty }=0.233$ being the fuel and oxidiser mass fractions in the pure fuel and pure air, respectively, and s is the stoichiometric oxygen-to-fuel mass ratio. $Y_F^{\prime }$ and $Y_O^{\prime }$ are the rms values of the respective scalar fields in the unburned gas, and $Y_{F0}^{\prime }$ and $Y_{O0}^{\prime }$ are their target values to be maintained. The parameter K is the proportional control constant, that must exceed approximately $K/(1/T_{\mathrm{turb}})>{10}^3$ for the rms value of the scalar fluctuation to be maintained effectively, with greater values being found to have no adverse effects on the results [24]. Quantities marked with a superscript asterisk (*) are altered by the forcing scheme throughout the simulation to maintain the mean mixture fraction $\langle \xi \rangle$ at the target values [23,24] which ensures that the scalar field does not diverge to a fully mixed state at one of the scalar bounds. These quantities in terms of mixture fraction are defined as ${\xi }_m^{*}=K^{*}\left(〈\xi 〉-{\xi }_m\right)+{\xi }_m$, ${\xi }_l^{*}={\xi }_u-2\left({\xi }_u-{\xi }_m^{*}\right)$, ${\xi }_u^{*}={\xi }_l+2\left({\xi }_m^{*}-{\xi }_l\right)$, where $K^{*}$ is the proportional control constant in the mean correction control system. A $K^{*}$ value exceeding $1.0$ is required to ensure that the forcing term can effectively prevent the scalar mean from drifting, where values up to 10 have been tested and the target mean value of the scalar is maintained more faithfully for higher values of $K^{*}$ [24]. The corresponding quantities for the species mass fractions are then evaluated from the mixture fraction using the relations $Y_F=Y_{F\infty }\xi$ and $Y_O=Y_{O\infty }(1-\xi )$.

It should be noted that it is possible to solve an additional transport equation for a passive scalar such as the mixture fraction $\xi$, and apply scalar forcing to its transport equation only. Then, $Y_F$ and $Y_O$ can be evaluated in the unburned gas only at the end of each timestep from the mixture fraction and reaction progress variable [24]. This is mathematically equivalent to forcing the species mass fractions directly. Interested readers are referred to Brearley et al. [24] for a more thorough discussion on the scalar forcing scheme with its derivation, validation and mathematical properties. The scalar forcing is employed only in the unburned gas where the chemical reaction is negligible, which is characterised by $c<c_{ϵ}=0.001$, where c is the reaction progress variable which monotonically increases from 0 to 1 from the unburned gas to the fully burned gas. The reaction progress variable c is defined as [1]

$$c=\frac{\xi Y_{F\infty }-Y_F}{\xi Y_{F\infty }-max\left[0,\frac{\xi -{\xi }_{st}}{1-{\xi }_{st}}\right]Y_{F\infty }}$$

(9)

The forcing scheme [23,24] does not have any impact during the reacting simulations as the forcing term is switched off in the reaction/heat release zone. The value of $c=0.001$ was chosen as the boundary between the unburned gas and the flame so that the pure mixing relations between the mixture fraction and the species mass fractions can be used without any significant loss in accuracy. In reality, $c=c_{ϵ}$ with $c_{ϵ}$ being a small positive fraction can be a suitable choice. It has been demonstrated elsewhere [24] that reducing $c_{ϵ}$ from 0.01 by up to two orders of magnitude has a negligible effect on the flame surface area and propagation rate, and will not be repeated in this paper for the sake of conciseness. Interested readers are referred to Brearley et al. [24] for the detailed description of the validation and performance of the aforementioned scalar forcing methodology for passive scalar mixing in non-reacting flows and the performance of this scalar forcing for different values of K and $K^{*}$. It was demonstrated that the mean and rms values of the forced scalar are faithfully maintained along with the prescribed PDF for large values of $K^{*}$ and K (i.e., $K^{*}\gg 1$ and $K\gg 1/T_{char}\gg 1$ where $T_{char}$ is the characteristic timescale which can be either chemical timescale or eddy turnover time for stratified-mixture combustion). The above information is not repeated here as this paper will principally focus on stratified-mixture combustion simulations in the presence of scalar forcing according to Ref. [24].

3. DNS Database

Table 1. Summary of simulation parameters. For decaying turbulence simulations the values correspond to initial conditions.

Case	Scalar Forcing	Velocity Forcing	${\mathit{u}}^{\mathbf{\prime }}/{\mathit{S}}_{\mathit{b}}$	$\mathit{\ell }\mathbf{/}{\mathit{\delta }}_{\mathit{L}\mathbf{,}\mathit{m}}$	$\mathbf{\langle }\mathit{\xi }\mathbf{\rangle }$ ($\mathbf{\langle }\mathit{\varphi }\mathbf{\rangle }$)	${\mathit{\xi }}^{\mathbf{\prime }}$ (${\mathit{\varphi }}^{\mathbf{\prime }}$)	Da	Ka	${\mathit{\ell }}_{\mathit{\varphi }}/\mathit{\ell }$	Domain	Grid
(a)	yes	yes	4.0	3.0	0.044 (0.80)	0.008 (0.14)	0.75	4.62	1.5	$47.9{\delta }_{Lm}\times {\left(19.2{\delta }_{Lm}\right)}^2$	$1000\times {400}^2$
(b)	yes	yes	8.0	3.0	0.044 (0.80)	0.008 (0.14)	0.37	13.1	1.5	$47.9{\delta }_{Lm}\times {\left(19.2{\delta }_{Lm}\right)}^2$	$1000\times {400}^2$
(c)	yes	no	4.0	3.0	0.044 (0.80)	0.008 (0.14)	0.75	4.62	1.5	$47.9{\delta }_{Lm}\times {\left(19.2{\delta }_{Lm}\right)}^2$	$1000\times {400}^2$
(d)	yes	no	8.0	3.0	0.044 (0.80)	0.008 (0.14)	0.37	13.1	1.5	$47.9{\delta }_{Lm}\times {\left(19.2{\delta }_{Lm}\right)}^2$	$1000\times {400}^2$
(e)	no	no	4.0	3.0	0.044 (0.8)	0.008 (0.14)	0.75	4.62	1.5	$47.9{\delta }_{Lm}\times {\left(19.2{\delta }_{Lm}\right)}^2$	$1000\times {400}^2$
(f)	no	no	8.0	3.0	0.044 (0.8)	0.008 (0.14)	0.37	13.1	1.5	$47.9{\delta }_{Lm}\times {\left(19.2{\delta }_{Lm}\right)}^2$	$1000\times {400}^2$

summarises the newly generated DNS database considered for this analysis. The cases (a) and (b) in Table 1 have been simulated under both scalar and velocity forcing, whereas simulations in cases (c) and (d) have been conducted only under scalar forcing and cases (e) and (f) are allowed to freely mix without the influence of any external forcing and flame-turbulence interaction takes place under decaying turbulence. Only cases (a) and (b) are able to reach a statistically quasi-stationary state as both the scalar and velocity fluctuations are required to be maintained. The remaining cases (c–f) are provided to highlight the influence of the newly developed scalar forcing scheme [24]. Table 1 shows the values of $u^{\prime }/S_b$, $\mathsf{\ell }/{\delta }_{L,m}$, $\langle \xi \rangle$, ${\xi }^{\prime }$, Damkohler number $Da=\mathsf{\ell }{S}_b/u^{\prime }{\delta }_{L,m}$, Karlovitz number $Ka={(u^{\prime }/S_b)}^{3/2}{(\mathsf{\ell }/{\delta }_{L,m})}^{-1/2}$, ${\mathsf{\ell }}_{\varphi }/\mathsf{\ell }$, domain size and the corresponding grid size, where ℓ and ${\mathsf{\ell }}_{\varphi }$ are the integral length scale of turbulence and equivalence ratio $\varphi =\xi (1-{\xi }_{st})/\left[{\xi }_{st}(1-\xi )\right]$ in the unburned gas, respectively, and $S_b$ and ${\delta }_{L.m}$ are the unstretched laminar burning velocity and thermal flame thickness of the unstretched laminar flame corresponding to $\varphi =0.8$, respectively. The flame thickness ${\delta }_{L,m}$ is defined as $(T_{ad(\varphi =0.8)}-T_0)/\max (\nabla {\widehat{T}}_L)$ where $T_0$, $T_{ad(\varphi =0.8)}$ and $\widehat{T}$ are the unburned gas temperature, adiabatic flame temperature for $\varphi =0.8$ and dimensional instantaneous temperature, respectively. The simulations consist of statistically planar methane-air flames propagating into an imperfectly mixed, globally lean fuel-air mixture corresponding to a mean equivalence ratio $\langle \varphi \rangle$ of 0.8 and an rms value of equivalence ratio of 0.14.

The cases considered here differ by the rms turbulent velocity fluctuation normalised by the burning velocity of the laminar premixed flame corresponding to the mean equivalence ratio $u^{\prime }/S_b$, and whether or not the scalar or velocity forcing schemes are used. All scalar forcing simulations are subject to $K/(1/T_{chem})=1.71\times {10}^6$ (where $T_{chem}={\delta }_{L,m}/S_b$ is the chemical timescale for $\varphi =0.8$), $K^{*}=5.0$ and the target passive scalar bounds are ${\xi }_l=0.0337$ and ${\xi }_r=0.055$ as these correspond to equivalence ratio values of ${\varphi }_l=0.6$ and ${\varphi }_u=1.0$.

The compressible 3D DNS code SENGA+ [27] was used for all simulations. The transport equations are solved in using a 10th-order central difference scheme to calculate spatial derivatives of internal grid points, with the order of accuracy gradually reducing to a one-sided 2nd-order scheme at non-periodic boundaries. Explicit time advancement uses low storage 3rd-order Runge-Kutta scheme [28]. The numerical technique used in this study is standard practice for combustion DNS and has been used in different DNS analyses in the past [1,2,3,4,5,6,7,8,9,10,11,12,13]. The four boundaries transverse to the mean direction of the flame propagation are considered periodic, while the two boundaries in the direction of the mean flame propagation are considered to be a partially non-reflecting turbulent inflow and outflow in line with the Navier-Stokes characteristic boundary conditions (NSCBC) [29]. The mean inlet velocity in the forced turbulence cases is gradually adjusted to match the turbulent flame speed to keep the flame within the computational domain. The partially non-reflecting boundaries allow for the acoustic waves to pass through them without any appreciable reflection while arresting the mean pressure drift [29]. The flame is kept sufficiently away from the non-periodic boundaries at all stages and thus the interaction of the order of accuracy of spatial differentiation with boundary condition implementation does not affect the flame dynamics in the canonical configuration considered for turbulent stratified-mixture combustion.

The chemical mechanism is simplified in this analysis by single-step Arrhenius-type chemistry given by 1 unit mass of fuel + s unit mass of oxidiser → ($1+s$) unit mass of products [30]. Here, s is the stoichiometric oxidiser–fuel mass ratio. The chemical reaction ${\mathrm{CH}}_4+2{\mathrm{O}}_2+7.52{\mathrm{N}}_2\to {\mathrm{CO}}_2+2{\mathrm{H}}_2\mathrm{O}+7.52{\mathrm{N}}_2$ yields a value of $s=4.0$ for methane–air combustion. Both the activation energy and heat release are taken to be functions of equivalence ratio [30]. This chemical mechanism was found to mimic the correct equivalence ratio dependence of the unstretched laminar burning velocity [3,30]. Since the scalar forcing is applied only in the unburned gas, it does not interact with the chemical processes within the flame. The scalar forcing term can be used for any number of species to ensure that the desired mean and standard deviations are maintained. Alternatively, this term can be expressed in terms of mixture fraction and the species mass fractions in the unburned gas in the multi-step chemical system can be tabulated as a function of mixture fraction, as used in the past for detailed chemistry DNS [31] and flame-resolved simulations [32]. Simple thermochemistry is used here as the proof of concept of the application of scalar forcing in DNS of turbulent stratified flames and the simplification of chemistry does not affect the performance of scalar forcing or the conclusions of this analysis.

The initial conditions were prescribed as follows. The isotropic turbulent velocity fluctuations were initialised following the well-known pseudo-spectral method by Rogallo [33], which yields an initially homogeneous, isotropic, divergence-free field for specified values of rms velocity $u^{\prime }$ and integral length scale ℓ following Batchelor-Townsend spectrum [34]. Mixture inhomogeneity in the unburned gas was initialised with a bimodal distribution according to the pseudo-spectral method by Eswaran & Pope [35] for $\langle \varphi \rangle =0.8$, rms ${\varphi }^{\prime }=0.14$ for a normalised integral length scale of equivalence ratio fluctuation ${\mathsf{\ell }}_{\varphi }/\mathsf{\ell }=1.5$.

The turbulence intensity in the cases of turbulent forcing is maintained by including a source term in the momentum equation, given by:

$$\overrightarrow{f}=(1-c)max\left[0,\frac{k_{target}-k}{\Delta t{k}_{target}}\right]{\overline{\overrightarrow{u}}}^{HP}$$

(10)

where $k_{target}$ is the desired turbulent kinetic energy value, $\Delta t$ is the timestep size, k is the current level of turbulent kinetic energy, ${{\overline{u}}_i}^{HP}=u_i-{\overline{u}}_i$ a high pass filtered velocity fluctuation with $\overline{\left(\dots \right)}$ being a conventional low pass filter typically used in the context of LES with a 1D Gaussian filter kernel given by $G\left(x\right)={\left(6/\pi {\mathsf{\ell }}_f^2\right)}^{1/2}exp\left(-6x^2/{\mathsf{\ell }}_f^2\right)$ and where ${\mathsf{\ell }}_f=0.25k^{3/2}/ϵ$ is a filter length scale where k and $ϵ$ are turbulent kinetic energy and its dissipation rate over the domain to be forced [26]. The factor $(1-c)$ in Equation (10) ensures that the turbulence forcing remains active in the unburned gas but gradually reduces to zero towards the burned gas. The turbulence intensity in flames within the thin reaction zones regime [36] often decays from the unburned gas side to the burned gas side of the flame brush and the integral length scale of turbulence increases due to dilatation and a rise in viscosity with heat release [37,38]. By contrast, in the corrugated flamelets regime, the turbulence intensity may increase from the leading edge to somewhere within the flame brush [37,38]. However, forcing turbulence everywhere in the domain tries to enforce a constant level of turbulence on both sides of the flame brush. In this sense, the flame-turbulence interaction will not be physical if the forcing is applied to the whole computational domain. This is explained in detail by Klein et al. [26]. Whilst, in principle, the turbulent velocity field can be forced throughout the domain, the same conclusions cannot be automatically applied to scalar forcing. The purpose of the scalar forcing scheme is to deliver an inhomogeneous unburned fuel-air mixture with prescribed values of mean and rms values of equivalence ratio to the flame. Scalar forcing within the flame will artificially alter the fuel and oxidiser concentrations, which, in turn, will affect the burning rate and subsequent mixing of species within the burned gas. Moreover, an active scalar forcing within the flame induces a lot of complexity in the calculation (e.g., scalar fluctuations introduced by forcing cannot be separated from the fluctuations due to chemical reaction), particularly for more detailed chemical mechanisms.

The scalar forcing scheme used was found to be very computationally efficient, adding just 0.7% to the overall computational cost. In contrast, the velocity forcing scheme used adds an additional 86% to the computational cost in comparison to the decaying turbulence simulations.

4. Results & Discussion

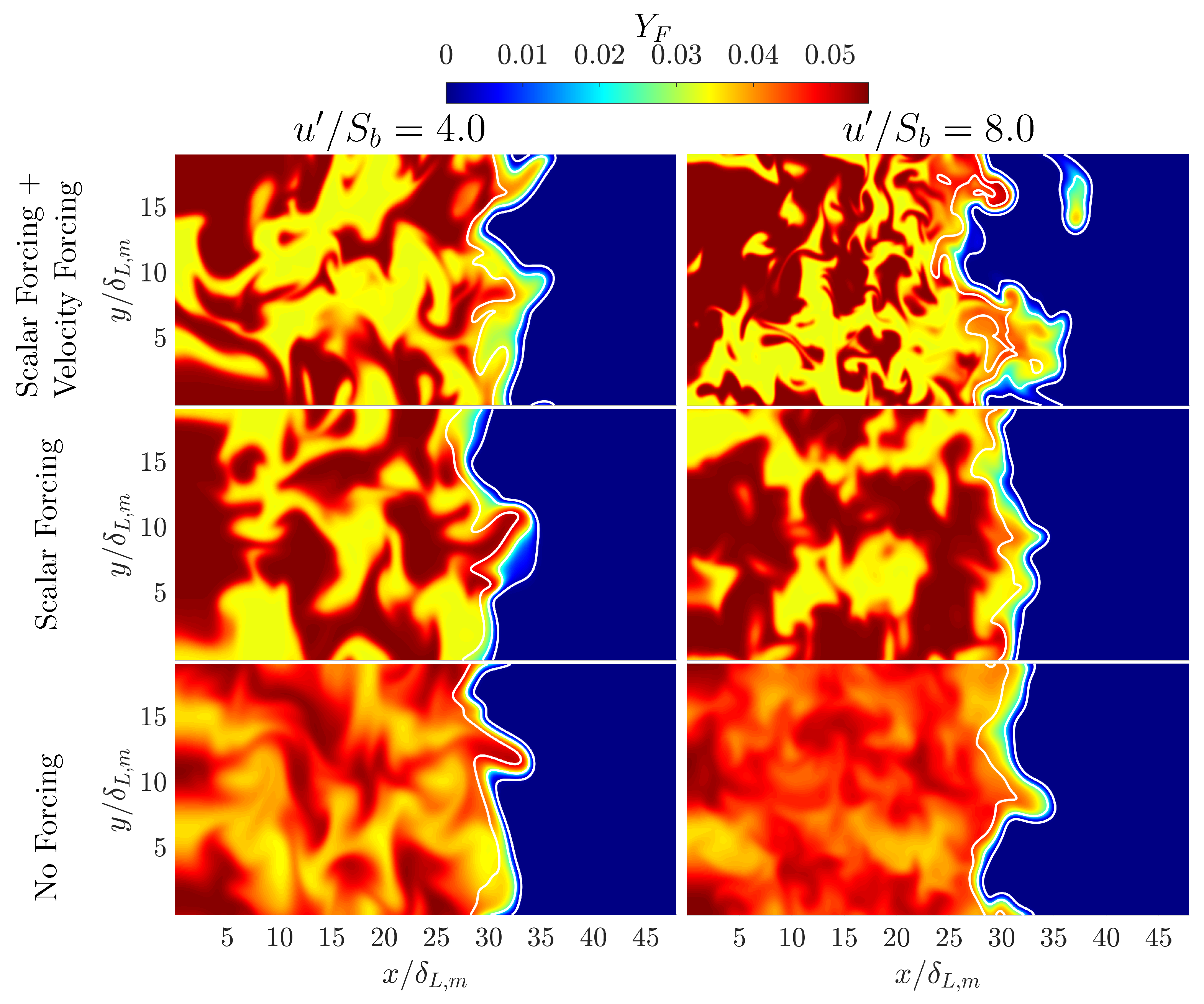
Figure 1 shows the distributions of the fuel mass fraction $Y_F$ and the contours of the reaction progress variable c equalling 0.1, 0.5 and 0.9 (left to right) on the central midplane of all simulation cases. The snapshots shown are after 2 chemical timescales (i.e., $t=2.0{\delta }_{L,m}/S_b$) have passed, where cases (a) and (b) (first row) have reached a statistically quasi-stationary state. In the remaining cases, achieving statistically stationary conditions is not possible due to the decaying nature of the turbulent velocity or scalar fields. The typical simulation time for stratified-mixture combustion in canonical configurations is limited to a couple of eddy turnover times [1,2,3,4,5,6,7,8,39] and all the cases considered here have shorter turbulent timescale than the chemical timescale. Therefore, the simulation time for the cases considered here ranges from 3.5 to 6.76 eddy turnover times, enabling a quasi-stationary state to be achieved.

Figure 1 shows the flame wrinkling increases with increasing turbulence intensity when the turbulence intensity is sustained with velocity forcing, which is evident by the greater extent of wrinkling of the c contours in $u^{\prime }/S_b=8.0$ case (i.e., case (b)) than in $u^{\prime }/S_b=4.0$ case (i.e., case (a)). Without turbulence forcing, turbulence intensity in cases (c–f) decays with time, which in turn leads to smaller extents of flame wrinkling in these cases in comparison to cases (a) and (b). Furthermore, when the velocity field is decaying, the extent of wrinkling of the c contours is approximately the same regardless of the initial $u^{\prime }/S_b$ value due to the higher kinetic energy dissipation rate associated with the initially higher $u^{\prime }/S_b$ cases, and consequently a faster rate of decay of $u^{\prime }/S_b$, which acts to make the turbulence intensities comparable when the statistics are extracted. Figure 1 shows that the mixture inhomogeneity in the unburned gas is sustained in cases (a–d), but the extent of mixture inhomogeneity is relatively smaller in cases (e) and (f) due to the absence of scalar fluctuation generating mechanisms (i.e., scalar forcing).

The extent of the mixing, decay of the turbulent velocity field and effectiveness of the relevant scalar forcing schemes can be seen from Figure 2, which shows the evolution of $u^{\prime }/S_b$ and ${\varphi }^{\prime }$ with time throughout the duration of the simulation. The scalar and velocity forcing schemes are clearly effective at maintaining the respective fields at the desired value. As expected, in the initially higher $u^{\prime }/S_b$ case (f), both the $u^{\prime }/S_b$ and ${\varphi }^{\prime }$ values decay at a greater rate than in case (e). Moreover, it can be seen from Figure 2 in case (f) the decays mentioned above occur at a faster rate than in case (e) due to greater dissipation rate of kinetic energy ($\sim u^{\prime 3}/\mathsf{\ell }$) for higher values of turbulence intensity for a given value of ℓ.

In order to demonstrate the effects of scalar forcing at maintaining the mixture PDF, the temporal evolution of the equivalence ratio $\varphi$ PDF for all simulations in the unburned gas ($c<0.05$) and in the flame ($0.05<c<0.95$) are shown in Figure 3. The scalar forcing scheme maintains the bimodal nature of mixture inhomogeneity in the unburned gas effectively throughout the simulation. However, the forcing does not directly control the $\varphi$ PDF within the flame as this would unnaturally interfere with the chemical reaction and would produce an unphysical solution. Thus, the mean value of the equivalence ratio $\langle \varphi \rangle$ within the flame cannot be directly controlled using the present scalar forcing scheme [24], although it is indirectly controlled by maintaining the PDF in the unburned gas. In its current incarnation, the forcing maintains the PDF sampled over the entire unburned gas volume, so cannot guarantee that the surface immediately upstream of the flame (e.g., $c=0.001$) will share the same mean scalar value as the entire unburned gas volume. Therefore, the overall burning rate is expected to fluctuate and the statistics will converge when time averaging over a sufficient duration. The turbulent burning velocity is not expected to reach a plateau in a true sense under a quasi-steady state and it shows oscillations around a mean value as shown in Figure 4. This was demonstrated elsewhere for premixed flames by other authors [40]. Ensuring a consistent $\langle \varphi \rangle$ immediately upstream of the flame would require modification to the forcing term to inconsistently modify the length scale and scalar dissipation rate in the unburned gas to redistribute mixture independently from the velocity field, which is possible but raises further questions as to the physicality of the solution.

The scalar and turbulent forcing schemes in the unburned gas have consequences on the turbulent burning velocity and the flame surface area. Figure 4 shows the temporal evolution of the normalised turbulent burning velocity $S_T=[1/\left({\rho }_0{A}_L\right)]{\int }_V{\dot{\omega }}_{c}dV$ (where $A_L$ is the projected flame surface area in the direction of mean flame propagation, ${\rho }_0$ is the unburned gas density) and turbulent flame surface area $A_T={\int }_V|\nabla c|dV$ for the different forcing configurations. Figure 4 shows the cases under the effects of velocity forcing that reach a quasi-stationary state. The sustained turbulence levels result in a higher level of flame wrinkling throughout the duration of the simulations, and thus causes the burning velocity and flame surface area to be higher than the other cases. It is evident from Figure 4 that $S_T$ and $A_T$ continue to oscillate around a constant time averaged value. The turbulent burning velocities $S_T$ for the initially $u^{\prime }/S_b=4.0$ cases are found to be counter-intuitively greater than the $u^{\prime }/S_b=8.0$ cases for the cases not subjected to velocity forcing. This can attributed to the greater decay in $u^{\prime }$ already discussed with regards to Figure 2, and also can be explained using the PDF of $\varphi$ within the flame ($0.05<c<0.95$) shown in Figure 3. The probability of finding a more reactive $0.8<\varphi <1.0$ mixture remains consistently higher in the $u^{\prime }/S_b=4.0$ case than in the $u^{\prime }/S_b=8.0$ case where the greater rate of mixing increases the probability of finding $\varphi \approx 0.8$ mixture. It can also be seen from Figure 4 that the combination of scalar and turbulence forcing yields higher values of $S_T$ and $A_T$ than the unforced and only scalar forced simulations. Without scalar forcing, the mixture inhomogeneity reduces with time and the PDF of $\varphi$ converges to a narrow distribution around $\varphi =0.8$ but the forced scalar simulation shows a greater probability of finding more reactive $0.8<\varphi <1.0$ mixture which acts to increase both $S_T$ and $A_T$. The turbulent forcing also increases the flame wrinkling due to turbulence in comparison to the unforced turbulence simulations, which in turn increases the flame area generation and the volume-integrated burning rate. It can be seen from Figure 4 that $S_T/S_b$ is similar to $A_T/A_L$ for most cases considered. Without the influence of scalar forcing (i.e., cases (e–f)), $S_T/S_b$ rises above $A_T/A_L$. With the addition of scalar forcing (i.e., (cases c–d)), the flame speed dips below the flame area for the initial $u^{\prime }/S_b=8$ case, but remains above the flame area for the initial $u^{\prime }/S_b=4$ case. These effects can be substantiated from the PDF of $\varphi$ within the flame in Figure 3b. The cases not subject to forcing (e–f) have a much higher chance of encountering $\varphi =0.8$ mixture within the flame, while case (d) has a greater probability of encountering the less reactive $0.6<\varphi <0.8$ mixture than case (c) due to the randomness of mixture inhomogeneity in the unburned gas, despite both cases being subject to scalar forcing.

It is demonstrated in Figure 2 that the desired values for the rms turbulent velocity and equivalence ratio are maintained in the cases where both velocity and scalar forcing are used. Figure 3 shows the PDFs of equivalence ratio in the unburned gas settle to a shape that does not change when the scalar forcing is employed. Finally, in Figure 4, both the turbulent burning velocity and flame surface area oscillate mildly around a mean value, reaching a quasi-steady state. In its current incarnation, the forcing maintains the PDF sampled over the entire unburned gas volume, so cannot guarantee that the surface immediately upstream of the flame (e.g., $c=0.001$) will share the same mean scalar value as the entire unburned gas volume. Therefore, the overall burning rate is expected to oscillate in an instantaneous sense, so the statistics will converge when time averaging over a sufficient duration. The turbulent burning velocity is not expected to reach a plateau in a true sense under a quasi-steady state and it shows oscillations around a mean value as shown in Figure 4. This was demonstrated elsewhere for premixed flames by other authors [40].

Figure 3 demonstrates that the flame propagates and experiences inhomogeneous mixture throughout its evolution. Thus, it is worthwhile to consider percentage contributions to $S_T$ and $A_T$ of front- and back-supported elements. Such elements can be identified by calculating the flame normal vector alignment with the local mixture fraction gradient, given as

$$cos{\theta }_{c\xi }=\frac{\nabla c·\nabla \xi }{|\nabla c||\nabla \xi |}$$

(11)

For $cos{\theta }_{c\xi }<0$, the flame is locally propagating into an increasingly rich mixture, and this is referred to as a front-supported flame. Conversely, when $cos{\theta }_{c\xi }>0$, the flame is propagating into an increasingly lean mixture, and this is referred to as a back-supported flame. Figure 5 is a histogram showing the proportion of front- and back-supported contributions to $S_T$ and $A_T$ at different times. These percentage shares for cases continue to fluctuate for all cases as the mixture within the flame changes. It can be seen from Figure 5 that generally, back-supported flame elements with the richer mixture behind the flame contribute mostly to the overall flame speed and area. The qualitative nature of the percentage shares of front- and back-supported flame elements to $S_T$ and $A_T$ remain unchanged in the presence of scalar forcing but the actual values of these percentage shares are different in cases depending on the presence of turbulence and scalar forcing. It is evident from Figure 5 that the percentage contributions of $S_T$ and $A_T$ to the back-supported and front-supported elements in the quasi-stationary state remain comparable to the only scalar forcing and no-forcing decaying turbulence scenarios for $u^{\prime }/S_b=4.0$. However, the percentage shares of back-supported elements increase in the $u^{\prime }/S_b=8.0$ cases with scalar forcing and turbulence forcing (i.e., case (b)), but decrease in the other cases (i.e., cases (d) and (f)). The alterations of percentage shares of front- and back-supported contributions to $S_T$ and $A_T$ with turbulence intensity are not the focus of this paper and thus are not discussed further. The findings from Figure 5 essentially demonstrate that the scalar forcing does not artificially alter the front-supported and back-supported contributions to the overall heat release rate in turbulent stratified flame simulations.

As the combustion takes place in inhomogeneous mixtures, it is worthwhile to analyse if the scalar forcing has any impact on the mode of combustion. The mode of combustion (i.e., premixed and non-premixed) can be quantified in terms of the flame index $\Psi$, which is defined as [41]:

$$\Psi =\frac{\nabla Y_F·\nabla Y_O}{|\nabla Y_F\left|\right|\nabla Y_O|}$$

(12)

A positive value of $\Psi$ (i.e., $\Psi >0$) is indicative of premixed combustion, whereas a negative value (i.e., $\Psi <0$) is indicative of non-premixed combustion [41]. The percentage shares of heat release rate arising from premixed (i.e., $\Psi >0$) and non-premixed (i.e., $\Psi <0$) modes of combustion are shown in Figure 6 for the cases considered here, where the total heat release rate is given by

$${\mathrm{HR}}_{\mathrm{total}}={\int }_V{H}_{\varphi }\left|{\dot{\omega }}_F\right|dV$$

(13)

where $H_{\varphi }$ is the heat release rate per unit mass of fuel, and ${\dot{\omega }}_F$ is the fuel reaction rate. It can be seen from Figure 6 that more than $99\%$ of the heat release rate occurs due to the premixed mode of combustion irrespective of the nature of scalar forcing. Therefore, scalar forcing does not affect the mode of combustion and thus does not introduce any artificial effects into the flame statistics.

The scalar dissipation rate of mixture fraction $N_{\xi }=D\nabla \xi ·\nabla \xi$ and reaction progress variable $N_c=D\nabla c·\nabla c$ and cross-scalar dissipation rate $N_{c\xi }=D\nabla c·\nabla \xi$ (where D is the species diffusivity) affect the reaction rate of reaction progress variable ${\dot{\omega }}_c\propto [{\dot{\omega }}_F+N_{\xi }{\partial }^2{Y}_F/\partial {\xi }^2+N_c{\partial }^2{Y}_F/\partial c^2+2N_{c\xi }{\partial }^2{Y}_F/\partial \xi \partial c]$ in turbulent stratified flames [11,42,43]. The cross-scalar dissipation rate $N_{c\xi }$ exists within the flame where the scalar forcing does not remain active. Moreover, the magnitude of $N_{c\xi }$ remains negligible in comparison to the magnitude of $N_c$ and thus ${\dot{\omega }}_c$ is principally determined by $N_c$ as $N_{\xi }$ remains small within the flame in stratified-mixture combustion [11,42,43]. Figure 7 shows the mean values of scalar dissipation rate for the mixture fraction $N_{\xi }$ and reaction progress variable $N_c$ averaged upon over bins of their respective scalars. The quantities $N_{\xi }$ and $N_c$ are evaluated as a postprocessing exercise by evaluating the gradients of $\nabla \xi$ and $\nabla c$ using the same spatial differentiation techniques used for DNS simulations. In the case of $N_{\xi }$, the mean values are shown for the unburned gas (i.e., $c<0.1$) only, as this is where the scalar forcing is applied. The mean values of $N_{\xi }$ within the unburned gas converge towards a steady value for the cases subject to both scalar forcing and velocity forcing (first column), whereas it gradually decays after rising from the initial simulation transients in the cases not subject to any external forcing (third column) and the cases subject to scalar forcing only (second column), with the effects being most pronounced in the case not subject to any forcing. The mean value of $N_{\xi }$ in the case without scalar forcing will eventually converge to zero as the unburned gas becomes entirely premixed, while in cases with scalar forcing the inhomogeneity is maintained and the mean $N_{\xi }$ converges to some non-zero value. Moreover, both the qualitative variation and peak mean value of $N_c$ remain unaffected by the nature of scalar forcing. Thus, scalar forcing does not introduce any artificiality in terms of micro-mixing within the flame and also in terms of mode of combustion within turbulent stratified flames. Therefore, scalar forcing does not introduce any artificiality in the flame structure in turbulent stratified-mixture combustion. Thus, it can be used to obtain a quasi-stationary state in DNS of stratified-mixture combustion in canonical configurations without any other scalar fluctuation generation mechanism.

5. Conclusions

Maintaining the mixture inhomogeneity in the unburned gas in DNS of turbulent stratified flames in the canonical ’flame-in-a-box’ configuration is a challenging task but with the potential to provide great insight into stratified flame physics. The implications of applying a newly developed scalar forcing methodology and its interaction with turbulence forcing in DNS of turbulent stratified flames in the canonical ’flame-in-a-box’ configuration have been analysed. The statistical behaviours of turbulent burning velocity, flame surface area and reaction zone structure (e.g., the fractional share of front- and back-supported combustion, and the contributions of heat release originating from different modes of combustion) extracted from DNS of turbulent stratified flame simulations where (a) both the scalar field and the turbulence field are forced, (b) only the scalar field is forced and (c) where neither fields are subject to external forcing have been analysed in detail. The main findings of this analysis are as follows

• The mean mixture composition within the flame may vary during the course of the simulation since the average quantities are maintained in the entire unburned gas volume, leading to fluctuations in the burning rate over time.
• Scalar forcing alongside turbulence forcing may lead to greater values of turbulent burning velocity and flame surface area in comparison to unforced simulations for globally fuel-lean turbulent stratified flames.
• The sustained unburned gas mixture inhomogeneity in the case of scalar forcing alters the percentage shares of back- and front-supported flame elements in comparison to unforced simulations, especially for high turbulence intensities.
• The heat release due to different modes of combustion and the micro-mixing rates characterised by scalar dissipation rates remain unaffected by scalar forcing, suggesting that the scalar forcing does not introduce any artificial influence on the flame structure.

The above findings indicate that the scalar forcing has a high potential for advancing our understanding of stratified-mixture combustion by obtaining well-converged time-averaged statistics using DNS in canonical configurations.