Abstract
This study comprehensively analyzes the impact of the novel HybridBridge method, developed by the authors, for generating a 3D mesh at contact points within packed beds within the effective thermal conductivity. It compares HybridBridge with alternative methodologies, highlights its superiority and outlines potential applications. The HybridBridge employs two independent geometry parameters to facilitate optimal flow mapping while maintaining physically accurate effective thermal conductivity and ensuring high mesh quality. A method is proposed to estimate the HybridBridge radius for a defined packed bed and cap height, enabling a presimulative determination of a suitable radius. Numerical analysis of a body-centered-cubic unit cell with varied HybridBridges is conducted alongside previous simulations involving a simple-cubic unit cell. Additionally, a physically based resistance model is introduced, delineating effective thermal conductivity as a function of the HybridBridge geometry and porosity. An equation for the HybridBridge radius, tailored to simulation parameters, is derived. Comparison with the unit cells and a randomly packed bed reveals an acceptable average deviation between the calculated and utilized radii, thereby streamlining and refining the implementation of the HybridBridge methodology.
1. Introduction
The versatility of packed beds in the energy and process industries knows virtually no bounds. Their remarkable ratio of surface area to volume renders them indispensable in myriad applications, serving as separators or as chemical reactors across diverse designs, as illustrated in [1]. Simultaneously, packed beds play pivotal roles in thermodynamic processes such as the cooling of cement clinker or in drying processes, for example within the natural gas storage.
Spanning from powder beds hosting dust-sized particles to pebble beds with pronounced boundary effects, their size distribution encompasses a broad spectrum. From a process engineering perspective, precision in describing transport phenomena within packed beds is paramount. Such precision facilitates the more accurate design of apparatuses and the optimization of existing processes. Consequently, packed beds have been subject to decades of intensive study employing experimental and analytical methods. With the burgeoning advancement in microelectronics, computer-aided techniques, particularly numerical simulations, have gained prominence in recent years.
These simulations offer a distinct advantage in visualizing heat and mass transfer within packed beds and other complex geometries. They have the capacity to incorporate local variables that significantly influence transport processes. Various modelling approaches, each with differing levels of complexity, find applicability in this domain.
For instance, the categorization proposed by Tsotsas [2] offers a valuable means of differentiation. While not inherently tied to numerical methodologies, this classification aids in achieving a more nuanced characterization. Tsotsas [2] delineates between homogeneous modelling and heterogeneous modelling. In homogeneous modelling, the fluid and solid phases are amalgamated, enabling the description of the packed bed solely through a characteristic transport parameter, such as the effective thermal conductivity . Conversely, heterogeneous modelling involves coupling the fluid phase of the packed bed to the solid phase through an additional coupling parameter. In the case of heat transfer, this coupling parameter is known as the heat transfer coefficient.
The heterogeneous methodologies mentioned above can further be categorized based on the level of geometry resolution. When particles are not explicitly modelled in their spatial arrangement, it is referred to as a porous media model. This approach can enhances modelling accuracy in comparison to homogeneous methods.
In contrast, heterogeneous particle-resolved simulations, such as those based on the finite volume method, aim to depict physical processes within packed beds with maximum fidelity. Nevertheless, generating the computational mesh for such simulations presents a significant challenge. This challenge stems from the contact points among particles themselves and between particles and the enclosing reactor walls. The nature of these points of contact can vary depending on the shapes and arrangements of the particles. In the simplest scenario, featuring a packed bed of monodisperse spherical particles with no consideration for particle elasticity, all contact points manifest as point contacts. Point contacts are characterised by infinitesimally small contact areas between the spheres.
In practical applications, meshing point contacts often lead to the creation of highly skewed cells, potentially triggering convergence issues. Alternatively, one may resort to utilizing very small cells to address this challenge. However, this approach inevitably inflates the number of cells within the model, consequently prolonging computation times.
In transient simulations, this extensive local refinement, coupled with adherence to the Courant–Friedrichs–Lewy condition—which mandates smaller predefined time steps for stability—further compounds the computation burden. This combination of factors can significantly escalate computation times.
To circumvent these challenges, a prevalent approach involves altering the spheres to eliminate point contact. When outlining the scientific consensus numerous approaches for consideration can be found. One group of methods, known for their simplicity in implementation, are the global methods, which modify the entire sphere. A widely employed technique, especially in earlier studies (e.g., [3,4,5]), involves reducing the sphere size, commonly referred to as the gaps method. In contrast, the overlaps method, introduced by Guardo et al. [6], involves enlarging the spheres to create overlaps. However, both these global methods have drawbacks, notably their potential to induce significant alterations in key parameters of packed beds, such as the porosity .
To address this limitation, local methods were developed, focusing on modifying spheres solely in the vicinity of the contact point. Two such methods are the bridges method introduced by Ookawara et al. [7] and the caps method proposed by Eppinger et al. [8]. In the bridges method, the spheres are connected to each other with bridges by enlarging the contact point. Conversely, the caps method, involves removing a portion of each sphere at the contact point, akin to cutting off a cap. These techniques are applicable not only to spherical particles but also to non-spherical ones. For instance, Eppinger and Wehinger [9] and Kutscherauer et al. [10] have extended the original caps method to accommodate diverse particle geometries.
With appropriate specifications, both of the local methods presented here are well-suited for the particle-resolved simulations of (spherical) packed beds. However, they share a common drawback in that they may not always accurately represent the effective thermal conductivity of the bed, or may do so only with significant additional effort.
In the caps method, the creation of an artificial fluid gap between contacting spheres may result in an underestimation of the thermal conductivity. Conversely, the bridges method tends to overestimate heat conduction. While this overestimation can be mitigated by introducing a third pseudophase as a bridge material, as demonstrated by Dixon et al. [11] or Wehinger et al. [12], such an approach requires substantial additional implementation effort and is notably detached from physical reality.
To address these issues, alternative strategies have been proposed. For instance, one can utilize very small bridges in the bridges method, as explored in [13], or significantly reduce the gap size in the caps method, as demonstrated in [10]. However, it is important to note that these adjustments do not offer a systematic and universally applicable solution to the contact point problem.
Henceforth, Szambien et al. [14], introduced the so-called HybridBridge method in their previous work. This method ingeniously amalgamates the advantages of both the caps and bridges techniques, allowing the effective thermal conductivity of the packed bed to remain intact and providing a reliable contact point modification. Thus, whenever the effective thermal conductivity is dominated by the thermal conduction between the spheres, the HybridBridge method offers an advantage over conventional local methods.
The aim of this work is to explain the theory of the HybridBridge in more detail and to investigate the effect of the HybridBridge on the effective thermal conductivity when used for particle-particle contact points. In addition, an initial approximate a priori approach for the design of the HybridBridge’s geometry is proposed.
2. Materials and Methods
2.1. Theoretical Context
In principle, the effective thermal conductivity of flowed-through packed beds can be divided into two parts: one that depends on the Péclet number (in the case of heat transfer, the following applies: ) and a non-flow-through share dominated by the effective thermal conductivity of the non flown-through packed bed . For , with x representing either axial or radial direction, the following applies [15,16]:
In this equation
is the Péclet number of the empty tube and is a specific constant.
When the influence of predominates, the contact points between particles can exert a significant impact on heat transfer. This scenario arises, for instance, when values are small, as indicated by Equation (1). Furthermore Aichlmayr and Kulacki [17], as well as Hsu et al. [18], stated that the influence of contact points may become important when the thermal conductivity of the particles is substantially greater than that of the fluid .
When conducting numerical investigations on a packed bed with a notable ensuring an accurate modeling of becomes imperative. The innovative new HybridBridge method has been introduced for this purpose. The rationale underlying the introduction of the HybridBridge is best illustrated by the following example:
In this scenario we compare the standard bridges method and the conventional caps method between two monosized particles with the radius . Both modifications utilize identical radii . We use the predefined height of the cap to calculate its radius:
The radius is selected to be sufficiently small to ensure that the flow in the context under consideration remains unaffected. The following assumption is made: the velocity within the fluid gap of the cap is set to exactly zero, as illustrated in [9]. Consequently, in this specific scenario, both methods give identical results for flow computations. However, when it comes to heat conduction between the particles, they exhibit notably divergent behaviour. While the bridges method tends to induce excessively high heat flows, the caps method tends to result in disproportionately low heat conduction.
As previously noted in the introduction, this issue can be avoided by the introduction of a pseudo phase as a bridge or by a reduction in the size of the bridge or cap. However, it is important to note that, due to the physical circumstances, the caps method can never provide a perfect representation of heat conduction. This limitation stems from the nature of surface contact.
As an alternative, it is possible to create a parallel arrangement of thermal resistances consisting of the high thermal conductivity solid phase and the low thermal conductivity stagnant fluid phase. This arrangement can effectively replicate the thermal resistance exhibited by the third pseudophase or that observed in real packed beds.
By adopting the simplest symmetrical geometry and appropriate phase assignment, the continuity of both phases can be seamlessly maintained without interruption. This concept aligns precisely with the HybridBridge methodology we have introduced: a solid centred cylinder encompassed by a concentric hollow fluid cylinder. Figure 1 illustrates a comparison between conventional methods and the new HybridBridge approach.
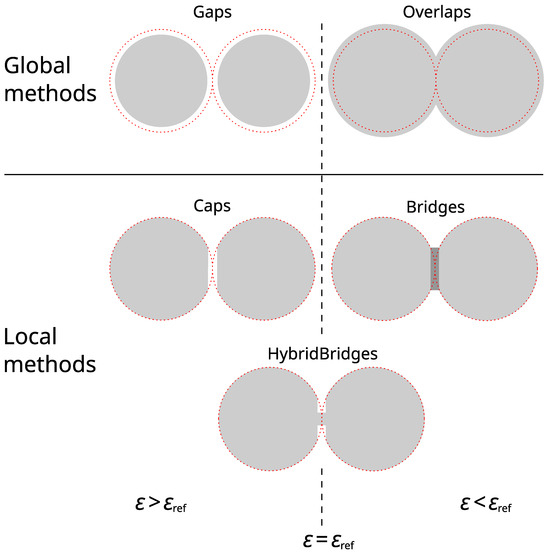
Figure 1.
Comparison of conventional contact point modification methods with the novel HybridBridge method. The white areas represent the fluid phase, the different shades of grey represent the solid phases. The red circles represent the circumferences of the original spheres.
In our prior research [14], we have demonstrated the meshing advantages offered by the HybridBridge. Based on our assessments, the mesh quality closely aligns with that of conventional caps. Additionally, significantly larger cells can be employed, and a reduced number of cells suffices when compared to conventional bridges with an equivalent radius. For fitting geometrical parameters, a replication of the effective thermal conductivity according to the Zehner–Bauer–Schlünder Model was achievable. Demonstration of real-world applicability of the Hybrid Bridge method has been successful.
The HybridBridge thus unites the advantages of both conventional methods: the meshing behavior of the caps method and the representation of thermal conductivity of the bridge method.
2.2. Geometrical Description
Unlike the conventional methods presented, HybridBridge contains two independent geometry parameters the height of the cap and the radius of the bridge , as shown in Figure 2. This dual-parameter setup enables control over two overarching properties of the packed bed. The initial objective is to ensure precise flow simulation by selecting an appropriate cap height . Subsequently, achieving the desired effective thermal conductivity becomes feasible by selecting a suitable bridge radius . Values for estimating the order of magnitude for of the HybridBridge can be found in the literature [9,10] but must be adjusted to the individual packed bed and flow regime. An option to calculate the corresponding radius will be introduced later in the paper (see Equation (16)).
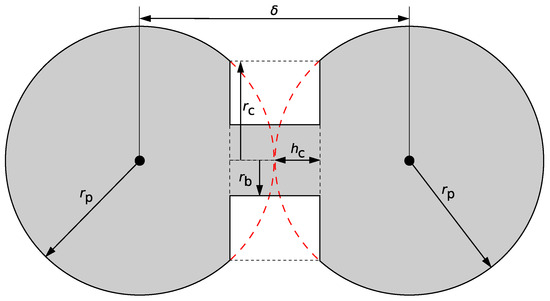
Figure 2.
Schematic representation of the geometrical parameters of a HybridBridge between two monosized spheres. In order to provide a clearer overview, the HybridBridge is shown larger than it should be used in practice.
Alternatively, adjustment of the effective thermal conductivity in combination with the porosity is also feasible. Herein lies a unique aspect of the HybridBridge method. Unlike conventional approaches, the HybridBridge method theoretically enables the preservation of the true porosity while modifying the contact points. Moreover, the alteration in porosity associated with the HybridBridge is consistently less pronounced compared to that of conventional caps of the equivalent height.
Furthermore, the HybridBridge can be regarded as a versatile local method for contact point modification. It inherently encompasses both the conventional bridges method as well as the conventional caps method as special cases of the HybridBridge method. The simultaneous availability of both conventional methods represents a significant advantage when implementing the HybridBridge in a workflow for meshing a numerical model. At the same time, this versatility ensures, that the usage of the HybridBridge method is as least as advantageous as conventional methods for any packed beds.
2.3. Analysis of a Body-Centred Cubic Unit Cell
Szambien et al. [14] investigated how various parameters of HybridBridge geometry impact the effective thermal conductivity within a unit cell structured in a simple-cubic (sc) grid arrangement. Initial insights into how the HybridBridge geometry adapts to the actual thermal conductivity of the scrutinized packed bed emerged from analyzing the results of this particular unit cell.
The simple-cubic lattice arrangement epitomizes the most basic unit cell. Moreover, heat conduction was assumed to occur in one direction only, running parallel to one of the main grid axis, traversing from midpoint to midpoint of the two spheres. Hence, within this unit cell, a solitary contact point enables the flow of heat. It is important to highlight that the assumption of one-dimensional heat conduction pertains exclusively to the modelling of effective thermal conductivity and the associated homogeneous perception of the packed bed. Within the numerical simulation model of unit cells, heat propagation is inherently three-dimensional. Consequently, it is deduced that heat flows occurring at interfaces perpendicular to the macroscopically imposed temperature gradient, as dictated by boundary conditions, are excluded.
The simple-cubic (sc) grid structure is characterized by a small number of contact points that affect heat conduction. Consequently, this unit cell tends to underestimate heat conduction compared to a realistically random packed bed. To address this discrepancy, in this work, we have carried out a numerical investigation of a unit cell featuring a body-centred-cubic (bcc) grid structure. In line with the aforementioned assumptions, this arrangement has a coordination number of 8 [19]. All eight contact points had to be modified with HybridBridge to ensure realistic heat conduction. No contact points were disregarded as irrelevant in this process.
To ensure a fair comparison with the simple-cubic grid, we adopted identical parameters for the simulation process. These simulation parameters are summarized in Table 1, while a qualitative representation can be observed in Figure 3. To generate the necessary .stl file we once more utilized our Python [20,21] tool in conjunction with Salome [22]. The numerical simulation was executed employing chtMultiRegionFoam within OpenFOAM (refer to [23,24]). The underlying mesh was generated using snappyHexMesh.

Table 1.
Parameters of the unit cell with relevant initial and boundary values.

Figure 3.
Body-centered-cubic unit cell with a qualitative temperature profile, red color indicates hotter temperatures and blue color indicates cooler temperatures.
2.4. Dimensioning of the HybridBridge
For achieving a high-quality multiphase particle-resolved numerical simulation of heat transport within packed beds, accurate modelling of heat conduction, as previously elucidated, is paramount. When applying the HybridBridge method for treating contact points, it becomes imperative to meticulously select the radius of the bridge in relation to the height of the caps . The effective thermal conductivity can be used to design the appropriate radius. To achieve this, the heterogeneous CFD model has to be homogenized. The homogenization of the model is based on Fourier’s Law of thermal conduction:
This equation must give the same results as the heterogeneous CFD model.
To determine the appropriate bridge radius , one must have knowledge of the target value for the effective thermal conductivity . This can be gleaned from a suitable model for the effective thermal conductivity, such as the model of Zehner, Bauer and Schlünder [25] or from experimental results.
This specification must be complemented with an understanding of how the geometry parameters of the HybridBridge influence the system. For this purpose, we conducted an extensive array of particle-resolved numerical simulations for unit cells (uc) both within the scope of this study and in our previous work [14].
Here, we computed the resulting values of the effective thermal conductivity of the unit cell, denoted as for various HybridBridges. From Equation (4), of the unit cell for a steady state is given by
with the cross-sectional area of the unit cell and their height . The heat flows are taken from the converged numerical simulations. Leveraging these unit cell results, we aim to derive an equation for the approximate estimation of the bridge radius.
3. Results
3.1. Assessment of the Body-Centred-Cubic Unit Cell
Figure 4 illustrates the effective thermal conductivity values, , derived utilizing Equation (5), alongside numerical simulation of the body-centered-cubic unit cell, incorporating various HybridBridge geometries. For comparison, the data corresponding to the simple-cubic unit cell, as presented in our earlier study [14], is provided in Figure 5. Both figures collectively demonstrate the HybridBridge’s capacity to encompass a wide spectrum of effective thermal conductivities within numerical simulations.
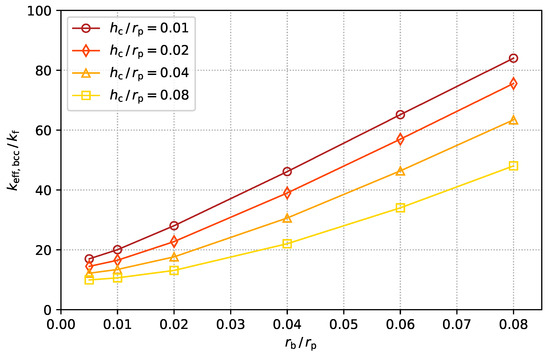
Figure 4.
Effective thermal conductivity of the HybridBridge with various ratios of for a body-centred-cubic arrangement of monodisperse spheres.
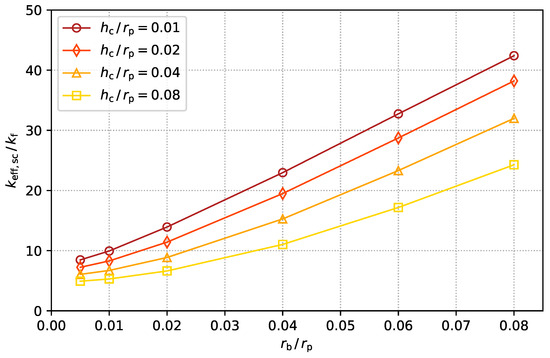
Figure 5.
Effective thermal conductivity of the HybridBridge with various ratios of for a simple-cubic arrangement of monodisperse spheres. Results taken from Szambien et al. [14].
Upon comparing the ratios of the effective thermal conductivities for the simple-cubic and body-centered-cubic unit cells, as illustrated in Figure 6, surprisingly it can be observed that the following approximation holds true:
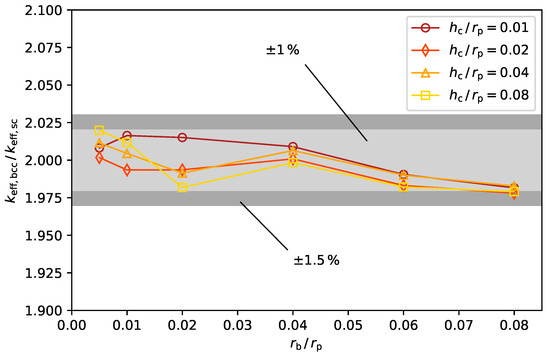
Figure 6.
Ratios of the effective thermal conductivities for body-centred-cubic (bcc) grid structure to simple-cubic (sc) grid structure.
Given that this observation holds across all examined HybridBridge geometries, it can be concluded that the HybridBridge exerts the most significant influence on the effective thermal conductivity in the conducted simulations. The factor of 2 can be explained by the number of HybridBridges per unit cell:
Starting with the simple-cubic unit cell, it is evident that the mean heat flux represented as remains identical for two identical unit cells. This straightforward observation underscores that altering the surface area by linking several unit cells in parallel does not affect the mean heat flux.
A similar analysis applies to the sequential alignment along the main direction of heat flow of two unit cells. Due to symmetry considerations, the gradient remains identical for both unit cells, resulting in an identical total gradient along the two unit cells. Consequently, the heat flow or mean heat flux remains identical when these two unit cells are aligned under the appropriate boundary conditions. These considerations further justify the use of a unit cell.
Moreover, in addition Figure 6, examination of the temperature profile within the unit cell (refer to Figure 3) reveals that the HybridBridge, or its corresponding contact point, significantly influences the total heat flow. This dominance stems from the substantial disparity between the thermal conductivities of the phases and the notably high thermal resistance at the contact point compared to the particle interior.
Considering all three factors, it becomes evident that is unaffected by changes in A or , but rather influenced by the number of HybridBridges per unit cell. It is crucial to differentiate whether the HybridBridges are arranged in parallel or in series with respect to the main direction of heat conduction. For clarification: A parallel connection describes the number of HybridBridges denoted as , on a plane parallel to A, whereas a serial connection counts the number of such parallel planes, denoted as , aligned along .
A straightforward resistance analysis of the HybridBridge reveals that is directly proportional to and inversely proportional to . Likewise, considering Equation (4), is proportional to and inversely proportional to . Applying this analysis to the body-centred-cubic unit cell yields the following result:
The subsequent relationship between and can be generalized to encompass the utilization of HybridBridge in any packed bed. For illustration we can state the descriptive equation
3.2. Predesign of the HybridBridge Geometry
As demonstrated earlier, the influence of the geometry of the HybridBridge on the effective thermal conductivity can be traced back to the results of the simple-cubic unit cell. Hence, we will formulate an approximate representation for drawing upon the insights garnered from the simple-cubic unit cell results.
To address this objective, we have crafted a straightforward thermal resistance model that is as close as possible to the physical situation. This adaptable model can be fine-tuned to align with CFD findings by adjusting empirical parameters. The model is based on the following equation:
In this equation and represent the dimensions of the simple-cubic unit cell, visually depicted in Figure 7. The equations governing the calculation of the total resistance are the following:
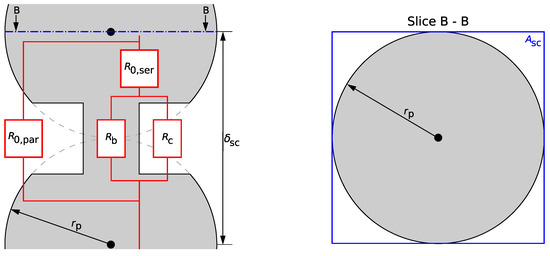
Figure 7.
Schematic representation of the main dimensions of the simple-cubic unit cell with the proposed resistance network model. Analogous to Figure 2, the HybridBridge is shown larger than it should be used in practice.
The graphical representation of the resistance network is provided in Figure 7. The resistance encompasses all the resistance connected in series with the HybridBridge, including those of the two hemispheres. The resistance amalgamates all resistances that are parallel to the HybridBridge, such as those pertaining to heat conduction through the fluid outside the generated cap region.
and are empirical values crucial for refining the accuracy of this simplified modelling approach. These values are determined through fitting the outcomes of the numerical model. For this purpose, and from the simulations performed (see Figure 5) were used in Equations (8)–(14) while adding missed fixed values from Table 1. The resulting relationship calculates values of for a given HybridBridge Geometry as a function of and . By calculating the deviation between values of , obtained using the procedure described, and the corresponding numerically computed values for , the optimal values of and were determined using the least squares method. The least squares method yields the following values:
Based on the findings presented in from Section 3.1 it is plausible to interpolate between the two unit cells using the contact points. However, determining the precise locations of these contact points is not always feasible, or conducting an analysis of their positions in relation to the main heat conduction direction can be excessively time-consuming. Hence, porosity emerges as a viable criterion for interpolation, as it correlates with the number of contact points, evident from the coordination number. This relationship is expressed as follows:
The incorporation of the porosity of the simple-cubic unit cell [19] and the porosity of the body-centered-cubic unit cell [19] yields the following for .
Now, we aim to derive a functional relationship using Equations (8)–(15) to approximate the radius of the HybridBridge for a given packed bed ( and given) and a selected cap radius.
To maintain the function’s complexity within manageable bounds, all predefined values for the examined unit cells from Table 1 have already been set and roughly consolidated, except those required for a dimensionless context. The transformations are partially based on [26]. The equation is presented below:
with
To validate this equation, simulation results for both unit cells were used. The calculated bridge radius was compared with the radius used in the underlying CFD model. For , the average deviation is about . Notably, the deviation increases significantly for . Across all simulation runs, including , the average deviation between the calculated and utilized radii is slightly below .
For a real packed bed with , investigated in [14], the equation yielded for the relative bridge radius. This results in a deviation of . To ascertain porosity, we employed our MATLAB [27] tool, capable of numerically computing porosity for geometrically defined beds, both in general and with local resolution in the axial and radial directions. The porosity of the examined packed bed was determined to be .
Accounting for all eventualities with a single equation is impractical due to the multitude of variables influencing the effective thermal conductivity . Models such as that proposed by Zehner, Bauer and Schlünder (e.g., [25]), illustrate the complexity inherent in this problem. Moreover, the wide variety of geometries and material combinations found in packed beds further complicate the issue.
The objective of Equation (16) is not to describe the effective thermal conductivity with a single equation, but to offer a method for implementing the new HybridBridge method in a more focused manner. Consequently, the formal validation of this equation is restricted to the packed bed parameters outlined in this work. The generalizability of Equation (16) cannot be reliably estimated due to the inherent variability in such systems. However, it is essential to note that this limitation is specific for Equation (16) alone. Regarding the resistance model in general, there is no evidence to suggest that it cannot be used to predesign the HybridBridge with other packed bed parameters.
Users are encouraged to test Equation (16) for their specific applications. Should the attained accuracy fail to meet the specified requirements, it is advisable to derive a more suitable empirical equation from our proposed resistance model, following the structure of Equation (16). This iterative process allows for refinement tailored to the intricacies of individual applications, ensuring optimal performance.
4. Discussion
The new HybridBridge method, introduced in [14], has undergone a thorough analysis. This method aims to address the contact point problem, ensuring that the effective thermal conductivity remains consistent with physical specifications while minimizing the impact of particle modifications on flow dynamics.
The theoretical framework demonstrates the potential advantages of the HybridBridge method over other local techniques, particularly evident for small Péclet numbers and significant ratios of particle thermal conductivity to fluid thermal conductivity . Furthermore, we have established the plausibility that the HybridBridge method typically induces a lesser alteration in porosity compared to conventional caps methods. In our previous work [14] we have illustrated that larger cells and thus a smaller number of cells using the HybridBridge method is sufficient to achieve comparable mesh quality to the conventional bridges method. This underscores the HybridBridge’s reliability in addressing the contact point problem across a broader range of scenarios than traditional methods could offer.
The comprehensive geometrical description highlights that the HybridBridge method inherently encompasses both the conventional bridges and caps methods as special cases. This simplifies its integration into workflow, as several local methods become available through the adoption of the HybridBridge approach.
Through an analysis of the body-centered-cubic unit cell, we have rectified a limitation in our prior work, where the porosity, and consequently the coordination number, was lower than observed in many real cases of randomly packed beds. We have specified how the HybridBridge can be adapted to physical reality using a homogenization approach and experimental values or models for the effective thermal conductivity .
Given that the HybridBridge method involves two independent geometric parameters and aims for a more accurate representation of the effective thermal conductivity, , the implementation effort required is greater compared to conventional methods. The primary challenge lies in the difficulty of designing the appropriate bridge radius for the given effective thermal conductivity and cap height prior to simulation.
Through a comprehensive assessment of our recent simulations involving both the body-centered-cubic and simple-cubic unit cells, we have outlined an initial methodology for the a priori design of the HybridBridge, intended for numerical simulations. This involved the development of a semi-empirical resistance model tailored to the effective thermal conductivity of the simple-cubic unit cell. Subsequently, we extended the applicability of this model to other packed beds by leveraging insights from the body-centered-cubic unit cell, employing interpolation techniques across varying porosities and their corresponding coordination numbers.
Building upon this model approach, we derived an equation to approximate the bridge radius. To validate the accuracy of this equation, we compared the calculated radius against the radius employed in unit cells and a previously examined randomly packed bed. The mean deviation was found to be less than , which is deemed satisfactory for the model’s intended purpose.
It is crucial to note that while this equation provides a valuable tool for estimating the bridge radius, it cannot be directly applied to other packed beds without adjustments and validation to the specific parameters of each individual bed under investigation. However, the underlying resistance network model approach remains unaffected and is applicable to other packed beds.
A potential avenue for future research is suggested: building upon the investigation into the impact of diverse lattice arrangements, coordination numbers, and porosities, it would be beneficial to extend the study to encompass various material combinations. In addition, the HybridBridge method should be extended to other forms of contact. This expanded scope will facilitate a deeper understanding of the possibilities and hurdles associated with the innovative HybridBridge method of contact point modification, enabling a more nuanced and targeted application of the HybridBridge approach.
Author Contributions
The authors have contributed to the work as follows: conceptualization, D.F.S., M.R.Z., C.U. and R.S.; methodology, D.F.S., M.R.Z., C.U. and R.S.; software, D.F.S., M.R.Z. and C.U.; validation, D.F.S.; formal analysis, D.F.S., M.R.Z. and R.S.; investigation, D.F.S., M.R.Z. and C.U.; resources, D.F.S., M.R.Z. and R.S.; data curation, D.F.S.; writing—original draft preparation, D.F.S. and M.R.Z.; writing—review and editing, D.F.S., M.R.Z. and R.S.; visualization, D.F.S. and M.R.Z.; supervision, R.S.; project administration, D.F.S.; funding acquisition, R.S. All authors have read and agreed to the published version of the manuscript.
Funding
Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—INST 187/742-1 FUGG; INST 187/592-1 FUGG.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| b | bridge |
| bcc | body-centered-cubic |
| c | cap |
| CFL | Courant–Friedrichs–Lewy |
| eff | effective |
| f | fluid |
| g | gap |
| HB | HybridBridge |
| p | particle |
| par | parallel |
| uc | unit-cell |
| s | solid |
| sc | simple-cubic |
| ser | serial |
| x | radial or axial coordinate |
References
- Eigenberger, G.; Ruppel, W. Catalytic Fixed–Bed Reactors. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH, Ed.; Wiley-VCH: Weinheim, Germany, 2012. [Google Scholar] [CrossRef]
- Tsotsas, E. Über die Wärme- und Stoffübertragung in durchströmten Festbetten: Experimente, Modelle, Theorien. Habilitation Thesis, VDI-Verlag, Düsseldorf, Germany, 1990; pp. 7–16. [Google Scholar]
- Dixon, A.G.; Nijemeisland, M. CFD as a Design Tool for Fixed-Bed Reactors. Ind. Eng. Chem. Res. 2001, 40, 5246–5254. [Google Scholar] [CrossRef]
- Romkes, S.; Dautzenberg, F.; van den Bleek, C.; Calis, H. CFD modelling and experimental validation of particle-to-fluid mass and heat transfer in a packed bed at very low channel to particle diameter ratio. Chem. Eng. J. 2003, 96, 3–13. [Google Scholar] [CrossRef]
- Bai, H.; Theuerkauf, J.; Gillis, P.A.; Witt, P.M. A Coupled DEM and CFD Simulation of Flow Field and Pressure Drop in Fixed Bed Reactor with Randomly Packed Catalyst Particles. Ind. Eng. Chem. Res. 2009, 48, 4060–4074. [Google Scholar] [CrossRef]
- Guardo, A.; Coussirat, M.; Larrayoz, M.A.; Recasens, F.; Egusquiza, E. CFD Flow and Heat Transfer in Nonregular Packings for Fixed Bed Equipment Design. Ind. Eng. Chem. Res. 2004, 43, 7049–7056. [Google Scholar] [CrossRef]
- Ookawara, S.; Kuroki, M.; Street, D.; Ogawaa, K. High-fidelity DEM-CFD modeling of packed bed reactors for process intensification. In Proceedings of the European Congress of Chemical Engineering (ECCE-6), Copenhagen, Denmark, 16–20 September 2007. [Google Scholar]
- Eppinger, T.; Seidler, K.; Kraume, M. DEM-CFD simulations of fixed bed reactors with small tube to particle diameter ratios. Chem. Eng. J. 2011, 166, 324–331. [Google Scholar] [CrossRef]
- Eppinger, T.; Wehinger, G.D. A Generalized Contact Modification for Fixed–Bed Reactor CFD Simulations. Chem. Ing. Tech. 2021, 93, 143–153. [Google Scholar] [CrossRef]
- Kutscherauer, M.; Böcklein, S.; Mestl, G.; Turek, T.; Wehinger, G.D. An improved contact modification routine for a computationally efficient CFD simulation of packed beds. Chem. Eng. J. Adv. 2022, 9, 100197. [Google Scholar] [CrossRef]
- Dixon, A.G.; Nijemeisland, M.; Stitt, E.H. Systematic mesh development for 3D CFD simulation of fixed beds: Contact points study. Comput. Chem. Eng. 2013, 48, 135–153. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Fütterer, C.; Kraume, M. Contact Modifications for CFD Simulations of Fixed-Bed Reactors: Cylindrical Particles. Ind. Eng. Chem. Res. 2017, 56, 87–99. [Google Scholar] [CrossRef]
- Bu, S.; Wang, J.; Sun, W.; Ma, Z.; Zhang, L.; Pan, L. Numerical and experimental study of stagnant effective thermal conductivity of a graphite pebble bed with high solid to fluid thermal conductivity ratios. Appl. Therm. Eng. 2020, 164, 114511. [Google Scholar] [CrossRef]
- Szambien, D.F.; Ulrich, C.; Ziegler, M.R.; Maaß, N.P.; Scharf, R. A Novel Method for Generating 3D Mesh at Contact Points in Packed Beds. In Proceedings of the 14. International Conference on Computational Heat and Mass Transfer (ICCHMT2023), Düsseldorf, Germany, 4–8 September 2023. [Google Scholar]
- Yagi, S.; Kunii, D. Studies on effective thermal conductivities in packed beds. AIChE J. 1957, 3, 373–381. [Google Scholar] [CrossRef]
- Tsotsas, E. M7 Wärmeleitung und Dispersion in durchströmten Schüttungen. In VDI-Wärmeatlas; Stephan, P., Kabelac, S., Kind, M., Mewes, D., Schaber, K., Wetzel, T., Eds.; Springer Vieweg: Berlin/Heidelberg, Germany, 2019; pp. 1753–1772. [Google Scholar] [CrossRef]
- Aichlmayr, H.T.; Kulacki, F.A. The Effective Thermal Conductivity of Saturated Porous Media. Adv. Heat Transf. 2006, 39, 377–460. [Google Scholar] [CrossRef]
- Hsu, C.T.; Cheng, P.; Wong, K.W. Modified Zehner-Schlunder models for stagnant thermal conductivity of porous media. Int. J. Heat Mass Transf. 1994, 37, 2751–2759. [Google Scholar] [CrossRef]
- von Seckendorff, J.; Hinrichsen, O. Review on the structure of random packed-beds. Can. J. Chem. Eng. 2021, 99, S703–S733. [Google Scholar] [CrossRef]
- van Rossum, G. Python Reference Manual: Report CS-R9525; Centrum Wiskunde & Informatica: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Anaconda, Inc. Anaconda Individual Edition 2021.05; Anaconda, Inc.: Austin, TX, USA, 2021. [Google Scholar]
- Open CASCADE. Salome: The Open Source Platform for Numerical Simulation. SALOME Version 9.10.0; Open CASCADE: Issy-Les-Moulineaux, France, 2023. [Google Scholar]
- Greenshields, C. OpenFOAM v9 User Guide; The OpenFOAM Foundation: London, UK, 2021. [Google Scholar]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Tsotsas, E. M11 Wärmeleitfähigkeit von Schüttschichten. In VDI-Wärmeatlas; Stephan, P., Kabelac, S., Kind, M., Mewes, D., Schaber, K., Wetzel, T., Eds.; Springer Vieweg: Berlin/Heidelberg, Germany, 2019; pp. 1831–1843. [Google Scholar] [CrossRef]
- Wolfram Alpha LLC. Wolfram|Alpha; Wolfram Research, Inc.: Champaign, IL, USA, 2024. [Google Scholar]
- The MathWorks Inc. MATLAB Version: 9.9.0. (R2020b), MathWorks Inc.: Natick, MA, USA, 2020.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).