A Symmetric Approach Elucidates Multisensory Information Integration
Abstract
:“A color is a physical object when we consider its dependence upon its luminous source; regarding, however, its dependence upon the retina, it becomes a psychological object, a sensation. Not the subject, but the direction of our investigation, is different in the two domains” (Mach 1885).
1. Classical vs. Current View
2. A Topological Model of Multisensory Integration
2.1. The Borsuk-Ulam Theorem.
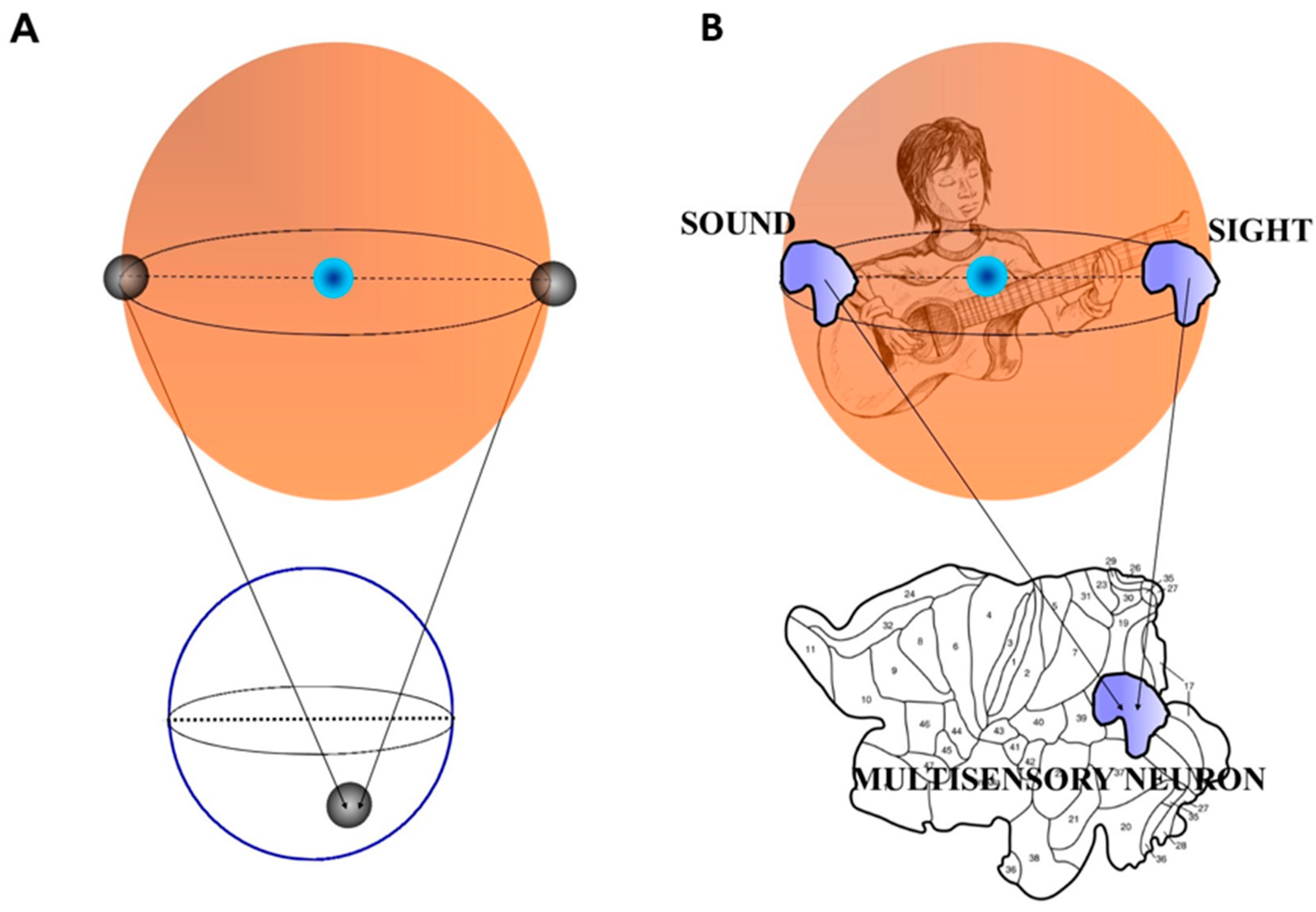
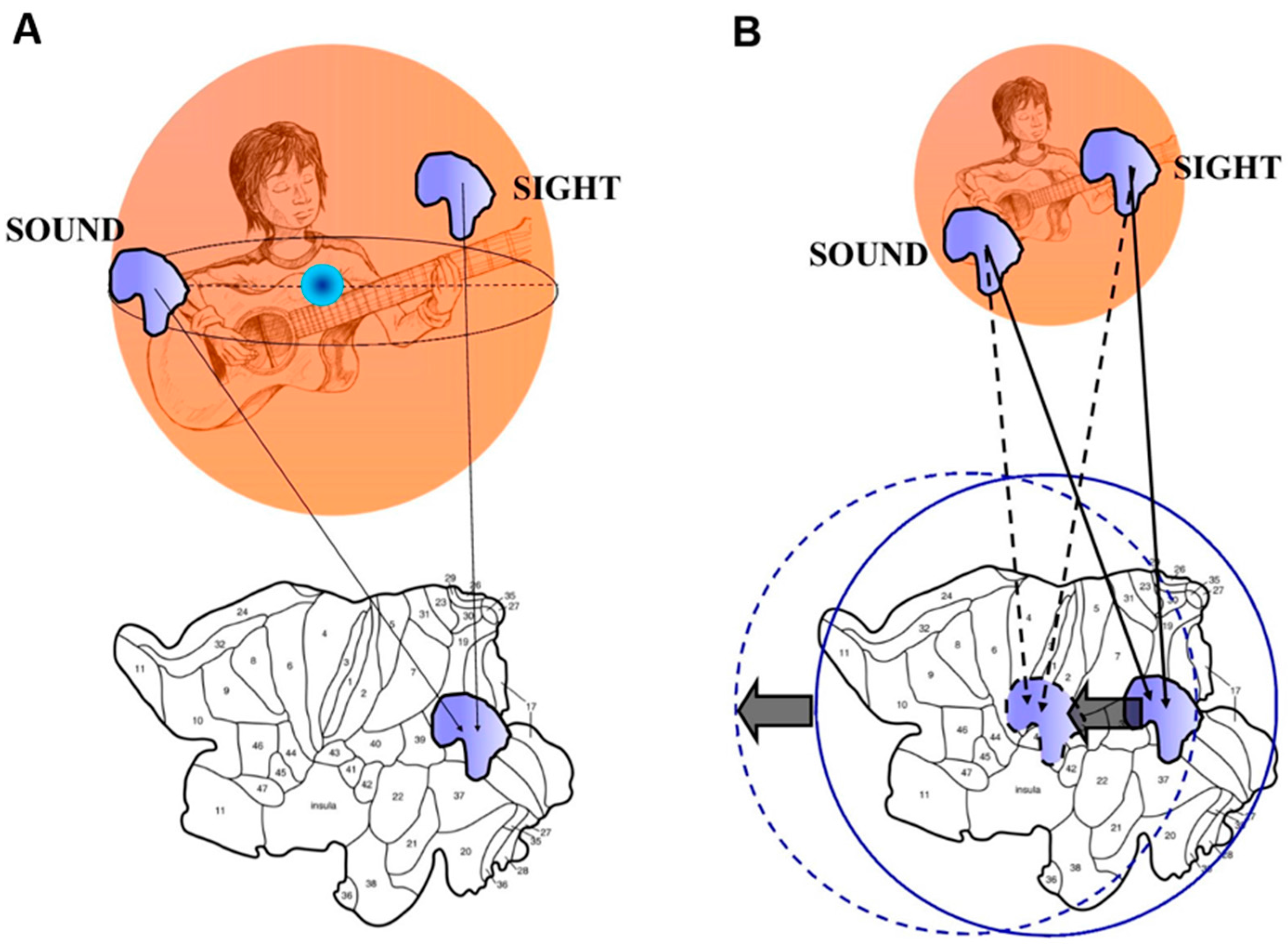
Points on Sn are antipodal, provided they are diametrically opposite. Examples of antipodal points are the endpoints of a line segment S1, or the opposite points along the circumference of a circle S2, or the poles of a sphere S3 [35]. An n-dimensional Euclidean vector space is denoted by [36,37]. Put simply, BUT states that a sphere displays two antipodal points that emit matching signals. When they are projected on a circumference, they give rise to a single point which a description matching both antipodal points (Figure 1A). Here “opposite points” means two points on the surface of a three-dimensional sphere (the surface of a beach ball is a good example) which share some characteristics in common and are at the same distance from the center of the beach ball [38]. For example, BUT dictates that on the earth’s surface there always exist two opposite points with the same pressure and temperature. Two opposite points embedded in a sphere project onto a single point on a circumference, and vice versa: this means that the projection from a higher dimension (equipped with two antipodal points) to a lower one gives rise to a single point (equipped with the characteristics of both the antipodal points). It is worth mentioning again that the two antipodal points display similar features: we will go through this central issue in the next paragraph.Every continuous map must identify a pair of antipodal points.
2.2. Borsuk-Ulam Theorem in Brain Signal Analysis.
- (Str. 1) Every union of sets in is a set in
- (Str. 2) Every finite intersection of sets in is a set in
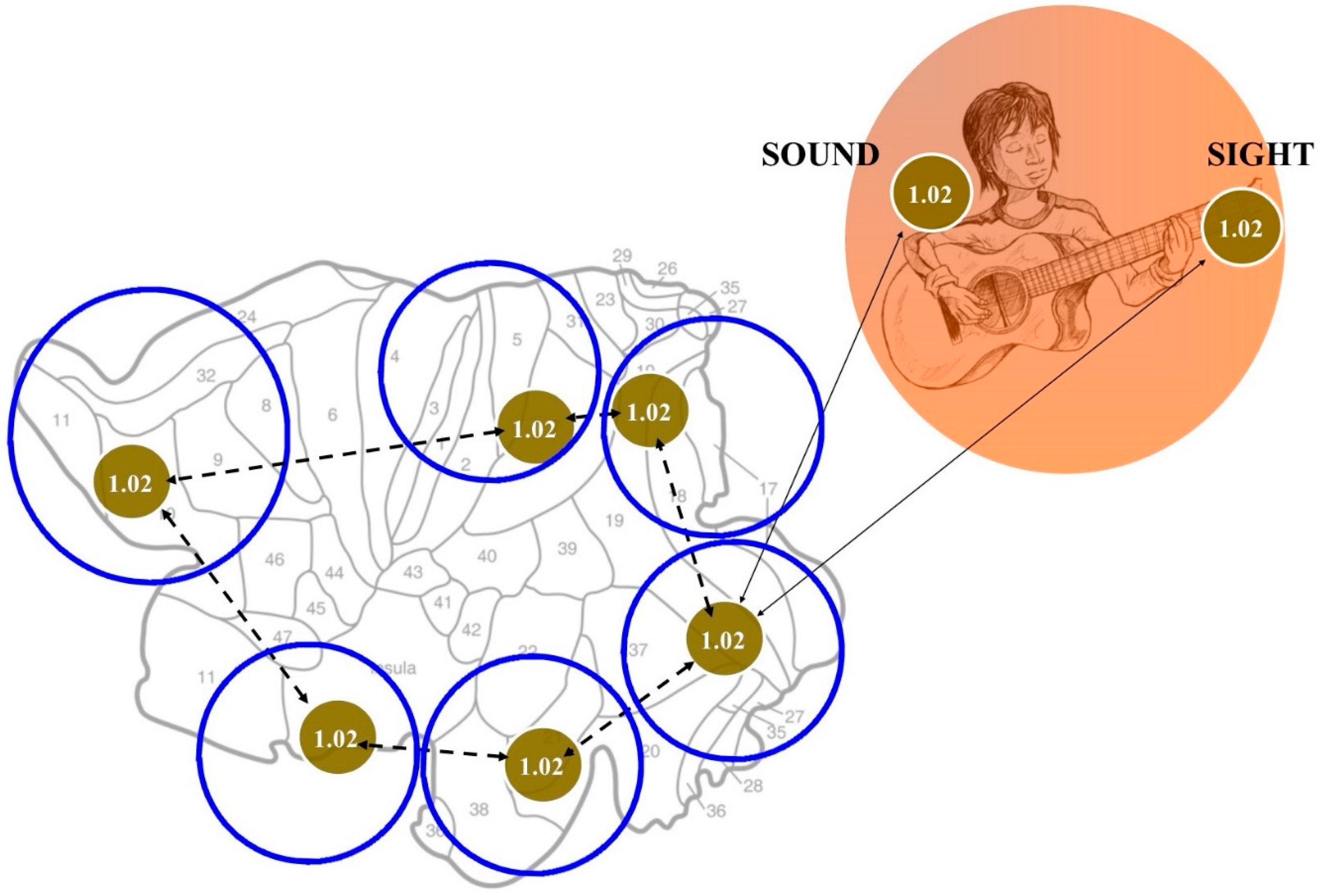
2.3 Borsuk-Ulam Theorem and Multisensory Integration.
3. An Answer for Current Issues
4. What Does Topology Bring to the Table?
Conflicts of Interest
References
- Krueger, J.; Royal, D.W.; Fister, M.C.; Wallace, M.T. Spatial receptive field organization of multisensory neurons and its impact on multisensory interactions. Hear. Res. 2009, 258, 47–54. [Google Scholar] [CrossRef] [PubMed]
- Fetsch, C.R.; DeAngelis, G.C.; Angelaki, D.E. Visual-vestibular cue integration for heading perception: Applications of optimal cue integration theory. Eur. J. Neurosci. 2010, 31, 1721–1729. [Google Scholar] [CrossRef] [PubMed]
- Werner, S.; Noppeney, U. Superadditive responses in superior temporal sulcus predict audiovisual benefits in object categorization. Cereb. Cortex 2009, 20, 1829–1842. [Google Scholar] [CrossRef] [PubMed]
- Stein, B.E.; Rowland, B.A. Organization and plasticity in multisensory integration: Early and late experience affects its governing principles. Prog. Brain Res. 2011, 191, 145–163. [Google Scholar] [PubMed]
- Royal, D.W.; Krueger, J.; Fister, M.C.; Wallace, M.T. Adult plasticity of spatiotemporal receptive fields of multisensory superior colliculus neurons following early visual deprivation. Restor. Neurol Neurosci. 2010, 28, 259–270. [Google Scholar] [PubMed]
- Burnett, L.R.; Stein, B.E.; Perrault, T.J., Jr.; Wallace, M.T. Excitotoxic lesions of the superior colliculus preferentially impact multisensory neurons and multisensory integration. Exp. Brain Res. 2007, 179, 325–338. [Google Scholar] [CrossRef] [PubMed]
- Stein, B.E.; Perrault, T.Y., Jr.; Stanford, T.R.; Rowland, B.A. Postnatal experiences influence how the brain integrates information from different senses. Front. Integr. Neurosci. 2009, 3. [Google Scholar] [CrossRef] [PubMed]
- Stein, B.E.; Stanford, T.R.; Rowland, B.A. Development of multisensory integration from the perspective of the individual neuron. Nat. Rev. Neurosci. 2014, 15, 520–535. [Google Scholar] [CrossRef] [PubMed]
- Johnson, S.P.; Amso, D.; Slemmer, J.A. Development of object concepts in infancy: Evidence for early learning in an eye-tracking paradigm. Proc. Natl. Acad. Sci. USA 2003, 100, 10568–10573. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Yu, L.; Rowland, B.A.; Stanford, T.R.; Stein, B.E. Incorporating cross-modal statistics in the development and maintenance of multisensory integration. J. Neurosci. 2012, 15, 2287–2298. [Google Scholar] [CrossRef] [PubMed]
- Porcu, E.; Keitel, C.; Müller, M.M. Visual, auditory and tactile stimuli compete for early sensory processing capacities within but not between senses. Neuroimage 2014, 97, 224–235. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Rowland, B.A.; Stein, B.E. Initiating the development of multisensory integration by manipulating sensory experience. J. Neurosci. 2010, 7, 4904–4913. [Google Scholar] [CrossRef] [PubMed]
- Borsuk, K. Drei Sätze über die n-dimensionale euklidische Sphäre. Fundam. Math. 1933, 20, 177–190. (In German) [Google Scholar]
- Nieuwenhuys, R.; Voogd, J.; van Huijzen, C. The Human Central Nervous System; Springer: Heidelberg, Germany, 2008. [Google Scholar]
- Pollmann, S.; Zinke, W.; Baumgartner, F.; Geringswald, F.; Hanke, M. The right temporo-parietal junction contributes to visual feature binding. Neuroimage 2014, 101, 289–297. [Google Scholar] [CrossRef] [PubMed]
- Van den Heuvel, M.P.; Sporns, O. Rich-club organization of the human connectome. J. Neurosci. 2011, 31, 15775–15786. [Google Scholar] [CrossRef] [PubMed]
- Allman, B.L.; Keniston, L.P.; Meredith, M.A. Not just for bimodal neurons anymore: The contribution of unimodal neurons to cortical multisensory processing. Brain Topogr. 2009, 21, 157–167. [Google Scholar] [CrossRef] [PubMed]
- Hackett, T.A.; Schroeder, C.E. Multisensory integration in auditory and auditory-related areas of Cortex. Hear. Res. 2009, 258, 72–79. [Google Scholar] [CrossRef] [PubMed]
- Shinder, M.E.; Newlands, S.D. Sensory convergence in the parieto-insular vestibular cortex. J. Neurophysiol. 2014, 111, 2445–2464. [Google Scholar] [CrossRef] [PubMed]
- Reig, R.; Silberberg, G. Multisensory integration in the mouse striatum. Neuron 2014, 83, 1200–1212. [Google Scholar] [CrossRef] [PubMed]
- Kuang, S.; Zhang, T. Smelling directions: Olfaction modulates ambiguous visual motion perception. Sci. Rep. 2014, 23. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.S.; Gomez-Ramirez, M.; Thakur, P.H.; Hsiao, S.S. Multimodal Interactions between Proprioceptive and Cutaneous Signals in Primary Somatosensory Cortex. Neuron 2015, 86, 555–566. [Google Scholar] [CrossRef] [PubMed]
- Murray, M.M.; Thelen, A.; Thut, G.; Romei, V.; Martuzzi, R.; Matusz, P.J. The multisensory function of the human primary visual cortex. Neuropsychologia 2015. [Google Scholar] [CrossRef] [PubMed]
- Nys, J.; Smolders, K.; Laramée, M.E.; Hofman, I.; Hu, T.T.; Arckens, L. Regional Specificity of GABAergic Regulation of Cross-Modal Plasticity in Mouse Visual Cortex after Unilateral Enucleation. J. Neurosci. 2015, 35, 11174–11189. [Google Scholar] [CrossRef] [PubMed]
- Bedny, M.; Richardson, H.; Saxe, R. “Visual” Cortex Responds to Spoken Language in Blind Children. J. Neurosci. 2015, 35, 11674–11681. [Google Scholar] [CrossRef] [PubMed]
- Yan, K.S.; Dando, R. A crossmodal role for audition in taste perception. J. Exp. Psychol. Hum. Percept. Perform. 2015, 41, 590–596. [Google Scholar] [CrossRef] [PubMed]
- Escanilla, O.D.; Victor, J.D.; di Lorenzo, P.M. Odor-taste convergence in the nucleus of the solitary tract of the awake freely licking rat. J. Neurosci. 2015, 35, 6284–6297. [Google Scholar] [CrossRef] [PubMed]
- Maier, J.X.; Blankenship, M.L.; Li, J.X.; Katz, D.B. A Multisensory Network for Olfactory Processing. Curr. Biol. 2015, 25, 2642–2650. [Google Scholar] [CrossRef] [PubMed]
- Klemen, J.; Chambers, C.D. Current perspectives and methods in studying neural mechanisms of multisensory interactions. Neurosci. Biobehav. Rev. 2012, 36, 111–133. [Google Scholar] [CrossRef] [PubMed]
- Bastos, A.M.; Litvak, V.; Moran, R.; Bosman, C.A.; Fries, P.; Friston, K.J. A DCM study of spectral asymmetries in feedforward and feedback connections between visual areas V1 and V4 in the monkey. Neuroimage 2015, 108, 460–475. [Google Scholar] [CrossRef] [PubMed]
- Dodson, C.T.J.; Parker, P.E. A User’s Guide to Algebraic Topology; Kluwer: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Matoušek, J. Using the Borsuk-Ulam Theorem; Lectures on Topological Methods in Combinatorics and Geometry; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Weisstein, E.W. Antipodal Points. Available online: http://mathworld.wolfram.com/AntipodalPoints.html (accessed on 15 November 2016).
- Borsuk, M.; Gmurczyk, A. On Homotopy Types of 2-Dimensional Polyhedral. Fundam. Math. 1980, 109, 123–142. [Google Scholar]
- Moura, E.; Henderson, D.G. Experiencing Geometry: On Plane and Sphere; Prentice Hall: Englewood Cliffs, NJ, USA, 1996. [Google Scholar]
- Tozzi, A.; Peters, J.F. Towards a Fourth Spatial Dimension of Brain Activity. Cogn. Neurodyn. 2016, 10, 189–199. [Google Scholar] [CrossRef] [PubMed]
- Tozzi, A.; Peters, J.F. A Topological Approach Unveils System Invariances and Broken Symmetries in the Brain. J. Neurosci. Res. 2016, 94, 351–365. [Google Scholar] [CrossRef] [PubMed]
- Marsaglia, G. Choosing a Point from the Surface of a Sphere. Ann. Math. Stat. 1972, 43, 645–646. [Google Scholar] [CrossRef]
- Van Essen, D.C. A Population-Average, Landmark—And Surface-based (PALS) atlas of human cerebral cortex. Neuroimage 2005, 28, 635–666. [Google Scholar] [CrossRef] [PubMed]
- Krantz, S.G. A Guide to Topology; The Mathematical Association of America: Washington, DC, USA, 2009; p. 107. [Google Scholar]
- Manetti, M. Topology; Springer: Heidelberg, Germany, 2015. [Google Scholar]
- Cohen, M.M. A Course in Simple Homotopy Theory; Springer: New York, NY, USA, 1973; p. MR0362320. [Google Scholar]
- Borsuk, K. Concerning the classification of topological spaces from the standpoint of the theory of retracts. Fundam. Math. 1959, 46, 321–330. [Google Scholar]
- Borsuk, K. Fundamental Retracts and Extensions of Fundamental Sequences. Fundam. Math. 1969, 64, 55–85. [Google Scholar]
- Collins, G.P. The Shapes of Space. Sci. Am. 2004, 291, 94–103. [Google Scholar] [CrossRef] [PubMed]
- Weeks, J.R. The Shape of Space, 2nd ed.; Marcel Dekker, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Peters, J.F. Topology of Digital Images. Visual Pattern Discovery in Proximity Spaces, Intelligent Systems Reference Library; Springer: Berlin, Germany, 2014; Volume 63, pp. 1–342. [Google Scholar]
- Peters, J.F. Computational Proximity. Excursions in the Topology of Digital Images, Intelligent Systems Reference Library; Springer: Berlin, Germany, 2016; pp. 1–468. [Google Scholar]
- Willard, S. General Topology; Dover Pub., Inc.: Mineola, NY, USA, 1970. [Google Scholar]
- Peters, J.F.; Tozzi, A. Region-Based Borsuk-Ulam Theorem. arXiv, 2016; arXiv:1605.02987. [Google Scholar]
- Perrault, T.J., Jr.; Stein, B.E.; Rowland, B.A. Non-stationarity in multisensory neurons in the superior colliculus. Front. Psychol. 2011, 2, 144. [Google Scholar] [CrossRef] [PubMed]
- Benson, K.; Raynor, H.A. Occurrence of habituation during repeated food exposure via the olfactory and gustatory systems. Eat Behav. 2014, 15, 331–333. [Google Scholar] [CrossRef] [PubMed]
- Schneidman, E.; Berry, M.J.; Segev, R.; Bialek, W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 2006, 440, 1007–1012. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, T.; Kan, S.; Koike, T.; Misaki, M.; Konishi, S.; Miyauchi, S.; Masuda, N. Network-dependent modulation of brain activity during sleep. NeuroImage 2014, 98, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Li, Y.; Childress, A.R.; Detre, J.A. Brain entropy mapping using fMRI. PLoS ONE 2014, 9, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Kida, T.; Tanaka, E.; Kakigi, R. Multi-Dimensional Dynamics of Human Electromagnetic Brain Activity. Front. Hum. Neurosci. 2016, 9, 713. [Google Scholar] [CrossRef] [PubMed]
- Sutter, C.; Drewing, K.; Müsseler, J. Multisensory integration in action control. Front. Psychol. 2014. [Google Scholar] [CrossRef] [PubMed]
- Drugowitsch, J.; de Angelis, G.C.; Klier, E.M.; Angelaki, D.E.; Pouget, A. Optimal multisensory decision-making in a reaction-time task. Elife 2014. [Google Scholar] [CrossRef] [PubMed]
- Jones, D.M.B. Models, Metaphors and Analogies. In The Blackwell Guide to the Philosophy of Science; Machamer, P., Silberstein, M., Eds.; Blackwell: Oxford, UK, 2002. [Google Scholar]
- Mach, E. Analysis of the Sensations; The Open Court Publishing Company: Chicago, IL, USA, 1896. [Google Scholar]
- Van Ackeren, M.J.; Schneider, T.R.; Müsch, K.; Rueschemeyer, S.A. Oscillatory neuronal activity reflects lexical-semantic feature integration within and across sensory modalities in distributed cortical networks. J. Neurosci. 2014, 34, 14318–14323. [Google Scholar] [CrossRef] [PubMed]
- Doehrmann, O.; Naumer, M.J. Semantics and the multisensory brain: How meaning modulates processes of audio-visual integration. Brain Res. 2008, 25, 136–150. [Google Scholar] [CrossRef] [PubMed]
- Diaconescu, A.O.; Alain, C.; McIntosh, A.R. The co-occurrence of multisensory facilitation and cross-modal conflict in the human brain. J. Neurophysiol. 2011, 106, 2896–2909. [Google Scholar] [CrossRef] [PubMed]
- Gärdenfors, P. Six Tenets of Cognitive Semantics. 2011. Available online: http://www.ling.gu.se/~biljana/ st1-97/ tenetsem.html (accessed on 11 December 2016).
- Gärdenfors, P. Conceptual Spaces: The Geometry of Thought; The MIT Press: Cambridge, UK, 2000. [Google Scholar]
- Kuhn, W. Why Information Science Needs Cognitive Semantics—And What It Has to Offer in Return; DRAFT Version 1.0; Meaning and Computation Laboratory, Department of Computer Science and Engineering, University of California at San Diego: La Jolla, CA, USA, 31 March 2003. [Google Scholar]
- Stevenson, R.A.; Fister, J.K.; Barnett, Z.P.; Nidiffer, A.R.; Wallace, M.T. Interactions between the spatial and temporal stimulus factors that influence multisensory integration in human performance. Exp. Brain Res. 2012, 219, 121–137. [Google Scholar] [CrossRef] [PubMed]
- Langacker, R.W. Cognitive Grammar—A Basic Introduction; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Fauconnier, G. Mappings in Thought and Language; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Kim, J. Making Sense of Emergence. Philos. Stud. 1999, 95, 3–36. [Google Scholar] [CrossRef]
- Parise, C.V.; Spence, C.; Ernst, M.O. When correlation implies causation in multisensory integration. Curr. Biol. 2012, 22, 46–49. [Google Scholar] [CrossRef] [PubMed]
- Körding, K.P.; Beierholm, U.; Ma, W.J.; Quartz, S.; Tenenbaum, J.B.; Shams, L. Causal inference in multisensory perception. PLoS ONE 2007, 26, e943. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. The free-energy principle: A unified brain theory? Nat. Rev. Neurosci. 2010, 11, 127–138. [Google Scholar] [CrossRef] [PubMed]
- Grush, R. Cognitive Science. In The Blackwell Guide to the Philosophy of Science; Machamer, P., Silberstein, M., Eds.; Blackwell: Oxford, UK, 2002. [Google Scholar]
- McLean, J.; Freed, M.A.; Segev, R.; Freed, M.A.; Berry, M.J.; Balasubramanian, V.; Sterling, P. How much the eye tells the brain. Curr. Biol. 2006, 25, 1428–1434. [Google Scholar]
- Royal, D.W.; Carriere, B.N.; Wallace, M.T. Spatiotemporal architecture of cortical receptive fields and its impact on multisensory interactions. Exp. Brain Res. 2009, 198, 127–136. [Google Scholar] [CrossRef] [PubMed]
- Méndez, J.C.; Pérez, O.; Prado, L.; Merchant, H. Linking perception, cognition, and action: Psychophysical observations and neural network modelling. PLoS ONE 2014, 9, e102553. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, B.; Tozzi, A.; Cooray, G.K.; Douglas, P.K.; Friston, K.J. Towards a Neuronal Gauge Theory. PLoS Biol. 2016, 14, e1002400. [Google Scholar] [CrossRef] [PubMed]
- Peters, J.F.; Tozzi, A.; Ramanna, S. Brain tissue tessellation shows absence of canonical microcircuits. Neurosci. Lett. 2016, in press. [Google Scholar] [CrossRef] [PubMed]
- Holldobler, B.; Wilson, E.O. Formiche—Storia di Un’Esplorazione Scientifica; Adelphi: Milano, Italy, 2002. [Google Scholar]
- Peirce, C.S. Philosophical Writings of Peirce; Buchler, J., Ed.; Courier Dover Publications: New York, NY, USA, 2011; p. 344. [Google Scholar]
- Goodman, R.B. Pragmatism: Critical Concepts in Philosophy; Taylor & Francis: New York, NY, USA, 2005; Volume 2, p. 345. [Google Scholar]
- Magosso, E.; Cuppini, C.; Serino, A.; di Pellegrino, G.; Ursino, M. A theoretical study of multisensory integration in the superior colliculus by a neural network model. Neural Netw. 2008, 21, 817–829. [Google Scholar] [CrossRef] [PubMed]
- Ohshiro, T.; Angelaki, D.E.; DeAngelis, G.C. A normalization model of multisensory integration. Nat. Neurosci. 2011, 14, 775–782. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tozzi, A.; Peters, J.F. A Symmetric Approach Elucidates Multisensory Information Integration. Information 2017, 8, 4. https://doi.org/10.3390/info8010004
Tozzi A, Peters JF. A Symmetric Approach Elucidates Multisensory Information Integration. Information. 2017; 8(1):4. https://doi.org/10.3390/info8010004
Chicago/Turabian StyleTozzi, Arturo, and James F. Peters. 2017. "A Symmetric Approach Elucidates Multisensory Information Integration" Information 8, no. 1: 4. https://doi.org/10.3390/info8010004
APA StyleTozzi, A., & Peters, J. F. (2017). A Symmetric Approach Elucidates Multisensory Information Integration. Information, 8(1), 4. https://doi.org/10.3390/info8010004






