Abstract
Radio Frequency Identification (RFID) technology is one of the most promising technologies in the IoT (The Internet of Things) era. Many RFID systems have been used in supermarkets or warehouses. There are two challenges for RFID anti-collision algorithms. The first challenge is accurately estimating the number of tags; the other is improving the efficiency of RFID systems. This paper proposes an optimal tag estimation method in which tags respond to the reader in assigned time slots instead of responding randomly. In order to improve the performance of the RFID system, a 4-ary query tree Additive Link On-line HAwaii (ALOHA) protocol is presented that combines the merits of query tree algorithm and frame slotted ALOHA, and avoids their weaknesses. Simulation results show that the proposed algorithm has a higher tag identification efficiency compared to other dynamic frame slotted ALOHA algorithms, and it can overcome the tag starvation phenomenon, because it traces each tag until all of them are identified successfully.
1. Introduction
Many large-sized chain supermarkets, such as Wal-Mart and Metro AG invest in innovative technology to improve the shopping experience for consumers. Supermarket smart payment systems (SSPS) based on Radio Frequency Identification (RFID) technology is an outstanding substitute for traditional payment patterns. With the development of low-cost RFID tags [1,2,3], the bar code will soon be eliminated [4]. RFID technology enables objects to be distinguished from a long distance [5], and furthermore, passive RFID tags which collect energy from the RFID reader offer several advantages such as battery-less operation, wireless communication, high flexibility, low cost, and fast deployment [6]. Because there is only one communication channel between RFID reader and RFID tags, collision is a familiar problem in RFID systems, easily resulting in missing information and inefficient use of resources—particularly hardware resources [7].
Anti-collision is essential for an RFID system. According to the difference of channel classification method, tag anti-collision algorithms can be divided into four types: Frequency Division Multiple Access (FDMA), Code Division Multiple Access (CDMA), Space Division Multiple Access (SDMA), and Time Division Multiple Access (TDMA). Most RFID anti-collision algorithms in previous works have adopted TDMA. Among them, Additive Link On-line HAwaii (ALOHA)-based algorithms and tree-based algorithms are more popular. A slotted ALOHA algorithm can decrease the probability of collision compared to a pure ALOHA algorithm [8]. In dynamic frame-slotted ALOHA (DFSA) [9,10,11], the length of the frame dynamically changes with the number of unidentified tags. In frame slotted ALOHA protocols, when the length of the frame is equal to the number of tags, the maximum system efficiency is attained, which is about 36.8% [7,12]. Tags select time slots to send their data packages randomly, so the performances of existing frame slotted ALOHA protocols are not stable, and the tag starvation phenomenon may occur.
Recently, plenty of improved ALOHA-based anti-collision algorithms have been published. Reference [10] proposes a new Enhanced Dynamic Framed Slotted (EDFSA) ALOHA algorithm in which the unread tags are divided into different groups, and only one group responds meanwhile. An anti-collision algorithm named Collision-Group-Based (CGA) was proposed in [13]. This algorithm has two reading cycles. In the first cycle, the reader sets frame size. In the second cycle, the reader decides the group size. The tag randomly selects a group, then it selects a slot to send its ID to the reader. EDFSA and CGA can improve the efficiency to some extent, but they still cannot avoid the tag starvation phenomenon and break through the restriction of 36.8%. Reference [14] presents a splitting Binary Tree Slotted ALOHA (BTSA) algorithm, which can adjust the frame length to a value close to the number of tags, and as a result, its identification efficiency can achieve the restriction of 42.5%. However, some tags may not be identified for a long time.
The tree-based algorithms are deterministic algorithms which can accurately identify all tags. Among them, the binary tree anti-collision algorithm (BT) [15] and the query tree algorithm (QTA) [16,17] are more well-known. Tree-based algorithms can be expressed as a B-ary tree, where B should be in the form of 2n (n ≥ 1) [17]. The 4-ary tree algorithm can decrease the number of collision cycles, and the efficiency of 4-ary tree outperforms that of 2-ary tree algorithm. This paper presents a novel algorithm to break through the restriction of existing methods, where tags respond to the reader in assigned time slots instead of responding randomly. Considering the advantages of ALOHA-based algorithms and tree-based algorithms, this paper proposes an improved 4-ary query tree ALOHA protocol that combines 4-ary query tree with dynamic frame slotted ALOHA. Simulation results indicate that the proposed algorithm can improve the efficiency of RFID systems to a great extent, and it can make sure the reader identifies all tags accurately.
The remainder of the article is organized as follows. First, the architecture of SSPS will be presented. Secondly, the optimal tag estimation method based on assigned time slots will be detailed. Thirdly, a 4-ary query tree ALOHA protocol based on optimal tag estimation method will be described. Then, simulation results will be provided and compared with previous algorithms. Finally, the main conclusions will be highlighted.
2. An Optimal Tag Estimation Method
When we estimate the number of unidentified tags, we should calculate optimal frame size that will maximize system efficiency. The frame size greatly influences the system efficiency. If the frame size is too large, plenty of idle time slots will occur; if the frame size is too small, there will be many collided time slots. In existing frame slotted algorithms, tags select time slots of a frame to send their data packages randomly, which will cause uncertainty in the number of collided time slots and idle time slots.
Schoute presented a method to estimate the number of unrecognized tags in multi-access RFID system in which tags choose time slot i of a frame to transmit their data packets that is Poisson distributed, the estimation of the number of tags (n’) which have not been recognized by the reader after the current frame is n’ = 2.39C, where C is the number of slots in which collisions arise [9]. Reference [10] proposes a new tag estimation method. Thus, if the number of tags is relatively small, it works well; however, if the number becomes large, it begins to show poor performance. Now, we will introduce a tag estimation method based on more reasonable probability analysis.
2.1. Description of Tag Estimation Method
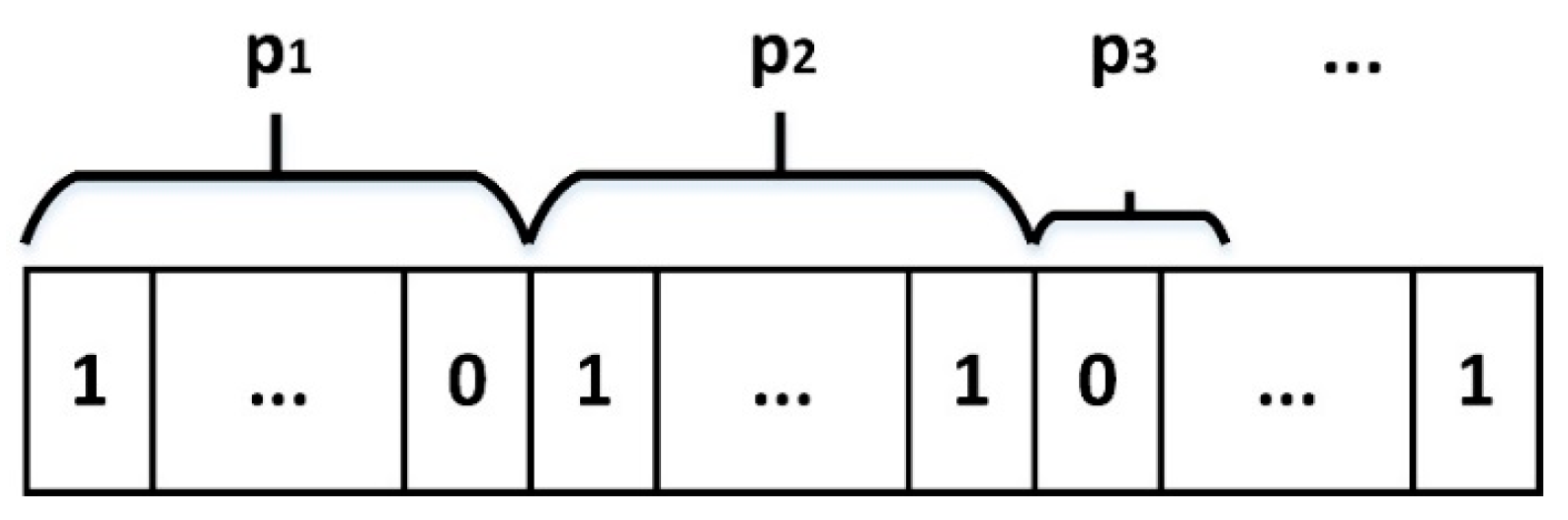
Given the number of unread tags is N, the number of time slots in a frame (the length of a frame) is L and p bit serial binary digits (named as assignment bits) in tag ID are used by each tag to select assigned time slot in a frame (as shown in Figure 1).
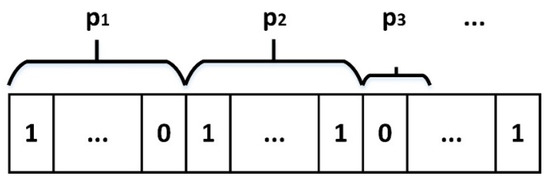
Figure 1.
Schematic diagram of assignment bits in tag ID.
The frame length is decided by the number of assignment bits, the relationship between p and L is:
When there are m tags responding in a time slot simultaneously, it means that their p assignment bits of tag ID are same. The probability can be defined as:
If there are m of all tags responding in a certain timeslot, the probability can be defined as:
If there is only one tag responding in a certain slot of frame (m = 1), the probability is:
where is a binomial expression.
S is the number of time slots in each one of which only one tag transmits its data packet successfully; E denotes the number of time slots in each one of which no tag transmits its data packet; and C denotes the number of time slots in each one of which more than one tag transmits their data packet.
We define the throughput T as follows:
We can obtain the number of assignment bits (p) that gives the maximum throughput by differentiating Equation (6).
Log2N may not be an integer, hence in order to getting more a reasonable frame length, we command that:
As shown in Figure 1, when there are collided tags in a frame, all collided tags will respond to the reader in the next frame. If the start bit of assignment bits is fixed, the tags colliding once may collide again, which will result in the tag starvation phenomenon. So, the start bit of p1 is the start bit of tag ID, and the start bit of pn+1 is next bit of the end bit of pn.
2.2. Example Analysis
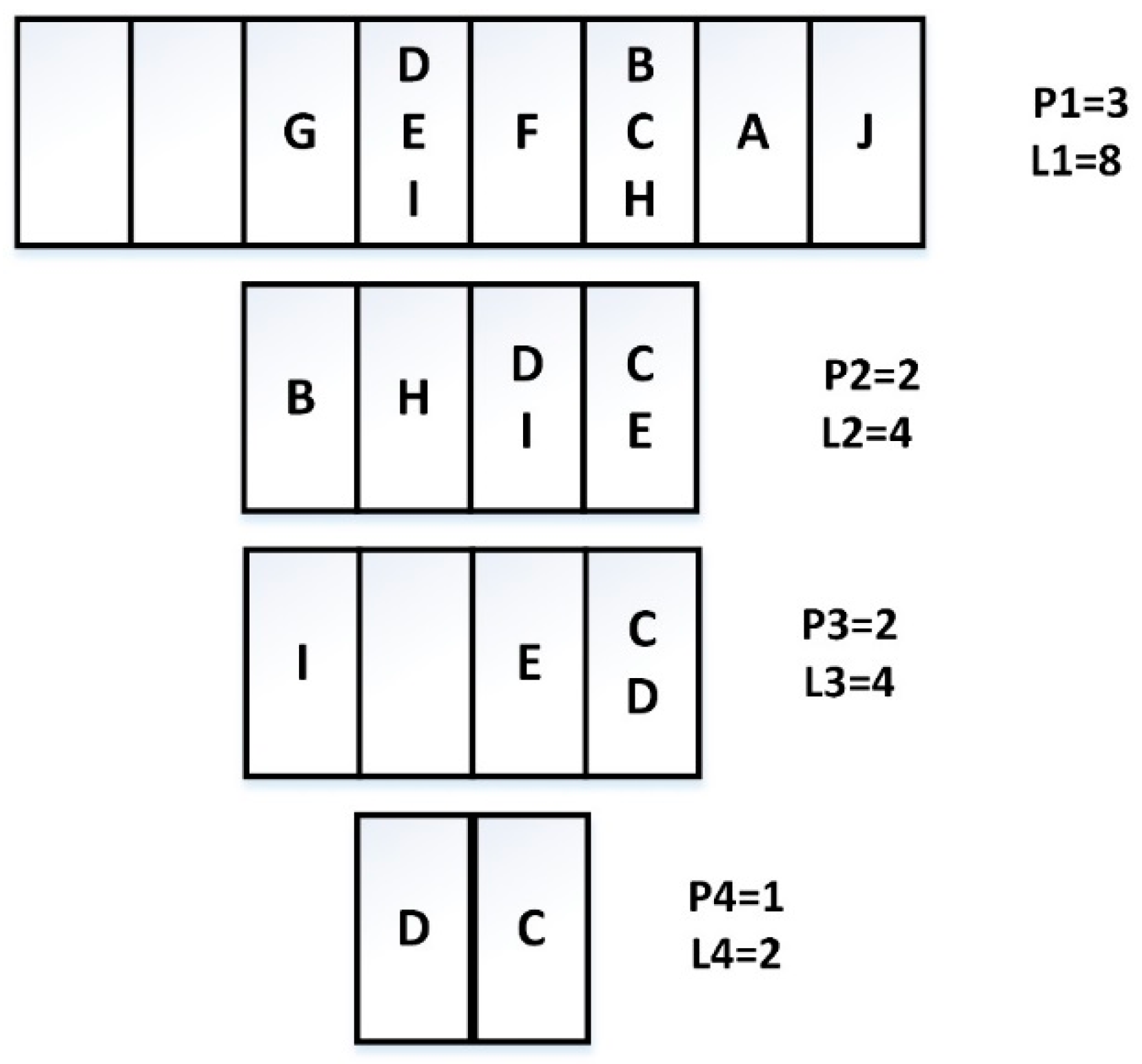
We suppose that there are 10 tags A–J. A: 1101010101, B: 1010000011, C: 1011111111, D: 0111011010, E: 0111110001, F: 1001010100, G: 0101011101, H: 1010101100, I: 0111000000, J: 1110001010. We can get the tag identification process as shown in Figure 2.
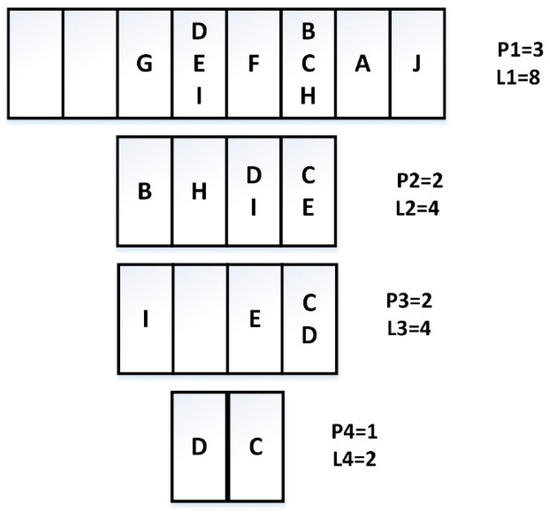
Figure 2.
Tag identification process.
3. A 4-Ary Query Tree ALOHA Protocol Based on Optimal Tag Estimation
3.1. QTA and 4-Ary QTA
Query Tree Algorithms (QTA) have the advantage of easy execution due to their simple structure and operating mode. In QTA protocol, the reader asks the tags whether their IDs contain the same prefix as the query strings q. If the prefix of tag ID is the same as the query strings q, the tag will respond to the reader, but when more than one tag answers, a collision is detected [13]. The reader then attaches bit 0 or 1 to generate the longer prefixes in a queue, and the reader repeats the process until all tags are uniquely identified. In 4-ary QTA, if a collision occurs in a tree node, two bits 00, 01, 10, and 11 are used by the reader to generate the longer prefixes in the queue, and it can decrease the collided cycles compared to 2-ary QTA.
Table 1 shows the identification process. We suppose there are four tags in the reader capture range; their tag IDs are 0001, 0011, 1000, and 1101, respectively. In round 1, the collision occurs because more than one tag responds, and in rounds 2, 5, and 7, there are no tags responding to the reader. In rounds 3, 4, 6, and 8, only one tag can be successfully identified.

Table 1.
The operating process of 4-ary query tree algorithm (QTA).
3.2. Description of the Proposed Algorithm
QTA can accurately identify all tags, but in each tree node, only one tag can be identified. ALOHA-based algorithms are more efficient than the tree-based algorithms, but tag starvation phenomena may occur. In this part, we present a 4-ary query tree ALOHA protocol (4QTAP) which combines 4-ary QTA with the dynamic frame slotted ALOHA. Firstly, the proposed algorithm is based on a 4-ary tree structure. Secondly, all the tree nodes adopt dynamic frame slotted ALOHA, and the tag estimation method presented in Section 3 is adopted in each node. Thirdly, if the tag IDs are known, the identification process can be predicted accurately, all tags can be identified efficiently.
In 4QTAP, the 4-ary tree is composed of the initial node and the leaf nodes, and they are frames consisting of some time slots. Each leaf node in the query tree corresponds to each the prefix in the queue, and the status of each node can be classified as follows.
- Empty node (En): There is no tag responding to the reader’s query, resulting in a waste of the time slot.
- Success node (Sn): All response tags are successfully identified by the reader, and there are no collided tags in Sn. The success node does not have branch nodes in the query tree, and the corresponding prefix will not generate new prefixes in the queue.
- Collision node (Cn): The collision occurs as multiple tags respond to the reader’s query simultaneously. The collided tags in Cn will be recognized in its branch nodes, and the reader will attach two binary bits 00, 01, 10, 11 to the corresponding prefix to generate the longer prefixes in queue.
Before the initial node works, the query string is null, so the procedure of the initial node is identical to the example presented in Section 3; each tag needs pinitial serial binary digits to assign a response time slot, and the number of time slots in initial node is Linitial = 2pinitial. If the initial node is Sn, it means that all tags have been successfully identified by the reader, and the process of identification is over. If the initial node is Cn, two bits 00, 01, 10, and 11 are added to queue as the longer query bits. We suppose the number of collided tags is Cinitial, the number of unread tags in each branch node of initial node is Cinitial/4 on average. The number of unread tags in each branch node of the initial node is expressed as notation Rxx, where xx is two serial binary digits on behalf of four branch nodes. Each collided tag in the initial node needs pxx serial binary digits of tag ID to assign a response time slot, and the pxx assignment bits are adjacent to the pinitial assignment bits in tag ID. The reader sends the query bits and assignment bits pxx to all unread tags; if the prefix of a tag matches the query bits, it selects a branch node and a response time slot, then transmits its ID to the reader.
We suppose that a leaf node is determined by the query bits , the number of unread tags in this node is , it is equal to (1/4) based on the probability (where is the number of collided tags in tree node ). Each tag needs assignment bits to select a response time slot. The reader sends the query bits and assignment bits to all unread tags; eligible tags will respond to the reader.
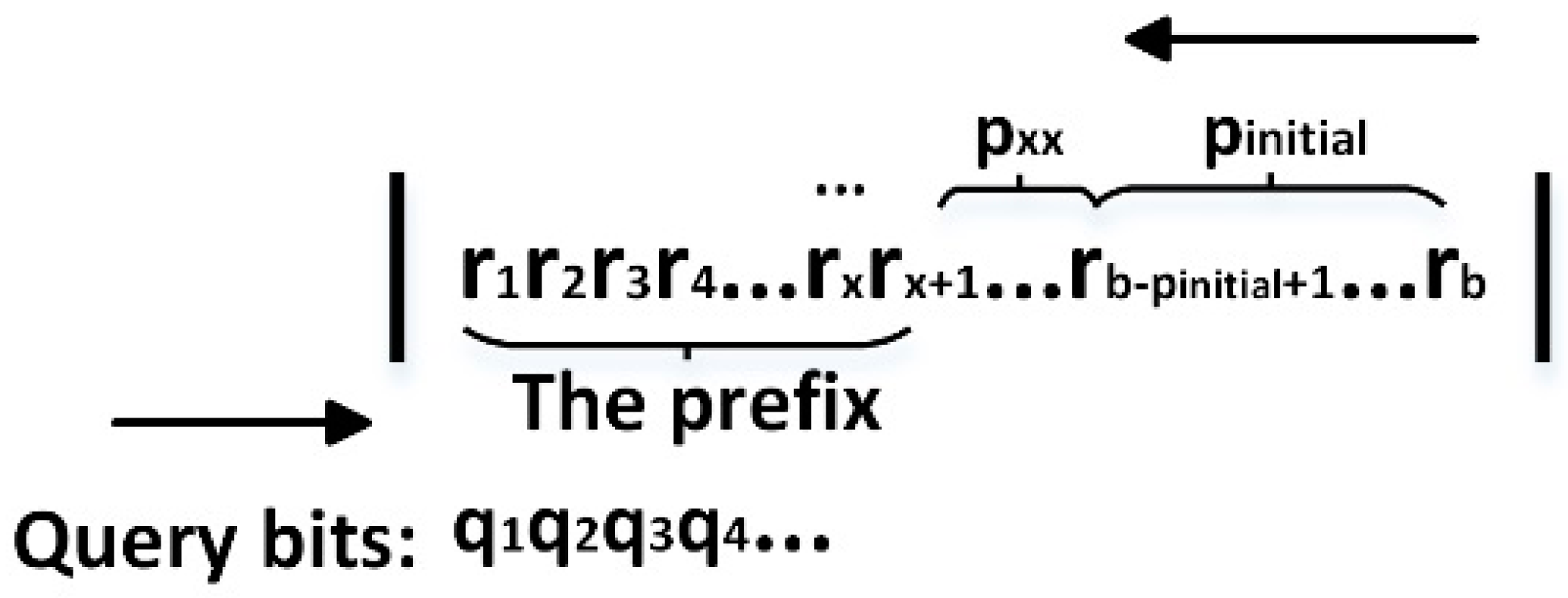
The assignment bits p are set from the beginning of tag ID like Figure 1. Some collided tags in a tree node may have the same prefixes, which generates a tag starvation phenomenon. In order to avoid this phenomenon, the assignment bits should be set from the end of tag ID (as shown in Figure 3), and they should keep away from the prefixes of tags. The tag ID is composed of a series of binary bits , where b is the number of bits in tag ID. When the query bits from the reader is , the prefix of a tag is , where 1 ≤ x ≤ b.
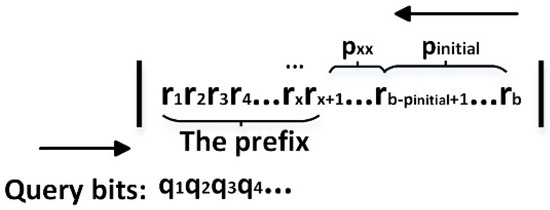
Figure 3.
The prefix and assignment bits in tag ID during the implementation of 4-ary query tree ALOHA protocol (4QTAP).
3.3. Flowchart of 4QTAP
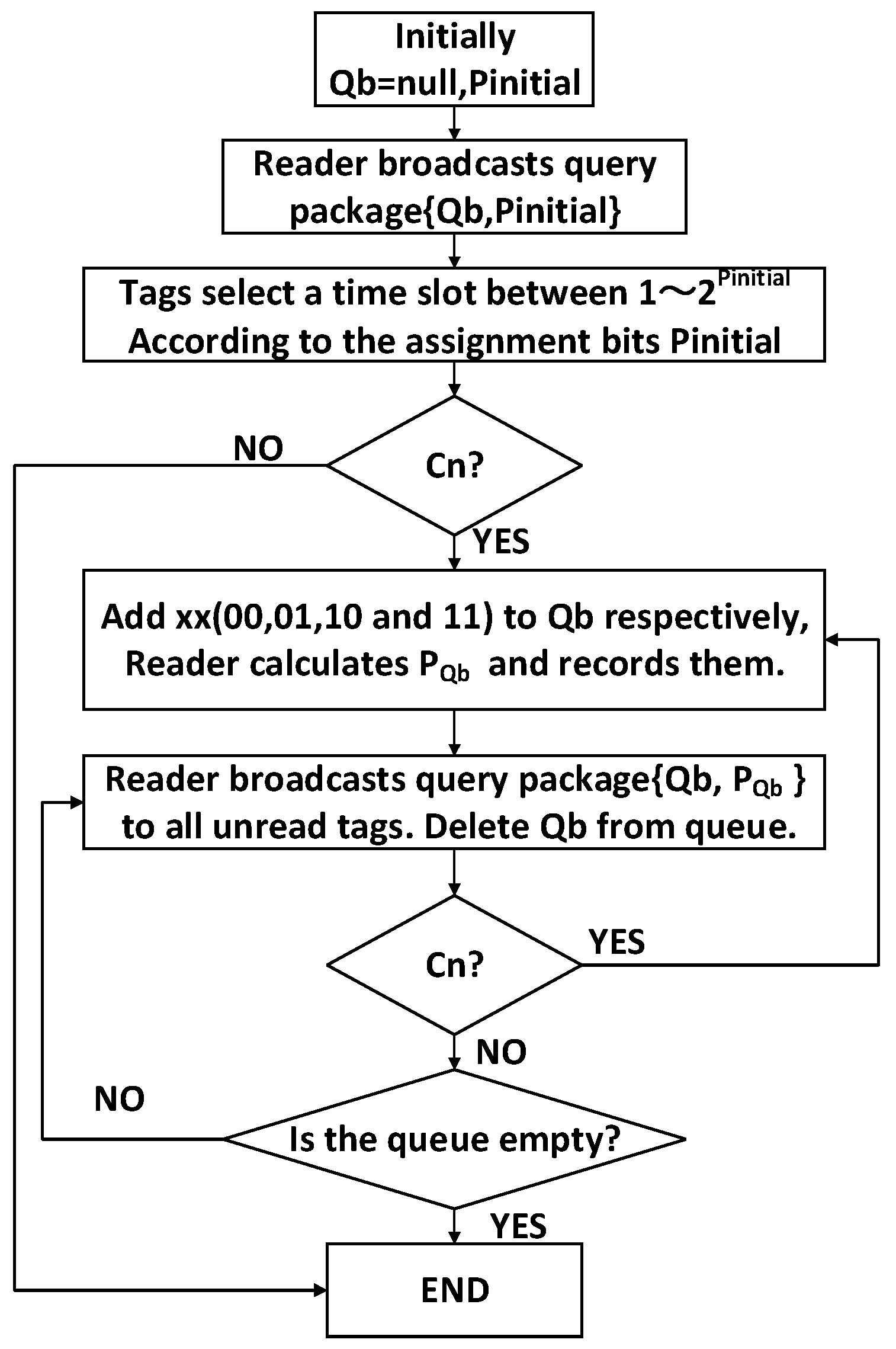
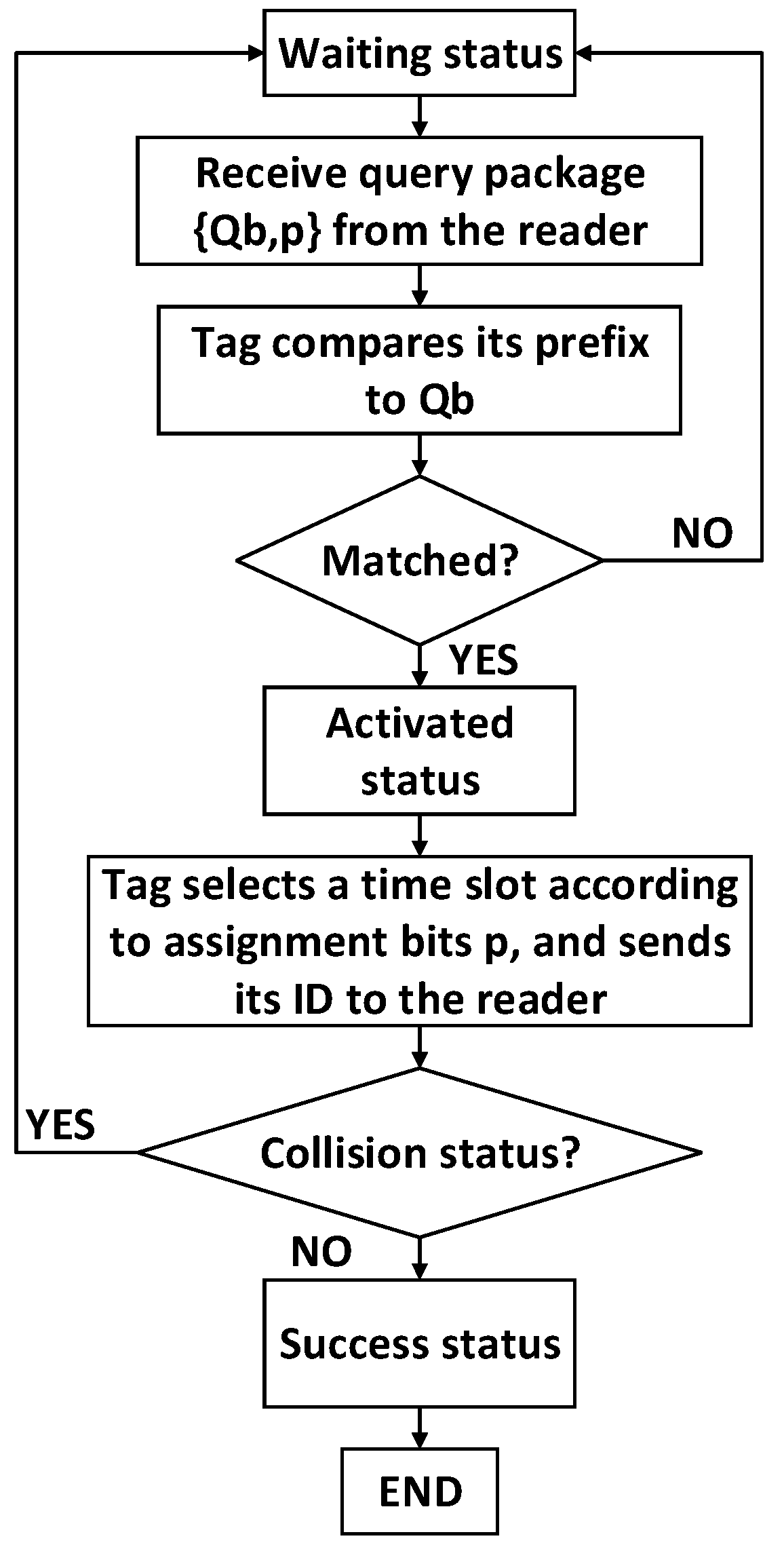
The reader’s query and the tag’s response of 4QTAP is an iterative processes as shown in Figure 4 and Figure 5. In order to implement 4QTAP, the necessary notations are listed as follows.
- Qb: The shorthand notation of query bits. It is a serial binary bits , where qx is 0 or 1, and 1 ≤ x ≤ b, b is the number of bits in the tag ID. Every Qb determines a leaf node in the 4-ary tree, and Qb has two statuses—in initial node of 4-ary tree, Qb is null; in leaf nodes of 4-ary tree, Qb is valid.
- p: The assignment bits of a tag; a tag can select a time slot according to p. In the initial node, it is expressed as pinitial; In leaf nodes of the 4-ary tree, it is expressed as pQb. The reader can calculate p based on Equation (11).
- Queue: The storage space in the reader, where all the Qbs are stored. If a Qb is used, it will be deleted from the Queue. If a node is Cn, four longer query bits Qb00, Qb01, Qb10, and Qb11 will be added to the Queue, and the reader will broadcast the longer Qbs to the unread tags in the subsequent process.
- Lookup table: In the process of identification, a lookup table is used to store all the assignment bits pQb.
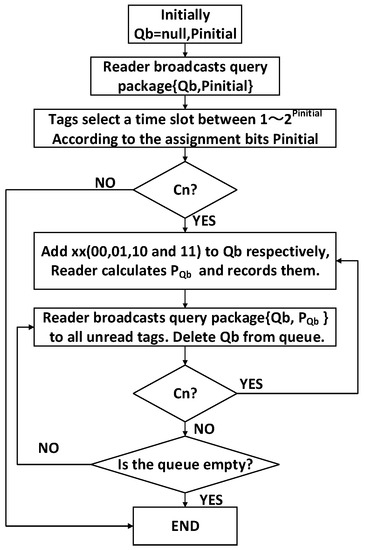
Figure 4.
The reader’s flowchart of 4QTAP.
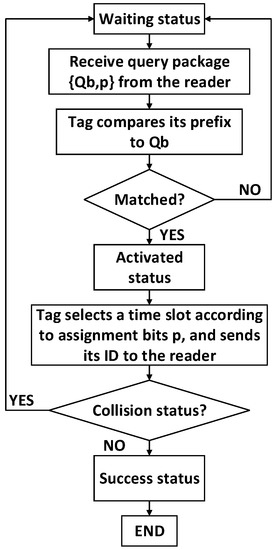
Figure 5.
A tag’s flowchart of 4QTAP.
The status of each tag can be divided into four types:
- Waiting status: Tags wait to receive the reader’s query package {Qb, pQb}.
- Activated status: If the prefix of a tag matches the query bits (Qb), the tag is activated, and it select an assigned time slot to send its ID to the reader.
- Success status: There is only one tag responding in a time slot, the tag is identified successfully.
- Collision status: More than one tag responds in a time slot, a collision occurs, and all collided tags in this time slot are not identified by the reader.
3.4. Example Analysis
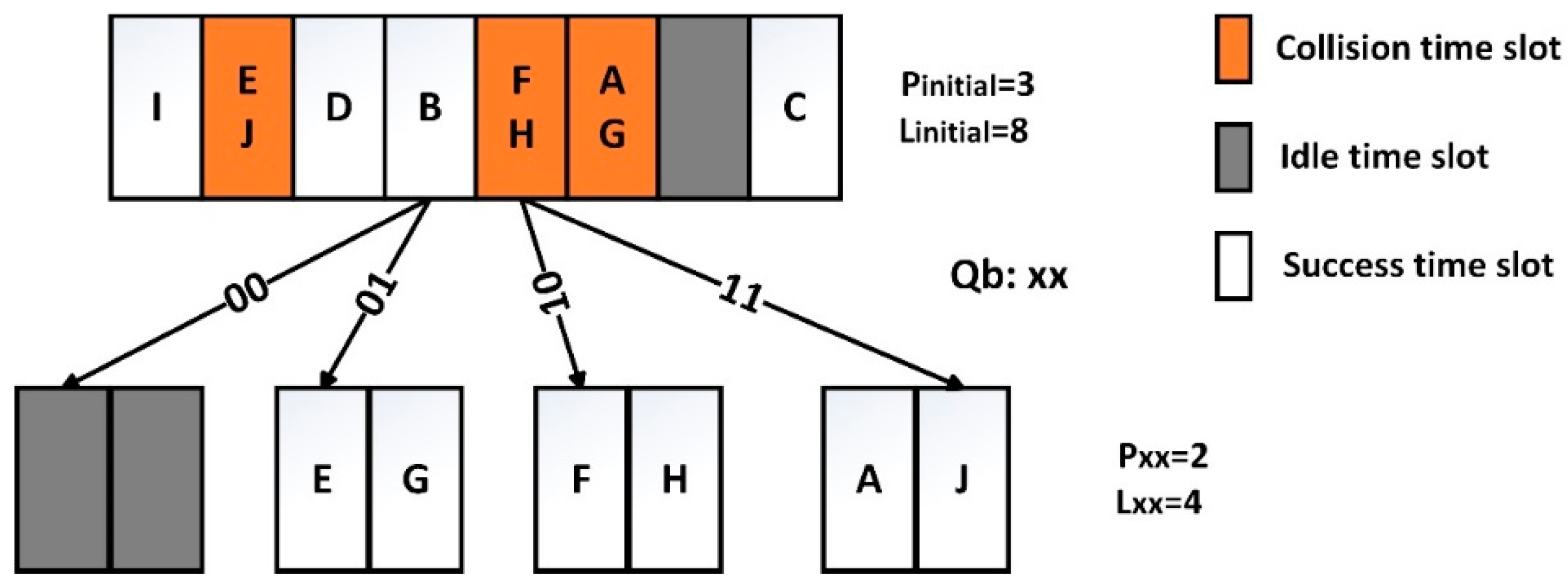
We suppose that there are 10 tags A–J. A: 1101010101, B: 1010000011, C: 1011111111, D: 0111011010, E: 0111110001, F: 1001010100, G: 0101011101, H: 1010101100, I: 0111000000, J: 1110001010. We can get the tag identification process as shown in Figure 6.
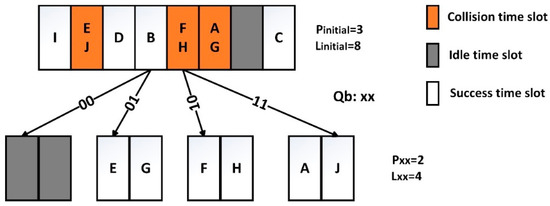
Figure 6.
Identification process of 4QTAP.
4. Simulation Results and Discussion
We evaluate the performances of 4QTAP and other former ALOHA-based algorithms by matlab simulation. The total time to identify all tags is equal to the total number of time slots multiplied by the slot time, which is an important evaluation factor for RFID anti-collision algorithms. Since the slot time is constant, we only take the total number of time slots into consideration. The smaller the total number of time slots, the better the performance of the algorithm. The system efficiency (throughput) is defined as the ratio of the slots filled with one tag to the number of all time slots, which is another evaluation factor that should be taken into consideration in our simulations. When the durations of collision slot, idle slot, and successful slot are the same (t0 = t1 = tk), the system efficiency is the same as the channel usage efficiency presented in paper [18], so the system efficiency in our paper is a special case of channel usage efficiency.
We compare 4QTAP with the Schoute DFSA algorithm [9], EDFSA [10], Query Tree Split (QTS) ALOHA protocol [19], and Q algorithm [20]. The basic ideas of these algorithms are described as follows:
- (1)
- EDFSA: The algorithm estimates the number of unidentified tags first, then compares with the given maximum frame size. If the number of tags is much larger than the one that gives the optimal system efficiency, it divides the unread tags into some groups and allows only one group to respond.
- (2)
- QTS ALOHA: The length of a frame is chosen in the set (8, 16, 32, 64, 128, 256). If the size of the next identification frame is selected, the total number of time slots will equal to all frames multiplied by their size.
- (3)
- Schoute DFSA: The DFSA algorithm was presented by Schoute in 1983, and the number of collided tags is equal to 2.39 times the number of collided time slots.
- (4)
- Q algorithm: In this algorithm, the value of Q is updated slot by slot according to the status of the preceding received slot, which can determine the frame size that can maximize the tag identification efficiency.
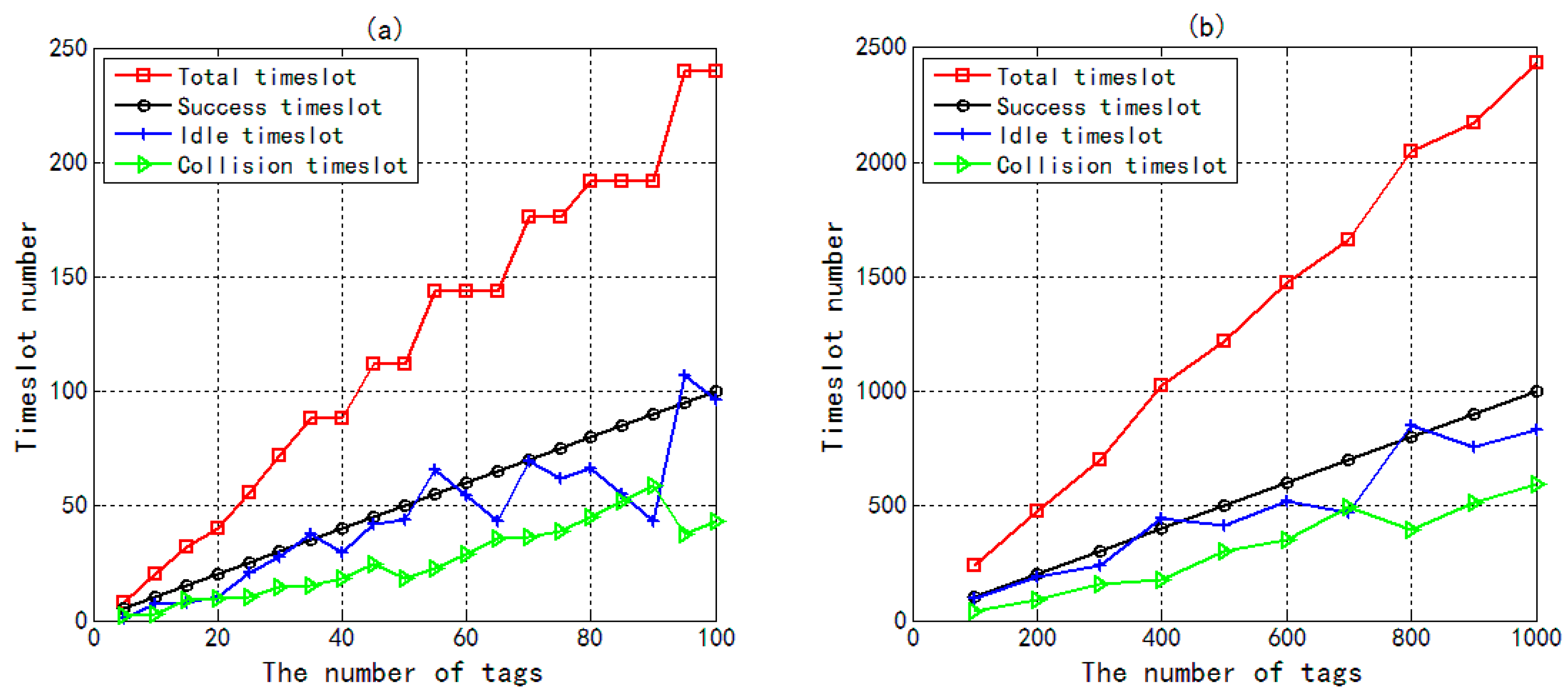
Figure 7a plots the number of total time slots, success time slots, idle time slots, and collision time slots in 4QTAP when the number of tags increases from 5 to 100. Figure 7b further describes the relationship between the number of time slots and the number of tags in the range 100 to 1000. Firstly, the number of total time slots is equal to the sum of success time slots, idle time slots, and collision time slots. Secondly, as the number of tags increases, the total number of time slots may be invariant, because when there is a small difference in the number of tags, corresponding frames may have the same number of time slots.
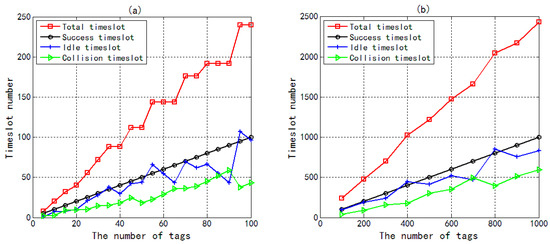
Figure 7.
The number of total timeslots, success timeslots, idle timeslots, and collision timeslots in 4QTAP vs. the number of tags. (a) The number of tags increases from 5 to 100; (b) The number of tags increases from 100 to 1000.
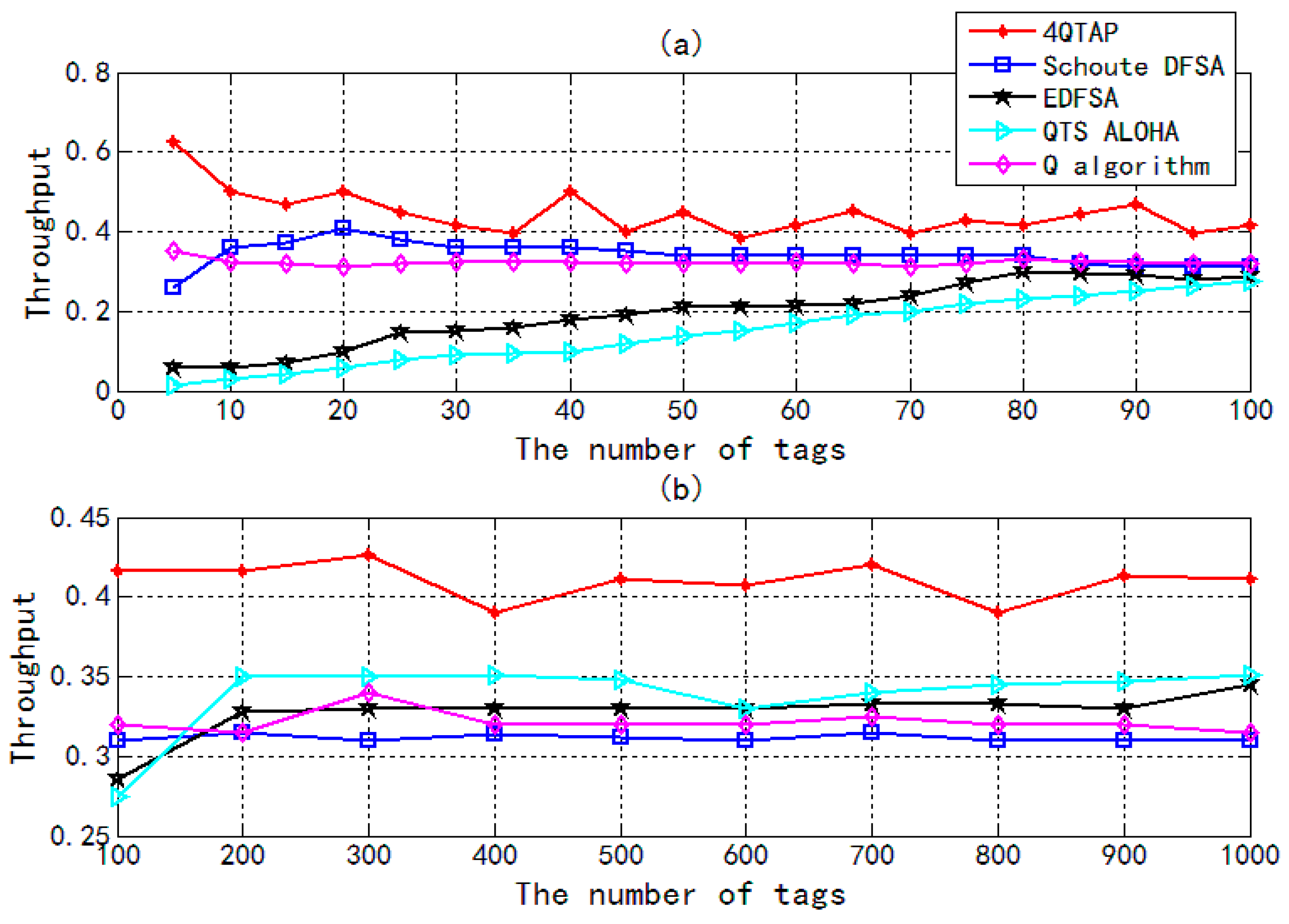
Figure 8 shows the efficiency of tag identification for different algorithms. When the number of tags increases from 5 to 100, the efficiency of Schoute DFSA and Q algorithms rapidly become stable, but the efficiency of EDFSA and QTS ALOHA slowly increase. When the number of tags is beyond 100, we can observe that the efficiency of each of 4QTAP, Schoute DFSA, QTS ALOHA, and Q algorithm becomes stable. For a large number of tags, the efficiency of 4QTAP varies around 40%, and that of the other four algorithms is only about 30%. In general, 4QTAP has better performance than other ALOHA protocols. When all the tag IDs are determinate, the procedure of 4-ary query tree and tag estimation method presented in this paper can be accurately predicted, so all tags will be traced in 4QTAP until each of them is identified.
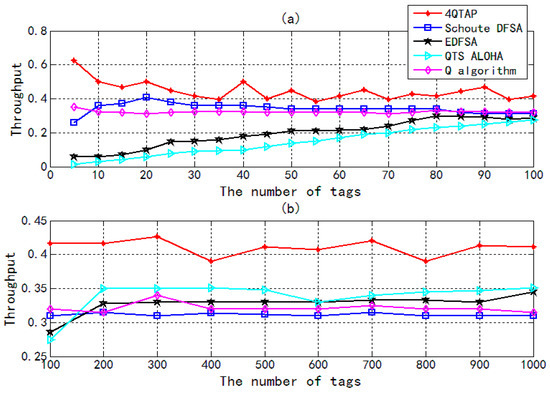
Figure 8.
Throughput of different algorithms vs. the number of tags. (a) The number of tags increases from 5 to 100; (b) The number of tags increases from 100 to 1000.
5. Conclusions
This paper presents a novel RFID anti-collision algorithm. When an RFID system identifies multiple tags, tag collision will happen. A 4-ary query tree ALOHA protocol with optimal tag estimation method is proposed, demonstrated, and discussed. In order to break through the constraint of traditional frame slotted ALOHA protocols, we design an optimal tag estimation method. The frame length changes with the number of tags, and each tag selects an assigned time slot to respond to the reader according to the assignment bits p. Simulation results indicate that the tag estimation method is more efficient. ALOHA-based algorithms have the tag starvation phenomenon. We combined a 4-ary query tree algorithm with the dynamical frame slotted ALOHA. Collision tags in a frame (node) will be identified in the branch nodes. The simulation results show that the whole performances of 4QTAP is better than the performances of current ALOHA-based algorithms.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (61663013), the Natural Science Foundation of Jiangxi Province (20161BAB212051) and the Key Research and Development Program of Jiangxi Province (20161BBE50076).
Author Contributions
Zhihui Fu and Xiang Wu undertake most of this work. Fangming Deng provides the instructions and helps during the design. All authors provide the helps in revisions of this manuscript. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dagan, H.; Shapira, A.; Teman, A.; Mordakhay, A.; Jameson, S.; Pikhay, E.; Dayan, V.; Roizin, Y.; Socher, E.; Fish, A. A Low-Power Low-Cost 24 GHz RFID Tag With a C-Flash Based Embedded Memory. IEEE J. Solid-State Circuits 2014, 49, 1942–1957. [Google Scholar] [CrossRef]
- Jang, S.; Kim, S.; Tentzeris, M.M. Low-cost flexible RFID tag for on-metal applications. In Proceedings of the IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Memphis, TN, USA, 6–11 July 2014; pp. 1298–1299.
- Wang, J.; Li, H.; Yu, F. Design of Secure and Low-cost RFID Tag Baseband. In Proceedings of the International Conference on Wireless Communications, Networking and Mobile Computing, Shanghai, China, 21–25 September 2007; pp. 2066–2069.
- Preradovic, S.; Karmakar, N.C. Chipless RFID: Bar code of the future. IEEE Microw. Mag. 2010, 11, 87–97. [Google Scholar] [CrossRef]
- Want, R. An Introduction to RFID Technology. IEEE Pervasive Comput. 2006, 5, 25–33. [Google Scholar] [CrossRef]
- Deng, F.; He, Y.; Li, B.; Zuo, L.; Wu, X.; Fu, Z. A CMOS pressure sensor tag chip for passive wireless applications. Sensors 2015, 15, 6872–6884. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Lai, S. ALOHA-Based Anti-Collision Algorithms Used in RFID System. In Proceedings of the International Conference on Wireless Communications, Networking and Mobile Computing, WiCOM 2006, Wuhan, China, 22–24 September 2006; pp. 1–4.
- Cheng, T.; Jin, L. Analysis and Simulation of RFID Anti-collision Algorithms. In Proceedings of the 9th International Conference on Advanced Communication Technology, Gangwon-Do, Korea, 12–14 February 2007; pp. 697–701.
- Schoute, F.C. Dynamic frame length ALOHA. IEEE Trans. Commun. 1983, 31, 565–568. [Google Scholar] [CrossRef]
- Lee, S.R.; Joo, S.D.; Lee, C.W. An enhanced dynamic framed slotted ALOHA algorithm for RFID tag identification. In Proceedings of the International Conference on Mobile and Ubiquitous Systems: Networking and Services, MOBIQUITOUS 2005, San Diego, CA, USA, 17–21 July 2005; pp. 166–174.
- Chen, W.T. An Accurate Tag Estimate Method for Improving the Performance of an RFID Anticollision Algorithm Based on Dynamic Frame Length ALOHA. IEEE Trans. Autom. Sci. Eng. 2009, 6, 9–15. [Google Scholar] [CrossRef]
- He, Y.; Wang, X. An ALOHA-based improved anti-collision algorithm for RFID systems. IEEE Wirel. Commun. 2013, 20, 152–158. [Google Scholar]
- Lin, C.F.; Lin, Y.S. Efficient Estimation and Collision-Group-Based Anticollision Algorithms for Dynamic Frame-Slotted ALOHA in RFID Networks. IEEE Trans. Autom. Sci. Eng. 2010, 7, 840–848. [Google Scholar] [CrossRef]
- Wu, H.; Zeng, Y.; Feng, J.; Gu, Y. Binary Tree Slotted ALOHA for Passive RFID Tag Anticollision. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 19–31. [Google Scholar] [CrossRef]
- Myung, J.; Lee, W.; Srivastava, J. Adaptive Binary Splitting for Efficient RFID Tag Anti-Collision. IEEE Commun. Lett. 2006, 10, 144–146. [Google Scholar] [CrossRef]
- Yang, C.N.; Hu, L.J.; Lai, J.B. Query Tree Algorithm for RFID Tag with Binary-Coded Decimal EPC. IEEE Commun. Lett. 2012, 16, 1616–1619. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, S.; Lee, S.; Ahn, K. Improved 4-ary Query Tree Algorithm for Anti-Collision in RFID System. In Proceedings of the 2009 International Conference on Advanced Information Networking and Applications, Bradford, UK, 26–29 May 2009; pp. 699–704.
- Shakiba, M.; Singh, M.J.; Sundararajan, E.; Zavvari, A.; Islam, M.T. Extending birthday paradox theory to estimate the number of tags in RFID systems. PLoS ONE 2014, 9, e95425. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.; Yin, Z.; Xiong, Y. QTS ALOHA: A Hybrid Collision Resolution Protocol for Dense RFID Networks. In Proceedings of the 2008 IEEE International Conference on E-Business Engineering, Xi’an, China, 22–24 October 2008; pp. 557–562.
- EPCglobal Standard Specification. EPC™ Radio-Frequency Identification Protocols Class-1 Generation-2 UHF RFID Protocol for Communications at 860 MHz–960 MHz Ver. 1.0.9; EPCglobal Inc.: Lawrenceville, NJ, USA, 2005; pp. 1–94. [Google Scholar]
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).