Abstract
First, mathematical formulae faithfully describing the distributions of amino acids and codons and reproducing the degeneracies in the various known genetic codes, including the standard genetic code, are constructed, by hand. Second, we summarize another mathematical approach relying on the use of q-deformations to describe these same genetic codes, and add a new application not considered before. Third, by considering these same genetic codes, we find, qualitatively, that an inverse symmetry-information relationship exists.
1. Introduction
Today, the two most important questions in science concern the origin of the universe and the origin of life on Earth and, maybe, in other places. As for the former, its understanding is well advanced thanks to the great discoveries made in the last century (particle physics and cosmology). This is certainly not the case for the latter, namely, where life came from and how it functions. However, two important breakthroughs were made in the second half of the last century with the (experimental) discovery of the DNA structure [1], and the deciphering of the genetic code [2], that is, how the information in DNA is ultimately converted into proteins. Unfortunately, there is no such fundamental mathematical laws in biology, as in physics (Newton’s laws in classical mechanics, Einstein’s equation in general relativity, Maxwell’s equations in electromagnetism, Navier Stokes in fluid dynamics, and so on) so, there is no way to derive the mathematical structure of the genetic code from first principles, taking into account biochemical and structural features. This is really a hard problem. In spite of this difficult problem, we have nonetheless tried, through the recent past years, to make some modest contributions to find mathematical models which, if not derived from “first principles”, at least could faithfully reproduce the experimental data for the standard genetic code [3,4,5] and, to some extent, its important variant the Vertebrate Mitochondrial genetic code [4] (one could also find in [3,4,5] reference to other older works by ourselves). Recently, we have used the formalism of q-deformations (see Section 3) to study the case of the various today known genetic code variants [6,7]. We also constructed, by hand, exact mathematical expressions, relying on the use of geometrical and arithmetical progressions describing the distributions of amino acids and codons and reproducing faithfully the degeneracies for the standard genetic code [6], and the Vertebrate Mitochondrial Code [7]. Here, in this new contribution, we go further and construct exact mathematical expressions for each one of all the genetic code variants which also reproduce, faithfully, the distribution of amino acids and codons as well as the degeneracies. This is the subject of Section 2. In Section 3, we summarize our recent approach, using the q-deformation of numbers and add, here, a new application case. In Section 4, as a contribution to this special issue, “Symmetry and Information”, we take a qualitative look at an interesting inverse relationship between symmetry and information in the various genetic code variants. Finally, in Section 5, we summarize our results and make some concluding remarks.
2. Formulae for the Standard Genetic Code and Its Variants
In this section, as mentioned in the introduction, we shall construct, by hand, several mathematical formulae describing (fitting), in detail, the codons distributions of the standard genetic code as well as all of its several presently-known variants. The genetic code is the set of rules for the translation of 64 mRNA triplet-codons into 20 amino acids. In the standard genetic code there are 61 meaningful codons, that is codons encoding amino acids, and three stop-codons or termination codons. As more than one different codon could code for the same amino acid, one speaks about degeneracy and results in a multiplet structure; the codons encoding the same amino acid form multiplets (singlets, doublets, triplets, quartets, and so on). For example, a quartet is composed of four codons, a sextet is composed of six codons, and so on. Also, we call frequency the number of times a given multiplet occurs. In the standard genetic code, for example, there are two singlets: Methionine (M) and Tryptophane (W); nine doublets: Phenylalanine (F), Tyrosine (Y), Cytosine (C), Asparagine (N), Lysine (K), Histidine (H), Glutamine (Q), Acid Aspartic (D), and Glutamic Acid (E); one triplet: Isoleucine (I); five quartets: Proline (P), Threonine (T), Valine (V), Alanine (A) and Glycine (G); and, finally, three sextets: Serine (S), Arginine (R), and Leucine (L) (see Table 1 and Figure 1). (Note that the term “multiplet” is used indifferently for the amino acids and their codons.)

Table 1.
The distribution of codons in the various genetic codes.
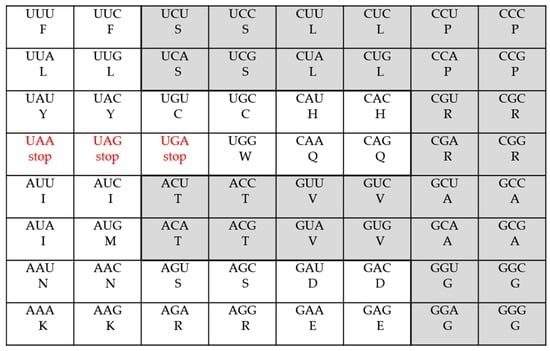
Figure 1.
The standard genetic code Table.
The genetic code is therefore said degenerate: as there 61 codons coding for amino acids and 20 amino acids, the total number of degenerate codons is equal to 41 (= 61–20). As another example, let us give the multiplets and their frequencies for the Vertebrate Mitochondrial genetic code, the most important after the standard genetic code. Here, there are twelve doublets (F, Y, C, N, K, H, Q, D, E, I, M, W), six quartets (P, T, V, A, G, R), and finally two sextets (S, L), see Table 1. In the latter table, we have gathered, from the database at NCBI [8], all the information—that is, the multiplet structure—for each one of the variants of the genetic code. In the first row, the various occurring multiplets—singlet (1), doublet (2), triplet (3), quartet (4), quintet (5), sextet (6), septet (7), and octet (8)—are indicated and, in the row of each one of these variants, the corresponding frequency for each multiplet is given. Let us also indicate in Table 2, from reference [8], the modifications in the various variants with respect to the standard genetic code

Table 2.
The modifications, in the genetic codes, with respect to the standard genetic code.
Now, the idea behind the construction of our mathematical (fitting) formulae has its origin in an interesting observation made in 1985 by Gavaudan in a paper entitled “The genetic code and the origin of life” [9]. Gavaudan observed, for the standard genetic code, that “the frequencies for the even multiplets are in accordance with a geometrical progression when the multiplets are inversely ordered by an arithmetical progression”. This means that to the doublets, quartets, and sextets (ordered arithmetic progression 2, 4, 6) correspond respectively the frequencies 9, 5 and 3 (inversely ordered geometric progression 23 + 1 = 9, 22 + 1 = 5, and 21 + 1 = 3). For the odd multiplets (two singlets and one triplet), no clear-cut equivalent was given by Gavaudan. Also, he gave no explicit mathematical formula for the supposed arithmetical progression for the frequencies, in both cases (even and odd multiplets). In [6], we have written the frequencies for the even multiplets, mentioned above, as the simple arithmetic progression 8 − 2k (k = 1, 2, 3), which gives 6, 4, and 2. We have therefore that the frequencies—3, 5, and 9—are in accordance with the geometrical progression 2k + 1 when the even multiplets—6, 4, and 2—are inversely ordered by the arithmetical progression 8 − 2k, for k = 1, 2, 3. In this case, the sum over k (= 1, 2, 3) of the product (2k + 1) × (8 − 2k) gives 3 × 6 + 5 × 4 + 9 × 2 = 56, i.e., the number of codons for the 17 amino acids encoded by the even multiplets of codons. In the case of the odd multiplets, we can apply the same reasoning: for k = 0, 1, the frequencies are in accordance with the geometrical progression 2k when multiplets are inversely ordered by the arithmetic progression 5 − 2(k + 1), and the sum over k of the product 2k × [5 − 2(k + 1)] gives 1 × 3 + 2 × 1 = 5, just the right total number of codons for the amino acids encoded by odd multiplets of codons. In the following, we shall generalize the construction to all known variants of the genetic code. In so doing, we shall introduce “perturbation” terms in the various geometrical and arithmetical progressions describing the frequencies and the multiplets. Let us provide an example. Consider the Thraustochytrium Mitochondrial code (see Table 1). Here we have two sextets, five quartets, nine doublets, one quintet, one triplet, and two singlets—that is, 2, 5, 9, 1, 1, 2 amino acids, or frequencies, and 6, 4, 2, 5, 3, 1, the corresponding multiplets, respectively. For the even multiplets, 6, 4 and 2, we modify the geometric progression giving the frequencies, considered above, and take now 2k + (1 − ), where we have introduced a Kronecker delta symbol, as a “perturbation” term. In this case, the arithmetic progression for the multiplets remains the same as above: (8 − 2k). For the odd multiplets, we modify both progressions, the new geometric one as 2k and the new arithmetic one as 5 − 2k (for k = 0, 1, 2). It is easily seen that the above new functions reproduce correctly all the numbers for this case (see Table 1 and Equation (2)). Below, in Equations (1)–(18), we give the various functions for all the genetic code variants collected in reference [8]. In each one of these equations, inside each sum, we show the frequency function (in the first position) and the multiplets function (in the second position). For example, in the Vertebrate Mitochondrial Code in Equation (1), the frequencies are given by the function [2k + 2(k − 1)] and the multiplets function is given by (8 − 2k). Also, below each equation, we write the numeric value of the sum of the products of the two above functions which gives the total number of encoding codons. In the example of the Vertebrate Mitochondrial Code, we have 2 sextets (2 × 6 = 12 codons), 6 quartets (6 × 4 = 24 codons), and 12 doublets (12 × 2 = 24 codons), that is, a total of 60 encoding codons.
- The Vertebrate Mitochondrial Code
- The Thraustochytrium Mitochondrial Code
- The Standard Genetic Code
- The Bacterial, Archeal and plant Plastid Code
- The Scenedesmus Oblicus Mitochondrial Code and Alternative Yeast Nuclear Code
- The Pashysolen Tannophilus Nuclear Code
- The Yeast Mitochondrial Code (In this case, the codons CGA and CGC, usually coding for Arginine, R, are absent [8], and there are only two stop codons (hence its location in Table 1).)
- The Mold, Protozoan, and Coelenterate Mitochondrial Code and the Mycoplasma/Spirolasma Code
- The Invertebrate Mitochondrial Code
- The Echinoderm and Flatworm Mitochondrial Code
- The Euploid Nuclear Code
- The Ascidian Mitochondrial Code
- The Chlorophycean Mitochondrial Code
- The Trematode Mitochondrial Code
- The Pterobranchia Mitochondrial Code
- The Candidate Division SR1 and Gracilibacteria Code
- The Ciliate Dascladacean and Hexamita Nuclear Code
- The Alternative Flatworm Mitochondrial Code
Let us note that the functions in the equations above could be used to get the total number of amino acids, 20, the same in all the cases. As an example, take the standard genetic code. We have, using only sums over the amino acids number functions
The same could be done for all the other cases, albeit with different amino acids number functions, but it could be easily verified the all the corresponding sums for all the genetic code variants give the same number 20. The above relations could also be exploited to compute, separately, the number of amino acids, as given above, and total degeneracy. It suffices to rearrange each equation for a given code (by adding and subtracting 1 in the multiplet functions). For example, in the case of the standard genetic code, we have
Here, the numbers in the second bracket are respectively the total number of degenerate codons corresponding to the number of amino acids in the first bracket (the adjective “degenerate” refers to the following: in a given multiplet of, say, n codons, the number of degenerate codons is equal to n − 1). For example, a sextet has five degenerate codons. Therefore, in Equation (20), the total degeneracy for the three sextets is computed as 3 × (6 − 1) = 15. We have thus constructed, by hand, for all the known genetic codes, a mathematical formula describing (fitting), faithfully, their codons distributions, and also the number of amino acids as well as the degeneracies. Looking at these formulae, Equations (1)–(18), we see that the frequency functions are all variations on the theme of the function, 2k. Added to this latter, are constants and/or k-dependent terms representing perturbations. Let us note, finally, that, in some rare cases, there are slight changes in a given code. For example, in the Invertebrate Mitochondrial Code, the codon AGG is absent in Drosophila. In this case, the only modification is that Serine, S, is now coded by seven codons instead of eight codons, and we could easily modify the frequency and multiplets functions in Equation (9). We shall return to these formulae in the fourth section and in the concluding remarks of Section 5.
3. The Genetic Codes via q-Deformations
In this short section, we summarize the results, obtained recently in [7], concerning another type of mathematical formulae which could be derived for the genetic codes using q-numbers, or q-deformed numbers, these latter being the all first ingredients from which many mathematical functions could be constructed. The q-numbers are used since many years in applications in mathematics and physics (see the references in [7] and some remarks in Section 5). The basic idea behind q-deformations is to introduce a deformation parameter, q, which could be real (or complex), in the “classical” mathematical expressions describing the studied system, and look at the effect(s) produced by the variation of the deformation parameter on these expressions when q is different from unity. In the limit where q = 1, the “classical” expressions are recovered and, for q ≠ 1, one expects new insights into the studied system. This is exactly what we are going to do for the genetic codes. Also, we shall include here a new application case, not yet known at the time of the publication of the above cited reference. There are several definitions of the q-numbers and we shall use the following one (used mainly by mathematicians) here, which proves interesting
where n is a natural number and q is a (real) deformation parameter (q ≥ 0). One has, [1]q = 1, [2]q = 1 + q, [3]q = 1 + q + q2, and so on and, for q = 1, one recovers the usual (natural) numbers. For q ≠ 1, one expects, as mentioned above, some new insights. This is exactly what we are going to show by considering the standard genetic code, as a starting point, and show that all its various variants could be seen as slight q-deformations of it. Thus, we first consider numeric expressions for the (standard) genetic code like (see Equation (20) above)
In the first bracket, we have the number of amino acids, 20. In the second bracket, we have the total degeneracy, 41, equal to the sum of the total degeneracies of the five multiplets. Next, in a first step, we chose to deform the numbers of the degeneracies only, keeping the number of amino acids unchanged. We have
or, explicitly, using Equation (21)
Of course, for q = 1, we get back to Equation (22): 20 + 41 = 61. Before giving the results, let us look at Table 1. The various genetic codes, including the standard one, are arranged according to decreasing stop codons numbers (given in the last column), from 4 to 1, and we see that there are four categories, noted Ci. If one takes, in each category, the product of the frequencies by the corresponding multiplets numbers, he/she finds the total number of coding codons, as it is indicated in the second line following each one of the Equations (1)–(18). On the other hand, as there is always a total of 64 codons, the number of stop codons is equal to 64 minus the total number of coding codons; this is precisely what is indicated in the fourth column. Using now Equation (24) and adjusting the deformation parameter q, for each category, we obtain
With the indicated q-values, all near 1, we describe therefore the total degeneracy of all the four categories. Note here that the special case of the Yeast Mitochondrial Code, although it has only two stop codons, is described by the value q~0.9959 (for category C4); it has 60 codons, coding for amino acids, two stop codons and two codons are absent. As mentioned above, we could also describe some cases, which were not yet published, when the above results were previously written in [7]. As a matter of fact, Záhonová et al., [10], have reported, very recently, the case of a non-canonical code (in a lineage of tripanosomatids) where all three termination codons (or stops)—UGA, UAG, and UAA—are reassigned to code for amino acids (UGA for Tryptophane and UAG and UAA for Glutamic Acid), with UAA and UAG serving, at the same time, as genuine termination codons. Furthermore very recently, Heaphy et al. [11] have identified a novel genetic code (Condylostoma magnum) where UAA, UAG, and UGA also specify amino acids and they provided evidence suggesting that the function of these codons depends on their location within mRNA. These two, and other cases (mentioned in the above two references) could be described by using our Equation (24) too. As a matter of fact, these last two cases are eventually classified in a new category, C0, and we can show that the value q~1.0116 leads to
Now, in a second step, starting again from Equation (22), we keep the degeneracy unchangedand q-deform the number of amino acids. We have
Or, explicitly, using again Equation (21)
For q = 1, we have 20+41. First, by deforming slightly the q-dependent part in Equation (31), we could describe additional amino acids (besides the 20 canonical ones). For q~1.0193, the term in bracket, in Equation (31), gives 21 and for q~1.0373, it gives 22. In the first case, we could describe either Selenocysteine (Sec) or Pyrrolysine (Pyl). In the second case, we could describe both, at the same time; this last case is known to occur in some organisms (see [7] for the details). Finally, the minimal value q = 0 leads to a minimal value for the number of amino acids which is here equal to 5. This later agrees well with claims concerning the number of “primordial” amino acids at the origin of life (see [7]).
4. An Inverse Symmetry-Information Relationship in the Genetic Codes
In this section, we shall consider, briefly and qualitatively, the relationship between symmetry and information in the various genetic codes. More than a century ago, British biologist William Bateson, studying biological systems, identified an inverse relationship between symmetry and information: an increase of symmetry = loss of information (see D. Peat [12] and also the references in the book by his son Gregory Bateson [13]). This inverse relationship has also been studied by Muller in his book [14] (by including also the concept of entropy). He summarized these “asymmetry relationships” in a table where high symmetry corresponds to low entropy (information) and low symmetry corresponds to high entropy (information). Before considering the inverse relationship between symmetry and information in the genetic codes, let us note that there is an abundant number of cases found in the biological literature where an “inverse” relationship exists. Let us mention, here, briefly, only some few examples. A global inverse relationship between the molecular weights of the 20 (canonical) amino acids and the number of triplets (codons) which code them was observed by Gavaudan et al. in 1969 [15]. Biro [16], has shown that there is a close internal inverse correlation between the codon usage bias (CBUs) of different codons. In the field of genomics, an inverse relationship between genome size and mutation rates has been observed in 1991 by Drake and is known as Drake’s rule [17]. Huang [18], reported an inverse relationship between genetic diversity and epigenetic complexity. With respect to the subject in our Section 3 above, we have also an inverse relationship between the frequencies and the multiplets; recall that, in our mathematical construction, the frequencies are in accordance with a geometrical progression when the multiplets are inversely ordered by an arithmetical progression, and this construction fits exactly the (experimental) distribution of the codons in all the genetic codes studied. In the case of the even multiplets, this inverse relationship is nicely verified (fitted). Take, for example, the case of the Thraustochytrium Mitochondrial Code (in Table 1 or in Equation (2)). Here, for the even multiplets 2, 4 and 6, we have the frequencies 9, 5 and 2, respectively and for the odd multiplets 1, 3, and 5, we have the frequencies 2, 1 and 1, respectively. In the (minor) case of the odd multiplets, it is almost well verified. This inverse relationship is globally nicely verified in all the variants shown in the table and is, of course, by construction, exactly reproduced, through our Equations (1)–(18). We can also mention another inverse global relationship concerning also the frequencies and the multiplets. Looking again at Table 1, we have that for all the genetic codes the number of amino acids for the smallest multiplets 1–3, is equal to 12 (with only two cases equal to 11, respectively 13) while, for the largest multiplets 4–8, the number of amino acids is 8 (with only two cases equal to 9, respectively 7). Now, we turn to the (inverse) relationship between information and symmetry in the genetic codes in Table 1. Here, the symmetry considered is related to Rumer’s symmetry [19], which is well known. Rumer, in 1966, defined the transformation U↔G, A↔C, where U, C, A and G denote the nitrogenous bases Uracyl, Cytosine, Adenine, and Guanine, respectively. This transformation divides the 64-codons table into two equal and symmetrical halves with 32 codons each (The 64 codons table is also divided into 16 “family-boxes” where, in each family, four codons share the same first two bases). In one half, call it M1, the third base, in a codon, is not necessary to define unambiguously an amino acid. In the other half of the symmetrical codons, call it M2, the third base is necessary to unambiguously define an amino acid. Also, in M2, the nature of the third base, pyrimidine (U/C) or purine (A/G) will be necessary to unambiguously define an amino acid. In the case of the standard genetic code, for example, M1 contains the five quartets: Proline (P), Threonine (T), Valine (V), Alanine (A), and Glycine (G); and also the three quartet-parts of the three sextets: Serine (SIV), Arginine (RIV) and Leucine (LIV). M2, on the other hand, contains the nine doublets: Phenylalanine (F), Tyrosine (Y), Cytosine (C), Asparagine (N), Lysine (K), Histidine (H), Glutamine (Q), Acid Aspartic (D), and Glutamic Acid (E); the three doublet-parts of the three sextets: (SII), (RII), (LII); the triplet Isoleucine (I); and, finally, the two singlets Methionine (M) and Tryptophane (W), see Figure 1 below where M1 is indicated in light grey.
The standard genetic code, described above, is not the most symmetric as we are going to explain below. On the other hand, we shall consider the data concerning the various genetic codes, in Table 1, as the information. This latter table summarizes, and shows the diversity of the frequencies and the multiplets of the various genetic codes. What is immediately apparent, when we look at Table 1, is that the genetic codes with high symmetry have very few multiplets (i.e., low information). Take, for example the two following genetic codes, the Vertebrate Mitochondrial Code, and the Ascidian Mitochondrial Code. Here, we have only even multiplets, that is, sextets, quartets and doublets. Also, if we consider the sextets, each, as the association of a quartet and a doublet, then the set M1 (see above) comprises only quartets and M2 comprises only doublets. Now, we perform a Rumer transformation (U↔G, A↔C) on the third base of all the 64 codons (shown in blue color in Figure 2). Such a transformation exists (see [20] and Figure 2), we call it R3 and, under this transformation, each one of the eight quartets in M1 is globally invariant (the meaning of the associated amino acid does not change) and the doublets in M2 are exchanged (the corresponding pairs of amino acids are exchanged). Equivalently, the “family-boxes” are invariant in M1 because each “family-box” correspond to a single amino acid but, in M2, the two doublets of each of the eight “family-boxes” are exchanged, that is the two amino acids in a “family box” are exchanged, thus we can only say that doublets remain doublets. In [20], we have constructed two another transformations, called R6 and R8 (see Figure 2). These two transformations, as does R3, act both only at the third codon position and contain, besides the Rumer transformation {U↔G, C↔A}, also other ones as {A↔U, C↔G} and {U↔C, A↔G}. Combined, these two transformations are equivalent to Rumer’s transformation; they are frequently called secondary Rumer’s transformations, see [20]. These latter, also, leave M1 and M2 globally invariant. In M2, R6 exchange the pairs of doublets of the four family-boxes in the upper half of the 64 codons table (shown in blue color for three family boxes, and in red color for one family box) and leaves invariant the doublets in the lower half of the table; the meaning of the corresponding amino acids does not change (shown in green color for three family boxes, and in black for one family box with strict invariance). R8, on the other hand, exchange the pairs of doublets of the four family-boxes in the lower half of the 64 codons table (shown in red color for three family boxes and in blue color for one family box) and leaves invariant the doublets in the upper half of the table (shown in black for three family boxes with strict invariance and in green color for one family box). In this latter case, the meaning of the corresponding amino acids does not change. These three transformations, together with the identity transformation, constitute a Klein group, itself a sub-group of a dihedral group D8 of eight transformations, including Rumer’s transformation, see [20]. Therefore, we have the result that, the two genetic codes mentioned above, are characterized by the “high” symmetry, mentioned above, and also low information: only sextets, quartets, and doublets, that is, only three multiplets out of eight possible.
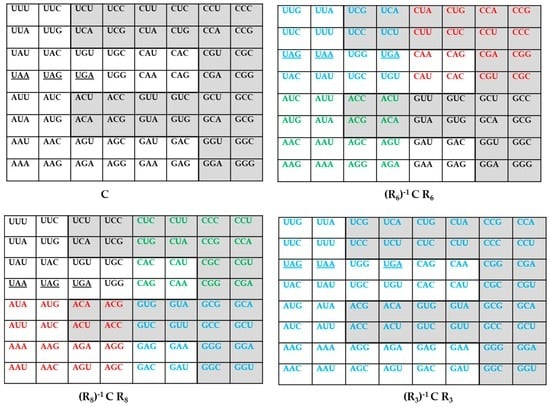
Figure 2.
The action of the transformations R3, R6, and R8 on the codon matrix C (see the text and [20]). The set M1 is indicated in light grey, as in Figure 1. The blue color corresponds to the substitutions {U↔G, A↔C}, the red color to the substitutions {A↔U, C↔G} and the green color to the substitutions to {U↔C, A↔G}; all the substitutions occur at the third base. For R6 and R8, the codons shown in black have their position strictly unchanged. The codons corresponding to the stop codons are underlined.
Now, two other codes also have only even multiplets: the Yeast Mitochondrial Code and the Invertebrate Mitochondrial Code and they both have one octet, that is, two different quartets (two different family-boxes) coding for the same amino acid, Threonine (H) for the former, where its two quartets are in M1, and Serine (S) for the latter, with one quartet in M1 and the other in M2. These latter two cases, therefore, also have a high symmetry, as for the two cases considered above, and also low information as only four multiplets out of eight are involved. Note also that, for the four most symmetric genetic code considered above (the Vertebrate Mitochondrial Code, the Ascidian Mitochondrial Code, the Yeast Mitochondrial Code, and the Invertebrate Mitochondrial Code) the mathematical functions constructed in Section 2 which describe them, respectively Equations (1), (12), (7) and (9), are not very complicated (low information) compared with the rest of the functions for the other genetic codes which need more terms (high information). Finally, the remaining genetic codes, including the standard genetic code, are characterized by five or more multiplets (five to seven coding codons, out of eight) and have a lower symmetry because there are frequently slight but disturbing changes(see these changes with respect to the standard genetic code after Table 1) which, in many cases, lead to the appearance of new multiplets: singlets, triplets, quintets, amino acids coded by five codons (quintet); septets, amino acids coded by seven codons (septet); octets, amino acids coded by eight codons (octet); and also new stop codons (as in the Scenedesmus Obliqus Mitochondrial Code) or stop codons reassigned to amino acids (as in the Alternative Flatworm Mitochondrial Code or in the Chlorophycean Mitochondrial Code, for example). In M1, changes can occur as for example, in the Alternative Yeast Nuclear Code where the codon CUG, which usually codes for Leucine, is now reassigned to code for Serine or in the Pachysolentannophilus Nuclear Code where this same codon (CUG) is reassigned to code for Alanine. Here, for example, under any one of the three transformations R3, R6 and R8, the reassigned codon for Serine or Alanine (CUG) is exchanged with one of the other three codons for Leucine so, in this case, at least one of the eight family-boxes in M1 has two of its amino acids exchanged and the global invariance in M1 is lost. In M2, there are more changes. For example, thereare appearances of new triplets as in the Echinoderm and Flatworm Mitochondrial Code, the Euplotid Nuclear Code, the Alternative Flaworm Mitochondrial Code, and the Trematode Mitochondrial Code. Here, one of the codons of the new triplet is exchanged with one codon of a singlet (in the same family-box) and so do the corresponding amino acids. The initial high symmetry, considered above for the four genetic codes (the Vertebrate Mitochondrial Code, the Ascidian Mitochondrial Code, the Yeast Mitochondrial Code, and the Invertebrate Mitochondrial Code) is now, for these remaining codes, anyway broken and, at the same time, the information becomes greater, as there is more and more diversity in the multiplets. In summary, we therefore have an inverse relationship between symmetry and information.
5. Summary and Concluding Remarks
We end this paper by summarizing our results and also by making some remarks. In the second section, we constructed, by hand, mathematical formulae reproducing faithfully (fitting), the frequencies of the various occurring multiplets for all the genetic code variants. It is important to mention here, as a first remark, that one might not grant the above formulae more than they deserve. They are only fits, obtained by elementary means, faithfully reproducing the frequencies and the multiplet structure of the genetic codes and extending earlier results by Gavaudan [9], concerning the existence of an inverse relationship between the frequencies and the multiplets (see Section 2). A genuine mathematical description (derivation) of the frequencies the multiplet structure of the genetic code(s), which takes into account the structural biochemical facts, is a truly hard problem and is far beyond what has been considered here. As a second remark, let us suggest that these formulae could have a practical pedagogical application: they could be used, via a small software program, to quickly give the several numeric characteristics (the frequencies and their number, the multiplets and their number, the degeneracies, and so on) of the genetic codes which are not directly and easily accessible for the reader from the tables of the genetic codes, as the ones at NCBI [8], or elsewhere. In the third section, we have summarized our recent approach to the description of the degeneracies of the genetic codes, using the concept of q-deformations. The q-deformations have been largely used in the last decades, especially in physics—and also in chemistry—with great success. For example, such important topics as the harmonic oscillator, the hydrogen atom, the Aufbau Prinzip which is at the root of the periodic system of the elements, and many others, have been considered (see [6] and the references therein). There are hundreds of papers published these latter few decades, in physics, concerning a great number of physical systems, where the q-deformations have been used successfully. In many of these works, tuning the parameter q to a given value, or to several given values, from an infinity of ones (q a real or complex number), could describe in an improved way the considered physical system, describing subtle effects. For example, starting from a mathematical formula for the spectrum of the hydrogen atom and introducing a q-deformation, we obtained the construction principle for the neutral atoms, positive ions, etc., [21]. As another example, the q-deformations have been linked to the smooth (non-linear) behavior of phenomena in atomic nuclei [22]. We gave here only two examples but in fact there are a hundreds of applications using the q-deformations (in statistical physics, solid-state physics, nuclear physics, particle physics, superstrings, branes, and so on). It is worth mentioning here that, in a theoretical biology context, attempts have been made, by physicists, in the study of the genetic code using q-deformations. As a matter of fact, so-called “quantum groups”, including a q-deformation parameter q, have been considered for the description of the genetic code degeneracies [23,24]. The question of the physical, chemical, or—as in this work—biological interpretation of the parameter q is an open question but, this has not prevented researchers from successfully obtaining interesting new insights and new results. In the fourth section, we have considered a particular symmetry group of transformations to study the relation between symmetry and information, in the genetic codes. The considered symmetry group of four transformations is a Klein group, itself a sub-group of a larger dihedral D8 group of eight transformations (including Rumer’s transformation), and the information was considered to be associated to the diversity of the multiplets of the various genetic codes. In particular we showed that, globally, there is an inverse relationship between symmetry and information: the larger the symmetry, the smaller the diversity of the multiplets in the genetic codes. It is important to mention, also, that the study of the symmetries of the genetic code(s) is not at all new; significant contributions have been made by several authors in the recent years, in particular those in references [25,26,27,28,29,30,31]. What we did, in the fourth section of this work, was to consider the concepts of information and symmetry together.
Acknowledgments
I would like to address my thanks to the reviewers for their constructive comments, criticisms and suggestions which have improved the quality of the paper.
Conflicts of Interest
The author declares no conflict of interest.
References
- Watson, J.D.; Crick, F.H.C. A Structure for deoxyribose nucleic acid. Nature 1953, 171, 737–738. [Google Scholar] [CrossRef] [PubMed]
- Nirenberg, M.; Leder, P.; Bernfield, M.; Brimacombe, R.; Trupin, J.; Rottman, F.; O’Neal, C. RNA codewords and protein synthesis, VII. On the general nature of the RNA code. Proc. Natl. Acad. Sci. USA 1965, 53, 1161–1168. [Google Scholar] [CrossRef] [PubMed]
- Négadi, T. The genetic code multiplet structure, in one number. Symmetry Cult. Sci. 2007, 18, 149–160. [Google Scholar] [CrossRef]
- Négadi, T. The genetic code via Gödel encoding. Open Phys. Chem. J. 2008, 2, 1–5. [Google Scholar] [CrossRef]
- Négadi, T. A taylor-made arithmetic model of the genetic code and applications. Symmetry Cult. Sci. 2009, 20, 51–76. [Google Scholar]
- Négadi, T. A Mathematical model of the genetic code(s) based on Fibonacci numbers and their q-analogues. NeuroQuantology 2015, 13, 259–272. [Google Scholar] [CrossRef]
- Négadi, T. Semi-phenomenological classification models of the genetic code(s) using q-deformed numbers. Symmetry Cult. Sci. 2016, 27, 81–94. [Google Scholar]
- The Genetic Codes. Available online: https://www.ncbi.nlm.nih.gov/Taxonomy/Utils/wprintgc.cgi (accessed on 12 August 2016).
- Gavaudan, P. The genetic code and the origin of life. In Chemical Evolution and the Origin of Life; Buvet, R., Ponnamperuma, C., Eds.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1971; pp. 432–445. [Google Scholar]
- Záhonová, K.; Kostygov, A.Y.; Ševčíková, T.; Yurchenko, V.; Eliás, M. An unprecedented non-canonical nuclear genetic code with all three termination codons reassigned as sense codons. Curr. Biol. 2016, 26, 2364–2369. [Google Scholar] [CrossRef] [PubMed]
- Heaphy, S.M.; Mariotti, M.; Gladyshev, V.N.; Atkins, J.F.; Baranov, P.V. Novel ciliate genetic code variants including the reassignment of all three stop codons to sense codons in Condylostoma magnum. Mol. Biol. Evol. 2016, 33, 2885–2889. [Google Scholar] [CrossRef] [PubMed]
- Meaning and Structure in Biology and Physics: Some Outstanding Questions. Available online: http://www.fdavidpeat.com/bibliography/essays/bermuda.htm (accessed on 26 October 2016).
- Bateson, G. Steps to an Ecology of Mind; Jason Aronson Inc.: Northvale, NJ, USA; London, UK, 1987. [Google Scholar]
- Muller, S.J. Asymmetry: The Foundation of Information; Springer: Berlin/Heidelberg, Germany, 2007; pp. 96–97. [Google Scholar]
- Schutzenberger, M.P.; Gavaudan, P.; Besson, J. Sur l’existence d’une certain correlation entre le poids moléculaire des acides aminés et le nombre de triplets intervenant dans leur codage. C. R. Acad. Sci. (Paris) 1969, 268, 1342–1344. [Google Scholar]
- Biro, J.C. Does codon bias have an evolutionary origin? Theor. Biol. Model. 2008, 5, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Drake, J.W. A constant rate of spontaneous mutation in DNA-based microbes. Proc. Natl. Acad. Sci. USA 1991, 88, 7160–7164. [Google Scholar] [CrossRef] [PubMed]
- Huang, S. Inverse relationship between genetic diversity and epigenetic complexity. In Cancer Epigenetics; Nature Proceedings; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Rumer, Y.B. About the codon’s systematization in the genetic code. Proc. Akad. Sci. USSR 1966, 167, 1393–1394. [Google Scholar]
- Négadi, T. Symmetry groups for the Rumer-Konopel’chenko-Shcherbak “bisections” of the Genetic Code and applications. Intern. Electron. J. Mol. Des. 2004, 3, 247–270. [Google Scholar]
- Négadi, T.; Kibler, M. A q-deformed Aufbau Prinzip. J. Phys. A Math. Gen. 1992, 25, L157–L160. [Google Scholar] [CrossRef]
- Sviratcheva, K.D.; Bahri, C.; Georgieva, A.I.; Draayer, J.P. Physical significance of q deformation and many-body interactions in nuclei. Phys. Rev. Lett. 2004, 93, 152501. [Google Scholar] [CrossRef]
- Frappat, L.; Sorba, P.; Sciarrino, A. A model of the genetic code. Int. J. Mod. Phys. 2000, B14, 2485. [Google Scholar] [CrossRef]
- Frappat, L.; Sorba, P.; Sciarrino, A. Quantum groups and the genetic code. Theor. Math. Phys. 2001, 128, 756–859. [Google Scholar] [CrossRef]
- Jestin, J.L. Degeneracy in the genetic code and its symmetries by base substitutions. C. R. Biol. 2006, 329, 168–171. [Google Scholar] [CrossRef] [PubMed]
- Jestin, J.L.; Soulé, C. Symmetries by base substitutions in the genetic code predict 2’ or 3’aminoacylation of tRNAs. J. Theor. Biol. 2007, 247, 391–394. [Google Scholar] [CrossRef] [PubMed]
- Koch, A.J.; Lehmann, J. About a symmetry of the genetic code. J. Theor. Biol. 1997, 189, 171–174. [Google Scholar] [CrossRef] [PubMed]
- Hornos, J.E.M.; Braggion, L.; Magini, M.; Forger, M. Symmetry preservation in the evolution of the genetic code. Life 2004, 56, 125–130. [Google Scholar] [CrossRef]
- Gonzalez, D.L. Can the genetic code be mathematically described? Med. Sci. Monit. 2004, 10, 11–17. [Google Scholar]
- Bashford, J.D.; Tsohantjis, I.; Jarvis, P.D. A supersymmetric model for the evolution of the genetic code. Proc. Natl. Acad. Sci. USA 1998, 95, 987–992. [Google Scholar] [CrossRef] [PubMed]
- Antoneli, F.; Forger, F.; Hornos, J.E.M. The search for symmetries in the genetic code: Finite groups. Mod. Phys.Lett. 2004, B18, 971. [Google Scholar] [CrossRef]
© 2016 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).