Abstract
Recent advances in neuronal multisensory integration suggest that the five senses do not exist in isolation of each other. Perception, cognition and action are integrated at very early levels of central processing, in a densely-coupled system equipped with multisensory interactions occurring at all temporal and spatial stages. In such a novel framework, a concept from the far-flung branch of topology, namely the Borsuk-Ulam theorem, comes into play. The theorem states that when two opposite points on a sphere are projected onto a circumference, they give rise to a single point containing their matching description. Here we show that the theorem applies also to multisensory integration: two environmental stimuli from different sensory modalities display similar features when mapped into cortical neurons. Topological tools not only shed new light on questions concerning the functional architecture of mind and the nature of mental states, but also provide an empirically assessable methodology. We argue that the Borsuk-Ulam theorem is a general principle underlying nervous multisensory integration, resulting in a framework that has the potential to be operationalized.
“A color is a physical object when we consider its dependence upon its luminous source; regarding, however, its dependence upon the retina, it becomes a psychological object, a sensation. Not the subject, but the direction of our investigation, is different in the two domains” (Mach 1885).
Current advances in human neurosciences shed new light on questions concerning the status of the mental and its relation to the physical. Multisensory neurons (we will also term them “heteromodal” or “multimodal”) receiving convergent inputs from multiple sensory modalities (independent sources of information called “cues”) integrate information from the five different senses []. When cues are available, combining them facilitates the detection of salient events and reduces perceptual uncertainty, in order to improve reactions to immediate dangers and to rapidly varying events []. Multisensory neurons are able as well to carry out complex brain activities, such as object categorization []. Heteromodal integration displays complicated temporal patterns: absent in the superior colliculus of newborn’s brain, it arises in the earlier weeks/months of postnatal life [,]. As time goes on, neurons develop their capacity to engage in multisensory integration, which determines whether stimuli are to be integrated or treated as independent events. Multisensory integration’s development is due to early sensory experience, extensive experience with heteromodal cues and, above all, maturation of cooperative interactions between superior colliculus and cortex [,]. The ability to engage in multisensory integration specifically requires cortical influences [,]: without the help of cortical activity, neurons become responsive to multiple sensory modalities, but are unable to integrate different sensory inputs []. To make the picture more intricate, multisensory experience is a plastic capacity depending on dynamic brain/environment interactions []: neurons indeed retain sensitivity to heteromodal experience well past the normal developmental period, in order that the brain learns a multisensory principle based on the specifics of experience and is able to apply it to novel incoming stimuli [].
In such a multifaceted framework, the Borsuk-Ulam theorem (BUT) from topology comes into play. This theorem tells us that two opposite points on a sphere, when projected on a one-dimension lower circumference, give rise to a single point displaying a matching description []. In this review, we will elucidate the underrated role of topology in multimodal integration, illustrating how simple concepts may be applied to brain processes of cues integration. This paper comprises four sections. In the first section, we will compare the traditional hierarchical view of multisensory integration with the very last developments: the latter talk about the nervous system as a sum of multisensory neurons that form extensive forward, backward and lateral connections at the very first steps of integration in the primary sensory areas. The second section provides a description of the BUT and its role in multisensory integration. Section three goes through the BUT’s theoretical and experimental consequences in theory of knowledge and in the explanation of mental states’ nature. The last section elucidates what the BUT brings on the table, when applied to multimodal neurons.
1. Classical vs. Current View
Traditional research on the basic science of sensation asks what types of information the brain receives from the external world. To elucidate the classical view, as an example we will go through the visual system, the best known and the most relevant among sensory systems in Primates. The retinal receptors are sensitive to simple signals related to the external world. The message is sent to the primary visual cortex V1, where specific aspects of vision such as form, motion or color are segregated in different parallel pathways. V1 projects to the associative areas termed “unimodal”, since they are influenced by a sole sensory modality (in this case, the vision) []. The visual unimodal associative cortex (secondary visual cortex) is arranged in two streams, devoted to the control of action and objects perception. Processing channels, each serving simultaneously specialized functions, are also present in the central auditory and somatosensory systems. The message is then conveyed from unimodal to associative areas termed “heteromodal”, since they are influenced by more than one sensory modality (visual, auditory, somatosensory, and so on) []. A high-order heteromodal area, the prefrontal cortex, collects the highly-processed inputs conveyed by other associative areas. In this classical view, the sequential processing of information is hierarchical, such that the initial, low-level inputs are transformed into representations and multisensory integration emerges at multiple processing cortical stages []. The hierarchical view is also embraced by the most successful model of cognitive architecture, i.e., the connectome, where hubs/nodes are characterized by preferential railways of information flows [].
In the last decade, neuroscience has witnessed major advances, emphasizing the potentially vast underestimation of multisensory processing in many brain areas. New mechanisms, such as the “unimodal multisensory neurons” [], have been demonstrated. In addition, multisensory interactions have been reported at system levels traditionally classified as strictly unimodal: both primary and secondary sensory areas receive substantial inputs from sources that carry information about events impacting other modalities [,,,,]. In particular, it has been well established in the case of the human V1, which is inherently multisensory []. In adult mice, vision loss through one eye leads whiskers to become a dominant nonvisual input source which attains extensive visual cortical reactivation []. In blind individuals, when visual inputs are absent, occipital (“visual”) brain regions respond to sound and spoken language []. A growing number of studies reports the presence of connectivity between V1 and primary auditory cortex (as well as other higher-level visual and auditory cortices). Non-visual stimuli have been shown to enhance the excitability of low-level visual cortices within the occipital pole. Research into cross-modal perception has also linked senses other than vision, such as taste with audition []. Escanilla et al. [] demonstrated odor-taste convergence in the nucleus of the solitary tract of the awake, freely licking rat. A multisensory network for olfactory processing, via primary gustatory cortex connections to primary olfactory cortex, once again suggests that sensory processing may be more intrinsically integrative than previously thought [].
In sum, the current broad consensus is that the multimodal model is widely diffused in the brain and that most, if not all, higher- as well as lower-level neural processes are in some form multisensory. Information from multiple senses is integrated already at very early levels of processing, leading to the concept of the whole neocortex as multisensory in function. Forward, backward and lateral extensive connections support communication in a densely-coupled system, where multisensory interactions occur at all temporal and spatial stages []. The content of the single neuronal outputs turns out to be increasingly complex. The functional wheel has come full circle when the highest polymodal areas send feedback messages to the primary sensory cortices. From now on, a ceaseless pathway of feedbacks and feedforwards takes place among cortical areas. The functional importance of the so called “backward” connections is worth of mention. The effects of the projections from higher areas to multimodal neurons play an important role both in multisensory development and in complex brain functions, providing meaningful adjustments to the ongoing activity of a given area. It has been argued that backward connections might embody the causal structure of the world, while forward connections just provide feedback about prediction errors to higher areas []. That is, anatomical forward connections are functional feedback connections. For backward connections to effectively modulate lower level processing, higher order areas would need to begin their processing at approximately the same time as lower areas. While this was originally thought not to be the case, we know now that the cross-modal interactions’ processing latencies are highly similar to the latencies at which initial sensory processing occurs in the respective primary cortices [].
2. A Topological Model of Multisensory Integration
2.1. The Borsuk-Ulam Theorem.
Continuous mappings from object spaces to feature spaces lead to various variants of the Borsuk-Ulam Theorem [,,]. Antipodal points are points opposite each other on a Sn sphere []. There are natural ties between Borsuk’s result for antipodes and mappings called homotopies. In fact, the early work on n-spheres and antipodal points eventually led Borsuk to the study of retraction mappings and homotopic mappings [].
The Borsuk-Ulam Theorem states that:
Points on Sn are antipodal, provided they are diametrically opposite. Examples of antipodal points are the endpoints of a line segment S1, or the opposite points along the circumference of a circle S2, or the poles of a sphere S3 []. An n-dimensional Euclidean vector space is denoted by [,]. Put simply, BUT states that a sphere displays two antipodal points that emit matching signals. When they are projected on a circumference, they give rise to a single point which a description matching both antipodal points (Figure 1A). Here “opposite points” means two points on the surface of a three-dimensional sphere (the surface of a beach ball is a good example) which share some characteristics in common and are at the same distance from the center of the beach ball []. For example, BUT dictates that on the earth’s surface there always exist two opposite points with the same pressure and temperature. Two opposite points embedded in a sphere project onto a single point on a circumference, and vice versa: this means that the projection from a higher dimension (equipped with two antipodal points) to a lower one gives rise to a single point (equipped with the characteristics of both the antipodal points). It is worth mentioning again that the two antipodal points display similar features: we will go through this central issue in the next paragraph.Every continuous map must identify a pair of antipodal points.
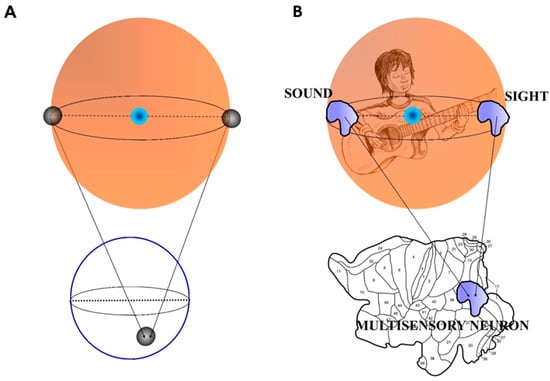
Figure 1.
(A) A simplified sketch of the Borsuk-Ulam theorem: two antipodal points (black spheres) on a three-dimensional sphere project to a single point on a two-dimensional circumference. (B) The Figure shows what happens when an observer is in front of a guitar player. The environmental inputs from different sensory modalities (in this case sound and sight are depicted in guise of shapes instead of points) converge on a single group of multisensory neurons in the cortical layers of brain’s observer. Note that the brain is flattened and displayed in 2D []. According to the dictates of the Borsuk-Ulam theorem, the single shape contains a melted message from the two modalities. Modified from Tozzi and Peters [].
2.2. Borsuk-Ulam Theorem in Brain Signal Analysis.
What does BUT mean in a physical/biological context? How could BUT be helpful in the evaluation of brain function? The two antipodal points can be used not just for the description of simple topological points, but also of broad-spectrum phenomena: i.e., either two antipodal shapes, or functions, or signals, or vectors. For example, a “point” may be described as a collection of signals or a surface shape, where every shape maps to another antipodal one. Here we provide, for technical readers, the underlying mathematical treatment. In order to evaluate the possible applications of the BUT in brain signal analysis, we view the surface of the brain as an n-sphere and the feature spaces for brain signals as finite Euclidean topological spaces. In terms of brain activity, a feature vector models the description of a brain signal. The BUT states that, for description for a brain signal , we expect to find an antipodal feature vector that describes a brain signal on the opposite (antipodal) side of the brain (or of the environment). The pair of antipodal brain/environmental signals have matching descriptions. Let denote a nonempty set of points on the brain surface. Recall that an open set does not encompass its boundary or limit points. A topological structure on (called a brain topological space) is a collection of open sets of , having the following properties:
- (Str. 1) Every union of sets in is a set in
- (Str. 2) Every finite intersection of sets in is a set in
The pair is called a topological space. Also by itself can be termed a topological space, provided has a topology on it. Let be topological spaces. A function or map on a set to a set is a subset , so that for each there is a unique such that (usually written ). The mapping is defined by a rule telling us how to find .
Provided is open, a mapping is continuous and the inverse is also open []. In this view of continuous mappings from the brain signal topological space on the brain surface to the brain signal feature space , we can consider not just one signal feature vector , but also mappings on to a set of signal feature vectors . This expanded view of brain signals has interest, since every connected set of feature vectors has a shape. In sum, this means that brain signal shapes can be compared. A consideration of (set of brain signal descriptions for a region X) instead of (description of a single brain signal ) leads to a region-based view of brain signals. This region-based view of the brain arises naturally in terms of a comparison of shapes produced by different mappings from (brain object space) to the brain feature space . An interest in continuous mappings from object spaces to feature spaces leads into homotopy theory and the study of shapes.
Let be continuous mappings from to . The continuous map is defined by
The mapping H is a homotopy, provided there is a continuous transformation (called a deformation) from f to g. The continuous maps f, g are called homotopic maps, provided continuously deforms into (denoted by ). The sets of points , are called shapes [].
For the mapping , where and are homotopic, provided and have the same shape. That is, and are homotopic, in case of:
An interest in continuous mappings from object spaces to feature spaces leads into homotopy theory and the study of shapes: antipodal points on a sphere have the same shape []. It was Borsuk who first associated the geometric notion of antipodal shapes and mappings, called homotopies [,,]. Borsuk’s discovery paves the way for a geometry of shapes and shapes of space [,]. To make an example, a pair of connected planar subsets in Euclidean space R2 have equivalent shapes, if the planer sets have the same number of holes []. This suggests yet another useful application of Borsuk’s view of the transformation of one shape into the other, in terms of brain signal analysis. Sets of brain signals not only will have similar descriptions, but also similar dynamic character. Moreover, the deformation of one brain signal shape into another occurs when they are descriptively near [,]. This expanded view of signals has interest, since every connected couple of antipodal points has a shape: therefore, signal shapes can be compared. If we evaluate physical and biological phenomena instead of “signals”, BUT leads naturally to the possibility of a region-based, not simply point-based, geometry, with many applications. In terms of activity, two antipodal regions model the description of a signal. The regions themselves live on what is known as a manifold, which is a topological space that is a snapshot (tiny part) of a locally Euclidean space. For a given signal on a sphere, we expect to find an antipodal region that describes a signal with a matching description. In sum, the mapping from the sphere to the circumference is defined by a rule which tells us how to find a single point/region []. The region-based view of the manifold arises naturally in terms of a comparison of shapes produced by different mappings from the sphere to the circumference [].
2.3 Borsuk-Ulam Theorem and Multisensory Integration.
Multisensory integration could be evaluated in terms of antipodal points and BUT. Figure 1B depicts an example of multisensory integration in the BUT framework. Consider an observer who hears the strumming of a guitar standing in the surrounding environment. A guitar player is embedded in the environment. The observer perceives, through his different sense organs such as ears and eyes, the sounds and the movements produced by the guitar player. According to the BUT dictates, the guitar player stands for an object embedded in a three-dimensional sphere. The two different sensory modalities produced by the guitar player (sounds and movements) stand for the antipodal points on the sphere’s surface. Objects belonging to antipodal regions can either be different or similar, depending on the features of objects []; however, the two antipodal points share the same features. Both sounds and movements come indeed from the same object embedded in the sphere, i.e., the guitar player. The two antipodal points are not true points, but instead shapes, or functions, which can also be portrayed as vectors containing all the features of the stimulus: in the case, for example, of the visual inputs, the vector contains information about the colours, the shape, the movements of the guitar player. The two antipodal points project at first to a two-dimensional layer, the brain cortex—where multisensory neurons lie—, then are integrated into a single multimodal signal, which takes into account the features of both. Cerebral hemispheres can be indeed unfolded and flattened into a two-dimensional reconstruction by computerized procedures []. We may think to a single vector, embedded in the two-dimensional brain, which contains the features of all the information from the two inputs.
A variant of the BUT theorem, called reBUT [], states that the two points (or regions, or vectors or whatsoever) with similar description do not need necessarily to be antipodal, in order to be described together (Figure 2A). This means that different inputs from different modalities do not need to be perfectly antipodal on the n-sphere (the environment). Sets of signals not only will have similar descriptions, but also dynamic character; moreover, the deformation of one signal shape into another occurs when they are descriptively near []. This elucidates an important feature of multisensory integration. Although multisensory interactions’ simulations at the neuronal level clearly show that the simple effect of heteromodal convergence is sufficient to generate multimodal properties, nonetheless the multisensory integration’s occurrence almost never could be predicted on the basis of a simple linear addition of their unisensory response profiles: the interactions may indeed be super-additive, sub-additive, or display inverse effectiveness and temporal changes [,,,]. In the BUT’s topological framework, this apparently bizarre behaviour is explained by the dynamical changes occurring at the antipodal points []. There is indeed the possibility that two inputs from different cues are not perfectly integrated. This means that the mapping of the two cues on the Sn−1 sphere does not match perfectly, and the sensation is doubtful (Figure 2B). A superimposition of two spheres with slightly different centers occurs. The brain thus might “move” its spheres, in order to restore the coherence between the two signals. Therefore, by an operational point of view, we might be able to evaluate the distance between the central points of the two spheres, in order to achieve the discrepancy values between the two multisensory signals projected from the environment to the brain.
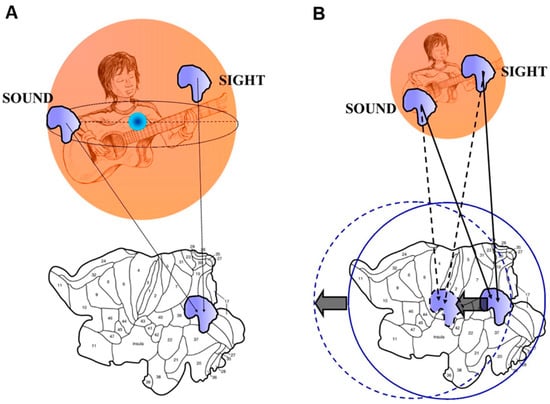
Figure 2.
(A) A simplified sketch of the reBUT (a variant of the Borsuk-Ulam theorem). The functions with matching description do not need necessarily to be antipodal. Thus, the two inputs from different sensory modalities may arise from every point of the environment, if they are just equipped with a signal matching. (B) When the two inputs from different modalities do not match on the 2-D brain surface, a discrepancy occurs between two brain spheres, which can be quantified by evaluating the distance between their two centres. Modified from Tozzi and Peters [].
The BUT is not simply a “metaphor”, rather a real computational tool. Indeed, there is room to use the description of the BUT and its variants in order to assess computations involved in multisensory integration, therefore providing both mechanisms and explanatory hypotheses. A BUT variant, termed energy-BUT, is particularly useful in our context. There exists a physical link between the abstract concept of BUT and the energetic features of the system formed by two manifolds Sn and Sn−1. We start from a manifold Sn equipped with a pair of antipodal points. When these opposite points map to an n-Euclidean manifold (where Sn−1 lies), a dimensionality reduction occurs, and a single point is achieved. However, it is widely recognized that a decrease in dimensions goes together with a decrease in information. Two antipodal points contain more information than their single projection in a lower dimension, because dropping down a dimension means that each point in the lower dimensional space is simpler: each point has one less coordinate. To make an example, a two-dimensional shadow of a cat encompasses less information than a three-dimensional cat. This means that the single mapping function on Sn−1 displays informational parameters lower than the two corresponding antipodal functions on Sn. Because information can be evaluated in terms of informational entropy, BUT and its variants yield physical quantities: we achieve a system in which entropy changes depend on affine connections and homotopies. Entropies can be evaluated in fMRI functional studies through different techniques, e.g., pairwise entropy [,,], Granger causality index, phase slope index, and so on []. Here we propose a topological procedure in order to assess changes in informational entropies in brain fMRI multisensory integration’s studies. The method is described in Figure 3. In our example, the visual and auditory cues stand for a continuous function, from the sphere surrounding the individual to his cortical multisensory neurons. Informational entropy values can be identified in multisensory neurons after their activation: in the hypothetical case of Figure 3, we choose a putative entropy value of 1.02. According to the BUT’s dictates, the same value 1.02 must be found both in the environmental cues (a single value of 1.02 for every one of the two different cues), and in every other cortical area involved in multisensory processing. We might not know the entropy values of the sound and sight in the external environment. However, this is not important: if we identify a group of cortical multisensory neurons that fire when a visual and auditory cue are presented together, we need just to know the entropy values of such neuronal assembly. Therefore, by knowing the sole entropy values of a Blood Oxygenation Level Dependent (BOLD)-activated multisensory brain area, we are allowed to correlate different brain zones involved in multisensory integration (Figure 3). Indeed, neurons equipped with the same entropy values are functionally linked, according to BUT. Therefore, we are able to assess the cortical zones that display the same entropy values, shedding light on the pathways involved in multisensory integration. This methodology paves also the way to experimentally evaluate which model, e.g., either the traditional or the current view of multisensory integration, is valid. Note that, in the proposed fMRI context, BUT is related to a meso-level of observation that involves cortical circuits and inter-areal massive interactions, through “Communication through Coherence”. Nevertheless, once neuro-techniques will be more advanced, BUT should be applicable also to micro-levels of observation, such as single-cell spiking activity.
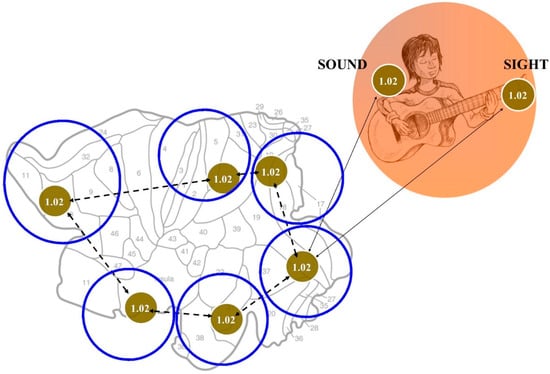
Figure 3.
The use of BUT in the evaluation of brain computations during multisensory integration. The figure displays a hypothetical case for illustrative purposes. The red circles are equipped with a number standing for the corresponding entropy value (in this hypothetical case: 1.02). The right Figure displays the environment containing two cues with matching description, e.g., equipped with entropy values: 1.02. The same entropy value can be found in the corresponding multisensory neuronal assembly located in the brain sensory cortex (left figure). This means that there must be at least a cortical area (or micro-area) with the same entropy value of the two matching points encompassed in the environment. Because multisensory interactions occur at all temporal and spatial stages, their extensive cortical connections must have something in common: they must display the same values of entropy (in this case, 1.02). This allows us to recognize which zones of the brain are functionally correlated during multisensory integration.
3. An Answer for Current Issues
In this section, we will go through the issues of the nature of mental states and theory of knowledge, through the lens of topology. The BUT model takes into account the content-bearing properties of physical neural networks, by reducing representational states to construct of observables and by providing a mechanistic account of the neural processes which underlie the mental processes of knowledge. BUT integration works not just at the so-called low-level processes—such as perception, motor control and simple mnemonic processing—[], but also at the high-levels—such as planning and reasoning—[]. In the above-described recent model of multisensory integration, sensory modalities outline a broadly interconnected network with multiple forward, backward and lateral connections, rather than a hierarchical system of parallel sensory streams that converge at higher levels. The key difference between the traditional and the novel view is whether the hierarchy comprises distinct and parallel streams that converge at higher levels, or whether there are dense interactions between all sensory streams, even at lower levels []. The BUT approach supports a model that assume rich cross-modal interconnectedness at all processing levels, suggesting that functional interplay between the senses occurs at all anatomical levels and across a varied time course. For example, the connections between the two secondary cortex’s visual pathways (the “where” and the “what” systems) provide evidence for a common and simultaneous neural substrate for action and perception.
The BUT allows us to establish the “metaphor” in a general cognitive theory. If a metaphor is a linguistic expression in which at least one part of the expression is transferred from one domain of application (source domain), where it is common, to another (target domain) in which it is unusual [], there are striking formal analogies with the topological concept of antipodal points. We hypothesize that the metaphor is produced by the convergence on a multisensory neurons’ assembly of both literal and figurative messages (corresponding to the antipodal points located in the environment). The heteromodal integration, aiming to gain insight through the metaphor that no literal paraphrase could ever capture, links together in a linguistic expression the domain of intuitive common-sense understanding of the “literal”, and the domain of application of the “figurative”. The peculiar nature of multisensory integration leads to a radical rethinking of mental representations. It takes into account the “cognitive” needs of theoretical representational states and provides a neuroanatomical frame to cognitive semantics. Can a single neuronal output contain more information than each of its countless inputs? The answer to this crucial question implies cognitive theoretical conclusions, concerned both with information and knowledge.
Multimodal neurons utilize the salient, meaningful information from different sensations and “melt” them into a novel message, which holds a “semantic” content. Consider the classical “leg of the table”. The leg “appears to us at first a single, indivisible whole. One name designates the whole”. But “the apparently indivisible thing is separated into parts” []: the world “leg” is not strictly a literal source domain, because it already contains the “merging” and integration of several features, such as the color, the shape, the temperature, the evoked feelings. In the framework of BUT, mental processes are not just cortical networks’ computations operating on the “syntax” of representation (i.e., Boolean logic), but they also throw a bridge between the latter and the “semantic” notion of mental content. The countless inputs become thus able to solve not-computable functions and to “fabricate” a cognitive process. BUT mechanisms underlying multisensory integration let us hypothesize that our “naïve” thoughts are semantic [], rather than syntactic, and that, during mental processes, the metaphor goes before the axiomatization and the formal syntax rules of the first-order predicate logic. Scientific data confirm heteromodal integration as “semantic” and show which cortical networks are most likely to mediate these effects, with the temporal area being more responsive to semantically congruent, and the frontal one to semantically incongruent audio-visual stimulation []. It has been suggested that multisensory facilitation is associated with posterior parietal activity as early as 100 ms after stimulus onset; as participants are required to classify heteromodal stimuli into semantic categories, multimodal processes extend in cingulate, temporal and prefrontal cortices 400 ms after stimulus onset [].
The BUT model displays astonishing connections with Gärdenfors’ [] “cognitive semantics”, which states that meanings are in the head, but are not independent of perception and bodily experience. Topology provides a conceptual bridge between “realistic” semantics (the meaning of an expression is something out there in the world) and “cognitive” semantics (meanings are expressions of mental entities independent of truth). Gardenfors states that semantic elements are based on spatial or topological rules [,], not on symbols: in touch also with BUT multisensory integration, cognitive models are primarily image-schemes transformed by metaphoric and metonymic operations []. Experimental data provide evidence for a complex inter-dependency between spatial location and temporal structure in determining the ultimate behavioral and perceptual outcome associated with paired multisensory stimuli []. This experience of time and two- or three-dimensional spatial configurations, together with the expressions pertaining to higher level of conceptual organization, can be easily explained by a topological mapping of the components onto the multisensory. The blending, a standpoint of cognitive semantics [], refers to a “mental” space configuration in which elements of two input spaces are projected into a third space, the blend, which thus contains elements of both []. If we figure this space not as “mental” but as “biological”, the blend turns out to be the BUT. Rather than just combining predicates, the semantic model/BUT structure blends behaviors from multiple (mental or anatomical) spaces and explains “apparently” emergent phenomena [].
Inferring which signals have a hypothetical common underlying cause—and hence should be integrated—is a primary challenge for a perceptual system dealing with multiple sensory inputs. The brain is able to efficiently infer the causes underlying our sensory events. Experiments demonstrate that we use the similarity in the temporal structure of multisensory cue combinations, in order to infer from correlation the causal structure as well as the location of causes []. This capacity is not limited to the high-level cognition, rather it is performed recurrently and effortlessly in perception too []. In case of abnormal multisensory experience (visual-auditory spatial disparity), an atypical multisensory integration takes place (Stein 2009). We hypothesize that inferences form a sort of “niche construction”, which shapes the common sense of a neural machinery operating in embodied/embedded interaction with the environment []. Our brain is also able of abstraction, i.e., to create its own representational endowment or potential, without recourse to external objects or states of affairs, such as causal antecedents or evolutionary history []. Truth conditions are not crucial for such a kind of representational content. How could multisensory neurons’ outputs abstract both causal and not causal events, in order to introduce new multifaceted elements into the thinking process? Perhaps heteromodal neurons are able to re-evoke complex data also in absence of the original external stimulus, by comparing and integrating the countless novel semantic messages included in the single bi-dimensional point predicted by BUT, in order that the brain is able to “look without seeing, listen without hearing” (Leonardo da Vinci) []. The role of the highest cortical areas could be crucial in activating multisensory neurons of lower levels, also in absence of external stimuli. Data from literature suggest this possibility. Two important temporal epochs have been described in the visual, auditory and multimodal response to stimuli: an early phase, during which both weak/no-unisensory and defined multisensory responses occur, and a late period, after which the unisensory responses have ended and the multisensory one remains []. In sum, in view of the BUT principles, the higher brain activities may be explained by a sole factor: the presence of a multi-dimensional structure equipped with antipodal points. It astonishingly resembles Godel’s suggestion of abstract terms more and more converging to the infinity in the sphere of our understanding.
4. What Does Topology Bring to the Table?
In conclusion, we provided a general topological mechanism which explains the elusive phenomenon of multisensory integration. The model is cast in a physical/biological fashion which has the potential of being operationalized and experimentally tested through fMRI studies. A shift in conceptualizations is evident in a theory of knowledge based on BUT multisensory integration: it is no longer the default position to assume that perception, cognition and motor control are unisensory processes []. In agreement with Ernst Mach [], objects are “combinations or complex of sensations”. Our senses do not exist in isolation of each other and, in order to fully answer to epistemological queries, the processes in question must be studied in a multimodal context []. The question here is: What for? What does a topologic reformulation add in the evaluation of multimodal integration? The opportunity to treat elusive mental phenomena as topological structures takes us into the realm of algebraic topology, allowing us to describe brain function in the language of powerful analytical tools, such as combinatorics, hereditary set systems [], homology theory and functional analysis. BUT and its extensions provide a methodological approach which makes it possible for us to study multisensory integration in terms of projections from real to abstract phase spaces. The importance of projections between environmental spaces, where objects lie, and brain phase spaces, where multimodal operations take place, is also suggested by Sengupta et al. [], who provide a way of measuring distance on concave neural manifolds. Note that the BUT requires the function to be continuous, while the nervous activity is at most piecewise continuous. However, the projections dictated by BUT might occur just in the periods in which brain activity is piecewise continuous, e.g., during a single multisensory task, and then be broken when another different task occurs. A methodological approach has been proved useful in the evaluation of brain symmetries, in order to assess the relationships and affinities among BOLD activated areas [] and among cortical histological images []. However, BUT and its variants are not just a methodological approach, but also display a physical meaning. Based on the antipodal cortical zones with co-occurring BOLD activation, it has been also recently suggested that brain trajectories might display donut-like trajectories [].
The different animals’ senses capture only bits and selected aspects of reality and display the world from limited points of view []. “The development of the human mind has practically extinguished all feelings, except a few sporadic kinds, sound, colors, smells, warmth, etc.” []. However, a realistic fraction, albeit incomplete, reaches our brain from outside and gives rise, thanks to the BUT, to an isomorphism between sensations and perceptions. As stated above, the BUT perspective allows a symmetry property located in the real space (the environment) to be translated to an abstract space, and vice versa, enabling us to achieve a map from one dynamical system to another. “A truth is like a map, which does not copy the ground, but uses signs to tell us where to find the hill, the stream and the village” []. If symmetry transformations (antipodal points) can be evaluated, we are allowed to use the pure mathematical tools of topological group theory. Symmetry transformations therefore furnish us with a topologic family of models able to explain the data. In the study of multisensory integration, promising empiric advances are forthcoming: cutting edge methods have been recently proposed, from oscillatory phase coherence, to multi-voxel pattern analysis applied to multisensory research at different system levels, to the TMS-adaptation paradigm (for a review, see []). The last but not the least, two computational frameworks that account for multisensory integration have been recently established [,]. In the context of BUT, such advances might provide a considerable experimental support and a unifying computational account of multisensory neurons’ features.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Krueger, J.; Royal, D.W.; Fister, M.C.; Wallace, M.T. Spatial receptive field organization of multisensory neurons and its impact on multisensory interactions. Hear. Res. 2009, 258, 47–54. [Google Scholar] [CrossRef] [PubMed]
- Fetsch, C.R.; DeAngelis, G.C.; Angelaki, D.E. Visual-vestibular cue integration for heading perception: Applications of optimal cue integration theory. Eur. J. Neurosci. 2010, 31, 1721–1729. [Google Scholar] [CrossRef] [PubMed]
- Werner, S.; Noppeney, U. Superadditive responses in superior temporal sulcus predict audiovisual benefits in object categorization. Cereb. Cortex 2009, 20, 1829–1842. [Google Scholar] [CrossRef] [PubMed]
- Stein, B.E.; Rowland, B.A. Organization and plasticity in multisensory integration: Early and late experience affects its governing principles. Prog. Brain Res. 2011, 191, 145–163. [Google Scholar] [PubMed]
- Royal, D.W.; Krueger, J.; Fister, M.C.; Wallace, M.T. Adult plasticity of spatiotemporal receptive fields of multisensory superior colliculus neurons following early visual deprivation. Restor. Neurol Neurosci. 2010, 28, 259–270. [Google Scholar] [PubMed]
- Burnett, L.R.; Stein, B.E.; Perrault, T.J., Jr.; Wallace, M.T. Excitotoxic lesions of the superior colliculus preferentially impact multisensory neurons and multisensory integration. Exp. Brain Res. 2007, 179, 325–338. [Google Scholar] [CrossRef] [PubMed]
- Stein, B.E.; Perrault, T.Y., Jr.; Stanford, T.R.; Rowland, B.A. Postnatal experiences influence how the brain integrates information from different senses. Front. Integr. Neurosci. 2009, 3. [Google Scholar] [CrossRef] [PubMed]
- Stein, B.E.; Stanford, T.R.; Rowland, B.A. Development of multisensory integration from the perspective of the individual neuron. Nat. Rev. Neurosci. 2014, 15, 520–535. [Google Scholar] [CrossRef] [PubMed]
- Johnson, S.P.; Amso, D.; Slemmer, J.A. Development of object concepts in infancy: Evidence for early learning in an eye-tracking paradigm. Proc. Natl. Acad. Sci. USA 2003, 100, 10568–10573. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Yu, L.; Rowland, B.A.; Stanford, T.R.; Stein, B.E. Incorporating cross-modal statistics in the development and maintenance of multisensory integration. J. Neurosci. 2012, 15, 2287–2298. [Google Scholar] [CrossRef] [PubMed]
- Porcu, E.; Keitel, C.; Müller, M.M. Visual, auditory and tactile stimuli compete for early sensory processing capacities within but not between senses. Neuroimage 2014, 97, 224–235. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Rowland, B.A.; Stein, B.E. Initiating the development of multisensory integration by manipulating sensory experience. J. Neurosci. 2010, 7, 4904–4913. [Google Scholar] [CrossRef] [PubMed]
- Borsuk, K. Drei Sätze über die n-dimensionale euklidische Sphäre. Fundam. Math. 1933, 20, 177–190. (In German) [Google Scholar]
- Nieuwenhuys, R.; Voogd, J.; van Huijzen, C. The Human Central Nervous System; Springer: Heidelberg, Germany, 2008. [Google Scholar]
- Pollmann, S.; Zinke, W.; Baumgartner, F.; Geringswald, F.; Hanke, M. The right temporo-parietal junction contributes to visual feature binding. Neuroimage 2014, 101, 289–297. [Google Scholar] [CrossRef] [PubMed]
- Van den Heuvel, M.P.; Sporns, O. Rich-club organization of the human connectome. J. Neurosci. 2011, 31, 15775–15786. [Google Scholar] [CrossRef] [PubMed]
- Allman, B.L.; Keniston, L.P.; Meredith, M.A. Not just for bimodal neurons anymore: The contribution of unimodal neurons to cortical multisensory processing. Brain Topogr. 2009, 21, 157–167. [Google Scholar] [CrossRef] [PubMed]
- Hackett, T.A.; Schroeder, C.E. Multisensory integration in auditory and auditory-related areas of Cortex. Hear. Res. 2009, 258, 72–79. [Google Scholar] [CrossRef] [PubMed]
- Shinder, M.E.; Newlands, S.D. Sensory convergence in the parieto-insular vestibular cortex. J. Neurophysiol. 2014, 111, 2445–2464. [Google Scholar] [CrossRef] [PubMed]
- Reig, R.; Silberberg, G. Multisensory integration in the mouse striatum. Neuron 2014, 83, 1200–1212. [Google Scholar] [CrossRef] [PubMed]
- Kuang, S.; Zhang, T. Smelling directions: Olfaction modulates ambiguous visual motion perception. Sci. Rep. 2014, 23. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.S.; Gomez-Ramirez, M.; Thakur, P.H.; Hsiao, S.S. Multimodal Interactions between Proprioceptive and Cutaneous Signals in Primary Somatosensory Cortex. Neuron 2015, 86, 555–566. [Google Scholar] [CrossRef] [PubMed]
- Murray, M.M.; Thelen, A.; Thut, G.; Romei, V.; Martuzzi, R.; Matusz, P.J. The multisensory function of the human primary visual cortex. Neuropsychologia 2015. [Google Scholar] [CrossRef] [PubMed]
- Nys, J.; Smolders, K.; Laramée, M.E.; Hofman, I.; Hu, T.T.; Arckens, L. Regional Specificity of GABAergic Regulation of Cross-Modal Plasticity in Mouse Visual Cortex after Unilateral Enucleation. J. Neurosci. 2015, 35, 11174–11189. [Google Scholar] [CrossRef] [PubMed]
- Bedny, M.; Richardson, H.; Saxe, R. “Visual” Cortex Responds to Spoken Language in Blind Children. J. Neurosci. 2015, 35, 11674–11681. [Google Scholar] [CrossRef] [PubMed]
- Yan, K.S.; Dando, R. A crossmodal role for audition in taste perception. J. Exp. Psychol. Hum. Percept. Perform. 2015, 41, 590–596. [Google Scholar] [CrossRef] [PubMed]
- Escanilla, O.D.; Victor, J.D.; di Lorenzo, P.M. Odor-taste convergence in the nucleus of the solitary tract of the awake freely licking rat. J. Neurosci. 2015, 35, 6284–6297. [Google Scholar] [CrossRef] [PubMed]
- Maier, J.X.; Blankenship, M.L.; Li, J.X.; Katz, D.B. A Multisensory Network for Olfactory Processing. Curr. Biol. 2015, 25, 2642–2650. [Google Scholar] [CrossRef] [PubMed]
- Klemen, J.; Chambers, C.D. Current perspectives and methods in studying neural mechanisms of multisensory interactions. Neurosci. Biobehav. Rev. 2012, 36, 111–133. [Google Scholar] [CrossRef] [PubMed]
- Bastos, A.M.; Litvak, V.; Moran, R.; Bosman, C.A.; Fries, P.; Friston, K.J. A DCM study of spectral asymmetries in feedforward and feedback connections between visual areas V1 and V4 in the monkey. Neuroimage 2015, 108, 460–475. [Google Scholar] [CrossRef] [PubMed]
- Dodson, C.T.J.; Parker, P.E. A User’s Guide to Algebraic Topology; Kluwer: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Matoušek, J. Using the Borsuk-Ulam Theorem; Lectures on Topological Methods in Combinatorics and Geometry; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Weisstein, E.W. Antipodal Points. Available online: http://mathworld.wolfram.com/AntipodalPoints.html (accessed on 15 November 2016).
- Borsuk, M.; Gmurczyk, A. On Homotopy Types of 2-Dimensional Polyhedral. Fundam. Math. 1980, 109, 123–142. [Google Scholar]
- Moura, E.; Henderson, D.G. Experiencing Geometry: On Plane and Sphere; Prentice Hall: Englewood Cliffs, NJ, USA, 1996. [Google Scholar]
- Tozzi, A.; Peters, J.F. Towards a Fourth Spatial Dimension of Brain Activity. Cogn. Neurodyn. 2016, 10, 189–199. [Google Scholar] [CrossRef] [PubMed]
- Tozzi, A.; Peters, J.F. A Topological Approach Unveils System Invariances and Broken Symmetries in the Brain. J. Neurosci. Res. 2016, 94, 351–365. [Google Scholar] [CrossRef] [PubMed]
- Marsaglia, G. Choosing a Point from the Surface of a Sphere. Ann. Math. Stat. 1972, 43, 645–646. [Google Scholar] [CrossRef]
- Van Essen, D.C. A Population-Average, Landmark—And Surface-based (PALS) atlas of human cerebral cortex. Neuroimage 2005, 28, 635–666. [Google Scholar] [CrossRef] [PubMed]
- Krantz, S.G. A Guide to Topology; The Mathematical Association of America: Washington, DC, USA, 2009; p. 107. [Google Scholar]
- Manetti, M. Topology; Springer: Heidelberg, Germany, 2015. [Google Scholar]
- Cohen, M.M. A Course in Simple Homotopy Theory; Springer: New York, NY, USA, 1973; p. MR0362320. [Google Scholar]
- Borsuk, K. Concerning the classification of topological spaces from the standpoint of the theory of retracts. Fundam. Math. 1959, 46, 321–330. [Google Scholar]
- Borsuk, K. Fundamental Retracts and Extensions of Fundamental Sequences. Fundam. Math. 1969, 64, 55–85. [Google Scholar]
- Collins, G.P. The Shapes of Space. Sci. Am. 2004, 291, 94–103. [Google Scholar] [CrossRef] [PubMed]
- Weeks, J.R. The Shape of Space, 2nd ed.; Marcel Dekker, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Peters, J.F. Topology of Digital Images. Visual Pattern Discovery in Proximity Spaces, Intelligent Systems Reference Library; Springer: Berlin, Germany, 2014; Volume 63, pp. 1–342. [Google Scholar]
- Peters, J.F. Computational Proximity. Excursions in the Topology of Digital Images, Intelligent Systems Reference Library; Springer: Berlin, Germany, 2016; pp. 1–468. [Google Scholar]
- Willard, S. General Topology; Dover Pub., Inc.: Mineola, NY, USA, 1970. [Google Scholar]
- Peters, J.F.; Tozzi, A. Region-Based Borsuk-Ulam Theorem. arXiv, 2016; arXiv:1605.02987. [Google Scholar]
- Perrault, T.J., Jr.; Stein, B.E.; Rowland, B.A. Non-stationarity in multisensory neurons in the superior colliculus. Front. Psychol. 2011, 2, 144. [Google Scholar] [CrossRef] [PubMed]
- Benson, K.; Raynor, H.A. Occurrence of habituation during repeated food exposure via the olfactory and gustatory systems. Eat Behav. 2014, 15, 331–333. [Google Scholar] [CrossRef] [PubMed]
- Schneidman, E.; Berry, M.J.; Segev, R.; Bialek, W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 2006, 440, 1007–1012. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, T.; Kan, S.; Koike, T.; Misaki, M.; Konishi, S.; Miyauchi, S.; Masuda, N. Network-dependent modulation of brain activity during sleep. NeuroImage 2014, 98, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Li, Y.; Childress, A.R.; Detre, J.A. Brain entropy mapping using fMRI. PLoS ONE 2014, 9, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Kida, T.; Tanaka, E.; Kakigi, R. Multi-Dimensional Dynamics of Human Electromagnetic Brain Activity. Front. Hum. Neurosci. 2016, 9, 713. [Google Scholar] [CrossRef] [PubMed]
- Sutter, C.; Drewing, K.; Müsseler, J. Multisensory integration in action control. Front. Psychol. 2014. [Google Scholar] [CrossRef] [PubMed]
- Drugowitsch, J.; de Angelis, G.C.; Klier, E.M.; Angelaki, D.E.; Pouget, A. Optimal multisensory decision-making in a reaction-time task. Elife 2014. [Google Scholar] [CrossRef] [PubMed]
- Jones, D.M.B. Models, Metaphors and Analogies. In The Blackwell Guide to the Philosophy of Science; Machamer, P., Silberstein, M., Eds.; Blackwell: Oxford, UK, 2002. [Google Scholar]
- Mach, E. Analysis of the Sensations; The Open Court Publishing Company: Chicago, IL, USA, 1896. [Google Scholar]
- Van Ackeren, M.J.; Schneider, T.R.; Müsch, K.; Rueschemeyer, S.A. Oscillatory neuronal activity reflects lexical-semantic feature integration within and across sensory modalities in distributed cortical networks. J. Neurosci. 2014, 34, 14318–14323. [Google Scholar] [CrossRef] [PubMed]
- Doehrmann, O.; Naumer, M.J. Semantics and the multisensory brain: How meaning modulates processes of audio-visual integration. Brain Res. 2008, 25, 136–150. [Google Scholar] [CrossRef] [PubMed]
- Diaconescu, A.O.; Alain, C.; McIntosh, A.R. The co-occurrence of multisensory facilitation and cross-modal conflict in the human brain. J. Neurophysiol. 2011, 106, 2896–2909. [Google Scholar] [CrossRef] [PubMed]
- Gärdenfors, P. Six Tenets of Cognitive Semantics. 2011. Available online: http://www.ling.gu.se/~biljana/ st1-97/ tenetsem.html (accessed on 11 December 2016).
- Gärdenfors, P. Conceptual Spaces: The Geometry of Thought; The MIT Press: Cambridge, UK, 2000. [Google Scholar]
- Kuhn, W. Why Information Science Needs Cognitive Semantics—And What It Has to Offer in Return; DRAFT Version 1.0; Meaning and Computation Laboratory, Department of Computer Science and Engineering, University of California at San Diego: La Jolla, CA, USA, 31 March 2003. [Google Scholar]
- Stevenson, R.A.; Fister, J.K.; Barnett, Z.P.; Nidiffer, A.R.; Wallace, M.T. Interactions between the spatial and temporal stimulus factors that influence multisensory integration in human performance. Exp. Brain Res. 2012, 219, 121–137. [Google Scholar] [CrossRef] [PubMed]
- Langacker, R.W. Cognitive Grammar—A Basic Introduction; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Fauconnier, G. Mappings in Thought and Language; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Kim, J. Making Sense of Emergence. Philos. Stud. 1999, 95, 3–36. [Google Scholar] [CrossRef]
- Parise, C.V.; Spence, C.; Ernst, M.O. When correlation implies causation in multisensory integration. Curr. Biol. 2012, 22, 46–49. [Google Scholar] [CrossRef] [PubMed]
- Körding, K.P.; Beierholm, U.; Ma, W.J.; Quartz, S.; Tenenbaum, J.B.; Shams, L. Causal inference in multisensory perception. PLoS ONE 2007, 26, e943. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. The free-energy principle: A unified brain theory? Nat. Rev. Neurosci. 2010, 11, 127–138. [Google Scholar] [CrossRef] [PubMed]
- Grush, R. Cognitive Science. In The Blackwell Guide to the Philosophy of Science; Machamer, P., Silberstein, M., Eds.; Blackwell: Oxford, UK, 2002. [Google Scholar]
- McLean, J.; Freed, M.A.; Segev, R.; Freed, M.A.; Berry, M.J.; Balasubramanian, V.; Sterling, P. How much the eye tells the brain. Curr. Biol. 2006, 25, 1428–1434. [Google Scholar]
- Royal, D.W.; Carriere, B.N.; Wallace, M.T. Spatiotemporal architecture of cortical receptive fields and its impact on multisensory interactions. Exp. Brain Res. 2009, 198, 127–136. [Google Scholar] [CrossRef] [PubMed]
- Méndez, J.C.; Pérez, O.; Prado, L.; Merchant, H. Linking perception, cognition, and action: Psychophysical observations and neural network modelling. PLoS ONE 2014, 9, e102553. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, B.; Tozzi, A.; Cooray, G.K.; Douglas, P.K.; Friston, K.J. Towards a Neuronal Gauge Theory. PLoS Biol. 2016, 14, e1002400. [Google Scholar] [CrossRef] [PubMed]
- Peters, J.F.; Tozzi, A.; Ramanna, S. Brain tissue tessellation shows absence of canonical microcircuits. Neurosci. Lett. 2016, in press. [Google Scholar] [CrossRef] [PubMed]
- Holldobler, B.; Wilson, E.O. Formiche—Storia di Un’Esplorazione Scientifica; Adelphi: Milano, Italy, 2002. [Google Scholar]
- Peirce, C.S. Philosophical Writings of Peirce; Buchler, J., Ed.; Courier Dover Publications: New York, NY, USA, 2011; p. 344. [Google Scholar]
- Goodman, R.B. Pragmatism: Critical Concepts in Philosophy; Taylor & Francis: New York, NY, USA, 2005; Volume 2, p. 345. [Google Scholar]
- Magosso, E.; Cuppini, C.; Serino, A.; di Pellegrino, G.; Ursino, M. A theoretical study of multisensory integration in the superior colliculus by a neural network model. Neural Netw. 2008, 21, 817–829. [Google Scholar] [CrossRef] [PubMed]
- Ohshiro, T.; Angelaki, D.E.; DeAngelis, G.C. A normalization model of multisensory integration. Nat. Neurosci. 2011, 14, 775–782. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).