Transforming Credit Risk Analysis: A Time-Series-Driven ResE-BiLSTM Framework for Post-Loan Default Detection

Abstract

Credit risk refers to the possibility that a borrower fails to meet contractual repayment obligations, posing potential losses to lenders. This study aims to enhance post-loan default prediction in credit risk management by constructing a time-series modeling framework based on repayment behavior data, enabling the capture of repayment risks that emerge after loan issuance. To achieve this objective, a Residual Enhanced Encoder Bidirectional Long Short-Term Memory (ResE-BiLSTM) model is proposed, in which the attention mechanism is responsible for discovering long-range correlations, while the residual connections ensure the preservation of distant information. This design mitigates the tendency of conventional recurrent architectures to overemphasize recent inputs while underrepresenting distant temporal information in long-term dependency modeling. Using the real-world large-scale Freddie Mac Single-Family Loan-Level Dataset, the model is evaluated on 44 independent cohorts and compared with five baseline models, including Long Short-Term Memory (LSTM), Bidirectional LSTM (BiLSTM), Gated Recurrent Unit (GRU), Convolutional Neural Network (CNN), and Recurrent Neural Network (RNN) across multiple evaluation metrics. The experimental results demonstrate that ResE-BiLSTM achieves superior performance on key indicators such as F1 and AUC, with average values of 0.92 and 0.97, respectively, and demonstrates robust performance across different feature window lengths and resampling settings. Ablation experiments and SHapley Additive exPlanations (SHAP)-based interpretability analyses further reveal that the model captures non-monotonic temporal importance patterns across key financial features. This study advances time-series–based anomaly detection for credit risk prediction by integrating global and local temporal learning. The findings offer practical value for financial institutions and risk management practitioners, while also providing methodological insights and a transferable modeling paradigm for future research on credit risk assessment.

1. Introduction

The significance of anomaly detection lies in its role in identifying unusual patterns in complex data, thus mitigating potential risks in various fields such as machine failure, financial fraud, web error logs, and medical health diagnosis [1]. In financial fraud detection, fraudulent activities usually fall into four categories [2]: banking, corporate, insurance, and cryptocurrency fraud. Banking fraud includes credit card, loan, and money laundering fraud. Corporate fraud consists of financial statement fraud and securities and commodities fraud, while insurance fraud involves life and auto insurance fraud [3].

This study focuses on anomaly detection in the loan domain, a context closely related to everyday life and directly affecting the financial security of individuals and households. Moreover, given the extreme scarcity of large-scale financial panel data available in the real world, the loan sector provides authentic long-term data suitable for modeling and validation, making it an ideal and practically representative application scenario for this research. The detection of financial loan anomalies consists of two primary phases: pre-loan fraud detection, known as the “application model”, and post-loan default prediction, identified as the “behavioral model” [4]. The purpose of pre-loan fraud detection is to intercept fraudulent activities during the loan application process [5], usually based on upfront audits [6]. These activities can involve falsifying financial or identity information and misrepresenting intentions. In contrast, using data analytics and machine learning, post-loan default prediction assesses risk by analyzing historical financial data of the borrowers [7]. This prediction assists financial institutions in implementing preventative strategies and modifying loan conditions to reduce non-performing loans, thereby ensuring asset quality assurance and stability. Despite its practical importance, research on post-loan default prediction remains limited compared with pre-loan fraud detection, partly due to the scarcity of publicly available large-scale panel datasets that capture borrowers’ repayment dynamics over time. Financial institutions typically withhold such data for privacy reasons, which restricts academic exploration of temporal credit risk modeling.

Financial loan data, typically documented on a monthly basis as time series, exhibits strong temporal dependencies that must be considered during anomaly detection. This complicates modeling compared to static data [8]. While LSTM-based models are widely used for capturing temporal dependencies [9,10], their unidirectional structure prevents effective modeling of bidirectional information. BiLSTM alleviates this limitation by incorporating forward and backward layers [11,12]. However, both LSTM and BiLSTM remain constrained in their ability to model global temporal patterns, and relatively few studies have leveraged post-loan repayment behavior to design default prediction systems. Furthermore, many deep learning–based credit risk models suffer from limited interpretability, which restricts their adoption in real financial decision-making [13]. Explainable AI (XAI) provides promising techniques to address this issue by enhancing the interpretability of machine learning (ML) models, particularly deep learning–based approaches, and helping users understand the contribution of different features to prediction outcomes [14].

Motivated by these challenges, this study focuses on the following core research question: How can the classification performance of imbalanced financial time series data in post-loan credit risk prediction be effectively improved?

To address this question, this study proposes ResE-BiLSTM, a BiLSTM-based model integrated with a residual-enhanced encoder to strengthen temporal feature extraction and improve out-of-sample (OOS) prediction accuracy. The model is applied to the real-world large-scale Freddie Mac Single-Family Loan-Level Dataset [15], and its performance is compared with five mainstream baseline models under different feature window lengths and resampling strategies. SHAP [16], a widely used post-hoc interpretability method for LSTM-based models [17], is further employed to reveal how key financial features influence prediction outcomes over time.

This research contributes to both theoretical and practical domains. From a theoretical perspective, it enhances the understanding of temporal modeling in credit risk prediction by demonstrating how global and local temporal dependencies jointly shape the evolution of borrower risk. The integration of a residual-enhanced encoder with a bidirectional recurrent structure addresses the limitations of conventional sequential models that overemphasize recent inputs, offering a clearer view of how distant and recent information interact within deep temporal learning. From a practical perspective, the study provides a robust and generalizable approach to post-loan default prediction in real-world financial settings. The model’s stable performance across varying levels of class imbalance and different feature window configurations underscores its adaptability, while the interpretability analysis reveals how repayment behaviors influence risk over time, offering actionable guidance for borrower monitoring, early-warning design, and data-driven risk management.

The structure of this paper is organized as follows. Section 2 provides a review of the relevant literature. Section 3 presents the dataset, preprocessing procedures, model architecture, and evaluation metrics. Section 4 reports the empirical results, including baseline comparisons, statistical significance tests, ablation studies, and interpretability findings. Section 5 concludes the study with a summary of key insights and directions for future research.

2. Review of Literature

2.1. Benchmark Datasets and Loan Default Prediction Model

Most prior studies have validated the performance of the default model using publicly accessible benchmark datasets from two primary sources, including Freddie Mac [15] and Lending Club [18]. In contrast, some studies used private datasets, making reproduction or replication of their results challenging for research purposes.

Specifically, Zandi et al. [19] introduced dynamic multi-layer graph neural networks (DYMGNN) using the Freddie Mac dataset, achieving a loan default prediction F1 of 0.851. The study contributes by incorporating default correlations among borrowers through graph neural representations, offering a dynamic modeling perspective that has been largely overlooked in previous research. However, its limitation lies in high computational complexity and an extended one-year prediction horizon, which reduce its practical applicability in large-scale financial settings. Wang et al. [20] adopted a survival model combined with neural networks on the same dataset, providing an interpretable model that elucidates the risk of default with factors such as loan maturity, origination year, and environmental influences. Its main contribution lies in integrating survival analysis into neural network architectures, thereby enhancing the interpretability of default timing. However, survival models require the complete life cycle of loans as training data, making them highly dependent on data integrity. Moreover, their modeling objectives and data utilization strategies fundamentally differ from ours. Survival analysis constructs a full credit cycle model spanning from loan origination to closure, which is particularly suitable for long-term strategic evaluation. In contrast, our model learns borrower behavioral patterns from shorter loan sequences without relying on full historical records, offering greater applicability in scenarios where data are limited or newly issued products lack complete lifecycle information. Karthika and Senthilselvi [21] developed an Extreme Gradient Boosting-based Bidirectional Gated Recurrent Unit with a self-attention mechanism (XGB-BiGRU-SAN), achieving more than 98% mean precision and recall on the Freddie Mac and Lending Club datasets. The hybrid design effectively enhances accuracy through attention-guided feature extraction, yet it depends heavily on cross-sectional transformations of temporal data, limiting its ability to model long-term repayment dynamics. Kanimozhi et al. [22] reported 89% accuracy using a logistic regression model, 78% with ridge regression, and 76% with k-nearest neighbors to predict loan prepayment, a bank risk indicator for mortgage-backed securities (MBS), using the Freddie Mac dataset. Although this study provides useful benchmark comparisons among traditional classifiers, it primarily focuses on prepayment risk rather than default behavior, which is crucial for dynamic risk assessment.

However, the Lending Club dataset is originally cross-sectional, and although it can be reformatted into a time series, it does not constitute the panel data required for this study. In contrast, the Freddie Mac dataset closely approximates the panel data collected by financial institutions, most of which are not publicly available due to privacy constraints. Prior research leveraging Freddie Mac data has largely overlooked the monthly repayment records, focusing only on the static information available at the pre-loan application stage, thereby failing to effectively exploit the information inherent in the time series, leaving an important research gap that this study seeks to address.

2.2. Design of BiLSTM and Its Variants in Anomaly Detection

Recent research has used BiLSTM models to detect financial anomalies, typically integrating them with various mechanisms such as attention, convolutional neural networks (CNN), and Transformer networks.

Chen et al. [23] used an attention-based BiLSTM model to analyze the data sequences to discover contract flaws with an accuracy of 95.40% and an F1 of 95.38% compared to baseline models such as LSTM, GRU and CNN. The study contributes by demonstrating that the attention mechanism can enhance BiLSTM’s ability to extract temporal features, but its limitation lies in the narrow evaluation scope, being confined to detecting smart contract defects. The contribution of this study lies in demonstrating that the attention mechanism enhances the temporal feature extraction capability of BiLSTM. However, its limitation is the restricted scope of evaluation, as the model’s generalization ability has not been validated on diverse real-world financial datasets. Narayan and Ganapathisamy [24] introduced a Hybrid Sampling (HS)—Similarity Attention Layer (SAL)—BiLSTM method to improve the classification performance in the detection of credit card fraud by removing redundant samples from the majority class and adding instances to the minority class. This approach effectively combines resampling and sequential modeling to enhance anomaly detection. However, it relies on synthetic oversampling and fails to consider the temporal evolution of anomalies, which may weaken its practical effectiveness.

Several studies analyzed the integration of BiLSTM, attention, and CNN for financial anomaly detection. Agarwal et al. [25] introduced a CNN-BiLSTM-Attention where CNN handles data initially, BiLSTM provides historical context next, and the attention mechanism discerns transaction multicollinearity, tested with 97% recall in IEEE-CIS Fraud Detection Dataset. Joy and R [26] presented a BiLSTM and CNN model driven by the attention mechanism, improving feature extraction and classification, outperforming CNN and BiLSTM-with-CNN on the Talking Data dataset. Prabhakar et al. [27] developed a structure that effectively uses CNN for feature extraction and BiLSTM for sequence learning, with the focus on words. This model improves Korean voice phishing detection with 99.32% accuracy and a 99.31% F1, which outperforms the CNN, LSTM, and BiLSTM baselines. Collectively, these studies have enriched the BiLSTM research landscape by demonstrating its flexibility for combining with attention or convolutional modules to capture complex temporal or spatial relationships. Nevertheless, most of them optimize architectures for specific datasets or tasks, with limited theoretical explanation of why such hybridization improves temporal representation. Moreover, the lack of evaluation on real-world financial panel data makes it unclear how well these models generalize under dynamic and imbalanced credit environments, resulting in a research gap that this study aims to address.

Several studies have proposed the integration of BiLSTM with Transformer networks, where Transformer, an algorithm based on the multi-headed self-attention mechanism introduced by Vaswani et al. [28], is capable of capturing long-range contextual information across the entire sequence. Cai et al. [29] developed a hybrid model with BiLSTM and Transformer to improve sentiment classification. Initially, BiLSTM derives contextual features, which are trained in several independent Transformer modules. The parameters of each Transformer are optimized during training to precisely determine sentiment polarity. Experiments on the SemEval dataset showed that this model outperforms traditional models such as CNN, LSTM, and BiLSTM in sentiment classification. Boussougou and Park [30] applied a similar approach, integrating Transformer and BiLSTM for portfolio return prediction. The input data fed into a post-BiLSTM three-layer encoder to produce predicted outputs, demonstrating the effectiveness of the BiLSTM-Transformer model in portfolio return prediction. These studies demonstrate the effectiveness of Transformer models in other application domains, providing theoretical support for our research.

LSTM, GRU, CNN, and RNN are commonly used standard models in time series data-based anomaly detection studies [31]. LSTM networks, with their gated design, effectively handle the problem of vanishing gradients seen in traditional RNNs, making them useful for capturing long-term dependencies in sequence data. CNNs are adept at detecting local patterns in sequences and are often combined with RNN models to improve spatio-temporal pattern tasks. The GRU, a simplified version of RNN, simplifies the gating functions of LSTM, offering similar performance with faster training, and is popular for anomaly detection and forecasting in time-series data [32].

2.3. XAI in Loan Default Prediction

Mill et al. [33] defines XAI as “AI systems that can explain their reasoning to humans, indicate their strengths and weaknesses, and predict their future behavior”. Unlike traditional “black-box” models, XAI offers insight into the internals of complex models, improving credibility and helping to comply with regulatory requirements in sectors such as finance, healthcare and law enforcement. XAI covers an array of methods designed for different objectives, offering various levels of insight. These methods are generally divided into pre-model, in-model, and post-model techniques [17]. The post-model technique, such as SHAP, Local Interpretable Model-Agnostic Explanations (LIME) [14], and Partial Dependence Plots (PDP) [14], is frequently utilized to clarify results from pre-trained models.

SHAP, derived from cooperative game theory [16], evaluates the impact of each input feature on the output of the model by assigning importance scores, highlighting the influential input features in the predictions. Conversely, LIME makes small data perturbations and builds an interpretable surrogate model to approximate the behavior of the black-box model. PDP shows how the values of a single input feature influence the predictions on average, which is explained by its global effect. Each method is suitable for specific domains. Li et al. [17] cataloged anomaly explanation techniques over 22 years, advocating for selection based on the model type. In particular, LSTM models often use SHAP to explain anomalies where the study by Ji [13] indicated that LIME offers slightly better interpretability than SHAP in the detection of credit card fraud.

Decision trees, linear regression, and rule-based classifiers are inherently interpretable in-model techniques due to their straightforward structures, allowing for transparency via human-readable decision rules or coefficients, directly correlating predictions with input features. In loan default prediction, these models can elucidate the impact of borrower behavior or demographic factors on default risk. However, there is a balance between interpretability and predictive accuracy, as highly interpretable models often do not perform optimally [34]. Raval et al. [35] demonstrated that pre-model strategies improve transparency in data preprocessing by employing an X-LSTM model with SHAP or LIME to identify crucial training features, with results documented on a blockchain. This method streamlines input data, improves performance and interpretability, and reveals key predictive features.

The existing literature has contributed to improving model transparency and promoting regulatory compliance in finance, illustrating how interpretability enhances trust in machine learning systems. However, most XAI studies remain descriptive and post hoc, rarely linking interpretability outcomes to model architecture or the temporal behavior of features. In the context of time-series credit data, few works explore how feature importance evolves across time or how interpretability insights can guide model refinement. This study advances this line of inquiry by using SHAP not only to interpret model predictions but also to explain how the Residual-Enhanced Encoder alters temporal focus compared to a standard BiLSTM, thereby connecting interpretability with architectural design.

In general, the use of XAI in predicting loan defaults improves the transparency of the model that could help build trust between financial institutions, aligns with regulatory standards, and optimizes model performance. Choosing suitable XAI tools based on specific application contexts effectively clarifies model decisions, guaranteeing the wide applicability of these models. For complex deep learning models, SHAP is mainly used to provide intuitive feature contribution values, aiding in understanding model decisions. Thus, this study uses SHAP as the interpretability method for model explanation.

3. Materials and Methods

3.1. Data Preprocessing

This study uses the Freddie Mac Single-Family Loan-Level Dataset [15], which contains more than 50 million entries from 1999 onward. Due to the reduced significance of older data and the incomplete nature of recent data, the study focuses on monthly repayment data from loans available between 1 January 2009, and  31 December 2019. Each quarter constitutes a separate dataset, with the first 1,000,000 records selected from each. The original dataset includes a large number of features, some of which have more than 50% missing values. Features with such a high proportion of missing values were excluded during the preprocessing stage, as they lack analytical value and may introduce additional noise. For the retained features, missing values are minimal. If any borrower has missing records in the selected features, the entire time-series data for that borrower is removed to ensure data completeness and consistency.

Table 1. Summary of the 44 independent cohorts in the Freddie Mac Single-Family Loan-Level Dataset.

Cohort	Number of Loans	Average Loan Length (Months)	Median Loan Length (Months)	Default Rate
2009Q1	17,604	56.805	42	1.755%
2009Q2	16,730	59.773	42	1.470%
2009Q3	15,728	63.581	44	2.893%
2009Q4	16,080	62.189	42	2.674%
2010Q1	15,779	63.375	42	2.884%
2010Q2	16,132	61.989	40	3.149%
2010Q3	15,525	64.412	46	2.209%
2010Q4	12,957	77.178	67	1.443%
2011Q1	13,969	71.587	61	2.098%
2011Q2	16,211	61.687	47	2.807%
2011Q3	15,196	65.807	55	2.165%
2011Q4	12,631	79.170	76	1.362%
2012Q1	12,304	81.274	85	1.756%
2012Q2	11,566	86.460	92	1.816%
2012Q3	11,209	89.214	95	1.963%
2012Q4	10,939	91.416	97	1.901%
2013Q1	11,138	89.783	96	2.182%
2013Q2	11,444	87.382	92	2.386%
2013Q3	12,733	78.536	83	2.592%
2013Q4	15,045	66.467	65	2.951%
2014Q1	16,002	62.492	62	3.412%
2014Q2	16,287	61.399	61	2.923%
2014Q3	15,715	63.633	67	2.660%
2014Q4	15,778	63.379	66	2.903%
2015Q1	15,638	63.947	67	2.954%
2015Q2	14,592	68.531	68	2.947%
2015Q3	15,923	62.802	63	3.410%
2015Q4	15,860	63.052	62	3.140%
2016Q1	17,180	58.207	59	3.423%
2016Q2	16,102	62.104	59	3.198%
2016Q3	15,871	63.008	60	3.459%
2016Q4	15,961	62.653	61	3.390%
2017Q1	19,386	51.584	49	4.354%
2017Q2	20,066	49.836	45	4.625%
2017Q3	20,019	49.953	44	4.311%
2017Q4	20,194	49.520	44	4.600%
2018Q1	22,999	43.480	39	4.913%
2018Q2	26,343	37.961	31	4.555%
2018Q3	29,629	33.751	27	4.398%
2018Q4	32,095	31.158	24	4.518%
2019Q1	36,704	27.245	22	4.795%
2019Q2	34,226	29.218	22	4.885%
2019Q3	32,061	31.191	24	4.429%
2019Q4	30,083	33.241	29	4.168%

displays the basic statistics for the 44 cohorts, including the number of loans, average and median loan history length, and default rate. Although these datasets are chronologically ordered, they are independent and represent the repayment records for a specific quarter across all subsequent years. The selected features are shown in

Table 2. Overview of the features in the Freddie Mac Single-Family Loan-Level Dataset.

No.	Feature	Description
1	Loan Sequence Number	Unique ID allocated for every loan.
2	Current Actual UPB	Indicates the reported final balance of the mortgage.
3	Current Loan Delinquency Status	Days overdue relative to the due date of the most recent payment made.
4	Defect Settlement Date	Date for resolution of Underwriting or Servicing Defects that are pending confirmation.
5	Modification Flag	Signifies that the loan has been altered.
6	Current Interest Rate (Current IR)	Displays the present interest rate on the mortgage note, with any modifications included.
7	Current Deferred UPB	The current non-interest bearing UPB of the modified loan.
8	Due Date Of Last Paid Installment (DDLPI)	Date until which the principal and interest on a loan are paid.
9	Estimated Loan To Value (ELTV)	LTV ratio using Freddie Mac’s AVM value.
10	Delinquency Due To Disaster	Indicator for hardship associated with disasters as reported by the Servicer.
11	Borrower Assistance Status Code	Type of support arrangement for interim loan payment mitigation.
12	Current Month Modification Cost	Monthly expense resulting from rate adjustment or UPB forbearance.
13	Interest Bearing UPB	The interest-bearing UPB of the adjusted loan.

.

The feature selection process involves removing features that mainly exhibit missing values and those linked to categorical attributes. The Current Loan Delinquency Status (CLDS) acts as the class label, where a value of 3 or more signifies that the borrower has not repaid the loan for at least 3 months, considering it a default, aligning with the industry standard definition according to Basel II guidelines [36]. Discrete features are transformed using hot encoding. Two additional features are introduced, including the difference in Interest Bearing Unpaid Principal Balance (UPB) and Current Actual UPB between the current month and the previous month. These differences generate new features labeled Interest Bearing UPB Delta and Current Actual UPB Delta, respectively.

Interest Bearing UPB, or Interest Bearing Unpaid Principal Balance, signifies the portion of a modified mortgage’s unpaid principal balance subject to interest. This amount is the basis for interest calculations and represents the remaining owed balance of a borrower. Calculating Interest Bearing UPB-Delta is valuable in loan default prediction and financial modeling, as it offers insights into repayment patterns. A negative value suggests principal repayment, indicating normal behavior, whereas a zero value might signal missed payments, indicating risk. A positive increase in principal may result from loan restructuring, deferred capitalization, or new debt, which requires further investigation.

The Current Actual UPB, combining both interest-bearing and non-interest-bearing UPB, offers a complete view of the borrower’s debt. This metric is important for risk management and thorough loan evaluation. The feature Current Actual UPB-Delta, indicating changes in deferred principal, adds further time-series insights by capturing adjustments such as additions, reductions, or re-amortizations. These elements improve the model’s capacity to differentiate typical repayment behavior from the distinct patterns linked to loan modifications.

The data is organized by Loan Sequence Number (loan ID). Within each group, a sliding window approach [37] is applied. Each time slice consists of three consecutive components: a feature window denoted as $\mathcal{L}$, which serves as the input for the model; a subsequent 2-month window serving as a blank gap; and a 3-month observation period used for generating labels. According to the definition of default adopted in this study, a default is identified when $\mathrm{CLDS}\ge 3$ occurs within the observation period. Accordingly, a label of $y=1$ is assigned if such an event occurs during the observation period; otherwise, $y=0$. To preserve the practical relevance of the task, samples with nonzero CLDS values (e.g., $\mathrm{CLDS}=1$ or 2) within the input feature window are excluded, ensuring that the model focuses on genuine early-stage prediction rather than detecting already evident delinquency signals. Consequently, defaults ($\mathrm{CLDS}\ge 3$) are constrained to occur no earlier than the third month following the input feature window. For this reason, a 2-month blank gap is designed between the input feature window and the observation period. The data is then randomly divided into 70% as the training set and 30% as the testing set (out-of-sample test) according to the original default ratio. To further prevent data leakage, time slices from the same borrower are strictly ensured not to appear in both the training and testing sets.

To address class imbalance, which can substantially influence the performance and generalization of ML models particularly in real-world scenarios such as loan default prediction, six resampling strategies were evaluated. These include random undersampling (RUS) [38], random oversampling (ROS) [38], Synthetic Minority Over-sampling Technique (SMOTE) [39], tSMOTE [40], TimeGAN [41,42], and a baseline without resampling. All resampling operations were performed only on the training sets. In the RUS procedure, all default (minority-class) samples were retained, while an equal number of non-default (majority-class) samples were randomly selected in each trial. In contrast, the ROS, SMOTE, tSMOTE, and TimeGAN methods adopted a two-stage procedure: the majority class was first randomly undersampled to obtain a default-to-non-default ratio of 1:2, followed by oversampling of the minority class until a default-to-non-default ratio of 1:1 was achieved. This design follows the findings of Chawla et al. [39], whose experiments demonstrated that combining undersampling with oversampling yields superior classification performance, while direct oversampling would have resulted in an impractically large dataset. For all resampling methods, the random selection of majority-class samples was independently repeated ten times to reduce the influence of randomness. The resulting ten training sets were then used to conduct ten independent experimental trials, and the final evaluation metrics were reported as the average values across these trials.

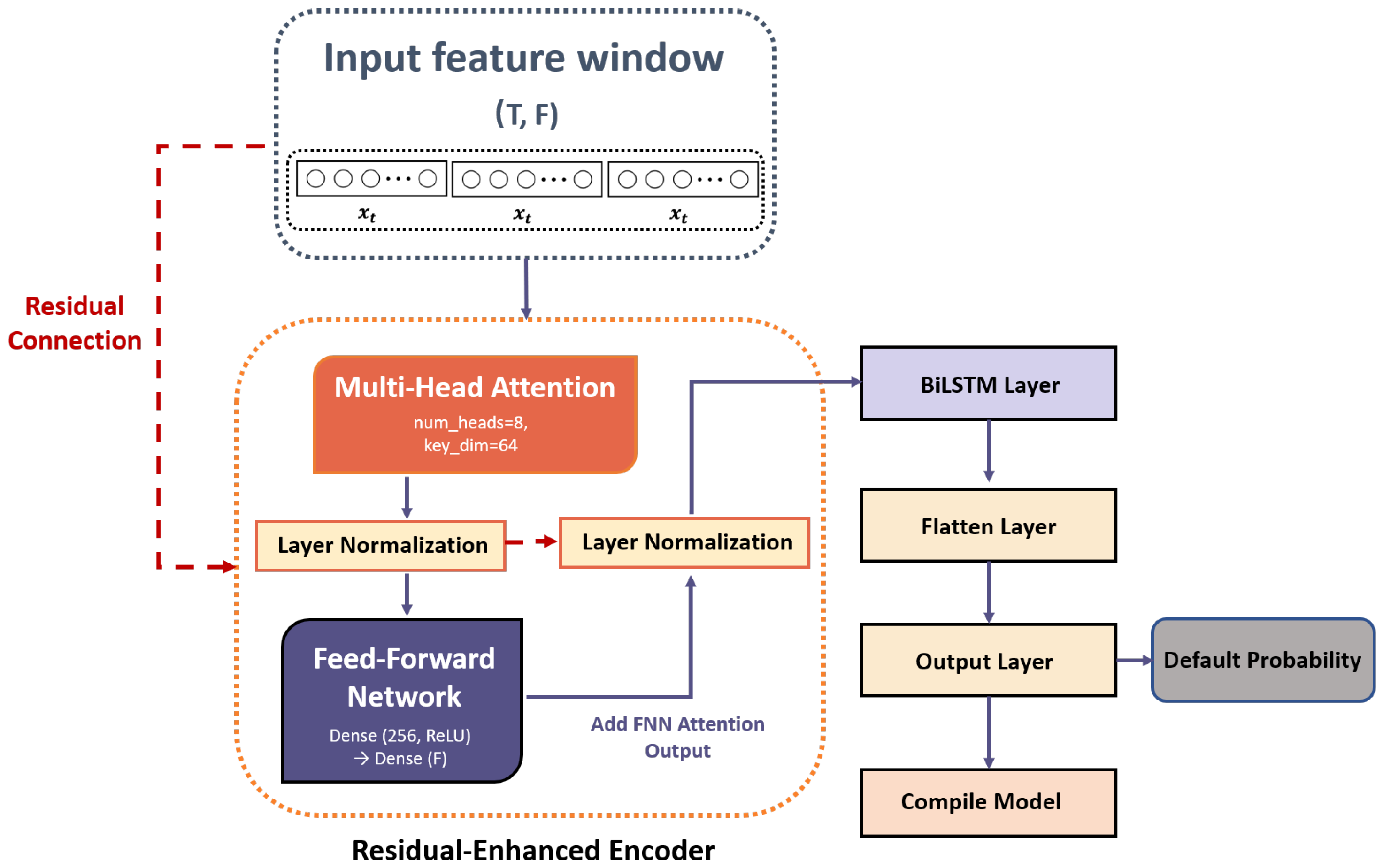
3.2. Proposed ResE-BiLSTM Model

The design of the ResE-BiLSTM model is grounded in the complementary characteristics of the Residual-enhanced Encoder (ResE) and BiLSTM in temporal representation learning. Conventional recurrent architectures (such as LSTM, BiLSTM, and GRU) can model sequential dependencies through gated mechanisms; however, due to the compression of information into hidden states, they struggle to explicitly preserve multiple long-range dependencies across time steps and features. As a result, the global contextual information that reflects the gradual accumulation of risk may become weakened or lost within the latent representations. To overcome this limitation, the residual-enhanced encoder introduces a global feature extraction mechanism based on multi-head self-attention. This structure allows each time step to directly attend to all others, thereby enabling the model to learn many-to-many temporal interactions and cross-feature dependencies without relying solely on recursive propagation [43]. The residual connections further stabilize gradient flow and preserve the original temporal signals, allowing the model to construct stable and expressive global semantics in deeper layers [44]. However, relying solely on attention mechanisms, while effective for capturing global structures, may be insufficient to characterize the local temporal continuity and direction-sensitive variations inherent in borrower behavior. Therefore, the BiLSTM is employed as a local dependency learner to refine the bidirectional sequential relationships on top of the globally contextualized embeddings, thereby enhancing fine-grained temporal order features. This global–local hybrid structure achieves hierarchical complementarity: the residual-enhanced encoder captures macro-level contextual dependencies, whereas the BiLSTM strengthens micro-level sequential dynamics and directionality.

Figure 1 illustrates the structure of the proposed ResE-BiLSTM model. As shown, the model first utilizes a multi-head attention mechanism, which serves to focus on the most relevant features within the time-series data, followed by a Feedforward Neural Network (FNN) that forms the encoder, enabling the model to learn richer representations. The output from the encoder is then passed into the BiLSTM layer, which captures both forward and backward dependencies in the time sequence. In addition to these components, the ResE-BiLSTM architecture incorporates residual connections, which help mitigate the vanishing gradient problem and enhance the flow of information across layers, improving model stability and convergence. The model handles input data of dimensions $(T,F)$, with T as the sequence length and F the number of features. The pseudocode for this model is presented in Algorithm 1, which outlines the detailed process for feature extraction, temporal dependency modeling, and prediction.

Algorithm 1: Pseudocode of the proposed ResE-BiLSTM

3.2.1. Residual-Enhanced Encoder (ResE) Layer

• Multi-Head Attention
  Multi-head attention [28] is a sophisticated attention mechanism integrating several attention processes in one model. It functions by projecting input into multiple subspaces via linear transformations with learned weight matrices. Each head processes its own transformed input independently, allowing the model to concentrate on different data aspects and grasp richer contextual details. This model utilizes a self-attention mechanism that computes attention using only the input, without external data. This method efficiently captures relationships and dependencies within the input sequence. Importantly, post-attention calculation maintains the output dimensionality consistent with the input, facilitating integration with subsequent layers.
  The query vector Q, key vector K, and value vector V are initially derived from linear transformations, with $Q=X{W}^Q$, $K=X{W}^K$, and $V=X{W}^V$, where X represents the input data and $W^Q,W^K,W^V$ are weight matrices randomly initialized. The algorithm utilizes h attention heads to derive the attention matrix $A_i$ via the scaled dot product ${\displaystyle \frac{Q_i{K}_i^T}{\sqrt{d_k}}}$, where $d_k$ denotes the key vector dimension, and subsequently employs the softmax function to produce a probability distribution. The output $Z_i$ for each attention head is derived by applying the attention weights $A_i$ to the value vector $V_i$. Finally, combining the outputs from all attention heads and projecting back into the input space with $W^O$ completes the multi-head attention layer.
• Normalization Layer and Residual Connection Mechanism
  The normalization layer follows the multi-head attention and feed-forward network to improve model stability and performance. The residual connection in layer normalization ensures balanced input and layer output contributions [45], preserving essential information from earlier layers and enabling deeper layers to learn more complex features. Moreover, the normalization layer mitigates issues like vanishing and exploding gradients through output standardization, improving training stability. It also reduces the influence of input scale variations on parameter updates, speeding up convergence and optimizing the efficiency of the training process. The normalization layer operates as follows:

  $$LN\left(x\right)={\displaystyle \frac{x-\mu }{\sqrt{{\sigma }^2+ϵ}}}\gamma +\beta$$

  (1)

  where $\mu$ represents the mean of each feature, ${\sigma }^2$ indicates their variance, $ϵ$ is a small constant (set at 1 × 10⁻⁶) to avoid division by zero, as well as $\gamma$ and $\beta$ are learnable parameters. As shown in Equation (1), layer normalization stabilizes the output distribution and improves training robustness.
  The residual connection mechanism incorporated within the ResE module plays a pivotal role in facilitating effective deep representation learning. Specifically, by introducing skip connections that directly add the input of a sub-layer (e.g., the multi-head attention or feed-forward layer) to its output prior to normalization, the model preserves the integrity of the original feature representations while enabling the training of deeper networks without degradation. This architectural design mitigates the vanishing gradient problem and ensures more stable and efficient gradient flow during backpropagation. Moreover, the integration of residual connections with layer normalization enhances the model’s capacity to learn complex temporal dependencies by stabilizing the output distributions across layers.
• Feed-Forward Network
  The feed-forward network processes each time step independently, refining and improving the fine-grained features to improve feature representation [46]. Using the ReLU activation function, the network applies non-linear transformations to capture more intricate patterns and relationships within the data. The feed-forward network in this model features two layers. The initial layer is fully connected, containing 256 neurons and employing ReLU activation. The second layer reshapes the feature dimension to match the original input, maintaining compatibility with the BiLSTM layer. The resultant output is shaped as batch size, sequence length, feature dimension. This is followed by layer normalization applied to the combined outputs of the feed-forward network and attention layer, improving stability and robustness of the model.

3.2.2. BiLSTM

BiLSTM processes time series data bidirectionally, capturing temporal relationships and contextual information [47]. Equipped with forget, input, and output gates, it selectively retains and updates information to capture dependencies, enhancing its applicability to predict loan default, where temporal patterns are crucial. Moreover, BiLSTM complements the residual-enhanced encoder by learning local time-series patterns, while the residual-enhanced encoder captures global dependencies. This combination promotes robust data representation.

The BiLSTM algorithm manages sequence processing through two states: the cell state (c) for long-term memory and the hidden state (h) for short-term context and time-step output. It operates bidirectionally over the sequence, forward from $t=1$ to $t=T$ and backward from $t=T$ to $t=1$. At each step, the hidden forward and backward states ($h_f$ and $h_b$) are concatenated to form the final output, integrating the dependencies of the past and future sequences. For process initialization, c and h of both forward LSTM ($c_f\left(0\right),h_f\left(0\right)$) and backward LSTM ($c_b(T+1),h_b(T+1)$) start as zero vectors.

• Forward LSTM Process
  The LSTM executes these operations at every time step:

  (a)

  Forget Gate

  This mechanism determines which part of the previous cell state ($c_f(t-1)$) is preserved in the cell state. The forget gate governing this mechanism is defined in Equation (2):

  $$f_t^{\left(f\right)}=\sigma (W_f^{\left(f\right)}[X_t,h_f(t-1)]+b_f^{\left(f\right)})$$

  (2)

  where $\sigma$ is the sigmoid activation function mapping values to [0, 1], $W_f^{\left(f\right)}$ represents the weights for the forward forget gate, $X_t$ is the input data, $h_f(t-1)$ denotes the prior hidden state, and $b_f^{\left(f\right)}$ is the forget gate bias.

  (b)

  Input Gate

  This operation determines the portion of current input ($X_t$) to be stored in the cell state. The input gate computation is defined by Equation (3):

  $$i_t^{\left(f\right)}=\sigma (W_i^{\left(f\right)}[X_t,h_f(t-1)]+b_i^{\left(f\right)})$$

  (3)

  where $W_i^{\left(f\right)}$ is the weights for the forward input gate, $h_f(t-1)$ is the hidden state from the preceding time step, $b_i^{\left(f\right)}$ is the bias term for the input gate.

  (c)

  Candidate Cell State

  This operation generates a candidate value (${\tilde{C}}_t^{\left(f\right)}$) for potential updates to the cell state. As specified in Equation (4), this candidate value is computed by:

  $${\tilde{C}}_t^{\left(f\right)}=tanh(W_c^{\left(f\right)}[X_t,h_f(t-1)]+b_c^{\left(f\right)})$$

  (4)

  where $W_c^{\left(f\right)}$ represents the weights for the candidate cell state, $h_f(t-1)$ is the previous time step’s hidden state, and $b_c^{\left(f\right)}$ is the bias term for the candidate cell state.

  (d)

  Output Gate

  This operation delineates the cell state fraction impacting the hidden state ($h_f\left(t\right)$). The output gate $o_t^{\left(f\right)}$ is determined by Equation (5):

  $$o_t^{\left(f\right)}=\sigma (W_o^{\left(f\right)}[X_t,h_f(t-1)]+b_o^{\left(f\right)})$$

  (5)

  where $W_o^{\left(f\right)}$ denotes the forward output gate weights, $h_f(t-1)$ is the previous hidden state, and $b_o^{\left(f\right)}$ stands for the output gate bias.

  (e)

  Updated Cell State

  The current cell state is updated by integrating information from the forget gate, input gate, and candidate cell state, as formalized in Equation (6):

  $$c_f\left(t\right)=f_t^{\left(f\right)}{c}_f(t-1)+i_t^{\left(f\right)}{\tilde{C}}_t^{\left(f\right)}$$

  (6)

  where $c_f(t-1)$ denotes the previous cell state, $f_t^{\left(f\right)}$ is the forget gate values, $i_t^{\left(f\right)}$ represents input gate values, and ${\tilde{C}}_t^{\left(f\right)}$ is the candidate cell state.

  (f)

  Updated Hidden State

  The updated hidden state $h_f\left(t\right)$ is computed by applying the output gate to the newly updated cell state, as defined in Equation (7):

  $$h_f\left(t\right)=o_t^{\left(f\right)}tanh\left(c_f\left(t\right)\right)$$

  (7)

  Following these six steps, the forward process refreshes the cell state ($c_f\left(t\right)$) and the hidden state ($h_f\left(t\right)$), producing an output ($o_t^{\left(f\right)}$) through the output gate.
• Backward LSTM Process
  The backward LSTM functions similarly, but processes in reverse, beginning from $t=T$ to $t=1$.

3.2.3. Flatten and Output Layers

The flatten layer transforms the multi-dimensional tensor output from the BiLSTM into a one-dimensional form appropriate for the fully connected layer. Subsequently, a fully connected two-layer network is used for prediction. To limit the output between [0, 1], a sigmoid activation function is used in the output layer.

3.3. Evaluation Metrics

This study uses five metrics to evaluate the ResE-BiLSTM model, including accuracy (ACC) [48], precision (PR) [49], recall (RC) [50], F1 [51], and the area under the ROC curve (AUC) [23]. Accuracy denotes the ratio of correctly predicted samples to the total number of samples, as defined in Equation (8). Precision indicates the proportion of true positives (TP) among all predicted positives (see Equation (9)). Recall, defined in Equation (10), represents the fraction of true positives successfully identified by the model. High recall aids in regulatory compliance by helping banks fully assess risks and enforce suitable controls. Recall (RC) and precision (PR) have a trade-off; increasing recall tends to reduce precision [52]. To balance precision and recall, the F1 reconciles these conflicting metrics through its formulation as the harmonic mean (see Equation (11). The AUC, ranging from 0 to 1, quantifies the model’s ability to differentiate between classes, with values near 1 indicating better performance.

The evaluation metrics are formally defined as follows:

$$\mathrm{ACC}={\displaystyle \frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FP}+\mathrm{FN}}}$$

(8)

$$\mathrm{PR}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}}$$

(9)

$$\mathrm{RC}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}}$$

(10)

$$\mathrm{F}1=2·{\displaystyle \frac{\mathrm{PR}·\mathrm{RC}}{\mathrm{PR}+\mathrm{RC}}}$$

(11)

where TP, TN, FP, and FN denote true positives, true negatives, false positives, and false negatives, respectively.

Given that different evaluation metrics might yield varying results, using a multi-metric approach ensures a comprehensive assessment of model performance. This study uses $AvgR$ [53] to evaluate overall model performance across different indicators. Models are first ranked according to their performance in ACC, PR, RC, F1, and AUC across different groups (e.g., quarterly or yearly). These rankings are then averaged to obtain the final $AvgR$ (see Section 4.3), where a lower $AvgR$ indicates better classifier performance.

4. Experiment Results Analysis

Five experiments are conducted to comprehensively evaluate the models from multiple perspectives, including the overall effects of different resampling methods across all models (Section 4.1), the influence of feature window lengths (Section 4.2), the detailed performance of the proposed ResE-BiLSTM model (Section 4.3), the ablation study (Section 4.4), and the interpretability analysis (Section 4.5).

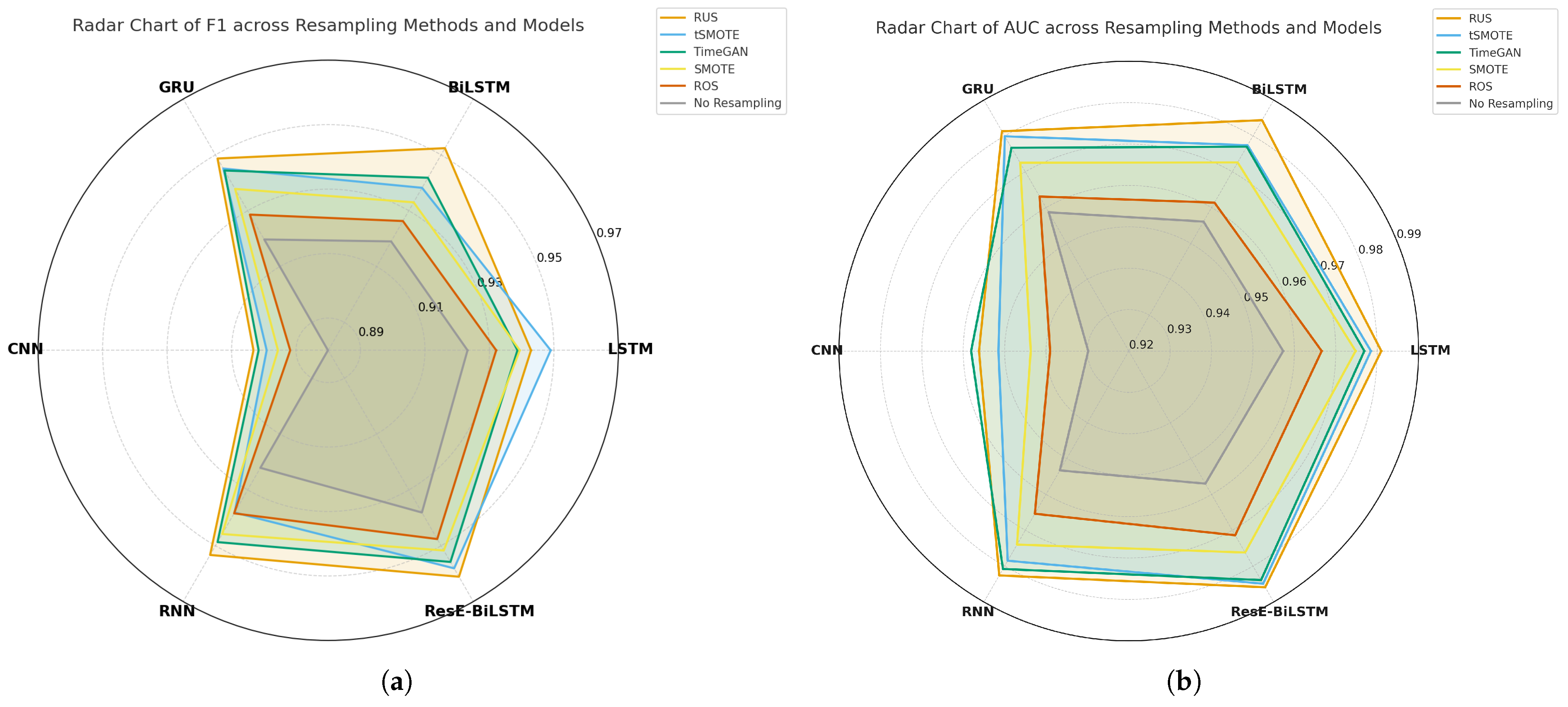
4.1. Resampling Methods Performance Analysis

To illustrate the impact of different resampling techniques on model performance, this subsection fixes the feature window lengths at 12 and 18 months, following the convention widely adopted in previous research on time series modeling. The average performance of the models is expressed by the ranking metric $Avg{R}_R$, where smaller rank values correspond to superior performance, and is defined as:

Let $\mathcal{D}$ denote the set of data cohorts ($\left|\mathcal{D}\right|=44$), $\mathcal{R}$ ($\left|\mathcal{R}\right|=6$) the set of resampling methods applied to the training set, and $\mathcal{M}$ ($\left|\mathcal{M}\right|=6$) the set of models, including one proposed model and five baselines. Let $AC{C}_{d,r,m}$, $P{R}_{d,r,m}$, $R{C}_{d,r,m}$, $F{1}_{d,r,m}$, and $AU{C}_{d,r,m}$ represent the mean accuracy, precision, recall, F1, and AUC over 10 independent trials obtained by applying resampling method $r\in \mathcal{R}$ and model $m\in \mathcal{M}$ to data cohort $d\in \mathcal{D}$. The quantities $ACC\_R_{R,M}(d,r,m)$, $PR\_R_{R,M}(d,r,m)$, $RC\_R_{R,M}(d,r,m)$, $F1\_R_{R,M}(d,r,m)$, and $AUC\_R_{R,M}(d,r,m)$ indicate their respective global rankings among all corresponding metrics computed across all resampling methods and models within each cohort. The total average ranking for data cohort d under resampling method r and model m, denoted by $Avg{R}_{R,M}(d,r,m)$, is then given as [53,54]:

$$Avg{R}_{R,M}(d,r,m)={\displaystyle \frac{ACC\_R_{R,M}(d,r,m)+PR\_R_{R,M}(d,r,m)+RC\_R_{R,M}(d,r,m)+F1\_R_{R,M}(d,r,m)+AUC\_R_{R,M}(d,r,m)}{5}}$$

(12)

where $d\in \mathcal{D}$, $r\in \mathcal{R}$, and $m\in \mathcal{M}$.

The obtained ranking values are subsequently grouped according to the resampling methods $\mathcal{R}=$ {RUS, SMOTE, TimeGAN, tSMOTE, ROS, and No Resampling}. For each resampling method $r\in \mathcal{R}$, its overall performance is quantified by averaging the rankings across all models, thereby facilitating the identification of the most generally effective method for subsequent experiments. The resulting average ranking is denoted as $Avg{R}_R$ and defined as [54]:

$$Avg{R}_R(d,r)={\displaystyle \frac{1}{\left|M\right(r\left)\right|}}\sum _{m\in M\left(r\right)}Avg{R}_{R,M}(d,r,m)$$

(13)

where $M\left(r\right)\subseteq \mathcal{M}$ denotes the subset of models evaluated under resampling method r, and $\left|M\right(r\left)\right|$ represents the number of models within this subset.

The comparative effects of different resampling techniques on the average predictive rankings of six models across 44 data cohorts are summarized in

Table 3. $Avg{R}_R(d,r)$ of the 44 data cohorts under different resampling methods when feature window length is 12 (lower values indicate better performance).

Data Cohorts	RUS	SMOTE	TimeGAN	tSMOTE	ROS	No Resampling
2009Q1	12.9	21.3	14.0	13.0	24.5	25.2
2009Q2	14.3	21.4	13.6	15.2	21.5	25.0
2009Q3	14.4	20.3	14.5	13.8	22.3	25.6
2009Q4	12.6	22.2	15.0	14.1	21.5	25.6
2010Q1	12.0	20.0	14.4	14.1	24.7	25.8
2010Q2	11.7	21.1	15.3	14.6	23.0	25.3
2010Q3	13.6	20.0	14.6	13.9	22.9	26.1
2010Q4	13.4	21.0	14.4	13.5	22.3	26.5
2011Q1	12.5	21.2	13.4	15.0	23.2	25.7
2011Q2	13.6	21.1	14.3	13.6	22.6	25.9
2011Q3	13.1	20.0	14.2	13.1	23.9	26.8
2011Q4	13.8	21.5	14.5	13.1	22.0	26.1
2012Q1	12.7	20.1	16.6	14.1	22.9	24.5
2012Q2	14.8	21.3	15.1	13.5	21.5	24.8
2012Q3	13.3	22.1	14.0	14.1	22.1	25.4
2012Q4	11.3	20.4	14.9	15.2	23.0	26.2
2013Q1	11.3	21.4	15.5	14.3	21.9	26.6
2013Q2	13.5	21.4	13.5	14.3	23.0	25.2
2013Q3	11.6	20.9	15.6	14.6	21.6	26.6
2013Q4	12.4	21.6	14.3	13.5	22.4	26.8
2014Q1	13.4	20.3	14.3	13.8	23.4	25.9
2014Q2	14.8	20.1	13.3	14.2	23.5	25.1
2014Q3	13.0	22.2	13.2	13.8	23.3	25.5
2014Q4	12.2	20.4	15.6	14.3	22.4	26.0
2015Q1	12.0	21.0	14.8	13.8	22.7	26.6
2015Q2	13.8	21.1	14.4	13.7	22.6	25.3
2015Q3	14.2	21.4	13.2	13.8	21.5	26.9
2015Q4	13.2	21.8	14.0	13.5	22.7	25.7
2016Q1	13.4	21.2	13.2	13.9	23.0	26.3
2016Q2	12.9	20.2	15.2	14.5	22.6	25.7
2016Q3	14.4	20.1	14.4	13.3	23.0	25.8
2016Q4	13.7	20.3	14.1	15.2	22.0	25.6
2017Q1	11.9	21.2	13.8	15.4	23.0	25.8
2017Q2	12.4	20.4	14.8	14.6	23.1	25.7
2017Q3	14.3	21.5	13.5	13.2	21.9	26.6
2017Q4	11.3	21.2	15.3	15.4	22.4	25.3
2018Q1	13.9	20.8	14.4	13.8	22.9	25.2
2018Q2	12.3	20.4	15.2	13.8	22.5	26.7
2018Q3	13.9	20.0	13.5	13.4	24.1	26.2
2018Q4	12.8	20.8	13.4	13.9	23.4	26.6
2019Q1	11.4	20.4	14.4	14.4	23.8	26.7
2019Q2	13.2	20.4	15.2	14.1	21.7	26.4
2019Q3	12.2	22.3	13.7	13.0	22.8	26.9
2019Q4	12.7	22.1	14.3	13.3	23.6	25.0
Average	13.0	21.0	14.3	14.0	22.8	25.9

Note: Values in bold indicate the best performance metric within each data cohort.

and

Table 4. $Avg{R}_R(d,r)$ of the 44 data cohorts under different resampling methods when feature window length is 18 (lower values indicate better performance).

Data Cohorts	RUS	SMOTE	TimeGAN	tSMOTE	ROS	No Resampling
2009Q1	8.1	19.9	12.9	13.6	25.2	31.3
2009Q2	10.6	18.6	14.2	13.7	23.7	30.1
2009Q3	6.8	19.7	12.8	12.5	26.3	32.8
2009Q4	10.0	18.8	14.2	14.1	24.1	29.8
2010Q1	6.6	19.7	12.4	12.4	26.8	33.1
2010Q2	8.5	19.1	13.4	13.4	25.1	31.4
2010Q3	9.9	18.8	13.9	14.3	24.2	29.8
2010Q4	10.1	18.5	13.7	13.8	24.1	30.9
2011Q1	10.5	19.1	14.3	14.1	23.8	29.2
2011Q2	9.2	19.4	13.7	13.7	24.4	30.7
2011Q3	11.3	18.7	14.9	14.5	22.9	28.7
2011Q4	10.5	19.6	14.3	13.7	23.8	29.2
2012Q1	11.2	19.1	14.5	14.7	22.9	28.5
2012Q2	11.1	19.0	14.7	14.3	23.2	28.7
2012Q3	10.4	18.9	14.7	14.6	23.5	28.8
2012Q4	8.4	19.6	13.1	12.9	25.3	31.8
2013Q1	10.8	19.4	14.7	14.6	23.4	28.1
2013Q2	10.5	18.7	14.3	14.0	24.0	29.6
2013Q3	11.5	19.1	14.3	14.3	23.4	28.4
2013Q4	10.3	18.8	14.2	14.6	23.9	29.2
2014Q1	10.0	19.3	13.9	13.9	23.9	29.9
2014Q2	9.8	19.2	13.4	14.0	24.7	29.9
2014Q3	7.3	19.1	13.2	13.0	25.6	32.7
2014Q4	10.5	19.0	14.1	14.2	23.7	29.6
2015Q1	11.1	19.0	14.2	14.4	23.5	28.7
2015Q2	11.4	18.5	12.5	12.3	24.8	31.5
2015Q3	9.8	18.8	14.1	14.3	24.2	29.8
2015Q4	10.1	19.3	14.1	14.5	24.0	29.1
2016Q1	10.3	18.8	14.6	14.3	23.9	29.0
2016Q2	9.5	19.0	13.7	13.4	24.4	31.1
2016Q3	9.9	19.0	14.2	14.3	23.9	29.7
2016Q4	9.4	18.4	14.3	13.5	24.3	31.0
2017Q1	9.1	19.3	13.7	14.0	24.4	30.5
2017Q2	10.4	18.8	14.3	14.4	23.8	29.4
2017Q3	12.8	19.4	12.3	12.1	24.3	30.1
2017Q4	9.3	19.1	14.3	14.0	23.9	30.4
2018Q1	7.7	19.6	13.3	13.6	25.2	31.6
2018Q2	8.9	19.2	13.8	13.2	25.2	30.7
2018Q3	11.6	19.7	11.3	12.8	25.1	30.5
2018Q4	9.4	18.7	13.9	13.4	25.0	30.5
2019Q1	8.8	19.3	13.3	12.7	25.2	31.7
2019Q2	9.5	19.5	13.2	12.2	25.3	31.4
2019Q3	9.1	19.0	13.6	13.9	24.8	30.6
2019Q4	10.6	19.4	14.2	14.6	23.8	28.4
Average	9.8	19.1	13.8	13.7	24.3	30.2

Note: Values in bold indicate the best performance metric within each data cohort.

, corresponding to feature window lengths of 12 and 18. The results indicate that, under the experimental conditions of this study, RUS consistently achieves the lowest $Avg{R}_R$ values, demonstrating superior overall performance across both window configurations. tSMOTE and TimeGAN exhibit comparable yet slightly inferior outcomes. Therefore, RUS is adopted as the resampling strategy in subsequent experiments to ensure methodological efficiency and robustness in performance evaluation.

In general, employing a feature window length of 18 results in higher evaluation scores across most data cohorts compared with a length of 12. As a representative case, Figure 2 presents radar charts of the average F1 and AUC values obtained from 10 independent trials for the six models using cohort 2019Q4, based on the 18-month feature window setting. The radar charts reveal that regardless of the resampling method applied, our proposed ResE-BiLSTM consistently outperforms the baseline models across the key evaluation metrics.

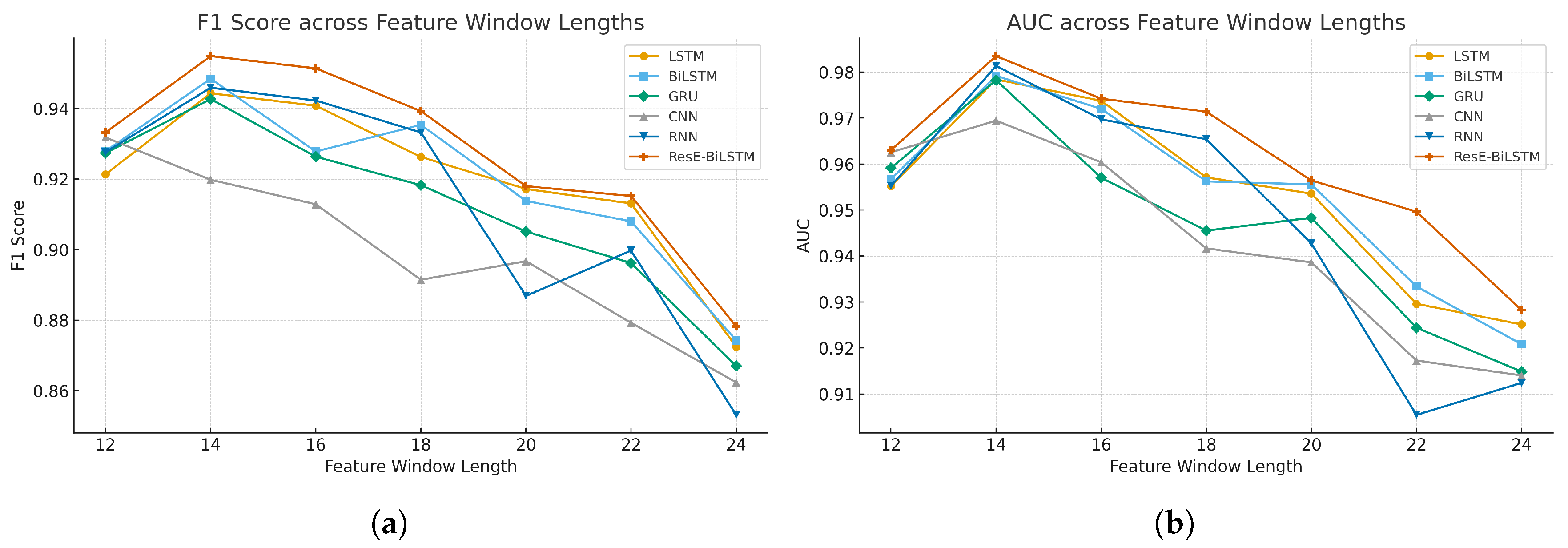
4.2. Feature Window Lengths Performance Analysis

To examine how the feature window length affects model performance, the feature window lengths are set to 12, 14, 16, 18, 20, 22, and 24 months. Each feature window serves as input to predict default events occurring within a 3-month observation period that follows a 2-month blank gap after the feature window. This analysis identifies the optimal feature window configuration for the benchmark datasets used in this study and further provides a sensitivity analysis of the models under different feature window lengths.

Let $\mathcal{L}$ represent the set of feature window lengths, where $\left|\mathcal{L}\right|=7$. The sets $\mathcal{D}$ and $\mathcal{M}$ follow the same definitions as provided in Section 4.1. For each data cohort $d\in \mathcal{D}$, feature window length $l\in \mathcal{L}$, and model $m\in \mathcal{M}$, let $AC{C}_{d,l,m}$, $P{R}_{d,l,m}$, $R{C}_{d,l,m}$, $F{1}_{d,l,m}$, and $AU{C}_{d,l,m}$ denote the mean accuracy, precision, recall, F1, and AUC values obtained from 10 independent trials. The corresponding global rankings, $ACC\_R_{L,M}(d,l,m)$, $PR\_R_{L,M}(d,l,m)$, $RC\_R_{L,M}(d,l,m)$, $F1\_R_{L,M}(d,l,m)$, and $AUC\_R_{L,M}(d,l,m)$, capture their relative positions among all feature window lengths and models within each data cohort. The overall average ranking for d, when using feature window length l and model m, is expressed as $Avg{R}_{L,M}(d,l,m)$ and defined as [53,54]:

$$Avg{R}_{L,M}(d,l,m)={\displaystyle \frac{ACC\_R_{L,M}(d,l,m)+PR\_R_{L,M}(d,l,m)+RC\_R_{L,M}(d,l,m)+F1\_R_{L,M}(d,l,m)+AUC\_R_{L,M}(d,l,m)}{5}}$$

(14)

where $d\in \mathcal{D}$, $m\in \mathcal{M}$, and $l\in \mathcal{L}$.

Afterward, the obtained ranking values are aggregated with respect to the feature window lengths defined in $\mathcal{L}$. The corresponding within-group averages are computed and denoted as $Avg{R}_L$ [54]:

$$Avg{R}_L(d,l)={\displaystyle \frac{1}{\left|M\right(l\left)\right|}}\sum _{m\in M\left(l\right)}Avg{R}_{L,M}(d,l,m)$$

(15)

where $l\in \mathcal{L}$, $M\left(l\right)\subset \mathcal{M}$ represents the subset of models applied with feature window length l, and $\left|M\right(l\left)\right|$ represents the number of models within this subset.

Table 5. $Avg{R}_L(d,l)$ of the 44 data cohorts under different feature window lengths (lower values indicate better performance).

Data Cohorts	Months
	12	14	16	18	20	22	24
2009Q1	19.7	11.8	15.2	16.5	27.5	28.7	31.1
2009Q2	22.6	8.4	13.0	18.2	24.9	27.6	35.8
2009Q3	20.3	13.2	12.9	12.4	24.4	30.2	37.1
2009Q4	18.1	10.6	13.5	15.7	25.5	27.2	39.9
2010Q1	19.5	7.6	14.2	14.8	27.8	27.8	38.8
2010Q2	18.7	11.9	14.4	14.5	24.5	27.3	39.2
2010Q3	17.5	11.6	13.3	13.4	25.7	29.6	39.4
2010Q4	18.9	14.9	13.2	17.4	24.6	27.2	34.3
2011Q1	20.8	10.8	8.7	13.4	28.2	29.5	39.1
2011Q2	17.3	11.8	12.3	17.0	27.1	30.6	34.4
2011Q3	21.5	9.4	13.9	13.8	28.2	27.8	35.9
2011Q4	21.2	8.7	12.8	12.6	27.7	28.0	39.5
2012Q1	20.5	10.7	13.3	12.8	23.9	28.0	41.3
2012Q2	21.0	10.6	11.5	18.4	25.8	28.4	34.8
2012Q3	17.8	14.3	15.7	13.6	22.8	30.6	35.7
2012Q4	21.8	9.2	12.8	15.0	26.5	29.7	35.5
2013Q1	17.5	11.8	12.5	15.9	28.2	27.8	36.8
2013Q2	19.4	9.2	8.4	18.0	27.6	27.4	40.5
2013Q3	21.6	10.5	15.2	18.3	24.6	24.1	36.2
2013Q4	21.6	11.9	14.4	9.2	24.7	27.1	41.6
2014Q1	18.8	8.3	15.4	16.5	27.9	29.5	34.1
2014Q2	17.2	11.4	11.4	18.6	27.7	29.9	34.3
2014Q3	19.2	10.7	14.9	17.8	26.1	29.9	31.9
2014Q4	21.3	12.6	12.1	14.4	25.3	27.7	37.1
2015Q1	19.2	12.8	7.7	18.9	24.2	30.6	37.1
2015Q2	19.3	8.7	15.6	17.6	24.5	31.6	33.2
2015Q3	18.3	9.5	11.7	17.9	26.8	27.8	38.5
2015Q4	20.9	10.9	15.1	12.0	24.7	27.5	39.4
2016Q1	21.8	10.6	7.7	16.2	24.3	30.9	39.0
2016Q2	17.7	12.7	8.2	16.5	27.2	30.0	38.2
2016Q3	19.0	8.7	14.6	15.1	25.6	28.0	39.5
2016Q4	20.3	9.3	12.6	17.6	26.5	28.9	35.3
2017Q1	18.7	12.5	13.7	12.4	24.3	30.4	38.5
2017Q2	18.7	11.3	13.7	12.8	25.7	31.3	37.0
2017Q3	19.9	12.4	13.7	17.9	28.4	29.8	28.4
2017Q4	17.7	12.1	9.5	13.7	25.3	29.2	43.0
2018Q1	17.3	11.6	13.5	14.2	27.6	29.0	37.3
2018Q2	20.1	9.0	11.5	15.3	26.1	28.2	40.3
2018Q3	20.2	12.2	14.6	18.2	27.2	31.7	26.4
2018Q4	19.9	11.5	14.4	14.5	24.4	27.4	38.4
2019Q1	20.7	10.7	15.2	12.1	25.8	27.3	38.7
2019Q2	20.4	11.9	11.4	15.9	27.6	27.1	36.2
2019Q3	18.7	7.6	12.4	18.0	27.1	29.8	36.9
2019Q4	19.3	12.7	13.4	13.7	26.4	28.7	36.3
Average	19.6	10.9	12.8	15.4	26.1	28.8	36.9

Note: Values in bold indicate the best performance metric within each data cohort.

presents the $Avg{R}_L(d,l)$ values of 44 data cohorts under different feature window lengths, reflecting the average performance across all models. Lower values indicate better performance. Overall, shorter to medium-length feature windows (12–18 months) generally yield higher predictive accuracy, while longer windows tend to result in performance degradation. Among these, the 14-month feature window performs best across most cohorts, achieving the lowest average $Avg{R}_L$ values and demonstrating an optimal balance between feature richness and noise suppression. Specifically, in 31 out of 44 data cohorts (approximately 70.5%), the 14-month feature window produces the minimum $Avg{R}_L(d,l)$ value. Based on this empirical finding, the subsequent experimental analyses adopt the 14-month feature window as the representative configuration for further model comparison and performance evaluation.

To provide a clearer visualization of how different feature window lengths affect model performance, Figure 3 illustrates the variation of average F1 and AUC values over 10 independent trials using the 2019Q3 dataset. Across all tested window lengths, the proposed ResE-BiLSTM consistently achieves superior performance on both metrics, exhibiting smoother trends that indicate higher robustness to temporal span variation. When the feature window extends from 12 to 14 months, all models reach their performance peaks, suggesting that this range captures sufficient behavioral and temporal information for accurate prediction. However, as the window length further increases (16–24 months), performance declines across all models, particularly for RNN and CNN, which are more sensitive to temporal noise. This degradation arises because overly long windows incorporate outdated behavioral patterns, diluting the relevance of recent credit risk signals. In contrast, the ResE-BiLSTM benefits from residual enhancement and bidirectional temporal learning, enabling it to retain long-term dependencies while mitigating the impact of historical noise.

4.3. ResE-BiLSTM Model Performance Analysis

Based on the optimal resampling method (RUS) identified in Section 4.1 and the optimal feature window length verified in Section 4.2,

Table A1. Accuracy of 6 models on 44 cohorts of the Freddie Mac dataset based on average results from 10 trials.

Cohort	LSTM [8]	BiLSTM [12]	GRU [56]	CNN [57]	RNN [58]	ResE-BiLSTM
2009Q1	0.918	0.913	0.914	0.892	0.914	0.923
2009Q2	0.895	0.880	0.887	0.897	0.883	0.921
2009Q3	0.914	0.914	0.915	0.911	0.919	0.924
2009Q4	0.926	0.924	0.945	0.906	0.937	0.924
2010Q1	0.939	0.935	0.938	0.935	0.940	0.946
2010Q2	0.901	0.900	0.903	0.887	0.901	0.913
2010Q3	0.909	0.919	0.913	0.893	0.911	0.922
2010Q4	0.899	0.900	0.896	0.911	0.910	0.890
2011Q1	0.925	0.933	0.927	0.904	0.924	0.903
2011Q2	0.922	0.921	0.919	0.895	0.920	0.923
2011Q3	0.922	0.929	0.935	0.896	0.910	0.906
2011Q4	0.920	0.916	0.912	0.886	0.920	0.925
2012Q1	0.904	0.890	0.905	0.875	0.919	0.894
2012Q2	0.830	0.817	0.827	0.848	0.855	0.863
2012Q3	0.911	0.910	0.911	0.863	0.902	0.913
2012Q4	0.948	0.953	0.949	0.935	0.947	0.954
2013Q1	0.878	0.878	0.884	0.868	0.865	0.916
2013Q2	0.926	0.931	0.923	0.889	0.913	0.932
2013Q3	0.893	0.890	0.897	0.857	0.885	0.909
2013Q4	0.914	0.914	0.910	0.887	0.924	0.930
2014Q1	0.921	0.915	0.924	0.886	0.927	0.931
2014Q2	0.918	0.917	0.912	0.885	0.918	0.924
2014Q3	0.931	0.933	0.924	0.919	0.927	0.935
2014Q4	0.875	0.865	0.862	0.869	0.884	0.891
2015Q1	0.896	0.885	0.879	0.892	0.910	0.913
2015Q2	0.911	0.912	0.904	0.890	0.903	0.916
2015Q3	0.926	0.930	0.924	0.894	0.914	0.931
2015Q4	0.927	0.936	0.928	0.884	0.928	0.908
2016Q1	0.913	0.920	0.916	0.886	0.919	0.927
2016Q2	0.908	0.909	0.913	0.886	0.913	0.923
2016Q3	0.912	0.901	0.909	0.879	0.907	0.915
2016Q4	0.930	0.925	0.934	0.913	0.940	0.941
2017Q1	0.927	0.925	0.923	0.902	0.929	0.933
2017Q2	0.921	0.918	0.910	0.897	0.909	0.930
2017Q3	0.916	0.916	0.914	0.883	0.914	0.923
2017Q4	0.925	0.925	0.923	0.901	0.923	0.930
2018Q1	0.937	0.936	0.937	0.915	0.935	0.939
2018Q2	0.928	0.926	0.925	0.899	0.923	0.934
2018Q3	0.930	0.930	0.930	0.911	0.932	0.935
2018Q4	0.919	0.923	0.922	0.900	0.926	0.927
2019Q1	0.926	0.924	0.923	0.907	0.927	0.930
2019Q2	0.932	0.930	0.927	0.923	0.937	0.942
2019Q3	0.944	0.949	0.943	0.921	0.946	0.951
2019Q4	0.951	0.941	0.947	0.903	0.953	0.955

Note: Values in bold indicate the best performance metric within each data cohort.

,

Table A2. Precision of 6 models on 44 cohorts of the Freddie Mac dataset based on average results from 10 trials.

Cohort	LSTM [8]	BiLSTM [12]	GRU [56]	CNN [57]	RNN [58]	ResE-BiLSTM
2009Q1	0.950	0.949	0.945	0.950	0.950	0.951
2009Q2	0.897	0.881	0.892	0.901	0.885	0.953
2009Q3	0.921	0.919	0.922	0.925	0.922	0.927
2009Q4	0.964	0.951	0.965	0.959	0.964	0.956
2010Q1	0.978	0.980	0.977	0.974	0.982	0.983
2010Q2	0.895	0.893	0.900	0.888	0.904	0.915
2010Q3	0.894	0.919	0.911	0.896	0.917	0.920
2010Q4	0.923	0.921	0.915	0.970	0.954	0.919
2011Q1	0.929	0.928	0.935	0.915	0.915	0.862
2011Q2	0.969	0.973	0.976	0.934	0.985	0.988
2011Q3	0.941	0.935	0.954	0.949	0.908	0.902
2011Q4	0.940	0.925	0.919	0.945	0.956	0.935
2012Q1	0.893	0.863	0.893	0.859	0.923	0.863
2012Q2	0.785	0.770	0.783	0.807	0.816	0.828
2012Q3	0.920	0.919	0.916	0.851	0.932	0.933
2012Q4	0.985	0.985	0.983	0.971	0.979	0.990
2013Q1	0.854	0.852	0.862	0.879	0.834	0.911
2013Q2	0.981	0.987	0.978	0.922	0.981	0.980
2013Q3	0.869	0.865	0.877	0.829	0.855	0.903
2013Q4	0.919	0.913	0.918	0.901	0.937	0.920
2014Q1	0.931	0.917	0.939	0.883	0.946	0.948
2014Q2	0.930	0.929	0.925	0.931	0.944	0.936
2014Q3	0.952	0.950	0.939	0.945	0.945	0.949
2014Q4	0.850	0.834	0.827	0.872	0.870	0.874
2015Q1	0.875	0.854	0.847	0.892	0.905	0.901
2015Q2	0.925	0.923	0.919	0.922	0.913	0.936
2015Q3	0.932	0.938	0.926	0.890	0.912	0.936
2015Q4	0.931	0.946	0.935	0.910	0.940	0.941
2016Q1	0.928	0.935	0.928	0.905	0.961	0.941
2016Q2	0.916	0.928	0.927	0.887	0.921	0.941
2016Q3	0.915	0.893	0.907	0.881	0.904	0.929
2016Q4	0.950	0.939	0.954	0.933	0.971	0.958
2017Q1	0.955	0.941	0.938	0.934	0.955	0.957
2017Q2	0.926	0.913	0.898	0.927	0.894	0.939
2017Q3	0.943	0.944	0.941	0.925	0.942	0.947
2017Q4	0.956	0.957	0.950	0.927	0.959	0.961
2018Q1	0.977	0.975	0.976	0.943	0.979	0.963
2018Q2	0.958	0.953	0.957	0.914	0.955	0.963
2018Q3	0.968	0.963	0.965	0.939	0.970	0.964
2018Q4	0.915	0.927	0.923	0.903	0.938	0.940
2019Q1	0.957	0.956	0.958	0.932	0.958	0.947
2019Q2	0.911	0.909	0.904	0.926	0.922	0.931
2019Q3	0.940	0.953	0.940	0.930	0.949	0.967
2019Q4	0.940	0.918	0.929	0.897	0.949	0.953

Note: Values in bold indicate the best performance metric within each data cohort.

,

Table A3. Recall rate of 6 models on 44 cohorts of the Freddie Mac dataset based on average results from 10 trials.

Cohort	LSTM [8]	BiLSTM [12]	GRU [56]	CNN [57]	RNN [58]	ResE-BiLSTM
2009Q1	0.883	0.872	0.880	0.829	0.874	0.883
2009Q2	0.892	0.880	0.881	0.892	0.879	0.896
2009Q3	0.905	0.909	0.907	0.894	0.915	0.921
2009Q4	0.886	0.894	0.923	0.849	0.908	0.889
2010Q1	0.898	0.889	0.897	0.894	0.896	0.908
2010Q2	0.910	0.909	0.906	0.887	0.897	0.911
2010Q3	0.929	0.918	0.916	0.891	0.905	0.934
2010Q4	0.870	0.876	0.873	0.847	0.861	0.856
2011Q1	0.921	0.938	0.918	0.892	0.936	0.961
2011Q2	0.873	0.866	0.860	0.851	0.854	0.874
2011Q3	0.902	0.923	0.915	0.837	0.914	0.912
2011Q4	0.897	0.907	0.905	0.820	0.880	0.914
2012Q1	0.917	0.927	0.922	0.900	0.913	0.937
2012Q2	0.914	0.907	0.908	0.916	0.919	0.922
2012Q3	0.900	0.899	0.905	0.881	0.868	0.912
2012Q4	0.910	0.920	0.914	0.897	0.913	0.928
2013Q1	0.912	0.914	0.915	0.854	0.912	0.922
2013Q2	0.869	0.873	0.865	0.851	0.843	0.883
2013Q3	0.925	0.926	0.925	0.900	0.928	0.917
2013Q4	0.909	0.915	0.900	0.870	0.908	0.941
2014Q1	0.910	0.912	0.908	0.891	0.905	0.913
2014Q2	0.903	0.904	0.897	0.831	0.890	0.910
2014Q3	0.909	0.913	0.907	0.891	0.907	0.920
2014Q4	0.911	0.912	0.917	0.866	0.902	0.919
2015Q1	0.924	0.928	0.929	0.894	0.916	0.932
2015Q2	0.895	0.898	0.887	0.853	0.891	0.899
2015Q3	0.918	0.921	0.921	0.898	0.917	0.926
2015Q4	0.923	0.925	0.921	0.853	0.915	0.931
2016Q1	0.895	0.902	0.902	0.863	0.873	0.904
2016Q2	0.898	0.888	0.896	0.886	0.903	0.890
2016Q3	0.909	0.911	0.913	0.877	0.911	0.897
2016Q4	0.909	0.909	0.913	0.891	0.906	0.923
2017Q1	0.897	0.906	0.906	0.867	0.901	0.907
2017Q2	0.916	0.924	0.925	0.864	0.927	0.930
2017Q3	0.885	0.884	0.884	0.833	0.882	0.896
2017Q4	0.891	0.890	0.893	0.871	0.885	0.907
2018Q1	0.896	0.894	0.896	0.884	0.889	0.908
2018Q2	0.895	0.896	0.891	0.882	0.889	0.903
2018Q3	0.890	0.894	0.892	0.879	0.891	0.904
2018Q4	0.923	0.918	0.920	0.896	0.913	0.923
2019Q1	0.892	0.888	0.885	0.878	0.895	0.911
2019Q2	0.957	0.957	0.957	0.920	0.955	0.958
2019Q3	0.948	0.944	0.946	0.910	0.942	0.942
2019Q4	0.964	0.969	0.968	0.910	0.957	0.970

Note: Values in bold indicate the best performance metric within each data cohort.

,

Table A4. Binary F1 of 6 models on 44 cohorts of the Freddie Mac dataset based on average results from 10 trials.

Cohort	LSTM [8]	BiLSTM [12]	GRU [56]	CNN [57]	RNN [58]	ResE-BiLSTM
2009Q1	0.915	0.909	0.911	0.885	0.910	0.916
2009Q2	0.894	0.880	0.886	0.896	0.882	0.924
2009Q3	0.913	0.914	0.914	0.909	0.919	0.924
2009Q4	0.923	0.921	0.943	0.900	0.935	0.921
2010Q1	0.936	0.932	0.935	0.932	0.937	0.944
2010Q2	0.902	0.901	0.903	0.887	0.900	0.913
2010Q3	0.911	0.918	0.914	0.893	0.911	0.927
2010Q4	0.896	0.898	0.894	0.904	0.905	0.886
2011Q1	0.925	0.933	0.926	0.903	0.925	0.909
2011Q2	0.918	0.916	0.914	0.890	0.915	0.927
2011Q3	0.921	0.929	0.934	0.889	0.911	0.907
2011Q4	0.918	0.916	0.911	0.877	0.916	0.924
2012Q1	0.905	0.894	0.907	0.878	0.918	0.898
2012Q2	0.844	0.833	0.840	0.858	0.864	0.873
2012Q3	0.910	0.909	0.911	0.865	0.899	0.922
2012Q4	0.946	0.951	0.947	0.932	0.945	0.958
2013Q1	0.882	0.882	0.887	0.866	0.871	0.917
2013Q2	0.921	0.927	0.918	0.885	0.907	0.929
2013Q3	0.896	0.894	0.900	0.863	0.890	0.910
2013Q4	0.914	0.914	0.909	0.885	0.922	0.930
2014Q1	0.920	0.915	0.923	0.887	0.925	0.930
2014Q2	0.916	0.916	0.911	0.878	0.916	0.923
2014Q3	0.930	0.932	0.922	0.917	0.925	0.934
2014Q4	0.879	0.871	0.869	0.869	0.886	0.896
2015Q1	0.899	0.890	0.885	0.892	0.910	0.916
2015Q2	0.909	0.910	0.903	0.886	0.902	0.917
2015Q3	0.925	0.929	0.923	0.894	0.914	0.931
2015Q4	0.927	0.935	0.928	0.880	0.927	0.936
2016Q1	0.911	0.918	0.914	0.884	0.915	0.922
2016Q2	0.907	0.907	0.911	0.886	0.912	0.915
2016Q3	0.912	0.902	0.910	0.879	0.907	0.913
2016Q4	0.929	0.924	0.933	0.911	0.938	0.940
2017Q1	0.925	0.923	0.922	0.898	0.927	0.931
2017Q2	0.921	0.918	0.911	0.894	0.910	0.935
2017Q3	0.913	0.913	0.911	0.876	0.911	0.921
2017Q4	0.922	0.922	0.921	0.898	0.920	0.933
2018Q1	0.934	0.933	0.934	0.913	0.931	0.935
2018Q2	0.925	0.924	0.923	0.897	0.921	0.932
2018Q3	0.927	0.927	0.927	0.908	0.929	0.933
2018Q4	0.919	0.922	0.922	0.899	0.925	0.931
2019Q1	0.923	0.921	0.920	0.904	0.925	0.928
2019Q2	0.934	0.932	0.930	0.923	0.938	0.944
2019Q3	0.944	0.948	0.943	0.920	0.945	0.954
2019Q4	0.952	0.943	0.948	0.903	0.953	0.961

Note: Values in bold indicate the best performance metric within each data cohort.

and

Table A5. AUC values of 6 models on 44 cohorts of the Freddie Mac dataset based on average results from 10 trials.

Cohort	LSTM [8]	BiLSTM [12]	GRU [56]	CNN [57]	RNN [58]	ResE-BiLSTM
2009Q1	0.968	0.967	0.969	0.954	0.964	0.971
2009Q2	0.955	0.956	0.958	0.952	0.948	0.969
2009Q3	0.970	0.971	0.969	0.966	0.971	0.972
2009Q4	0.977	0.976	0.980	0.963	0.979	0.972
2010Q1	0.985	0.983	0.983	0.977	0.985	0.986
2010Q2	0.957	0.958	0.961	0.946	0.955	0.963
2010Q3	0.970	0.970	0.968	0.957	0.964	0.972
2010Q4	0.963	0.965	0.952	0.975	0.957	0.955
2011Q1	0.972	0.975	0.970	0.962	0.972	0.974
2011Q2	0.973	0.973	0.975	0.964	0.979	0.981
2011Q3	0.967	0.969	0.971	0.960	0.964	0.966
2011Q4	0.968	0.966	0.965	0.958	0.971	0.973
2012Q1	0.968	0.967	0.970	0.943	0.972	0.966
2012Q2	0.930	0.925	0.930	0.928	0.943	0.945
2012Q3	0.969	0.971	0.968	0.938	0.965	0.974
2012Q4	0.975	0.976	0.979	0.973	0.979	0.981
2013Q1	0.956	0.959	0.960	0.931	0.955	0.962
2013Q2	0.977	0.977	0.978	0.959	0.977	0.979
2013Q3	0.958	0.958	0.959	0.938	0.951	0.960
2013Q4	0.968	0.968	0.967	0.949	0.972	0.974
2014Q1	0.969	0.968	0.970	0.949	0.972	0.973
2014Q2	0.970	0.970	0.967	0.948	0.972	0.977
2014Q3	0.968	0.970	0.965	0.964	0.970	0.971
2014Q4	0.952	0.951	0.946	0.932	0.949	0.953
2015Q1	0.961	0.958	0.957	0.948	0.964	0.966
2015Q2	0.962	0.962	0.960	0.949	0.959	0.963
2015Q3	0.966	0.965	0.963	0.948	0.960	0.967
2015Q4	0.971	0.972	0.971	0.946	0.970	0.965
2016Q1	0.957	0.965	0.965	0.948	0.965	0.969
2016Q2	0.952	0.950	0.952	0.944	0.953	0.949
2016Q3	0.959	0.955	0.960	0.939	0.956	0.958
2016Q4	0.966	0.964	0.967	0.960	0.971	0.971
2017Q1	0.960	0.960	0.960	0.952	0.962	0.970
2017Q2	0.960	0.962	0.959	0.945	0.959	0.963
2017Q3	0.958	0.960	0.957	0.938	0.959	0.964
2017Q4	0.963	0.964	0.962	0.946	0.961	0.973
2018Q1	0.969	0.970	0.969	0.960	0.971	0.972
2018Q2	0.967	0.966	0.966	0.953	0.967	0.969
2018Q3	0.965	0.967	0.967	0.956	0.969	0.973
2018Q4	0.970	0.969	0.969	0.959	0.971	0.973
2019Q1	0.975	0.973	0.974	0.968	0.978	0.978
2019Q2	0.980	0.980	0.979	0.972	0.980	0.983
2019Q3	0.978	0.979	0.978	0.969	0.981	0.983
2019Q4	0.984	0.980	0.982	0.956	0.983	0.986

Note: Values in bold indicate the best performance metric within each data cohort.

in the Appendix A display the average performance of the six models on five metrics, based on 10 independent trials per cohort. The analysis reveals that although individual model performance varied across cohorts, ResE-BiLSTM consistently outperformed the other models on all metrics.

ResE-BiLSTM achieved the highest accuracy in 38 cohorts, or 86.36% of the total, clearly outperforming other models, highlighting the ability of ResE-BiLSTM to capture complex features. In contrast, models such as BiLSTM and GRU showed the best performance in two cohorts, and other models achieved the highest performance in two cohorts. Furthermore, ResE-BiLSTM led in precision, with the highest precision in 26 cohorts, representing 59.09% of the total, compared to LSTM, BiLSTM, GRU, CNN and RNN, which outperformed in 1, 3, 4, 1 and 9 cohorts respectively.

ResE-BiLSTM achieved the highest recall in 37 cohorts, highlighting its effectiveness in reducing false negatives. Furthermore, it achieved the highest F1 in 39 out of 44 cohorts (88.64%), showing an excellent precision-recall balance. The results of the AUC demonstrated that ResE-BiLSTM maintained high true positive rates and low false positive rates in 36 cohorts.

4.3.1. AvgR Performance Analysis

The sets $\mathcal{D}$ and $\mathcal{M}$ follow the same definitions as provided in Section 4.1. For each data cohort $d\in \mathcal{D}$ and model $m\in \mathcal{M}$, let $AC{C}_{d,m}$, $P{R}_{d,m}$, $R{C}_{d,m}$, $F{1}_{d,m}$, and $AU{C}_{d,m}$ denote the mean accuracy, precision, recall, F1, and AUC values obtained from 10 independent trials. $ACC\_R_M(d,m)$, $PR\_R_M(d,m)$, $RC\_R_M(d,m)$, $F1\_R_M(d,m)$, and $AUC\_R_M(d,m)$ denote the rank of model m among all models in $\mathcal{M}$ with respect to accuracy, precision, recall, F1, and AUC, respectively. Lower ranks indicate better performance. The overall average ranking of model m in cohort d is defined as [53,54]:

$$Avg{R}_M(d,m)={\displaystyle \frac{ACC\_R_M(d,m)+PR\_R_M(d,m)+RC\_R_M(d,m)+F1\_R_M(d,m)+AUC\_R_M(d,m)}{5}}$$

(16)

where $d\in \mathcal{D}$, and $m\in \mathcal{M}$.

Table 6. Summary of the overall average ranking $Avg{R}_M(d,m)$ for model m within each cohort (lower values indicate better performance).

Quarter	LSTM	BiLSTM	GRU	CNN	RNN	ResE-BiLSTM
2009Q1	2.2	4.8	3.4	5.4	4.2	1
2009Q2	3	5.2	3.6	2.8	5.4	1
2009Q3	4.8	4	3.8	5.2	2.2	1
2009Q4	3.4	4.2	1	5.6	2	4.8
2010Q1	2.8	4.8	4.2	5.6	2.6	1
2010Q2	3.2	4	2.6	6	4.2	1
2010Q3	4	2.2	3.6	5.8	4.4	1
2010Q4	3.4	2.6	4.8	2.2	2.6	5.4
2011Q1	3.4	1.6	3	5.4	3.6	4
2011Q2	3.2	3.4	4	6	3.4	1
2011Q3	3.4	2.2	1.2	5.2	4.2	4.8
2011Q4	2.8	3.8	4.8	5.2	2.6	1.6
2012Q1	3	4	2.4	6	1.8	3.8
2012Q2	4	6	4.6	3.4	2	1
2012Q3	3	3.6	3	5.8	4.6	1
2012Q4	4.2	2.4	3.2	6	4.2	1
2013Q1	3.6	3.8	2.2	5	5.4	1
2013Q2	3.4	2.2	3.8	5.8	4.2	1.6
2013Q3	3	3.6	2.4	6	4.2	1.8
2013Q4	3.6	3.2	4.8	6	2.2	1.2
2014Q1	3.8	4.4	3.2	6	2.6	1
2014Q2	3	3.8	5	5.4	2.6	1.2
2014Q3	2.8	2.2	5.2	5.6	3.8	1.4
2014Q4	3.2	4	4.8	4.8	3.2	1
2015Q1	3.4	4.4	5	4.6	2.4	1.2
2015Q2	2.6	2.4	4.4	5.6	5	1
2015Q3	3	2	3.8	6	5	1.2
2015Q4	4	1.4	3	6	3.8	2.8
2016Q1	4.6	2.6	3.8	6	2.8	1.2
2016Q2	3.8	3.8	2.8	6	2	2.4
2016Q3	2.4	4.4	2.2	6	3.8	2.2
2016Q4	4	4.6	2.8	6	2.4	1.2
2017Q1	3.6	3.4	4.6	6	2.4	1
2017Q2	3	3.2	4	5.2	4.6	1
2017Q3	3	2.4	4.4	6	4.2	1
2017Q4	3.2	2.6	4	6	4.2	1
2018Q1	2.4	3.8	3.4	6	3.6	1.8
2018Q2	2.4	3.4	4	6	4.2	1
2018Q3	3.6	3.8	3.8	6	2.2	1.6
2018Q4	4	3.6	3.8	6	2.6	1
2019Q1	3	4.2	4	6	2	1.8
2019Q2	3.2	3.8	4.8	5.2	3	1
2019Q3	3.6	2.4	4.2	6	3	1.8
2019Q4	3	4.4	3.8	6	2.8	1

Note: Values in bold indicate the best performance metric within each data cohort.

shows the $Avg{R}_M(d,m)$ for each model in five evaluation metrics for 44 data cohorts. The ResE-BiLSTM model significantly outperforms other models, obtaining the top ranking in 37 of 44 cohorts. In contrast, although other models perform well on specific cohorts, their overall rankings are particularly lower. Specifically, BiLSTM, GRU, and RNN have the highest average rank in two cohorts each, CNN in one, and none for LSTM.

4.3.2. Ranking Performance Grouped by Year

Cohorts within the same year, while independently collected, can be effectively grouped by year for model performance evaluation. This approach is valid since all four cohorts from the same year are likely to be affected by similar social and market conditions. Factors such as macroeconomic trends, policy shifts, and industry-specific cycles may similarly influence data across these cohorts. By analyzing data from one year collectively, this study gains a more complete assessment of model performance stability throughout the entire year, rather than examining each quarter separately.

Using the year as a grouping unit helps mitigate the effects of seasonal variations, unexpected events, and short-term economic changes that could impact the independence of cohorts, thus improving the robustness and generalizability of the model analysis. In finance, model stability and adaptability across years are crucial due to the significant fluctuations in financial markets and economic activities. The aggregation of yearly data avoids overemphasis on fluctuations in a single quarter, offering a more suitable evaluation of the performance of the model. This approach supports a more comprehensive performance assessment, reducing the influence of individual quarter volatility.

For each data cohort $d\in \mathcal{D}$ and model $m\in \mathcal{M}$, let $AC{C}_{d,m}$, $P{R}_{d,m}$, $R{C}_{d,m}$, $F{1}_{d,m}$, and $AU{C}_{d,m}$ denote the mean accuracy, precision, recall, F1, and AUC values obtained from 10 independent trials. The average ranking method enables a hierarchical evaluation process, in which cohort-level results are first grouped annually and then ranked within each group. Specifically, the 44 quarterly cohorts are derived from 11 consecutive years, with four cohorts per year and six models evaluated under five metrics (accuracy, precision, recall, F1, and AUC). For a given year Y and a given metric, all 24 values (4 cohorts × 6 models) are ranked, such that the rank value represents the relative position of a model within these 24 results for that year and metric, where a lower rank indicates better performance. Subsequently, for each model m, the average of its four quarterly rankings within year Y is computed to obtain the annual ranking under each metric, denoted as $ACC\_R_M(Y,m)$, $PR\_R_M(Y,m)$, $RC\_R_M(Y,m)$, $F1\_R_M(Y,m)$, and $AUC\_R_M(Y,m)$ respectively. Finally, the overall average ranking of model m in year Y is determined by averaging its annual rankings across the five metrics, as defined below [54]:

$$Avg{R}_M(Y,m)={\displaystyle \frac{ACC\_R_M(Y,m)+PR\_R_M(Y,m)+RC\_R_M(Y,m)+F1\_R_M(Y,m)+AUC\_R_M(Y,m)}{5}}$$

(17)

where $m\in \mathcal{M}$, $Y\in \mathcal{Y}=\{$2009, …, 2019}.

Table 7. Summary of the annual average ranking $Avg{R}_M(Y,m)$ for model m in year Y (lower values indicate better performance).

Year	LSTM	BiLSTM	GRU	CNN	RNN	ResE-BiLSTM
2009	12.10	14.10	11.65	17.30	12.40	7.45
2010	12.15	11.80	12.70	15.70	12.35	10.30
2011	10.75	9.55	10.55	20.20	12.25	11.65
2012	12.50	12.80	12.10	16.45	11.80	9.35
2013	12.15	11.40	11.80	19.40	13.20	7.05
2014	11.85	12.40	13.95	18.55	11.40	6.85
2015	11.30	9.95	12.75	20.65	12.90	7.45
2016	12.60	12.70	10.70	20.25	10.65	8.05
2017	11.05	10.75	13.70	21.75	12.60	5.15
2018	11.45	11.80	12.20	21.60	11.60	6.35
2019	11.10	12.45	12.80	20.85	10.15	7.65

Note: Values in bold indicate the best performance metric within each data cohort.

presents the relative performance ranking of six models in different years grouped from the 44 cohorts. The results reveal that ResE-BiLSTM outperformed the other models in 10 of 11 years, accounting for 90.91% of the total years. In contrast, while models such as BiLSTM displayed strong performance in some individual years, they generally exhibited lower performance compared to ResE-BiLSTM. This highlights the good consistency of the proposed ResE-BiLSTM model in delivering high performance in different annual cohorts.

4.3.3. Wilcoxon Signed-Rank Tests

To further substantiate the empirical finding that ResE-BiLSTM ranks first in most cohorts, non-parametric statistical significance tests are conducted to determine whether its superiority over the two best-performing baseline models (LSTM and BiLSTM) is statistically significant. The Wilcoxon signed-rank test [55] is employed for this comparison using the two key evaluation metrics, F1 and AUC. One-sided tests are performed, with the null hypothesis stating that the proposed ResE-BiLSTM exhibits equal or worse performance compared to the baseline models, while the alternative hypothesis posits that the ResE-BiLSTM model performs better. A small p-value indicates a statistically significant difference between the two models, with the significance level set to $\alpha =0.005$. Each cohort was tested independently, and the proportion of significant results was reported as evidence of consistency, rather than as multiple evaluations of a single overarching hypothesis; therefore, no cross-cohort corrections for the family-wise error rate or the false discovery rate were applied.

Table 8. Wilcoxon signed-rank test results (p-values) for comparing ResE-BiLSTM with the baseline models LSTM and BiLSTM. Values in bold indicate statistical significance at the 0.5% significance level.

Data Cohort	p-Value for F1		p-Value for AUC
	LSTM	BiLSTM	LSTM	BiLSTM
2009Q1	4.12$\times {10}^{-1}$	2.68$\times {10}^{-2}$	2.28$\times {10}^{-1}$	5.87$\times {10}^{-1}$
2009Q2	$\mathbf{6.84} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{9.77} \times {\mathbf{10}}^{-\mathbf{4}}$	$\mathbf{2.49} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.10} \times {\mathbf{10}}^{-\mathbf{3}}$
2009Q3	$\mathbf{3.24} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{2.47} \times {\mathbf{10}}^{-\mathbf{3}}$	1.98$\times {10}^{-2}$	1.14$\times {10}^{-2}$
2009Q4	7.40$\times {10}^{-1}$	3.21$\times {10}^{-1}$	6.25$\times {10}^{-1}$	4.85$\times {10}^{-1}$
2010Q1	$\mathbf{2.91} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{4.11} \times {\mathbf{10}}^{-\mathbf{3}}$	1.33$\times {10}^{-1}$	2.88$\times {10}^{-1}$
2010Q2	$\mathbf{4.62} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{2.18} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{4.74} \times {\mathbf{10}}^{-\mathbf{3}}$	9.33$\times {10}^{-3}$
2010Q3	$\mathbf{2.89} \times {\mathbf{10}}^{-\mathbf{3}}$	2.28$\times {10}^{-1}$	3.60$\times {10}^{-2}$	2.28$\times {10}^{-1}$
2010Q4	5.12$\times {10}^{-1}$	6.18$\times {10}^{-1}$	7.40$\times {10}^{-1}$	8.32$\times {10}^{-1}$
2011Q1	6.25$\times {10}^{-1}$	3.60$\times {10}^{-2}$	9.83$\times {10}^{-2}$	5.20$\times {10}^{-2}$
2011Q2	$\mathbf{1.68} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{9.77} \times {\mathbf{10}}^{-\mathbf{4}}$	$\mathbf{9.77} \times {\mathbf{10}}^{-\mathbf{4}}$	$\mathbf{1.60} \times {\mathbf{10}}^{-\mathbf{3}}$
2011Q3	3.60$\times {10}^{-1}$	3.28$\times {10}^{-1}$	2.28$\times {10}^{-1}$	3.60$\times {10}^{-2}$
2011Q4	$\mathbf{2.05} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{3.29} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{2.61} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.42} \times {\mathbf{10}}^{-\mathbf{3}}$
2012Q1	4.85$\times {10}^{-1}$	6.25$\times {10}^{-1}$	4.12$\times {10}^{-1}$	3.60$\times {10}^{-2}$
2012Q2	$\mathbf{2.14} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{4.81} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{3.41} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{9.77} \times {\mathbf{10}}^{-\mathbf{4}}$
2012Q3	$\mathbf{1.86} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{4.03} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{4.82} \times {\mathbf{10}}^{-\mathbf{3}}$	1.01$\times {10}^{-1}$
2012Q4	$\mathbf{1.39} \times {\mathbf{10}}^{-\mathbf{3}}$	7.24$\times {10}^{-3}$	$\mathbf{1.93} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{4.28} \times {\mathbf{10}}^{-\mathbf{3}}$
2013Q1	$\mathbf{2.74} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{4.57} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{3.44} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.18} \times {\mathbf{10}}^{-\mathbf{3}}$
2013Q2	$\mathbf{3.05} \times {\mathbf{10}}^{-\mathbf{3}}$	8.21$\times {10}^{-2}$	3.60$\times {10}^{-2}$	4.85$\times {10}^{-1}$
2013Q3	$\mathbf{2.63} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.41} \times {\mathbf{10}}^{-\mathbf{3}}$	4.91$\times {10}^{-1}$	2.28$\times {10}^{-1}$
2013Q4	$\mathbf{1.58} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.02} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.24} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.72} \times {\mathbf{10}}^{-\mathbf{3}}$
2014Q1	3.60$\times {10}^{-2}$	$\mathbf{2.28} \times {\mathbf{10}}^{-\mathbf{3}}$	1.01$\times {10}^{-2}$	$\mathbf{4.33} \times {\mathbf{10}}^{-\mathbf{3}}$
2014Q2	5.47$\times {10}^{-3}$	6.41$\times {10}^{-3}$	$\mathbf{3.18} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{2.24} \times {\mathbf{10}}^{-\mathbf{3}}$
2014Q3	2.24$\times {10}^{-2}$	1.51$\times {10}^{-2}$	2.17$\times {10}^{-2}$	1.83$\times {10}^{-2}$
2014Q4	$\mathbf{2.06} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.42} \times {\mathbf{10}}^{-\mathbf{3}}$	7.36$\times {10}^{-3}$	5.57$\times {10}^{-3}$
2015Q1	$\mathbf{1.13} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{4.22} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.21} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.07} \times {\mathbf{10}}^{-\mathbf{3}}$
2015Q2	$\mathbf{3.29} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{2.87} \times {\mathbf{10}}^{-\mathbf{3}}$	2.38$\times {10}^{-2}$	1.64$\times {10}^{-2}$
2015Q3	$\mathbf{1.99} \times {\mathbf{10}}^{-\mathbf{3}}$	8.91$\times {10}^{-2}$	1.28$\times {10}^{-2}$	1.09$\times {10}^{-3}$
2015Q4	$\mathbf{1.82} \times {\mathbf{10}}^{-\mathbf{3}}$	1.06$\times {10}^{-2}$	7.53$\times {10}^{-1}$	6.76$\times {10}^{-1}$
2016Q1	2.28$\times {10}^{-1}$	6.25$\times {10}^{-1}$	$\mathbf{2.548} \times {\mathbf{10}}^{-\mathbf{3}}$	1.01$\times {10}^{-1}$
2016Q2	$\mathbf{3.61} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{4.12} \times {\mathbf{10}}^{-\mathbf{3}}$	1.01$\times {10}^{-1}$	4.61$\times {10}^{-1}$
2016Q3	3.22$\times {10}^{-2}$	$\mathbf{2.44} \times {\mathbf{10}}^{-\mathbf{3}}$	3.59$\times {10}^{-1}$	1.95$\times {10}^{-1}$
2016Q4	$\mathbf{2.57} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.91} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{4.28} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{4.95} \times {\mathbf{10}}^{-\mathbf{3}}$
2017Q1	9.71$\times {10}^{-2}$	$\mathbf{2.18} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{2.07} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.43} \times {\mathbf{10}}^{-\mathbf{3}}$
2017Q2	$\mathbf{1.92} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.25} \times {\mathbf{10}}^{-\mathbf{3}}$	1.86$\times {10}^{-2}$	1.52$\times {10}^{-2}$
2017Q3	3.41$\times {10}^{-2}$	7.13$\times {10}^{-2}$	$\mathbf{2.95} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.88} \times {\mathbf{10}}^{-\mathbf{3}}$
2017Q4	$\mathbf{2.49} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.33} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.62} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.11} \times {\mathbf{10}}^{-\mathbf{3}}$
2018Q1	5.20$\times {10}^{-2}$	6.80$\times {10}^{-2}$	4.91$\times {10}^{-2}$	6.39$\times {10}^{-2}$
2018Q2	$\mathbf{2.71} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.93} \times {\mathbf{10}}^{-\mathbf{3}}$	2.12$\times {10}^{-2}$	$\mathbf{4.57} \times {\mathbf{10}}^{-\mathbf{3}}$
2018Q3	$\mathbf{1.64} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.08} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.26} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.02} \times {\mathbf{10}}^{-\mathbf{3}}$
2018Q4	$\mathbf{2.36} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.79} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{4.34} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{4.17} \times {\mathbf{10}}^{-\mathbf{3}}$
2019Q1	2.85$\times {10}^{-2}$	2.23$\times {10}^{-2}$	1.58$\times {10}^{-2}$	$\mathbf{4.13} \times {\mathbf{10}}^{-\mathbf{3}}$
2019Q2	$\mathbf{1.42} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.03} \times {\mathbf{10}}^{-\mathbf{3}}$	1.12$\times {10}^{-2}$	9.77$\times {10}^{-3}$
2019Q3	$\mathbf{1.27} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{1.86} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{3.05} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{2.98} \times {\mathbf{10}}^{-\mathbf{3}}$
2019Q4	$\mathbf{4.12} \times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{3.25} \times {\mathbf{10}}^{-\mathbf{3}}$	2.08$\times {10}^{-2}$	$\mathbf{3.44} \times {\mathbf{10}}^{-\mathbf{3}}$

reports the results of the Wilcoxon signed-rank tests comparing ResE-BiLSTM with the top two baseline models, LSTM and BiLSTM, using F1 and AUC as evaluation metrics. The results demonstrate that ResE-BiLSTM achieves statistically significant improvements ($p<0.005$) in 32 out of 44 cohorts (72.7%) for F1 and 23 out of 44 cohorts (52.3%) for AUC. When comparing against LSTM alone, significant superiority is observed in 65.9% of cohorts for F1 and 43.2% for AUC, while against BiLSTM, the significance rates are 61.4% and 45.5%, respectively. At the 0.5% significance level, these results indicate that the null hypothesis, which states that ResE-BiLSTM performs no better than the baseline models, can be rejected with 99.5% confidence in the majority of cases. The consistently low p-values suggest that the observed performance improvements are unlikely to have occurred by chance, demonstrating the robustness and generalizability of the proposed model’s superiority across different data cohorts.

4.4. Ablation Study

An ablation study was conducted to evaluate the behavior of ResE-BiLSTM by excluding specific components. Four model variations were created: M1 omits the residual connection mechanism, M2 omits the feedforward network, M3 omits the residual-enhanced encoder, and M4 removes the bidirectional feature of the BiLSTM. Data were grouped by merging three-year periods into cohorts, minimizing previous partition bias and ensuring generalizability of the results.

Table 9. Overview evaluation of ablation study performance with proposed ResE-BiLSTM, E-BiLSTM, A-BiLSTM, BiLSTM, and LSTM.

Cohort	Metrics	ResE-BiLSTM	E-BiLSTM (M1)	A-BiLSTM (M2)	BiLSTM (M3)	LSTM (M4)
2009; 2010; 2011	Accuracy	0.9283	0.9151	0.7514	0.9121	0.9040
	Precision	0.9614	0.9493	0.9451	0.9467	0.9534
	Recall	0.8917	0.8670	0.5347	0.8734	0.8497
	F1	0.9252	0.9063	0.6812	0.9085	0.8984
	AUC	0.9709	0.9618	0.8702	0.9614	0.9594
2012; 2013; 2014	Accuracy	0.9311	0.9184	0.7460	0.9086	0.9079
	Precision	0.9317	0.9191	0.7421	0.8930	0.8957
	Recall	0.9404	0.9267	0.7750	0.9286	0.9234
	F1	0.9360	0.9229	0.7535	0.9104	0.9093
	AUC	0.9724	0.9612	0.8475	0.9577	0.9556
2015; 2016; 2017	Accuracy	0.9203	0.9050	0.7047	0.8933	0.8882
	Precision	0.8945	0.8843	0.6839	0.8811	0.8696
	Recall	0.9312	0.9184	0.7763	0.9094	0.9132
	F1	0.9125	0.9010	0.7241	0.8950	0.8909
	AUC	0.9678	0.9572	0.8101	0.9561	0.9549
2018; 2019; 2020	Accuracy	0.9331	0.9196	0.7950	0.9154	0.9120
	Precision	0.9791	0.9687	0.9599	0.9579	0.9579
	Recall	0.8671	0.8496	0.6967	0.8325	0.8257
	F1	0.9197	0.9052	0.8074	0.8908	0.8869
	AUC	0.9736	0.9619	0.9059	0.9593	0.9599

concisely presents the results of the ablation study, demonstrating that all the variations of the model underperformed compared to the ResE-BiLSTM model.

The ResE-BiLSTM model consistently achieves an accuracy of over 92% across all cohorts. In contrast, E-BiLSTM (M1) shows slightly lower performance, indicating that removing the residual connections has some impact on overall performance, but it is not a decisive factor. A-BiLSTM (M2) exhibits the most significant performance drop, suggesting that the feedforward neural network (FNN) plays a more critical role in enhancing the model’s predictive capability. Although the M2 model incorporates an attention mechanism on BiLSTM, the absence of the FNN support leads to the attention output failing to effectively convert into discriminative features. Instead, it may increase the focus on noise or the majority class, resulting in worse performance compared to the basic BiLSTM and LSTM models. This phenomenon emphasizes the importance of the collaborative relationship between modules in this task.

Moreover, ResE-BiLSTM demonstrates excellent precision, recall, and F1 across all cohorts, validating the effectiveness of its structural design. E-BiLSTM (M1) shows a performance decline after the removal of residual connections, especially in recall, indicating that residual connections play a significant role in capturing deep temporal information and improving the recognition of the minority class. In contrast, A-BiLSTM (M2) experiences a more drastic performance drop after the removal of the feedforward neural network (FNN), with an average recall decrease of 23.48% across the four cohorts, highlighting the critical importance of FNN in enhancing feature discriminability. Although BiLSTM and LSTM, which do not incorporate residual or feedforward structures, show relatively stable performance, they consistently fall short of ResE-BiLSTM in terms of all evaluation metrics.

Overall, the ablation study results indicate that each key component in the ResE-BiLSTM structure plays an irreplaceable role in model performance. Removing any of these modules leads to performance degradation across various dimensions, providing crucial insights for structural optimization in future model design.

4.5. Interpretability Performance Analysis

4.5.1. Barplot Analysis

Figure A1a–f in the Appendix A show SHAP barplots for the proposed ResE-BiLSTM and five baseline models, ranked over 238 features. These barplots are derived from the third cohort in the ablation study, covering years 2015 to 2017. The barplots reveal that the models prioritize different features with varying emphasis on their temporal order.

Table 10. The number of months each feature appears in the top 50 feature importance rankings (up to a maximum of 14).

Feature	ResE-BiLSTM	BiLSTM	LSTM	GRU	RNN	CNN
Interest Bearing UPB-Delta	14	14	14	14	14	14
Current Actual UPB-Delta	14	14	14	14	14	14
Estimated Loan to Value (ELTV)	12	11	14	14	11	14
Borrower Assistance Status Code_F	3	3	4	3	3	-
Delinquency Due To Disaster_Y	4	3	3	2	3	-
Current Deferred UPB	3	3	-	3	4	8
Delinquency Due To Disaster_NAN	-	1	-	-	1	-
Borrower Assistance Status Code_NAN	-	1	-	-	-	-
Current Interest Rate	-	-	1	-	-	-

presents the number of months each feature appears among the top 50 in feature importance rankings. The findings indicate variations in feature emphasis in all six models, which explain the differences in their contributions.

For the ResE-BiLSTM model, six key features consistently rank among the top-50 over 14 months. Features such as Interest Bearing UPB-Delta, Current Actual UPB-Delta, and Estimated Loan to Value (ELTV) were significant for 14 months, 14 months and 12 months, respectively, making up 80% of these top features, with no direct relation between feature importance and time. In contrast, the BiLSTM model identifies eight features in the top 50, with Interest Bearing UPB-Delta prominent for 14 months. Unlike ResE-BiLSTM, BiLSTM ranks feature importance chronologically, generally decreasing from recent to past months, with minor fluctuations in some months.

The difference in temporal feature importance between the ResE-BiLSTM and BiLSTM models arises from their distinct emphases in modeling temporal dependencies. In the ResE-BiLSTM, the attention mechanism is responsible for discovering long-range correlations, while the residual connections ensure the preservation of distant information, an advantage that the BiLSTM architecture lacks. Specifically, the residual-enhanced encoder employs multi-head self-attention to establish pairwise associations and dynamic weighting across the entire temporal dimension, enabling the model to recognize both distant and recent key signals simultaneously. For example, the model can concurrently focus on early-stage variations in the ELTV and recent changes in Current Actual UPB or Interest Bearing UPB, thereby linking long-term asset risk with short-term repayment pressure. The residual connections further preserve the original temporal cues, preventing early features from being completely diluted in deeper representations. This not only stabilizes gradient flow numerically but also reshapes the temporal attention distribution mechanistically. In this structure, each layer’s output is added to the original input, allowing the attention mechanism to repeatedly leverage earlier temporal signals when redistributing weights. Through this mechanism, the attention pattern along the timeline becomes less monotonic and often exhibits a flatter or even bimodal form, reinforcing the model’s responsiveness to both distant and recent time steps. In other words, the model learns to dynamically revisit distant periods, transitioning from a short-term recency bias toward a more globally balanced focus on both long- and short-term signals.

In the LSTM model, six features are most prominent, with Interest Bearing UPB-Delta, Current Actual UPB-Delta, and ELTV consistently appearing over 14 months, making up 84% of the top 50 features. Unlike ResE-BiLSTM, the Current Actual UPB-Delta was identified as the most significant feature. The GRU model highlights six features, similar to the ResE-BiLSTM model, where the importance of the feature is not linearly related to the time order in both models. However, the GRU’s ranking of feature importance over time is more unpredictable and lacks a consistent pattern. Moreover, the GRU prioritizes Current Actual UPB-Delta over Interest Bearing UPB-Delta.

The results of the RNN model are the same as those of the GRU model, with the current actual UPB-Delta as the key feature. However, the ranking of feature importance throughout the sequence varies from the GRU model, showing less regularity. In contrast, the CNN model concentrates on four features, highlighting Interest Bearing UPB-Delta as most significant. For all six models, Interest Bearing UPB-Delta, Current Actual UPB-Delta, and ELTV are the most significant features. Line charts showing how feature importance evolves across months are presented in Figure 4a–c for further analysis. The horizontal axis represents the month index, where each value corresponds to a specific month (e.g., 14 indicates the 14th month, which is the month closest to the observation period in our experimental setting), while the vertical axis shows the feature importance in the top 50 rankings, where 50 signifies the most important feature.

For Interest Bearing UPB-Delta, the ResE-BiLSTM and GRU models indicate that data from both distant and recent times are important for predictions, whereas intermediate periods are less significant. In contrast, the BiLSTM and CNN models show a nearly linear decrease in feature importance from recent to past data. In contrast, the LSTM and RNN models demonstrate a variable pattern without consistent changes in the importance of the features.

For Current Actual UPB-Delta, all six models show a double-peak pattern in feature importance over time, initially decreasing from recent to distant points, then rising and falling again. This pattern suggests that both recent and distant data may contain meaningful signals. Interestingly, in the GRU and CNN models, feature importance starts to increase at the month 8 (6 months before the most recent point), while in other models, this rise begins at the month 5 (9 months earlier).

For ELTV, the general importance of the features over the 14 months is less than the previous two features, usually ranking in the bottom half of the top 50 with mild month-to-month variation. Besides the CNN model, the other five models show lower feature importance in the mid-periods, increasing at both timeline extremes. Moreover, the evaluation of the importance of the features in different models reveals similar trends in similar time frames.

4.5.2. SHAP Summary Plot Analysis

The SHAP summary plot (Figure A2a–f in Appendix A) depicts the influence and significance of each feature on the model outcome, both positively and negatively. The distribution of positions and colors reveals how variations in feature values affect prediction results. Specifically, each dot represents a sample, with the vertical stacking of dots indicating sample density. The horizontal position corresponds to the SHAP value of the feature, which reflects the magnitude and direction of the feature’s contribution to the model prediction. The vertical axis ranks features based on the sum of SHAP values across all samples, following the same order as in the bar plot. A SHAP value positioned further to the right indicates a stronger positive contribution to the prediction, while values further to the left indicate a stronger negative contribution. A larger horizontal spread signifies that the range of the feature’s values has a more significant impact on the model’s predictions. The color coding represents the magnitude of the feature values, with red indicating higher values and blue indicating lower values.

The findings demonstrate that the lower values of Interest Bearing UPB-Delta and Current Actual UPB-Delta significantly improve the model computation, while the lower value of ELTV negatively impacts it, as the blue dots are concentrated on the negative side (left). Furthermore, five models (besides the CNN model) displayed varying patterns, suggesting that these features may impact positively or negatively based on the model. Moreover, the CNN model uniquely assessed the significance of these two features. The CNN model’s differing assessment of the importance of these two key features may explain why its performance is inferior to that of the other models.

The six models also differ in how they assess the impact of ELTV on prediction outcomes. The ResE-BiLSTM model indicates that ELTV has a dual effect, sometimes exerting minimal influence. For BiLSTM and LSTM models, ELTV’s impact fluctuates, potentially due to the sensitivity of the time series data or shifts in its relationship with the prediction target over time. For features of lesser importance, such as Delinquency due to Disaster_Y, all models similarly evaluate their contribution. Likewise, Current Deferred UPB exhibited both positive and negative impacts across models. Thus, these features are not the main factors differentiating model performance.

In summary, the different models show variation in their assessments of feature importance, and the impact of features on prediction results changes over time. The differences in model responses and the assessment of feature importance reveal the models’ varying abilities to capture feature complexity and time-series characteristics.

5. Conclusions and Discussion

This study addresses loan default prediction by introducing the ResE-BiLSTM model, which consistently outperforms baseline models in accuracy, precision, recall, F1, and AUC across most cohorts, demonstrating the effectiveness of combining the residual-enhanced encoder and BiLSTM components in capturing complex temporal dependencies and improving prediction accuracy. The interpretability analysis examines the significance of features and their temporal variations, providing insight into the model’s internal mechanisms and guiding future optimization.

5.1. Theoretical Implications

From a theoretical perspective, this study builds upon prior research on time-series-based financial anomaly detection, such as the works of Chen et al. [23], Agarwal et al. [25], and Boussougou and Park [30], by clarifying how a residual-enhanced encoder modifies the temporal focus of conventional recurrent architectures in modeling sequential financial data. Previous studies demonstrated that BiLSTM and attention mechanisms could improve predictive performance but rarely explained the underlying reason for such improvement. This study contributes new theoretical insight by showing that the residual-enhanced encoder reshapes temporal attention through residual information flow, allowing the model to revisit and preserve distant information that traditional recurrent models tend to underemphasize. The SHAP-based interpretability analysis further supports this finding by revealing a flatter or dual-peaked temporal importance pattern in ResE-BiLSTM, indicating that both distant and recent time steps contribute meaningfully to risk assessment. This explains why the proposed model achieves more balanced temporal representation and stronger predictive stability in credit risk modeling.

5.2. Practical Implications

From a practical perspective, the ResE-BiLSTM provides a data-driven framework that can be directly applied to post-loan default prediction for financial institutions. The model can dynamically identify the evolution of repayment risks within loan portfolios and reveal how the temporal importance of key repayment features such as Current Actual UPB, Interest Bearing UPB, and ELTV changes over time. This helps institutions determine when risk signals are most pronounced, enabling the optimization of early-warning thresholds and repayment adjustment strategies. The model demonstrates stable performance across different feature window lengths and resampling settings, indicating its adaptability to class imbalance and the variability of financial environments. Banks and other lending institutions can incorporate this model into their monitoring systems for long-term loans to enhance borrower risk tracking, reduce non-performing loans, and improve overall asset quality. Moreover, practitioners can extend the model by incorporating additional features that reflect product- or region-specific characteristics, thereby improving its suitability for different credit products and market contexts.

5.3. Research Limitations

Despite the positive outcomes achieved, certain limitations should be acknowledged. The analysis in this study is based on the Freddie Mac Single-Family Loan-Level dataset, which primarily contains records of U.S. residential mortgage loans. This dataset features long-term, monthly panel data that reflect loan structures secured by single-family housing assets with fixed or adjustable interest rates. Such data typically exhibit relatively stable repayment patterns, consistent borrower characteristics, and transparent reporting standards, which are representative of the U.S. mortgage market but may not adequately capture the characteristics of other forms of consumer or commercial credit.

These characteristics may constrain the model’s direct applicability to other loan products, such as small business loans or credit card portfolios. In these contexts, borrowing behavior is often influenced by short-term cash flow fluctuations, revolving credit limits, and heterogeneous financing purposes. Compared with residential mortgages, these credit products are driven more by transactional dynamics and liquidity conditions than by collateral value or long-term contractual obligations. Consequently, the temporal dependency patterns learned from mortgage data provide a transferable modeling framework for other credit domains, though practical applications may require appropriate adjustments based on product-specific characteristics. For example, the temporal window length and observation intervals could be redefined according to the repayment cycle and data availability of the target loan type. At the model level, retraining or fine-tuning on domain-specific data could help adapt the model to new temporal dependency structures. At the feature level, incorporating variables that better reflect domain-specific risk characteristics, such as cash flow indicators in small business lending or transaction frequency and credit utilization in credit card data, would further enhance the model’s ability to capture product-specific risk dynamics.

Furthermore, the Freddie Mac dataset reflects the regulatory environment, institutional framework, and macroeconomic conditions specific to the U.S. housing finance system. Differences in legal structures, credit scoring practices, and market maturity across countries suggest that applying the model to other geographical markets would require recalibration or fine-tuning based on local economic structures and risk characteristics. For example, this may involve adjusting the feature window length or redistributing feature weights using local loan data to account for differences in borrower behavior patterns, repayment cycles, interest rate policies, and default triggers. In addition, incorporating locally relevant variables, such as regional economic indices or sectoral indicators, could further enhance the model’s ability to capture market-specific risk dynamics.

5.4. Directions for Future Research

Future research could therefore extend this work by validating the model’s transferability across multiple datasets and credit products to evaluate its robustness and adaptability under diverse lending conditions. However, such cross-market validation is often constrained by limited data availability. Due to privacy and confidentiality concerns, relevant datasets in many countries are not publicly disclosed, which restricts the practical feasibility of future research. Hence, financial institutions are encouraged to share properly anonymized datasets with researchers to facilitate advances in credit risk modeling and promote broader academic–industry collaboration in this field.

In addition, this study primarily addresses class imbalance at the data level. Model-level techniques, such as cost-sensitive learning and class weighting, have not yet been incorporated and could be explored in future work to further enhance model robustness under imbalanced conditions. Building on these directions, future research will focus on developing more efficient architectures for real-time anomaly detection and mitigating the negative effects of concept drift. These efforts aim to assist financial institutions in identifying high-risk borrowers, minimizing non-performing loans, and ultimately improving asset quality and financial stability.