Interest as the Engine: Leveraging Diverse Hybrid Propagation for Influence Maximization in Interest-Based Social Networks

Abstract

Influence maximization is a crucial research domain in social network analysis, playing a vital role in optimizing information dissemination and managing online public opinion. Traditional IM models focus on network topology, often overlooking user heterogeneity and server-driven propagation dynamics, which often leads to limited model adaptability. To overcome these shortcomings, this study proposes the “Social–Interest Hybrid Influence Maximization” (SIHIM) problem, which explicitly models the joint influence of social topology and user interest in server-mediated propagation, aiming to enhance the effectiveness of information propagation by integrating users’ social relationships and interest preferences. To model this problem, we develop a Server-Based Independent Cascading (SB-IC) model that captures the dynamics of influence propagation. Based on this model, we further propose a novel hybrid centrality algorithm named Pascal Centrality (PaC), which integrates both topological and interest-based attributes to efficiently identify key seed nodes while minimizing influence overlap. Experimental evaluations on ten real-world social network datasets demonstrate that PaC improves influence spread by 5.22% under the standard IC model and by 7.04% under the SB-IC model, outperforming nine state-of-the-art algorithms. These findings underscore the effectiveness and adaptability of the proposed algorithm in complex scenarios.

1. Introduction

In recent years, with the rapid development of the internet, social networks have gradually become an important platform for information dissemination and social interaction [1]. The Influence Maximization (IM) problem is one of the hottest research directions in the field of social networks [2]. The concept of the IM problem originated from viral marketing, where companies rewarded influential users to encourage them to promote products within their social circles. The objective of this problem is to select the most influential users in the network as seed nodes to maximize the scope of information dissemination, thereby achieving broader information diffusion and more effective marketing promotion [3].

Domingos and Richardson’s seminal [4] work established the foundation for Influence Maximization by introducing the concept of “expected network value.” This expanded the view of customer value beyond independent attributes to include social influence, and they utilized a Markov random field model to formalize and maximize this combined value. This work laid the ideological foundation for influence maximization. Building upon this, Kempe et al. [5] were the first to formally define the Influence Maximization (IM) problem as a discrete optimization problem. In their study, they systematically analyzed and popularized the Independent Cascade (IC) model and the Linear Threshold (LT) model, establishing them as the theoretical cornerstone of the field. The intellectual roots of the LT model, in particular, can be traced back to the earlier work of Granovetter [6] on collective behavior. Furthermore, Kempe et al. [5] proved that the IM problem is NP-hard under both the IC and LT models. Additionally, IM research has drawn upon classic propagation models from epidemiology, such as the SIR and SIS models [7]. These models were originally developed to describe the spread of infectious diseases, but their underlying concepts and methodologies have been widely adopted in studies of influence propagation.

Traditional IM methods primarily rely on users’ social networks, specifically analyzing the friendship relationships between users to identify nodes with greater influence. Common methods include greedy algorithms [5,8,9,10,11,12,13,14,15], heuristic methods [16,17,18,19,20,21,22,23,24,25,26,27], and others. Kempe et al. [5] first proposed a greedy algorithm called Greedy, which constructs a seed set by progressively selecting the most influential nodes. However, this method has high computational complexity. To improve computational efficiency, Leskovec et al. [8] and Goyal et al. [9] proposed the CELF and CELF++ methods, respectively. Although these methods enhance computational efficiency to some extent, they remain unsuitable for large-scale networks. Consequently, researchers have introduced various computationally efficient heuristic centrality metrics from network analysis, such as degree centrality [16], K-Shell [17], and closeness centrality [18], for the rapid and approximate identification of high-influence nodes. These centrality-based approaches can efficiently locate nodes with high centrality values; however, they often fail to account for interactions between nodes and struggle to avoid the influence overlap problem. Additionally, methods such as graph neural networks [28,29,30], reinforcement learning [31,32], and community detection [2] have been partially utilized by some scholars in IM problem research.

Traditional IM problems typically treat nodes in a network as homogeneous in their reception of information, regardless of content, ignoring differences in users’ interest preferences. However, this simplifying assumption often has limitations in practical applications, as users’ interest preferences significantly influence the efficiency and scope of influence spreading. In recent years, to more accurately model real-world information propagation mechanisms, researchers have increasingly focused on IM problems incorporating users’ interest preferences. Currently, IM research, which integrates users’ interest, primarily focuses on the Topic-aware Influence Maximization (TIM) problem [33,34,35,36,37,38,39,40,41,42]. TIM optimizes the information dissemination process by introducing users’ preferences for different topics, making dissemination strategies more aligned with users’ actual needs and interests. Additionally, Li et al. [33] proposed an influence maximization problem based on interest coverage maximization, aiming to enhance the overall influence spreading by maximizing the coverage of users’ interests. However, existing research primarily focuses on word-of-mouth dissemination patterns between users, neglecting the influence propagation generated by Servers in Interest-Based Social Networks (ISNs) through interest-based content recommendations.

In traditional social networks, information dissemination typically follow a word-of-mouth pattern among acquaintances; only direct user-to-user ties are taken into account. ISNs, by contrast, allow users to be influenced not only by their immediate social neighbors but also by like-minded others with whom they share no direct connection. By leveraging individuals’ interest preferences, these platforms recommend content favored by users with similar interests, thereby substantially accelerating information diffusion, enriching its modalities, and delivering content that more precisely matches users’ interests. For example, in ISNs like BiliBili and TikTok, users may share information about a particular topic with their friends because they are interested in it. At the same time, Servers also recommend topics to users based on their interests. This dissemination mechanism breaks through the limitations of traditional networks, where users must engage in direct interaction with one another. As a result, existing solutions to IM problems are unable to accurately simulate the information dissemination process in ISNs.

The research on Influence Maximization primarily encompasses two aspects: the design of propagation models and the design of Influence Maximization algorithms. Focusing on the scope of this paper, we need to address the following problems:

• How to define an information propagation model within ISNs. This model must be capable of modeling not only the information propagation between users but also the platform’s interest-based information delivery to users.
• How to design an Influence Maximization algorithm suitable for ISNs. This algorithm needs to select a set of highly influential nodes in the Interest-driven Social Network while also mitigating the influence overlap problem as much as possible.

Based on the above background, this study defines the problem of maximizing influence in ISN as the “Social–Interest Hybrid Influence Maximization Problem” (SIHIM) and models the influence propagation process in ISNs as the Server-Based Independent Cascade (SB-IC) model. Meanwhile, we innovatively propose an effective method for identifying influential nodes in ISNs using centrality, namely PaC (Pascal Centrality). Specifically, the main contributions of this study are as follows:

• We first define the SIHIM problem, considering influence propagation under both “node–node” and “Server–node” mechanisms. We prove that its objective function is monotonic and submodular and that influence estimation for this problem is NP-hard.
• We design a propagation model named Server-Based Independent Cascade (SB-IC), which fully considers the impact of users’ interest characteristics on influence propagation. This enables more accurate modeling of the information propagation process in ISNs.
• We propose a new IM algorithm called PaC. This method fully considers the multi-attribute characteristics of nodes, thereby accurately identifying influential nodes in the network while effectively avoiding the problem of influence overlap between nodes.
• We conducted extensive experiments on ten real-world datasets, comparing our proposed algorithm with several recent high-performance algorithms. The results demonstrate that our algorithm achieved an average improvement in influence spreading by 5.22% and 7.04% on the IC model and SB-IC model, respectively, compared to the other nine comparison algorithms.

The remainder of this paper is organized as follows. Section 2 reviews the related work. Section 3 presents the problem definition of SIHIM and the proposed SB-IC model. Section 4 details the PaC algorithm. Section 5 reports the experimental results and analysis. Finally, Section 6 concludes the paper and discusses future research.

2. Related Work

In this section, we provide a brief overview of the relevant work on solutions to IM problems, including greedy-based methods, heuristic-based methods, and Influence maximization with users’ interests.

2.1. Greedy-Based Methods

The greedy algorithm is one of the most representative methods for IM, primarily achieved by iteratively selecting nodes that yield the greatest marginal gain as seed nodes. The theoretical foundation of this class of methods stems from the pioneering work of Kempe et al. [5] in 2003, who proved that under certain conditions, the IM problem exhibits sub-modularity. This means that using a greedy algorithm can guarantee obtaining an approximation of at least $(1-1/e)$ of the optimal solution. Although the greedy algorithm they proposed has strong theoretical guarantees, its high computational cost limits its application scenarios. To improve algorithm efficiency, Leskovec et al. [8] proposed the CELF algorithm, which significantly enhances efficiency by leveraging monotonic sub-modularity. Subsequently, Chen et al. [10] introduced the NewGreedy and MixedGreedy algorithms, which select edges based on the influence factor between nodes to construct a new subgraph. During subsequent influence expectation calculations, influence propagation is performed only on the optimized subnetwork, thereby improving efficiency. The StaticGreedy [11] and UBLF [12] algorithms further reduce the number of Monte Carlo simulations by utilizing static snapshots and quickly estimating upper bounds for influence propagation, respectively, thereby significantly improving computational efficiency.

As social networks and other information networks continue to expand, the number of nodes and edges may reach hundreds of millions or even billions, making it challenging for even the most advanced greedy algorithms to obtain solutions within a reasonable timeframe. To address this challenge, researchers are exploring additional strategies, such as parallel and distributed computing methods, as well as utilizing graph decomposition techniques to reduce the scale of the problem. Biswas et al. [13] developed a novel influence maximization algorithm to identify a set of seed nodes in complex networks. This algorithm uses the VIKOR method to filter out low-influence nodes from candidate seeds and introduces the EDV function with submodular properties into the greedy algorithm framework. Yang et al. [14] derived an independent cascading model based on ternary closures to study the influence maximization problem and further proposed a heuristic influence maximization algorithm that evaluated a node’s expected propagation influence by comprehensively considering ternary closure-weighted propagation probabilities and ternary closure-weighted degrees. Based on multi-dimensional attributes such as users’ social relationships, historical records, and topological structures, Li et al. [15] put forward a cross-comparison improved K-kernel heuristic algorithm based on heterogeneous information entropy to identify the most influential seed set in a hypergraph. Although these improved greedy algorithms have achieved significant improvements in efficiency, they still face challenges when dealing with large-scale networks.

2.2. Heuristic-Based Methods

Heuristic methods provide a relatively efficient approach to estimating and selecting the set of seed nodes with the greatest influence by simplifying the complexity of the problem when maximizing influence. The core idea of heuristic algorithms is to utilize the topological structure features of a network, such as node centrality metrics, to predict node influence. These algorithms typically select seed nodes based on their centrality metrics. For example, Degree Centrality (DC) [16] posits that a node’s influence is proportional to the number of nodes it is connected to. This method is simple and intuitive, suitable for scenarios where information propagation probabilities are assumed to be equal. The K-Shell decomposition method [17] partitions a network into multiple layers, such that nodes within the same layer share an identical coreness number. This method highlights that a node’s potential influence is determined by its position (rather than just its degree) within the network topology. Nodes residing in the innermost core layer—the one with the highest K-Shell value—are considered to have significant influential potential due to their central location, and are likely to play a critical role in information dissemination. Freeman proposed two classic algorithms based on global information from the perspective of the shortest path between nodes: betweenness centrality [19] and closeness centrality [20]. Betweenness centrality suggests that the more times a node appears on the shortest path between all nodes in the network, the more important it is in the information dissemination process. Closeness centrality measures a node’s influence by quantifying the average shortest distance between the node and the remaining nodes in the network. This algorithm asserts that the shorter the average shortest distance between a node and the remaining nodes, the faster the information transmission speed from that node as a source and the higher the node’s importance ranking. Lei et al. [21] quantified a node’s influence by analyzing changes in network structure after node removal, combining information from first and second-order neighboring nodes and using Tsallis entropy to measure influence.

However, relying solely on a single node attribute is insufficient for complex and diverse network structures. Agneessens et al. [22] introduced a generalized centrality method that considered information from a node’s direct neighbors and the distances between each pair of nodes to identify key nodes in a network. Besides, Li et al. [23] developed the GGC model to pick up the most influential nodes in a network, taking into account the closeness between a node and its neighboring nodes through the local clustering coefficient. Ullah [24] presented the NPIC algorithm, which identifies the most influential key nodes in a network by evaluating both the local attributes of nodes and the path information between nodes. Ibnoulouaf et al. [25] formulated a multi-attribute centrality metric to address the influential node identification problem, integrating the position information of nodes in the network and the local information of their nearest neighbors. Additionally, some scholars have attempted to rank the importance of nodes by simultaneously considering both local and global information in the network. Ullah et al. [26,27] proposed the LGC and LSS algorithms to identify key nodes in a network, which simultaneously account for both local and global network information to enhance accuracy. Inspired by potential energy, the EPC [18] centrality method was also introduced for identifying key nodes in a network, reflecting not only the local influence of a node but also aggregating the influence of surrounding nodes to ensure a comprehensive assessment of a node’s influence.

2.3. Influence Maximization with Users’ Interests

To better model the spread of influence in real life, an increasing number of scholars are attempting to model the influence propagation process using users’ interest factors. Recognizing that users exert varying levels of influence across different topics, Aslay et al. [34] introduced the TIM problem, which accounts for users’ interest topics. They also proposed an efficient indexing framework called INFLEX that can process TIM queries in milliseconds. Building on this work, Chen et al. [35] developed two topic-aware influence maximization algorithms: Best Effort and Topic Sample. The Best Effort algorithm estimates the upper limit of each user’s influence and uses these limits to prune users with lower influence, thereby efficiently selecting seed users. The Topic Sample algorithm precomputes the influence distribution for some topics and uses this precomputed information to estimate upper and lower bounds, enabling rapid selection of seed users. Bingöl et al. [36] investigated a topic-based influence calculation approach designed to recognize social interactions and postings of a limited number of users, aiming to discover and sustain the dynamic trends and activities of influential users under limited resources. Qin et al. [37] expanded the topic-aware model to the community level and introduced the community-topic feature-based dynamic social network influence maximization algorithm CFDI, aimed at diminishing the computational complexity of the dynamic IM problem.

Traditional topic-aware models primarily ignore users’ actual interest in marketing information or lack specific quantification of users’ interest. To address this, Galhotra et al. [38] proposed a comprehensive solution called Holistic Influence Maximization (HIM), which introduces the Opinion-cum-Interaction (OI) model. This model simultaneously considers nodes’ personal opinions and the probability of interaction between nodes to more realistically simulate the information dissemination process. Cai et al. [39] further investigated target user groups based on HIM, considering network relationships, spatial relationships, and preference similarities among users. They proposed the Target-aware HIM problem to better adapt to the complex requirements of real-world application scenarios. Additionally, Li et al. [33] conceived the Topic-Aware Information Coverage Maximization problem to maximize the sum of the expected numbers of active and known nodes in a topic-aware social network.

Recent research focuses on improving the efficiency and adaptability of TIM. To address issues such as high online query latency, significant indexing overhead, or reliance on static parameters in existing solutions, several studies have proposed efficient approaches. Tang et al. [43] combined hashing and sketching techniques, achieving significant efficiency improvements in both offline and online phases. Halal et al. [44] integrated deep reinforcement learning with graph attention networks, modeling the topical nature of diffusion using real cascade data and accelerating queries via cross-attention mechanisms. Ahmadikia et al. [45] employed reinforcement learning to dynamically adjust the weights of node centrality measures, adapting to different network structures and enhancing solution robustness and scalability. In terms of underlying modeling, Sang et al. [46] constructed dynamic heterogeneous graphs to uniformly describe spatio-temporal information interactions, improving the accuracy of cascade prediction. Chakraborty et al. [47] innovatively introduced a topic and opinion-infused hypergraph model, enhancing diffusion efficiency through novel seed selection criteria and propagation settings.

Beyond discussing influence propagation for specific topics, Li et al. [40] proposed an influence maximization method based on group sentiment to study the multidimensional characteristics of information propagation influenced by users’ sentiment and group features. They addressed the Two-Factor Information Propagation (TFIP) model. Huang et al. [41] formulated the SentiRank method, which constructs an emotion map considering positive and negative sentiment systems from social networks to identify sentiment leaders. Zareie [42] calculated the degree of users’ interest in marketing information by computing the Jeffrey divergence between users’ interest vectors and marketing information vectors, and put forward the IMUD method to maximize information propagation in viral marketing. However, while the aforementioned methods consider node heterogeneity, they overlook the influence propagation resulting from users’ interest-based recommendations by Servers, making it difficult to simulate influence propagation in ISNs.

3. Model and Problem Definition

In this section, we first introduce ISNs and the SB-IC propagation model, along with their related definitions. We then formally describe the SIHIM problem in ISNs.

3.1. Interest-Driven Social Network and Diffusion Model

Unlike traditional social networks, Interest-driven Social Networks (ISNs) such as TikTok and BiliBili do not rely solely on direct user interactions to transmit information. Instead, Servers in these ISNs can actively deliver messages to users based on their interests. Inspired by [48] and based on the IC model, this paper proposes a new propagation model, SB-IC, to describe the influence propagation process in ISNs. The SB-IC model utilizes Server nodes to model the interest-based information delivery in ISNs.

The ISN can be represented as $G=(V,E,I)$, where $V=\{1,2,\dots ,n\}$ denotes the set of all nodes in the network; $E\subseteq V\times V$ denotes the set of all edges in the network; if there is a directed edge from node u to node v, it is denoted as $(u,v)\in E$; $I=(i_1,i_2,\dots ,i_n)$ denotes the set of interest vectors for all nodes in the network.

The SB-IC model defines two states for nodes: inactive and active. At the initial moment $t=0$, only the seed nodes are in the active state, while all other nodes are in the inactive state. At any time step $t>0$, nodes that were activated at time $t-1$ will simultaneously propagate their influence through the following two propagation methods:

• Information propagation based on social relationships: Each node u activated at time step $t-1$ will attempt to activate its inactive neighbor node v with probability $p_N$.
• Information propagation based on node interests: The Servers will attempt to activate each inactive interest neighbor node w of node u that was activated at time step $t-1$ with probability $p_I$.

If a node is successfully activated, its status changes from inactive to active. The process continues iteratively until no new nodes can be activated in the network. As illustrated in Figure 1.

In the SB-IC model, the influence of a node can be spread not only to neighboring nodes but also to nodes that are not directly connected but have more similar interests. The model defines the interest neighbor set to reflect the potential interaction relationships between users based on interest similarity. Given an interest-based social network $G=(V,E,I)$, for each node u in the network, its interest neighbor set ${\mathrm{IN}}_u$ can be obtained by Equation (1):

$${\mathrm{IN}}_u=\{v\mid v\in V,v\notin {\mathsf{\Gamma }}_u,\mathrm{rank}(v,u)\le {\mathrm{PI}}_u\}$$

(1)

where ${\mathrm{IN}}_u$ denotes the interest neighbor set of node u, ${\mathsf{\Gamma }}_u$ denotes the set of direct neighbors of node u, $\mathrm{rank}(v,u)$ denotes the interest similarity rank between nodes v and u, and ${\mathrm{PI}}_u$ denotes the potential interest neighbors of node u.

In ISNs, the potential influence of a node is usually closely related to its position in the network. The more high-quality neighboring nodes a node has and the more central its position in the network, the greater its potential influence. To more comprehensively measure the potential influence of a node, this paper proposes the concept of Potential Interest Expansion Degree (PIED). The formula for calculating PIED is as follows:

$${\mathrm{PIED}}_u=\sqrt{d_u·{\mathrm{ks}}_u}\times {\mathrm{cloness}}_u$$

(2)

$${\mathrm{cloness}}_u={\displaystyle \frac{2E_u}{d_u(d_u-1)}}$$

(3)

where $d_u$ represents the degree of node u, ${\mathrm{ks}}_u$ represents the K-Shell value of node u, ${\mathsf{\Gamma }}_u$ represents the set of neighboring nodes of node u, and ${\mathrm{cloness}}_u$ represents the local clustering coefficient of u, which is defined as shown in Equation (3), where $E_u$ is the actual number of edges between node u and its neighboring nodes.

In ISNs, Servers typically prioritize recommending information from other users with similar interests to users based on the degree of interest similarity, thereby enhancing the precision of information dissemination. In the SB-IC model, interest similarity is calculated based on the interest vectors of any two distinct nodes in the network, with values ranging from [0, 1]. The closer the value is to 1, the more similar the interests of the two nodes; the closer the value is to 0, the greater the difference in interests. Given the interest vectors ${\mathbf{i}}_u=[i_u^1,i_u^2,\dots ,i_u^k,\dots ,i_u^h]$ and ${\mathbf{i}}_v=[i_v^1,i_v^2,\dots ,i_v^k,\dots ,i_v^h]$, the similarity between nodes u and v, $\mathrm{Sim}(u,v)$, can be calculated using Equation (4):

$$\mathrm{Sim}(u,v)={\displaystyle \frac{{\sum }_{i=1}^h{i}_u^i·i_v^i}{\sqrt{{\sum }_{i=1}^h{\left(i_u^i\right)}^2}·\sqrt{{\sum }_{i=1}^h{\left(i_v^i\right)}^2}}}$$

(4)

where $u,v\in V$, ${\mathbf{i}}_u,{\mathbf{i}}_v\in I$, and $i_u^k$ and $i_v^k$ represent the k-th dimensional interest vectors of node u and node v, respectively.

3.2. Problem Definition

The IM problem focuses on how to select seeds with the greatest influence based on the interaction relationships between nodes, while ignoring the impact of user interests on influence propagation. In contrast, the SIHIM problem considers the dual influence propagation mechanism of user propagation and Servers’ recommendations, making it more suitable for real-world ISNs.

To formally define the SIHIM problem, let ${\sigma }_N(·)$ denote the influence function based on social relationships, and ${\sigma }_I(·)$ denote the influence function based on node interests. Given a seed set S, let ${\sigma }_N\left(S\right)$ denote the influence propagation value based on social relationships, and ${\sigma }_I\left(S\right)$ denote the influence propagation value based on node interests. Then, the SIHIM problem can be formally defined as follows:

Definition 1 (Social–Interest Hybrid Influence Maximization Problem). 

Given an interest-based social network G, a propagation model SB-IC, and a positive integer k ($k=1,2,\dots ,n$), the SIHIM problem aims to find an optimal seed set $S^{*}$ of size k such that the sum of ${\sigma }_N\left(S\right)$ and ${\sigma }_I\left(S\right)$ is maximized, i.e.:

$$S^{*}=argma{x}_{S\subseteq V,\left|S\right|=k}\left({\sigma }_N\left(S\right)+{\sigma }_I\left(S\right)\right)$$

(5)

Since Kempe et al. [5] have proven that the influence maximization problem based on the traditional independent cascade (IC) model is NP-hard, when only social-relationship-based propagation is considered in the network, the SB-IC model degenerates into the traditional IC model. Therefore, the influence maximization problem under the SB-IC model is identical to the classical IM problem, whose NP-hardness has been thoroughly proven. Additionally, the SB-IC model is designed based on the traditional IC model with a propagation mechanism based on interest similarity, which does not reduce the problem’s complexity, so the influence maximization problem under the SB-IC model is also an NP-hard problem.

In the SIHIM problem, let the total influence propagation be $\sigma \left(S\right)={\sigma }_N\left(S\right)+{\sigma }_I\left(S\right)$, where ${\sigma }_N\left(S\right)$ denotes the influence based on social relationships propagation and ${\sigma }_I\left(S\right)$ denotes the influence based on interests propagation. Then, the SIHIM problem based on the SB-IC model is monotonic and submodular.

Proof. 

(1)

Monotonicity of the SIHIM problem

For any seed sets S and T, if $S\subseteq T$, then the influence ${\sigma }_N\left(S\right)$ based on social relationships propagation is monotonic. Because the traditional IC model has proven its monotonicity [5], i.e., ${\sigma }_N\left(S\right)\le {\sigma }_N\left(T\right)$. Similarly, the influence based on interest propagation ${\sigma }_I\left(S\right)$ also exhibits monotonicity. The reason is that ${\sigma }_I\left(S\right)$ depends on the size of the seed set and interest similarity. A larger seed set T covers all propagation paths of S and may introduce new paths, thus ${\sigma }_I\left(S\right)\le {\sigma }_I\left(T\right)$. In summary, $\sigma \left(S\right)\le \sigma \left(T\right)$, so the SB-IC model exhibits monotonicity.

(2)

Sub-modularity of SIHIM problem

In the SIHIM problem, the sub-modularity of the SB-IC model is considered for any sets $S\subseteq T$ and $e\notin T$. Kempe et al. [5] have proven that the IC model satisfies the submodular property, so the propagation ${\sigma }_N\left(S\right)$ based on social relationships is submodular, i.e., ${\sigma }_N(S\cup \left\{e\right\})-{\sigma }_N\left(S\right)\ge {\sigma }_N(T\cup \left\{e\right\})-{\sigma }_N\left(T\right)$. For the interest-based propagation influence ${\sigma }_I\left(S\right)$, since the calculation of interest similarity is based on cosine similarity, which has a normalization property, the marginal gain of the newly added node e for S decreases as S increases. Therefore, $\sigma (S\cup \{ϵ\left\}\right)-\sigma \left(S\right)\ge \sigma (T\cup \{ϵ\left\}\right)-\sigma \left(T\right)$, thereby the sub-modularity of the SB-IC model is proved. □

4. Proposed Method

In this section, we propose a heuristic algorithm for addressing maximization problems in ISNs. Firstly, we describe the overall framework of the algorithm, and then elaborate on some of its details.

4.1. The Framework of Pascal Centrality

The adoption of physical-world principles and mathematical formulas for algorithm design is a prevalent and potent paradigm within IM research, as evidenced by prior work such as [18,23]. The propagation of influence in a network is a typical process of communication dynamics, where the influence of key nodes plays a crucial role in information dissemination. Inspired by the characteristics of pressure transmission in fluid mechanics, this study treats key nodes as the “source points” of influence propagation. According to Pascal’s law, changes in fluid pressure can be transmitted without loss through the fluid medium in all directions. Similarly, the influence of key nodes can efficiently diffuse along the network’s connection paths to other nodes. Based on the above principles, this section models the propagation of influence among nodes in a network. The liquid density $\rho$, which characterizes the local influence profile of nodes and captures their ability to directly activate neighbors, represents the local characteristics of nodes in the network. The gravitational acceleration g describes the global characteristics of nodes. This metric effectively quantifies these characteristics and provides a stable, interpretable framework for global assessment, and the relative height $\mathsf{\Delta }h$, which modulates the interactions between nodes and addresses the influence overlap problem through a dynamic adjustment mechanism, indicates the interactions between nodes. Therefore, the pressure at node u can be expressed as:

$$P_u={\rho }_u·g_u·\mathsf{\Delta }{h}_u$$

(6)

Figure 2 shows the complete process of the proposed interest social network analysis and PaC calculation method.

• Obtain the propagation matrix: The algorithm first constructs a Pascal centrality propagation matrix based on the initial propagation probabilities between nodes.
• Assess the initial influence: The algorithm then calculates the density and gravitational acceleration of each node to perform a preliminary assessment of the node’s influence.
• Select seed nodes: After completing the preliminary assessment, the algorithm iteratively updates the relative height of each node and finally outputs the node sequence based on the size of the PaC value.

Figure 2. Flowchart of PaC algorithm.

Figure 2. Flowchart of PaC algorithm.

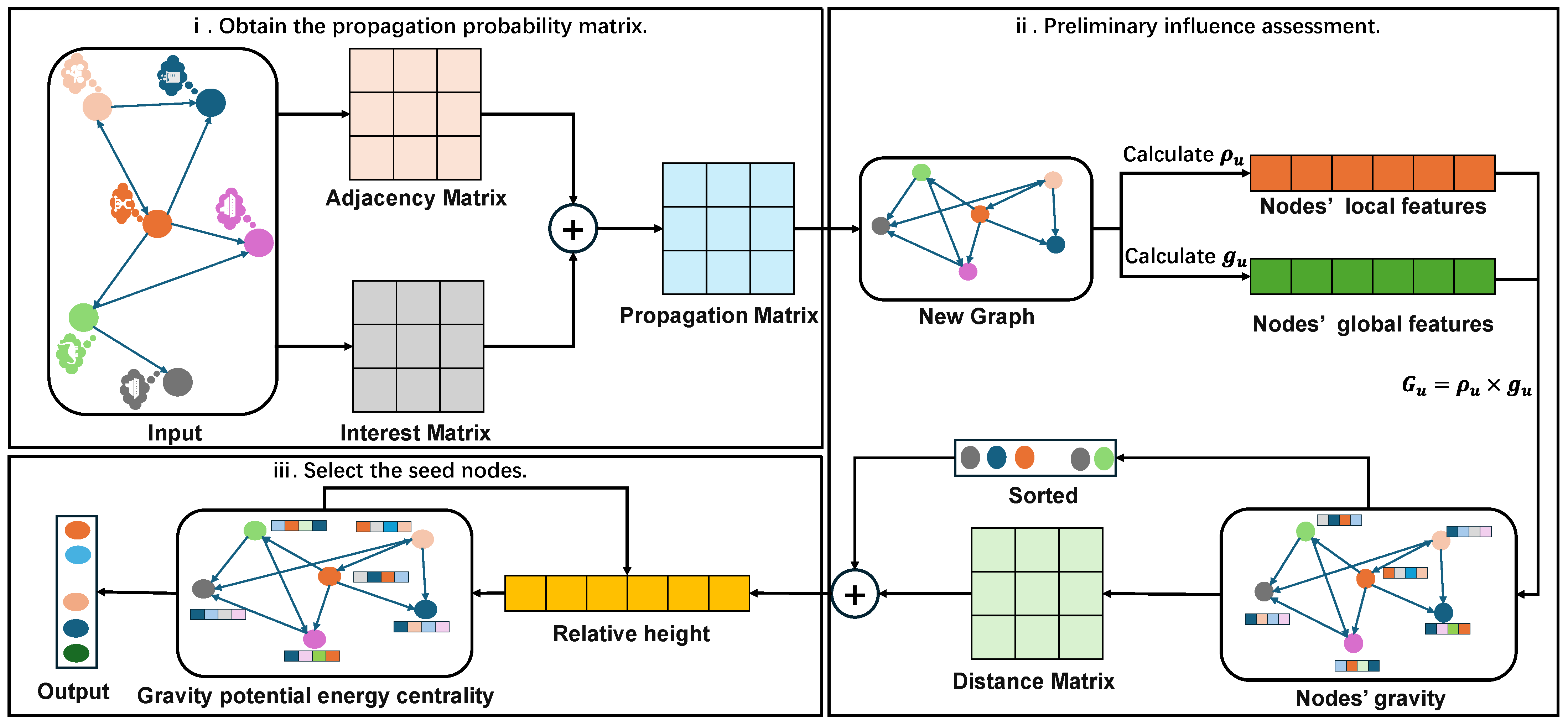
4.2. Propagation Matrix

In the real world, there are significant differences in the ability of different users to accept information. These differences depend not only on the recipient’s own ability to accept information but also on the source of the information. Even when faced with the same information, users’ willingness to accept it varies depending on the channel through which they obtain it. To quantify these differences, we propose the concept of propagation probability matrix. In SIHIM problems, the influence propagation of nodes mainly includes two methods: the influence of interest propagation and the influence of social relationship propagation. Based on this, the propagation matrix of nodes can be formulated as Equation (7):

$$PM=P{M}_I+{PM}_N$$

(7)

where $PM$ denotes the propagation probability matrix of the interest social network G, $P{M}_I$ denotes the probability matrix of G based on interest propagation, and $P{M}_N$ denotes the social relation probability matrix.

4.3. Assess the Initial Influence

A node’s influence is determined by both its local influence and global influence. Local influence establishes the foundation of a node’s influence within its neighborhood, while global characteristics determine the node’s position within the network. PaC performs an initial assessment of a node’s influence based on its local and global influence. For any node $u\in G$, its energy $Q_u$ is calculated by multiplying the node’s density ${\rho }_u$ by its acceleration $g_u$, as shown in Equation (8):

$$Q_u={\rho }_u·g_u$$

(8)

In Equation (8), ${\rho }_u$ is used to describe the influence within the node’s domain of node u. It is determined by two parts: the local activation expectation $LA{E}_u$ and the connectivity factor $c{f}_u$ of node u. The calculation of ${\rho }_u$ is as follows:

$${\rho }_u=LA{E}_u\times c{f}_u$$

(9)

It has been proven that the influence of a node decreases exponentially with distance from the node [49]. Therefore, the size of the local activation expectation value of node u within one hop is an important factor in node influence, and its calculation formula is shown in Equation (10):

$$LA{E}_u=M_u·PM·\mathbf{1}$$

(10)

Among them, $\mathbf{1}$ is a column vector of length $\left|V\right|$ with all elements being 1, $PM$ is the propagation probability matrix, and the vector $M_u$ is the mapping of node u in $PM$, where $M_u=[m_1,m_2,\dots ,m_u,\dots ,m_n]=[0,0,\dots ,m_u,\dots ,0]=[0,0,\dots ,1,\dots ,0].$ However, considering only the local activation expectation value may overlook the connections between neighboring nodes. To more accurately estimate a node’s local influence, we propose the local connectivity factor. The connectivity factor $c{f}_u$ is a metric that measures the connectivity between node u and its neighboring nodes in G. It combines node degree and the number of triangles to comprehensively evaluate node importance from both direct influence and information flow capacity. $c{f}_u$ for node u is shown in Equation (11).

$$c{f}_u={\displaystyle \frac{d_u+{\alpha }_u}{d_u}}$$

(11)

where, $d_u$ is the degree of node u, and ${\alpha }_u$ is the number of triangles formed by node u.

The influence of a node depends not only on its own attributes but also on the influence of neighboring nodes. In fact, nodes with higher local activation expectations are more likely to have higher importance. However, the status of a node in a network is difficult to reflect by its local influence alone. Therefore, to more comprehensively measure the global influence of a node, we use the gravitational acceleration $g_u$ of node u to measure the global influence of node u, thereby reflecting the status of node u in the network. The calculation method is as follows:

$$g_u=\sum _{\begin{array}{c}v\in V\backslash \left\{u\right\},\\ \mathrm{dist}(u,v)\le r\end{array}}{\displaystyle \frac{LA{E}_v}{\mathrm{dist}{(u,v)}^2}}$$

(12)

The gravitational acceleration $g_u$ of node u is obtained by calculating the weighted sum of the local activation expectation value $LA{E}_v$ of node v within the truncated radius r and the inverse of the square of the distance $\mathrm{dist}(u,v)$ between node u and node v. Specifically, the global influence contribution of node v to node u is directly proportional to its local activation expectation value and inversely proportional to the square of the distance between node v and node u. This calculation method comprehensively considers the local influence of nodes and their spatial distribution in the network, thereby more accurately reflecting the global influence of node u and its position in the network, and preliminarily evaluating the influence of nodes through Equation (8).

4.4. Seed Node Selection

After calculating the initial influence of all nodes, the next step is to select seed nodes based on these evaluation results. However, the selection of seed nodes is essentially a complex combinatorial optimization problem. If seed nodes are selected directly based on the initial influence evaluation results, the overlapping influence between nodes will lead to an optimistic estimate of the overall influence, thereby reducing the overall effectiveness of the algorithm. To address this issue, we designed a relative height $\mathsf{\Delta }h$ during the seed node selection phase to reduce influence overlap and thereby improve the overall performance of the algorithm. The relative height $\mathsf{\Delta }{h}_u$ of node u is calculated as follows:

$$\mathsf{\Delta }{h}_u=1-\prod _{\begin{array}{c}b\in B,\\ v\in V\backslash B,\\ \mathrm{dist}(b,v)\le r\end{array}}\left(1-e^{p·\mathrm{dist}(b,v)}\right)$$

(13)

Among them, p is a free parameter between $(0,1)$, and b is any node in the current optimal node list B. This formula calculates the $\mathsf{\Delta }h$ to dynamically assess the interactions between nodes, thereby reducing the problem of influence overlapping. The overall procedure of the algorithm is shown in Algorithm 1:

Algorithm 1 Pascal Centrality.

1: Input: $G=(V,E,I)$, the number of seeds k   2: Output: seed set S   3: Initialize:   4: $S=\varnothing$, $B=\left[\right]$   5: Get the Propagation Matrix according to Equation (7)   6: for each node $u\in V$ do   7:       Calculate the preliminary influence assessment of node u by Equation (8)   8: end for   9: while $\left|B\right|<\left|V\right|$ do 10:       for each node $u\in V$ do 11:             Calculate the Relative Height of node u by Equation (13) 12:             Calculate the PaC of node u by Equation (6) 13:             Select the node with the highest PaC value and add it to the list B 14:       end for 15: end while 16: Select the top k nodes from list B and add them to set S 17: return S

4.5. Complexity Analysis of the PaC Algorithm

Time Complexity Analysis: The computational cost of the PaC algorithm mainly focuses on three stages: constructing the propagation matrix, assessing the initial influence, and selecting seed nodes. Firstly, when constructing the propagation probability matrix $PM$, the algorithm leverages the sparse characteristics of interest-based social networks and employs a sparse storage structure for initialization, with a time complexity of $O\left(\right|E\left|\right)$. Second, during the initial influence assessment, the local activation expectation $LAE$ is computed via sparse matrix-vector multiplication, with complexity $O\left(\right|E\left|\right)$; the gravitational acceleration $g_u$ for each node requires traversing all nodes within the truncated radius r, with the total computation cost for all nodes denoted as $C_g$. In the worst case, $O\left(\right|V{|}^2)$, while it is typically much smaller when r is bounded and the network is locally sparse. Finally, during the seed selection stage, the relative height $\mathsf{\Delta }h$ of all nodes is calculated only once during initialization. In subsequent iterations, $\mathsf{\Delta }h$ is incrementally updated for all candidate nodes affected by each newly added seed, with each update costing $\mathsf{\Delta }h$. A max-heap structure is used to maintain PaC values for efficiently selecting the node with the highest score, with selection cost per iteration bounded by $O(log|V\left|\right)$. Consequently, selecting k seeds has a total complexity of $O(k·|V\left|\right)$. Considering all three stages, the overall time complexity of the PaC algorithm can be expressed as $O\left(\right|E|+C_g+k·|V\left|\right)$. Under the worst-case scenario for $C_g$ and assuming $k=\left|V\right|$, this complexity simplifies to $O\left(\right|E|+|V{|}^2)$. The dominant term is therefore $O\left(\right|V{|}^2)$.

Space Complexity Analysis: The space consumption of the PaC algorithm primarily comes from storing the network structure, the propagation matrix, and node-related attributes. The input network is represented by an adjacency list, occupying $O\left(\right|E|+|V\left|\right)$ space. The sparse propagation probability matrix $PM$ requires $O\left(\right|E\left|\right)$ space. During the computation process, intermediate variables such as local activation expectation $LAE$, density $\rho$, gravitational acceleration g, relative height $\mathsf{\Delta }h$, and PaC value need to be maintained for each node, all stored in list form, occupying $O\left(\right|V\left|\right)$ space. Additional auxiliary structures, including the max-heap and the selected seed set, also require $O\left(\right|V\left|\right)$ space. Therefore, without caching all r-hop neighborhoods and reusing temporary traversal structures, the total space complexity of the algorithm is $O\left(\right|E|+|V\left|\right)$ which is dominated by the network topology and the sparse propagation matrix.

5. Performance Analysis

To systematically validate the research objectives of this paper, we propose the following core research hypotheses, which will be tested in subsequent experiments.

Hypothesis 1. 

The proposed SB-IC model is capable of modeling the information propagation process in interest-based social networks more accurately, thereby achieving a larger influence propagation range than the traditional IC model under the same seed set.

Hypothesis 2. 

The proposed PaC, by integrating both topological and interest attributes of nodes, can identify a set of seed nodes with greater influence compared to existing mainstream algorithms.

Hypothesis 3. 

The relative height $\mathsf{\Delta }h$ mechanism in the PaC can effectively reduce influence overlap among seed nodes and optimize their distribution.

To evaluate the performance of the proposed PaC algorithm in ISNs, we conducted experiments on nine real-world social networks. Every experiment was conducted using the identical computer setup to guarantee the impartiality of the comparative analysis. The experiments were implemented and executed using the Python 3.9 programming language and the NetworkX library. The computer configuration used for the experiments was as follows: Intel Core i5 13400F 2.5 GHz processor (10 cores), Windows 11 operating system, and 32 GB of memory. This configuration provided sufficient computational power and memory support for the experiments, ensuring their accuracy and efficiency.

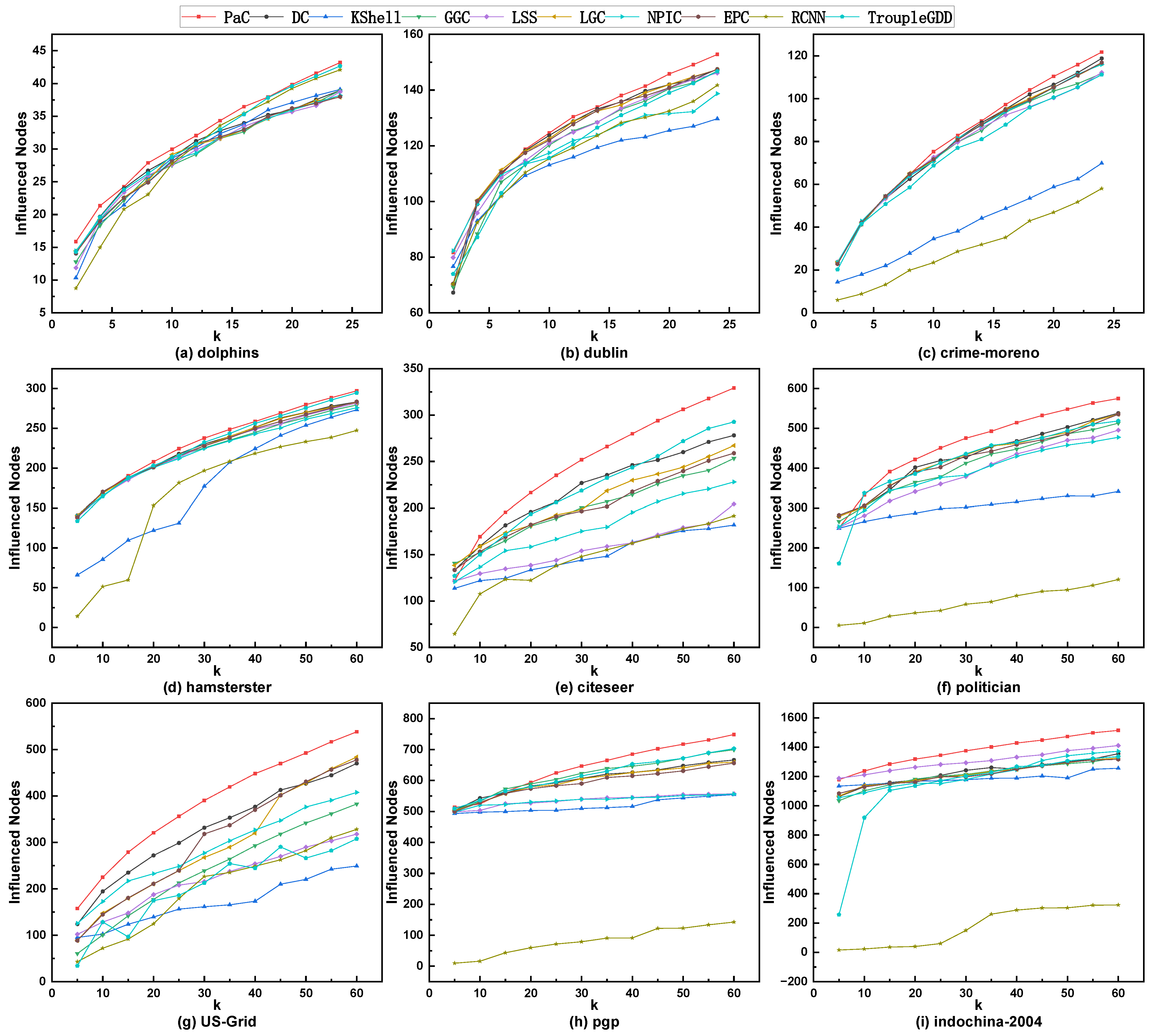
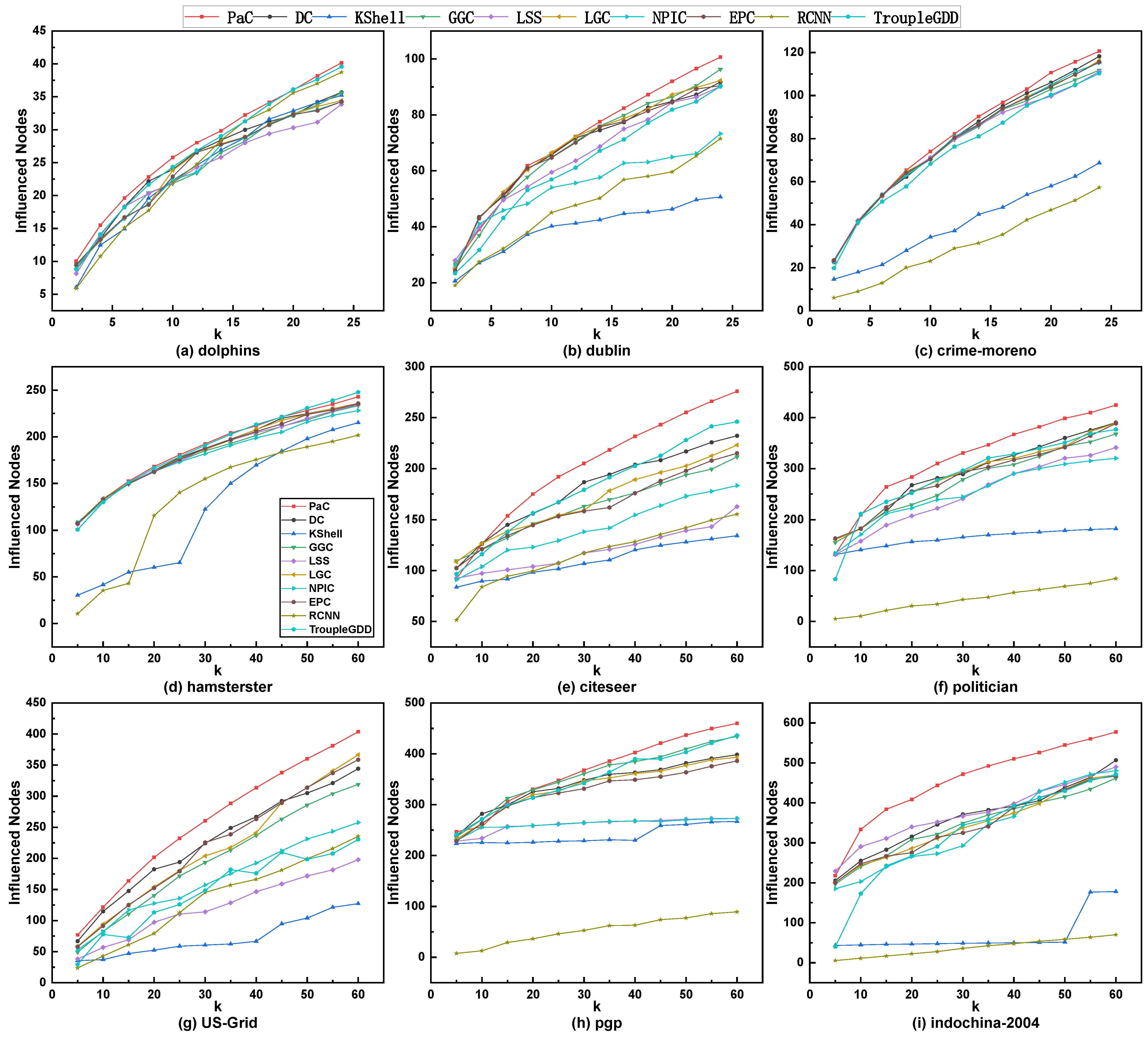
5.1. Datasets and Compared Algorithms

Guided by the aforementioned hypotheses, we conducted experiments on real-world networks, including dolphins [50], dublin [50], crime-moreno [50], hamsterster [50], citeseer [50], politician [50], US-Grid [50], pgp [50], indochina-2004 [50] and Sinanet [51]. These networks encompass a variety of relationships, such as data contact networks, social friendships, and Facebook follow relationships, providing diverse data for performance testing. Since there are currently no datasets that include interest vectors, we randomly generated a 10-dimensional vector for each node to simulate and validate the experiments. The datasets are detailed below, with some key parameters summarized in Table 1, where $\left|V\right|$ and $\left|E\right|$ represent the number of nodes and edges in the network, respectively; $\langle \widehat{d}\rangle$ and $\langle d\rangle$ represent the maximum degree and average degree in the network, respectively; k represents the maximum k-core value of the network; and c represents the local clustering coefficient of the network:

• dolphins: The social network of 62 bottlenose dolphins in New Zealand was constructed based on their frequent interaction patterns.
• dublin: This network records the contact network of an influenza outbreak at a school in Dublin.
• crime-moreno: This network is constructed based on the relationships between criminal cases and suspects, victims, witnesses, and other parties involved.
• Hamsterster: This represents a social network dataset containing anonymized friendships and family relationships among users, sourced from real-world interactions.
• Citeseer: This network is composed of citation relationships among 3312 publications across six categories.
• Politician: This includes mutual-follow data between blue-badge-certified pages crawled from Facebook.
• US-Grid: This is an undirected graph constructed using information about power grids in western US states.
• pgp: This dataset records the interaction and relationship network among users of the Pretty Good Privacy algorithm.
• indochina-2004: A large-scale web-crawling dataset covering webpage data from domain names in Indochina countries.
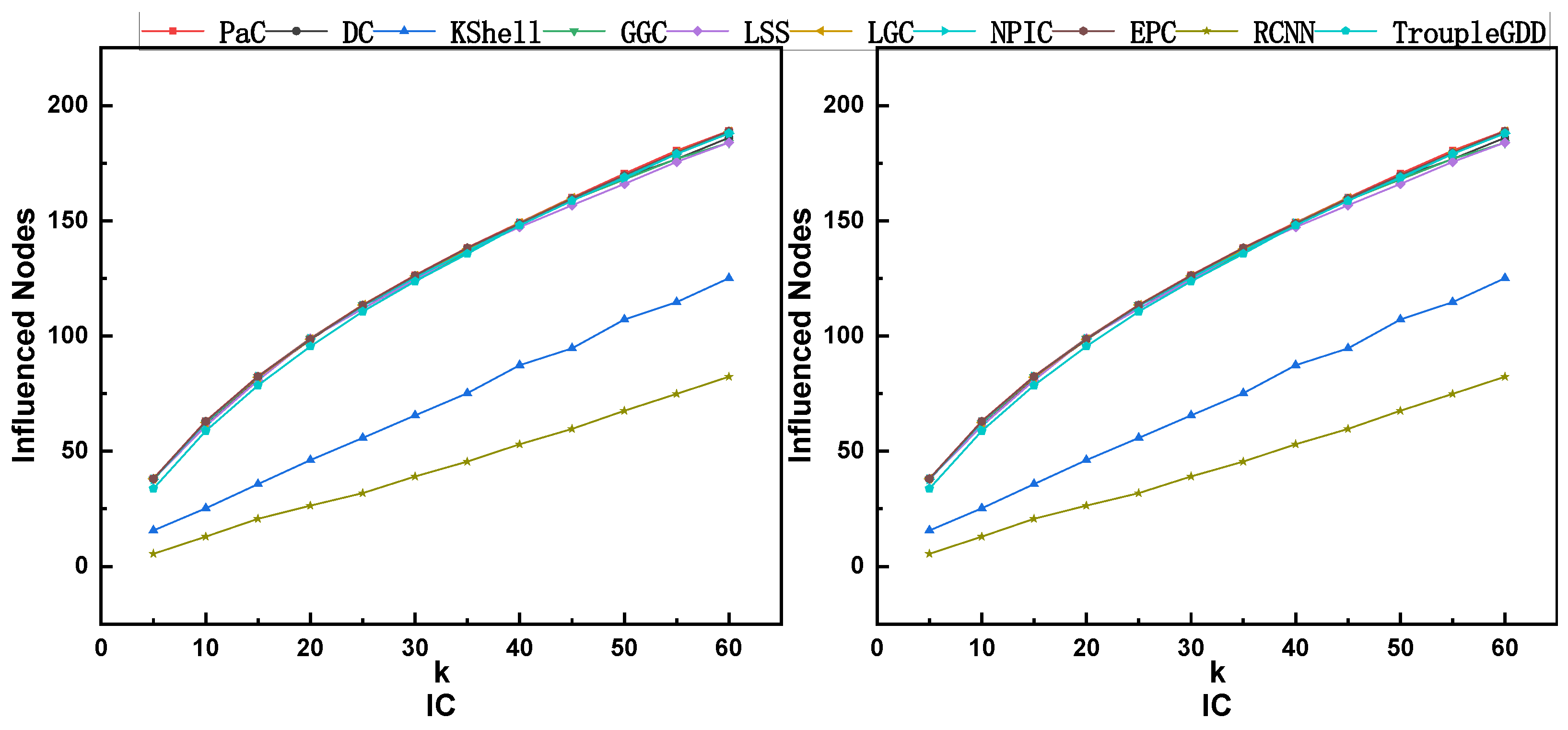
• Sinanet: This network is constructed based on the follower/followee relationships between microblog users extracted from Sina Weibo, along with their interests characterized by topic distributions in 10 forums.

Table 1. The detailed information of datasets.

Network	$\left|\mathit{V}\right|$	$\left|\mathit{E}\right|$	$\widehat{\mathit{d}}$	$\langle \mathit{d}\rangle$	k	c
dolphins	62	159	12	5.129	4	0.259
dublin	410	2765	50	13.488	17	0.456
crime-moreno	829	1473	25	3.554	3	0.006
hamsterster	2426	16,630	273	13.710	24	0.538
citeseer	3264	4536	99	2.779	7	0.145
politician	5908	41,706	323	14.119	31	0.385
US-Grid	4941	6594	19	2.669	5	0.080
pgp	10,682	24,317	205	4.553	31	0.266
indochina-2004	11,358	47,606	199	8.383	49	0.710
Sinanet	3490	28,657	799	16.5313	20	0.179

Table 1. The detailed information of datasets.

Network	$\left|\mathit{V}\right|$	$\left|\mathit{E}\right|$	$\widehat{\mathit{d}}$	$\langle \mathit{d}\rangle$	k	c
dolphins	62	159	12	5.129	4	0.259
dublin	410	2765	50	13.488	17	0.456
crime-moreno	829	1473	25	3.554	3	0.006
hamsterster	2426	16,630	273	13.710	24	0.538
citeseer	3264	4536	99	2.779	7	0.145
politician	5908	41,706	323	14.119	31	0.385
US-Grid	4941	6594	19	2.669	5	0.080
pgp	10,682	24,317	205	4.553	31	0.266
indochina-2004	11,358	47,606	199	8.383	49	0.710
Sinanet	3490	28,657	799	16.5313	20	0.179

In our experiment, we compared the performance of nine algorithms—DC [16], K-Shell [17], GGC [23], LSS [27], LGC [26], NPIC [24] EPC [18], RCNN [30], and ToupleGDD [32]—with the proposed PaC method. The following is a brief introduction to these algorithms, outlining their basic concepts and methods.

• DC (1994): DC evaluates the importance of a node based on its degree, i.e., the number of edges connected to the node. Nodes with higher degrees are deemed more influential in the network, as they can directly influence more other nodes.
• K-Shell (2010): K-Shell assesses a node’s robustness and connectivity by iteratively removing nodes with degrees below a certain threshold. The higher a node’s K-Shell value, the more influential it is within the network.
• LGC (2021): LGC identifies critical nodes in complex networks by integrating both local and global topological information, effectively overcoming the limitations of focusing solely on local structure or global information.
• GGC (2021): GGC measures a node’s propagation capability by combining its local clustering coefficient and degree. This approach is more comprehensive than traditional gravity models and enables more accurate identification of influential nodes in complex networks.
• LSS (2023): LSS is a novel heuristic algorithm that evaluates a node’s influence by combining degree centrality, K-Shell values, and node connectivity. It features low computational complexity and requires no parameter tuning.
• NPIC (2024): NPIC assesses a node’s influence by integrating local attributes and global path information, providing a comprehensive method for evaluating node importance.
• EPC (2024): EPC is a complex-network key-node identification method based on potential centrality. It comprehensively considers both local and global topological information and measures the influence of nodes based on their degree and distance.
• RCNN (2020): RCNN is a complex network key node identification method based on graph convolutional networks. It converts the critical node identification problem into a regression problem, utilizes adjacency matrices and convolutional neural networks to learn and predict node influence.
• ToupleGDD (2024): ToupleGDD is an influence maximization method based on deep reinforcement learning. It incorporates three coupled graph neural networks and double deep Q-networks, uses personalized DeepWalk for node embedding, and optimizes seed selection policies through reinforcement learning.

5.2. The Comparison of Influence Spreading

The influence spreading refers to the propagation range when influence propagation reaches a steady state under a given number of seed nodes, reflecting the extent of influence that a given seed set can ultimately cover. To compare the influence spreading of seed sets mined by the PaC algorithm in networks with different seed node scales, we designed experiments based on the scale of the dataset. Specifically, for smaller datasets (e.g., dolphins, dublin, and crime-moreno), we selected seed nodes ranging from 2 to 24 with a step size of 2; for larger datasets (e.g., hamsterster, citeseer, politician, US-Grid, pgp, and indochina-2004), we selected seed nodes ranging from 5 to 60 with a step size of 5 as initial activation nodes. In terms of the propagation model, we adopted the SB-IC model. To avoid rapid diffusion of influence in the network due to excessively high propagation probabilities, we adjusted the activation probabilities $p_N$ and $p_I$ of node u for node v based on differences in network topology. Specifically, $p_N$ and $p_I$ are calculated as $\langle d\rangle /\langle d^2\rangle$ and $(\langle d\rangle /\langle d^2\rangle ·\mathrm{Sim}(u,v))$, respectively, where $\langle d\rangle$ and $\langle d^2\rangle$ represent the average degree and the mean square of the degree of the network, respectively, and $\mathrm{Sim}(u,v)$ denotes the interest similarity between nodes u and v. To ensure the reliability of the results, we performed 10,000 Monte Carlo simulations and calculated the average influence spreading as the final metric. The experimental results are illustrated in Figure 3.

Figure 3 illustrates the performance comparison of different algorithms in terms of influence spread under the SB-IC model, with the red curve representing the PaC algorithm. Across the nine datasets evaluated, the PaC algorithm demonstrates a notable average improvement of 7.04% in influence spreading compared to the other nine benchmark algorithms. The performance advantage of PaC is particularly significant in the indochina-2004 network, where it achieves a remarkable improvement of 22.25%. However, in the hamsterster network, the performance gain of PaC is relatively limited at just 0.9%, which may be attributed to the low network density of hamsterster affecting algorithm effectiveness. Despite this exception, PaC exhibits substantial performance enhancements in most scenarios. Concurrently, we observe that the performance of RCNN tends to degrade as network scale increases, a phenomenon particularly evident in the pgh and indochina-2004 networks. This decline can be attributed to the challenge faced by graph embedding-based methods in capturing complex network structures as network size grows, ultimately leading to compromised generalization performance. Additionally, as depicted in Figure 3, the advantage of the PaC in influence spreading becomes increasingly pronounced as the number of seed nodes increases. This trend can be attributed to the influence overlapping effect. When the number of seed nodes is small, the influence overlapping effect is not yet prominent, and thus the PaC algorithm’s advantages are not fully realized. However, as the number of seed nodes increases, influence overlapping becomes more pronounced. The PaC effectively mitigates this overlap by evaluating interactions between nodes, thereby demonstrating higher performance with a larger number of seed nodes.

In addition, to verify the applicability of the algorithm on the IC model, the SB-IC model was replaced with the IC propagation model, the propagation probability was set to $p=\langle d\rangle /\langle d^2\rangle$, and 10,000 Monte Carlo simulations were conducted on the IC model. The average value was taken as the final influence spreading result. The experimental results of the influence spreading are shown in Figure 4.

Figure 4 presents the performance of different algorithms in terms of influence spreading under the IC model, with the red curve representing the PaC algorithm. Across nine datasets, the PaC algorithm consistently demonstrated superior influence spreading performance compared to other benchmark algorithms in most cases, achieving an average improvement of 5.22%. Notably, it attained a significant enhancement of up to 18.21% in the indochina-2004 network, while a modest average increase of 0.1% was observed in the hamsterster network. As the network scale expanded and structural complexity increased (e.g., in politician, pgh, and indochina-2004 datasets), the performance of the RCNN algorithm declined. This was primarily due to its difficulty in effectively fitting the intricate network structures to accurately model the influence spreading process. Meanwhile, the K-Shell algorithm exhibited specific trends in the hamsterster, pgp, and indochina-2004 datasets: before the number of seeds exceeds a threshold, the improvement in influence spreading is relatively slow; however, once the number of seeds reaches a tipping point, influence spreading improves rapidly before leveling off. This phenomenon can be attributed to the K-Shell algorithm’s seed node selection strategy. The algorithm tends to select key nodes with high K-Shell values as seed nodes. When the number of seeds is small, although key nodes have high individual influence, their influence ranges overlap significantly, leading to slow growth in influence spreading. Once the number of seeds reaches the threshold, the K-Shell algorithm shifts to selecting edge nodes, whose influence ranges overlap less with key nodes, significantly expanding the influence range and causing the expansion rate to rise rapidly. However, as the number of seed nodes continues to increase, the algorithm resumes selecting key nodes with influence ranges that overlap significantly with existing seed nodes, resulting in reduced expansion of new influence ranges and a subsequent flattening of expansion rate growth. In contrast, the PaC algorithm’s curve is the smoothest, indicating its superiority in avoiding influence overlapping compared to other algorithms. Additionally, as the number of seed nodes grows, the PaC algorithm’s advantage over other comparison algorithms becomes increasingly pronounced, further demonstrating its ability to effectively avoid influence overlapping and achieve more efficient influence spreading.

5.3. The Comparison of Influence Propagation Rate

The influence propagation rate compares how the influence spreading changes over time given a certain number of seed nodes, reflecting the efficiency of influence diffusion over time. To further compare the propagation capabilities of the proposed method with other methods, we selected the top 20 nodes from the node sets obtained by each algorithm as the initial activation nodes for the SB-IC model and observed the total number of activated nodes in the SB-IC model over 25 timesteps. The activation probabilities $p_N$ and $p_I$ of node u activating node v on different networks were set as $\langle d\rangle /\langle d^2\rangle$ and $(\langle d\rangle /\langle d^2\rangle ·\mathrm{Sim}(u,v))$, respectively. We conducted 10,000 Monte Carlo simulations and took the average value as the final result of influence propagation. The experimental results on nine real-world datasets are shown in Figure 5.

Figure 5 illustrates the temporal change in influence propagation when the first 20 nodes are selected as the initial activation nodes for the SB-IC model. The red curve represents the temporal change in influence using the PaC algorithm. Although the PaC algorithm’s influence may not be optimal during the initial stages of propagation, its performance consistently outperforms other algorithms as the propagation process stabilizes. In terms of propagation speed and steady-state influence coverage, the PaC algorithm demonstrates superior propagation efficiency compared to the other nine comparison algorithms across eight networks: dolphins, dublin, crime-moreno, citeseer, politician, US-Grid, pgp, and indochina-2004. Particularly in the dolphins, crime-moreno, citeseer, US-Grid, and indochina-2004 networks, the PaC algorithm’s performance is especially outstanding. However, in the hamsterster network, when the influence propagation in the network has not yet reached a steady state, the PaC algorithm’s performance is comparable to that of DC, GGC, LSS, LGC, NPIC, and EPC. This is primarily because the hamsterster network contains a large number of nodes with degree 1, while a small number of nodes occupy the core positions of the network, making it difficult to establish a significant lead during the initial stages of propagation. However, as the propagation process progresses, by the 7th time step, the propagation ranges of other algorithms gradually stabilize, while the PaC algorithm’s propagation range continues to grow, ultimately achieving a steady-state influence coverage range that remains superior to that of other comparison algorithms. Research indicates that the PaC algorithm possesses a significant advantage in terms of absolute influence coverage.

5.4. The Comparison of Coverage Redundancy

According to the literature [52], the more dispersed the distribution of seed nodes, the smaller the overlapping areas of their propagation influence become, thereby making the propagation effects triggered by the seed nodes more pronounced. To quantify the dispersion of seed nodes, we used the average distance between seed nodes as a metric. A larger average distance indicates that the seed nodes are more dispersed, resulting in smaller overlapping influence areas. Specifically, we calculated the average of the shortest paths between seed nodes to represent this distance. If there was no path between nodes u and v, the shortest path between nodes u and v was defined as $r+1$, where r was the network diameter.

Table 2. Influence spreading comparison across datasets and algorithms.

Dataset	k	Algorithms
		PaC	DC	KShell	GGC	LSS	LGC	NPIC	EPC
dolphins	2	5.500	5.000	5.000	5.000	5.000	5.000	5.000	5.000
	4	4.500	3.375	3.375	3.375	3.875	3.250	3.250	3.250
	6	3.944	3.389	2.722	2.778	3.222	2.889	2.889	2.889
	8	3.563	3.313	2.906	2.719	2.750	2.594	2.594	2.594
	10	3.340	3.060	2.860	2.480	2.60	2.90	2.640	2.820
	12	3.181	3.125	2.708	2.403	2.556	2.958	2.444	2.958
	14	3.265	3.031	2.745	2.551	2.500	2.745	2.745	2.745
	16	3.352	2.906	2.703	2.484	2.508	2.633	2.633	2.633
	18	3.556	2.975	2.846	2.630	2.463	2.759	2.759	2.759
	20	3.625	2.905	2.890	2.605	2.375	2.745	2.745	2.745
	22	3.868	2.872	2.851	2.574	2.322	2.694	2.686	2.686
	24	3.931	2.816	2.792	2.611	2.417	2.656	2.656	2.656
dublin	2	5.500	6.000	5.500	6.000	6.000	6.000	5.500	6.000
	4	3.875	3.875	3.500	3.500	3.625	3.875	3.625	3.875
	6	3.111	3.111	2.778	3.000	3.167	3.167	2.944	3.111
	8	3.094	2.875	2.375	2.719	2.750	2.875	2.563	2.875
	10	2.920	2.760	2.100	2.680	2.500	2.640	2.360	2.620
	12	3.056	2.681	1.972	2.542	2.444	2.639	2.194	2.528
	14	3.010	2.663	1.918	2.490	2.337	2.561	2.051	2.561
	16	2.914	2.531	1.820	2.430	2.320	2.469	2.039	2.492
	18	2.975	2.562	1.710	2.377	2.290	2.444	1.963	2.444
	20	3.050	2.500	1.645	2.350	2.300	2.465	1.905	2.400
	22	3.140	2.475	1.649	2.360	2.264	2.426	1.855	2.426
	24	3.229	2.524	1.597	2.500	2.302	2.417	1.913	2.385
crime-moreno	2	7.000	7.000	6.000	7.000	7.000	7.000	7.000	7.000
	4	4.750	4.750	3.875	4.750	4.750	4.750	4.750	4.750
	6	4.389	4.056	3.444	4.056	4.056	4.056	4.056	4.056
	8	4.063	3.938	3.156	3.781	3.781	3.969	3.781	3.969
	10	3.960	3.700	2.960	3.620	3.580	3.700	3.700	3.700
	12	3.917	3.667	2.819	3.556	3.556	3.667	3.667	3.667
	14	3.929	3.592	2.714	3.520	3.490	3.510	3.510	3.510
	16	3.891	3.602	2.633	3.469	3.453	3.508	3.508	3.508
	18	3.883	3.568	2.568	3.395	3.383	3.500	3.457	3.457
	20	3.910	3.535	2.505	3.380	3.315	3.480	3.445	3.445
	22	3.942	3.521	2.603	3.339	3.335	3.446	3.446	3.446
	24	3.983	3.545	2.712	3.337	3.358	3.465	3.441	3.441
hamsterster	5	3.160	3.400	3.000	3.240	3.080	3.240	3.240	3.240
	10	2.500	2.400	2.000	2.300	2.420	2.400	2.300	2.400
	15	2.333	2.129	1.667	2.084	2.147	2.129	2.129	2.129
	20	2.350	2.010	1.500	1.940	2.035	1.970	1.975	1.970
	25	2.302	1.944	1.400	1.902	1.938	1.944	1.886	1.922
	30	2.316	1.922	1.836	1.873	1.933	1.907	1.867	1.907
	35	2.564	1.904	2.055	1.847	1.909	1.893	1.828	1.883
	40	2.636	1.893	2.195	1.839	1.884	1.893	1.801	1.873
	45	2.794	1.892	2.246	1.846	1.853	1.878	1.779	1.844
	50	2.818	1.868	2.218	1.837	1.862	1.850	1.792	1.839
	55	2.831	1.836	2.205	1.830	1.853	1.837	1.774	1.825
	60	2.936	1.816	2.186	1.822	1.847	1.816	1.770	1.813
citeseer	5	7.560	8.840	6.840	8.520	7.080	8.760	7.000	8.520
	10	6.980	5.720	4.140	5.320	4.400	5.720	4.460	5.360
	15	6.796	5.471	3.222	4.342	3.578	4.973	4.244	4.644
	20	6.735	5.380	2.960	4.055	3.170	4.355	3.675	4.360
	25	6.667	5.195	2.882	3.746	2.987	4.018	3.387	3.995
	30	6.578	5.704	2.776	3.747	2.882	3.969	3.282	3.818
	35	6.582	5.346	2.770	3.648	2.788	4.350	3.137	3.761
	40	7.046	5.255	3.645	3.553	2.701	4.630	3.284	3.878
	45	7.157	5.140	4.184	3.651	2.680	4.512	3.398	4.108
	50	7.271	4.978	4.040	3.838	2.705	4.384	3.423	4.262
	55	7.530	4.964	3.898	3.740	2.701	4.420	3.346	4.281
	60	7.661	4.928	3.779	3.882	2.857	4.391	3.307	4.171
politician	5	3.800	4.440	3.880	4.200	3.800	4.360	3.800	4.360
	10	3.200	2.860	2.560	2.820	2.560	2.820	2.720	2.820
	15	3.222	2.858	2.040	2.404	2.236	2.502	2.449	2.502
	20	3.040	2.780	1.840	2.290	2.040	2.480	2.255	2.480
	25	2.978	2.661	1.723	2.270	1.960	2.347	2.107	2.315
	30	3.047	2.547	1.696	2.269	1.947	2.442	1.984	2.347
	35	3.083	2.520	1.612	2.282	1.981	2.487	2.017	2.370
	40	3.156	2.529	1.603	2.243	2.089	2.421	2.054	2.390
	45	3.209	2.492	1.584	2.286	2.126	2.415	2.075	2.360
	50	3.240	2.506	1.558	2.295	2.152	2.398	2.101	2.382
	55	3.304	2.528	1.549	2.279	2.149	2.467	2.059	2.428
	60	3.319	2.565	1.540	2.307	2.217	2.497	2.137	2.497
US-Grid	5	21.640	26.040	10.520	17.400	10.680	15.240	17.560	15.240
	10	16.160	19.080	6.040	12.820	9.680	12.680	16.620	11.300
	15	16.084	15.978	7.098	10.884	10.716	11.604	16.164	11.604
	20	16.250	15.525	7.080	10.880	13.330	12.100	15.330	11.625
	25	16.181	17.470	6.670	12.670	13.707	12.014	14.747	11.611
	30	16.196	17.311	6.118	12.231	12.713	12.309	14.544	12.180
	35	16.019	16.432	5.767	11.828	12.817	11.540	14.822	11.356
	40	16.239	15.748	6.365	12.226	13.899	11.333	14.644	11.726
	45	15.960	15.511	9.611	12.616	14.705	12.003	14.371	11.597
	50	15.779	16.338	12.365	12.835	14.878	11.865	14.666	11.865
	55	15.961	16.753	14.548	12.752	14.845	12.129	14.658	11.760
	60	15.974	16.627	15.972	13.081	15.172	12.082	14.679	11.711
pgp	5	6.120	6.360	5.80	6.360	5.960	5.960	5.960	5.960
	10	4.280	4.680	3.460	3.960	3.640	3.940	3.780	3.940
	15	3.827	4.040	2.627	3.516	3.000	3.364	2.991	3.364
	20	3.880	3.555	2.230	3.205	2.645	3.170	2.630	3.100
	25	3.979	3.317	2.002	2.978	2.466	2.990	2.389	2.949
	30	4.047	3.291	1.849	2.940	2.522	3.044	2.351	2.787
	35	4.024	3.242	1.749	2.909	2.419	2.956	2.365	2.783
	40	4.151	3.116	1.685	2.815	2.464	2.960	2.309	2.736
	45	4.318	3.034	1.726	2.784	2.421	2.934	2.211	2.714
	50	4.282	2.984	1.936	2.853	2.397	2.931	2.121	2.793
	55	4.319	2.925	1.992	2.893	2.377	2.896	2.132	2.751
	60	4.449	2.885	2.034	2.871	2.383	2.829	2.141	2.767
indochina-2004	5	8.080	7.920	6.400	8.240	8.720	7.200	6.400	7.200
	10	6.160	5.940	3.700	5.640	5.520	4.660	3.700	4.660
	15	5.724	5.200	2.800	5.173	4.293	3.813	3.209	3.813
	20	5.620	5.260	2.350	4.815	4.315	3.425	2.860	3.210
	25	5.363	5.206	2.080	4.611	3.779	3.456	2.499	3.456
	30	5.256	4.896	1.900	4.420	3.400	3.507	2.293	3.293
	35	5.144	4.596	1.771	4.377	3.229	3.445	2.460	3.198
	40	5.095	4.294	1.675	4.316	3.344	3.609	2.365	3.336
	45	5.146	4.090	1.600	4.118	3.323	4.041	2.655	3.670
	50	5.151	4.076	1.540	4.039	3.318	3.911	2.660	3.911
	55	5.120	3.915	2.446	4.005	3.326	3.786	2.784	3.759
	60	5.268	3.919	3.083	3.937	3.312	3.708	3.298	3.696

shows the average distance corresponding to different numbers of seed nodes in nine real networks.

As indicated by the results in Table 2, the PaC algorithm we proposed outperforms the other nine algorithms in both the dolphins and crime-moreno networks. In the seven networks of dublin, hamsterster, citeseer, politician, pgp, and indochina-2004, the PaC algorithm also demonstrates superior performance compared to other algorithms in the majority of cases. Through the analysis of Table 2, we also found that as the number of seed nodes selected in the network increases, the advantage of the PaC algorithm in terms of average distance becomes increasingly evident, showing a more pronounced superiority over other algorithms. However, in the US-Grid network, the PaC algorithm’s optimal average distance is second only to the DC algorithm.

As shown in

Table 3. Network Data Statistics of US-Grid.

Density	0.0005
Maximum degree	19
Average number of triangles	0.3953
Average clustering coefficient	0.08010

, the US-Grid is characterized by an extremely low density (0.0005), together with a low average number of triangles (0.3953) and a low average clustering coefficient (0.08010). These metrics collectively reveal a topology that can be described as a “tree-star” hybrid structure. The sparse connectivity inherent in such a topology reduces redundant paths, thereby simplifying path-selection decisions. Furthermore, this structure naturally designates a small set of high-degree nodes as key nodes. Consequently, the DC algorithm can leverage these hub nodes effectively, which explains its improved average-path-length performance in this network. However, across most datasets, the PaC algorithm demonstrates a significant advantage over the nine comparison algorithms in terms of avoiding influence overlapping.

5.5. Ablation Experiment

To verify the effectiveness of the PaC algorithm in reducing the problem of influence overlapping by measuring the interaction relationships between seed nodes, we conducted experiments comparing the average distance between seed nodes using the PaC algorithm and the PaC-h algorithm. The PaC-h algorithm removed the relative height $\mathsf{\Delta }h$ component from the PaC algorithm and directly selectd the k nodes with the highest influence values as seed nodes after completing the initial influence assessment. The experimental results are shown in Figure 6.

Figure 6 clearly illustrates the comparison between the PaC and the PaC-h in terms of average distance. In the figure, the yellow bar and the green bar represent the average distance between nodes under different numbers of seed nodes for the PaC and the PaC-h, respectively. The experimental results demonstrate that under all tested conditions, the average distance achieved by the PaC is consistently better than that of the PaC-h algorithm. Unlike the PaC-h, which only performs an initial influence assessment, the PaC further considers the interactions between seed nodes. By incorporating a well-designed $\mathsf{\Delta }h$, the PaC effectively mitigates the issue of influence overlapping, resulting in a more dispersed distribution of the selected seed nodes. This strategic design enables the PaC to better balance node influence and distribution uniformity when selecting seed nodes, thereby significantly enhancing the overall influence spreading effect.

Furthermore, we conducted a detailed comparison of the substantial impact of different values of the free parameter p on the influence spreading of the PaC algorithm to evaluate its sensitivity to this parameter. We selected 10, 20, and 30 nodes as the initially activated nodes in the SB-IC model, and assigned the free parameter $p=\langle d\rangle /\langle d^2\rangle$, $p=0.1$, $p=0.5$, and also examined the case where the free parameter p was removed. The total number of activated nodes in the SB-IC model was observed after the information propagation reached a steady state. Monte Carlo simulations were performed 10,000 times, and the average value was taken as the final result of influence propagation.

As evidenced by the results in

Table 4. Comparison of the influence spreading of free parameter p in the PaC algorithm.

	(a) dolphins				(b) dublin				(c) crime-moreno
	PaC	PaC, p = 0.1	PaC, p = 0.5	PaC-p	PaC	PaC, p = 0.1	PaC, p = 0.5	PaC-p	PaC	PaC, p = 0.1	PaC, p = 0.5	PaC-p
10	29.79	28.35	29.51	27.66	124.49	118.06	122.07	113.80	75.38	72.12	74.00	71.12
20	39.76	36.73	38.48	35.61	146.21	141.58	143.25	128.28	109.61	105.71	108.78	104.11
30	47.87	42.52	47.18	41.16	162.57	154.81	160.66	140.68	138.69	133.81	136.09	125.75
	(d) hamsterster				(e) citeseer				(f) politician
	PaC	PaC, p = 0.1	PaC, p = 0.5	PaC-p	PaC	PaC, p = 0.1	PaC, p = 0.5	PaC-p	PaC	PaC, p = 0.1	PaC, p = 0.5	PaC-p
10	168.09	166.19	164.04	163.54	168.12	134.66	152.84	128.58	330.06	298.21	331.31	267.98
20	208.69	194.71	205.25	192.78	214.75	181.55	209.99	161.76	422.59	355.27	417.38	351.22
30	236.48	224.51	236.28	212.51	248.97	209.03	244.10	172.37	474.58	434.98	459.09	375.31
	(g) US-Grid				(h) pgp				(i) indochina-2004
	PaC	PaC, p = 0.1	PaC, p = 0.5	PaC-p	PaC	PaC, p = 0.1	PaC, p = 0.5	PaC-p	PaC	PaC, p = 0.1	PaC, p = 0.5	PaC-p
10	226.36	197.74	216.78	167.65	524.56	500.50	522.18	500.71	1245.81	1220.87	1228.70	1195.42
20	317.27	287.24	307.78	198.98	593.33	531.56	564.49	506.63	1319.11	1278.30	1302.22	1220.15
30	386.11	352.54	378.62	258.71	647.42	539.63	623.83	530.57	1371.87	1322.95	1355.90	1236.27

, when the free parameter $p=\langle d\rangle /\langle d^2\rangle$, the algorithm demonstrates superior performance across all nine datasets, significantly outperforming the control groups (where $p=0.1$, $p=0.5$, or the parameter p is entirely removed). Concurrently, the most pronounced performance degradation is observed upon the removal of the free parameter p, with an average decline of 18.79%. This declining trend is most prominent in the US-Grid dataset, where the average performance drop reaches 47.91%. Specifically, for the US-Grid dataset with 20 initially selected seed nodes, the PaC algorithm achieves a 59.45% improvement over the PaC-p variant. This remarkable discrepancy arises because, in the absence of the parameter p, the metric $\mathsf{\Delta }{h}_u$ fails to effectively capture the interactions between nodes. Consequently, the algorithm exhibits a bias towards selecting nodes with high initial influence. Due to the presence of influence overlap effects, this bias can trap the algorithm in local optima during seed selection, preventing it from identifying the global optimal solution.

5.6. The Comparison of Influence Spreading on ISNs

To validate the performance of algorithms and diffusion models in real ISNs, we conducted a comparative evaluation on the Sinanet dataset, measuring the influence spreading of the PaC method against nine other baseline algorithms under both the SB-IC and IC models. The Sinanet dataset is constructed as a microblog user relationship network extracted from the sina-microblog website. It characterizes user interests by leveraging topic distributions derived from user activities across 10 forums, with these distributions obtained through the LDA topic model. The comparative results are illustrated in Figure 7.

In the Sinanet, the PaC achieved performance improvements of 2.25% and 0.1% in terms of influence spreading under the SB-IC and IC models, respectively. This effectively demonstrates the applicability and effectiveness of our algorithm and model in ISNs. However, it should be noted that the Sinanet was constructed by extracting user relationships limited to within three layers, which restricted the depth of the network. This structural constraint may have limited the full performance potential of PaC from being realized. Furthermore, compared to other algorithms, both K-shell and RCNN showed limitations in sufficiently identifying key nodes within the network. The K-shell method demonstrates a fundamental limitation in its reliance on core decomposition, which fails to discriminate nodes with identical core values—a critical shortcoming in networks containing structurally equivalent nodes. This simplification undermines its discriminative capacity, leading to suboptimal node rankings. RCNN exhibits notable limitations in generalizability when deployed across heterogeneous network topologies. The method’s strong dependency on localized structural features—while effective for homogeneous networks—impedes its adaptability to networks with divergent topological characteristics, such as scale-free or hierarchical structures. This constraint arises from the model’s insufficient capacity to encapsulate global influence propagation patterns, particularly in dynamic or large-scale networks where topological complexity escalates.

5.7. Statistical Comparison of PaC and DC Performance

To evaluate the performance of the PaC, we compared it with the DC on the SB-IC model using 10,000 Monte Carlo simulations for each method. Given the large sample size—which satisfies the Central Limit Theorem—and the confirmation of homogeneity of variances via Levene’s test ($F=0.074$, $p=0.785$), an independent-samples t-test was conducted to examine the difference in mean performance between the two algorithms. The results are presented in

Table 5. Statistical comparison of performance between PaC and DC algorithms.

Metric	PaC	DC
Sample size (n)	10,000	10,000
Mean (M)	100.95	100.31
Standard deviation ($SD$)	10.91	10.94
95% CI of the mean	[100.74, 101.16]	[100.09, 100.52]
Mean difference ($\mathsf{\Delta }M$)	0.64
95% CI of the mean difference	[0.34, 0.94]
t-statistic	4.14
Degrees of freedom ($df$)	19,998
p-value	$3.435607\times {10}^{-5}$

* Note: CI = confidence interval.

.

The independent-samples t-test revealed that PaC significantly outperformed DC, with $t\left(19,998\right)=4.14$, $p<0.001$. Specifically, the mean score of PaC ($M=100.95$, $SD=10.91$) was 0.64 points higher than that of DC ($M=100.31$, $SD=10.94$). The 95% confidence interval for this mean difference was [0.34, 0.94], which does not include zero. These results indicate that PaC exhibits a statistically significant and stable performance advantage over DC on the SB-IC model.

The SB-IC model and the PaC algorithm designed in this study can provide support for optimizing recommendation systems in e-commerce platforms. For instance, they enable dynamic adjustment of display strategies for related products, reducing influence overlap in word-of-mouth propagation. Simultaneously, by integrating findings from eWOM credibility researches [53,54], platforms can further incorporate user emotional response data, thereby refining marketing strategies and enhancing service efficiency.

6. Conclusions

This paper investigates the influence maximization problem in Interest-Based Social Networks (ISNs). Considering the impact of user interest preferences and server recommendation mechanisms on information diffusion, we first defined a “Social–Interest Hybrid Influence Maximization” (SIHIM) problem that integrates users’ social relationships and interest preferences. We then constructed a Server-Based Independent Cascading (SB-IC) model to simulate the influence propagation process. Evaluations based on influence spread and experiments on real-world datasets demonstrate that the proposed SB-IC model can more effectively model influence propagation in interest-based social networks compared to the conventional IC model. Furthermore, we propose the Pascal Centrality (PaC) method, which incorporates multi-attribute node features to identify key influential nodes in the network. Extensive experiments on nine real-world datasets showed that the proposed PaC method significantly outperforms baseline approaches, achieving average influence spread improvements of 7.04% under the SB-IC model and 5.22% under the IC model, surpassing nine other baseline methods. Additionally, ablation studies were conducted, fully verifying the role of relative height $\mathsf{\Delta }h$ alleviating influence overlap. In summary, this research provides a comprehensive solution for the influence maximization problem in interest-based social networks, and its superiority was thoroughly validated through extensive experiments.

The managerial implications of this study lie in providing a novel perspective for enterprises to conduct targeted marketing and public opinion management on interest-based social platforms. By synergistically considering social influence and interest matching, businesses can more precisely identify high-value influencers, optimize the allocation of marketing budgets, and achieve a dual dissemination effect combining word-of-mouth recommendations and platform-driven propagation. However, the current approach still has certain limitations, primarily including insufficient adaptability to the dynamic nature of user interests, an oversimplified simulation of complex platform recommendation algorithms, and a reliance on static network assumptions that cannot fully capture fully capture the dynamic evolution of network structures.

In future research, we plan to introduce social simulation techniques to construct dynamic models that better reflect real-world social networks, thereby further validating the applicability and effectiveness of the proposed method in complex network environments. Additionally, we will explore the method based on deep learning and data mining techniques to predict changes in user interests, thereby optimizing the selection strategy for seed nodes.