On Measuring Large Language Models Performance with Inferential Statistics
Abstract
1. Introduction
1.1. Objectives
- Develop a robust and efficient evaluation framework capable of withstanding the variability introduced by non-deterministic models.
- Establish confidence intervals for performance metrics in the evaluation scenario where access to individual outputs and gold standard labels is available.
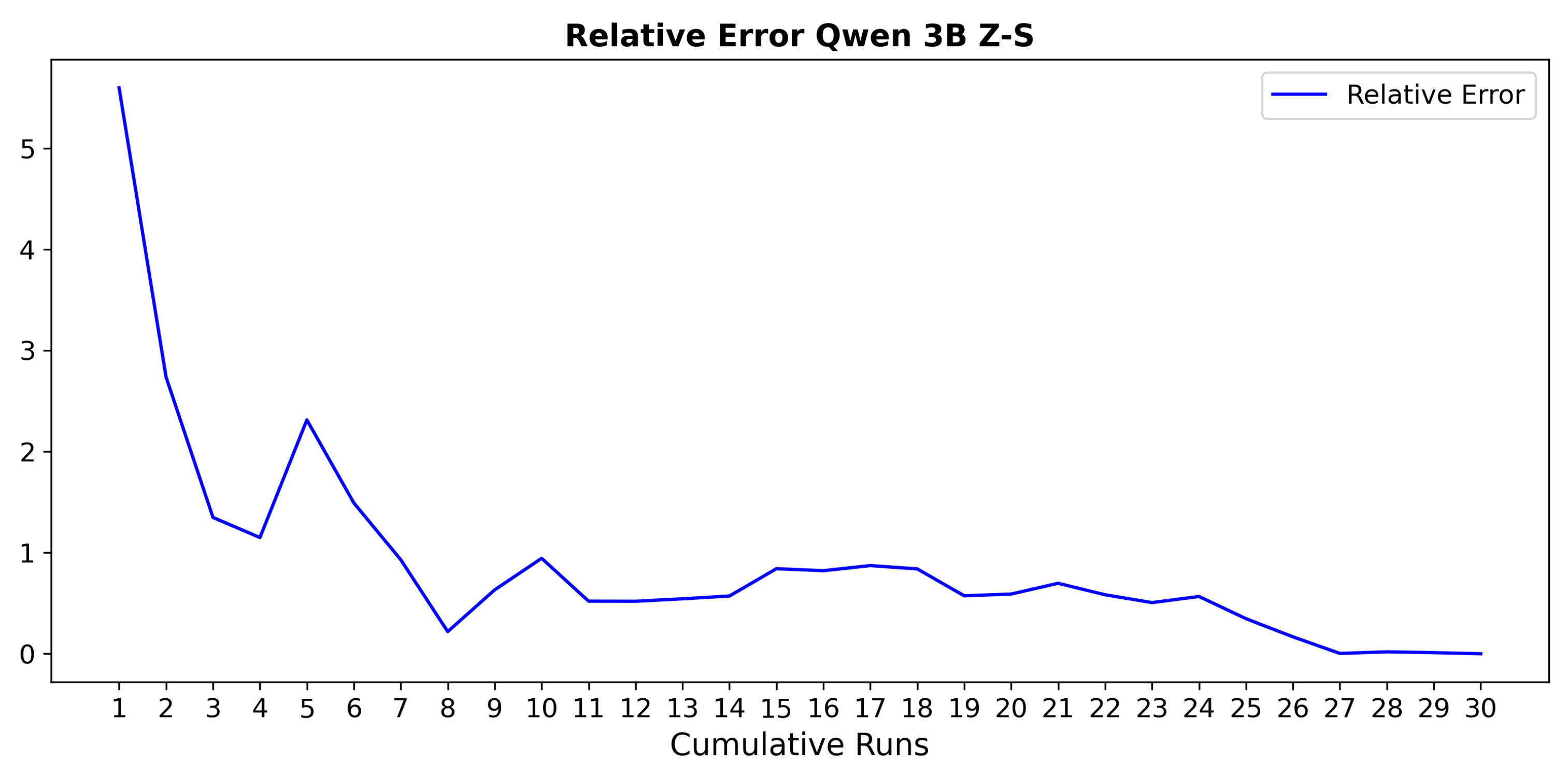
- Provide empirical evidence demonstrating the variability across multiple runs of a non-deterministic model and illustrate how the use of the proposed evaluation system can lead to more reliable and informative performance assessments.
1.2. Contributions
- Statistical analysis of evaluation variability: We provide empirical evidence showing that performance metrics obtained from single runs can vary significantly, highlighting the need for repeated evaluations to obtain reliable performance estimates.
- Confidence interval estimation: We propose a methodology for calculating confidence intervals for performance metrics. This method allows the uncertainty associated with model evaluation to be quantified.
- Model-independent assessment framework: The proposed methodology is designed to be robust to different model architectures and prompts.
1.3. Research Questions
- RQ1.
- Is a single run enough to evaluate the performance of a generative model, and do the results of multiple runs vary in a statistically significant way?
- RQ2.
- Can we estimate the true performance of a given approach by aggregating multiple runs with identical configurations?
- RQ3.
- Which statistical techniques provide the most reliable and efficient approximation of model performance variability in non-deterministic settings?
2. Experimentation Setting
2.1. Dataset
2.2. Evaluation Measure
3. Methodology
3.1. Performing Multiple Executions
3.2. Approximation of the Theoretical Distribution of Model Performance
- Let be the set of predicted labels and their corresponding true labels for run r, where l is the number of instances in the test set. The sample size l should be sufficiently large to obtain meaningful performance distributions. (A sufficiently large sample size reduces variability and ensures stable F1 estimates. Empirically, at least 30–50 examples per class are recommended, with larger sets (>300–1000) needed for reliable distributions and >5000 for complex or industrial settings. Small samples yield unstable, high-variance, or biased estimates.)
- Generate B bootstrap samples with replacement from the original set , obtaining B new datasets (), each of size l. Each contains a resampled set of predicted–true label pairs.
- For each bootstrap sample , compute the F1 score, denoted . This represents the model’s performance on the b-th resampled dataset.
- The set of bootstrap F1 scores defines the empirical distribution of model performance for run r, which we denote as .
- Estimate the theoretical F1 value for run r as the mean of the bootstrap scores:where provides a point estimate of the model’s expected F1 for this run.
3.3. Analysis of Aggregated F1 Means
3.4. Confidence Interval Estimation
- The B bootstrap values are sorted in ascending order to approximate the empirical distribution of .
- The confidence interval at level is defined by the and percentiles of the ordered bootstrap distribution:where denotes the j-th smallest value among the B estimates.
3.5. Proposed Evaluation Framework
| Algorithm 1 Instance-Level Bootstrapping Evaluation Framework |
| Require: Predictions from n runs, gold standard of size l, number of bootstrap samples B, confidence level Ensure: Combined distribution , mean estimate , confidence interval Concatenate predictions from all n runs into dataset of size for do Sample l pairs with replacement from Compute on end for Define empirical distribution Estimate mean performance: Define confidence interval: |
4. Running Example
4.1. Performing Multiple Executions
4.2. Approximation of the Theoretical Distribution of Model Performance
4.3. Analysis of Aggregated F1 Means
4.4. Confidence Interval Estimation
5. Comparison with State-of-the-Art Evaluation Methods
6. Discussion
7. Conclusions
8. Hardware and Computational Resources
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LLMs | Large Language Models |
| NLP | Natural Language Processing |
| CI | Confidence Interval |
Appendix A. Prompt Structure
- Blue: Instructional introduction or task formulation presented to the model.
- Green: Titles of narratives.
- Grey: Descriptive content associated with each narrative or sub-narrative.
- Red: System-level instructions or control tokens, where applicable.
- 1: The West as Immoral and Hostile:Identify tweets that depict Western countries, especially the US, as immoral, hostile, or decadent. Look for content where China is positioned as a victim of Western actions or policies.
- 2: China as a Benevolent Power:Classify tweets highlighting China’s peaceful and cooperative international stance. Include tweets that mention China’s contributions to global peace, support for international law, and economic development in other nations.
- 3: China’s Epic History:Detect tweets that discuss China’s historical resilience and achievements, particularly those crediting the Chinese Communist Party with overcoming adversities and leading national modernisation.
- 4: China’s Political System and Values:Look for tweets advocating for socialism with Chinese characteristics and portraying it as aligned with the will of the Chinese people. Tweets should suggest that China’s political system supports genuine democracy and global peace.
- 5: Success of the Chinese Communist Party’s Government:Identify tweets focusing on the government’s role in driving China’s technological, economic, and social advancements, such as achievements in 5G technology.
- 6: China’s Cultural, Natural, and Heritage Appeal:Classify tweets that promote Chinese culture, traditions, natural beauty, or heritage sites. This includes mentions of historical cities, cultural festivities, and natural landscapes.
- 1. Read carefully the tweet {tweet}
- 2. Determine which narrative(s) it supports based on the content and sentiment expressed. A tweet may align with at most 2 narratives if it incorporates elements from more than one category. It is possible that the tweet does not support any narrative.
- 3. You have to generate a JSON structure:
References
- Atil, B.; Aykent, S.; Chittams, A.; Fu, L.; Passonneau, R.J.; Radcliffe, E.; Rajagopal, G.R.; Sloan, A.; Tudrej, T.; Ture, F.; et al. Non-Determinism of “Deterministic” LLM Settings. arXiv 2025, arXiv:2408.04667. [Google Scholar] [CrossRef]
- Zhou, H.; Savova, G.; Wang, L. Assessing the Macro and Micro Effects of Random Seeds on Fine-Tuning Large Language Models. arXiv 2025, arXiv:2503.07329. [Google Scholar] [CrossRef]
- Xiao, Y.; Liang, P.P.; Bhatt, U.; Neiswanger, W.; Salakhutdinov, R.; Morency, L.P. Uncertainty Quantification with Pre-trained Language Models: A Large-Scale Empirical Analysis. arXiv 2022, arXiv:2210.04714. [Google Scholar] [CrossRef]
- Hendrycks, D.; Burns, C.; Basart, S.; Zou, A.; Mazeika, M.; Song, D.; Steinhardt, J. Measuring Massive Multitask Language Understanding. arXiv 2020, arXiv:2009.03300. [Google Scholar]
- Rein, D.; Hou, B.L.; Stickland, A.C.; Petty, J.; Pang, R.Y.; Dirani, J.; Michael, J.; Bowman, S.R. GPQA: A Graduate-Level Google-Proof Q&A Benchmark. arXiv 2023, arXiv:2311.12022. [Google Scholar] [CrossRef]
- Suzgun, M.; Scales, N.; Schärli, N.; Gehrmann, S.; Tay, Y.; Chung, H.W.; Chowdhery, A.; Le, Q.; Chi, E.; Zhou, D.; et al. Challenging BIG-Bench Tasks and Whether Chain-of-Thought Can Solve Them. In Proceedings of the Findings of the Association for Computational Linguistics: ACL 2023, Toronto, ON, Canada, 9–14 July 2023; Rogers, A., Boyd-Graber, J., Okazaki, N., Eds.; pp. 13003–13051. [Google Scholar] [CrossRef]
- Gema, A.P.; Leang, J.O.J.; Hong, G.; Devoto, A.; Mancino, A.C.M.; Saxena, R.; He, X.; Zhao, Y.; Du, X.; Madani, M.R.G.; et al. Are We Done with MMLU? arXiv 2025, arXiv:2406.04127. [Google Scholar] [CrossRef]
- Dietterich, T.G. Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithms. Neural Comput. 1998, 10, 1895–1923. [Google Scholar] [CrossRef]
- McNemar, Q. Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika 1947, 12, 153–157. [Google Scholar] [CrossRef]
- Bouckaert, R.R. Choosing Between Two Learning Algorithms Based on Calibrated Tests. In Proceedings of the Twentieth International Conference on International Conference on Machine Learning, Washington, DC, USA, 21–24 August 2003. [Google Scholar]
- Bouckaert, R.R. Estimating replicability of classifier learning experiments. In Proceedings of the Twenty-First International Conference on Machine Learning—ICML ’04, Banff, AB, Canada, 4–8 July 2004; p. 15. [Google Scholar] [CrossRef]
- Claridge-Chang, A.; Assam, P.N. Estimation statistics should replace significance testing. Nat. Methods 2016, 13, 108–109. [Google Scholar] [CrossRef]
- Masson, M.E.J. Using confidence intervals for graphically based data interpretation. Can. J. Exp. Psychol. = Rev. Can. Psychol. Exp. 2003, 57, 203–220. [Google Scholar] [CrossRef]
- Cai, B.; Luo, Y.; Guo, X.; Pellegrini, F.; Pang, M.; Moor, C.d.; Shen, C.; Charu, V.; Tian, L. Bootstrapping the Cross-Validation Estimate. arXiv 2025, arXiv:2307.00260. [Google Scholar] [CrossRef]
- Cumming, G. Understanding the New Statistics: Effect Sizes, Confidence Intervals, and Meta-Analysis; Routledge: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Bestgen, Y. Please, Don’t Forget the Difference and the Confidence Interval when Seeking for the State-of-the-Art Status. In Proceedings of the Thirteenth Language Resources and Evaluation Conference, Marseille, France, 20–25 June 2022; pp. 5956–5962. [Google Scholar]
- Berrar, D.; Lozano, J.A. Significance tests or confidence intervals: Which are preferable for the comparison of classifiers? J. Exp. Theor. Artif. Intell. 2013, 25, 189–206. [Google Scholar] [CrossRef]
- Soboroff, I. Computing Confidence Intervals for Common IR Measures. In Proceedings of the EVIA@ NTCIR, Tokyo, Japan, 9–12 December 2014. [Google Scholar]
- Liapunov, A.M. Nouvelle Forme du Théorème sur la Limite de Probabilité; Imperatorskaia akademīia nauk,1901; Google-Books-ID: XDZinQEACAAJ. Available online: https://books.google.co.jp/books/about/Nouvelle_forme_du_th%C3%A9or%C3%A8me_sur_la_limi.html?id=XDZinQEACAAJ&redir_esc=y (accessed on 6 September 2025).
- Fraile-Hernández, J.M.; Peńas, A.; Moral, P. Automatic Identification of Narratives: Evaluation Framework, Annotation Methodology, and Dataset Creation. IEEE Access 2025, 13, 11734–11753. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap Methods: Another Look at the Jackknife. Ann. Stat. 1979, 7, 569–593. [Google Scholar] [CrossRef]
- Hall, P. Theoretical Comparison of Bootstrap Confidence Intervals. Ann. Stat. 1988, 16, 927–953. [Google Scholar] [CrossRef]
- Qwen; Yang, A.; Yang, B.; Zhang, B.; Hui, B.; Zheng, B.; Yu, B.; Li, C.; Liu, D.; Huang, F.; et al. Qwen2.5 Technical Report. arXiv 2025, arXiv:2412.15115. [Google Scholar] [CrossRef]
- Bouthillier, X.; Delaunay, P.; Bronzi, M.; Trofimov, A.; Nichyporuk, B.; Szeto, J.; Sepah, N.; Raff, E.; Madan, K.; Voleti, V.; et al. Accounting for Variance in Machine Learning Benchmarks. arXiv 2021, arXiv:2103.03098. [Google Scholar] [CrossRef]
- Bayle, P.; Bayle, A.; Janson, L.; Mackey, L. Cross-validation Confidence Intervals for Test Error. arXiv 2020, arXiv:2007.12671. [Google Scholar] [CrossRef]
- Jayasinghe, G.K.; Webber, W.; Sanderson, M.; Dharmasena, L.S.; Culpepper, J.S. Evaluating non-deterministic retrieval systems. In Proceedings of the 37th International ACM SIGIR Conference on Research & Development in Information Retrieval, Gold Coast, Australia, 6–11 July 2014; pp. 911–914. [Google Scholar] [CrossRef]
- Efron, B. Better Bootstrap Confidence Intervals. J. Am. Stat. Assoc. 1987, 82, 171–185. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall/CRC: New York, NY, USA, 1994. [Google Scholar] [CrossRef]
- Quenouille, M.H. Approximate Tests of Correlation in Time-Series. J. R. Stat. Soc. Ser. B (Methodol.) 1949, 11, 68–84. [Google Scholar] [CrossRef]
- Politis, D.N.; Romano, J.P. The Stationary Bootstrap. J. Am. Stat. Assoc. 1994, 89, 1303–1313. [Google Scholar] [CrossRef]

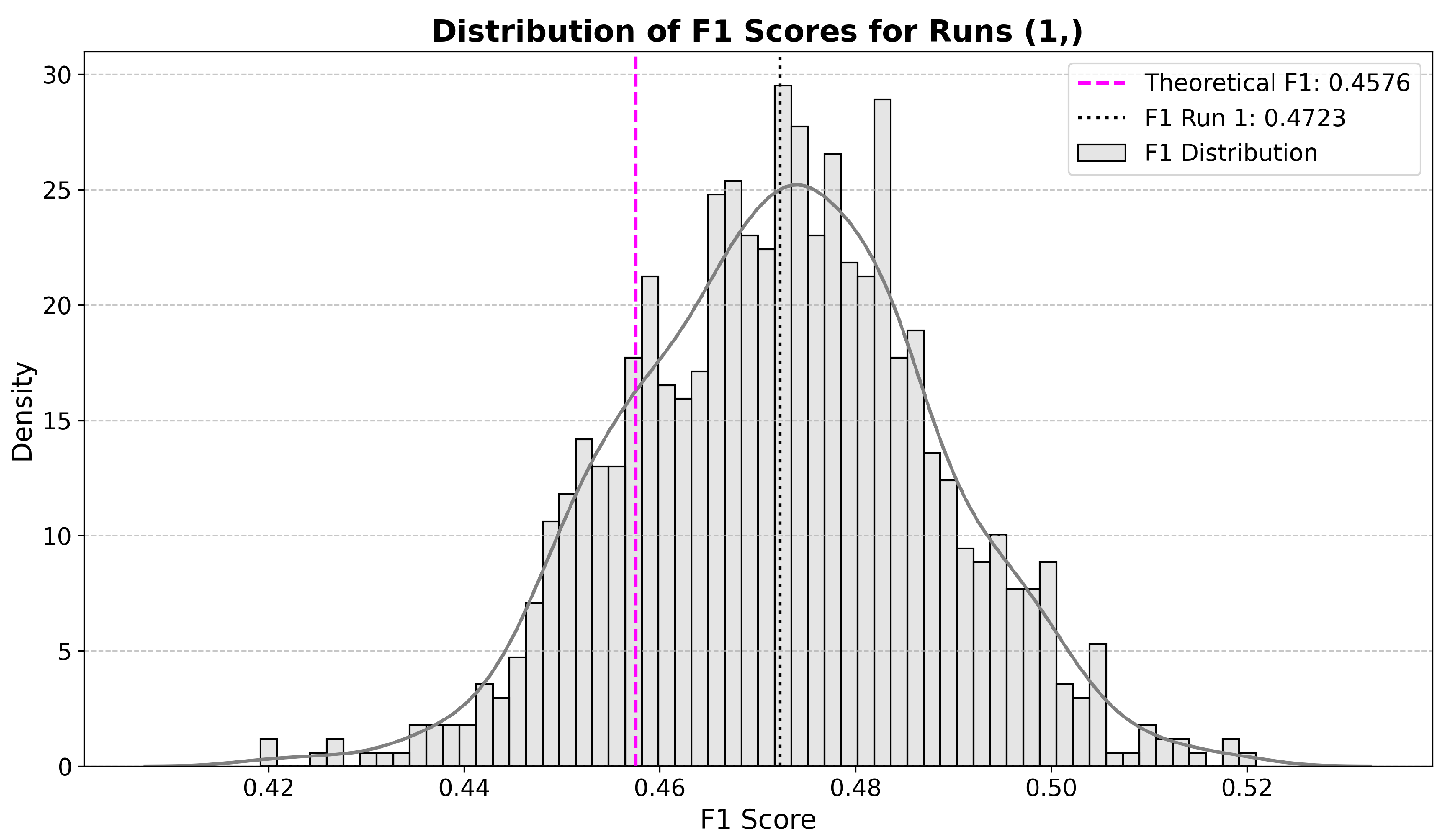
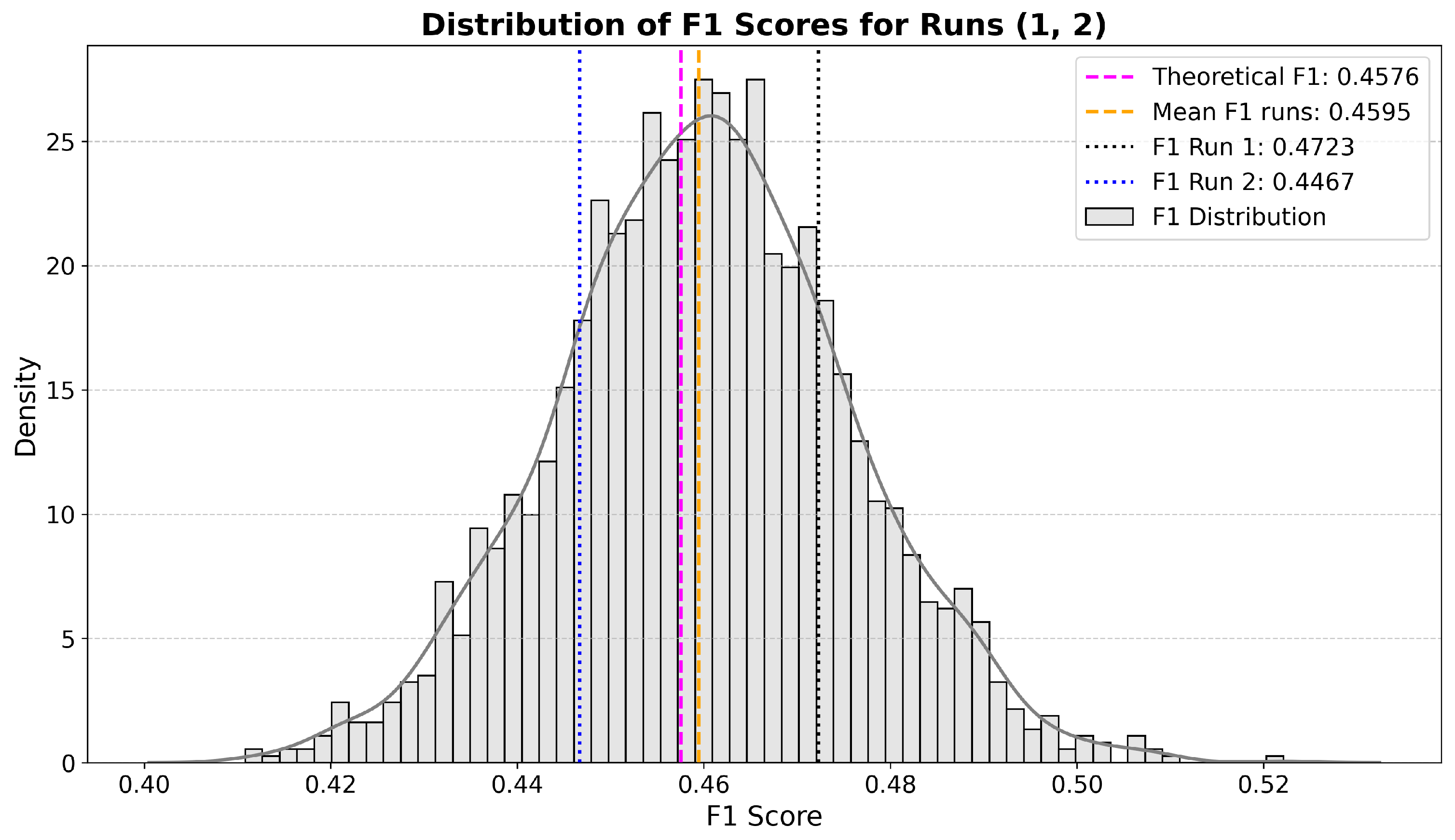
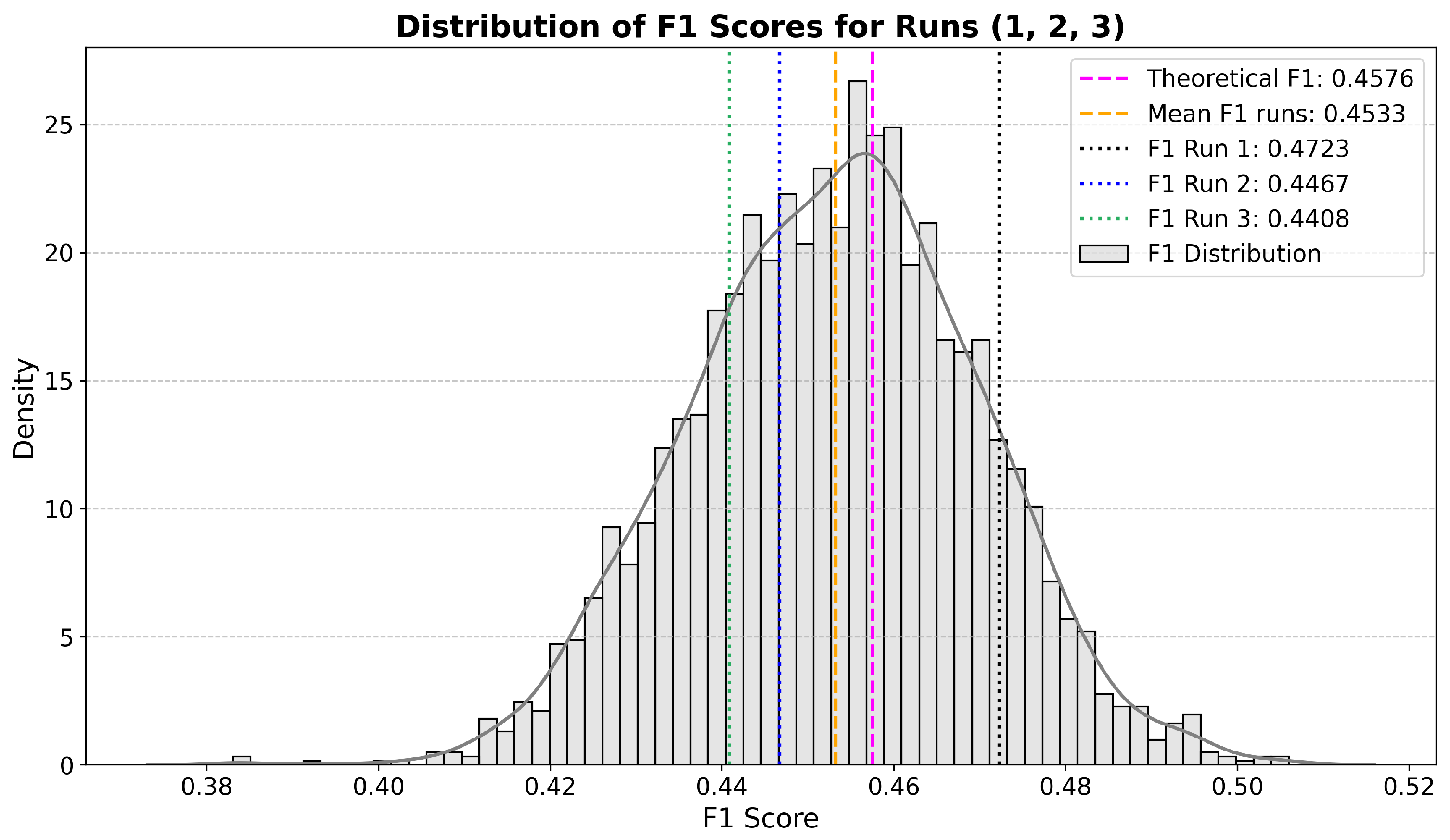
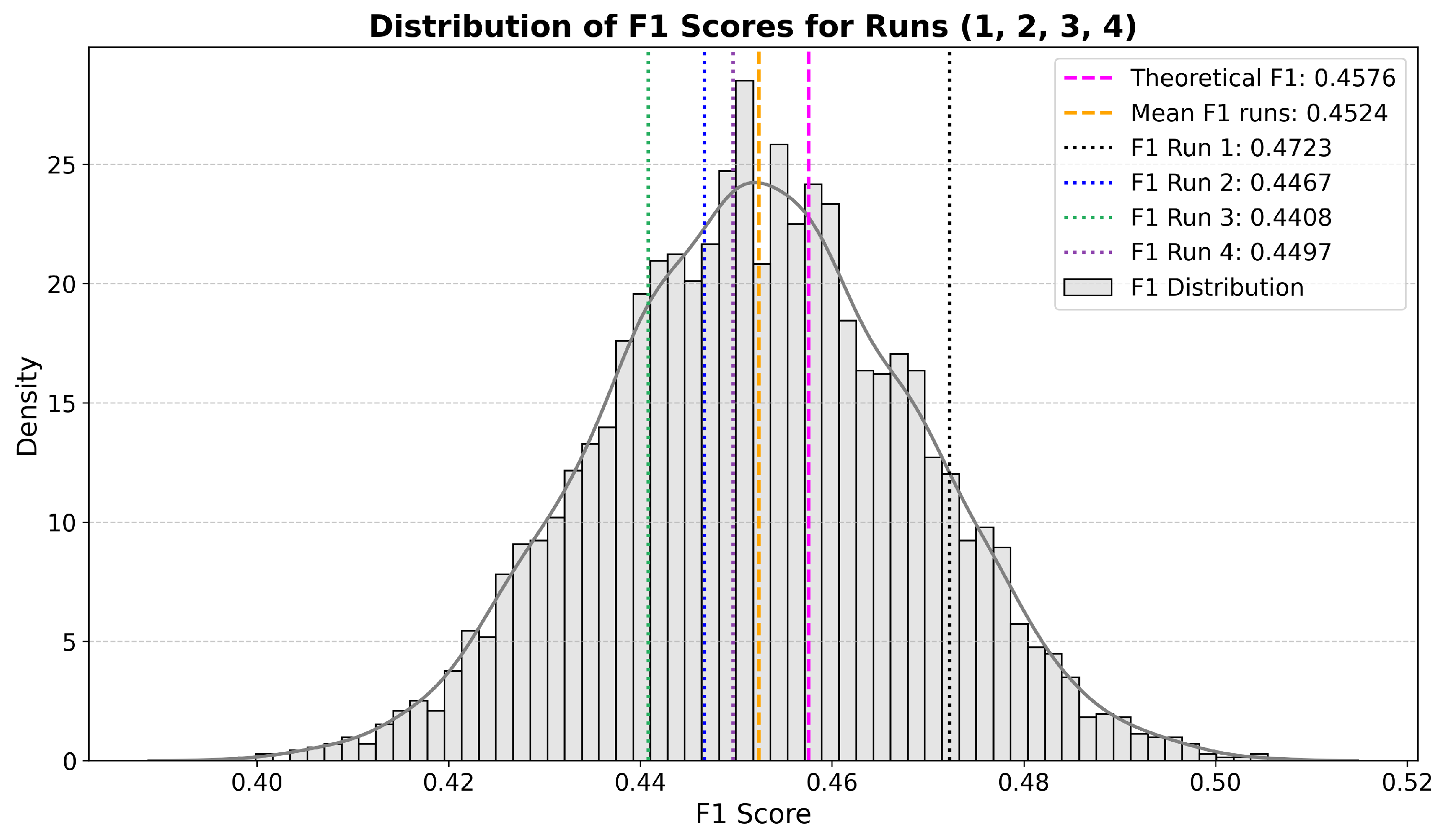
| Region/Nar. | Yes | Leaning | No | Region/Nar. | Yes | Leaning | No |
|---|---|---|---|---|---|---|---|
| CH1 | 21 | 8 | 171 | RU1 | 34 | 12 | 154 |
| CH2 | 65 | 9 | 126 | RU2 | 4 | 15 | 181 |
| CH3 | 6 | 0 | 194 | RU3 | 30 | 28 | 142 |
| CH4 | 24 | 24 | 152 | RU4 | 25 | 19 | 156 |
| CH5 | 12 | 21 | 167 | RU5 | 22 | 25 | 153 |
| CH6 | 22 | 11 | 167 | RU6 | 14 | 10 | 176 |
| China | 150 | 73 | 977 | Russia | 129 | 109 | 962 |
| EU1 | 14 | 10 | 176 | US1 | 23 | 1 | 175 |
| EU2 | 29 | 21 | 150 | US2 | 19 | 5 | 175 |
| EU3 | 24 | 23 | 153 | US3 | 46 | 11 | 142 |
| EU4 | 31 | 23 | 146 | US4 | 66 | 23 | 110 |
| EU5 | 79 | 33 | 88 | US5 | 37 | 18 | 144 |
| EU6 | 48 | 65 | 87 | US6 | 11 | 4 | 184 |
| European Union | 225 | 175 | 800 | USA | 202 | 62 | 930 |
| Runs | CI | CI |
|---|---|---|
| (1) | (0.4424, 0.5027) | 0.0602 |
| (1, 2) | (0.4292, 0.4905) | 0.0613 |
| (0.4211, 0.4841) | 0.0630 | |
| (0.4203, 0.4838) | 0.0634 | |
| (0.4255, 0.4889) | 0.0634 |
| Sorted Runs | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| … | |||||||||
| ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | |
| - | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | |
| - | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | |
| - | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | |
| - | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | |
| - | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | |
| - | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | |
| - | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | |
| - | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | |
| - | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | |
| - | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | |
| - | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | |
| - | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | |
| - | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | |
| - | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | |
| - | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | |
| - | - | - | - | - | - | - | ✓ | ✗ | |
| - | - | - | - | - | - | - | - | ✗ | |
| Runs | Our | % | t Student | % | Percentile | % | BCa | % | t-Bootstrap | % |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | (0.44, 0.50) | 63 | - | - | - | - | - | - | - | - |
| 2 | (0.43, 0.49) | 83 | (0.30, 0.62) | 100 | (0.45, 0.47) | 56 | (0.45, 0.47) | 56 | (0.46, 0.46) | 0 |
| 3 | (0.42, 0.48) | 100 | (0.41, 0.49) | 100 | (0.44, 0.47) | 66 | (0.44, 0.47) | 66 | (0.44, 0.51) | 66 |
| 4 | (0.42, 0.48) | 100 | (0.43, 0.47) | 80 | (0.44, 0.47) | 53 | (0.44, 0.47) | 53 | (0.44, 0.50) | 73 |
| 5 | (0.43, 0.49) | 97 | (0.44, 0.48) | 70 | (0.44, 0.47) | 53 | (0.45, 0.47) | 53 | (0.44, 0.52) | 70 |
| 6 | (0.42, 0.49) | 100 | (0.44, 0.47) | 70 | (0.44, 0.47) | 53 | (0.44, 0.47) | 56 | (0.44, 0.49) | 73 |
| 7 | (0.42, 0.48) | 100 | (0.44, 0.47) | 70 | (0.44, 0.46) | 53 | (0.44, 0.47) | 56 | (0.44, 0.49) | 73 |
| 8 | (0.42, 0.48) | 100 | (0.43, 0.46) | 63 | (0.44, 0.46) | 57 | (0.44, 0.46) | 57 | (0.44, 0.48) | 73 |
| 9 | (0.42, 0.48) | 100 | (0.44, 0.46) | 60 | (0.44, 0.46) | 53 | (0.44, 0.46) | 53 | (0.44, 0.47) | 63 |
| 10 | (0.42, 0.48) | 100 | (0.44, 0.46) | 57 | (0.44, 0.46) | 50 | (0.44, 0.46) | 50 | (0.44, 0.47) | 60 |
| 11 | (0.42, 0.48) | 100 | (0.44, 0.46) | 57 | (0.44, 0.46) | 50 | (0.44, 0.46) | 53 | (0.44, 0.46) | 57 |
| 12 | (0.42, 0.48) | 100 | (0.44, 0.46) | 57 | (0.44, 0.46) | 50 | (0.44, 0.46) | 50 | (0.44, 0.46) | 53 |
| 13 | (0.42, 0.48) | 100 | (0.44, 0.46) | 50 | (0.44, 0.46) | 47 | (0.44, 0.46) | 47 | (0.44, 0.46) | 53 |
| 14 | (0.42, 0.48) | 100 | (0.44, 0.46) | 50 | (0.44, 0.46) | 43 | (0.44, 0.46) | 43 | (0.44, 0.46) | 47 |
| 15 | (0.42, 0.48) | 100 | (0.44, 0.46) | 43 | (0.44, 0.46) | 40 | (0.44, 0.46) | 40 | (0.44, 0.46) | 47 |
| 16 | (0.42, 0.48) | 100 | (0.44, 0.46) | 43 | (0.44, 0.46) | 40 | (0.44, 0.46) | 40 | (0.44, 0.46) | 43 |
| 17 | (0.42, 0.48) | 100 | (0.44, 0.46) | 40 | (0.44, 0.46) | 40 | (0.44, 0.46) | 40 | (0.44, 0.46) | 40 |
| 18 | (0.42, 0.48) | 100 | (0.44, 0.46) | 40 | (0.44, 0.46) | 40 | (0.44, 0.46) | 40 | (0.44, 0.46) | 40 |
| 19 | (0.42, 0.48) | 100 | (0.44, 0.46) | 43 | (0.44, 0.46) | 40 | (0.44, 0.46) | 40 | (0.44, 0.46) | 43 |
| 20 | (0.42, 0.48) | 100 | (0.44, 0.46) | 43 | (0.44, 0.46) | 36 | (0.44, 0.46) | 40 | (0.44, 0.46) | 43 |
| 21 | (0.42, 0.48) | 100 | (0.44, 0.46) | 40 | (0.44, 0.46) | 40 | (0.44, 0.46) | 40 | (0.44, 0.46) | 40 |
| 22 | (0.42, 0.48) | 100 | (0.44, 0.46) | 40 | (0.44, 0.46) | 36 | (0.44, 0.46) | 36 | (0.44, 0.46) | 40 |
| 23 | (0.42, 0.48) | 100 | (0.44, 0.46) | 36 | (0.44, 0.46) | 36 | (0.44, 0.46) | 36 | (0.44, 0.46) | 36 |
| 24 | (0.42, 0.48) | 100 | (0.44, 0.46) | 36 | (0.44, 0.45) | 36 | (0.44, 0.45) | 36 | (0.44, 0.46) | 36 |
| 25 | (0.42, 0.48) | 100 | (0.44, 0.45) | 36 | (0.44, 0.45) | 33 | (0.44, 0.45) | 33 | (0.44, 0.45) | 40 |
| 26 | (0.42, 0.48) | 100 | (0.44, 0.45) | 36 | (0.44, 0.45) | 36 | (0.44, 0.45) | 36 | (0.44, 0.45) | 36 |
| 27 | (0.41, 0.48) | 100 | (0.44, 0.45) | 40 | (0.44, 0.45) | 40 | (0.44, 0.45) | 40 | (0.44, 0.45) | 40 |
| 28 | (0.41, 0.48) | 100 | (0.44, 0.45) | 40 | (0.44, 0.45) | 36 | (0.44, 0.45) | 36 | (0.44, 0.45) | 40 |
| 29 | (0.42, 0.48) | 100 | (0.44, 0.45) | 40 | (0.44, 0.45) | 36 | (0.44, 0.45) | 36 | (0.44, 0.45) | 40 |
| 30 | (0.41, 0.48) | 100 | (0.44, 0.45) | 36 | (0.44, 0.45) | 36 | (0.44, 0.45) | 36 | (0.44, 0.45) | 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fraile-Hernández, J.M.; Peñas, A. On Measuring Large Language Models Performance with Inferential Statistics. Information 2025, 16, 817. https://doi.org/10.3390/info16090817
Fraile-Hernández JM, Peñas A. On Measuring Large Language Models Performance with Inferential Statistics. Information. 2025; 16(9):817. https://doi.org/10.3390/info16090817
Chicago/Turabian StyleFraile-Hernández, Jesús M., and Anselmo Peñas. 2025. "On Measuring Large Language Models Performance with Inferential Statistics" Information 16, no. 9: 817. https://doi.org/10.3390/info16090817
APA StyleFraile-Hernández, J. M., & Peñas, A. (2025). On Measuring Large Language Models Performance with Inferential Statistics. Information, 16(9), 817. https://doi.org/10.3390/info16090817








