Post-Quantum Key Exchange and Subscriber Identity Encryption in 5G Using ML-KEM (Kyber) ^†

Abstract

5G addresses user privacy concerns in cellular networking by encrypting a subscriber identifier with elliptic-curve-based encryption and then transmitting it as ciphertext known as a Subscriber Concealed Identifier (SUCI). However, an adversary equipped with a quantum computer can break a discrete-logarithm-based elliptic curve algorithm. Consequently, the user privacy in 5G is at stake against quantum attacks. In this paper, we study the incorporation of the post-quantum ciphers in the SUCI calculation both at the user equipment and at the core network, which involves the shared-key exchange and then using the resulting key for the ID encryption. We experiment on different hardware platforms to analyze the PQC key exchange and encryption using NIST-standardized CRYSTALS-Kyber (which is now called an ML-KEM after the standardization selection by NIST). Our analyses focus on the performances and compare the Kyber-based key exchange and encryption with the current (pre-quantum) elliptic curve Diffie–Hellman (ECDH). The performance analyses are critical because mobile networking involves resource-limited and battery-operating mobile devices. We measure and analyze not only the time and CPU-processing performances but also the energy and power performances. Our analyses show that Kyber-512 is the most efficient and even has better performance (i.e., faster computations and lower energy consumption) than ECDH.

1. Introduction

In telecommunications networking, user privacy is important against tracking the behavior and the location of the mobile user. Before 5G, cellular networking provided no ID confidentiality protection. The ID of the user equipment (UE) was transmitted in plaintext before 5G, including 4G and any of the previous cellular generations. Because cellular connections in wireless rely on an open-air medium, the adversary can access, capture, and track the UE ID, e.g., IMSI catching [1,2]. UE tracking can result in the breach of the location (where the mobile UE is located) and behavior (how and when it uses the connectivity) of the mobile UE and the human owner using the UE. To address such an issue, 5G introduced authentication and key agreement (AKA), which conceal the actual permanent identity of the user to enable the confidentiality protection of the user ID to protect the user privacy. In contrast, previous generations do not conceal user identities. While enabling other security objectives (confidentiality, integrity, authentication, and non-repudiation), 5G AKA includes key exchange and encryption. More specifically, 5G AKA uses the Elliptic Curve Integrated Encryption Scheme (ECIES) [3]. The ECIES involves public-key key exchange to establish the shared key, which in turn can be used for encryption for the confidentiality protection of the ID. The ciphertext of the user equipment ID is called a Subscriber Concealed Identifier (SUCI).

Such 5G user equipment ID encryption, however, is vulnerable against quantum-equipped adversary. Assuming quantum computing, Shor’s algorithm [4] can break the mathematical problem (discrete-logarithm problem in this case) anchoring the cipher security and finding the key. Recent prototypes in quantum computing, e.g., IBM and Google, continue to evolve to support greater qubits to realize such threats in order to break the current ciphers. To defend against future quantum attackers, the National Institute of Standards and Technology (NIST) has solicited post-quantum public-key ciphers since 2016 and standardized CRYSTALS-Kyber for the key encapsulation mechanism or KEM cipher standardization in 2022. After standardization, CRYSTALS-Kyber evolved into ML-KEM [5], which is our “Kyber” cipher in this paper. (There are three NIST-standardized post-quantum digital signature ciphers that are less relevant to this paper, as our work focuses on encryption for confidentiality protection.)

We incorporate PQC on 5G UE ID and analyze the performance impacts of the post-quantum transition for 5G SUCI, which is important since the cellular UE is constrained in resources (mobile, lightweight, and battery-operating). Our performance analyses are more relevant to such mobile/5G networking than other applications with greater resources and looser performance requirements.

In this research work, we study the performance analyses of post-quantum ciphers in the 5G AKA identification and registration. We build our scheme on the 3rd Generation Partnership Project (3GPP) standard 5G-AKA protocol [6]. While the current 3GPP-defined 5G-AKA protocol uses the pre-quantum elliptic curve algorithms that are vulnerable against the quantum-equipped adversary (specifically, secp256r1 and X22519), we replace the pre-quantum ciphers and incorporate the post-quantum Kyber-512 [7] into 5G AKA and analyze the pre-quantum vs. post-quantum 5G AKA.

We compare the performances of the existing pre-quantum ciphers (the elliptic curve KEM ciphers of secp256r1 and X22519) with the post-quantum cipher (CRYSTALS-Kyber-512) when implemented in 5G AKA. For fairness, we compare the ciphers with the same security levels and fix the computing platform on which we simulate the 5G AKA. Because the mobile UE is resource-constrained, we compare the performances of the ciphers with the shortest key/parameter lengths. We implement and measure performance in processing time, power, energy, and CPU cycles. While the memory and byte overhead increases from pre-quantum to post-quantum, our results show that the post-quantum Kyber is more efficient in terms of time and energy than pre-quantum PKE/KEM.

The rest of the paper is organized as follows: Section 2 describes the motivation and background, which highlight the rationale and context of the research. We discuss the related work in Section 3. While Section 2 describes the background that is more foundational and established, Section 3 describes the state-of-the-art research. Section 5 describes our implementation and experimentation procedure. Section 6 focuses on the experimentation analysis, presenting the results and observations. Section 7 concludes the paper, summarizing the key findings, contributions, implications of the study, and future directions.

2. Motivation and Background

2.1. Motivation: PQC Transition

Public-key ciphers are vulnerable to quantum computers due to the challenges posed by prime factorization and discrete logarithms. In 1994, Peter Shor introduced quantum algorithms for prime factorization [4], while Grover’s algorithm [8] significantly accelerates key searches. The combined impact of Shor’s and Grover’s algorithms compromises the security of current cryptographic systems, as demonstrated in

Table 1. Security level for pre-quantum vs. post-quantum ciphers. Shor’s algorithm breaks the pre-quantum RSA and EC ciphers by finding the key in polynomial time.

Security Level (bits)	Symmetric	RSA	EC	Post-Quantum (NIST Round 4)
128	AES-128	3072 bits	256 bits	Kyber-512
192	AES-192	7680 bits	384 bits	Kyber-768
256	AES-256	15,360 bits	512 bits	Kyber-1024

.

In October 2023, IBM announced the development of the latest quantum computer, with a processor containing over 1000 qubits [9]. Martin et al. [10] have shown that calculating the elliptic curve discrete logarithm on a quantum computer requires a considerably smaller number of quantum bits (qubits) compared to addressing the integer factorization problem. While breaking RSA-2048 would necessitate millions of qubits, which is still years away, the urgency for considering quantum attacks arises from several factors: the compatibility of PQC with classical computers, the uncertainty surrounding the development of quantum computers globally, the security of PQC ciphers against both quantum and classical attacks, and government agencies taking early steps to use PQC for better security.

The National Institute of Standards and Technology (NIST) introduced post-quantum cryptographic algorithms in 2016 to address quantum resistance issues; the timeline of PQC is shown in Figure 1. In late 2017, 82 candidate ciphers were submitted for review, and in December of the same year, 69 algorithms were selected in the first round based on meeting the minimum suitability criteria. By January 2019, NIST advanced 26 ciphers to the second round, based on internal analysis, theoretical security assessments, and public feedback. By July 2020, 15 ciphers were chosen for round 3 and categorized into finalized and alternative groups based on factors such as performance, computational cost, data transfer cost, and implementation feasibility.

After a comprehensive evaluation across multiple rounds, NIST identified four candidate ciphers for potential standardization in July 2022. These include one PKE/KEM, namely CRYSTALS-Kyber, and three digital signatures (DSs), namely CRYSTALS-Dilithium, FALCON, and SPHINCS+, all originating from the third round. PKE/KEM is employed to ensure message confidentiality, while DSs are used to ensure message integrity.

NIST conducted a thorough analysis of the security strengths of post-quantum ciphers and compared the brute-force difficulty with pre-quantum ciphers. Table 1 outlines the pre-quantum security levels of symmetric (AES) and public-key ciphers, including RSA and elliptic curve (EC) algorithms, in 128-bit, 192-bit, and 256-bit security contexts. It contrasts these with the Kyber family of post-quantum cryptographic schemes, specifically Kyber-512, Kyber-768, and Kyber-1024. The table demonstrates that Kyber-512 offers 128-bit security equivalent to EC-256 (including algorithms like X25519 and secp256r1). Furthermore, it highlights the vulnerability of traditional public-key algorithms to quantum attacks, notably Shor’s algorithm, whereas Kyber-512 remains secure against quantum threats due to its reliance on different mathematical hard problems.

We utilize NIST security-level analyses to ensure fairness in our comparison study, selecting ciphers of the same security levels for comparison purposes.

2.2. Background on 5G AKA and Cryptographic Primitives

In this paper, we use acronyms standardized by 3GPP for 5G telecommunication networks.

Table 2. Acronyms used in this research.

AKA	Authentication and Key Agreement
CN	Core Network
ECIES	Elliptic Curve Integrated Encryption Scheme
IMSI	International Mobile Subscriber Identity
KEM	Key Encapsulation Mechanism
KDF	Key Derivation Function
MSIN	Mobile Subscriber Identity Number
PQC	Post-Quantum Cryptography
SUCI	Subscriber Concealed Identifier
SUPI	Subscriber Permanent Identifier
UE	User Equipment
USIM	Universal Subscriber Identity Module

provides a list of the acronyms used throughout this paper.

2.2.1. 5G-AKA and SUCI

Fifth-generation Authentication and Key Agreement (5G-AKA) is a mutual authentication protocol in the 5G cellular network between the user equipment (UE) and the core network (CN). The UE is the beneficiary of the cellular service provision receiving the connectivity access, while the CN is the cellular service provider network providing the connectivity access to the UE. The 5G-AKA protocol consists of two phases: the identification phase and the challenge–response phase. The identification phase starts with a registration request by the UE. Upon powering on, the UE initiates the registration request to the CN by sending its subscription identifier. This identifier is stored on an integrated chip called the Universal Subscriber Identifier Module (USIM). The USIM in the UE also stores a public key of the CN. In 4G, the International Mobile Subscriber Identity (IMSI) is sent in plaintext during authentication initialization.

In 5G, the identifier is known as a Subscriber Permanent Identifier (SUPI), which is sent in an encrypted format known as an SUCI. The CN public key stored in the USIM encrypts the SUPI into the SUCI. Figure 2 shows the SUCI format. The SUCI contains an SUPI-type indicator, a home network identifier, a protection scheme ID, a home network public-key ID, and a protection scheme’s output. The protection scheme’s output contains a public key, message authentication code (MAC), and encrypted MSIN (Mobile Subscriber Identity Number), either an SUPI or IMSI. When the UE sends the SUCI to the core network, it decrypts the SUCI using its private key and identifies the subscriber successfully. The SUCI format protection scheme identifies the algorithm used for the encrypt and decrypt function.

Table 3. Protection schemes standardized by 3GPP [6].

Scheme	Scheme ID	Algorithms	Output Scheme
Null scheme	0	N/A	Size of MSIN (if using IMSI)
Profile A	1	ECIES (X25519)	256 bits public keys + 64 bits MAC + cipher-text value
Profile B	2	ECIES (secp256r1)	256 bits public keys + 64 bits MAC + cipher-text value
Reserved for future standardization	3–11	N/A	N/A
Reserved for proprietary (home operator)	12–15	N/A	N/A

describes the protection schemes, where the protection scheme ID is a numerical value ranging from 0 to 15. It signifies whether a protection scheme is null (0) or non-null (1-15) for the given SUCI value. When an SUPI value is provided, the protection scheme ID determines the corresponding scheme applied, resulting in an output scheme. In the null scheme, no encryption is applied to the provided SUPI. Instead, the output scheme consists of the MSIN component of the IMSI. Our work focuses on the 5G protection schemes beyond the null scheme, which uses encryption to protect the confidentiality of the UE ID. More specifically, we focus on the two schemes called Profile A and Profile B using distinct ciphers. In both Profiles A and B, the ECIES generates the SUCI from a given SUPI value at the UE side. Similarly, at the CN side, the ECIES is utilized to decipher the SUPI value from the received SUCI value. The key difference between Profile A and Profile B arises in the elliptic curve domain parameters, elliptic curve Diffie–Hellman (ECDH) primitive, and point compression. However, other elements remain consistent across both profiles. Profile A uses Curve25519 as its domain parameter and X25519 as an ECDH primitive while Profile B uses secp256r1 as its domain parameter and elliptic curve cofactor Diffie–Hellman as an ECDH primitive. Additionally, Profile B implements point compression to reduce overhead, while Profile A does not apply this compression technique.

2.2.2. Pre-Quantum (X25519 and secp256r1)

X25519 and secp256r1 (NIST P-256) are both elliptic curve cryptography (ECC) algorithms used for key exchange but they differ in terms of the elliptic curve that they use, the underlying mathematics, and certain characteristics.

Although X25519 is not NIST-standardized, it is widely used and considered secure and is defined in RFC 7748 [11]. Curve25519 is designed to be fast and secure. It is a Montgomery curve, which provides certain performance advantages in implementations. X25519 uses the elliptic curve Curve25519, defined over a prime field defined by the prime number $2^{255}-19$. X25519 is often faster in computation, which makes it particularly efficient for key exchange in various protocols. Secp256r1, also known as NIST P-256, is an NIST-recommended elliptic curve [12]. Secp256r1 is a Weierstrass curve and is widely implemented in cryptographic libraries and security protocols, including TLS.

2.2.3. Post-Quantum, CRYSTALS-Kyber

CRYSTALS-Kyber [7] is the only PKE/KEM cryptographic algorithm selected by NIST in the fourth round of the post-quantum cryptography standardization process. Kyber is specifically a post-quantum cryptographic algorithm, which means that it provides security against attacks from both classical and quantum computers. The mathematical hardness of the Kyber relies on problems believed to be hard even for quantum computers. One such problem is the hardness of solving certain instances of the learning with errors (LWE) problem over module lattices. These problems involve finding a secret vector given some noisy linear equations.

When the protection scheme ID is 1, then X25519 is used, and when the ID is 2, secp256r1 is used. 3GPP also standardizes protection scheme ID 3∼11 for future use, while it standardizes 12∼15 for the use of the proprietary home operator.

2.2.4. Key Encapsulation Mechanism (KEM)

Because symmetric-key cryptography is more efficient than public-key cryptography, the general cryptographic practices use the public-key encryption (PKE) for the key encapsulation mechanism (KEM) to share and establish the symmetric key (which can then be used to encrypt the communications and messages). KEM/PKE solves the problem by securely transmitting the symmetric key while encrypting the symmetric key with public-key cryptography. Hence, the KEM enables two communicating parties to derive a shared key by leveraging public-key cryptographic encryption. This section fills the gap between the SUCI calculation and our implementation design.

The KEM consists of the following three algorithms. The details of KEM inclusion in SUCI calculation are described in Section 5.2.

• KEM.KeyGen: A probabilistic key generation algorithm, KEM.KeyGen, that generates a public–private key pair.
• KEM.Encapsulation: A probabilistic encapsulation algorithm, KEM.Encapsulate, that takes the public key of the receiver as input. Then, it selects a shared key randomly, encrypts the shared key using the receiver public key, and outputs the ciphertext, which is also known as an encapsulated shared key.
• KEM.Decapsulation: A deterministic decapsulation algorithm that takes as input a ciphertext (encapsulated shared key) and private key of the receiver to generate the shared key or report a failure.

3. Related Work

3.1. SUCI Protection in 5G

The introduction of encrypted subscriber identity in 5G comes from the fact that, in the technology of previous generations (2G, 3G, 4G), the plaintext transmission of subscriber identity (e.g., IMSI) during user registration suffers from user privacy leakages. An attacker, with open-source hardware and software tools, can act as a man-in-the-middle between the UE and the base station to eavesdrop on the plaintext IMSI without the knowledge of the network operator or the user. The captured IMSI is then utilized to track the user location and eavesdrop on user private conversations [1]. For example, Mjølsnes et al. [13] realized this attack (also known as an IMSI catcher) in a 4G/LTE network using software-defined radios (Ettus USRP B210) and open-source software tools (OpenBTS and Open Air Interface). While there are research works conducted to reveal the presence of IMSI catchers [14,15,16], the 3GPP standard addresses the issue by introducing a Subscription Concealed Identifier (SUCI) in the 5G authentication and key agreement protocol [6].

In 5G, the user encrypts its identifier (IMSI/SUPI) using public-key cryptography, turning it into a concealed identifier (SUCI) that serves as a component of 5G-AKA during the authentication and key agreement protocol. The 3GPP proposes two discrete-logarithm-based elliptic curve cryptography (ECC) algorithms to calculate the SUCI. The protection scheme identifier field in the SUCI format specifies the algorithms as X25519 and secp256r1 as discussed in Section 2.2.1.

3.2. Post-Quantum for 5G KEM

Among the research carried out to study the incorporation of PQC into 5G networking, Refs. [17,18,19] present a roadmap for the incorporation while Khan et al. [20,21] introduce post-quantum digital signatures for authentication and CN public-key delivery in 5G subscription data provisioning (USIM provisioning). However, the research study most closely related to our work is by Ulitzsch et al. [22] and Damir et al. [23]. Damir et al. [23] propose a novel authentication and key agreement protocol based on a KEM for 5G where the user identity and forward secrecy are preserved. Their proposed protocol is compatible with post-quantum cryptography and analyzes the performance of the scheme using NIST round 4 finalists. Ulitzsch et al. [22] focus more on the SUCI calculation of 5G-AKA. They propose a post-quantum secure SUCI calculation scheme called a KEMSUCI. They also evaluate their framework with NIST round 3 finalists using a standard SIM card. However, both of the research studies identify Kyber as the best suitable KEM among post-quantum algorithms. Our work builds on these previous works providing proof-of-concepts [22,23], but further analyzes the performances to include the comparison between post-quantum (Kyber-512) vs. pre-quantum (X25519 and secp256r1) and to measure energy and power for applications constrained by mobile resources. We measure the performance of three different algorithms (Kyber-512, X25519, and secp256r1) on three different platforms (computer, MiniPC, and Raspberry Pi) while providing the time duration, energy consumption, and CPU cycle count analysis, focusing on the UE.

4. Security and Cryptanalysis on PQC KEM: How Kyber Was Selected

In this section, we focus on the security of NIST PQC. To evaluate the security of candidate algorithms, NIST defined three security definitions—two for encryption (for general-use and ephemeral cases) and one for digital signatures as discussed in [24]—and categorized them into five security levels (they require resources at least equivalent to breaking AES with 128/192/256-bit keys or finding collisions in SHA-256/384 hash functions) based on how hard it would be for an attacker to break them. NIST also highlighted other important security features, like forward secrecy, protection against side-channel and multi-key attacks, and resistance to misuse, which remain important.

NIST selected Kyber as the standardized KEM cipher in 2022 [25], informed by the cryptanalysis conducted by the cryptographers and security researchers around the world. Section 4.2 describes the cryptanalysis, much of which is based on side-channel vulnerabilities. Informed by them, Kyber improved and advanced its security and design from 2017 [26] to 2019 [27] to 2021 [28].

The first and second rounds focused more on performance and hardware compatibility, while the third round informed the security strength and cryptanalysis, described in Section 4.2. Saber [29], another KEM cipher candidate from the third round, is based on a lattice-based problem like Kyber, but the math problem is based on modular learning with rounding or MLWR. However, because MLWR is less analyzed from the attacker perspective (i.e., fewer cryptanalysis studies), NIST selected SABER.

4.1. PQC Requirements

NIST evaluates post-quantum algorithms based on security, performance, and practicality. Among these, security is the most important. NIST aims to select algorithms that can withstand both classical and quantum attacks in real-world applications like TLS, SSH, and IPsec. Encryption and key-establishment schemes should be secure against indistinguishability under chosen ciphertext attack (IND-CCA2), and digital signature must be hard to forge. The second most important criteria are cost and performance, which refers to the efficiency with which the algorithm runs, memory use, key/ciphertext size, and decryption failure rates. Finally, practicality focuses on how usable and adaptable an algorithm is in real-world settings, including factors such as simplicity of implementation, cross-platform compatibility, and support for parallelism.

4.2. Side-Channel Attack on NIST’s Third Round

Side-channel attack is the process of extracting secret and information from the system or chip by measuring and examining the physical factors. Common side-channel analyses are timing, power, electromagnet, cold boot, correlation power, etc., when the adversary has physical access to the system computing cryptographic algorithms. These types are considered as side-channel attacks. There are several parameters or factors (NTT, sample distribution, secret key, polynomial degree, etc.) in lattice-based schemes (SIS or LWE) that can be targeted. Lee et al. [30] in 2010 demonstrated a simple power attack on typical software implementation of NTRU. They implemented over a low-end device (Tmoto sky) and showed the results of first- and second-order correlation power analysis (CPA) attacks. Lee also proposed three countermeasures against SPA and CPA attacks on NTRU. After three years, in 2013, Zheng et al. [31] introduced a collision attack against Lee’s proposed countermeasure that resulted in 78% efficiency. One of the parameters that is used in NTRUprime is the school-book polynomial multiplier, where the coefficient is calculated specifically. It was attacked by Huang et al. [32] using vertical CPA and online temple attack.

Lattice-based crytosystems that use LWE are also vulnerable to side-channel attack. Primas [33] found some leakage in NTT, which is used in almost all cryptosystems based on LWE lattices, and proposed a new side-channel attack on single decryption; this attack is also effective for mask implementation to recover individual shares and then to combine and perform a full key recovery attack. Aysu [34] introduced an attack that targeted the matrix and polynomial multiplication based on hardware implementation on FPGA and found vulnerabilities in the NewHope and Frodo KEM cryptosystem. In their attack, they used horizontal DPA, which resulted in full key recovery in a single trace. Bos et al. [35] demonstrated a software implementation in the ARM cortex M0 process and investigated a single trace of Frodo KEM, which is a ringless cryptosystem based on LWE. Some LWE cryptosytems use error-correcting code to minimize the failure decryption probability. D’Anvers [36] used a timing attack to find error correcting and illustrate a key recovery attack on the LAC scheme, which uses error-correcting code. Ravi [37] showed vulnerabilities based on EM in the error correction code of round 5 and LAC, and also found a similar vulnerability in the FO transform (Fujisaki-Okamoto), implemented in the ARM cortex process microcontroller using the public library pqm4. Sim et al. [38] presented a clustering attack on Kyber and target leakage of Barette reduction in the decapsulation phase, implemented in the ARM cortex-M4 microcontroller.

D’Anvers [39] investigated the impact of the failure in the chosen cipher security of a lattice-based system, used the failure boosting technique, which boosts the failure rate, and then analyzed the amount of information. Ravi et al. [40] described a fault attack on the round 3 NIST finalized algorithm (NewHope, Dilithium, Frodo and Kyber) and showed, misuse-nonce, result key recovery, and message attack. Xu et al. [41] proposed an EM side-channel attack on the ciphertext on Kyber and also described a full key extraction through simple power analysis. Additionally, Hermelink et al. [42] introduced a fault attack on Kyber and showed that the combination of the chosen cipher attack and fault injection can compromise and threaten implementation.

Ravi et al. [43] discussed the security of crystal Dilithium in contrast to the combination of a classical attack and side-channel attack. The author divided the research into two parts. One concerned using the power analysis and retrieving the partial secret key, and the second concerned showing that the signature can be forged even by partial knowledge of the secret key, which can be retrieved by using power analysis. Islam et al. [44] presented a correlation attack on Dilithium, which is the NIST fourth-round finalized digital signature. They used a rawhammer target and an attack on a single flip bit in a secret vector, and successfully recovered 1851 bits out of 3072 bits.

5. Our PQC Incorporation and Implementation

We implement PQC in the 4G/5G context for empirical performance analyses and validations. This section describes our implementation scope, i.e., using the 5G information fields and simulating the participating entities and their SUCI protocol. Our implementation follows the standardized 5G protocol because we focus on the 5G application, and our implementation and experimentation focus on the KEM involving public-key cryptography (requiring the PQC transition for quantum resistance) and not on the symmetric cryptographic operations.

5.1. SUCI in Existing 5G

This section describes the SUCI calculation in existing 5G that builds on Section 2.2.1. In the current standard of 5G AKA, two protection schemes X25519 and secp256r1 exist. Below are the steps for generating the SUCI protection scheme output fields for both the ECDH algorithms. We refer to each relevant field in the SUCI format depicted in Figure 2.

The CN generates public–private key pairs of the elliptic curve (EC) and shares the public key with the user by integrating it into the USIM. This is the core network public key discussed in Section 2.2.1. Further discussion on each of these steps follows below.

• Public–Private Key Generation at UE: During the registration process, the UE generates the EC public–private key pair. The UE’s public key is used by the CN to de-conceal the SUPI from the received SUCI while the UE’s private key serves as input for the key agreement function in the subsequent step.
• Key Agreement: The input to this function includes the CN’s public key stored in the USIM and the UE’s private key obtained from step 1, resulting in the generation of a shared key. In contrast to the use of ECDH in other contexts that exchange the public keys via digital networking, our key agreement makes use of the public keys shared during the UE registration, as described in Section 2.2.
• Encryption Key: The UE then uses a key derivation function on the shared key to generate an encryption key $k_{enc}$ for the symmetric cipher, an initial counter block (ICB), and a $k_{mac}$ for the message authentication code (MAC).
• Symmetric Encryption: The UE uses the encryption key $k_{enc}$ and the ICB to encrypt the plaintext (SUPI or IMSI) depending on the SUPI type field in the SUCI format. Also, the UE generates the MAC field using $k_{mac}$. The output ciphertext value becomes the part of the scheme output of the SUCI.
  The UE then transmits the finalized output of the UE-side encryption process to the CN for registration and identification. This output consists of the concatenation of the UE’s public key, ciphertext, and MAC.
• Decryption: When the CN receives the registration request along with the SUCI, it uses the UE’s public key (from step 1) and CN’s private key to generate the shared key at the CN side. The shared key is further used to generate a decryption key $k_{dec}$ that is the same as $k_{enc}$ to decrypt the SUCI, using a key derivation function.

In our experimentation, we implement steps 1, 2, and the shared key part of step 5 for our performance analysis of the existing SUCI calculation. Steps 3 and 4 use symmetric cryptography, which is not in our research contribution.

5.2. Post-Quantum Cryptography for Subscriber Concealed Identifier (SUCI)

In this section, we describe the SUCI generation using post-quantum cryptography. Unlike Section 5.1, the post-quantum cryptography algorithms use a KEM to generate a shared key. We describe the related background information for the KEM in Section 2.2.4 and build on it. Although we use a KEM, the information elements of the SUCI format are intact; hence, we omit redundant information about the fields in the SUCI because it is already described in Section 5.1. The steps for generating the protection scheme output for the SUCI are given below:

The CN generates the public–private key pair using the KEM.KeyGen function. The resulting CN’s public key is stored in the USIM.

• Public–Private Key Generation (UE): The UE generates the public–private key pair using the KEM.KeyGen function.
• Encapsulation (UE): To encrypt SUPI/IMSI, the UE uses the function KEM.Encapsulate to generate initial randomness, derive the shared key from this randomness, and compute a ciphertext using the CN’s public key. The generated ciphertext is the encapsulated shared key.
• Symmetric Encryption: After generating the shared key, the UE encrypts the plaintext (SUPI or IMSI) with a shared key that is computed using function KEM.Encapsulate.
  The UE then sends the encapsulated shared key and encrypted data to the CN.
• Decapsulation: When the CN receives the registration request, the CN uses its private key and encapsulated shared key to generate a shared key by using the decapsulation function KEM.Decapsulate, and further uses that generated shared key for decryption to verify the subscriber.

In our implementation, we use steps 1, 2, and 4 to measure the computational performance of the post-quantum KEM. We also calculate the byte size of the public keys because the key lengths in post-quantum cryptography are much greater than the pre-quantum ciphers. Since the SUCI generation occurs at the USIM, which is an integrated chip and has memory size limitations (e.g., 256 KB), we show the byte size of the public keys in our comparison in

Table 4. Protection scheme output comparison. Protection scheme output corresponds to the scheme output described in the last column of Table 3.

Protection Scheme	Ciphertext (Bytes)	Public Key (Bytes)	Scheme Output (Bytes)
Kyber-512	768	800	847
X25519	32	32	111
secp256r1	33	33	112

.

5.3. Subscription Concealment Protection Schemes (Modified for Post-Quantum Scheme—Kyber Profile C)

This specifies the protection schemes used for concealing the SUPI in 5G networks. Each protection scheme is uniquely identified by a protection scheme identification. The currently defined identifiers are as follows: 0x0 (null scheme or no protection), 0x1 (Profile A), and 0x2 (Profile B), where Profiles A and B are defined by 3GPP and described briefly in Section 2.2.1.

For our scheme, which we call Profile C, we use the same data field but assign different identifier encoding: 0x3 (Profile C).

The output size for each protection scheme varies based on its cryptographic components. The null scheme produces an output equal to the input size (e.g., MSIN or NAI username). Profile A includes a 256-bit (32 bytes) public key and a 64-bit (8 bytes) MAC, in addition to the input size. Profile B consists of a 264-bit (33 bytes) public key, a 64-bit (8 bytes) MAC, and the input size. Profile C, which uses the Kyber-512 post-quantum algorithm, generates a larger output due to its quantum-resistant components: it includes an 800-byte public key, a 768-byte ciphertext (encapsulation output), and a 64-bit (8 bytes) MAC, resulting in a total output size of approximately 768 bytes plus the MAC and the input size.

The maximum size of the scheme output for proprietary or quantum-resistant protection schemes shall not exceed 3000 octets + input size [6]. This maximum was chosen to accommodate future post-quantum encryption schemes, such as lattice-based KEMs, without violating SUCI transport constraints. The UE shall not transmit an SUCI whose scheme output exceeds the defined maximum. The network may reject any SUCI message that surpasses this size limit to ensure protocol compliance and processing efficiency.

6. Experimentation and Performance Analysis

We focus on and compare the post-quantum (Kyber-512) vs. pre-quantum (X25519 and secp256r1) ciphers that are relevant to mobile computing in 5G. We use the key-exchange ECDH utilized in the 3GPP standardized protocol, more specifically, X25519 and secp256r1, which are used in the 5G protection scheme for key exchange as discussed in Section 2.2.1. To provide a fair comparison, we compare the ciphers that correspond to 128-bit security.

NIST’s recommendations for cryptographic algorithms often include different security levels, typically ranging from 80 bits to 256 bits. NIST analyzed such security levels based on the brute-force difficulty, as described in Section 2.1. Each level corresponds to a different expected level of security, with higher levels offering stronger protection but potentially requiring more computational resources. We focus on 128-bit security because the UE implementing and applying the ciphers is often mobile and resource-constrained.

This section provides our experimental setup, experimentation, and performance analyses. We measure the computational time in the experimentation and analyze the performance for 100,000 samples. We present average values with a $95\%$ confidence interval of the sample data in the analysis, except for power/energy analysis. We also make our experimental scripts and data available in a public repository [45].

6.1. Hardware and Software Setup

Table 5. Hardware specification of our experimental setup.

Device	Entity	CPU Specs	RAM (GB)	OS
Computer	CN & UE	AMD Ryzen 7 5700U 1.8 GHz	16	Ubuntu 16.04 LTS
MiniPC	UE	Intel 12th N95 3.4 GHz	8	Ubuntu 16.04 LTS
Raspberry Pi B+	UE	BCM2711, Quad-core Cortex-A72 1.8 GHz	4	Ubuntu 16.04 LTS

shows the hardware and software specification that we use in our experimental setup. We implement our system using a computer with an AMD Ryzen 7 5700U running at $1.8$ GHz with 16GB RAM to simulate both user equipment and the core network. Additionally, we also perform our experimentation with resource constraints, such as a Mini-PC equipped with an Intel 12th N95 processor running at $3.4$ GHz with 8 GB RAM, as well as a Raspberry Pi featuring a BCM2711, Quad-core Cortex-A72 (ARM v8) 64-bit SoC clocked at $1.8$ GHz with 4 GB RAM, to represent the UE, and implement all three ciphers on both devices for measuring the computational time of public-key generation and shared-key generation. All of the machines are running Ubuntu 22.04 LTS as their operation system (OS).

We perform our experimentation as the implementation design described in Section 5. We follow steps 1, 2, and 5 of Section 5.1 for the pre-quantum ECIES and use open-source python library cryptography version 42.0.5 [46] for the implementation. For the post-quantum algorithm, we follow steps 1, 2, and 4 of Section 5.2. We use the open-source Open Quantum Safe (oqs) library liboqs version 0.10.0 [47] to realize the steps. We write Python scripts to run the experiments on a computer, a MiniPC, and a Raspberry Pi hardware as mentioned earlier, while the compiler version installed on each machine is Python 3.10.6. For our experimental data analyses, we collect the time and power measurement data. We measure only the computation time required by each algorithm in key pair generation, encapsulation/encryption, and decapsulation/decryption. The computational time gives us an indication of the energy required for each computation in the user equipment.

For the power measurements, we use a power analyzer hardware (ZHURUI PR10-E US15A power recorder [48]; Shenzhen Zhurui Technology CO., LTD.; Shenzhen, China) to measure power consumption during the execution of our cryptographic processes. Specifically, for the pre-quantum ECIES, we measure power consumption during steps 1, 2, and 5 of Section 5.1. Meanwhile, for Kyber-512, we follow the procedures outlined in steps 1, 2, and 4 of Section 5.2. After collecting this data, we compute the average power consumption and multiply it by the time duration of the process to obtain the total energy consumed.

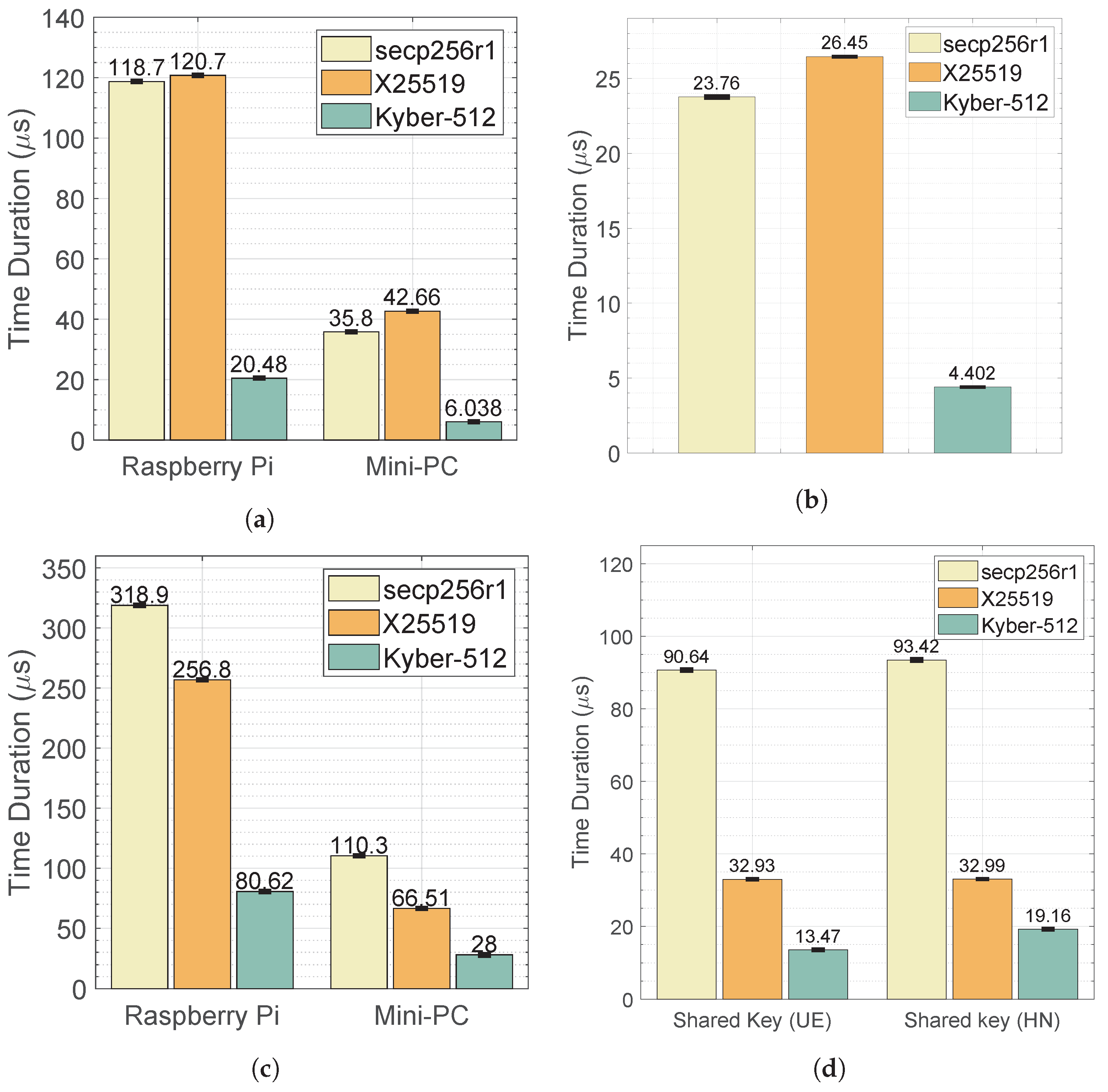
6.2. Computational Time Performance Analysis

As described in Section 5 the UE performs public- and shared-key generation, encapsulation, and encryption processes before transmitting the data to the CN side for decapsulation and decryption. We evaluate and compare the computation times required for generating public keys and shared keys using pre-quantum ciphers (X25519 and secp256r1) and a post-quantum cipher (Kyber-512) on two resource-constrained devices (Raspberry Pi and Mini-PC) at the UE side, as shown in Figure 3a and Figure 3c, respectively. We also compare the computational time duration for public-key generation among three ciphers at the CN side. This is essential because the CN requires a more robust device, and the Mini-PC and Raspberry Pi are not suitable for serving as the primary CN device due to limited computing resources, such as processing power, memory, storage, and energy, but the UE can be resource-constrained devices. The CN uses a computer to generate its public key, which the UE then uses to conceal the SUPI during the SUCI generation process. The speed at which the CN can generate this public key directly impacts the overall authentication latency. As shown in Figure 3b, Kyber-512 completes public-key generation in just 3.95 $\mathsf{\mu }$s, while X25519 and secp256r1 take 27.3 $\mathsf{\mu }$s and 22.5 $\mathsf{\mu }$s, respectively. This means that Kyber-512 is approximately $85.5\%$ faster than X25519 and $82.4\%$ faster than secp256r1. The substantial reduction in computation time makes Kyber-512 a highly efficient choice for the CN, enabling faster response times and better scalability in post-quantum secure 5G authentication.

Figure 3a shows the computation time for public key generation on the Raspberry Pi and Mini-PC because the UE’s public key is used by the CN to de-conceal the SUPI from the received SUCI. By using the Raspberry Pi as a UE, the computational time comparison shows that, for Kyber-512, the public-key generation requires $20.48\mathsf{\mu }$s, which is $82.88\%$ and $82.67\%$ less time consumption than X25519 and secp256r1 have, with 120.7 $\mathsf{\mu }$s and 118.7 $\mathsf{\mu }$s, respectively. For the Mini-PC, Kyber-512 consumes $6.038\mathsf{\mu }$s, X25519 takes $42.66\mathsf{\mu }$s, and secp256r1 requires $35.8\mathsf{\mu }$s. Kyber-512 exhibits a significant advantage, taking $85.76\%$ and $82.95\%$ less time than X25519 and secp256r1, respectively. Figure 3a also shows that the Raspberry Pi requires more time compared to the Mini-PC for all three ciphers. This is because the computing resources of Raspberry Pi are fewer than the Mini-PC.

Similarly, we also measure the computational time for shared-key generation on the Raspberry Pi and Mini-PC as shown in Figure 3c because the shared key is used for encapsulation at the UE side and decapsulation at the CN side. The shared-key generation time on the Raspberry Pi is reduced significantly, standing at $68.57\%$ and $74.69\%$ less than X25519 and secp256r1, respectively, while the results of the time required to generate a shared key on the Mini-PC show that the post-quantum cipher Kyber-512 takes $28\mathsf{\mu }$s, demonstrating efficiency, utilizing $57.90\%$ and $74.66\%$ less time than X25519 and secp256r1, with $66.51\mathsf{\mu }$s and 110.3 $\mathsf{\mu }$s, respectively.

We also measure the computation time required for shared-key generation on the same device (computer) at both the UE and CN sides. Our results demonstrate that Kyber-512 exhibits less computational time at the UE side compared to the CN side, attributable to differing functions performed on the UE and CN, as shown in Figure 3d. Regarding the share key generation for encapsulation/encryption at the UE side, using Kyber-512 utilizes $13.47\mathsf{\mu }$s, which utilizes $59.13\%$ and $85.12\%$ less time than X25519 ($32.93\mathsf{\mu }$s) and secp256r1 ($90.64\mathsf{\mu }$s), respectively. The shared-key generation time at the CN for decapsulation/decryption is illustrated in Figure 3d. Kyber-512 consumes $19.16\mathsf{\mu }$s, that is, $41.97\%$ and $79.52\%$ less time than X25519 ($32.0\mathsf{\mu }$s) and secp256r1 ($93.42\mathsf{\mu }$s), respectively.

• Summary: The above results compare the computational time measurements of public-key generation and shared-key generation for encapsulation/decapsulation operations in the SUCI calculation process as described in Section 5. Regarding the post-quantum KEM, Kyber-512 demonstrates shorter processing times for key generation compared to pre-quantum ciphers X25519 and secp256r1, both at UE and CN sides, across different platforms, including the computer, Mini-PCs, and Raspberry Pi, which can improve the overall performance and responsiveness of mobile devices, crucial for tasks requiring secure communication and data transmission.

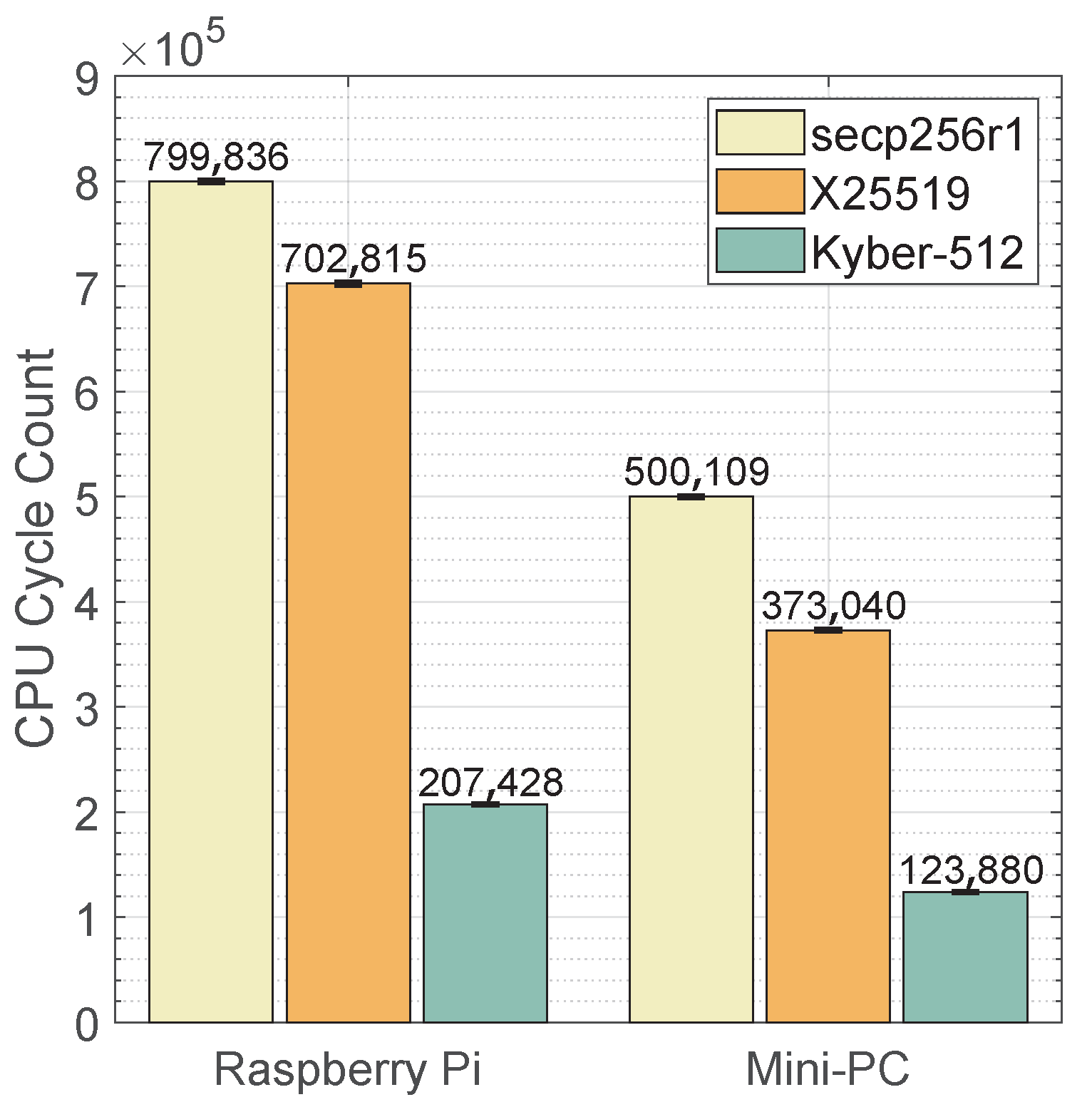
6.3. CPU Processor Analysis

We analyze CPU performance by measuring the CPU usage and the CPU cycle count. Because we run our experiments and the respective cryptographic operations repeatedly to take the statistical measurements while not running other processes, CPU usage is at $100\%$.

We also measure CPU cycles, which helps to select efficient cryptographic algorithms. Lower CPU cycle counts indicate more efficient algorithms, as they result in reduced processing time and energy consumption, which helps to conserve the battery life of the mobile device. In our experiment, we compute the cycle counts for the pre-quantum ciphers (X25519 and secp25r1) described in steps 1, 2, and 5 of Section 5.1. Furthermore, we followed the procedures outlined in steps 1, 2, and 4 of Section 5.2 for the post-quantum cipher (Kyber-512) using both the Mini-PC and Raspberry Pi. Our analysis involves computing the cycle count for 100,000 samples and utilizing a $95\%$ confidence interval to calculate the results.

Figure 4 shows a CPU cycle count comparison of pre-quantum and post-quantum ciphers on both the Mini-PC and Raspberry Pi. As shown in Figure 4, the Raspberry Pi has a low-performance processor and thus requires more CPU cycles to execute tasks than a Mini PC. The Mini-PC has a higher performance processor for all ciphers compared to the Raspberry Pi.

For the Raspberry Pi, secp256r1 takes an average of 799,836 cycles during steps 1, 2, and 5 of the existing SUCI calculation as shown in Section 5.1, which is $73.34\%$ higher than Kyber-512, which takes 207,428 cycles for the SUCI calculation, while X25519 takes 702,814 cycles. In the Mini-PC, secp256r1 again takes more cycles than X25519 and Kyber-512. secp256r1 takes an average of 500,109 cycles, which is $75.23\%$ higher than Kyber-512, which takes 123,880 cycles.

• Summary: The analysis provides significant differences in cycle counts between pre-quantum (X25519 and secp256r1) and post-quantum (Kyber-512) ciphers on both the Raspberry Pi and Mini-PC. Kyber-512 stands out favorably in the CPU cycle comparison for mobile devices due to its relatively lower cycle count compared to other cryptographic ciphers like secp256r1 and X25519. This lower cycle count indicates that Kyber-512 requires fewer computational resources, making it more efficient and suitable for resource-constrained devices like mobile devices. Lower cycle counts enable Kyber-512 to execute cryptographic operations more efficiently, resulting in reduced processing time and low energy, which helps to conserve battery life, as discussed in Section 6.4.

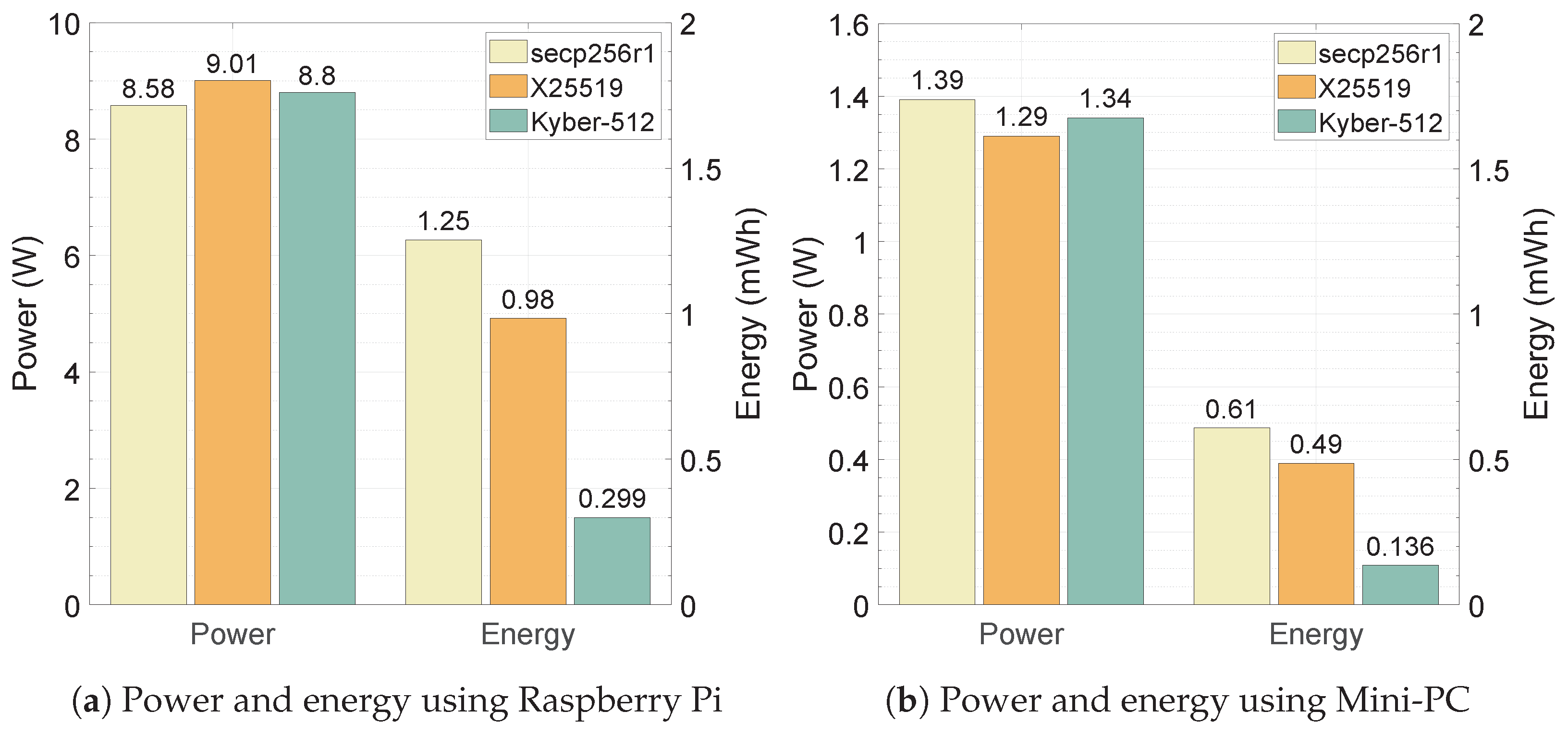
6.4. Computational Battery Performance Analysis

Because the UE can be mobile and battery-operating, we measure the power and energy performance using two different lightweight platforms; the results using the Raspberry Pi are shown in Figure 5a and the results of the Mini-PC are shown in Figure 5b. We measure the power values in watts (W) and then derive and calculate the energy values in milliwatt-hours (mWh); the energy is a product of the power measurements in this section and the time measurements in Section 6.2.

In Figure 5a, when simulating the UE with a Raspberry Pi, the power consumption of each cipher is closely comparable, ranging from a minimum of $8.58$ W for secp256r1 to a maximum of $9.01$ W for X25519, with Kyber-512 falling in between at $8.8$ W. However, when considering energy consumption, the results are incomparable due to the cumulative computational time of the public-key generation and shared-key generation. Kyber-512 proves to be more efficient, requiring only $0.299$ mWh due to a low computational time, which is notably $69.49\%$ and $76.08\%$ lower than the energy consumption of the X25519 and secp256r1, with $0.98$ mWh and $1.25$ mWh, respectively.

Similarly, for the Mini-PC, the power consumption is comparable and the values are closely related, with $1.39$ W, $1.29$ W, and $1.34$ W for secp256r1, X25519, and Kyber-512, respectively. While the energy consumption shows variation, Kyber-512 shows better energy efficiency on the Raspberry Pi, consuming only $0.136$ mWh. This is significantly lower than the energy consumption of secp256r1 and X25519, which consume $0.61$ mWh and $0.49$ mWh, respectively, as described in Figure 5b.

Additionally, Figure 5a,b illustrate that power and energy consumption are higher on the Raspberry Pi compared to the Mini-PC, attributed to the lower computing resources of the Raspberry Pi.

• Summary: We aim to compare the power and energy performances of all three ciphers on resource-constrained devices. The power consumption among all three ciphers is closely comparable on both the Mini-PC and Raspberry Pi, while post-quantum KEM Kyber-512 demonstrates superior energy efficiency, consuming notably less energy compared to pre-quantum ciphers, secp256r1 and X25519, on both Mini-PC and Raspberry Pi platforms, helping to conserve battery life, thereby allowing users to use their devices for longer periods without needing to recharge.

6.5. Byte Overhead Analysis

We also compare the protection scheme output byte size analysis in our experimentation. The protection scheme output consists of an encrypted public key or cipher text, MAC code, and the encrypted SUPI. Table 4 summarizes the protection scheme output among all three ciphers considering the 64-bytes MAC size and 15-bytes SUPI size. The Kyber-512 has a greater scheme output size than the ECIES ciphers because of the ciphertext output size (768 bytes). Since the protection scheme output is transmitted to the CN from the UE, the communication networking overhead will increase significantly.

However, in our future work, we experiment with the impact of the increased byte size in networking while prototyping our implementation using open-source software. In terms of the storage requirement of the public keys in the USIM (refer to Section 5), the Kyber-512 consumes (${\displaystyle \frac{800}{32}}=25$) magnitudes more memory size than the ECIES ciphers. The memory size of a standard USIM card is 256 KB [49]; hence, the USIM can store the public keys of the Kyber-512 algorithm and is feasible to use.

• Summary: Table 4 describes protection scheme output sizes among cryptographic ciphers, with Kyber-512 having a larger output due to its ciphertext size. While this may increase communication overhead, it remains feasible for the storage of public keys within a standard USIM card (with 256 KB memory), facilitating its practical usage in mobile devices.

7. Conclusions and Future Directions

In this research work, we study the performance analysis of post-quantum (Kyber-512, the only selected KEM cipher by NIST) and pre-quantum (X25519 and secp256r1, currently used for 5G SUCI) ciphers in the identification phase of 5G-AKA during registration. The UE calculates the Subscriber Concealed Identifier (SUCI) and sends it to the CN during the 5G-AKA protocol for registration. In this study, we show that the SUCI calculation, using the post-quantum Kyber-512 at the UE and CN, performs better than the pre-quantum ECIES ciphers. Focusing on the lightweight ciphers for the UE in 5G, the PQC KEM and encryption based on Kyber-512 performs better in computational time and energy consumption than the pre-quantum equivalent. Due to the low energy and time consumption, Kyber-512 has positive effects, including an extended battery life, data transmission, optimized resource utilization, and enhanced overall performance.

While we focus specifically on the SUCI calculation operations (which utilize the SIM-hardcoded core network’s public key and occur within the UE before the 5G networking) in this research, taking a systems approach to further analyze the rest of the 5G operations can go beyond the scope of this paper. Hands-on implementations of such a 5G networking system, for example, using a software-defined radio and 5G software of srsRAN and Open5GS, can validate the 5G integration and facilitate practicality. In addition to the validations, such implementation will enable measuring the networking byte size overhead, the communication overhead in terms of initiating the registration request, and the energy consumption of the user equipment within the 5G networking communication session. To measure the scalability of the core network, we plan to measure the maximum number of subscriber identifications that the core network can carry out with the three ciphers (Kyber-512, X25519, and secp256r1) and compare the latency and throughput of network communication.

While our work simulated and emulated mobile devices using a Raspberry Pi and Mini-PC, we can further use a jail-broken phone or an embedded software, which is mobile-device friendly. For example, the wolfSSL-embedded TLS library is a lightweight and portable SSL/TLS library. It is specifically designed for IoT, embedded, and real-time operating system (RTOS) environments, prioritizing a small size, high speed, and comprehensive features. wolfSSL supports the ECIES with elliptic curves defined by NIST, which can be compromised by quantum computers.

While our research focuses on the current 5G New Radio technology (and shows that it supports the NIST-standardized, post-quantum Kyber), we expect this research to inform the future designs and incorporation of post-quantum ciphers in the next generations of mobile networking (beyond 5G and 6G). The post-quantum Kyber can have comparable or even better time/power performances than the ECIES; however, it introduces additional byte overheads in storing the public key and in transmitting the ciphertext.