Uncovering Key Factors of Student Performance in Math: An Explainable Deep Learning Approach Using TIMSS 2019 Data

Abstract

In 2019, the TIMSS study offered a closer look at how Moroccan eighth-grade students were doing in mathematics. The data came from a sample of 8390 students; 37% performed well, while the remaining 63% struggled. The goal was to better understand which contextual factors truly influence academic success. The dataset was dense, with over 700 variables drawn from students, teachers, and school questionnaires. To make sense of it, advanced machine learning techniques were applied, including an autoencoder to reduce dimensionality. This process helped narrow things down to 20 key variables that strongly correlated with student performance. These factors covered a range of influences, from teaching strategies and student engagement to teacher training and school-level resources. The insights from the study offer practical guidance for educators and policymakers looking to design targeted, effective interventions. At its core, the study underscores a familiar truth: success in math does not hinge on a single element but on a web of interconnected conditions. Improving outcomes requires a holistic approach, one that supports both learners and the people guiding them.

1. Introduction

The Trends in International Mathematics and Science Study (TIMSS), conducted every four years by the International Association for the Evaluation of Educational Achievement (IEA), has become a key benchmark for assessing student performance in mathematics and science across the globe [1]. TIMSS evaluates fourth- and eighth-grade students through standardized assessments and collects rich contextual data via student, teacher, and school questionnaires. Its primary aims are to monitor trends in academic achievement, analyze the influence of curricula and instructional practices, and provide data for evidence-based education reform. The study employs a stratified random sampling approach and uses plausible values (PVs) to estimate students’ proficiencies with robust psychometric accuracy [2,3]. In its 2019 cycle, the study gathered data from over 250,000 students, 30,000 teachers, and 8000 school leaders across 39 countries, including Morocco. This extensive dataset offers a rare opportunity to gain insights into the mathematics performance of Moroccan eighth-grade students. Unfortunately, as in previous cycles, Morocco’s performance remained below the international average [4], raising significant concerns regarding the quality of instruction and learning conditions. These persistent gaps often reflect broader systemic issues, including insufficient human capital and structural challenges within the national education system, factors that have long-term implications for employability, economic growth, and social development. In Morocco, student underperformance in mathematics is closely linked to a set of well-documented educational challenges. Socio-economic inequalities remain a major concern, particularly between urban centers and rural or remote areas. Many schools in underprivileged regions suffer from a limited infrastructure, overcrowded classrooms, and a shortage of trained teachers. Additionally, the use of multiple languages in instruction, Arabic, French, and Amazigh, can create comprehension difficulties, especially in mathematics, which requires conceptual clarity. These realities must be considered when interpreting the TIMSS 2019 results, as they reflect broader systemic issues that continue to affect students’ learning conditions across the country [5]. Nevertheless, TIMSS 2019 is not merely a diagnostic tool [6]. The study provides rich contextual data that enables researchers to explore the multifaceted determinants of student achievement. Identifying these driving factors is crucial for developing targeted and effective educational interventions capable of producing lasting improvements in mathematics teaching and learning in Morocco [7].

Up to now, most studies tackling this issue have relied on traditional statistical methods like regression models, principal component analysis, or multilevel modeling. While these techniques have helped uncover general trends, they often fall short when faced with large, complex datasets, like those provided by TIMSS. In contrast, machine learning and deep learning methods are proving increasingly useful in educational research. These approaches can detect hidden patterns and capture non-linear relationships that conventional methods tend to overlook.

In this study, we tapped into the power of deep learning, specifically using autoencoders, to uncover the most influential contextual factors shaping mathematics achievement among Moroccan eighth-grade students. By analyzing more than 700 variables related to students, teachers, and schools, we aimed to identify the strongest predictors of academic success. The goal was not just to boost prediction accuracy but also to generate meaningful, data-driven insights that can help shape smarter education policies and teaching practices in Morocco.

To better understand these challenges, our study is guided by two central questions:

(i)

What are the most influential contextual factors, drawn from the TIMSS 2019 data, that predict mathematics performance among Moroccan eighth-grade students?

(ii)

How can explainable machine learning techniques help uncover these factors and translate them into actionable insights for teachers and policymakers?

To address these questions, the paper is structured as follows: Section 2 presents related studies on mathematics achievement and educational data mining. Section 3 outlines our methodology, including data preprocessing, model training, and the interpretation strategy. Section 4 reports the results of the classification models. Section 5 explores the selected features in detail. Section 6 offers practical recommendations. Finally, Section 7 concludes the study and discusses its limitations and possible future directions.

2. Related Works

A growing body of research has been dedicated to understanding the factors that shape student achievement in mathematics, often drawing on data from large-scale international assessments like TIMSS. These datasets have become vital tools for evaluating the effectiveness of education systems, enabling meaningful cross-national comparisons and helping researchers and policymakers identify both the key drivers of academic success and the areas where targeted improvements are needed [8,9,10].

For example, Hammouri [11] highlighted the importance of eighth-grade students’ attitudes toward mathematics, along with their self-confidence, sense of accomplishment, and perception of the subject’s value, all of which significantly impact performance. Liu and Meng [12], using TIMSS 2003 data, compared high- and low-achieving eighth-grade students in East Asia and the United States, emphasizing how cultural and educational differences shape learning outcomes. In another comparative study, Topçu, Erbilgin, and Arkan [13] examined eighth-grade student performance in mathematics and science between Turkey and South Korea to uncover influencing factors. Similarly, Kılıç-Depren et al. [14] applied various classification methods, including Decision Trees, naïve Bayes, logistic regression, and neural networks, to classify Turkish eighth graders based on their math proficiency. On a more conceptual level, Baranyi and Gilanyi [15] and Chmielewska [16] introduced the concept of Mathability, stressing the synergy between human cognitive abilities and technology when solving complex mathematical problems. Their work illustrates how integrating educational technologies can enhance mathematics learning. In more recent contributions, Yoo [17] applied the Elastic Net algorithm to TIMSS 2011 data to predict mathematics achievement of Korean fourth-grade students. The study successfully selected 17 significant variables out of 162, demonstrating the effectiveness of machine learning in handling large-scale educational data. Wardat et al. [8] analyzed TIMSS 2015 data from Abu Dhabi and highlighted the importance of school resources, parental support, and the disciplinary climate as key predictors of mathematics achievement. AlSalouli et al. [18] performed a multilevel analysis based on TIMSS 2019 data in the USA, finding that eighth-grade students’ attitudes, school climate, and teacher engagement significantly contribute to science achievement, explaining 33% of variance between schools. Badri et al. [19] examined the relationships among student attitudes, perceptions, and mathematics achievement using TIMSS 2015 data from the UAE, confirming that attitudes toward mathematics and its perceived relevance to real life play a decisive role.

In the Moroccan context, research is still limited. However, Khoudi, Nachaoui, and Lyaqini [20] addressed this gap by applying the XGBoost algorithm to TIMSS 2019 data of 8390 Moroccan eighth graders. They successfully identified 12 key contextual factors differentiating high and low achievers, covering student-, teacher-, and school-level variables. Building on these previous works, our study applies a deep learning approach, specifically autoencoders, to further explore the determinants of mathematics achievement in Morocco using the TIMSS 2019 dataset.

In parallel with these country-specific studies, recent research in educational data mining has increasingly embraced advanced machine learning techniques, particularly deep learning and explainable AI, to analyze large-scale assessments, such as TIMSS. Jang et al. (2022) used SHAP-based models to predict student success and interpret feature contributions, highlighting the role of interpretable AI in supporting early intervention strategies [21]. Khosravi et al. (2022) reviewed how explainable AI frameworks, including SHAP and LIME, can help educators make informed decisions by revealing how input variables influence predictions [22]. Furthermore, Bitton et al. (2022) proposed the Latent SHAP method for interpreting compressed representations from deep neural networks, a strategy highly relevant to our autoencoder-based approach [23]. These studies underscore the potential of combining deep learning with interpretability techniques to generate both predictive accuracy and actionable educational insights. Our work builds on this trend, aiming to bridge data-driven modeling with transparent recommendations for educational improvement in Morocco.

3. Material and Methods

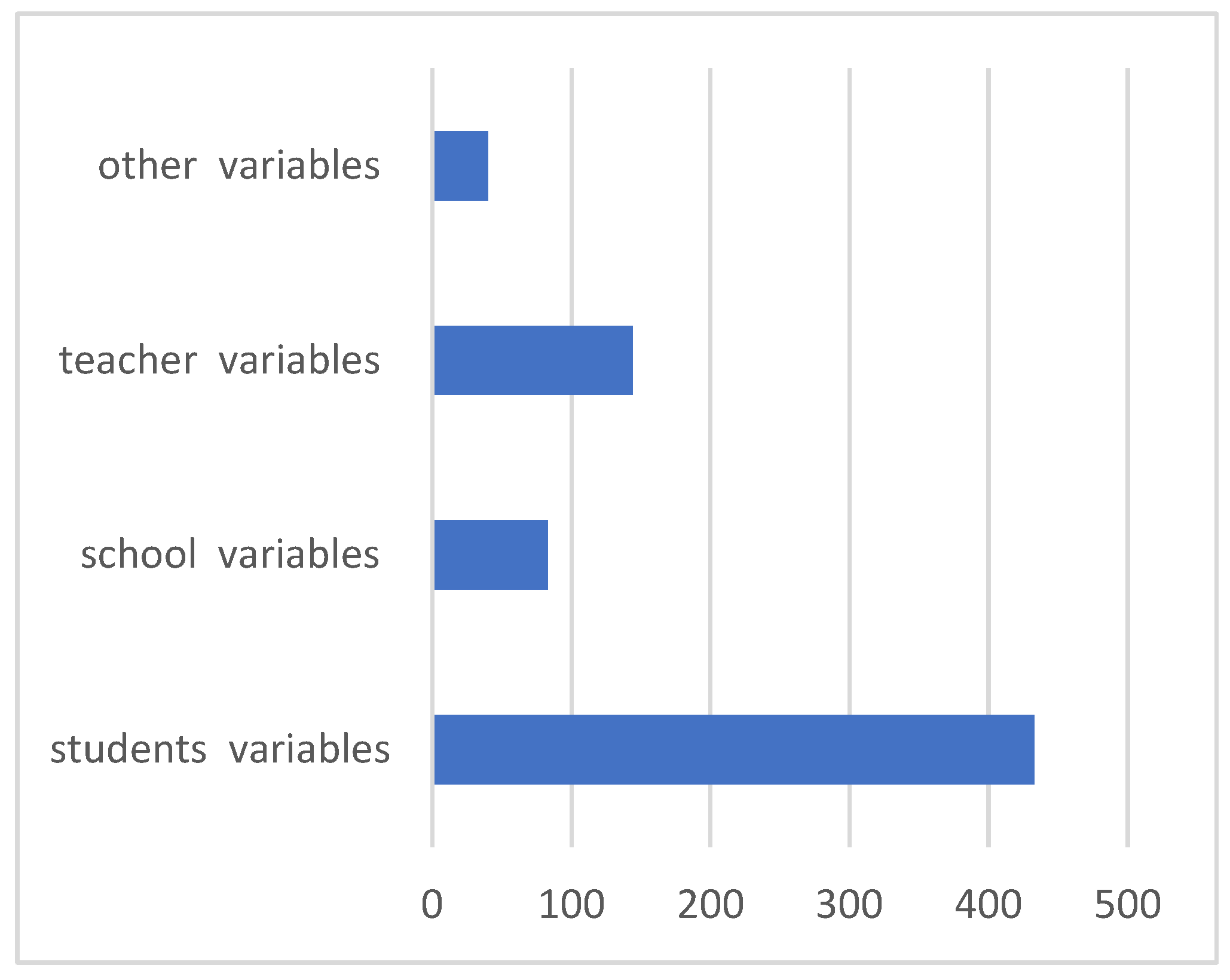
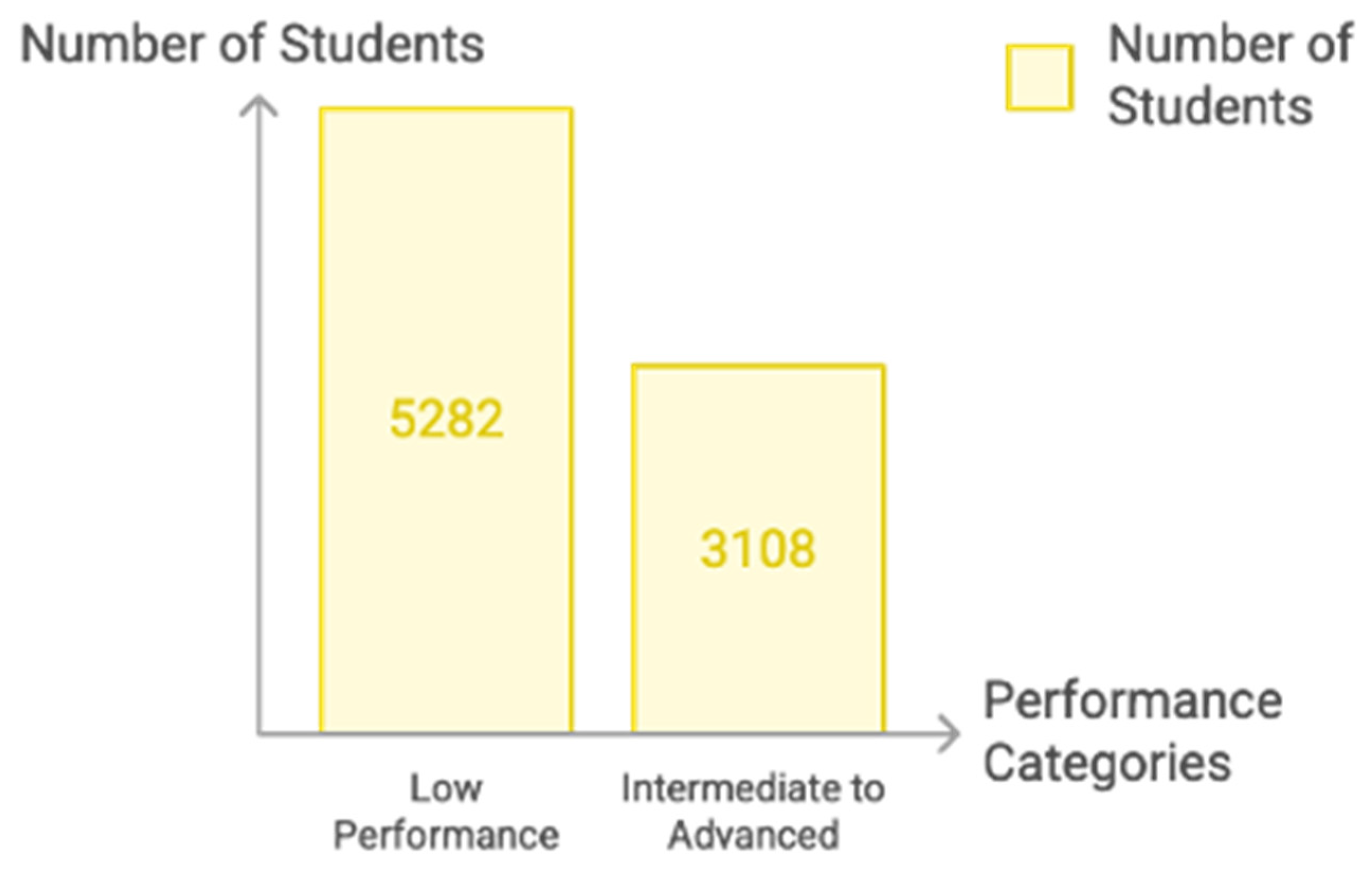
3.1. Data Description

The data utilized in this research were extracted from the TIMSS 2019 international database, curated by the IEA, Amsterdam, The Netherlands (TIMSS 2019 Database). The analysis focused exclusively on Moroccan students enrolled in the eighth grade. In the Moroccan education system, the eighth grade corresponds to the final year of lower secondary education (collège), with students typically aged between 13 and 14 years old. This level follows six years of primary schooling and precedes upper secondary education, forming part of the compulsory education system governed by a national curriculum. To build the dataset, information was obtained from three distinct sources, student, teacher, and school questionnaires.

The final dataset contained 8458 individual student entries following the data-integration process. This dataset comprised approximately 700 variables, offering detailed information on various aspects, such as students’ backgrounds, teacher characteristics, and school-level factors (Figure 1). The diversity and depth of these variables provided an extensive and valuable dataset to investigate the contextual determinants of mathematics achievement among Moroccan students.

The dataset comprises a total of 700 variables, organized into four main categories. Specifically, 433 variables relate to student background information (prefixed with BS), such as BSBG11A (students’ confidence in learning mathematics), BSBG09C (frequency of absenteeism), and BSBM16A (students’ sense of belonging at school). A total of 144 variables describes teacher characteristics (prefixed with BT), including BTBG12B (how often teachers ask students to explain their answers), BTBG08A (teachers’ participation in professional development), and BTBM20C (integration of technology in math lessons). In addition, 83 variables pertain to the school context (prefixed with BC), such as BCBG10A (availability of a school library), BCBG13BA (shortage of qualified teachers), and BCBG07 (number of available computers). In addition, 40 technical variables, including identifiers, weights, and metadata, are included for data management purposes but were excluded from the predictive modeling phase, as they do not contribute directly to the analysis of student performance. From a demographic perspective, the student population was balanced in terms of sex, with approximately 50.4% male and 49.6% female students. This party ensured that the analysis was not skewed by gender imbalances. Regarding the geographic distribution of schools, the dataset included institutions located in both urban and rural areas, with a relatively equitable representation across these environments. This balance made it possible to investigate potential geographic disparities in student achievement while maintaining a fair comparison base between different school locations.

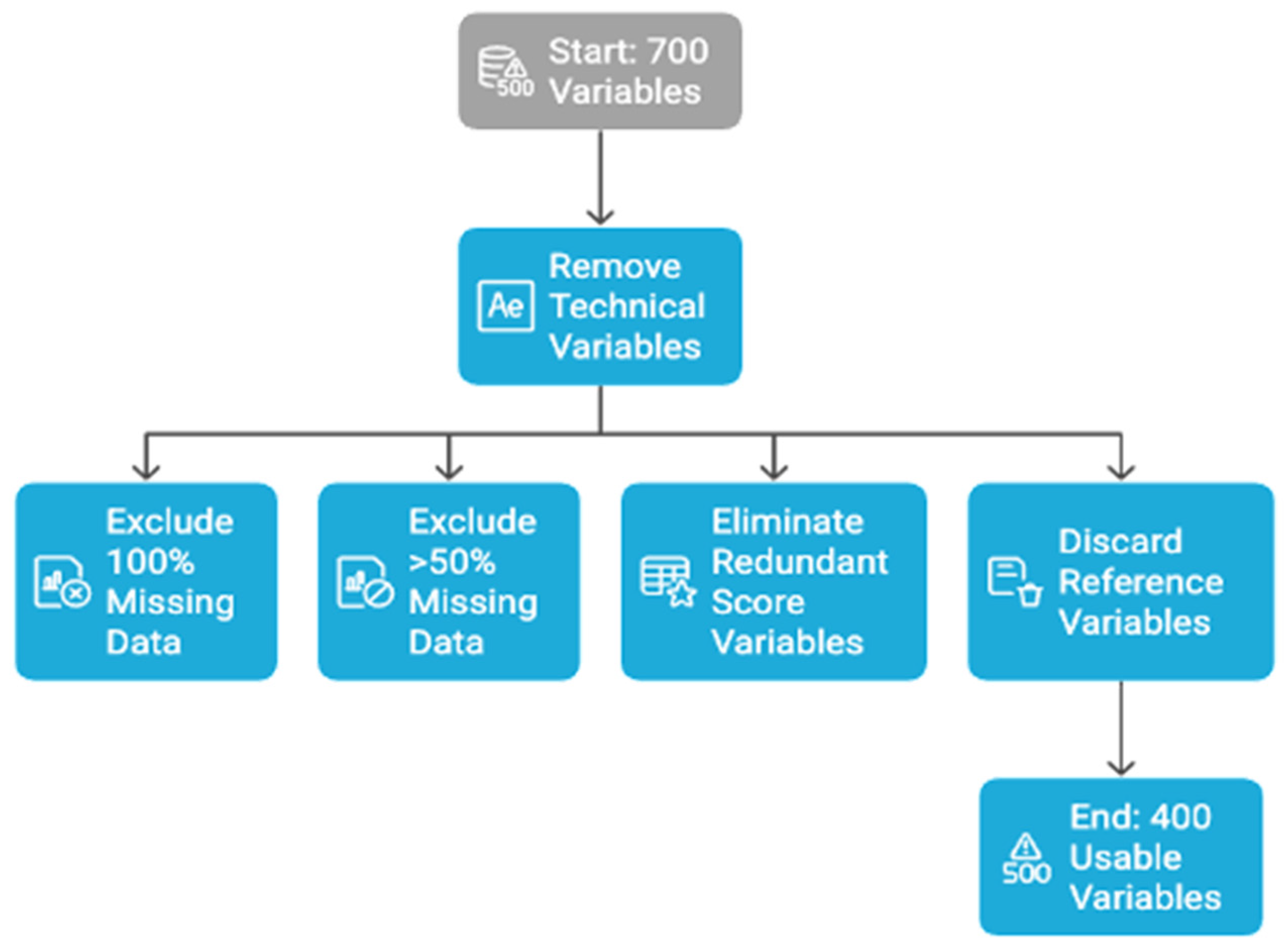
3.2. Data Pre-Processing

The data-cleaning process began with an initial pool of 700 variables extracted from the TIMSS 2019 database. Figure 2 outlines the key stages of this process. Several steps were taken to refine the dataset and ensure its reliability. First, 41 technical variables, including identifiers, weights, metadata, and duplicates, were removed, as they held no analytical value. Then, 61 variables with 100% missing values were excluded; these included items that were not administered in the Moroccan version of the survey, such as country-specific curriculum questions. An additional 74 variables with more than 50% missing data were also removed, as they related to rarely implemented school policies. To eliminate redundancy, 29 variables representing numerical scores already captured in alternative formats were discarded. Finally, 95 reference variables, particularly the plausible values (PVs), were excluded to avoid introducing bias into the predictive models. After this careful and systematic cleaning process, 400 variables remained, forming a robust and well-structured dataset suitable for the exploratory analysis and machine learning applications.

Once the dataset was thoroughly cleaned and refined, the next logical step involved identifying and defining the target variable that would guide our predictive modeling efforts. For this purpose, we used the plausible values (PVs) provided by the TIMSS 2019 assessment to construct a binary indicator of students’ mathematics performance. Each student in the dataset is assigned five PVs, which represent estimates of their achievement level. These values are categorized into five performance tiers: Below Low, Low, Intermediate, High, and Very High (Advanced). A descriptive analysis revealed that most students were concentrated in the “Low” and “Intermediate” categories.

The other levels showed highly unequal distributions: for instance, the “Intermediate” level included 2378 observations, with the “High” level 637 and the “Very High” level only including 5. To reduce class imbalance and simplify the predictive analysis, we decided to merge the “Intermediate,” “High,” and “Very High” levels into a single grouped category. This transformation enabled us to generate a binary target variable, coded as follows: 0 for the “Low” level, and 1 for the higher levels. This binary target was then used in training our machine learning classification models.

As a result, the final classification retained only two categories, as illustrated in Figure 3, the first representing students with low performance and the second grouping those with performance ranging from intermediate to advanced. This binary distinction facilitated the application of classification algorithms, while also enhancing the stability and interpretability of the predictive models.

3.3. Classification Models

After conducting the necessary preprocessing and cleaning steps, we obtained a structured dataset composed of 400 variables derived from TIMSS questionnaires, covering students, teacher, school, and contextual characteristics. The goal was to identify the most relevant predictors of students’ mathematics performance by leveraging advanced machine learning techniques.

In this study, an autoencoder was employed to reduce the dimensionality of the dataset [24]. The objective was to transform this high-dimensional input into a more compact latent representation, Figure 4, while preserving the essential information required for accurate predictions. The encoder architecture consists of two successive dense layers: the first maps the 400 input variables to a hidden layer of 100 neurons, and the second compresses this representation into a 20-dimensional latent space, denoted as Z. The choice of compressing the input space into 20 latent dimensions was based on empirical validation. Several configurations (10, 15, 20, 25, and 30 latent units) were tested during model tuning. The 20-dimensional representation consistently produced the best balance between classification accuracy and latent space interpretability. Smaller encodings led to a loss of predictive power, while higher-dimensional encodings resulted in marginal performance gains but increased complexity. Thus, 20 latent variables were retained as the optimal dimensionality for our analysis.

The autoencoder was trained by minimizing reconstruction loss, encouraging the model to capture the most informative and structured patterns within the data. The resulting latent variables served as an efficient encoding of the original data, supporting robust learning and reducing redundancy.

Once the latent space Z was generated, it was used as input to various supervised learning algorithms, namely Random Forest, XGBoost, Support Vector Machine, and Decision Tree to predict student achievement in mathematics. These models were selected based on their ability to handle structured, nonlinear data and because no single algorithm consistently provides optimal performance across all contexts. Experimental results confirmed that the latent features retained enough relevant information to ensure high prediction accuracy, validating the autoencoder’s dimensionality reduction.

To provide more context, the following brief descriptions outline the core principles and characteristics of the models applied:

• Random Forest (RF) is an ensemble learning technique that constructs many Decision Trees during the training phase and combines their predictions to enhance overall model accuracy. By aggregating the results of individual trees often through majority voting in classification tasks, Random Forest reduces the risk of overfitting, a common issue in single Decision Trees. This method proves especially effective when dealing with high-dimensional datasets, as it can automatically capture complex feature interactions and identify the most influential variables, making it a robust tool for both prediction and feature importance analysis [25].
• XGBoost (Extreme Gradient Boosting) is a highly efficient and scalable implementation of gradient boosting that builds Decision Trees in a sequential manner. Each new tree is trained to correct the errors made by the previous ones, allowing the model to progressively refine its predictions. What sets XGBoost apart is its incorporation of advanced regularization techniques, which help prevent overfitting—a common challenge in complex models. Additionally, XGBoost is optimized for both computational speed and predictive accuracy, making it a preferred choice for high-dimensional datasets and competitive machine learning tasks [26].
• Support Vector Machine (SVM) is a classification algorithm that aims to find the optimal hyperplane separating different classes with the maximum margin. It is well-suited for high-dimensional spaces and non-linear classification when used with kernel functions, such as the radial basis function (RBF) [27].
• Decision Tree (DT) is a tree structured classifier where each internal node represents a test based on an attribute, each branch corresponds to an outcome, and each leaf node represents a class label. Although it is prone to overfitting when used alone, its interpretability makes it valuable for understanding classification rules [28].

However, due to the abstract nature of the latent variables, a key challenge remained: how to interpret and trace their influence back to the original variables X. To address this, we adopted a hybrid interpretability strategy based on both neural network weight analysis and SHAP (SHapley Additive exPlanations) values [29].

The interpretative process unfolded through the following steps:

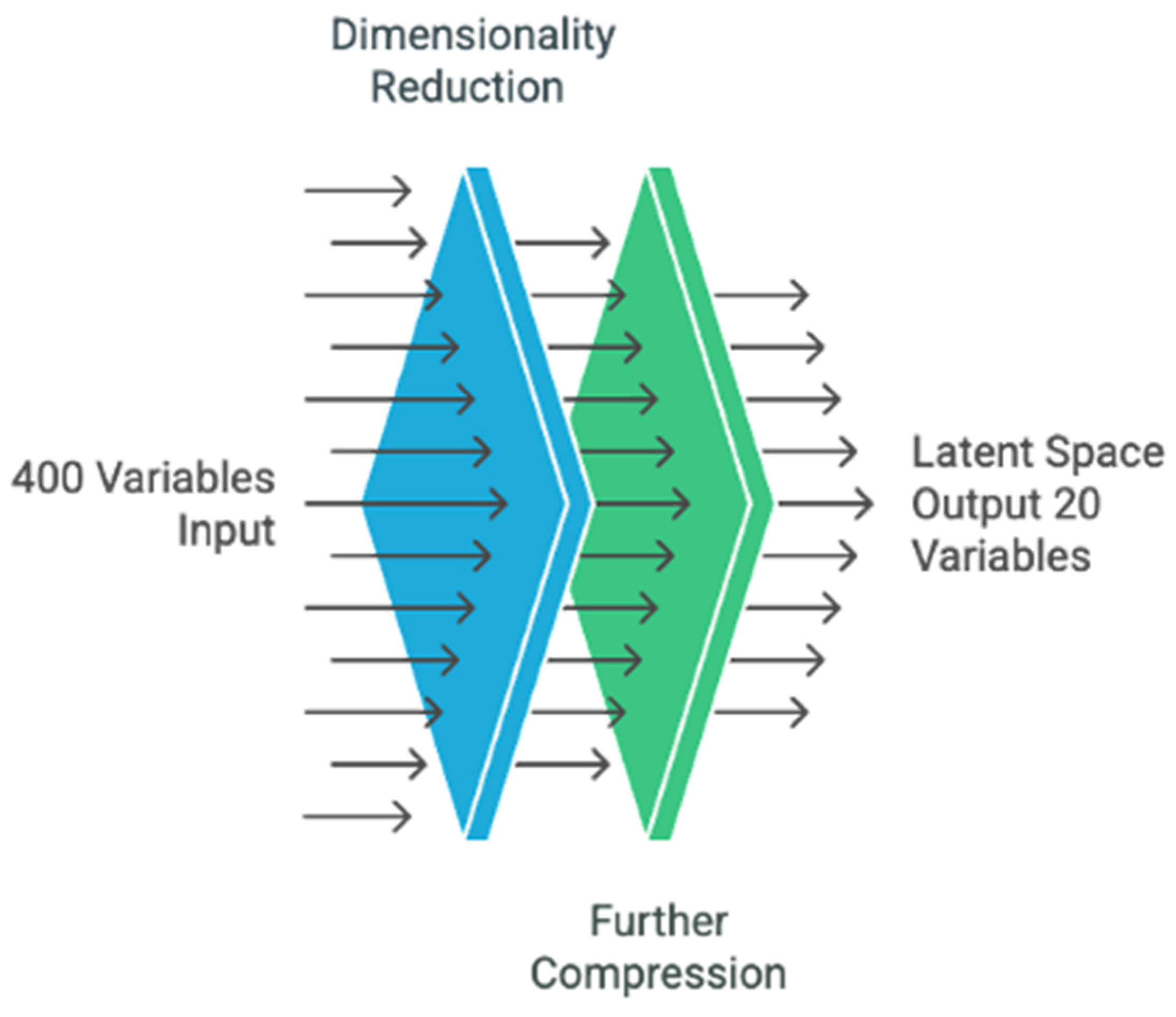
• Extraction of encoder weights: From the trained autoencoder, we retrieved the two core weight matrices: W1, which connects the input layer (original variables) to the first hidden layer, and W2, which connects the hidden layer to the latent space Z. By multiplying these matrices, we constructed a composite matrix Wx-z, which captures the contribution of each original input variable to each latent dimension.
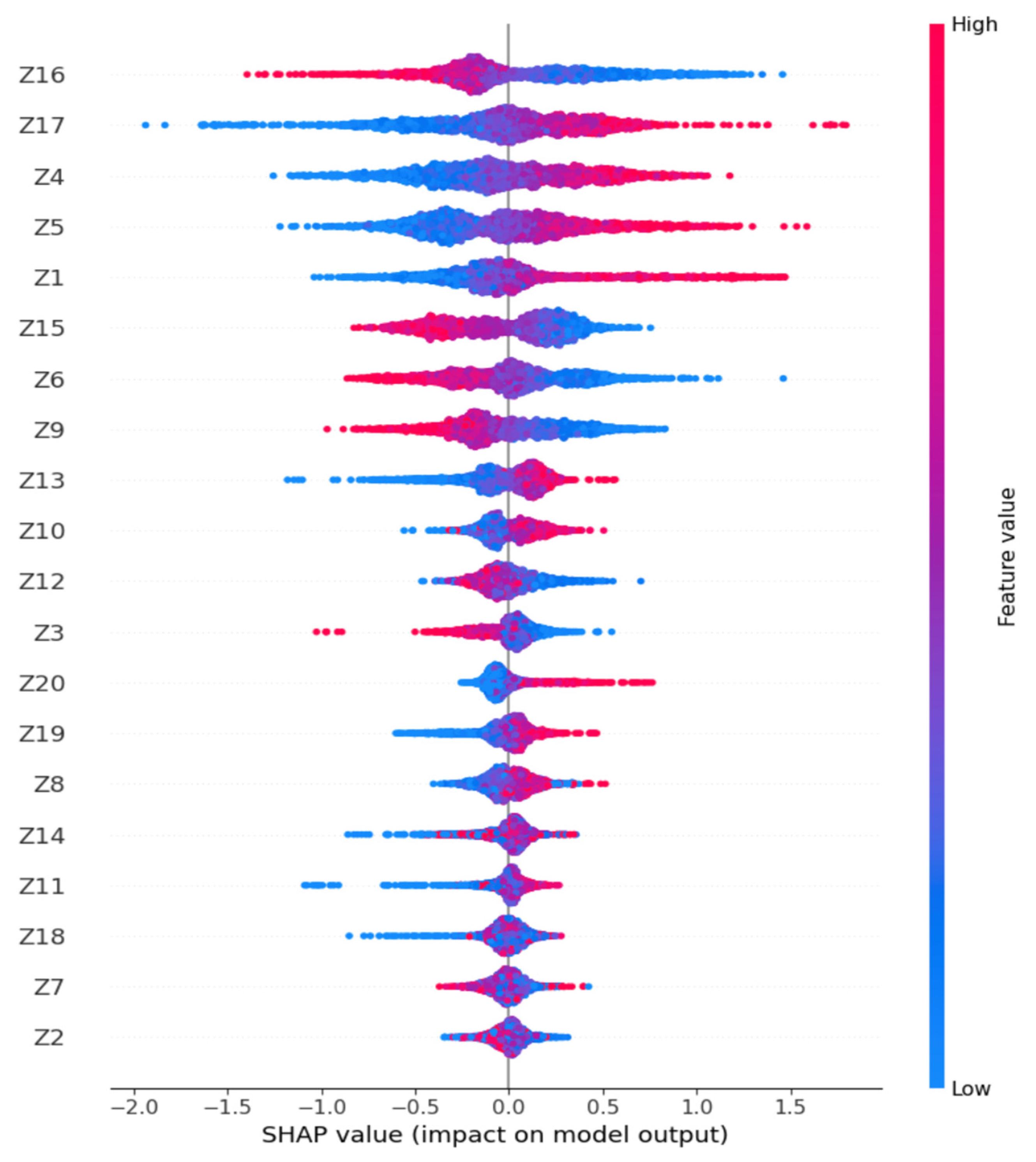
• SHAP-based importance estimation: Next, we trained an XGBoost classifier on the latent variables Z and computed SHAP values for each of these dimensions. These SHAP values quantify the contribution of each latent feature to the final prediction. Averaging the absolute SHAP values across all samples enabled us to identify which latent dimensions were most influential in driving the model’s output.
• Projection to input space: To understand which original variables most contributed to these key latent dimensions, we projected the SHAP importance scores from the latent space back to the original variable space using the Wx-z matrix. This allowed us to compute a global importance score for each input variable, reflecting its indirect impact on the prediction via the latent representations.
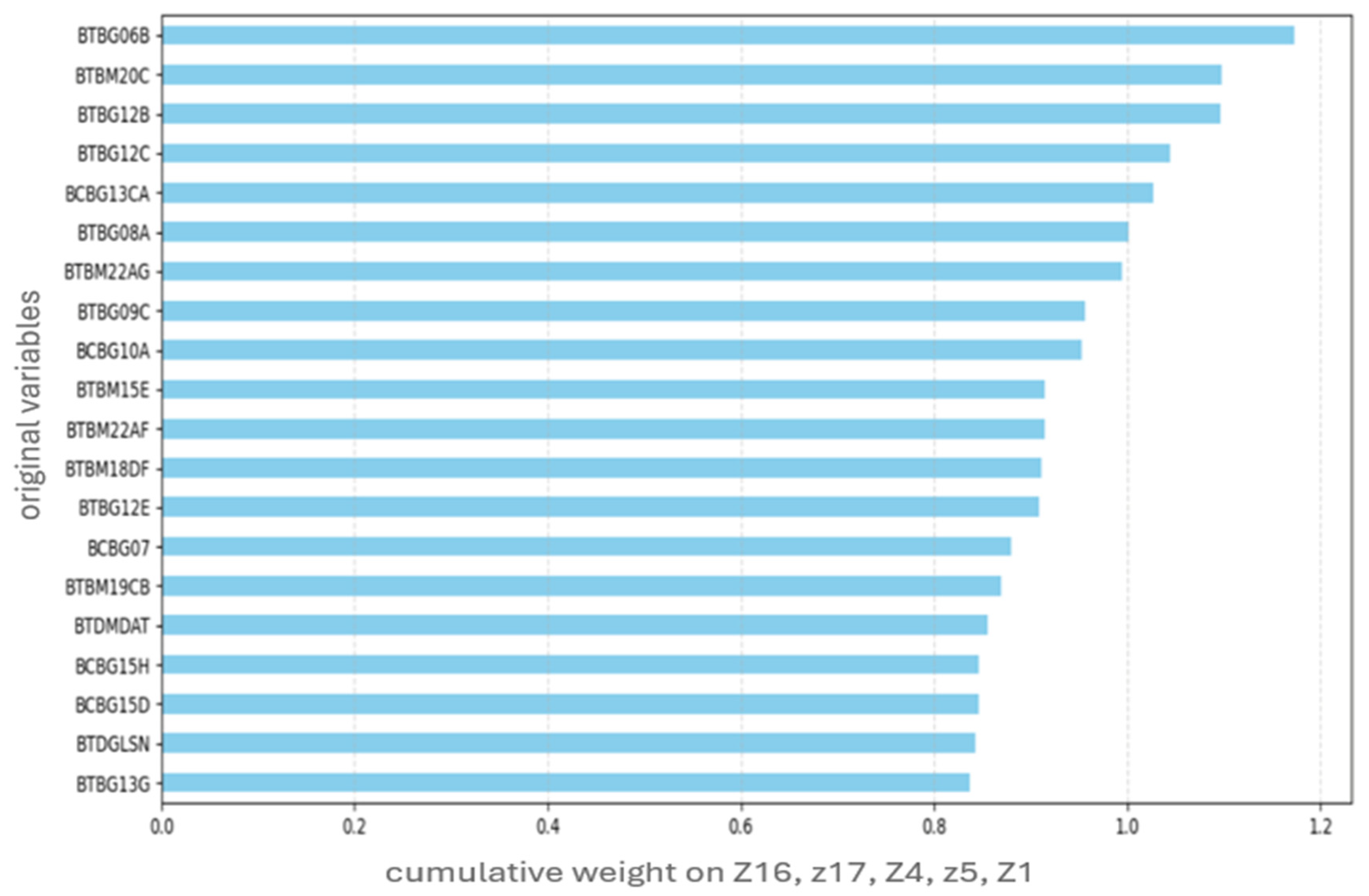
• Feature selection: Based on the aggregated importance scores, we ranked the original variables and selected the top contributors with the greatest influence on the predictive process. These variables capture the most meaningful educational, behavioral, and contextual indicators linked to students’ performance in mathematics.

This methodology not only validates the predictive strength of the latent space but also bridges the gap between deep learning and interpretability. By tracing the predictive impact back to understandable features, it offers actionable insights for educators and policymakers alike. In doing so, it supports the more transparent and responsible use of machine learning in the educational field.

4. Experimental Results

After presenting the classification models, this section explores the results obtained by applying them to the 20-dimensional latent features, extracted using the autoencoder. These compressed features serve as a distilled representation of the original 400 variables from the TIMSS dataset, capturing the most relevant information for prediction while reducing noise and redundancy. We trained four classification models, Random Forest, XGBoost, Support Vector Machine (SVM), and Decision Tree, on this latent space to classify students based on their academic performance. This comparative analysis allowed us to evaluate how well each model handles simplified, lower-dimensional input data and how effectively it distinguishes between different performance levels.

To assess each model’s performance, we used a set of standard evaluation metrics. A key tool in this process was the confusion matrix (

Table 1. Confusion matrix in general.

	Predicted Positive	Predicted Negative
Actual Positive	True Positive (TP)	False Negative (FN)
Actual Negative	False Positive (FP)	True Negative (TN)

), which gives a detailed view of how accurately each model classifies both high- and low-performing students. In our setup, the positive class represents high achievers, while the negative class includes students with lower performance. Alongside the confusion matrix, we also considered the accuracy, precision, recall, F1-score, and the Area Under the ROC Curve (AUC) to develop a comprehensive picture of each model’s strengths and limitations.

As shown in Table 1, the model achieves strong performance in distinguishing between low-performing and higher performing students. However, a limited number of false positives instances where low-performing students were misclassified as higher-performing can still be observed. While the false negative rate (i.e., high-performing students misclassified as low) remains lower, the presence of such false positives is particularly significant in educational contexts, where failing to identify students at risk may limit opportunities for timely intervention. These cases highlight the importance of combining predictive models with teacher judgment and continuous assessment to support equitable decision-making.

To evaluate the effectiveness of our classification models, we used four key performance metrics, with a particular focus on the accuracy and F1-score. Accuracy reflects the overall proportion of correct predictions and is calculated as follows:

$$\mathrm{Accuracy}={\displaystyle \frac{\mathrm{T}\mathrm{P}+\mathrm{T}\mathrm{N}}{\mathrm{T}\mathrm{P}+\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P}+\mathrm{F}\mathrm{N}}}$$

(1)

While accuracy gives a general sense of correctness, it can be misleading when class distributions are imbalanced. To address this, we used the F1-score, which balances precision (the proportion of true positives among all predicted positives) and recall (the proportion of true positives among all actual positives). The F1-score is calculated using the harmonic means of precision and recall:

$$\mathrm{F}1\text{-}\mathrm{score}={\displaystyle \frac{2.(\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}.\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l})}{\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}+\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}}}$$

(2)

In addition, we evaluated each model’s ability to distinguish between classes using the Area Under the Curve (AUC) of the Receiver Operating Characteristic (ROC). While binary classification often relies on a fixed threshold typically 0.5, the AUC provides a broader perspective by assessing model performance across all possible thresholds. This makes it a more robust and reliable measure of a model’s overall discriminative power.

5. Results and Discussion

The results of our performance evaluation are summarized in

Table 2. Performance evaluation of classification models based on latent features (accuracy and F1-score).

Models	Accuracy	F1-Score
Random Forest	0.71	0.69
Decision Tree	0.65	0.64
XGBoost	0.73	0.71
SVM	0.74	0.73

, highlighting key indicators associated with students’ mathematics achievement. Four classification models were assessed in this study: Random Forest, Decision Tree, XGBoost, and Support Vector Machine (SVM). Among these, SVM achieved the highest overall performance, with an accuracy of 0.74 and an F1-score of 0.73. These metrics reflect a strong balance between precision and recall, indicating that the SVM was particularly effective at distinguishing between high- and low-performing students.

XGBoost followed closely behind SVM, with an accuracy of 0.73 and an F1-score of 0.71. These results highlight its effectiveness in handling high-dimensional data, such as the latent variables generated by the autoencoder. The Random Forest model also performed well, achieving an accuracy of 0.71 and an F1-score of 0.69, indicating reliable but slightly lower predictive strength. In contrast, the Decision Tree classifier produced the weakest results, with an accuracy of 0.65 and an F1-score of 0.64, underscoring its limited ability to generalize within this modeling framework.

To complement the evaluation based on the accuracy and F1-score, we also assessed each model’s discriminative ability using the Receiver Operating Characteristic (ROC) curve and its corresponding Area Under the Curve (AUC). The ROC curve provides a detailed picture of each classifier’s ability to distinguish between high- and low-performing students across the full range of classification thresholds. While the SVM model achieved an AUC of 0.79, which is considered moderate in absolute terms, it reflects a reasonably strong performance in the context of high-dimensional, imbalanced, and noisy educational data. The accompanying F1-score of 0.73 reinforces the model’s ability to maintain a balance between precision and recall, making it a useful tool for identifying at-risk students with acceptable reliability.

Figure 5 compares the ROC curves of the four classification models, providing a visual summary of their discriminative ability based on the 20-dimensional latent features. The Area Under the Curve (AUC) values serve as concise indicators of each model’s ability to distinguish between high- and low-performing students, with values closer to 1 representing stronger performance.

Among the tested models, SVM achieved the highest AUC at 0.79, reflecting both strong discriminative power and robustness. This result is consistent with its leading F1-score and demonstrates its reliability when applied to compressed feature spaces. From a practical standpoint, such performance suggests that SVM is well-suited for the early identification of students at risk of underperformance, particularly in imbalanced and noisy educational datasets.

XGBoost followed closely with an AUC of 0.76, highlighting its effectiveness in capturing non-linear relationships and maintaining generalization. As a widely used model for structured data, XGBoost’s high sensitivity across classification thresholds reinforces its suitability for practical deployment in education systems, especially where nuanced patterns must be captured.

Random Forest posted an AUC of 0.75, showing solid but slightly lower performance. While it still offers balanced predictive capacity, its lower F1-score may reflect a degree of sensitivity to class imbalance, which could impact its reliability in high-stakes educational decision-making.

In contrast, the Decision Tree model recorded the lowest AUC at 0.68, indicating limited performance in this context. Although Decision Trees are valued for their interpretability, this result suggests that without ensemble reinforcement, they are less capable of capturing complex interactions within high-dimensional latent spaces.

Overall, the ROC-AUC analysis reinforces the conclusion that SVM and XGBoost are the most effective models in this study. Their superior AUC values and general performance make them promising candidates for practical integration into school-level monitoring systems. When combined with explainability tools, these models offer the dual benefits of predictive accuracy and interpretability, key components for designing targeted, data-driven educational interventions.

5.1. Feature Selection

Feature selection is a vital step in the machine learning pipeline, especially when working with high-dimensional datasets. Its primary goal is to identify and keep the most relevant variables while removing those that are redundant or noisy or add little predictive value. This process simplifies the dataset while retaining the essential information needed for accurate predictions. By reducing the dimensionality, feature selection improves the computational efficiency, reduces memory usage, and often enhances a model’s ability to generalize to new data. At the core of this process lies the concept of feature importance, which helps quantify how much each input variable influences the target outcome. This analysis strengthens the interpretability by shedding light on the most influential factors driving model predictions, offering a clearer understanding of the data’s underlying patterns.

In our study, feature selection was carried out using an autoencoder, which compressed the original 400 variables into a 20-dimensional latent space. Figure 6 displays a summary of SHAP values calculated for these latent features, highlighting the most impactful dimensions in predicting students’ mathematics performance. Each latent variable, labeled Z₁ through Z₂₀, represents a learned feature extracted during the encoding process. The horizontal axis in the figure shows the SHAP value, which reflects the contribution of each latent variable to the final prediction. Positive SHAP values indicate that a feature increases the likelihood of a high-performance classification, while negative values suggest a dampening effect. To enhance model transparency, we applied SHAP, a method based on cooperative game theory that provides consistent and locally accurate feature attributions [30]. SHAP has been successfully used in various domains, including healthcare and education, to interpret complex models, such as XGBoost and neural networks [31]. Its ability to explain individual predictions makes it particularly useful in educational settings, where interpretability is essential for informed decision-making. While SHAP values clearly identify influential latent variables such as Z₄, Z₅, Z₁₆, and Z₁₇, their semantic meaning remains abstract, as they do not directly correspond to specific educational indicators. These variables represent compressed patterns that integrate multiple aspects of the student background, teaching practices, and school conditions. To better interpret their educational significance, future work could involve inverse projection methods or correlation analyses with the original input features.

This approach not only enhances model performance but also improves transparency, bridging the gap between abstract latent features and clear, interpretable insights that can inform decision making.

The color scale further enriches the interpretation by mapping the raw value of each latent variable: red denotes high values, and blue indicates low values.

The results reveal that certain latent dimensions play a decisive role in the classification process. Notably, variables Z₁₆, Z₁₇, Z₄, Z₅, and Z₁ emerge as the most influential, as evidenced by their wider SHAP value distributions and greater distance from zero. For example, high values of Z₁₆ (shown in red) are predominantly located on the right side of the graph, suggesting a strong positive impact on the prediction of high academic performance. In contrast, other variables, such as Z₁₅ or Z₆, exhibit more ambiguous behavior, where the effect depends on the specific value taken by the latent feature itself.

By summing the absolute weights associated with these five latent dimensions, we were able to extract the top 20 original input variables that exerted the strongest influence on the construction of the latent space. In other words, these variables played a critical role in shaping the internal representations learned by the autoencoder.

Table 3. Absolute weights of original variables contributing to latent dimensions.

	Z16	Z17	Z4	Z5	Z1	Z15	Z6
BCBG13BA	Nan	Nan	0.300745	0.369664	Nan	Nan	Nan
BCBG13BB	0.335501	Nan	Nan	Nan	Nan	Nan	Nan
BCBG13CA	Nan	0.918100	Nan	0.180115	Nan	Nan	Nan
BCBG13CC	0.280674	Nan	Nan	Nan	Nan	Nan	Nan
BCBG14H	Nan	Nan	Nan	Nan	Nan	Nan	Nan
BCBG16B	Nan	Nan	Nan	0.356161	Nan	Nan	Nan
BCBG16J	Nan	Nan	0.298822	Nan	Nan	Nan	Nan
BCBG16K	0.344207	Nan	Nan	Nan	Nan	Nan	Nan
BCBG10A	Nan	Nan	0.694093	0.199053	Nan	Nan	Nan
BTBG01	Nan	0.328356	Nan	Nan	Nan	Nan	Nan
BTBG06A	Nan	Nan	0.299234	Nan	Nan	Nan	Nan
BTBG12B	0.852109	Nan	Nan	Nan	Nan	0.218380	Nan
BTBG08A	Nan	0.709116	0.300014	Nan	Nan	Nan	Nan
BTBG06B	0.801001	Nan	0.327315	Nan	Nan	Nan	Nan
BTBG12C	Nan	0.623100	Nan	Nan	0.779116	Nan	Nan
BTBG09C	Nan	Nan	0.784053	Nan	Nan	0.184053	Nan
BTBG09H	Nan	Nan	Nan	Nan	Nan	0.220638	Nan
BTBG13F	Nan	Nan	Nan	0.318046	Nan	Nan	Nan
BTBM20C	0.753100	Nan	0.322244	Nan	Nan	Nan	Nan
BTBM18BF	Nan	Nan	Nan	Nan	0.332814	Nan	Nan
BTBM22AF	Nan	Nan	Nan	0.656161	Nan	Nan	0.286259
BTBM18CB	Nan	Nan	Nan	Nan	Nan	0.303042	Nan

presents the original variables that contributed the most to the formation of the five most influential latent dimensions (Z₁₆, Z₁₇, Z₄, Z₅, and Z₁), as identified through the combined analysis of the autoencoder model’s weight matrix. These latent dimensions result from the dimensionality reduction applied to the 400 variables in the TIMSS 2019 dataset.

The values shown in the table correspond to the absolute weights linking each input variable to a specific latent dimension. These weights were derived from the Wx-z matrix, obtained by multiplying the internal weights of the network. Thus, they quantify the indirect impact of the original variables on the compact representations learned by the autoencoder.

For example

• The variable BTBG12B shows a significant weight of 0.852 based on latent dimension Z₁₆ and a non-negligible weight based on Z₁₅ (0.218), indicating that it plays a structuring role in at least two model dimensions.
• The variable BTBM20C strongly contributes to Z₁₆ (0.753) and Z₄ (0.322), suggesting cross-influence across multiple latent aspects.
• Similarly, BCBG10A stands out with contributions to Z₄ (0.694) and Z₅ (0.199), highlighting its importance in shaping latent representations.

Figure 7 illustrates this relationship by highlighting the original TIMSS variables that most significantly contributed to the formation of these influential latent features. Notably, the analysis shows that most of these variables are directly related to teachers, including their pedagogical practices and classroom management, and experiences well as to students’ classroom behavior, such as attentiveness, discipline, and participation. These aspects are particularly relevant in understanding academic outcomes, as they reflect the teaching environment and behavioral engagement within the classroom. The following Table 3 summarizes these key features, which can be considered major predictive variables based on their content and influence. These findings reinforce the importance of classroom dynamics and instructional quality in shaping students’ mathematics performance [32].

5.2. Evaluation of Top 20 Original Variables for Classification

To evaluate the predictive power of the top 20 original variables identified using the autoencoder’s contribution matrix, we trained a second set of classification models using only these selected features. These variables were chosen based on their strong influence on the most predictive latent dimensions (Z₁₆, Z₁₇, Z₄, Z₅, and Z₁), as determined by their absolute weights in the Wx-z matrix and their relevance highlighted through SHAP analysis. The same four supervised learning models used in the previous experiment Random Forest, XGBoost, Support Vector Machine (SVM), and Decision Tree were applied to this reduced set of features. The objective was to assess whether these 20 variables alone could capture enough information to reliably distinguish between students with low and high mathematics achievement, The results of this experiment are presented in

Table 4. Classification performance using the top 20 original variables.

Models	Accuracy	F1-Score
Random Forest	0.68	0.67
Decision Tree	0.63	0.62
XGBoost	0.72	0.70
SVM	0.73	0.72

.

As demonstrated, the accuracy and F1-score values of the SVM and XGBoost classifiers were comparable to those obtained using the 20-dimensional latent features, confirming their continued strong predictive capabilities. These findings suggest that the selected original variables contain substantial discriminative information, making them suitable for classification tasks that are both accurate and interpretable. This validation confirms that the top 20 variables are sufficient not only to maintain strong model performance but also to enhance interpretability and essential consideration in educational contexts where actionable insights are critical for informed decision-making, a detailed description of these 20 variables is presented in

Table 5. Description of essential characteristics.

Feature	Description
BTBG06B	Frequency with which the teacher faces students lacking prerequisite knowledge
BTBM20C	How often students use computers/tablets to search for ideas/information in math
BTBG12B	How often teachers ask students to explain their answers
BTBG12C	How often teachers give challenging exercises to students
BCBG13CA	Shortage of specialized science teachers according to the school
BTBG08A	Frequency of teacher participation in professional development on math content
BTBM22AG	Teacher’s recent professional development focus: addressing student needs
BTBG09C	Agreement with the statement “Too many teaching hours are required”
BCBG10A	Whether the school has a functioning library
BTBM15E	How often teachers ask students to apply what they have learned in math
BTBM22AF	Professional development focused on mathematics assessment
BTBM18DF	Coverage of probability compound events in the curriculum
BTBG12E	How often teachers help students link new knowledge with prior knowledge
BCBG07	Total number of computers available in the school
BTBM19CB	Whether students are asked to correct their own math homework
BTDMDAT	Percentage of students taught data and probability topics
BCBG15H	Agreement with the statement students need extra time to complete tasks
BCBG15D	Total number of students taught in the mathematics class
BTDGLSN	Extent to which teaching is limited by students’ needs or abilities
BTBG13G	Teacher’s level of agreement with the statement “Students are not motivated to do well in school.”

.

The analysis of contextual variables in this study highlights the distinct influence of school-related factors, such as available resources, classroom size, and the presence of a functioning library (BCBG07, BCBG10A, BCBG15D), versus those directly tied to instructional practices and teacher challenges, the frequency of pedagogical strategies, students’ lack of prerequisites, and perceived motivation (BTBG06B, BTBG12B, BTBG13G). This distinction is critical for understanding the multiple dimensions that affect student achievement in mathematics. The results suggest that while infrastructure provides foundational support, it is primarily the quality of instructional strategies, the extent of teacher professional development (BTBM22AG, BTBM22AF), and teachers’ ability to adapt lessons to diverse student needs (BTDGLSN, BTBM20C) that significantly impact outcomes. Variables such as asking students to explain reasoning (BTBG12B) or connecting new knowledge with a prior understanding (BTBG12E) point to an active pedagogy that encourages autonomy and critical thinking skills that are essential for mathematics proficiency.

6. Implication and Recommendations

Based on the key findings of this study, several practical recommendations can be made to improve mathematics achievement among Moroccan students:

▪

Promote Interactive Teaching Practices: Variables such as BTBG12B (teachers asking students to explain their answers) and BTBG12E (linking new knowledge to prior understanding) show strong positive associations with higher achievement. Training programs should emphasize active pedagogy that fosters reasoning and autonomy.

▪

Improve Access to Educational Resources: Features like BTBM20C (use of digital tools) and BCBG10A (availability of school libraries) highlight the importance of infrastructure. Ensuring equitable access to these resources can reduce achievement gaps.

▪

Support Targeted Teacher Development: The role of teacher professional development (e.g., BTBG08A, BTBM22AF) emerged as a key factor. Investment in tailored training focused on formative assessment and differentiated instruction is essential.

▪

Address Foundational Learning Gaps: BTBG06B reflects the frequent challenge of students lacking prerequisite knowledge. Schools should implement diagnostic assessments and remediation programs to support at-risk learners.

These recommendations, derived from explainable deep learning models and contextualized within the TIMSS 2019 Moroccan dataset, provide concrete pathways for educational stakeholders to design data-informed interventions aimed at improving student outcomes in mathematics.

7. Conclusions

The findings of this study highlight the combined influence of instructional practices and school-level conditions on students’ performance in mathematics. While access to material resources (such as libraries and digital tools) plays a supportive role, it is ultimately the quality of classroom strategies, the extent of teacher professional development, and the ability to address diverse learning needs that emerge as the most decisive factors in student achievement. In response to the guiding questions, the analysis reveals the following:

• Teachers often face students who lack foundational knowledge, underlining the critical need for diagnostic assessments and differentiated instruction.
• Teachers who have received professional development focused on student needs and formative assessment demonstrate greater instructional effectiveness.
• Low student motivation, as perceived by teachers, presents a persistent barrier to success, but one that can be addressed by engaging, learner-centered pedagogical approaches.
• Although school infrastructure contributes to the learning environment, it must be paired with the empowerment and support of teachers to yield meaningful academic improvement.

This study not only confirms known challenges but also introduces a novel methodological perspective. By compressing over 400 variables into 20 latent features using autoencoders and interpreting them via SHAP values, the study provides an explainable deep learning framework that identifies subtle, non-linear patterns influencing performance patterns that traditional statistical models may overlook. This approach not only improves the predictive accuracy, but also enhances transparency, offering educators and policymakers interpretable, data driven insights. Beyond descriptive findings, this research also offers a predictive lens. The variables identified as most influential can serve as reliable indicators for anticipating students’ mathematics outcomes. Their integration into explainable machine learning models provides not only predictive capacity but also actionable insights to inform pedagogical strategies and policy decisions.

The practical implications of these findings are particularly relevant for educational stakeholders. For educators, the results highlight the need to strengthen diagnostic assessments and diversify instructional methods to address varying student readiness levels. For policymakers, the study underscores the importance of investing in teacher professional development focused on formative practices and inclusive pedagogy. Lastly, for curriculum developers, the findings support the integration of motivational and student-centered components into math instruction, as well as an alignment with the real-life experiences of learners. Together, these targeted actions could contribute to narrowing performance gaps and enhancing overall educational equity in Morocco.

That said, several limitations must be acknowledged. TIMSS 2019 remains a valuable resource, but the data collected more than five years ago may not fully reflect current educational conditions in Morocco. Additionally, many variables are self-reported and may introduce perception biases. The study is also context-specific, and its findings may not be directly generalized to other educational systems. Finally, while machine learning enhances predictive power, it does not establish causality.

Future research should address these limitations by integrating longitudinal data, conducting qualitative studies with educators, and updating models with more recent datasets. This would ensure greater relevance, applicability, and depth in understanding the evolving landscape of mathematics education. Although a binary classification was adopted due to the strong class imbalance in the current dataset, future studies may explore multi-class models combined with advanced oversampling techniques. Such approaches could help preserve performance granularity and better capture the nuanced differences across achievement levels.

To guide future investigations, several research directions are worth exploring. First, the integration of longitudinal data would help assess how contextual factors influence student performance over time, enabling the identification of causal trends. Second, combining this approach with qualitative studies, such as teacher interviews or classroom observations, could enrich the quantitative findings with contextual depth. Third, future models may adopt a multi-class classification framework with advanced oversampling techniques to better capture performance gradations among students. Additionally, inverse mapping or correlation analysis could be applied to interpret the latent variables produced by the autoencoder and clarify their educational meaning. Finally, adapting this explainable AI framework to real-time school-based monitoring systems could support early interventions and informed decision-making in classroom settings.