Search Heuristics and Constructive Algorithms for Maximally Idempotent Integers

Abstract

Previous work established the set of square-free integers n with at least one factorization $n=\overline{p}\overline{q}$ for which $\overline{p}$ and $\overline{q}$ are valid RSA keys, whether they are prime or composite. These integers are exactly those with the property $\lambda \left(n\right)\mid (\overline{p}-1)(\overline{q}-1)$, where $\lambda$ is the Carmichael totient function. We refer to these integers as idempotent, because $\forall a\in Z_n,a^{k(\overline{p}-1)(\overline{q}-1)+1}\underset{n}{\equiv }a$ for any positive integer k. This set was initially known to contain only the semiprimes, and later expanded to include some of the Carmichael numbers. Recent work by the author gave the explicit formulation for the set, showing that the set includes numbers that are neither semiprimes nor Carmichael numbers. Numbers in this last category had not been previously analyzed in the literature. While only the semiprimes have useful cryptographic properties, idempotent integers are deserving of study in their own right as they lie at the border of hard problems in number theory and computer science. Some idempotent integers, the maximally idempotent integers, have the property that all their factorizations are idempotent. We discuss their structure here, heuristics to assist in finding them, and algorithms from graph theory that can be used to construct examples of arbitrary size.

1. Introduction

Take two integers $\overline{p}$ and $\overline{q}$, let $n=\overline{p}\overline{q}$. Let ${\varphi }^{\prime }\left(n\right)=(\overline{p}-1)(\overline{q}-1)$. Find two integers d and e such that $de\underset{{\varphi }^{\prime }\left(n\right)}{\equiv }1$. Publish e, keep d secret. Let M be a message, let its encrypted version be given by by $E\underset{n}{\equiv }{M}^e$. Let the decryption operation be given by $D\underset{n}{\equiv }{E}^d$. What are the conditions on $\overline{p}$ and $\overline{q}$ such that $D=M$?

Readers will recognize this as the RSA protocol [1], with the required conditions constraining encryption and decryption to “work”: Encrypting and decrypting in this manner will recover the original message. Ref. [1] showed that choosing $\overline{p}$ and $\overline{q}$ as prime numbers will not only meet this required condition, but also provides the valuable property of making n empirically difficult to factor (when $\overline{p}$ and $\overline{q}$ are sufficiently large). This in turn leads to the security of RSA.

While choosing n as a semiprime provides the necessary security properties, and reduces ${\varphi }^{\prime }$ to Euler’s totient function, semiprimes are not the only integers for which the correctness of this protocol is preserved. Ten years after [1,2] implicitly showed, without explicitly stating, that the set of these integers also includes some of the Carmichael numbers. Whether there were other possible values of $n=\overline{p}\overline{q}$ that were neither semiprimes nor Carmichael numbers remained unknown.

In [3], we introduced the notion of idempotent integers, the set of square-free integers n that can be factored into two positive integers $\overline{p}$ and $\overline{q}$ such that $\lambda \left(n\right)\mid (\overline{p}-1)(\overline{q}-1)$, where $\lambda$ is the Carmichael totient function. We refer to these integers as idempotent because $\forall a\in Z_n,a^{k(\overline{p}-1)(\overline{q}-1)+1}\underset{n}{\equiv }a$ for any positive integer k. These integers are exactly those for which $\overline{p}$ and $\overline{q}$ generate valid keys in the 2-prime RSA protocol, regardless of whether they are prime or composite [3].

While only the semiprimes have useful cryptographic properties [4], idempotent integers are deserving of study in their own right, as they lie at the border of hard problems in number theory and computer science. Some idempotent integers, the maximally idempotent integers, have the property that all their factorizations are idempotent. We discuss their structure here, heuristics to assist in finding them, and algorithms from graph theory that can be used to construct examples of arbitrary size. We discuss what is currently known, present new results since [3], and discuss open problems.

2. Materials and Methods

2.1. Definitions

Let $n=p_1{p}_2\dots p_m$ be a square-free integer, where $p_1<p_2<\dots <p_m$ are primes. Let $a_i=p_i-1:i=1\dots m$. We will call $a_i$ the predecessor of $p_i$ and $p_i$ the successor of $a_i$. It is a known property of the function $\lambda$ that $\lambda \left(n\right)=\mathrm{lcm}(a_1,a_2,\dots ,a_m)$, where lcm denotes the least common multiple. We will write $\lambda$ instead of $\lambda \left(n\right)$ when the meaning is clear. We write ${\overline{p}}_i$ as shorthand for ${\displaystyle \prod _{i=1\dots m}}{p}_i$.

Let $n=p_1{p}_2\dots p_m$. Let P be the set $\{p_1,p_2\dots p_m\}$. Sets A and B are said to partition P if (a) $\forall p\in P,$ either $p\in A$ or $p\in B$, (b) $A\bigcap B=\varnothing$, and (c) $A\bigcup B=P$. A factorization of n into $\overline{p}\overline{q}$ is any $\overline{p},\overline{q}$ such that $\overline{p}={\displaystyle \prod _{p\in A}p,\overline{q}=\prod _{p\in B}}p$ where A and B partition P. An idempotent factorization is a factorization $n=\overline{p}\overline{q}$ for which $\lambda \left(n\right)\mid (\overline{p}-1)(\overline{q}-1)$. We will refer to an integer n that has an idempotent factorization as idempotent when the meaning is clear.

Let $p,q$ be prime, consider a semiprime $n=pq$. It is a known property of $\lambda$ that $\lambda \left(n\right)\mid \varphi \left(n\right)$. Since $\varphi \left(n\right)=(p-1)(q-1)$, all semiprimes are trivially idempotent. We do not consider them further here.

Any square-free integer with m factors has $\left(\genfrac{}{}{0pt}{}{m}{1}\right)=m$ factorizations of the form $\overline{p}=p_i,\overline{q}={\displaystyle \prod _{j\ne i}}{p}_j,\left(\genfrac{}{}{0pt}{}{m}{2}\right)$ factorizations of the form $\overline{p}=p_i{p}_j,\overline{q}={\displaystyle \prod _{k\ne i,j}}{p}_k$, and so forth. Each factorization corresponds to a single equation in $n, \overline{p}$ and $\overline{q}$ that represents a possible idempotent factorization. We refer to these as single-factor equations/factorizations, double-factor, etc. We call idempotent single-factor factorizations semi-composite factorizations of n, because $\overline{p}$ is prime while $\overline{q}$ is composite. All other factorizations are fully composite.

The first eight square-free n with three or more factors and fully composite idempotent factorizations are shown in

Table 1. The first 8 integers with fully composite idempotent factorizations.

n	Prime Factorization	Idempotent Factorization n = $\overline{\mathit{p}}\overline{\mathit{q}}$	$\mathit{\lambda }$
210	2*3*5*7	10*21	12
462	2*3*7*11	21*22	30
570	2*3*5*19	10*57	36
1155	3*5*7*11	21*55	60
1302	2*3*7*31	6*217	60
1330	2*5*7*19	10*133	36
1365	3*5*7*13	15*91	12
1785	3*5*7*17	21*85	48

[3].

The smallest integer with two fully composite idempotent factorizations is 2730, when factored into 10*273 and 21*130. The complete list of all $n<2^{27}$ with fully composite idempotent factorizations is available at [5].

2.2. Maximally Idempotent Integers

An integer is maximally idempotent if all its factorizations are idempotent. These integers have the property that all their factorizations $n=\overline{p}\overline{q}$ produce correctly functioning RSA keys.

The first 16 maximally idempotent n with 3 and 4 prime factors are shown in

Table 2. Maximally idempotent integers with 3, 4 and 5 factors.

3 Factors	$\mathit{\lambda }$	4 Factors	$\mathit{\lambda }$	5 Factors	$\mathit{\lambda }$
273 = 3*7*13	12	63,973 = 7*13*19*37	36	72,719,023 = 13*19*37*73*109	216
455 = 5*7 *13	12	137,555 = 5*11*41*61	120	213,224,231 = 11*31*41*101*151	300
1729 = 7*13*19	36	145,607 = 7*11*31*61	60
2109 = 3*19*37	36	245,791 = 7*13*37*73	72
2255 = 5*11*41	40	356,595 = 5*19*37*73	72
2387 = 7*11*31	30	270,413 = 11*13*31*61	60
3367 = 7*13*37	36	536,389 = 7*19*37*109	108
3515 = 5*19*37	72	667,147 = 13*19*37*73	72
4433 = 11*13*31	60	996,151 = 13*19*37*109	108
4697 = 7*11*61	60	1,007,903 = 13*31*41*61	120
4921 = 7*19*37	36	1,847,747 = 11*17*41*241	240
5673 = 3*31*61	60	1,965,379 = 13*19*73*109	216
6643 = 7*13*73	72	2,060,863 = 7*37*73*109	216
6935 = 5*19*73	72	2,395,897 = 7*31*61*181	180
7667 = 11*17*41	80	2,778,611 = 11*41*61*101	600
8103 = 3*37*73	72	3,140,951 = 11*31*61*151	300

, along with the two 5-factor cases <$2^{30}$ [3]. Carmichael numbers are underlined.

Maximally idempotent integers are rare. Below $2^{30}$ there are 15,189 with three prime factors, 315 with 4, and 2 with 5.

The smallest and smallest known maximally idempotent integers with m factors for $3\le m\le 9$ are shown below in

Table 3. Smallest or smallest known (m = 8, 9) maximally idempotent integers with m factors.

m	n	Factorization
3	273	3*7*13
4	63,973	7*13*19*37
5	72,719,023	13*19*37*73*109
6	13,006,678,091	11*31*41*61*101*151
7	7,817,013,532,691	11*31*41*61*101*151*601
8	1,461,152,759,521,471,960,628,611	31*211*421*631*2521*4201*6301*12,601
9	35 digits	61*2021*3061*6121*8161*12,241*24,481*40,801*122,401

:

3. Results

3.1. Some Structural Properties of Maximally Idempotent Integers

A number of quantities affect whether or not an integer is maximally idempotent: The smallest prime $p_1$, the largest prime $p_m$, the number of factors m, the GCD of each distinct set of factorizations, and the least common multiple of the $a_i$.

We begin with a universal property of maximally idempotent integers:

Theorem 1.

All maximally idempotent integers with at least three factors are odd.

Proof. 

First, we consider the case $m=3$. There are three equations that must be satisfied for n to be maximally idempotent:

$$\begin{array}{c}(p_1-1)(p_2{p}_3-1)\underset{\lambda }{\equiv }0\\ (p_2-1)(p_1{p}_3-1)\underset{\lambda }{\equiv }0\\ (p_3-1)(p_1{p}_2-1)\underset{\lambda }{\equiv }0\end{array}$$

Assume $p_1=2$. Plugging it into the above, we obtain:

$$\begin{array}{c}(p_2{p}_3-1)\underset{\lambda }{\equiv }0\to p_2{p}_3\underset{\lambda }{\equiv }1\\ (p_2-1)(2p_3-1)\underset{\lambda }{\equiv }0\to 2p_2{p}_3-p_2-2p_3+1\underset{\lambda }{\equiv }0\\ (p_3-1)(2p_2-1)\underset{\lambda }{\equiv }0\to 2p_2{p}_3-p_3-2p_2+1\underset{\lambda }{\equiv }0\end{array}$$

Applying the first equation to the second and third, we have:

$$\begin{array}{c}2-p_2-2p_3+1\underset{\lambda }{\equiv }0\to p_2+2p_3\underset{\lambda }{\equiv }3\\ 2-p_3-2p_2+1\underset{\lambda }{\equiv }0\to 2p_2+p_3\underset{\lambda }{\equiv }3\\ \to p_2+2p_3\underset{\lambda }{\equiv }2p_2+p_3\to p_3\underset{\lambda }{\equiv }{p}_2\to a_3\underset{\lambda }{\equiv }{a}_2\end{array}$$

For distinct $a_i$ with $a_2<a_3, \lambda =\mathrm{lcm}(a_1,a_2,a_3)=\mathrm{lcm}(1,a_2,a_3)\ge a_3$, so the above is impossible.

Now, let $n=p_1{p}_2\dots p_m$ be a maximally idempotent integer with $m>3$. There are m single-factor equations that n satisfies:

$$\begin{array}{c}(p_1-1)(p_2{p}_3\dots p_m-1)\underset{\lambda }{\equiv }0\\ (p_2-1)(p_1{p}_3\dots p_m-1)\underset{\lambda }{\equiv }0\\ \dots \\ (p_m-1)(p_1{p}_2\dots p_{m-1}-1)\underset{\lambda }{\equiv }0\end{array}$$

Assume $p_1=2$ and substitute. We have

$$\begin{array}{c}(2-1)(p_2{p}_3\dots p_m-1)\underset{\lambda }{\equiv }0\to p_2{p}_3\dots p_m\underset{\lambda }{\equiv }1(i=1)\\ (p_i-1)(2p_{j\ne 1,i}-1)\underset{\lambda }{\equiv }0(i>1)\end{array}$$

Multiplying out the second equation and substituting the first, we have

$$\begin{array}{c}(p_i-1)(2p_{j\ne 1,i}-1)\underset{\lambda }{\equiv }0\to 2p_2{p}_3\dots p_m-p_i-2p_{j\ne 1,i}+1\underset{\lambda }{\equiv }0\\ \to {\forall }_{i>1}:p_i+2\prod _{j\ne 1,i}{p}_j\underset{\lambda }{\equiv }3\end{array}$$

Now, consider the double factor equations resulting from moving $p_1=2$ from the right side of a single-factor equation for $i>1$. Since n is maximally idempotent, it satisfies these equations as well. We have:

$$\begin{array}{c}(2p_i-1)(p_{j\ne 1,i}-1)\underset{\lambda }{\equiv }0\to 2p_2{p}_3\dots p_m-2p_i-p_{j\ne 1,i}+1\underset{\lambda }{\equiv }0\\ \to {\forall }_{i>1}:2p_i+\prod _{j\ne 1,i}{p}_j\underset{\lambda }{\equiv }3\end{array}$$

By setting all these equations equal to each other mod $\lambda$ and working through the algebra, we find the mutual equivalences from the single and double factor equations imply $\forall i{p}_i\underset{\lambda }{\equiv }{p}_j,\to a_i\underset{\lambda }{\equiv }{a}_j$. For $\lambda$ as defined previously with distinct $a_i$, this is impossible. □

The above is an example of a restriction on $p_1$ as a result of increasing m (since for $m=2$, the result does not hold). A similar result can be obtained showing that $m=4\to p_1>3$, omitted here due to space limitations. We offer the following:

Conjecture 1.

If $p_i$ is the smallest prime factor of an m-factor maximally idempotent integer, and $p_j$ is the smallest prime factor of an $m+1$-factor maximally idempotent integer, then $p_i\le p_j$.

This is consistent with all empirical results so far. Below

Table 4. Smallest $p_1$ for given m for which maximally idempotent integers are known.

m	Smallest ${\mathit{p}}_{\mathbf{1}}$
3	3
4	5
5	5
6	5
7	11
8	29
9	61

are the smallest $p_1$, for which maximally idempotent integers are known for $m=3,\dots ,9$.

It is unknown if maximally idempotent integers exist for ($m=7$, $p_1<11$), ($m=8$, $p_1<29$) or ($m=9$, $p_1<61$). We propose these and the conjecture above as open problems, waiting for proofs of nonexistence or counterexamples.

3.2. A Structure Theorem for Maximally Idempotent Integers

Let $n=p_1{p}_2\dots p_m$ be an m-factor maximally idempotent integer, $p_1<p_2\dots <p_m$. Let $a_i=p_i-1,\lambda (a_2\dots a_m)=\lambda =lcm(a_2\dots a_m)$ (note we are deliberately omitting $a_1$). Let $p_1=N$. Consider the first two single-factor equations, where the first term is $(p_i-1)$, under modulo $a_2$. (The equation with a left factor of $p_2-1$ is trivially true mod $a_2$, so we consider the equations with left factors of $(p_1-1)$ and $(p_3-1)$). We obtain

$$\begin{array}{c}(N-1)(p_2\dots p_m)\underset{a_2}{\equiv }0\to (N-1)(p_3\dots p_m)\underset{a_2}{\equiv }(N-1)\\ (p_3-1)(N{p}_4\dots p_m-1)\underset{a_2}{\equiv }0\\ \to N{p}_3\dots p_m-p_3-N{p}_4\dots p_m+1\underset{a_2}{\equiv }0\end{array}$$

(Recall that $p_i\underset{a_i}{\equiv }1$). Next, consider the factorization equation $(p_1{p}_3-1)(p_2{p}_4\dots p_m-1)$. By the requirements of maximal idempotency, we have

$$\begin{array}{c}(p_1{p}_3-1)(p_2{p}_4\dots p_m-1)\underset{a_2}{\equiv }0\\ \to (N{p}_3-1)(p_4\dots p_m-1)\underset{a_2}{\equiv }0\\ \to N{p}_3\dots p_m-N{p}_3-p_4\dots p_m+1\underset{a_2}{\equiv }0\end{array}$$

Multiplying this equation by N and then subtracting the previous result, we get

$$\begin{array}{c}(N^2-N)p_3\dots p_m+(1-N^2)p_3+N-1\underset{a_2}{\equiv }0\\ \to N(N-1)p_3\dots p_m+(1-N^2)p_3+N-1\underset{a_2}{\equiv }0\\ \to N(N-1)+(1-N^2)p_3+N-1\underset{a_2}{\equiv }0\\ \to N^2-1-(N^2-1)p_3\underset{a_2}{\equiv }0\\ \to (N^2-1)(1-p_3)\underset{a_2}{\equiv }0\\ \to (N^2-1)(p_3-1)\underset{a_2}{\equiv }0\\ \to (N^2-1)a_3\underset{a_2}{\equiv }0\end{array}$$

Applying this to the other mod $a_2$ equations, and then to the other moduli $a_3,a_4,a_5$, we obtain

$$\begin{array}{c}(N^2-1)a_2\underset{a_2}{\equiv }(N^2-1)a_2\underset{a_3}{\equiv }\cdots \equiv (N^2-1)a_2\underset{a_m}{\equiv }0\\ (N^2-1)a_3\underset{a_2}{\equiv }(N^2-1)a_3\underset{a_3}{\equiv }\cdots \equiv (N^2-1)a_3\underset{a_m}{\equiv }0\\ \dots \\ (N^2-1)a_m\underset{a_2}{\equiv }(N^2-1)a_m\underset{a_3}{\equiv }\cdots \equiv (N^2-1)a_m\underset{a_m}{\equiv }0\end{array}$$

Letting $(N^2-1)=C$, it is easily shown that for distinct $a_i$, we must have $a_m\le C{a}_2$, and that a set of distinct positive $a_i$ is a solution $⟺\forall a_i,\lambda /a_i\mid C,i>1$. So any maximally idempotent integer has the property $\forall a_i,\lambda /a_i\mid ({p_1}^2-1),i>1$.

Since $a_m\le C{a}_2$, there are a finite number of m-factor maximally idempotent integers with a given $p_1$ and $p_2$.

The results above are expressed in terms of $p_1$. We noted previously that for the resulting system of modular equations, $a_m\le ({p_1}^2-1)a_2$. In fact, we may fix any factor, not just $p_1$. This gives a Ratio Theorem for Maximally Idempotent Integers:

Theorem 2.

Let n be a maximally idempotent integer with factors $p_1<p_2\cdots <p_m$. For any $p_j>p_i,\frac{p_j}{p_i}<{p_k}^2-1,k\ne i,j$.

The Ratio Theorem means that all but one of the prime factors of maximally idempotent integers are constrained to be within a certain range of one another; there can be at most one outlier. For example, the primes [7, 11, 127, 211, 853] could not form a maximally idempotent integer, because $853/7>{11}^2-1$. However, the primes [7, 727, 1453, 2179, 4357] can and do form a maximally idempotent integer. Note for this integer $\lambda =4356,\{\lambda /a_2,\lambda /a_3,\lambda /a_4,\lambda /a_5\}=\{\{6,3,2,1\}$, all of which divide $48={p_1}^2-1)$. Note as well that the Ratio Theorem holds.

The Ratio Theorem also has computational implications. It means fixing any two prime factors permits the enumeration of all maximally impotent integers containing those factors.

We have not yet considered the equations corresponding to the factorization $(N-1)$$(p_2\dots p_m-1)$, for moduli $>a_1$:

$$\begin{array}{c}(N-1)(p_2\dots p_m-1)\underset{a_i}{\equiv }0\end{array}$$

These also form a set of modular equations similar to the one considered above. This time the constant C is $(N-1)(p_2\dots p_m-1)$, which here implies that for any solution $a_2,\dots ,a_m$ we must have $\lambda /gcd(a_2,\dots ,a_m)\mid (N-1)(p_2\dots p_m-1)$.

We sum up the results of this section as a Structure Theorem for Maximally Idempotent Integers:

Theorem 3.

Let $n=p_1{p}_2\dots p_m$ be a maximally idempotent integer with m factors, $m\ge 4,p_i$ prime. Let $a_i=p_i-1,\lambda (a_2,\dots ,a_m)=\lambda =lcm(a_2,\dots ,a_m)$. n must satisfy the following conditions:

(1) $\forall a_i\lambda /a_i\mid ({p_1}^2-1),i>1$

(2) $\lambda \mid (p_1-1)(p_2...p_m-1)$

We emphasize that these are necessary conditions, but not sufficient. [5, 7, 13, 19] satisfies both criteria, but does not form a maximally idempotent integer.

The smallest possible value of $\lambda$ is $a_m$. Thus, for small $p_1$, condition 2 will most likely be met when $\lambda$ is at or close to $a_m$. For example, the four smallest maximally idempotent integers with $p_1=5$ and $m=4$ are 137,555 = 5*11*41*61, 356,595 = 5*19*37*73, 5,521,745 = 5*29*113*337, and 23,988,515 = 5*59*233*349. In these cases, $\lambda$ is either $2a_m$ or $a_m$. For $m=5$ and $p_1=5$, the smallest maximally idempotent integer is 146,168,311,505 = 5*101*401*601*1201, with $\lambda$ at the minimum value $a_m=1200$. Similarly, for the previously considered maximally idempotent example 70,200,928,349,251 = 7*727*1453*2179*4357, $\lambda$ also has minimum value of $a_m=4356$. Note that both these examples meet Condition 1. We will have more to say about the value of $\lambda$ in the sections that follow.

Condition 1 imposes a crude lower limit on $p_1$ as a function of m, in that $({p_1}^2-1)$ must contain at least $m-1$ divisors. These limits for small m are shown in the

Table 5. These limits for small m are shown.

${\mathit{p}}_1$	Max m = D + 1
	D = #divisors of ${{\mathit{p}}_1}^2-1$
3	5
5	9
7	11
11	17
13	17
17	19

below:

In some cases, tighter bounds have already been established by the work previously shown. Cases where gaps remain are offered as open problems.

3.3. The Role of Factorization Equation GCD’s

Let $D_i\left(n\right)$ denote the gcd of all factorization equations of n with i factors on the left side. For example, with $n=p_1{p}_2{p}_3{p}_4$ = 43*79*223*331, we have

$$\begin{array}{c}{D}_1\left(n\right)=\gcd ((p_1-1)(p_2{p}_3{p}_4-1),(p_2-1)(p_1{p}_3{p}_4-1),\\ (p_3-1)(p_1{p}_2{p}_4-1),(p_4-1)\left(p_1{p}_2{p}_{3}01\right))=108\\ D_2\left(n\right)=\gcd (p_1{p}_2-1)(p_3{p}_4-1),(p_1{p}_3-1)(p_2{p}_4-1),\\ (p_1{p}_4-1)(p_2{p}_3-1))=144\end{array}$$

We will omit the argument n if the meaning is clear. It is easily seen that n is maximally idempotent if $\lambda \mid D_i$ for all i for which i-factor factorizations exist.

Empirically, $D_1$ and $D_2$ are almost always equal, with the probability rapidly approaching 1 as m increases, $D_i$ becomes smaller. Below

Table 6. Data for $m=4.12$, based on a million random permutations of length m from the first 100,000 primes.

m	${\mathit{D}}_{\mathbf{1}}={\mathit{D}}_{\mathbf{2}}$	${\mathit{D}}_{\mathbf{1}}\mid {\mathit{D}}_{\mathbf{2}}$	${\mathit{D}}_{\mathbf{2}}\mid {\mathit{D}}_{\mathbf{1}}$	Neither
4	699,799	298,253	1534	414
5	996,571	235	3194	0
6	931,969	64,968	2946	117
7	997,686	32	2282	0
8	983,371	15,292	1322	15
9	999,280	0	720	0
10	996,162	3536	301	1
11	999,875	0	125	0
12	999,149	797	54	0

shows data for $m=4.12$, based on a million random permutations of length m from the first 100,000 primes.

The fact that $D_1=D_2$ so often has implications for improving the efficiency of search algorithms for maximally idempotent integers.

3.4. Finding Maximally Idempotent Integers

The equations of idempotency have some redundancy. In particular, let $\overline{p}$ and $\overline{q}$ be a factorization of n. Because $p_k\underset{\lambda }{\equiv }1$, any $p_k$ may be moved from $\overline{q}$ to $\overline{p}$ without affecting the product mod $a_k:(\overline{p}-1)(\overline{q}-1)\underset{\lambda }{\equiv }0\to (\overline{p}{p}_k-1)(\overline{q}/k-1)\underset{a_k}{\equiv }0$. Thus, in addition to the explicit equivalence equation of a given factorization, there are implied equivalences mod $a_k$. If equations are chosen such that a given equivalence is implied for all $a_k$, then it holds for $\lambda$ even if it is not explicitly given (recall that $\forall i,a_i\mid \lambda$).

This has implications when testing for maximal idempotency. For example, only the single factor equations need to be tested for $m=3,4$, as they imply the three double factor ones. For $m=5$, only 12 of the possible 15 equations need be tested, and so forth.

However, based on the results regarding $D_1$ and $D_2$ above, it is empirically more efficient to check the single factor equations first. If any one of them fail, n is not maximally idempotent. If they all pass, then the double factorizations can be checked, and so forth. It is also more efficient to compute $D_i$ one equation at a time. If the current value $D_i$ ever drops below $\lambda$, further testing is not required since $\lambda$ can never divide it.

One way to find maximally idempotent integers is to simply iterate through a range of integers n, factor them, calculate $\lambda$ for the ones that are square free, and then see if the equations for maximal idempotency are satisfied. As this requires factoring, this is computationally intensive. A more productive approach is to start with the primes in a given range and test products for $m=3,4\dots$ etc. In particular, we may fix $p_1$ and $p_m$ and then identify all the maximally idempotent integers with factors inclusively between those two values.

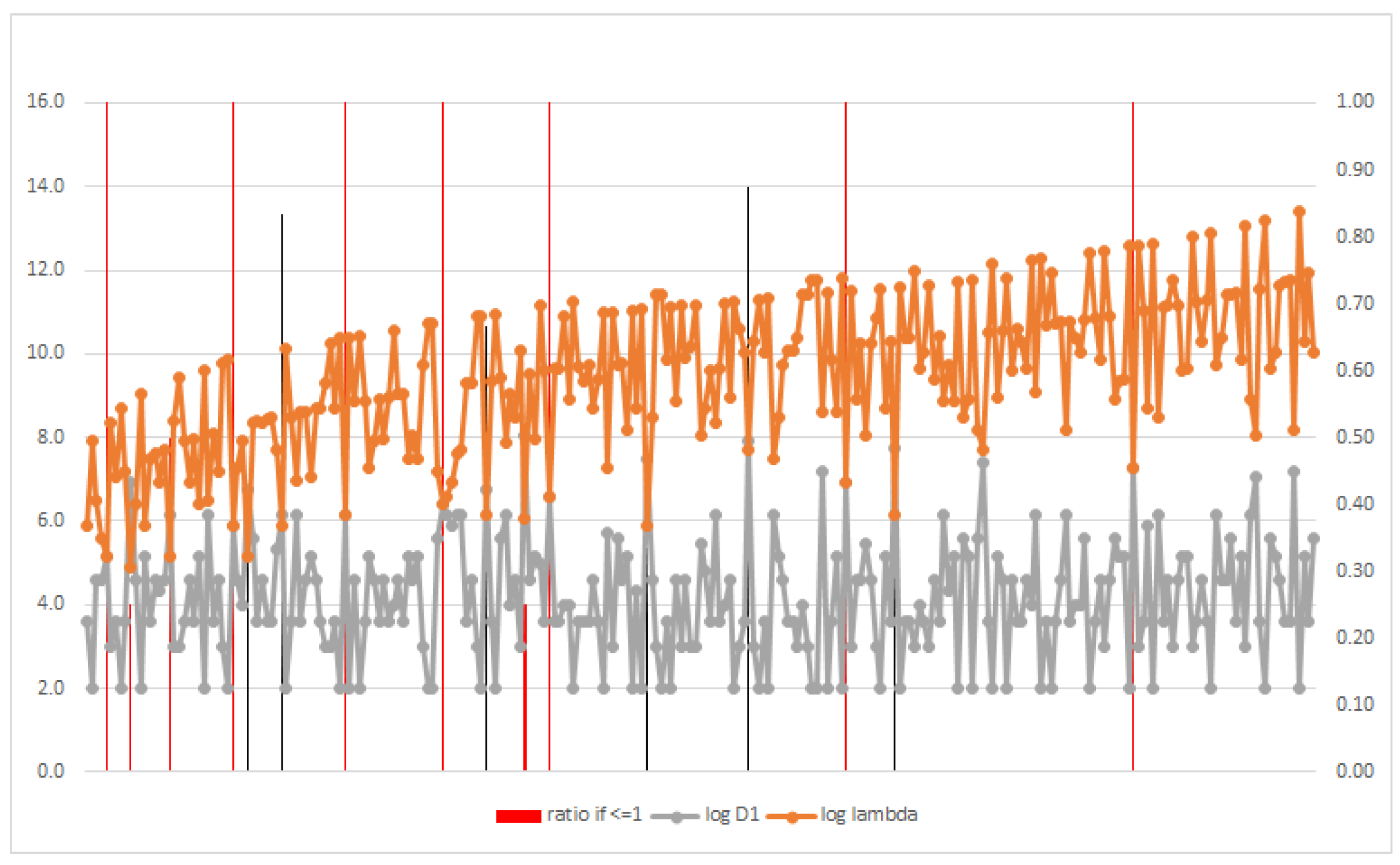
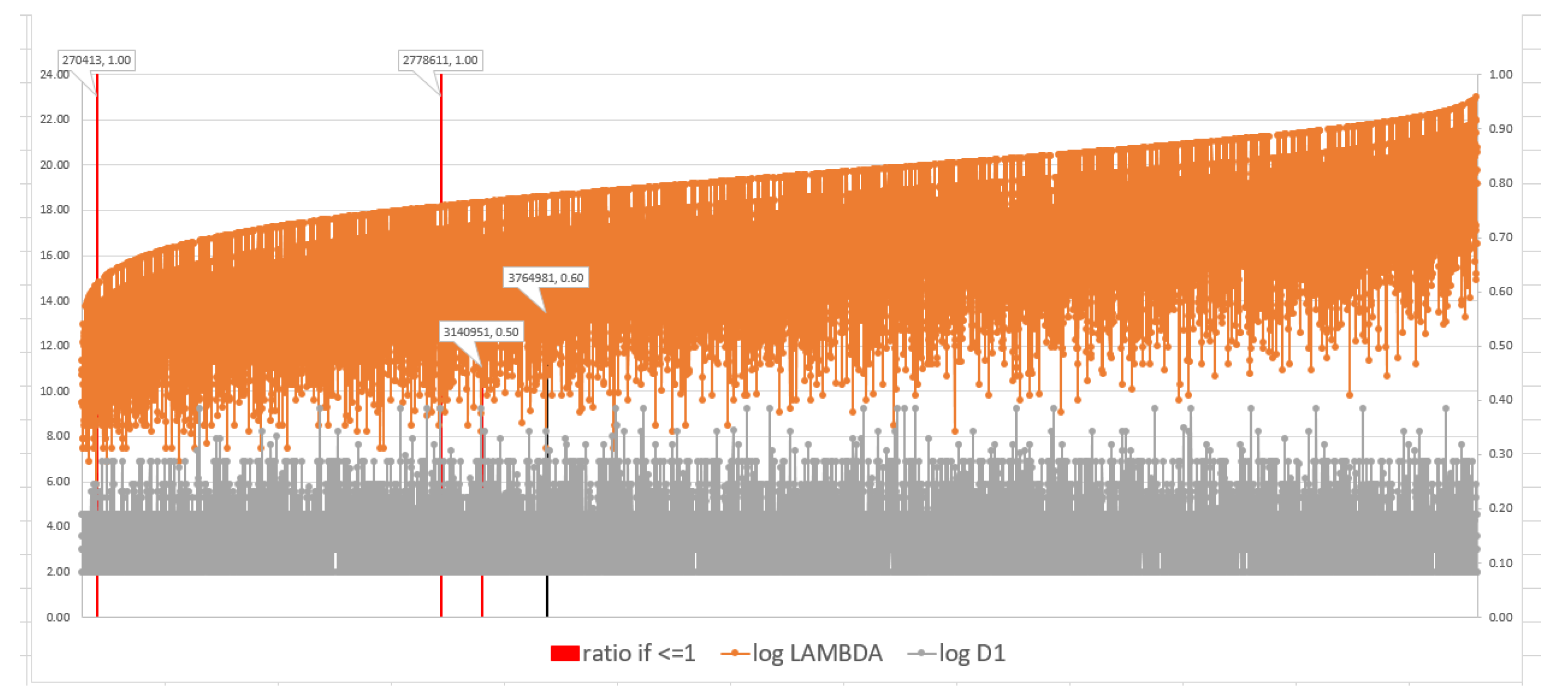
Based on the results previously discussed, we may expect maximally idempotent integers to be found only when $\lambda$ is at a local minimum ($a_m$ or a small multiple thereof) and the $D_i$’s are at a local maximum. This confirmed in the figures below, which show ${log}_2{D}_1$ and ${log}_2\lambda$ as a function of n. Logarithmic values are used due to the differences in magnitude between $\lambda$ and $D_1$.

Figure 1 shows this plot for $p_1=7,m=3,p_m\le 97$. The orange data set is the log of $\lambda$, the gray is the log of $D_1$. Each data point is for a value of $n=p_1{p}_2{p}_3$, sorted in increasing order. The values of n where $\lambda \le D_1$ are marked with vertical lines. The value of that ratio is read from the right vertical axis. Red lines correspond to those cases where $D_1/\lambda$ is an integer, and indicate all the maximally idempotent integers in this range.

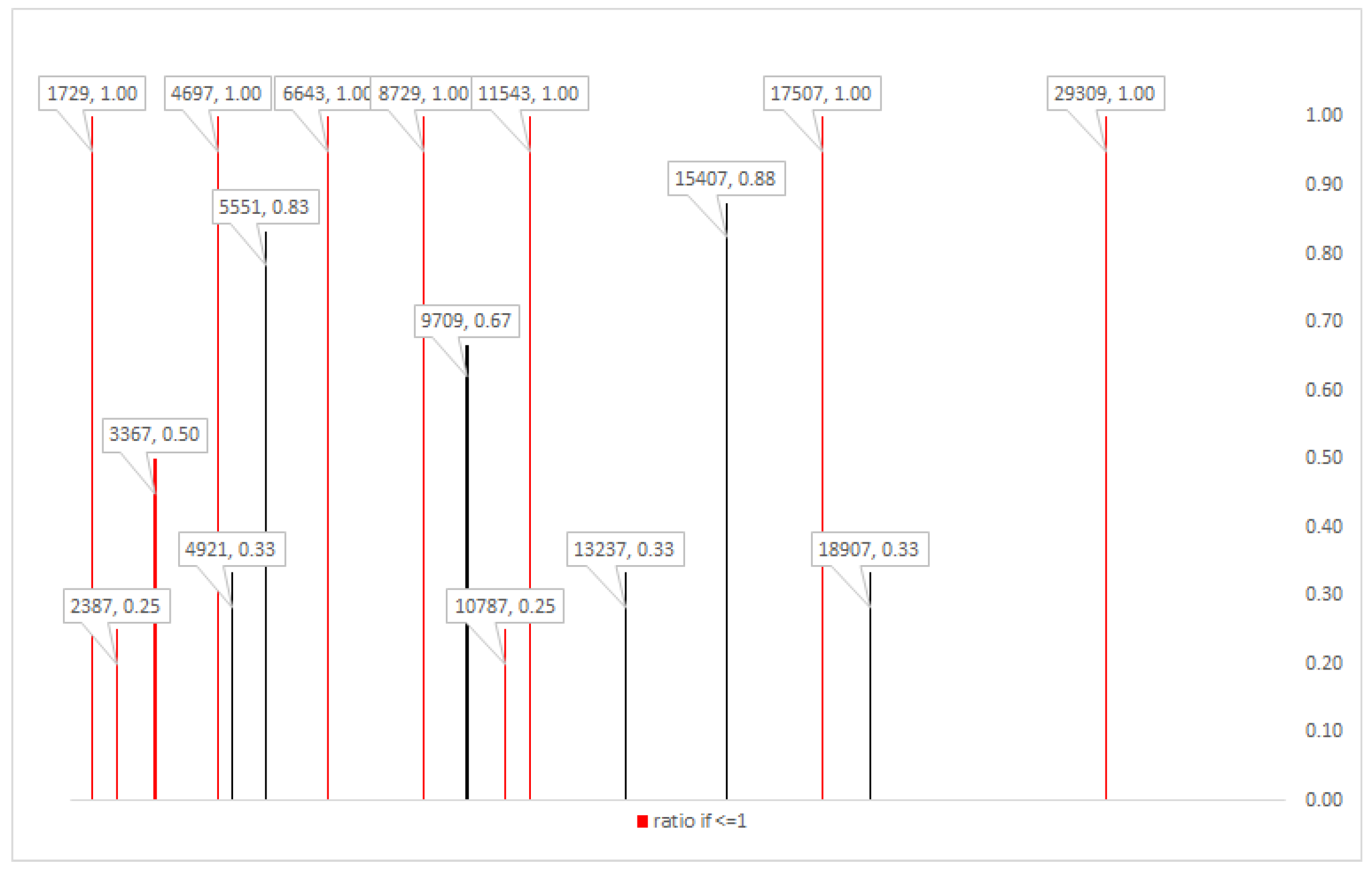
Figure 2 shows these lines alone, along with their data values. The left value in each label with a reciprocal integer ratio (indicated with a red line) is a maximally idempotent integer.

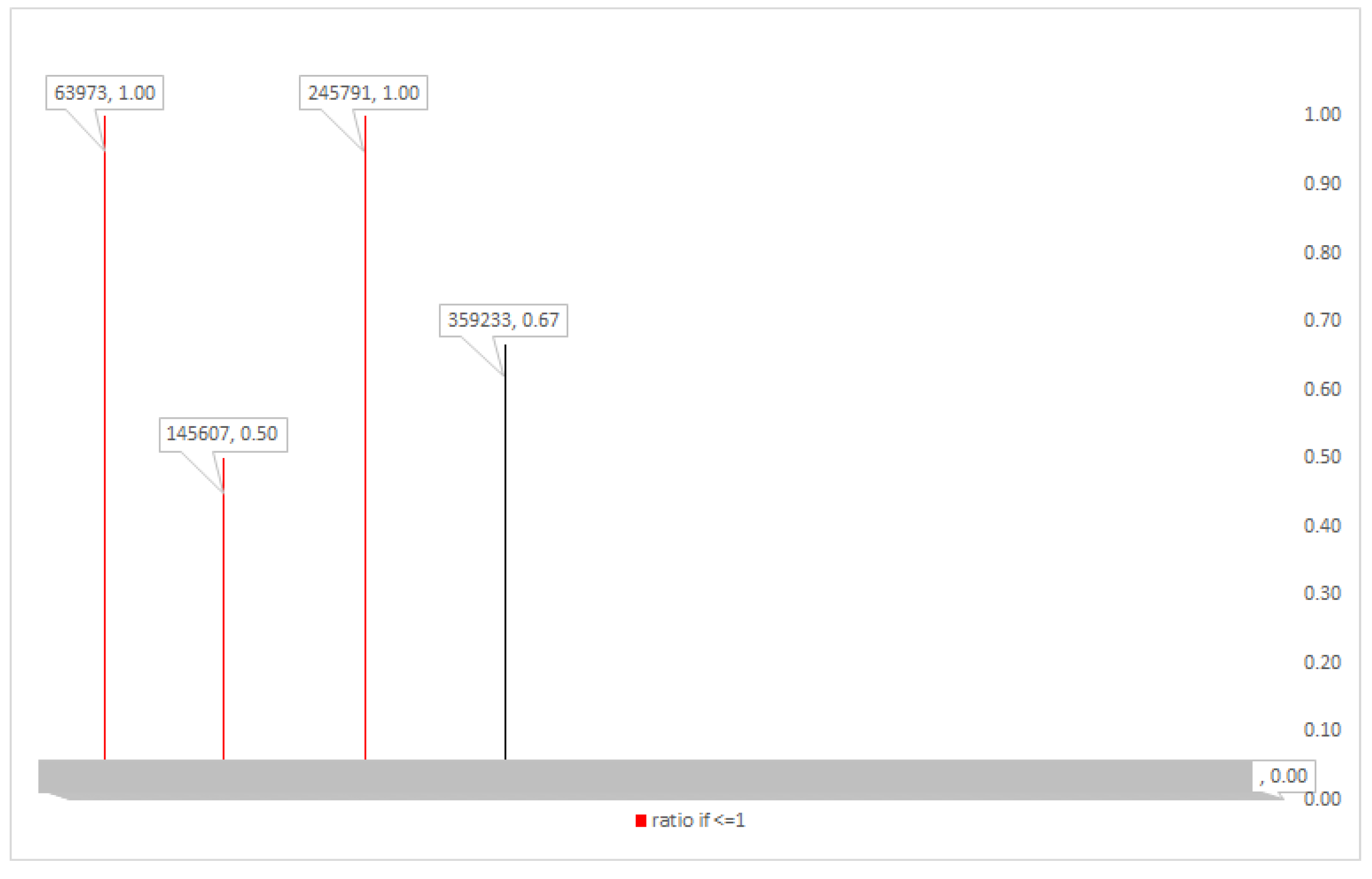
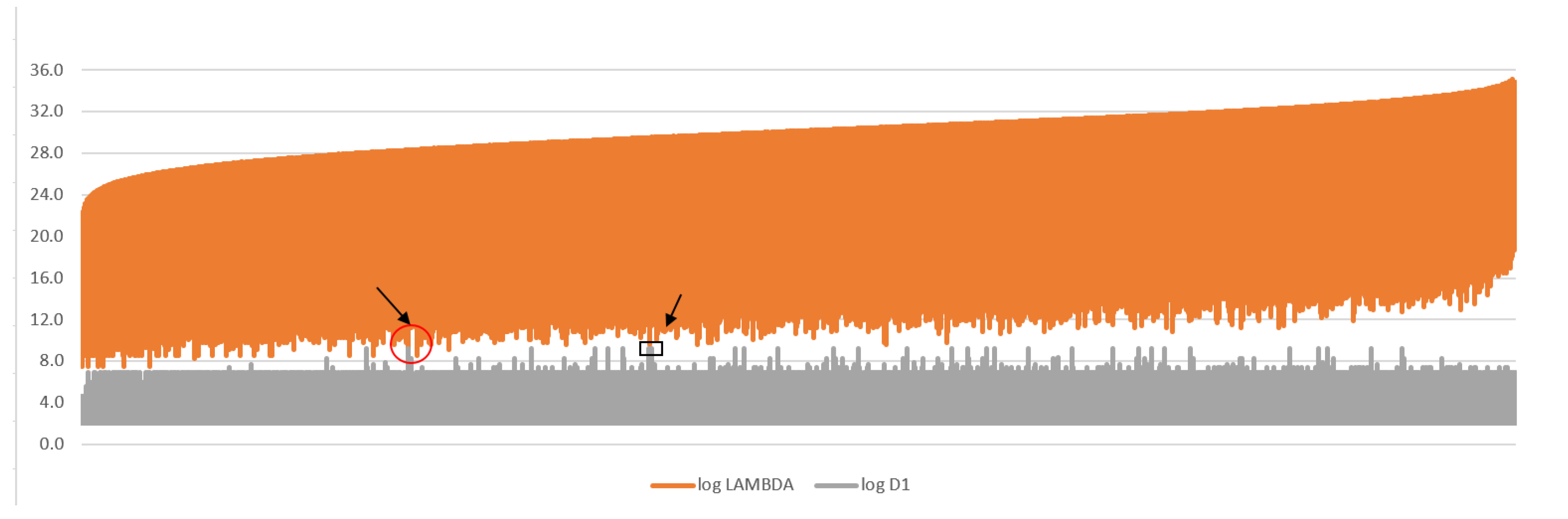
Figure 3 and Figure 4 show similar plots with $m=4$. Increasing the number of factors to 4 increases the number of data points, but it also increases $\lambda$ as it starts to pull away from $D_i$. (Recall that logarithmic scales are used, making the absolute difference exponentially larger than that depicted in the figure). The overall effect is to decrease the number of integers with $\lambda \le D_1$. We note, however, that the proportion of those integers which are maximally idempotent increases. We conjecture this ratio approaches 1 with increasing m.

Figure 5 increases $p_1$ from 7 to 11. Increasing $p_1$ increases the average $D_1$ slightly, but significantly increases $\lambda$. It also reduces the number of candidates that can satisfy the Ratio Theorem. The overall effect is a net decrease in the number of integers with $\lambda \le D_1$, and therefore the number of maximally idempotent integers. No maximally idempotent integers exist in this range with $p_1\ge 17$.

Figure 6 increases $p_m$ from 97 to 199. Doubling $p_m$ increases the number of candidates in the combinatorially expected manner, which increases the probability of an maximally idempotent integer being found. On the other hand, their asymptotic density decreases. We conjecture the asymptotic density of maximally idempotent integers for a given $p_1$ approaches zero. It is unknown if for a given $p_1$ for which an maximally idempotent integer exists, there is a maximum $p_m$ beyond which no more maximally idempotent integers can be found, or if there are infinitely many.

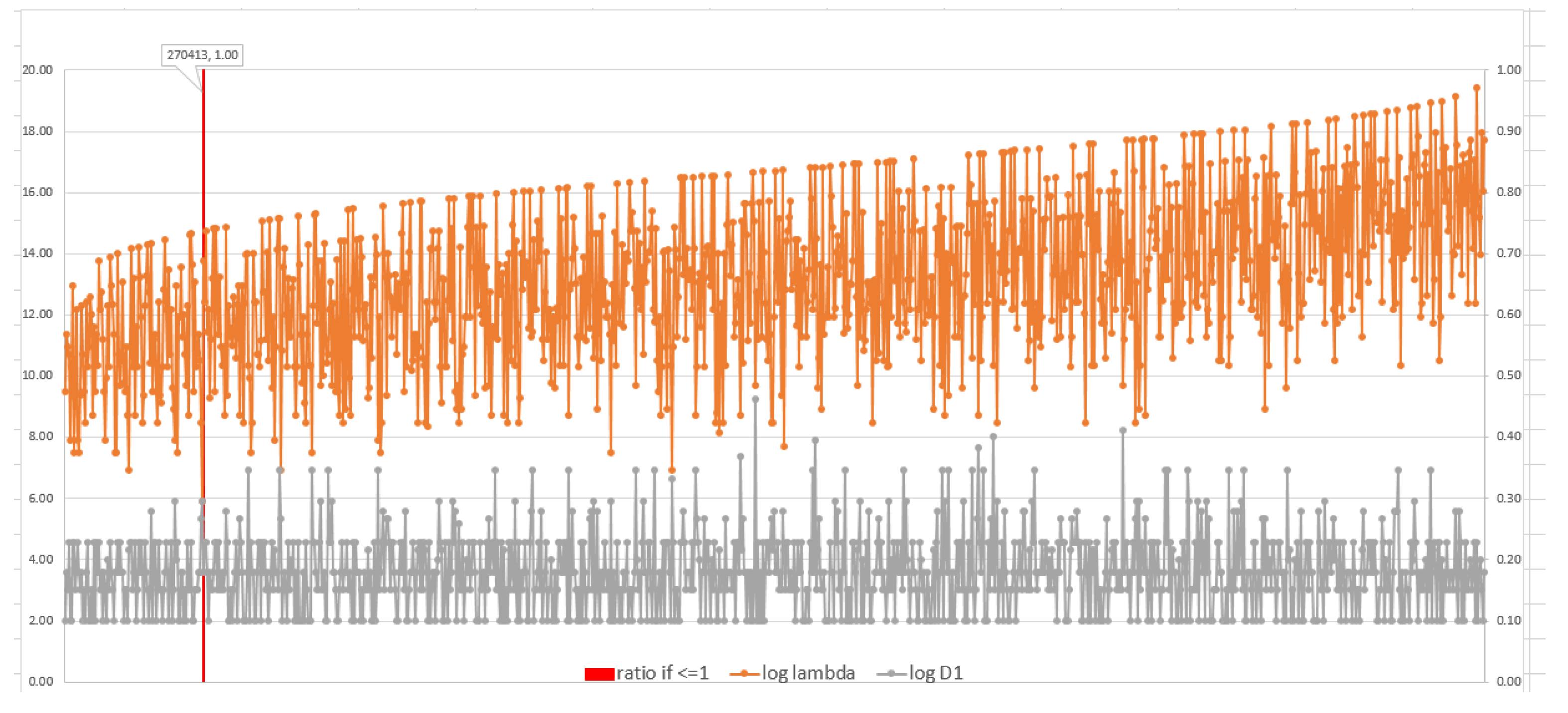
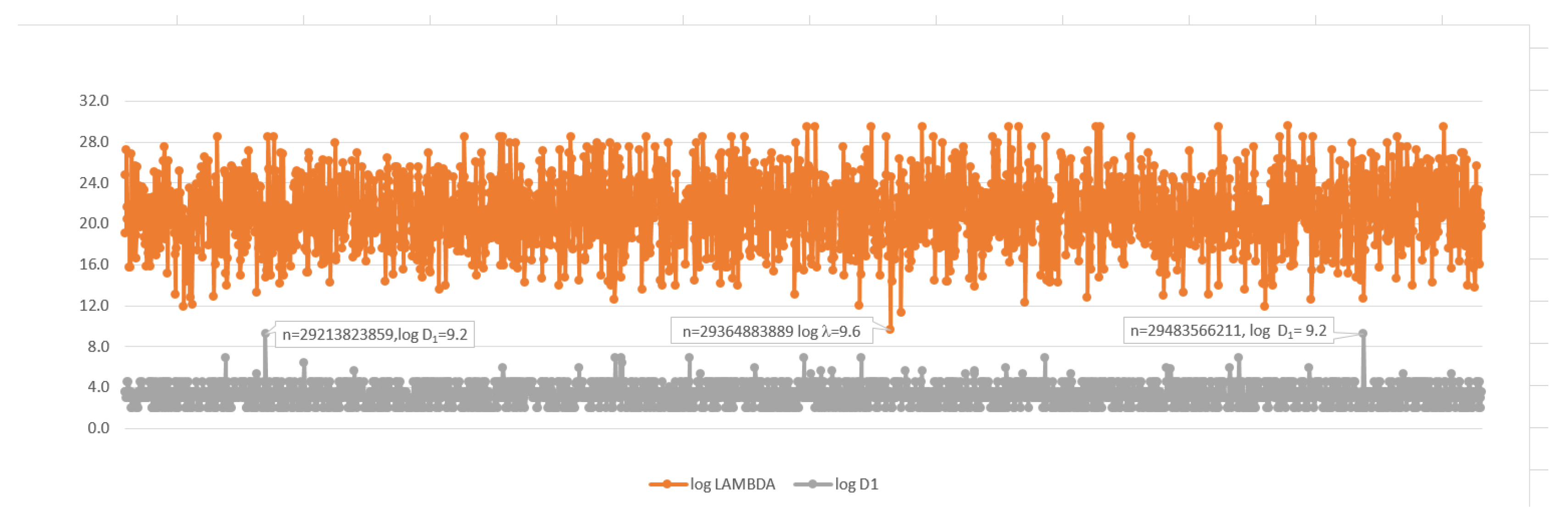
Figure 7 further increases m to 6, showing the smallest 6-factor maximally idempotent integer in the given range (indicated with a red circle). This is the entry for $m=6$ in Table 2. The black rectangle appears to indicate a second example, but that is an artifact of scale, due to both the large number of points on the x axis (approximately 750 million) and the logarithmic scales employed on the y axis. While in both of the indicated areas there are $D_1$ values at the maximum of 600, with ${log}_2\left(D_i\right)\approx 9.2$, the minimum $\lambda$ in the rectangle is 760, ${log}_2\left(\lambda \right)\approx 9.6$. The apparent match in the rectangle is in fact a local minimum $\lambda$ between two local maximum $D_1$. Figure 8 makes this clearer.

Thus, there is only one maximally idempotent integer with $m=6$ in the indicated range, the smallest one with 6-factors. There are none with $m=7,8$. We conjecture there are no other maximally idempotent integers with $p_i\ge 11,p_m\le 199$ for $m\ge 6$.

3.5. Constructive Techniques

3.5.1. Improving the Odds with Divisor Sequences

More than half of the entries in Table 2 are primes in arithmetic progression, where each factor is of the form $a_{1}k+1$. As m increases, more and more maximally idempotent integers take this form. This is because sequences of increasing $a_i$ where all $a_i$ divide $a_m$ iff $\lambda =a_m$, the minimum possible value. This is more likely to occur with primes in arithmetic progression. This not a sufficient condition, due to the influence of the $D_i$, nor is it necessary, since $\lambda$ may still be a local minimum if all the $a_i$ divide a small multiple of $a_m$. Nonetheless, as a heuristic it is useful for finding maximally idempotent integers faster than brute force or searching arbitrary combinations of m primes.

To find an maximally idempotent integer with m factors, we begin with a desired $p_1$ and a number N that contains at least m divisors $d_i$, with $(N-1)\ast (p_1-1)+1$ prime. Next, we identify those $d_i$ such that $d_i\ast (p_1-1)+1$ is prime, discarding the rest. The resulting subsets will have $(a_1,\dots ,a_{max})$ such that $\lambda$ will be at its smallest possible value $a_{max}$. These subsets can then be tested for maximal idempotency. We refer to these subsets as divisor sequences, since all of them are divisors of $a_{max}$.

For example, suppose we are searching for 6-factor maximally idempotent integers with $p_1=11$. 300 has 8 divisors, but 301 is not prime. Additionally, 40 has 8 divisors and 401 is prime, but only four of them have the property that $10d_i+1$ is prime. Additionally, 60 has 12 divisors, of which 7 have $10d_i+1$ prime, giving the divisor sequence {$10,30,40,60,100,150,600$}. (Note that all $a_i$ divide the largest value of 600). There are seven possible subsets of size 6 to test, one of which produces the maximally idempotent integer 11*31*41*101*151*601. Note that this not the smallest 6-factor example, which has the corresponding divisor set {$10,30,40,60,100,150$}. These are not all divisors of 150, so this is a case of an maximally idempotent integer where $\lambda$ is not equal to $a_m$.

The complete subset of all seven primes above is also maximally imdepotent; it is the smallest seven-factor example. All maximally idempotent integers known to the author with seven or more factors have either been found using this technique, or explicitly constructed using a technique from graph theory. We discuss that next.

3.5.2. Constructing Large Maximally Idempotent Integers Using k-Cliques in Congruence Graphs

Random primes in modern cryptography are hundreds of bits long, found efficiently using probabilistic algorithms [6]. Do similarly large maximally idempotent integers exist, and if so, can they be found? The answer is yes, and probabalistic techniques are not required. They can be constructed explicitly, of any size desired.

It is not difficult to show that every equation for idempotency is a linear sum of products of $a_i$, where each term is of length $\ge 2$. For maximal idempotency, all such sums must be $\underset{\lambda }{\equiv }0$. Any set of $a_i$ for which all distinct products $a_i{a}_j\underset{\lambda }{\equiv }0$ will have this property, and will therefore correspond to a maximally idempotent integer. This is not a necessary condition, but it is sufficient.

Such sets of $a_i$ can be constructed in the following way. (1) Choose ${\lambda }_0$ a highly composite number. (2) Make nodes in a graph corresponding to all divisors $a_i$ of ${\lambda }_0$ such that the successor of $a_i$ is prime. (3) Connect all node pairs $a_i,a_j$ such that $a_i{a}_j\underset{{\lambda }_0}{\equiv }0$. We call the resulting graph a congruence graph.

For any congruence graph, $\lambda$ of any subset of its nodes is their lcm, which in turn must divide ${\lambda }_0$. For all pairs of nodes in a k-clique, $a_i{a}_j$ is congruent to 0 mod ${\lambda }_0$. Therefore all $a_i{a}_j$ are congruent to zero mod the lcm of any subset of divisors of ${\lambda }_0$, including the members of the clique themselves.

Thus, every $a_i{a}_j\underset{\lambda }{\equiv }0$, where $\lambda$ is the lcm of every node in the clique. This means that every k-clique corresponds to a maximally idempotent integer with k factors. Similarly, any divisor of a maximally idempotent integer constructed in this way is also maximally idempotent. Thus, a k-clique in a congruence graph contains $\left(\genfrac{}{}{0pt}{}{k}{m_i}\right)$ maximally idempotent integers with $3\le m_i\le k$ factors, for a total of $2^k-\left(\genfrac{}{}{0pt}{}{k}{2}\right)-\left(\genfrac{}{}{0pt}{}{k}{1}\right)$ (we ignore the primes and semiprimes).

For example, consider ${\lambda }_0=36$. The resulting divisors $a_i$ with $p_i=a_i+1$ prime are $1,2,4,12,18,36$. This produces the congruence graph of Figure 9.

This graph contains six 3-cliques and one 4-clique. These correspond to seven maximally idempotent integers with $\lambda =36$. Five of the six 3-cliques correspond to integers in Table 2. The 4-clique is the smallest maximally idempotent integer with four factors, also shown in Table 2.

In general, to construct a maximally idempotent integer with a large number of factors, choose ${\lambda }_0$ highly composite. The divisor graph will then have a large number of nodes, high connectivity and a greater likelihood of k-cliques for larger k.

Table 7. Smallest ${\lambda }_0$ where k-cliques first appear in congruence graph.

k	Prime Factorization of ${\mathit{\lambda }}_0$	Divisors	Nodes	Edges	#Digits in Largest Max Idempotent Integer
3	$2^{2}3$	6	5	6	3
4	$2^2{3}^2$	9	7	11	5
5	$2^3{3}^3$	16	9	15	9
6	$2^2{3}^{4}5$	30	17	58	16
7	$2^2{3}^2{11}^2$	27	15	46	21
8	$2^7{3}^4$	40	20	71	25
9	$2^4{3}^{5}5$	60	30	149	32
10	$2^2{3}^2{5}^2{7}^2$	81	31	129	36
11	$2^4{3}^2{5}^2{7}^2$	135	53	311	45
12	$2^6{3}^2{5}^2$	126	51	381	58
13	$2^6{3}^2{5}^2{7}^2$	1889	71	424	57
14	$2^8{3}^5{5}^2$	162	63	386	66
15	$2^6{3}^3{5}^2{7}^2$	252	93	743	72
16	$2^7{3}^3{5}^2{7}^2$	288	104	963	84
17	$2^2{3}^2{5}^2{7}^2{11}^2$	243	73	531	87
18	$2^8{3}^3{5}^2{7}^2$	324	115	1203	99
19–22	$2^4{3}^2{5}^2{7}^2{11}^2$	405	125	1237	120
23–24	$2^6{3}^2{5}^2{7}^2{11}^2$	567	168	1866	143
25–26	$2^7{3}^2{5}^2{7}^2{11}^2$	648	195	2326	161
27–28	$2^4{3}^4{5}^2{7}^2{11}^2$	675	200	2976	181
29	$2^8{3}^2{5}^2{7}^2{11}^2$	729	215	2738	182
30–34	$2^6{3}^4{5}^2{7}^2{11}^2$	945	275	4657	232
35–39	$2^8{3}^4{5}^2{7}^2{11}^2$ (${\lambda }_0$ $conjectured$)	1215	353	6374	272
40–41	$2^8{3}^6{5}^2{7}^2{11}^2$ (${\lambda }_0$ $conjectured$)	1701	471	9453	315

shows the values of ${\lambda }_0$ when the first cliques of size k appear using this method, along with some information about the graph and the size of the largest maximally idempotent integer it contains.

Figure 10 shows the congruence graph for ${\lambda }_0$ = 44,100 = $2^2{3}^2{5}^2{7}^2$, corresponding to k = 10 in Table 7.

The largest k-clique currently constructed by the author has 141 nodes, corresponding to an maximally idempotent integer of 2081 digits. It contains approximately ${10}^{43}$ maximally idempotent integers as divisors.

Idempotent factorizations can also be constructed from a congruence graph. It can be shown that any complete $(j,k)$ bipartite subgraph of the congruence subgraph corresponds to an idempotent factorization of an integer n with j and k factors, respectively, where n is the product of the successors of the corresponding $a_i$’s. For example, Figure 9 has a complete $(2,2)$ bipartite subgraph on $(4,6)$ and $(18,36)$, shown in Figure 11. This corresponds to the idempotent factorization $\overline{p}=5\ast 7,\overline{q}=19\ast 37$. n = $5\ast 7\ast 19\ast 37$ is not maximally idempotent, but it does have the indicated fully composite idempotent factorization. Complete subgraphs of congruence graphs correspond to maximally idempotent integers, while complete bipartite graphs correspond to idempotent integers. Again, we emphasize these are sufficient conditions, not necessary ones.

4. Discussion, Conclusions, and Directions for Future Work

We define the class of idempotent integers as those n which can be factored into $\overline{p}\overline{q}$ such that $\lambda \left(n\right)\mid (\overline{p}-1)(\overline{q}-1)$. This set includes the primes, semiprimes, and Carmichael numbers, but is not unique to them. Maximally idempotent integers are those for which all factorizations are idempotent. This last category presents interesting open problems. For maximally idempotent integers as defined above, for a given $p_1$ and a given m is the number of maximally idempotent integers infinite? Of those n for which $\lambda \le D_i$, does the proportion for which $\lambda /D_i=1$ approach 1 as n increases? What lower bounds on $p_1$ can be proven as a function of m?

Rather than regard idempotency as a discrete property of factorizations and integers, idempotency could be viewed on a continuum. Factorizations of n that are not fully idempotent may be viewed as partially idempotent, depending on the $(e,d)$ pair chosen according to the RSA protocol [7]. In this case, the k in the definition of idempotency is replaced by $ed$. Some integers may then be regarded as minimally idempotent, meaning that no $(e,d)$ pairs for any factorization are idempotent. The $a_i$ values for minimally idempotent integers are solutions to a system of nonlinear modular equations, a known NP-complete problem. The statistical properties of partial idempotency and heuristics for finding minimal idempotency are a work in progress.