Radar Emitter Identification under Transfer Learning and Online Learning
Abstract
1. Introduction
2. Relevant Research
2.1. Transfer Learning
2.2. Online Learning
3. Radar Emitter Identification under Transfer Learning and Online Learning
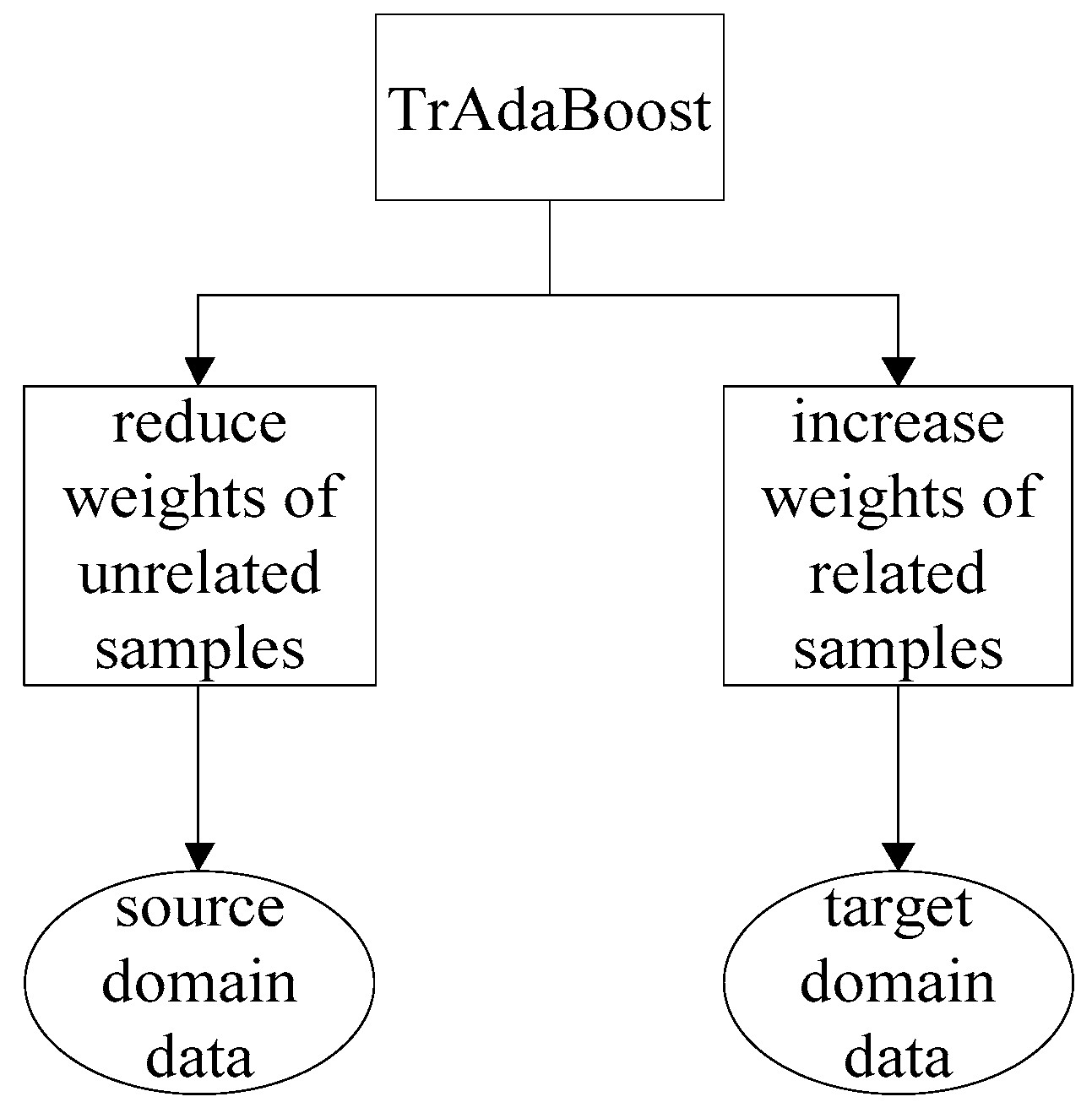
3.1. Support Vector Machine Model Based on the TrAdaBoost Method
| Algorithm 1. Support vector machine model based on the TrAdaBoost method |
|
3.2. Transductive Transfer Learning Based on EM Algorithm
| Algorithm 2. Transductive transfer learning based on EM algorithm |
|
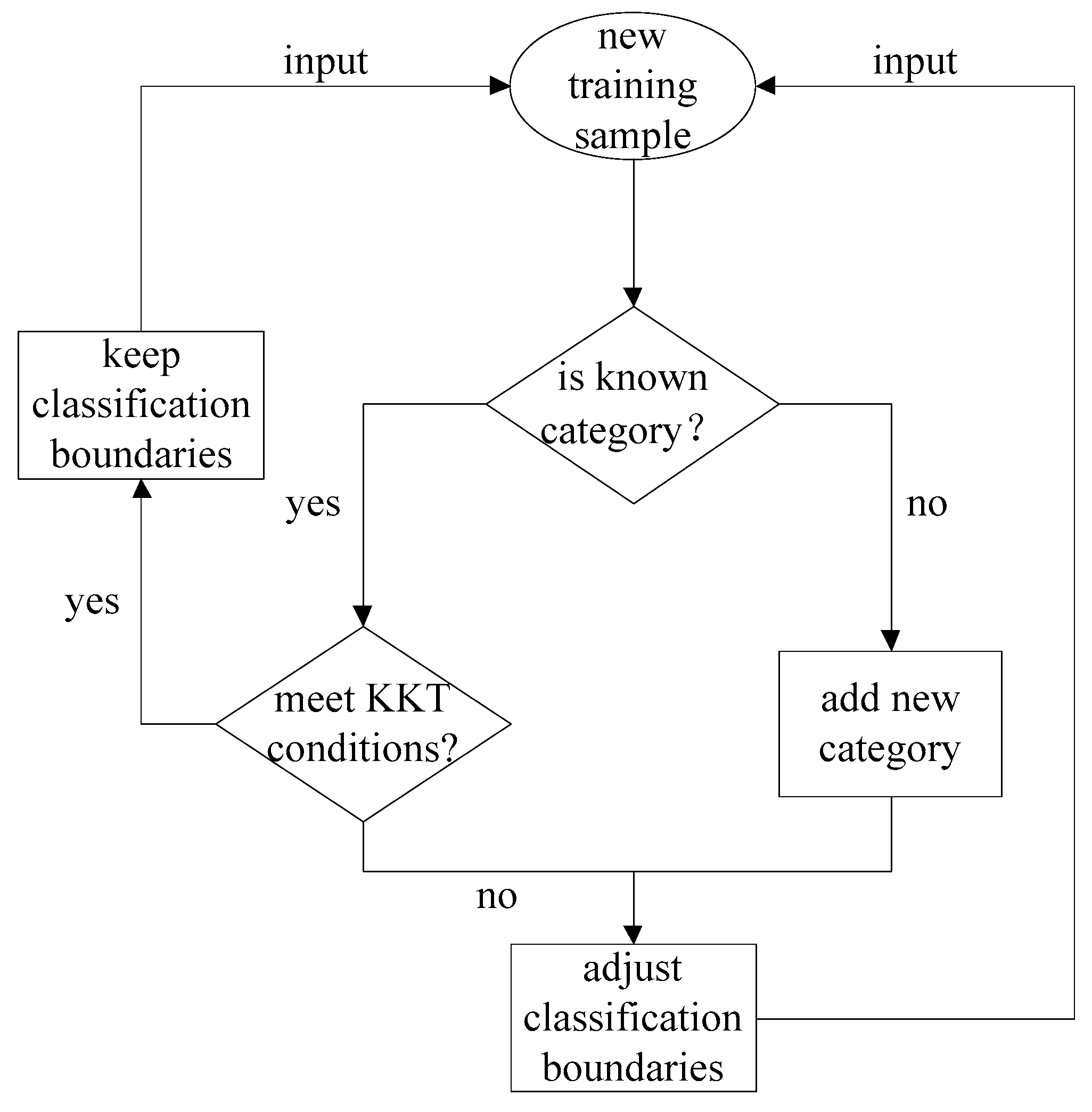
3.3. Radar Emitter Identification Based on Online Learning
4. Experiments
4.1. Experiment Settings
4.1.1. Experiment Environment
4.1.2. Experiment Data
4.1.3. Experiment Scenario
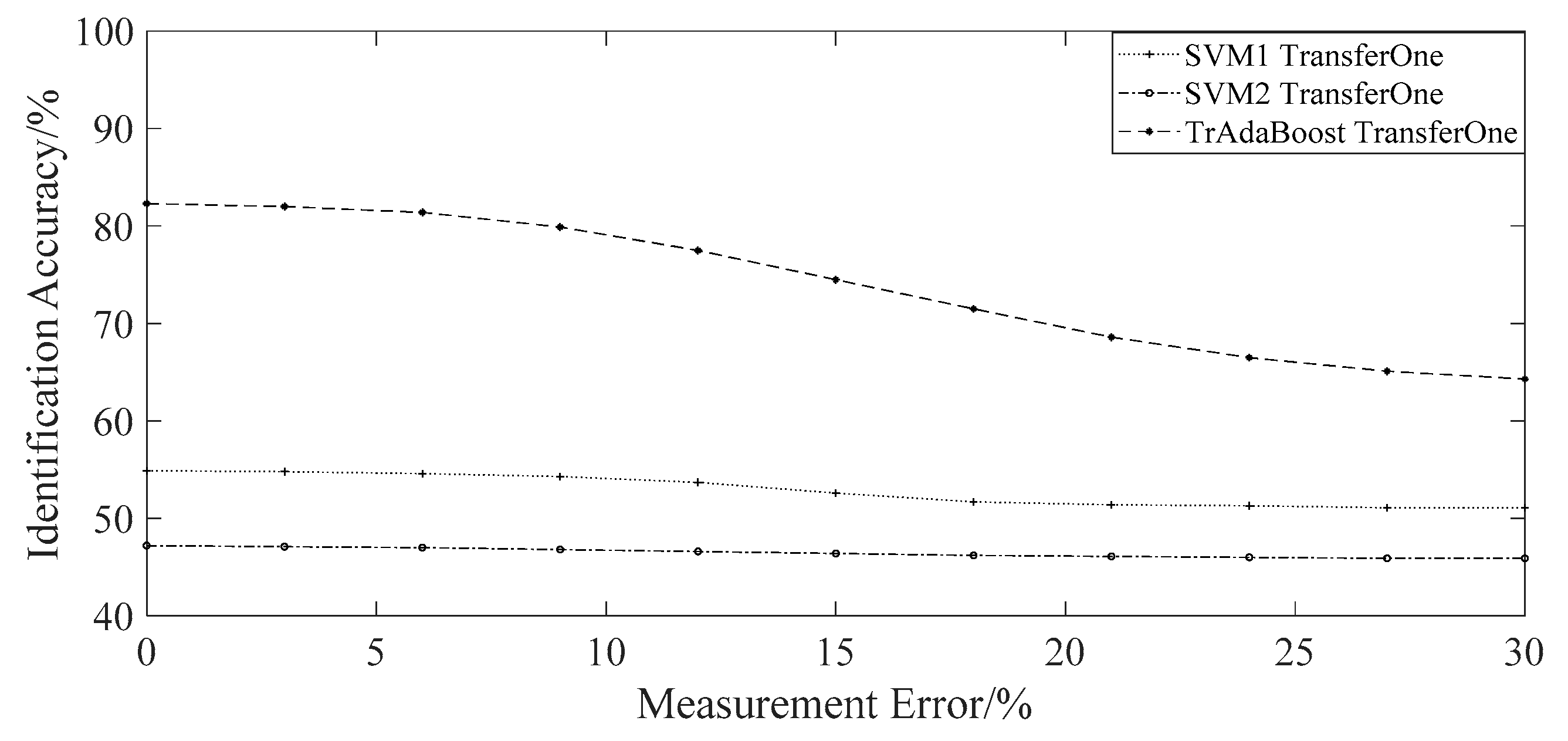
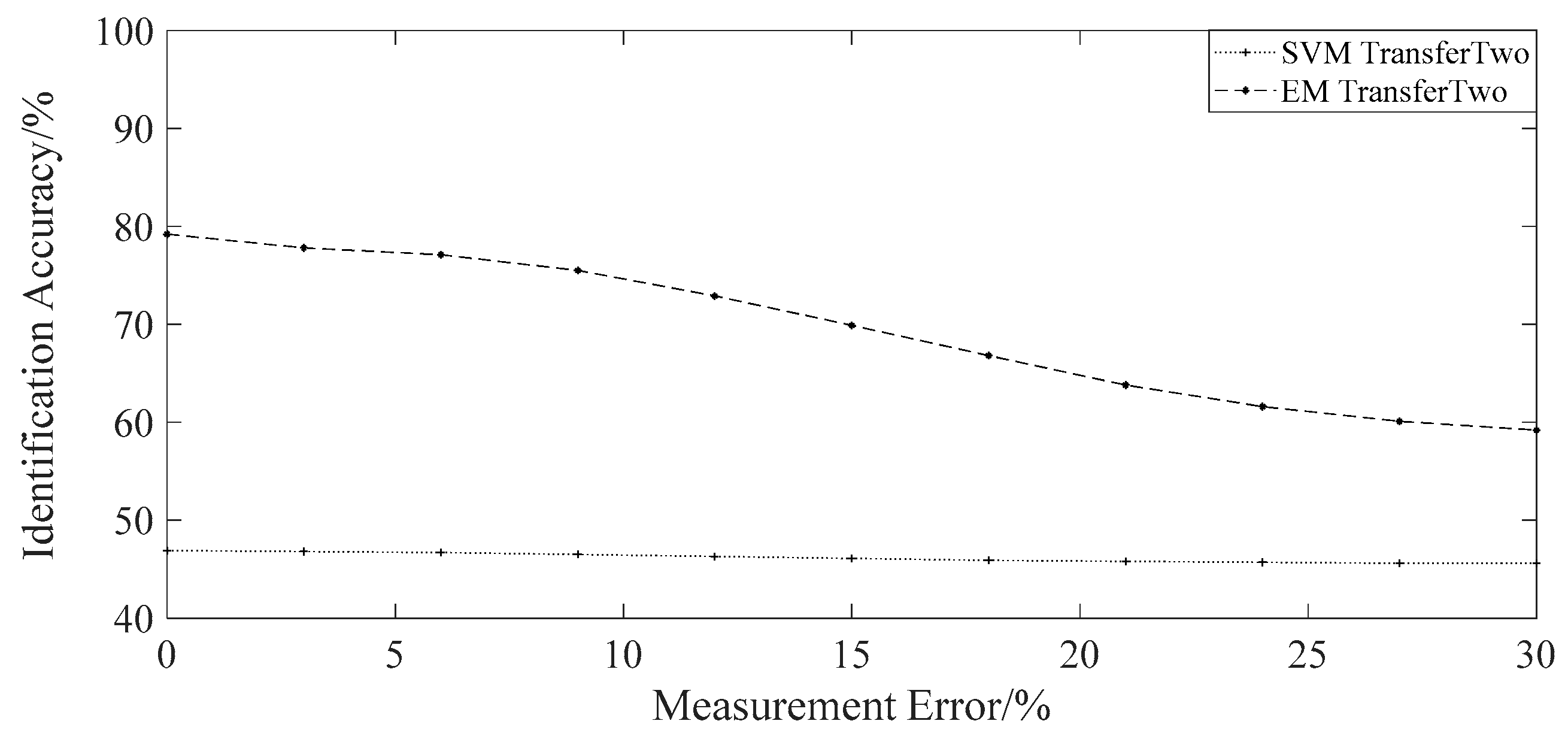
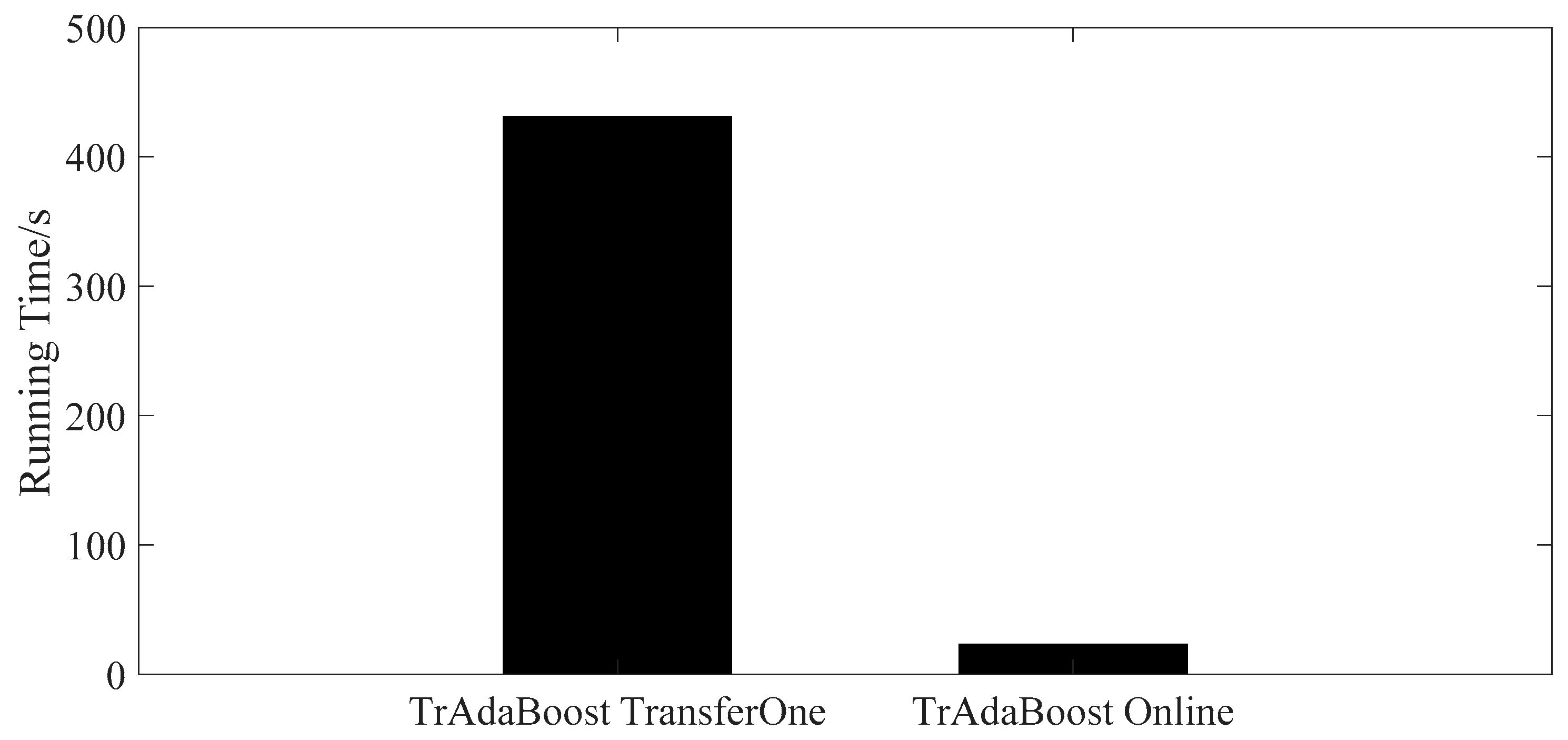
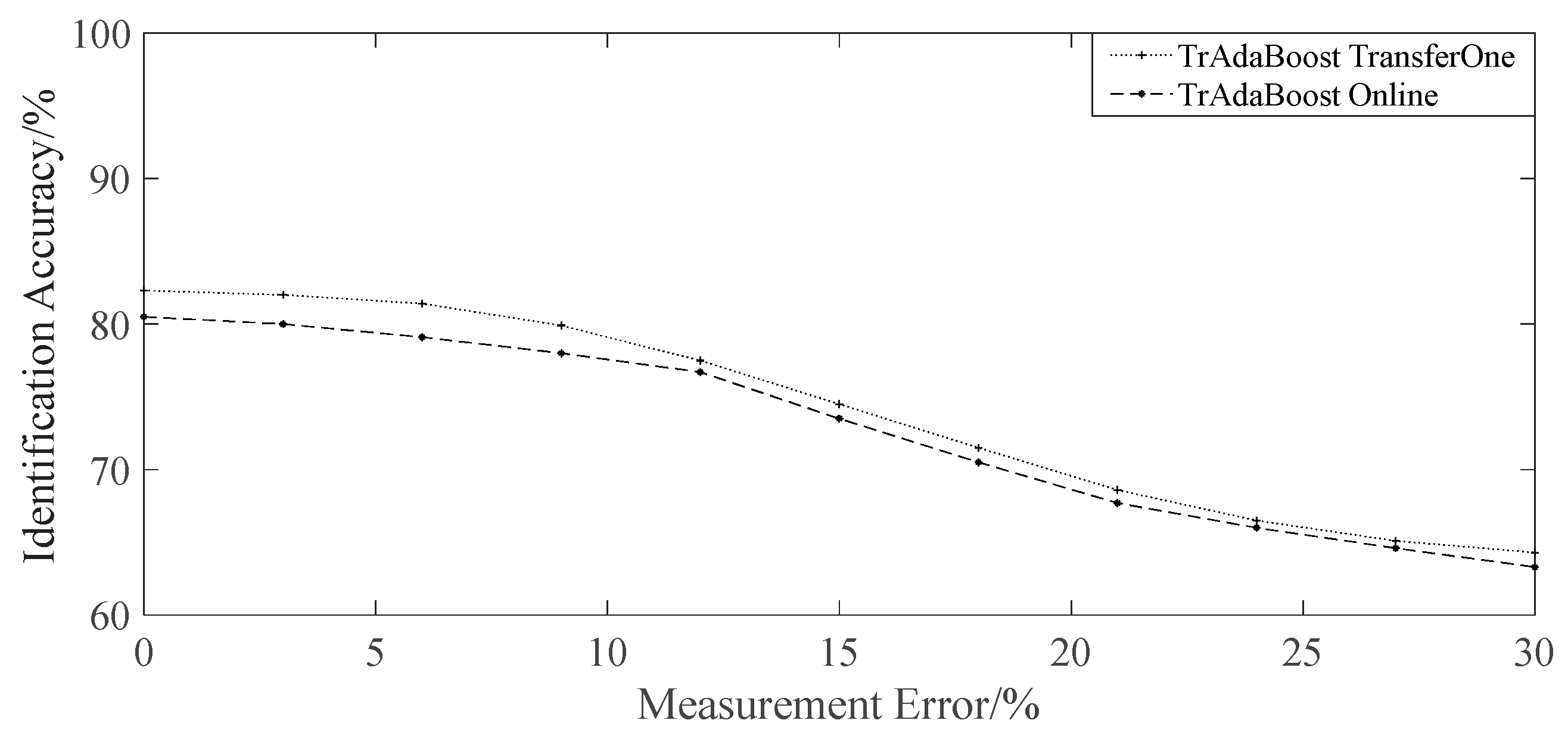
4.2. Contrast Experiments under Transfer Learning
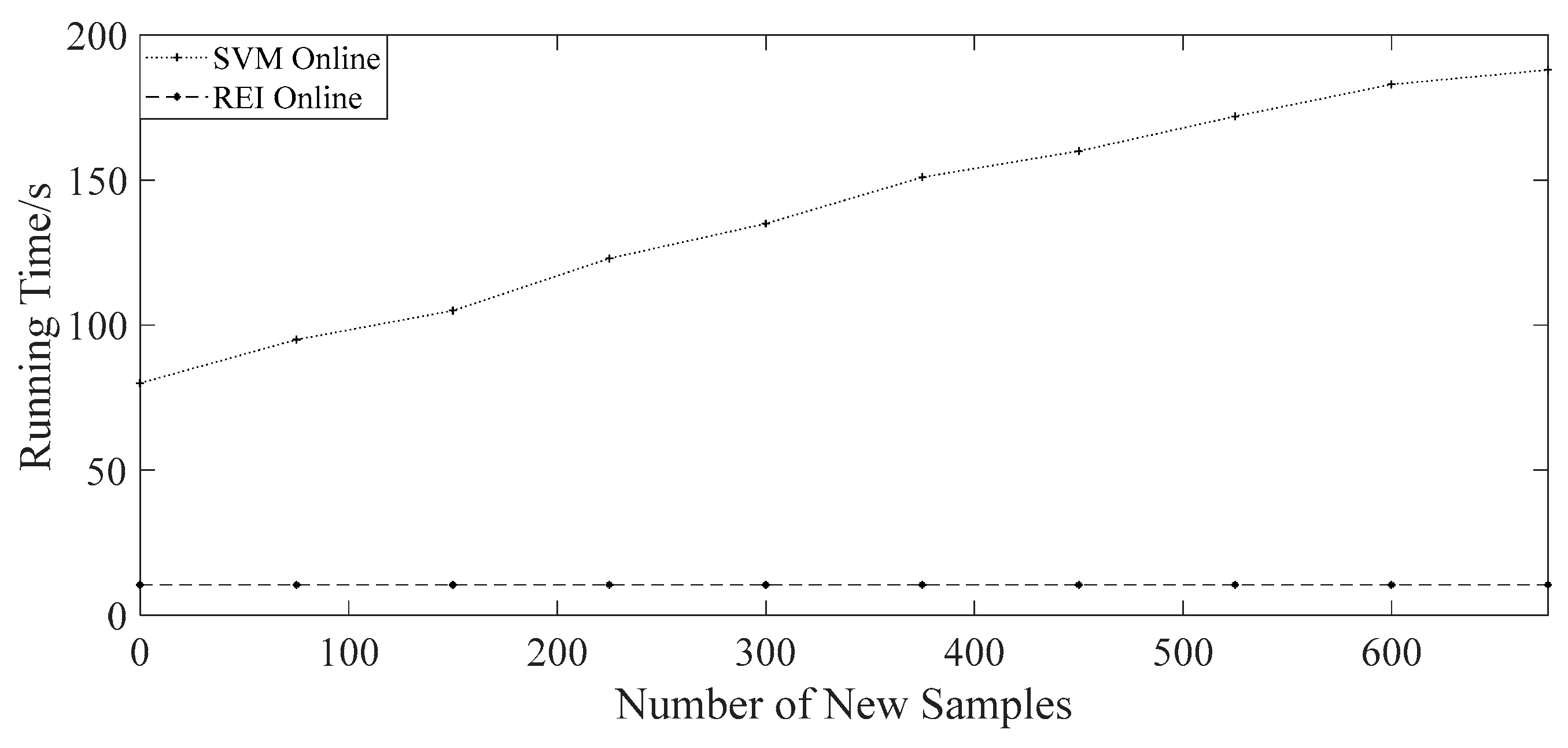
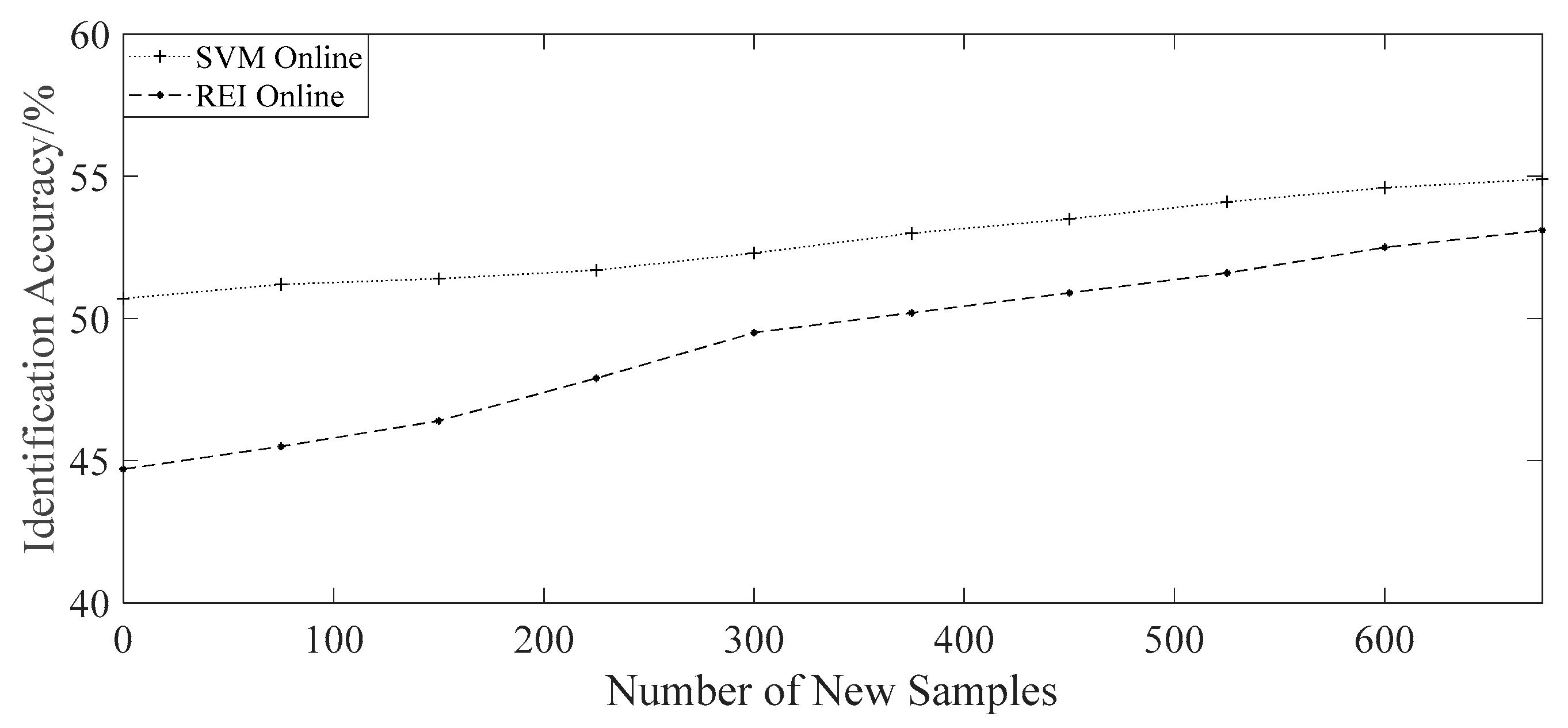
4.3. Contrast Experiments under Online Learning
4.4. A Combination of Transfer Learning Method and Online Learning Method
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hugh, G. ELINT: The Interception and Analysis of Radar Signals R.G. Wiley Artech House, 46 Gillingham Street, London, SW1V 1AH. 2006. 451pp. Illustrated. £82.00. ISBN 1-58053-925-4. Aeronaut. J. 2007, 111, 280. [Google Scholar]
- Lei, W.; Ji, H. Optimizing zero-slice feature of ambiguity function for radar emitter identification. In Proceedings of the 7th International Conference on Information, Communications and Signal Processing (ICICS), Macau, China, 8–10 December 2009. [Google Scholar]
- Bian, M.; Wang, S.; Hu, W.; Ma, L.; Liu, S.; An, D. Radiation source and scattering characteristics analysis of space-borne terahertz cloud radar. J. Terahertz Sci. Electron. Inf. Technol. 2015, 13, 712–717. (In Chinese) [Google Scholar]
- Nguyen, M.N.; Rajapakse, J.C. Two-Stage support vector machines for protein secondary structure prediction. Neural Parallel Sci. Comput. 2003, 11, 1–18. [Google Scholar]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Shalevshwartz, S. Online Learning and Online Convex Optimization. Found. Trends Mach. Learn. 2012, 4, 107–194. [Google Scholar] [CrossRef]
- Lu, J.; Zhao, P.; Hoi, S.C.H. Online Passive-Aggressive Active learning. Mach. Learn. 2016, 103, 141–183. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, P.; Hoi, S.C.H. Exact soft confidence-weighted learning. arXiv 2012, arXiv:1206.4612. [Google Scholar]
- Bistarelli, S.; Gennari, R.; Rossi, F. General Properties and Termination Conditions for Soft Constraint Propagation. Constraints 2003, 8, 79–97. [Google Scholar] [CrossRef]
- Crammer, K.; Kulesza, A.; Dredze, M. Adaptive regularization of weight vectors. Mach. Learn. 2013, 91, 155–187. [Google Scholar] [CrossRef]
- Tsuruoka, Y.; Tsujii, J.; Ananiadou, S. Stochastic Gradient Descent Training for L1-regularized Log-linear Models with Cumulative Penalty. In Proceedings of the Joint Conference of the 47th Annual Meeting of the ACL and the 4th International Joint Conference on Natural Language Processing of the AFNLP, Suntec, Singapore, 2–7 August 2009; Association for Computational Linguistics: Stroudsburg, PA, USA, 2009; pp. 477–485. [Google Scholar]
- Lu, J.; Hoi, S.C.H.; Wang, J.; Zhao, P.; Liu, Z.Y. Large Scale Online Kernel Learning. J. Mach. Learn. Res. 2016, 17, 1613–1655. [Google Scholar]
- Peter, L.; Bartlett, E.H.; Alexander, R. Adaptive Online Gradient Descent. In Advances in Neural Information Processing Systems, Proceedings of the Twenty-First Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 3–6 December 2007; Curran Associates Inc.: Red Hook, NY, USA, 2007. [Google Scholar]
- Zhang, Q.; Li, H.; Zhang, Y.; Li, M. Instance Transfer Learning with Multisource Dynamic TrAdaBoost. Sci. World J. 2014, 2014, 282747. [Google Scholar] [CrossRef]
- Papaconstadopoulos, P.; Levesque, I.R.; Maglieri, R.; Seuntjens, J. Direct reconstruction of the source intensity distribution of a clinical linear accelerator using a maximum likelihood expectation maximization algorithm. Phys. Med. Biol. 2016, 61, 1078–1094. [Google Scholar] [CrossRef]
| Working Mode | PA | CF/MHz | / | / | / |
|---|---|---|---|---|---|
| search | [16, 20] | [3121, 3333] | [7.1, 7.2] | [800, 860] | [66, 68] |
| tracking | [6, 16] | [2019, 2020] | [1.1, 1.3] | [400, 550] | [46, 48] |
| guidance | [2, 12] | [2150, 2250] | [0.3, 0.5] | [300, 400] | [62, 64] |
| Working Mode | PA | CF/MHz | / | / | / |
|---|---|---|---|---|---|
| unknown mode1 | [22, 30] | [2850, 3098] | [4.5, 4.6] | [620, 680] | [45, 47] |
| unknown mode2 | [11, 13] | [2550, 2551] | [0.4, 0.6] | [700, 760] | [25, 27] |
| unknown mode3 | [4, 7] | [2748, 2758] | [0.5, 0.7] | [220, 300] | [50, 52] |
| Source Domain Data | Target Domain Data | |||
|---|---|---|---|---|
| Characteristic Parameter | Mean Value | Standard Deviation | Mean Value | Standard Deviation |
| PA | 0.72 | 0.21 | 0.86 | 0.09 |
| CF/MHz | 0.81 | 0.12 | 0.61 | 0.26 |
| PW/ | 0.76 | 0.32 | 0.44 | 0.13 |
| PRI/ | 0.86 | 0.24 | 0.54 | 0.09 |
| AOA/ | 0.59 | 0.03 | 0.78 | 0.16 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Cheng, Y.; Wang, G.; Xu, X.; Han, H.; Wu, R. Radar Emitter Identification under Transfer Learning and Online Learning. Information 2020, 11, 15. https://doi.org/10.3390/info11010015
Feng Y, Cheng Y, Wang G, Xu X, Han H, Wu R. Radar Emitter Identification under Transfer Learning and Online Learning. Information. 2020; 11(1):15. https://doi.org/10.3390/info11010015
Chicago/Turabian StyleFeng, Yuntian, Yanjie Cheng, Guoliang Wang, Xiong Xu, Hui Han, and Ruowu Wu. 2020. "Radar Emitter Identification under Transfer Learning and Online Learning" Information 11, no. 1: 15. https://doi.org/10.3390/info11010015
APA StyleFeng, Y., Cheng, Y., Wang, G., Xu, X., Han, H., & Wu, R. (2020). Radar Emitter Identification under Transfer Learning and Online Learning. Information, 11(1), 15. https://doi.org/10.3390/info11010015




