Gain Adaptation in Sliding Mode Control Using Model Predictive Control and Disturbance Compensation with Application to Actuators
Abstract
1. Introduction and Literature Review
1.1. Adaptive Sliding Mode Control and Model Predictive Control
1.2. Estimation and Kalman Filters
1.3. Actuators
1.4. Main Contribution
- Section 2 presents the physically-based model of a DC drive that is affected by a nonlinear friction torque and model uncertainty.
- The feedback control design is described in Section 3, where
- Section 3.1 contains details on the employed SMC techniques which involve a combination of a continuous control action and a discontinuous switching part, and where
- in Section 3.2, the height of the switching control action is adapted using MPC techniques to counteract undesired chattering.
- Moreover, an unknown lumped disturbance—accounting for nonlinear friction and model uncertainty in the equation of motion—is estimated in Section 3.3 by a KF. This estimate is employed subsequently in the error dynamics for compensation purposes and, as a result, contributes to the reduction of the necessary switching height determined by MPC.
- The benefits are shown by meaningful simulation results in Section 4.
- Finally, conclusions are given in Section 5.
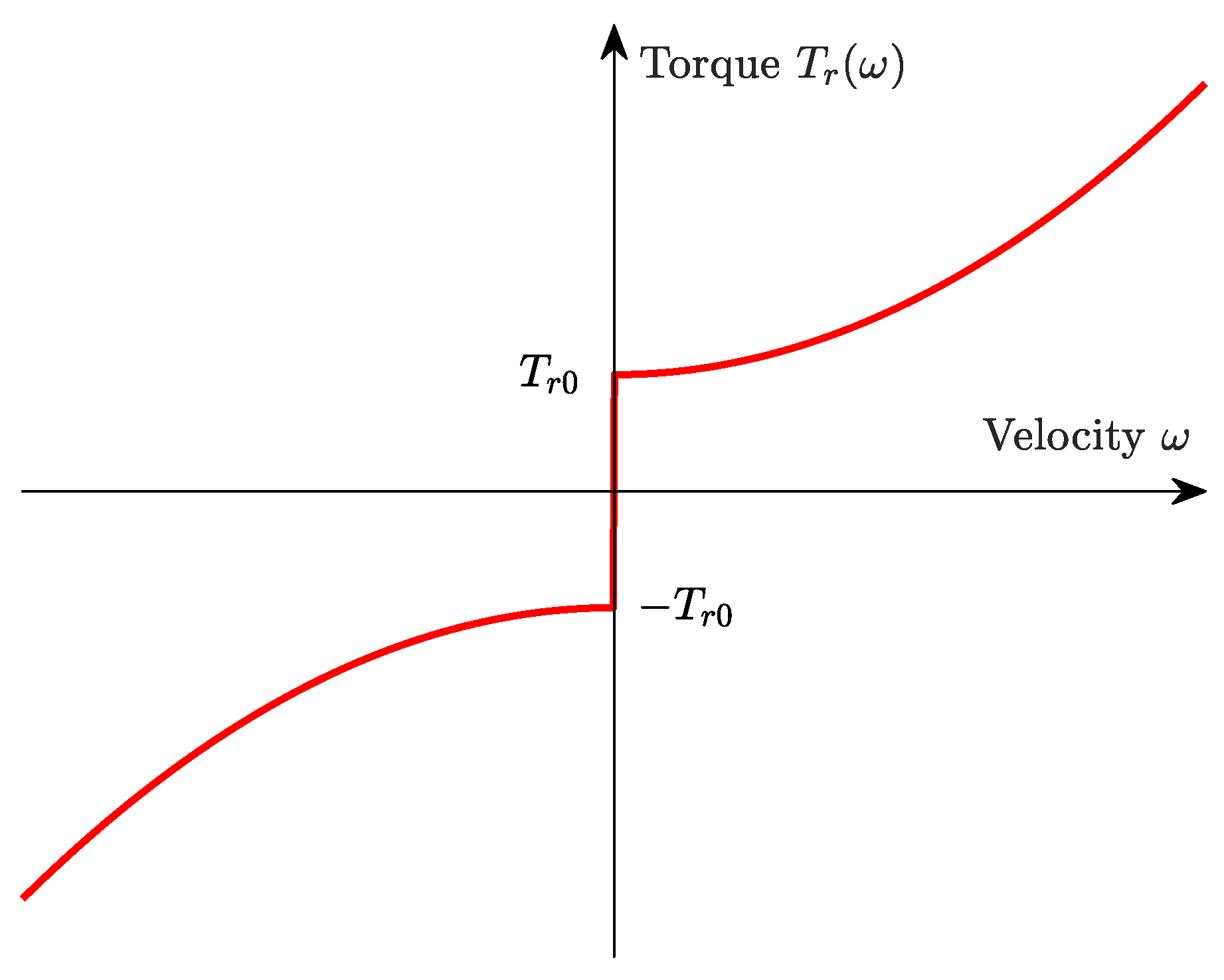
2. System Modelling
- Feedback disturbance compensation: In this solution, the friction term (3) is assumed as known and explicitly included in the sliding mode control design. The corresponding parameters are identified beforehand by the least-squares method. In the envisaged sliding-mode control design this would involve a time differentiation of the friction model and a compensation by means of feedback. It is clear that any changes of the friction model afterwards results in an imperfect compensation.
- Estimator-based disturbance compensation: In this approach, the detailed physical model for the nonlinear friction (3) is not employed at all in the control design. Instead, nonlinear friction is estimated by a Kalman filter. It turns out that the approach can be generalized by considering a lumped disturbance torque , where represents any further external loads torques, unmodelled dynamic effects and model uncertainty. The estimate can be subsequently used for a disturbance compensation. The modified system model is then given by
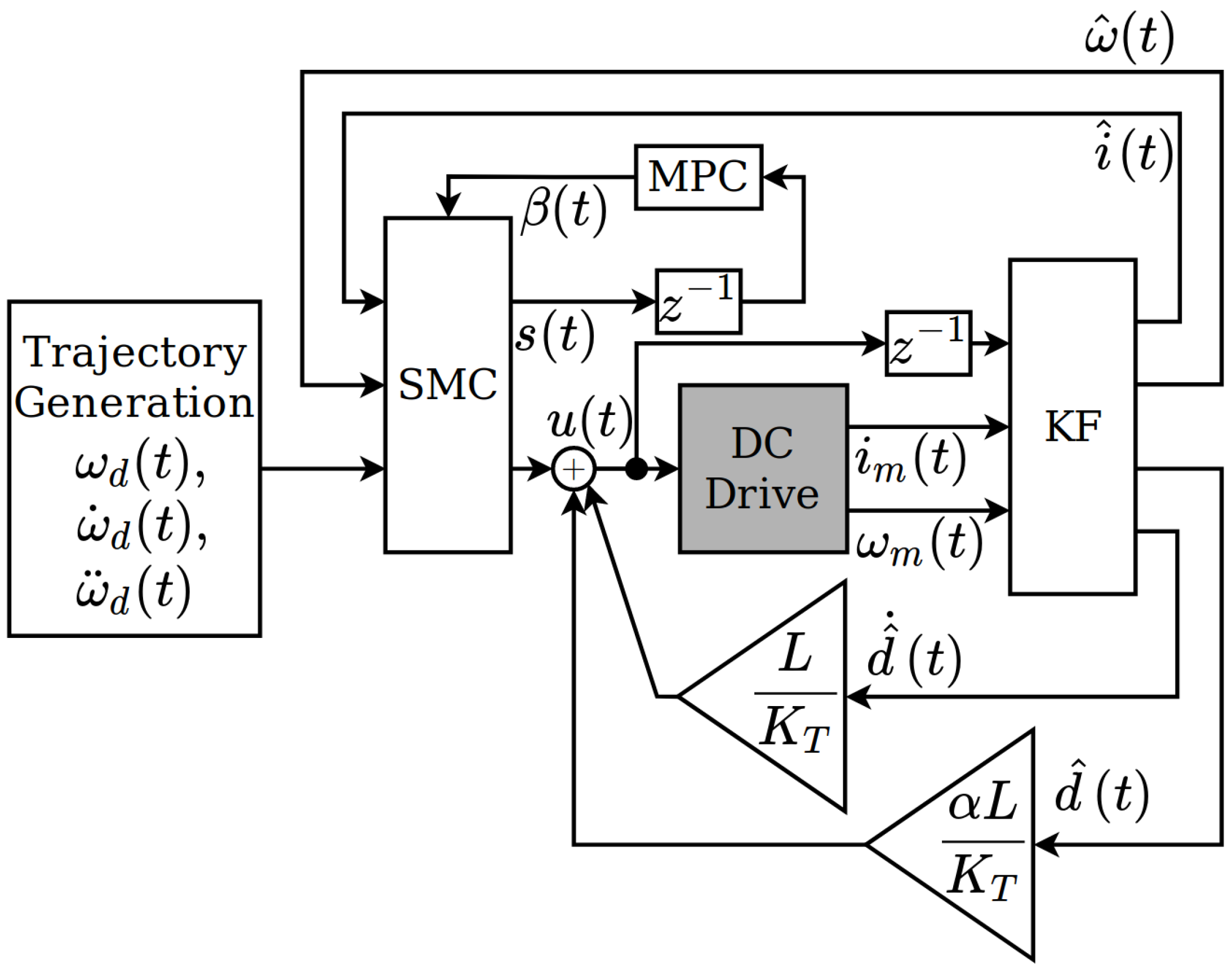
3. Control Design
3.1. Feedback Control Design Using SMC
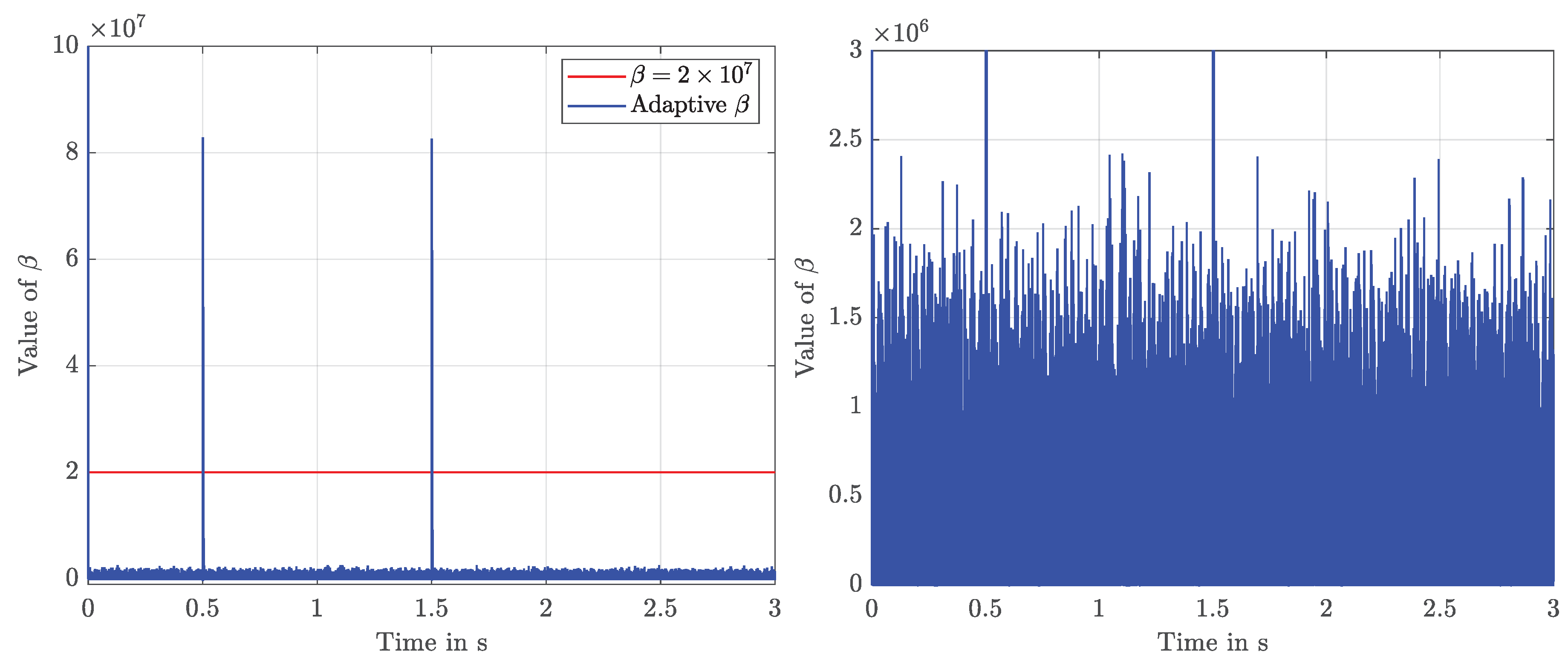
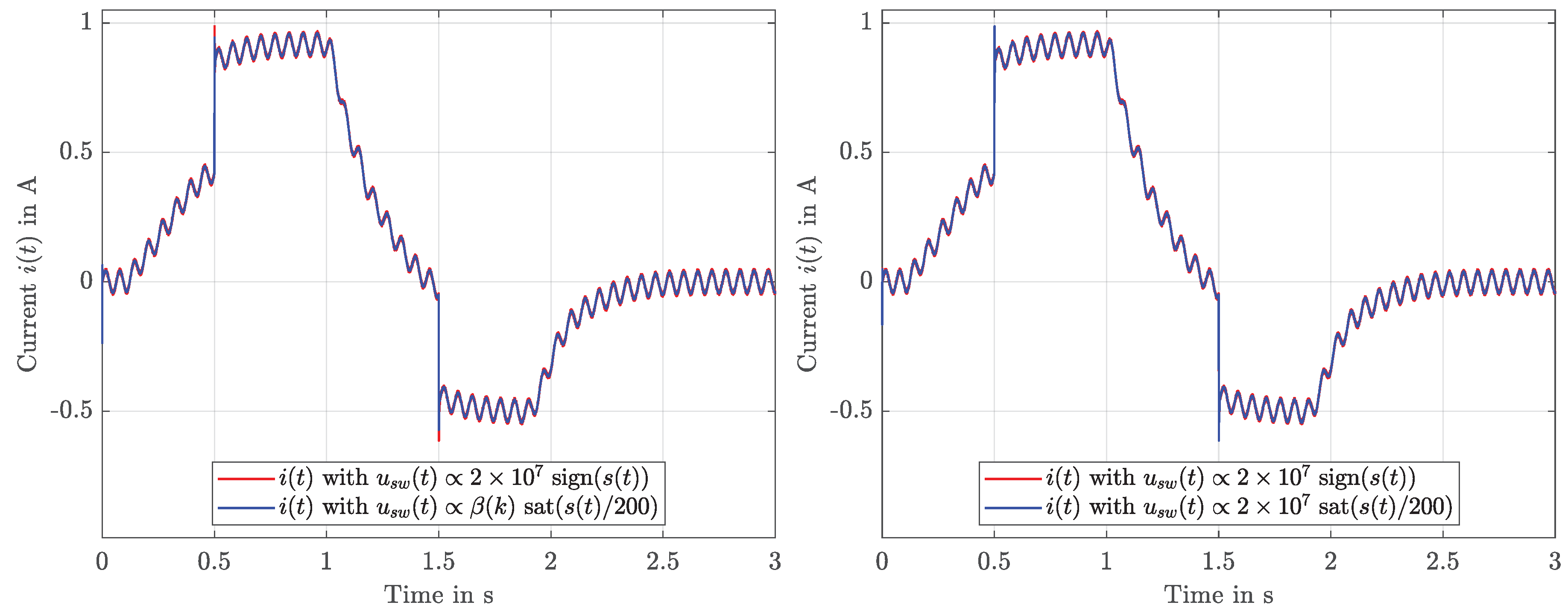
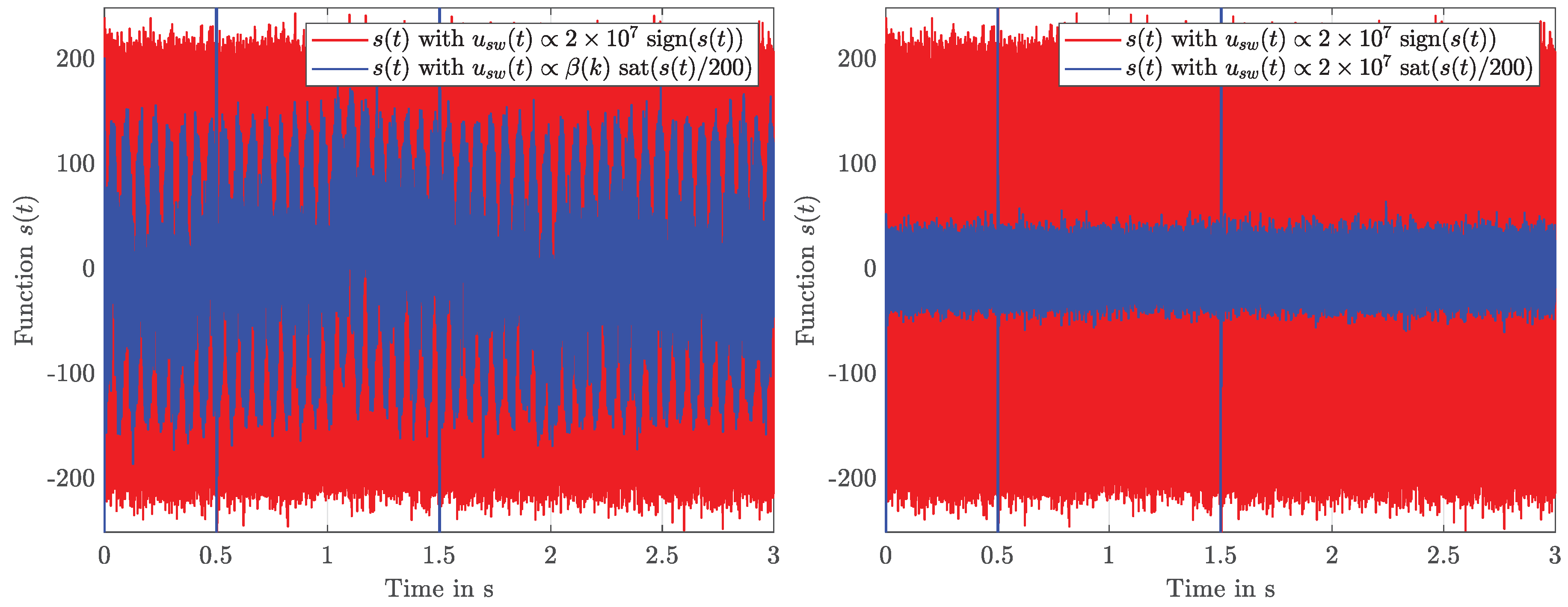
3.2. Adaption of the Switching Height Using MPC
3.2.1. Converge Properties Outside the Boundary Layer
3.2.2. Convergence Properties Inside the Boundary Layer
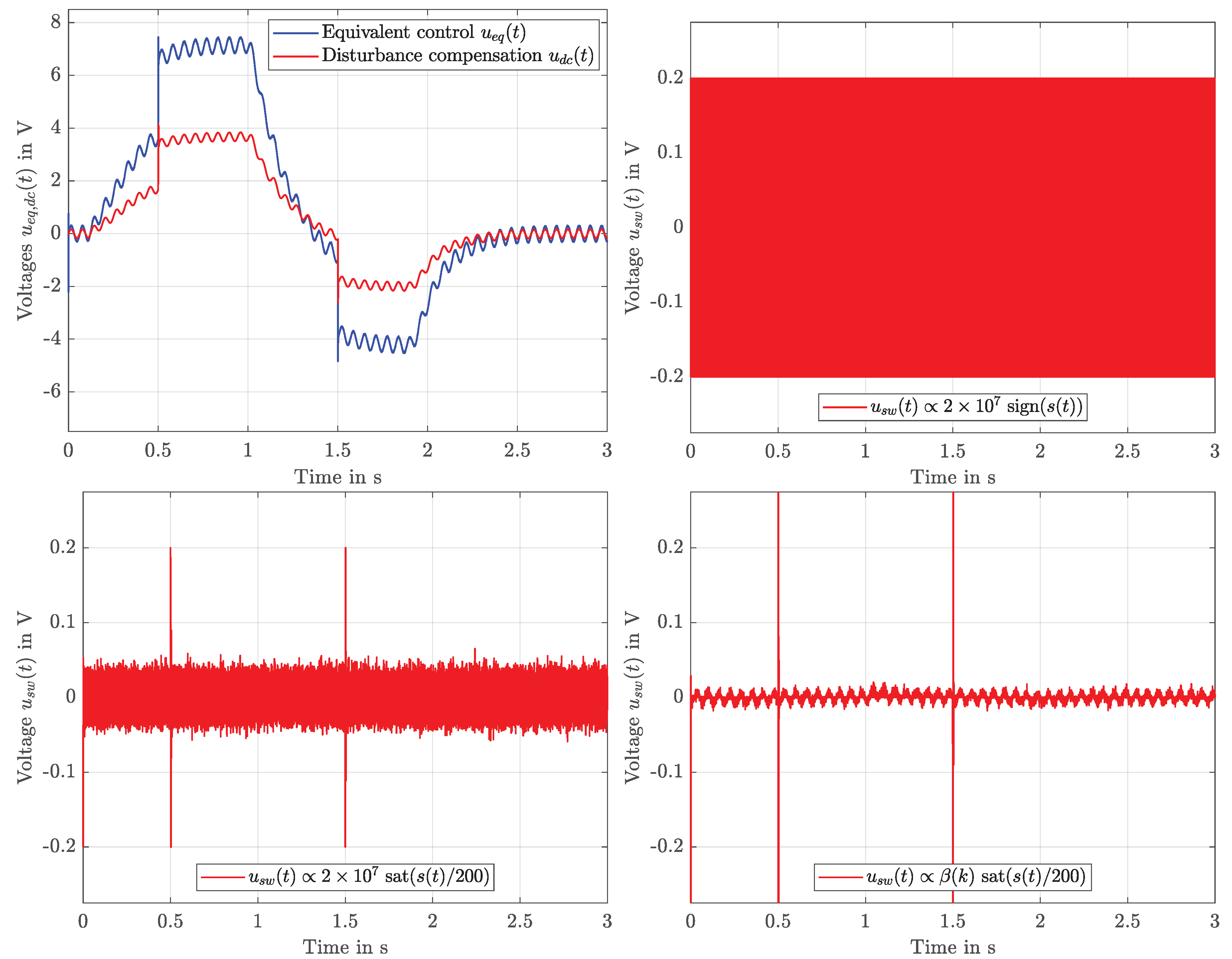
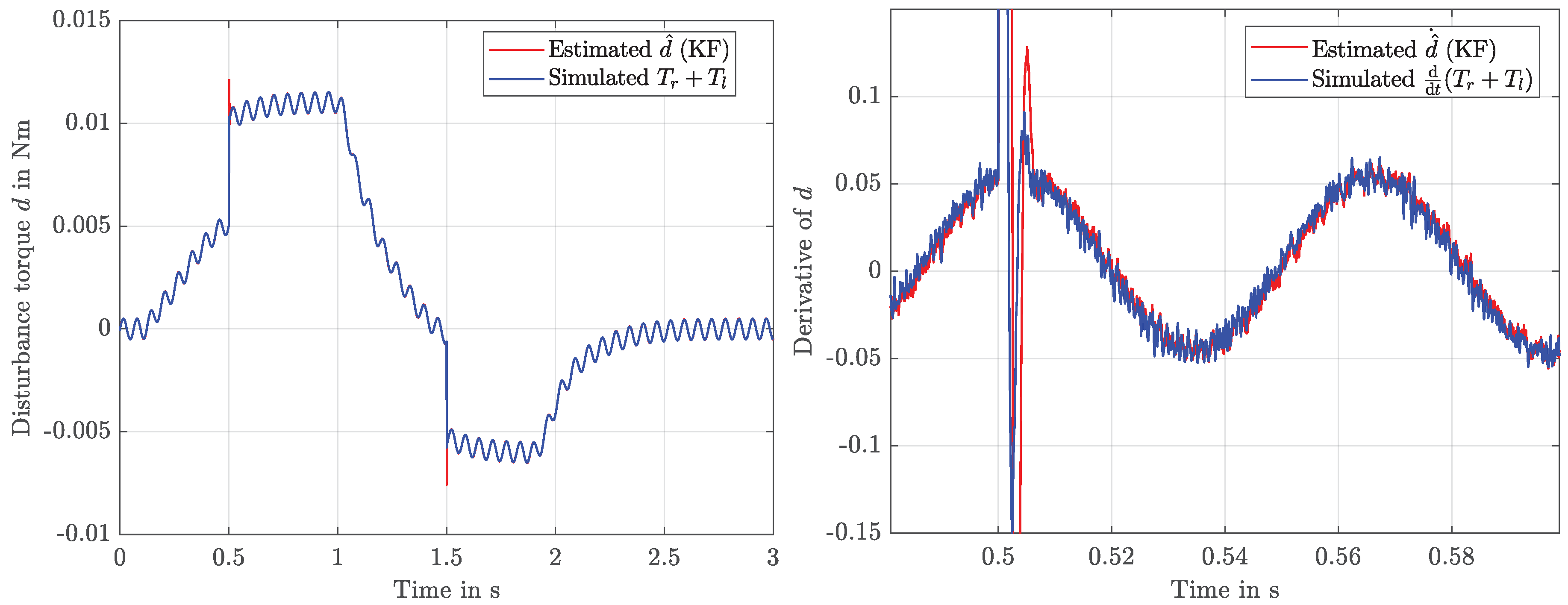
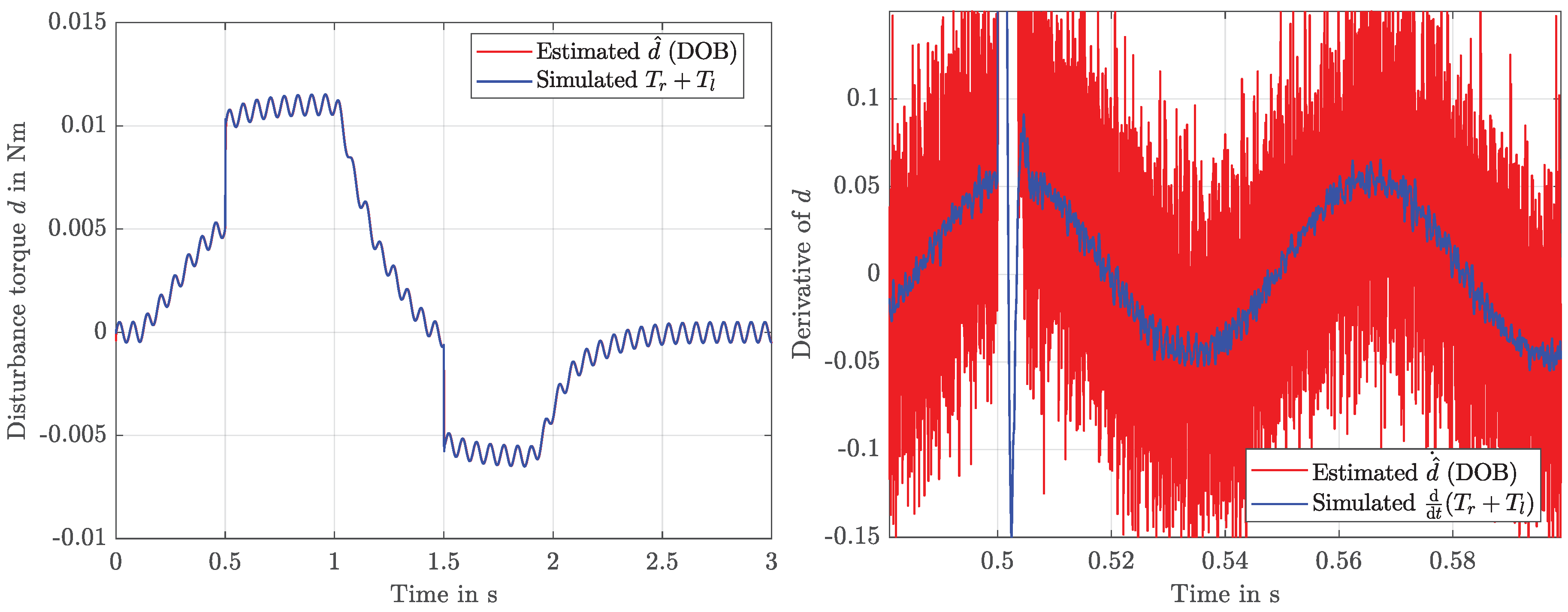
3.3. KF for the Estimation of a Lumped Disturbance Torque
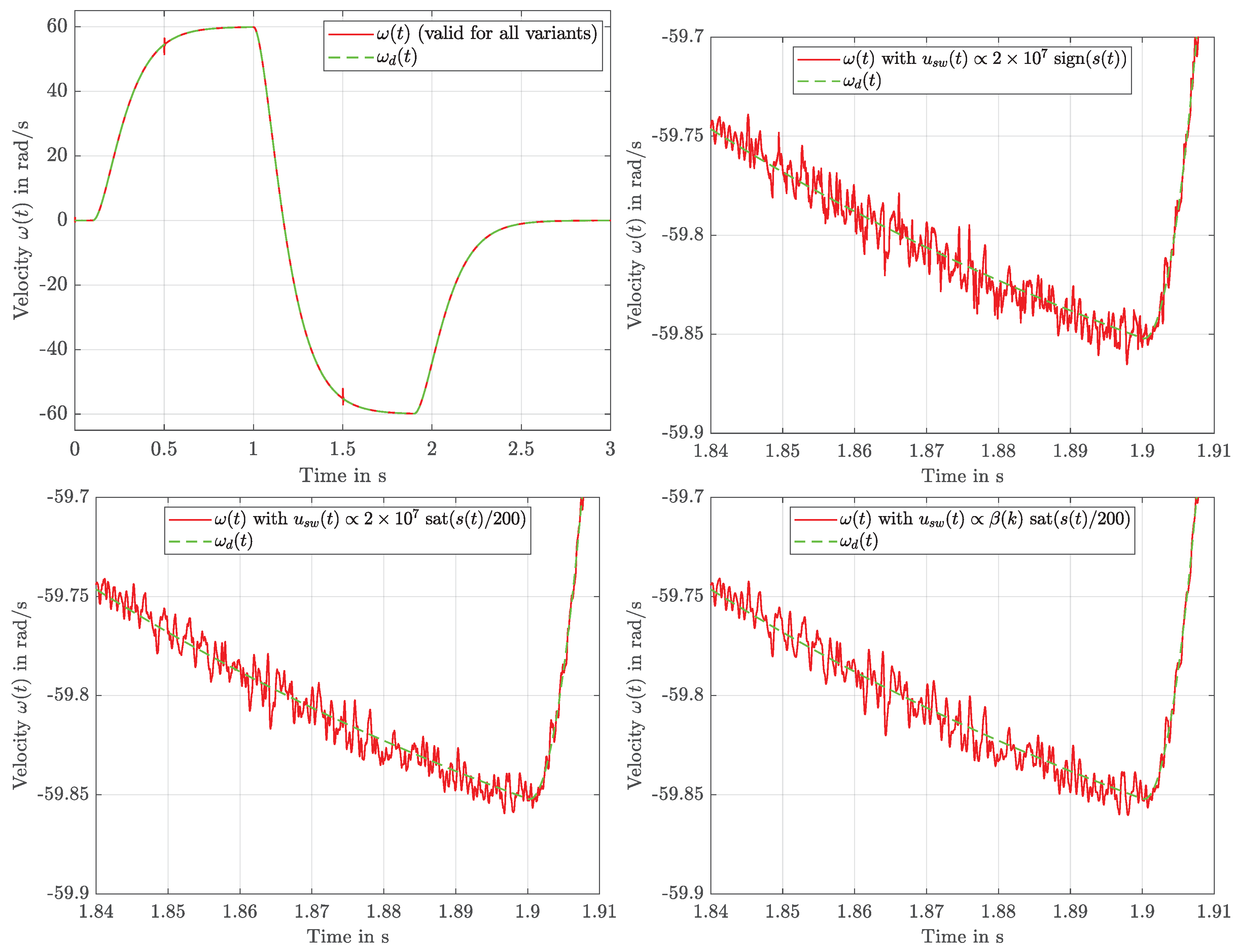
4. Simulations
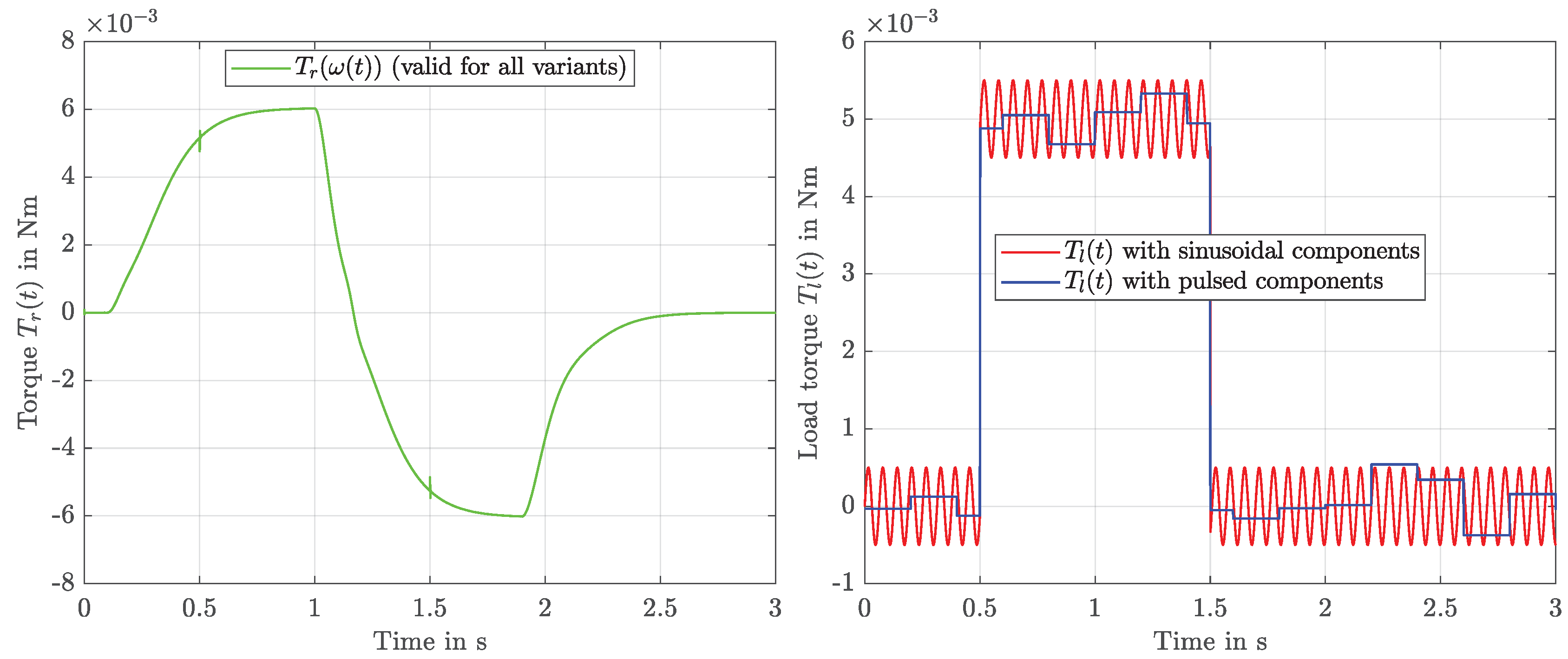
4.1. Simulation Settings and Scenarios
- SMC with and switching control law (14),
- SMC with and ,
- SMC with adaptive and , i.e., the proposed strategy.
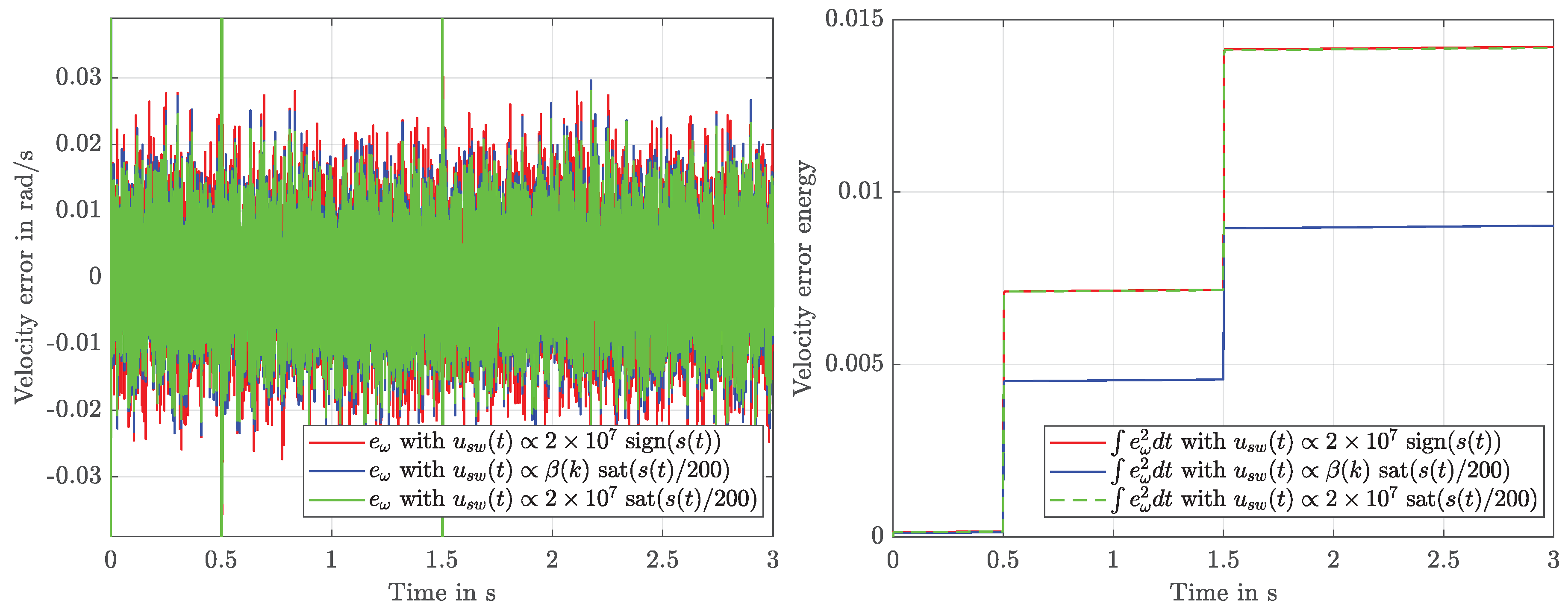
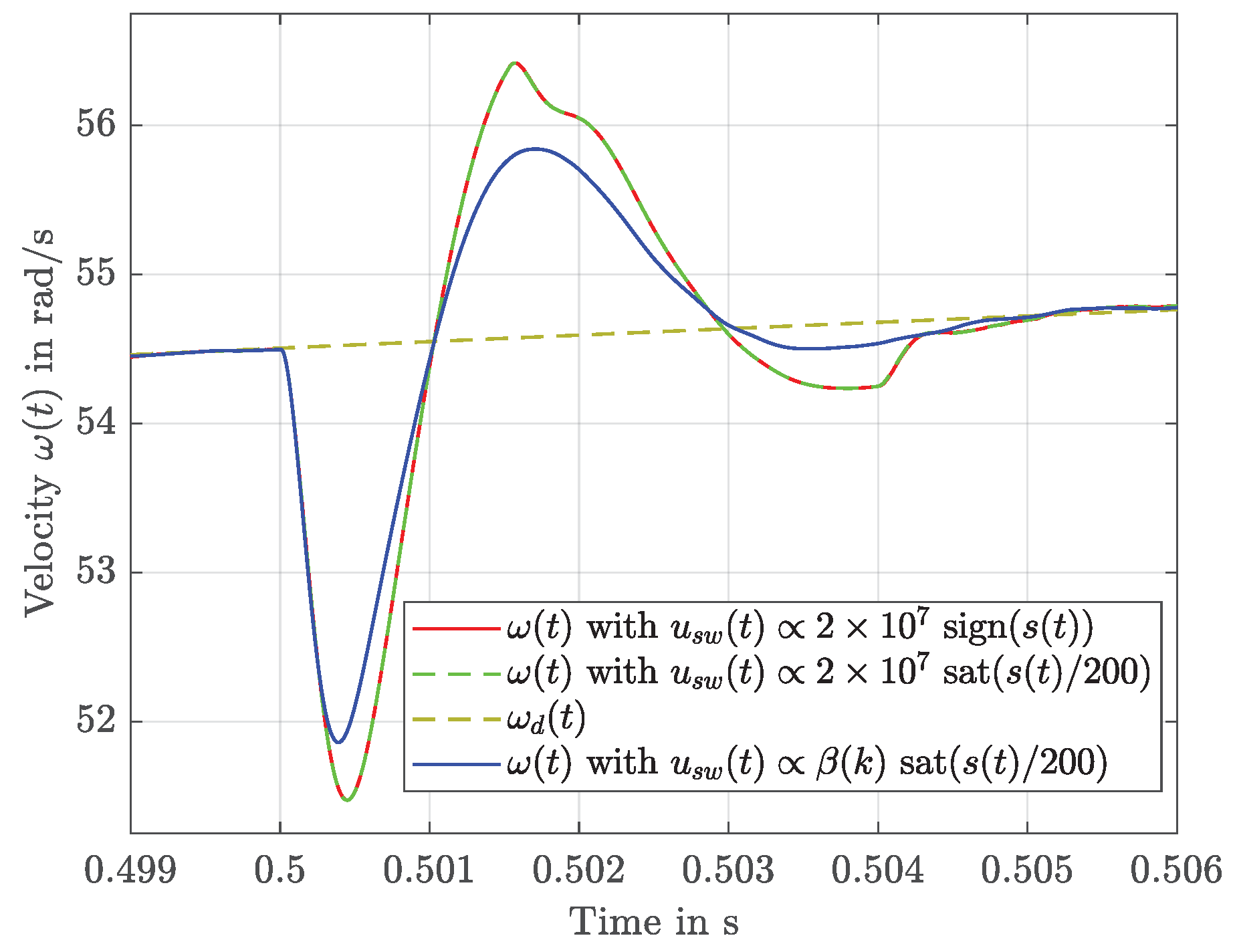
4.2. Results
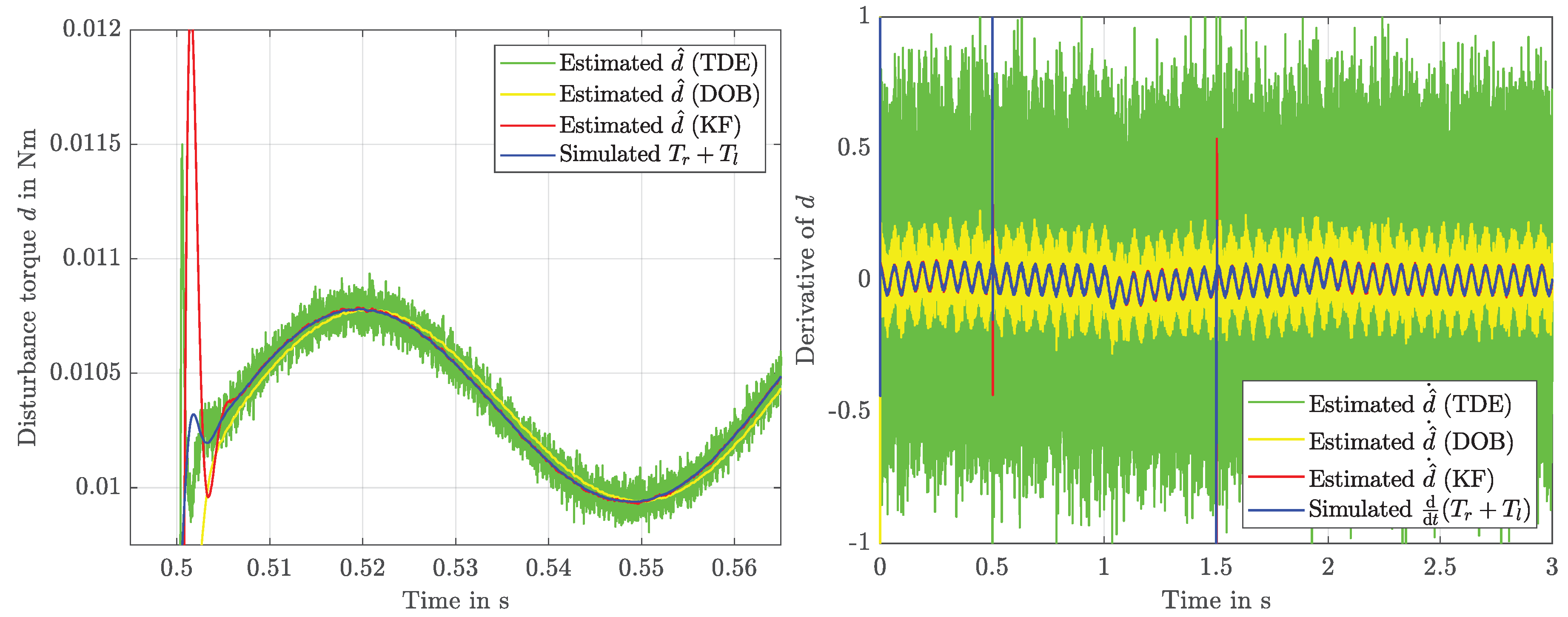
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kachroo, P.; Tomizuka, M. Chattering reduction and error convergence in the sliding-mode control of a class of nonlinear systems. IEEE Trans. Autom. Control 1996, 41, 1063–1068. [Google Scholar] [CrossRef]
- Bartolini, G.; Ferrara, A.; Usai, E. Chattering avoidance by second-order sliding mode control. IEEE Trans. Autom. Control 1998, 43, 241–246. [Google Scholar] [CrossRef]
- Aschemann, H.; Haus, B.; Mercorelli, P. Second-Order Sliding Mode Control with State and Disturbance Estimation for a Permanent Magnet Linear Motor. In Proceedings of the 23rd International Conference on Methods Models in Automation Robotics (MMAR), Miedzyzdroje, Poland, 27–30 August 2018; pp. 345–350. [Google Scholar] [CrossRef]
- Xia, C.; Jiang, G.; Chen, W.; Shi, T. Switching-Gain Adaptation Current Control for Brushless DC Motors. IEEE Trans. Ind. Electron. 2016, 63, 2044–2052. [Google Scholar] [CrossRef]
- Roy, S.; Kar, I.N.; Lee, J.; Jin, M. Adaptive-Robust Time-Delay Control for a Class of Uncertain Euler-Lagrange Systems. IEEE Trans. Ind. Electron. 2017, 64, 7109–7119. [Google Scholar] [CrossRef]
- Plestan, F.; Shtessel, Y.; Brégeault, V.; Poznyak, A. New methodologies for adaptive sliding mode control. Int. J. Control 2010, 83, 1907–1919. [Google Scholar] [CrossRef]
- Liu, J.; Li, H.; Deng, Y. Torque Ripple Minimization of PMSM Based on Robust ILC Via Adaptive Sliding Mode Control. IEEE Trans. Power Electron. 2018, 33, 3655–3671. [Google Scholar] [CrossRef]
- Moon, H.T.; Kim, H.S.; Youn, M.J. A discrete-time predictive current control for PMSM. IEEE Trans. Power Electron. 2003, 18, 464–472. [Google Scholar] [CrossRef]
- Mercorelli, P. Linear Generalised Model Predictive Control to Avoid Input Saturation through Matrix Conditions. WSEAS Trans. Syst. 2017, 16, 313–322. [Google Scholar]
- Mercorelli, P. A Sufficient Asymptotic Stability Condition in Generalised Model Predictive Control to Avoid Input Saturation. In Applied Physics, System Science and Computers II; Ntalianis, K., Croitoru, A., Eds.; Springer: Berlin, Germany, 2018. [Google Scholar]
- Mercorelli, P. A Motion-Sensorless Control for Intake Valves in Combustion Engines. IEEE Trans. Ind. Electron. 2017, 64, 3402–3412. [Google Scholar] [CrossRef]
- Mercorelli, P. A Two-Stage Sliding-Mode High-Gain Observer to Reduce Uncertainties and Disturbances Effects for Sensorless Control in Automotive Applications. IEEE Trans. Ind. Electron. 2015, 62, 5929–5940. [Google Scholar] [CrossRef]
- Hsieh, C.S. Robust two-stage Kalman filters for systems with unknown inputs. IEEE Trans. Autom. Control 2000, 45, 2374–2378. [Google Scholar] [CrossRef]
- Hsieh, C.S.; Chen, F.C. Optimal solution of the two-stage Kalman estimator. IEEE Trans. Autom. Control 1999, 44, 194–199. [Google Scholar] [CrossRef]
- Hsieh, C.S. General two-stage extended Kalman filters. IEEE Trans. Autom. Control 2003, 48, 289–293. [Google Scholar] [CrossRef]
- Haessig, D.; Friedland, B. Separate-bias estimation with reduced-order Kalman filters. IEEE Trans. Autom. Control 1998, 43, 983–987. [Google Scholar] [CrossRef]
- Chen, L.; Mercorelli, P.; Liu, S. A Kalman estimator for detecting repetitive disturbances. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; Volume 3, pp. 1631–1636. [Google Scholar] [CrossRef]
- Armstrong-Hélouvry, B.; Dupont, P.; Wit, C.C.D. A survey of models, analysis tools and compensation methods for the control of machines with friction. Automatica 1994, 30, 1083–1138. [Google Scholar] [CrossRef]
- Aschemann, H.; Haus, B.; Mercorelli, P. Sliding Mode Control and Observer-Based Disturbance Compensation for a Permanent Magnet Linear Motor. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 4141–4146. [Google Scholar] [CrossRef]
- Haus, B.; Röhl, J.H.; Mercorelli, P.; Aschemann, H. Model Predictive Control for Switching Gain Adaptation in a Sliding Mode Controller of a DC Drive with Nonlinear Friction. In Proceedings of the 22nd International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 10–12 October 2018; pp. 765–770. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Pearson: Upper Saddle River, NJ, USA, 1991. [Google Scholar]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter. Available online: https://www.cs.unc.edu/~welch/media/pdf/kalman_intro.pdf (accessed on 15 May 2019).
- Chen, W.H. Disturbance observer based control for nonlinear systems. IEEE/ASME Trans. Mechatron. 2004, 9, 706–710. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haus, B.; Mercorelli, P.; Aschemann, H. Gain Adaptation in Sliding Mode Control Using Model Predictive Control and Disturbance Compensation with Application to Actuators. Information 2019, 10, 182. https://doi.org/10.3390/info10050182
Haus B, Mercorelli P, Aschemann H. Gain Adaptation in Sliding Mode Control Using Model Predictive Control and Disturbance Compensation with Application to Actuators. Information. 2019; 10(5):182. https://doi.org/10.3390/info10050182
Chicago/Turabian StyleHaus, Benedikt, Paolo Mercorelli, and Harald Aschemann. 2019. "Gain Adaptation in Sliding Mode Control Using Model Predictive Control and Disturbance Compensation with Application to Actuators" Information 10, no. 5: 182. https://doi.org/10.3390/info10050182
APA StyleHaus, B., Mercorelli, P., & Aschemann, H. (2019). Gain Adaptation in Sliding Mode Control Using Model Predictive Control and Disturbance Compensation with Application to Actuators. Information, 10(5), 182. https://doi.org/10.3390/info10050182






