Abstract
Buildings play a critical role in the stability and resilience of modern smart grids, leading to a refocusing of large-scale energy-management strategies from the supply side to the consumer side. When buildings integrate local renewable-energy generation in the form of renewable-energy resources, they become prosumers, and this adds more complexity to the operation of interconnected complex energy systems. A class of methods of modelling the energy-consumption patterns of the building have recently emerged as black-box input–output approaches with the ability to capture underlying consumption trends. These make use and require large quantities of quality data produced by nondeterministic processes underlying energy consumption. We present an application of a class of neural networks, namely, deep-learning techniques for time-series sequence modelling, with the goal of accurate and reliable building energy-load forecasting. Recurrent Neural Network implementation uses Long Short-Term Memory layers in increasing density of nodes to quantify prediction accuracy. The case study is illustrated on four university buildings from temperate climates over one year of operation using a reference benchmarking dataset that allows replicable results. The obtained results are discussed in terms of accuracy metrics and computational and network architecture aspects, and are considered suitable for further use in future in situ energy management at the building and neighborhood levels.
1. Introduction
Complex energy systems that support global urbanization tendencies play an important role in the definition, implementation, and evaluation of future smart cities. Within the built environment, making use of modern technologies in the areas of sensing, computing, communication, and control leads to improving the operations of various systems and the well-being of its inhabitants. Of particular relevance is the reliable, clean, and cost-effective energy-supply electrical grid, thereby catering to ever-increasing urban needs. The main target of our work is developing improved models for load forecasting of medium and large commercial buildings that act in a determining role as consumers, prosumers, or balancing entities for grid stability. Statistical-learning algorithms, such as classical and deep neural networks, represent a prime example. The back-box model, achieved thorough such techniques, has proven able to accurately model underlying patterns and trends driving energy consumption that can be used to forecast load profiles and improve high-level control strategies. In such a way, significant economic, through cost savings, and environmental, through limited use of scarce energy resources, benefits can be achieved.
An often quoted figure in the scientific literature [1] places building energy use at almost 40% of primary energy use in many developed countries with an increasing trend. In modern buildings, a centralized software solution, often denoted as a Building Management System (BMS), collects all relevant data streams originating in building subsystems and provides means for intelligent algorithms to act based on processed data. Energy-relevant data, generated through heterogeneous instrumentation networks, are subsequently leveraged to control relevant energy parameters in daily operation. For an existing older building, new technology can be used to upgrade legacy devices, such as electrical meters, and integrate them into wired or wireless communication networks in a cost-effective manner. Finally, the resulting preprocessed energy-measurement time series serve as input for accurate models of energy prediction and control.
Statistical-learning algorithms have become robust and well-adopted in the last few years through concentrated efforts in both research and industry. This was stimulated by data availability and exponentially increasing computing resources at lower costs, including cloud systems. Neural networks are one example of such an algorithm, which offers good results in many application areas, including the modelling and prediction of energy systems. This is valid for both classification and as regression tasks, where the objective is to predict an output numerical value of interest. Deep-learning networks are highly intricate neural networks with many hidden layers that are able to learn patterns of increasing complexity in input datasets. Initially deployed through industry-driven initiatives in the areas of multimedia processing and translation systems, other technical applications currently stand to benefit from the availability of open-source algorithms and tools. For time series and sensor data, a particular type is gaining traction with the research community, namely, sequence models based on a recurrent neural network that can capture long-term dependencies in input examples. In the nomenclature described by Reference [2] of machine-learning (ML) taxonomy for smart buildings, our work fits within the area of using ML to estimate aspects related to either energy or devices, in particular, energy profiling and demand estimation.
Within this approach, large commercial buildings provide the operators/owners with economic incentives and returns of investment related to energy-efficiency projects, where small-percentage gains on large absolute values of energy use become more attractive. An equally large market exists for improving energy-forecasting accuracy in the residential sector, which is, however, more fragmented, and the incentives to deploy such approaches have to be present at the energy supplier or through public large-scale programs.
The main contributions of the paper can be thus summarised:
- illustrating a deep-learning approach to model large-commercial-building electrical-energy usage as alternative to conventional modelling techniques;
- presenting an experimental case study using the chosen deep learning techniques enabling reliable forecasting of building energy use;
- analysis of the results in terms of accuracy metrics, both absolute and relative, which provide a way for replicable result towards other related research.
Additional contributions that extend the previous conference paper [3] are summarised. We provided, as the main goal for the extended version, new experiment results for recurrent neural-network modelling of large-commercial-building energy consumption. These were further analyzed, also taking into account several performance metrics and computational aspects. More technical clarifications regarding the methods and data-processing and -modelling pipeline are also included. Significant revisions and extensions were also carried out in the related work section for more timely and focused state of the art to frame the work, as well as to other parts of the paper to improve readability and allow the replication of the results by interested researchers on neural-network architectures presented in an energy-management system.
We further briefly discuss the structure of the paper. Section 2 discusses a timely recent publication that deal with four models of electrical-energy consumption of direct relevance to the previously stated contribution areas. In Section 3, sequence models are introduced as computational intelligence methods for this task. Most notably, Recurrent Neural Networks (RNN) are used through units of Long Short-Term Memory (LSTM) neurons. The selected deep-learning methods are applied as a case study in Section 4 on publicly available data stemming from four large commercial buildings. The salient findings are also discussed in detail, including computational aspects pertaining to the architectures of the learning algorithms that were implemented. Section 5 concludes the paper with regard to the applicability of the derived black-box models for in situ electrical-load forecasting.
2. Related Work
We first state three key factors identified as drivers of the implementation of a statistical-learning methodology, and algorithms to energy-system modelling and control:
- more computational resources are currently easily available that allow testing and validation of the designed approaches on better-quality public datasets;
- open-source libraries and software packages have been developed that implement advanced statistical-learning techniques with good documentation for research outside the core mathematical and computer-science fields of expertise;
- customized development of new deep-learning architectures through joint work in teams with computing, algorithm, and domain expertise (energy in this case), which has yielded suitable and good results for the challenges discussed in this article.
Fayaz et al. [4] describe an approach and case study for the prediction of household energy consumption using feed-forward back-propagation neural networks. The authors discuss their outcomes based on data collected from four residential buildings in South Korea, including the preprocessing and tuning of the algorithms. The evaluation is based on models built on raw data, normalized data, and data with statistical moments, with the conclusion that accuracy metrics are best in the latter case. Learning customer behaviors for effective load forecasting is discussed by [5], who implemented Sparse Continuous Conditional Random Fields (sCCRF) to effectively identify different customer behaviors through learning. A hierarchical clustering process was subsequently used to aggregate customers according to the identified behaviors.
Time-series change-point detection, along with preprocessing approaches, are introduced in [6]. The SEP algorithm was evaluated on smart-home data, both real and artificial. This algorithm uses separation distance as a divergence measure to detect change points in high-dimensional time series. Building-occupancy influence on energy consumption through indirect sensing is elaborated upon by [7], where the system was able to infer occupancy counts using “proxy” measures of temperature and indoor CO2 concentrations. Two types of sequence models using long short-term memory units were tested in [8] in conjunction with an electrical-energy modelling application. As a salient discovery, the authors showed that performance metrics were improved when working on aggregated collected data that require the consideration of long-term dependencies. The validated model was subsequently leveraged for missing value imputation on input time data. Refererence [9] discussed the application of autoencoders and generative networks as a deep-learning alternative to conventional feature engineering in learning models for electrical-energy load forecasting. A method based on Support Vector Regression (SVR) was presented by [10].
Extensive building energy modelling from the thermal energy perspective is analysed in [11] by using approximate data to derive simplified grey-box models of the building based on electrical circuit analogies. The derived building element-wise RC-models are validated by means of an optimisation routine.The authors of [12] further perform a study with R5C1 simulation models for a typical average day in mediterranean climate conditions. The models have been validated and implemented in a large energy consumption study simulation, given the fact that the Heating, Ventilation and Air Conditioning (HVAC) subsystem in a major driver of the building electrical energy consumption for several climate regions. In this context also deep learning approaches might be relevant given enough input data as historical measurement from the Building Management System over several seasons and external conditions, to be compared with an analytical large scale solution.
While defining the context of the current work, we also mentioned previous implementation that analyzed conventional system identification using Autoregressive Integrated Moving Average (ARIMA) models versus classical Artificial Neural Networks (ANN) [13]. Multiple ANN versions have been tested [14] in terms of number of hidden layers and number of neurons per layer. The deep-learning approach offers better results for our test scenarios. The final aim is to integrate the resulting validated models in a building energy decision support system, in a similar fashion to [15].
3. Electrical-Energy Modelling Using Sequence Model RNNs
RNNs represent a currently highly relevant modelling instrument in applications where input data consist of time-related sequences of “events”. The inherent loop present in an RNN carries long-term dependencies toward the final outcome. By simultaneously processing multiple items in a sequence of input data, they are directly applicable for the evaluation of nonlinear time-series problems, as is the case with electrical-energy load forecasting. Given the differences with conventional artificial neural networks (ANN), RNNs use back-propagation-through-time (BPTT) [16] or real-time recurrent-learning (RTRL) [17] algorithms to compute the gradient descent after each iteration for solving the optimization problem. As summary, RNNs are a type of deep-learning method that includes supplementary weights in the structure by creating cycles so that the internal graph is able to control and adjust the internal state of the network.
3.1. RNN Implementation with LSTM
A recurrent neural network can be implemented by using typical sigmoid, tanh, and rectifier linear unit activation functions, or by more advanced units that help to better manage the information flow throughout the network. Of the latter category, the currently most popular with researchers are Gated Recurrent Units (GRU) and LSTM units. The main purpose of such techniques is to mitigate the effect of vanishing or exploding gradients during training with long sequences of input data, which creates significant numerical computation problems during the optimization steps. Enhancing gradient flow by means of the LSTM [18] architecture in long sequences during training is achieved by self-connected “gates” in the hidden units. Basic primitives to manage the flow of information pieces in the network are handled with reading, writing, and removing information in the cells [19,20].
A time series x of length n, () passing by a single LSTM layer is shown in Figure 1. h represents the output or hidden state, and c represents the cell state. The initial state of the network, (, ) in input to the first cell as initialization along with the first time step of the sequence . The first output is computed, and and the new cell state is further propagated to the next computational cell in an iterative fashion.
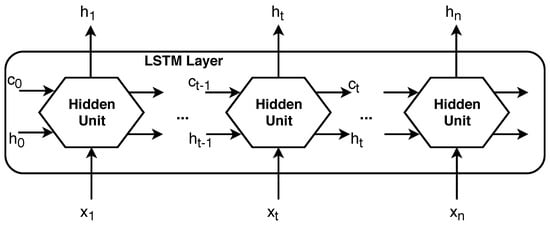
Figure 1.
Long Short-Term Memory (LSTM) layer diagram.
The state of the LSTM layer consists of output state and cell state . On the one hand, the output state at time step t is achieved by means of combining the current output of the LSTM layer with the cell-state information that accounts for previous extracted information. This cell state is iteratively updated by write or erase operations that are controlled using symbolic gates that filter the underlying effects at each step. Following are the four gate types in an LSTM cell and their respective effects [20]:
- input gate —level of cell state update;
- layer update —add information to cell state;
- forget gate —remove information from cell state;
- output gate —effect of cell state on output.
Figure 2 presents a diagram concerning the data flow at time instance t inside one hidden unit.
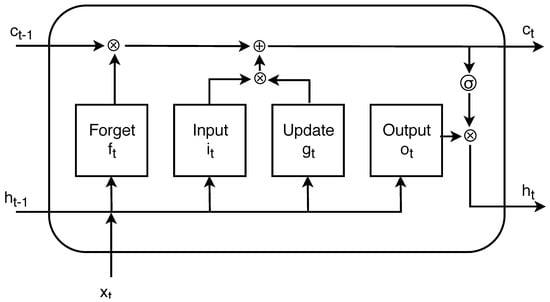
Figure 2.
Schematic diagram and data flow for one LSTM cell.
During training, an LSTM network also learns conventional parameters such as input weights and bias while adding an extra set of parameters in the form of recurrent weights , and b is achieved through the concatenations of input weights, recurrent weights, and bias at the component-wise level. Matrices are constructed as follows:
with i, f, g and o accounting for the input gate, forget gate, layer input, and output gate, respectively.
The state of the cell memory at time step t is updated recursively using the following formula [18]:
with ⊗ standing for the Hadamard product. The equations governing the updates at each time instance t are written as:
represents the sigmoid activation function, and tanh the hyperbolic tangent activation function.
Output gate combined as a reading operation with cell state produces the output state for time instance t, as reflected by the following equations:
where
A simplified version of LSTM was introduced by [21], namely, a GRU. In this case, the RNN cell uses a sole update gate and merges the cell and output states into a single value that is propagated across the network. A recent application of GRU vs. LSTM in electrical-energy load forecasting was provided by [22].
3.2. Benchmarking Datasets
We leveraged and acknowledge the datasets within the Building Data Genome at the Building and Urban Data Science (BUDS) Group at the National University of Singapore (http://www.budslab.org). This includes active power load traces that are part of a data collection of several hundreds of nonresidential buildings, mainly academic venues, proposed for performance analysis and algorithm benchmarking to a common baseline [14,23].
The current study investigated an RNN LSTM modelling approach by using various neural-network configurations and the performance assessment between all forecasting LSTM models.
A key joint characteristic of the benchmarking datasets is the sampling period of measurement of 60 min over a one-year period. We selected four educational buildings with an approximate surface area of 9000 square meters. The chosen buildings for the study were from university campuses in Chicago (USA), two reference buildings, New York (USA) and Zurich (Europe). After preprocessing noise and missing data in the initial dataset using the median filter technique, two time-series datasets were obtained with approximately 8.670data points each. The median filter [24] is expressed as:
where is the filtered output of the input sequence. The sole parameter used for tuning the filter is represented by filter length . In our case, a 15th-order median filter was used by the preprocessing implementation.
The key criteria for the selection were: medium-to-large building, mixed usage pattern—office, laboratory space, some classrooms—and nonextreme temperate climate, with four distinct seasons [14]. A guiding choice in selecting the four candidates from the 508 entities in the dataset was also similarity to a local university building from our campus, where a data-collection study is currently ongoing.
4. Experiment Evaluation for Building-Energy Time-Series Forecasting
We first present the preprocessed time series for the buildings that make up our study and consist of hourly active power measurement from the electrical meters. Figure 3 presents the input data for the buildings in Zurich and Chicago, while Figure 4 presents the input data for the buildings in New York and the second Chicago building. All are from academic campuses and, in terms of absolute electrical energy load, New York uses the most energy, followed by Zurich and Chicago in a similar range, with Chicago 2 having the least energy needs.
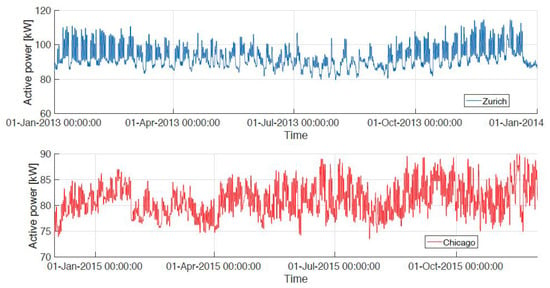
Figure 3.
Input data for LSTM training and validation: Zurich and Chicago buildings.
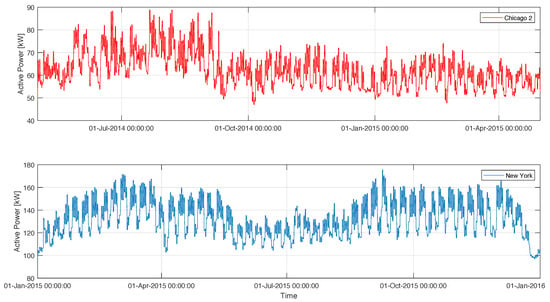
Figure 4.
Input data for LSTM training and validation: Chicago 2 and New York buildings.
The classical LSTM algorithm was implemented for experiment assessment and forecasting. The base network architecture consisted of one sequence input layer, one hidden LSTM layer of varying unit numbers, one fully connected layer, and one regression output layer for the resulting forecasted output value. Each network has a different configuration represented by the number of hidden units from the LSTM layer. Based on this, the following network structures were implemented; in total, 25 networks were trained, validated, and evaluated: C-0, C-1, C-2, C-3, C-4, Z-0, Z-1, Z-2, Z-3, Z-4, C2-0, C2-1, C2-2, C2-3, C2-4, NY-0, NY-1, NY-2, NY-3, NY-4. In our case, the identifier before the dash sign reflects the analyzed building: C stands for the Chicago building, Z for the Zurich building, for the second building from Chicago, and for the New York building. The number after the building identifier marks the complexity of the network in terms of hidden units of LSTM that were implemented in the hidden layer, using a linear increase. This ranges from five hidden units for ID 0, 25 hidden units for ID 1, 50 hidden units for ID 2, 100 hidden units for ID 3, and, finall, y 125 hidden units for ID 4.
The optimization method of choice for training the neural networks was through the Adaptive Moment Estimation (ADAM) algorithm [25]. This is an often-used general optimization method for first-order gradient-based optimisation of stochastic objective functions with momentum. One of the key optimization parameters for carrying out neural-network training is learning rate. This allows implementing a trade-off between the speed of the processing and its precision, in the sense that a large learning rate can in many situations miss the optimal value of the objective metric. In our case, the learning rate was established through an empirical adjustment process. The initial value was set at 0.1, followed by subsequent decreases with a factor of 0.2 every 200 iterations. From observing the performance over multiple initial training runs, a second parameter, the number of training iterations, was set at 200.
Figure 5, Figure 6, Figure 7 and Figure 8 present the prediction response by the LSTM neural network, with 50 hidden units in the LSTM layer versus real data for the Chicago building and the Zurich building, respectively. The plots demonstrate that the forecasting performance of the LSTM models for the testing datasets was very good.
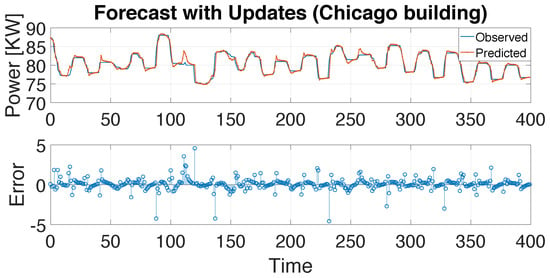
Figure 5.
Building load forecasting with 50 unit recurrent neural network (RNN) LSTM: Chicago.
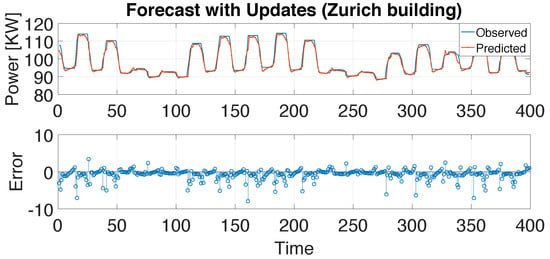
Figure 6.
Building load forecasting with 50 unit RNN LSTM: Zurich.
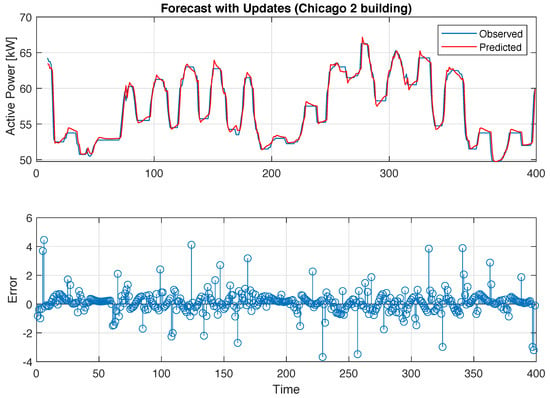
Figure 7.
Building load forecasting with 50 unit RNN LSTM: Chicago 2.
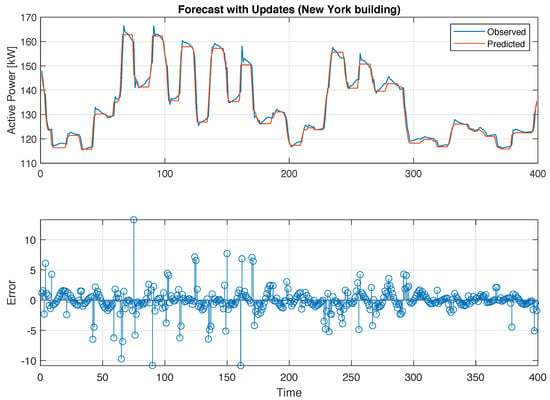
Figure 8.
Building load forecasting with 50 unit RNN LSTM: New York.
To evaluate the prediction models, three performance metrics were used: Mean Squared Error (MSE), Root MSE (RMSE), and Mean Absolute Percentage Error (MAPE). In addition, we included the Coefficient of Variation (CV) of the RMSE based on the evaluation discussed in [9]. The metrics were computed according to the following equations:
where n represents the number of samples, and stand for the actual data and predicted data, respectively.
A summary of the experiment results is listed in Table 1, Table 2, Table 3 and Table 4 show These include: the error metrics MSE, RMSE, CV (RMSE) and MAPE as well as training/computation time for the previously defined RNN LSTM networks. The figures in bold style mark the best results achieved.

Table 1.
Summary of accuracy metrics for RNN LSTM model forecasting: Chicago. Note: MSE, Mean Squared Error; RMSE, Root MSE; CV, Coefficient of Variation; MAPE, Mean Absolute Percentage Error.

Table 2.
Summary of accuracy metrics for RNN LSTM model forecasting: Zurich.

Table 3.
Summary of accuracy metrics for RNN LSTM model forecasting: Chicago 2.

Table 4.
Summary of accuracy metrics for RNN LSTM model forecasting: New York.
The main outcome of the learning models, as reflected by the aggregate performance metrics from Table 1, Table 2, Table 3 and Table 4, pinpoints the best network architecture for all four testing scenarios to be the one with 50 LSTM units in the hidden layer. Figure 9 also presents the evolution of the MAPE and computation time for each building over each defined network. It can be seen that computation time increases linearly with the number of neurons in the LSTM layers, which can be helpful for deploying more tests. We can affirm that, until we achieve the best value for MAPE, 50 neurons in the LSTM layer, this is a good compromise, but after this point, computation time increases too much without better performance. The reference computer includes a 2.6 GHz seventh-generation Intel i5 CPU, 8 GB of RAM, and a solid-state disk, with Windows 10 as the operating system. This is the baseline for the reported computation/training time for all test cases. Algorithms were written and run under MATLAB, version R2018a, which provides a robust high-level technical programming environment. We leveraged built-in functions from the machine- and deep-learning toolboxes, as well as dedicated scripts for data ingestion and preprocessing.
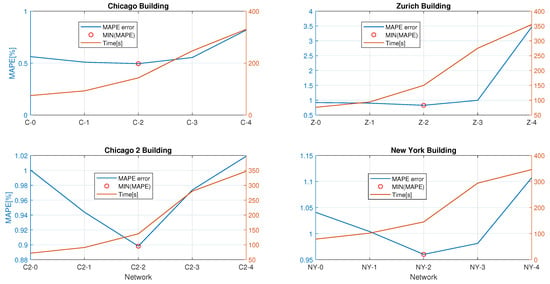
Figure 9.
Computation time vs. MAPE evolution for each building.
Table 5 provides a summary of the statistical indicators for the comparable relative accuracy metrics: CV (RMSE) and MAPE over the tested scenarios, four buildings with five networks each. The reported statistical indicators are: minimum, maximum, mean , standard deviation , skewness, and kurtosis.

Table 5.
Statistical indicators for relative performance metrics, CV (RMSE) and MAPE.
Performance evolution during training for the Zurich and New York buildings is graphically depicted in Figure 10 and Figure 11. The graphic represents the gradual decrease in the RMSE metric over 200 iterations, with the worst- and best-case scenarios. In the first case, the worst performance is seen on the Z4 network, which tried to overfit the data given the more complex structure. As such, the RMSE presented multiple increases and decreases over the training horizon. In the positive case, Z2, we observed convergence in just under 100 training iterations, as compared to the previous 120 iterations needed by the denser network. Similar networks were represented for the New York dataset. Different behavior was observed in this case, with the best-case convergence of the RMSE being slower at the beginning, with a more gentle slope of the graphic over the first steps.
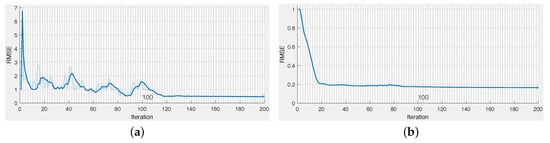
Figure 10.
RMSE accuracy during training: Zurich. (a) Z-4 (b) Z-2.
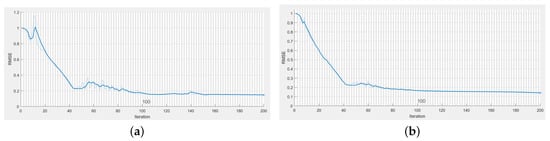
Figure 11.
RMSE accuracy during training: New York, (a) NY-4 (b) NY-2.
5. Conclusions
We presented an application of sequence models, implemented by means of a Recurrent Neural Network with Long Short-Term Memory units, for electrical-energy load forecasting in large commercial buildings. Results showed good performance for modelling and forecasting accuracy while evaluating against typical time series-based metrics, namely, MSE, RMSE, CV-RMSE and MAPE. Generally, based on the number of layers that were selected, a value of around 50 LSTM units in the hidden layer was found to yield the best estimates for the underlying time series. Beyond this, the network had a strong tendency to overfit the input data and perform poorly on the testing samples. The results were evaluated on year-long selected building-energy traces from a reference benchmarking dataset, and the MAPE relative metric was found to be between and for all investigated buildings. The CV (RMSE) was stable between the various scenarios.
For future work, we aim to validate the presented approaches in this article on the full BUDS dataset of 508 buildings using an appropriate that goes beyond the available resources on a single local machine or server. For this, the use of a cloud based on a GPU computing infrastructure is planned in order to reach a feasible computing time. Similar to the approach [26], hardware-in-the-loop architecture is envisioned to deploy the resulting black-box models on an embedded device for inference while streaming data from a real building. In such scenarios, the models would be pretrained with only partial retraining, and model updates locally based on continuously streamed energy-consumption values from local smart meters. Other types of applications can stand to benefit from the described approach, such as several industry applications for energy and cost optimization in smart-production environments.
Author Contributions
Formal analysis, I.S.; investigation, C.N.; methodology, C.N.; software, G.S.; supervision, I.F.; validation, I.F.; writing—original draft, G.S.; writing—review and editing, I.S.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ADAM | Adaptive Moment Estimation |
| ARIMA | Autoregressive Integrated Moving Average |
| BPTT | Back-Propagation Through Time |
| CV (RMSE) | Coefficient of Variation of RMSE |
| LSTM | Long Short-Term Memory |
| DL | Deep Learning |
| GRU | Gated Recurrent Unit |
| MAPE | Mean Absolute Percentage Error |
| MSE | Mean Squared Error |
| RMSE | Root Mean Squared Error |
| RNN | Recurrent Neural Network |
| RTRL | Real-Time Recurrent Learning |
References
- Berardi, U. Building Energy Consumption in US, EU, and BRIC Countries. Procedia Eng. 2015, 118, 128–136. [Google Scholar] [CrossRef]
- Djenouri, D.; Laidi, R.; Djenouri, Y.; Balasingham, I. Machine Learning for Smart Building Applications: Review and Taxonomy. ACM Comput. Surv. 2019, 52, 24:1–24:36. [Google Scholar] [CrossRef]
- Nichiforov, C.; Stamatescu, G.; Stamatescu, I.; Calofir, V.; Fagarasan, I.; Iliescu, S.S. Deep Learning Techniques for Load Forecasting in Large Commercial Buildings. In Proceedings of the 2018 22nd International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 10–12 October 2018; pp. 492–497. [Google Scholar] [CrossRef]
- Fayaz, M.; Shah, H.; Aseere, A.M.; Mashwani, W.K.; Shah, A.S. A Framework for Prediction of Household Energy Consumption Using Feed Forward Back Propagation Neural Network. Technologies 2019, 7, 30. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, M.; Ren, F. Learning Customer Behaviors for Effective Load Forecasting. IEEE Trans. Knowl. Data Eng. 2019, 31, 938–951. [Google Scholar] [CrossRef]
- Aminikhanghahi, S.; Wang, T.; Cook, D.J. Real-Time Change Point Detection with Application to Smart Home Time Series Data. IEEE Trans. Knowl. Data Eng. 2019, 31, 1010–1023. [Google Scholar] [CrossRef]
- Jin, M.; Bekiaris-Liberis, N.; Weekly, K.; Spanos, C.J.; Bayen, A.M. Occupancy Detection via Environmental Sensing. IEEE Trans. Autom. Sci. Eng. 2018, 15, 443–455. [Google Scholar] [CrossRef]
- Rahman, A.; Srikumar, V.; Smith, A.D. Predicting electricity consumption for commercial and residential buildings using deep recurrent neural networks. Appl. Energy 2018, 212, 372–385. [Google Scholar] [CrossRef]
- Fan, C.; Sun, Y.; Zhao, Y.; Song, M.; Wang, J. Deep learning-based feature engineering methods for improved building energy prediction. Appl. Energy 2019, 240, 35–45. [Google Scholar] [CrossRef]
- Zhong, H.; Wang, J.; Jia, H.; Mu, Y.; Lv, S. Vector field-based support vector regression for building energy consumption prediction. Appl. Energy 2019, 242, 403–414. [Google Scholar] [CrossRef]
- Harish, V.; Kumar, A. Reduced order modeling and parameter identification of a building energy system model through an optimization routine. Appl. Energy 2016, 162, 1010–1023. [Google Scholar] [CrossRef]
- Capizzi, G.; Sciuto, G.L.; Cammarata, G.; Cammarata, M. Thermal transients simulations of a building by a dynamic model based on thermal-electrical analogy: Evaluation and implementation issue. Appl. Energy 2017, 199, 323–334. [Google Scholar] [CrossRef]
- Nichiforov, C.; Stamatescu, I.; Făgărăşan, I.; Stamatescu, G. Energy consumption forecasting using ARIMA and neural network models. In Proceedings of the 2017 5th International Symposium on Electrical and Electronics Engineering (ISEEE), Galaţi, Romania, 20–22 October 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Nichiforov, C.; Stamatescu, G.; Stamatescu, I.; Fagarasan, I.; Iliescu, S.S. Intelligent Load Forecasting for Building Energy Management. In Proceedings of the 2018 14th IEEE International Conference on Control and Automation (ICCA), Anchorage, AK, USA, 12–15 June 2018. [Google Scholar]
- Stamatescu, I.; Arghira, N.; Fagarasan, I.; Stamatescu, G.; Iliescu, S.S.; Calofir, V. Decision Support System for a Low Voltage Renewable Energy System. Energies 2017, 10, 118. [Google Scholar] [CrossRef]
- Werbos, P.J. Backpropagation through time: What it does and how to do it. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef]
- Williams, R.J.; Zipser, D. Gradient-based learning algorithms for recurrent networks and their computational complexity. In Developments in Connectionist Theory. Backpropagation: Theory, Architectures, and Applications; Erlbaum Associates Inc.: Hillsdale, NJ, USA, 1995; pp. 433–486. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Marino, D.L.; Amarasinghe, K.; Manic, M. Building Energy Load Forecasting using Deep Neural Networks. arXiv 2016, arXiv:1610.09460. [Google Scholar]
- Srivastava, S.; Lessmann, S. A comparative study of LSTM neural networks in forecasting day-ahead global horizontal irradiance with satellite data. Sol. Energy 2018, 162, 232–247. [Google Scholar] [CrossRef]
- Chung, J.; Gülçehre, Ç.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Ugurlu, U.; Oksuz, I.; Tas, O. Electricity Price Forecasting Using Recurrent Neural Networks. Energies 2018, 11, 1255. [Google Scholar] [CrossRef]
- Miller, C.; Meggers, F. The Building Data Genome Project: An open, public data set from non-residential building electrical meters. Energy Procedia 2017, 122, 439–444. [Google Scholar] [CrossRef]
- Broesch, J.D. Chapter 7—Applications of DSP. In Digital Signal Processing; Broesch, J.D., Ed.; Instant Access, Newnes: Burlington, NJ, USA, 2009; pp. 125–134. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Stamatescu, G.; Stamatescu, I.; Arghira, N.; Făgărăsan, I.; Iliescu, S.S. Embedded networked monitoring and control for renewable energy storage systems. In Proceedings of the 2014 International Conference on Development and Application Systems (DAS), Suceava, Romania, 15–17 May 2014; pp. 1–6. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).