An Efficient Monte-Carlo Simulation for the Dynamic Reliability Analysis of Jacket Platforms Subjected to Random Wave Loads
Abstract
1. Introduction
2. Equation of Motion
3. Explicit Formulation of Structural Responses
3.1. Explicit Expressions of Structural Responses
3.2. Truncated Explicit Expressions of Structural Responses
4. System Reliability Analysis with MCS Based on ETDM
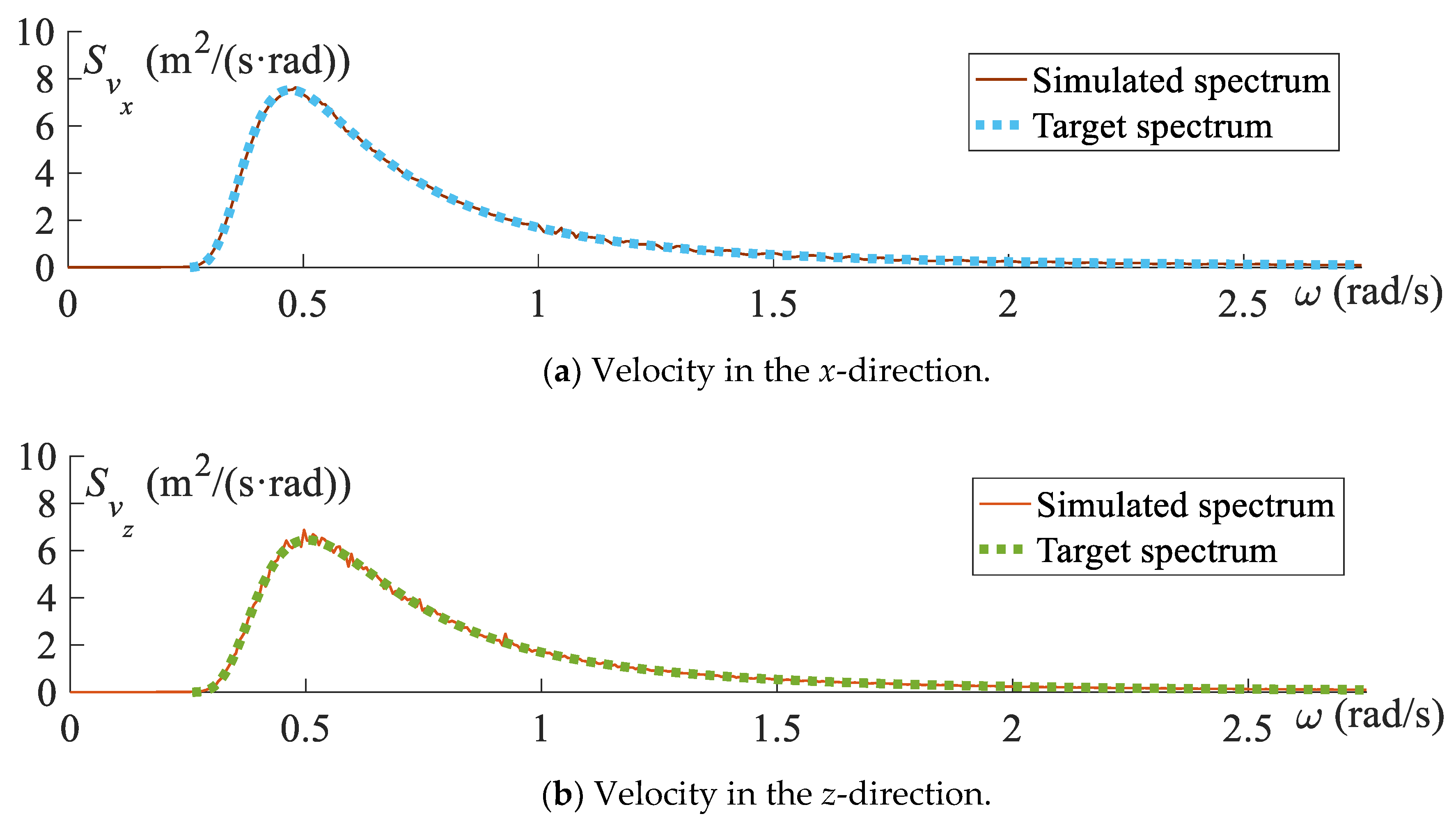
4.1. Simulation of Wave–Particle Velocities and Accelerations
4.2. System Limit-State Function
4.3. ETDM-Based MCS for System Reliability Analysis
5. Engineering Example
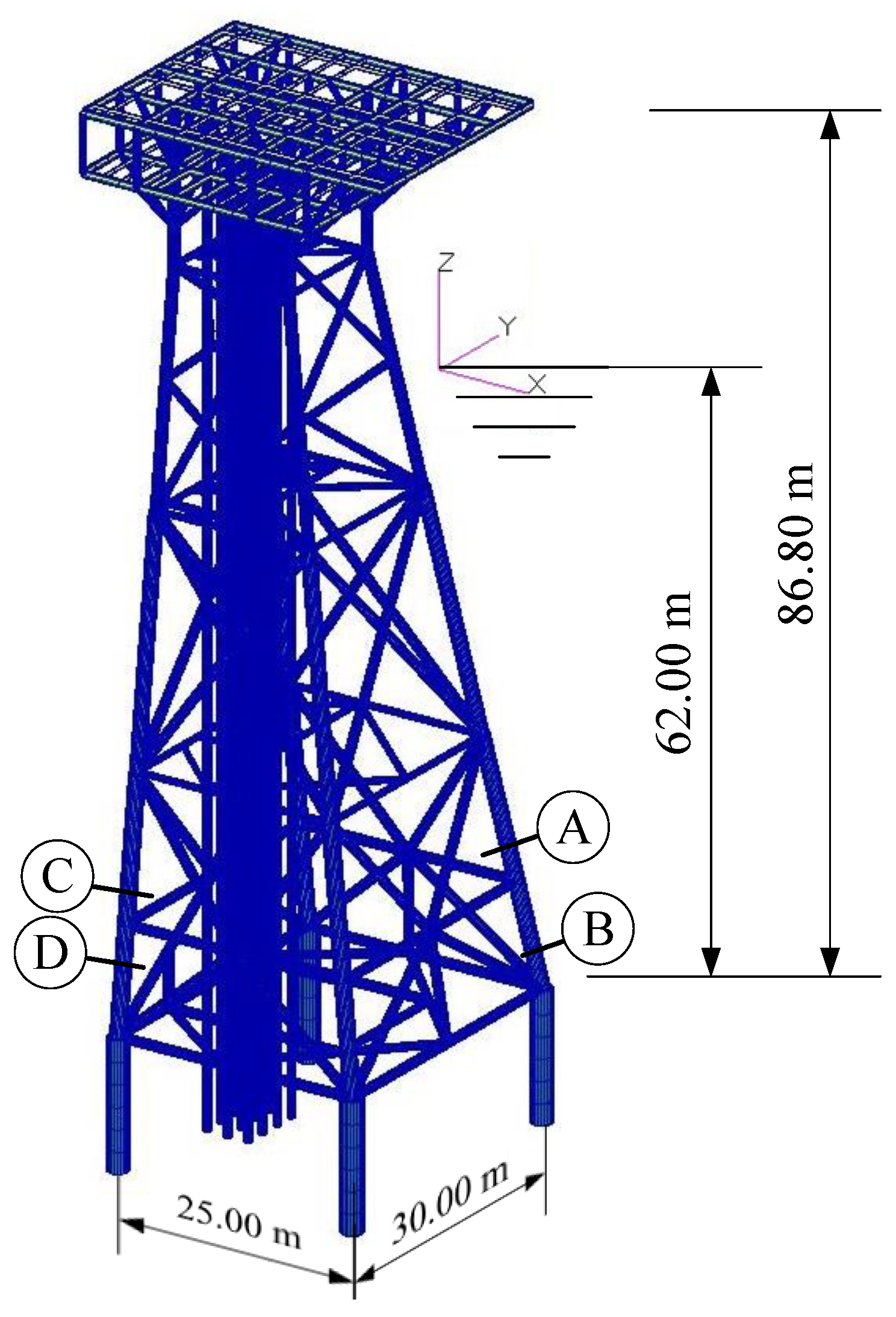
5.1. Jacket Platform and Sea Condition
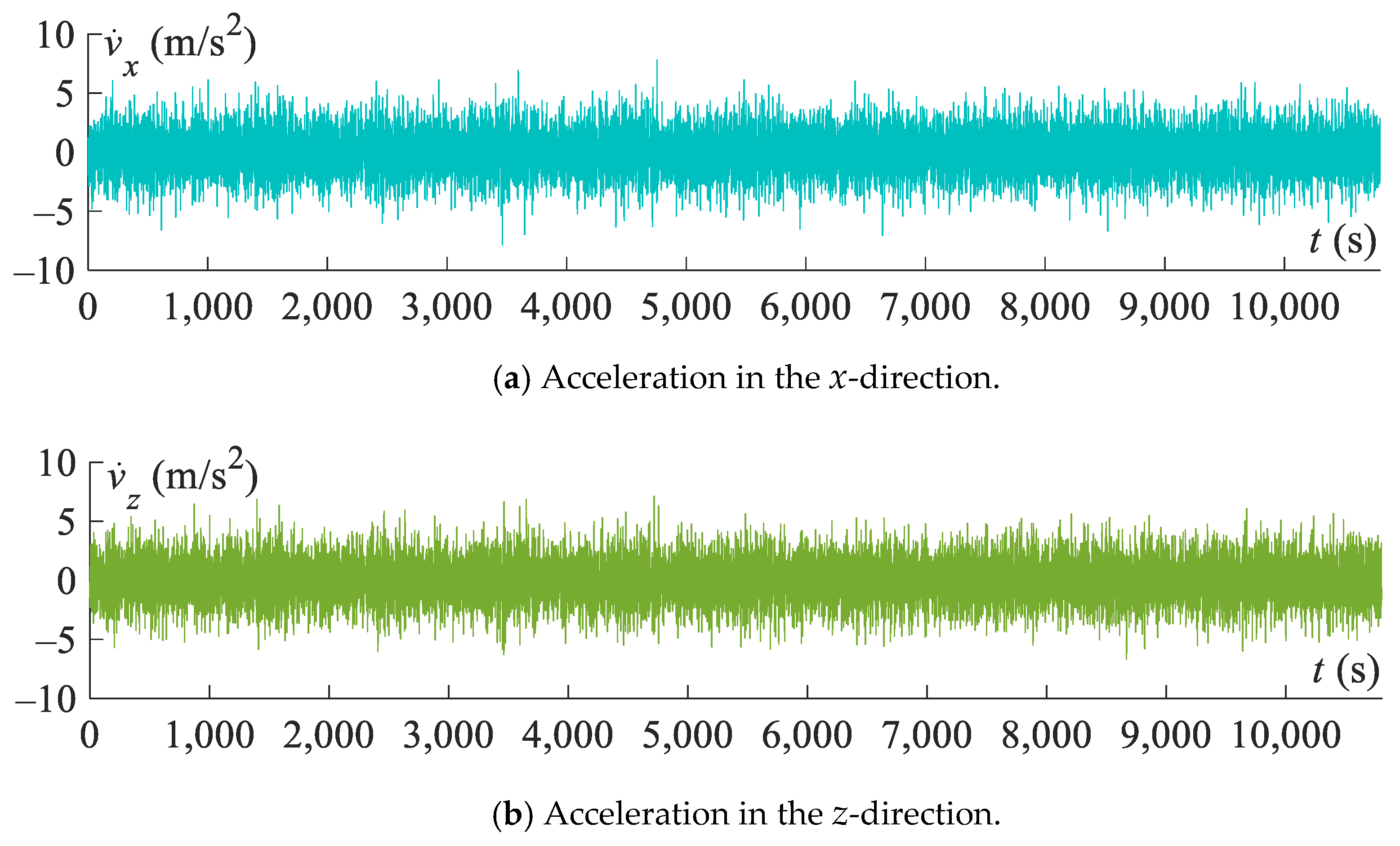
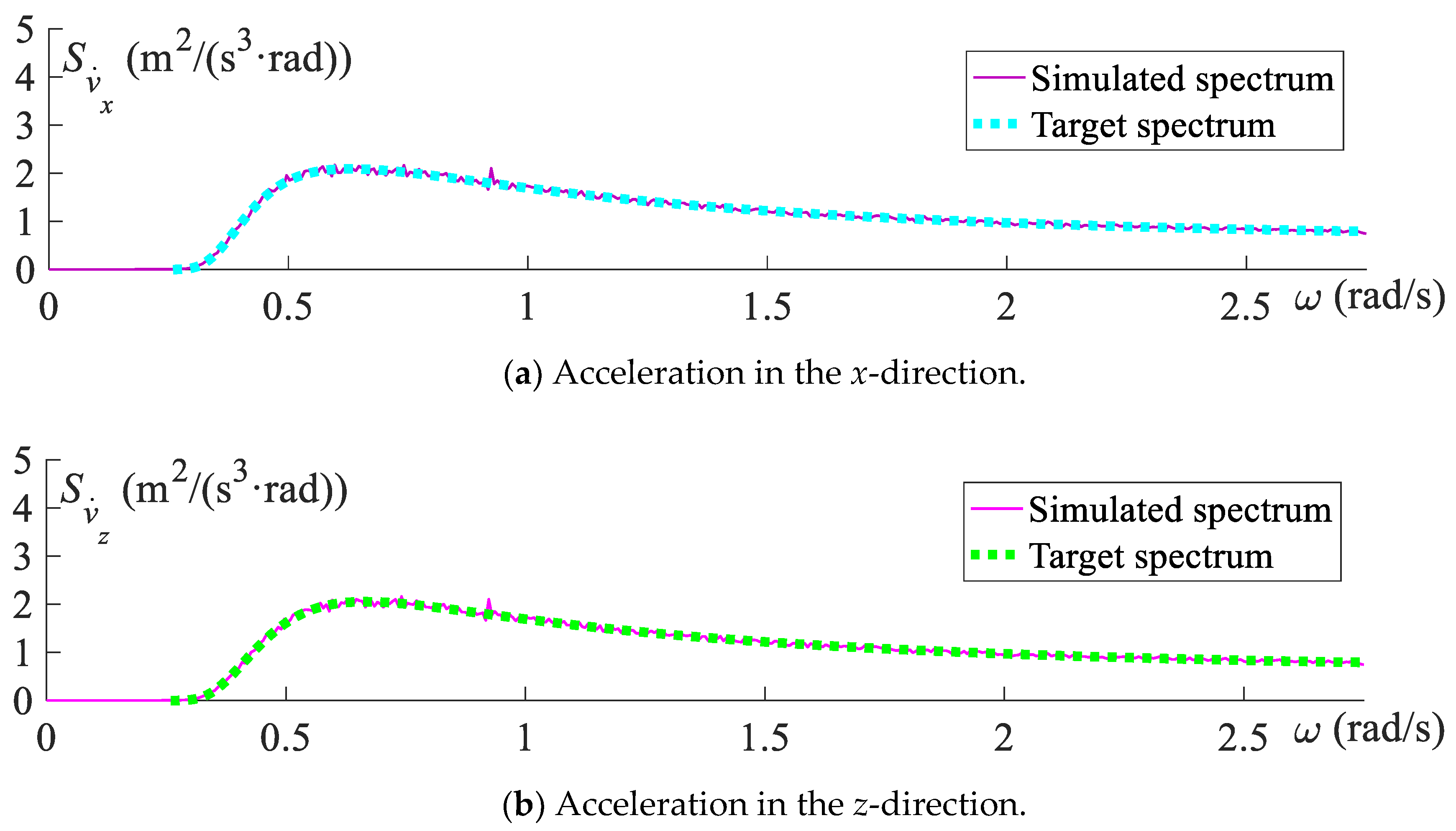
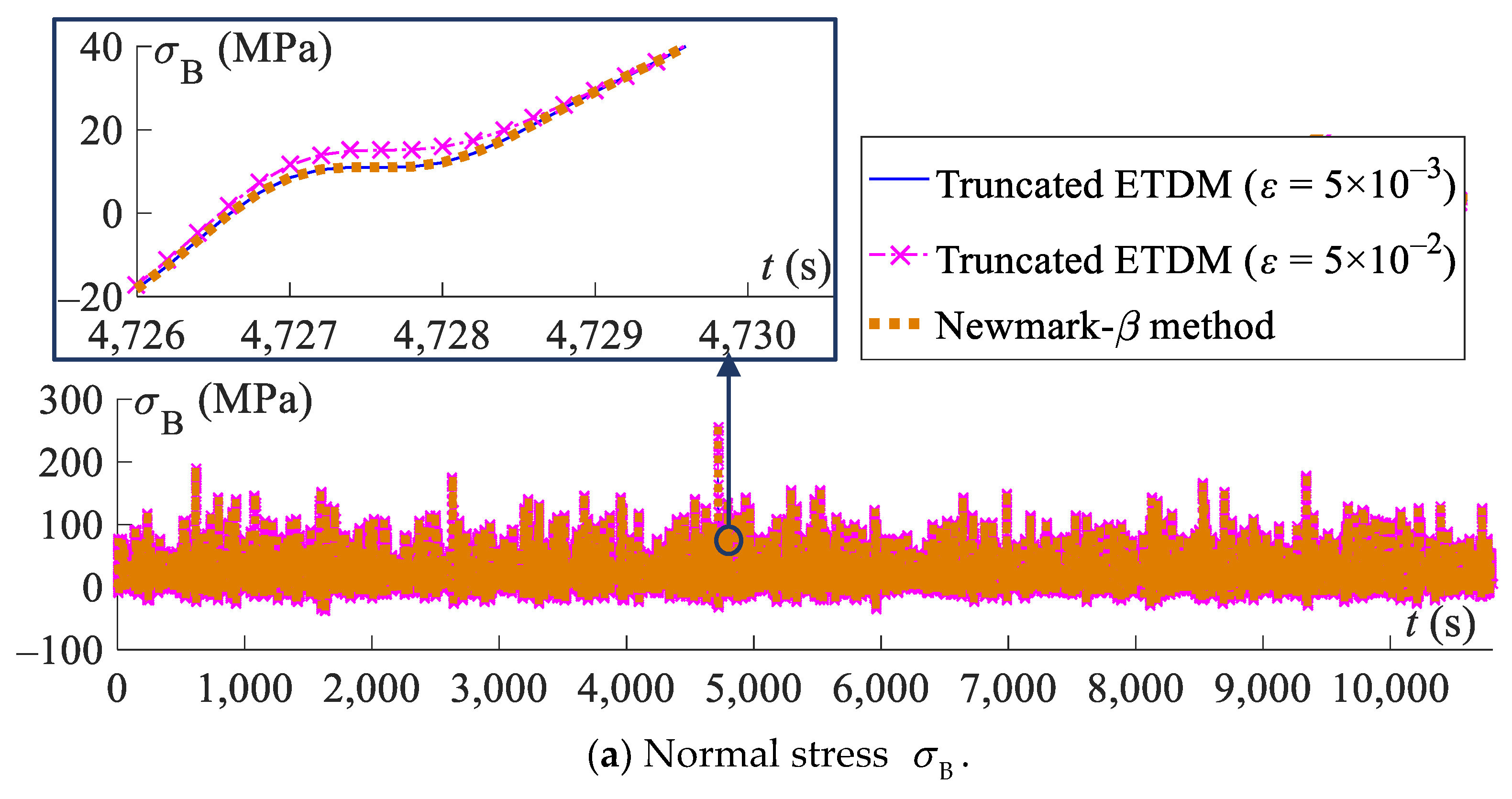
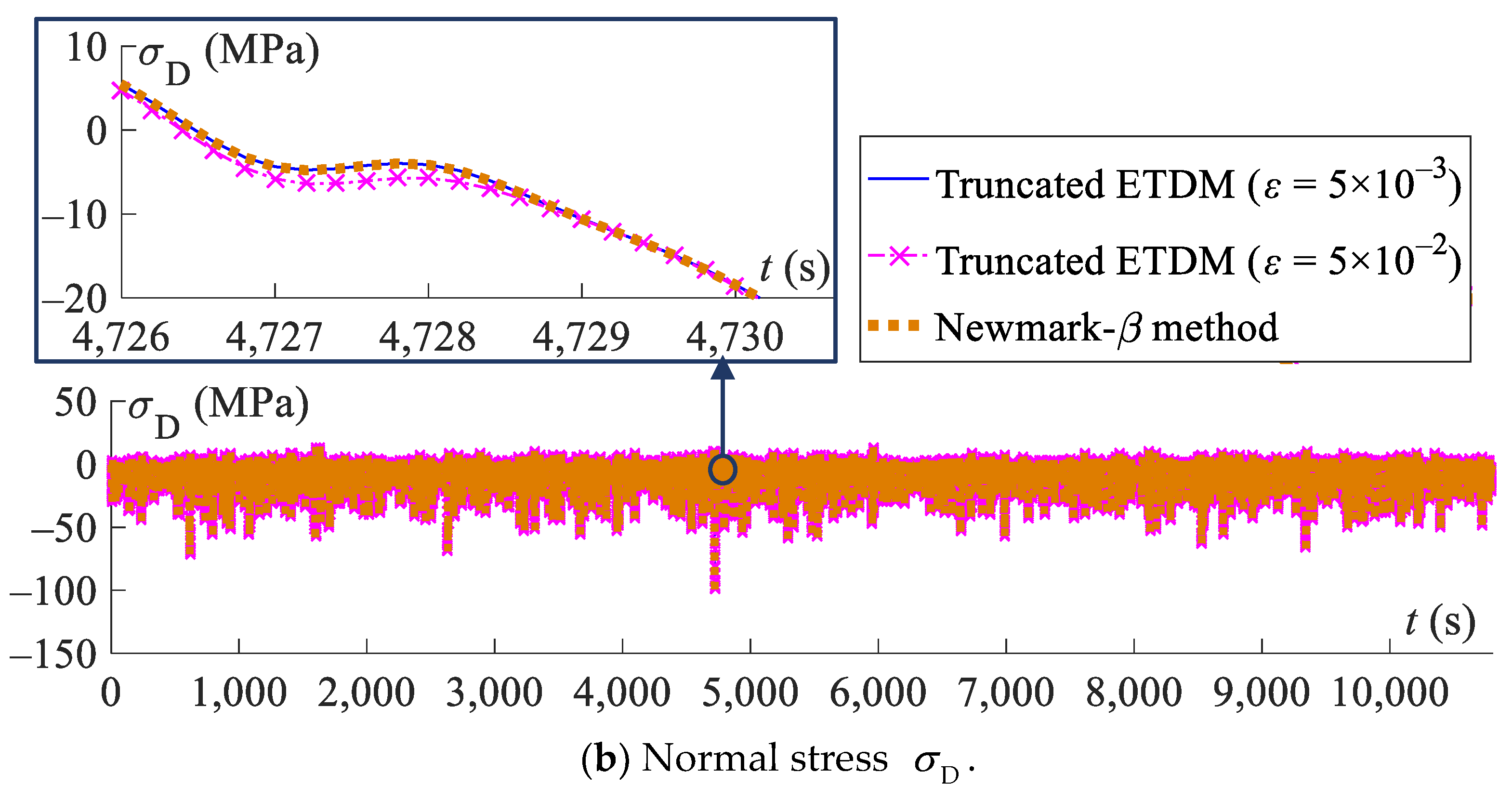
5.2. Three-Hour-History Analysis of Jacket Platform with ETDM
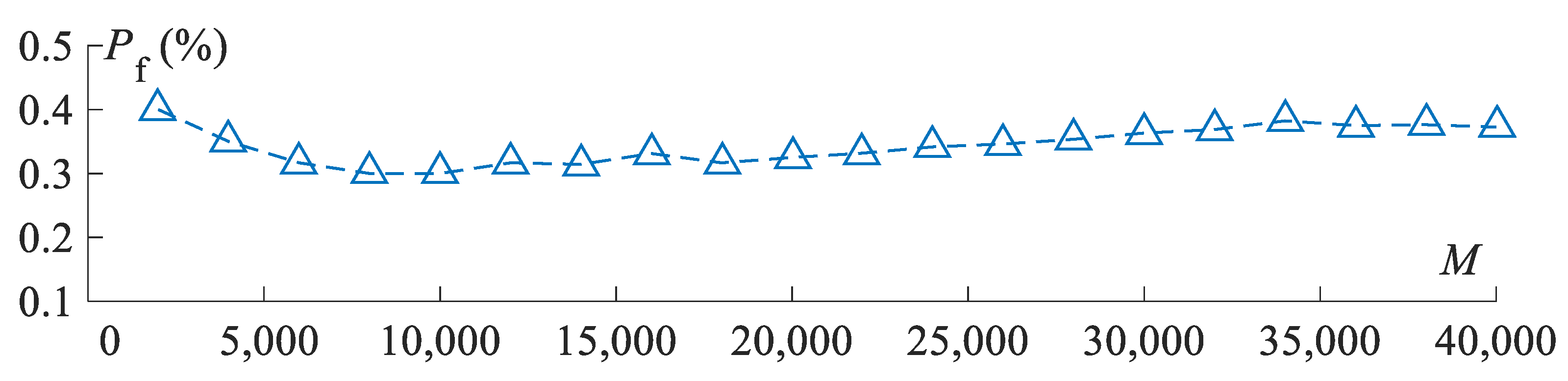
5.3. Dynamic Reliability Analysis of Jacket Platform with ETDM-Based MCS
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- American Petroleum Institute. Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms—Load and Resistance Factor Design, RP 2A-LRFD, 1st ed.; American Petroleum Institute: Washington, DC, USA, 1993. [Google Scholar]
- Onoufriou, T.; Forbes, V.J. Developments in structural system reliability assessment of fixed steel offshore platforms. Reliab. Eng. Syst. Saf. 2001, 71, 189–199. [Google Scholar] [CrossRef]
- Murotsu, Y.; Okada, H.; Taguchi, K.; Grimmelt, M.; Yonezawa, M. Automatic generation of stochastically dominant failure modes of frame structures. Struct. Saf. 1984, 2, 17–25. [Google Scholar] [CrossRef]
- Feng, Y.S. Enumerating significant failure modes of a structural system by using criterion methods. Comput. Struct. 1988, 30, 1152–1157. [Google Scholar] [CrossRef]
- Dier, A.F.; Morandi, A.C.; Smith, D.; Birkinshaw, M.; Dixon, A. A comparison of jacket and jack-up structural reliability. Mar. Struct. 2001, 14, 507–521. [Google Scholar] [CrossRef]
- Bai, Y.; Cao, Y.; Kim, Y.; Yang, Y.; Jiang, H. Time-dependent reliability assessment of offshore jacket platforms. Ships Offshore Struct. 2015, 11, 591–602. [Google Scholar] [CrossRef]
- Alibrandi, U.; Alani, A.M.; Ricciardi, G. A new sampling strategy for SVM-based response surface for structural reliability analysis. Probabilistic Eng. Mech. 2015, 41, 1–12. [Google Scholar] [CrossRef]
- Borgman, L.E. Random hydrodynamic forces on objects. Ann. Math. Stat. 1967, 38, 37–51. [Google Scholar] [CrossRef]
- Borgman, L.E. Spectral analysis of ocean wave forces on piling. J. Waterw. Harbors Div. 1967, 93, 129–156. [Google Scholar] [CrossRef]
- Kawano, K.; Venkataramana, K. Dynamic response and reliability analysis of large offshore structures. Comput. Methods Appl. Mech. Eng. 1999, 168, 255–272. [Google Scholar] [CrossRef]
- Ghazizadeh, S.; Barbato, M.; Tubaldi, E. New analytical solution of the first-passage reliability problem for linear oscillators. J. Eng. Mech. 2011, 138, 695–706. [Google Scholar] [CrossRef]
- Naess, A. Approximate first-passage and extremes of narrow-band Gaussian and non-Gaussian random vibrations. J. Sound Vib. 1990, 138, 365–380. [Google Scholar] [CrossRef]
- Chen, J.J.; Duan, B.Y.; Zeng, Y.G. Study on dynamic reliability analysis of the structures with multi-degree-of-freedom. Comput. Struct. 1997, 62, 877–881. [Google Scholar] [CrossRef]
- American Petroleum Institute. Recommended Practice for Planning, Designing, and Constructing Fixed Offshore Platforms–Working Stress Design, API RP2A-WSD, 21st ed.; American Petroleum Institute: Washington, DC, USA, 2000. [Google Scholar]
- Det Norske Veritas. Environmental Conditions and Environmental Loads, DNV-RP-C205; Det Norske Veritas: Oslo, Norway, 2014. [Google Scholar]
- Au, S.K.; Beck, J.L. First excursion probabilities for linear systems by very efficient importance sampling. Probabilistic Eng. Mech. 2001, 16, 193–207. [Google Scholar] [CrossRef]
- Bichon, B.J.; Eldred, M.S.; Swiler, L.P.; Mahadevan, S.; McFarland, J.M. Efficient global reliability analysis for nonlinear implicit performance functions. AIAA J. 2008, 46, 2459–2468. [Google Scholar] [CrossRef]
- Valdebenito, M.A.; Jensen, H.A.; Labarca, A.A. Estimation of first excursion probabilities for uncertain stochastic linear systems subject to Gaussian load. Comput. Struct. 2014, 138, 36–48. [Google Scholar] [CrossRef]
- Au, S.K.; Beck, J.L. Estimation of small failure probabilities in high dimensions by subset simulation. Probabilistic Eng. Mech. 2001, 16, 263–277. [Google Scholar] [CrossRef]
- Ching, J.; Au, S.K.; Beck, J.L. Reliability estimation for dynamical systems subject to stochastic excitation using subset simulation with splitting. Comput. Methods Appl. Mech. Eng. 2005, 194, 1557–1579. [Google Scholar] [CrossRef]
- Norouzi, M.; Nikolaidis, E. Integrating subset simulation with probabilistic re-analysis to estimate reliability of dynamic systems. Struct. Multidiscip. Optim. 2013, 48, 533–548. [Google Scholar] [CrossRef]
- Tromans, P.S.; Anaturk, A.R.; Hagemeijer, P. A new model for the kinematics of large ocean waves-application as a design wave. In Proceedings of the 1st International Offshore and Polar Engineering Conference, Edinburgh, UK, 11–16 August 1991; pp. 64–71. [Google Scholar]
- Cassidy, M.J.; Eatock Taylor, R.; Houlsby, G.T. Analysis of jack-up units using a Constrained NewWave methodology. Appl. Ocean Res. 2001, 23, 221–234. [Google Scholar] [CrossRef]
- Cassidy, M.J.; Houlsby, G.T.; Eatock Taylor, R. Probabilistic models applicable to the short-term extreme response analysis of jack-up platforms. J. Offshore Mech. Arct. Eng. 2003, 125, 249–263. [Google Scholar] [CrossRef]
- Mirzadeh, J.; Kimiaei, M.; Cassidy, M.J. A framework to efficiently calculate the probability of failure of dynamically sensitive structures in a random sea. Ocean Eng. 2015, 110, 215–226. [Google Scholar] [CrossRef]
- Zeinoddini, M.; Nikoo, H.M.; Estekanchi, H. Endurance Wave Analysis (EWA) and its application for assessment of offshore structures under extreme waves. Appl. Ocean Res. 2012, 37, 98–110. [Google Scholar] [CrossRef]
- Zeinoddini, M.; Namin, Y.Y.; Nikoo, H.M.; Estekanchi, H.; Kimiaei, M. An EWA framework for the probabilistic-based structural integrity assessment of offshore platforms. Mar. Struct. 2018, 59, 60–79. [Google Scholar] [CrossRef]
- Su, C.; Liu, X.; Li, B.; Huang, Z. Inelastic response analysis of bridges subjected to non-stationary seismic excitations by efficient MCS based on explicit time-domain method. Nonlinear Dyn. 2018, 94, 2097–2114. [Google Scholar] [CrossRef]
- Su, C.; Li, B.; Chen, T.; Dai, X. Stochastic optimal design of nonlinear viscous dampers for large-scale structures subjected to non-stationary seismic excitations based on dimension-reduced explicit method. Eng. Struct. 2018, 175, 217–230. [Google Scholar] [CrossRef]
- Lin, W.; Su, C.; Tang, Y.H. Explicit time-domain approach for random vibration analysis of jacket platforms subjected to wave loads. J. Mar. Sci. Eng. 2020, 8, 1001. [Google Scholar] [CrossRef]
- Sarpkaya, T. In-line forces on a cylinder translating in oscillatory flow. Appl. Ocean Res. 1985, 7, 188–196. [Google Scholar] [CrossRef]
- Rahman, M. Wave diffraction by large offshore structures: An exact second-order theory. Appl. Ocean Res. 1984, 6, 90–100. [Google Scholar] [CrossRef]
- Lighthill, M.J. Fundamentals concerning wave loading on offshore structures. J. Fluid Mech. 1986, 173, 667–681. [Google Scholar] [CrossRef]
- Santo, H.; Taylor, P.H.; Day, A.H.; Nixon, E.; Choo, Y.S. Blockage and relative velocity Morison forces on a dynamically-responding jacket in large waves and current. J. Fluids Struct. 2018, 81, 161–178. [Google Scholar] [CrossRef]
- Borgman, L.E. Computation of the ocean-wave forces on inclined cylinders. Trans. Am. Geophys. Union 1958, 39, 885–888. [Google Scholar] [CrossRef]
- Charkrabarti, S.K. Laboratory generated waves and wave theories. J. Waterw. Port Coast. Ocean Eng. Div. 1980, 106, 349–368. [Google Scholar]
- Shinozuka, M. Monte Carlo solution of structural dynamics, Comput. Struct. 1972, 2, 855–874. [Google Scholar] [CrossRef]
- Su, C.; Han, D.J.; Yan, Q.S.; Au, F.T.K.; Tham, L.G.; Lee, P.K.K.; Lam, K.M.; Wong, K.Y. Wind-induced vibration analysis of the Hong Kong Ting Kau Bridge. Proc. Inst. Civ. Eng. Struct. Build. 2003, 156, 263–272. [Google Scholar] [CrossRef]
- Nash, A.W. Schaum’s Outline of Theory and Problems of Statics and Mechanics of Material; McGraw-Hill: New York, NY, USA, 1983. [Google Scholar]
- Xian, J.H.; Su, C.; Guo, H.Z. Seismic reliability analysis of energy-dissipation structures by combining probability density evolution method and explicit time-domain method. Struct. Saf. 2021, 88, 102010. [Google Scholar] [CrossRef]
- American Bureau of Shipping. Guidance Notes on Dynamic Analysis Procedure for Self-Elevating Drilling Units; American Bureau of Shipping: Houston, TX, USA, 2004. [Google Scholar]
- Wang, D.J. Hydrodynamic Behavior of Large Moored Offshore Structures during Adverse Weather Conditions. Ph.D. Thesis, Hong Kong Polytechnic, Hong Kong, China, 1993. [Google Scholar]
- Rubinstein, R.Y. Simulation and the Monte-Carlo Method; John Wiley & Sons Inc.: New York, NY, USA, 1981. [Google Scholar]
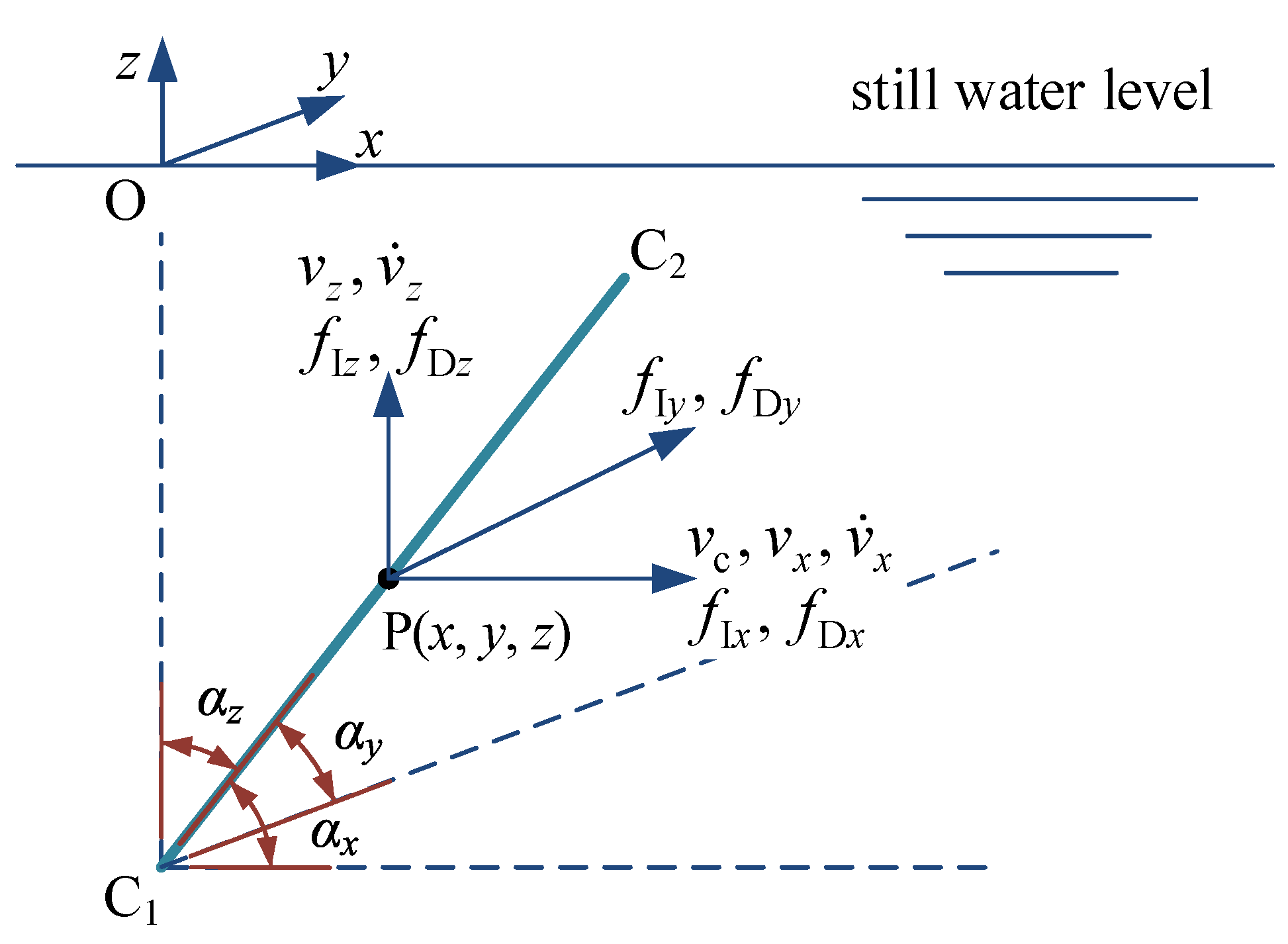


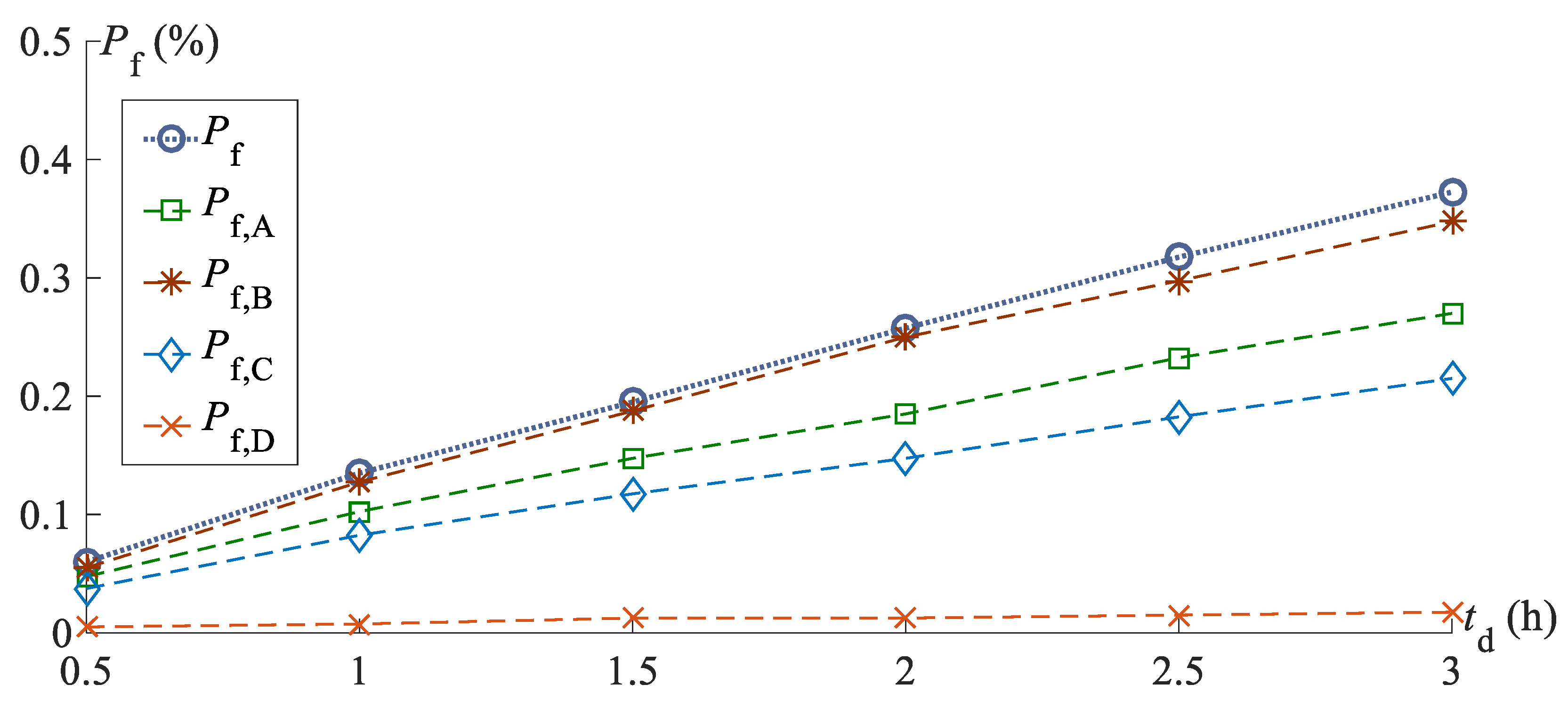
| Method | Elapsed Time (s) |
|---|---|
| Truncated ETDM | 56.45 |
| Newmark-β method | 2980 |
| Calculation of Coefficient Matrices in Equation (15) (s) | MCS Based on Equation (15) (M = 30,000) (s) | Total (s) |
|---|---|---|
| 56 | 13,500 | 13,556 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, W.; Su, C. An Efficient Monte-Carlo Simulation for the Dynamic Reliability Analysis of Jacket Platforms Subjected to Random Wave Loads. J. Mar. Sci. Eng. 2021, 9, 380. https://doi.org/10.3390/jmse9040380
Lin W, Su C. An Efficient Monte-Carlo Simulation for the Dynamic Reliability Analysis of Jacket Platforms Subjected to Random Wave Loads. Journal of Marine Science and Engineering. 2021; 9(4):380. https://doi.org/10.3390/jmse9040380
Chicago/Turabian StyleLin, Wei, and Cheng Su. 2021. "An Efficient Monte-Carlo Simulation for the Dynamic Reliability Analysis of Jacket Platforms Subjected to Random Wave Loads" Journal of Marine Science and Engineering 9, no. 4: 380. https://doi.org/10.3390/jmse9040380
APA StyleLin, W., & Su, C. (2021). An Efficient Monte-Carlo Simulation for the Dynamic Reliability Analysis of Jacket Platforms Subjected to Random Wave Loads. Journal of Marine Science and Engineering, 9(4), 380. https://doi.org/10.3390/jmse9040380






