1. Introduction
The propeller is the main part of a propulsion system by which engine power can move the marine vessels. Marine propellers work in an intense and complicated flow field and high-risk work conditions; those two aspects must be considered to design a new propeller. First, evaluating the hydrodynamic coefficients like efficiency and thrust and torque coefficient. Second, strength due to loads and manufactured material. The propeller blade strength role is essential in the cavitation phenomenon and propellers’ efficiency. In essence, the blades’ structural behavior has fully interacted with the hydrodynamic propulsion qualification, particularly propeller efficiency. There are two main approaches for hydrodynamic calculations of marine propellers. The first, the inviscid numerical methodologies, involve the lifting line method, the boundary element method (BEM) [
1], and the vortex lattice method (VLM) [
2]. The second is computational fluid dynamic (CFD) involving large eddy simulation (LES) [
3], or Reynolds-averaged Navier–Stokes (RANS) [
4,
5,
6]. Because marine propeller operates in a viscous flow and complex current of the wake, CFD methods are more suitable and efficient than the inviscid methods (BEM, VLM), albeit some researchers use the inviscid method for propeller simulation due to the low-cost and lower simulation power needed.
Many researchers have used the RANS method to overcome the rotating blades’ solution complexity, especially for marine propellers. Maksoud et al. [
7] carried out how the propeller hub could change the propeller efficiency by using CFX. Another main factor in operational marine propeller condition is the propeller and rudder interaction, investigated by Simenson et al. [
8]. Valentine [
9] used the RANS equations to predict the propeller blades’ flow characteristics by considering turbulence inflow characteristics. In this paper, two main issues should be evaluated; first hydrodynamic calculations based on the RANS method. Second, structural analysis, that fluid–structure interaction must be engaged in the computational prediction approach. The nonlinear hydrodynamic load exerted on propeller blades due to the propeller’s rotational motion inducing a centrifugal force.
The majority of the fluid-structure interaction studies on marine propeller focus on the composite propeller; Das et al. [
10] used a reverse-rotation propeller in a CFD analysis. Mulcahy [
11] investigated a comprehensive study on the composite propellers’ hydro-elastic tailoring. In 2011, Blasques et al. [
12] investigated the propeller’s hydrodynamic improvements using different laminate layups for optimal speed and fuel consumption. In 2008, Young [
13] investigated marine propeller fluid-structure interaction analysis to assess the composite blade’s behavior. Also, the Tsai-Wu strength criterion is considered to evaluate the blade strength. Lee et al. [
14] investigated a two-way coupling approach consisting of added mass based on the coupling between boundary element and finite element method. He et al. [
15] used a hydro-elastic approach to evaluate composite propeller’s performance, especially vibration due to loads on propeller hub and the composite layup scheme shaped based on coupling CFD and FEM methods. Finally, a comprehensive study for four propellers with different concerning materials was published in 2018 by Maljaars et al. [
16], consisting of RANS–FEM and BEM–FEM results versus experimental results. Hong et al. [
17] developed a pre-twist approach to gentrify the propeller’s hydrodynamic characteristics using FEM/CFD-based software, ANSYS/CFX. Han et al. [
18] used Star-CCM+ and Abaqus coupling approach to study the marine composite propellers; the results were reasonably close to experimental outputs. Paik et al. [
19] investigated different composite propellers numerically and experimentally. In 2020, Shayanpoor et al. [
20] performed an analysis by considering the CFD–FEM-based approach under the two-way coupling method on the KP458 propeller.
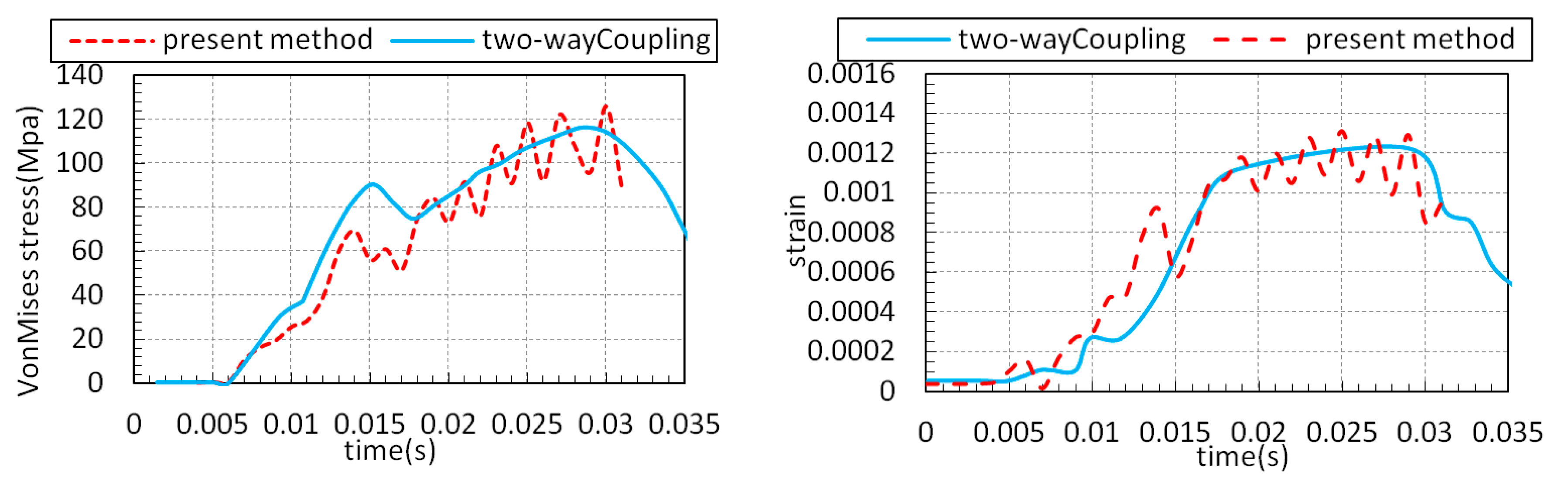
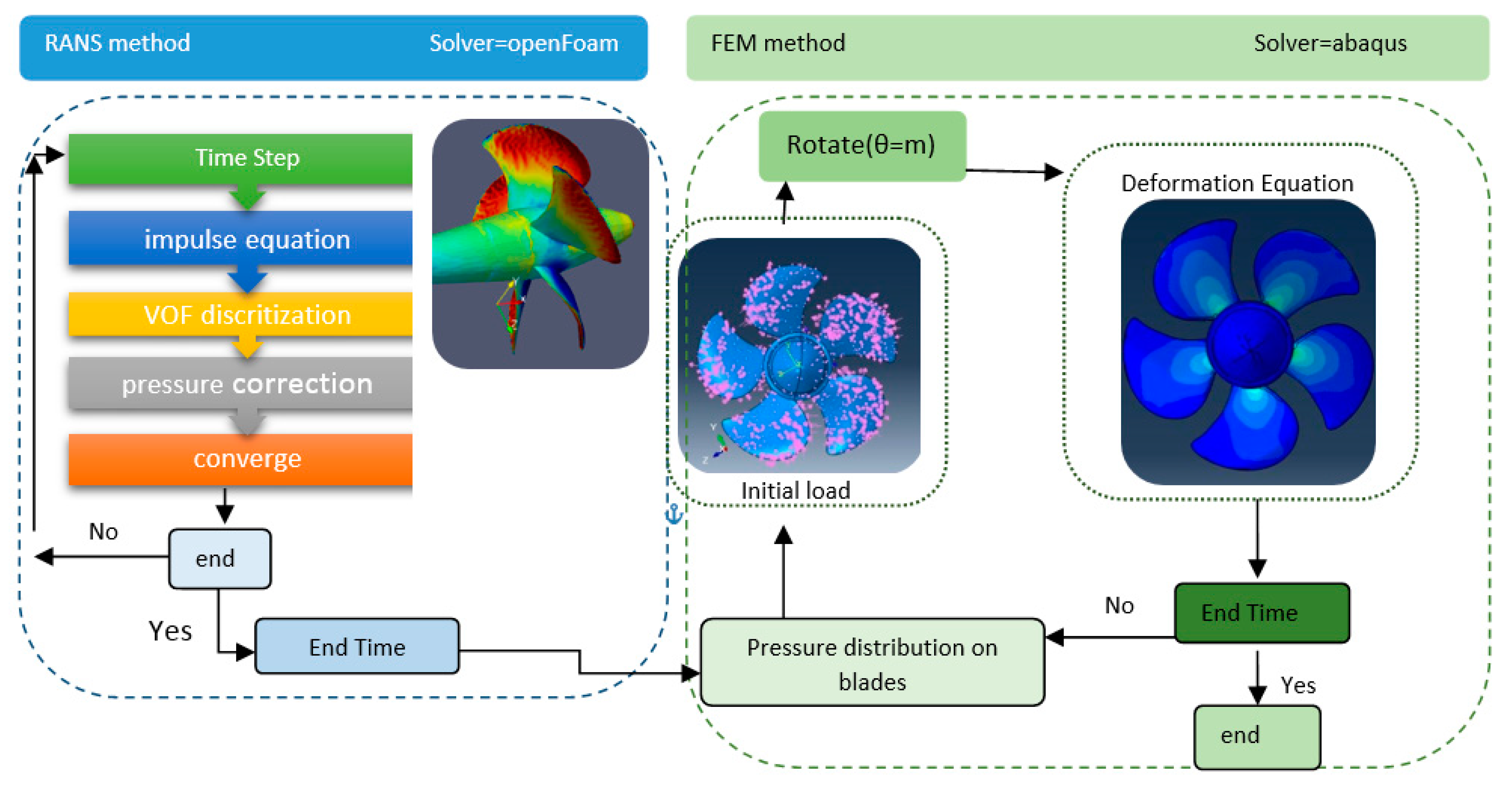
A simple FSI surrogate modeling is introduced in the present study by considering two distinct solvers, Linux-based/open access solvers (OpenFOAM) and windows-based/commercial software (Abaqus); thus, the major challenge is the coupling approach by considering the propeller’s dynamic motion. Accordingly, the pressures extracted from OpenFOAM transfer to Abaqus in each predetermined time-step, to use as structural load, the rotation rate and the number of time-steps should be first evaluated. In the following sections, for the first step, hydrodynamic solution verified with experimental tests. For the structural solution, the current FSI approach compared with the wedge impact case was verified later; the justification of using the wedge impact verification is the similarity of the two cases. For the second step, the verified numerical model performs to analyze the advance coefficients’ effect on the forces and stresses imposed on the propeller blades.
2. Materials and Methods
Fluid–structure interaction approaches are divided into monolithic and partitioned methods. In addition, partitioned methods are divided into one-way and two-way approaches. Moreover, two-way coupled is divided into strong and weak approaches [
21]. From the accuracy aspect, the two-way coupling approach is more accurate than the one-way approach, especially for cases with more significant deformations and deflections. On the other hand, the one-way coupling requires less data for a single iteration per time-step. In addition, the mesh advocated for the fluid domain needless to be recalculated at each time-step. This leads the numerical solution to remain stable with unchanged mesh quality. Thus, the needed time related to the numerical solution is lower than two-way coupling, updated only after each time-step for a new iteration. Therefore, an overriding advantage of the one-way coupling approach is decreasing in the numerical solution time. Piro’s [
22] compared the one-way and two-way coupling approaches (RQS-RDyn-TC) for different plate thicknesses, the discrepancies between the methods were small for thick plates; whatever the plate’s thickness becomes small, the accuracy of one-way coupling decrease. Due to the small deflection that occurred for the propeller blades in the present study, the one-way coupling method could be accurate enough.
2.1. Governing Equations of the Flow Around the Propeller
The most applicable and usable approach for simulating turbulent regimes is based on solving the Reynolds-averaged Navier–Stokes (RANS) equations. In the present study, InterDymFoam, a multiphase solver of OpenFOAM libraries, is used for hydrodynamic simulation. InterDymFoam is a proper solver based on the RANS equation by considering multi turbulence models [
23] for dynamic mesh cases. The fluid is regarded as an incompressible Newtonian fluid that should inherently satisfy the mass conservation and momentum equations. The RANS equations are based on time-averaged variables decomposing the velocity, pressure fields into:
represents coordinates,
are the component of Reynolds-averaged velocity. ƒ
i denotes the body forces presented as forces per unit volume and in the present study assumed that
. Moreover,
u,
, and P are fluid velocity vectors, density, and pressure, respectively. The Boussinesq assumption is considered to represent the Reynolds stress for incompressible flows, which is commented below:
where
represent the turbulence eddy viscosity, k denotes turbulent kinetic energy (TKE) per mass. In addition,
surrogate as the Kronecker delta.
is time-averaged velocity, in which
and
are the mean and variance velocity, respectively. A two-equation turbulence model (k-ε) is used for the present study. ε denotes the dissipation rate of energy per mass, which determines the amount of energy lost by the viscous forces in the turbulent flow that should be introduced. (
is turbulent viscosity:
To track the particles and capture the interface for the multiphase solution easily, the volume of fluid (VOF) could be a practical approach. The VOF method uses a volume fraction variable α to represent the air and water portion in each finite volume cell [
24], where
and
represent the physical properties of water, and
and
also mean the physical properties of air, which introduces new conservation equations:
The two-phase dynamic solution similar to the present case (propeller in water) is transient with a high turbulent regime that caused the solution to be inherently unstable. There were some algorithms to couple the mass conservation and momentum equations, the semi-implicit method for pressure-linked equations (SIMPLE), and the pressure implicit with the splitting of operators (PISO) that in the present study, the high-fidelity algorithm based on merging the PISO and SIMPLE called PIMPLE used.There are two important parameters, inner and outer correctors; inner corrector is the number of times the pressure is corrected, and the outer corrector is the number of times the equations are solved in each time-step. Outer corrector puts an obligation to stop the solution for each time-step apart from the solution be converged or not.
2.2. Governing the Structural Equations
Structural analysis is an essential step for one-way coupling approaches that should be performed correctly. The cantilever beam model is the initial theory to calculate the propeller blade strength introduced by Taylor [
25]. This method was implemented and developed by some researchers. The method’s drawback was poor results for the points with a low thickness on the propeller’s blade compared to thicker blade’s sections near the propeller’s root. This problem continued until the introduction of shell theories developed by Cohen [
26] and Conolly [
27], the limitation of this method was the propellers’ geometry complexity. For instance, wide-blade or high-skew propellers could not be assessed accurately, but in recent years, the finite element method used widely by dividing into solid or shell element approaches. Many investigations are based on both approaches, but Young [
13] and Blasques et al. [
12] performed a study to evaluate the output results’ differences. Their investigation indicates that, although both methods are sufficient, the Shell element model needs lower computational power than the solid element method. Moreover, the solid element method has some prominency rather than a shell element model, Young [
13]; this is why most FSI problems used a solid element model for the structural solver.
The deflection due to the structure’s imposing loads is the main issue [
28] performed by the finite element method. This technique broadly consists of discretizing a structure into several elements that should be assembled at the end. In addition, internal stresses are in equilibrium due to the continuity of stress for interface elements. The present finite element uses the explicit method, in which a time-based approach (central difference method) is used to integrate the equations of motion. In this method, the period is considered small enough to prevent divergence [
29]. The equation of motion for the structural deformation corresponding to the propeller blade fixed coordinate is introduced by Equation (9):
where
is the mass matrix,
belongs to damping matrix and
represent the matrix for the structure stiffness. the variables
are the acceleration, velocity, and displacement, respectively.
is the summation of all loads imposed on the structure. Importantly, for the cases like a propeller, this load comprises force due to rotation, centrifugal force and moments, Coriolis force, and external load on the structure. For the case in hand, due to static analysis of the propeller and motionless blades in each time-step, the only pressure used for calculation is the fluid pressure extracted from the CFD solution. The calculation algorithm’s first step is to solve the dynamic equilibrium relation, Equation (11). The kinematic conditions solve the next iteration’s kinematic constraint in each distinct increment.
All of these parameters belong to nodal points, where M is the nodal mass matrix, U is nodal displacement and is nodal acceleration. To govern net forces act on nodal points (P–I) is used, that p is the external loads imposed on the structure. This parameter is considered nodal forces. The integrated accelerations are used to calculate velocity variations; this new added velocity value from the previous middle increment determines the middle of the current increment Equation (11). then The time-integrated velocities are added to the beginning displacements’ increment to determine the final displacements’ increment, Equation (12); after estimation of the nodal displacement in time(t), the element strain increments are calculated from the strain rate, The stress components can be calculated from constitutive equations and the solution process repeated for time (t + ∆t).
2.3. Modeling and Computational Setup
2.3.1. Open Water Test Characteristic
The present study’s framework is a numerical solution related to the Potsdam propeller test case (PPTC). For this purpose, the same propellers’ geometry with the same material is accepted from the experiment cases, represented in
Table 1 and
Table 2, respectively [
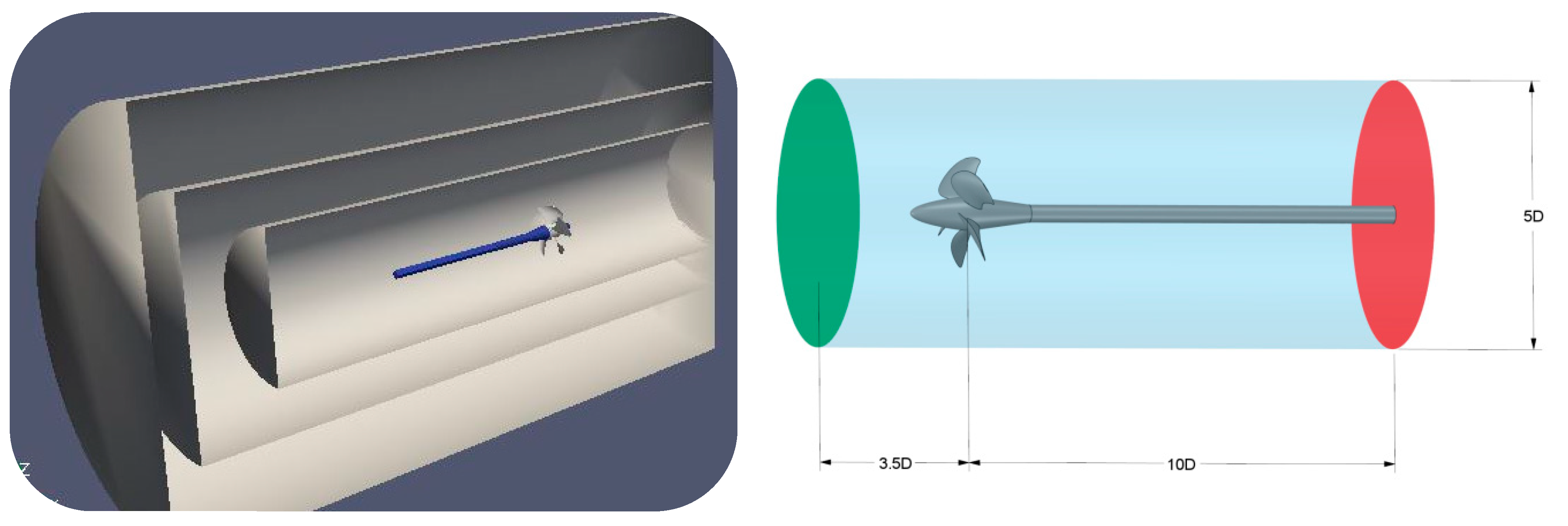
29]. The International Towing Tank Conference (ITTC) recommended that the propeller rotational speed is considered constant, but propellers’ advanced speed varies for different advance coefficients. The incident flow into the propeller is the opposite of real working conditions; propellers must be rotated in the opposite direction. We will hereafter comply with this rule to perform open water tests. The solution domain is modeled cylindrically with the following dimensions; 3.5 D forward, 10 D rearward, and 5 D in diameter, D is propeller diameter [
30] (
Figure 1).
For the open water tests, The main parameters are the thrust coefficient
, and torque coefficient
, represented by the dimensionless values mentioned in equation (13). The coefficients are directly related to rotational speed, n, diameter, D of the propeller, and water density,
. Furthermore, T represents thrust [N], Q is equal to torque [Nm],
denote the advance speed [m/s], and η is proportional to the efficiency [-].
2.3.2. Applied Boundry Condition and Dynamic Motions Method
Although various boundary conditions can be devoted to, accurate results without divergence need a proper allocation of boundary conditions In the present case, the inlet and outlet boundary condition was set based on the downstream of the outlet boundary domain. For the inlet boundary condition, free-flow velocity is considered constant, dependent on advance velocity for each advance coefficient. Moreover, the inlets’ turbulence intensity is considered, I = 5%. Two main approaches could simulate the propeller’s dynamic motions, multi-reference frame (MRF) and arbitrary mesh interface (AMI), since the AMI is more practical for propeller case studies used in the present numerical solution. This method is based on the interpolation between two distinct but adjacent domains connected with an interface [
30]. Two similar cylindrical domains encompass the propeller, one is static, and another one is dynamic, moves with the propeller’s rotation. Although there was no physical relationship between the two zones, the fluid and numerical calculations were transported through the interface.
An appropriate mesh quality and structural-based domain around the propeller needs some consecutive cylinders for dividing the domain into some sub-domain. The smallest cylinder is a small grid size, and the subsequent cylinder is larger than the former cylinder. In this regard, snappyHexMesh is used as the main tool and rhinoceros’ role as an assistant tool to generate the numerical solution mesh. As shown in
Figure 2, a high-quality structured mesh can be obtained by considering these techniques. A mesh independence study was established for the accuracy of the CFD solutions besides keep the computational cost.
The mesh generation framework is explained, but the mesh independence study must be performed simultaneously. The mechanism whereby the performance of griding qualified is highly dependant on the main propeller characteristics shown in Equation (12); that is how the mesh could be alleviated the computational cost without losing the accuracy. The propeller rotational speed, ω = 15 rps, and advance speed,
= 2 m/s, the advance coefficient, J = 0.53 [-] is considered to perform the numerical solution,
Table 3. The calculation for this advanced coefficient involved five different initial grid sizes,
Table 4, dynamic multiphase solutions, InterDyMFoam, which comes from OpenFOAM libraries with the same underlying physics relative to InterFoam. The thrust and torque are extracted from the postprocessing tool as the initial value; then these values substitute in Equation (13); finally, the results for each simulation are gathered in
Table 4; all these cases provided acceptable results. Consequently, fine (IIII) resolution leads to a reasonable prediction of thrust and torque coefficient with optimum computational cost compared with other cases.
4. Conclusions
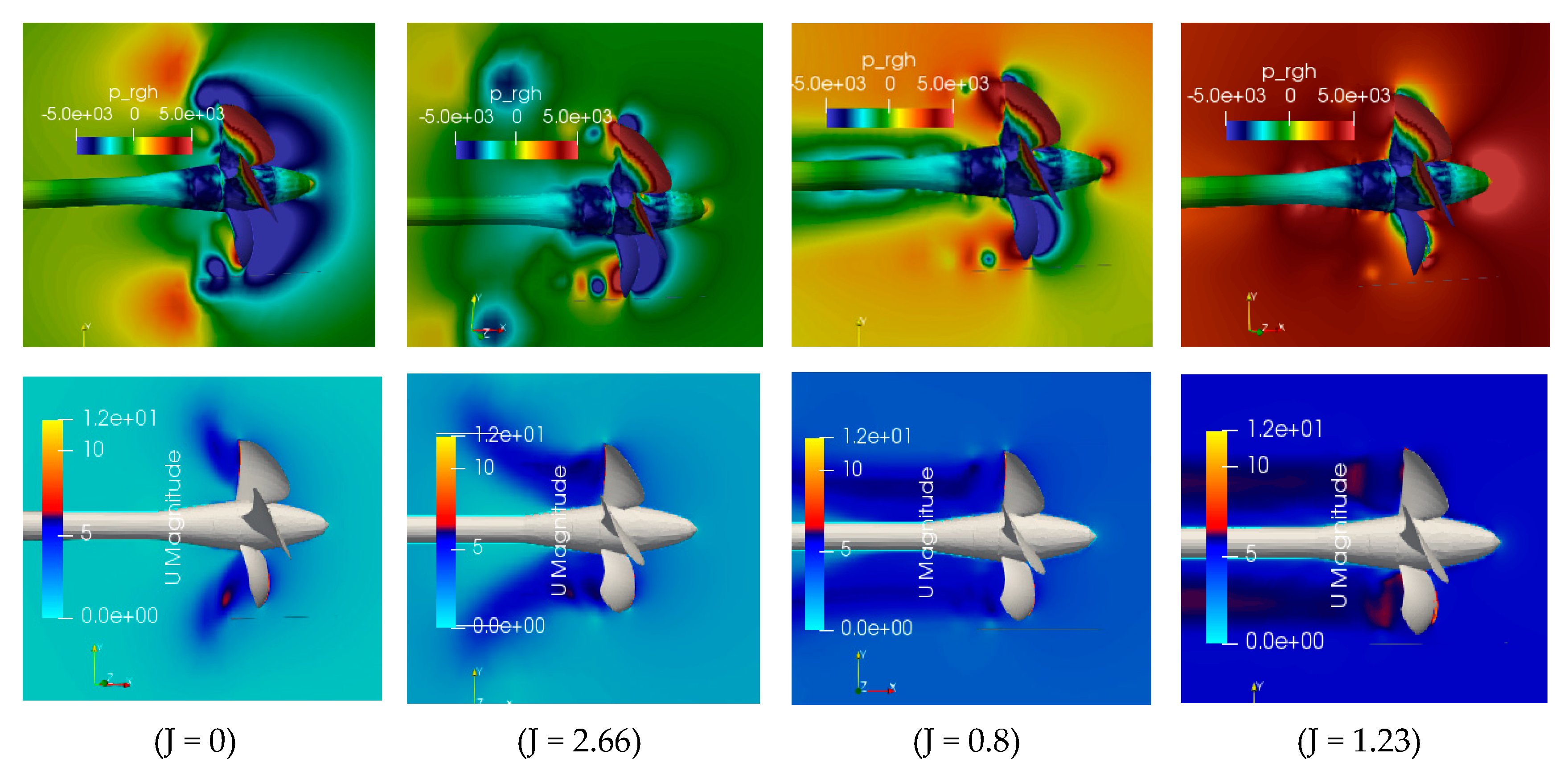
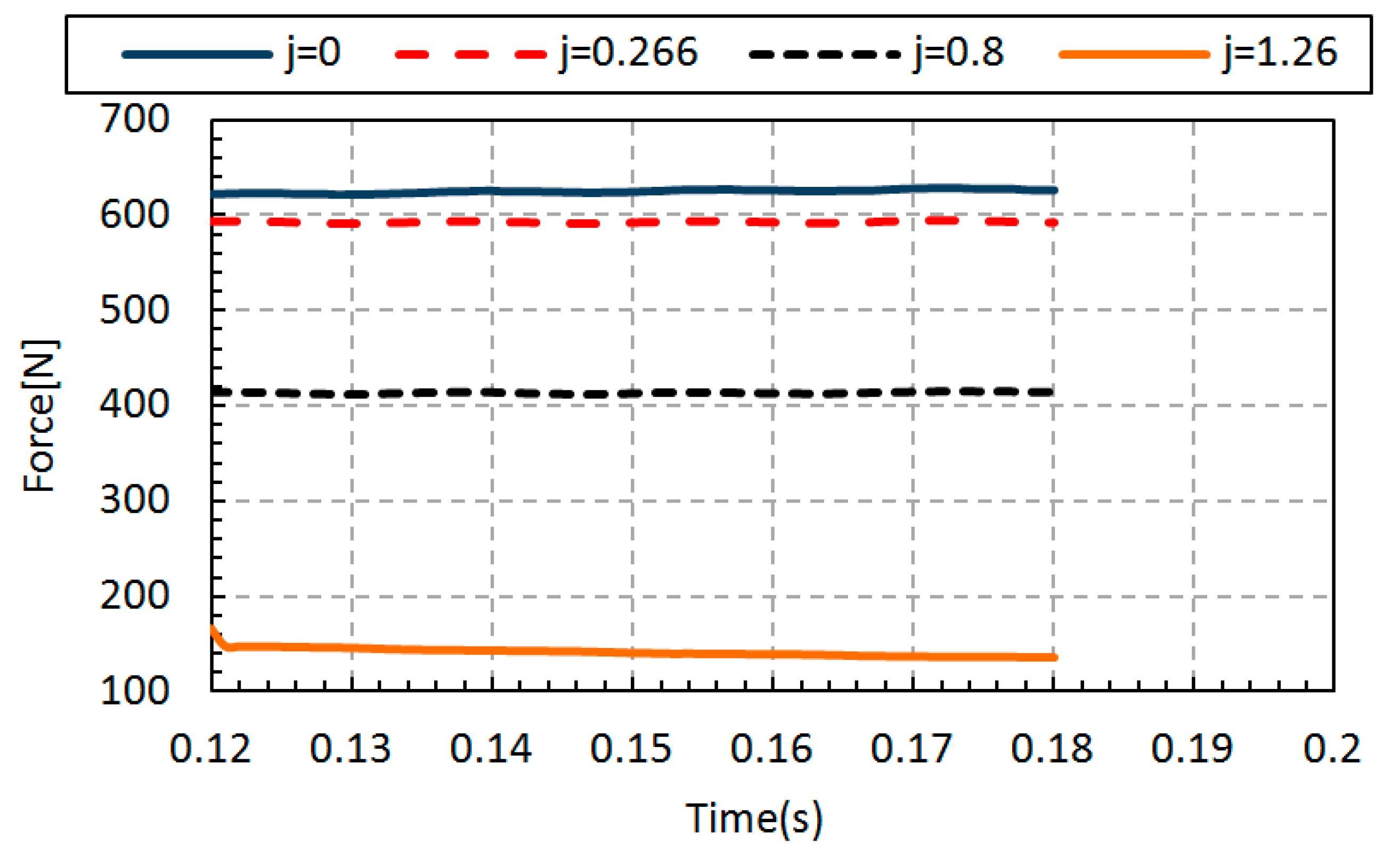
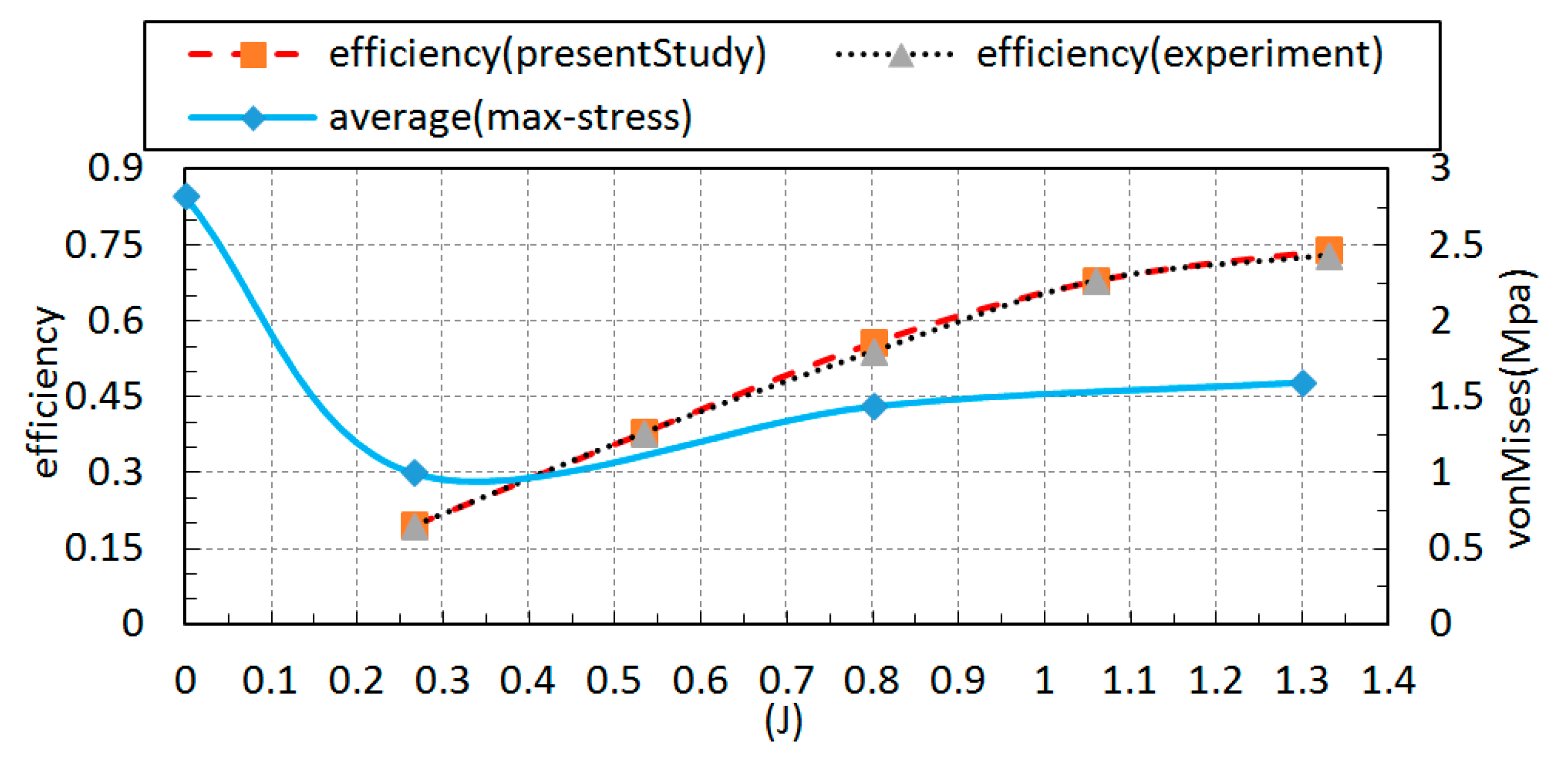
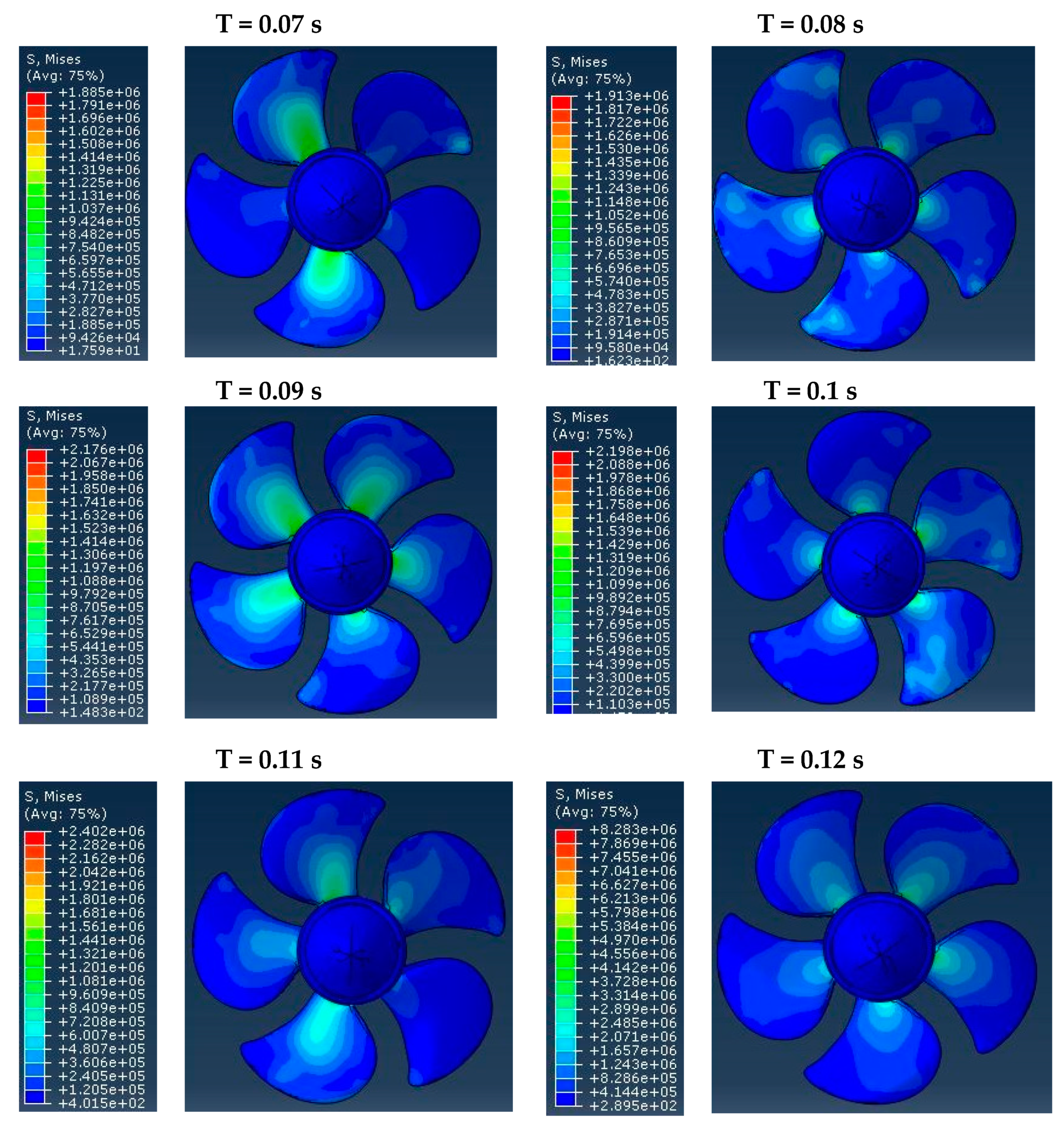
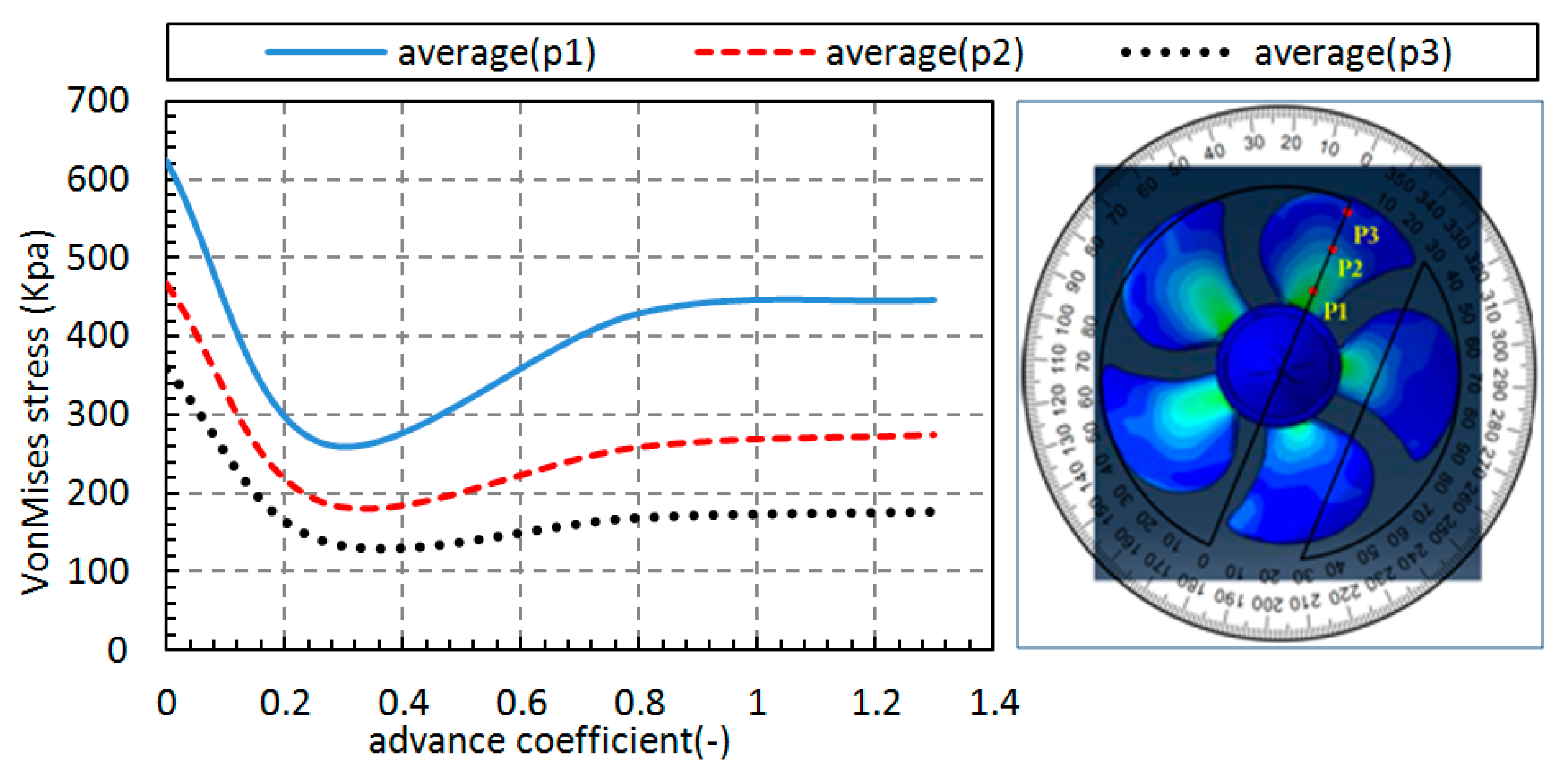
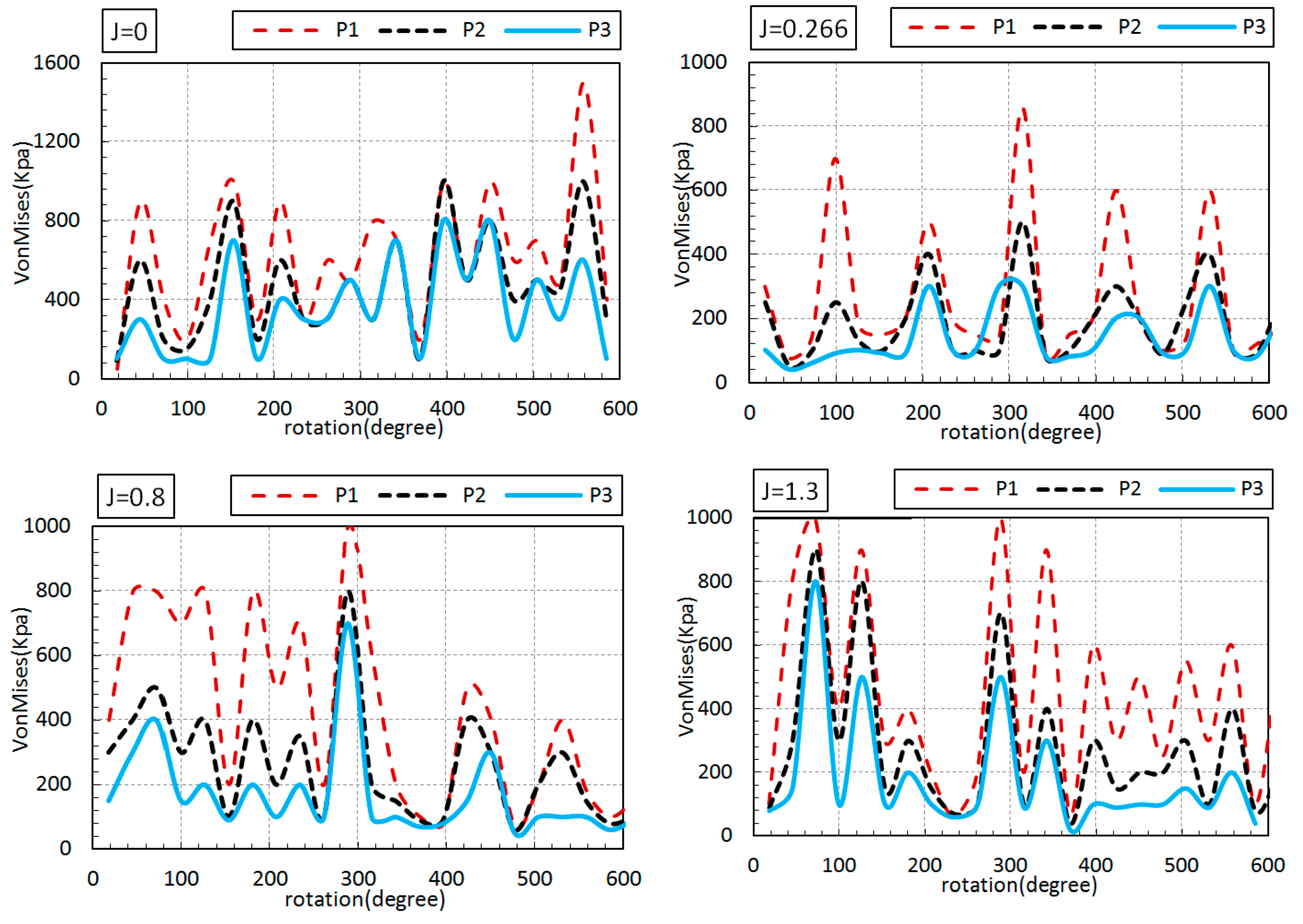
In the present study, simple surrogate modeling for rigid/quasi-static approach is used to investigate hydroelastic simulation for open water propeller test cases (PPTC); the coupling approach comprises a CFD-FEM method solved separately. In the first step, the hydrodynamic solver, InterDyMFoam, is verified with an experimental study that the average efficiency error for different advanced coefficients was about e = 7.5% for efficiency on average. For further evaluation in the hydrodynamic section, a force analysis was performed using the ParaView postprocessing toolkit for each advanced coefficient; also, pressure and velocity contours were demonstrated versus different advance coefficients.
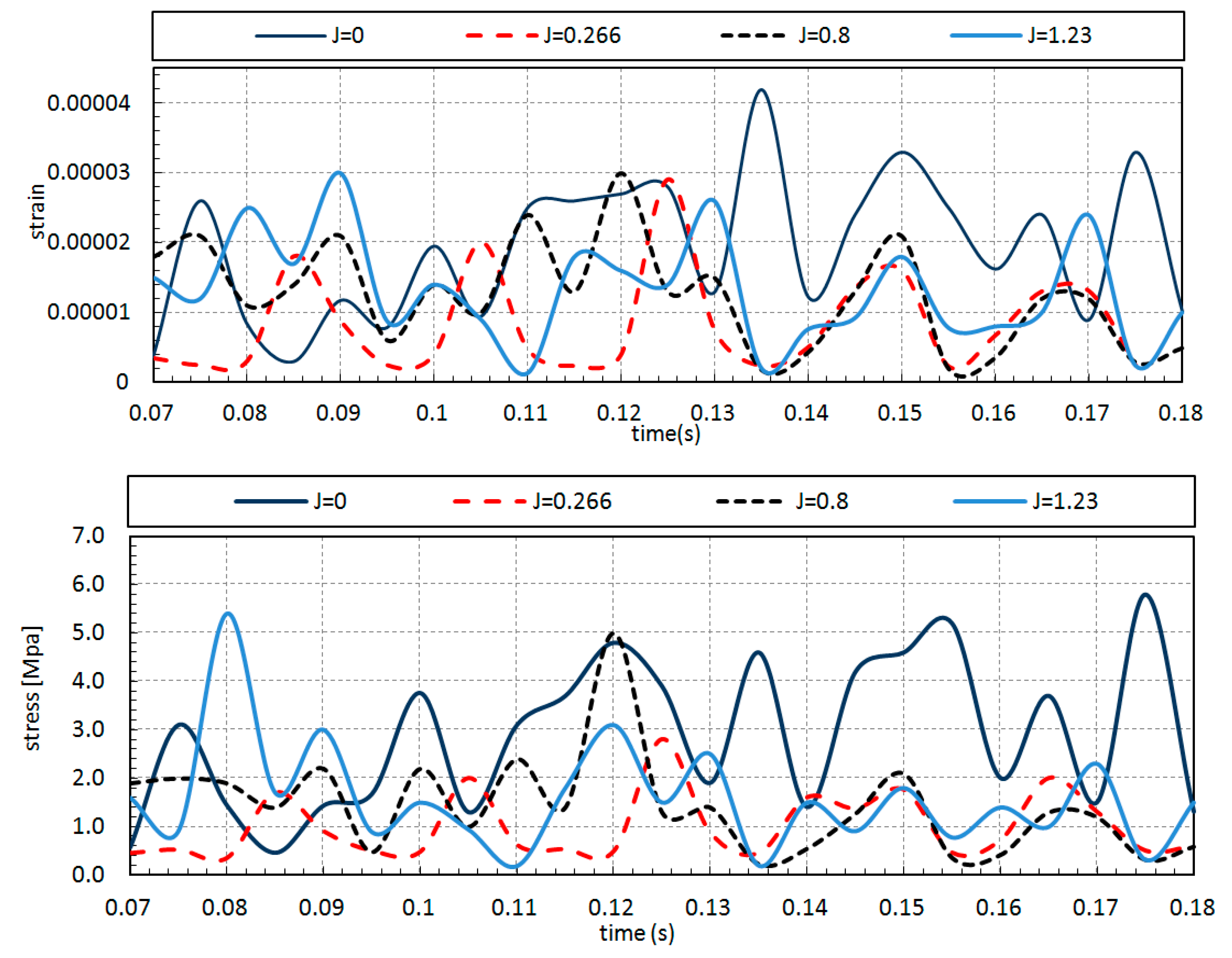
For the second step, the pressure distributions were obtained from OpenFOAM visualization software, ParaView, and used as the initial structural loads in Abaqus software. The point is that the propeller must have an appropriate rotational motion in each time-step; this procedure continued until it reaches any complete revolutions needed. Emphasis is put on von Mises stress, which is vital for evaluating the propeller’s structural strength. A fact that is borne out is that the maximum stress occurs at the bollard pull state, J = 0. In addition, j = 0.266 has the minimum stress value apart from the advance coefficient. Although von Mises stress’s value remained stable without a notable change after J = 0.8, the value and maximum stress position could be changeable for each advance coefficient under different work conditions. Consequently, the propeller’s structural behavior can effectively be analyzed by the one-way coupling approach, which is a simple, but efficient model by considering the OpenFOAM and Abaqus solvers as the CFD and FEM solutions, respectively. The present method aims to assess the appropriate material or design framework for a wide range of propellers and working conditions with an accurate and low-cost method.