Next Article in Journal
PoC (Proof of Concept) for Performance Monitoring Platform of Container Terminals
Next Article in Special Issue
A Modeling Comparison of the Potential Effects on Marine Mammals from Sounds Produced by Marine Vibroseis and Air Gun Seismic Sources
Previous Article in Journal
A Hybrid BEM-CFD Virtual Blade Model to Predict Interactions between Tidal Stream Turbines under Wave Conditions
Previous Article in Special Issue
Above and below: Military Aircraft Noise in Air and under Water at Whidbey Island, Washington
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
JMSE
Volume 8
Issue 12
10.3390/jmse8120970
jmse-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Acoustic Characteristics of Small Research Vessels

by
Miles Parsons
* and
Mark Meekan
Australian Institute of Marine Science, Perth, WA 6009, Australia
*
Author to whom correspondence should be addressed.
J. Mar. Sci. Eng. 2020, 8(12), 970; https://doi.org/10.3390/jmse8120970
Submission received: 20 October 2020 / Revised: 19 November 2020 / Accepted: 19 November 2020 / Published: 27 November 2020
(This article belongs to the Special Issue Ocean Noise: From Science to Management)
Browse Figures
Review Reports Versions Notes

Abstract

Vessel noise is an acute and chronic stressor of a wide variety of marine fauna. Understanding, modelling and mitigating the impacts of this pollutant requires quantification of acoustic signatures for various vessel classes for input into propagation models and at present there is a paucity of such data for small vessels (<25 m). Our study provides this information for three small vessels (<6 m length and 30, 90 and 180 hp engines). The closest point of approach was recorded at various ranges across a flat, ≈10 m deep sandy lagoon, for multiple passes at multiple speeds (≈5, 10, 20, 30 km h−1) by each vessel at Lizard Island, Great Barrier Reef, Australia. Radiated noise levels (RNLs) and environment-affected source levels (ASLs) determined by linear regression were estimated for each vessel and speed. From the slowest to fastest speeds, median RNLs ranged between 153.4 and 166.1 dB re 1 µPa m, whereas ASLs ranged from 146.7 to 160.0 dB re 1 µPa m. One-third octave band-level RNLs are provided for each vessel–speed scenario, together with their interpolated received levels with range. Our study provides data on source spectra of small vessels to assist in understanding and modelling of acoustic exposure experienced by marine fauna.

1. Introduction

Through evolutionary time, sound has become an important sensory cue for many marine taxa. The efficient transmission of sound underwater has meant that a wide variety of species have developed frequency-specific hearing sensitivity and rely on the detection of acoustic cues and subtle changes in the biophony of their local soundscape during vital life functions [1,2,3,4,5]. These important signals, such as the spawning calls of fishes or the sound of healthy habitat in which larvae will settle, can be masked by anthropogenic noise, disrupting natural behaviors [6,7,8]. Sound produced by vessels is a major element of marine anthrophony and has been recognized as a chronic stressor [9], negatively impacting communication, health and behavior of many species [4,10,11,12,13,14,15]. As human populations have increased, so too has anthrophony in oceans and inland waterways [16,17,18,19,20,21], creating what has now been termed the ‘Ocean soundscape of the Anthropocene’ [22].
Management strategies that aim to mitigate the impact of vessel noise on marine fauna [23,24,25,26,27,28] require information about source levels and vessel movements. Although the Automatic Information System (AIS) can be used to track passages of the majority of commercial vessels [29,30], noise is also dependent on vessel size, speed, load and power, as well as other design characteristics [24,31,32]. This requires characterization of source signatures from different types and sizes of vessels.
At present, there is little data on the noise characteristics of small (<25 m length) vessels [26,33,34,35,36,37]. This is important because in coastal waters, these vessels often vastly outnumber larger ships ferrying commercial cargos. The data required to accurately model the propagation of signals from small vessels are rarely reported, or typically provided as one or two measures at limited numbers of speeds [36]. For this reason, we lack data on the variability in noise among vessels of different classes (e.g., monohull, catamarans, tugs, landing craft) within this size range or even different passes of the same vessel. This is problematic for management strategies that aim to set useful guidelines to mitigate noise for boating activities [38], particularly in shallow coastal waters, inland waterways, and coral reefs, where small vessels have the potential to significantly change the local soundscape and, due to proximity, are more likely to affect fishes, invertebrates and small marine mammals [38,39,40,41,42].
To address these issues, our study aimed to characterize the source spectra of three small vessels under 10 m length that are commonly used in shallow coastal marine environments. We took multiple measurements at the closest point of approach (CPA) at multiple ranges and speeds, over multiple passes, in shallow water. Source characteristics of noise can be specific to a vessel and have multiple engine-, propeller- and hull-related origins [43] and their impacts on fauna are frequency-dependent. Therefore, one-third octave levels were also calculated, and their propagation across the measured ranges investigated.

2. Materials and Methods

The International Standards Organization (ISO) protocols for the measurement of vessel radiated noise levels (RNLs) and monopole source level (MSL) focus on large vessels in deep water (see ISO 17208-1 [44] and 17208-2 [45]). The ISO criteria require a minimum water depth equal to the greater of 150 m or 1.5 times the overall ship length. For the highest standard of estimates, this comprises the deployment of three hydrophones positioned vertically at depths that result in 15°, 30°, and 45° angles from the sea surface at a CPA distance of either 100 m or one overall ship length, whichever is greater. Neither are these requirements achievable, nor is the procedure applicable, in shallow water. Indeed, meeting these requirements in Australia would require vessels to travel a significant distance offshore, which may not be appropriate for all classes of small vessels. Standards for measurements of RNL in shallow water are under development. However, we had sufficient replication of measurements to accurately estimate both RNLs and affected source levels (ASLs), in lieu of any current shallow-water ISO protocols.

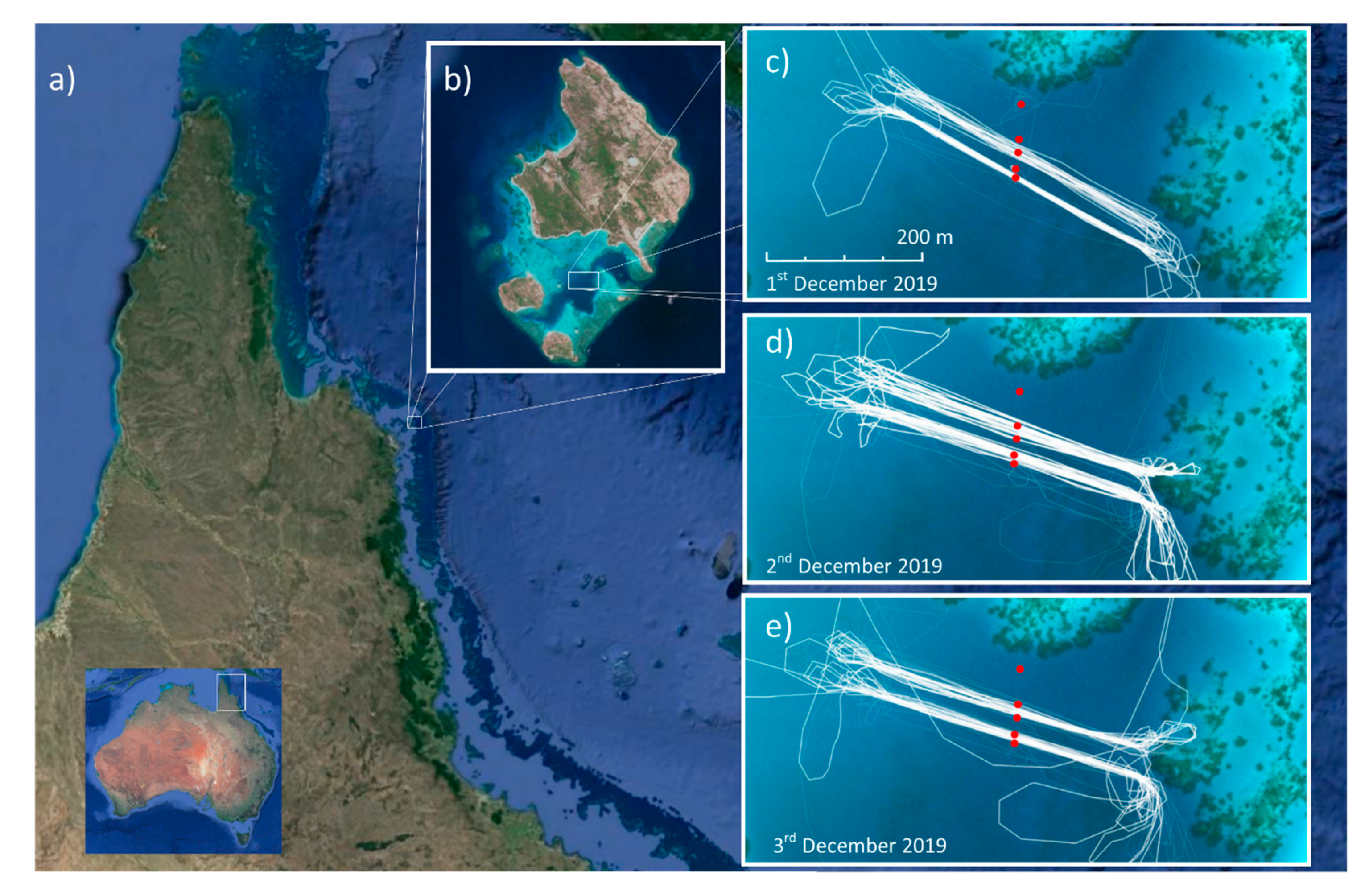
2.1. Study Site

Lizard Island is a granitic island located approximately 30 km off the north Queensland coastline (14°40.88′ S, 145°27.82′ E, Figure 1). The Lizard Island group comprises four late-Permian granite islands—Lizard, Palfrey, South and Bird Islands—which, together with the surrounding fringing reef, encircle an up to 10 m-deep flat, sandy-bottomed lagoon [46]. Tidal range at Lizard Island reaches a maximum of 3 m and current speeds into the lagoon can be >30 cm s−1 [47,48]. Measurements were collected in the 10 m deep area of the lagoon, to the south of Lizard Island (Figure 1).

2.2. Vessel Recordings

Vessel recordings were acquired using Ocean Instruments ST300 SoundTraps. These are piston-phone calibrated passive acoustic pressure sensors with a flat response of ±3 dB over the 20 Hz to 60 kHz system bandwidth, calibrated by the manufacturer using a 121 dB re 1 µPa source at 250 Hz. Divers deployed 10 ST300s on the seafloor of the lagoon, each orientated vertically, attached to the top of a star picket, and positioned approximately 50 cm above the sand. Two ST300s were deployed, 1 m apart, at each of five sites, forming a 100 m-long transect with relative spacing of 0, 10, 33.5, 52.1 and 100 m from the first site, running approximately north-south, at the northern end of the lagoon (Figure 1, red dots). All SoundTraps recorded 290 of every 300 s, at a sampling frequency of 48 kHz. Gaps between the recordings were kept to separate files into manageable sizes and minimize the potential for losing recordings due to buffering issues, and the 97% duty cycle minimized the likelihood of missing the CPA of a vessel pass. At each SoundTrap, a tight vertical line was run from the ST300 to a surface buoy where the exact GPS location was recorded with a Garmin 64SX.
Between the 1st and 3rd December 2019, three vessels (Figure 2, characteristics shown in Table 1) each conducted ten transects at speeds as close as possible to 5, 10, 20, and 30 km h−1 (1.4, 2.8, 5.6, and 8.3 m s−1, respectively). For each speed, five transects were conducted across the southern end of the line of SoundTraps and five across the midway point (Figure 1, white lines), totaling 100 potential recordings of each vessel at each speed. Vessel transects were planned to be orthogonal to the line of SoundTraps, though in reality were not completely perpendicular to the SoundTrap transect (Figure 1). Each vessel conducted all transects over a three-hour period, with one vessel completed each day. Vessel positions were recorded using a handheld Garmin 64SX. Wind over the three days remained at Beaufort scale two or below.

2.3. Data Analysis

Data processing involved the following steps: (1) calibrating recordings, (2) selecting sections that matched the known time of each vessel pass, (3) computing mean squared pressure and power spectral density for the CPA of each transect, (4) computing RNL for each pass, and (5) least squares linear regression modelling of the recordings across all ranges to produce dipole source spectra and ASL for each vessel and speed.
The 290-s recordings were extracted, and each dataset processed with a MATLAB (version R2014, The MathWorks Inc., Nantucket, MA, USA) user interface designed for analysis of underwater passive acoustic recordings, CHORUS [49] and purpose-written functions, as well as inspected via audio and visual scrutiny of the recordings and spectrograms, respectively. Spectrograms were created in MATLAB (version R2019) using the spectrogram function with 1-s Hanning windows and 80% (=0.8) overlap. Mean squared pressure was calculated for each transect and the 1-s window that contained the maximum mean square pressure was selected to represent the received level (RL) for the vessel’s CPA. Background noise levels were calculated from one-minute periods without vessel noise from each day, for each SoundTrap. RLs for each CPA were compared between pairs of SoundTraps at the same recording distance and any CPA RL with a difference greater than 5 dB were removed from analysis. CPA distance for each SoundTrap and vessel pass were determined from the known recorder positions and depth, and the GPS track of the vessel. In each case, the SoundTrap and Garmin 64SX CPA time were compared to confirm a match.
Spherical spreading losses, in the form of 20log10(range), were back-propagated to a range of 1 m for each slant range and vessel pass to provide an estimate of RNL [50]. However, the shallow-water depth in the study area means these estimates are for comparison only as spherical spreading is unlikely reflective of the actual propagation losses (PL) at the site. Estimation of MSL is conducted by collecting measurements in the far-field and combining these with an appropriate PL model for the site, to determine the effective source level, accounting for the surface ghost, i.e., an effective RL at 1 m range [26]. However, propagation modelling, particularly in shallow water, also requires precise knowledge of the local seafloor geology, sometimes multiple meters into the substrate [37]. As this information was not available at the study site, RLs were recorded at multiple ranges from the source CPA during each transect, and broadband PLs were estimated empirically using least squares regression for a best fit curve of the RLs with range in the form of:
SL = CPL × log10(range)
where CPL is the PL coefficient. As these RLs are a function of the propagation environment of the signal (i.e., the signal is affected by the surface reflections and interactions [51]), the value of the curve at a range of 1 m from the source may be considered an environment-affected source level (ASL).
Although hydrophones positioned directly beneath the vessel were within the acoustic near-field (for frequencies approximately ≤200 Hz) [50], these ranges reflected the type of exposure likely experienced on shallows reefs. We therefore modelled the PLs and resulting ASL estimates for each vessel and speed scenario using all data and with data from within 15 m slant range excluded, to minimize the effect of frequencies still in the near field. RNLs calculated in a shallow-water environment using spherical spreading are unlikely reflective of true PL. However, the regression-modelled PLs provide a useful proxy for acoustic propagation models, thus the broadband RLs were also back-propagated to 1 m using the average of all the regression-modelled PLs (i.e. mean CPL) across all vessels and speeds (as calculated with and without measurements from the <15 m range), for comparison. Median and quartile estimates were then produced for each vessel and speed for all RNLs and ASLs. Thus, this study provides results on the RNL (percentiles are given for data including and excluding measurements taken at <15 m), the empirically measured and linear regression-modelled ASLs (with and without data from within the 15 m range) of three small vessels in shallow water.
As acoustic signals are vessel and speed specific [31,36,37,42,52], linear regression models were applied to the estimated RNL and ASLs, to investigate the relationship between source level and speed, in the form of:
SL-SLref = Cv1 × 10log10(v/vref),
where SL and SLref were the source levels at the tested and reference speeds, respectively, v and vref were the tested and reference vessel speeds, respectively, and Cv1 was the velocity-related coefficient of the slope of the curve (Ross, 1976). If a single-coefficient, log-based regression model failed to produce a clear fit for the data, it was also investigated with a polynomial function with two coefficients:
SL-SLref = Cv1 × (v/vref)2 + Cv2 × (v/vref),
where Cv2 was the second velocity-related coefficient.
Finally, received spectra for each CPA measurement were also integrated into one-third octave band levels. These band levels were interpolated across one-third octave frequency bands and range in logarithmic bins to compare the one-third octave band PL in the environment, again for each speed and vessel. One-third octave band RNLs were calculated and the frequency-dependent CPL for each one-third octave band determined using linear regression of the respective band RLs recorded at various ranges, using the form of Equation (1).

3. Results

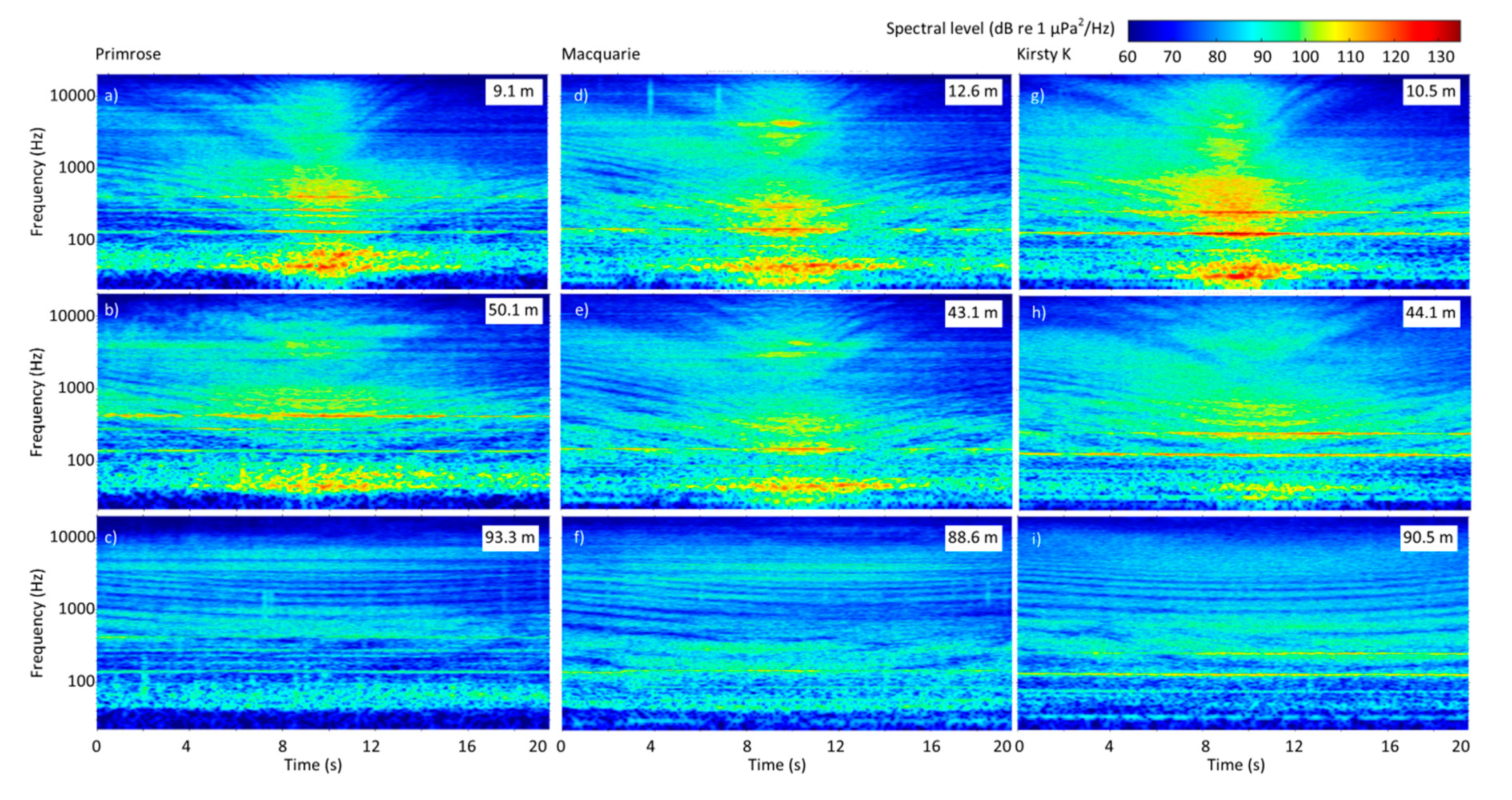
3.1. Measurements

A total of 120 transects were conducted across all three vessels and speeds (Table 2). One SoundTrap failed to provide calibrated recordings, leaving nine datasets. Of the remaining 1080 potential recordings of passes (360 for each vessel), 330, 336 and 344 CPAs were recorded of the Primrose, Macquarie and Kirsty K, respectively, at slant ranges between 9.0 m (almost directly below the vessel) and 98.8 m. Only two recordings were removed due to the RL of a CPA as noted by two SoundTraps at the same range differed by more than 5 dB. Average background noise levels across all sites and days were 106.8 dB re 1 µPa (max = 109.8, min = 102.3, s.d. 1.4 dB). Although the SoundTraps positioned at the greatest range were closer to the reef to the north and did contain more sounds of snapping shrimp than at the other recording sites, the mean noise at that location was <2 dB greater (108 compared with 106.2 dB re 1 µPa, respectively).
The approach of the vessel could be heard and observed in all recordings and spectrograms, respectively (Figure 3), though the exact CPA was more difficult to discern at the furthest ranges (>50 m) and slowest speed (5 km h−1category). Lloyd’s mirror interference pattern was evident on all spectrograms and propeller and engine/motor tones visible from 20 Hz through 24 000 Hz (the Nyquist frequency in this recording, Figure 3). Additionally, while not investigated fully in this study, at the close ranges (<50 m) energy in the 1–10 kHz band was typically higher in the final seconds of approach than the initial seconds of departure (Figure 3, rows a and b).

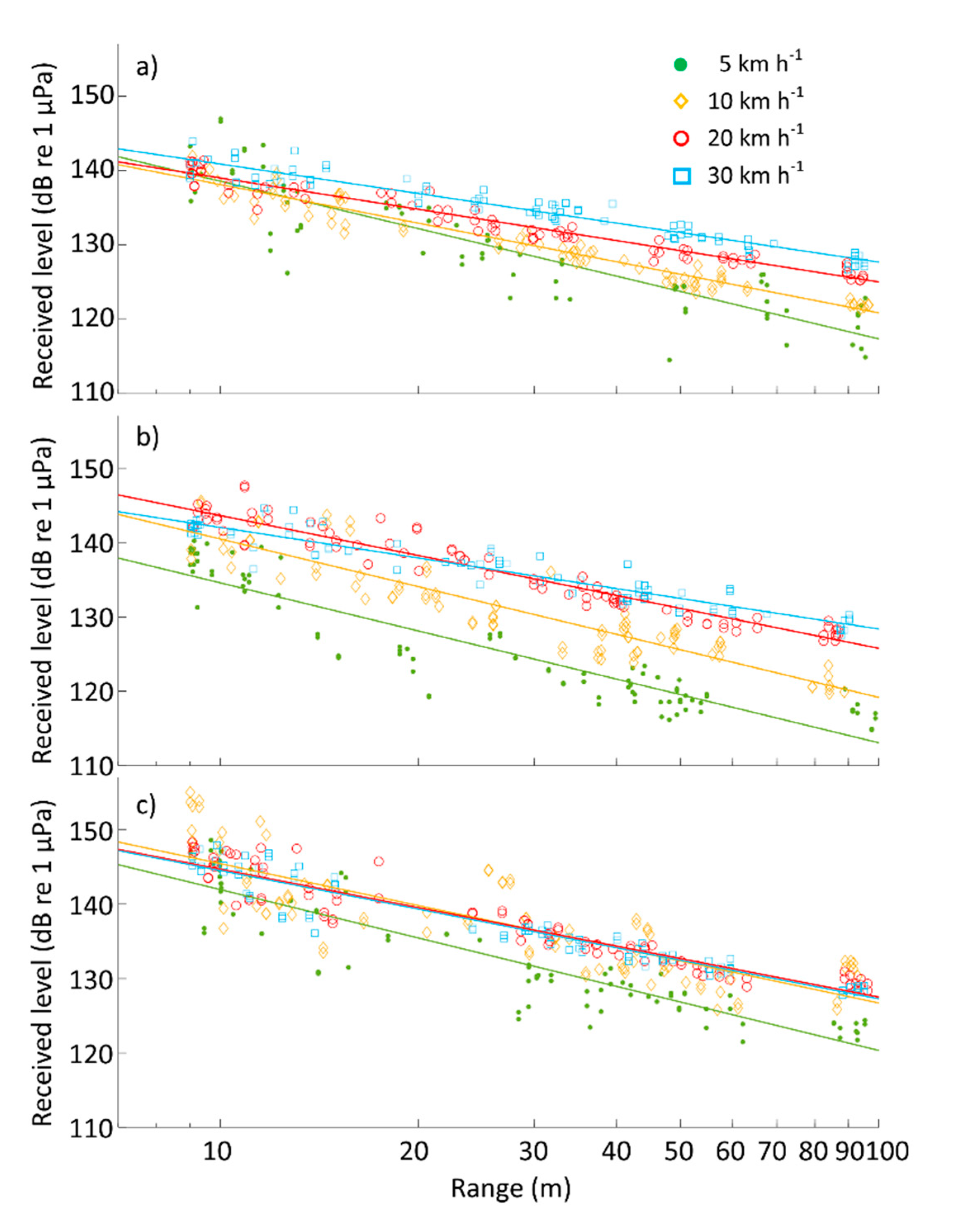
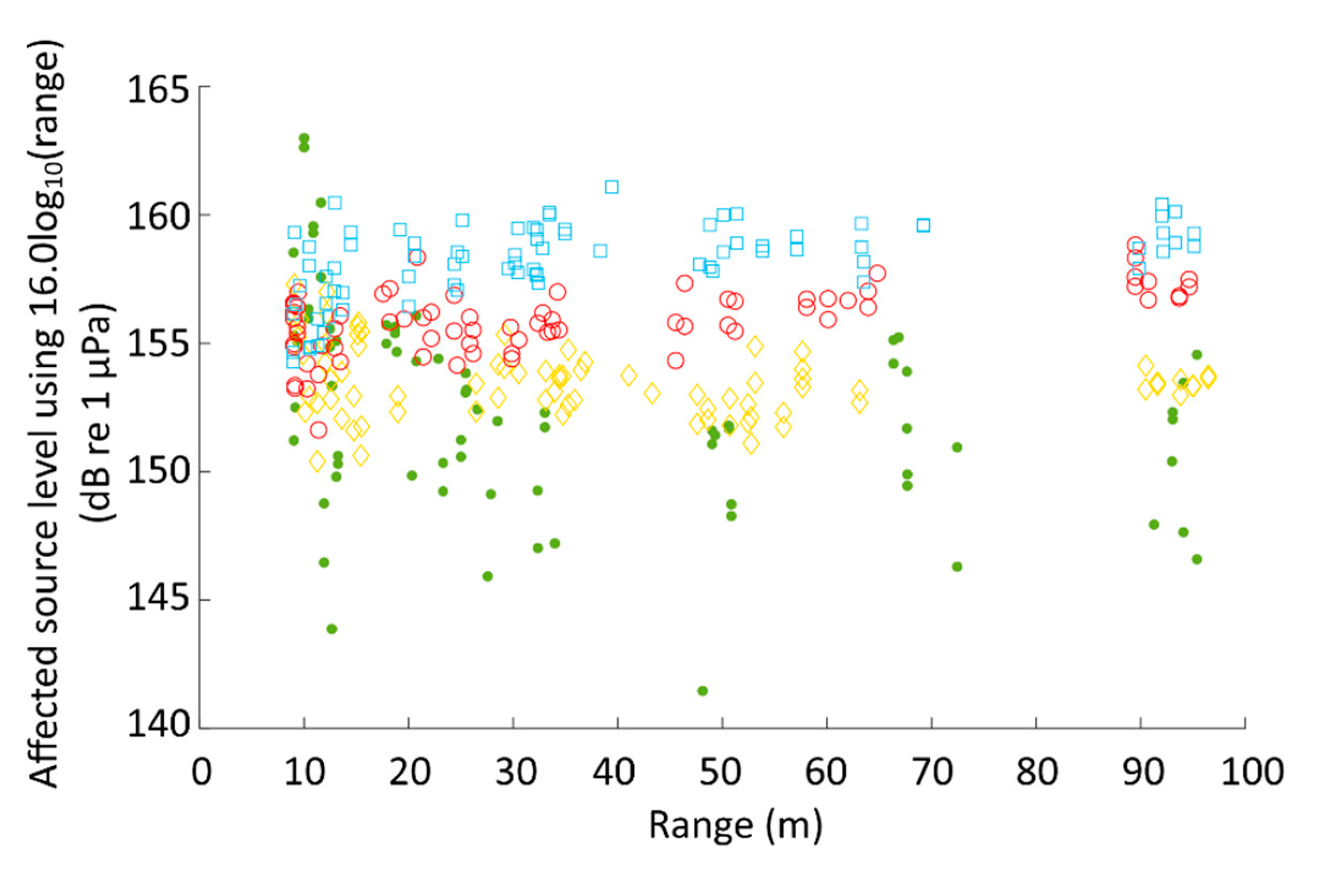
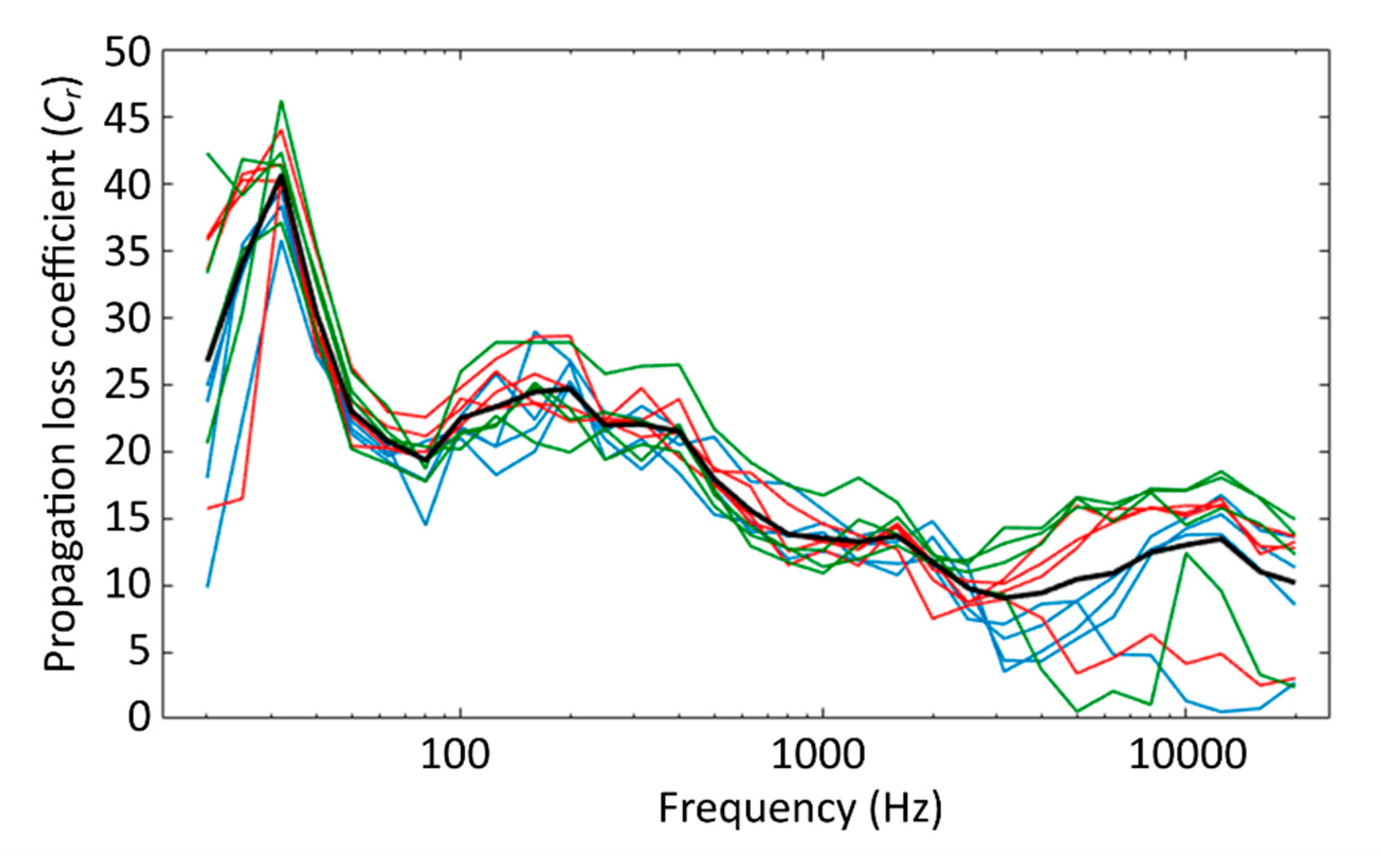
3.2. Received Levels with Range

In general, at a given range, RLs increased with speed for Primrose and Macquarie, though this was not as evident for the Kirsty K (Figure 4). Standard deviations in RLs at the same approximate speed were greatest closest to the source and standard deviations in RLs at the same range were greatest at the slowest speed category (Supplementary information). Regression models of PL varied between vessels and speeds and correlation with the recorded data was greater for transects conducted at 20 and 30 km h−1 than 5 and 10 km h−1 (Table 3). This variation was still evident when the recordings at the closest (<15 m) ranges were removed, though less so than when analyzing the full datasets. The average PL for individual datasets (vessels and speeds) for recordings across all ranges was 17.9log10(range), becoming 16.0log10(range) when data from <15 m were excluded. Standard deviation of all modelled losses decreased from 3.1 to 2.3 when removing the data taken at the <15 m range (Table 3). Percentiles of RNLs (with and without data from the <15 m range) and ASLs (using average PL with and without data from the <15 m range) all increased with increasing engine size and speed, except the Kirsty K between 10 and 20 km h−1and 20 and 30 km h−1.
When PL has been estimated correctly, the resulting RNL or ASL should not increase if plotted against the original range at which the measurement was taken, as can be seen for Primrose, using the averaged PL with data from <15 m removed (i.e., using 16.0log10(range), Figure 5). This plot also illustrates the increased variation in RLs taken at ranges <15 m, compared with those at greater ranges at all speeds (Figure 5). The reduction in RL over the entire measured range would be 40 dB for spherical spreading RNLs and 32 dB for the average modelled losses at 16.0log10(range). Therefore, the median ASLs, using 16.0log10(range), for the Primrose (at 5, 10, 20 and 30 km h−1, respectively) were 151.7, 153.3, 156.2, and 158.7; for the Macquarie, they were 146.7, 152.9, 158.2, and 159.2; and for the Kirsty K, they were 154.4, 159.5, 160.0, and 159.7, respectively (Table 4).

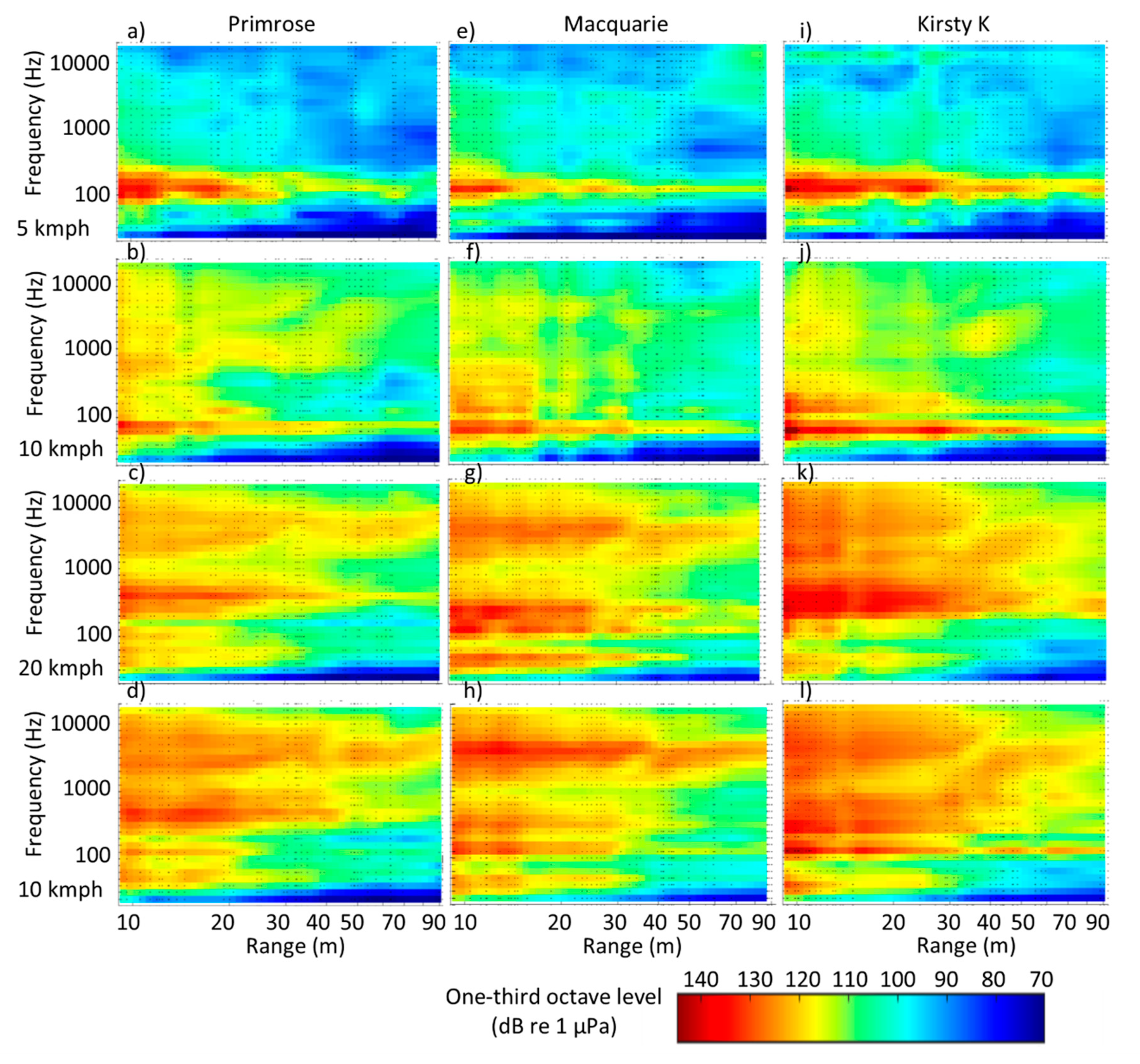
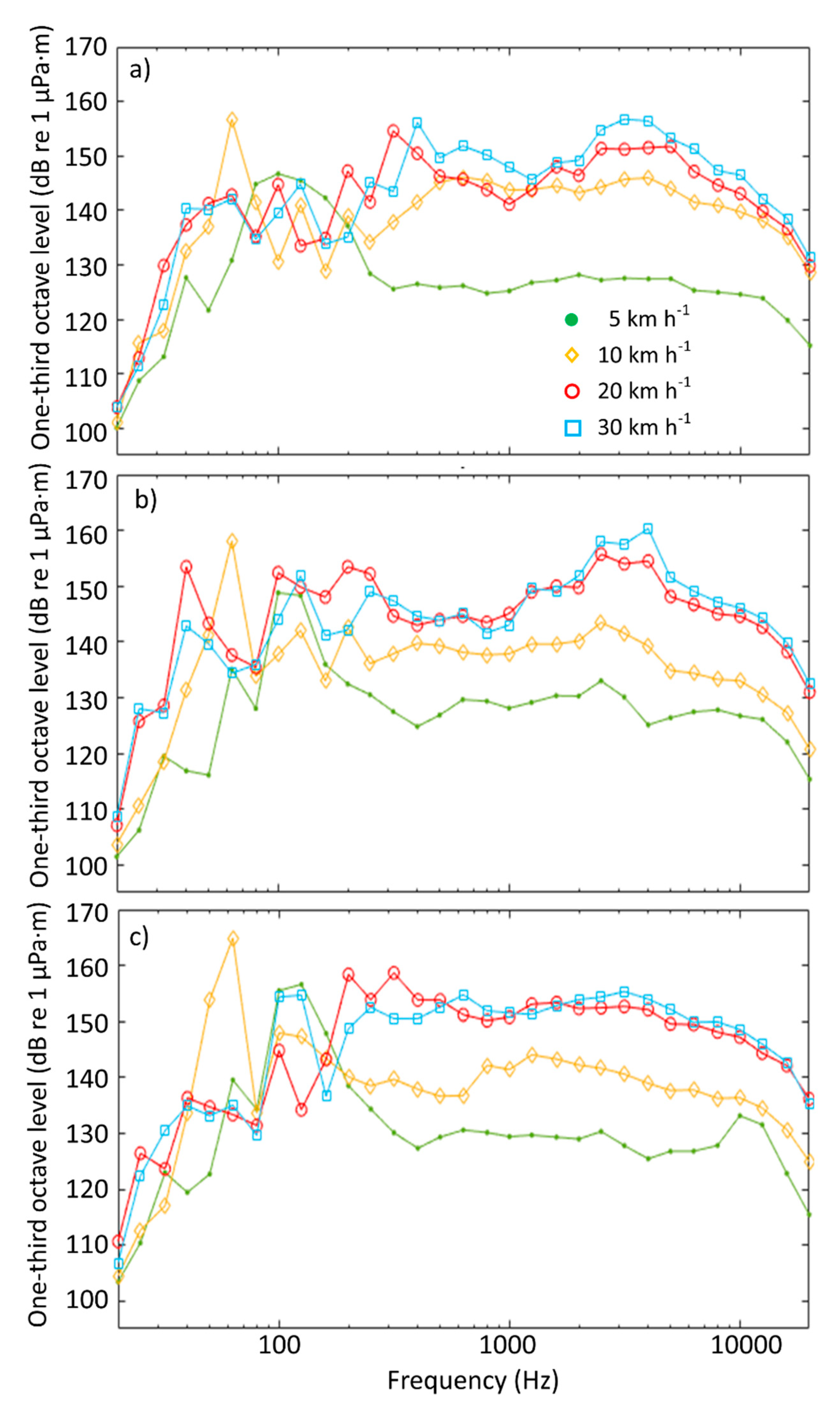
3.3. One-Third Octave Band Levels

The interpolated one-third octave band levels received across the different slant ranges illustrate the interference pattern with frequency and range (Figure 6). In all three vessels, the higher frequencies increased with increasing speed, shown by the one-third octave band levels and RNLs for each vessel (Figure 6 and Figure 7).
Linear regression determined one-third octave band PLs decreased with increasing frequency (Figure 8) from between 20 and 40 at frequencies below 50 Hz, to between 10 and 25 for frequencies between 50 and 2000 Hz. Above 2000 Hz, the propagation loss coefficients split with the vessels travelling at 5 km h−1 that exhibited little energy at these frequencies having coefficients of <10 (Figure 8, dots at >2000 Hz) and models for vessels with greater power and faster speeds displaying higher coefficients of 5 to 15 (Figure 8, red and green lines at >2000 Hz). Applying these frequency-dependent PL coefficients to the one-third octave band RLs produced ASL estimates higher than those derived using a single frequency-independent PL coefficient (Supplementary information).

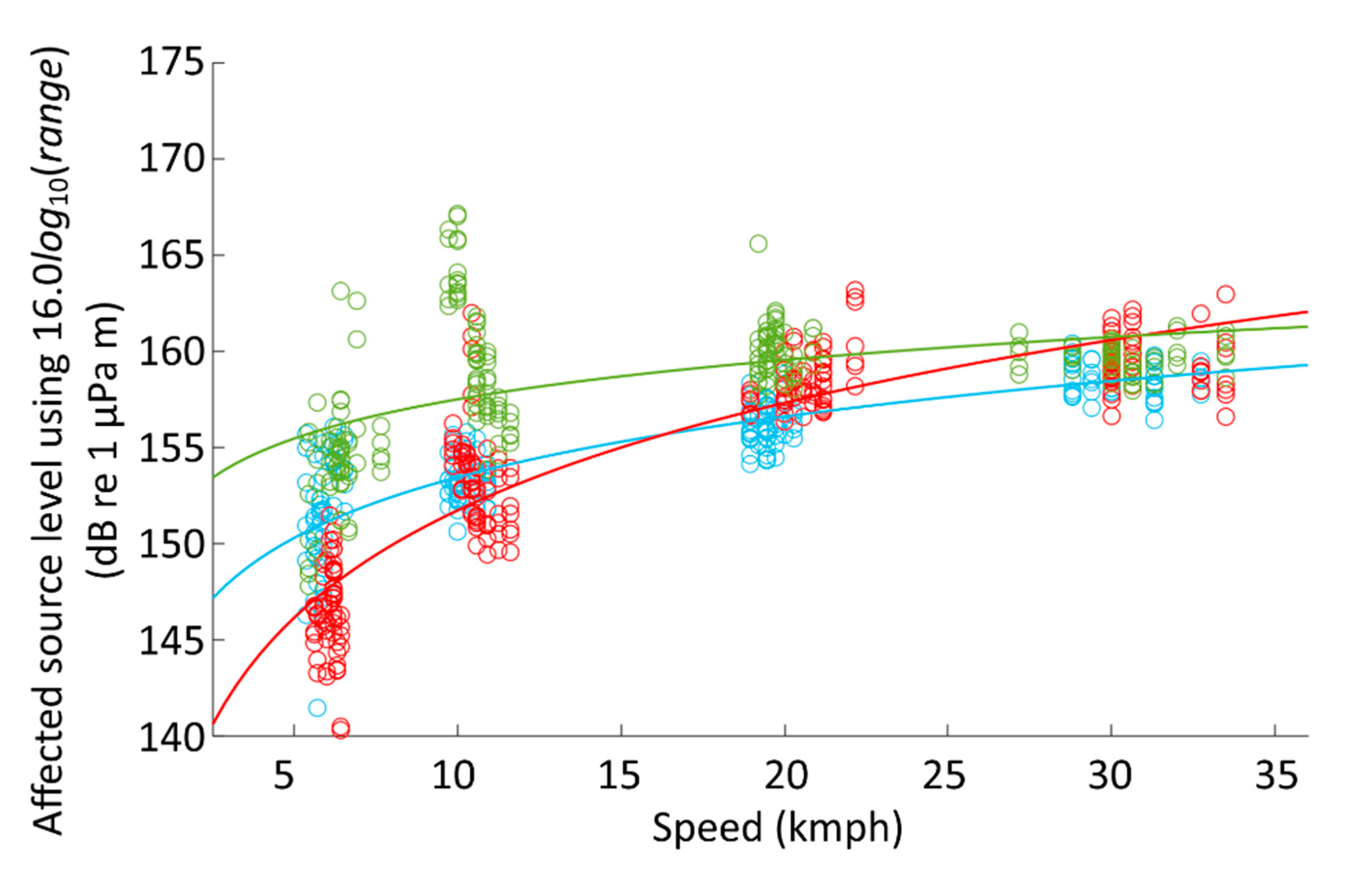
3.4. Received Levels with Speed

All three vessels displayed a general increasing trend in source level with speed, with Cv1 values of 1.05 (s.d. = 0.09), 1.86 (0.11), and 0.68 (0.15) for the Primrose, Macquarie and Kirsty K, respectively (Table 5). While the Primrose ASLs clearly increased with each speed increase, the Macquarie appeared close to asymptote by 30 km h−1 and the Kirsty K appeared to reduce in source level after 20 km h−1 (Figure 9).

4. Discussion

Management strategies to mitigate the impacts of noise pollution by vessels in marine environments rely on an understanding of the acoustic signature of different vessel types. The variation in frequency bands in which species can detect sound means that reporting broadband RNLs or MSLs alone is insufficient information to support management decisions [36,43]. We characterized the acoustic pressure signatures for the CPA of three small (<10 m length) vessels of similar lengths, but differing engine power, at multiple speeds. We empirically measured the propagation of their noise in shallow water (10 m depth) over the flat, sandy lagoon of a tropical granitic island, from within the near field (directly beneath the vessels at the 9 m range), out to the 100 m range. RNL and empirically modelled ASL have been determined for each speed and vessel. RNLs for small vessels, particularly those under 10 m length, are rarely reported and MSLs even less so [26,36,37,53]. Thus, the estimated RNLs, ASLs, and one-third octave band levels described here provide useful information on both shallow-water propagation of these signals and the source levels and spectra that can be applied to modelling of vessel noise.
The ISO have provided criteria for quantifying RNLs. However, the highest criteria cannot be met in Australia’s shallow coastal waters. Estimation of MSLs require accurate knowledge of seafloor geomorphology (and other marine geophysical characteristics) to ensure that PL is modelled appropriately, otherwise unexpected features may arise, potentially resulting in misleading estimates [42]. Our study recorded >80 measurements at a slant ranges of between 9 and 100 m for each vessel–speed scenario to ensure PL could be estimated with confidence. RLs recorded within the closest 15 m displayed greater variation than those taken at greater ranges (Supplementary information), justifying the removal of these data from PL models on the basis that they were in the acoustic near field. This still left >50 measurements for each scenario. PL coefficients in individual vessel/speed models excluding these data ranged between 13.6 and 19.8 and produced an average coefficient of 16.0 across the 12 PL models (Table 3), approximately halfway between cylindrical and spherical spreading losses, a reasonable estimate of PL in the tested conditions [54]. As the level of required information makes the accuracy of MSL estimates difficult to assess retrospectively, we argue that measurement of RLs for multiple passes at multiple ranges to model PL through linear regression of empirical measurements was an appropriate alternative to propagation modelling for similar shallow-water cases.
Not all low-frequency energy is accounted for in this method, as indicated by the low RNLs (Figure 7) and high propagation losses (Figure 8) of one-third octave bands at frequencies below 80 Hz, as would be expected with estimates made using a dipole model. However, similar errors may also often be found in the determination of MSLs in shallow water where geomorphological information has not been accurately identified. Thus, the RNL and ASL estimates provided here are representative of the 80-20,000 Hz band. Applying linear-regression to the one-third octave band RLs to determine frequency-dependent PLs can identify where some of the low-frequency energy is missed in the RNL and ASL estimates (Figure 8, Supplementary information). However, using the vessel noise as a source can be misleading as it does not necessarily contain sufficient energy across the desired bandwidth to provide accurate PLs from linear regression. For example, vessels travelling at 5 km h−1 emitted relatively little sound above 2 kHz, thus the PLs appeared to be low (Figure 8, lower values of Cr at frequencies above 2 kHz). This can be alleviated by using a standardized source, such as a speaker and tone generator at the desired frequencies, though these unfortunately not available during this study. The difference between estimates of RNL (excluding data at the <15 m range) and ASL (using averaged PL models and excluding data at the <15 m range) across all vessels and speeds was 6.4 dB, while the mean difference between ASLs with and without data within the 15 m range for each scenario was -3.2 dB (s.d. = 4.9 dB, Table 3 and Table 4). Additionally, the average correlation coefficient (R2) of the individual models decreased from 0.87 to 0.80 when the data <15 m were removed (Table 3). The average difference between 25th and 75th percentiles for RNLs and averaged-loss ASLs was 2.8 dB (s.d. = 1.3, Table 4), whereas the average range was 8.8 dB (s.d. = 3.3 dB). In contrast, the average standard deviation in ASL estimates from individual speed-/vessel-specific models was 6.7 dB (Table 3). These findings show that multiple measurements of an individual vessel at the same speed can be variable and greater than the changes found by moving from a spherical spreading calculation of RNL to the linear regression-modelled ASL. Removing the near-field measurements was prudent, as this reduced the PL estimate in almost every model and the resulting estimated ASLs, albeit by less than 3 dB (Table 3).
Wladichuk et al. [36] measured multiple vessel categories, of which rigid hull inflatable boats (RHIBs) were the most similar to the vessels in this study. Broadband RNLs for these vessels were 160.9 and 167.0 dB re 1 µPa m for ≈13 and 28 km h−1, respectively [36], though RHIBs were larger both in length (5.2 to 8.2 m) and engine power (150 to 700 hp) than the vessels we recorded at Lizard Island. The Kirsty K, the closest vessel in size and power measured here to the previously measured RHIBs [36], produced ASLs of ≈160 dB re 1 µPa m and spherical spreading RNLs of 165–166 dB re 1 µPa, at both of these speeds (Table 4). Erbe [26] and Erbe et al. [37] estimated RNLs and MSLs of various RHIBs, ranging from 7 to 9.1 m length and engine powers from 90 to 450 hp. Differences in estimated levels at any one speed, across all vessels, were found to be up to >20 dB, comparable with the variation found between the Primrose, Macquarie and Kirsty K (Table 3 and Table 4). One vessel (6.5 m length, 90 hp) in Erbe et al. [37], produced MSLs of approximately 154, 156 and 153 dB re 1 µPa m at speeds of approximately 12, 20 and 30 km h−1, respectively, in 8 m of flat water. ASL estimates of the Macquarie, the vessel of most similar size and power measured at Lizard Island were 152.9, 158.2 and 159.2 dB re 1 µPa m, respectively, for similar speeds (Table 4). Thus, the ASLs estimated here using PLs of 16log10(range) were comparable with previous measures.
Estimations of RNL and MSL typically use recordings of the CPA, or an averaged azimuth about the CPA, and assume that maximum broadband levels are received when broadside to the vessel or that there is no horizontal source directionality [37,44]. However, recorded noise levels can depend on azimuth and inclination, with some reports suggesting acoustic shielding at fore, aft or broadside, depending on the vessel design [42,55]. For example, similar to Parsons et al. [42], the recordings taken at Lizard Island displayed higher levels of acoustic energy in front of the vessel than behind, suggesting that entrained bubbles behind the vessels, generated by cavitation, have a shadowing effect after the vessel has passed. In this study, maximum levels were assumed to be broadside and directionality to be symmetrical about the centerline of the vessels, thus data from both port and starboard recordings were pooled during analysis. Any adjustment (e.g., altering power or trim) to maintain the correct speed and direction to account for wind and current can alter acoustic output of the vessel. Variations in RL recorded at Lizard Island were greatest at the slowest speed, which matched anecdotal comments from the skipper that holding the appropriate direction and line was more difficult when moving slowly. Erbe et al. [37] noted similar variability in their estimates of RNLs and MSLs of rigid-hulled inflatable boats (RHIBS) and hypothesized potential reasons for them. Acoustic output and potential shielding (e.g., by factors such as the bubble cloud and vessel hull) both contribute to the RL. Thus, changes to hull inclination and size of the cavitation vortices in the vessel wake, which occur with changes in speed or power, may be indicative of both acoustic output and dampening. Measurement of these factors could provide greater information to characterize the acoustic signature.
Ross [31] defined a relationship between vessel speed and changes in source level that Erbe [26] and then Wladichuk et al. [36] investigated for small vessels, albeit with few measures at different speeds. Broadband level increases with speed in this study comprised Cv values of 1.05, 1.86 and 0.68 for the Primrose, Macquarie and Kirsty K, respectively (Table 5). Wladichuk et al. [36] also observed a wide range in the same coefficient for their RHIB class (1.3 to 1.8), though they were generally higher than the three vessels studied here (Table 5). It is possible that the greater variability found at the slower speeds tested at Lizard Island (5 km h−1), lack of measurements at the higher speeds (>30 km h−1), yet significantly more measurements at speeds in between, can account for this difference. However, Wladichuk et al. [36] also found a much greater variation in Cv for monohulls ranging between 1.0 and 3.6, thus it is likely that the relationship between source spectra and speed is highly vessel specific.
Erbe et al. [37] noted that the decline in MSL after 20 km h−1 (which continued to speeds of ≈40 km h−1) was likely due to reaching its ‘hump’ speed, when the bow-up angle was largest, producing a large trim and water resistance and therefore propeller loading. Above this speed, the vessel begins to plane, resistance and propeller loading drops, and so too does the noise level. The three vessels at Lizard Island did not display a distinct hump across the speeds measured (Figure 9). However, the asymptotic nature of the Macquarie and Kirsty K RNL and ASL curves with speed suggest that this could have occurred between 20 and 30 km h−1 or about to occur with increasing speed. If measures at Lizard Island had extended to the maximum speeds of each vessel, such a relationship might have been observed. At planing speeds, Erbe et al. [37] also found that variation in RLs increased with speed, attributing this to the additional sound of vessel slap on the water for some measurements, highlighting that multiple measures are required, even for an individual speed.
At the slower speeds tested at Lizard Island, almost all energy in all three vessels occurred below 200 Hz, increasing up to 10 kHz at the faster speeds (Figure 7). Energy at all frequencies was detected at the furthest ranges for the highest vessel speeds (Figure 6). Ideally, for the same speed and vessel, the interpolated measurements of one-third octave levels would represent the similar Lloyd’s mirror pattern seen in the spectrograms of the individual recordings as the vessel approaches and passes the hydrophone. This pattern can be seen to varying degrees in all scenarios in Figure 6. However, these patterns are blurred by the interpolation across range and the integration of the spectra into one-third octave bands, which blurs the narrowband energy. These frequencies were all within the hearing sensitivity range of most fishes and overlapped with those of many cetaceans [22], with the majority of energy at the most sensitive frequencies and main communication band of most fishes [56,57,58,59,60]. Although several studies have been conducted on the impacts of noise from such vessels on the ecology of fishes and invertebrates in recent years [61,62,63,64], and specific ways to mitigate these impacts in shallow water are being investigated [38,42], there remains a knowledge gap in this area.
Together with previous studies, the data from the Primrose, Macquarie and Kirsty K highlight that to fully understand a vessel’s acoustic signature requires taking multiple measurements at multiple speeds and that within a given vessel class, large differences can be observed between vessels. Additional measures (e.g., data on vessel inclination, wake and size or vortices behind the vessel) may help assess the noise signature and understand differences between vessels and speeds. For appropriate modelling to be conducted with a view to mitigating the impact of noise from small vessels, a meta-analysis of all reported data is required.

Supplementary Materials

The following are available online at https://www.mdpi.com/2077-1312/8/12/970/s1, Table S1: Standard deviation in RNL estimates within shown range brackets for the various vessels and speeds, Table S2: Percentiles and maximum ranges of affected source levels calculated using propagation loss coefficients derived from linear regression of one-third octave band received levels at multiple ranges

Author Contributions

Conceptualization, M.P.; methodology, M.P. and M.M.; formal analysis, M.P.; writing—original draft preparation, M.P.; writing—review and editing, M.P. and M.M.; visualization, M.P. and M.M..; funding acquisition, M.M. All authors have read and agreed to the published version of the manuscript.

Funding

This work was undertaken for the Marine Biodiversity Hub, a collaborative partnership supported through funding from the Australian Government’s National Environmental Science Program.

Acknowledgments

The authors would like to thank Drs. Mark McCormick and Jen Kelley, and the Lizard Island Research Station for logistical support and assistance during data collection. The authors would also like to thank three reviewers for the time to consider the manuscript and for their valuable suggestions.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Winn, H.E. The biological significance of fish sounds. Mar. Bioacoust. 1964, 2, 213–231. [Google Scholar]
  2. Au, W.W.L.; Hastings, M.C. Principles of Marine Bioacoustics, 2nd ed.; Springer: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
  3. Radford, C.A.; Stanley, J.A.; Hole, W.; Montgomery, J.C.; Jeffs, A. Localised coastal habitats have distinct underwater sound signatures. Mar. Ecol. Prog. Ser. 2010, 401, 21–29. [Google Scholar] [CrossRef]
  4. Erbe, C.; Reichmuth, C.; Cunningham, K.; Lucke, K.; Dooling, R. Communication masking in marine mammals: A review and research strategy. Mar. Pollut. Bull. 2016, 103, 15–38. [Google Scholar] [CrossRef] [PubMed]
  5. Simpson, S.; Meekan, M.G.; Montgomery, J.; McCauley, R.D.; Jeffs, A. Homeward Sound. Science 2005, 308, 221. [Google Scholar] [CrossRef]
  6. Simpson, S.; Radford, A.; Nedelec, S.; Ferrari, M.C.O.; Chivers, D.P.; McCormick, M.I.; Meekan, M.G. Anthropogenic noise increases fish mortality by predation. Nat. Commun. 2016, 7, 10544. [Google Scholar] [CrossRef]
  7. Parsons, M.J.G.; McCauley, R.D.; Mackie, M.C.; Siwabessy, P.J.; Duncan, A.J. In situ source levels of mulloway (Argyrosomus japonicus) calls. J. Acoust. Soc. Am. 2012, 132, 3559–3568. [Google Scholar] [CrossRef]
  8. Stanley, J.A.; Van Parijs, S.M.; Hatch, L.T. Underwater sound from vessel traffic reduces the effective communication range in Atlantic cod and haddock. Sci. Rep. 2017, 7, 14633. [Google Scholar] [CrossRef]
  9. Van der Graaf, A.J.; Ainslie, M.A.; Andre, M.; Brensing, K.; Dalen, J.; Dekeling, R.P.A.; Robinson, S.M.; Tasker, M.I.; Thomsen, F.; Werner, S. European Marine Strategy Framework Directive-Good Environmental Status (MSFD GES): Report of the Technical Subgroup on Underwater Noise and Other Forms of Energy (JRC Scientific and Technical Report); TSG Noise & Milieu Ltd.: Brussels, Belgium, 2012; 75p. [Google Scholar]
  10. Weilgart, L.S. The impacts of anthropogenic ocean noise on cetaceans and implications for management. Can. J. Zool. 2007, 85, 1091–1116. [Google Scholar] [CrossRef]
  11. Graham, A.L.; Cooke, S.J. The effects of noise disturbance from various recreational boating activities common to inland waters on the cardiac physiology of a freshwater fish, the largemouth bass (Micropterus salmoides). Aquat. Cons. Mar. Fresh. Ecosyst. 2008, 18, 1315–1324. [Google Scholar] [CrossRef]
  12. Williams, R.; Erbe, C.; Ashe, E.; Beerman, A.; Smith, J. Severity of killer whale behavioral responses to ship noise: A dose response study. Mar. Poll. Bull. 2014, 79, 254–260. [Google Scholar] [CrossRef]
  13. Simpson, S.D.; Radford, A.N.; Holles, S.; Ferarri, M.C.O.; Chivers, D.P.; McCormick, M.I.; Meekan, M.G. Small-Boat Noise Impacts Natural Settlement Behavior of Coral Reef Fish Larvae. In The Effects of Noise on Aquatic Life II. Advances in Experimental Medicine and Biology; Popper, A., Hawkins, A., Eds.; Springer: New York, NY, USA, 2016; Volume 875. [Google Scholar] [CrossRef]
  14. Nedelec, S.L.; Mills, S.C.; Radford, A.N.; Belade, R.; Simpson, S.D.; Nedelec, B.; Côté, I.M. Motorboat noise disrupts co-operative interspecific interactions. Sci. Rep. 2017, 7, 6987. [Google Scholar] [CrossRef] [PubMed]
  15. Erbe, C.; Marley, S.; Schoeman, R.; Smith, J.N.; Trigg, L.; Embling, C.B. The effects of ship noise on marine mammals—A review. Front. Mar. Sci. 2019, 6, 606. [Google Scholar] [CrossRef]
  16. Ross, D. Ship sources of ambient noise. IEEE J. Ocean. Eng. 2005, 30, 257–261. [Google Scholar] [CrossRef]
  17. McDonald, M.A. Increase in deep ocean ambient noise in the Northeast Pacific west of San Nocolas Island. J. Acoust. Soc. Am. 2006, 120, 711–718. [Google Scholar] [CrossRef] [PubMed]
  18. Hildebrand, J.A. Anthropogenic and natural sources of ambient noise in the ocean. Mar. Ecol. Prog. Ser. 2009, 395, 5–20. [Google Scholar] [CrossRef]
  19. Frisk, G. Noiseonomics: The relationship between ambient noise levels in the sea and global economic trends. Sci. Rep. 2012, 2, 437. [Google Scholar] [CrossRef]
  20. Williams, R.; Wright, A.J.; Ashe, E.; Blight, L.K.; Bruintjes, R.; Canessa, R.; Clark, C.W.; Cullis-Suzuki, S.; Dakin, D.T.; Erbe, C.; et al. Impacts of anthropogenic noise on marine life: Publication patterns, new discoveries, and future directions in research and management. Ocean Coast. Man. 2015, 115, 17–24. [Google Scholar] [CrossRef]
  21. McWhinnie, L.; Smallshaw, L.; Serra-Sogas, N.; O’Hara, P.D.; Canessa, R. The grand challenges in researching marine noise pollution from vessels: A horizon scan for 2017. Front. Mar. Sci. 2017, 4, 31. [Google Scholar] [CrossRef]
  22. Duarte, C.M.; Chapuis, L.; Collin, S.P.; Costa, D.P.; Devassy, R.P.; Eguiluz, V.M.; Erbe, C.; Halpern, B.S.; Harding, H.R.; Havlik, M.N.; et al. The Ocean Soundscape of the Anthropocene. Science 2020. accepted. [Google Scholar]
  23. Blane, J.; Jaakson, R. The impact of ecotourism boats on the St. Lawrence beluga whales. Environ. Cons. 1994, 21, 267–269. [Google Scholar] [CrossRef]
  24. Erbe, C. Underwater noise of whale-watching boats and potential effects on killer whales (Orcinus orca), based on an acoustic impact model. Mar. Mamm. Sci. 2002, 18, 394–418. [Google Scholar] [CrossRef]
  25. Erbe, C.; Williams, R.; Sandilands, D.; Ashe, E. Identifying modeled ship noise hotspots for marine mammals of Canadas’ Pacific Region. PLoS ONE 2014, 9, e89820. [Google Scholar] [CrossRef] [PubMed]
  26. Merchant, N.D.; Pirotta, E.; Barton, T.R.; Thompson, P.M. Monitoring ship noise to assess the impact of coastal developments on marine mammals. Mar. Poll. Bull. 2014, 78, 85–95. [Google Scholar] [CrossRef] [PubMed]
  27. New, L.F.; Hall, A.J.; Harcourt, R.; Kaufman, G.; Parsons, E.C.M.; Pearson, H.C.; Cosentino, A.M.; Schick, R.S. The modelling and assessment of whale-watching impacts. Ocean Coast. Manag. 2015, 115, 10–16. [Google Scholar] [CrossRef]
  28. Cominelli, S.; Devillers, R.; Yurk, H.; MacGillivray, A.O.; McWhinnie, L.; Canessa, R. Noise exposure from commercial shipping for the southern resident killer whale population. Mar. Poll. Bull. 2018, 136, 177–200. [Google Scholar] [CrossRef] [PubMed]
  29. Hatch, L.; Clark, C.W.; Merrick, R.; Van Parijs, S.M.; Ponirakis, D.; Schwehr, K.; Thompson, M.; Wiley, D. Characterizing the relative contributions of large vessels to total ocean noise fields: A case study using the Gerry E. Studds Stellwagen Bank National Marine Sanctuary. Environ. Man. 2008, 42, 735–752. [Google Scholar]
  30. Erbe, C.; MacGillivray, A.O.; Williams, R. Mapping cumulative noise from shipping to inform marine spatial planning. J. Acoust. Soc. Am. 2012, 132, EL423–EL428. [Google Scholar] [CrossRef]
  31. Ross, D. Mechanics of Underwater Noise; Pergamon Press: New York, NY, USA, 1976. [Google Scholar]
  32. Chion, C.; Lagrois, D.; Dupras, J. A meta-analysis to understand the variability in reported source levels of noise radiated by ships from opportunistic studies. Front. Mar. Sci. 2019, 6, 714. [Google Scholar]
  33. Au, W.W.L.; Green, M. Acoustics interaction of humpback whales and whale-watching boats. Mar. Environ. Res. 2000, 49, 469–481. [Google Scholar] [CrossRef]
  34. Buckstaff, K.C. Effects of watercraft noise on the acoustic behaviour of bottlenose dolphins Tursiops truncates in Sarasota Bay. Fla. Mar. Mam. Sci. 2004, 20, 709–725. [Google Scholar] [CrossRef]
  35. Brooker, A.; Humphrey, V. Measurement of radiated underwater noise from a small research vessel in shallow water. Ocean Eng. 2015, 120, 182–189. [Google Scholar] [CrossRef]
  36. Wladichuk, J.L.; Hannay, D.E.; MacGillivray, A.O.; Li, Z.; Thornton, S.J. Systematic source level measurements of whale watching vessels and other small boats. J. Ocean. Technol. 2019, 14, 110–126. [Google Scholar]
  37. Erbe, C.; Liong, S.; Koessler, M.W.; Duncan, A.J.; Gourlay, T. Underwater sound of rigid-hulled inflatable boats. J. Acoust. Soc. Am. 2016, 139, EL223–EL227. [Google Scholar] [CrossRef] [PubMed]
  38. McCloskey, K.P.; Chapman, K.E.; Chapuis, L.; McCormick, M.I.; Radford, A.N.; Simpson, S.D. Assessing and mitigating impacts of motorboat noise on nesting damselfish. Environ. Poll. 2020, 266, 115376. [Google Scholar] [CrossRef]
  39. Marley, S.A.; Erbe, C.; Salgado-Kent, C.P.; Parsons, M.J.G.; Parnum, I.M. Spatial and Temporal Variation in the Acoustic Habitat of Bottlenose Dolphins (Tursiops aduncus) within a Highly Urbanized Estuary. Front. Mar. Sci. 2017, 4, 197. [Google Scholar] [CrossRef]
  40. Parsons, M.J.G.; McCauley, R.D.; Mackie, M.C. Characterisation of mulloway (Argyrosomus japonicus) advertisement sounds. Acoust. Aust. 2013, 196, 196–201. [Google Scholar]
  41. Nedelec, S.L.; Radford, A.N.; Pearl, L.; Nedelec, B.; McCormick, M.I.; Meekan, M.G.; Simpson, S.D. Motorboat noise impacts parental behaviour and offspring survival in a reef fish. Proc. R. Soc. B. 2017, 284, 20170143. [Google Scholar] [CrossRef]
  42. Parsons, M.J.G.; Duncan, A.J.; Parsons, S.K.; Erbe, C. Reducing vessel noise: An example of a solar-electric passenger ferry. J. Acoust. Soc. Am. 2020, 147, 3575–3583. [Google Scholar] [CrossRef]
  43. Malinowski, S.J.; Gloza, I. Underwater noise characteristics of small ships. Acta Acust. United Acust. 2002, 88, 718–721. [Google Scholar]
  44. International Organization for Standardization. Underwater Acoustics—Quantities and Procedures for Description and Measurement of Underwater Sound from Ships—Part 1: Requirements for Precision Measurements in Deep Water Used for Comparison Purposes (ISO 17208-1); International Organization for Standardization: Geneva, Switzerland, 2016; 20p. [Google Scholar]
  45. International Organization for Standardization. Underwater Acoustics—Quantities and Procedures for Description and Measurement of Underwater Sound from Ships—Part 2: Determination of Source Levels from Deep Water Measurements (ISO 17208-2); International Organization for Standardization: Geneva, Switzerland, 2019; 13p. [Google Scholar]
  46. Hamylton, S.M.; Leon, J.X.; Saunders, M.I.; Woodroffe, C.D. Simulating reef response to sea-level rise at Lizard Island: A geospatial approach. Geomorphology 2014, 222, 151–161. [Google Scholar] [CrossRef]
  47. Daly, M. Wave Energy and Shoreline Response on a Fringing Reef Complex, Lizard Island, Qld, Australia. Bachelor’s Thesis, Env. Sci., University of New South Wales, Sydney, Australia, 2005; 105p. [Google Scholar]
  48. Frith, C.; Leis, J.; Goldmand, B. Currents in the Lizard Island region of the Great Barrier Reef Lagoon and their relevance to potential movements of larvae. Coral Reefs 1986, 5, 81–92. [Google Scholar] [CrossRef]
  49. Gavrilov, A.G.; Parsons, M.J.G. A Matlab toolbox for the Characterisation of Recorded Underwater Sound (CHORUS). Acoust. Aust. 2014, 42, 191–196. [Google Scholar]
  50. Urick, R.J. Principles of Underwater Sound, 3rd ed.; McGraw Hill: New York, NY, USA, 1983. [Google Scholar]
  51. De Jong, C.A.F. Characterization of ships as sources of underwater noise. In Proceedings of the NAG-DAGA 2009, Rotterdam, The Netherlands, 23–26 March 2009; pp. 271–274. [Google Scholar]
  52. Veirs, S.; Veirs, V. Vessel noise measurements underwater in the Haro Strait, WA. J. Acoust. Soc. Am. 2006, 120, 3382. [Google Scholar] [CrossRef]
  53. Kipple, B.; Gabriele, C. Underwater noise from skiffs to ships. In Proceedings of the Fourth Glacier Bay Science Symposium, Junea, AK, USA, 26–28 October 2004; Piatt, J.F., Gende, S.M., Eds.; U.S. Geological Survey Scientific Investigations Report 2007-5047; 2007 U.S. Geological Survey. pp. 172–175. [Google Scholar]
  54. Cato, D.H. Simple methods of estimating source levels and locations of marine animal sounds. J. Acoust. Soc. Am. 1998, 104, 1667–1678. [Google Scholar] [CrossRef] [PubMed]
  55. McCauley, R.D.; Cato, D.H.; Jeffrey, A.F. A Study of Impacts of the Impacts of Vessel Noise on Humpback Whales in Hervey Bay; Report to the Queensland Department of Environment and Heritage; Maryborough Branch: Queensland, Australia, 1996; 163p. [Google Scholar]
  56. Ladich, F.; Fay, R.R. Auditory evoked potential audiometry in fish. Rev. Fish. Biol. Fish. 2013, 23, 317–364. [Google Scholar] [CrossRef] [PubMed]
  57. Kasumyan, A.O. Acoustic signaling in fish. J. Ichthyol. 2009, 49, 963–1020. [Google Scholar] [CrossRef]
  58. Parsons, M.J.G.; Longbottom, S.; Lewis, P.; McCauley, R.D.; Fairclough, D.V. Sound production by the West Australian dhufish (Glaucosoma hebraicum). J. Acoust. Soc. Am. 2013, 134, 2701–2709. [Google Scholar] [CrossRef]
  59. McWilliam, J.N.; McCauley, R.D.; Erbe, C.; Parsons, M.J.G. Patterns of biophonic periodicity on coral reefs in the Great Barrier Reef. Sci. Rep. 2017, 7, 17459. [Google Scholar] [CrossRef]
  60. Montgomery, J.C.; Jeffs, A.; Simpson, S.D.; Meekan, M.G.; Tindle, C. Sound as an Orientation Cue for the Pelagic Larvae of Reef Fishes and Decapod Crustaceans. Adv. Mar. Biol. 2006, 51, 143–196. [Google Scholar]
  61. Radford, A.N.; Kerridge, E.; Simpson, S.D. Acoustic communication in a noisy world: Can fish compete with anthropogenic noise? Behav. Ecol. 2014, 25, 1022–1030. [Google Scholar] [CrossRef]
  62. Nedelec, S.L.; Mills, S.C.; Lecchini, D.; Nedelec, B.; Simpson, S.D.; Radford, A.N. Repeated exposure to noise increases tolerance in a coral reef fish. Environ. Pollut. 2016, 216, 428–436. [Google Scholar] [CrossRef] [PubMed]
  63. Putland, R.L.; Merchant, N.D.; Farcas, A.; Radford, C.A. Vessel noise cuts down communication space for vocalizing fish and marine mammals. Glob. Chang. Biol. 2018, 24, 1708–1721. [Google Scholar] [CrossRef] [PubMed]
  64. Mensinger, A.F.; Putland, R.L.; Radford, C.A. The effect of motorboat sound on Australian snapper Pagrus auratus inside and outside a marine reserve. Ecol. Evol. 2018, 8, 6438–6448. [Google Scholar] [CrossRef] [PubMed]
Jmse 08 00970 g001
Figure 1. (a) Map of Australia with expansion of Cape York Peninsula, Queensland; (b) expansion of Lizard Island on the Great Barrier Reef; (c–e) expansions of the island lagoon with the vessel tracks from three consecutive survey days (c, d, and e, respectively) displayed in white and the positions of pairs of seafloor-mounted SoundTraps shown by the red dots.
Figure 1. (a) Map of Australia with expansion of Cape York Peninsula, Queensland; (b) expansion of Lizard Island on the Great Barrier Reef; (c–e) expansions of the island lagoon with the vessel tracks from three consecutive survey days (c, d, and e, respectively) displayed in white and the positions of pairs of seafloor-mounted SoundTraps shown by the red dots.
Jmse 08 00970 g001
Jmse 08 00970 g002
Figure 2. Photos of research vessels (a) Primrose, (b) Macquarie 2 and (c) Kirsty K.
Figure 2. Photos of research vessels (a) Primrose, (b) Macquarie 2 and (c) Kirsty K.
Jmse 08 00970 g002
Jmse 08 00970 g003
Figure 3. Spectrograms of 20 s recordings of individual passes of (a–c) Primrose, (d–f) Macquarie and (g–i) Kirsty K (all travelling at ≈30 km h−1), as recorded almost directly (a,d,g) beneath the vessel (≈9 m range), (b,e,h) at the 25 m and (c,f,i) the ≈100 m ranges. CPA distance shown in top right of each spectrogram.
Figure 3. Spectrograms of 20 s recordings of individual passes of (a–c) Primrose, (d–f) Macquarie and (g–i) Kirsty K (all travelling at ≈30 km h−1), as recorded almost directly (a,d,g) beneath the vessel (≈9 m range), (b,e,h) at the 25 m and (c,f,i) the ≈100 m ranges. CPA distance shown in top right of each spectrogram.
Jmse 08 00970 g003
Jmse 08 00970 g004
Figure 4. Received sound pressure levels from directly beneath the vessel (9 m range) to the 100 m range for (a) Primrose, (b) Macquarie and (c) Kirsty K, at speeds of 5, 10, 20 and 30 km h−1 (green circles, beige diamonds, red circles and blue squares, respectively).
Figure 4. Received sound pressure levels from directly beneath the vessel (9 m range) to the 100 m range for (a) Primrose, (b) Macquarie and (c) Kirsty K, at speeds of 5, 10, 20 and 30 km h−1 (green circles, beige diamonds, red circles and blue squares, respectively).
Jmse 08 00970 g004
Jmse 08 00970 g005
Figure 5. Affected source levels using the average linear regression-determined propagation loss across all vessels, excluding ranges below 15 m (16.0log10{range}) for Primrose at category speeds of 5, 10, 20 and 30 km h−1 (green dots, beige diamonds, red circles and blue square, respectively).
Figure 5. Affected source levels using the average linear regression-determined propagation loss across all vessels, excluding ranges below 15 m (16.0log10{range}) for Primrose at category speeds of 5, 10, 20 and 30 km h−1 (green dots, beige diamonds, red circles and blue square, respectively).
Jmse 08 00970 g005
Jmse 08 00970 g006
Figure 6. Interpolated (in log frequency and log range bins) one-third octave band received levels with range for each vessel (a–d, Primrose; e–h, Macquarie; i–l, Kirsty K), at each speed. (a,e,i, 5 km h−1; b,f,j, 10 km h−1; c,g,k, 20 km h−1; d,h,l, 30 km h−1). Black dots show the ranges at which measurements were taken to highlight gaps in interpolated data.
Figure 6. Interpolated (in log frequency and log range bins) one-third octave band received levels with range for each vessel (a–d, Primrose; e–h, Macquarie; i–l, Kirsty K), at each speed. (a,e,i, 5 km h−1; b,f,j, 10 km h−1; c,g,k, 20 km h−1; d,h,l, 30 km h−1). Black dots show the ranges at which measurements were taken to highlight gaps in interpolated data.
Jmse 08 00970 g006
Jmse 08 00970 g007
Figure 7. One-third octave radiated noise levels for (a) Primrose, (b) Macquarie, and (c) Kirsty K, at speeds of 5, 10, 20 and 30 km h−1 (green circles, beige diamonds, red circles and blue squares, respectively).
Figure 7. One-third octave radiated noise levels for (a) Primrose, (b) Macquarie, and (c) Kirsty K, at speeds of 5, 10, 20 and 30 km h−1 (green circles, beige diamonds, red circles and blue squares, respectively).
Jmse 08 00970 g007
Jmse 08 00970 g008
Figure 8. One-third octave band propagation loss coefficients (Cr) determined from linear regression for Primrose, Macquarie and Kirsty K (blue, red and green, respectively). Mean one-third octave band propagation loss coefficients across all vessels and speeds shown by the black line.
Figure 8. One-third octave band propagation loss coefficients (Cr) determined from linear regression for Primrose, Macquarie and Kirsty K (blue, red and green, respectively). Mean one-third octave band propagation loss coefficients across all vessels and speeds shown by the black line.
Jmse 08 00970 g008
Jmse 08 00970 g009
Figure 9. Relationships between affected source levels using the average linear regression-determined propagation loss across all vessels, excluding ranges below 15 m and speed for the Primrose (blue circles), Macquarie (red circles) and Kirsty K (green circles).
Figure 9. Relationships between affected source levels using the average linear regression-determined propagation loss across all vessels, excluding ranges below 15 m and speed for the Primrose (blue circles), Macquarie (red circles) and Kirsty K (green circles).
Jmse 08 00970 g009
Table 1. Specifications of vessels recorded in Lizard Island lagoon.
Table 1. Specifications of vessels recorded in Lizard Island lagoon.
PrimroseMacquarie 2Kirsty K
Vessel specificationsLength (m)55.965.95
Width (m)2.12.42.6
Draught (cm)0.91.181.23
Mass (kg)3608251500
PropellerNo. blades333
Prop radius (cm)2532.532.5
Depth below water (cm)477063
EngineEngineSuzukiSuzukiSuzuki
Horsepower30902x90
FuelPetrol (4 stroke)Petrol (4 stroke)Petrol (4 stroke)
Table 2. Transect speeds conducted by each vessel (standard deviation, minimum and maximum speeds and the number of analyzed recordings shown in parentheses).
Table 2. Transect speeds conducted by each vessel (standard deviation, minimum and maximum speeds and the number of analyzed recordings shown in parentheses).
Target Speed (km h−1)Primrose
(km h−1)		Macquarie
(km h−1)		Kirsty K
(km h−1)
55.86 (0.12, 5.37, 6.55, 73)6.12 (0.23, 5.63, 6.43, 88)6.41 (0.61, 5.45, 7.66, 83)
1010.32 (0.50, 9.73, 10.91, 79)10.61 (1.64, 9.86, 11.61, 85)10.62 (0.59, 9.73, 11.61, 92)
2019.44 (0.39, 18.95, 20.28, 75)20.63 (3.32, 18.95, 3.32, 86)19.74 (0.52, 19.20, 20.87, 88)
3030.23 (1.23, 28.80, 32.73, 81)30.75 (3.30, 30.0, 33.49, 82)30.40 (1.72, 27.17, 33.49, 86)
Table 3. Propagation loss coefficients (CPL) and affected source levels for individual vessels and speeds determine from Equation (1) for all ranges and for only ranges >15 m. Mean log10(range) loss values (and standard deviation) found across all regression models with all data and for ranges >15 m are also included.
Table 3. Propagation loss coefficients (CPL) and affected source levels for individual vessels and speeds determine from Equation (1) for all ranges and for only ranges >15 m. Mean log10(range) loss values (and standard deviation) found across all regression models with all data and for ranges >15 m are also included.
All RangesExcluding <15 m Range
VesselSpeedCPLASL
(dB re 1 µPa)		R2CPLASL
(dB re 1 µPa)		R2
Primrose5−21.2 (−23.79, −18.64)159.8 (156.1, 163.6)0.79−19.5 (−22.98, −15.96)156.9 (151.2, 162.7)0.72
10−17.3 (−18.20, −16.33)155.4 (154.0, 156.8)0.95−16.2 (−17.44, −14.90)153.5 (151.4, 155.6)0.92
20−14.0 (−14.72, −13.24)153.0 (151.9, 154.1)0.95−13.6 (−14.70, −12.50)152.4 (150.6, 154.2)0.92
30−13.2 (−14.02, −12.38)154.1 (152.9, 155.3)0.93−14.5 (−15.65, −13.41)156.4 (154.5, 158.2)0.92
Macquarie5−21.5 (−23.50, −19.52)156.1 (153.2, 159.0)0.84−12.2 (−14.95, −9.43)140.5 (135.9, 145.0)0.58
10−21.3 (−23.31, −19.31)161.8 (158.8, 164.8)0.85−19.8 (−22.43, −17.10)159.2 (155.0, 163.4)0.78
20−17.9 (−18.96, −16.75)161.5 (159.9, 163.1)0.93−18.3 (−19.92, −16.67)162.2 (159.6, 164.8)0.90
30−13.7 (−14.68, −12.64)155.7 (154.2, 157.2)0.90−14.3 (−16.05, −12.57)156.7 (153.9, 159.6)0.84
Kirsty K5−21.6 (−23.83, −19.43)163.6 (160.4, 166.8)0.83−16.7 (−20.03, −13.42)155.3 (149.9, 160.7)0.67
10−18.7 (−21.38, −16.11)164.2 (160.3, 168.0)0.69−15.3 (−18.33, −12.21)158.5 (153.7, 163.2)0.58
20−17.2 (−18.41, −15.97)161.9 (160.1, 163.7)0.90−15.0 (−16.62, −13.43)158.3 (155.7, 160.8)0.86
30−17.3 (−18.40, −16.13)161.8 (160.1, 163.4)0.92−16.9 (−18.09, −15.71)161.2 (159.2, 163.1)0.94
Mean CPL (s.d.)−17.9 (3.1) −16.0 (2.3)
Table 4. Percentiles and maximum ranges of radiated noise levels and of affected source levels for the average log10(range) losses across modelled losses for individual vessels and speeds using all ranges and using all ranges >15 m.
Table 4. Percentiles and maximum ranges of radiated noise levels and of affected source levels for the average log10(range) losses across modelled losses for individual vessels and speeds using all ranges and using all ranges >15 m.
Percentiles of Radiated Noise Level
(dB re 1 µPa m)		Percentiles of Affected Source Level
(dB re 1 µPa m)
All RangesExcluding <15 m RangeLoss = 17.9log10 (range)Loss = 16.0log10 (range)
VesselSpeed25%50%75%Range25%50%75%Range25%50%75%Range25%50%75%Range
Primrose5155.5158.4160.218.8155.6158.3159.914.3152.4155.1157.420.2149.3151.7153.914.6
10158.6159.7160.57.3159.0159.9160.76.6155.4156.6157.26.7152.6153.3153.95.2
20160.3161.6163.510.8161.3162.3163.96.9157.6158.4159.98.9155.5156.2156.94.7
30163.6164.8166.19.4164.1165.4166.46.6160.1161.3162.48.1158.1158.7159.54.7
Macquarie5151.5153.4155.515.1151.5153.2155.28.6148.7150.5153.315.6145.4146.7148.411.2
10158.1159.6161.211.4158.0159.3161.010.6154.8156.4158.012.2151.4152.9154.310.7
20163.8164.6165.98.0163.8164.5165.96.6160.5161.3162.48.1157.5158.2159.36.8
30163.9165.4166.612.0164.7165.8167.17.9160.0161.9163.110.8158.6159.2160.46.4
Kirsty K5159.7161.2162.714.3159.8161.0162.414.3156.6158.1160.115.7153.2154.4155.415.3
10162.9165.3169.016.2163.5165.5169.711.9159.7162.1166.017.1157.1159.5162.713.3
20165.1166.0167.19.7165.5166.3167.26.6161.8163.0164.19.8159.1160.0160.97.9
30165.2166.1167.19.6165.7166.2167.14.5162.0162.9163.69.5158.9159.7160.23.4
Table 5. Linear regression logistic (or polynomial for the modelled affected source levels for Macquarie) relationship between radiated noise levels, ASLs and averaged log10(range) ASLs with speed, showing the theoretical source level at 0 km h−1 and remaining coefficients. Standard deviations shown in parentheses.
Table 5. Linear regression logistic (or polynomial for the modelled affected source levels for Macquarie) relationship between radiated noise levels, ASLs and averaged log10(range) ASLs with speed, showing the theoretical source level at 0 km h−1 and remaining coefficients. Standard deviations shown in parentheses.
VesselLevel at 0 km h−1Coefficient Cv1Coefficient Cv2R2RMSE
RNLPrimrose155.9 (0.7)0.84 (0.11)--0.432.60
Macquarie151.5 (0.7)1.55 (0.11)--0.682.87
Kirsty K161.6 (0.9)0.53 (0.14)--0.143.33
ASLPrimrose160.1 (0.7)−0.78 (0.11)--0.432.44
Macquarie150.1 (1.2)0.94 (0.12)−0.50 (0.06)0.502.62
Kirsty K165.1 (0.8)−0.37 0.12)--0.092.97
Full data (17.9 loss)Primrose152.9 (0.6)0.84 (0.1)--0.482.37
Macquarie148.4 (0.75)1.56 (0.11)--0.692.82
Kirsty K158.6 (0.9)0.53 (0.14)--0.153.32
Range >15 m (16.0 loss)Primrose148.8 (0.55)1.05 (0.09)--0.731.73
Macquarie143.5 (0.75)1.86 (0.12)--0.812.36
Kirsty K154.5 (11.0)0.68 (0.15)--0.272.86
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Parsons, M.; Meekan, M. Acoustic Characteristics of Small Research Vessels. J. Mar. Sci. Eng. 2020, 8, 970. https://doi.org/10.3390/jmse8120970

AMA Style

Parsons M, Meekan M. Acoustic Characteristics of Small Research Vessels. Journal of Marine Science and Engineering. 2020; 8(12):970. https://doi.org/10.3390/jmse8120970

Chicago/Turabian Style

Parsons, Miles, and Mark Meekan. 2020. "Acoustic Characteristics of Small Research Vessels" Journal of Marine Science and Engineering 8, no. 12: 970. https://doi.org/10.3390/jmse8120970

APA Style

Parsons, M., & Meekan, M. (2020). Acoustic Characteristics of Small Research Vessels. Journal of Marine Science and Engineering, 8(12), 970. https://doi.org/10.3390/jmse8120970

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop