Energy-Efficient Scheduling for Resilient Container-Supply Hybrid Flow Shops Under Transportation Constraints and Stochastic Arrivals
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Modeling
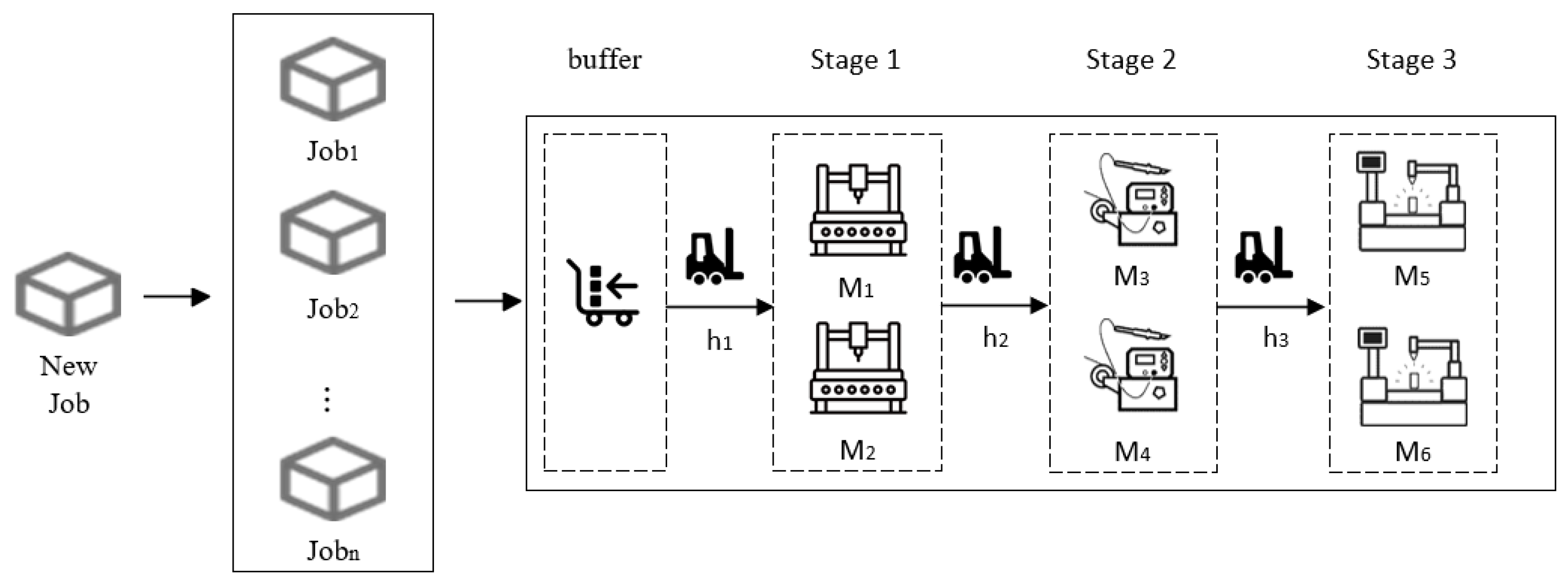
2.1.1. Problem Formulation
- Each machine can process only one task at any given moment.
- Every job must be processed by exactly one designated machine per operation.
- Job processing must proceed continuously once initiated, without suspension or interruption.
- All resources (machines/transport units) remain fully operational and available throughout the production timeline.
- Each operation can be executed on any eligible machine from the available set.
- Machines operate in four distinct modes: active processing, standby, maintenance, and shutdown, each with unique energy consumption patterns.
- Transport speed varies between the loaded and unloaded states of the transfer unit.
- Initial locations of all jobs and transport units reside in an unbounded-capacity buffer zone.
- Transportation assignments are exclusive—each task requires dedicated transporter allocation, and each transporter handles only one task concurrently.
- Potential conflicts or collision avoidance between transporters are excluded from consideration.
- Transport distance computations employ Manhattan metric principles.
- Existing schedules remain reconfigurable for unprocessed operations when new jobs arrive.
- New job arrivals occur stochastically without predefined temporal patterns.
2.1.2. Modeling Building
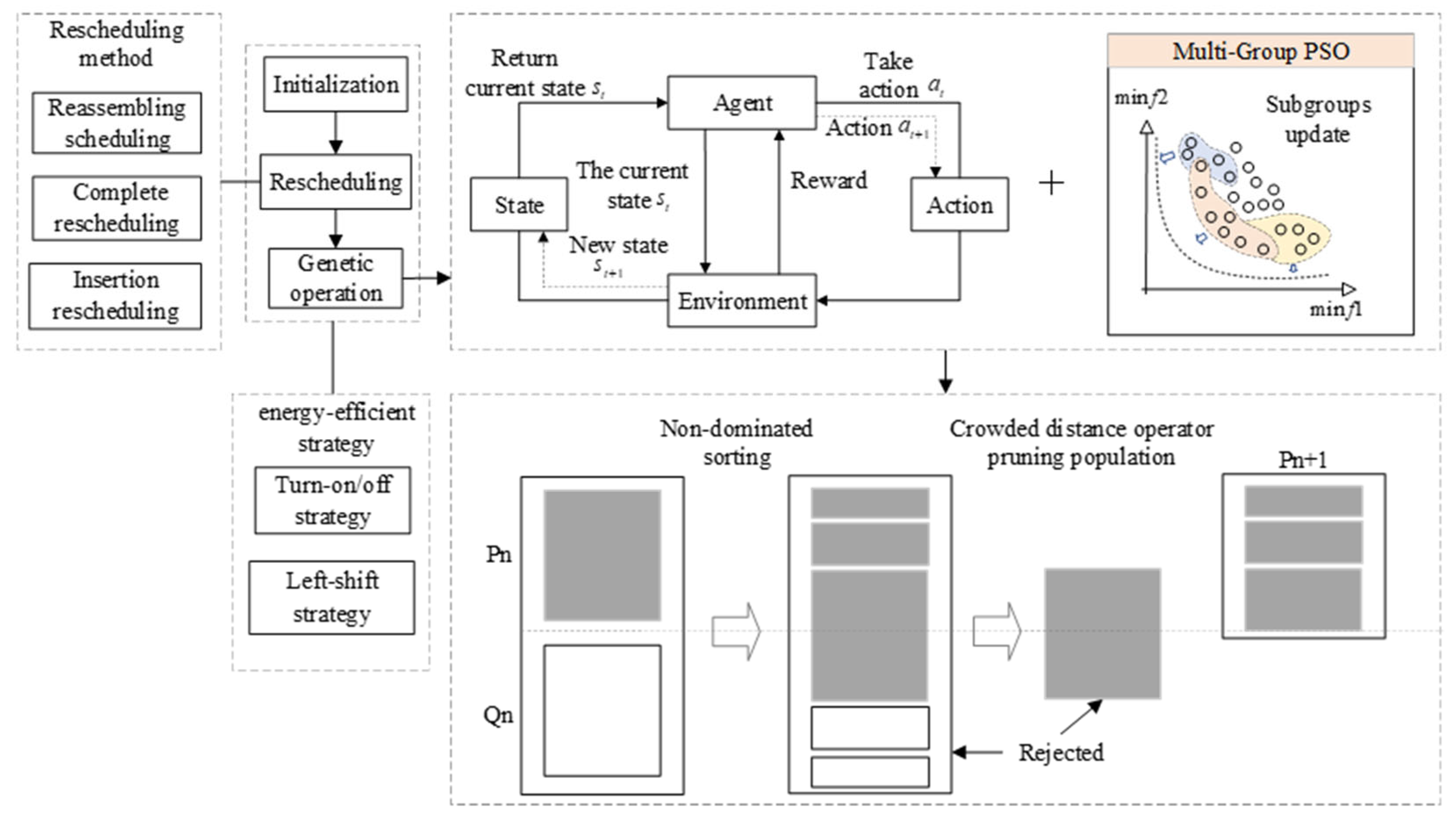
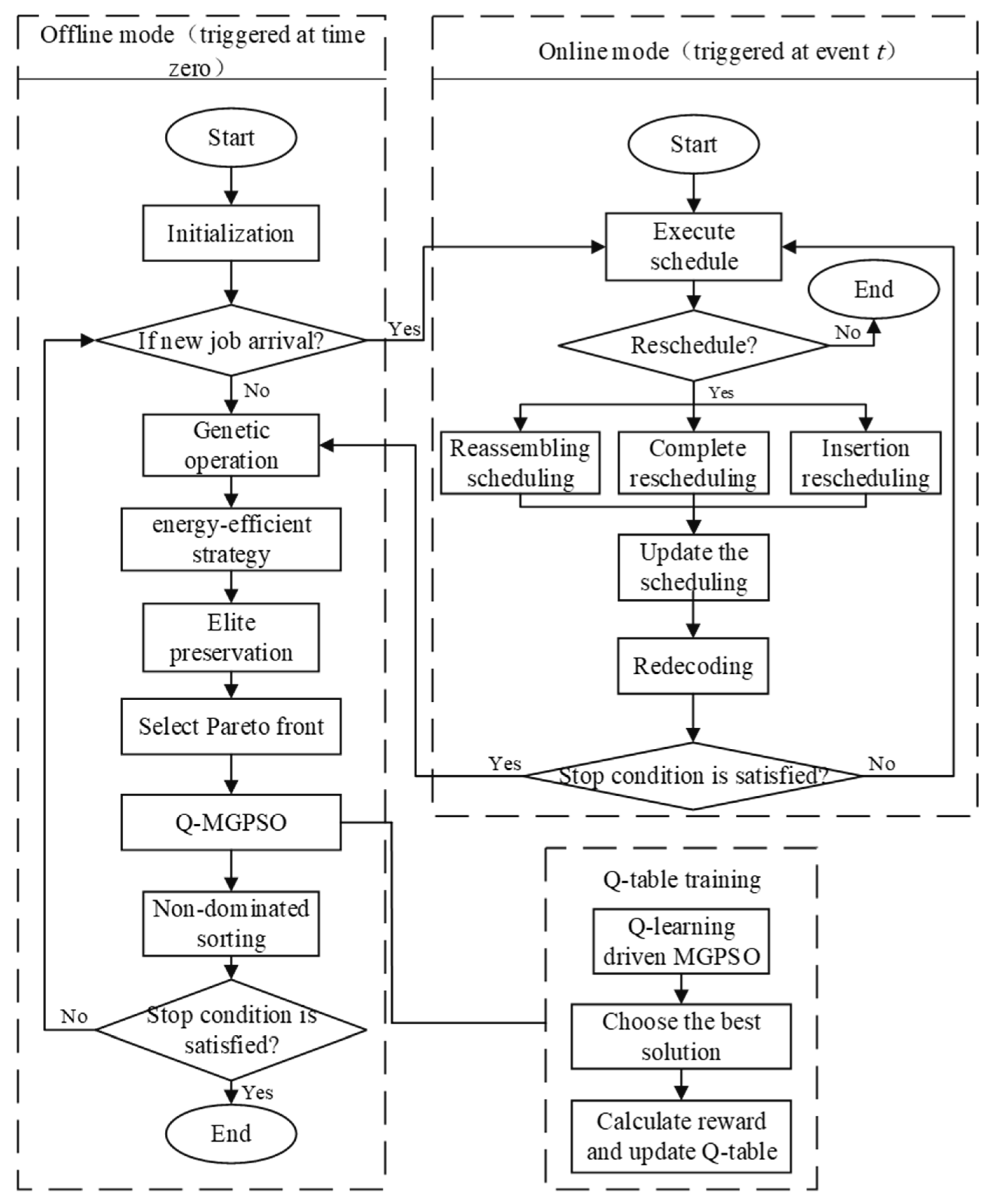
2.2. Rescheduling Strategies
- Reassembling scheduling: When new jobs arrive, the original schedule is preserved, but the system dynamically selects the optimal machine based on real-time load balancing and future time-unit predictions.
- Complete rescheduling: This method reorganizes all pending tasks and new jobs upon events rather than fixed intervals. It employs heuristics to dynamically adjust task assignments based on real-time device availability and delay risks, leveraging sliding window convolution for future gap detection.
- Insertion rescheduling: By leveraging sliding window algorithms, the system identifies idle time slots on each machine. New tasks are inserted into the earliest feasible slot to reduce makespan.
2.3. Energy-Efficient Strategy
3. Q-MGCOA Algorithm
3.1. Encoding and Decoding
3.2. Initialization
3.3. Genetic Operation and Elite Preservation
3.4. Neighborhood Structure and Local Search
| Algorithm 1: MGPSO with Q-Learning process |
| Input: parameters learning factor , discount factor , Epsilon-greedy factor , initial solution , state set , , action set , , the number of episodes , Non-progressing iterations highest number: Iter_Max Output: Best solution , Q-tables Q1, Q2 1: Initialise Q-tables Q1, Q2 as zero matrices 2: Initialise global best solution = 3: Divide particles into subpopulations 4: Initialise particle positions and velocities Initialise personal best positions pi for each particle Initialise neighbourhood structure for each particle # Particle Search and Q1 Training 5: For : Max-iter do 6: For each subpopulation m in do 7: For each particle in subpopulation do 8: Select action from using Epsilon-greedy(Q1) 9: Apply Destruction-Construction to particle based on 10: Evaluate new position 11: Update personal best position pi if is better 12: Calculate reward 13: Update Q1 using Q-learning 14: End for 15: End for # Local Search and Q2 Training 16: Identify and update global best solution 17: Update collaborative archive with new non-dominated solutions 18: For each particle in do 19: Select action from using Epsilon-greedy(Q2) 20: Apply local search operator to particle based on 21: Evaluate new position 22: Update personal best position pi if is better 23: Calculate reward 24: Update Q2 using Q-learning 25: End for # Update Velocity and Position 26: For each particle in do 27: Update velocity and position using PSO equations and collaborative archive 28: End for # Check for Stopping Criteria 29: If no improvement in for Max-iter iterations then 30: Break 31: End if 32: End for 33: Return best solution |
4. Experiment Validation and Result Analysis
4.1. Experiment Settings
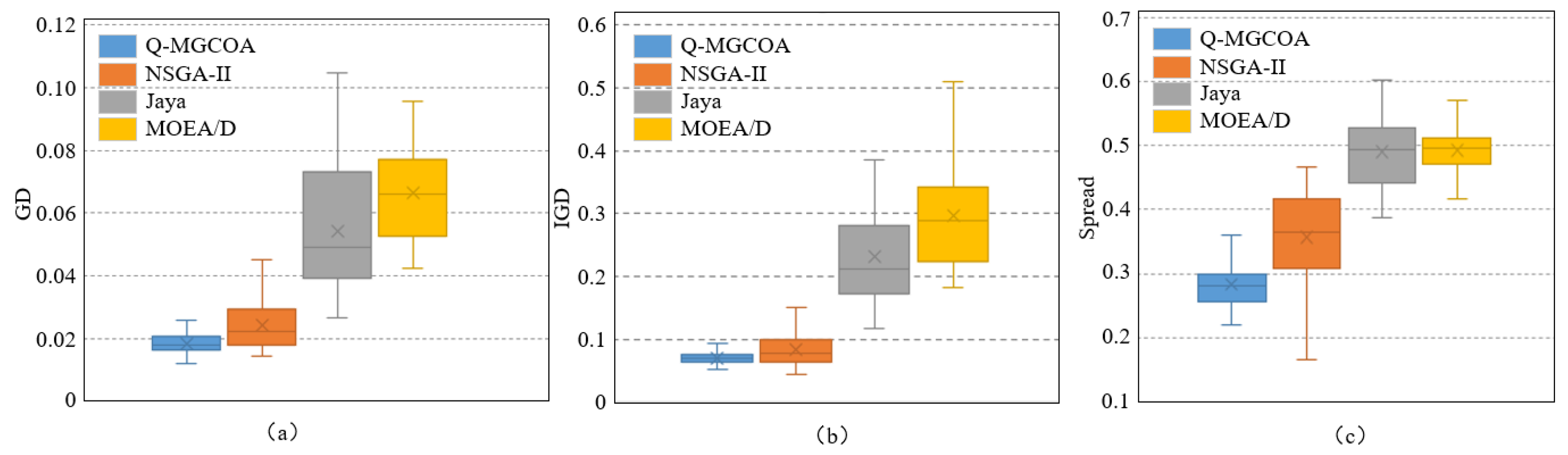
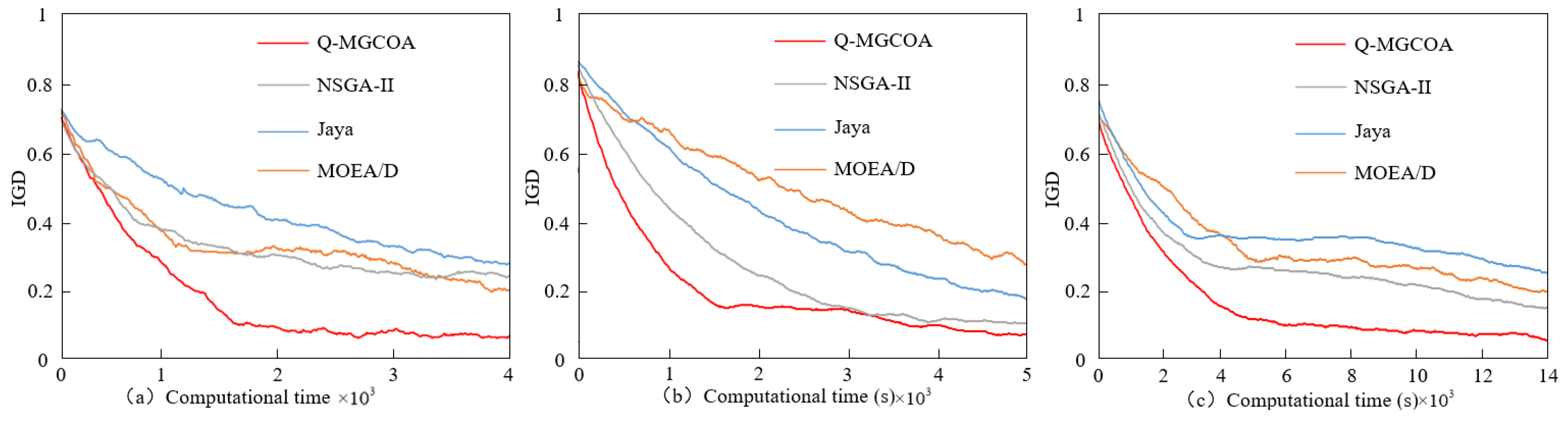
4.2. Evaluation Indicators
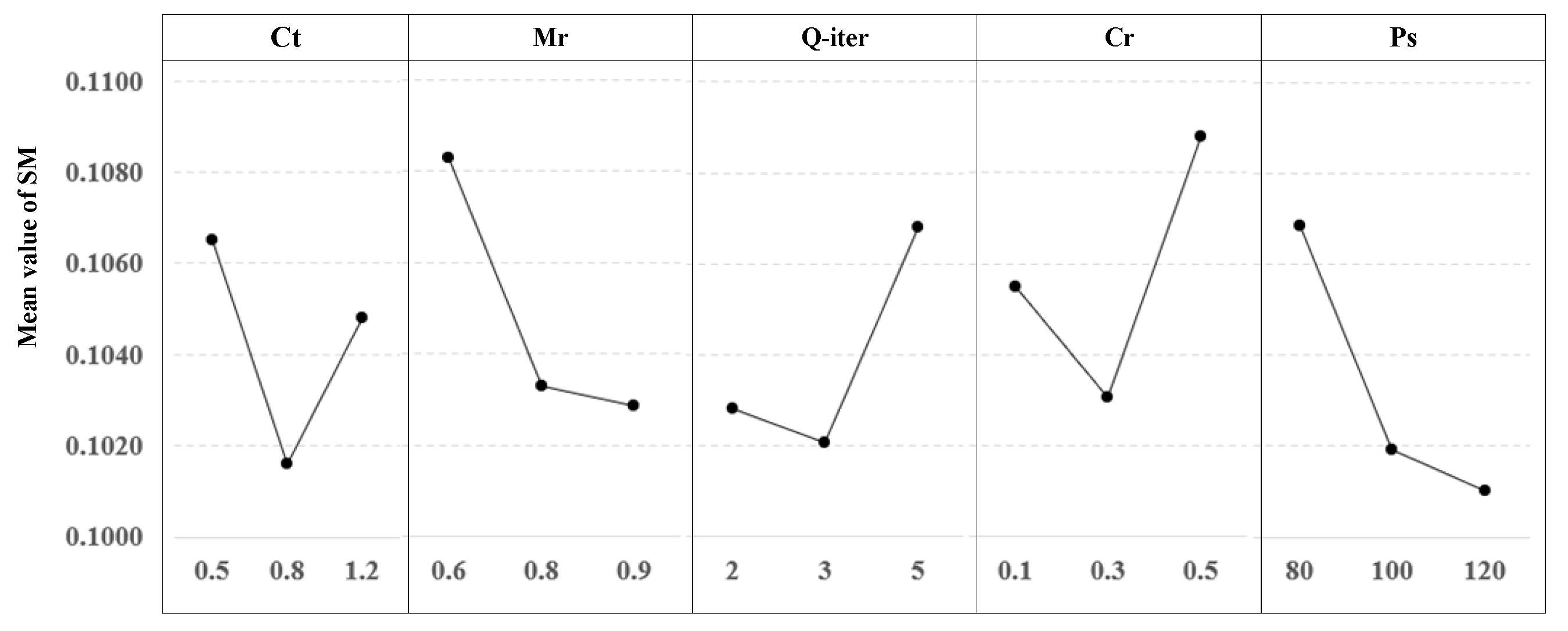
4.3. The Result of Parameter Tuning
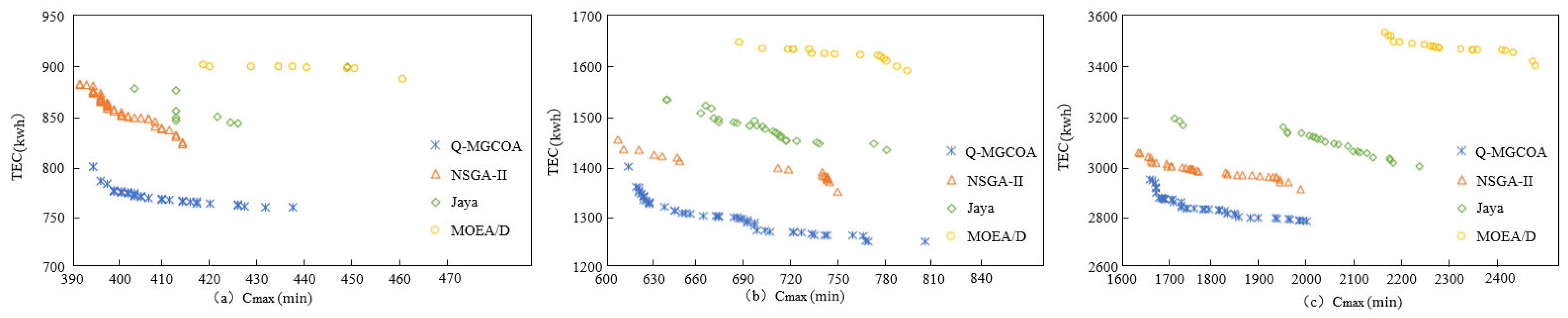
4.4. Algorithm Comparison and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.J.; Li, J.; Wang, G.G. Fuzzy correlation entropy-based NSGA-II for energy-efficient hybrid flow-shop scheduling problem. Knowl.-Based Syst. 2023, 277, 110808. [Google Scholar] [CrossRef]
- Wang, Z.; Shen, L.; Li, X.; Gao, L. An improved multi-objective firefly algorithm for energy-efficient hybrid flowshop rescheduling problem. J. Clean. Prod. 2023, 385, 135738. [Google Scholar] [CrossRef]
- Goli, A.; Ala, A.; Hajiaghaei-Keshteli, M. Efficient multi-objective meta-heuristic algorithms for energy-aware non-permutation flow-shop scheduling problem. Expert Syst. Appl. 2023, 213, 119077. [Google Scholar] [CrossRef]
- Geng, K.; Liu, L.; Wu, Z. Energy-efficient distributed heterogeneous re-entrant hybrid flow shop scheduling problem with sequence dependent setup times considering factory eligibility constraints. Sci. Rep. 2022, 12, 18741. [Google Scholar] [CrossRef]
- Ho, M.H.; Hnaien, F.; Dugardin, F. Exact method to optimise the total electricity cost in two-machine permutation flow shop scheduling problem under Time-of-use tariff. Comput. Oper. Res. 2022, 144, 105788. [Google Scholar] [CrossRef]
- Cui, D.; Zheng, J.; Sun, Y.; He, X.; Zhao, Z. Deploying Liquefied Natural Gas-Powered Ships in Response to the Maritime Emission Trading System: From the Perspective of Shipping Alliances. J. Mar. Sci. Eng. 2025, 13, 551. [Google Scholar]
- Zhang, F.; Mu, H.; Wang, Z.; Chen, J.; Zhang, G.; Wang, S. A Flow Shop Scheduling Method Based on Dual BP Neural Networks with Multi-Layer Topology Feature Parameters. Systems 2024, 12, 339. [Google Scholar] [CrossRef]
- Tao, X.R.; Pan, Q.K.; Sang, H.Y.; Gao, L.; Yang, A.-L.; Rong, M. Nondominated sorting genetic algorithm-II with Q-learning for the distributed permutation flowshop rescheduling problem. Knowl.-Based Syst. 2023, 278, 110880. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, Z.; Chen, S.; Li, J.; Wang, H.; Xiang, J.; Xiao, W. Attention-shared multi-agent actor–critic-based deep reinforcement learning approach for mobile charging dynamic scheduling in wireless rechargeable sensor networks. Entropy 2022, 24, 965. [Google Scholar] [CrossRef]
- Luo, H.; Fang, J.; Huang, G.Q. Real-time scheduling for hybrid flowshop in ubiquitous manufacturing environment. Comput. Ind. Eng. 2015, 84, 12–23. [Google Scholar] [CrossRef]
- Ghaleb, M.; Zolfagharinia, H.; Taghipour, S. Real-time production scheduling in the Industry-4.0 context: Addressing uncertainties in job arrivals and machine breakdowns. Comput. Oper. Res. 2020, 123, 105031. [Google Scholar] [CrossRef]
- Khan, M.A.; Ahmed, T.; Ashraf, S.; Arfeen, Z.A. SLM-OJ: Surrogate Learning Mechanism during Outbreak Juncture. August 2022 2020, 6, 162–167. [Google Scholar]
- Al-Hinai, N.; ElMekkawy, T.Y. Robust and stable flexible job shop scheduling with random machine breakdowns using a hybrid genetic algorithm. Int. J. Prod. Econ. 2011, 132, 279–291. [Google Scholar] [CrossRef]
- Duan, J.; Wang, J. Robust scheduling for flexible machining job shop subject to machine breakdowns and new job arrivals considering system reusability and task recurrence. Expert Syst. Appl. 2022, 203, 117489. [Google Scholar] [CrossRef]
- Fujimura, S.; Plazolles, B.; Luo, J.; El Baz, D. GPU based parallel genetic algorithm for solving an energy efficient dynamic flexible flow shop scheduling problem. J. Parallel Distrib. Comput. 2019, 133, 244–257. [Google Scholar]
- Ghaleb, M.; Taghipour, S.; Zolfagharinia, H. Real-time integrated production-scheduling and maintenance-planning in a flexible job shop with machine deterioration and condition-based maintenance. J. Manuf. Syst. 2021, 61, 423–449. [Google Scholar] [CrossRef]
- Li, W.; Gao, L.; Han, D.; Li, Y.; Li, X. Integrated production and transportation scheduling method in hybrid flow shop. Chin. J. Mech. Eng. 2022, 35, 12. [Google Scholar] [CrossRef]
- Gong, G.; Zhao, X.; Luo, Q.; Guo, X.; Chen, L.; Deng, Q. Modelling and optimisation of distributed assembly hybrid flowshop scheduling problem with transportation resource scheduling. Comput. Ind. Eng. 2023, 186, 109717. [Google Scholar]
- Cai, J.; Wang, J.; Wang, L.; Lei, D. A novel shuffled frog-leaping algorithm with reinforcement learning for distributed assembly hybrid flow shop scheduling. Int. J. Prod. Res. 2023, 61, 1233–1251. [Google Scholar] [CrossRef]
- Peng, K.-K.; Gao, L.; Zhang, B.; Pan, Q.-K.; Meng, L.-L.; Li, X.-Y. A three-stage multiobjective approach based on decomposition for an energy-efficient hybrid flow shop scheduling problem. IEEE Trans. Syst. Man Cybern. Syst. 2019, 50, 4984–4999. [Google Scholar]
- Zhang, Z.Q.; Qian, B.; Hu, R.; Yang, J.-B. Q-learning-based hyper-heuristic evolutionary algorithm for the distributed assembly blocking flowshop scheduling problem. Appl. Soft Comput. 2023, 146, 110695. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Wu, F.C.; Qian, B.; Hu, R.; Wang, L.; Jin, H.-P. A Q-learning-based hyper-heuristic evolutionary algorithm for the distributed flexible job-shop scheduling problem with crane transportation. Expert Syst. Appl. 2023, 234, 121050. [Google Scholar] [CrossRef]
- Jia, Y.; Yan, Q.; Wang, H. Q-learning driven multi-population memetic algorithm for distributed three-stage assembly hybrid flow shop scheduling with flexible preventive maintenance. Expert Syst. Appl. 2023, 232, 120837. [Google Scholar] [CrossRef]
- Xue, Q.; Zhou, D.; Zhang, Z.; Chen, J.; Li, P. Multi-objective energy-efficient hybrid flow shop scheduling using Q-learning and GVNS driven NSGA-II. Comput. Oper. Res. 2023, 159, 106360. [Google Scholar]
- Zhang, W.; Li, C.; Gen, M.; Yang, W.; Zhang, G. A multiobjective memetic algorithm with particle swarm optimisation and Q-learning-based local search for energy-efficient distributed heterogeneous hybrid flow-shop scheduling problem. Expert Syst. Appl. 2024, 237, 121570. [Google Scholar] [CrossRef]
- Zhang, Q.; Duan, J.; Qin, J.; Zhou, Y.; Shi, H.; Nie, L.; Si, H. Double Deep Q-Network-Based Solution to a Dynamic, Energy-Efficient Hybrid Flow Shop Scheduling System with the Transport Process. Systems 2025, 13, 170. [Google Scholar] [CrossRef]
- Zhang, W.; Gen, M.; Jo, J. Hybrid sampling strategy-based multiobjective evolutionary algorithm for process planning and scheduling problem. J. Intell. Manuf. 2014, 25, 881–897. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Zhang, L.; Gao, K.; An, Y. Multiobjective flexible job-shop rescheduling with new job insertion and machine preventive maintenance. IEEE Trans. Cybern. 2022, 53, 3101–3113. [Google Scholar]
- Li, Z.; Mumtaz, J.; Yue, L.; Wang, H.; Rauf, M. Energy-efficient scheduling of a two-stage flexible printed circuit board flow shop using a hybrid Pareto spider monkey optimisation algorithm. J. Ind. Inf. Integr. 2023, 31, 100412. [Google Scholar]
- Meyer, P.; Mohammadi, M.; Pasdeloup, B.; Karimi-Mamaghan, M. Learning to select operators in meta-heuristics: An integration of Q-learning into the iterated greedy algorithm for the permutation flowshop scheduling problem. Eur. J. Oper. Res. 2023, 304, 1296–1330. [Google Scholar]
- Luo, H.; Du, B.; Huang, G.Q.; Chen, H.; Li, X. Hybrid flow shop scheduling considering machine electricity consumption cost. Int. J. Prod. Econ. 2013, 146, 423–439. [Google Scholar] [CrossRef]
- Li, Z.; Gao, K.; Wu, N.; Pan, Y. Solving biobjective distributed flow-shop scheduling problems with lot-streaming using an improved Jaya algorithm. IEEE Trans. Cybern. 2022, 53, 3818–3828. [Google Scholar]
- Li, X.; Li, P.; Wang, G.; Gao, L. Energy-efficient distributed heterogeneous welding flow shop scheduling problem using a modified MOEA/D. Swarm Evol. Comput. 2021, 62, 100858. [Google Scholar]

| Parameters | Definition | Parameters | Definition |
|---|---|---|---|
| Sum of jobs number. | The -th transport task, () | ||
| Sum of stages number | Transport vehicle , | ||
| Sum of corresponding workshop machines | No-load/load transport speed of transport vehicles | ||
| Stage index | -th operation of job | ||
| Job index | Horizontal coordinate of the buffer | ||
| New job index | Coordinates of | ||
| ) | Processing/standby power of | ||
| Transportation time of the first job | Ending time of final stage jobs | ||
| No-load/load transport power of transport vehicles | Turn-on/off power of | ||
| Turn-on/off time of | Time constant | ||
| Idle time of | Time to start processing of new jobs | ||
| Processing time of on | Arrival time of new jobs | ||
| Starting/ending time of the no-load transport task | Starting/ending time of the load transport task | ||
| Variables | |||
| 1 if the operation is dealt with on the machine , 0 otherwise. | |||
| 1 if job is the subsequent job of job dealt with by machine , 0 otherwise. | |||
| 1 if job is dealt with on the machine and is transported by the transport vehicle , 0 otherwise. | |||
| 1 if operation is is a post-operation dealt with on machine , 0 otherwise. | |||
| 1 if the subsequent operation of job after processing in machine is carried out in machine , 0 otherwise. | |||
| Factors | Levels |
|---|---|
| Sum of jobs | {10, 20, 50} |
| Sum of stages | {3, 5} |
| Sum of machines per stage | {3, 4, 5} |
| Number of new jobs arrived | {3, 5} |
| Number of transport vehicles per stage | 2 |
| Processing time per operation | (20, 30) min |
| Power of machine | (5, 10) W |
| Speed of no-load/load transport vehicles | 30\20 m/min |
| Power of no-load/load transport vehicles | 100\200 W |
| Standby power of the machine | 2 |
| Reset power of the machine | 4 |
| Factors | Factor Levels | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| 0.5 | 0.8 | 1.2 | |
| 0.6 | 0.8 | 0.9 | |
| Q- | 2 | 3 | 5 |
| 0.1 | 0.3 | 0.5 | |
| 80 | 100 | 120 | |
| NSGA-II | Jaya | MOEA/D | Q-MGCOA | |||||
|---|---|---|---|---|---|---|---|---|
| AVG | STD | AVG | STD | AVG | STD | AVG | STD | |
| 10-3-3-3 | 0.0196 | 0.0084 | 0.0372 | 0.0071 | 0.0614 | 0.0179 | 0.0253 | 0.0082 |
| 10-3-3-5 | 0.0239 | 0.0066 | 0.0404 | 0.0239 | 0.0484 | 0.0155 | 0.0384 | 0.0209 |
| 10-3-4-3 | 0.0269 | 0.0051 | 0.0573 | 0.0277 | 0.0457 | 0.0136 | 0.0187 | 0.0034 |
| 10-3-4-5 | 0.0290 | 0.0123 | 0.0763 | 0.0255 | 0.0614 | 0.0191 | 0.0218 | 0.0022 |
| 10-3-6-3 | 0.0624 | 0.0138 | 0.0406 | 0.0206 | 0.0552 | 0.0104 | 0.0205 | 0.0113 |
| 10-3-6-5 | 0.0236 | 0.0051 | 0.0397 | 0.0179 | 0.0716 | 0.0400 | 0.0185 | 0.0039 |
| 10-5-3-3 | 0.0678 | 0.0630 | 0.0858 | 0.0412 | 0.0531 | 0.0070 | 0.0164 | 0.0021 |
| 10-5-3-5 | 0.0332 | 0.0145 | 0.0616 | 0.0255 | 0.0501 | 0.0186 | 0.0232 | 0.0078 |
| 10-5-4-3 | 0.0208 | 0.0054 | 0.1047 | 0.0627 | 0.0515 | 0.0238 | 0.0232 | 0.0084 |
| 10-5-4-5 | 0.0204 | 0.0064 | 0.0459 | 0.0200 | 0.1732 | 0.1732 | 0.0189 | 0.0020 |
| 10-5-6-3 | 0.0449 | 0.0364 | 0.0649 | 0.0372 | 0.0770 | 0.0586 | 0.0207 | 0.0022 |
| 10-5-6-5 | 0.0295 | 0.0064 | 0.0745 | 0.0572 | 0.1732 | 0.1732 | 0.0147 | 0.0021 |
| 20-3-3-3 | 0.0168 | 0.0050 | 0.0272 | 0.0055 | 0.0611 | 0.0463 | 0.0175 | 0.0028 |
| 20-3-3-5 | 0.0176 | 0.0026 | 0.0265 | 0.0059 | 0.0659 | 0.0602 | 0.0191 | 0.0068 |
| 20-3-4-3 | 0.0158 | 0.0033 | 0.0344 | 0.0064 | 0.0661 | 0.0604 | 0.0177 | 0.0032 |
| 20-3-4-5 | 0.0184 | 0.0038 | 0.0451 | 0.0170 | 0.0641 | 0.0204 | 0.0173 | 0.0023 |
| 20-3-6-3 | 0.0225 | 0.0079 | 0.0465 | 0.0256 | 0.0476 | 0.0288 | 0.0185 | 0.0022 |
| 20-3-6-5 | 0.0252 | 0.0088 | 0.0534 | 0.0254 | 0.0424 | 0.0119 | 0.0309 | 0.0101 |
| 20-5-3-3 | 0.0389 | 0.0318 | 0.0459 | 0.0141 | 0.0771 | 0.0209 | 0.0179 | 0.0033 |
| 20-5-3-5 | 0.0293 | 0.0153 | 0.0454 | 0.0133 | 0.0734 | 0.0570 | 0.0166 | 0.0032 |
| 20-5-4-3 | 0.0305 | 0.0083 | 0.0747 | 0.0277 | 0.0765 | 0.0552 | 0.0215 | 0.0044 |
| 20-5-4-5 | 0.0216 | 0.0050 | 0.0643 | 0.0267 | 0.0956 | 0.0612 | 0.0206 | 0.0045 |
| 20-5-6-3 | 0.0213 | 0.0032 | 0.0401 | 0.0316 | 0.1183 | 0.0335 | 0.0162 | 0.0039 |
| 20-5-6-5 | 0.0292 | 0.0081 | 0.1732 | 0.1732 | 0.0551 | 0.0251 | 0.0184 | 0.0049 |
| 50-3-3-3 | 0.0150 | 0.0045 | 0.0516 | 0.0227 | 0.0910 | 0.0522 | 0.0177 | 0.0038 |
| 50-3-3-5 | 0.0162 | 0.0021 | 0.0757 | 0.0571 | 0.1081 | 0.0477 | 0.0176 | 0.0051 |
| 50-3-4-3 | 0.0260 | 0.0082 | 0.0386 | 0.0054 | 0.0749 | 0.0250 | 0.0172 | 0.0039 |
| 50-3-4-5 | 0.0192 | 0.0073 | 0.0580 | 0.0288 | 0.0662 | 0.0175 | 0.0159 | 0.0035 |
| 50-3-6-3 | 0.0162 | 0.0039 | 0.0390 | 0.0125 | 0.0672 | 0.0175 | 0.0151 | 0.0077 |
| 50-3-6-5 | 0.0144 | 0.0022 | 0.0539 | 0.0243 | 0.0522 | 0.0194 | 0.0134 | 0.0013 |
| 50-5-3-3 | 0.0219 | 0.0048 | 0.0781 | 0.0563 | 0.0732 | 0.0273 | 0.0132 | 0.0039 |
| 50-5-3-5 | 0.0217 | 0.0072 | 0.0368 | 0.0072 | 0.0674 | 0.0138 | 0.0160 | 0.0018 |
| 50-5-4-3 | 0.0282 | 0.0101 | 0.1732 | 0.1732 | 0.0801 | 0.0578 | 0.0169 | 0.0033 |
| 50-5-4-5 | 0.0170 | 0.0045 | 0.0358 | 0.0095 | 0.0476 | 0.0153 | 0.0125 | 0.0018 |
| 50-5-6-3 | 0.0158 | 0.0044 | 0.0312 | 0.0058 | 0.0912 | 0.0496 | 0.0121 | 0.0013 |
| 50-5-6-5 | 0.0248 | 0.0114 | 0.0782 | 0.0534 | 0.0507 | 0.0161 | 0.0204 | 0.0122 |
| Hit rate | 9/36 | 8/36 | 0/36 | 0/36 | 0/36 | 0/36 | 27/36 | 28/36 |
| NSGA-II | Jaya | MOEA/D | Q-MGCOA | |||||
|---|---|---|---|---|---|---|---|---|
| AVG | STD | AVG | STD | AVG | STD | AVG | STD | |
| 10-3-3-3 | 0.0438 | 0.0061 | 0.1414 | 0.0303 | 0.2610 | 0.0717 | 0.0696 | 0.0045 |
| 10-3-3-5 | 0.0821 | 0.0211 | 0.1818 | 0.1108 | 0.2132 | 0.0706 | 0.1240 | 0.0392 |
| 10-3-4-3 | 0.0898 | 0.0388 | 0.2151 | 0.1456 | 0.2077 | 0.0697 | 0.0797 | 0.0192 |
| 10-3-4-5 | 0.0783 | 0.0336 | 0.3230 | 0.1192 | 0.2984 | 0.1078 | 0.0724 | 0.0100 |
| 10-3-6-3 | 0.0436 | 0.0106 | 0.1348 | 0.0501 | 0.2470 | 0.0769 | 0.0546 | 0.0195 |
| 10-3-6-5 | 0.0649 | 0.0130 | 0.1742 | 0.0908 | 0.2939 | 0.1698 | 0.0633 | 0.0171 |
| 10-5-3-3 | 0.2684 | 0.3571 | 0.3379 | 0.1383 | 0.2118 | 0.0627 | 0.0637 | 0.0074 |
| 10-5-3-5 | 0.1182 | 0.0644 | 0.2754 | 0.1194 | 0.2219 | 0.0853 | 0.0924 | 0.0295 |
| 10-5-4-3 | 0.0630 | 0.0201 | 0.5256 | 0.3428 | 0.2248 | 0.1433 | 0.0828 | 0.0232 |
| 10-5-4-5 | 0.0678 | 0.0142 | 0.1907 | 0.0672 | 0.9000 | 0.9000 | 0.0790 | 0.0055 |
| 10-5-6-3 | 0.1144 | 0.1033 | 0.2749 | 0.1819 | 0.3808 | 0.3120 | 0.0698 | 0.0088 |
| 10-5-6-5 | 0.0880 | 0.0334 | 0.3570 | 0.3119 | 0.9000 | 0.9000 | 0.0543 | 0.0033 |
| 20-3-3-3 | 0.0598 | 0.0211 | 0.1173 | 0.0279 | 0.2583 | 0.1792 | 0.0669 | 0.0146 |
| 20-3-3-5 | 0.0761 | 0.0217 | 0.1221 | 0.0304 | 0.3086 | 0.3312 | 0.0832 | 0.0302 |
| 20-3-4-3 | 0.0670 | 0.0159 | 0.1604 | 0.0390 | 0.3145 | 0.3283 | 0.0704 | 0.0158 |
| 20-3-4-5 | 0.0527 | 0.0043 | 0.1962 | 0.0974 | 0.2874 | 0.0833 | 0.0599 | 0.0095 |
| 20-3-6-3 | 0.0870 | 0.0322 | 0.2120 | 0.1345 | 0.2098 | 0.1350 | 0.0677 | 0.0139 |
| 20-3-6-5 | 0.0716 | 0.0333 | 0.2224 | 0.1197 | 0.1825 | 0.0491 | 0.1247 | 0.0544 |
| 20-5-3-3 | 0.1500 | 0.1264 | 0.2209 | 0.0647 | 0.3240 | 0.0845 | 0.0728 | 0.0151 |
| 20-5-3-5 | 0.1300 | 0.0855 | 0.1845 | 0.0688 | 0.3514 | 0.3114 | 0.0715 | 0.0163 |
| 20-5-4-3 | 0.1202 | 0.0315 | 0.3405 | 0.1305 | 0.3656 | 0.3022 | 0.0819 | 0.0282 |
| 20-5-4-5 | 0.0875 | 0.0102 | 0.2852 | 0.1302 | 0.4374 | 0.3031 | 0.0867 | 0.0239 |
| 20-5-6-3 | 0.0983 | 0.0206 | 0.1830 | 0.1516 | 0.5681 | 0.1927 | 0.0657 | 0.0109 |
| 20-5-6-5 | 0.1084 | 0.0303 | 0.9000 | 0.9000 | 0.2380 | 0.1072 | 0.0717 | 0.0245 |
| 50-3-3-3 | 0.0611 | 0.0222 | 0.2466 | 0.1233 | 0.4474 | 0.2762 | 0.0711 | 0.0136 |
| 50-3-3-5 | 0.0576 | 0.0063 | 0.3677 | 0.3066 | 0.5104 | 0.2527 | 0.0705 | 0.0201 |
| 50-3-4-3 | 0.0976 | 0.0364 | 0.1773 | 0.0313 | 0.3253 | 0.1463 | 0.0740 | 0.0132 |
| 50-3-4-5 | 0.0723 | 0.0204 | 0.2678 | 0.1182 | 0.2776 | 0.0697 | 0.0657 | 0.0160 |
| 50-3-6-3 | 0.0633 | 0.0216 | 0.1867 | 0.0710 | 0.2880 | 0.0862 | 0.0607 | 0.0341 |
| 50-3-6-5 | 0.0619 | 0.0122 | 0.2538 | 0.1252 | 0.2183 | 0.0759 | 0.0561 | 0.0070 |
| 50-5-3-3 | 0.0917 | 0.0253 | 0.3859 | 0.2989 | 0.3329 | 0.1387 | 0.0562 | 0.0201 |
| 50-5-3-5 | 0.0940 | 0.0322 | 0.1652 | 0.0367 | 0.3044 | 0.0736 | 0.0675 | 0.0077 |
| 50-5-4-3 | 0.1259 | 0.0453 | 0.9000 | 0.9000 | 0.3886 | 0.3059 | 0.0701 | 0.0173 |
| 50-5-4-5 | 0.0734 | 0.0247 | 0.1688 | 0.0510 | 0.2128 | 0.0755 | 0.0549 | 0.0110 |
| 50-5-6-3 | 0.0646 | 0.0153 | 0.1562 | 0.0284 | 0.4282 | 0.2778 | 0.0524 | 0.0065 |
| 50-5-6-5 | 0.1094 | 0.0576 | 0.3813 | 0.2926 | 0.2245 | 0.0670 | 0.0858 | 0.0503 |
| Hit rate | 11/36 | 10/36 | 0/36 | 0/36 | 0/36 | 0/36 | 25/36 | 26/36 |
| NSGA-II | Jaya | MOEA/D | Q-MGCOA | |||||
|---|---|---|---|---|---|---|---|---|
| AVG | STD | AVG | STD | AVG | STD | AVG | STD | |
| 10-3-3-3 | 0.3013 | 0.0928 | 0.4808 | 0.0739 | 0.5019 | 0.0256 | 0.2482 | 0.0227 |
| 10-3-3-5 | 0.2856 | 0.0383 | 0.3869 | 0.0783 | 0.5320 | 0.0338 | 0.4257 | 0.0262 |
| 10-3-4-3 | 0.4361 | 0.0736 | 0.4980 | 0.0581 | 0.5195 | 0.0519 | 0.2832 | 0.0695 |
| 10-3-4-5 | 0.3800 | 0.0922 | 0.5257 | 0.0695 | 0.5937 | 0.0370 | 0.2994 | 0.0433 |
| 10-3-6-3 | 0.1667 | 0.0393 | 0.4326 | 0.0856 | 0.5990 | 0.0460 | 0.1766 | 0.0309 |
| 10-3-6-5 | 0.3450 | 0.1039 | 0.4333 | 0.0642 | 0.5241 | 0.0786 | 0.2322 | 0.0554 |
| 10-5-3-3 | 0.4227 | 0.0814 | 0.4346 | 0.0492 | 0.4929 | 0.0387 | 0.2542 | 0.0378 |
| 10-5-3-5 | 0.4275 | 0.1076 | 0.5295 | 0.0846 | 0.4958 | 0.0702 | 0.2929 | 0.0330 |
| 10-5-4-3 | 0.2501 | 0.0557 | 0.4325 | 0.1146 | 0.5131 | 0.0167 | 0.2833 | 0.0816 |
| 10-5-4-5 | 0.3934 | 0.0649 | 0.5342 | 0.0574 | 0.4790 | 0.0971 | 0.2633 | 0.0307 |
| 10-5-6-3 | 0.4020 | 0.1018 | 0.4387 | 0.0677 | 0.4874 | 0.1029 | 0.3210 | 0.0357 |
| 10-5-6-5 | 0.2842 | 0.0376 | 0.4373 | 0.0474 | 0.5429 | 0.0491 | 0.1806 | 0.0254 |
| 20-3-3-3 | 0.2844 | 0.0949 | 0.4016 | 0.0367 | 0.5696 | 0.0467 | 0.2204 | 0.0382 |
| 20-3-3-5 | 0.3248 | 0.0462 | 0.4592 | 0.0162 | 0.5076 | 0.0728 | 0.2804 | 0.0440 |
| 20-3-4-3 | 0.2339 | 0.0495 | 0.4603 | 0.0619 | 0.4689 | 0.0607 | 0.2566 | 0.0510 |
| 20-3-4-5 | 0.3481 | 0.0452 | 0.5097 | 0.1092 | 0.4727 | 0.0543 | 0.3489 | 0.0632 |
| 20-3-6-3 | 0.3671 | 0.1033 | 0.5195 | 0.0687 | 0.5073 | 0.0664 | 0.2959 | 0.0500 |
| 20-3-6-5 | 0.4153 | 0.0563 | 0.5119 | 0.0954 | 0.4566 | 0.0506 | 0.3598 | 0.0538 |
| 20-5-3-3 | 0.3886 | 0.0970 | 0.5797 | 0.0797 | 0.4451 | 0.0575 | 0.2714 | 0.0597 |
| 20-5-3-5 | 0.4510 | 0.0516 | 0.4707 | 0.0880 | 0.5026 | 0.0990 | 0.2967 | 0.0228 |
| 20-5-4-3 | 0.3528 | 0.0487 | 0.4711 | 0.0657 | 0.5122 | 0.1099 | 0.3582 | 0.0461 |
| 20-5-4-5 | 0.3458 | 0.0835 | 0.4149 | 0.0424 | 0.4965 | 0.0907 | 0.3221 | 0.0228 |
| 20-5-6-3 | 0.3160 | 0.0518 | 0.5113 | 0.1079 | 0.4629 | 0.1117 | 0.2546 | 0.0765 |
| 20-5-6-5 | 0.4670 | 0.0570 | 0.5314 | 0.0440 | 0.4167 | 0.0327 | 0.2705 | 0.0409 |
| 50-3-3-3 | 0.3265 | 0.0624 | 0.4936 | 0.0617 | 0.4900 | 0.0653 | 0.3163 | 0.0591 |
| 50-3-3-5 | 0.2469 | 0.0363 | 0.4700 | 0.0718 | 0.4970 | 0.1210 | 0.2615 | 0.0688 |
| 50-3-4-3 | 0.4303 | 0.0389 | 0.5199 | 0.0950 | 0.4732 | 0.0334 | 0.2924 | 0.0346 |
| 50-3-4-5 | 0.4173 | 0.0824 | 0.5723 | 0.0441 | 0.4913 | 0.0622 | 0.2765 | 0.0236 |
| 50-3-6-3 | 0.3619 | 0.0620 | 0.5538 | 0.0643 | 0.5094 | 0.0323 | 0.2842 | 0.0616 |
| 50-3-6-5 | 0.3846 | 0.0403 | 0.5293 | 0.0467 | 0.5255 | 0.0560 | 0.2695 | 0.0425 |
| 50-5-3-3 | 0.4619 | 0.1154 | 0.5527 | 0.0906 | 0.4637 | 0.0493 | 0.2952 | 0.0788 |
| 50-5-3-5 | 0.3318 | 0.0547 | 0.5187 | 0.0880 | 0.5210 | 0.0688 | 0.2525 | 0.0376 |
| 50-5-4-3 | 0.4240 | 0.0690 | 0.4457 | 0.0536 | 0.5073 | 0.0859 | 0.3274 | 0.0410 |
| 50-5-4-5 | 0.3732 | 0.0719 | 0.4947 | 0.0674 | 0.4490 | 0.0942 | 0.2770 | 0.0648 |
| 50-5-6-3 | 0.3067 | 0.0369 | 0.6015 | 0.0375 | 0.4715 | 0.0607 | 0.2268 | 0.0380 |
| 50-5-6-5 | 0.3864 | 0.0490 | 0.4828 | 0.1024 | 0.4364 | 0.0534 | 0.2517 | 0.0558 |
| Hit rate | 7/36 | 7/36 | 0/36 | 2/36 | 0/36 | 6/36 | 29/36 | 21/36 |
| NSGA-II | Jaya | MOEA/D | Q-MGCOA | |
|---|---|---|---|---|
| 10-5-3-3 | 823 | 847 | 878 | 758 |
| 20-5-3-3 | 1348 | 1447 | 1596 | 1236 |
| 50-5-3-3 | 2908 | 3004 | 3321 | 2745 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, H.; Si, H.; Qin, J. Energy-Efficient Scheduling for Resilient Container-Supply Hybrid Flow Shops Under Transportation Constraints and Stochastic Arrivals. J. Mar. Sci. Eng. 2025, 13, 1153. https://doi.org/10.3390/jmse13061153
Shi H, Si H, Qin J. Energy-Efficient Scheduling for Resilient Container-Supply Hybrid Flow Shops Under Transportation Constraints and Stochastic Arrivals. Journal of Marine Science and Engineering. 2025; 13(6):1153. https://doi.org/10.3390/jmse13061153
Chicago/Turabian StyleShi, Huaixia, Huaqiang Si, and Jiyun Qin. 2025. "Energy-Efficient Scheduling for Resilient Container-Supply Hybrid Flow Shops Under Transportation Constraints and Stochastic Arrivals" Journal of Marine Science and Engineering 13, no. 6: 1153. https://doi.org/10.3390/jmse13061153
APA StyleShi, H., Si, H., & Qin, J. (2025). Energy-Efficient Scheduling for Resilient Container-Supply Hybrid Flow Shops Under Transportation Constraints and Stochastic Arrivals. Journal of Marine Science and Engineering, 13(6), 1153. https://doi.org/10.3390/jmse13061153





