Deploying Liquefied Natural Gas-Powered Ships in Response to the Maritime Emission Trading System: From the Perspective of Shipping Alliances
Abstract
1. Introduction
- How does the METS affect the LNG-powered ship deployment of liner alliances?
- How does the cooperation of liner carriers affect the cost of deploying LNG-powered ships?
- Different from previous studies conducted from a shipping carrier’s perspective, this paper investigates the deployment of LNG-powered ships from the perspective of liner alliances. Under the METS, our study aims to reduce the liner alliance’s cost and accelerate the deployment of LNG-powered ships through the cooperation of liner carriers.
- This paper proposes an LFDP to determine the deployment of LNG-powered ships and VLSFO-powered ships, sailing speeds, container shipment, slots co-chartering and the trading of CEPs. To solve the LFDP, we develop an MILP model.
- Numerical experiments show that the implementation of METS has an obvious impact on the fleet deployment of liner alliances, and the increase in CEP trading prices promotes the deployment of LNG-powered ships for liner alliances. Furthermore, compared with a single liner carrier, forming liner alliances can effectively reduce the total cost considering the METS.
2. Literature Review
2.1. Maritime Emission Trading System
2.2. LNG-Powered Ships
2.3. Research Gap
3. Problem Descriptions
3.1. Problem Assumptions
- (1)
- For our considered liner shipping network, the demand of container transportation per week is fixed.
- (2)
- For the time structure of any liner route, we consider sailing time and berthing time.
- (3)
- For the cost structure of any liner route, we consider fixed costs for ship deployment and variable costs for fuel consumptions and trading CEPs.
- (4)
- For all ports covered by the liner shipping network, the handling time per container is fixed.
3.2. Main Notations
3.3. Liner Shipping Network Service
3.4. Cost and Time Structure
3.5. Allocation, Trading and Cap of Emission Permits
3.6. Slot Co-Chartering Among Cooperative Liner Carriers
4. Model Development
4.1. Decision Variables
4.2. Mathematical Model
5. Numerical Experiments
5.1. Parameter Sets
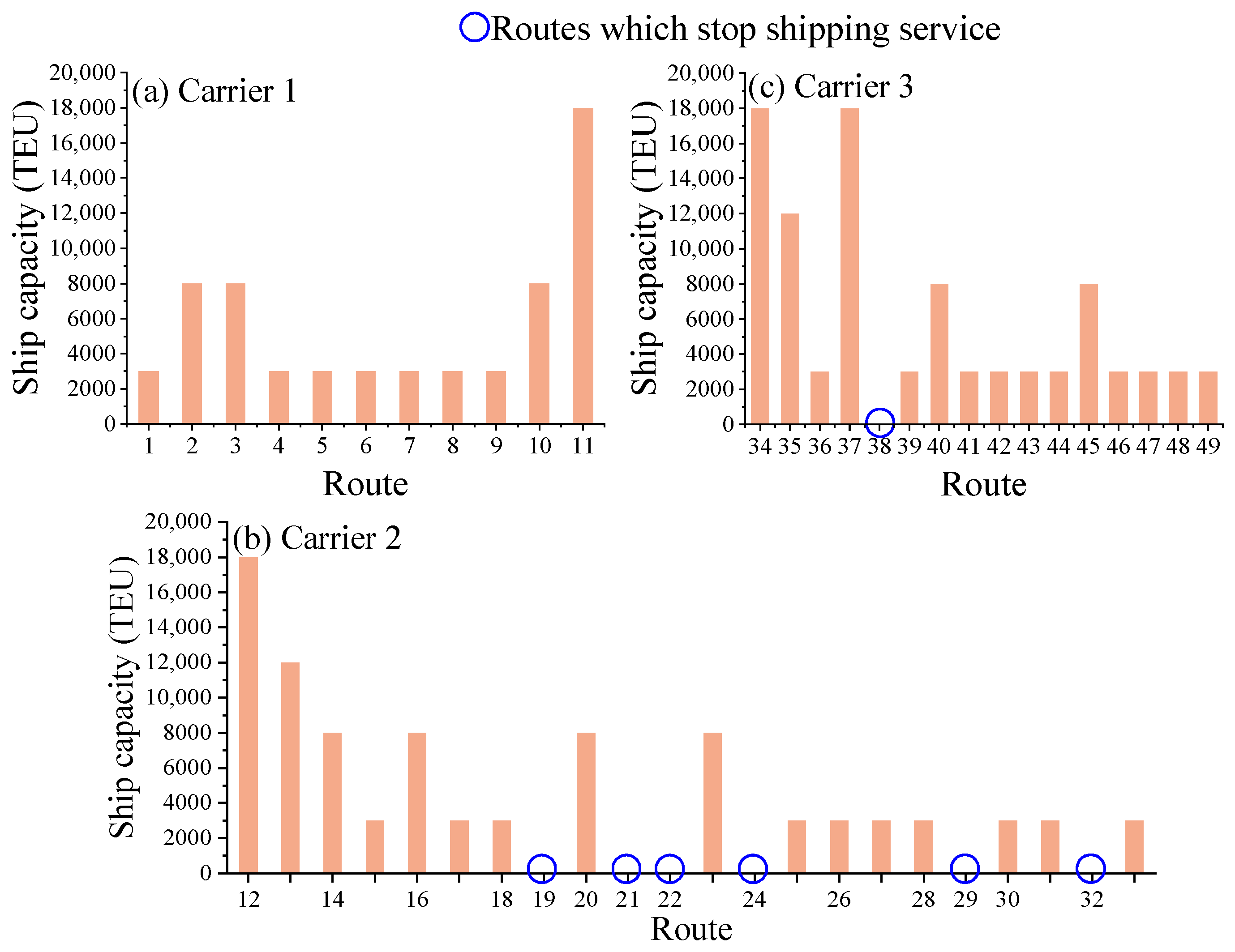
5.2. Comparison Analysis
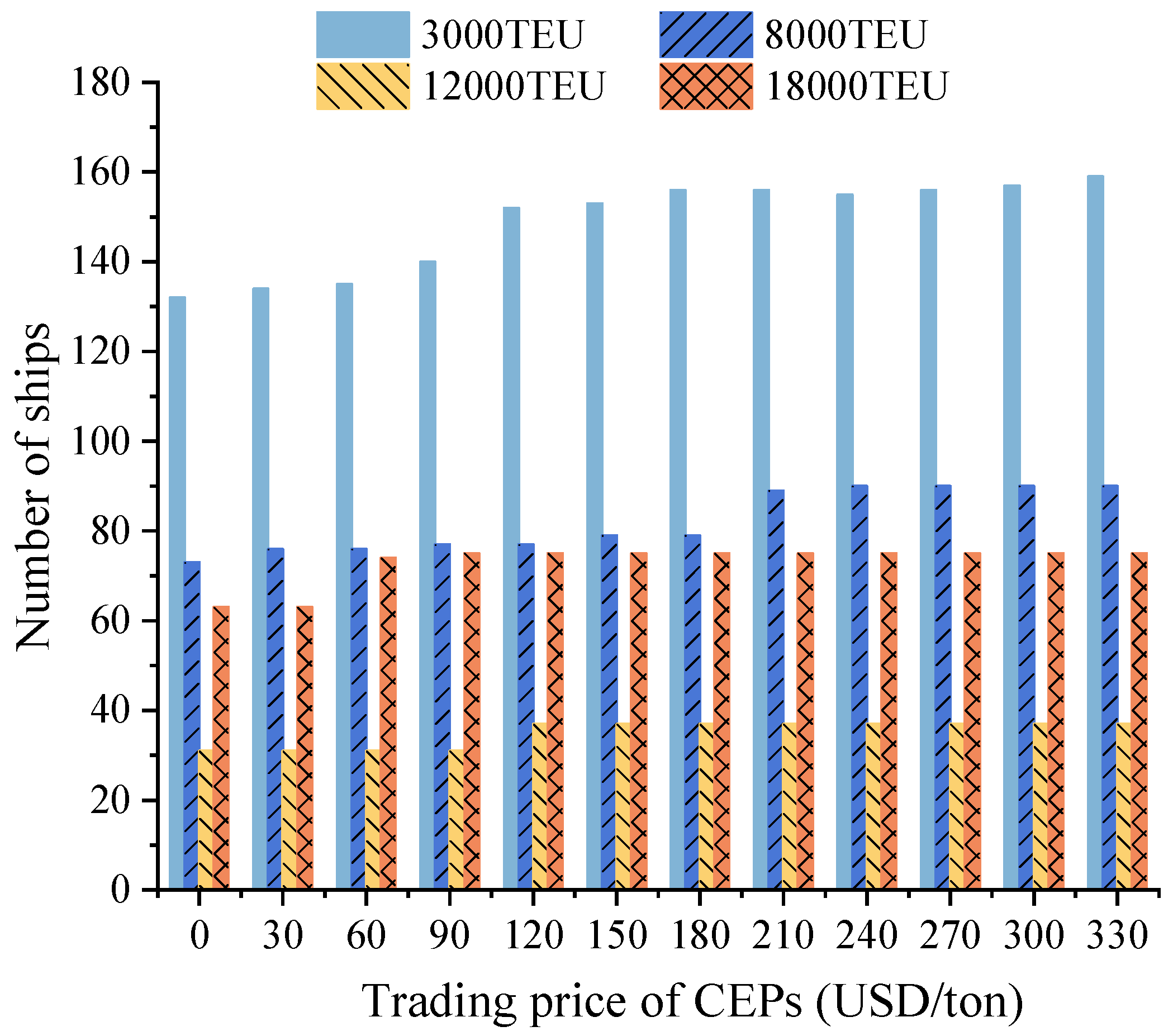
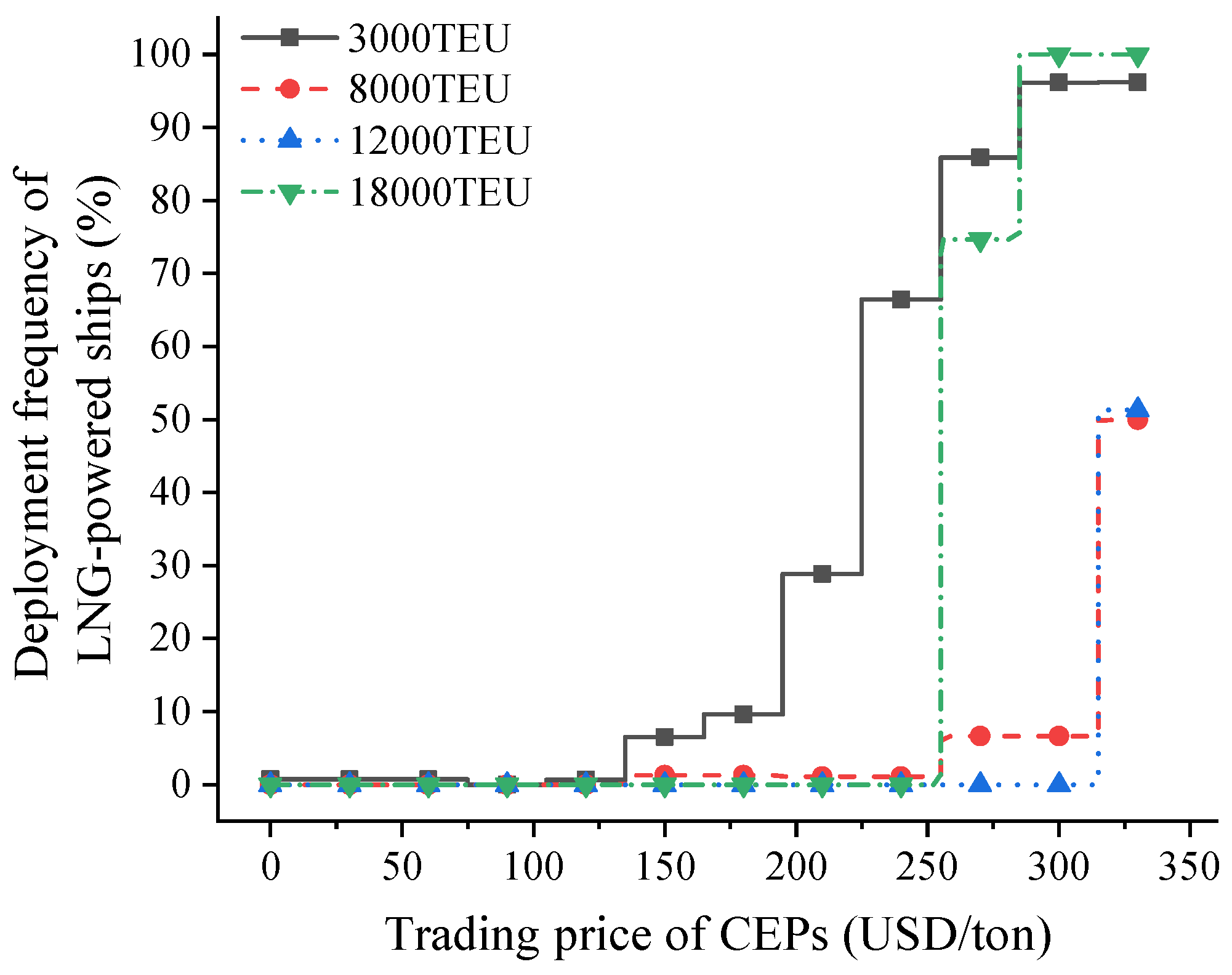
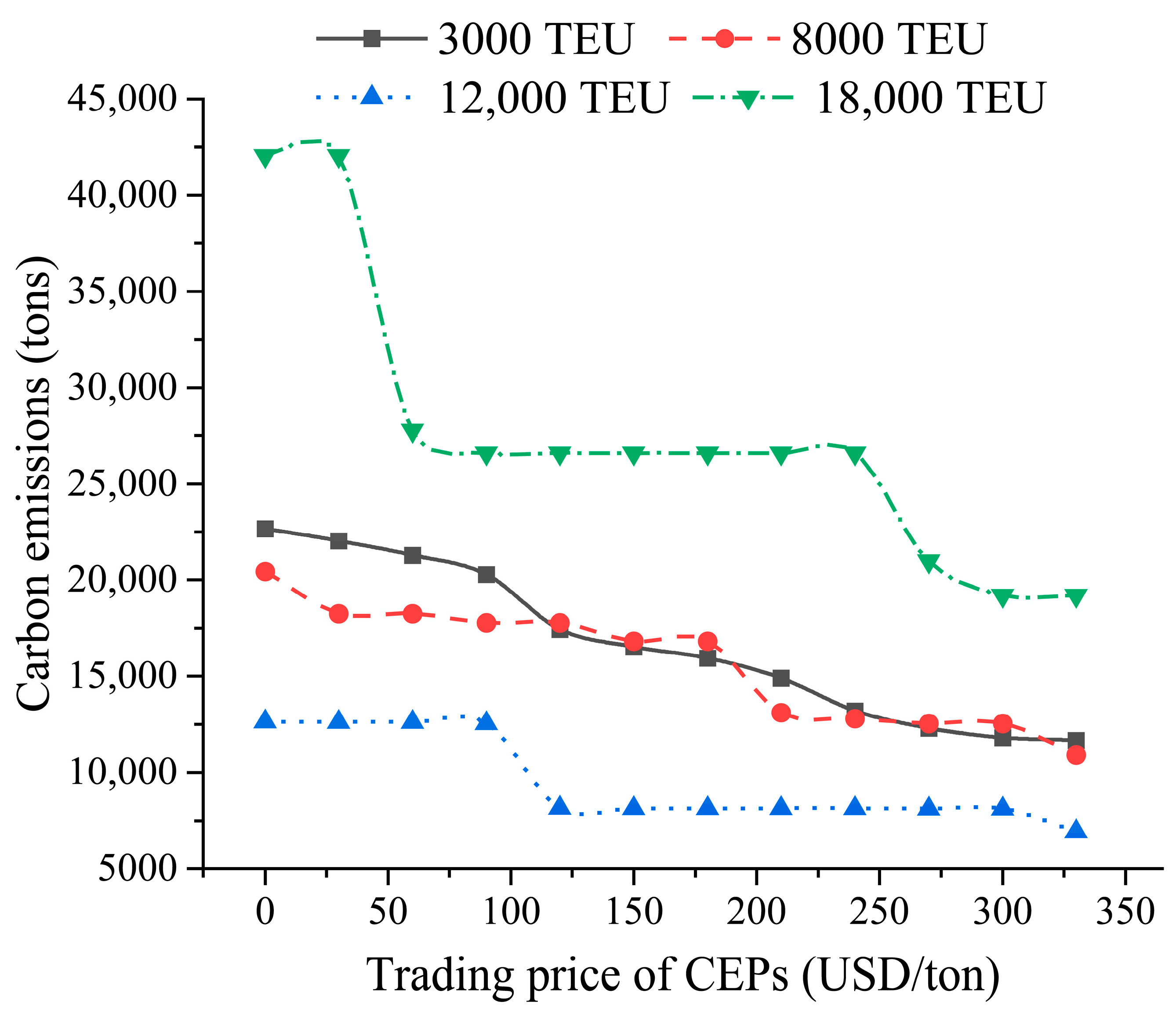
5.3. Results with Different CEP Trading Prices
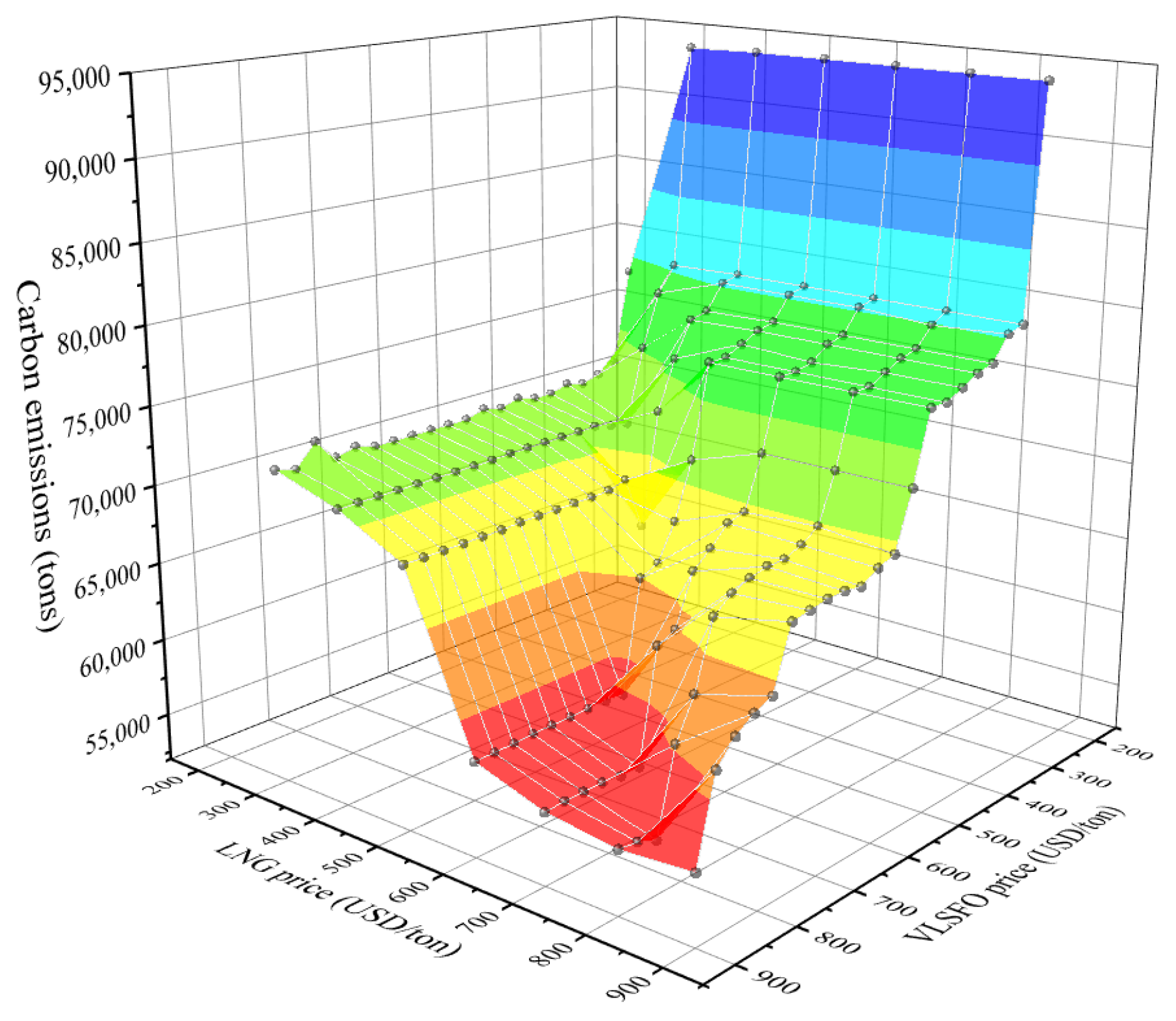
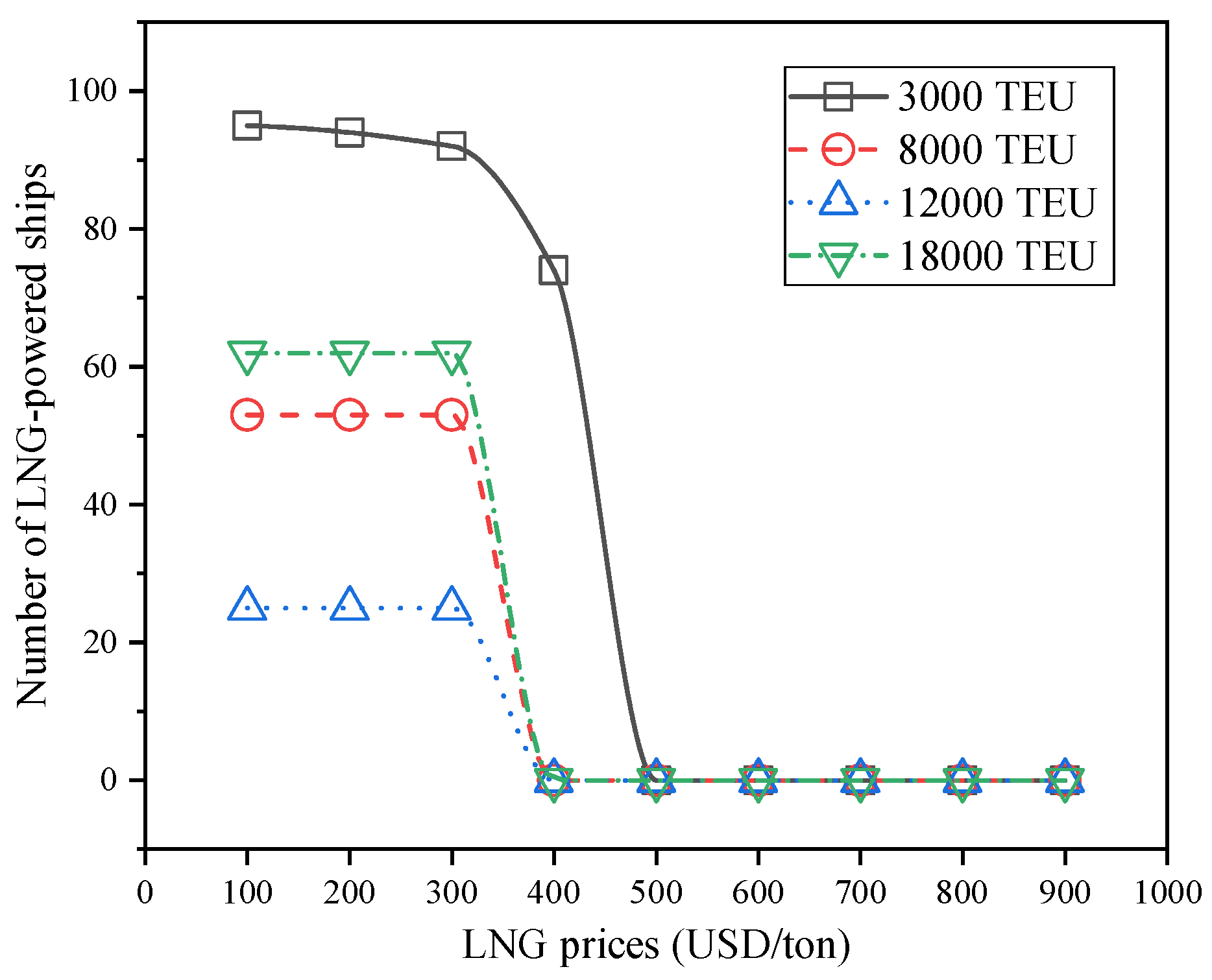
5.4. Results with Different Fuel Prices
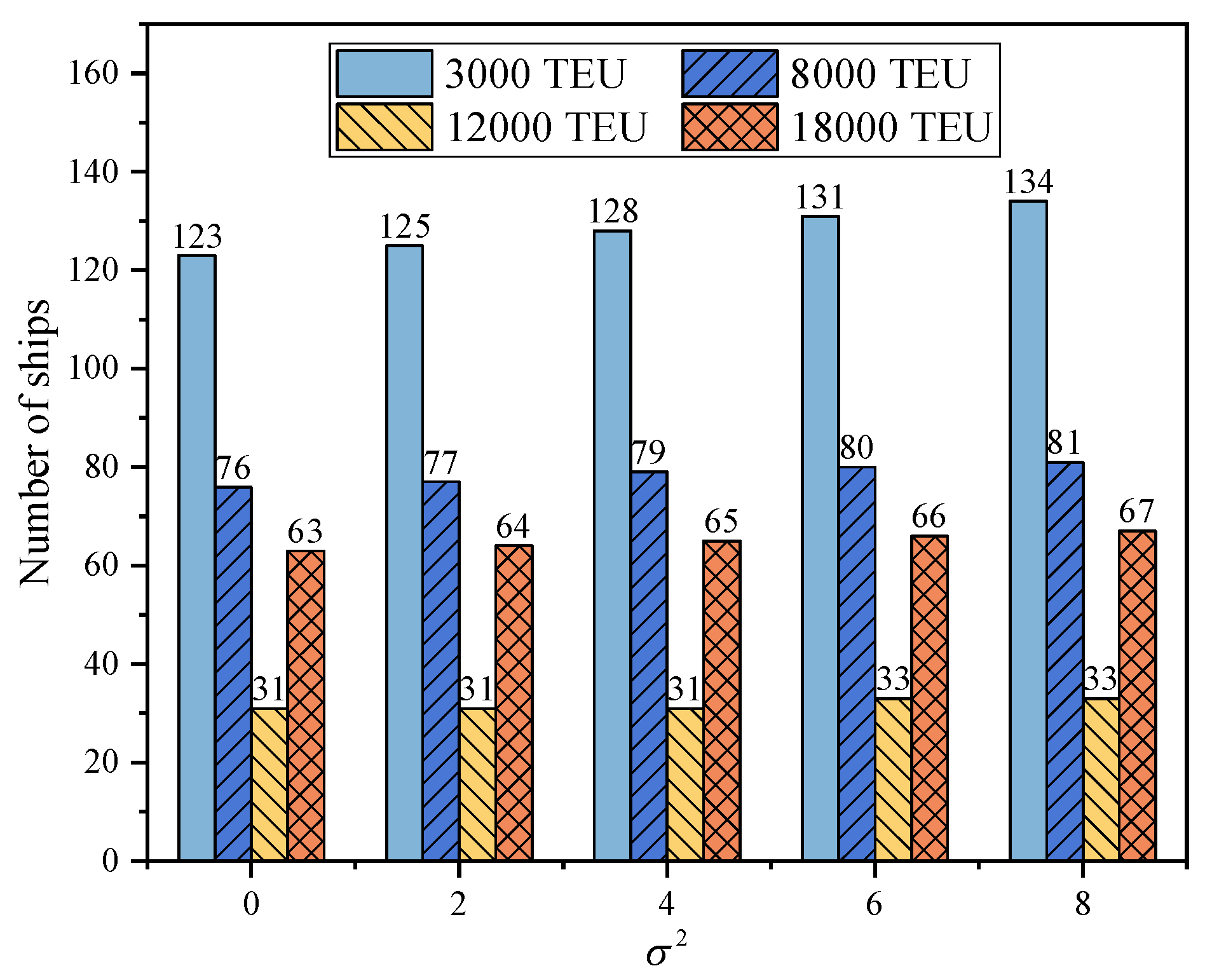
5.5. Expanded Results Considering Uncertain Navigational Risks
6. Conclusions
- (i)
- Compared with the results without considering the cooperation of liner carriers, the formation of liner alliances reduces the total cost of cooperative liner carriers, which consider the deployment of LNG-powered ships in response to the METS. To reduce the additional cost of CEP trading and deploying LNG-powered ships, shipping carriers can form a coalition to participate in the allocation and trading of CEPs for accelerating the deployment of LNG-powered ships. For our numerical experiments, the cooperation of liner carriers can reduce the total cost by about 3~11% with various CEP trading prices.
- (ii)
- The trading price of CEPs determines the total cost and ship carbon emissions of liner alliances. When the trading price of CEPs is low, it is economical for cooperative liner carriers to adopt the slow-down strategy to reduce carbon emissions from VLSFO-powered ships. The low trading price of CEPs (e.g., less than 150 USD/ton) hardly encourages shipping carriers to deploy LNG-powered ships. For accelerating the deployment of LNG-powered ships, METS regulators can raise the CEP trading price above 150 USD/ton through regulatory adjustments.
- (iii)
- When the CEP trading price is high (more than 150 USD/ton), shipping carriers should deploy small LNG-powered ships (e.g., 3000-TEU) first to reduce carbon emissions and the additional cost of trading CEPs. Then, as the CEP trading price increases, shipping carriers should complete the fuel conversion from VLSFO to LNG for small LNG-powered ships and mega LNG-powered ships (e.g., 18,000-TEU), which have the maximum deployed number and the maximum fixed cost.
- (i)
- The allocation and trading of CEPs encourage shipping carriers to invest in green shipping technologies including the reconstruction of LNG-powered ships. However, the economic interaction between CEP trading and the reconstruction cost of LNG-powered ships is not assessed in this paper. In future work, we will analyze the impact of CEP trading on the reconstruction of LNG-powered ships.
- (ii)
- Sulphur emission regulations (e.g., ECAs and the global sulphur limit) bring more operation costs for oil-powered ships, and these regulations also encourage shipping carriers to adopt LNG-powered ships, which produce virtually no sulphur emissions. In future work, we will investigate the deployment of LNG-powered ships in response to various sulphur emission regulations, as well as regulations pertaining to both sulphur and carbon emission reductions.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| CEP Trading Price (USD/ton) | Route 18 | Route 19 | Route 20 | Route 21 | Route 22 | Route 23 | Route 24 |
|---|---|---|---|---|---|---|---|
| 30 | 1414.12 | 0 | 3838.34 | 0 | 0 | 1912.21 | 0 |
| 60 | 1418.51 | 0 | 3838.34 | 0 | 0 | 1912.21 | 0 |
| 90 | 1405.64 | 0 | 3295.28 | 0 | 0 | 1912.21 | 0 |
| 120 | 1170.72 | 0 | 3295.28 | 0 | 0 | 1912.21 | 0 |
| 150 | 1161.33 | 0 | 3295.28 | 0 | 0 | 1461.09 | 0 |
| 180 | 1163.22 | 0 | 3295.28 | 0 | 0 | 1459.31 | 0 |
| 210 | 845.77 | 0 | 2547.72 | 0 | 0 | 1126.85 | 0 |
| 240 | 829.96 | 0 | 2547.72 | 0 | 0 | 1126.85 | 0 |
| 270 | 832.72 | 0 | 2547.72 | 0 | 0 | 1126.85 | 0 |
| 300 | 829.2 | 0 | 2547.72 | 0 | 0 | 1126.85 | 0 |
| 330 | 831.83 | 0 | 1838.56 | 0 | 0 | 1126.85 | 0 |
| CEP Trading Price (USD/ton) | Route 29 | Route 30 | Route 31 | Route 32 | Route 33 | Route 34 | Route 35 |
| 30 | 0 | 510.29 | 544.84 | 0 | 145.75 | 10,754.8 | 6556.39 |
| 60 | 0 | 510.29 | 544.84 | 0 | 145.75 | 6878.23 | 6556.39 |
| 90 | 0 | 510.29 | 544.84 | 0 | 145.75 | 6632.49 | 6481.78 |
| 120 | 0 | 510.29 | 544.84 | 0 | 145.75 | 6632.49 | 4292.33 |
| 150 | 0 | 368.25 | 393.18 | 0 | 145.75 | 6617.35 | 4257.1 |
| 180 | 0 | 368.25 | 393.18 | 0 | 105.18 | 6616.89 | 4257.36 |
| 210 | 0 | 368.25 | 393.18 | 0 | 105.18 | 6616.89 | 4257.36 |
| 240 | 0 | 368.25 | 393.18 | 0 | 105.18 | 6616.89 | 4257.36 |
| 270 | 0 | 368.25 | 393.18 | 0 | 105.18 | 4788.48 | 4245.24 |
| 300 | 0 | 368.25 | 255.55 | 0 | 105.18 | 4788.48 | 4245.24 |
| 330 | 0 | 368.25 | 255.55 | 0 | 105.18 | 4775.07 | 3072.32 |
| LNG Price (USD/ton) | Route 18 | Route 19 | Route 20 | Route 21 | Route 22 | Route 23 | Route 24 |
|---|---|---|---|---|---|---|---|
| 300 | 2147 | 0 | 5604.14 | 0 | 0 | 2801.18 | 0 |
| 400 | 1309.73 | 0 | 2769.93 | 0 | 0 | 1384.99 | 0 |
| 500 | 1025.37 | 0 | 3838.34 | 0 | 0 | 1912.21 | 0 |
| 600 | 1418.51 | 0 | 3838.34 | 0 | 0 | 1912.21 | 0 |
| 700 | 1404.96 | 0 | 3838.34 | 0 | 0 | 1912.21 | 0 |
| 800 | 1417.2 | 0 | 3838.34 | 0 | 0 | 1912.21 | 0 |
| 900 | 1415.85 | 0 | 3838.34 | 0 | 0 | 1912.21 | 0 |
| LNG price (USD/ton) | Route 29 | Route 30 | Route 31 | Route 32 | Route 33 | Route 34 | Route 35 |
| 300 | 0 | 771.91 | 393.18 | 0 | 105.18 | 7811.04 | 5976.81 |
| 400 | 0 | 368.25 | 393.18 | 0 | 105.18 | 7811.04 | 4756.4 |
| 500 | 0 | 368.25 | 393.18 | 0 | 145.75 | 6878.23 | 6556.39 |
| 600 | 0 | 510.29 | 544.84 | 0 | 145.75 | 6878.23 | 6556.39 |
| 700 | 0 | 510.29 | 544.84 | 0 | 145.75 | 6878.23 | 6556.39 |
| 800 | 0 | 510.29 | 544.84 | 0 | 145.75 | 6878.23 | 6556.39 |
| 900 | 0 | 510.29 | 544.84 | 0 | 145.75 | 6878.23 | 6556.39 |
References
- UNCTAD. Review of Maritime Transportation 2022; Paper Presented at the United Nations Conference on Trade and Development; UNCTAD: New York, NY, USA; Geneva, Switzerland, 2023. [Google Scholar]
- Gu, Y.; Wallace, S.; Wang, X. Can an Emission Trading Scheme really reduce CO2 emissions in the short term? Evidence from a maritime fleet composition and deployment model. Transp. Res. Part D Transp. Environ. 2019, 74, 318–338. [Google Scholar] [CrossRef]
- Davies, M. Emissions trading for ships—A European perspective. Nav. Eng. J. 2006, 118, 131–138. [Google Scholar] [CrossRef]
- Kågeson, P. Linking CO2 Emissions from International Shipping to the EU ETS. 2007. Available online: http://www.natureassociates.se/wp-content/uploads/2011/03/Linking-CO2-Emissions-from-International-Shipping-to-the-EU-ETS.pdf (accessed on 15 February 2018).
- Schinas, O.; Bergmann, N. Emissions trading in the aviation and maritime sector: Findings from a revised taxonomy. Clean. Logist. Supply Chain. 2021, 1, 100003. [Google Scholar] [CrossRef]
- Ye, J.; Chen, J.; Shi, J.; Jiang, X.; Zhou, S. Novel synergy mechanism for carbon emissions abatement in shipping decarbonization. Transp. Res. Part D Transp. Environ. 2024, 127, 104059. [Google Scholar] [CrossRef]
- Christodoulou, A.; Dalaklis, D.; Olcer, A.; Masodzadeh, P. Inclusion of Shipping in the EU-ETS: Assessing the direct costs for the maritime sector using the MRV data. Energies 2021, 14, 3915. [Google Scholar] [CrossRef]
- Wang, T.; Cheng, P.; Wang, Y. How the establishment of carbon emission trading system affects ship emission reduction strategies designed for sulfur emission control area. Transp. Policy 2025, 160, 138–153. [Google Scholar] [CrossRef]
- Kim, J.; Kim, H.; Lee, P. Optimizing containership speed and fleet size under a carbon tax and an emission trading scheme. Int. J. Shipp. Transp. Logist. 2013, 5, 571–590. [Google Scholar] [CrossRef]
- Haehl, C.; Spinler, S. Technology choice under emission regulation uncertainty in international container shipping. Eur. J. Oper. Res. 2019, 284, 383–396. [Google Scholar] [CrossRef]
- Kenan, N.; Jebali, A.; Diabat, A. The integrated quay crane assignment and scheduling problems with carbon emissions considerations. Comput. Ind. Eng. 2022, 165, 107734. [Google Scholar] [CrossRef]
- Xue, Y.; Lai, K.; Wang, C. How to invest decarbonization technology in shipping operations? Evidence from a game-theoretic investigation. Ocean Coast. Manag. 2024, 251, 107076. [Google Scholar] [CrossRef]
- Wang, T.; Cheng, P.; Zhen, L. Green development of the maritime industry: Overview, perspectives, and future research opportunities. Transp. Res. Part E Logist. Transp. Rev. 2023, 179, 138–153. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, S.; Chen, Y.; Chang, D. Evaluation of liquefied natural gas as a ship fuel for liner shipping using evolutionary game theory. Asia-Pac. J. Oper. Res. 2021, 38, 2140022. [Google Scholar] [CrossRef]
- Li, D.; Yang, H.; Xing, Y. Economic and emission assessment of LNG-fuelled ships for inland waterway transportation. Ocean Coast. Manag. 2023, 246, 106906. [Google Scholar] [CrossRef]
- Qi, J.; Wang, H.; Zheng, J. Promoting liquefied natural gas (LNG) bunkering for maritime transportation: Should ports or ships be subsidized? Sustainability 2022, 14, 6928. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, X.; Wang, H.; Cheng, S.; Liu, W. Fleet deployment optimization for LNG shipping vessels considering the influence of mixed factors. J. Mar. Sci. Eng. 2022, 10, 2034. [Google Scholar] [CrossRef]
- Yuan, J.; Shi, X.; He, J. LNG market liberalization and LNG transportation: Evaluation based on fleet size and composition model. Appl. Energy 2024, 358, 122657. [Google Scholar] [CrossRef]
- Shih, Y.C.; Tzeng, Y.; Cheng, C.; Huang, C. Speed and fuel ratio optimization for a dual-fuel ship to minimize its carbon emissions and cost. J. Mar. Sci. Eng. 2023, 11, 758. [Google Scholar] [CrossRef]
- He, P.; Jin, J.; Pan, W.; Chen, J. Route, speed, and bunkering optimization for LNG-fueled tramp ship with alternative bunkering ports. Ocean Eng. 2024, 305, 117957. [Google Scholar] [CrossRef]
- Sun, L.; Wang, X.; Hu, Z.; Liu, W.; Ning, Z. Carbon reduction and cost control of container shipping in response to the European Union Emission Trading System. Environ. Sci. Pollut. Res. 2024, 31, 21172–21188. [Google Scholar] [CrossRef]
- Christiansen, M.; Fagerholt, K.; Ronen, D. Ship routing and scheduling: Status and perspectives. Transp. Sci. 2004, 38, 1–120. [Google Scholar] [CrossRef]
- Dulebenets, M.; Pasha, J.; Abioye, O.; Kavoosi, M. Vessel scheduling in liner shipping: A critical literature review and future research needs. Flex. Serv. Manuf. J. 2019, 33, 43–106. [Google Scholar] [CrossRef]
- Chen, J.; Ye, J.; Zhuang, C.; Qin, Q.; Shu, Y. Liner shipping alliance management: Overview and future research directions. Ocean. Coast. Manag. 2022, 219, 106039. [Google Scholar] [CrossRef]
- Sun, Y.; Zheng, J.; Yang, L.; Li, X. Allocation and trading schemes of the maritime emissions trading system: Liner shipping route choice and carbon emissions. Transp. Policy 2024, 148, 60–78. [Google Scholar] [CrossRef]
- Haites, E. Linking emissions trading schemes for international aviation and shipping emissions. Clim. Policy 2009, 9, 415–430. [Google Scholar] [CrossRef]
- Schinas, O.; Butler, M. Feasibility and commercial considerations of LNG-fueled ships. Ocean Eng. 2016, 122, 84–96. [Google Scholar] [CrossRef]
- Jeong, H.; Yun, H. A stochastic approach for economic valuation of alternative fuels: The case of container ship investments. J. Clean. Prod. 2023, 418, 138182. [Google Scholar] [CrossRef]
- Xu, H.; Yang, D. LNG-fuelled container ship sailing on the Arctic Sea: Economic and emission assessment. Transp. Res. Part D Transp. Environ. 2020, 87, 102556. [Google Scholar] [CrossRef]
- Hermeling, C.; Klement, J.; Koesler, S.; Köhler, J.; Klement, D. Sailing into a dilemma: An economic and legal analysis of an EU trading scheme for maritime emissions. Transp. Res. Part A Policy Pract. 2015, 78, 34–53. [Google Scholar] [CrossRef]
- Wang, K.; Fu, X.; Luo, M. Modeling the impacts of alternative emission trading schemes on international shipping. Transp. Res. Part A Policy Pract. 2015, 77, 35–49. [Google Scholar] [CrossRef]
- Mao, Z.; Ma, A.; Zhang, Z. Towards carbon neutrality in shipping: Impact of European Union’s emissions trading system for shipping and China’s response. Ocean Coast. Manag. 2024, 249, 107006. [Google Scholar] [CrossRef]
- Wang, S.; Zhen, L.; Psaraftis, H.N.; Yan, R. Implications of the EU’s inclusion of maritime transport in the emissions trading system for shipping companies. Engineering 2021, 7, 554–557. [Google Scholar] [CrossRef]
- Meng, B.; Chen, S.; Haralambides, H.; Kuang, H.; Fan, L. Information spillovers between carbon emissions trading prices and shipping markets: A time-frequency analysis. Energy Econ. 2023, 120, 106604. [Google Scholar] [CrossRef]
- Wang, T.; Wu, Z.; Cheng, P.; Wang, Y. The effect of carbon quota allocation methods on maritime supply chain emission reduction. Transp. Policy 2024, 157, 155–166. [Google Scholar] [CrossRef]
- Cariou, P.; Lindstad, E.; Jia, H. The impact of an EU maritime emissions trading system on oil trades. Transp. Res. Part D Transp. Environ. 2021, 99, 102992. [Google Scholar] [CrossRef]
- Zhu, M.; Yuen, K.; Ge, J.; Li, K. Impact of maritime emissions trading system on fleet deployment and mitigation of CO2 emission. Transp. Res. Part D Transp. Environ. 2018, 62, 474–488. [Google Scholar] [CrossRef]
- Chua, Y.; Soudagar, I.; Ng, S.; Meng, Q. Impact analysis of environmental policies on shipping fleet planning under demand uncertainty. Transp. Res. Part D Transp. Environ. 2023, 120, 103744. [Google Scholar] [CrossRef]
- Sun, Y.; Zheng, J.; Han, J.; Liu, H.; Zhao, Z. Allocation and reallocation of ship emission permits for liner shipping. Ocean. Eng. 2022, 266, 112976. [Google Scholar] [CrossRef]
- Zhu, M.; Shen, S.; Shi, W. Carbon emission allowance allocation based on a bi-level multi-objective model in maritime shipping. Ocean Coast. Manag. 2023, 241, 106665. [Google Scholar] [CrossRef]
- Tan, Z.; Shao, S.; Zhang, D.; Shang, W.; Ochieng, W.; Han, Y. Decarbonizing the inland container fleet with carbon cap-and-trade scheme. Appl. Energy 2024, 376, 124251. [Google Scholar] [CrossRef]
- Burel, F.; Taccani, R.; Zuliani, N. Improving sustainability of maritime transport through utilization of liquefied natural gas (LNG) for propulsion. Energy 2013, 57, 412–420. [Google Scholar] [CrossRef]
- Adachi, M.; Kosaka, H.; Fukuda, T.; Ohashi, S.; Harumi, K. Economic analysis of trans-ocean LNG-fueled container ship. J. Mar. Sci. Technol. 2014, 19, 470–478. [Google Scholar] [CrossRef]
- He, Y.; Yan, X.; Fan, A.; Yin, X.; Meng, Q.; Zhang, L.; Liu, P. Assessing the influence of actual LNG emission factors within the EU emissions trading system. Transp. Policy 2024, 159, 345–358. [Google Scholar] [CrossRef]
- Lee, S.; Jo, C.; Pettersen, B.; Chung, H.; Kim, S.; Chang, D. Concept design and cost benefit analysis of pile-guide mooring system for an offshore LNG bunkering terminal. Ocean Eng. 2018, 154, 59–69. [Google Scholar] [CrossRef]
- Yu, Y.; Ahn, Y.; Kim, J. Determination of the LNG bunkering optimization method for ports based on geometric aggregation score calculation. J. Mar. Sci. Eng. 2021, 9, 1116. [Google Scholar] [CrossRef]
- Ha, M.; Park, H.; Seo, Y. Understanding core determinants in LNG bunkering port selection: Policy implications for the maritime industry. Mar. Policy 2023, 152, 105608. [Google Scholar] [CrossRef]
- Qi, J.; Wang, S. LNG bunkering station deployment problem—A case study of a Chinese container shipping network. Mathematics 2023, 11, 813. [Google Scholar] [CrossRef]
- Xu, J.; Testa, D.; Mukherjee, P. The use of LNG as a marine fuel: The international regulatory framework. Ocean Dev. Int. Law 2015, 46, 225–240. [Google Scholar] [CrossRef]
- Wan, C.; Yan, X.; Zhang, D.; Yang, Z. A novel policy making aid model for the development of LNG fuelled ships. Transp. Res. Part A 2019, 119, 29–44. [Google Scholar] [CrossRef]
- Wang, S.; Qi, J.; Laporte, G. Governmental subsidy plan modeling and optimization for liquefied natural gas as fuel for maritime transportation. Transp. Res. Part B Methodol. 2022, 155, 304–321. [Google Scholar] [CrossRef]
- Shang, T.; Wu, H.; Wang, K.; Yang, D.; Jiang, C.; Yang, H. Would the shipping alliance promote or discourage green shipping investment? Transp. Res. Part D Transp. Environ. 2024, 128, 104102. [Google Scholar] [CrossRef]
- Tai, H.; Chang, Y.; Chang, C.; Wang, Y. Analysis of the carbon intensity of container shipping on trunk routes: Referring to the decarbonization trajectory of the Poseidon principle. Atmosphere 2022, 13, 1580. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Z.; Qu, X. Weekly container delivery patterns in liner shipping planning models. Marit. Policy Manag. 2017, 44, 442–457. [Google Scholar] [CrossRef]
- Zheng, J.; Gao, Z.; Yang, D.; Sun, Z. Network design and capacity exchange for liner alliances with fixed and variable container demands. Transp. Sci. 2015, 49, 886–899. [Google Scholar] [CrossRef]
- Wang, S.; Zhuge, D.; Zhen, L.; Lee, C. Liner shipping service planning under sulfur emission regulations. Transp. Sci. 2021, 55, 491–509. [Google Scholar] [CrossRef]
- Fagerholt, K.; Gausel, N.; Rakke, J.; Psaraftis, H. Maritime routing and speed optimization with emission control areas. Transp. Res. Part C Emerg. Technol. 2015, 52, 57–73. [Google Scholar] [CrossRef]
- Song, C.; Wang, Y. Slot allocation and exchange for container shipping alliance under profit-sharing agreement and uncertain demand. Ocean Coast. Manag. 2022, 299, 106335. [Google Scholar] [CrossRef]
- Yang, L.; Yang, Y.; Zhou, Y.; Shi, X. Research the synergistic carbon reduction effects of sulfur dioxide emissions trading policy. J. Clean. Prod. 2024, 447, 141483. [Google Scholar] [CrossRef]
- Zhen, L.; Chang, D. A bi-objective model for robust berth allocation scheduling. Comput. Ind. Eng. 2012, 63, 262–273. [Google Scholar] [CrossRef]
- Guo, L.; Zheng, J.; Du, H.; Du, J.; Zhu, Z. The berth assignment and allocation problem considering cooperative liner carriers. Transp. Res. Part E Logist. Transp. Rev. 2022, 164, 102793. [Google Scholar] [CrossRef]
- Wang, S.; Meng, Q. Schedule design and container routing in liner shipping. Transp. Res. Rec. 2011, 2222, 25–33. [Google Scholar] [CrossRef]
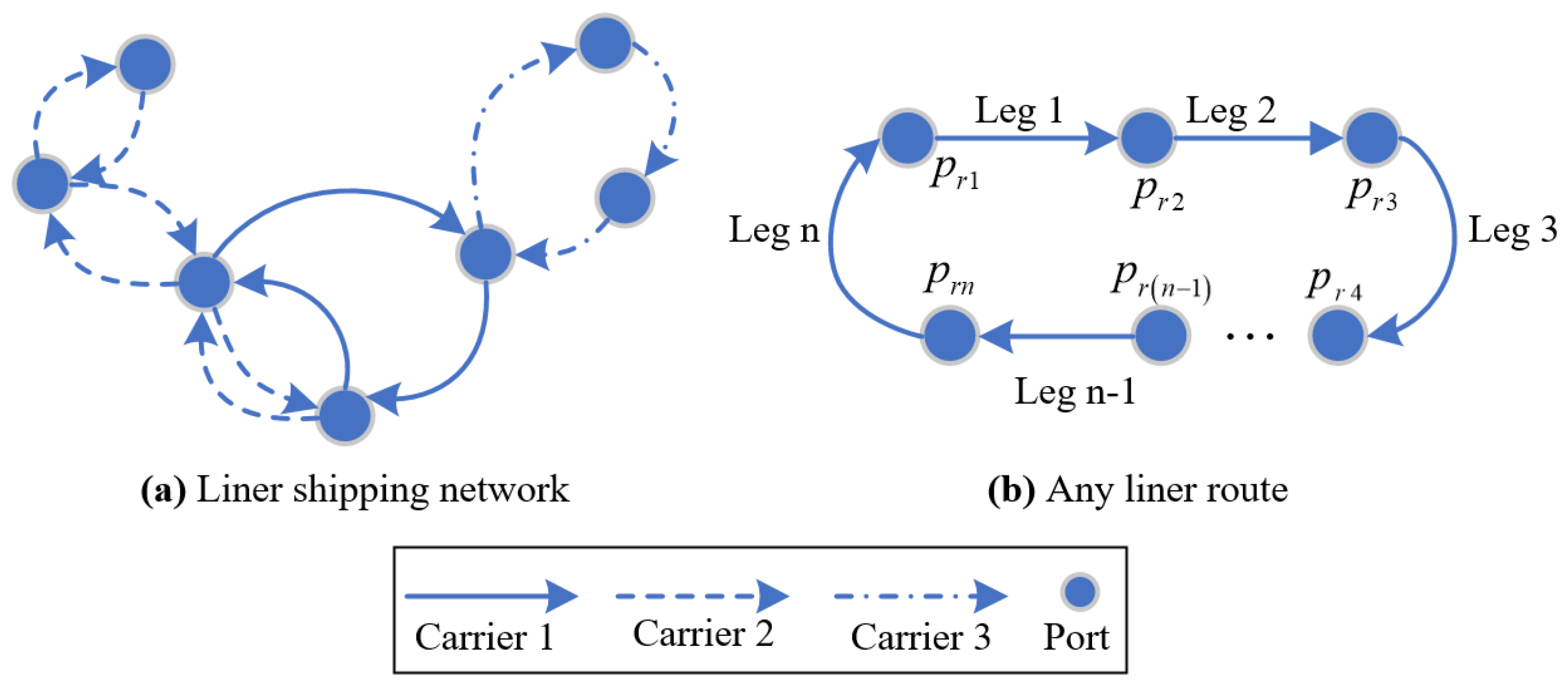
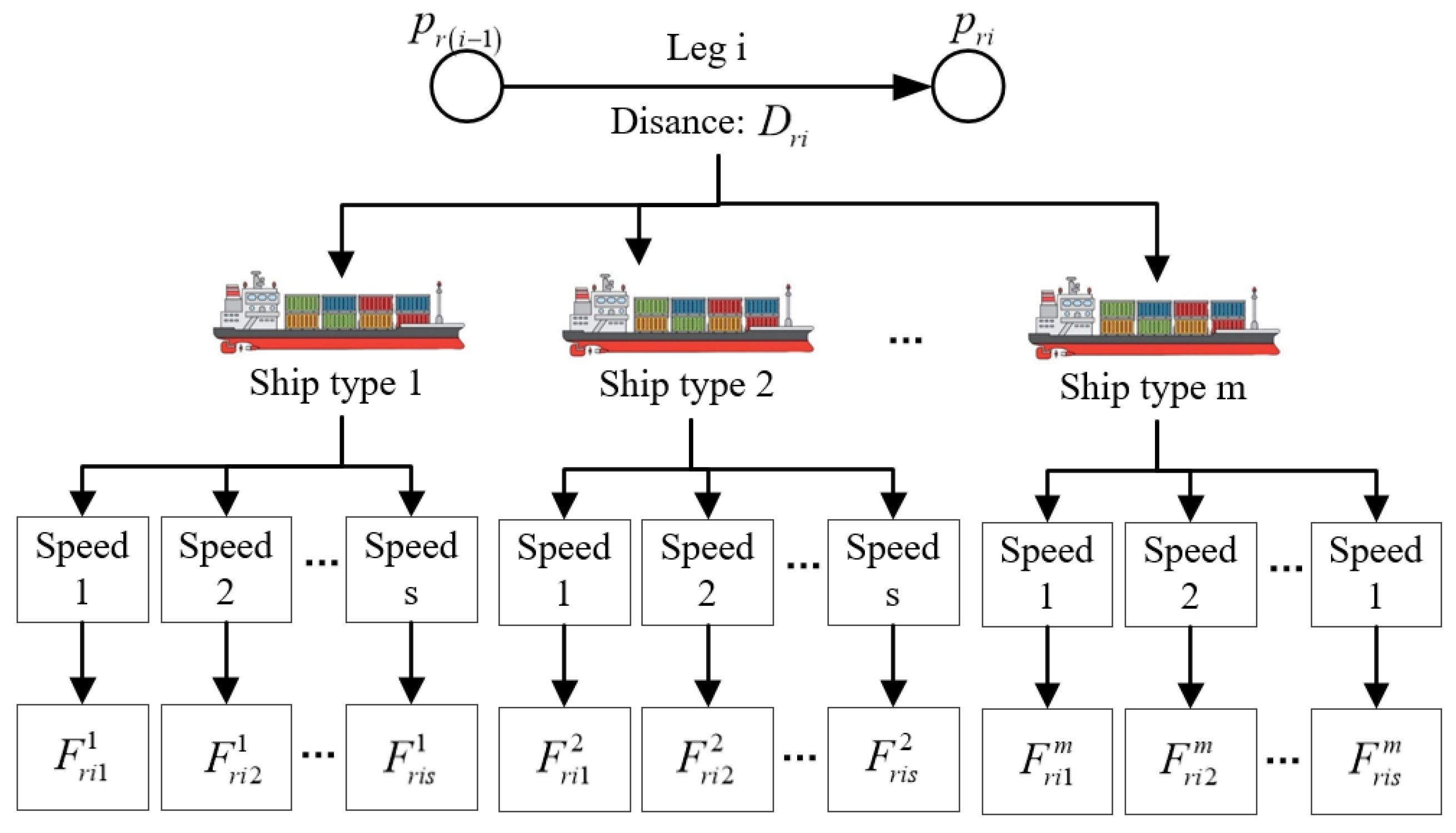

| Fuel | VLSFO | LNG |
|---|---|---|
| Main advantage | (i) Mature technology (ii) The supply network is mature and easy to access (iii) The price is stable | (i) High reserve (ii) The price is competitive with existing fuels |
| Main disadvantage | Compared with LNG, it offers poorer environmental protection | (i) High investment cost (ii) High fixed operation cost for ships (iii) The price is unstable |
| Carbon emission factor | 3.151 | 2.75 |
| Net calorific value (MWh/ton) | 11.28 | 13.5 |
| Research | METS | LNG-Powered Ships | Shipping (or Liner) Alliance | Investigations | Methodology |
|---|---|---|---|---|---|
| Tai et al. [53] | √ | Empirical analysis of carbon emissions | Activity-based model | ||
| Wang et al. [8] | √ | √ | Impact of the METS on sulphur emission regulations | A mixed-integer programming model | |
| Shang et al. [52] | √ | Green investment for shipping alliances | Economic model | ||
| He et al. [44] | √ | √ | Assessing the economic impact of LNG-powered ships on CEP trading | All-performance carbon emission test | |
| Tan et al. [41] | √ | √ | Ship operation planning of inland container ships | Bi-level programming | |
| Gu et al. [2] | √ | Fleet deployment | Mixed-integer programming model | ||
| Shih et al. [19] | √ | Speed and fuel ratio optimization for LNG dual-fuel ships | NSGA-II | ||
| This paper | √ | √ | √ | Deploying LNG-powered ships for liner alliances | Mixed-integer programming model |
| Ship Type | 1 | 2 | 3 | 4 |
| Capacity (TEU) | 3000 | 8000 | 12,000 | 18,000 |
| Powered by | Fuel | Fuel | Fuel | Fuel |
| 0.012 | 0.0108 | 0.013 | 0.015 | |
| 2.815 | 3.026 | 3.207 | 3.371 | |
| 1 | 1 | 1 | 1 | |
| Fixed cost (USD 103 ) | 70.9 | 142.7 | 216.8 | 285.8 |
| Ship Type | 5 | 6 | 7 | 8 |
| Capacity (TEU) | 3000 | 8000 | 12,000 | 18,000 |
| Powered by | LNG | LNG | LNG | LNG |
| 0.012 | 0.0108 | 0.013 | 0.015 | |
| 2.815 | 3.026 | 3.207 | 3.371 | |
| 0.84 | 0.84 | 0.84 | 0.84 | |
| Fixed cost (USD 103) | 85.08 | 171.24 | 260.16 | 342.96 |
| Trading Price of CEPs (USD/tons) | Liner Alliance | Single Liner Carrier | Cost Reduction Rate (%) | |||
|---|---|---|---|---|---|---|
| Carrier 1 | Carrier 2 | Carrier 3 | Sum | |||
| 0 | 55.36 | 5.93 | 28.86 | 23.13 | 57.92 | 3.54% |
| 30 | 56.46 | 6.00 | 29.16 | 23.37 | 58.53 | 3.00% |
| 60 | 57.26 | 6.05 | 29.41 | 23.57 | 59.03 | 2.51% |
| 90 | 57.82 | 6.08 | 29.55 | 23.68 | 59.31 | 1.84% |
| 120 | 58.30 | 6.09 | 29.59 | 23.71 | 59.39 | 3.86% |
| 150 | 58.58 | 6.08 | 30.56 | 24.29 | 60.93 | 4.57% |
| 180 | 58.83 | 6.06 | 30.97 | 24.62 | 61.65 | 5.89% |
| 210 | 58.97 | 6.04 | 31.38 | 25.24 | 62.66 | 7.43% |
| 240 | 59.05 | 6.00 | 32.01 | 25.78 | 63.79 | 9.14% |
| 270 | 59.02 | 5.94 | 32.88 | 26.14 | 64.96 | 10.79% |
| 300 | 58.80 | 5.87 | 33.15 | 26.89 | 65.91 | 11.43% |
| 330 | 58.52 | 5.80 | 33.98 | 26.29 | 66.07 | 3.54% |
| Route | Rate | Route | Rate | Route | Rate |
|---|---|---|---|---|---|
| 1 | 37.89% | 15 | 18.54% | 35 | 18.05% |
| 2 | 21.45% | 16 | 24.31% | 36 | 23.37% |
| 3 | 0.00% | 17 | 17.86% | 37 | 15.70% |
| 4 | 0.00% | 18 | 10.28% | 39 | 19.19% |
| 5 | 17.07% | 20 | 17.91% | 40 | 16.70% |
| 6 | 0.00% | 23 | 21.72% | 41 | 18.22% |
| 7 | 44.37% | 25 | 0.11% | 42 | 17.01% |
| 8 | 21.57% | 26 | 16.60% | 43 | 21.63% |
| 9 | 19.60% | 27 | 0.00% | 44 | 0.11% |
| 10 | 0.00% | 28 | 0.00% | 45 | 20.57% |
| 11 | 18.08% | 30 | 0.00% | 46 | 17.27% |
| 12 | 17.26% | 31 | 20.95% | 47 | 16.52% |
| 13 | 17.98% | 33 | 0.00% | 48 | 0.00% |
| 14 | 18.36% | 34 | 18.35% | 49 | 0.00% |
| Trading Price of CEPs (USD/ton) | Total Cost (USD 106) | Carbon Emissions (tons) | Traded CEPs (tons) | ||
|---|---|---|---|---|---|
| Carrier 1 | Carrier 2 | Carrier 3 | |||
| 0 | 55.36 | 97,789.52 | 9259 | 12,597 | 16,453 |
| 30 | 56.46 | 94,925.76 | 8246.11 | 11,877.63 | 15,319.97 |
| 60 | 57.26 | 79,898.41 | 3935.41 | 7984.15 | 8496.81 |
| 90 | 57.82 | 77,182.47 | 3776.58 | 6877.85 | 7045.98 |
| 120 | 58.30 | 69,936.91 | 3717.19 | 3752.64 | 2985.01 |
| 150 | 58.58 | 68,042.45 | 3249.59 | 2994.25 | 2316.56 |
| 180 | 58.83 | 67,442.03 | 3249.59 | 2748.78 | 1961.61 |
| 210 | 58.97 | 62,684.05 | 2677.83 | −877.43 | 1401.6 |
| 240 | 59.05 | 60,692.84 | 2677.83 | −1639.48 | 172.44 |
| 270 | 59.02 | 53,893.86 | 691.4 | −3880.55 | −2399.04 |
| 300 | 58.80 | 51,620.82 | 477.5 | −4018.19 | −4320.53 |
| 330 | 58.52 | 48,679.92 | 52.14 | −4727.35 | −6126.92 |
| CEP Price (USD/ton) | VLSFO-Powered Ships | LNG-Powered Ships | Sum | |||
|---|---|---|---|---|---|---|
| Cost (USD 106) | Carbon Emissions (103 tons) | Cost (USD 106) | Carbon Emissions (103 tons) | Cost (USD 106) | Carbon Emissions (103 tons) | |
| 30 | 55.40 | 94.93 | 0.00 | 0.00 | 55.40 | 94.93 |
| 60 | 55.84 | 79.60 | 0.14 | 0.30 | 55.97 | 79.90 |
| 90 | 56.23 | 77.18 | 0.00 | 0.00 | 56.23 | 77.18 |
| 120 | 56.95 | 69.78 | 0.10 | 0.15 | 57.05 | 69.94 |
| 150 | 56.05 | 66.49 | 1.18 | 1.56 | 57.23 | 68.04 |
| 180 | 55.75 | 65.37 | 1.65 | 2.07 | 57.39 | 67.44 |
| 210 | 54.28 | 58.40 | 3.95 | 4.29 | 58.24 | 62.68 |
| 240 | 48.80 | 51.08 | 9.96 | 9.62 | 58.76 | 60.69 |
| 270 | 28.10 | 27.16 | 32.43 | 26.74 | 60.53 | 53.89 |
| 300 | 21.52 | 19.99 | 39.57 | 31.63 | 61.09 | 51.62 |
| 330 | 11.23 | 9.92 | 50.86 | 38.76 | 62.09 | 48.68 |
| LNG Price (USD/ton) | VLSFO-Powered Ships | LNG-Powered Ships | Total | |||
|---|---|---|---|---|---|---|
| Cost (USD 106) | Carbon Emissions (103 tons) | Cost (USD 106) | Carbon Emissions (103 tons) | Cost (USD 106) | Carbon Emissions (103 tons) | |
| 100 | 0.49 | 0.30 | 40.94 | 106.40 | 41.43 | 106.7 |
| 200 | 0.49 | 0.35 | 44.32 | 106.36 | 44.81 | 106.71 |
| 300 | 0.70 | 0.51 | 48.55 | 99.94 | 49.25 | 100.45 |
| 400 | 45.88 | 81.29 | 6.70 | 10.37 | 52.58 | 91.66 |
| 500 | 52.43 | 94.93 | / | / | 52.43 | 94.93 |
| 600 | 52.43 | 94.93 | / | / | 52.43 | 94.93 |
| 700 | 52.43 | 94.93 | / | / | 52.43 | 94.93 |
| 800 | 52.43 | 94.93 | / | / | 52.43 | 94.93 |
| 900 | 52.43 | 94.93 | / | / | 52.43 | 94.93 |
| Total Cost (USD 106) | Carbon Emissions (103 tons) | Ship Power | |
|---|---|---|---|
| 0 | 54.56 | 94.93 | VLSFO |
| 2 | 55.19 | 95.52 | VLSFO |
| 4 | 56.01 | 96.15 | VLSFO |
| 6 | 56.59 | 93.70 | VLSFO |
| 8 | 57.36 | 94.40 | VLSFO |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zheng, J.; He, X.; Zhao, Z.; Cui, D. Deploying Liquefied Natural Gas-Powered Ships in Response to the Maritime Emission Trading System: From the Perspective of Shipping Alliances. J. Mar. Sci. Eng. 2025, 13, 551. https://doi.org/10.3390/jmse13030551
Sun Y, Zheng J, He X, Zhao Z, Cui D. Deploying Liquefied Natural Gas-Powered Ships in Response to the Maritime Emission Trading System: From the Perspective of Shipping Alliances. Journal of Marine Science and Engineering. 2025; 13(3):551. https://doi.org/10.3390/jmse13030551
Chicago/Turabian StyleSun, Yulong, Jianfeng Zheng, Xin He, Zhihao Zhao, and Di Cui. 2025. "Deploying Liquefied Natural Gas-Powered Ships in Response to the Maritime Emission Trading System: From the Perspective of Shipping Alliances" Journal of Marine Science and Engineering 13, no. 3: 551. https://doi.org/10.3390/jmse13030551
APA StyleSun, Y., Zheng, J., He, X., Zhao, Z., & Cui, D. (2025). Deploying Liquefied Natural Gas-Powered Ships in Response to the Maritime Emission Trading System: From the Perspective of Shipping Alliances. Journal of Marine Science and Engineering, 13(3), 551. https://doi.org/10.3390/jmse13030551







