Theoretical and Experimental Analysis of the Global Response of a Flexible Pipe Under Combined Axisymmetric and Bending Loads
Abstract
1. Introduction
2. Experimental Tests
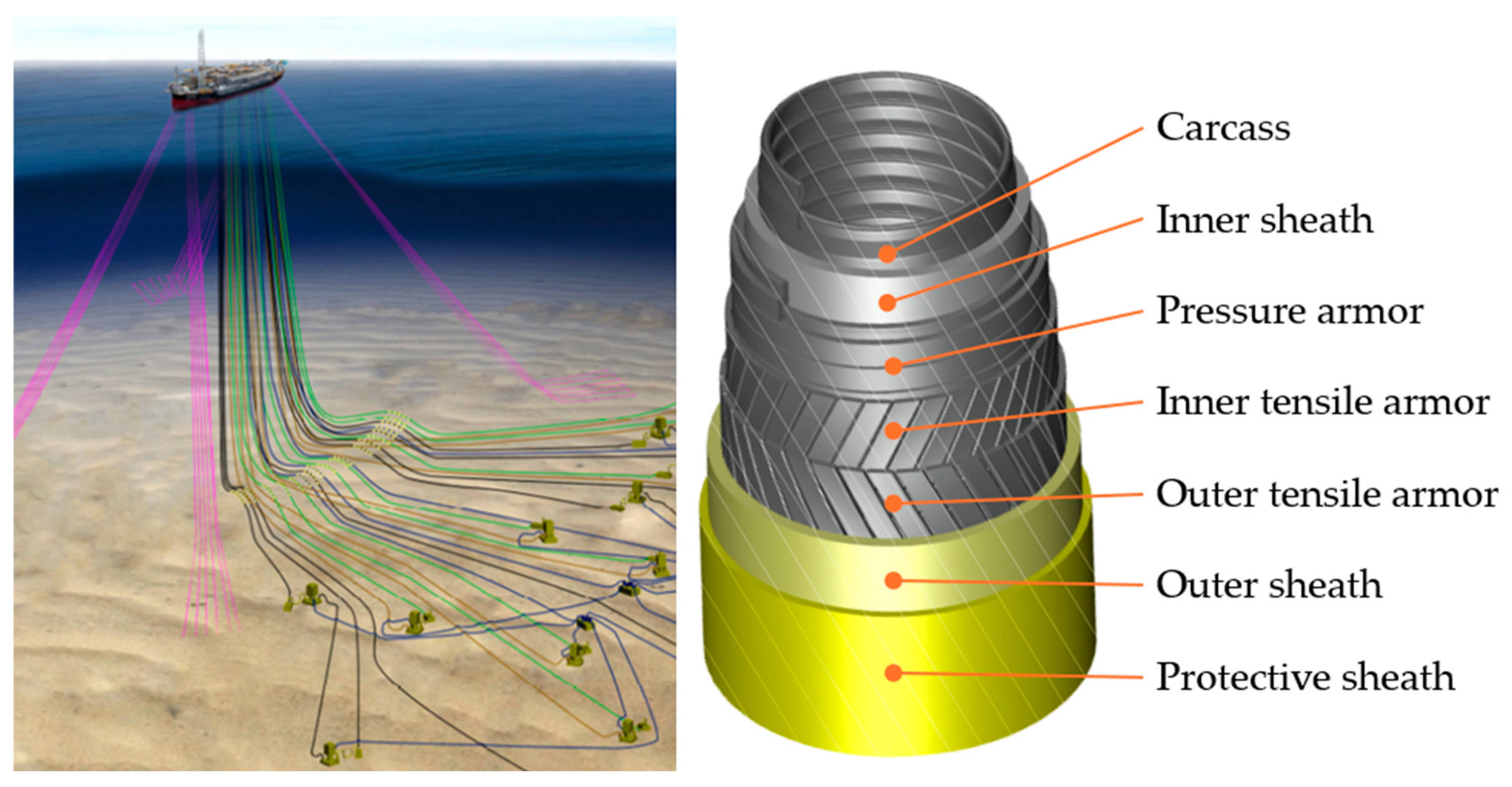
2.1. Flexible Pipe Characteristics
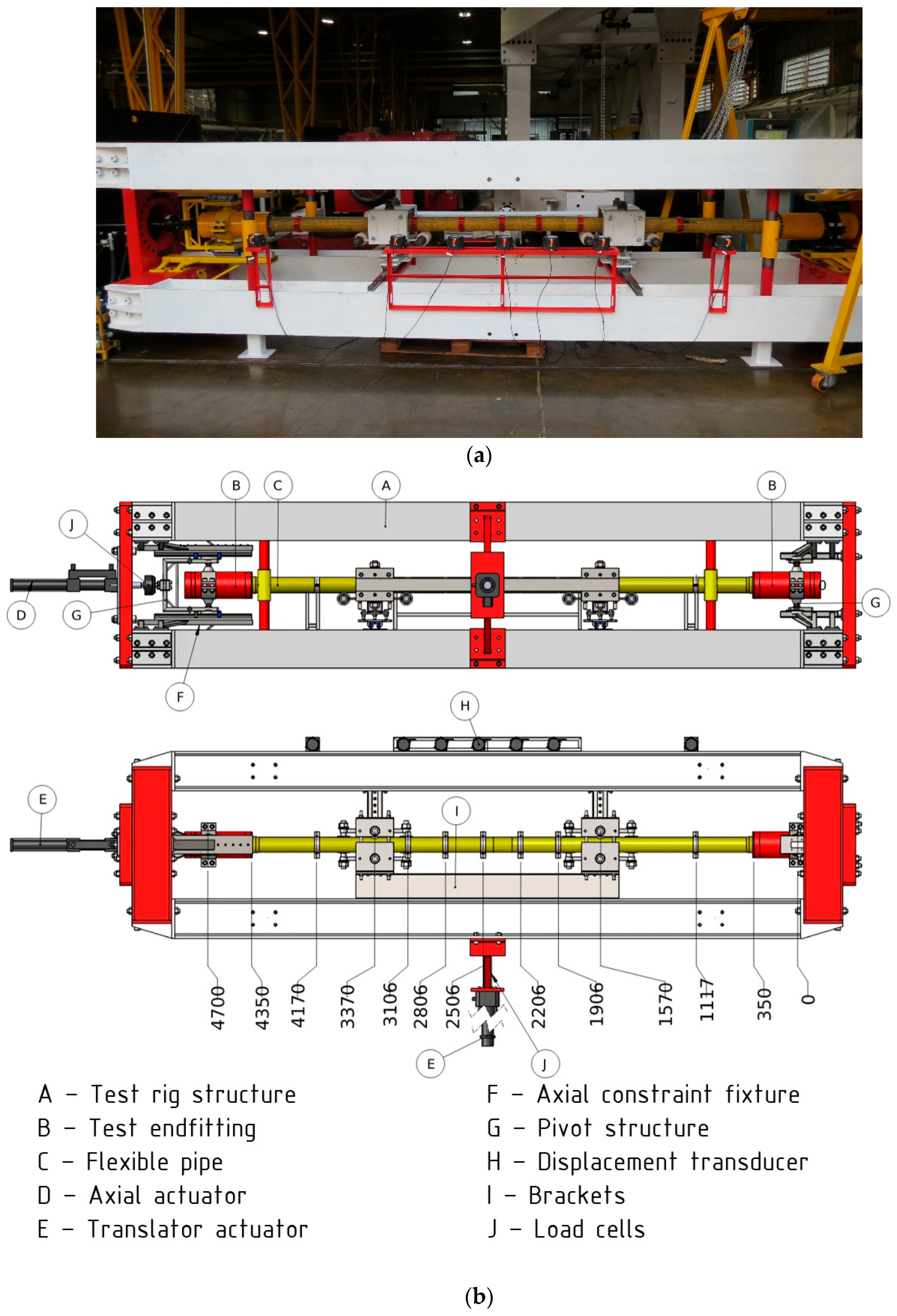
2.2. Experimental Apparatus
2.3. Test Execution
3. Theoretical Approach
3.1. Overview
3.2. Local Models
3.2.1. Axisymmetric Loads
- Small displacements.
- The same elongation and twist in all layers.
- Negligible contribution of plastic layers to the pipe’s mechanical resistance. These layers only transmit pressure.
- No gaps occur between layers.
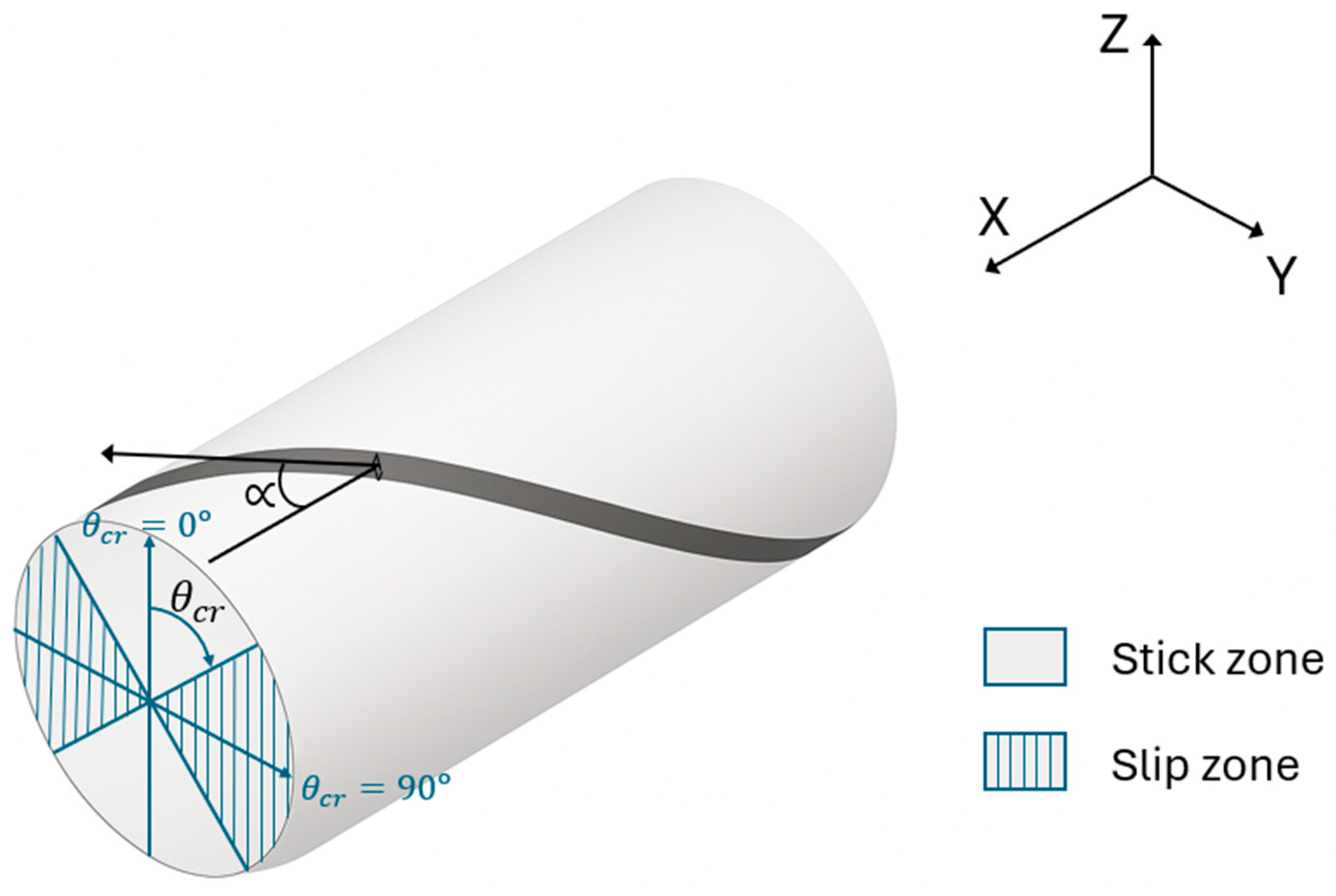
3.2.2. Bending Loads
Monotonic Loading
Cyclic Loading
- The bending response does not depend on the load rate: the pipe’s response to bending only depends on the acting bending moment, curvature, and contact pressures resulting from the axisymmetric loading at a given time. This hypothesis is reasonable to represent the experimental tests in this study, as the loads were imposed to minimize dynamic effects, and it finds support in previous experimental and numerical studies [11,36,38,41].
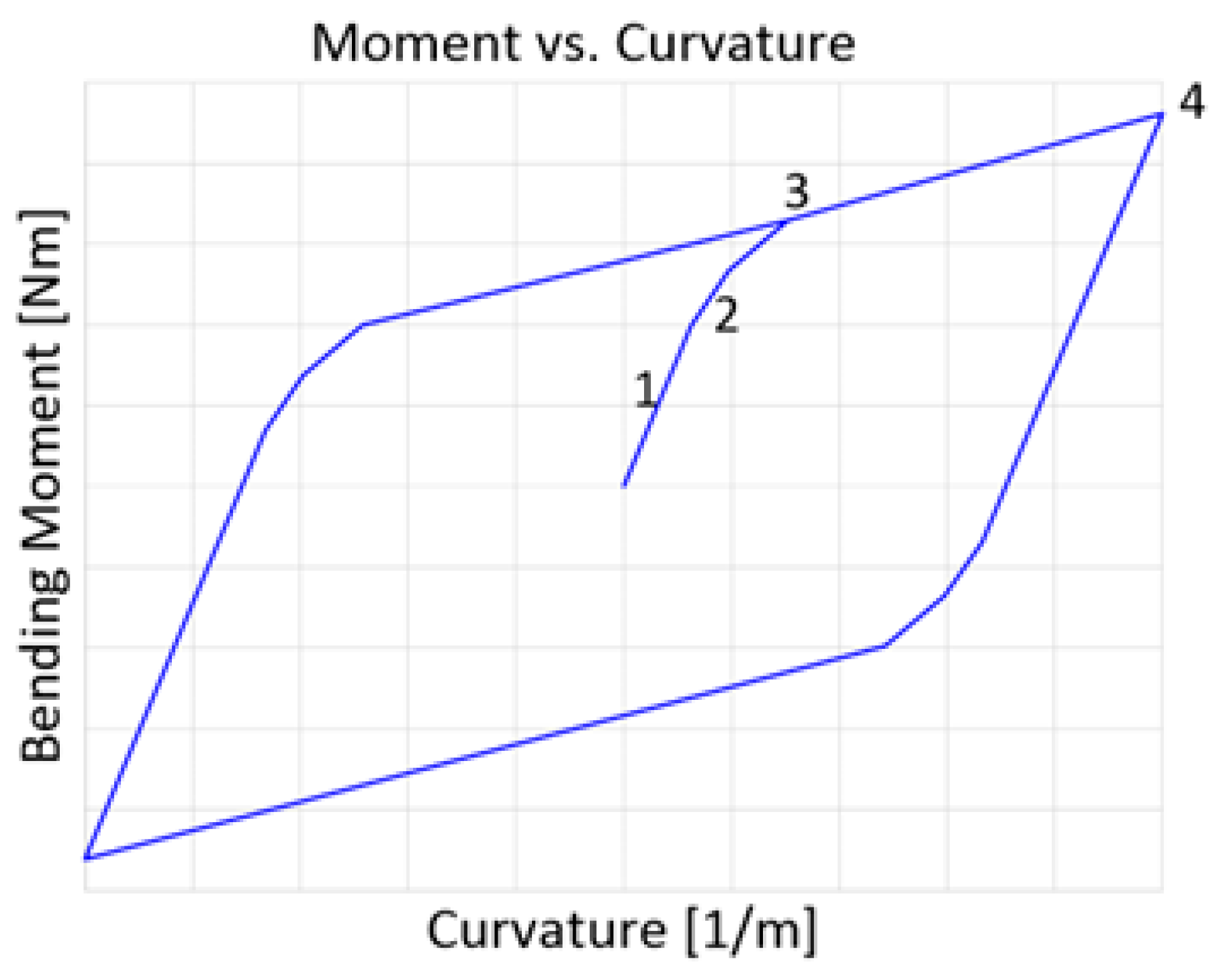
- The sliding surface translates without changing its size: this hypothesis ensures that the pipe retains memory of the loading direction, allowing the position of the critical curvature to adjust with the cyclic load. As qualitatively shown in Figure 2, the critical curvature varies with load reversal, exhibiting a response similar to the Bauschinger effect observed in metals.
3.3. Global Model
3.3.1. Differential Equation
3.3.2. Discretization
3.3.3. Solution
4. Results
4.1. Axisymmetric Loading Test (T0)
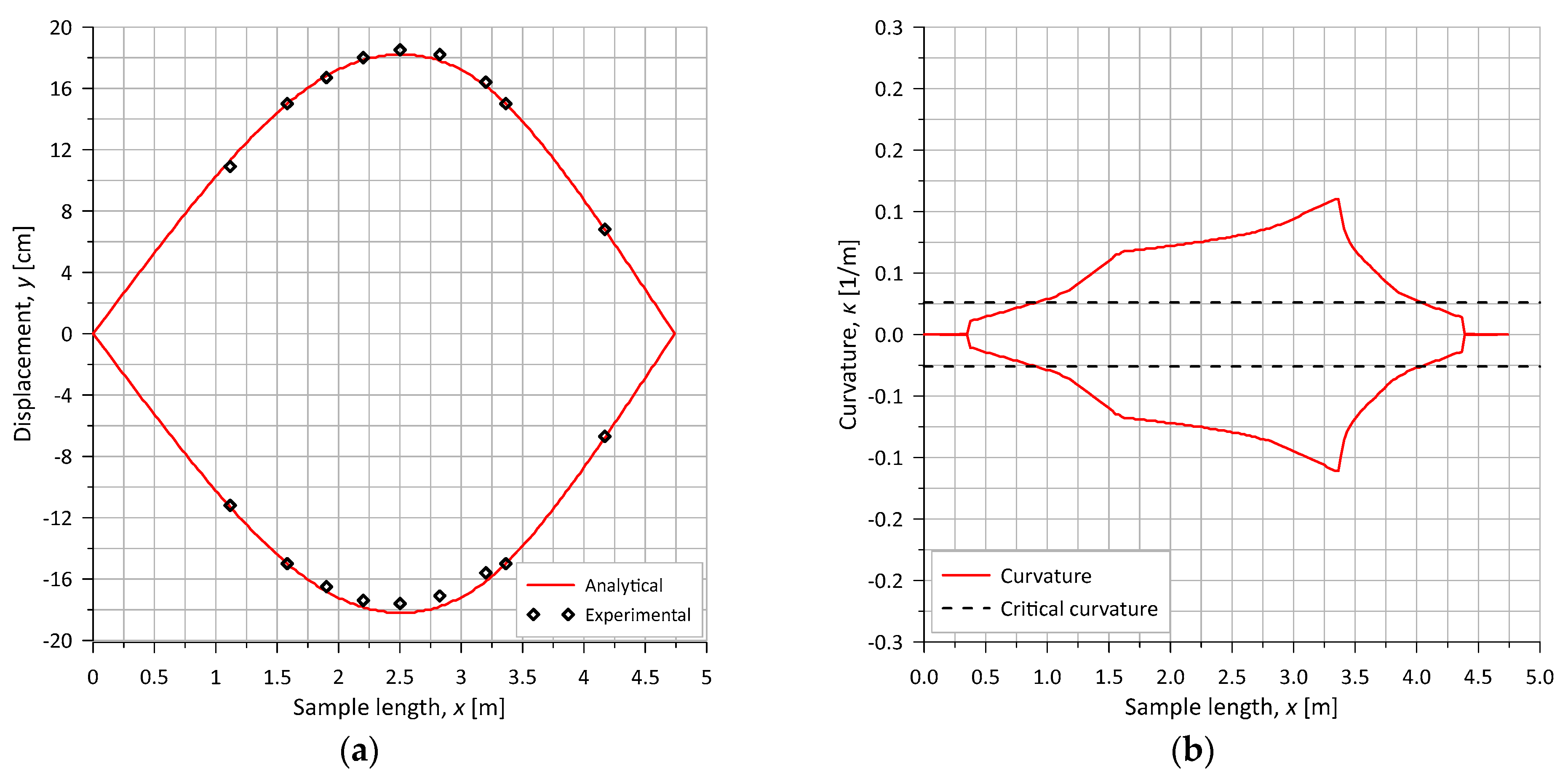
4.2. Pure Bending Test (T1-1)
4.2.1. Mesh and Load Increment Sensitivities
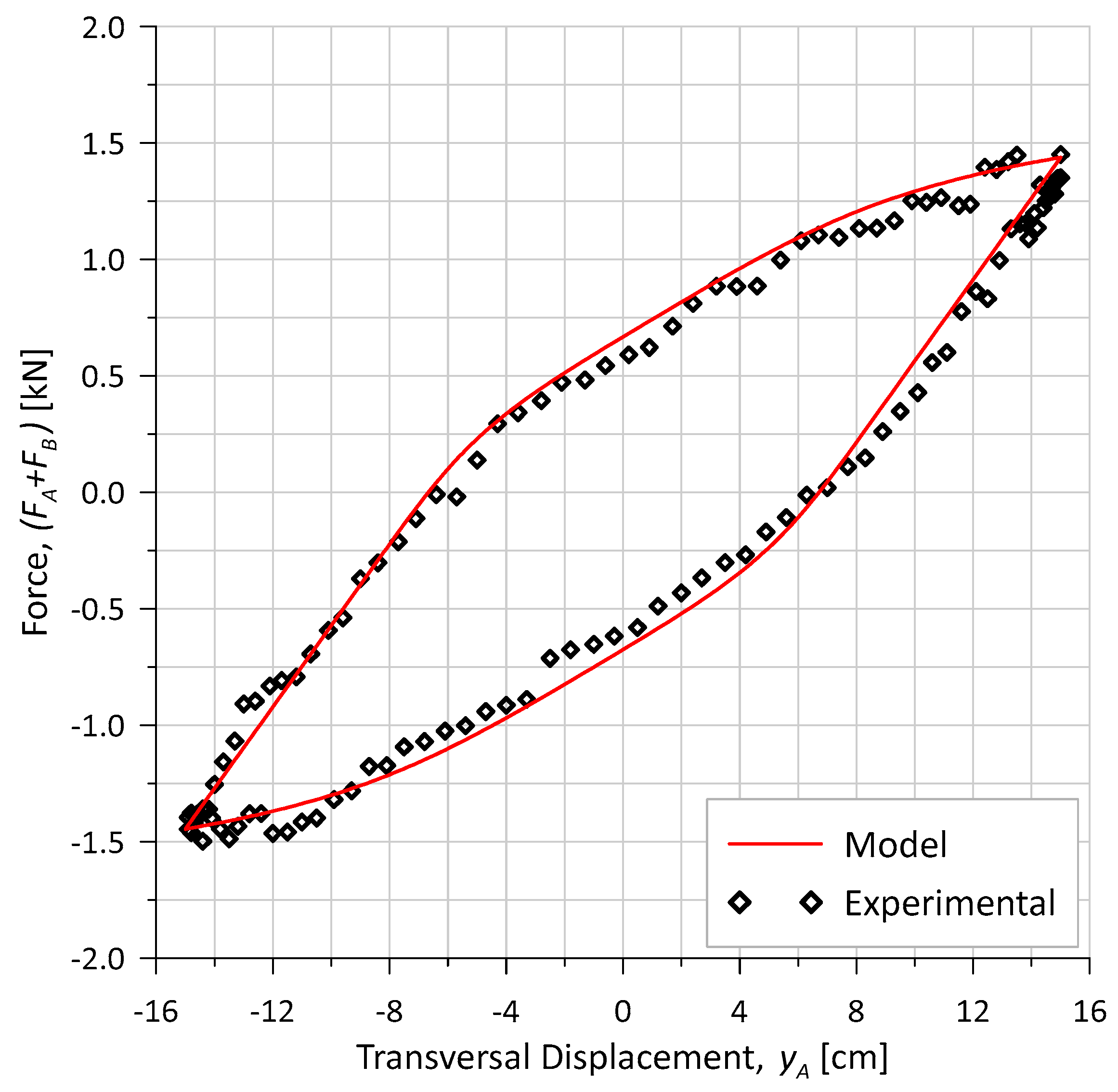
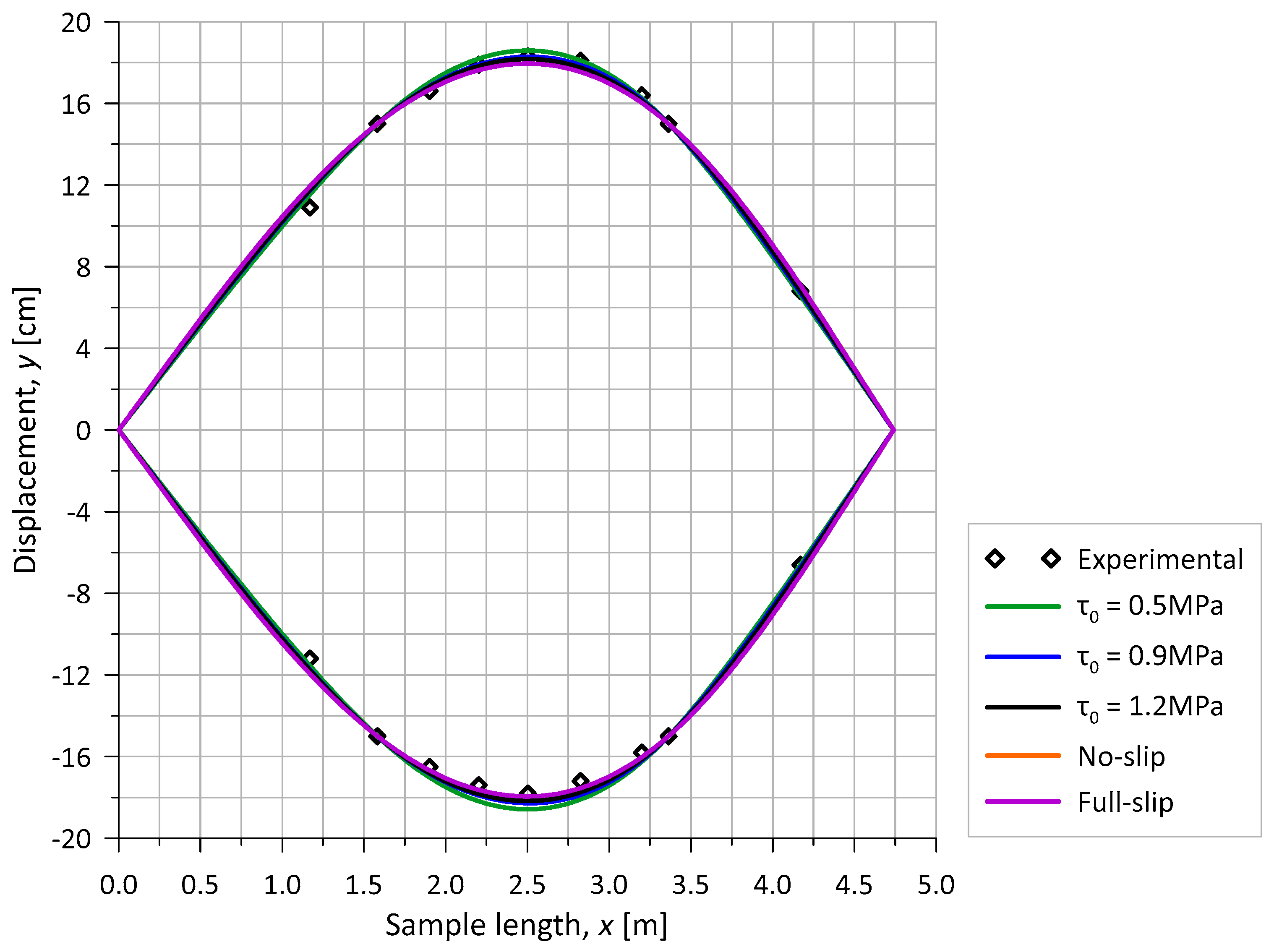
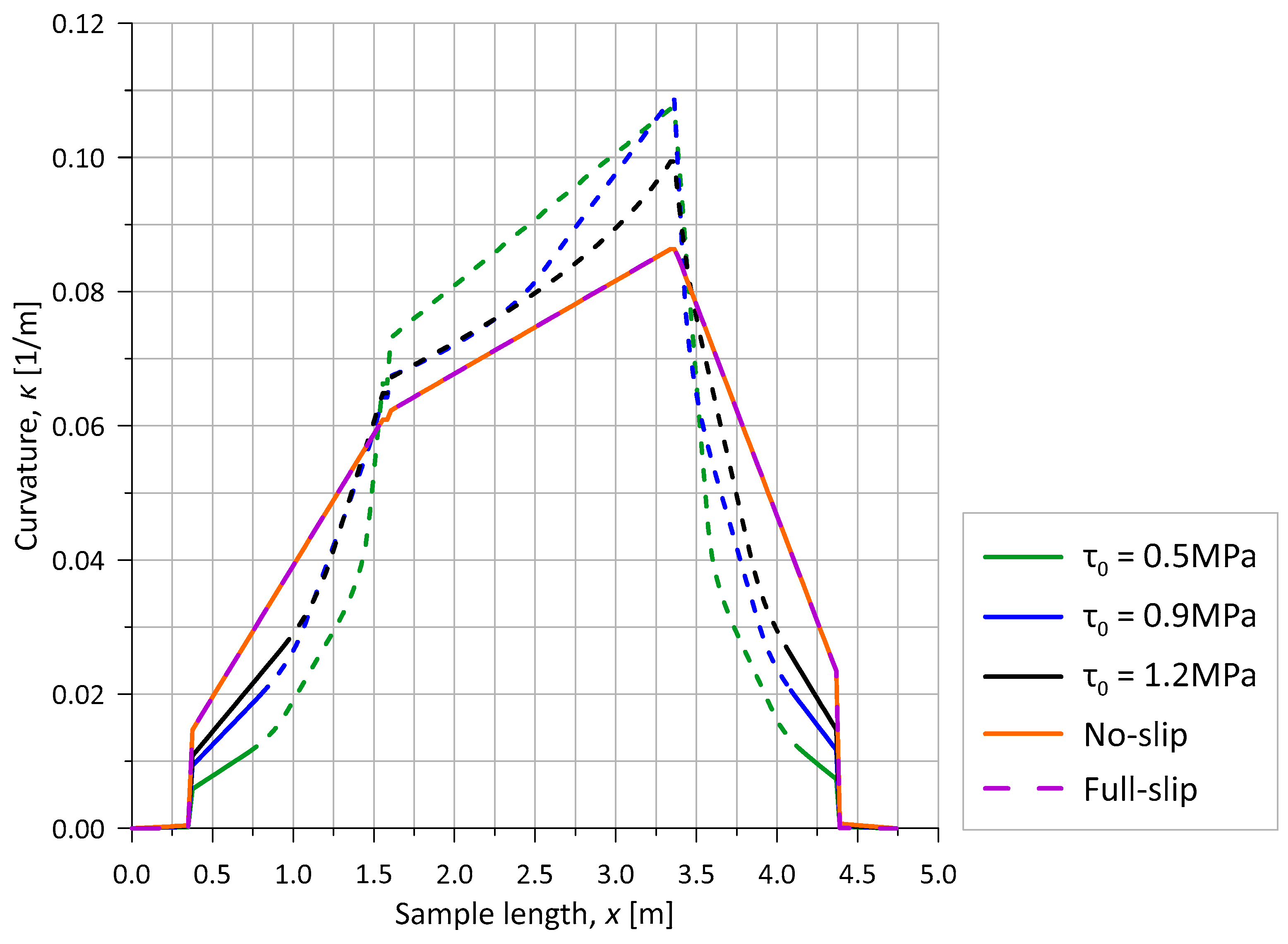
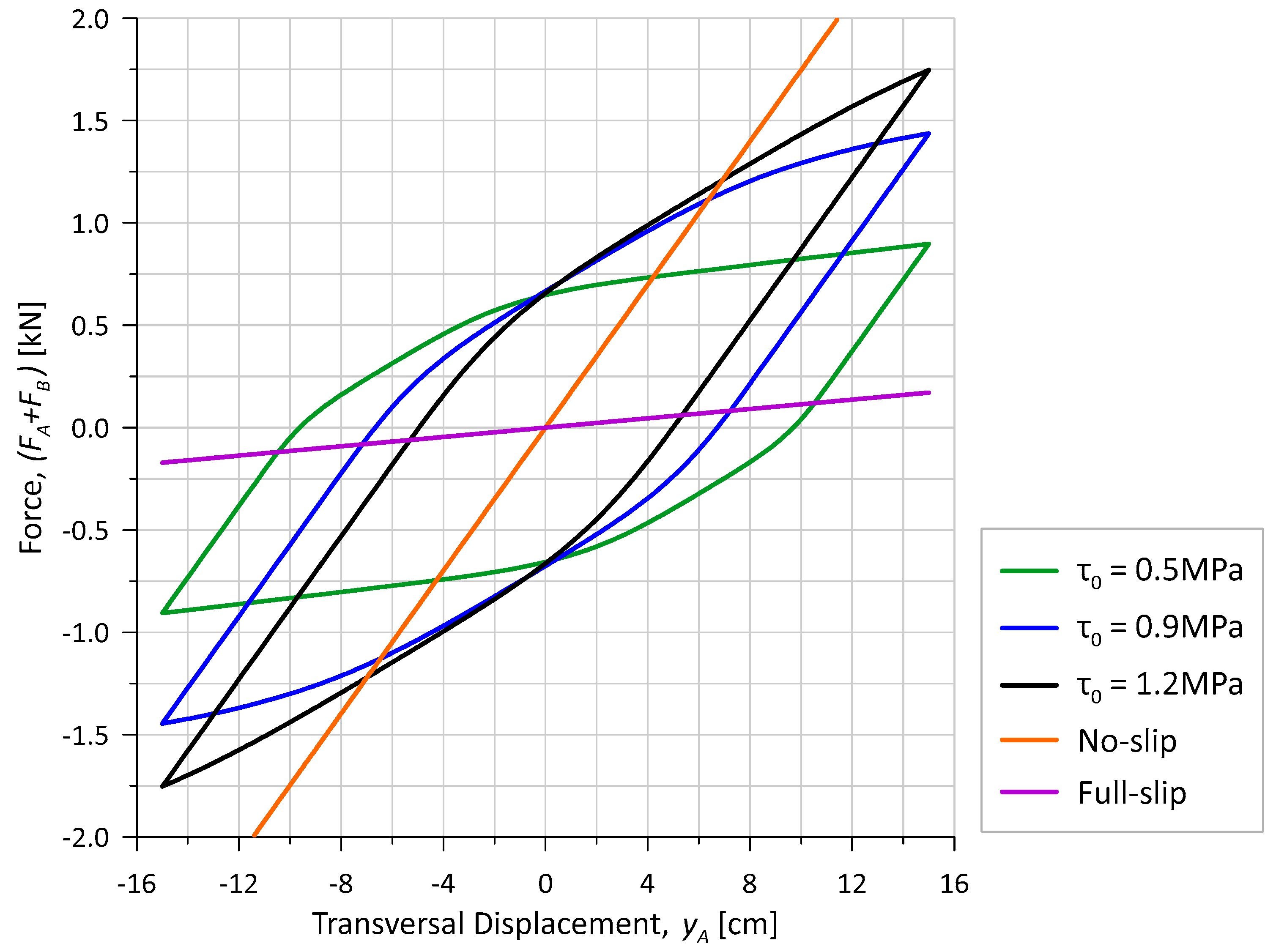
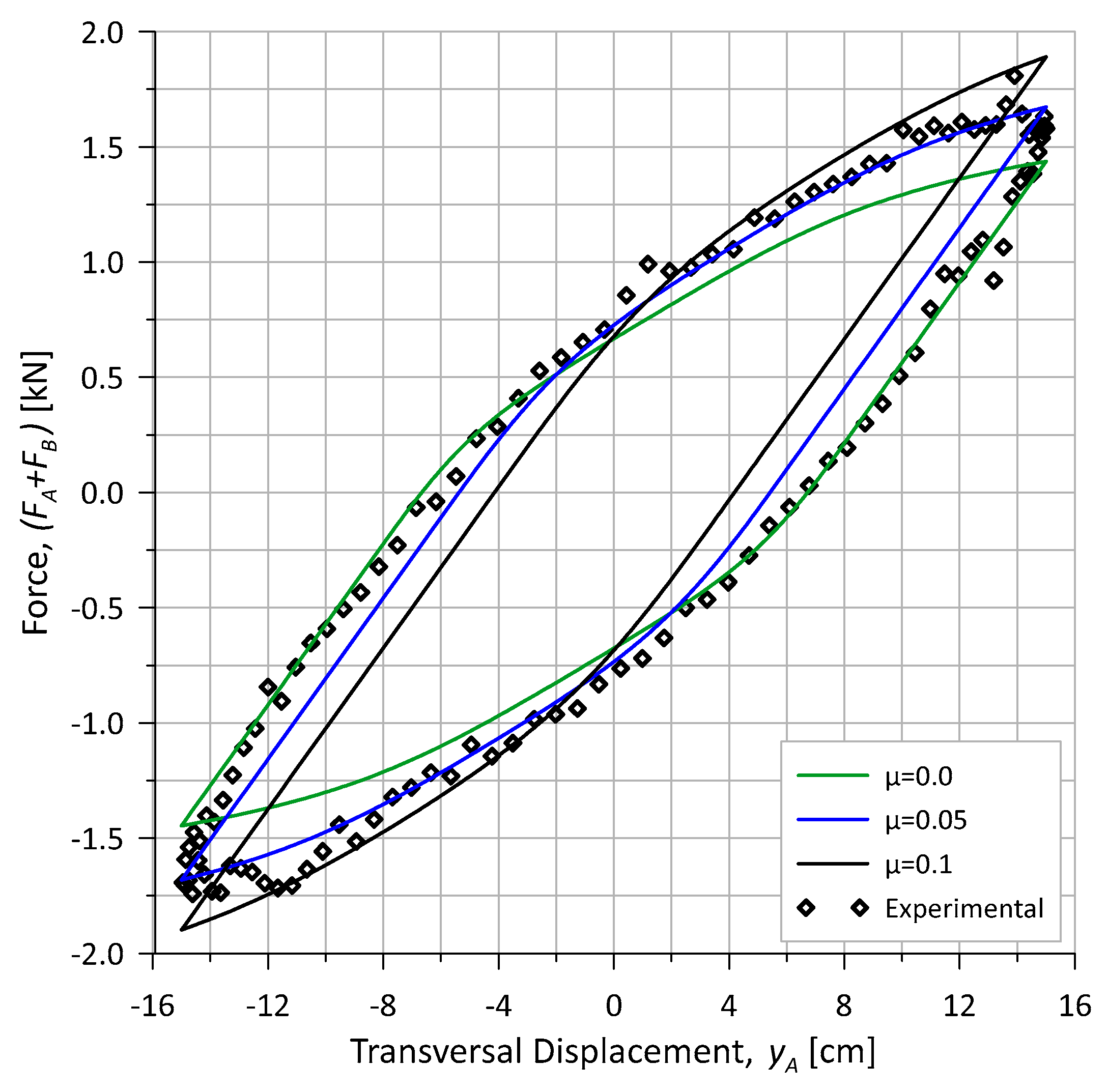
4.2.2. Adhesion Investigation
4.3. Bending Combined with Internal Pressure (T1-2)
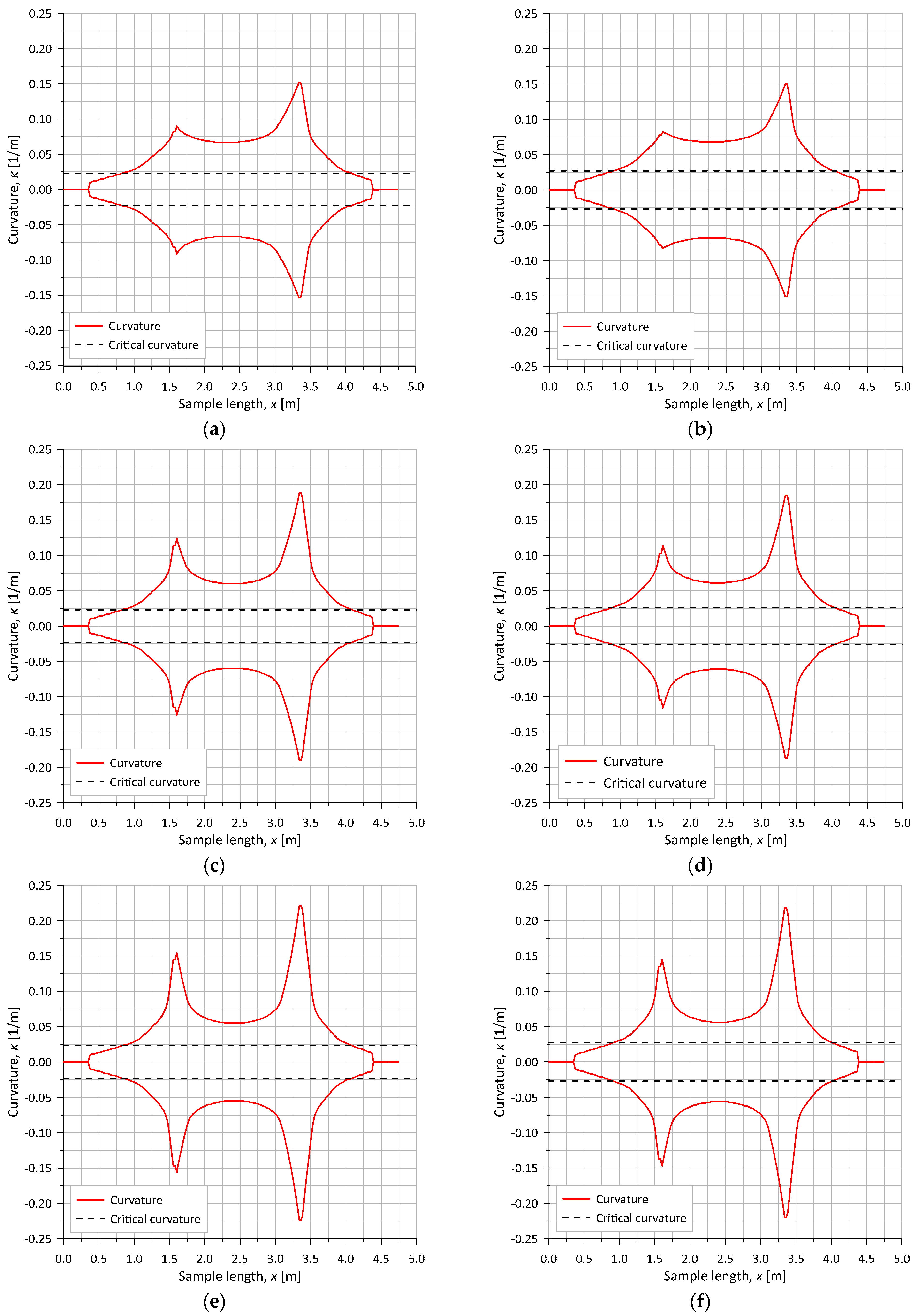
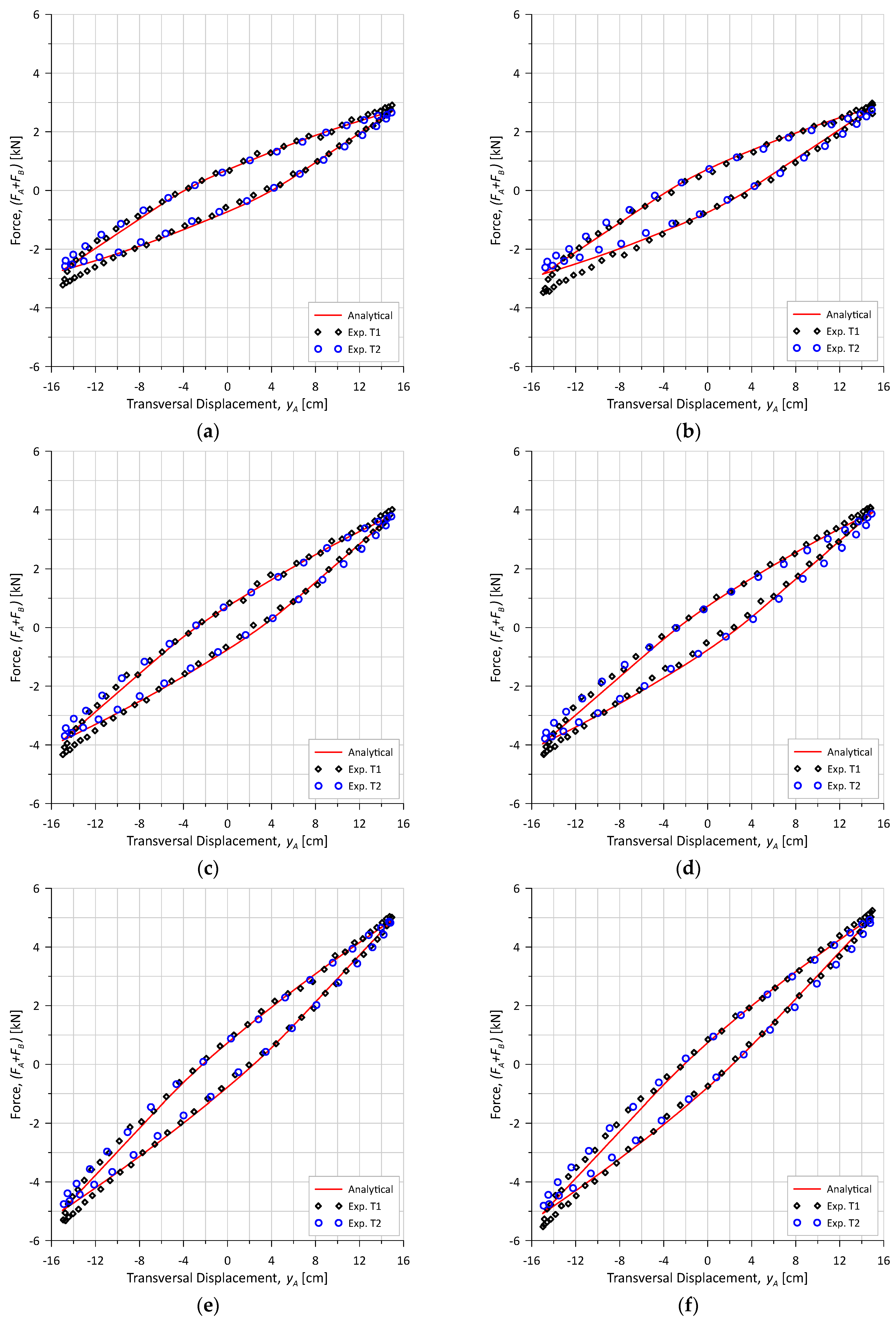
4.4. Bending Combined with Internal Pressure and Tension (T1-3 to T1-8)
4.5. Bending Tests After Degradation (T2-9 to T2-16)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- API SP 17J; Specification for Unbonded Flexible Pipe. 5th ed. American Petroleum Institute: Washington, DC, USA, 2024.
- Lobo, C.V.F.; Ribeiro, M.L. SCC-CO2 Failure Mode: Literature Review and Available Technologies Used to Inspect and Access the Integrity of the Flexible Pipes. In Proceedings of the Offshore Technology Conference (OTC), Houston, TX, USA, 1–4 May 2023. [Google Scholar]
- MacLeod, I.; Picksley, J.; Cruickshank, K. Flexible Pipe Integrity Management Guidance & Good Practice; Rev. 05; Wood: Aberdeen, Scotland, UK, 2023. [Google Scholar]
- Larsen, C.M.; Saevik, S.; Qvist, J. Design analysis. In Handbook on Design and Operation of Flexible Pipes; Part B; Fergestad, D., Lotveit, S.A., Eds.; NTNU/4Subsea/SINTEF Ocean: Trondheim, Norway, 2017. [Google Scholar]
- Custódio, A.B.; Vaz, M.A. A Nonlinear Formulation for the Axisymmetric Response of Umbilical Cables and Flexible Pipes. Appl. Ocean Res. 2002, 24, 21–29. [Google Scholar] [CrossRef]
- Féret, J.J.; Bournazel, C.L. Calculation of Stresses and Slip in Structural Layers of Unbonded Flexible Pipes. J. Offshore Mech. Arct. Eng. 1987, 109, 263–269. [Google Scholar] [CrossRef]
- Batista, R.C.; Bogarin, J.A.; Ebecken, N.F.F. Local Mechanical Behaviour of Multilayered Flexible Risers. In Proceedings of the 7th Symposium on Offshore Engineering, Rio de Janeiro, Brazil, 21–25 August 1989; pp. 494–510. [Google Scholar]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity, 4th ed.; Cambridge University Press: London, UK, 2017; ISBN 978-1107618091. [Google Scholar]
- Witz, J.A.; Tan, Z. On the Axial-Torsional Structural Behaviour of Flexible Pipes, Umbilicals and Marine Cables. Mar. Struct. 1992, 5, 205–227. [Google Scholar] [CrossRef]
- McIver, D.B. A Method of Modelling the Detailed Component and Overall Structural Behaviour of Flexible Pipe Sections. Eng. Struct. 1995, 17, 254–266. [Google Scholar] [CrossRef]
- Witz, J.A. A Case Study in the Cross-Section Analysis of Flexible Risers. Mar. Struct. 1996, 9, 885–904. [Google Scholar] [CrossRef]
- Ramos, R., Jr.; Martins, C.A.; Pesce, C.P.; Roveri, F.E. A Case Study on the Axial-Torsional Behavior of Flexible Risers. In Proceedings of the 27th International Conference on Offshore Mechanics and Arctic Engineering (OMAE 2008), Estoril, Portugal, 15–20 June 2008. [Google Scholar]
- de Sousa, J.R.M.; Magluta, C.; Roitman, N.; Campello, G.C. On the Extensional-Torsional Response of a Flexible Pipe with Damaged Tensile Armor Wires. Ocean Eng. 2018, 161, 350–383. [Google Scholar] [CrossRef]
- Liu, J.; Tan, Z.; Sheldrake, T. An Analytical Model for the Unbonded Flexible Pipe Stress Analysis with Consideration of Nonlinear Material Properties of Metal Layers. In Proceedings of the 29th International Conference on Offshore Mechanics and Arctic Engineering (OMAE 2010), Shanghai, China, 6–11 June 2010. [Google Scholar]
- Liu, J.; Ma, J.; Vaz, M.A.; Duan, M. Viscoelastic Damping of Flexible Risers: Theoretical Model. Ocean Eng. 2020, 217, 107974. [Google Scholar] [CrossRef]
- Ramos, R., Jr.; Kawano, A. Local Structural Analysis of Flexible Pipes Subjected to Traction, Torsion and Pressure Loads. Mar. Struct. 2015, 42, 95–114. [Google Scholar] [CrossRef]
- Lu, H.; Vaz, M.A.; Caire, M. Alternative Analytical and Finite Element Models for Unbonded Flexible Pipes under Axisymmetric Loads. Ocean Eng. 2021, 225, 108766. [Google Scholar] [CrossRef]
- de Sousa, J.R.M.; dos Santos, A.C. Symbolic Regression Equations to Predict the Maximum Stress Concentration Factors in Flexible Pipes with Damaged Tensile Armors. In Proceedings of the ASME 43rd International Conference on Offshore Mechanics and Arctic Engineering (OMAE 2024), Singapore, 9–14 June 2024. [Google Scholar]
- Li, X.; Jiang, X.; Hopman, H. Predicting the Wet Collapse Pressure for Flexible Risers with Initial Ovalization and Gap: An Analytical Solution. Mar. Struct. 2020, 71, 102732. [Google Scholar] [CrossRef]
- Gay Neto, A.; Martins, C.A.; Pesce, C.P.; Meirelles, C.O.C.; Malta, E.R.; Barbosa Neto, T.F.; Godinho, C.A.F. Prediction of Burst in Flexible Pipes. J. Offshore Mech. Arct. Eng. 2013, 135, 011401. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, Q.; He, J.; Liu, Q.; Li, M.; Wang, G. Coupled Burst and Fracture Failure Characteristics of Unbonded Flexible Riser under Internal Pressure and Axial Tension. J. Mar. Sci. Eng. 2025, 13, 1866. [Google Scholar] [CrossRef]
- Saevik, S.; Thorsen, M.J. Techniques for Predicting Tensile Armour Buckling and Fatigue in Deep Water Flexible Pipes. In Proceedings of the ASME 31st International Conference on Offshore Mechanics and Arctic Engineering (OMAE 2012), Rio de Janeiro, Brazil, 1–6 July 2012. [Google Scholar]
- Li, X.; Vaz, M.A.; Custódio, A.B. Analytical Model for Tensile Armors Lateral Deflections and Buckling in Flexible Pipes. Mar. Struct. 2019, 64, 211–228. [Google Scholar] [CrossRef]
- Saevik, S. Theoretical and Experimental Studies of Stresses in Flexible Pipes. Comput. Struct. 2011, 89, 2273–2291. [Google Scholar] [CrossRef]
- Muñoz, H.E.M.; de Sousa, J.R.M.; Magluta, C.; Roitman, N. Improvements on the Numerical Analysis of the Coupled Extensional-Torsional Response of a Flexible Pipe. J. Offshore Mech. Arct. Eng. 2016, 138, 011701. [Google Scholar] [CrossRef]
- Yoo, D.H.; Jang, B.S.; Yim, K.H. Nonlinear Finite Element Analysis of Failure Modes and Ultimate Strength of Flexible Pipes. Mar. Struct. 2017, 54, 50–72. [Google Scholar] [CrossRef]
- Malta, E.R.; Martins, C.A. Finite Element Analysis of Flexible Pipes under Axial Compression: Influence of the Sample Length. J. Offshore Mech. Arct. Eng. 2017, 139, 011701. [Google Scholar] [CrossRef]
- Lukassen, T.V.; Gunnarsson, E.; Krenk, S.; Glejbol, K.; Lyckegaard, A.; Berggreen, C. Tension-Bending Analysis of Flexible Pipe by a Repeated Unit Cell Finite Element. Mar. Struct. 2019, 64, 401–420. [Google Scholar] [CrossRef]
- Provasi, R.; Toni, F.G.; Martins, C.A. Friction Coefficient Influence in a Flexible Pipe: A Macroelement Model. Ocean Eng. 2022, 266, 112719. [Google Scholar] [CrossRef]
- de Sousa, J.R.M.; Magluta, C.; Roitman, N.; Londoño, T.V.; Campello, G.C. A Study on the Response of a Flexible Pipe to Combined Axisymmetric Loads. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering (OMAE 2013), Nantes, France, 9–14 June 2013. [Google Scholar]
- de Sousa, J.R.M.; Sagrilo, L.V.S.; Rocha, D.M. Semi-Empirical Equations to Predict the Bisymmetric Dry and Wet Hydrostatic Collapse Strengths of Flexible Pipes. Appl. Ocean Res. 2022, 122, 1013129. [Google Scholar] [CrossRef]
- Cuamatzi-Melendez, R.; Castillo-Hernández, O.; Vázquez-Hernández, A.O.; Albiter, A.; Vaz, M.A. Finite Element Modeling of Burst Failure in Unbonded Flexible Risers. Eng. Struct. 2015, 87, 58–69. [Google Scholar] [CrossRef]
- Gay Neto, A.; Martins, C.A. Flexible Pipes: Influence of the Pressure Armor in the Wet Collapse Resistance. J. Offshore Mech. Arct. Eng. 2014, 136, 031401. [Google Scholar] [CrossRef]
- Axelsson, G.; Skjerve, H. Flexible Riser Carcass Collapse Analyses—Sensitivity on Radial Gaps and Bending. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering (OMAE2014), San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Cuamatzi-Melendez, R.; Castillo-Hernández, O.; Vásquez-Hernández, A.O. Finite Element and Theoretical Analyses of Bisymmetric Collapses in Flexible Risers for Deepwaters Developments. Ocean Eng. 2017, 140, 195–208. [Google Scholar] [CrossRef]
- Dong, L.; Huang, Y.; Zhang, Q.; Liu, G. An Analytical Model to Predict the Bending Behavior of Unbonded Flexible Pipes. J. Ship Res. 2013, 57, 171–177. [Google Scholar] [CrossRef]
- Kebadze, E.; Krainkanic, I. Nonlinear Bending Behaviour of Offshore Flexible Pipes. In Proceedings of the Ninth International Offshore and Polar Engineering Conference (ISOPE), Brest, France, 30 May–4 June 1999. [Google Scholar]
- Ye, N.; Saevik, S.; Zhou, C. Investigation of Antiwear Tape’s Influence on Bending Behavior of One Flexible Riser. In Proceedings of the Twenty-fourth International Ocean and Polar Engineering Conference (ISOPE), Busan, South Korea, 15–20 June 2014. [Google Scholar]
- Kim, J.D.; Jang, B.S.; Yun, R.H. Application of Analytical Model in the Prediction of Dynamic Responses and Fatigue Damage of Flexible Risers: Part I—Improvement of Analytical Model Considering Shear Deformation and Varying Tension Effects. Mar. Struct. 2021, 79, 103044. [Google Scholar] [CrossRef]
- Dai, T.; Sævik, S.; Ye, N. Friction Models for Evaluating Dynamic Stresses in Non-Bonded Flexible Risers. Mar. Struct. 2017, 55, 137–161. [Google Scholar] [CrossRef]
- Wang, L.; Ye, N.; Yue, Q. A Novel Helix Contact Model for Predicting Hysteretic Behavior of Unbonded Flexible Pipes. Ocean Eng. 2022, 264, 112407. [Google Scholar] [CrossRef]
- Fang, P.; Li, X.; Jiang, X.; Hopman, H.; Bai, Y. Study of the Effects of Cross Section Shape on the Structural Behaviour of Helical Wires on a Bent Flexible Structure. In Proceedings of the 33rd International Ocean and Polar Engineering Conference (ISOPE), Ottawa, ON, Canada, 19–23 June 2023. [Google Scholar]
- Tang, M.; Li, S.; Zhang, H.; Bian, X.; Zhao, X. Monitoring the Slip of Helical Wires in a Flexible Riser under Combined Tension and Bending. Ocean Eng. 2022, 256, 111512. [Google Scholar] [CrossRef]
- Tan, Z.; Quiggin, P.; Sheldrake, T. Time Domain Simulation of the 3D Bending Hysteresis Behaviour of an Unbonded Flexible Riser. J. Offshore Mech. Arct. Eng. 2009, 131, 031301. [Google Scholar] [CrossRef]
- He, Y.; Lu, H.; Vaz, M.A.; Caire, M. Flexible Riser Connection Analysis with I-Tube Interface and Bending Hysteresis Effect. In Proceedings of the ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2019), Glasgow, Scotland, UK, 9–14 June 2019. [Google Scholar]
- Dai, T.; Zhang, J.; Ren, C.; Xing, Y.; Saevik, S.; Ye, N.; Jin, X.; Wu, J. Application of a Data-Driven Approach for Maximum Fatigue Damage Prediction of an Unbonded Flexible Riser. Ocean Eng. 2024, 256, 118053. [Google Scholar] [CrossRef]
- Gundersen, P.; Doynov, K.; Andersen, T.; Haakonsen, R. Methodology for Determining Remnant Fatigue Life of Flexible Risers Subjected to Slugging and Irregular Waves. In Proceedings of the ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering (OMAE 2012), Rio de Janeiro, Brazil, 1–6 June 2012. [Google Scholar]
- de Sousa, J.R.M.; de Sousa, F.J.M.; de Siqueira, M.Q.; Sagrilo, L.V.S.; de Lemos, C.A.D. A Theoretical Approach to Predict the Fatigue Life of Flexible Pipes. J. Appl. Math. 2012, 2012, 983819. [Google Scholar] [CrossRef]
- ASTM D638-22; Standard Test Method for Tensile Porperties of Plastics. American Society for Testing and Materials: West Conshohocken, PA, USA, 2022.
- Nitta, K.; Yam, M. Poisson’s Ratio and Mechanical Nonlinearity Under Tensile Deformation in Crystalline Polymers. In Rheology; de Vicente, J., Ed.; InTech: Vienna, Austria, 2012. [Google Scholar] [CrossRef]
- API RP 17B; Recommended Practice for Flexible Pipe, 6th ed. American Petroleum Institute: Washington, DC, USA, 2024.
- Sparks, C.P. Fundamentals of Marine Riser Mechanics: Basic Principles and Simplified Analyses, 1st ed.; PennWell Corp: Tulsa, OK, USA, 2007; ISBN 978-1-59370-070-6. [Google Scholar]
- Simo, J.C.; Hughes, T.J.R. Computational Ineslasticity; Springer: New York, NY, USA, 1998; ISBN 0-387-97520-0. [Google Scholar]
- Singh, A.K.; Bhadauria, B.S. Finite Difference Formulae for Unequal Sub-Intervals Using Lagrange’s Interpolation Formula. Int. J. Math. Anal. 2009, 3, 815–827. [Google Scholar]
- Mathcad, version 15.0; PTC Inc: Woburn, MA, USA, 2015.
- Coser, T.B.; de Negreiros, L.A.S.; Campelo, G.C.; Radke, E.D.; Rosa, C.D.; de Souza, D.F.; Rodrigues, L.F.V.; Renck, T.S.; Tagliari, M.R.; Borges, M.F. Flexible Pipe Fatigue Life Evaluation Based on a Dynamic Full-Scale Test Considering a Preconditioning Corrosion Procedure. In Proceedings of the ASME 2023 42nd International Conference on Ocean, Offshore and Artic Engineering (OMAE2023), Melbourne, Australia, 11–16 June 2023. [Google Scholar]
- Krishman, V.R.; Asher, S.; Kan, W.C.; Popelar, C. Effect of Piting Corrosion on Fatigue LIfe of Flexible Armor Wires. In Proceedings of the Twenty-sixth International Ocean and Polar Engineering Conference (ISOPE), Rhodes, Greece, 26 June–1 July 2016. [Google Scholar]












| Layer (Material) | Properties |
|---|---|
| Inner carcass (Stainless 316 L) | Thickness = 3.50 mm, No. of tendons = 1, Lay angle = 87.7°, Interlocked profile, Area = 16.00 mm2, Moment of inertia = 11.24 mm4, Young modulus = 193 GPa, Poisson coefficient = 0.3 |
| Internal plastic (Polyamide 12) | Thickness = 5.00 mm, Young modulus = 372 MPa, Poisson coefficient = 0.45 |
| Pressure armor (Carbon steel) | Thickness = 6.35 mm, No. of tendons = 1, Lay angle = 87.9°, Z-profile, Area = 49.95 mm2, Moment of inertia = 186.29 mm4, Young modulus = 205 GPa, Poisson coefficient = 0.30 |
| Antiwear layer (Polypropylene) | Thickness = 0.3 mm, Young modulus = 350 MPa, Poisson coefficient = 0.30 |
| Inner tensile armor (Carbon steel) | Thickness = 2.01 mm, No. of wires = 43, Lay angle = 38°, Rectangular profile, Width = 5.00 mm, Young modulus = 205 GPa, Poisson coefficient = 0.30 |
| Antiwear layer (Polypropylene) | Thickness = 0.6 mm, Young modulus = 350 MPa, Poisson coefficient = 0.30 |
| Anti-buckling tape (Glass filament) | Thickness = 0.81 mm, Young modulus = 350 MPa, Poisson coefficient = 0.30 |
| Antiwear layer (Polypropylene) | Thickness = 0.30 mm Young modulus = 350 MPa, Poisson coefficient = 0.30 |
| Outer tensile armor (Carbon steel) | Thickness = 2.01 mm, No. of wires = 47, Lay angle = 36°, Rectangular profile, Width = 5.0 mm Young modulus = 205 GPa, Poisson coefficient = 0.30 |
| Antiwear layer (Polypropylene) | Thickness = 0.30 mm, Young modulus = 350 MPa, Poisson coefficient = 0.30 |
| Anti-buckling tape (Glass filament) | Thickness = 0.81 mm, Young modulus = 350 MPa, Poisson coefficient = 0 |
| Antiwear tape (Polypropylene) | Thickness = 0.3 mm, Young modulus = 350 MPa, Poisson coefficient = 0 |
| Outer sheath (HDPE) | Thickness = 6.55 mm Young modulus = 622 MPa, Poisson coefficient = 0.45 |
| Test | Young Modulus (MPa) | |
|---|---|---|
| Inner Sheath (PA) | Outer Sheath (PE) | |
| 1 | 358 | 601 |
| 2 | 373 | 650 |
| 3 | 408 | 619 |
| 4 | 372 | 577 |
| 5 | 405 | 644 |
| 6 | 323 | 640 |
| 7 | 361 | - |
| Average | 372 | 622 |
| Std. deviation | 29.1 | 28.5 |
| Campaign | Test | [Bar] | [kN] | Annulus Degradation |
|---|---|---|---|---|
| T0 | 0 | 200 | 2 | No degradation |
| T1 | 1 | 0 | 0 | No degradation |
| 2 | 200 | 0 | ||
| 3 | 100 | 5 | ||
| 4 | 100 | 10 | ||
| 5 | 100 | 15 | ||
| 6 | 200 | 5 | ||
| 7 | 200 | 10 | ||
| 8 | 200 | 15 | ||
| T2 | 9 | 0 | 0 | 18 months—Flooded annulus with saturated water 1 bar CO2 at 40 °C |
| 10 | 200 | 0 | ||
| 11 | 100 | 5 | ||
| 12 | 100 | 10 | ||
| 13 | 100 | 15 | ||
| 14 | 200 | 5 | ||
| 15 | 200 | 10 | ||
| 16 | 200 | 15 |
[bar] | [kN] | Contact Pressures 1 | Corresponding Tests | |
|---|---|---|---|---|
| [MPa] | [MPa] | |||
| 0 | 0 | 0 | 0 | 1, 9 |
| 100 | 5 | 3.34 | 1.22 | 3, 11 |
| 100 | 10 | 3.63 | 1.31 | 4, 12 |
| 100 | 15 | 3.91 | 1.40 | 5, 13 |
| 200 | 0 | 5.93 | 2.05 | 2, 10 |
| 200 | 5 | 6.21 | 2.14 | 6, 14 |
| 200 | 10 | 6.50 | 2.23 | 7, 15 |
| 200 | 15 | 6.79 | 2.32 | 8, 16 |
| Mesh | [N] | [N] | [N] | ||||
|---|---|---|---|---|---|---|---|
| 1 | 10 | 15 | 10 | 33 | 582.1 | 851.5 | 1433.6 |
| 2 | 15 | 20 | 15 | 48 | 582.9 | 845.8 | 1428.7 |
| 3 | 30 | 40 | 30 | 98 | 584.6 | 838.2 | 1422.8 |
| 4 | 60 | 80 | 60 | 198 | 585.4 | 834.7 | 1420.1 |
| 5 | 90 | 120 | 90 | 298 | 585.6 | 833.6 | 1419.2 |
| 6 | 120 | 160 | 120 | 398 | 585.7 | 833.0 | 1418.7 |
| [mm] | [N] | [N] | [N] |
|---|---|---|---|
| 6.00 | 584.9 | 809 | 1393.9 |
| 3.00 | 585.4 | 834.7 | 1420.1 |
| 1.50 | 585.7 | 847.2 | 1432.9 |
| 1.00 | 585.8 | 851.4 | 1437.2 |
| 0.50 | 586.0 | 855.5 | 1441.5 |
| 0.25 | 586.0 | 857.5 | 1443.5 |
| Positive Stroke [mm] | |||||
| Sensor | #2 | #3 | #4 | #5 | #6 |
| Experimental | 164 | 181 | 183 | 179 | 166 |
| Full slip | 167 | 177 | 179 | 175 | 160 |
| No slip | 167 | 177 | 179 | 175 | 160 |
| τ0 = 0.5 MPa | 170 | 182 | 186 | 181 | 162 |
| τ0 = 0.9 MPa | 168 | 179 | 183 | 179 | 162 |
| τ0 = 1.2 MPa | 168 | 179 | 182 | 178 | 161 |
| Negative Stroke [mm] | |||||
| Sensor | #2 | #3 | #4 | #5 | #6 |
| Experimental | 158 | 172 | 178 | 174 | 165 |
| Full slip | 160 | 175 | 179 | 176 | 167 |
| No slip | 160 | 175 | 179 | 176 | 167 |
| τ0 = 0.5 MPa | 162 | 181 | 186 | 182 | 170 |
| τ0 = 0.9 MPa | 161 | 179 | 183 | 179 | 168 |
| τ0 = 1.2 MPa | 161 | 178 | 182 | 177 | 167 |
| [MPa] | [1/m] | |||
|---|---|---|---|---|
| 0.5 | 0.0107 | 0.592 | 1.03 | 0.848 |
| 0.7 | 0.0150 | 0.772 | 1.131 | 0.963 |
| 0.8 | 0.0171 | 0.86 | 1.117 | 0.988 |
| 0.9 | 0.0193 | 0.946 | 1.074 | 0.993 |
| 1.0 | 0.0214 | 1.023 | 1.02 | 0.983 |
| 1.1 | 0.0236 | 1.091 | 0.967 | 0.961 |
| 1.2 | 0.0257 | 1.148 | 0.927 | 0.933 |
| [1/m] | ||||
|---|---|---|---|---|
| 0 | 0.019 | 0.81 | 0.919 | 0.982 |
| 0.03 | 0.023 | 0.890 | 0.916 | 0.993 |
| 0.04 | 0.024 | 0.917 | 0.910 | 0.992 |
| 0.05 | 0.026 | 0.942 | 0.901 | 0.993 |
| 0.06 | 0.027 | 0.968 | 0.889 | 0.984 |
| 0.07 | 0.028 | 0.992 | 0.875 | 0.977 |
| 0.10 | 0.032 | 1.060 | 0.820 | 0.945 |
| Test | |||
|---|---|---|---|
| T1-1 | 0.946 | 1.074 | 0.993 |
| T1-2 | 0.942 | 0.901 | 0.989 |
| T1-3 | 0.885 | 0.997 | 0.990 |
| T1-4 | 0.918 | 1.008 | 0.996 |
| T1-5 | 0.950 | 0.954 | 0.997 |
| T1-6 | 0.874 | 0.975 | 0.990 |
| T1-7 | 0.930 | 0.992 | 0.995 |
| T1-8 | 0.938 | 0.933 | 0.996 |
| T2-9 | 1.010 | 0.965 | 0.984 |
| T2-10 | 1.082 | 1.015 | 0.983 |
| T2-11 | 1.031 | 1.025 | 0.994 |
| T2-12 | 1.020 | 0.990 | 0.994 |
| T2-13 | 1.021 | 0.982 | 0.995 |
| T2-14 | 1.057 | 1.081 | 0.988 |
| T2-15 | 1.023 | 0.948 | 0.993 |
| T2-16 | 1.031 | 0.898 | 0.992 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, B.d.P.M.d.; Sousa, J.R.M.d.; Roitman, N.; Radke, E. Theoretical and Experimental Analysis of the Global Response of a Flexible Pipe Under Combined Axisymmetric and Bending Loads. J. Mar. Sci. Eng. 2025, 13, 2180. https://doi.org/10.3390/jmse13112180
Costa BdPMd, Sousa JRMd, Roitman N, Radke E. Theoretical and Experimental Analysis of the Global Response of a Flexible Pipe Under Combined Axisymmetric and Bending Loads. Journal of Marine Science and Engineering. 2025; 13(11):2180. https://doi.org/10.3390/jmse13112180
Chicago/Turabian StyleCosta, Bernardo de P. M. da, José Renato M. de Sousa, Ney Roitman, and Erik Radke. 2025. "Theoretical and Experimental Analysis of the Global Response of a Flexible Pipe Under Combined Axisymmetric and Bending Loads" Journal of Marine Science and Engineering 13, no. 11: 2180. https://doi.org/10.3390/jmse13112180
APA StyleCosta, B. d. P. M. d., Sousa, J. R. M. d., Roitman, N., & Radke, E. (2025). Theoretical and Experimental Analysis of the Global Response of a Flexible Pipe Under Combined Axisymmetric and Bending Loads. Journal of Marine Science and Engineering, 13(11), 2180. https://doi.org/10.3390/jmse13112180







