Coupled Burst and Fracture Failure Characteristics of Unbonded Flexible Riser Under Internal Pressure and Axial Tension
Abstract
1. Introduction
2. Theoretical Model of Mixed Failure in Unbonded Flexible Risers Under Axisymmetric Loads
2.1. Limitations of the Model
- Both ends of each layer are fixedly installed on the terminal device to form an integral whole, and it is postulated that the axial elongation rates of each layer are the same. It ensures that all layers are synchronized in axial deformation, so that the multi-layer structure can be regarded as a whole for mechanical analysis, which greatly simplifies the establishment of control equations.
- The theoretical model does not consider the gap between layers in the initial calculation stage, so that the classical elastic mechanics theory can be applied to calculate the initial stress state.
- The materials of each layer are homogeneous and change within the linear elastic range, permitting the application of the generalized Hooke’s law.
- Neglect the initial defects formed in the production process. The aim is to analyze the performance of an idealized, flawless structure so as to establish a performance upper bound benchmark.
- Neglect the impact of the boundary effect and consider that the thickness of each layer changes consistently along the pipe’s length and in the radial direction. It is beneficial to analyze the mechanical behavior of any cross-section of the pipeline independently without considering the influence of end constraints.
- Ignore the energy caused by friction from the relative movement between the layers. It can simplify the derivation process of the energy method.
- It is assumed that the pressure-armor layer can still support a certain level of internal pressure when it reaches yield stress, making the model closer to the actual engineering judgment.
2.2. Equilibrium Equations of Cylindrical Shell Layers Under Axisymmetric Loads
2.3. Equilibrium Equation of Helical Layer Under Axisymmetric Load
2.4. Overall Equilibrium Equations Under Axisymmetric Loads
2.5. Failure Model
2.5.1. Tensile Failure Model
2.5.2. Internal Pressure Failure Model
3. Numerical Simulation
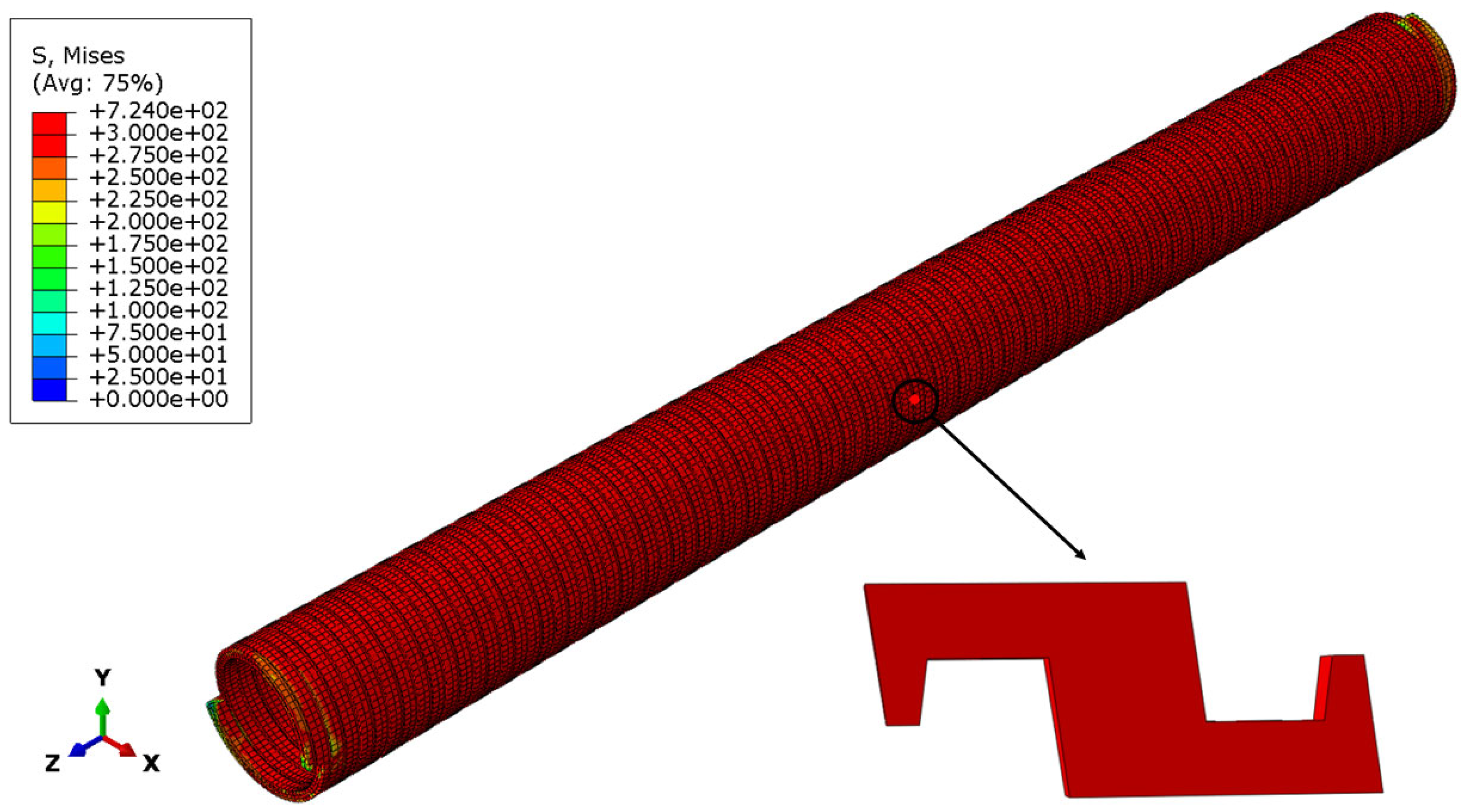
3.1. Finite Element Model of Unbonded Flexible Riser
3.2. Failure Criterion
3.2.1. Determination of Failure of Tensile-Armor Layer
3.2.2. Determination of Failure of Pressure–Tensile-Armor Layer
4. Discussion
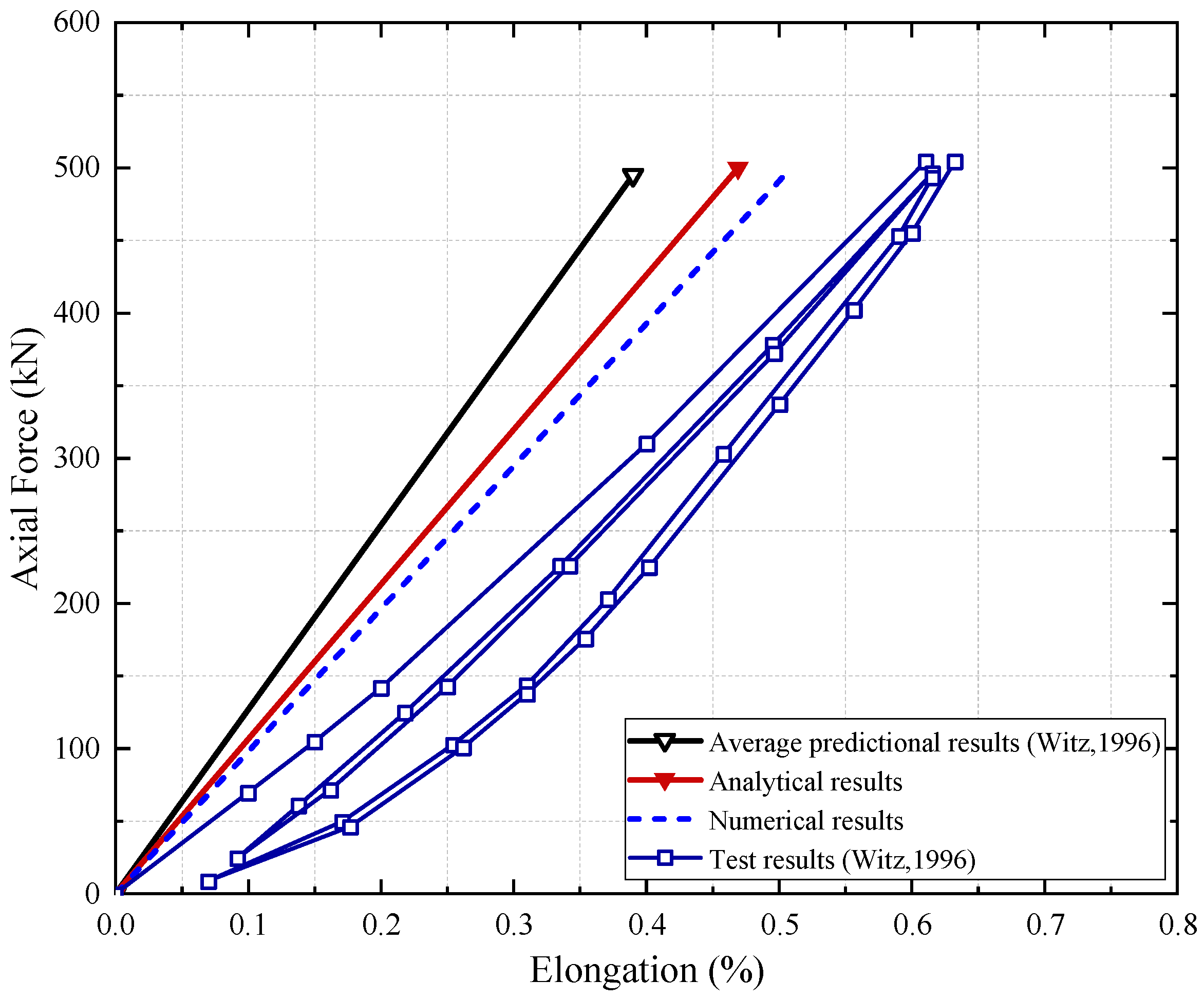
4.1. Model Verification
4.2. Failure Characteristic
4.2.1. Tensile Failure Characteristics
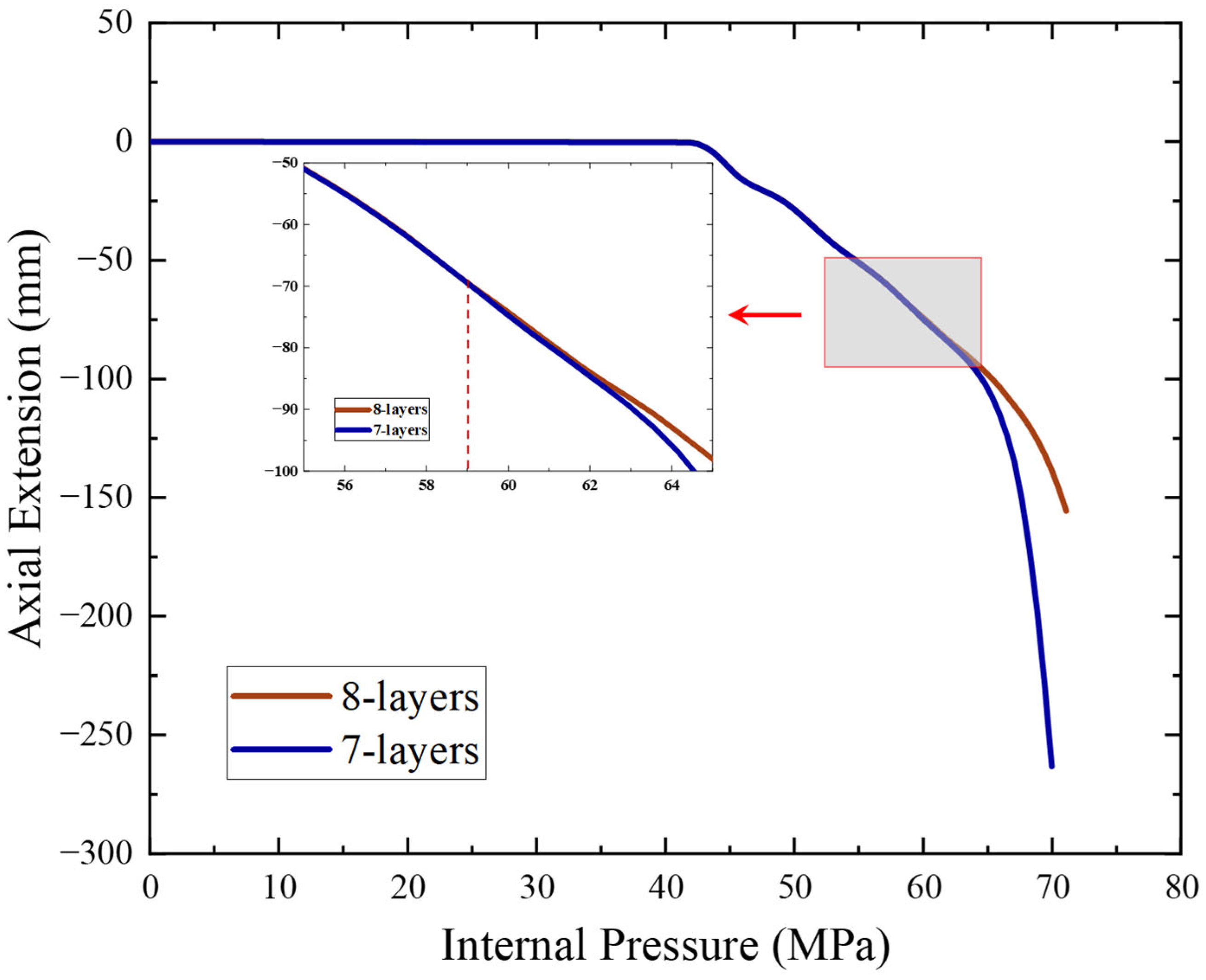
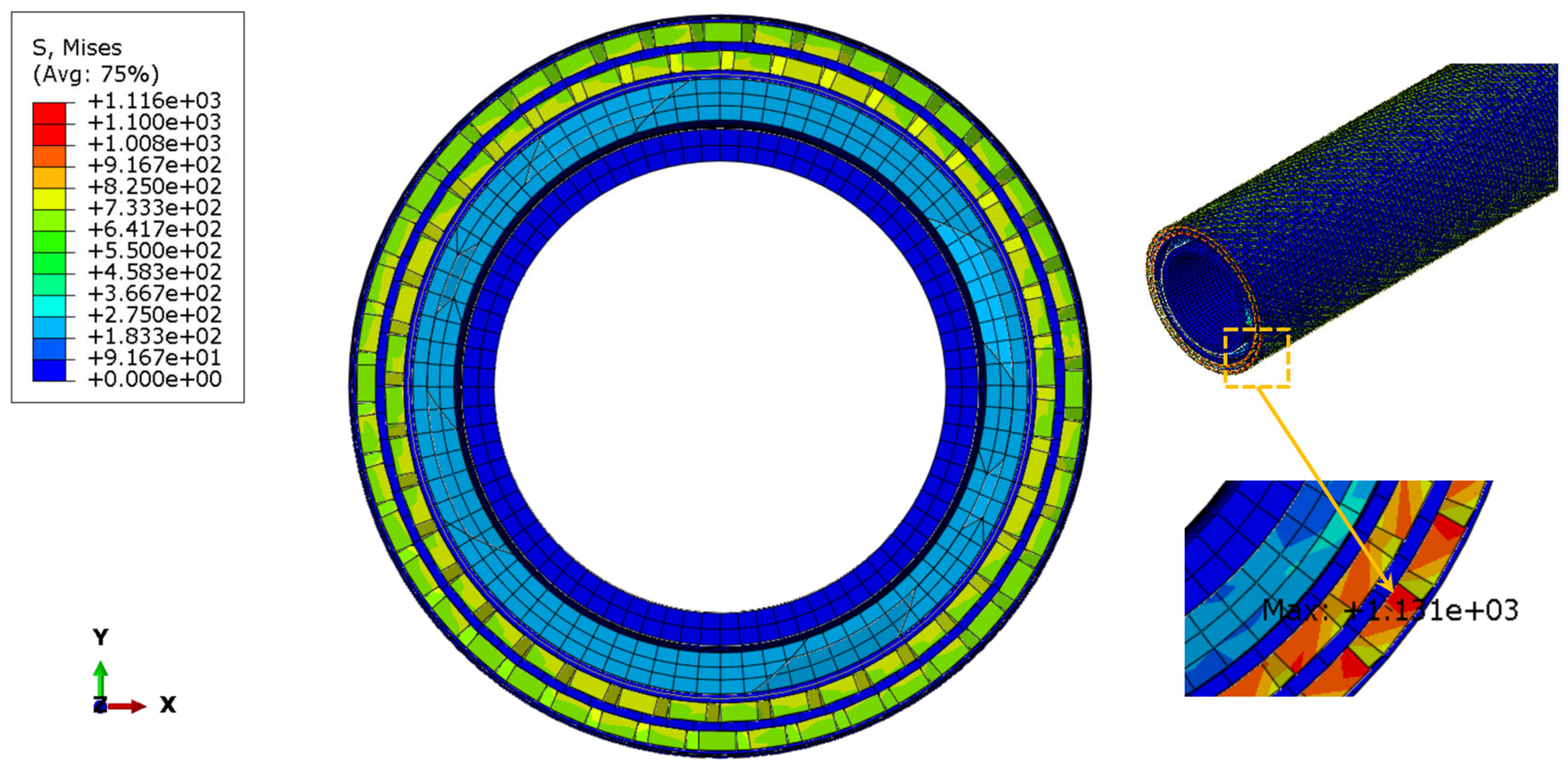
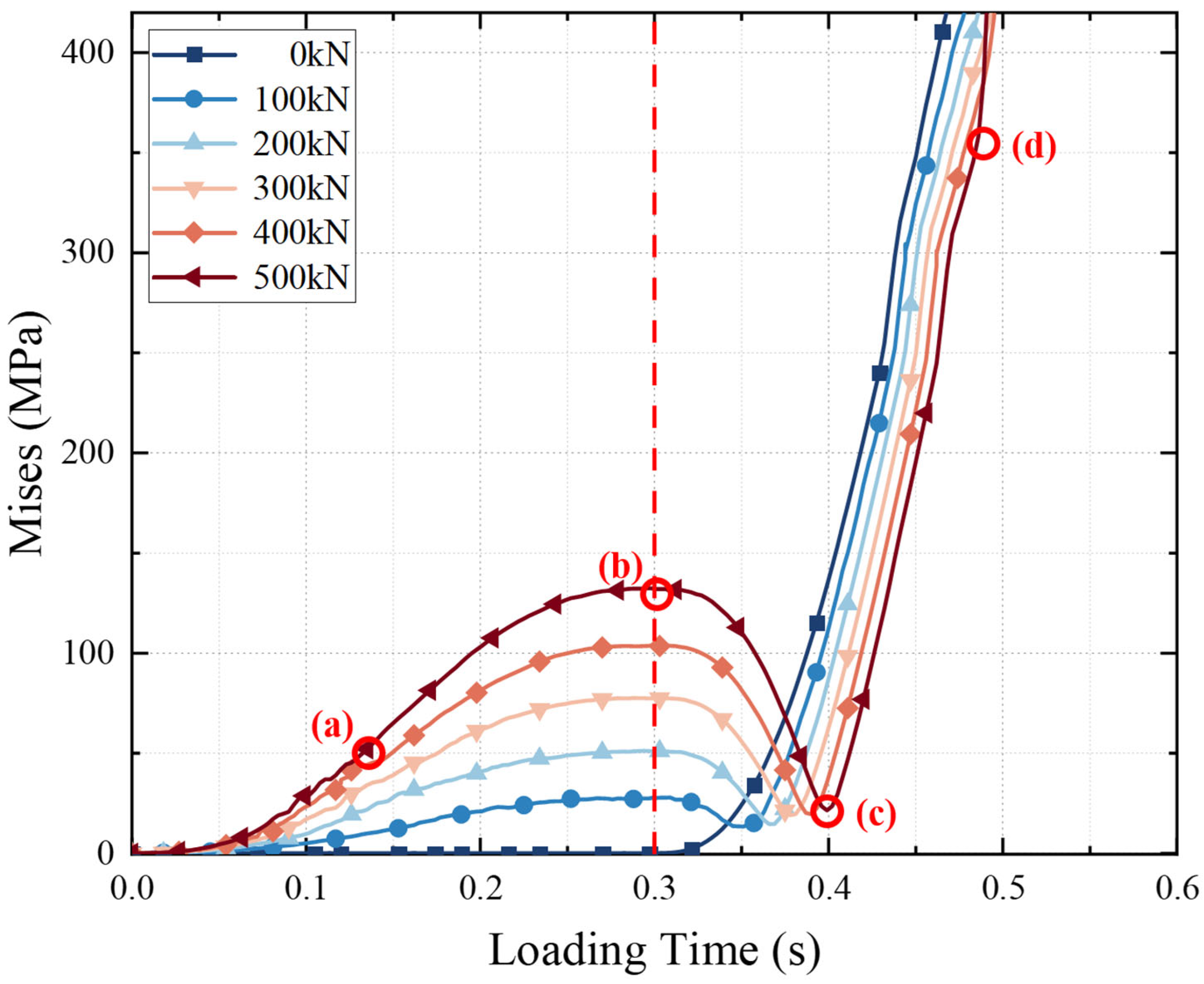
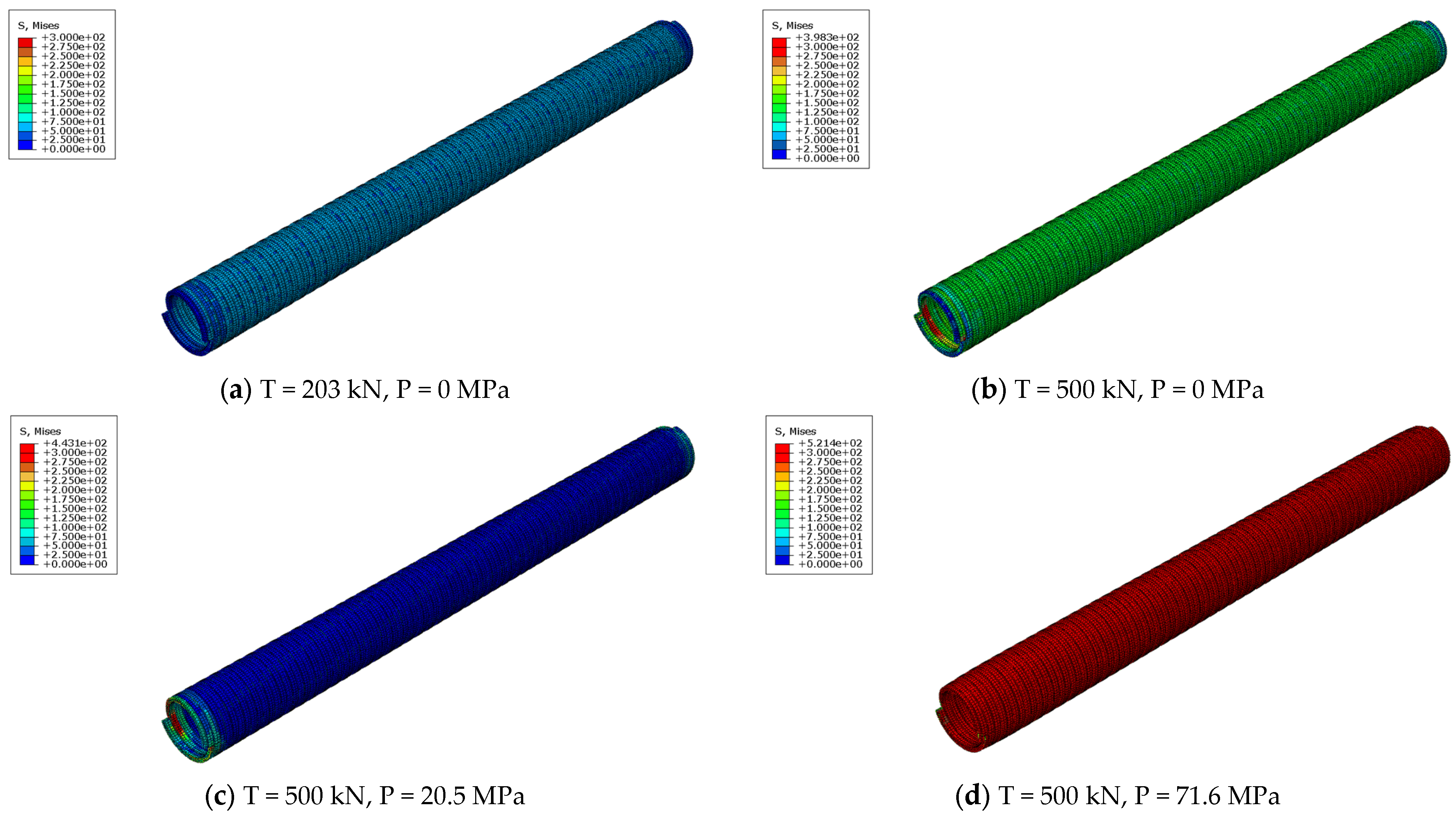
4.2.2. Characteristics of Burst Failure
4.3. Parameter Analysis
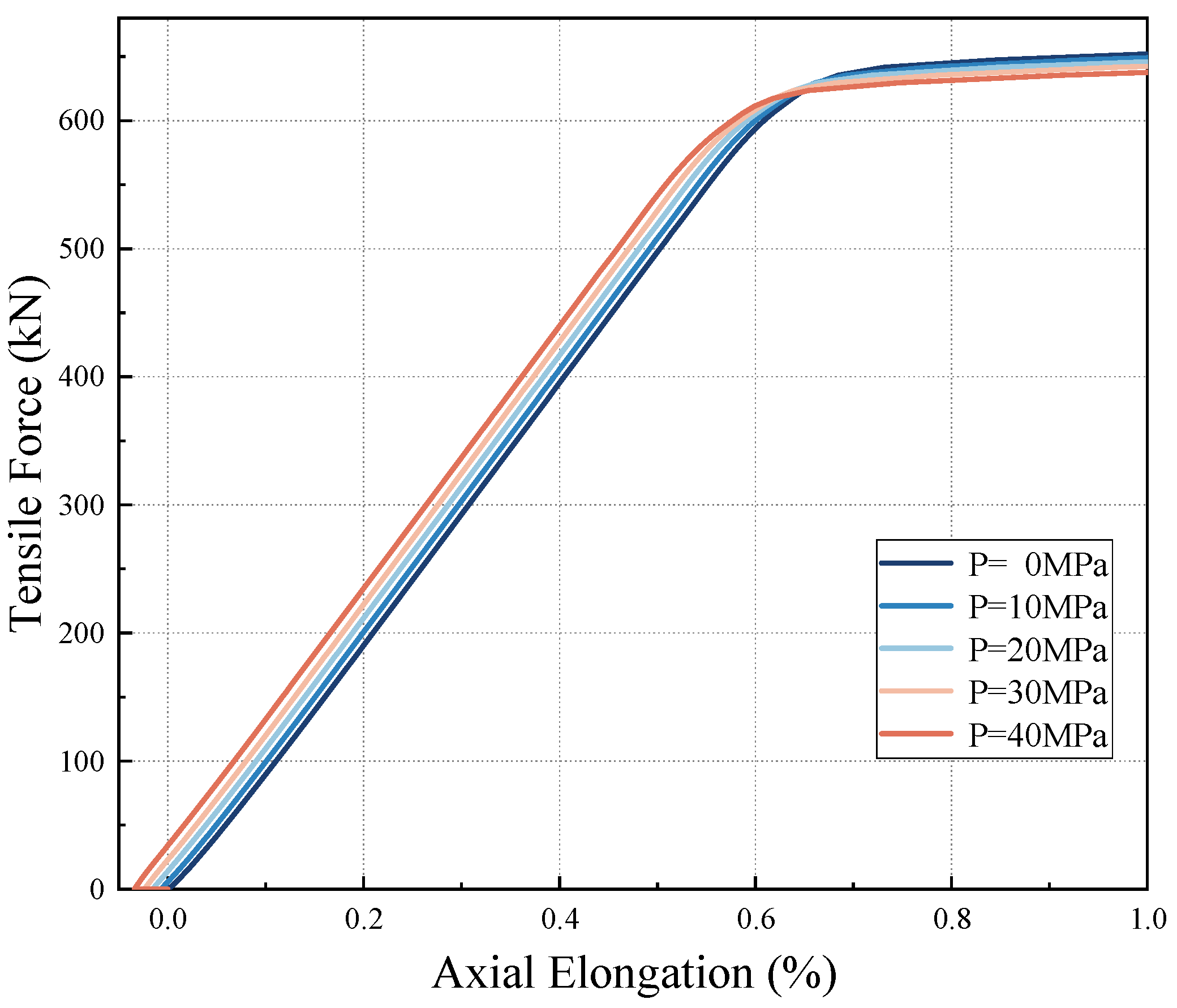
4.3.1. Tensile Mechanical Response of Risers Under Combined Loads
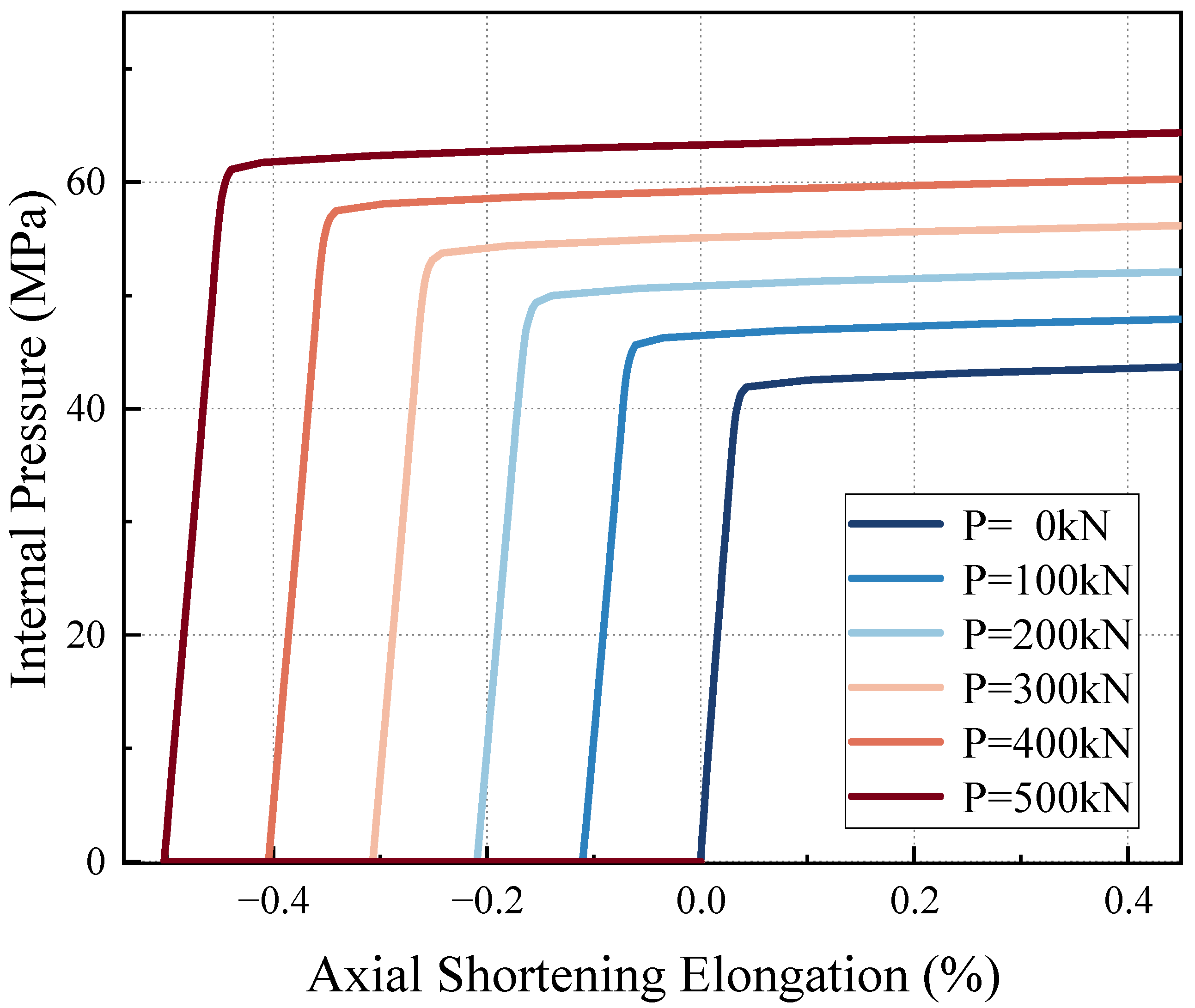
4.3.2. Pressure Mechanical Response of Risers Under Combined Loads
5. Conclusions
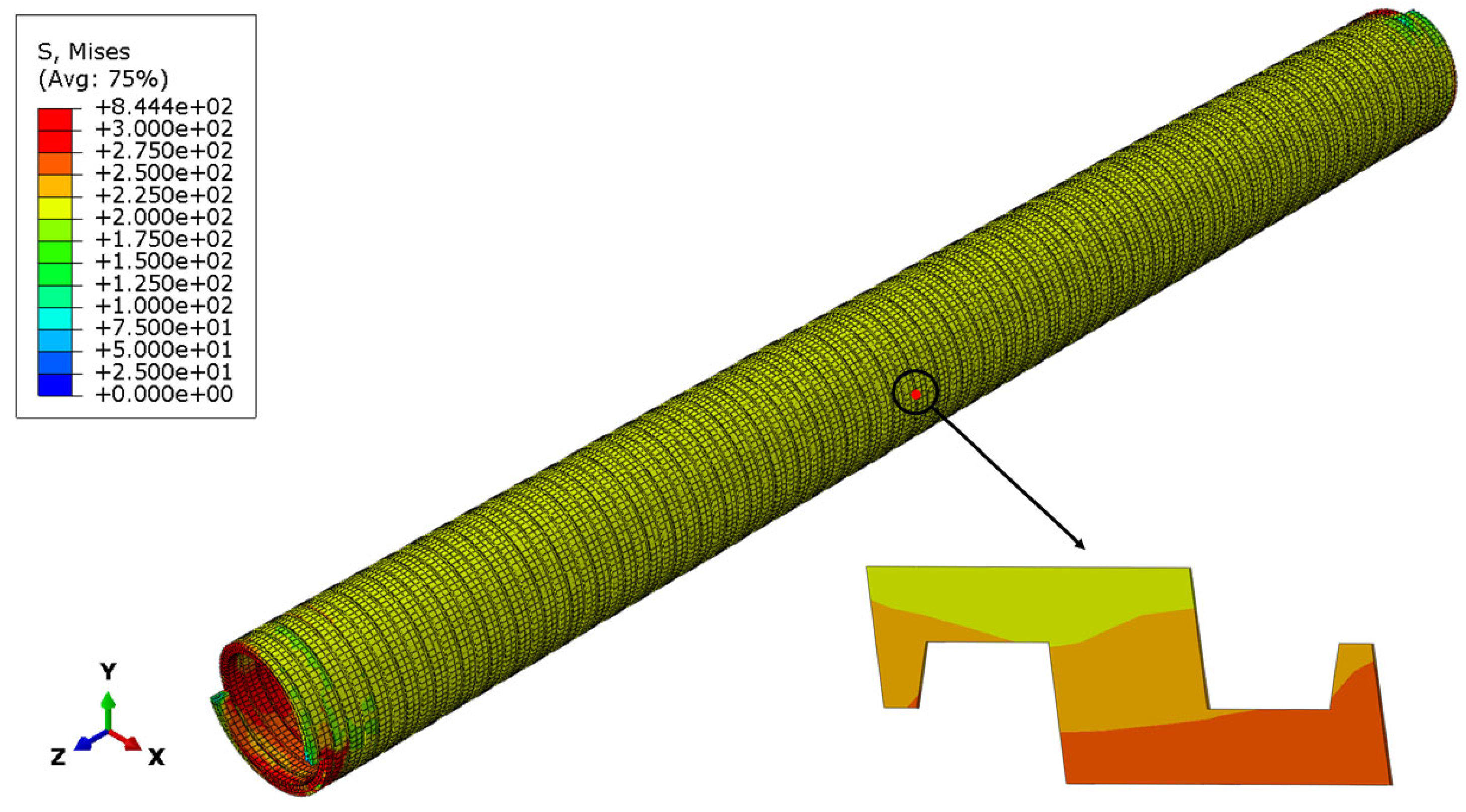
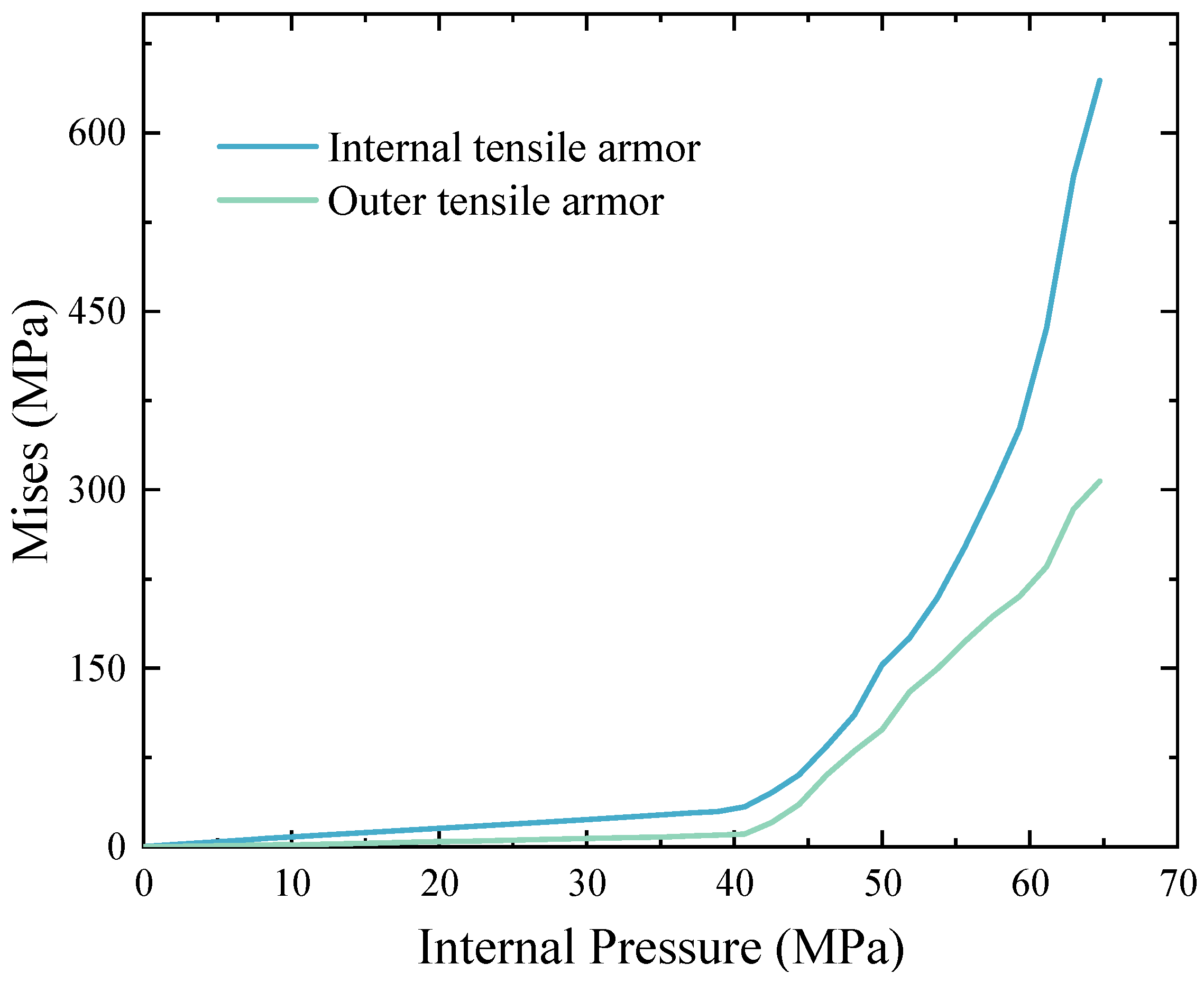
- During tensile failure of unbonded flexible risers, both inner and outer tensile-armor layers assume primary load-bearing responsibility. Stress magnitudes within the internal tensile-armor layer exceed those sustained by the external counterpart. Moreover, when the riser is subjected to axial tension, the stress does not change strictly and evenly along its axial direction. This is especially obvious at the end.
- Pre-applied internal pressure has no significant impact on the stiffness of unbonded flexible riser. Moreover, as the initial internal pressure increases from 0 MPa to 40 MPa, the axial tensile load capacity of the riser gradually diminishes. Although the deformation amount of the riser is reduced to a certain extent, it is more likely to experience axial failure. This is because the axial tensile load and the internal and external pressures will cause the contact pressure effect between the layers of the non-bonded flexible riser, so increasing the external pressure has a negative effect on the tensile strength of the composite riser.
- Under combined loading, the pressure-armor layer carries most of the load and its Z-section stress grows from the inner edge to the outer edge. This layer first undergoes a stress drop, then re-loads until burst. After burst, the inner tensile-armor layer immediately takes over as the primary pressure-bearing component, its peak stress exceeding that of the outer layer and serving as a secondary barrier.
- The initial axial tensile force magnitude significantly influences the failure characteristics of the pressure-armor layer. A higher initial tensile force endows it with a greater anti-burst ability; the failure pressure increases by 35% when the tensile force is 500 kN. This increase far exceeds the material’s own strain-hardening effect, primarily because the axial pre-compression suppresses radial ovalisation of the armor coil, thereby delaying the local buckling-yield coupling failure. Moreover, a larger initial axial tensile force results in a higher initial stress.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Q.S.; Xue, H.X.; Tang, W.Y.; Yuan, Y. Theoretical and numerical methods to predict the behavior of unbonded flexible riser with composite armor layers subjected to axial tension. Ocean Eng. 2020, 199, 107038. [Google Scholar] [CrossRef]
- Tchalala, M.R.; El-Demellawi, J.K.; Kalakonda, P.; Chaieb, S. High thermally stable hybrid materials based on amorphous porous silicon nanoparticles and imidazolium-based ionic liquids: Structural and chemical analysis. Mater. Today Proc. 2021, 39, 1132–1140. [Google Scholar] [CrossRef]
- Kalakonda, P.; Thudumu, S.; Mynepally, S.L.; Mandal, P.; Banne, S.; Kalakonda, P.B.; Podili, B.B. Engineering micro/nano-fibrous scaffolds with silver coating for tailored wound repair applications. J. Nanoparticle Res. 2023, 25, 254. [Google Scholar] [CrossRef]
- Dabbeta, N.K.; Kante, M.; Konda, R.; Devarala, A.; Kalakonda, P.B.; Khanam, S.J.; Savu, R.N.; Banovath, M.; Siddey, L.S.R.; Bommaji, V.N.; et al. ECO-inspired Cu-Zn bimetallic nanoparticles for Enhanced Water Purification Technologies. Mater. Chem. Phys. Sustain. Energy 2025, 2, 100013. [Google Scholar] [CrossRef]
- Hasan, I.; Bassi, A.; Kalakonda, P. CuO surface functionalized β-cyclodextrin grafted PMMA hybrid nanocomposite for advance oxidative mineralization of methyl orange. Surf. Interfaces 2025, 56, 105456. [Google Scholar] [CrossRef]
- Witz, J.A. A case study in the cross-section analysis of flexible risers. Mar. Struct. 1996, 9, 885–904. [Google Scholar] [CrossRef]
- Yue, Q.J.; Lu, Q.Z.; Yan, J.; Zheng, J.; Palmer, A. Tension behavior prediction of flexible pipelines in shallow water. Ocean Eng. 2013, 58, 201–207. [Google Scholar] [CrossRef]
- Vargas-Londoño, T.; de Sousa, J.R.M.; Magluta, C.; Rotiman, N. A theoretical and experimental analysis of the bending behavior of unbonded flexible pipes. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. OMAE2014-24247. [Google Scholar]
- Zhou, C.; Ye, N.; Sævik, S. Effect of anti-wear tape on behavior of flexible risers. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. OMAE2014-24261. [Google Scholar]
- Shao, W.Z.; Lin, Y.; Yan, J.H. Modeling the reeling process of offshore pipelines: A theoretical framework based on updated Voce-Chaboche model. Ocean Eng. 2025, 332, 121383. [Google Scholar] [CrossRef]
- Kebadze, E. Theoretical Modelling of Unbonded Flexible Pipe Cross-Sections. Doctoral Thesis, South Bank University, London, UK, 2000. [Google Scholar]
- Dong, L.L. Theoretical Calculation of Cross-Sectional Properties and Fatigue Analysis of Unbonded Flexible Risers in BSR Region. Doctoral Thesis, Dalian University of Technology, Dalian, China, 2013. [Google Scholar]
- Bahtui, A. Development of a Constitutive Model to Simulate Unbonded Flexible Riser Pipe Elements. Doctoral Thesis, Brunel University, London, UK, 2008. [Google Scholar]
- Ren, S.F.; Tang, W.Y.; Kang, Z.; Geng, H. Numerical study on the axial-torsional response of an unbonded flexible riser with damaged tensile armor wires. Appl. Ocean Res. 2020, 97, 102045. [Google Scholar] [CrossRef]
- Cornacchia, F.; Liu, T.; Bai, Y.; Fantuzzi, N. Tensile strength of the unbonded flexible pipes. Compos. Struct. 2019, 218, 142–151. [Google Scholar] [CrossRef]
- De Sousa, J.R.M.; Campello, G.C.; Kwietniewski, C.E.F.; Ellwanger, G.B.; Strohaecker, T.R. Structural response of a flexible pipe with damaged tensile armor wires under pure tension. Mar. Struct. 2014, 39, 1–38. [Google Scholar] [CrossRef]
- Liu, Q.S.; Xue, H.X.; Tang, W.Y. Behavior of unbonded flexible riser with composite armor layers under coupling loads. Ocean Eng. 2021, 229, 109907. [Google Scholar] [CrossRef]
- Jiang, H.; Yang, H.Z. Mechanical analysis of deep water unbonded flexible riser under combined loads. China Ocean Eng. 2014, 32, 93–99. [Google Scholar]
- Wang, B.D.; Zhang, H.; Liu, X.B.; Xu, L.X.; Fu, Y. Analysis of the Mechanical Behaviors of Fiber Reinforced Unbonded Flexible Pipe Under Combined Load. In Proceedings of the 13th International Pipeline Conference, Calgary, AB, Canada, 28–30 September 2020. IPC2020-9346. [Google Scholar]
- Sun, H.B.; Wang, Y.Y.; Jia, L.S.; Lin, Z.Q.; Yu, H. Theoretical and numerical methods for predicting the structural stiffness of unbonded flexible riser for deep-sea mining under axial tension and internal pressure. Ocean Eng. 2024, 310, 118672. [Google Scholar] [CrossRef]
- Tang, L.P.; He, W.; Zhu, X.H.; Zhou, Y.L. Mechanical analysis of un-bonded flexible pipe tensile armor under combined loads. Int. J. Press. Vessel. Pip. 2019, 171, 217–223. [Google Scholar] [CrossRef]
- Yoo, D.H.; Jang, B.S.; Yim, K.H. Nonlinear finite element analysis of failure modes and ultimate strength of flexible pipes. Mar. Struct. 2017, 54, 50–72. [Google Scholar] [CrossRef]
- Berge, S.; Wang, T.; Langhelle, N. Surface characterization and fatigue strength of corroded armor wire. In Proceedings of the 33rd International Conference on Offshore Mechanics and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. OMAE2014-24140. [Google Scholar]
- Antoine, F.H. Prevention and monitoring of fatigue-corrosion of flexible risers’ steel reinforcements. In Proceedings of the 21st International Conference on Offshore Mechanics and Arctic Engineering, San Diego, CA, USA, 10–15 June 2007. OMAE2007-29186. [Google Scholar]
- Ebrahimi, A.; Kenny, S.; Hussein, A. Finite Element Investigation on the Tensile Armor Wire Response of Flexible Pipe for Axisymmetric Loading Conditions Using an Implicit Solver. J. Offshore Mech. Arct. Eng. 2018, 140, 041402. [Google Scholar] [CrossRef]
- Zhu, X.-K.; Leis, B.N. Theoretical and numerical predictions of burst pressure of pipelines. J. Press. Vessel Technol. 2007, 129, 644–652. [Google Scholar] [CrossRef]
- Kamaya, M.; Suzuki, T.; Meshii, T. Failure pressure of straight pipe with wall thinning under internal pressure. Int. J. Press. Vessel. Pip. 2008, 85, 628–634. [Google Scholar] [CrossRef]
- Neto, A.; Martins, C.; Pesce, C.; Meirelles, C.; Malta, E.; Neto, T.; Godinho, C. Prediction of burst in flexible pipes. J. Offshore Mech. Arct. Eng. 2013, 135, 011401. [Google Scholar] [CrossRef]
- Zeng, D.Z.; Wang, X.; Ming, K.J.; Yu, C.X.; Zhang, Y.H.; Yu, Z.M.; Yan, J.; Li, F.G. Analysis and optimization design of internal pressure resistance of flexible composite pipe. Int. J. Press. Vessel. Pip. 2024, 210, 105271. [Google Scholar] [CrossRef]
- Liu, X.Y.; Qu, Z.Y.; Liu, Y.; He, J.W.; Si, G.J.; Wang, S.C.; Liu, Q.S. Numerical Simulation of Burst Failure in 2.5-Inch Unbonded Flexible Riser Pressure Armor Layers. Metals 2024, 14, 762. [Google Scholar] [CrossRef]
- Wei, R.; Li, X.; Vaz, M.A.; Custódio, A.B. Finite Element Modelling of Pressure Armor Unlocking Failure in Unbonded Flexible Risers. J. Mar. Sci. Eng. 2025, 13, 411. [Google Scholar] [CrossRef]
- Ren, S.F. Mechanical Properties and Typical Failure Characteristics of Unbonded Flexible Riser Cross-Sections. Doctoral Thesis, Shanghai Jiao Tong University, Shanghai, China, 2015. [Google Scholar]
- Zhang, X.J.; Chang, Z.Y. Advance of research of unbonded flexible risers. In Proceedings of the International Conference on Applied Mechanics and Materials, Sanya, China, 15–16 November 2014. ICAMM1015–1019. [Google Scholar]
- Grytå, G. Fatigue of Flexible Riser in Bend Stiffener Area. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2011. [Google Scholar]
- Zhang, M.M.; Chen, X.Q.; Fu, S.X.; Guo, Y.; Ma, L. Theoretical and numerical analysis of bending behavior of unbonded flexible risers. Mar. Struct. 2015, 44, 311–325. [Google Scholar] [CrossRef]
- Cuamatzi-Melendez, R.; Castillo-Hernández, O.; Vázquez-Hernández, A.; Albiter5, A.; Váz, M. Finite element modeling of burst failure in unbonded flexible risers. Eng. Struct. 2015, 87, 58–69. [Google Scholar] [CrossRef]
- Lei, Q.L.; Chen, C.Y.; Zhu, X.H. Tensile failure behavior of unbonded flexible riser with damaged tensile armor wires. Ocean Eng. 2023, 267, 113112. [Google Scholar] [CrossRef]
- De Sousa, J.R.M.; Viero, P.F.; Magluta, C.; Roitman, N. An Experimental and Numerical Study on the Axial Compression Response of Flexible Pipes. J. Offshore Mech. Arct. Eng. 2012, 134, 031703. [Google Scholar] [CrossRef]
- Ramos, R., Jr.; Martins, C.d.A.; Pesce, C.P. A case study on the axial-torsional behavior of flexible risers. In Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008. OMAE2008-57514. [Google Scholar]
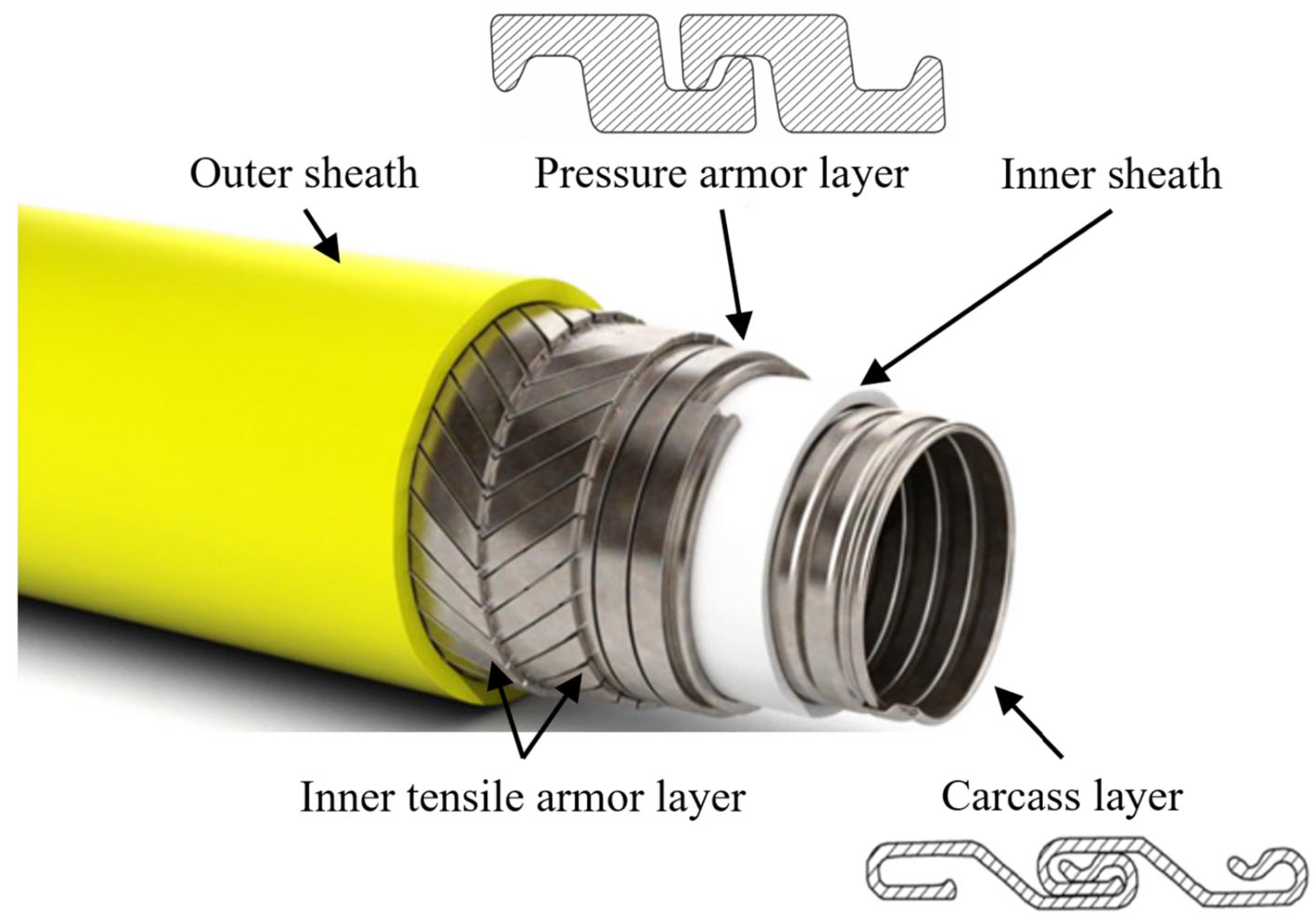
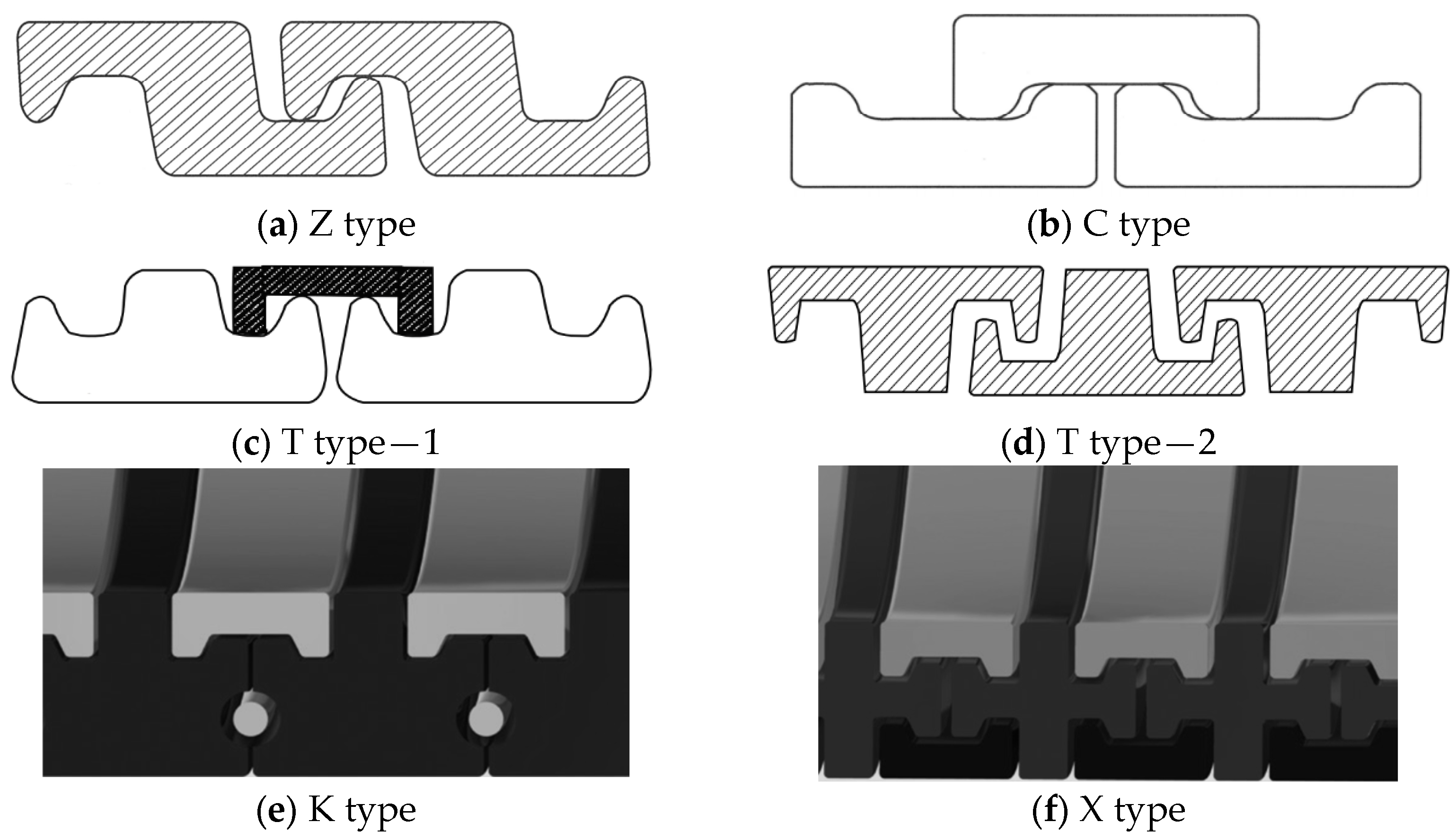


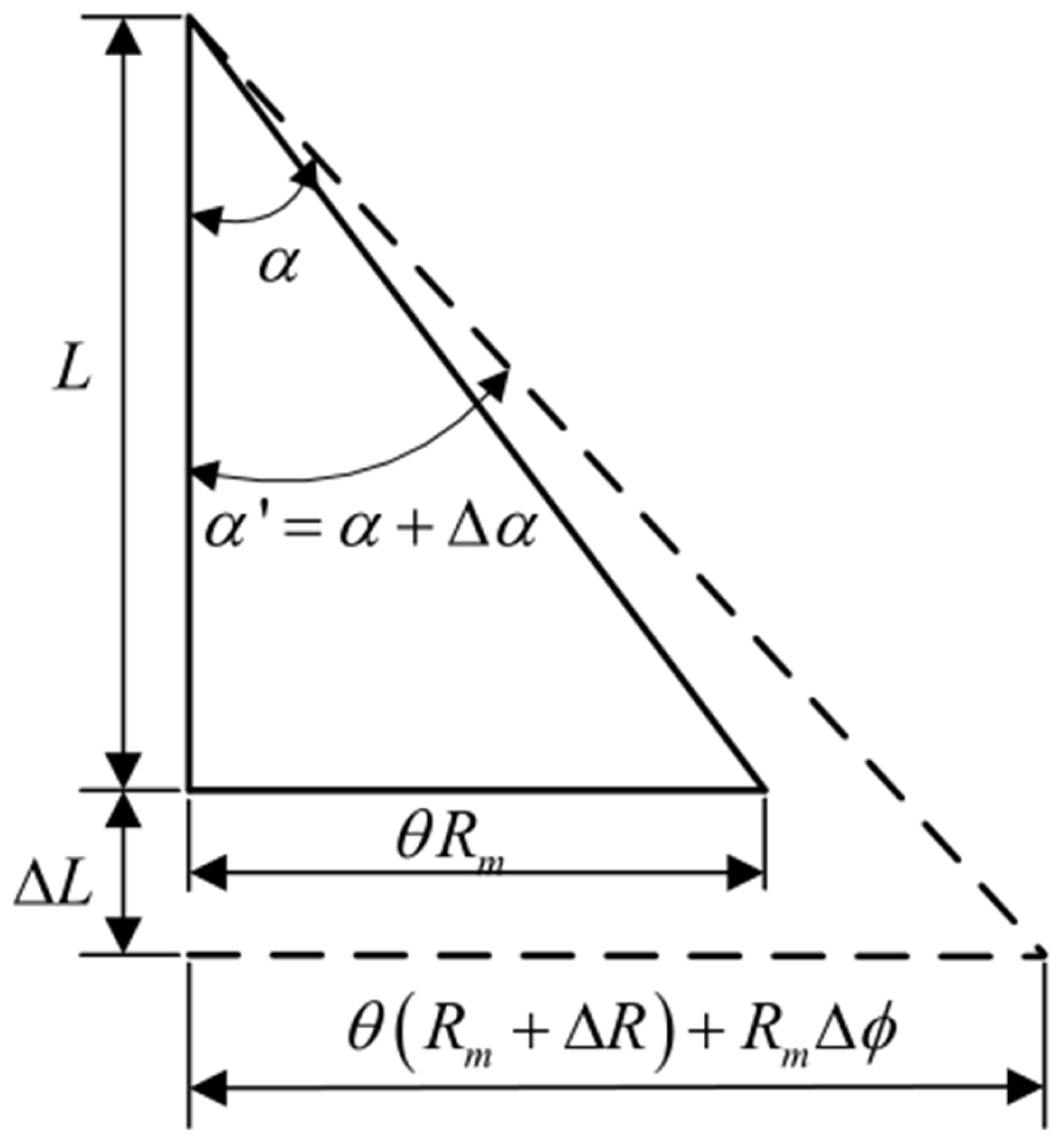

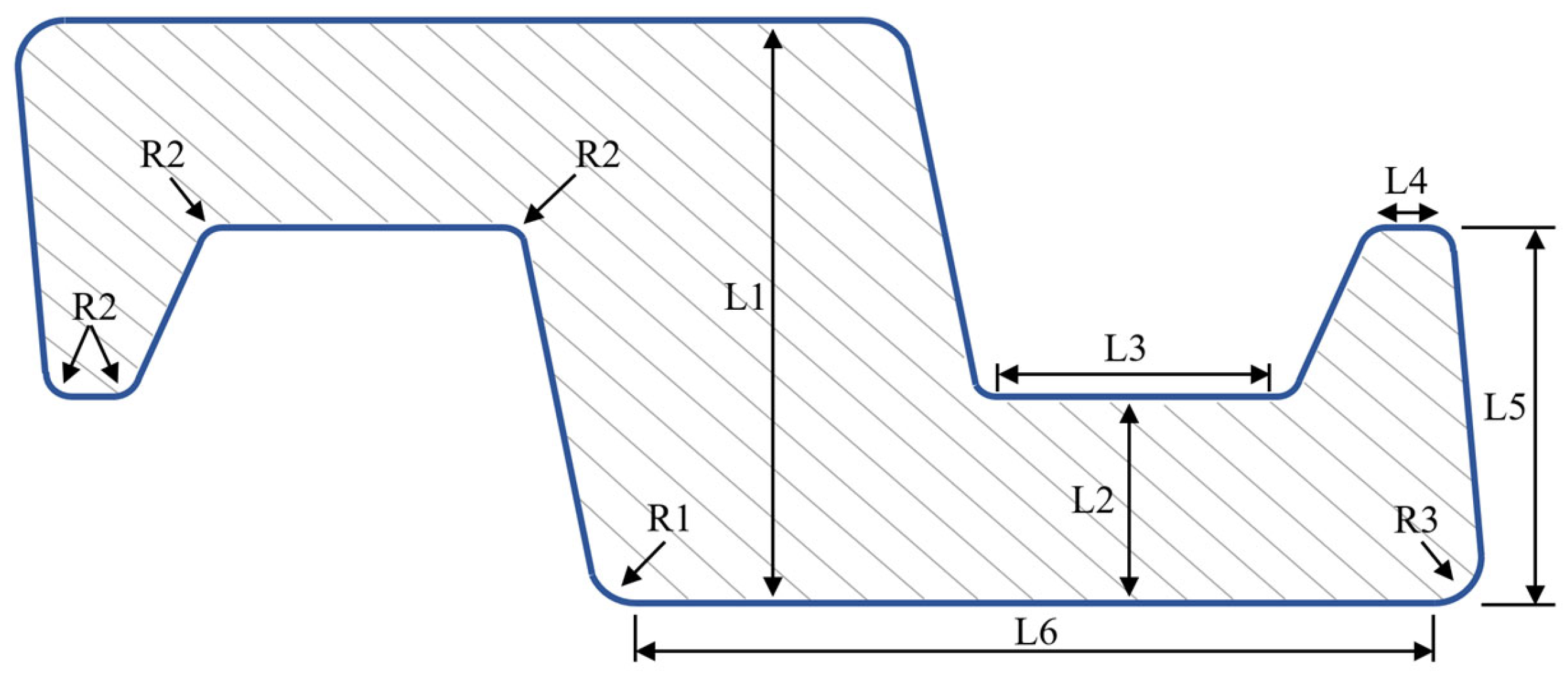








| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| L1 | 6.2 mm | L4 | 0.5 mm | R1 | 1.0 mm |
| L2 | 2.2 mm | L5 | 4.0 mm | R2 | 0.5 mm |
| L3 | 3.0 mm | L6 | 8.5 mm | R3 | 1.0 mm |
| Layer Number | Layer Type | Section Size (mm2) | Inner Radius (mm) | Outer Radius (mm) | Number of Tendons | Laying Angle (°) | Material |
|---|---|---|---|---|---|---|---|
| 1 | Carcass layer | 28 × 0.7 | 31.60 | 35.10 | 1 | −87.5 | AISI 304 |
| 2 | Pressure sheath | - | 35.10 | 40.00 | - | - | Nylon 12 |
| 3 | Pressure armor layer | 9.25 × 0.6 | 40.05 | 46.25 | 2 | −85.5 | FI-15 |
| 4 | Anti-friction tape | - | 46.25 | 47.75 | - | - | Nylon 11 |
| 5 | Inner tensile armor | 6 × 3 | 47.75 | 50.75 | 40 | −35.0 | FI-41 |
| 6 | Anti-friction tape | - | 50.75 | 52.25 | - | - | Nylon 11 |
| 7 | Outer tensile armor | 6 × 3 | 52.25 | 55.25 | 44 | 35.0 | FI-41 |
| 8 | Fabric tape | - | 55.25 | 55.75 | - | - | - |
| Axial Tensile Stiffness | Relative Deviation | References |
|---|---|---|
| 86.8 MN | 12.4% | Numerical (Lei et al., 2023) [37] |
| 108.7 MN | 9.6% | Numerical (Tang et al., 2019) [21] |
| 105.1 MN | 6% | Experiment (de Sousa et al., 2012) [38] |
| 127 MN | 28.1% | Analytical (Ramos, 2008) [39] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wu, Q.; He, J.; Liu, Q.; Li, M.; Wang, G. Coupled Burst and Fracture Failure Characteristics of Unbonded Flexible Riser Under Internal Pressure and Axial Tension. J. Mar. Sci. Eng. 2025, 13, 1866. https://doi.org/10.3390/jmse13101866
Liu Y, Wu Q, He J, Liu Q, Li M, Wang G. Coupled Burst and Fracture Failure Characteristics of Unbonded Flexible Riser Under Internal Pressure and Axial Tension. Journal of Marine Science and Engineering. 2025; 13(10):1866. https://doi.org/10.3390/jmse13101866
Chicago/Turabian StyleLiu, Yi, Qitao Wu, Jiawei He, Qingsheng Liu, Ming Li, and Gang Wang. 2025. "Coupled Burst and Fracture Failure Characteristics of Unbonded Flexible Riser Under Internal Pressure and Axial Tension" Journal of Marine Science and Engineering 13, no. 10: 1866. https://doi.org/10.3390/jmse13101866
APA StyleLiu, Y., Wu, Q., He, J., Liu, Q., Li, M., & Wang, G. (2025). Coupled Burst and Fracture Failure Characteristics of Unbonded Flexible Riser Under Internal Pressure and Axial Tension. Journal of Marine Science and Engineering, 13(10), 1866. https://doi.org/10.3390/jmse13101866






