Global Fixed-Time Target Enclosing Tracking Control for an Unmanned Surface Vehicle Under Unknown Velocity States and Actuator Saturation
Abstract
1. Introduction
- (1)
- In the design of the target enclosing task in this study, practical ocean navigation conditions are fully taken into account. To address the unknown velocity of the follower vessel and the unmeasurable relative velocity states of the target vessel, a fixed-time velocity observer is developed. In addition, a high-dimensional fixed-time extended state observer (HFTESO) is proposed to estimate the unknown state variables of the system. With the aid of this set of observers, the unknown system information can be accurately estimated within a fixed-time interval.
- (2)
- A novel FTTELOS guidance law is proposed in this paper. It ensures that both the enclosing distance error and angular error converge to an arbitrarily small neighborhood of the origin within a fixed time. The FTTELOS framework integrates guidance laws for both heading angle and surge velocity, resulting in accelerated convergence. Additionally, an adaptive update law for the look-ahead distance, driven by the enclosing distance error, is introduced to further enhance the convergence rate of the system.
- (3)
- A fixed-time saturated sliding mode controller under a fixed-threshold event-triggered mechanism is proposed in this paper to address two key challenges in target enclosing tasks: frequent actuator chattering and actuator saturation. To further enhance control performance, a Gaussian-function-based sliding mode reaching law is designed, which effectively suppresses chattering and ensures smoother control output.
2. Preliminary and Problem Formation
2.1. Preliminary
2.2. USV Model
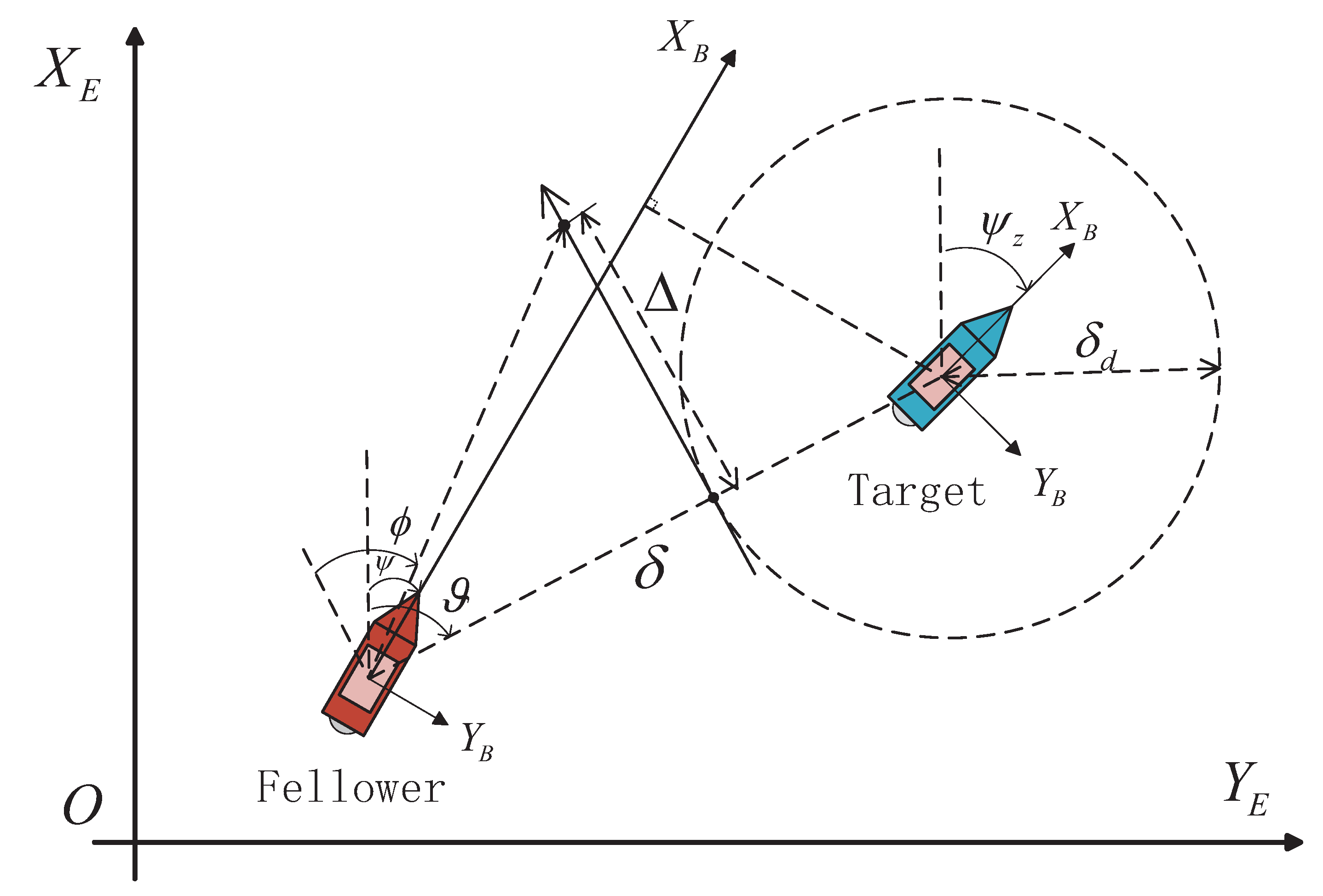
2.3. Problem Formulation
3. FTTELOS Guidance System Design
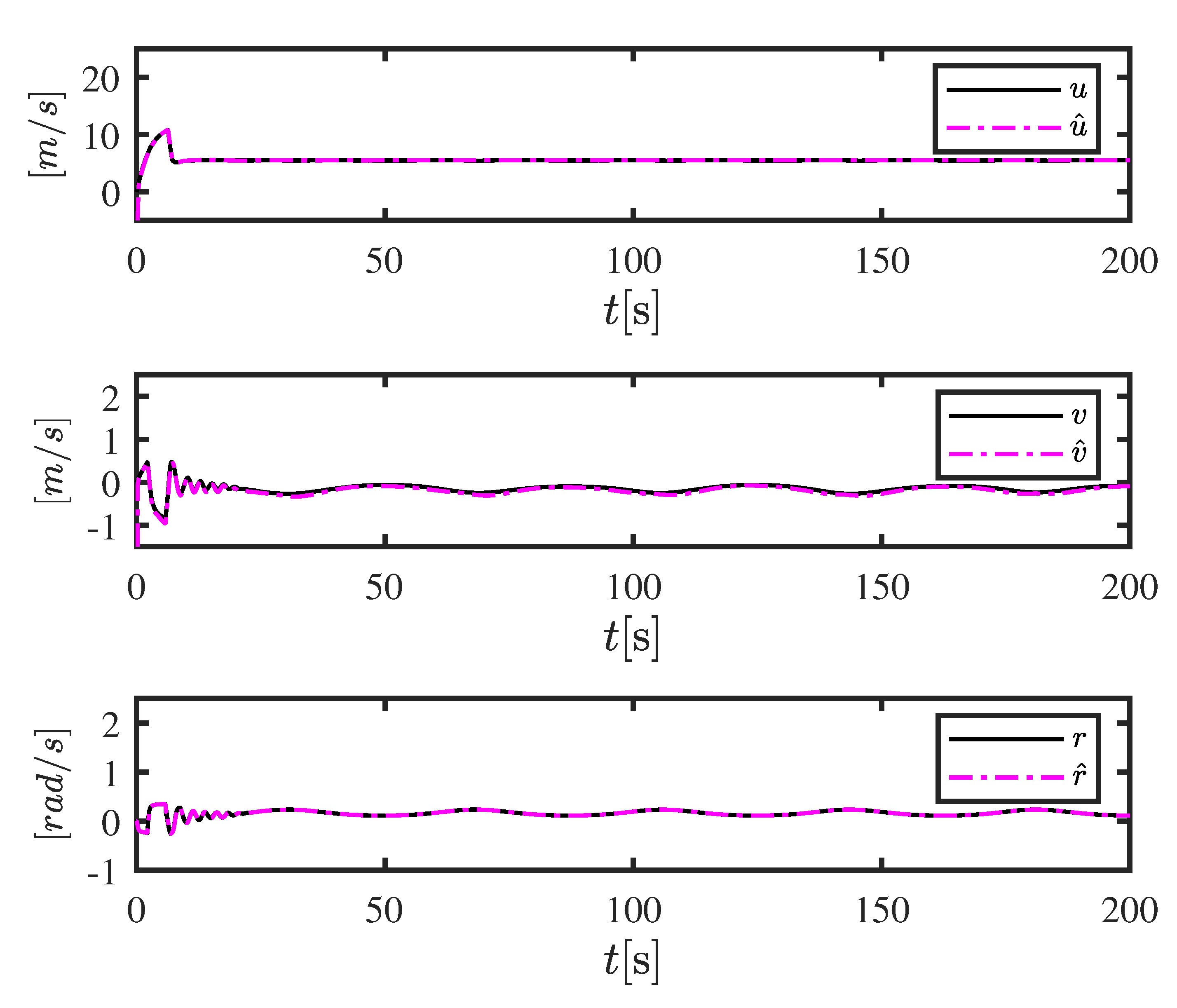
3.1. Observer Design
3.2. FTTELOS Guidance Law Design
4. Target Encircling Controller Design
4.1. Design of an FTSM-Based Surge Controller
4.2. Design of an FTSM-Based Heading Controller
4.3. Design of the Differentiator
4.4. Design of a Fixed-Threshold Event-Triggered Controller
4.5. Stability Analysis
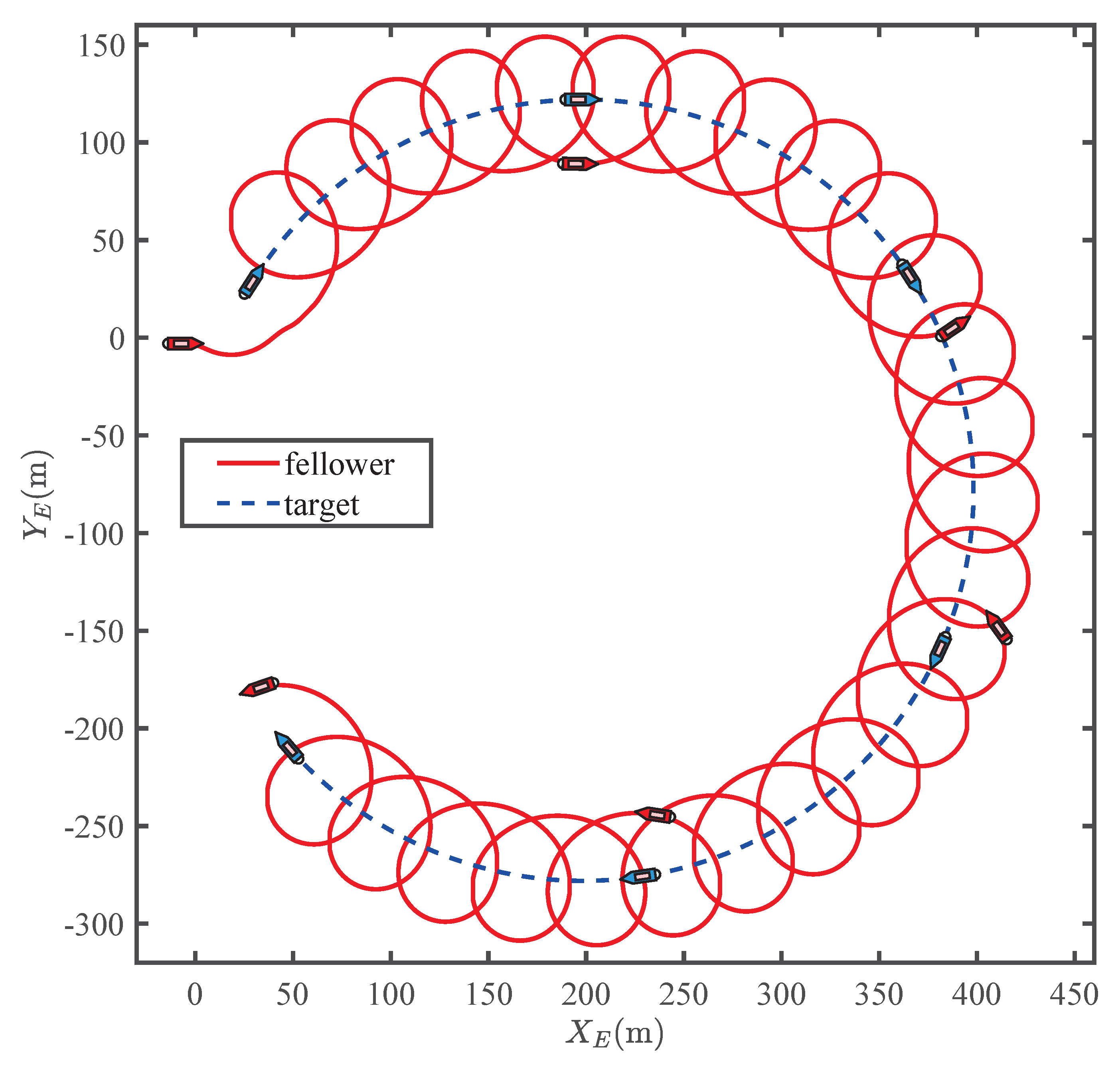
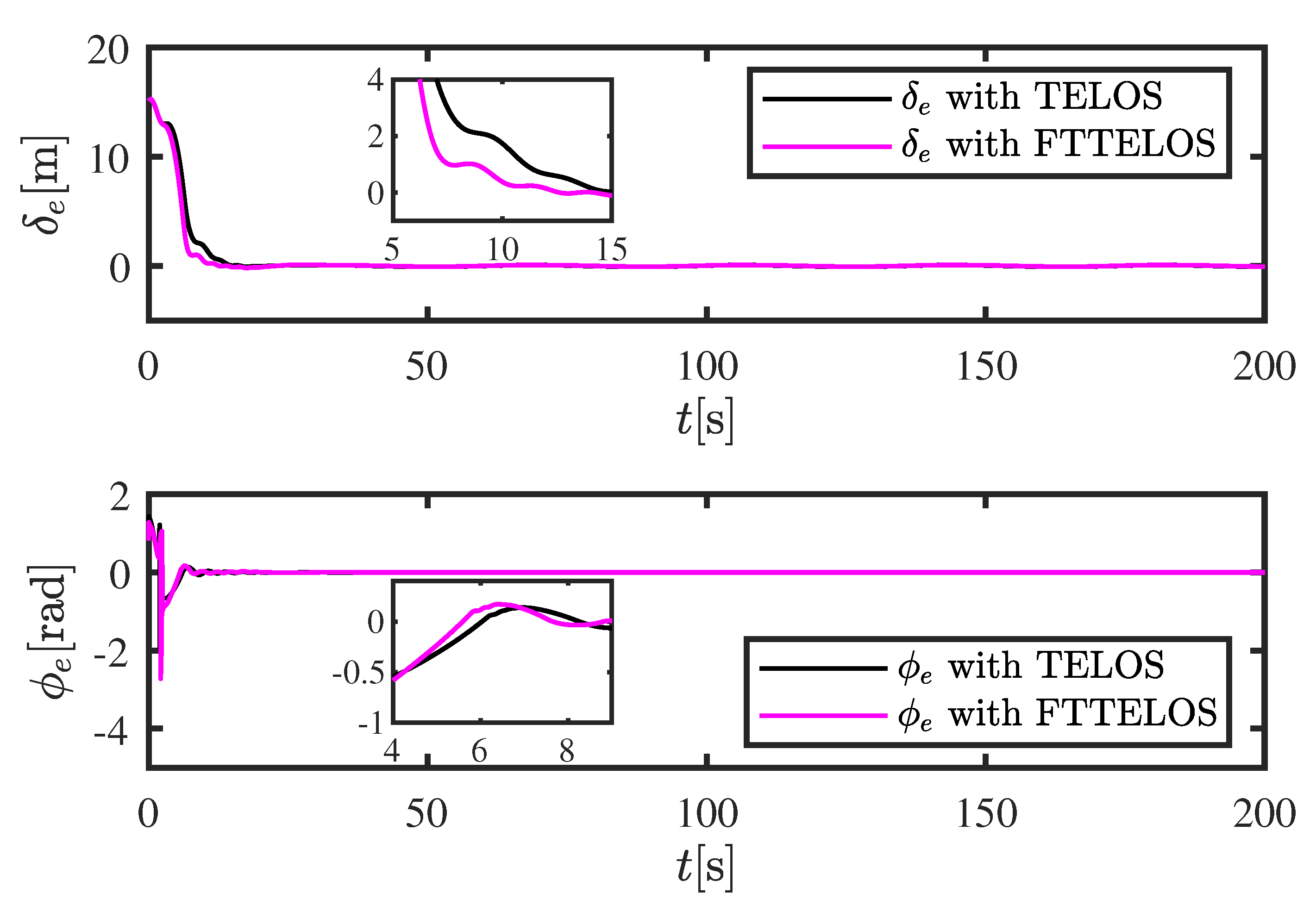
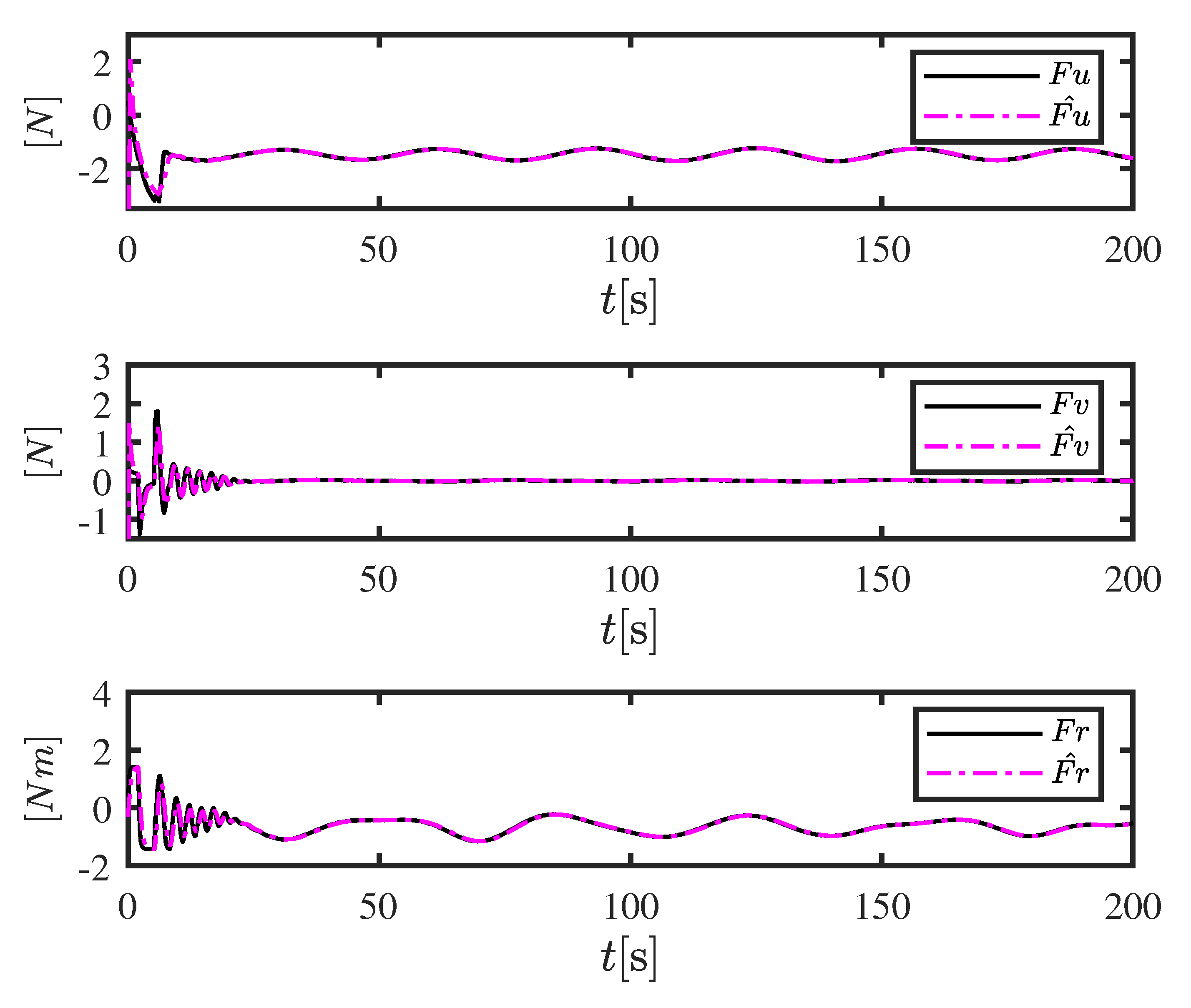
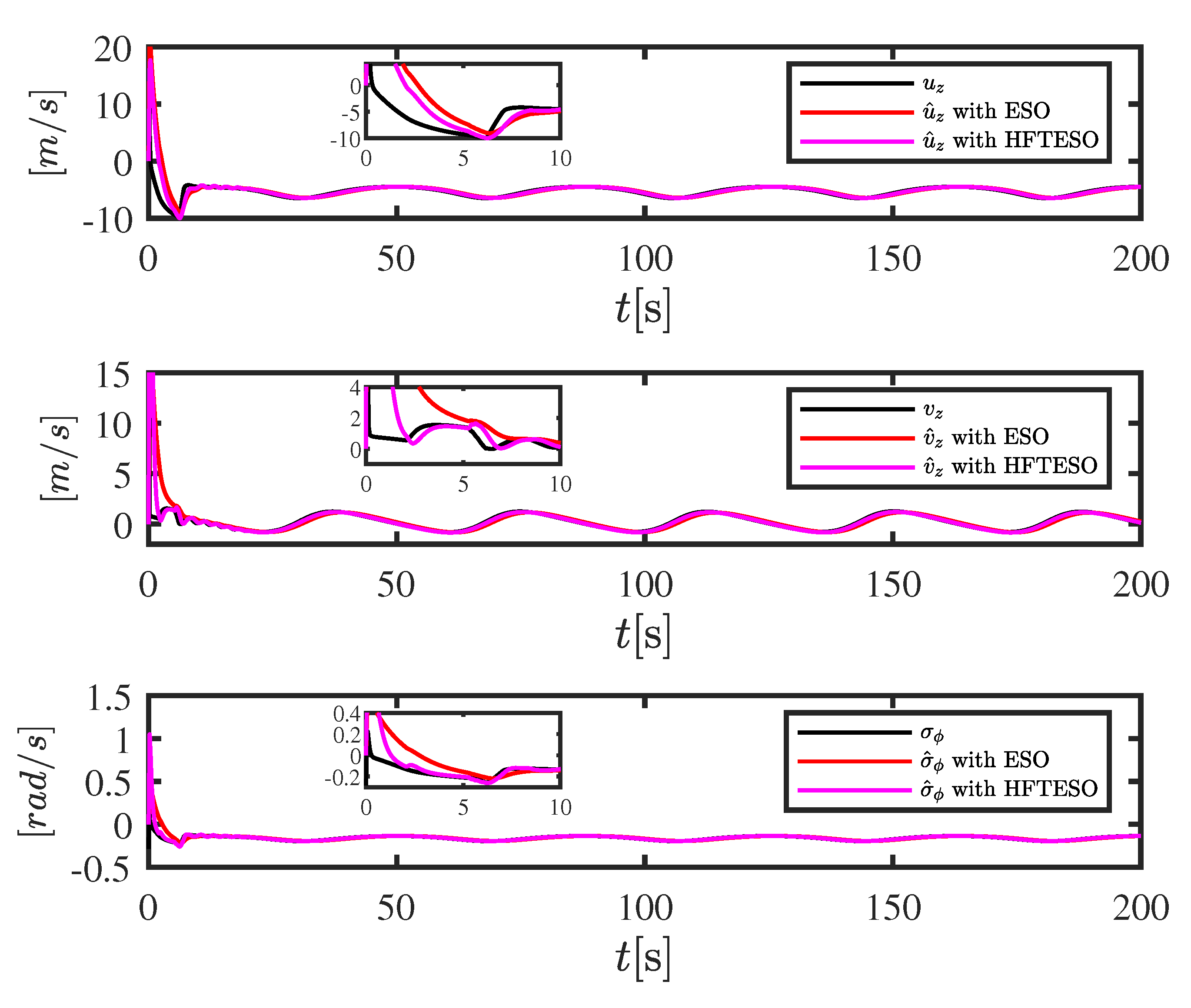
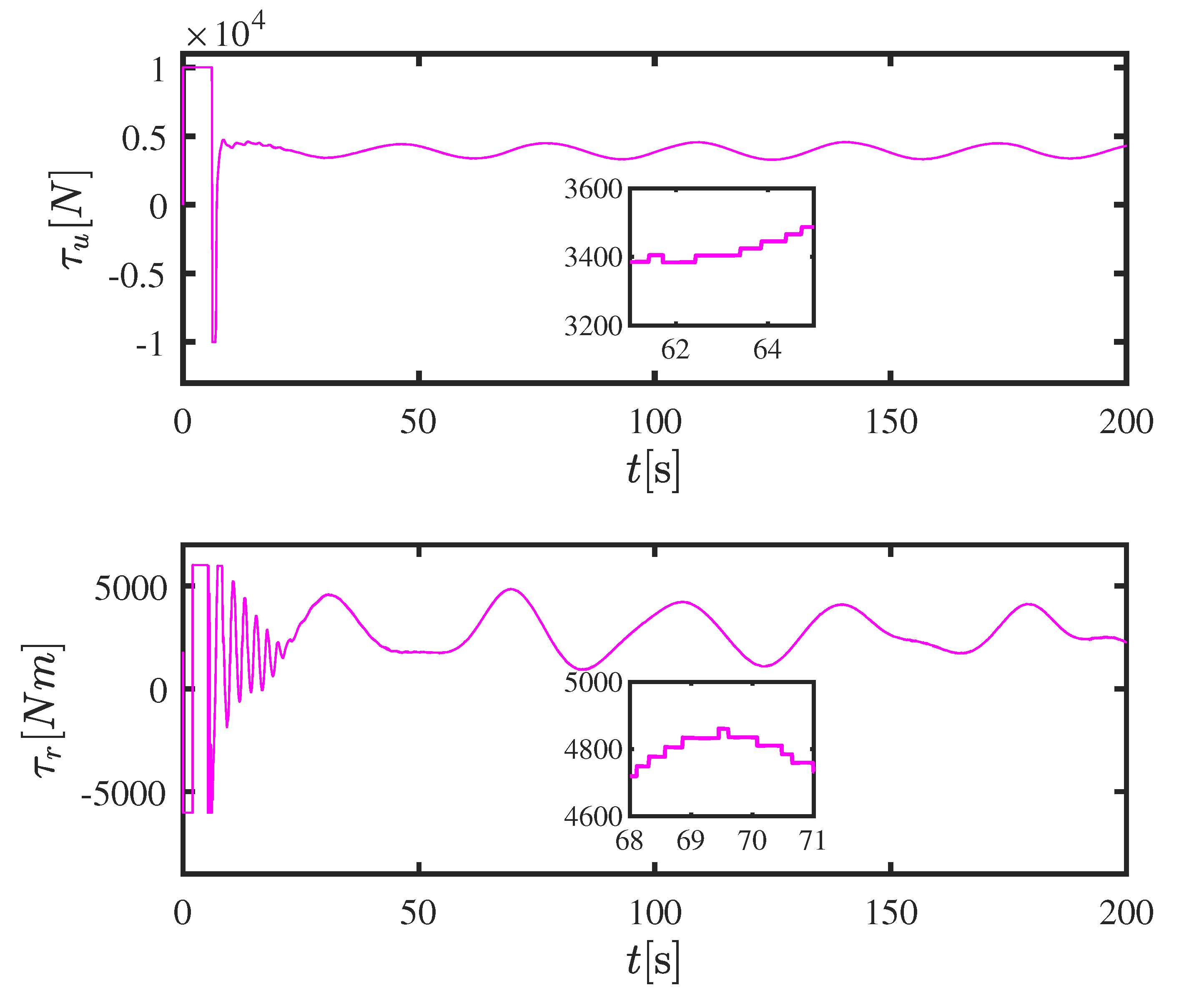
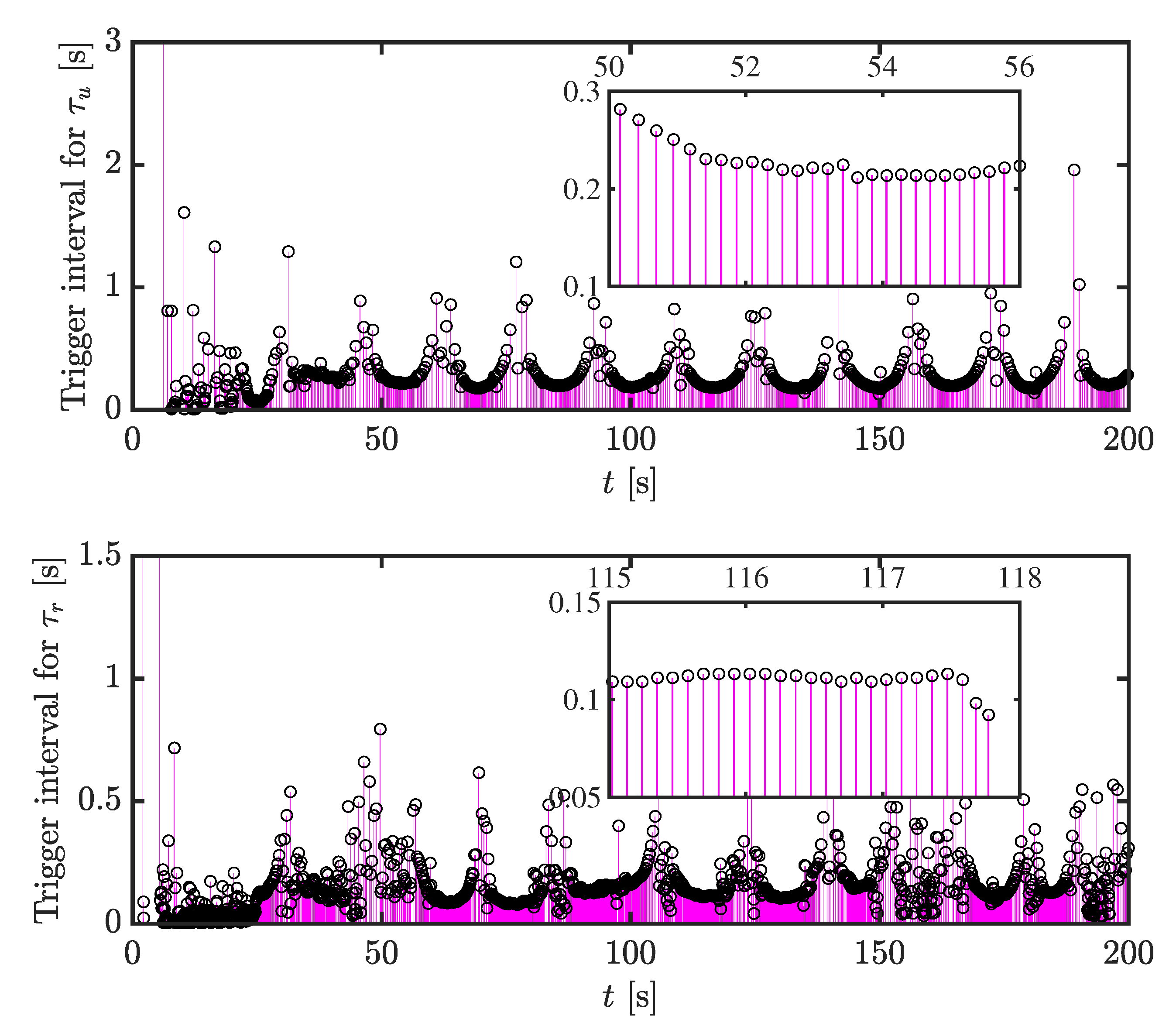
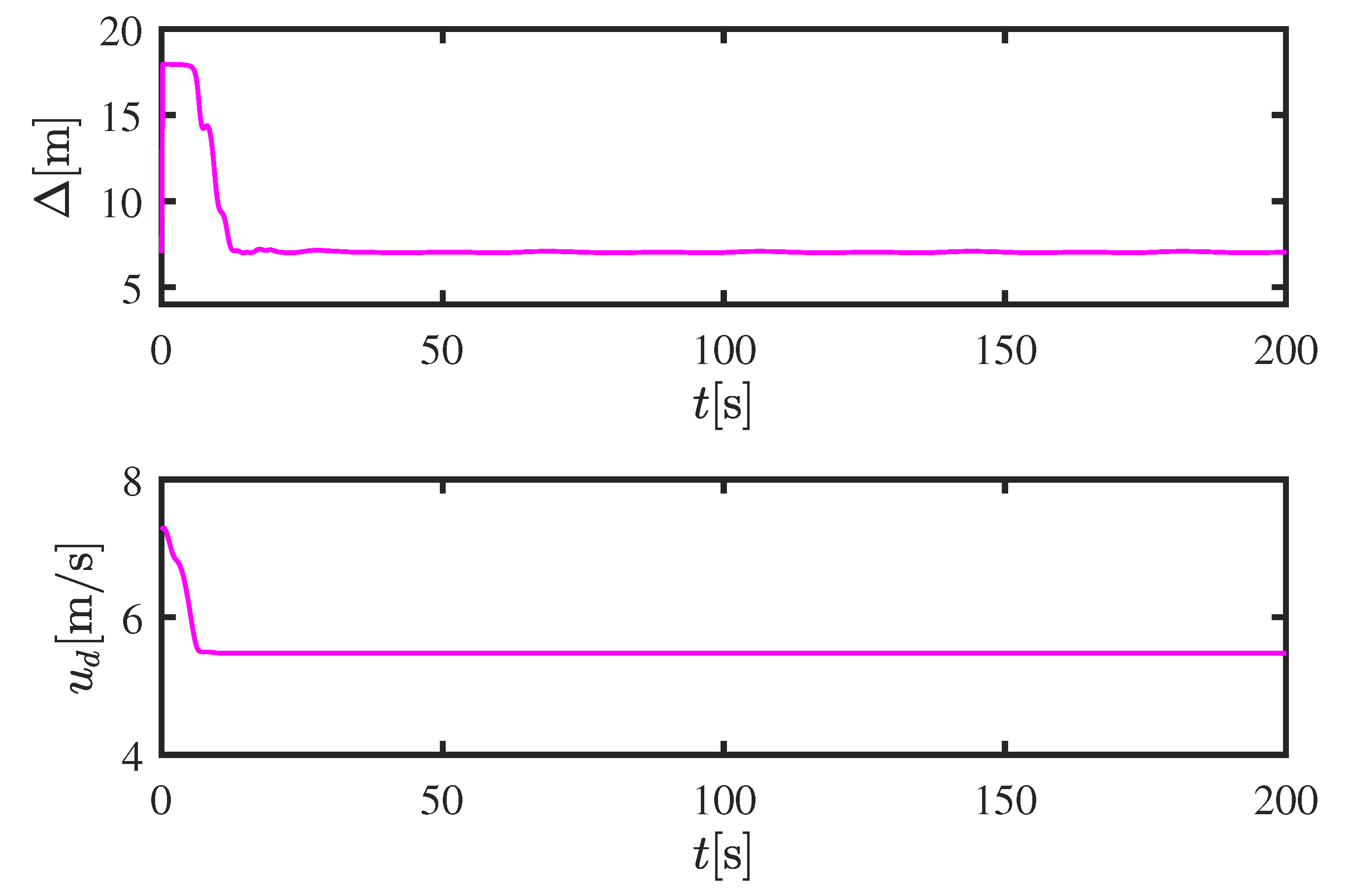
5. Simulation Results
6. Limitations and Practical Deployment Challenges
7. Real-World Implementation and Expectations
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fan, Y.; Shi, Y.; Mu, D.; Liu, J.; Li, Z. Global fixed-time adaptive fuzzy path following control for unmanned surface vehicles subject to lumped uncertainties and actuator saturation. Ocean Eng. 2023, 286, 115533. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, D.; Wang, W.; Liu, L. Containment control of networked autonomous underwater vehicles: A predictor-based neural DSC design. ISA Trans. 2015, 59, 160–171. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, X.; Zheng, Y. Adaptive neural path-following control for underactuated ships in fields of marine practice. Ocean Eng. 2015, 104, 558–567. [Google Scholar] [CrossRef]
- Shen, C.; Shi, Y.; Buckham, B. Integrated path planning and tracking control of an AUV: A unified receding horizon optimization approach. IEEE/ASME Trans. Mechatron. 2016, 22, 1163–1173. [Google Scholar] [CrossRef]
- Xiang, X.; Yu, C.; Zhang, Q. Robust fuzzy 3D path following for autonomous underwater vehicle subject to uncertainties. Comput. Oper. Res. 2017, 84, 165–177. [Google Scholar] [CrossRef]
- Cui, R.; Yang, C.; Li, Y.; Sharma, S. Adaptive neural network control of AUVs with control input nonlinearities using reinforcement learning. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1019–1029. [Google Scholar] [CrossRef]
- Shen, C.; Shi, Y.; Buckham, B. Trajectory tracking control of an autonomous underwater vehicle using Lyapunov-based model predictive control. IEEE Trans. Ind. Electron. 2017, 65, 5796–5805. [Google Scholar] [CrossRef]
- Yue, Y.; Ning, J.; Hu, X.; Li, W. Event-triggered anti-disturbance trajectory tracking for under-actuated surface vehicle under multiple constraints and input quantization. Ocean Eng. 2025, 329, 121111. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.; Peng, Z.; Chen, C.P.; Li, T. Bounded neural network control for target tracking of underactuated autonomous surface vehicles in the presence of uncertain target dynamics. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 1241–1249. [Google Scholar] [CrossRef]
- Fan, Y.; Qiao, S.; Wang, G.; Chen, S.; Zhang, H. A modified adaptive Kalman filtering method for maneuvering target tracking of unmanned surface vehicles. Ocean Eng. 2022, 266, 112890. [Google Scholar] [CrossRef]
- Marshall, J.A.; Broucke, M.E.; Francis, B.A. Pursuit formations of unicycles. Automatica 2006, 42, 3–12. [Google Scholar] [CrossRef]
- Lan, Y.; Yan, G.; Lin, Z. Distributed control of cooperative target enclosing based on reachability and invariance analysis. Syst. Control Lett. 2010, 59, 381–389. [Google Scholar] [CrossRef]
- Zheng, R.; Liu, Y.; Sun, D. Enclosing a target by nonholonomic mobile robots with bearing-only measurements. Automatica 2015, 53, 400–407. [Google Scholar] [CrossRef]
- Shames, I.; Dasgupta, S.; Fidan, B.; Anderson, B.D. Circumnavigation using distance measurements under slow drift. IEEE Trans. Autom. Control 2011, 57, 889–903. [Google Scholar] [CrossRef]
- Ma, L.; Cao, C.; Hovakimyan, N.; Dobrokhodov, V.; Kaminer, I. Adaptive vision-based guidance law with guaranteed performance bounds. J. Guid. Control Dyn. 2010, 33, 834–852. [Google Scholar] [CrossRef]
- Ghommam, J.; Fethalla, N.; Saad, M. Quadrotor circumnavigation of an unknown moving target using camera vision-based measurements. IET Control Theory Appl. 2016, 10, 1874–1887. [Google Scholar] [CrossRef]
- Yu, X.; Liu, L.; Feng, G. Distributed circular formation control of nonholonomic vehicles without direct distance measurements. IEEE Trans. Autom. Control 2018, 63, 2730–2737. [Google Scholar] [CrossRef]
- Xiang, X.; Lapierre, L.; Jouvencel, B. Smooth transition of AUV motion control: From fully-actuated to under-actuated configuration. Robot. Auton. Syst. 2015, 67, 14–22. [Google Scholar] [CrossRef]
- Lekkas, A.M.; Fossen, T.I. Integral LOS path following for curved paths based on a monotone cubic Hermite spline parametrization. IEEE Trans. Control Syst. Technol. 2014, 22, 2287–2301. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.; Peng, Z. ESO-based line-of-sight guidance law for path following of underactuated marine surface vehicles with exact sideslip compensation. IEEE J. Ocean. Eng. 2016, 42, 477–487. [Google Scholar] [CrossRef]
- Jiang, Y.; Peng, Z.; Wang, D.; Chen, C.P. Line-of-sight target enclosing of an underactuated autonomous surface vehicle with experiment results. IEEE Trans. Ind. Inform. 2019, 16, 832–841. [Google Scholar] [CrossRef]
- Wang, N.; Lv, S.; Zhang, W.; Liu, Z.; Er, M.J. Finite-time observer based accurate tracking control of a marine vehicle with complex unknowns. Ocean Eng. 2017, 145, 406–415. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, S.; Yan, Y. Fixed-time output feedback trajectory tracking control of marine surface vessels subject to unknown external disturbances and uncertainties. ISA Trans. 2019, 93, 145–155. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Gao, X.; Yu, Y. Dual Deep Neural Networks for Improving Trajectory Tracking Control of Unmanned Surface Vehicle. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 3441–3446. [Google Scholar]
- Majidiyan, H.; Enshaei, H.; Howe, D. A Concise Account for Challenges of Machine Learning in Seakeeping. Procedia Comput. Sci. 2025, 253, 2849–2858. [Google Scholar] [CrossRef]
- Yu, Y.; Guo, C.; Yu, H. Finite-time PLOS-based integral sliding-mode adaptive neural path following for unmanned surface vessels with unknown dynamics and disturbances. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1500–1511. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, G.; Yi, B.; Zhang, W. Practical proportional integral sliding mode control for underactuated surface ships in the fields of marine practice. Ocean Eng. 2017, 142, 217–223. [Google Scholar] [CrossRef]
- Li, T.; Zhao, R.; Chen, C.P.; Fang, L.; Liu, C. Finite-time formation control of under-actuated ships using nonlinear sliding mode control. IEEE Trans. Cybern. 2018, 48, 3243–3253. [Google Scholar] [CrossRef]
- Ashrafiuon, H.; Muske, K.R.; McNinch, L.C.; Soltan, R.A. Sliding-mode tracking control of surface vessels. IEEE Trans. Ind. Electron. 2008, 55, 4004–4012. [Google Scholar] [CrossRef]
- Yu, R.; Zhu, Q.; Xia, G.; Liu, Z. Sliding mode tracking control of an underactuated surface vessel. IET Control Theory Appl. 2012, 6, 461–466. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, W. Adaptive non-singular integral terminal sliding mode tracking control for autonomous underwater vehicles. IET Control Theory Appl. 2017, 11, 1293–1306. [Google Scholar] [CrossRef]
- Ding, L.; Han, Q.L.; Ge, X.; Zhang, X.M. An overview of recent advances in event-triggered consensus of multiagent systems. IEEE Trans. Cybern. 2017, 48, 1110–1123. [Google Scholar] [CrossRef]
- Mazo Jr, M.; Anta, A.; Tabuada, P. An ISS self-triggered implementation of linear controllers. Automatica 2010, 46, 1310–1314. [Google Scholar] [CrossRef]
- Xing, L.; Wen, C.; Liu, Z.; Su, H.; Cai, J. Event-triggered adaptive control for a class of uncertain nonlinear systems. IEEE Trans. Autom. Control 2016, 62, 2071–2076. [Google Scholar] [CrossRef]
- Ge, X.; Han, Q.L.; Zhang, X.M. Achieving cluster formation of multi-agent systems under aperiodic sampling and communication delays. IEEE Trans. Ind. Electron. 2017, 65, 3417–3426. [Google Scholar] [CrossRef]
- Postoyan, R.; Bragagnolo, M.C.; Galbrun, E.; Daafouz, J.; Nešić, D.; Castelan, E.B. Event-triggered tracking control of unicycle mobile robots. Automatica 2015, 52, 302–308. [Google Scholar] [CrossRef]
- Jain, R.P.; Aguiar, A.P.; de Sousa, J.B. Cooperative path following of robotic vehicles using an event-based control and communication strategy. IEEE Robot. Autom. Lett. 2018, 3, 1941–1948. [Google Scholar] [CrossRef]
- Ge, X.; Han, Q.L. Distributed formation control of networked multi-agent systems using a dynamic event-triggered communication mechanism. IEEE Trans. Ind. Electron. 2017, 64, 8118–8127. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2011, 57, 2106–2110. [Google Scholar] [CrossRef]
- Chen, M.; Wang, H.; Liu, X. Adaptive fuzzy practical fixed-time tracking control of nonlinear systems. IEEE Trans. Fuzzy Syst. 2019, 29, 664–673. [Google Scholar] [CrossRef]
- Wang, S.; Sun, M.; Xu, Y.; Liu, J.; Sun, C. Predictor-based fixed-time LOS path following control of underactuated USV with unknown disturbances. IEEE Trans. Intell. Veh. 2023, 8, 2088–2096. [Google Scholar] [CrossRef]
- Zuo, Z.; Tian, B.; Defoort, M.; Ding, Z. Fixed-time consensus tracking for multiagent systems with high-order integrator dynamics. IEEE Trans. Autom. Control 2017, 63, 563–570. [Google Scholar] [CrossRef]
- Fan, Y.; Qiu, B.; Liu, L.; Yang, Y. Global fixed-time trajectory tracking control of underactuated USV based on fixed-time extended state observer. ISA Trans. 2023, 132, 267–277. [Google Scholar] [CrossRef] [PubMed]


| Parameters | Value | Parameters | Value |
|---|---|---|---|
| (1, 1, 1) | 0.45 | ||
| (5, 15, 6) | 0.6 | ||
| (5, 5, 6) | 2 | ||
| (5, 18, 6) | 1 | ||
| 6/7 | m | 6/7 | |
| 7/6 | n | 7/6 | |
| (0.1, 0.1, 0.1) | 1 | ||
| (0.01, 0.01, 0.01) | 1 | ||
| (0.01, 0.01, 0.01) | 0.1 | ||
| (3, 3, 3) | |||
| 5/6 | 7 | ||
| 6/5 | 18 | ||
| (10, 10, 9, 1) | c | 1 | |
| (3, 6, 9, 9) | h | 2 | |
| (3, 10, 9, 9) | 1.4 | ||
| 0.7 | 1 | ||
| 1.2 | 0.3 | ||
| 0.1 | 0.2 | ||
| 0.01 | 7/6 | ||
| 5/6 | 6/7 | ||
| 2/3 | 5/4 | ||
| 6/5 | 2.6 | ||
| 31/30 | 0.46 | ||
| 0.96 | 0.6 | ||
| 0.43 | 0.4 | ||
| 1.3 | 1 | ||
| 1 | 1 | ||
| 1 | 3 | ||
| 0.01 | 20 | ||
| 0.02 | 25 |
| Method | of (s) | of (s) |
|---|---|---|
| TELOS | 13.64 | 10.46 |
| FTTELOS | 10.22 | 7.52 |
| Method | ||
|---|---|---|
| Time triggered | 20,000 | 20,000 |
| Fixed threshold triggered | 1259 | 3344 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.; Ma, G.; Fan, Y.; Mu, D.; Sun, F.; Shi, L.; Li, H. Global Fixed-Time Target Enclosing Tracking Control for an Unmanned Surface Vehicle Under Unknown Velocity States and Actuator Saturation. J. Mar. Sci. Eng. 2025, 13, 2094. https://doi.org/10.3390/jmse13112094
Han X, Ma G, Fan Y, Mu D, Sun F, Shi L, Li H. Global Fixed-Time Target Enclosing Tracking Control for an Unmanned Surface Vehicle Under Unknown Velocity States and Actuator Saturation. Journal of Marine Science and Engineering. 2025; 13(11):2094. https://doi.org/10.3390/jmse13112094
Chicago/Turabian StyleHan, Xinjie, Guanglu Ma, Yunsheng Fan, Dongdong Mu, Feng Sun, Linlong Shi, and Hongbiao Li. 2025. "Global Fixed-Time Target Enclosing Tracking Control for an Unmanned Surface Vehicle Under Unknown Velocity States and Actuator Saturation" Journal of Marine Science and Engineering 13, no. 11: 2094. https://doi.org/10.3390/jmse13112094
APA StyleHan, X., Ma, G., Fan, Y., Mu, D., Sun, F., Shi, L., & Li, H. (2025). Global Fixed-Time Target Enclosing Tracking Control for an Unmanned Surface Vehicle Under Unknown Velocity States and Actuator Saturation. Journal of Marine Science and Engineering, 13(11), 2094. https://doi.org/10.3390/jmse13112094








