Numerical Analysis of Impact-Freezing and Spreading Dynamics of Supercooled Saline Droplets on Offshore Wind Turbine Blades Using the VOF–Enthalpy–Porosity Method

Abstract

The impact-freezing phenomenon of supercooled saline droplets on cold surfaces poses a serious threat to the operational stability and structural integrity of offshore wind turbines. Compared to freshwater droplets, numerical models for analyzing the impact-freezing behavior of saline droplets typically involve complex physical mechanisms, resulting in high computational costs. This study employs a simplified two-dimensional axisymmetric numerical model that integrates the Volume of Fluid (VOF) method with the enthalpy–porosity approach, enabling rapid analysis of the saline droplet impact-freezing process under marine environmental conditions. The model is validated by comparing the spreading factor curve of saline droplets with a salinity of 35‰ against existing experimental data. Results show that the salinity corresponding to the peak relative deviation shifts with varying impact parameters, depending on the competition between impact dynamics and solidification. Furthermore, the maximum spreading factor decreases with increasing supercooling degree and contact angle but increases with higher Weber number. These findings provide useful correction parameters for improving existing droplet motion and icing prediction models.

1. Introduction

Offshore wind turbines in cold regions face severe icing problems, which directly threaten their stable operation, structural integrity, and service life [1]. For example, ice accretion on blades significantly reduces aerodynamic performance, while the increased mass may induce resonance and accelerate fatigue damage [2,3]. The fundamental reason for such icing events lies in the impact and subsequent freezing of supercooled droplets on cold surfaces, as illustrated in Figure 1. Therefore, accurate ice accretion prediction for offshore wind turbines in cold regions requires a detailed study of the droplet impact-freezing process [4,5].

The droplet impact-freezing phenomenon can be regarded as a coupling of two processes: impacting and solidification. Existing studies have revealed the basic behaviors of droplet impact, such as spreading, retraction, oscillation, and adhesion, and summarized the main stages of the freezing process, such as supercooling, nucleation, and recalescence [6]. The complex coupling between these two processes makes the impact-freezing phenomenon highly sensitive to factors such as ambient temperature, impact velocity, and surface wettability, resulting in significant changes in morphology [7]. Specifically, droplets usually exhibit different morphological characteristics under different impact parameters. Due to the heat exchange between the droplet and the cold surface during the impact process, the heat transfer rate and freezing rate of the droplet will also be affected [8]. These variations in morphology and freezing rate at the mesoscopic scale govern distinct ice-growth behaviors during continuous accumulation of supercooled droplets, ultimately producing diverse ice types (e.g., rime ice, glaze ice, and mixed ice) and different spatial distributions. Therefore, the key factors governing macroscopic ice accretion can be summarized through the study of droplet impact-freezing characteristics. Analyzing these characteristics enables the incorporation of corresponding corrections into existing icing prediction models, thereby improving their accuracy.

The study of the droplet impact-freezing characteristics has primarily been conducted using experimental and numerical methods. By utilizing high-speed imaging, the subtle dynamic evolution during the impact process can be clearly captured. Such experiments not only provide a direct way to understand the impact-freezing process but also supply essential initial input parameters for numerical simulations, such as droplet physics properties and contact angle. Yao et al. [9] revealed that the decrease in surface temperature led to a reduction in droplet retraction rate, equilibrium height, and freezing delay time while increasing the final contact area. Pan et al. [10] demonstrated that increased surface hydrophobicity resulted in a higher magnitude of oscillations, prolonged the time to reach equilibrium, and reduced the heat transfer rate. Fang et al. [11] showed that the final freezing morphology of droplets after impact depends on the competition between impact dynamics and solidification processes. By adjusting impact velocity and substrate temperature, five distinct freezing morphologies were observed. However, the droplet impact-freezing process is extremely sensitive and is easily disturbed by external factors in experiments. This not only increases the difficulty of the experiment but also affects the stability of the results. Moreover, owing to the limitations in directly observing internal droplet characteristics and acquiring essential parameters, experimental methods are primarily restricted to a validating role in the field of engineering.

As an effective supplement to experimental methods, the coupled VOF model and enthalpy–porosity method have been widely applied to the study of supercooled droplet impact-freezing process [12,13]. Zhang et al. [14] revealed that supercooled droplets have slower spreading and retraction rates. This effect is amplified with an increase in the Weber number, higher supercooling, and smaller contact angles. Wang et al. [15] investigated the impact-freezing process of supercooled droplets, finding that hydrophilic surfaces accelerated the heat transfer rate due to larger contact areas, thereby shortening the freezing time. Zhang et al. [16] studied the impact dynamics of ellipsoidal droplets. It was found that high aspect ratio droplets have shorter initial contact lines and less viscous dissipation, leading to larger maximum spreading times and factors. Chang et al. [17] found that the initial supercooling temperature has the greatest influence on the heat transfer rate between the droplet and the substrate. At the same time, droplets with lower initial supercooling temperatures completed freezing within the same period, while droplets with higher initial supercooling temperatures remained in the liquid state. Therefore, the coupled VOF model and enthalpy–porosity method can effectively capture the impact-freezing behavior of freshwater droplets at the mesoscopic scale. However, droplets in marine environments inherently contain salt, leading to differences in the impact-freezing process compared with supercooled freshwater droplets. Although the freezing of saline droplets has been extensively investigated [18,19,20,21,22], most studies have focused on exploring the fundamental physical mechanisms, with limited attention to engineering applications that utilize the deviations between freshwater and saline droplet impact-freezing processes.

More complex models, such as the lattice Boltzmann method [23], can resolve the unique mechanisms during the impact-freezing process of supercooled saline droplets, as illustrated in Figure 2. Song et al. [24] developed a coupled LBM–phase-field model to investigate ice-crystal growth during seawater freezing. Their results revealed that seawater flow effectively promotes the diffusion of discharged salt and enhances crystal growth, thereby reducing the probability of dendrite closure. Liu et al. [6] employed the same approach to study the impact-freezing process of supercooled saline droplets and found that lower surface temperatures lead to salt solution enrichment between dendrites structures. Nevertheless, the requirement for multiphysics coupling with numerous parameters inevitably imposes substantial computational costs, which makes such methods unsuitable for engineering applications such as icing prediction model correction.

Based on the investigations of single droplet, recent studies have sought to establish connections between mesoscopic droplet behavior and macroscopic ice-accretion models. Liu et al. [25] employed the coupled Level-Set and VOF methods together with the Enthalpy–Porosity approach to develop a numerical model for droplet impact-freezing process. Furthermore, they proposed a mathematical model to predict ice-layer thickness on flat surfaces based on the freezing fraction corresponding to the liquid water content (LWC) of a single droplet. Therefore, by analyzing the differences between saline and freshwater droplets during the impact-freezing process, the ice accumulation model derived from the study of single droplet can be effectively corrected, enabling real-time and efficient icing prediction for offshore environments in cold regions.

To address this issue, this study employs a simplified two-dimensional axisymmetric numerical model based on the VOF method and the enthalpy–porosity method. The numerical framework employs an equivalent physical property correction method to systematically evaluate the first-order effects of salinity on droplet impact behavior. This paper summarizes the regularities of the relative deviation of spreading factors under various salinities and impact parameters, including supercooling degree, contact angle, and Weber number. The results provide inspiration for refining ice prediction models for offshore wind turbines. Furthermore, this framework provides a foundation for incorporating more complex mechanisms in future studies. Section 2 introduces the numerical methods and calculation process. Section 3 validates the accuracy of the numerical model. Section 4 presents and analyzes the simulation results in detail. Section 5 discusses the limitations of this study along with potential directions for future work. Section 6 summarizes the key findings.

2. Theoretical Methods and Calculation Process

2.1. Volume of Fluid (VOF) Model

Since droplet spreading and retraction dynamics represent a typical two-phase flow phenomenon, the VOF method proposed by Hirt and Nichols [26] is employed to capture mass and momentum transfer between phases. As a widely adopted surface-tracking technique for multiphase flow simulations, the VOF method is particularly suitable for flows with complex interfaces.

In the VOF model, the computational domain is discretized into small cells, with each cell assigned a volume fraction representing the proportion of each fluid phase. This fraction evolves with time, enabling accurate tracking of the interface motion. The volume fraction of the phase p in each cell is defined as:

$${\alpha }_p={\displaystyle \frac{V_{pth}}{V_{\mathrm{cell}}}}$$

(1)

where $V_{pth}$ is the volume of the phase $p$, $V_{\mathrm{cell}}$ is the cell volume. In this paper, the Solidification/Melting model considers unfrozen water and frozen ice as the same liquid phase. Therefore, the air phase ($p=1$) and the ice/water phase ($p=2$) exist in each cell and satisfy ${\alpha }_1+{\alpha }_2=1$.

The mass conservation equations of the liquid and gas phases are expressed by:

$${\displaystyle \frac{1}{{\rho }_p}}\left[{\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_p{\rho }_p\right)+\nabla \cdot \left({\alpha }_p{\rho }_p{\overrightarrow{v}}_p\right)\right]=0$$

(2)

Throughout the computational domain, the different fluid phases use the unified momentum conservation equation.

$${\displaystyle \frac{\partial }{\partial t}}(\rho \overrightarrow{v}\overrightarrow{v})+\nabla \cdot (\rho \overrightarrow{v}\overrightarrow{v})=-\nabla p+\nabla \cdot \mu [(\nabla \overrightarrow{v}+\nabla {\overrightarrow{v}}^T)]+\rho \overrightarrow{g}+{\overrightarrow{F}}_{\mathrm{ST}}+{\overrightarrow{S}}_{\mathrm{M}}$$

(3)

where ${\overrightarrow{F}}_{\mathrm{ST}}$ denotes the source term of the momentum equation for the gas–liquid surface tension, and ${\overrightarrow{S}}_M$ is the momentum source term which is introduced due to the phase transition and obtained from Equation (10). In this study the continuous surface tension model proposed by Brackbill et al. [27] is used to calculate the interaction between the gas–liquid two-phase flow.

$${\overrightarrow{F}}_{\mathrm{ST}}=\sigma {\displaystyle \frac{\rho \kappa \nabla {\alpha }_1}{({\rho }_1+{\rho }_2)/2}}$$

(4)

where $\kappa =\nabla \overrightarrow{n}$ denotes the curvature of the interface and $\overrightarrow{n}=\nabla {\alpha }_1/|\nabla {\alpha }_1|$ is the unit normal vector.

The energy equation for all phases can be expressed as:

$${\displaystyle \frac{\partial }{\partial t}}(\rho h_{\mathrm{total}})+\nabla \cdot (\rho \overrightarrow{v}{h}_{\mathrm{total}})=\nabla \cdot (k\nabla T)$$

(5)

where $h_{\mathrm{total}}$ is the weighted total enthalpy of each phase in the control body, including sensible enthalpy and latent heat of phase change.

The physical parameters involved in Equations (2), (3) and (5) are weighted effective physical parameters.

$$\rho ={\displaystyle \sum _p{\alpha }_p}{\rho }_p;\mu ={\displaystyle \sum _p{\alpha }_p}{\mu }_p;k={\displaystyle \sum _p{\alpha }_p}{k}_p; p=1, 2$$

(6)

2.2. Solidification/Melting Model

This study utilizes the Solidification/Melting model in Ansys Fluent 2023 R1 to simulate the droplet freezing process. The model uses the enthalpy–porosity method to capture the phase transition phenomenon. The liquid fraction in each computational cell is determined through enthalpy balance calculations. Regions with liquid fractions between 0 and 1 are termed the mushy zone. Upon complete solidification, the liquid fraction, porosity, and velocity reach zero.

The total enthalpy per cell is expressed as the sum of sensible enthalpy and latent heat of the solid–liquid mixture:

$$h_{\mathrm{total}}=h+h_{\mathrm{latent}}$$

(7)

where $h$ is the sensible enthalpy, which can be expressed as:

$$h=h_{\mathrm{ref}}+{\displaystyle {\int }_{T_{\mathrm{ref}}}^{T}c}dT$$

(8)

where $h_{\mathrm{ref}}$ is the value of sensible enthalpy of the reference state, $T_{\mathrm{ref}}$ is the temperature of the reference state, and $c$ is the specific heat capacity at constant pressure. $h_{\mathrm{latent}}$ denotes the latent heat of a solid–liquid mixture under a certain liquid fraction.

$$h_{\mathrm{latent}}={\alpha }_{\mathrm{liquid}}{L}_{\mathrm{mix}}$$

(9)

in which ${\alpha }_{\mathrm{liquid}}$ is the liquid fraction, and $L_{\mathrm{mix}}$ is the latent heat of the water-ice mixture.

The Solidification/Melting model treats the phase transition region as a porous medium where the internal flow follows Darcy’s flow law and the Carman-Kozeny assumption. Therefore, the source term in the momentum equation ${\overrightarrow{S}}_M$ can be expressed as:

$${\overrightarrow{S}}_{\mathrm{M}}={\displaystyle \frac{{(1-{\alpha }_{\mathrm{liquid}})}^2}{{\alpha }_{\mathrm{liquid}}^3+\epsilon }}{A}_{\mathrm{mush}}\overrightarrow{\nu }$$

(10)

where $\epsilon$ is a small number that prevents the denominator from being zero, and $A_{\mathrm{mush}}$ is the mushy zone constant, which is related to the porosity of the porous medium.

In the enthalpy–porosity method, the solid skeleton in the porous medium imposes resistance to liquid-phase flow, thereby simulating the phase change process. The mushy zone constant $A_{\mathrm{mush}}$ is a key parameter that quantifies this flow resistance within the mushy region. ANSYS Fluent recommends $A_{\mathrm{mush}}$ value in the range from ${10}^4$ to ${10}^7$. When $A_{\mathrm{mush}}$ is relatively small, the fluid in the solidifying region can still maintain a certain velocity, representing a slower solidification rate. In contrast, a larger $A_{\mathrm{mush}}$ rapidly suppresses the fluid velocity in the solidifying region, corresponding to a faster solidification rate [28]. During the droplet impact-freezing process, the solidification rate is governed by the supercooling degree. Therefore, the value of $A_{\mathrm{mush}}$ varies with the supercooling degree. The $A_{\mathrm{mush}}$ values selected in this paper are shown in

Table 1. Mushy zone constant values.

$\mathit{\Delta }\mathit{T}(\mathbf{K})$	5	10	15	20	25	30	35
$A_{\mathrm{mush}}$	$1.0\times {10}^4$	$2.5\times {10}^4$	$5.0\times {10}^4$	$1.0\times {10}^5$	$5.0\times {10}^5$	$1.0\times {10}^6$	$1.0\times {10}^7$

.

Upon impacting the surface, a room-temperature droplet undergoes distinct phases: spreading, retraction, oscillation, and stabilization [29]. However, the impact dynamics of supercooled droplets involve coupled fluid flow and phase change. Compared to their room-temperature counterparts, supercooled droplets simultaneously experience supercooling, nucleation, recalescence, and freezing stages. Impact significantly enhances the nucleation probability of supercooled droplets, with the nucleation rate substantially exceeding the droplet spreading rate [30].

Therefore, this study assumes that the nucleation and recalescence stages complete instantaneously upon droplet impact. Specifically, the supercooling effect is incorporated into the initial conditions by modifying the initial volume and associated physical parameters. Salinity effects on supercooling are excluded to ensure consistent volume conditions for subsequent salinity investigations. The ice phase fractions corresponding to different supercooling degrees are listed in

Table 2. Ice phase ratio after the recalescence stage.

$\mathbf{\Delta }\mathit{T}$	Salinity	Ice Phase Ratio (%)
15 K	$20‰$	18.2
15 K	$35‰$	24.3
15 K	$50‰$	30.4
20 K	$20‰$	17.8
20 K	$35‰$	23.7
20 K	$50‰$	29.6
25 K	$20‰$	17.3
25 K	$35‰$	23.0
25 K	$50‰$	28.8

. Other relevant physical parameters were updated using Equation (11).

$$L_{\mathrm{mix}}=(1-{\gamma }_i)L_{sw};c_{\mathrm{mix}}=c_{sw}(1-{\gamma }_i)+c_i{\gamma }_i;k_{\mathrm{mix}}=k_{sw}(1-{\gamma }_i)+k_i{\gamma }_i$$

(11)

2.3. Dynamic Contact Angle Model

One of the most important steps in the simulation process is modeling the contact angle of saline droplets. A common approach is to set the contact angle as a static value. However, this approach is restricted to idealized smooth surfaces.

As illustrated in Figure 3, the droplet spreads to the right during its motion because of its initial kinetic energy, while contact angle hysteresis, caused by factors such as surface roughness, resists this spreading [28]. Consequently, the contact angle between the droplet and the surface changes dynamically. To capture this feature more accurately, a dynamic contact angle model is introduced in this paper. Figure 3 shows the schematic diagram of contact angle hysteresis. ${\theta }_{\mathrm{adv}}$ denotes the advancing contact angle, and ${\theta }_{\mathrm{rec}}$ denotes the receding contact angle.

Hoffman [31] proposed the Hoffman function to describe the dynamic contact angle.

$$f_{\mathrm{Hoff}}=\arccos \left\{1-2tanh\left[5.16{\left({\displaystyle \frac{x}{1+1.31x^{0.99}}}\right)}^{0.706}\right]\right\}$$

(12)

Based on the above studies, Kistler further improved the contact angle model and introduced the contact angle hysteresis effect. The dynamic contact angle can be expressed as:

$${\theta }_d=f_{\mathrm{Hoff}}[Ca+f_{\mathrm{Hoff}}^{-1}({\theta }_{\mathrm{eq}})]$$

(13)

where $Ca=\mu U_{\mathrm{CL}}/\sigma$ is the capillary number, $U_{\mathrm{CL}}$ is the contact line velocity, and ${\theta }_{\mathrm{eq}}$ has different values for spreading and retraction processes.

$${\theta }_{\mathrm{eq}}=\left\{\begin{array}{lll}{\theta }_{\mathrm{adv}},\hfill & \hspace{1em}\hfill & U_{\mathrm{cL}}>0\hfill \\ {\theta }_{\mathrm{rec}},\hfill & \hspace{1em}\hfill & U_{\mathrm{cL}}<0\hfill \end{array}\right.$$

(14)

The Kistler model is expressed as the following inverse function.

$$f_{\mathrm{Hoff}}^{-1}({\theta }_d)-f_{\mathrm{Hoff}}^{-1}({\theta }_{\mathrm{eq}})=Ca$$

(15)

2.4. Supercooled Saline Droplets Impact-Freezing Analysis Process

As illustrated in Figure 4, the saline droplet impact analysis process comprises three sequential stages: geometric modeling, numerical solution, and post-processing. Initially, a two-dimensional axisymmetric model is established based on the boundary conditions and assumptions specified in Section 3.1. Subsequently, the computational domain is discretized, and a saline droplet is numerically generated. At each time step, the governing equations (Equations (2), (3) and (5)) are solved iteratively, with updates to the gas–liquid interface, surface tension, and dynamic contact angle. Finally, corresponding cloud maps and numerical values are output at the monitoring interface for visualization and quantitative analysis.

3. Computational Model and Model Validation

3.1. Boundary Conditions and Parameter Settings

The process of supercooled saline droplets impacting and freezing on a cold surface involves complex fluid dynamics and phase transitions. To facilitate modeling and reduce computational complexity, the following assumptions are made:

Assumption 1. 

The entire process is assumed to be axisymmetric with respect to the plane perpendicular to the impact surface, implying that the droplet geometry and motion are symmetric about the central axis.

Assumption 2. 

It is assumed that the droplets are regarded as a continuous fluid medium during the impact process, thus neglecting the influence of microscopic bubbles and impurities inside the droplets and simplifying the hydrodynamic analysis.

Assumption 3. 

It is assumed that the recalescence stage is completed instantaneously upon impact with the surface, and no secondary recalescence is considered during the subsequent impact-freezing process.

Assumption 4. 

In the calculation process, the influence of salt rejection on the physical properties of the droplet is not considered. Accordingly, the physical properties of saline droplets are treated as constant throughout the impact-freezing process in this study.

When a droplet impinges vertically on a horizontal surface, it usually presents a diffuse state, with its internal flow field circumferentially uniform. In this case, it is desirable to use a two-dimensional axisymmetric model to simulate the dynamic behavior of the impinging droplet, as illustrated in Figure 5. This approach enables focused analysis of the critical flow region, improving computational efficiency and significantly reducing the computational cost compared to full three-dimensional simulations.

As shown in Figure 5, the cold surface is defined as a no-slip wall, the left boundary is set as the axis of rotational symmetry, and the right and upper sides are set as the pressure outlets. The width and height of the computational domain are both $12 \mathrm{mm}$, and the height from the top of the droplet to the lower wall is set as the diameter of the droplet $D_0$, and the initial velocity of the bottom of the droplet when it first touches the wall is $U_0$.

In this study, the droplet is tangent to the surface at the initial moment, i.e., the morphology change in the droplet due to gravity is not considered. During the freezing process, impact-induced vibrations significantly enhance nucleation, leading to its occurrence as the droplet first contacts the cold surface. Since the diffusion velocity of recalescence is much higher than that of the contact line, nucleation and recalescence are completed within a very short time after the onset of impact (Assumption 3), and the initial parameters need to be modified by Equation (11). Furthermore, the droplets investigated in this study are small and experience the intense impact process within a few milliseconds. Therefore, to simplify the modeling of saline droplet impact freezing, only the initial physical property parameters caused by salinity are considered, while the further phenomenon of salt rejection is neglected (Assumption 4). Similar simplifications have also been employed in previous studies on the freezing of sessile saline droplets [32,33].

In previous numerical studies, most physical property parameters are provided in the form of tables, typically derived from experimental measurements conducted decades ago. These datasets often cover only a limited range of temperatures or salinities, and the rest needed to be obtained by interpolation or extrapolation. While many saline properties resemble freshwater properties and can be described as functions of temperature and pressure, the presence of sea salt requires salinity to be incorporated into the correlation functions. Consequently, relevant physical parameters for saline droplets are functions of temperature, salinity, and pressure. The key physical parameters examined in this study include density, dynamic viscosity, surface tension, freezing point, latent heat, specific heat capacity, and thermal conductivity. Specifically, these parameters are calculated using the following equations [34,35].

In this study, the pressure is taken as standard atmospheric pressure, i.e., $P_0=0.1 \mathrm{Mpa}$. The salinity $S$ was taken as 20‰, 35‰, and 50‰, which represent 20 g, 35 g, and 50 g of salt dissolved per kilogram of water, respectively. The density of the saline droplet is defined by the following equation.

$$\begin{array}{l}{\rho }_{sw}(T,S_1,P_0)=(a_1+a_{2}T+a_3{T}^2+a_4{T}^3+a_5{T}^4)+\\ \left(b_1{S}_1+b_2{S}_{1}T+b_3{S}_1{T}^2+b_4{S}_1{T}^3+b_5{S}_1^2{T}^2\right)\end{array}$$

(16)

where $S_1=S/1000$, other parameters are given in

Table 3. Parameter settings for density equation.

Parameter (a)	Value	Parameter (b)	Value
$a_1$	$9.999\times {10}^2$	$b_1$	$8.02\times {10}^2$
$a_2$	$2.034\times {10}^{-2}$	$b_2$	$-2.001$
$a_3$	$-6.162\times {10}^{-3}$	$b_3$	$1.677\times {10}^{-2}$
$a_4$	$2.261\times {10}^{-5}$	$b_4$	$-3.06\times {10}^{-5}$
$a_5$	$-4.657\times {10}^{-8}$	$b_5$	$-1.613\times {10}^{-5}$

.

The dynamic viscosity of saline droplets can be defined by the following equation:

$${\mu }_{sw}={\mu }_w\left(1+A{S}_1+B{S}_1^2\right)$$

(17)

where ${\mu }_w$ is the dynamic viscosity of freshwater droplets, and other parameters are given in

Table 4. Parameter settings for dynamic viscosity and specific heat equations.

Parameters	Value
A	$1.541+1.998\times {10}^{-2}t-9.52\times {10}^{-5}{t}^2$
B	$7.974-7.561\times {10}^{-2}t+4.724\times {10}^{-4}{t}^2$
C	$5.328-9.76\times {10}^{-2}S+4.04\times {10}^{-4}{S}^2$
D	$-6.913\times {10}^{-3}+7.351\times {10}^{-4}S-3.15\times {10}^{-6}{S}^2$
E	$9.6\times {10}^{-6}-1.927\times {10}^{-6}S+8.23\times {10}^{-9}{S}^2$
F	$2.5\times {10}^{-9}+1.666\times {10}^{-9}S-7.125\times {10}^{-12}{S}^2$

.

The surface tension of saline droplets can be defined by the following equation.

$$\left\{\begin{array}{cc}{\sigma }_{sw}={\sigma }_w(1+3.766\times {10}^{-4}S+2.347\times {10}^{-6}ST)\hfill & \hfill \\ {\sigma }_w=235.8{\left(1-{\displaystyle \frac{T+273.15}{647.096}}\right)}^{1.256}\left[1-0.625\left(1-{\displaystyle \frac{T+273.15}{647.096}}\right)\right]\hfill & \hfill \end{array}\right.$$

(18)

where ${\sigma }_w$ is the surface tension of freshwater droplets.

The freezing point of saline droplets can be defined by the following equation.

$$T_f=-0.0137-0.05199S-0.00007225S^2$$

(19)

The latent heat, specific heat and thermal conductivity of saline droplets can be defined by the following equations.

$$L_{sw}=4.184\left(\begin{array}{c}79.68-0.505t-0.0273S_1+\\ 4.3115{\displaystyle \frac{S_1}{T}}+0.0008S_{1}T-0.0009T^2\end{array}\right)$$

(20)

$$c_{sw}(T,S,P_0)=C+D(T+273.15)+E{(T+273.15)}^2+F{(T+273.15)}^3$$

(21)

$$\begin{array}{l}{k}_{sw}(t,S,P_0)={\displaystyle \frac{1}{0.00022\times S+1}}\times (0.797015\times T^{\ast -0.194}-\\ 0.251242\times T^{\ast -4.717}+0.096437\times T^{\ast -6.385}-0.032696\times T^{\ast -2.134})\end{array}$$

(22)

where the parameters for specific heat equation are given in Table 4, and $T^{\ast }$ is defined as a dimensionless constant.

$$T^{\ast }={\displaystyle \frac{T+273.15}{300}}$$

(23)

In summary, the physical parameters of freshwater droplets, saline droplets, and ice taken in this study are shown in

Table 5. Physical parameters of saline droplets.

Salinity	${\mathit{T}}_{\mathbf{f}}$ $(\mathbf{K})$	${\mathit{\rho }}_{\mathbf{sw}}$ $({\mathbf{kg}/\mathbf{m}}^3)$	${\mathit{\mu }}_{\mathbf{sw}}$ $(\mathsf{\mu }\mathbf{Pa}\cdot \mathbf{s})$	${\mathit{\sigma }}_{\mathbf{sw}}$ $(\mathbf{mN}/\mathbf{m})$	${\mathit{L}}_{\mathbf{sw}}$ $(\mathbf{kJ}/\mathbf{kg})$	${\mathit{c}}_{\mathbf{sw}}$ $[\mathbf{kJ}/(\mathbf{kg}\cdot \mathbf{K})]$	${\mathit{k}}_{\mathbf{sw}}$ $[\mathbf{W}/(\mathbf{m}\cdot \mathbf{K})]$
20‰	271.92	1015.95	1851.3	76.21	335.328	4.079	0.554
35‰	271.08	1028.04	1903.1	76.63	337.095	3.989	0.552
50‰	270.21	1040.18	1960.7	77.05	338.926	3.904	0.550

and

Table 6. Physical parameters of freshwater droplets and ice.

Substance	${\mathit{T}}_{\mathbf{f}}$ $(\mathbf{K})$	$\mathit{\rho }$ $({\mathbf{kg}/\mathbf{m}}^{\mathbf{3}})$	${\mathit{\mu }}_{\mathbf{w}}$ $(\mathbf{\mu }\mathbf{Pa}\mathit{\cdot }\mathbf{s})$	${\mathit{\sigma }}_{\mathbf{w}}$ $(\mathbf{mN}/\mathbf{m})$	${\mathit{L}}_{\mathbf{w}}$ $(\mathbf{kJ}/\mathbf{kg})$	$\mathit{c}$ $[\mathbf{kJ}/(\mathbf{kg}\cdot \mathbf{K})]$	$\mathit{k}$ $[\mathbf{W}/(\mathbf{m}\cdot \mathbf{K})]$
Freshwater	273.15	999.80	1791.1	75.65	333.400	4.220	0.556
Ice	/	916.70	/	/	/	2.100	2.160

.

3.2. Grid Independence Validation

In order to validate that the grid size does not affect the computational results, three sets of square grids with different sizes: $20 \mathsf{\mu }\mathrm{m}\times 20 \mathsf{\mu }\mathrm{m}$, $10 \mathsf{\mu }\mathrm{m}\times 10 \mathsf{\mu }\mathrm{m}$ and $5 \mathsf{\mu }\mathrm{m}\times 5 \mathsf{\mu }\mathrm{m}$ are computed in this paper. The spreading factor (defined as the ratio of the droplet spreading diameter to its initial diameter) served as the validation criterion. Based on the working conditions in the literature [36], the validation settings in this section are $D_0=2.45 \mathrm{mm}$, $U_0=1.64 \mathrm{m}/\mathrm{s}$, ${\theta }_{\mathrm{adv}}=105°$, ${\theta }_{\mathrm{rec}}=95°$. The spreading factors of the impact process obtained by using three sets of grids are shown in Figure 6.

In this study, the transient calculation method is adopted, the pressure solver is pressure-based, and the coupling mode of pressure and velocity is SIMPLE. This algorithm is suitable for most flow problems, offering lower computational costs and improved convergence. The least squares cell-based method is used for the spatial discrete gradient, whereas the second-order upwind scheme is used for the momentum and energy control equations. The discrete format of the pressure governing equation is PRESTO!. The volume fraction discrete format is the modified HRIC format. This algorithm is suitable for most flow problems, offering lower computational costs and improved convergence. The discrete format of the time item is in first-order implicit format, and the residual control is set to ${10}^{-6}$.

During the calculation process, a variable time step is used. The calculation duration is set to total time, the Courant number is set to 0.1, the minimum time step is set to ${10}^{-7}$, and the maximum time step is set to ${10}^{-5}$. Moreover, the maximum and minimum step change factors are set to 1.2 and 0.8, respectively, to ensure the stability of the calculation. The time step in the actual calculation fluctuates between ${10}^{-7}$ and ${10}^{-5}$.

From Figure 6, it can be clearly seen that the curves of the spreading factor gradually overlap as the grid size decreases. Notably, the curve corresponding to the coarsest grid shows a pronounced deviation between $2 \mathrm{ms}$ and $4 \mathrm{ms}$. The difference between the two grid sizes of $10 \mathsf{\mu }\mathrm{m}\times 10 \mathsf{\mu }\mathrm{m}$ and $5 \mathsf{\mu }\mathrm{m}\times 5 \mathsf{\mu }\mathrm{m}$ is very small, demonstrating that the numerical model has reached stability. Considering the accuracy and the time required for the calculation, the grid size of $10 \mathsf{\mu }\mathrm{m}\times 10 \mathsf{\mu }\mathrm{m}$ is used for the subsequent simulations.

3.3. Accuracy Validation

In order to ensure the accuracy of the numerical method used in this study, we compared the computational results with the existing experimental results [7]. Figure 7 demonstrates the results of the comparison. The static contact angle in the experiment is $135.8°$, and the salinity is $35‰$. The other settings are as follows: $D_0=2.46 \mathrm{mm}$, $We=40$, with the droplet and surface temperature set to $298.15 \mathrm{K}$ and $263.15 \mathrm{K}$, respectively.

The results indicate that the simulated morphology evolution and the overall trend of spreading factor curve are in good agreement with the experimental data. In the spreading stage, the simulation results are basically consistent with the test results, but there are some differences in the retraction stage. Compared with the simulation results, the maximum error is $5.1\%$, where the experimental value is 1.96 and the simulated value is 2.06 at $4.5 \mathrm{ms}$. The simulation results show excellent agreement with the reference data, with a root mean square error (RMSE) of 0.09, corresponding to only 3–9% of the typical spreading factor range.

Figure 7b presents a comparison of droplet morphologies. At the same moment, the simulated and experimental droplets exhibit similar major characteristics. The experimental droplet underwent free fall before impacting the cold surface, resulting in deformation before contact. Therefore, slight discrepancies are observed at the early stage of the spreading phase ($2 \mathrm{ms}$). Based on the above analysis, the model established in this paper is accurate and can be used to simulate the impact-freezing process of saline droplets.

4. Results and Discussion

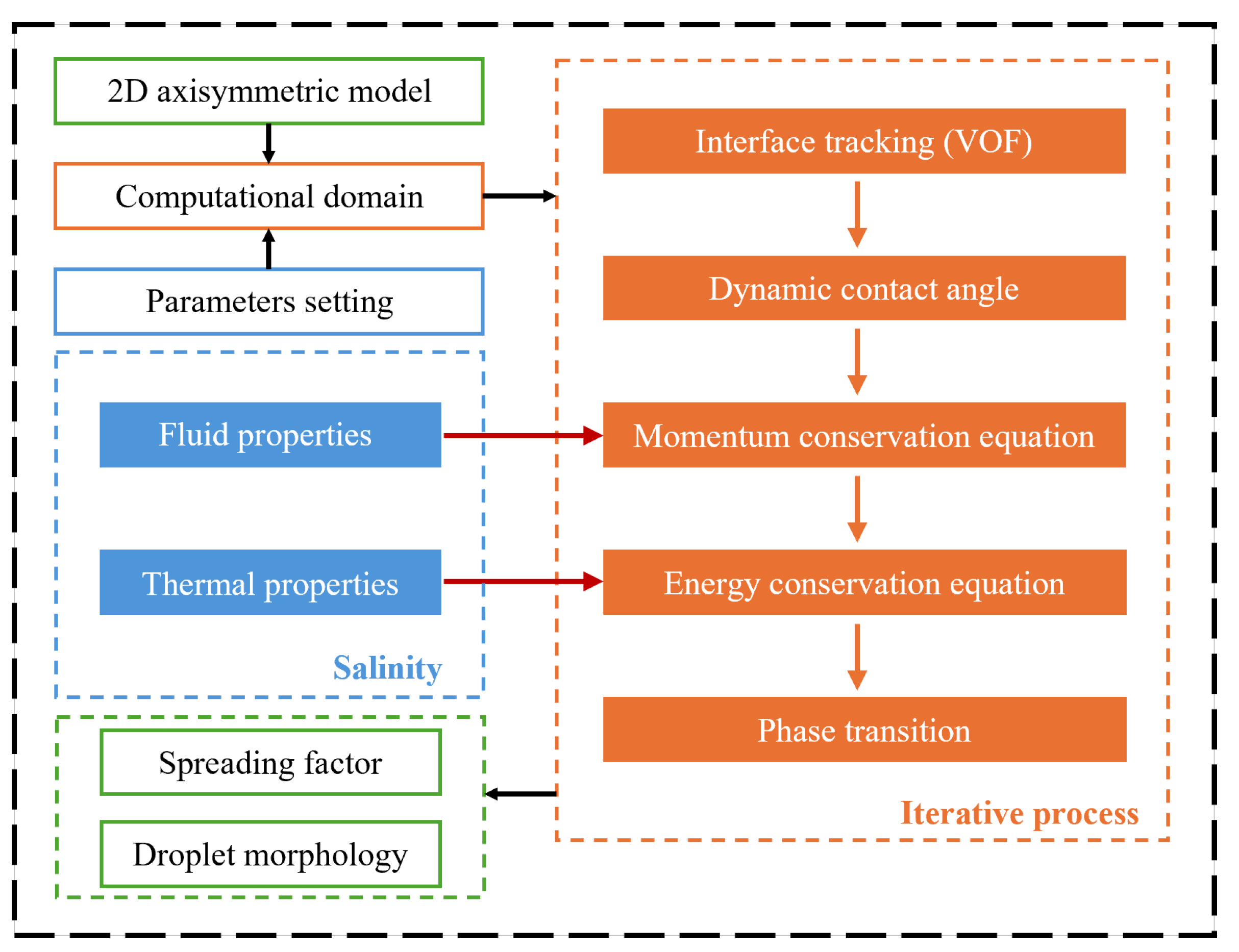
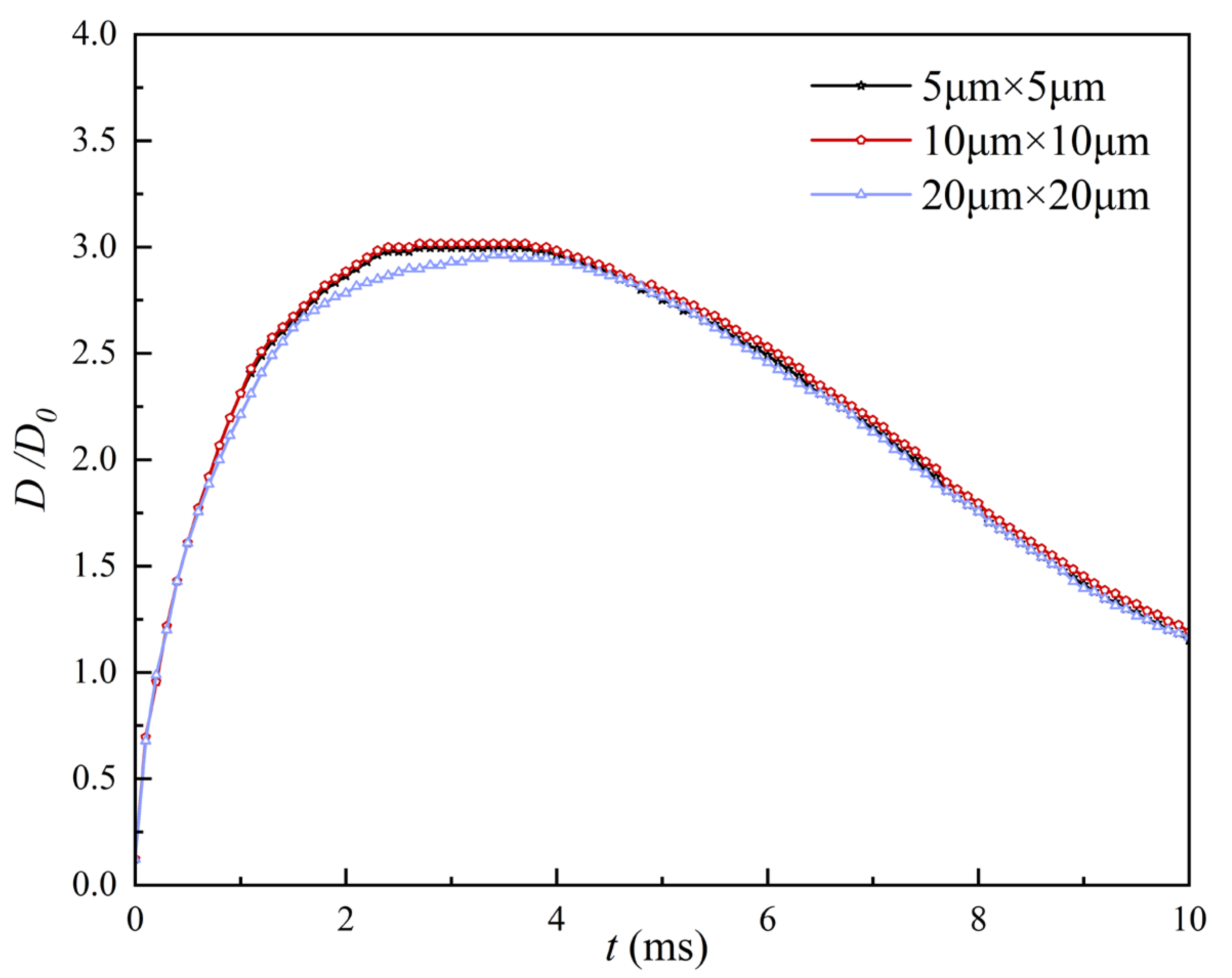
4.1. Effects of Salinity and Supercooling Degree on the Droplet Impact-Freezing Process

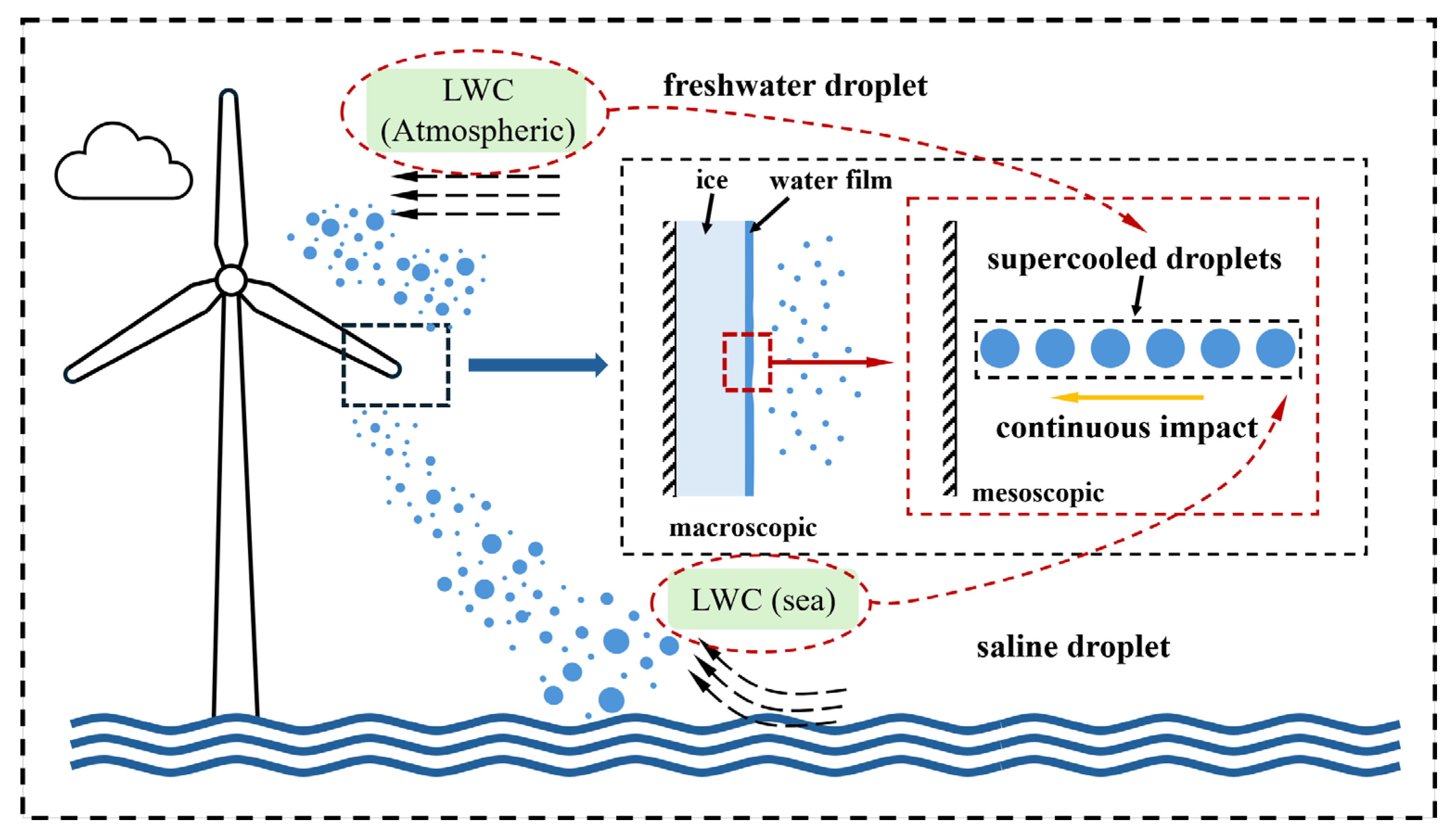
The salinity levels in global oceans exhibit significant spatial variability, with distinct differences observed even within specific regions of a single ocean. As salinity is a key factor affecting the freezing behavior of water droplets, this study investigates the impact-freezing characteristics of saline droplets with varying salinities under different conditions.

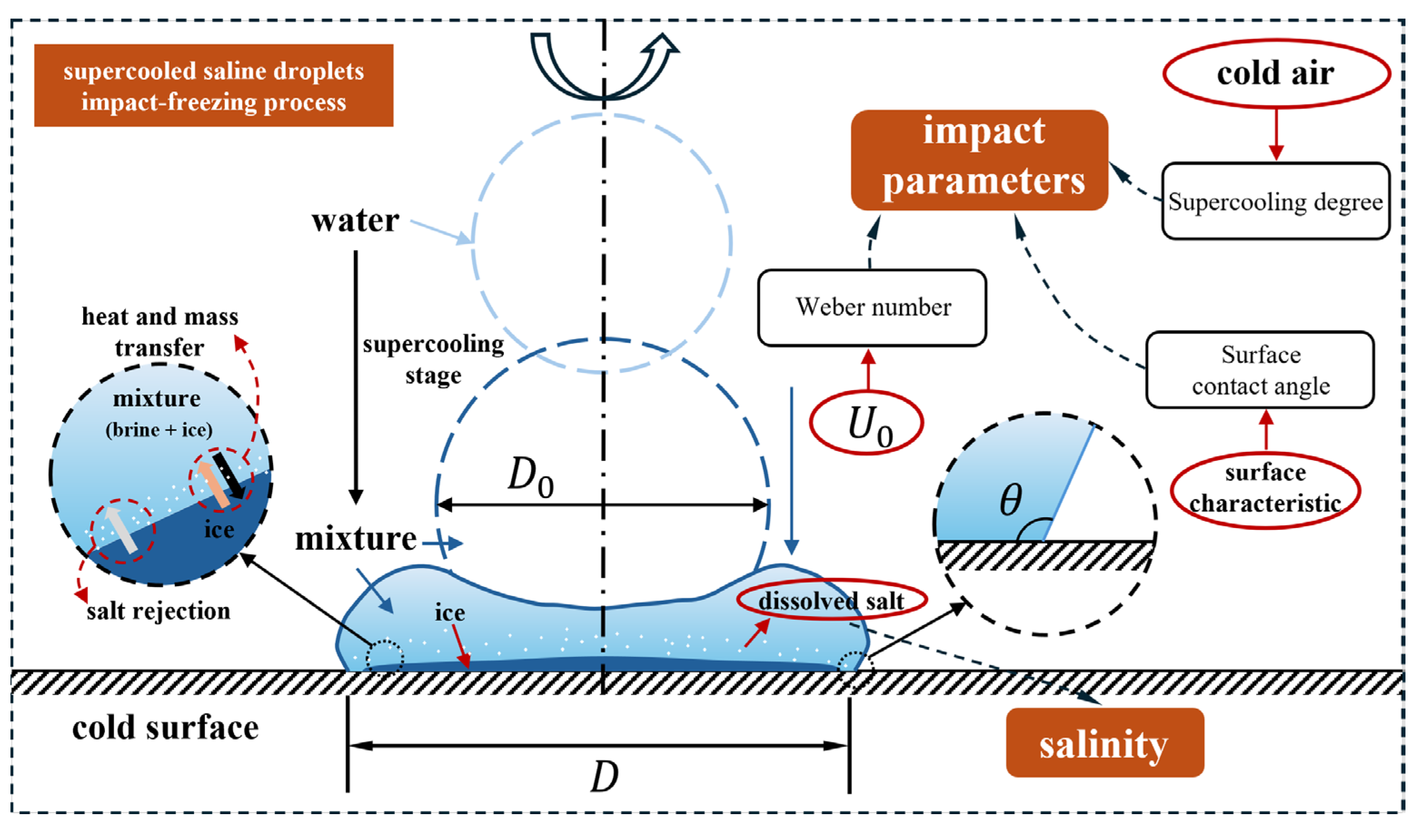
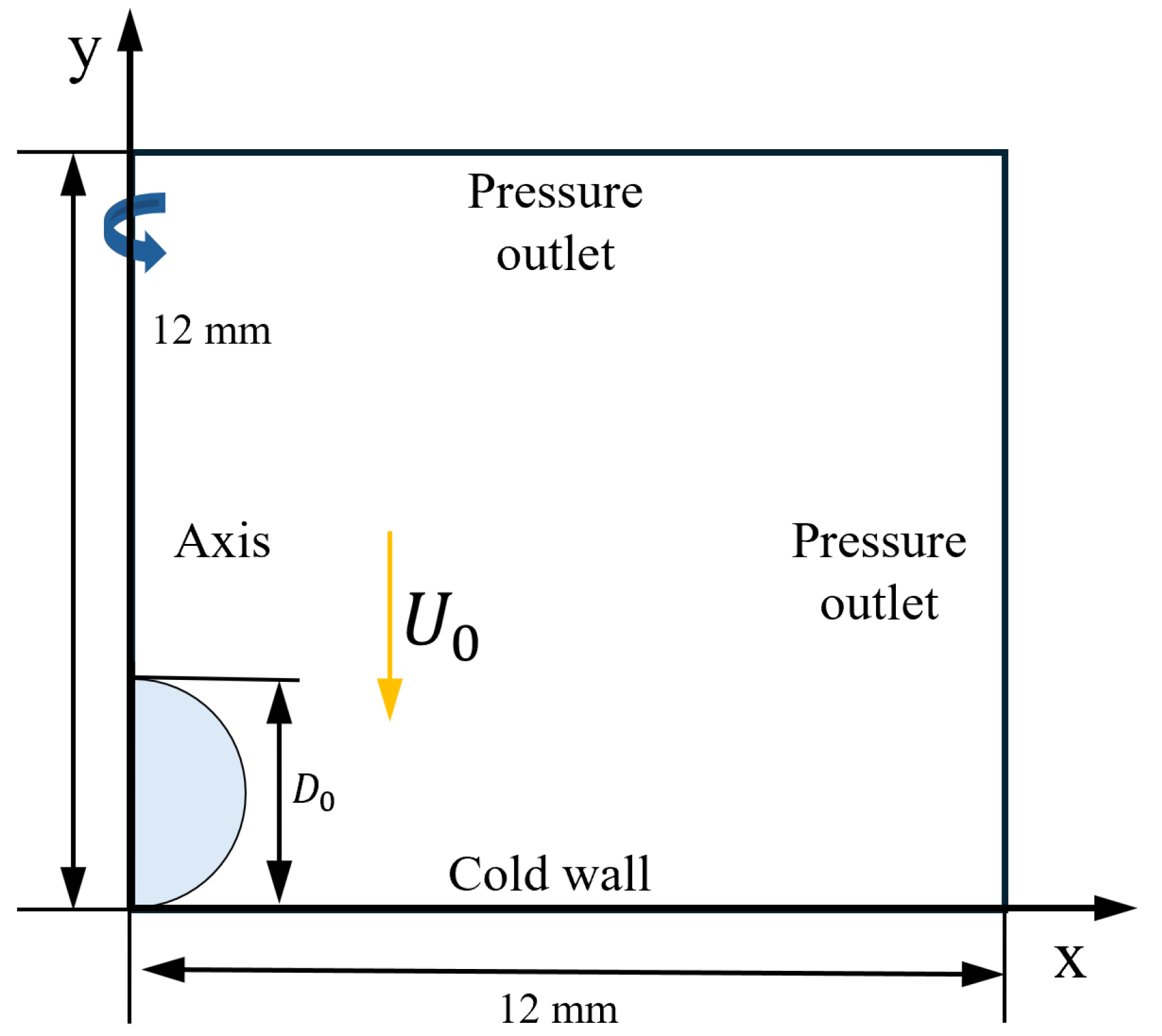
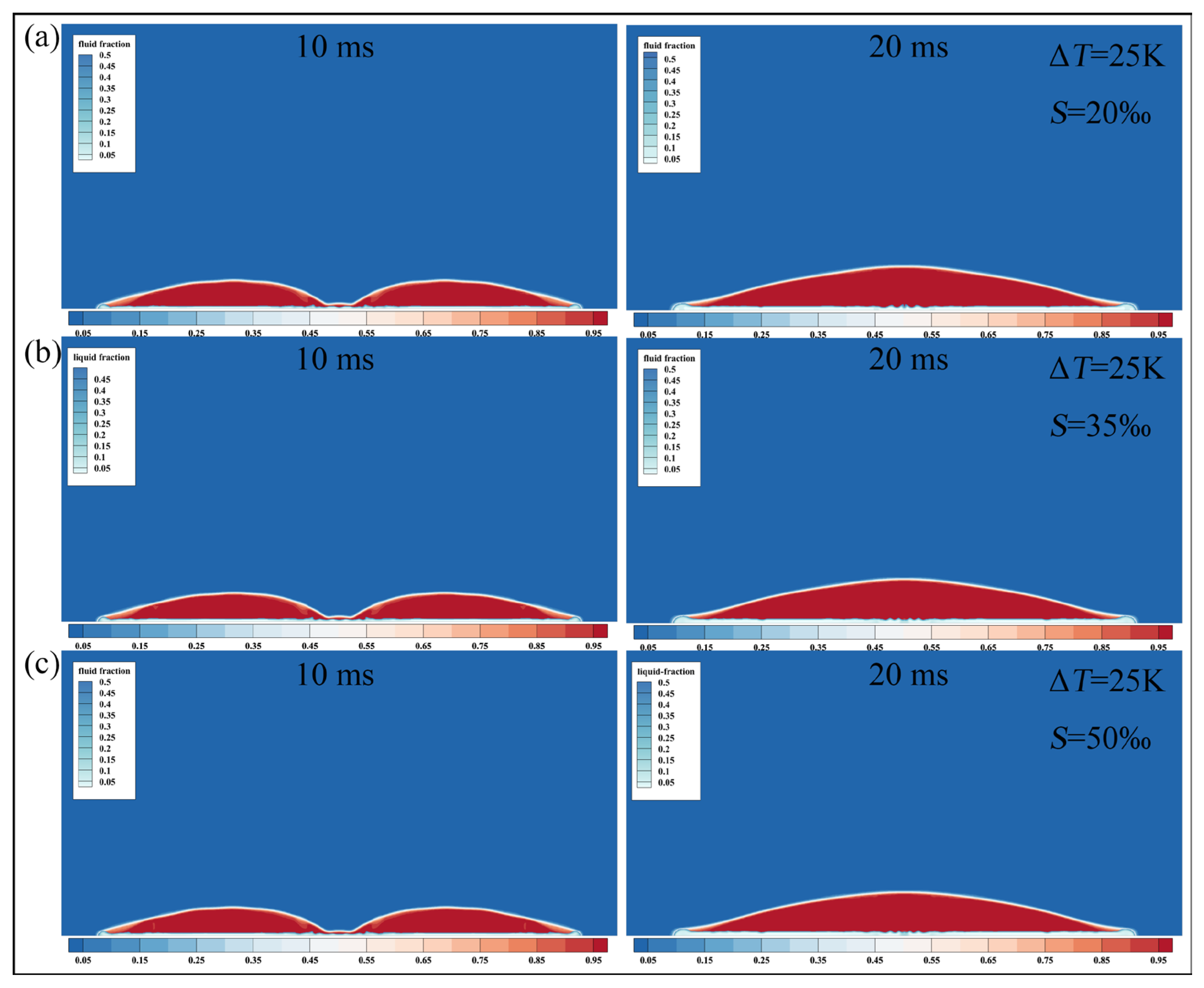
The working conditions in this section are hydrophobic surfaces, ${\theta }_{\mathrm{adv}}=105°$, ${\theta }_{\mathrm{rec}}=85°$. The droplets have Weber number of 60, salinity of $20‰$, $35‰$, and $50‰$, and a size of $10 \mathsf{\mu }\mathrm{L}$ (radius of $1.34 \mathrm{mm}$). Numerical simulations of droplets with supercooling degrees of $15 \mathrm{K}$, $20 \mathrm{K}$, and $25 \mathrm{K}$ are performed to investigate the effect of supercooling degrees on the impact-freezing process of the droplets by comparing their spreading factors and relative deviation.

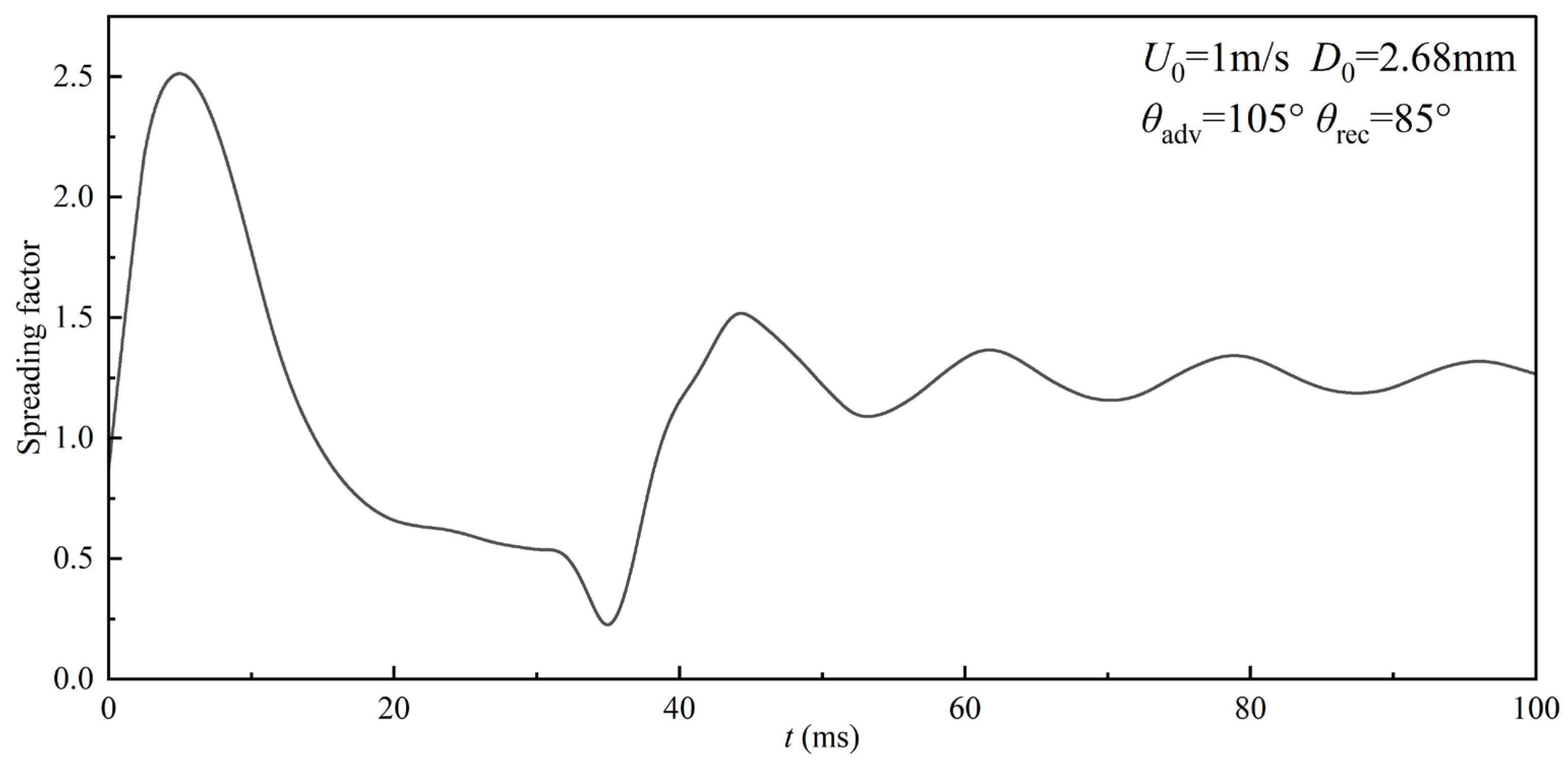
Figure 8 illustrates the temporal evolution of the spreading factor for a room-temperature droplet. The impact process comprises four stages: spreading, retraction, oscillation, and stabilization. Initial kinetic and gravitational energies drive rapid droplet spreading, while partial energy dissipates through wall adhesion and surface roughness. The remaining energy is converted into surface and internal energies. Once the kinetic energy is depleted, the spreading ceases, marking the maximum spreading extent. At this point ($5 \mathrm{ms}$), the droplet assumes a disk-like shape, characterized by a thinner center and a thicker rim, along with fluctuating contact angles. During the retraction phase (from $5 \mathrm{ms}$ to $35 \mathrm{ms}$), surface tension becomes dominant, converting surface energy back into kinetic energy. This initiates periodic spreading-retraction oscillations, which continue until the system reaches equilibrium.

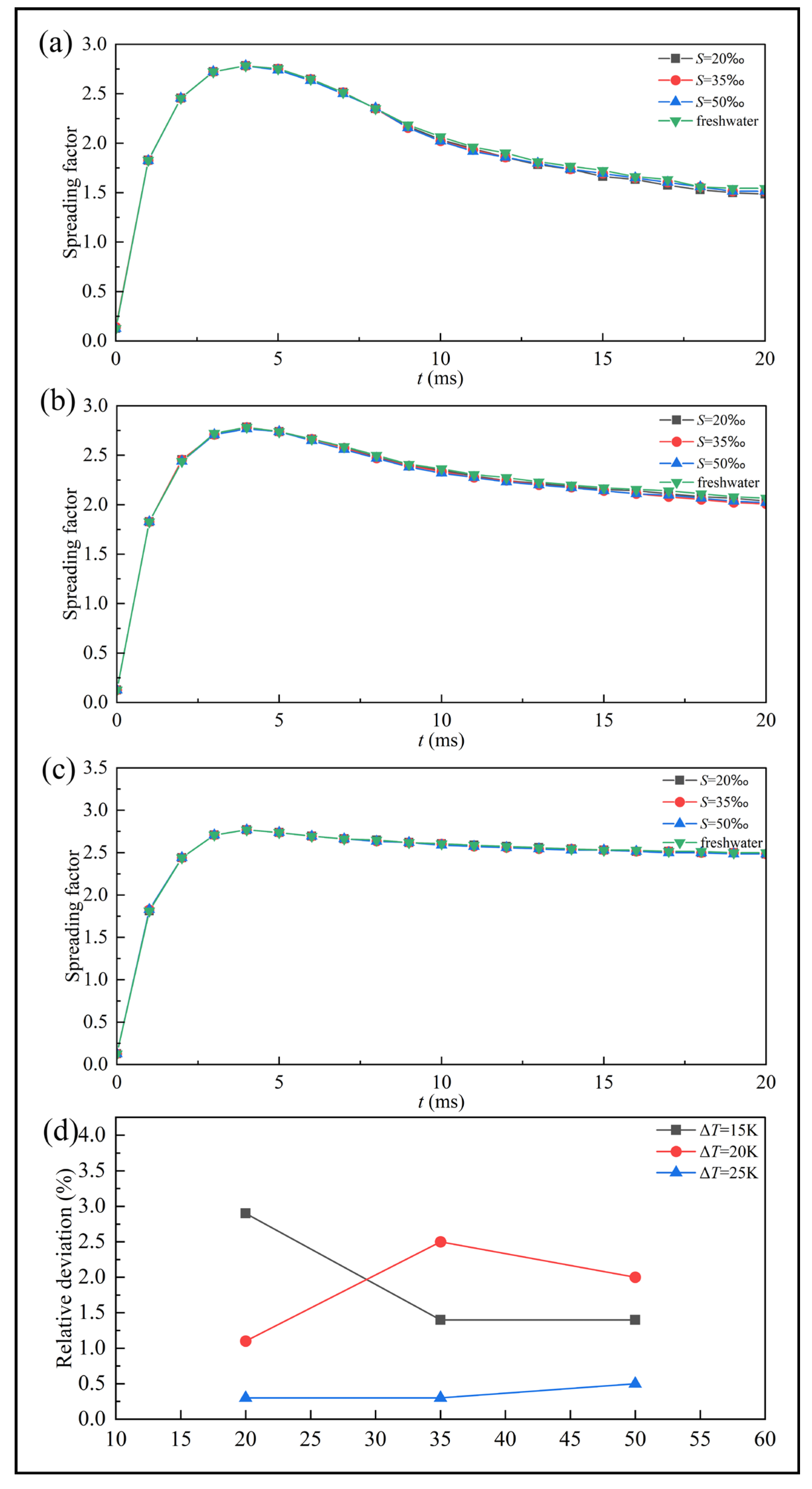
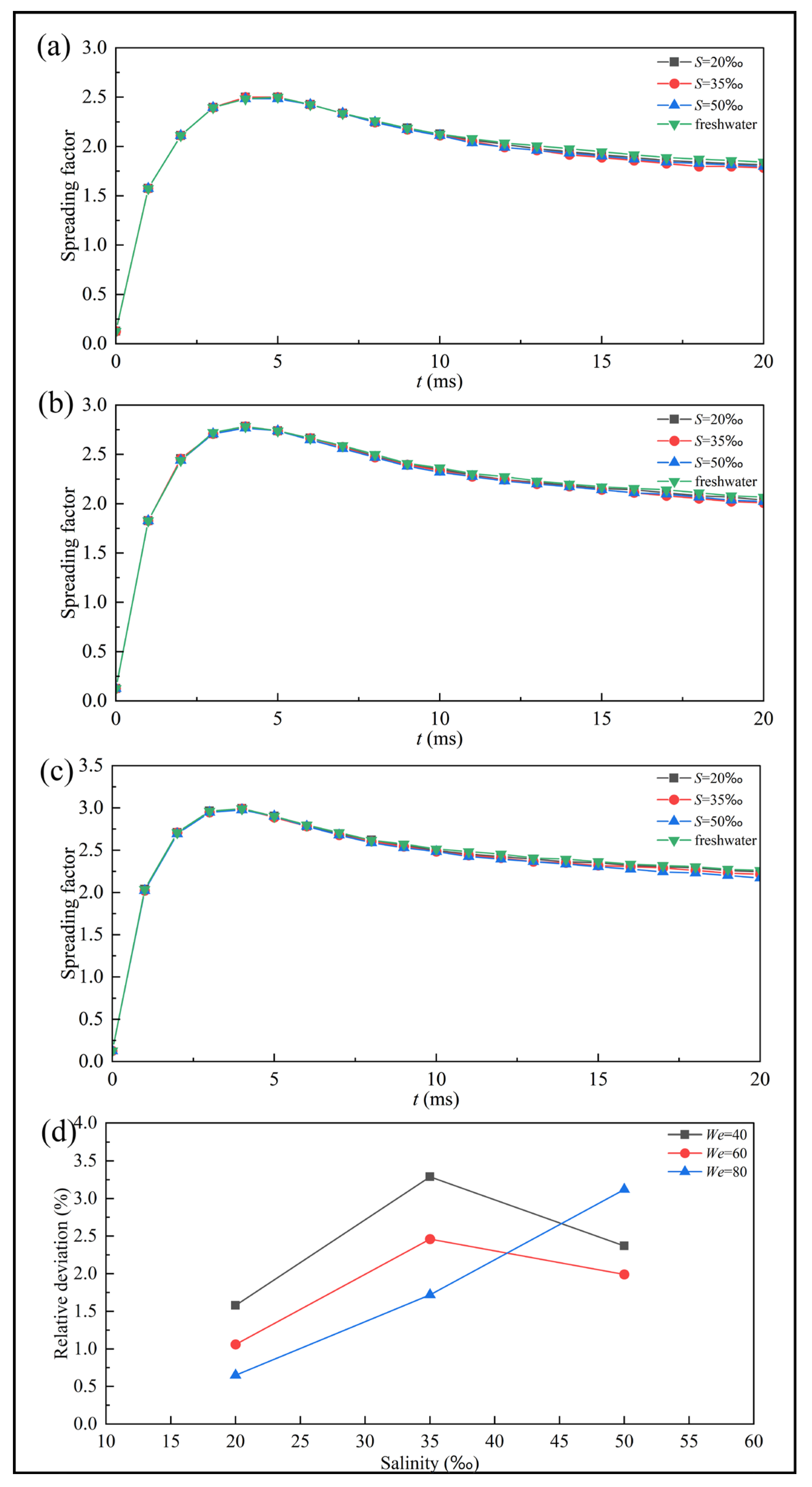
Figure 9 presents the spreading factor curves of freshwater and saline droplets under different supercooling degrees. Distinct differences are observed between supercooled and room-temperature droplets during the retraction stage. At room temperature, droplets retract rapidly after reaching their maximum spreading state. In contrast, supercooled droplets exhibit a gradual decrease in spreading factor, and this retraction trend becomes progressively weaker as the supercooling degree increases. When the supercooling degree reaches $25 \mathrm{K}$, the droplets experience almost no noticeable retraction and transition directly into the freezing stabilization stage. Throughout the entire impact-freezing process, the spreading factors of saline droplets remain consistently lower than those of freshwater droplets, particularly during the retraction and stabilization stage.

Figure 9d shows the maximum relative deviations of the spreading factor between saline and pure water droplets at different supercooling degrees. These peak values consistently occur at $20 \mathrm{ms}$, a stage during which the spreading factor is relatively small. Consequently, even minor disturbances caused by variations in physics properties can lead to noticeable deviations. Moreover, as the supercooling degree increases, the salinity corresponding to the peak relative deviation also shifts, changing from a lower salinity ($20‰$) at $15 \mathrm{K}$ to a higher salinity ($50‰$) at $25 \mathrm{K}$. And the peak relative deviation decreased from 2.39% to 0.5%, a decrease of 82.9%. This indicates that supercooling alters the mechanism by which salinity influences droplet impact-freezing process. The effect of salinity on the impact-freezing process is twofold. On one hand, salinity modifies fluid properties. For example, increasing viscosity enhances viscous dissipation and suppresses droplet retraction. On the other hand, salinity affects the solidification rate, which in turn influences droplet motion. Consequently, the retraction behavior of saline droplets is primarily governed by the competition between impact dynamics and solidification. Supercooling acts as one of the key parameters that determines which of these effects dominates.

An increase in supercooling degree leads to earlier freezing at the droplet base, slightly reducing the maximum spreading factor. From

Table 7. Maximum spreading factor under different supercooling degrees.

Temperature	$\mathbf{\Delta }\mathit{T}=15 \mathbf{K}$	$\mathbf{\Delta }\mathit{T}=20 \mathbf{K}$	$\mathbf{\Delta }\mathit{T}=25 \mathbf{K}$
$D/D_0$	2.79	2.78	2.76

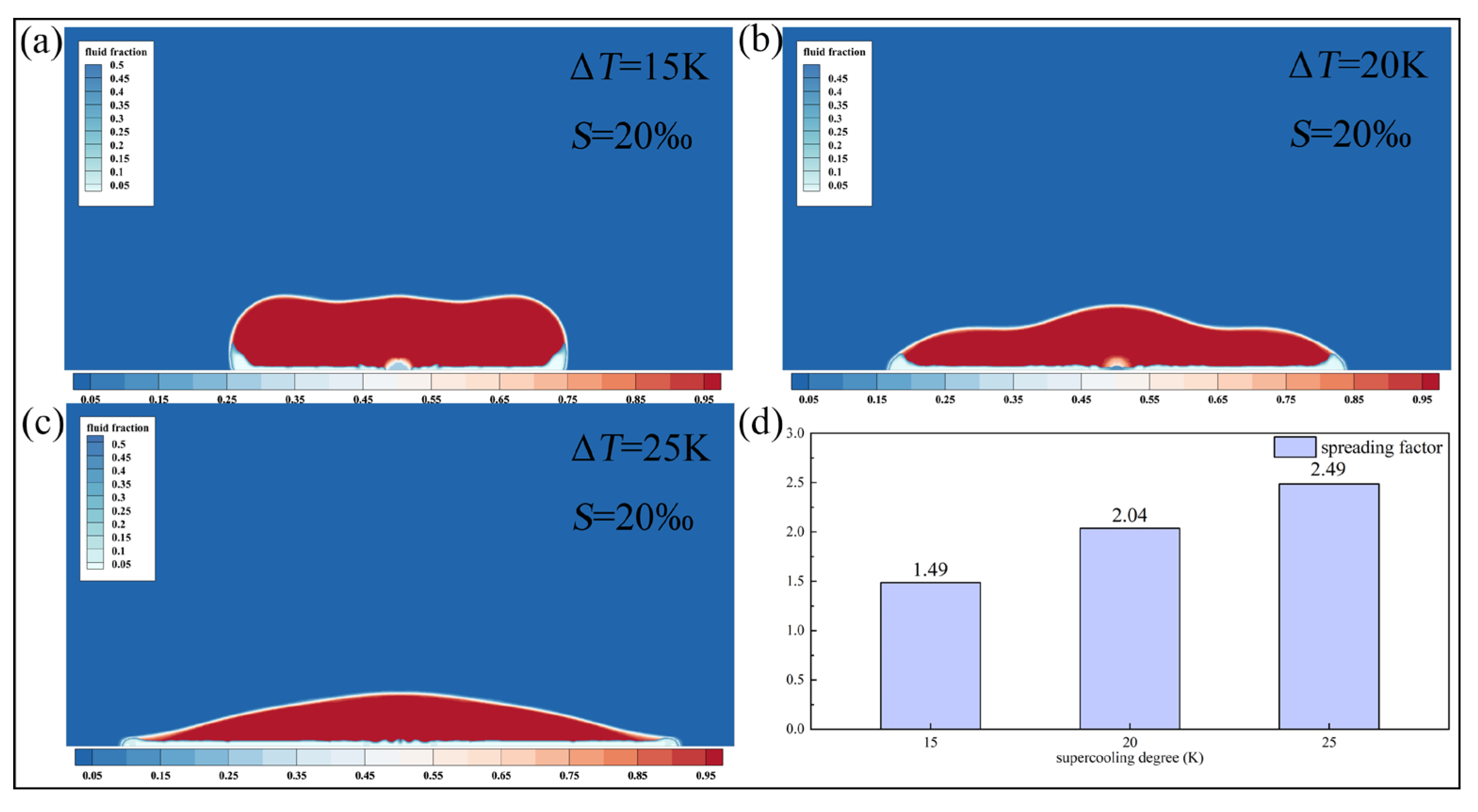
, the maximum spreading factor decreases slightly from 2.79 to 2.76 as the supercooling degree increases, corresponding to a reduction of 1.1%. Figure 10 presents the morphologies of saline droplets with a salinity of $20‰$ at $20 \mathrm{ms}$ under different supercooling conditions, along with their corresponding spreading factors. As the supercooling degree increases from $15 \mathrm{K}$ to $25 \mathrm{K}$, the spreading factor rises from 1.49 to 2.49, representing a 67.1% increase. At $20 \mathrm{K}$ and $25 \mathrm{K}$, the droplets remain in a spreading state at this moment, indicating that higher supercooling degree enhances heat transfer between the droplet and the cold surface, thereby accelerating the solidification process. Meanwhile, with increasing supercooling degree, the phase-change driving force becomes more pronounced during the retraction stage. As a result, droplets with higher salinity, which exhibit delayed freezing characteristics, display larger relative deviations in spreading factor compared with freshwater droplets.

At lower supercooling degree ($15 \mathrm{K}$), droplet dynamics are primarily governed by hydrodynamic effects. Low-salinity droplets ($20‰$), characterized by lower viscosity and reduced viscous dissipation, encounter less resistance during retraction and retract more completely, thereby producing larger maximum relative deviations. As the supercooling degree increases, the freezing phase transition gradually becomes the dominant mechanism controlling droplet motion. High-salinity droplets, which exhibit delayed solidification due to salt inhibition, undergo more pronounced retraction and thus exhibit greater relative deviations. However, at extremely high supercooling degrees (e.g., 25 K), both saline and freshwater droplets are strongly constrained by rapid solidification, leading to overall smaller relative deviations in spreading factor compared with those at lower supercooling conditions.

The above analysis indicates that salinity induces observable relative deviations in the spreading factor during the retraction stage of droplet impact-freezing process. These deviations reflect the systematic effects caused by variations in physics properties. It is worth noting that, as shown in Figure 11, changes in salinity exert limited influence on the overall morphological evolution of droplets under identical conditions. The differences are primarily manifested through variations in the spreading factor. This feature ensures that applying corrections based on relative deviations does not introduce additional errors associated with morphological differences. Although the relative deviations for individual droplets remain relatively small, the cumulative effect of repeated droplet impacts in natural environments can lead to significant differences in macroscopic ice accretion. Furthermore, the quantifiable nature of these deviations provides a solid basis for incorporating them as correction factors into existing droplet dynamic models.

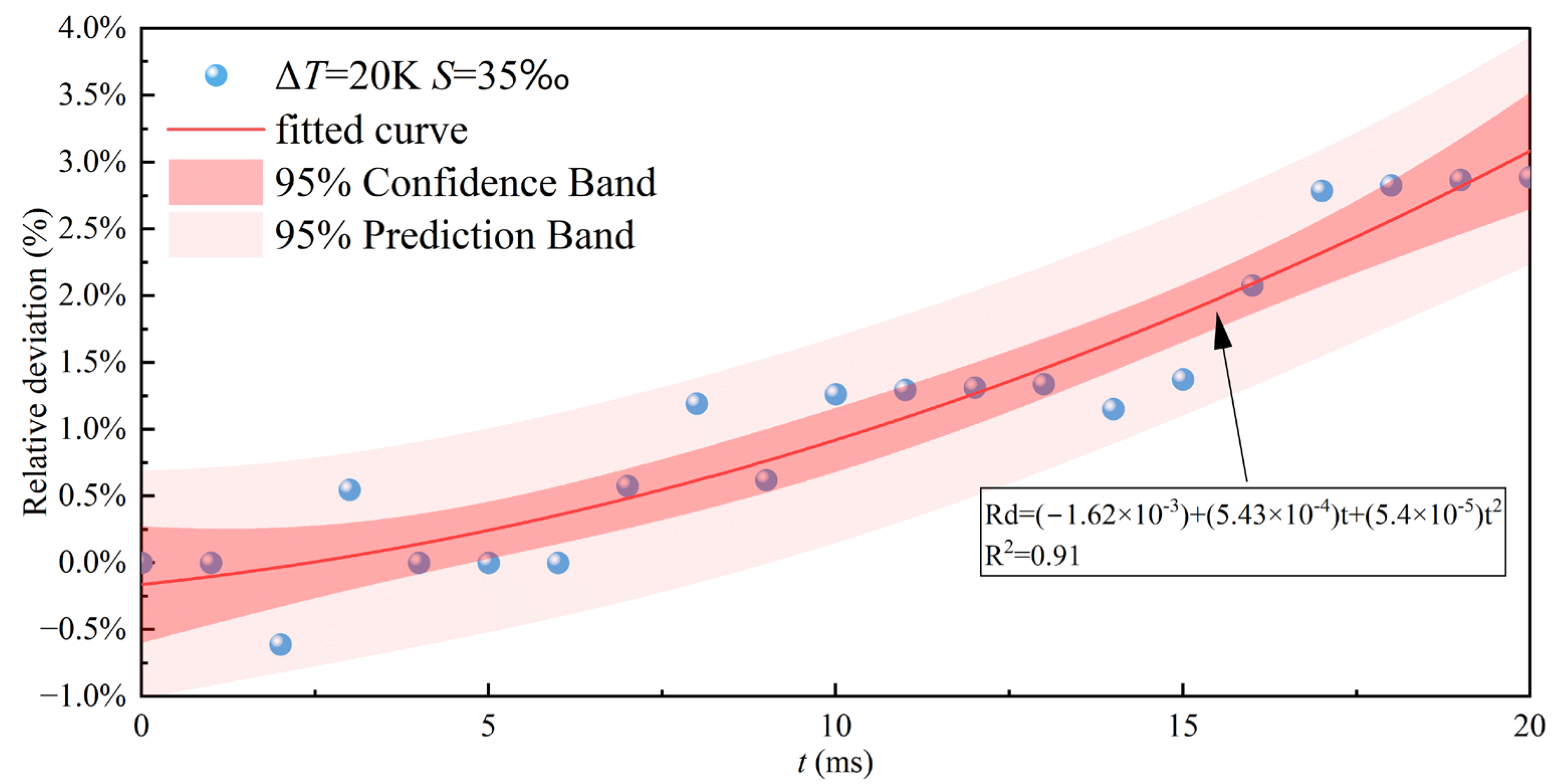
Figure 12 presents the fitted curve of the relative deviation over time for droplets with a salinity of $35‰$ at a supercooling degree of $20 \mathrm{K}$. The curve exhibits a nonlinear increasing trend, with smaller deviations during the early stage and larger deviations during the retraction and stabilization stages. This behavior indicates that the influence of salinity on the impact-freezing process primarily emerges in the middle and later stages. By applying relative-deviation-based corrections to the spreading factor, the impact-freezing process of saline droplets under different impact conditions can be more accurately represented. Moreover, such correction factors can provide essential parameters for macroscopic icing prediction models, enhancing their applicability in saline marine environments without significantly increasing computational cost.

It should be noted that the fitted curves presented in this study are derived under specific parameter conditions and are therefore strictly applicable only to the corresponding environments. To enhance the generality of this correction approach, a systematic and rapid analysis can be performed across a wide range of operating conditions to obtain multiple fitted curves and establish a comprehensive database of correction parameters. In practical applications, environmental data such as ambient temperature, wind speed, and Liquid Water Content (LWC) can be obtained in real time from onboard monitoring systems. The corresponding correction parameters can then be rapidly retrieved and integrated into existing ice prediction models, enabling adaptive, accurate, and computationally efficient forecasting of ice accretion on offshore wind turbine blades.

4.2. Effects of Salinity and Surface Contact Angle on the Droplet Impact-Freezing Process

To investigate the effect of contact angle on the dynamic characteristics of supercooled droplets, the concept of contact angle hysteresis, defined as ${\theta }_h={\theta }_{\mathrm{adv}}-{\theta }_{\mathrm{rec}}$, is introduced. The simulations in this section set the Weber number to 60, the droplet size to $10 \mathsf{\mu }\mathrm{L}$ (radius of $1.34 \mathrm{mm}$), the supercooling degree to $20 \mathrm{K}$, salinity from $20‰$ to $50‰$, and ${\theta }_h$ to $20°$. In this paper, the impact-freezing process of droplets on three different wettability surfaces is simulated (i.e., ${\theta }_{\mathrm{adv}}=90°, 105°, \mathrm{and} 120°$).

Figure 13 presents the spreading factor curves of freshwater droplets and saline droplets with three different salinities at various contact angles. A dynamic contact angle model was introduced in this study to account for contact angle hysteresis; therefore, a contact angle of 90° actually corresponds to a hydrophilic surface. Under this condition (Figure 13a), the spreading factor curve decreases slowly after reaching its maximum value, indicating weak droplet retraction. As the contact angle increases, the spreading factor curve decreases more rapidly, implying more pronounced retraction on hydrophobic surfaces, as shown in Figure 13b,c. Consistent with the results shown in Figure 9, the spreading factor curves of freshwater droplets are consistently higher than those of saline droplets, with the maximum relative deviation occurring at $20 \mathrm{ms}$, as illustrated in Figure 13d. The red curve corresponds to the case with a supercooling degree of 20 K analyzed in Section 4.1, under the current condition of a contact angle of 105°. From Figure 13d, it can be observed that for contact angles of 90° and 120°, the maximum relative deviation increases with salinity. This indicates that variations in surface wettability influence the competition between impact dynamics and solidification, as discussed in Section 4.1.

Increasing the contact angle intensifies retraction, resulting in a nearly linear decrease in the maximum spreading factor. From

Table 8. Maximum spreading factor under different contact angle conditions.

Contact Angle	${\mathit{\theta }}_{\mathbf{adv}}=90°$	${\mathit{\theta }}_{\mathbf{adv}}=105°$	${\mathit{\theta }}_{\mathbf{adv}}=120°$
$D/D_0$	2.96	2.78	2.63

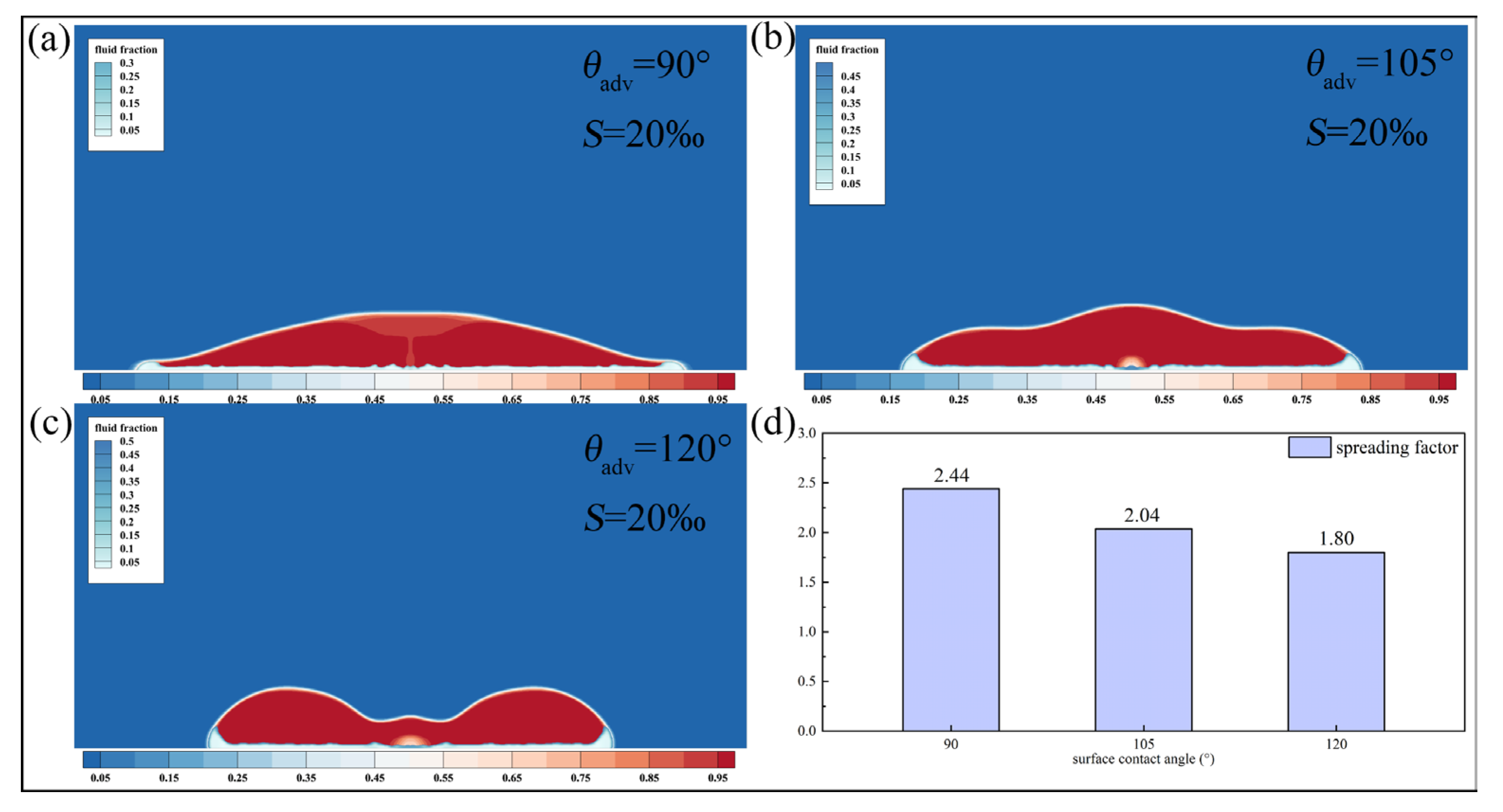
, the maximum spreading factor decreases from 2.96 to 2.63 as the contact angle increases, representing a reduction of 11.1%. Figure 14 shows the morphology of saline droplets with a salinity of $20‰$ on surfaces with different wettability at $20 \mathrm{ms}$. As the contact angle increases from 90° to 120°, the droplet shape transitions from a spread state with a convex center to a retracted state with a concave center. Correspondingly, the spreading factor at this time decreases from 2.44 to 1.80, a reduction of 26.2%.

On hydrophilic surfaces, the larger spreading area enhances heat exchange with the substrate, making the spreading factor curve more sensitive to the effects of phase change. As a result, high-salinity droplets ($50‰$), which have lower thermal conductivity and slower phase-change rates, exhibit more pronounced retraction and the highest maximum relative deviation on hydrophilic surfaces. This behavior is consistent with the characteristics observed for saline droplets at high supercooling degrees ($25 \mathrm{K}$) in Section 4.1.

On strongly hydrophobic surfaces with a contact angle of 120°, the weaker adhesion between the droplet and the wall reduces resistance during retraction, allowing surface tension to dominate the droplet motion and accelerating retraction. This corresponds to the rapid decrease observed in the spreading factor curves in Figure 13. Consequently, hydrophobic surfaces suppress the influence of phase change by rapidly reducing the heat exchange area through faster retraction. Moreover, as salinity increases, the enhanced surface tension of the droplet leads to greater retraction, resulting in larger relative deviations from freshwater droplets.

4.3. Effects of Salinity and Weber Number on the Droplet Impact-Freezing Process

To describe the dynamic behavior of droplets more accurately, the Weber number ($We$) is introduced in this section. When $We$ is small, the surface tension effect dominates. When $We$ is much greater than 1, the effect of surface tension is negligible. Under the simulated operating conditions, the droplet diameter is $2.68 \mathrm{mm}$. In this section, the effect of the Weber number and salinity on the impact-freezing process is investigated. Specifically, the salinities are $20‰$, $35‰$, and $50‰$, and the Weber numbers are 40, 60, and 80. The rest of the conditions are ${\theta }_{\mathrm{adv}}=105°$, ${\theta }_{\mathrm{rec}}=85°$, and $\mathrm{\Delta }T=20 \mathrm{K}$.

Figure 15 presents the spreading factor curves of saline and freshwater droplets at different Weber numbers. The results indicate that the spreading factor curves of freshwater droplets are consistently higher than those of saline droplets, and the maximum relative deviation for saline droplets still occurs at approximately $20 \mathrm{ms}$. The overall trends of the spreading factor curves for saline and freshwater droplets remain similar across different Weber numbers, with the primary differences in the maximum spreading factor.

An increase in the Weber number significantly enhances spreading capacity. From

Table 9. Maximum spreading factor under different Weber number conditions.

Weber Number	$\mathit{W}\mathit{e}=40$	$\mathit{W}\mathit{e}=60$	$\mathit{W}\mathit{e}=80$
$D/D_0$	2.5	2.78	2.99

, the maximum spreading factor increases from 2.50 to 2.99 as the Weber number increases, corresponding to a 19.6% rise. As shown in Figure 15d, the relative deviation trends with increasing salinity are similar for Weber numbers of 40 and 60. However, at a Weber number of 80, this trend changes, with the relative deviation progressively increasing as salinity rises.

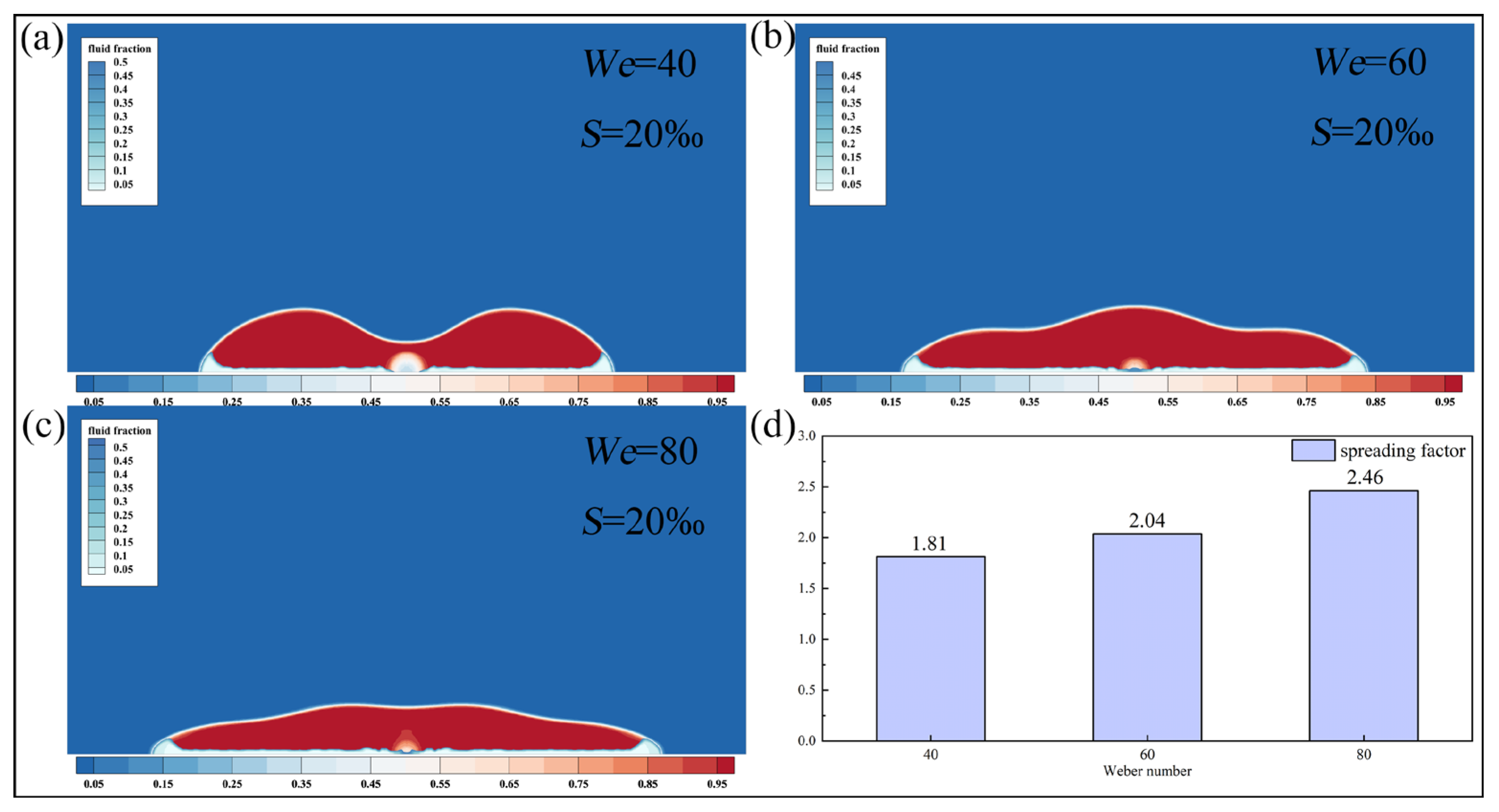
Figure 16 illustrates the morphology of saline droplets as the Weber number increases from 40 to 80. Elevated impact velocity enhances the initial kinetic energy, leading to broader droplet spreading. At $20 \mathrm{ms}$, the droplet with high Weber number exhibits slow retraction state and maintains a spread morphology. In contrast, the droplet with low Weber number has already entered a significant retraction state. Therefore, as the Weber number increases, the spreading coefficient at $20 \mathrm{ms}$ increases from 1.81 to 2.46, an increase of 35.9%.

Under high Weber number conditions, droplets possess greater initial kinetic energy, resulting in stronger radial spreading upon impact. Upon reaching the maximum spreading state, surface tension must overcome greater inertial resistance to drive droplet retraction. Furthermore, the high Weber number often corresponds to the high Reynolds number, leading to more intense internal flow within the droplet. This increases viscous dissipation and consequently weakens the power of retraction. The droplet with low Weber number can directly convert surface energy into kinetic energy during retraction, resulting in significantly faster retraction speeds.

The case with a Weber number of 60 corresponds to the supercooling degree of 20 K analyzed in Section 4.1. As discussed earlier, the non-monotonic variation in the maximum relative deviation at $We=60$ primarily arises from the competition between impact dynamics and solidification. At $20 \mathrm{K}$, the droplets of moderate salinity ($35‰$) exhibit the largest relative deviation due to a balanced combination of moderate viscous dissipation and relatively slow solidification rates. When the Weber number decreases to 40, the initial kinetic energy of all droplets is lower, and the relative deviation still follows a similar trend to that observed at $We=60$. In contrast, increasing the Weber number intensifies the initial kinetic energy, causing droplet behavior during the retraction stage to be dominated by hydrodynamics. Additionally, droplets with higher salinity have greater density, which enhances their inertia. As a result, under high Weber number conditions, droplets with higher salinity exhibit stronger retraction, leading to larger maximum relative deviations.

In addition to the time-dependent fitting curve method proposed in Section 4.1 for refining icing prediction models in cold marine environments, the maximum relative deviation can be treated as a single scalar parameter that can be directly embedded into droplet motion models or macroscopic icing prediction models to correct the impact-freezing process of saline droplets.

Because the maximum relative deviation typically occurs during the retraction and stabilization phase, where deviations are most pronounced, this parameter effectively captures the combined influence of salinity on droplet dynamics and phase-change coupling. Moreover, the analysis indicates that variations in salinity have a limited impact on overall droplet morphology and primarily affect the spreading factor, providing a robust foundation for quantitative corrections based on relative deviation. By systematically compiling maximum relative deviations under various conditions, a correction parameter database can be established, enabling rapid model adjustments as shown in

Table 10. Maximum relative deviation between freshwater and saline droplets.

	$\mathit{S}=20‰$	$\mathit{S}=35‰$	$\mathit{S}=50‰$
$\mathrm{\Delta }T=15 \mathrm{K}$  ${\theta }_{\mathrm{adv}}=105°$  $We=60$	2.93%	1.39%	1.39%
$\mathrm{\Delta }T=20 \mathrm{K}$  ${\theta }_{\mathrm{adv}}=105°$  $We=60$	1.06%	2.46%	2.00%
$\mathrm{\Delta }T=25 \mathrm{K}$  ${\theta }_{\mathrm{adv}}=105°$  $We=60$	0.30%	0.30%	0.50%
$\mathrm{\Delta }T=20 \mathrm{K}$  ${\theta }_{\mathrm{adv}}=90°$  $We=60$	0.60%	2.09%	2.49%
$\mathrm{\Delta }T=20 \mathrm{K}$  ${\theta }_{\mathrm{adv}}=105°$  $We=60$	1.06%	2.46%	2.00%
$\mathrm{\Delta }T=20 \mathrm{K}$  ${\theta }_{\mathrm{adv}}=120°$  $We=60$	0.81%	2.42%	4.03%
$\mathrm{\Delta }T=20 \mathrm{K}$  ${\theta }_{\mathrm{adv}}=105°$  $We=40$	1.58%	3.29%	2.37%
$\mathrm{\Delta }T=20 \mathrm{K}$  ${\theta }_{\mathrm{adv}}=105°$  $We=60$	1.06%	2.46%	2.00%
$\mathrm{\Delta }T=20 \mathrm{K}$  ${\theta }_{\mathrm{adv}}=105°$  $We=80$	0.65%	1.72%	3.12%

. Compared with the fitting-curve method, this approach eliminates the need to account for temporal variations and can enable direct model correction through empirical coefficients. Such simplicity makes it well suited for practical engineering applications, such as icing prediction for offshore wind turbines.

5. Limitations Analysis of the Adopted Method

The numerical model assumes an idealized circular droplet profile and neglects the gravitational effects on the initial morphology for simplicity. However, gravity, along with other environmental factors such as flow fields, can deform the droplet shape. This deformation alters the initial shape and affects the droplet impact-freezing process [13,16,37]. Such shape variations can influence the impact behavior, affecting both heat transfer and adhesion on the droplet-surface interface. These effects are crucial, particularly in larger droplets where gravity-induced shape distortion becomes more pronounced. Although the idealized circular assumption simplifies the model, the influence of gravity on droplet morphology must be considered in future studies for the accuracy simulation of the impact-freezing process.

In the current model, it is assumed that the heat transfer process is transient, and the heat exchange between the droplet and the surface reaches dynamic equilibrium within a very short time scale. Based on this assumption, the recalescence stage is considered to occur instantaneously upon impact, with no secondary recalescence during the subsequent freezing process. While this assumption simplifies the modeling and captures the dominant effects of recalescence, it neglects the possibility of secondary recalescence that may occur during prolonged freezing or under specific conditions. Future studies may need to incorporate a more detailed treatment of the recalescence stage to account for these potential secondary effects.

The numerical model employed in this study assumes constant physical parameters throughout the impact-freezing process, which is a common approach when modeling freshwater droplets. However, this assumption presents significant limitations when applied to solute-laden droplets, such as saline droplets. During solidification, the solutes (salts) in the droplet concentrate within the residual liquid phase, leading to the formation of high-concentration brine [19,38,39]. This concentration gradient alters the physical properties of the droplet, including viscosity, thermal conductivity, and specific heat capacity, which are time dependent. Therefore, the assumption of constant physical properties is not suitable for modeling the behavior of saline droplets accurately. In future studies, the temporal variations in salinity and the associated changes in physical properties should be incorporated into the model, such as a solute transport equation, to improve its realism and precision.

In this study, a two-dimensional axisymmetric model was employed to simplify the numerical computation. Given the relatively low Weber and Reynolds numbers used, the droplets did not reach a turbulent state or experience splashing during the entire impact-freezing process. As a result, the droplets maintained strong axial symmetry throughout the simulations. However, when future studies involve pronounced asymmetry or extreme environmental conditions, extending the current model to three dimensions will become essential. For instance, under high wind speeds, aerodynamic effects on the droplets cannot be neglected. Similarly, when investigating droplet impacts on inclined surfaces or interactions between multiple droplets, the inherently three-dimensional nature of such phenomena makes axisymmetric simplifications no longer applicable.

6. Conclusions

This study employs an equivalent physical property correction method to refine the existing two-dimensional axisymmetric numerical analysis framework, achieving high computational efficiency while enhancing engineering applicability. Using the droplet spreading factor and the corresponding relative deviation as a benchmark, the first-order effects of salinity on the impact-freezing process are systematically evaluated. Furthermore, this simplified numerical approach enables visualization of ice-phase distributions, thereby supporting qualitative analysis of freezing mechanisms. These findings offer theoretical support for improving the accuracy of icing prediction models for offshore wind turbines in cold regions. The following conclusions can be drawn:

(1)

With increasing supercooling degree, the salinity corresponding to the peak relative deviation exhibits a clear shift, rising from $20‰$ at $15 \mathrm{K}$ to $50‰$ at $25 \mathrm{K}$. And the peak relative deviation decreased from 2.39% to 0.5%, a decrease of 82.9%. This indicates that the supercooling degree changes the dominant mechanism of salinity on droplet motion. At low supercooling degrees, dynamics effects prevail, and low-salinity droplets show larger relative deviations due to reduced viscous dissipation and more extensive retraction. At higher supercooling degrees, stronger phase-change driving forces enhance freezing process, and high-salinity droplets display larger deviation peaks due to slow solidification. The maximum spreading factor decreases slightly from 2.79 to 2.76 as the supercooling degree increases, corresponding to a 1.1% reduction.

(2)

For contact angles of 90° and 120°, the maximum relative deviation increases with salinity, depending on solidification and dynamics factor, respectively. At 105°, however, the deviation first rises and then falls as salinity increases, reflecting a shift in the competition between impact dynamics and solidification at intermediate wettability. The maximum spreading factor decreases from 2.96 to 2.63 as the contact angle increases from 90° to 120°, corresponding to an 11.1% reduction.

(3)

The relationship between relative deviation and salinity varies with Weber numbers. At $We=40$ and 60, the deviation trends both first rise and then fall. However, at $We=80$, the relative deviation increases progressively with salinity. This is attributed to stronger inertia at high Weber numbers, which amplifies retraction effects in high-salinity droplets. The maximum spreading factor increases from 2.50 to 2.99 as the Weber number rises from 40 to 80, representing a 19.6% increase.

(4)

Two correction strategies based on relative deviation are proposed to enhance the applicability of droplet motion and icing prediction models in saline marine environments. The first employs time-dependent fitted curves of relative deviation to dynamically correct saline droplet impact-freezing behavior across different stages. The second uses the maximum relative deviation as an empirical coefficient to correct the saline droplet motion, making it well suited for integration into practical engineering models. The former offers higher accuracy for detailed simulations, while the latter provides improved computational efficiency and generality for engineering applications. Based on the proposed correction strategies, the single-droplet correction parameters can be dynamically adjusted in real time according to measured environmental conditions, thereby improving the accuracy of icing prediction.