Development of New Jack-Up Substructure Supporting Offshore Wind Turbines in Multi-Layered Soils: Geotechnical Aspects
Abstract
1. Introduction
2. Theory
2.1. Vertical Bearing Capacity of Jack-Up Spudcan
2.1.1. ISO 19905-1:2023 [16] Method
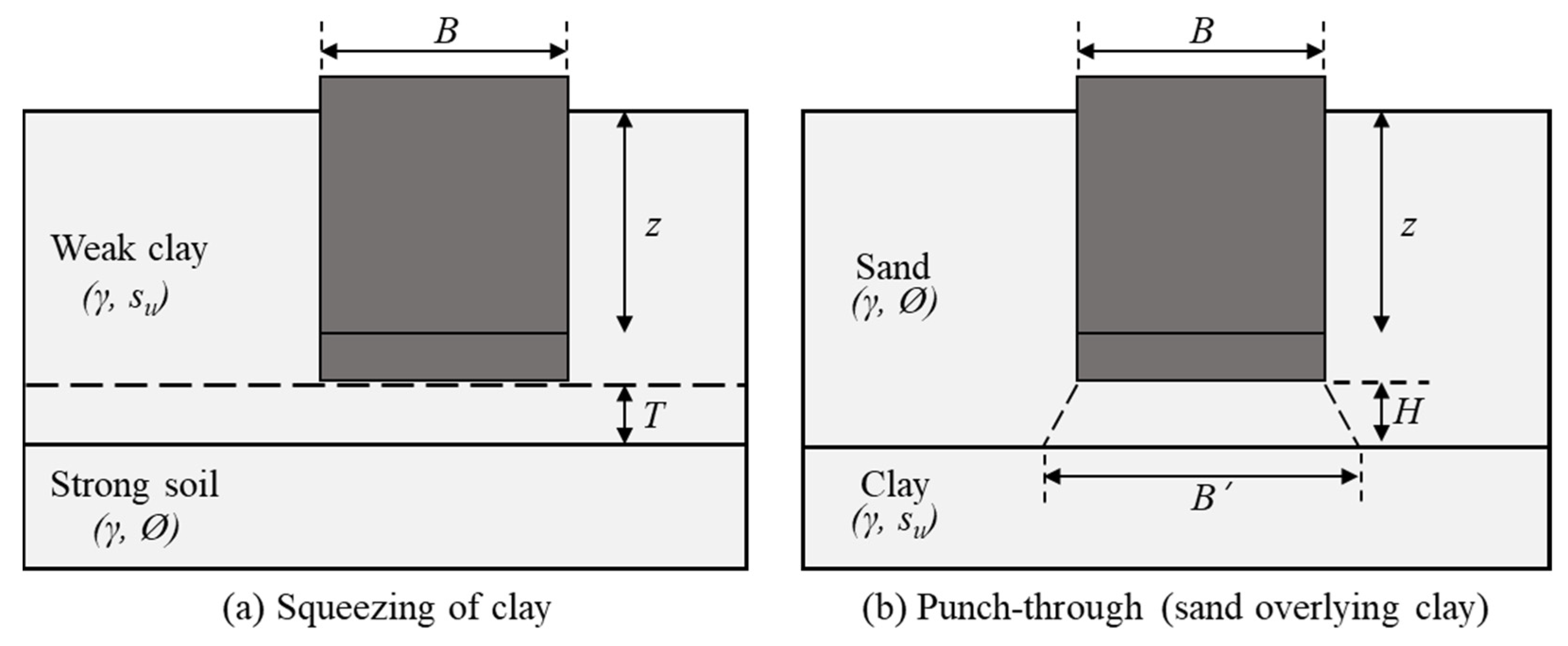
- Squeezing of clay
- 2.
- Punch-through (sand overlying clay)
2.1.2. InSafeJIP [18] Method for Two-Layered System
- Soft over strong soils
- 2.
- Strong over soft soils (sand-over-clay)
2.1.3. Evaluation of Methods
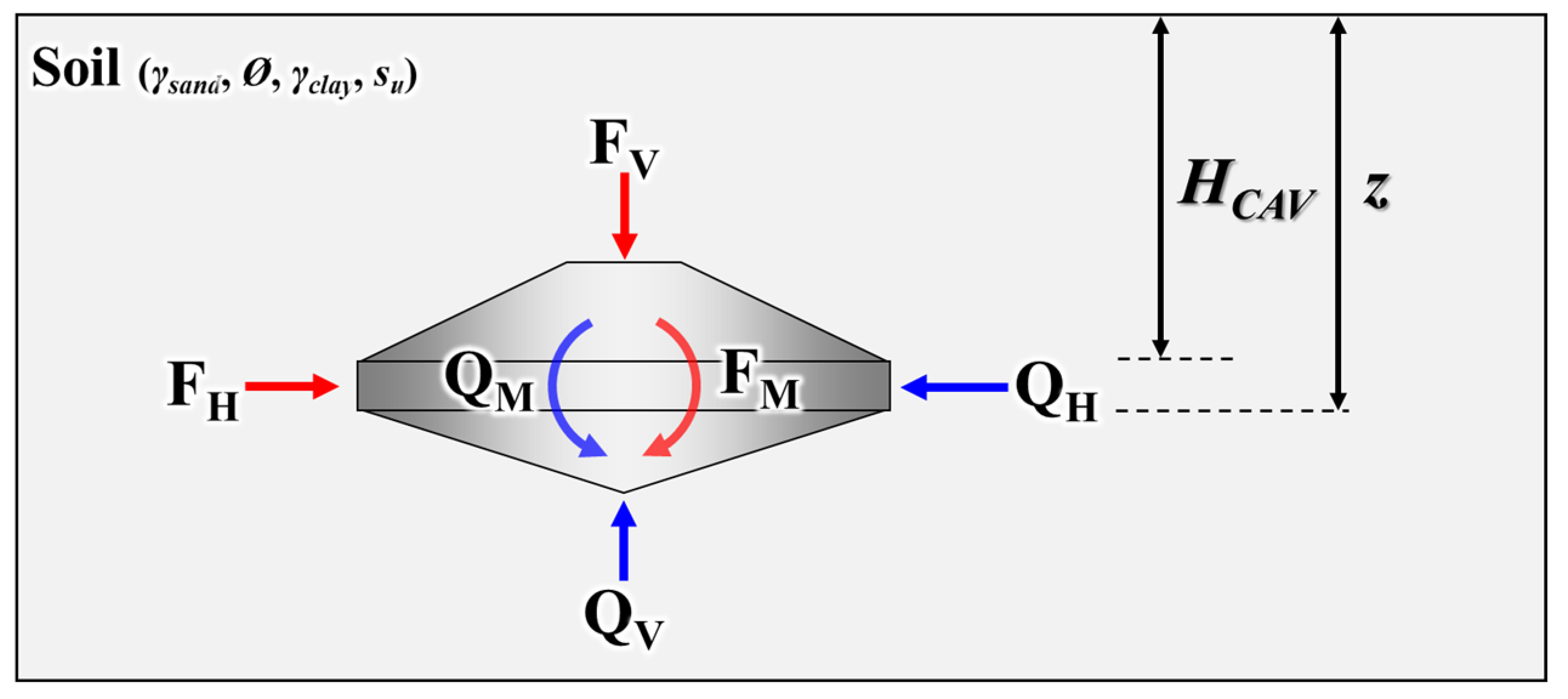
2.2. The Vertical–Horizontal–Moment Capacity Envelope
3. New Jack-Up Substructure Design Conditions
3.1. Site Conditions
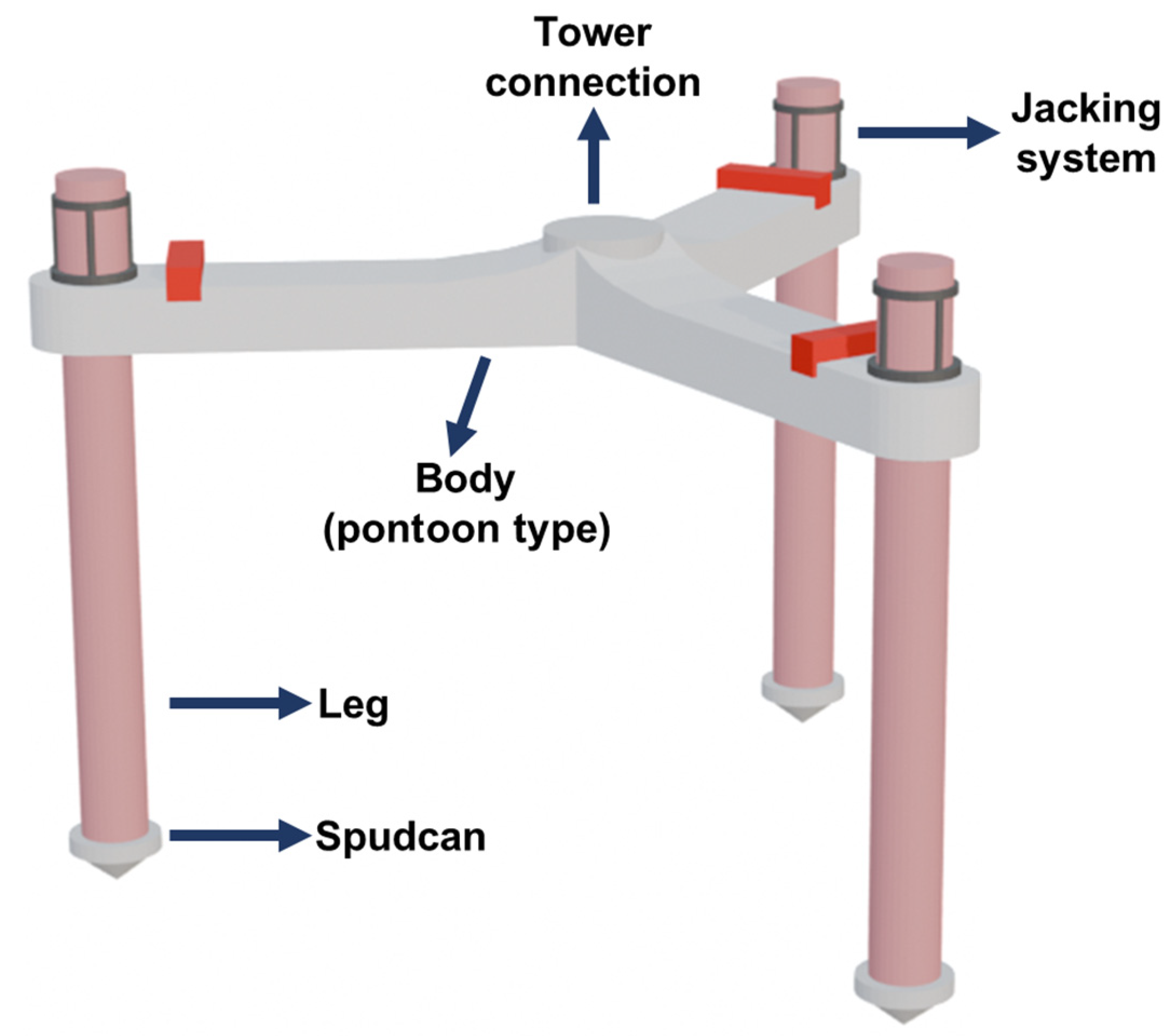
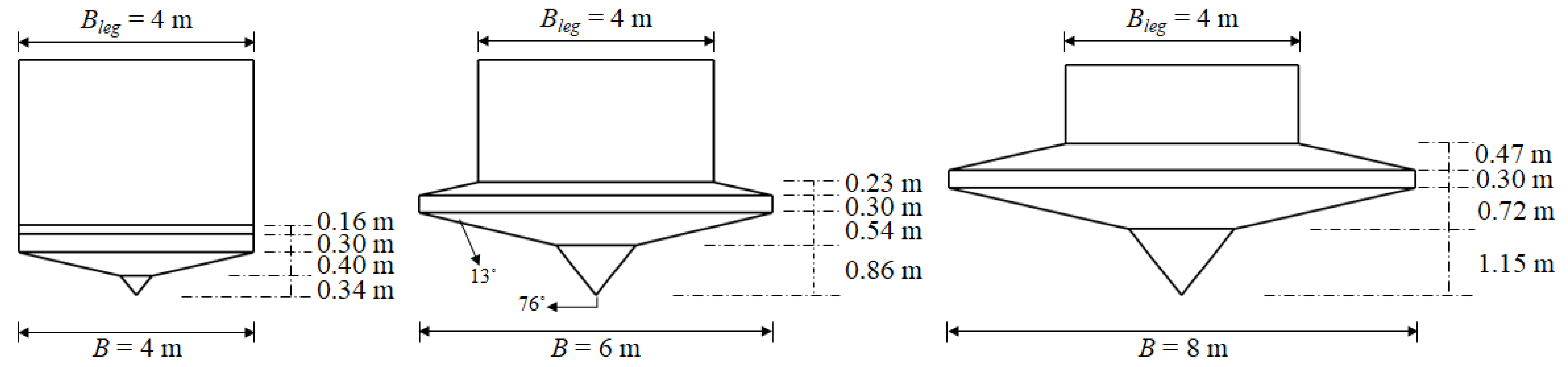
3.2. Model Foundation Cases
3.3. Experimental Verification for Vertical Capacity
3.3.1. Centrifuge Model Test
3.3.2. Test Condition
4. Results
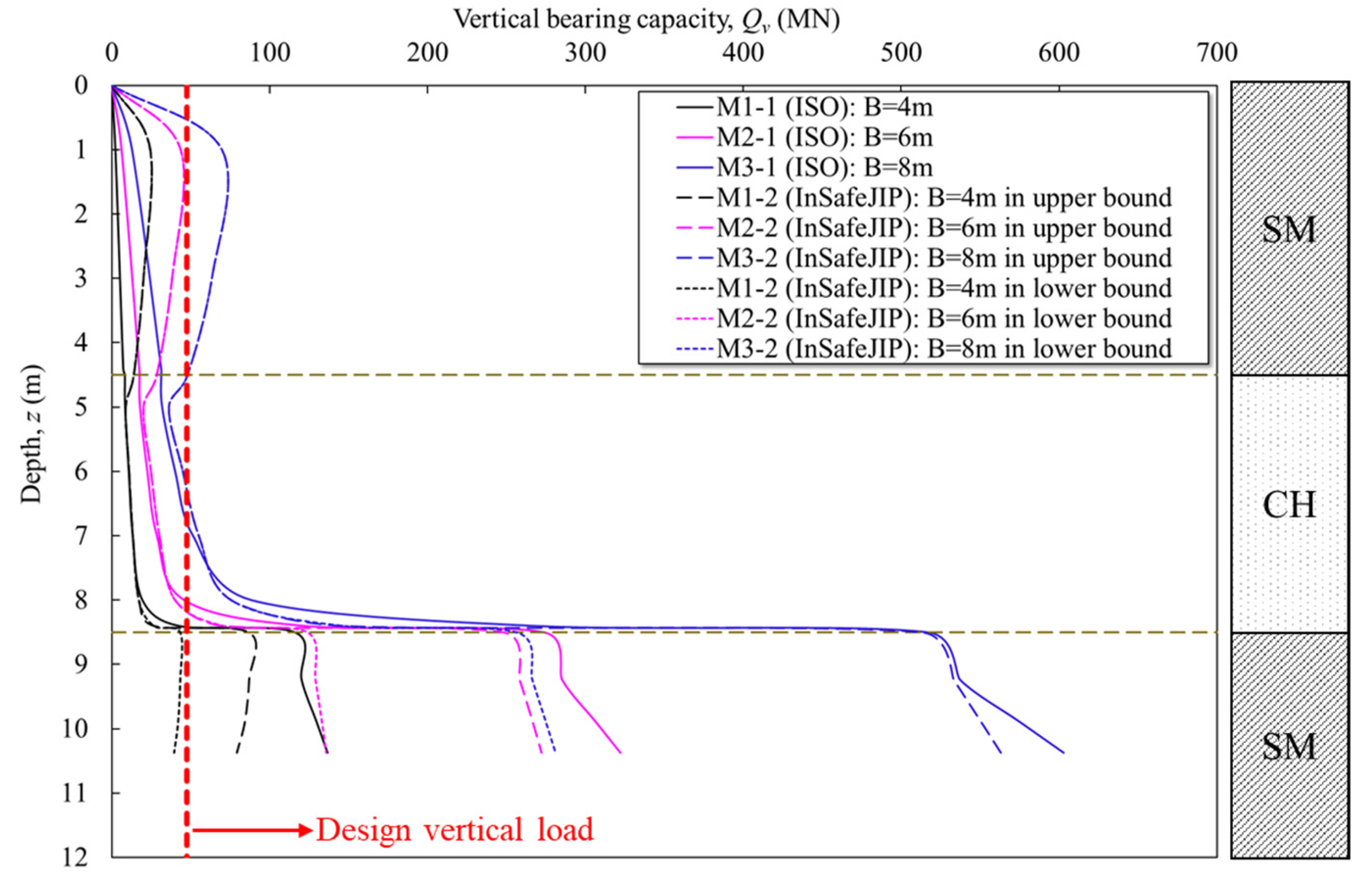
4.1. Vertical Capacities of Jack-Up Spudcans
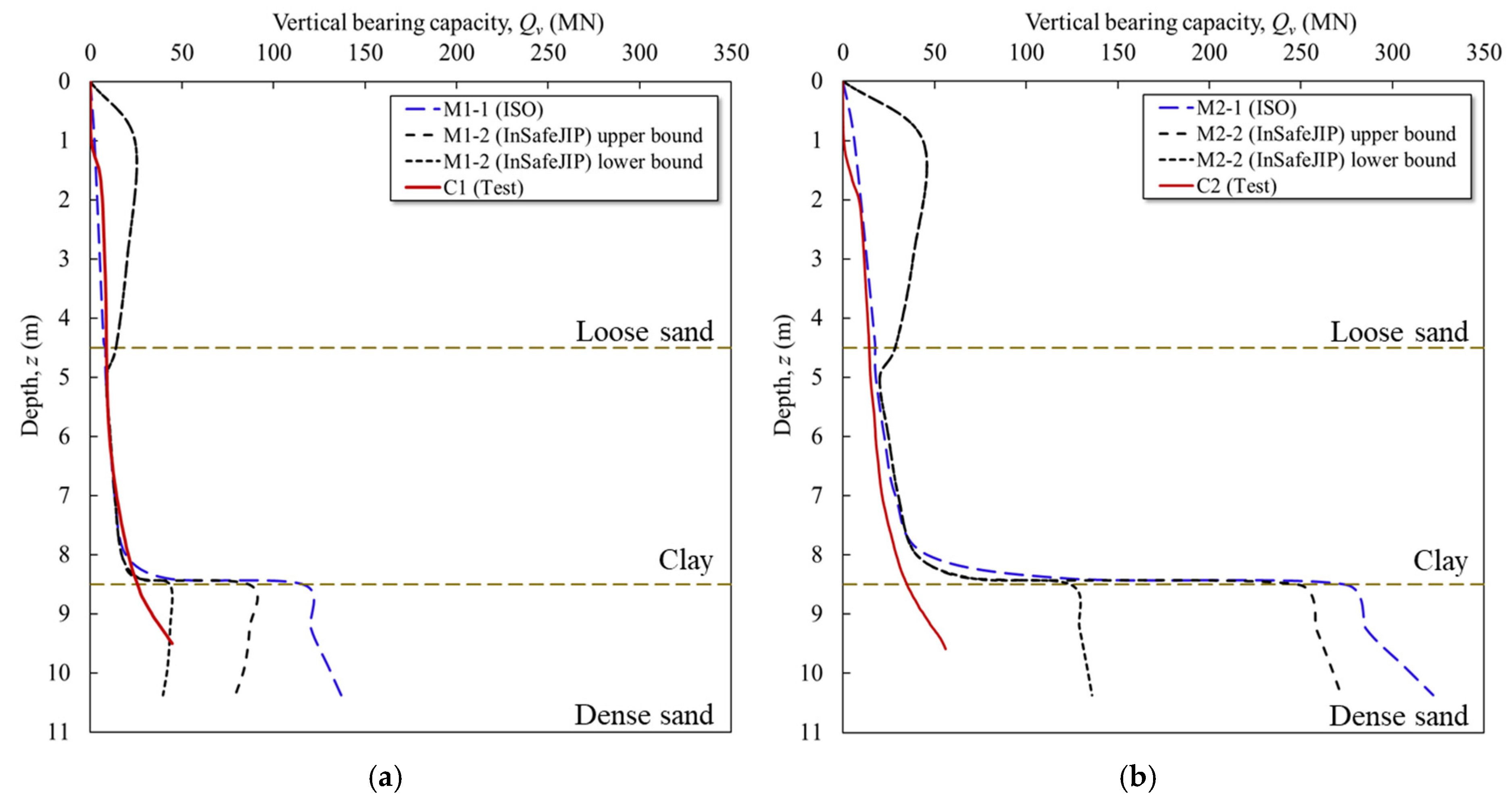
4.2. Experimental Validation of Vertical Capacity
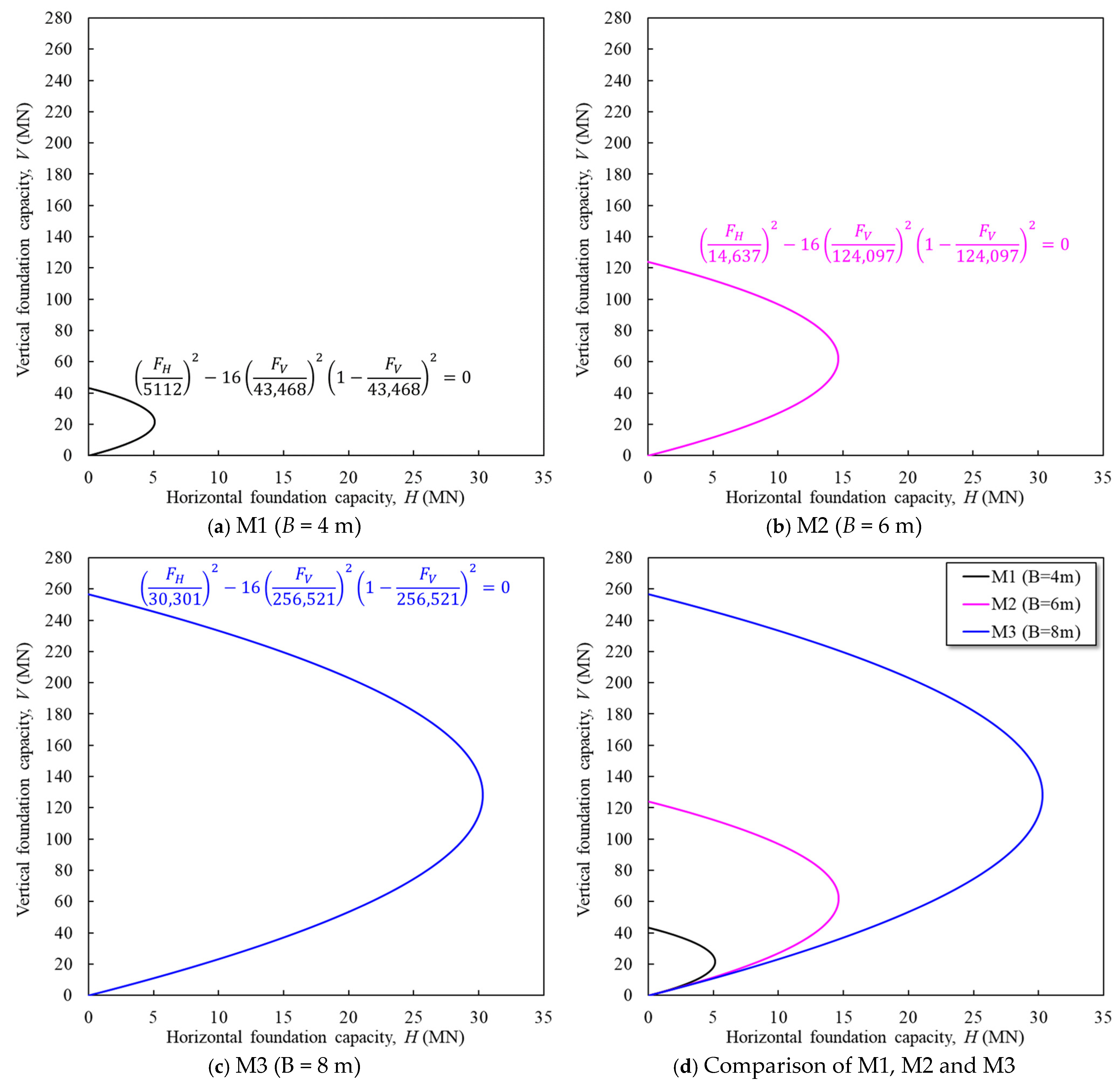
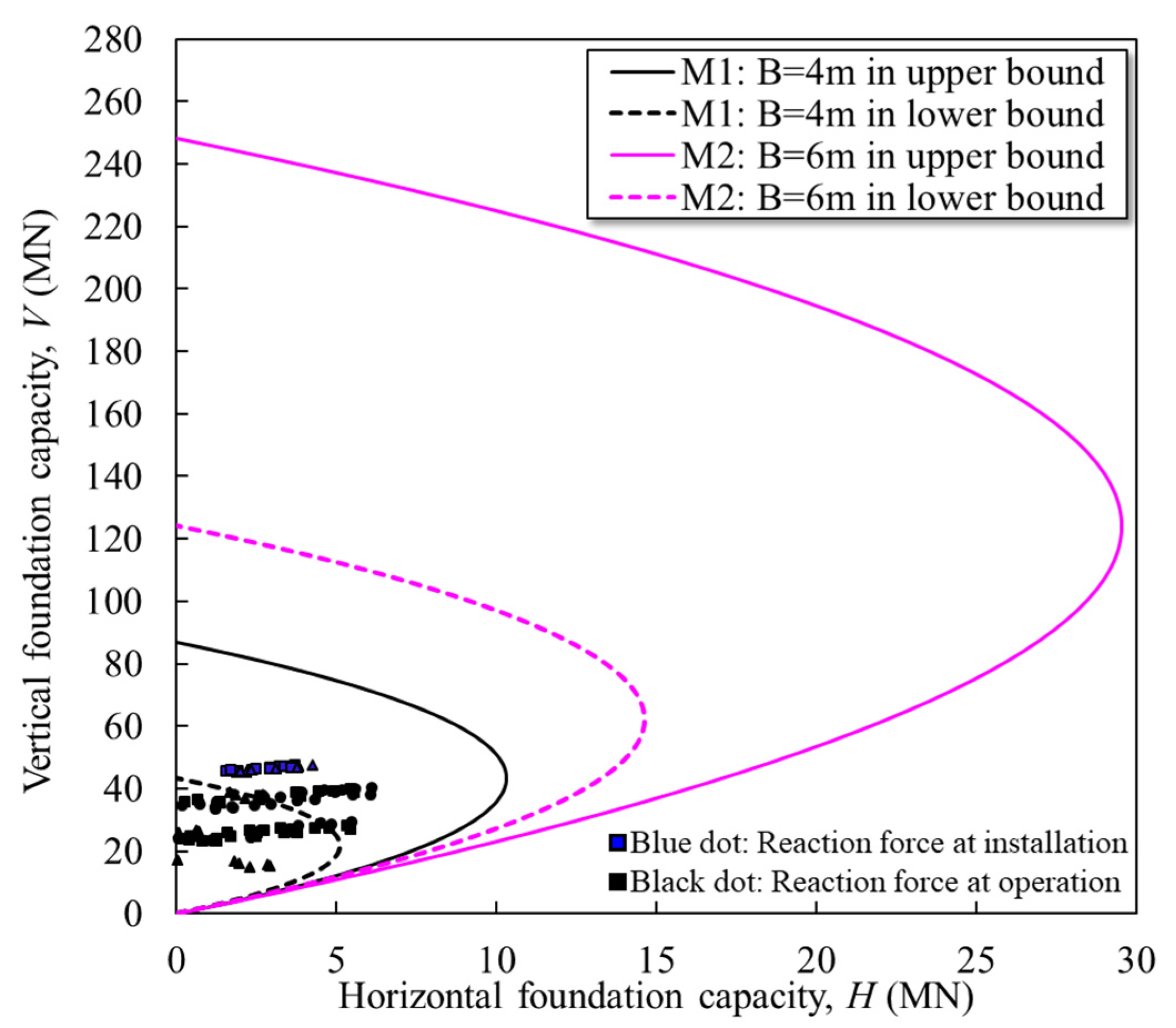
4.3. Capacity Yield Envelopes for Combined Horizontal Load and Moment
5. Discussion and Recommendation for Practice
6. Conclusions
- This study evaluated the applicability of a jack-up spudcan foundation design for typical Korean offshore seabed conditions consisting of a weak sand layer over clay, underlain by dense sand.
- The ISO design method showed good agreement with the experimental results for sand-over-clay and clay conditions; however, it tended to overestimate vertical capacity in sandy soils. Thus, considering strength reduction factors, such as the mobilization factor from the InSafeJIP method, is recommended to better predict the actual offshore soil behavior to design the foundation.
- Vertical–horizontal capacity envelopes expanded with spudcan diameter due to the larger bearing area and the formation of backfill on the spudcan shoulder.
- Finally, this study examines the influence of spudcan foundation size and the effects of multi-layered ground conditions, provides a foundation design based on integrated load analysis, and investigates a methodology for selecting an appropriate foundation for a 10 MW offshore wind turbine substructure.
- The current study aims to establish design procedures for an offshore three-leg jack-up substructure equipped with a spudcan installed in multiple layers for short-term performance. The result of the current work is limited to the short-term loading condition. Thus, further study is necessary to verify the long-term performance under cyclic loading.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Choo, Y.W.; Kim, D.; Park, J.H.; Kwak, K.; Kim, J.H.; Kim, D.S. Lateral Response of Large-diameter Monopiles for Offshore Wind Turbines from Centrifuge Model Tests. Geotech. Test. J. 2014, 37, 107–120. [Google Scholar] [CrossRef]
- Kim, D.; Choo, Y.W.; Kwak, K. Comparison of Lateral Behavior of Rock-socketed Large-diameter Offshore Monopiles in Sands with Different Relative Densities. Int. J. Offshore Polar Eng. 2015, 25, 156–160. [Google Scholar] [CrossRef]
- Kim, D.J.; Choo, Y.W.; Kim, J.H.; Kim, S.; Kim, D.S. Investigation of Monotonic and Cyclic Behavior of Tripod Suction Bucket Foundations for Offshore Wind Towers Using Centrifuge Modeling. J. Geotech. Geoenviron. Eng. 2014, 140, 04014008. [Google Scholar] [CrossRef]
- Choo, Y.W.; Seo, J.H.; Kim, Y.N.; Goo, J.M.; Kim, Y.H. Numerical Studies on Piled Gravity Base Foundation for Offshore Wind Turbine. Mar. Georesour. Geotechnol. 2016, 34, 729–740. [Google Scholar] [CrossRef]
- Shin, M.Y.; Sung, J.Y.; Park, C.I.; Kim, H.K. Introduction to 10 MW Jack-up Type Fixed Offshore Wind Power Design (K-WIND). In Proceedings of the 2023 Fall Conference of the Korea Society of Ocean Engineers, Gyeongju, Republic of Korea, 25–27 October 2023; pp. 162–163. [Google Scholar]
- Lee, M.J.; Choo, Y.W. Penetration Behavior of Jack-up Leg with Spudcan for Offshore Wind Turbine to Multi-layered Soils Using Centrifuge Tests. J. Ocean Eng. Technol. 2024, 38, 30–42. [Google Scholar] [CrossRef]
- Howarth, S.; Hassrick, J.; Grismala, R.; Diller, E.; Kerbs, J.; Manhard, R. Comparison of Environmental Effects from Different Offshore Wind Turbine Foundations. In Report No. OCS Study BOEM 2020-041; U.S. Department of the Interior: Sterling, VA, USA, 2020. [Google Scholar]
- Choo, Y.W.; Lee, M.J.; Hong, I.B. Technical Consideration on Jackup-spudcan Structures for Offshore Wind Substructure. In Proceedings of the 2023 Fall Conference of the Korea Society of Ocean Engineers, Gyeongju, Republic of Korea, 25–27 October 2023; pp. 156–157. [Google Scholar]
- Gilo, A.; Lee, M.J.; Choo, Y.W. Numerical Analysis of the Effect of an Inverted Cone Angle on the Penetration Behavior of the Jack-Up Leg Foundation for Offshore Wind Turbines in Uniform Clay. J. Ocean Eng. Technol. 2024, 38, 438–448. [Google Scholar] [CrossRef]
- Kim, Y.J.; Choe, J.W.; Lim, J.; Choi, S.W. Foundation types of fixed offshore wind turbine. J. Ocean Eng. Technol. 2024, 38, 74–85. [Google Scholar] [CrossRef]
- Ali, S.; Park, H.; Lee, D. Multi-Criteria Optimization of Wind Turbines in an Offshore Wind Farm with Monopile Foundation Considering Structural Integrity and Energy Generation. J. Mar. Sci. Eng. 2024, 12, 2313. [Google Scholar] [CrossRef]
- Tran, T.T.; Lee, D. Development of jacket substructure systems supporting 3MW offshore wind turbine for deep water sites in South Korea. Int. J. Nav. Archit. Ocean Eng. 2022, 14, 100451. [Google Scholar] [CrossRef]
- Park, J.S.; Lee, D.H.; Yi, M.S. Structural Analysis Procedure and Applicability Review of Spudcan Considering Soil Types. J. Mar. Sci. Eng. 2023, 11, 1833. [Google Scholar] [CrossRef]
- Falcon, S.S.D.; Choo, Y.W.; Leung, C.F. Spudcan–pile interaction in sand-over-clay: Centrifuge modelling. Géotechnique 2023, 73, 480–494. [Google Scholar] [CrossRef]
- Baek, S.H.; Choi, C.; Cho, J.; Chung, C.K. Assessment of py Behaviors of a Cyclic Laterally Loaded Pile in Saturated Dense Silty Sand. J. Korean Geotech. Soc. 2019, 35, 97–110. [Google Scholar]
- ISO 19905-1:2023; Petroleum and Natural Gas Industries: Site Specific Assessment of Mobile Offshore Unit—Part 1: Jack-Ups Elevated at a Site. International Organization for Standardization (ISO): Geneva, Switzerland, 2023.
- The Society of Naval Architects and Marine Engineers (SNAME). Guidelines for Site Specific Assessment of Mobile Jack-Up Units; Technical & Reasearch Bulletin 5-5A; SNAME: Alexandria, VA, USA, 2008. [Google Scholar]
- Osborne, J.J.; Teh, K.L.; Houlsby, G.T.; Cassidy, M.J.; Bienen, B.; Leung, C.F. Improved Guidelines for the Prediction of Geotechnical Performance of Spudcan Foundations during Installation and Removal of Jack-up nits. In Offshore Technology Development; InSafeJIP; RPS Engergy: Abingdon, UK, 2011. [Google Scholar]
- Brown, J.D.; Meyerhof, G.G. Experimental Study of Bearing Capacity in Layered Clays. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, Mexico, 25–29 August 1969. [Google Scholar]
- Vesic, A.S. Bearing Capacity of Shallow Foundations, Winterkorn. In Foundation Engineering Handbook; Winterkorn, H.F., Fang, H.Y., Eds.; Van Nostrand: Scarborough, ON, Canada, 1975; pp. 121–147. [Google Scholar]
- Young, A.G.; Remmes, B.; Meyer, B. Foundation Performance of Offshore Jack-UP Drilling Rigs. J. Geotech. Eng. Geotech. 2012, 42, 89–97. [Google Scholar] [CrossRef]
- Houlsby, G.T.; Martin, C.T. Undrained Bearing Capacity Factors for Conical Footings on Clay. Geotechnique 2003, 5, 513–520. [Google Scholar] [CrossRef]
- Young, A.G.; Focht, J.A. Subsurface Hazards Affect Mobile Jack-up Rig Operations. Sounding 1981, 3, 4–9. [Google Scholar]
- Martine, C.M. User Guide for ABC—Analysis of Bearing Capacity; Department of Engineering Science, University of Oxford: Oxford, UK, 2004. [Google Scholar]
- Brinch Hansen, J. Revised and Extended Formula for Bearing Capacity; Bulletin in Danish Geotechnical Institute: Copenhagen, Denmark, 1970; Volume 28. [Google Scholar]
- Graham, J.; Stuart, J.G. Scale and Boundary Effects in Foundation Analysis. J. Soil Mech. Found. Div. 1971, 97, 1533–1548. [Google Scholar] [CrossRef]
- James, R.G.; Tanaka, H. An Investigation of the Bearing Capacity of footings under Eccentric and Inclined Loading in Sand in a Geotechnical Centrifuge. In Proceedings of the Symposium Recent Advances in Geotechnical Centrifuge Modelling, Davis, CA, USA, 18–20 July 1984; pp. 88–115. [Google Scholar]
- Kimura, T.; Kusakabe, O.; Saitoh, K. Geotechnical Model Tests of Bearing Capacity Problems in Centrifuge. Geotechnique 1985, 35, 33–45. [Google Scholar] [CrossRef]
- Lee, M.J.; Gilo, A.; Choo, Y.W. Geotechnical Analysis of Jack-Up Leg Mounted on Spudcan for Offshore Wind Turbines Considering Installation and Operation. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Singapore, 9–14 June 2024; American Society of Mechanical Engineers: New York, NY, USA, 2024; p. V008T10A008. [Google Scholar]
- Meyerhof, G.G.; Hanna, A.M. Ultimate Bearing Capacity of Foundations on Layered Soils under Inclined Load. Can. Geotech. J. 1978, 15, 565–572. [Google Scholar] [CrossRef]
- Craig, W.H.; Chua, K. Deep Penetration of Spudcan Foundations on Sand and Clay. Géotechnique 1990, 40, 541–556. [Google Scholar] [CrossRef]
- Teh, K.L. Punch-Through of Spudcan Foundation in Sand Overlying Clay. Ph.D Thesis, National University of Singapore, Singapore, 2007. [Google Scholar]
- Lee, K.K. Investigation of Potential Spudcan Punch-Through Failure on Sand Overlying Clay Soils. PhD. Thesis, The University of Western Australia, Perth, Australia, 2009. [Google Scholar]
- Templeton, J.S.; Brekke, J.N.; Lewis, D.R. Spudcan Fixity in Clay, Final Findings of an IADC Study. In Proceedings of the 10th International Conference on Jack-Up Platform Design, Construction & Operation, London, UK, 13–14 September 2005. [Google Scholar]
- Templeton, J.S. Jackup Foundation Performance in Clay. In Proceedings of the 38th Offshore Technology Conference, OTC 18367, Huston, TX, USA, 1–4 May 2006. [Google Scholar]
- Falcon, S.S.D.; Choo, Y.W.; Leung, C.F. Pile Behavior due to Adjacent Jack-up Spudcan Penetration. Int. J. Offshore Polar Eng. 2021, 31, 472–479. [Google Scholar] [CrossRef]
- Falcon, S.S.D.; Sespene, S.M.; Choo, Y.W.; Leung, C.F. Model Study on Spudcan-pile Interaction in Uniform Clay and Sand-over-clay. In Proceedings of the 29th International Ocean Polar Engineering Conference, Honolulu, HI, USA, 16–21 June 2019; Volume 2, pp. 2042–2048. [Google Scholar]
- Schofield, A.N. Cambridge geotechnical centrifuge operations. Géotechnique 1980, 30, 227–268. [Google Scholar] [CrossRef]
- Kim, D.S.; Lee, S.H.; Choo, Y.W.; Perdriat, J. Self-balanced Earthquake Simulator on Centrifuge and Dynamic Performance Verification. KSCE J. Civ. Eng. 2013, 17, 651–661. [Google Scholar] [CrossRef]
- Yun, J.W.; Han, J.T. Dynamic Behavior of Pile-supported Wharves by Slope Failure during Earthquake via Centrifuge Tests. Int. J. Geo-Eng. 2021, 12, 33. [Google Scholar] [CrossRef]
- Yun, J.S.; Park, S.J.; Falcon, S.S.; Han, J.T.; Kim, D.; Choo, Y.W. Seismic Response of Braced Excavation Wall Supporting Deep Sand Layer Using Dynamic Centrifuge Tests. Soil Dyn. Earthq. Eng. 2024, 183, 108782. [Google Scholar] [CrossRef]
- Sakr, M.; Nasr, A.; Khaffaf, M.; Basha, A. Behavior of Under-reamed Piles under Inclined Uplift Loads in Sand. Int. J. Geo-Eng. 2025, 16, 9. [Google Scholar] [CrossRef]
- Raju, K.V.S.B.; Lakshmi, V. Pullout and Oblique Pullout Resistance of Enlarged Base Piles in Geogrid Reinforced Sand. Int. J. Geo-Eng. 2025, 16, 12. [Google Scholar] [CrossRef]
- Basha, A.M.; Eldisouky, E.A. Effect of Eccentric Loads on the Behavior of Circular Footing With/without Skirts Resting on Sand Soil. Int. J. Geo-Eng. 2023, 14, 13. [Google Scholar] [CrossRef]
- Park, S.; Kim, G.Y.; Chang, I. Experimental Study on the Effect of Surface-projected Conditions on the Mechanical Behavior of Pile Embedded in Sand. Int. J. Geo-Eng. 2024, 15, 22. [Google Scholar] [CrossRef]
- Ullah, S.N.; Hu, Y.; Stanier, S.; White, D. Lateral boundary effects in centrifuge foundation tests. Int. J. Phys. Model. Geotech. 2017, 17, 144–160. [Google Scholar] [CrossRef]




| Conditions | ISO Method | InSafeJIP Method | |
|---|---|---|---|
| Punch-through mechanism | Upper sand |
|
|
| Lower clay |
|
| |
| Squeezing mechanism | Upper weak soil |
|
|
| Lower strong soil |
|
| |
| Reduction factor | Sand |
|
|
| Clay |
|
|
| Soil Layers | Depth (m) | Thickness (m) | N-Value |
|---|---|---|---|
| Silty sand | 0~4.5 | 4.5 | 1~6/30 |
| Clayey soil | 4.5~8.5 | 4.0 | 10~31/30 |
| Silty sand | 8.5~10.7 | 2.2 | 46~50/30 |
| Items | Footings | Leg |
|---|---|---|
| Type | Spudcan | Pile |
| Material | Stainless steel (E 1 = 210 GPa) | |
| Diameter, B (m) | 4, 6, 8 | 4 (all cases) |
| Embedded length, L (m) | Full penetration | 8.5 from the spudcan shoulder |
| Items | 1st Layer | 2nd Layer | 3rd Layer |
|---|---|---|---|
| Soil type | Silty sand | Clay | Silty sand |
| Depth, z (m) | 0~4.5 | 4.5~8.5 | 8.5~10.7 |
| Thickness (m) | 4.5 | 4.0 | 2.2 |
| Relative density, Dr (%) | - | ||
| Submerged unit weight, γ′ (kN/m3) | 8.278 | 6.207 | 9.395 |
| Undrained shear strength, su (kPa) | - | 85.175~161.514 | - |
| Friction angle, ϕ (°) | 28 | - | 42 |
| Models | C1 | C2 | ||
|---|---|---|---|---|
| (Scales) | Model | Prototype | Model | Prototype |
| Spudcan diameter, B (mm) | 80 | 4000 | 120 | 6000 |
| Leg diameter, Bleg (mm) | 80 | 4000 | 80 | 4000 |
| Embedded length of foundation, Lem (mm) | 170 | 8500 | 170 | 8500 |
| Model Name | Spudcan Diameter, B (m) | Analysis Methodology |
|---|---|---|
| M1-1 | 4.0 | ISO method for the vertical capacities |
| M2-1 | 6.0 | |
| M3-1 | 8.0 | |
| M1-2 | 4.0 | InSafeJIP method for the vertical capacities |
| M2-2 | 6.0 | |
| M3-2 | 8.0 | |
| M1 | 4.0 | ISO method for vertical/horizontal/rotational capacity interaction function |
| M2 | 6.0 | |
| M3 | 8.0 |
| Foundations | The Yield Interaction Formula |
|---|---|
| M1 (B = 4 m) | |
| M2 (B = 6 m) | |
| M3 (B = 8 m) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, M.J.; Choo, Y.W. Development of New Jack-Up Substructure Supporting Offshore Wind Turbines in Multi-Layered Soils: Geotechnical Aspects. J. Mar. Sci. Eng. 2025, 13, 2060. https://doi.org/10.3390/jmse13112060
Lee MJ, Choo YW. Development of New Jack-Up Substructure Supporting Offshore Wind Turbines in Multi-Layered Soils: Geotechnical Aspects. Journal of Marine Science and Engineering. 2025; 13(11):2060. https://doi.org/10.3390/jmse13112060
Chicago/Turabian StyleLee, Min Jy, and Yun Wook Choo. 2025. "Development of New Jack-Up Substructure Supporting Offshore Wind Turbines in Multi-Layered Soils: Geotechnical Aspects" Journal of Marine Science and Engineering 13, no. 11: 2060. https://doi.org/10.3390/jmse13112060
APA StyleLee, M. J., & Choo, Y. W. (2025). Development of New Jack-Up Substructure Supporting Offshore Wind Turbines in Multi-Layered Soils: Geotechnical Aspects. Journal of Marine Science and Engineering, 13(11), 2060. https://doi.org/10.3390/jmse13112060







