Uplift Behavior of Suction Bucket Foundations in Sands: Experimental and Numerical Investigations

Abstract

Suction bucket foundations offer efficient installation and reusability for offshore wind turbines, yet their uplift behavior in sands with different permeabilities remains insufficiently understood. This study investigates the uplift behavior of suction bucket foundations in sands with varying permeabilities. Uplift capacity increases by up to 102% as permeability decreases from 7 × 10⁻² to 7 × 10⁻³ cm/s, with a diminishing rate of improvement beyond k ≈ 10⁻⁴ cm/s. A recommended uplift rate range of 10⁻⁵–10⁻⁴ m/s was found to optimize performance, minimizing hydraulic demand and seabed disturbance. The study highlights the critical role of passive suction in enhancing uplift capacity under partially drained conditions and provides key insights for offshore foundation design.

1. Introduction

Wind energy has become a cornerstone of global efforts toward carbon neutrality and sustainable development. Offshore wind power, benefiting from stronger and more consistent winds and fewer spatial constraints than onshore systems, has witnessed rapid expansion worldwide. With increasing turbine sizes and water depths, traditional monopile and gravity-based foundations face installation and economic limitations. In this context, suction bucket foundations—a type of caisson foundation installed by creating negative pressure within a hollow steel skirt—have gained attention for their advantages in ease of installation, reusability, and minimal environmental impact [1,2,3].

Suction foundations were first studied in Europe in the late 20th century, with a focus on their ultimate bearing capacity and failure mechanisms under vertical and combined loads [4,5,6]. Early studies by Christensen and Steensen-Bach [7,8] classified three fundamental uplift failure modes—local shear, base resistance, and overall failure—corresponding, respectively, to drained, partially drained, and undrained conditions. Later, Andersen [9] performed laboratory and field investigations on suction anchors under monotonic and cyclic loading, developing practical design procedures to predict uplift resistance under storm conditions.

The Norwegian Geotechnical Institute [10] also conducted uplift testing and limit-equilibrium analyses to characterize suction bucket capacity, identifying multiple potential slip surfaces. Model testing by several researchers [11,12] further confirmed that uplift capacity in suction buckets is rate-dependent: faster loading rates produce greater negative pressure beneath the lid, thereby increasing uplift resistance. Tests in clay by Luke et al. [13], Rao et al. [14], and Byrne and Houlsby [15] demonstrated that side friction under drained and undrained conditions remains comparable, with friction coefficients of approximately 0.5–0.8, while base resistance coefficients range from 13 to 21. Finite element analyses by Deng and Carter [16] reproduced the three uplift failure modes and yielded capacity relationships consistent with experimental findings.

Subsequent investigations further advanced the understanding of suction bucket behavior under more complex loading and drainage conditions. Clukey et al. [17] and Byrne et al. [18] examined combined loading responses, while Zhang et al. [19] and Zhu et al. [20] revealed that uplift capacity in sand and silt is highly sensitive to loading rate and drainage duration, identifying a clear transition between drained and undrained responses. Du [21] and Xu et al. [22] quantified rate-dependent uplift strength and demonstrated that suction formation and dissipation influence not only the failure mechanism but also soil deformation patterns. Numerical analyses, such as those by Thieken et al. [23], provided insight into the coupled influence of permeability and uplift rate, though primarily in coarse or medium sands. More recent studies have extended these investigations to offshore wind foundations and fine-grained soils, highlighting the importance of rate-dependent and permeability-controlled responses [24]. These findings demonstrate that suction redistribution and partial drainage can significantly affect uplift resistance, emphasizing the need for coupled flow–deformation analyses [25,26].

Despite these advances, several critical issues remain unresolved. First, the interaction between suction development, seepage, and soil–bucket interface friction in low-permeability fine sands is not fully understood. Second, the influence of bucket geometry (aspect ratio) and uplift rate on the transition between drained and undrained behavior has not been systematically quantified. Third, while prior work has recognized the role of internal suction, few studies have examined how the semi-enclosed structure and partial drainage condition jointly control uplift resistance, especially through experimentally validated coupled numerical models.

Accordingly, the present study addresses these gaps by integrating comprehensive physical model tests with fully coupled finite element (FE) analyses to investigate the uplift behavior of suction bucket foundations in fine sands with varying permeabilities. Specifically, this work:

• identifies and classifies uplift failure modes under different drainage conditions;
• quantifies the coupled effects of uplift rate, soil permeability, and bucket aspect ratio on uplift resistance; and
• elucidates the mechanism by which passive suction redistributes shaft friction and influences overall failure behavior.

The findings provide new insight into the rate–permeability coupling effects that govern suction bucket uplift performance, offering engineering guidance for retrieval strategies and capacity assessment of bucket foundations in offshore wind applications.

2. Methods

2.1. Physical Model Test

2.1.1. Model Box

The physical model tests were conducted in a rigid box with internal dimensions of 1.0 m × 1.0 m × 1.2 m (length × width × height). This size was selected to minimize boundary effects during loading. The sidewalls were stiffened with steel pipes to minimize lateral deformation. A drainage valve at the base enabled controlled draw-down during consolidation. The reaction frame supported a hydraulic servo actuator, which applied vertical uplift through a steel strand routed over a pulley to maintain proper alignment of the vertical load. The box base comprised a 0.20 m gravel drainage layer covered by geotextile to prevent sand loss and promote uniform saturation (Figure 1).

2.1.2. Foundation Soils

The test soil used was fine sand. Its permeability was adjusted by mixing the sand with different proportions of clay particles, which allowed simulation of various drainage conditions. In this experiment, particle-size distribution curves of the three sands with contrasting permeabilities were obtained by sieve analysis and are presented in Figure 2. The permeability of the sand was mainly influenced by grain size, grading, porosity, saturation, and mineral composition.

Three types of sand mixtures were prepared:

(a).

Pure fine sand;

(b).

Fine sand + 10% clay;

(c).

Fine sand + 15% clay.

The permeability coefficients of these mixtures were measured using constant-head and falling-head tests. The physical properties of the three soils are summarized in

Table 1. Physical properties of the test soils.

Soil Type	Bulk Density ${\mathit{\gamma }}_{\mathit{d}}$ (kN/m3)	Dry Density ${\mathit{\gamma }}^{\prime }$ (kN/m3)	Minimum Void Ratios emin	Maximum Void Ratios emax	Relative Density Dr	Permeability k (cm/s)	Internal Friction Angle $\mathit{\phi }$ (°)
I (0% clay)	17.56	8.53	0.62	0.9	0.64	8 × 10−3	36.3
II (10% clay)	16.88	7.85	0.64	0.92	0.68	7 × 10−4	35.7
III (15% clay)	19.95	10.55	0.65	0.89	0.7	7 × 10−5	35

.

2.1.3. Model Buckets and Instrumentation

Three types of model caissons were used in the tests. Two of them were made of acrylic to allow visual observation of soil plug behavior and seepage during uplift. These acrylic caissons had an outer diameter of 135 mm and 180 mm, a length of 270 mm, and a wall thickness of 5 mm, corresponding to aspect ratios of 2.0 and 1.5, respectively.

The third caisson was made of Q235 steel, with the same dimensions as the 180 mm acrylic model, used to simulate realistic material stiffness. The bucket lid was equipped with three openings for installing a valve, a lifting ring, and a pressure sensor, as shown in Figure 3.

For clarity, the caissons are denoted as:

(a).

SB: steel caisson;

(b).

AB-1: acrylic caisson with diameter 180 mm (aspect ratio 1.5);

(c).

AB-2: acrylic caisson with diameter 135 mm (aspect ratio 2.0).

The detailed geometric parameters and weights of these caissons are listed in

Table 2. Bucket model size in test and numerical simulations.

Caisson ID	Length L (mm)	Diameter D (mm)	Wall Thickness t (mm)	Aspect Ratio (L/D)	Weight (with Lid)/N
SB	270	180	5	1.5	72.6
AB-1	270	180	5	1.5	12.2
AB-2	270	135	5	2	9.2

.

Although the laboratory tests were conducted at a reduced scale, the setup was designed to preserve the key dimensionless relationships governing drainage behavior. The ratio between uplift rate, bucket diameter, and soil permeability (R = vD/k) was maintained within the range typical of field conditions, ensuring that the transition between drained and partially drained responses was properly captured. The effective stress levels in the tests (about 10~30 kPa) are comparable to those in the shallow seabed, where suction buckets commonly operate. Although geometric effects related to drainage path length may influence absolute capacity, the mechanisms of suction generation and pore-pressure redistribution are expected to remain representative of prototype behavior.

During testing, uplift loading was applied using the hydraulic servo system. Pore pressure sensors were installed at the mid-height and bottom of both the inner and outer sides of the caisson to monitor excess pore water pressure during uplift. Given the assumed isotropy of the soil, a single-sided sensor layout was adopted.

2.1.4. Testing Procedure

The uplift bearing behavior of the bucket foundation is highly dependent on the drainage conditions of the surrounding soil, which are influenced by both uplift rate and soil permeability. To explore this relationship, a series of model tests were conducted using three types of sand with different permeability levels:

(a)

I: k = 8 × 10⁻³ cm/s;

(b)

II: k = 7 × 10⁻⁴ cm/s;

(c)

III: k = 7 × 10⁻⁵ cm/s.

Each sand type was tested under three different uplift rates: 0.1 mm/s, 0.5 mm/s, and 2 mm/s.

Due to scale effects, small-scale model tests tend to deviate from the true uplift bearing capacity of full-scale structures, particularly at higher uplift rates. The discrepancy is generally minor at low uplift rates but increases as the rate rises [27]. Based on previous studies and preliminary tests, the three selected uplift rates were deemed appropriate for capturing the drainage-dependent behavior of the system.

To further investigate inner and outer shaft friction, additional open-top tests and soil pressure measurements were conducted. Soil pressure was measured only in test AB-1 under an uplift rate of 0.1 mm/s. Earth pressure cells were installed symmetrically on both the inner and outer caisson walls at 1/3L, 2/3L, and L depth from the top.

In total, the experimental campaign included: 1 pre-test, 6 open-top tests, 15 closed-top tests and 2 soil pressure tests. Details of all test configurations are provided in

Table 3. Summary of test configurations.

Group	Permeability k (cm/s)	Caisson ID	Aspect Ratio (L/D)	Uplift Rate v (mm/s)	Test Type
I-AB1-V0.5-P	8 × 10−3	AB-1	1.5	0.5	Closed
I-AB1-V0.1-O	8 × 10−3	AB-1	1.5	0.1	Open
I-AB1-V2-O	8 × 10−3	AB-1	1.5	2	Open
II-AB1-V0.1-O	7 × 10−4	AB-1	1.5	0.1	Open
II-AB1-V2-O	7 × 10−4	AB-1	1.5	2	Open
III-AB1-V0.1-O	7 × 10−5	AB-1	1.5	0.1	Open
III-AB1-V2-O	7 × 10−5	AB-1	1.5	2	Open
I-AB1-V0.1	8 × 10−3	AB-1	1.5	0.1	Closed
I-AB1-V0.5	8 × 10−3	AB-1	1.5	0.5	Closed
I-AB1-V2	8 × 10−3	AB-1	1.5	2	Closed
I-AB2V-0.5	8 × 10−3	AB-2	2	0.1	Closed
I-AB2-V2	8 × 10−3	AB-2	2	2	Closed
I-SB1-V0.5	8 × 10−3	SB	1.5	0.5	Closed
II-AB1-V0.1	7 × 10−4	AB-1	1.5	0.1	Closed
II-AB1-V0.5	7 × 10−4	AB-1	1.5	0.5	Closed
II-AB1-V2	7 × 10−4	AB-1	1.5	2	Closed
II-AB2-V0.1	7 × 10−4	AB-2	2	0.1	Closed
II-AB2-V2	7 × 10−4	AB-2	2	2	Closed
II-SB1-V0.5	7 × 10−4	SB	2	0.5	Closed
III-AB1-V0.1	7 × 10−5	AB-1	1.5	0.1	Closed
III-AB1-V0.5	7 × 10−5	AB-1	1.5	0.5	Closed
III-AB1-V2	7 × 10−5	AB-1	2	2	Closed
II-AB1-V0.1-SP	7 × 10−4	AB-1	1.5	0.1	Closed
III-AB1V0.1-SP	7 × 10−5	AB-1	1.5	0.1	Closed

Note: “Closed” = closed-top test, “Open” = open-top test, “Soil Pressure (SP)” = test with soil pressure measurement. AB/SB are acronyms for acrylic/steel bucket foundations as defined in Table 2.

.

2.2. Numerical Simulation

Coupled FE analyses were conducted in ABAQUS to extend the test envelope and visualize variables not directly observable—soil deformation, seepage fields, and excess pore pressure.

To complement the physical tests, a series of numerical simulations were conducted using ABAQUS. These simulations aimed to expand the range of uplift rates and soil permeabilities and to better understand the soil–caisson interaction mechanisms during uplift.

2.2.1. Model Setup

Finite element models were developed in ABAQUS to replicate both the model-scale and full-scale conditions. To verify the reliability of the numerical results, one model was constructed with the same dimensions as the AB-1 caisson used in the physical test. The calibrated parameters from this comparison were then applied to larger-scale models.

Due to the axisymmetric geometry of the bucket foundation and the loading setup, all simulations used two-dimensional axisymmetric elements. The horizontal extent of the soil domain was set to three times the caisson diameter, and the vertical extent was three times the caisson height, to minimize boundary effects.

Table 4. Finite element model dimensions.

Scale	Model ID	Diameter D (mm)	Height L (mm)	Aspect Ratio L/D	Wall Thickness t1 (mm)	Lid Thickness t2 (mm)
1:50	I	180	270	1.5	3	10
1:1	II	9000	13,500	1.5	30	100
	III	6250	13,500	2	30	100

summarizes the dimensions of the three numerical models.

A typical mesh layout is shown in Figure 4. The mesh was refined near the caisson and gradually coarsened outward to reduce computational cost while maintaining accuracy.

2.2.2. Constitutive Models and Coupling

The simulations used a fully coupled stress–pore pressure analysis, implemented through the ABAQUS/Standard solver. Soil permeability was modeled using a simplified Darcy–Forchheimer law. The analysis adopted transient steps to track the evolution of excess pore water pressure and displacement over time.

The soil was modeled as a saturated granular material governed by the effective stress principle, using the linear elastic Mohr–Coulomb model. This simplification was adopted because both the experimental and numerical uplift processes involved relatively small strains, generally below the yield range of dense fine sand, where the stress–strain response can be regarded as approximately linear. Although sands may show nonlinear stiffness degradation at higher strain levels, the stress range in this study remained moderate, making such effects negligible for the present simulations. Similar assumptions have been adopted in previous analyses of suction caisson uplift behavior [16,23].

To capture the behavior of the water plug formed between the bucket lid and soil plug, a “water unit” was introduced. This unit mimics the accumulation of water in this gap and its contribution to suction pressure. Following previous research [24,25], the water unit was modeled as a soft porous elastic material with parameters:

(a).

Elastic modulus: 10⁻⁵ kPa

(b).

Poisson’s ratio: 0.3;

(c).

Unit weight: 10 kN/m³;

(d).

Permeability: same as surrounding soil

The water unit was inserted at the interface between the bucket lid and soil plug, as shown in Figure 5.

The material parameters of the soil and the bucket foundation were determined based on results from laboratory direct shear tests and calibration against previous model test data. The detailed values are listed in

Table 5. Material parameter settings.

Material	Unit Weight γ′ (kN/m3)	Elastic Modulus E (Gpa)	Poisson’s Ratio μ	Friction Angle φ (°)	Dila-tion Angle ψ (°)	Permeability k (cm/s)	Void Ratio e	Interface Friction Coefficient μk	Lateral Earth Pressure Coefficient K0
caisson	68.5	210	0.3	\	\	\	\	\	\
Saturated Sand	10	0.03	0.3	30	1	0.007	0.7	0.46	0.5

.

2.2.3. Mesh and Boundary Conditions

Structured meshing was used for both the caisson and the surrounding soil. To ensure the numerical model provided sufficient accuracy without excessive computational demand, a mesh-sensitivity analysis was performed prior to finalizing the finite element configuration. The mesh was refined progressively in regions of high stress and pore-pressure gradients—particularly around the skirt tip, lid edge, and the “water plug” zone beneath the bucket—while larger elements were used farther away to reduce model size. The element dimensions were reduced stepwise, and the variation in the predicted peak uplift load was monitored until the difference between successive refinements fell below about 3%.

Three mesh densities were examined. Near the caisson wall and base, element sizes ranged from roughly 3–6 mm, gradually increasing to about 12–25 mm toward the outer and lower boundaries of the soil domain. The medium-density mesh produced uplift capacities within approximately 3% of the fine-mesh result, while cutting the computational time by nearly half. Considering both convergence and efficiency, this mesh was adopted for the subsequent analyses.

The final model contained on the order of 30,000 elements. The adopted graded mesh ensured accurate representation of the stress transfer at the bucket–soil interface and stable convergence of the coupled pore-pressure–displacement solution, providing a reasonable balance between precision and computational cost.

The soil and water plug were modeled using 4-node axisymmetric pore pressure–displacement elements (CAX4P), which allow coupled flow–deformation analysis. The bucket foundation was modeled as a non-permeable linear elastic material using 4-node axisymmetric displacement elements (CAX4).

The interaction between the caisson wall and the soil was defined using a surface-to-surface contact algorithm. The caisson wall (stiffer material) was set as the master surface, and the soil was set as the slave surface. Normal contact was defined as “hard contact” with no separation, while tangential behavior followed the Coulomb friction law.

The water unit was tied to both lid and surrounding soil to prevent numerical separation. The boundary conditions of the numerical model were defined to replicate realistic soil–bucket interaction while minimizing boundary effects. The bottom of the soil domain was fully fixed in all directions (u_x = u_y = u_z = 0), and the lateral boundaries were set as rollers (u_n = 0) to restrict horizontal movement but allow vertical displacement. The lateral distance between the bucket skirt and the model boundary was not less than 3D, ensuring that the boundaries did not influence stress or pore-pressure fields. Hydraulic boundary conditions were applied as no-flow on the lateral and bottom boundaries. The ground surface was set as drained for open-top cases and as undrained for closed-top cases, while the internal lid pressure was coupled with the pore pressure inside the bucket cavity. A sensitivity check showed that increasing the lateral extent from 3D to 5D changed the peak uplift capacity by less than 6%, confirming that the adopted boundary configuration was sufficient for accurate simulation. The ground surface was zero-pore-pressure (free-draining) to allow dissipation during uplift.

2.3. Validation of Numerical Modeling

To verify the accuracy of the finite element model, numerical results from Model I (scaled to match AB-1) were compared with physical test results under two test conditions: (a) Group I–AB1–V0.1 (uplift rate v= 0.1 mm/s) and (b) Group I–AB1–V2 (uplift rate v = 2 mm/s)

The comparison focused on two key metrics: uplift load–displacement curves and negative pressure–displacement curves.

Figure 6 shows the comparison between numerical and experimental results. The overall trend and magnitude of the curves were in good agreement, especially in the 2 mm/s test. A small deviation was observed in the 0.1 mm/s test, particularly for the negative pressure, which is more sensitive to drainage effects and material heterogeneity.

Table 6. Comparison between simulation and experimental Peak values.

Uplift Rate (mm/s)	Parameter	FEM Result	Experimental Result	Error (%)
0.1	Uplift Load (N)	134.4	124.5	7.95%
	Negative Pressure (kPa)	−1.54	−1.32	16.67%
2	Uplift Load (N)	264.5	287.6	8.7%
	Negative Pressure (kPa)	−5.95	−6.48	8.9%

summarizes the peak values from both simulation and physical tests. Except for the 0.1 mm/s case, where negative pressure deviated by 16.67%, all other results showed less than 9% error. These results confirm that the numerical model accurately reflects the uplift behavior of the bucket foundation under both low and high uplift rates.

To verify the robustness of the experimental data used for model validation, a series of duplicate uplift tests was conducted under identical conditions for selected combinations of soil permeability and uplift rate. The measured uplift capacities and displacement responses showed variations in less than 12%, and the patterns of suction development and friction redistribution remained consistent among repeated runs. These results confirm that random experimental uncertainty had a negligible influence on the observed uplift behavior, ensuring the reliability of the data employed for numerical validation and subsequent analyses.

3. Results

3.1. Uplift Failure Mechanisms

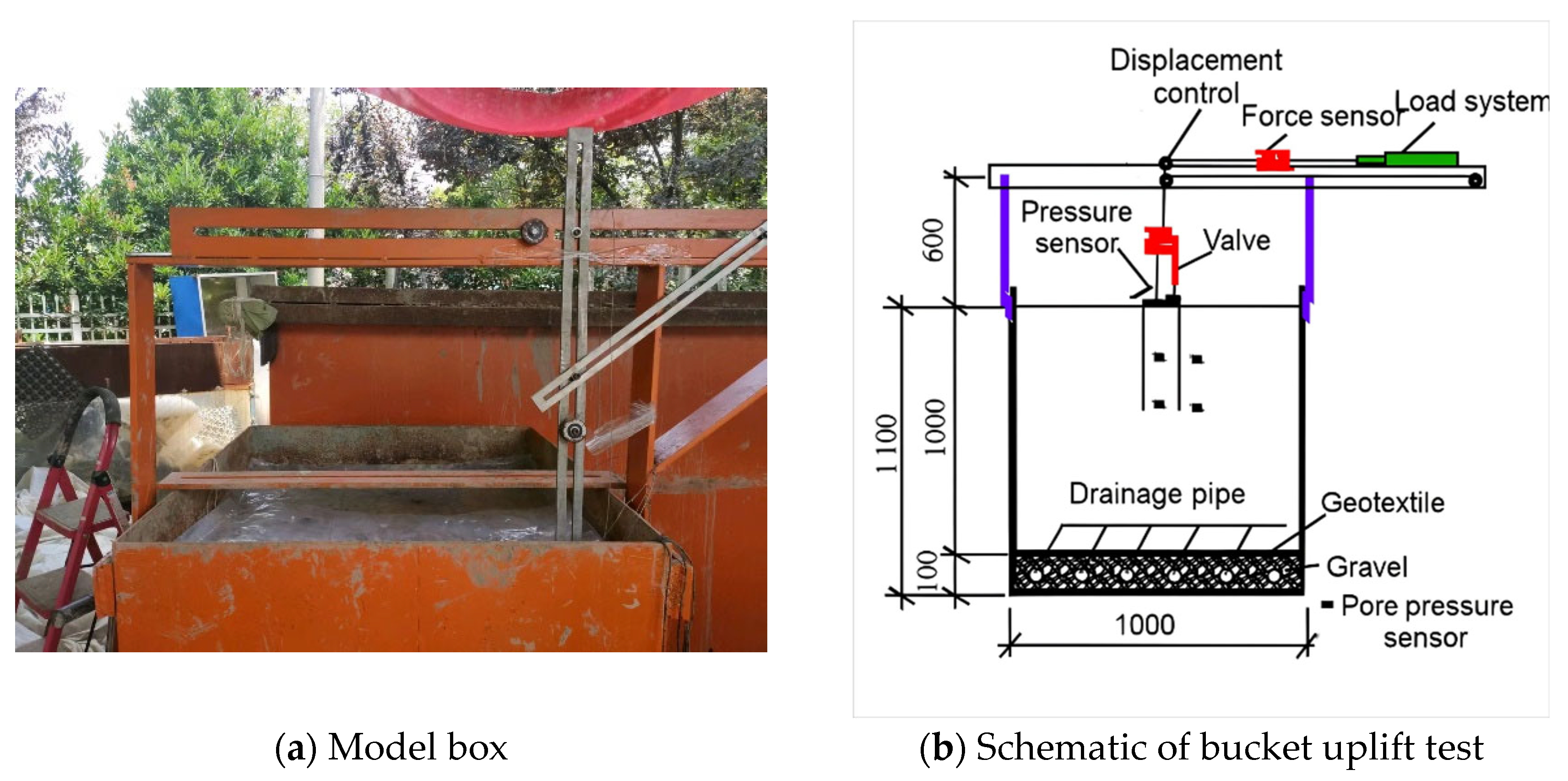
The uplift failure mechanisms of suction bucket foundations were analyzed by examining the evolution of negative pressure at the bucket lid and pore water pressure inside and outside the caisson during loading. Observations from the physical tests were used to support the interpretation of the results.

3.1.1. Results of Open-Top (Vented-Lid) Uplift Tests

To examine shaft friction development without the influence of internal suction, open-top uplift tests were conducted using the acrylic model caisson AB-1 (aspect ratio L/D = 1.5). In these tests, the caisson was fully extracted without carrying the soil plug (Figure 7). The measured uplift load corresponded primarily to the caisson’s self-weight and any frictional resistance.

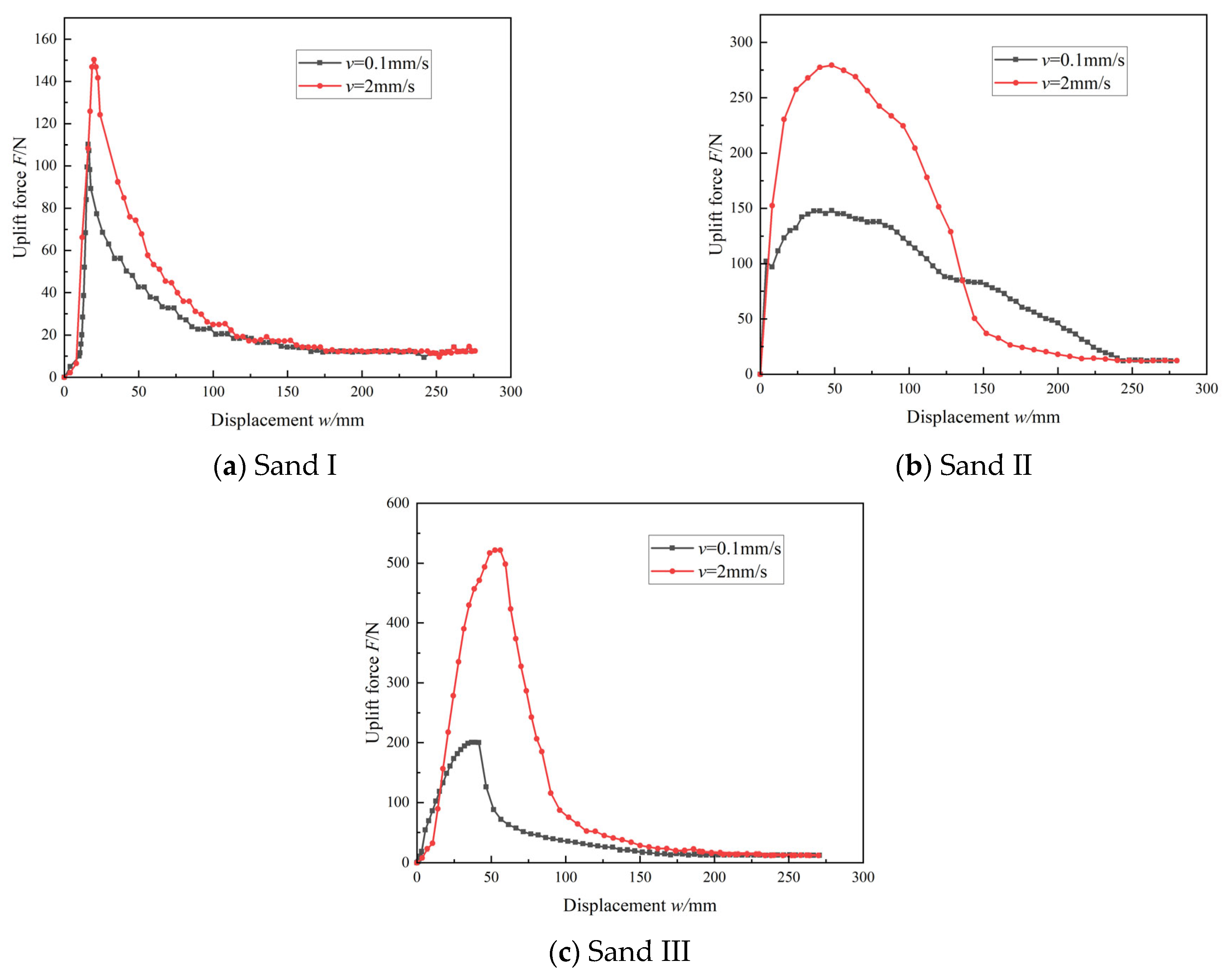
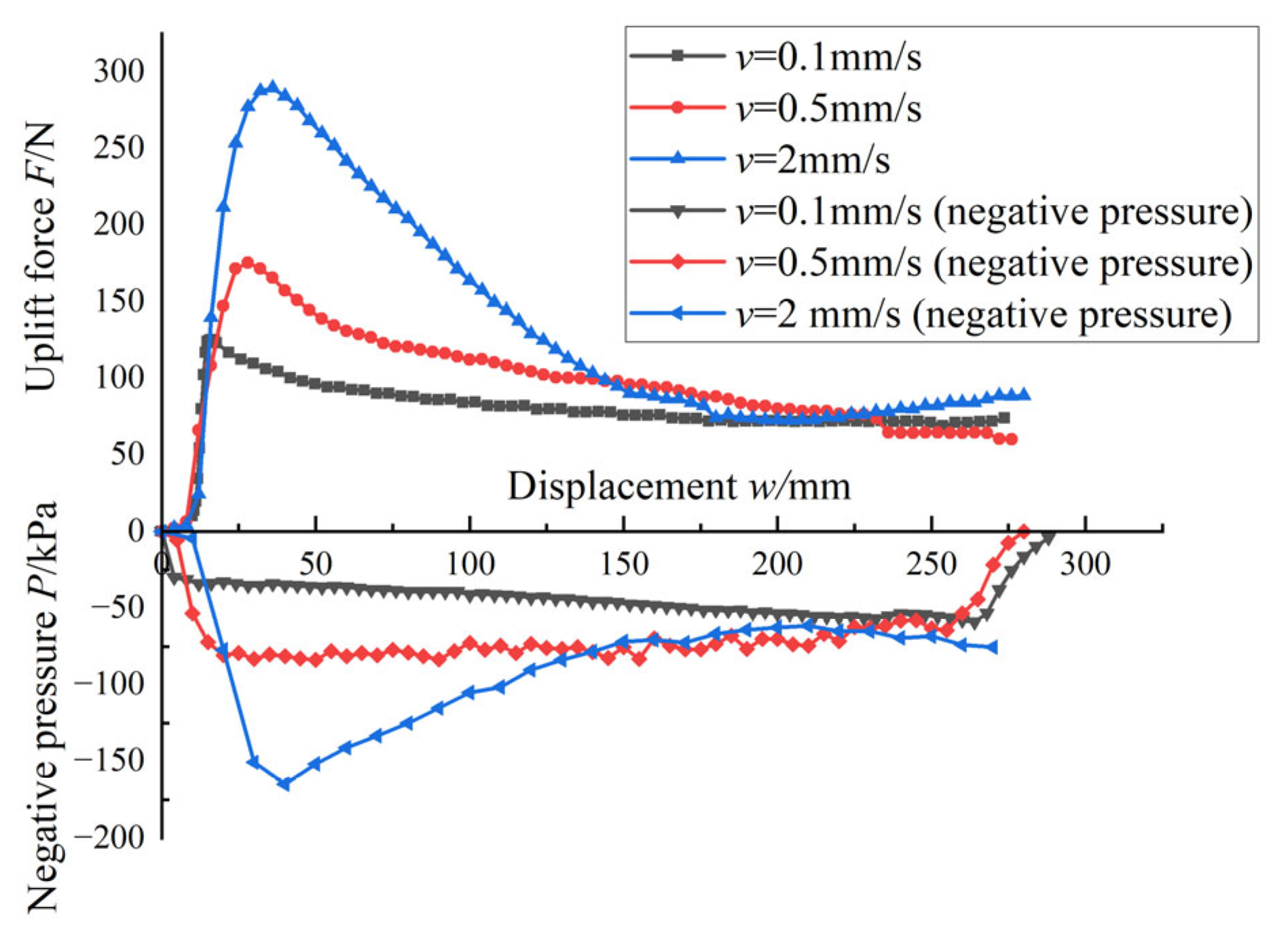
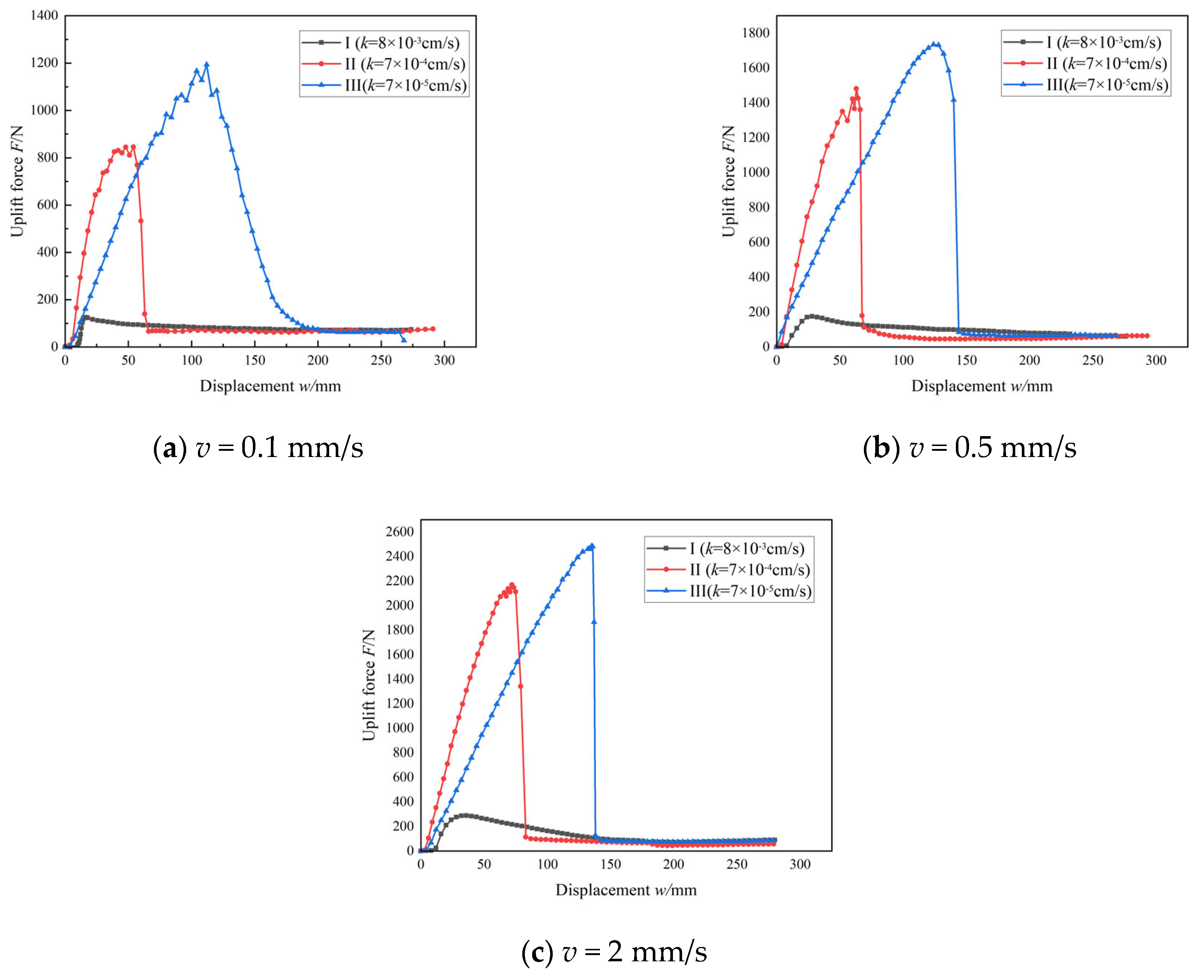
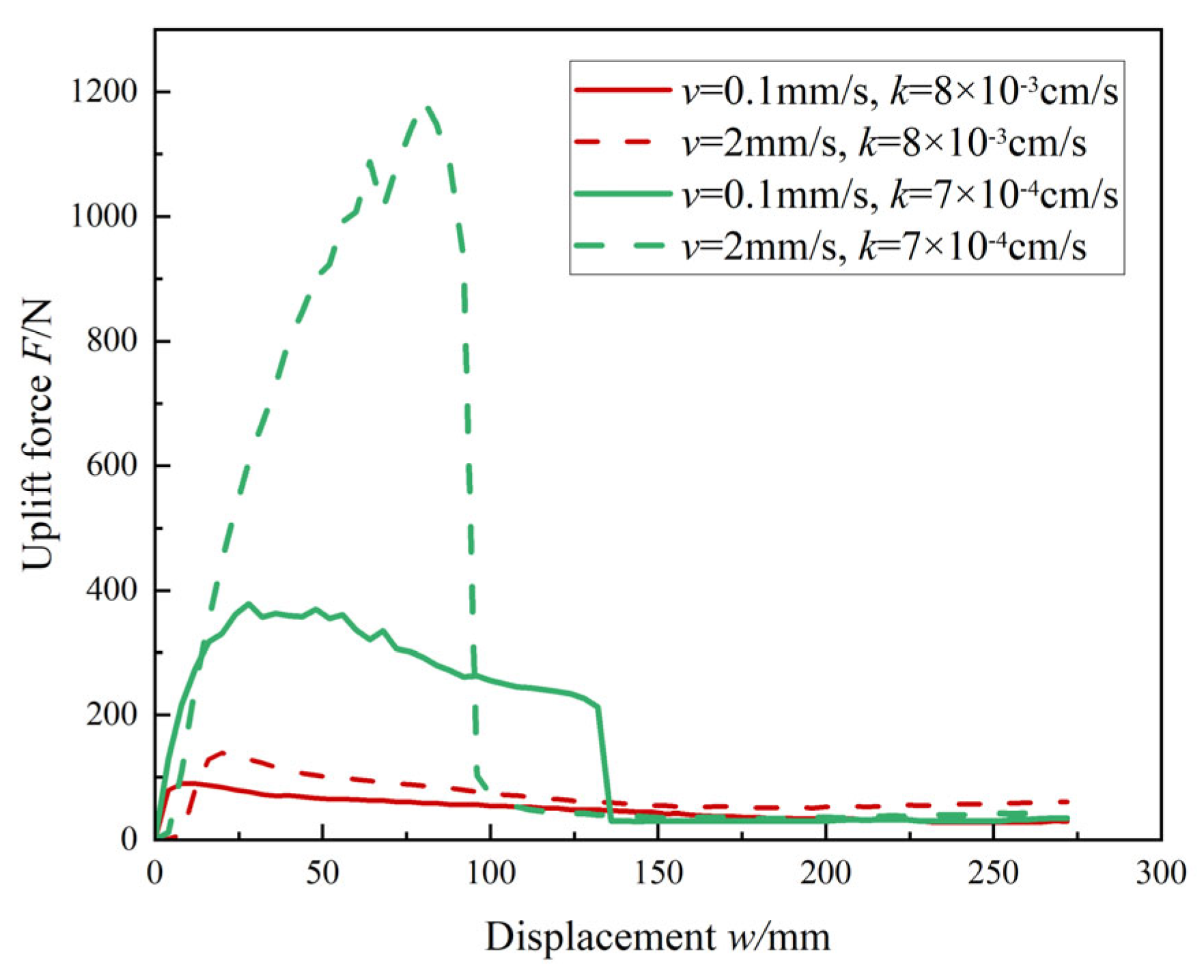
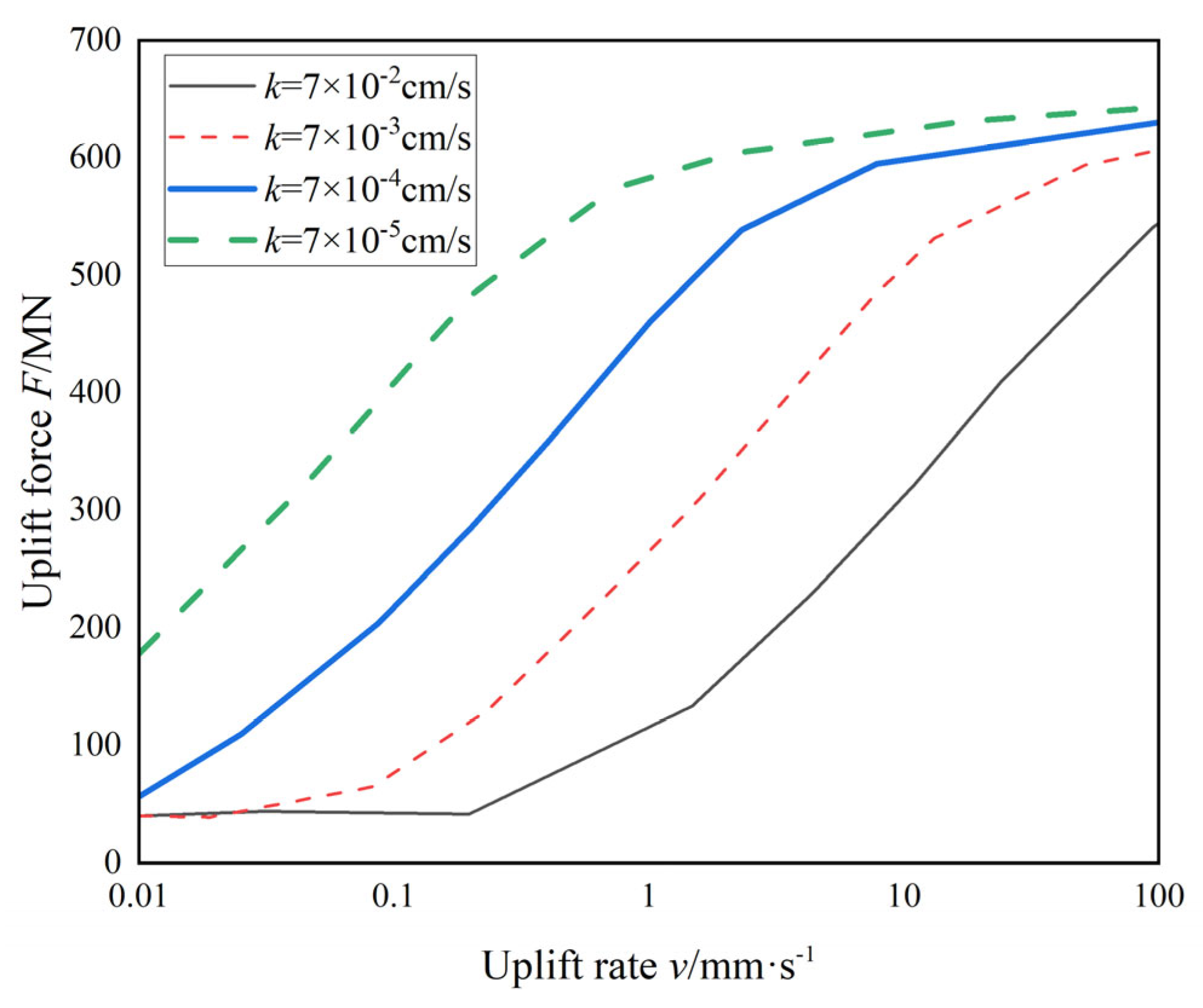
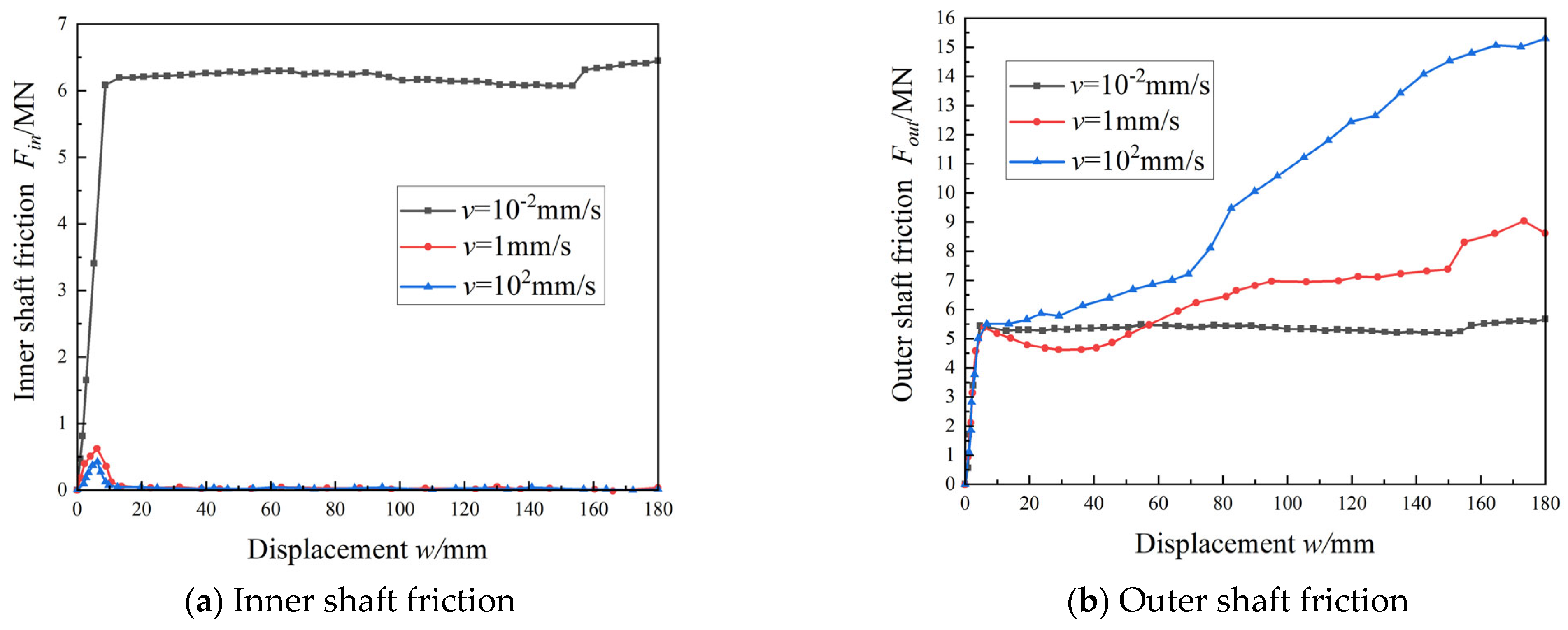
Figure 8 shows the load–displacement curves for different sand types (I, II, and III) under uplift rates of 0.1 mm/s and 2 mm/s. According to the local shear failure mode proposed by Deng et al. [16], when there is no negative pressure at the lid, the uplift bearing capacity mainly consists of the caisson’s self-weight and shaft friction along both the inner and outer walls. These components should theoretically not be sensitive to the uplift rate. However, test results demonstrated that higher uplift rates resulted in significantly larger uplift loads, particularly in low-permeability soils. This implies that, in addition to shaft friction and self-weight, other resistance mechanisms contributed to the overall uplift resistance.

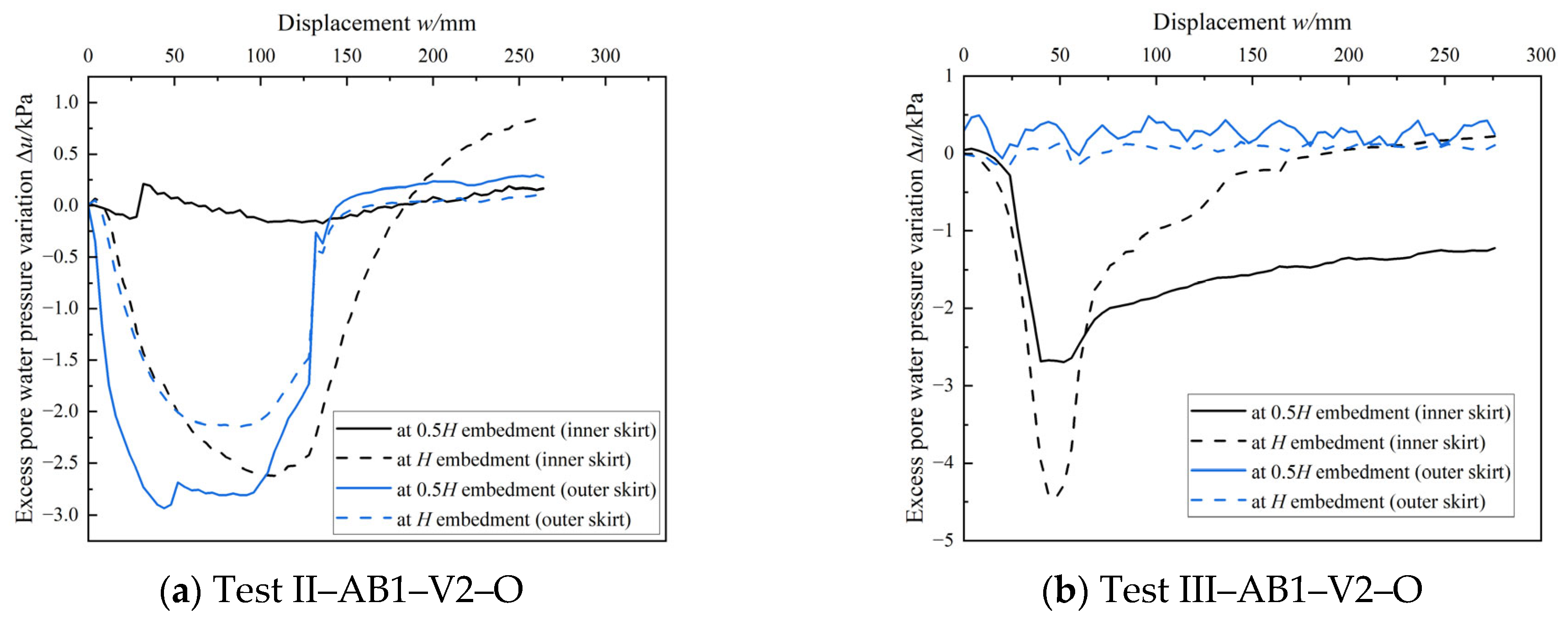
Further analysis of pore pressure data (Figure 9) showed negative pore pressure developing near the base of the caisson during the 2 mm/s tests. This indicates reverse end-bearing resistance, even without a soil plug. In contrast, no obvious pore pressure change was observed at the lower uplift rate (0.1 mm/s), suggesting the end-bearing effect could be neglected.

Based on these results, shaft friction in each sand type at low uplift rate (0.1 mm/s) was estimated as follows:

(a)

Sand I (k = 8 × 10⁻³ cm/s): approximately 108.3 N;

(b)

Sand II (k = 7 × 10⁻⁴ cm/s): approximately 147.84 N;

(c)

Sand III (k = 7 × 10⁻⁵ cm/s): approximately 200.2 N.

These values show a clear trend of increasing shaft friction with decreasing permeability, which can be attributed to reduced seepage loss and higher effective stress along the bucket-soil interface.

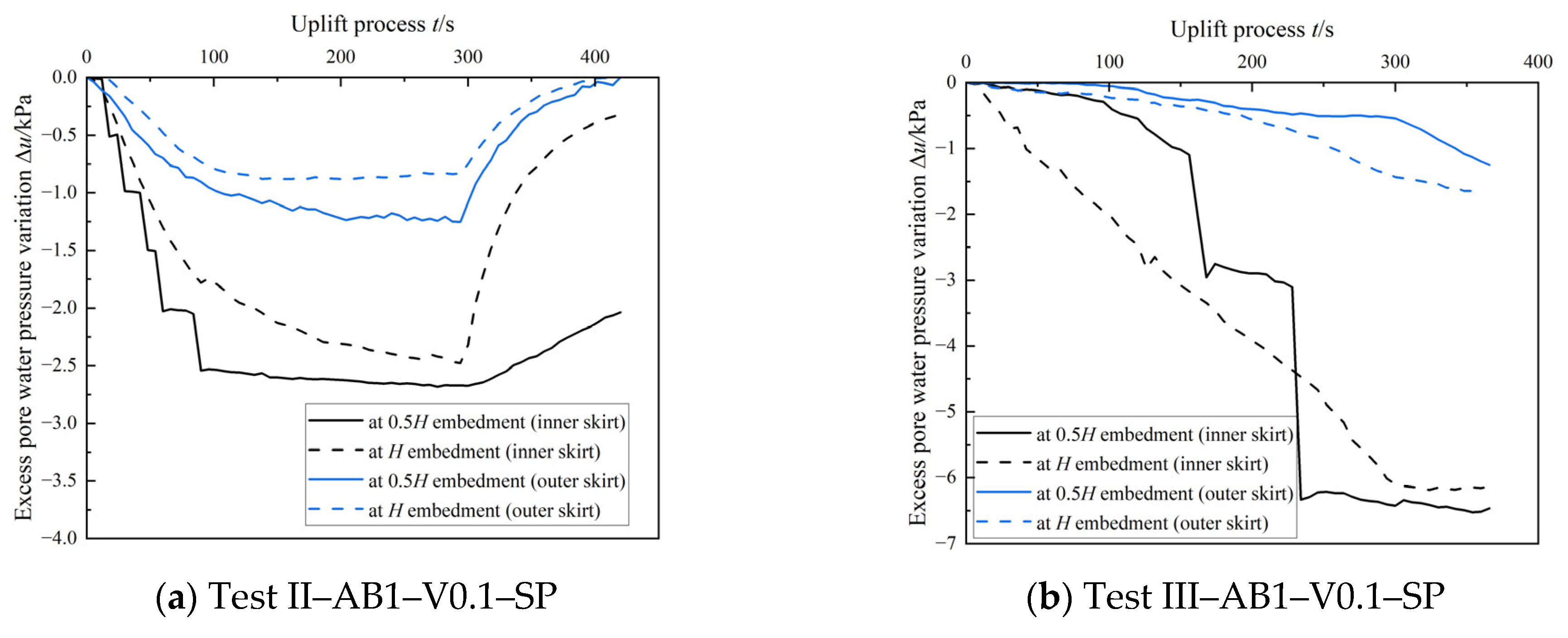
To explore shaft friction evolution during uplift, soil pressure tests were conducted for caisson AB-1 in Sands II and III. Since earth pressure cells can detach or disturb soil during rapid motion, tests were conducted at an uplift rate of 0.1 mm/s with a target displacement of 30 mm. All measurements were recorded as relative changes, with the system zeroed before testing.

As shown in Figure 10, pore water pressure on both the inner and outer sides of the caisson gradually decreased, eventually becoming negative. For Sand II, pore pressures at 0.5H and H depths inside the caisson were −2.68 kPa and −2.48 kPa, respectively. For Sand III, corresponding values were −6.52 kPa and −6.19 kPa. The pressure gradient was small in both cases, indicating uniform negative pressure distribution inside the caisson. Moreover, the magnitude of negative pressure increased with decreasing permeability.

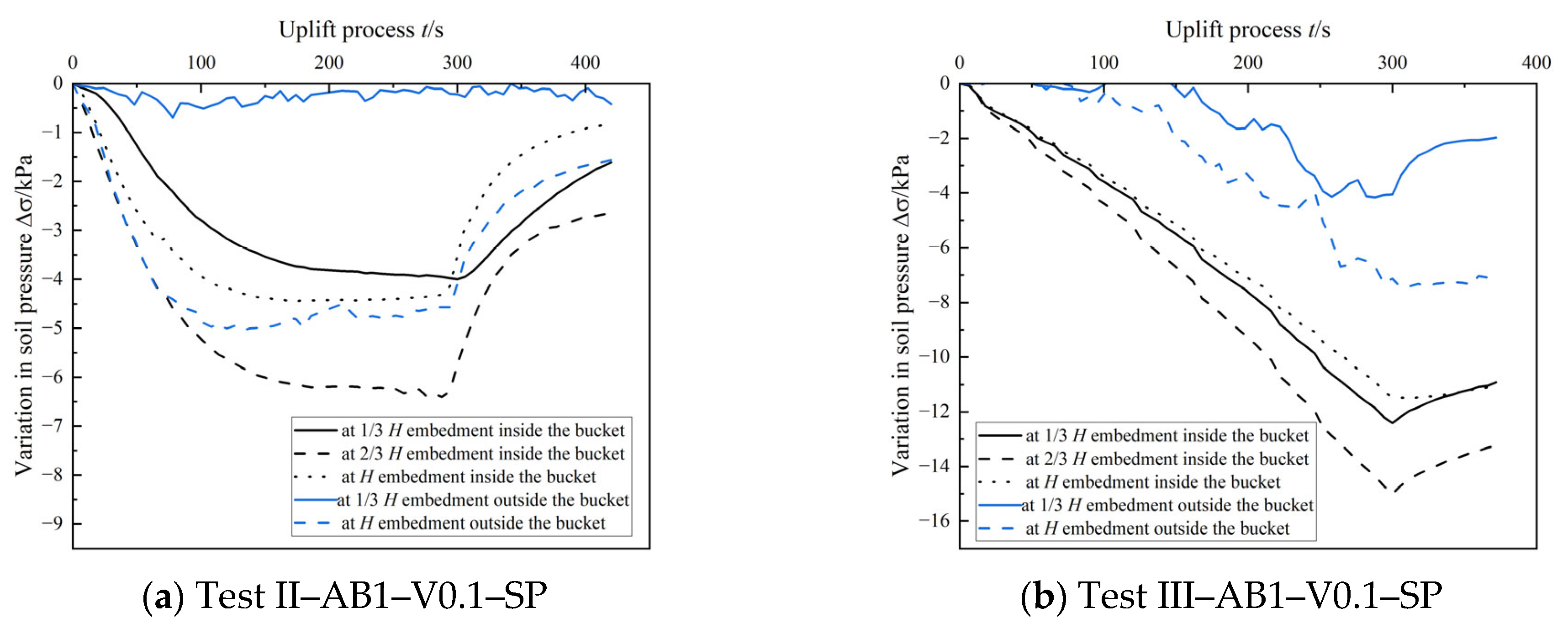
The soil pressure variations measured during uplift are shown in Figure 11. Some abnormal values were excluded from analysis (e.g., outer 2/3H sensor in Test II, and outer 1/3H sensor in Test III). In general, soil pressure decreased with uplift, and the reduction was more pronounced on the inner wall.

Since total stress was measured by the sensors, and frictional resistance depends on effective stress, effective stress was estimated based on the difference between total and pore water pressure at each depth. The results are summarized in

Table 7. Changes in effective stress inside and outside the caisson.

Group	Inner 1/3L $\Delta {\mathit{\sigma }}^{\prime }$ (kPa)	Inner 2/3L $\Delta {\mathit{\sigma }}^{\prime }$ (kPa)	Inner L $\Delta {\mathit{\sigma }}^{\prime }$(kPa)	Outer 1/3L $\Delta {\mathit{\sigma }}^{\prime }$ (kPa)	Outer 2/3L $\Delta {\mathit{\sigma }}^{\prime }$ (kPa)	Outer L $\Delta {\mathit{\sigma }}^{\prime }$
II-AB1V0.1SP	−1.32	−3.72	−1.76	0.55	/	−2.05
III-AB1V0.1SP	−5.89	−8.5	−5.31	/	−2.92	−5.79

.

In all cases, the reduction in effective stress was greater in Sand III than in Sand II, and the greatest drop occurred at the 2/3H position inside the caisson. Overall, the inner wall experienced more stress reduction than the outer wall, and this difference became more prominent in lower-permeability soils.

This trend may be attributed to the negative pressure formed inside the caisson, as well as upward drag forces. These results suggest that using pre-uplift effective stress alone may underestimate or misrepresent the actual shaft resistance, especially under partially drained or undrained conditions.

3.1.2. Results of Closed-Top (Sealed-Lid) Uplift Tests

As revealed in the vented-lid tests, the total uplift resistance F primarily consists of the bucket self-weight W_f, inner and outer shaft friction F_s, and reverse end bearing resistance F_fb (excluding the soil plug). In Sand I, under an uplift rate of 0.1 mm/s, the excess pore water pressure remained nearly constant, allowing the end bearing resistance to be considered negligible. Thus, the load–displacement curve primarily reflects the evolution of shaft friction, which peaked at 110.2 N when the displacement reached 16 mm, indicating full mobilization of shaft friction (Figure 8a).

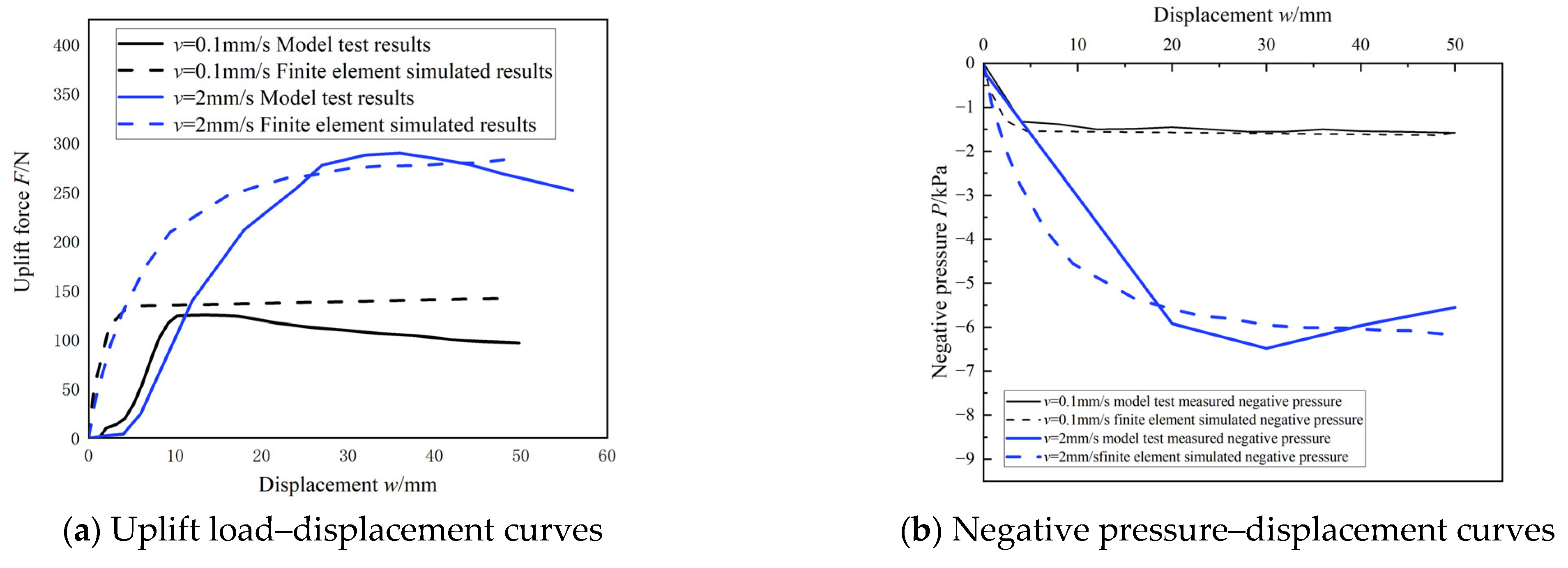
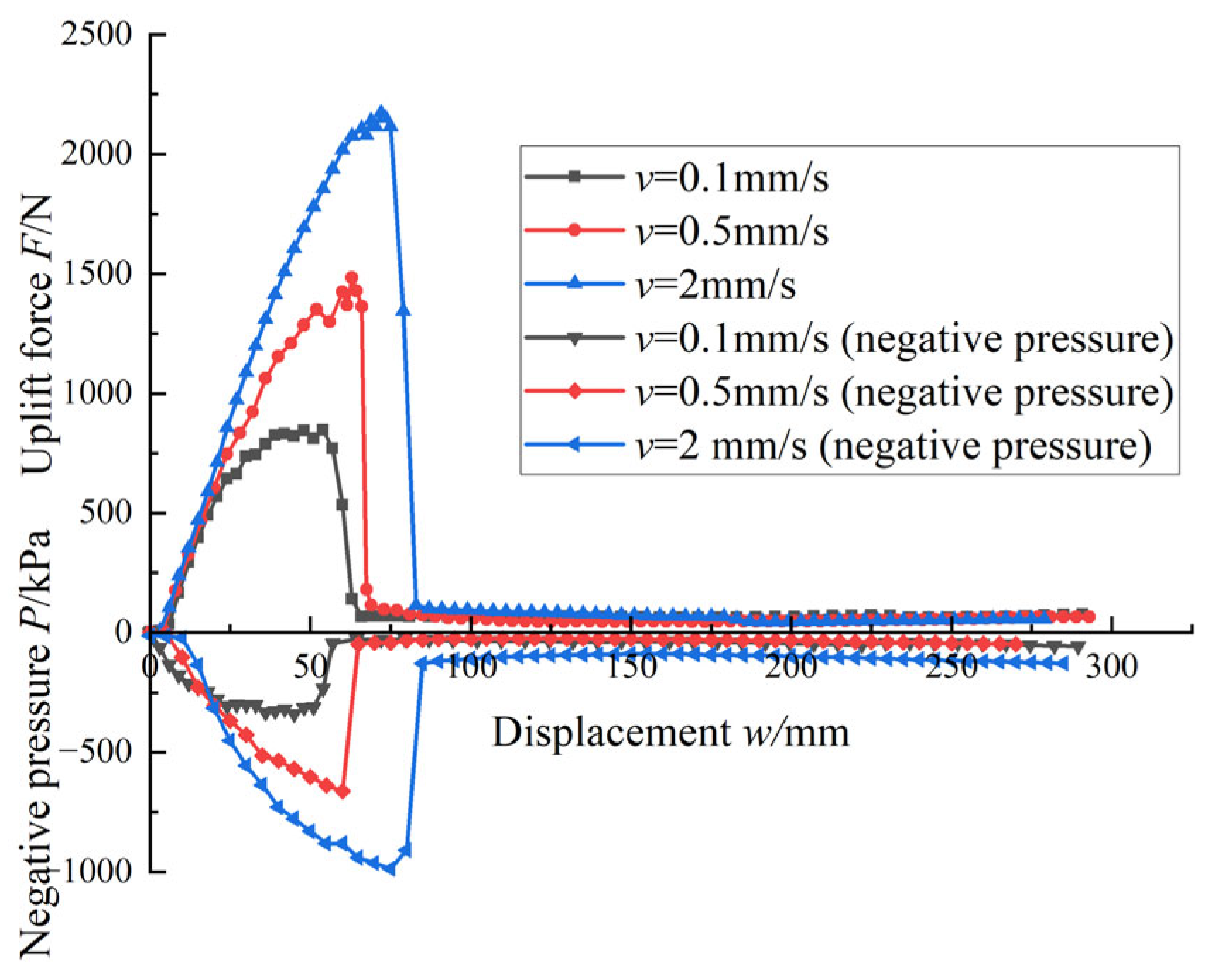
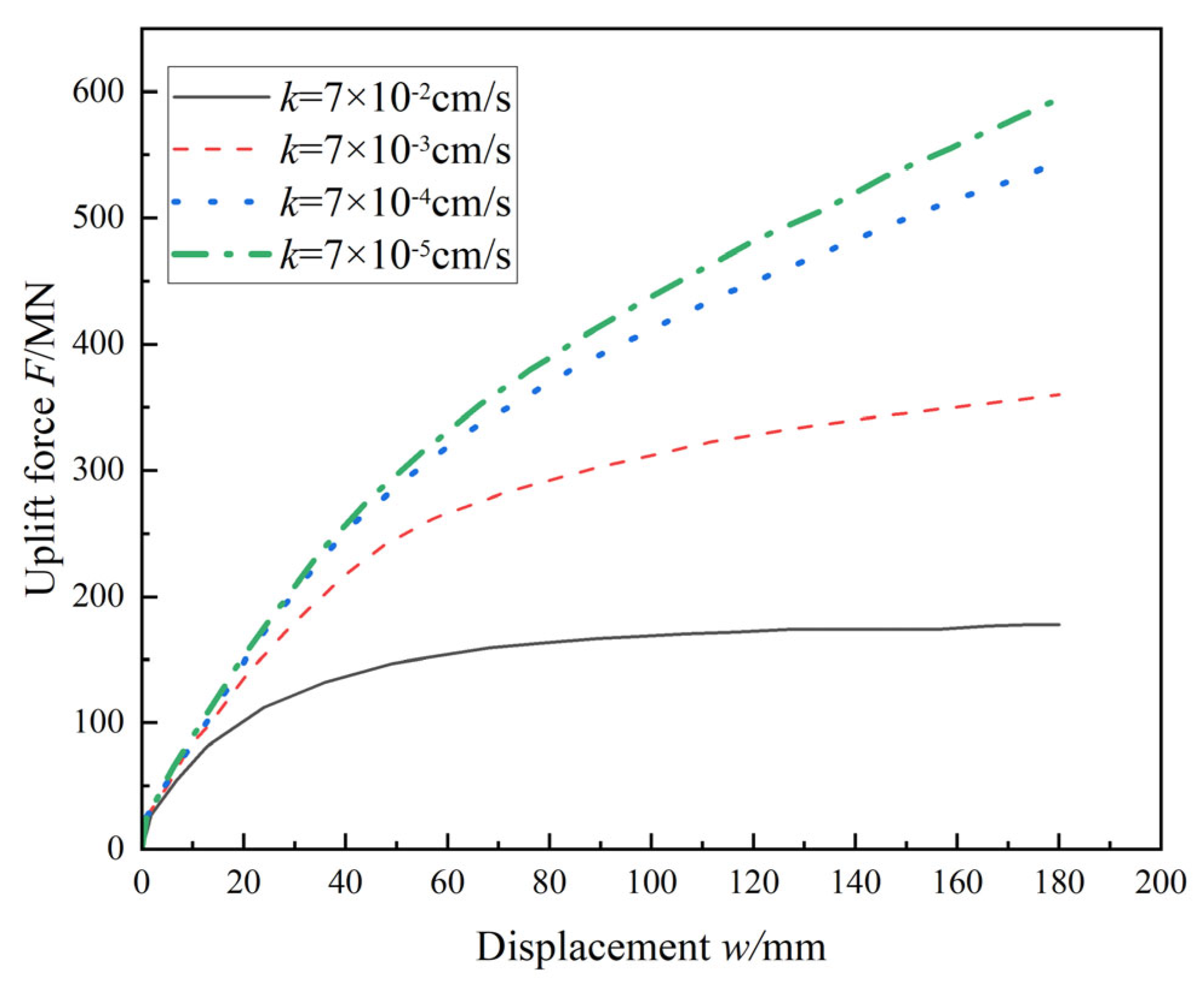
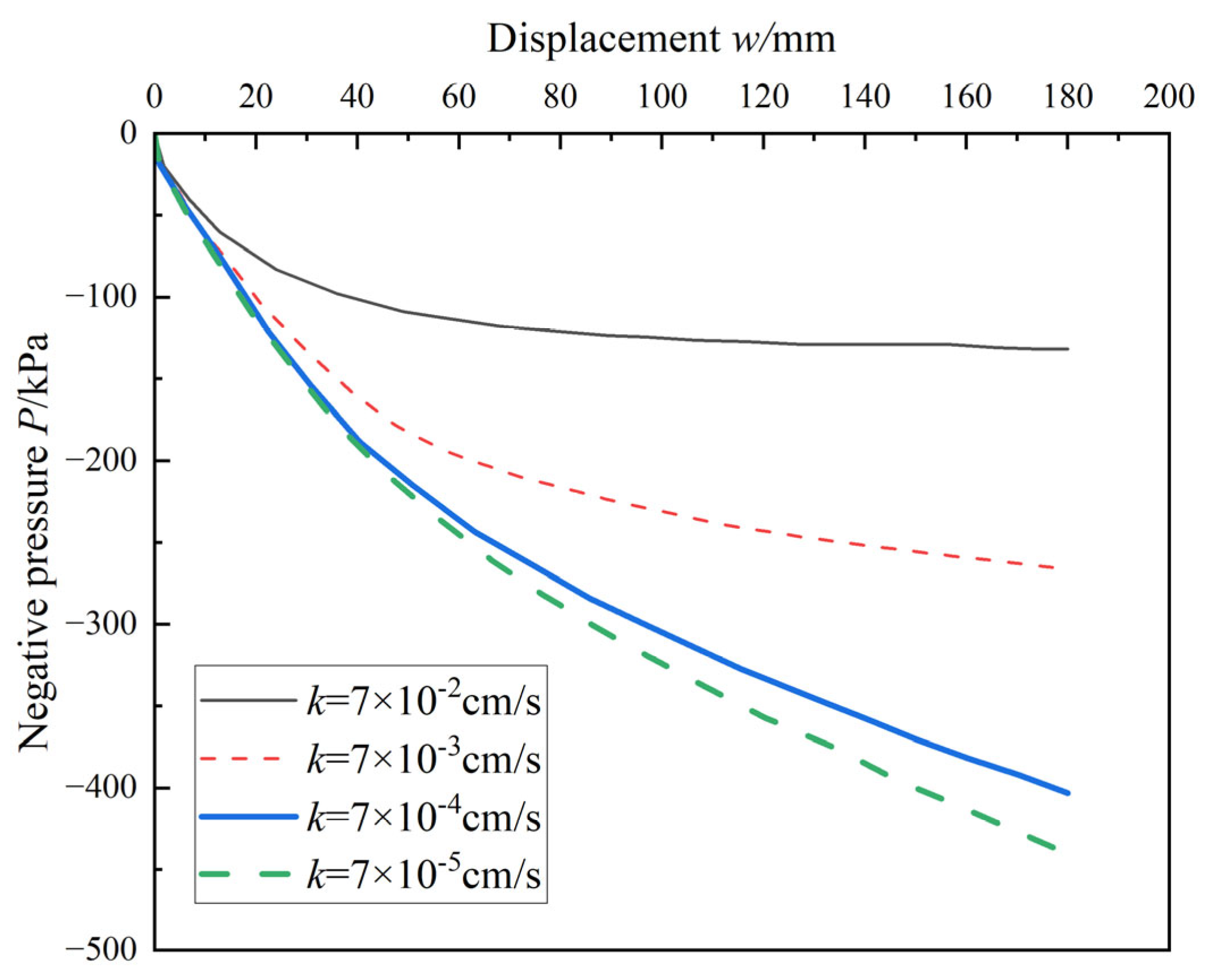
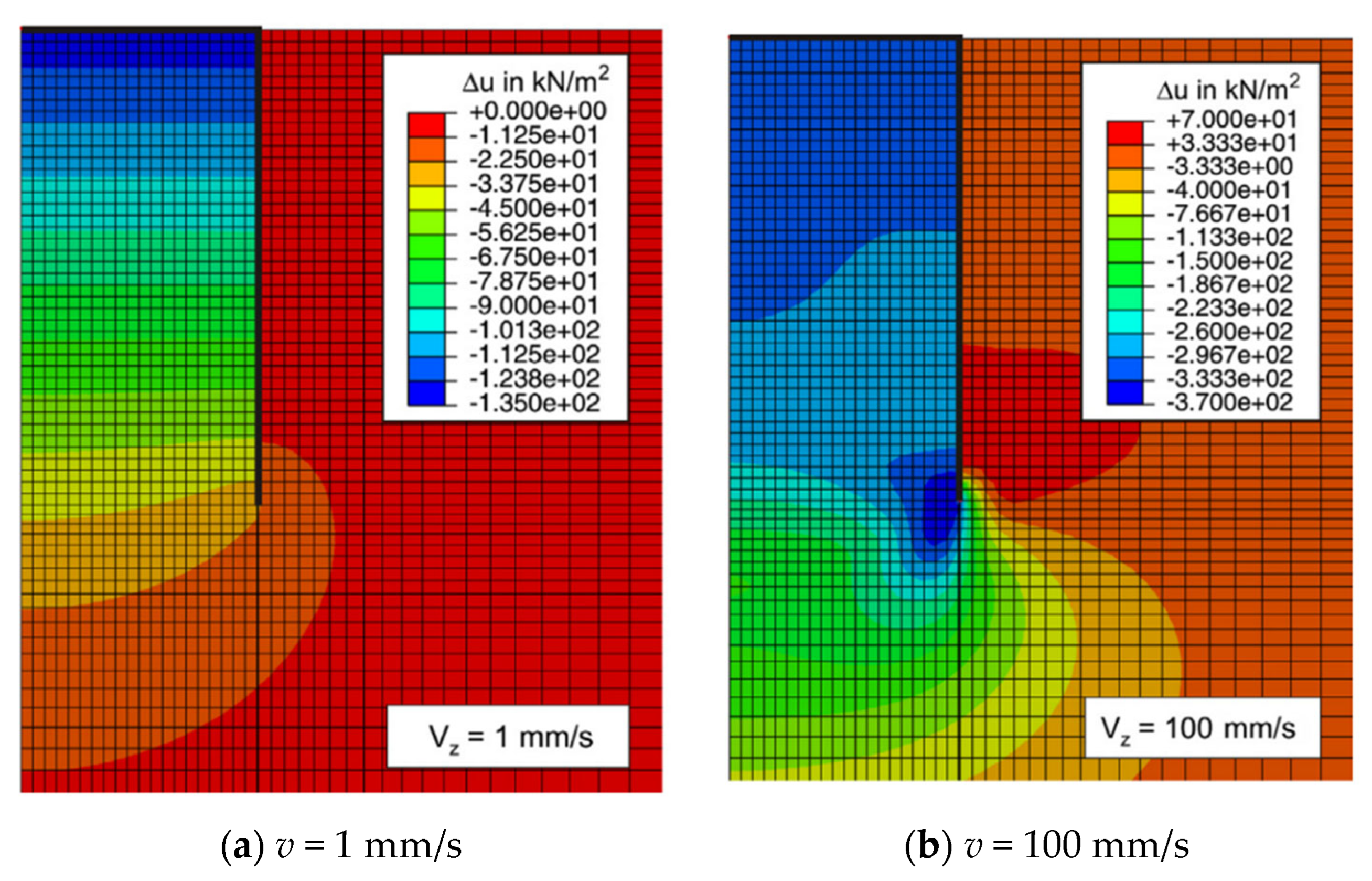
In the sealed-lid uplift tests, load and negative pressure at the bucket lid were recorded under different uplift rates (Figure 12). At 0.1 mm/s, the test condition corresponded to fully drained behavior, and failure occurred through localized shear. Initially, a water plug formed within the bucket. As uplift progressed, the contact area between the soil and shaft decreased, leading to a reduction in shaft friction. Meanwhile, the elevation difference between the water plug and the free surface increased, requiring higher negative pressure to maintain equilibrium. When uplift reached 175 mm, the load stabilized, suggesting complete loss of shaft friction. At this point, the uplift resistance was mainly attributed to the weight of the bucket and the water plug, with the surrounding soil becoming disturbed and detached.

When the uplift rate increased to 0.5 mm/s, noticeable negative pressure developed at the bucket lid, indicating partially drained conditions. At the initial stage, the soil plug was dragged upward, providing additional end resistance. The uplift load and negative pressure peaked simultaneously at a displacement of 28 mm, with values exceeding those in the 0.1 mm/s test (Figure 12). Observations (Figure 13) revealed the formation of seepage channels between the inner wall and the soil plug, through which sand particles were carried upward. The space between the lid and the plug was rapidly filled with water. After this stage, the height of the soil plug remained unchanged, and end resistance gradually dissipated, causing the load to decline. However, the sustained seepage maintained high negative pressure, contrasting with the fully drained case.

At a higher rate of 2 mm/s, suction developed before the uplift capacity reached its peak, indicating the test remained under partially drained conditions. The soil plug was also pulled out. At 36 mm of uplift, both uplift load and negative pressure reached maximum values. Air bubbles were observed outside the bucket, suggesting the development of seepage channels along the outer shaft wall (Figure 14), although no significant seepage failure was observed within the soil plug. After the peak, the plug continued to rise, but both load and suction dropped sharply, indicating rapid dissipation of bottom resistance.

In Sand II (k = 7 × 10⁻⁴ cm/s), sealed-lid uplift tests showed that under 0.1 mm/s loading, clear suction developed at the lid, implying partially drained conditions. The soil plug was pulled upward early in the test, and both uplift load and negative pressure rose sharply, then entered a plateau stage before peaking at 54 mm displacement (Figure 15). Seepage was observed from the top of the bucket, and a pit formed 0.25D away from the shaft wall, accompanied by visible seepage (Figure 16). After peaking, bottom resistance rapidly dissipated, and both load and suction dropped to near zero. After the test, the water in the box was drained to observe residual failure features. A pit was found to have penetrated from the ground surface to the outer wall of the bucket (Figure 17), validating a through-going failure path formed by negative pressure-driven seepage.

When the uplift rate increased to 0.5 mm/s, the test still showed partially drained behavior. Uplift load and suction rose rapidly and peaked at 63 mm of uplift, followed by a sharp decline. Collapse of the surrounding soil was observed, but the soil plug remained intact (Figure 18), similar to the 0.1 mm/s condition.

At 2 mm/s, peak uplift load and suction occurred at 72 mm. Prior to the peak, cracks formed around the outer shaft wall, eventually developing into a collapse pit with strong seepage (Figure 19). The sudden post-peak drop in capacity suggests a large void channel had formed between the bucket and surrounding soil, releasing suction rapidly.

In the low-permeability Sand III (k = 7 × 10⁻⁵ cm/s), the load and suction response is shown in Figure 20. At 0.1 mm/s, the soil plug was pulled out, but peak capacity was delayed until 112 mm of uplift. Before reaching the peak, cracks were observed between the outer shaft and surrounding soil, without obvious seepage. Observations (Figure 21) revealed intermittent seepage between the soil plug and inner wall, indicating alternating blockage and reopening of seepage channels. This likely results from temporary formation of channels during uplift, allowing pressure to partially dissipate. As seepage slows, channels are re-blocked by soil particles. When suction reaccumulates, new channels reopen. This cycle of buildup and release causes the gradual decline in uplift load and suction.

At higher uplift rates (0.5 mm/s and 2 mm/s), Sand III showed similar behavior to Sand II. Outer soil collapse was observed after the peak, but the soil plug remained intact. The rapid decline in load and suction was again caused by the formation of continuous seepage channels, leading to suction loss.

Across all nine sealed-lid uplift scenarios, two failure modes were identified:

(a).

Shear failure under fully drained conditions;

(b).

Base resistance failure under partially drained conditions.

In partially drained conditions, negative pressure forms in two key areas:

(a).

Between the bucket lid and soil plug, where limited water inflow prevents pressure equalization and causes the plug to be lifted.

(b).

At the bucket base, where suction forms due to water replenishment lag, increasing the uplift capacity.

Two mechanisms for suction dissipation were identified:

(I).

Seepage-induced piping: Water flow along the bucket–soil interface carries particles away, forming continuous flow paths and releasing suction.

(II).

Soil collapse: Uplift-induced deformation creates voids connecting the bucket base to the surface, leading to rapid pressure equalization.

The first mechanism tends to occur under lower uplift rates with longer durations.

Comparing sealed- and vented-lid tests shows that in vented-lid tests, free drainage at the lid prevents soil plug mobilization, resulting in localized shear failure. Uplift resistance primarily comes from shaft friction and bucket self-weight. In contrast, sealed-lid tests promote negative pressure buildup at both the lid and base, often leading to soil plug uplift, seepage channel development, and outer soil collapse. Uplift resistance arises from combined contributions of shaft friction, suction at the lid and base, and plug self-weight, producing more complex mechanical responses. Moreover, uplift rate and soil permeability significantly influence suction development and seepage formation in sealed-lid conditions, while their effect is limited in vented-lid tests.

The identification of distinct uplift failure modes under drained and partially drained conditions provides critical guidance for retrieval strategy selection. In high-permeability soils, uplift resistance is predominantly governed by shaft friction, indicating that retrieval loads can be reduced by minimizing wall–soil adhesion through pre-loosening measures or lid venting. In contrast, in low-permeability soils where suction-induced base resistance dominates, gradual depressurization or controlled creation of seepage paths is advisable to prevent excessive extraction forces and mitigate seabed disturbance.

3.2. Mechanistic Implications

The physical model tests demonstrated that both uplift rate and soil permeability play critical roles in governing the uplift response of bucket foundations, particularly through their combined effects on suction development and shaft friction. To extend these findings, a series of finite-element (FE) simulations was performed over a wider range of uplift rates and permeabilities. The aim was to explore the underlying mechanisms controlling uplift bearing capacity and to provide practical guidance for foundation retrieval.

3.2.1. Effect of Uplift Rate

Figure 22 compares the load–displacement curves from sealed-lid tests on model AB-1 in three different sands with different uplift rates. In all cases, increasing the uplift rate resulted in a higher ultimate uplift bearing capacity and a larger displacement at this load. For example, in Sand I, the capacity rose steadily as the rate increased from 0.1 mm/s to 2 mm/s, with the peak displacement expanding from about 16 mm to over 30 mm. The same pattern was observed in Sands II and III, though absolute capacities were higher in the lower-permeability soils.

To explore this behavior in more detail, full-scale FE models with aspect ratios L/D = 1.5 (Model II) and L/D = 2.0 (Model III) were analyzed for rates ranging from 0.001 mm/s to 100 mm/s. Following the approach of [23], the uplift load at a displacement of 0.02D (180 mm) was taken as the representative capacity to avoid mesh distortion and unrealistic post-peak artifacts.

For Model II (Figure 23a), at the lowest rate of 0.001 mm/s, yielding occurred at 10 mm displacement, and the capacity was governed almost entirely by bucket self-weight and mobilized shaft friction—a drained local shear failure mode. At intermediate rates such as 0.1 mm/s, suction began to contribute noticeably, raising the capacity. At the highest rate of 100 mm/s, the soil had not yielded even at 180 mm uplift, and the capacity was several times higher than at the slowest rate. This progression indicates a transition in failure mode from drained local shear to undrained global failure, with large capacity gains at higher rates. Notably, the initial stiffness of the load–displacement curves was only weakly rate-dependent; the main differences appeared at larger displacements, when suction was fully mobilized.

Model III (Figure 23b) showed the same qualitative behavior, but absolute capacities were lower than those of Model II at the same rate. Figure 24 directly compares the two, showing that the shorter bucket consistently achieved higher capacities. This is attributed to its smaller embedded length, which accelerates pore pressure build-up and suction development for a given uplift displacement.

From a practical engineering perspective, high uplift rates can significantly enhance capacity by mobilizing suction more effectively, but they require higher hydraulic forces and can cause greater disturbance to the surrounding soil. For foundation retrieval in offshore wind applications, moderate-to-low uplift rates are preferable to balance the required load and seabed stability.

3.2.2. Effect of Permeability

Both tests and simulations confirm that soil permeability strongly influences uplift capacity under sealed-lid conditions. Figure 25 shows AB-1 test results in three sands. Reducing permeability from 8 × 10⁻³ cm/s (Sand I) to 7 × 10⁻⁴ cm/s (Sand II) increased the peak uplift load substantially, along with the displacement to peak. A further reduction to 7 × 10⁻⁵ cm/s (Sand III) brought smaller additional gains, suggesting diminishing returns at very low permeability.

Table 8. Ultimate uplift bearing capacity of suction buckets in open-top and closed-top tests.

Soil Sample ID	Open-Top Test Ultimate Load at 0.1 mm/s (N)	Closed-Top Test Ultimate Load at 0.1 mm/s (N)	Deviation (N)	Open-Top Test Ultimate Load at 2 mm/s (N)	Closed-Top Test Ultimate Load at 2 mm/s (N)	Deviation (N)
I	108.3	124.5	16.2	150.2	289.5	48.1
II	147.8	846.3	698.5	279.3	2170.7	1891.4
III	200.2	1193.2	993	521.4	2481.4	1960

quantifies this effect by comparing open- and closed-top results. In high-permeability Sand I, differences were small, indicating minimal suction contribution. In Sands II and III, however, sealed-lid capacities were far higher, confirming suction as the dominant factor. Tests on AB-2 (Figure 26), with a larger aspect ratio, displayed the same pattern: lower permeability produced higher capacities and larger peak displacements, implying more soil mass mobilized before failure.

FE simulations for Model II at 1 mm/s (Figure 27) further illustrate the trend. Reducing k from 7 × 10⁻² cm/s to 7 × 10⁻³ cm/s increased capacity by 102.2%; reducing further to 7 × 10⁻⁴ cm/s added another 51.2%; but lowering to 7 × 10⁻⁵ cm/s yielded only a 9.3% increase. Figure 28 summarizes the interaction between permeability and uplift rate: in fully drained (<0.01 mm/s) and fully undrained (>100 mm/s) regimes, permeability had little effect, while in the partially drained range (0.01–100 mm/s) it strongly influenced suction growth rate and magnitude.

In engineering practice, this means that low-permeability soils can generate high suction and uplift resistance under sealed-lid conditions, but retrieval can also benefit any soil by using lower uplift rates, which reduce hydraulic demand and seabed disturbance.

3.3. Suction and Friction Interaction

3.3.1. Effect of Uplift Rate

Model tests and FE analyses both confirm that in partially drained or undrained conditions, uplift capacity is largely governed by passive suction. Figure 29 shows FE results for Model II in soil with k = 7 × 10⁻³ cm/s across various uplift rates. At very low rates (0.01 mm/s), lid negative pressure stayed near zero throughout extraction, and the load–displacement curve showed two nearly linear stages, typical of fully drained behavior where resistance comes from shaft friction alone.

As the uplift rate increases, negative pressure develops beneath the bucket lid and continues to grow during uplift, with its magnitude strongly dependent on the uplift rate. This relationship is nonlinear: the most significant changes occur between 0.01 mm/s and 10 mm/s. Beyond this range, the variation in passive suction becomes minimal—for example, at v = 100 mm/s, suction shows little change compared with the 10 mm/s case.

Further simulations were conducted at an uplift rate of 1 mm/s for soils with different permeability coefficients. As shown in Figure 30, passive suction increases as soil permeability decreases. The relationship is also nonlinear: when permeability decreases from 7 × 10⁻² cm/s to 7 × 10⁻⁴ cm/s, each one-order-of-magnitude reduction leads to a marked increase in negative pressure. However, when permeability is further reduced from 7 × 10⁻⁴ cm/s to 7 × 10⁻⁵ cm/s, the change in suction becomes negligible. This suggests that, for sandy soils with permeability below 7 × 10⁻⁵ cm/s, the negative pressure at the top of the foundation stabilizes.

This trend is consistent with the variation in uplift resistance, confirming that passive suction is the dominant factor governing uplift performance under these conditions.

3.3.2. Effect of Passive Suction on Side Friction

Figure 31 shows the variation in inner and outer shaft friction with uplift displacement for a bucket foundation in soil with a permeability coefficient of 7 × 10⁻³ cm/s, tested at uplift rates of 10⁻², 1, and 10² mm/s. The results indicate that the uplift rate has a significant effect on shaft friction. When the uplift rate is 10⁻² mm/s, the difference between the inner and outer shaft friction is relatively small, with a magnitude of about 6 MN. This can be explained by the fact that, at low uplift rates, the passive suction generated inside the bucket is small and has sufficient time to dissipate. The uplift process is therefore in a fully drained state, and the effective stress in the soil on both sides of the bucket wall changes very little.

When the uplift rate increases to 1 or 10² mm/s, the inner shaft friction decreases while the outer shaft friction increases substantially. At higher uplift rates, the passive suction inside the bucket accumulates continuously and cannot dissipate in time, resulting in a partially drained condition. In this case, the soil plug inside the bucket is pulled out together with the bucket under the action of seepage forces. The relative displacement between the bucket’s inner wall and the soil plug decreases, and the seepage from outside to inside reduces the effective stress in the soil plug. Consequently, the inner shaft friction decreases, while the outer shaft friction increases.

Further finite element simulations were performed to obtain the pore water pressure distribution for the same conditions, as shown in Figure 32. The results for uplift rates of 1 and 100 mm/s were selected for analysis. At v = 1 mm/s, the negative pressure at the top of the bucket is small and concentrated near the bucket lid, dissipating gradually with depth. At v = 100 mm/s, the rapid uplift of the soil plug results in a more complex pore water pressure distribution, with limited suction dissipation throughout the process. The movement of the soil plug also drives the surrounding soil beneath and outside the bucket, causing an increase in pore water pressure in these regions. This, in turn, reduces the effective stress in the outer soil and weakens the external shear resistance.

However, during rapid uplift, two competing effects are observed. On one hand, a high uplift rate generates a significant pore pressure difference between the inside and outside of the bucket, inducing downward seepage that increases the effective stress in the external soil and enhances shear resistance. On the other hand, the increased displacement of the soil plug with higher uplift rates reduces the effective stress near the outer skirt of the bucket, thereby lowering the frictional resistance. The combined action of these effects makes the evolution of external shaft friction more complex.

The influence of passive suction on shaft friction distribution underscores the need for rate control during retrieval. At elevated uplift rates, the reduction in inner wall friction and the concurrent increase in outer wall friction should be considered in both design and operational planning. Monitoring pore pressure during extraction can assist in managing this frictional redistribution, thereby ensuring structural stability and preventing soil plug jamming or outer wall collapse. Design strategies should explicitly incorporate these rate-dependent frictional asymmetries for both installation and removal phases.

This effect is quantified using two indicators. First, the depth-averaged change in effective stress along each side of the skirt, computed from the earth-pressure data. Using the 1/3L–L sensors (Table 7), the mean reduction on the inner wall is about 3.0× the outer wall in Sand II and ~1.5× in Sand III. This matches the sign pattern in the measurements: larger negative effective-stress change inside, smaller change outside. Second, the side-friction evolution provides an independent check. The inner-wall component drops as uplift proceeds, while the outer-wall component rises (Figure 31), consistent with the stress redistribution inferred from Table 7. The pore-pressure records (Figure 10) also show stronger negative pressures within the bucket than outside during sealed-lid uplift, which is compatible with the larger inner effective-stress reduction.

3.4. Water Plug Height and Soil Deformation

3.4.1. Effect of Water Plug Height

Due to the high permeability of sandy soil, a water-filled gap often forms between the bucket lid and the soil plug during uplift. This water-filled section is referred to in this study as the water plug, with its height denoted as h_g. Analyzing the variation of h_g under different operating conditions is essential for a comprehensive understanding of the uplift bearing behavior of bucket foundations. Figure 33 presents finite element results for h_g under various uplift rates, with the soil permeability coefficient set to 7 × 10⁻³ cm/s.

The results show that when the uplift rate is low (v = 0.01 mm/s), the water plug fully develops. During uplift, the gap formed between the lid and soil plug is completely filled by seepage water, and the negative pressure inside the bucket can dissipate in time. In this case, the drainage condition is fully drained. As the uplift rate increases, the development of the water plug becomes increasingly restricted: the water plug height decreases while the soil plug height increases. This lengthens the dissipation path for pore water pressure, causing passive suction to be retained within the foundation, corresponding to an undrained condition.

For an intermediate uplift rate (v = 1 mm/s), the gap expansion falls between the fully drained and fully undrained extremes, and its height remains smaller than the upward displacement of the bucket foundation. Under such partially drained conditions, the soil plug height increases with uplift rate, which also induces deformation in the external soil surrounding the bucket.

3.4.2. Soil Deformation

The deformation of foundation soil under different operating conditions was further analyzed to supplement the understanding of the uplift bearing behavior of bucket foundations. Two representative uplift rates, v = 1 and 10 mm/s, were selected for calculation. Figure 34 shows the simulated displacement fields of the soil around the foundation for these two rates.

As the uplift rate increases, both the maximum deformation magnitude and the affected zone expand. At both v = 1 and 10 mm/s, the bottom of the soil plug exhibits an outward bulge, indicating the generation of reverse end bearing resistance. The distribution of the displacement field also allows identification of the soil slip surface. With higher uplift rates, the failure mode transitions from local shear failure to a broader, overall shear failure.

Comparing the deformation contours shows that at v = 1 mm/s, the maximum soil deformation around the foundation is 39.8 mm, whereas at v = 10 mm/s, it reaches 198.4 mm.

The role of water plug height in suction retention and dissipation has direct operational relevance. In high-permeability sands, regulating the water plug height through controlled uplift or lid venting can promote drained conditions, thereby lowering extraction loads. Conversely, high-rate uplift produces extensive deformation zones and shifts failure from localized to global shear, increasing the risk of seabed instability. Retrieval planning should therefore account for permissible deformation limits to safeguard adjacent infrastructure and protect sensitive seabed environments.

4. Discussion

The combined experimental and numerical results demonstrate that the uplift behavior of suction bucket foundations in sand is governed by the coupled effects of soil permeability and uplift rate. Variations in drainage condition largely determine whether failure is controlled by local shear or by suction-induced base resistance. Passive suction also alters the distribution of shaft friction, influencing both the mobilized resistance and the mode of failure. These interactions explain the observed transition between drained and partially drained responses and provide a consistent framework for interpreting rate-dependent uplift performance.

To quantify this transition, a dimensionless rate–permeability number R = vD/k was introduced, representing the competition between the uplift rate and the soil’s drainage capacity. Here, v is the uplift rate, D is the bucket diameter, and k is the soil permeability. In the present tests (v = 10⁻⁵~10⁻³ m/s, D = 0.18 m, k = 7 × 10⁻⁴~10⁻⁷ m/s), R ranges from about 1 to 2.6 × 10⁵, covering drained, partially drained, and suction-dominated conditions. The results indicate that uplift behavior is drained when R < 10³, partially drained for 10³ < R < 10⁴, and suction-dominated when R > 10⁴. This physically meaningful criterion provides a consistent basis for comparing drainage regimes across different soil types and scales.

The overall trends identified here are broadly consistent with previous studies on suction caissons and bucket foundations. The observed shift from drained to suction-dominated behavior aligns with the experimental findings of Byrne and Houlsby [15] and the numerical results of Deng and Carter [16]. However, compared with these studies, the present work indicates a more pronounced influence of soil permeability, particularly in fine sands, which can be attributed to the stricter drainage boundaries and smaller particle sizes used in the current model tests. While the linear-elastic Mohr–Coulomb model is appropriate for small-strain conditions, it may not fully capture rate-dependent or cyclic effects that could influence uplift behavior, particularly in dynamic or high-strain scenarios. Our findings also complement the work of Thieken et al. [23], who emphasized the role of pore-pressure buildup under partially drained conditions; here, this mechanism is further quantified through coupled flow–deformation simulations across a wider range of parameters.

In contrast, the nonlinear rate–capacity relationship obtained in this study differs from the nearly linear trend reported by Zhang et al. [19] for dense sand. This discrepancy likely arises from differences in soil gradation, boundary control, and drainage conditions, which can affect suction generation and dissipation during uplift. Such distinctions highlight the importance of accurately representing seepage-induced suction and soil–structure interaction in numerical modeling.

From an engineering perspective, the results reinforce the significance of considering permeability–rate coupling when assessing the uplift capacity of suction buckets. Simplified approaches that assume fully drained behavior may underestimate resistance in low-permeability seabeds. Incorporating partially drained effects and suction-driven mechanisms, as demonstrated in this study, can therefore improve predictive reliability and inform safer, more efficient foundation retrieval strategies in offshore engineering practice.

Moreover, the findings provide useful insights for refining current offshore design frameworks, such as API RP 2GEO [28], ISO 19905-1 [29], and DNVGL-ST-0126 [30], which commonly assume either fully drained or undrained soil conditions in uplift assessments. The present results highlight that intermediate, partially drained responses can govern performance in many practical cases, suggesting that accounting for rate–permeability coupling would enhance the predictive consistency of these standards and support the development of more performance-based design guidelines for suction-installed foundations.

5. Conclusions

• The uplift behavior of suction bucket foundations in sands is jointly controlled by soil permeability and uplift rate, which act in a nonlinear and coupled manner.
• Two failure mechanisms were observed: (i) drained local shear under high permeability or slow uplift and (ii) suction-driven base resistance under partially drained or undrained conditions.
• Decreasing permeability substantially increases uplift capacity. The capacity improves by approximately 102% when k decreases from 7 × 10⁻² to 7 × 10⁻³ cm/s, and by 51% from 7 × 10⁻³ to 7 × 10⁻⁴ cm/s, but only by 9% when further reduced to 7 × 10⁻⁵ cm/s, indicating a diminishing benefit below k ≈ 10⁻⁴ cm/s.
• Passive suction redistributes shaft friction, reducing inner-wall friction while enhancing outer-wall friction, which contributes to soil plug stability and greater end resistance.
• For engineering applications, moderate-to-low uplift rates are recommended during retrieval to mitigate hydraulic requirements and minimize seabed disturbance, while the established capacity trends provide valuable reference for foundation design.

Based on the results, moderate-to-low uplift rates are recommended for retrieving suction bucket foundations, particularly in low-permeability soils. This approach will help minimize hydraulic demands and reduce seabed disturbance, facilitating a smoother decommissioning process. Additionally, foundation design should carefully consider the permeability of the soil to optimize uplift capacity in real-world applications.

For future research, it is essential to explore the effects of soil heterogeneity and the interaction between different soil layers on uplift behavior. Investigating the long-term behavior of suction foundations under cyclic loading and environmental factors, such as wave and temperature variations, would be valuable. Furthermore, the performance of alternative foundation shapes should be explored to enhance uplift capacity in challenging offshore environments. Incorporating real-time monitoring during installation and retrieval processes could also improve predictive models and increase the safety and efficiency of offshore foundation operations.