MNAT: A Simulation Tool for Underwater Radiated Noise
Abstract
1. Introduction
2. Related Work
2.1. Foundations and Advances in Underwater Acoustic Modeling
2.2. Methods and Applications in AIS Data Preprocessing
2.3. Simulation Tools for Underwater Noise Analysis
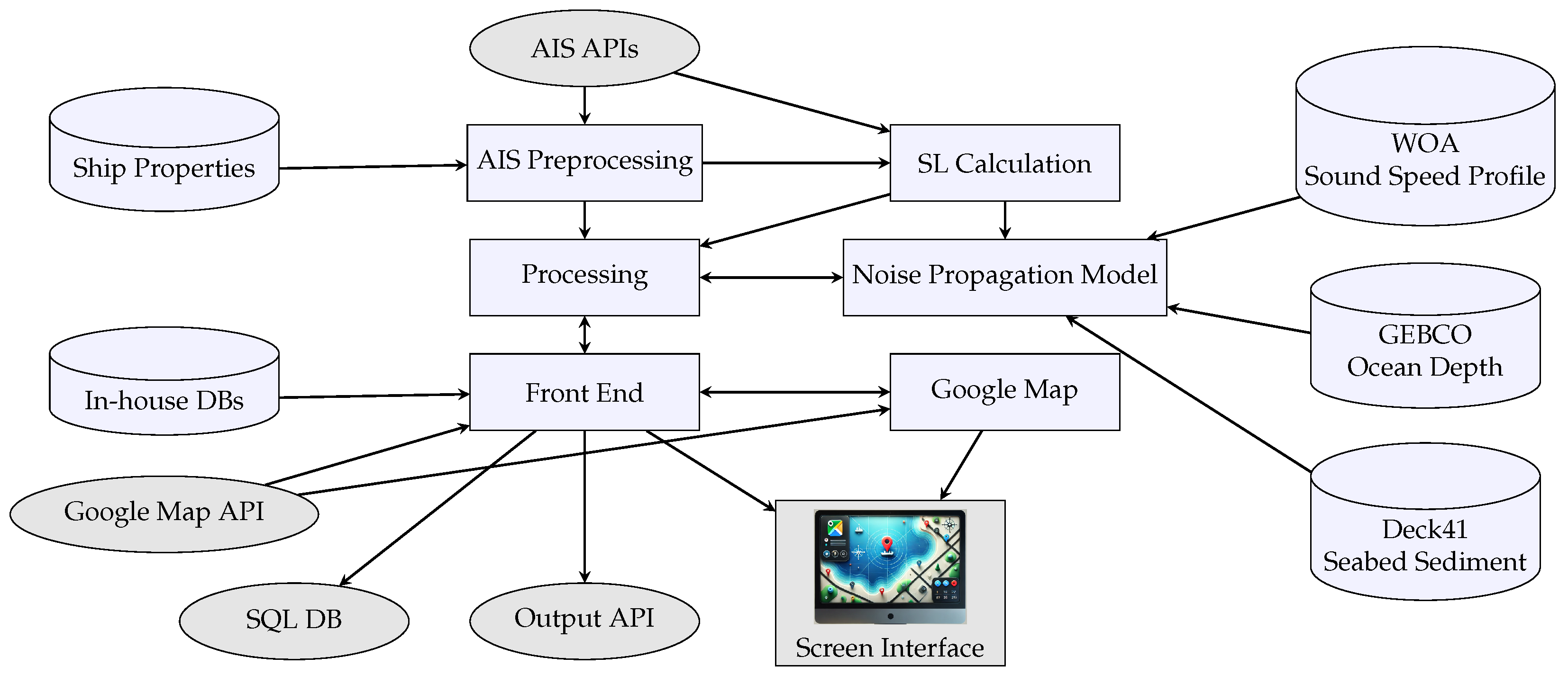
3. MNAT Modeling Architecture and Functional Capabilities
3.1. Data Acquisition and Preparation
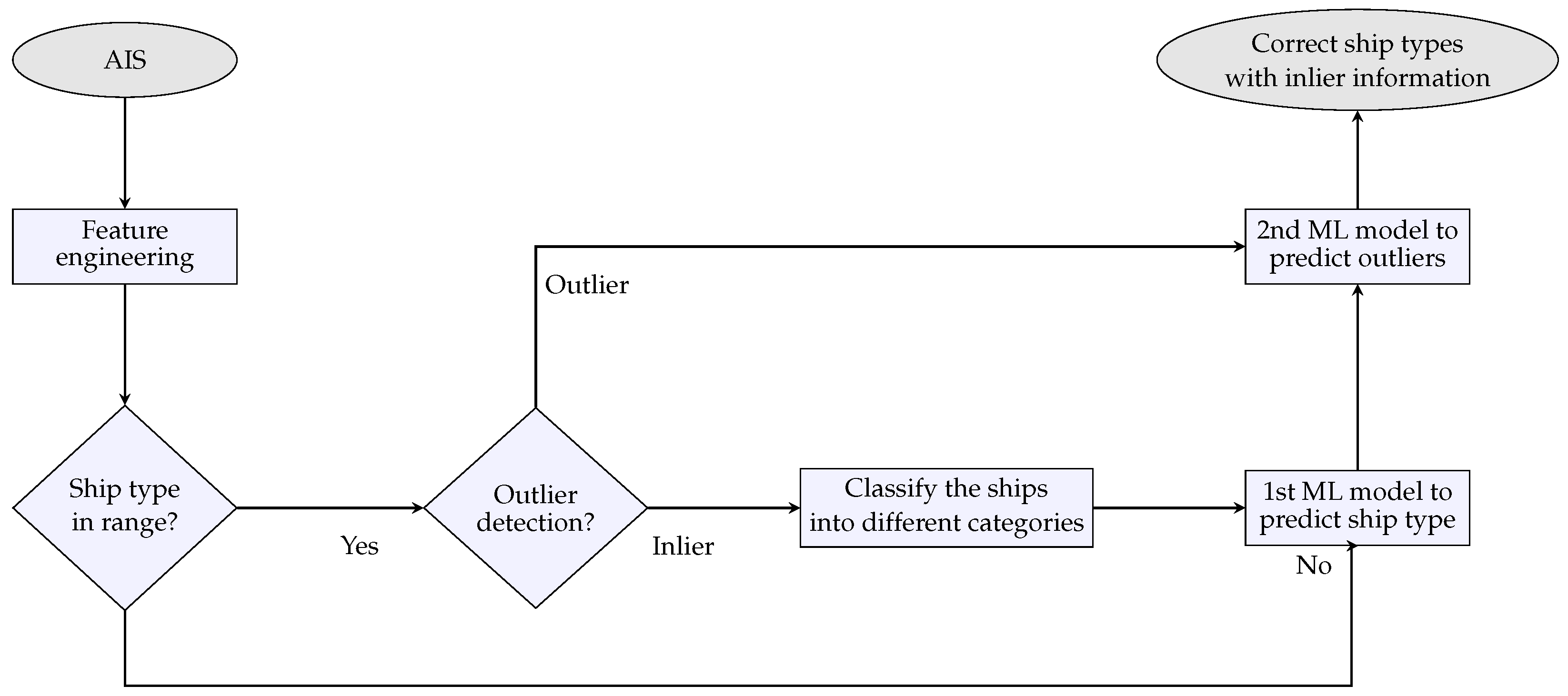
3.2. Data Processing, Cleaning, and Imputation Pipelines
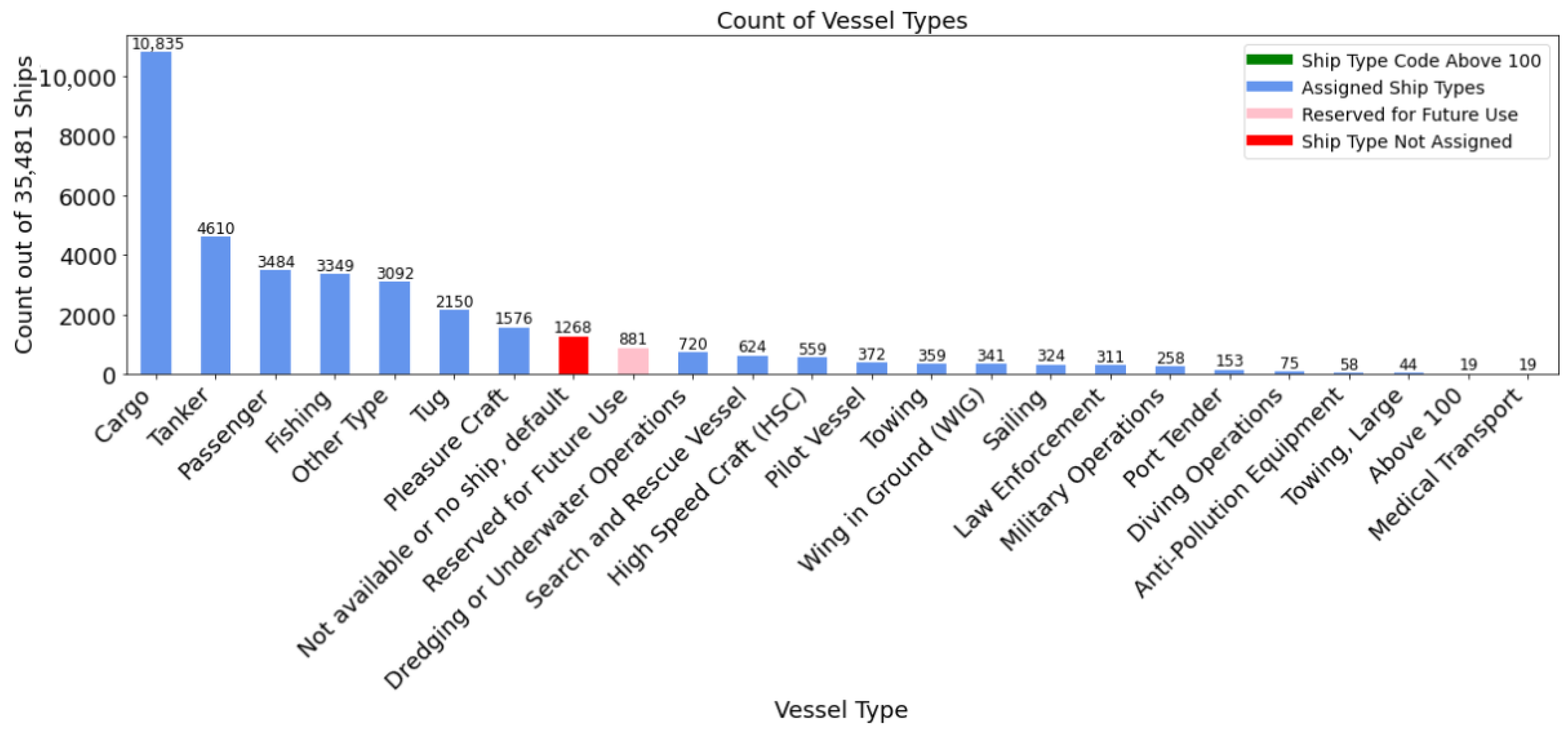
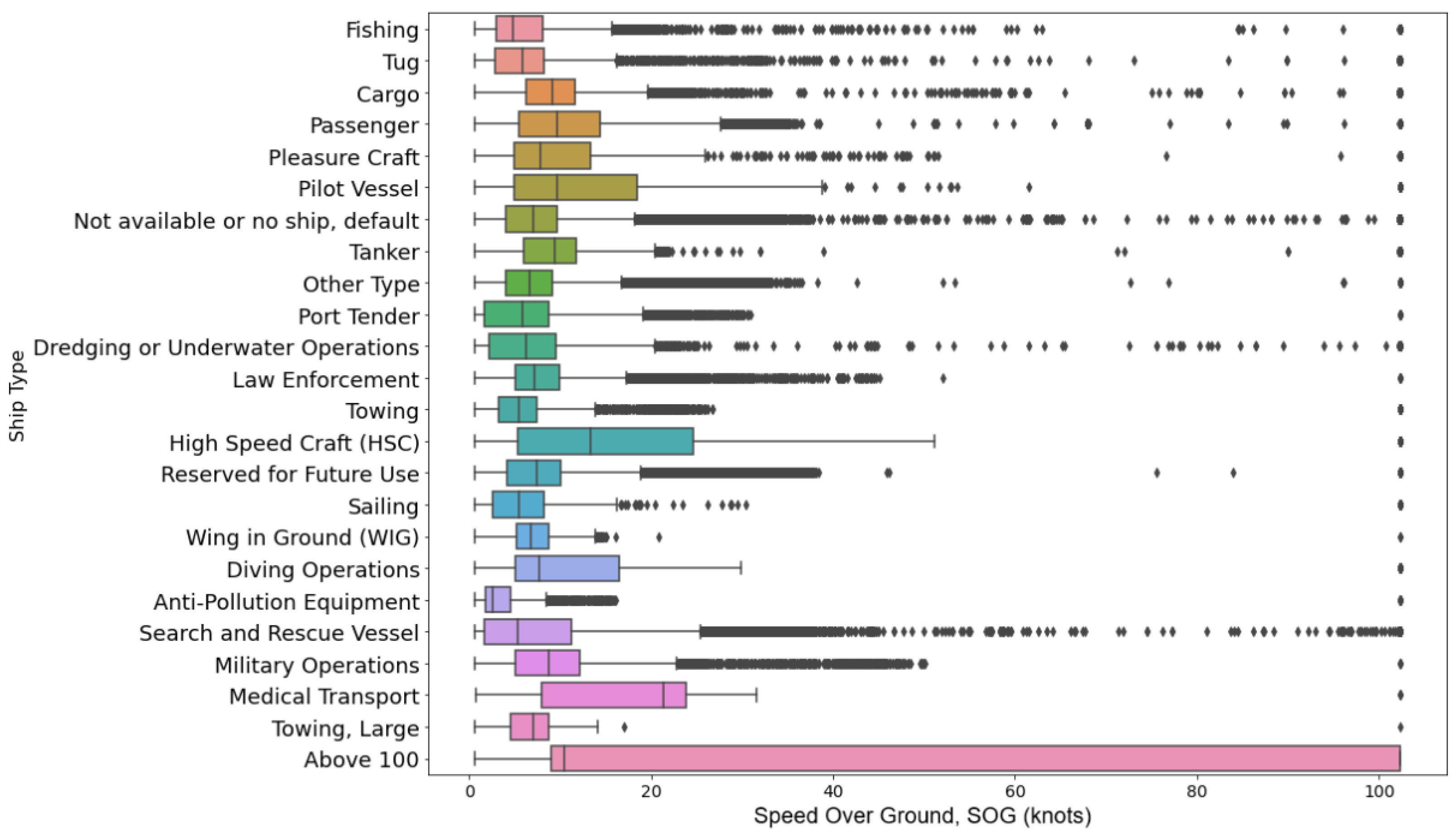
3.2.1. AIS Data Preprocessing
- Geometric features:
- -
- is the length of the vessel;
- -
- is the width of the vessel;
- -
- approximates the perimeter of the vessel;
- -
- approximates the area of a ship’s deck;
- -
- indicates the overall shape of the vessel;
- -
- measures the complexity of the shape or form of a vessel;
- -
- quantifies the position of the vessel in terms of its total length.
- Navigation features:
- -
- SOGmed represents the median value of the SOG, i.e., the speed of the vessel relative to the ground, measured in knots;
- -
- SOG75q represent the 75th quantiles of the SOG;
- -
- PerimeterToSpeed: , where is a small loading factor that avoids divisions by zero;
- -
- COGmed: Represents the median of the ships’ COG, i.e., the actual direction a vessel moves over the sea, considering the impact of elements such as the wind and currents;
- -
- COG25q and COG75q represent the 25th and 75th quantiles of the COG;
- -
- SogCogmed: equals the product ;
- -
- : equals ;
- -
- SpeedRatio: equals ;
- -
- LengthToWidth: ;
- -
- CogRange is ;
- -
- SogRange is .
- Data split: A three-way split is applied to data, using 60%, 20%, and 20%, respectively, for training, validation, and test sets.
- Feature selection: From the original 17 candidate features, Recursive Feature Elimination (RFE) is applied to select the most informative features for each method.
- Data augmentation: To address class imbalance in the training data, the Synthetic Minority Oversampling TEchnique (SMOTE) is applied on the training split only.
- Evaluation: A comprehensive evaluation is performed using multiple complementary metrics such as accuracy and F1-score as the harmonic mean of precision and recall:where , , , and represent the number of true positives, true negatives, false positives, and false negatives, respectively.
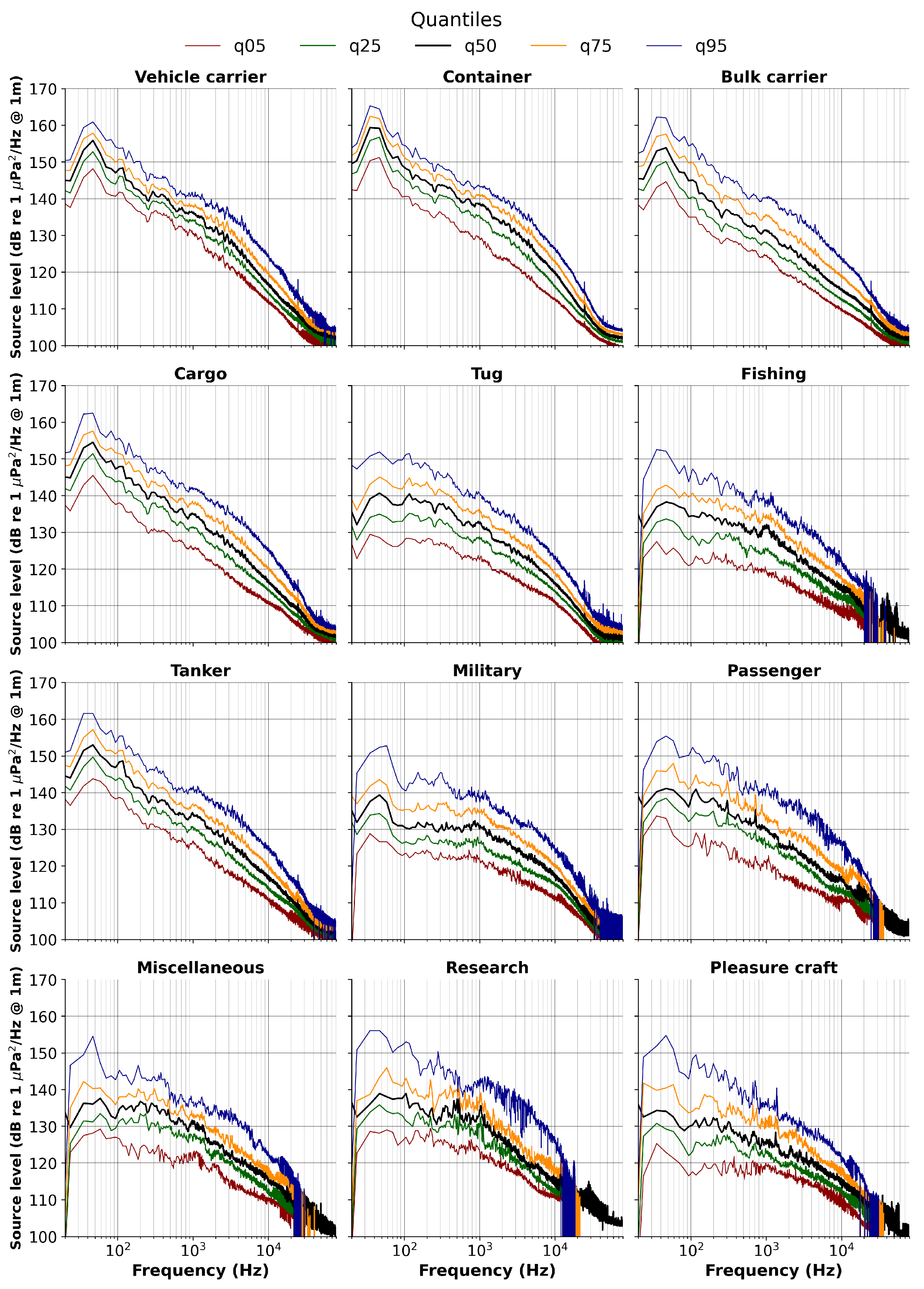
3.2.2. Finding Source Noise Levels
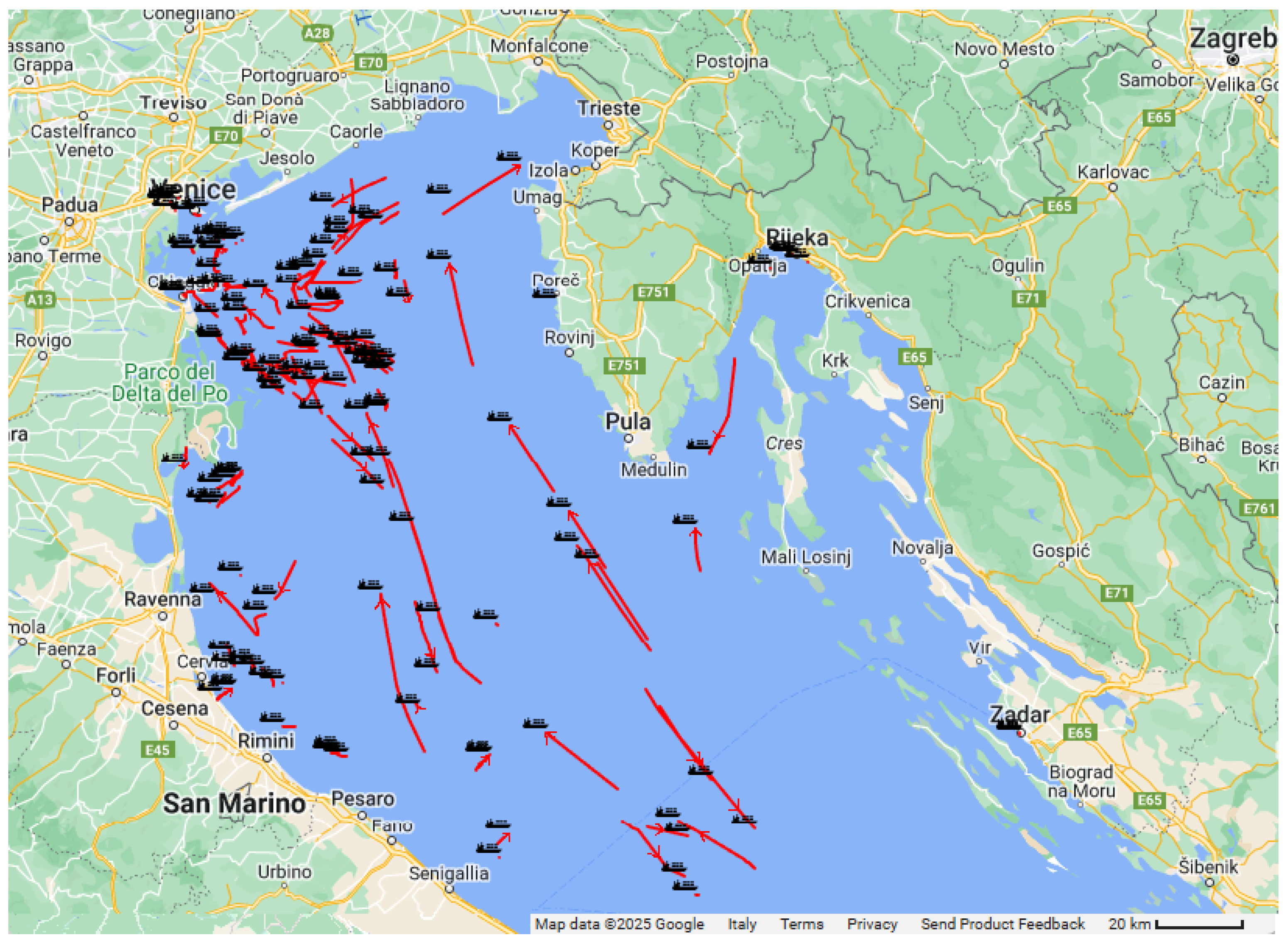
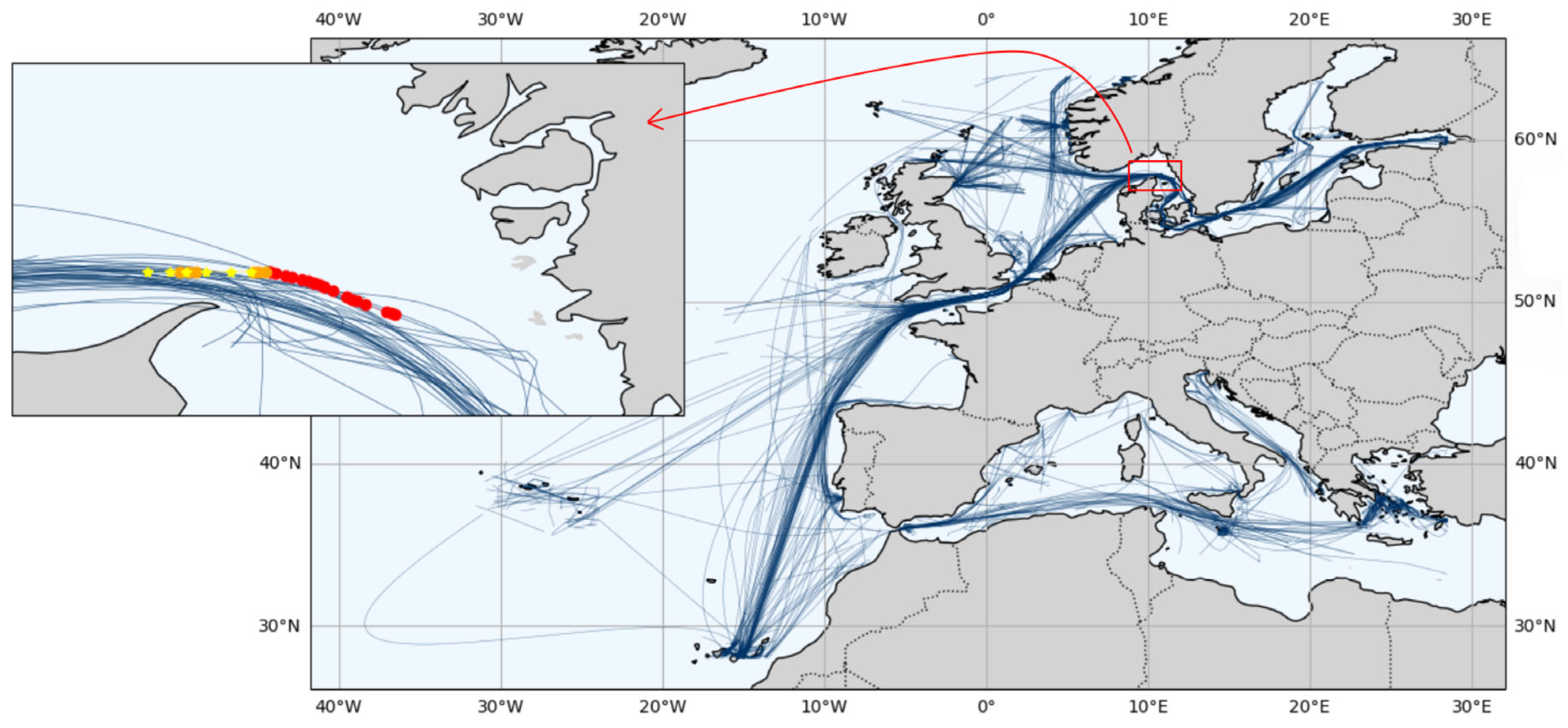
3.2.3. Vessel Trajectory Prediction Using AIS Data
3.3. Noise Prediction Using Machine Learning Models
- A.
- Base Models:
- Extra trees regressor: A robust ensemble method that builds multiple decision trees to reduce the variance of the noise predictions.
- XGBoost regressor [37]: A gradient boosting algorithm that efficiently handles complex patterns in data.
- LightGBM regressor [49]: A gradient boosting framework optimized for speed and efficiency.
- CatBoost regressor [50]: A gradient boosting model that performs well with categorical features and avoids over-fitting.
- B.
- Final Estimator: A ridge regression [51] model was used as the meta-model to combine the outputs of the base models.
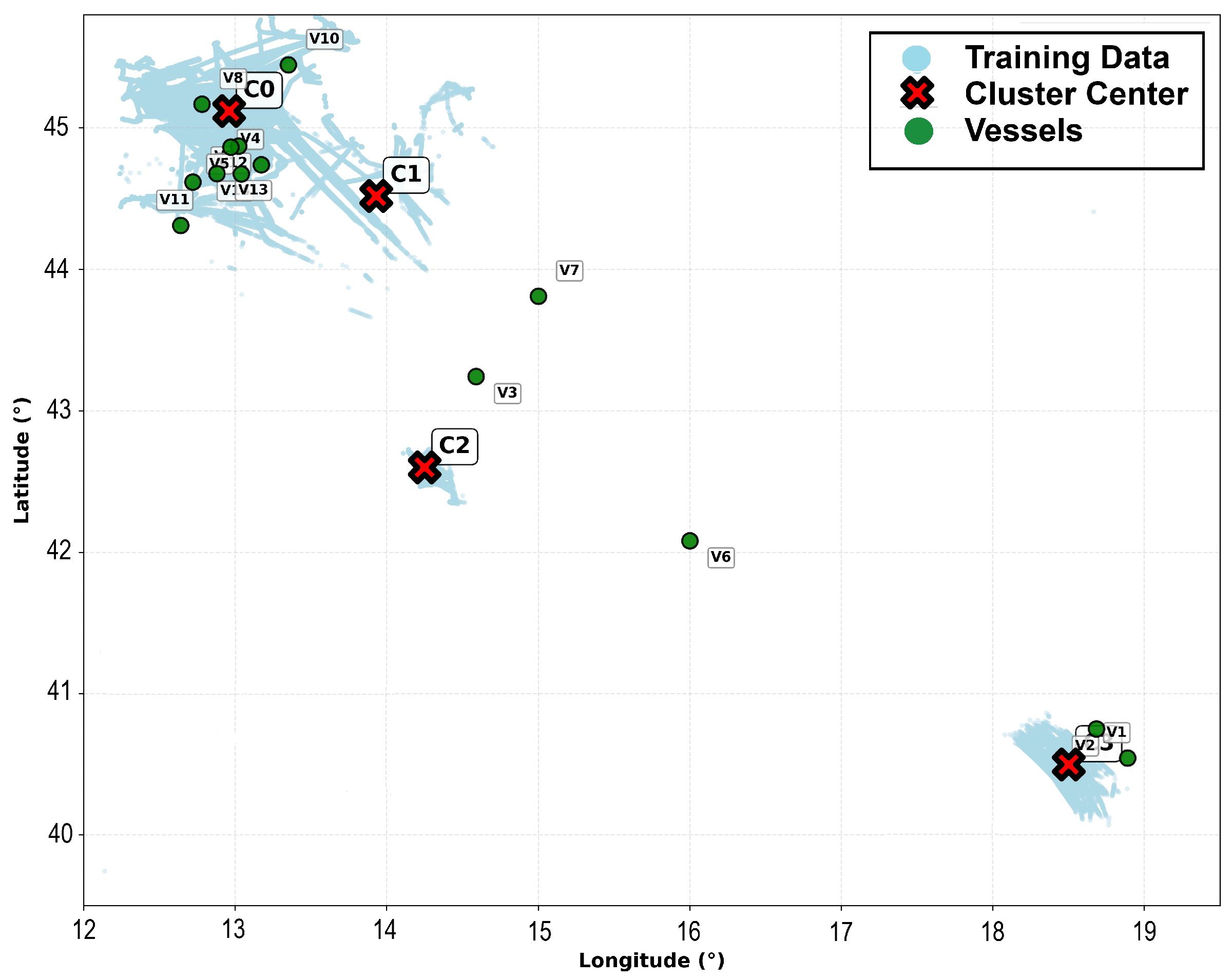
3.3.1. Vessel Clustering and Scoring via a Gaussian Mixture Model
3.3.2. Sorting Vessels for Training the Stacking Regressor
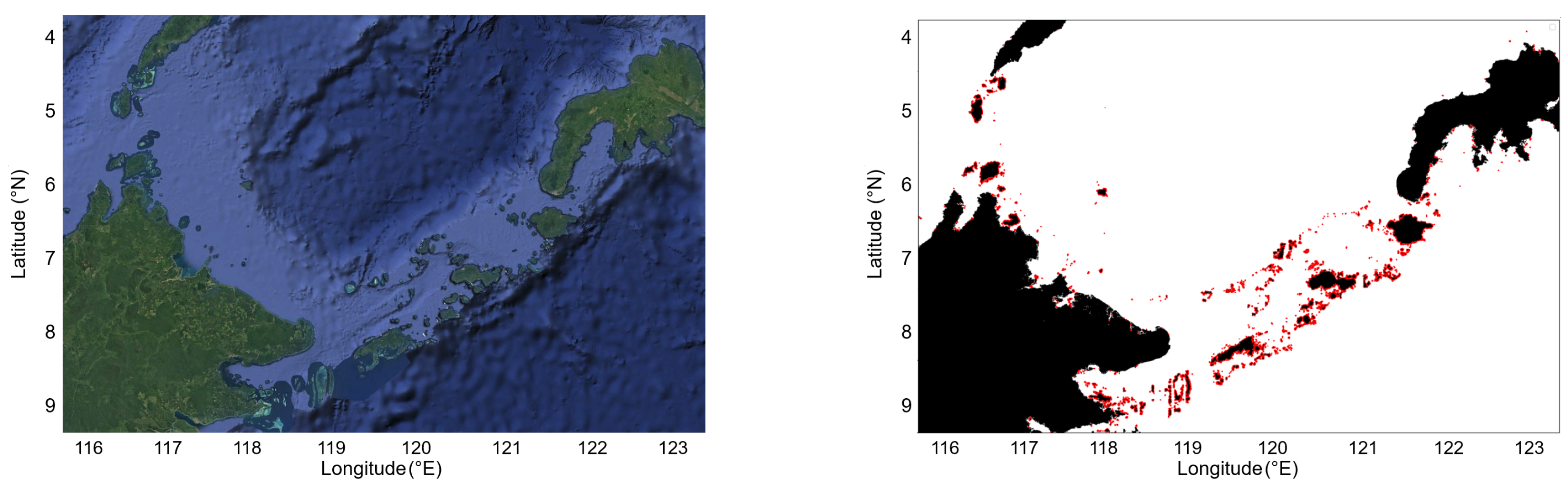
3.3.3. Sea and Coastline Data Preprocessing
- ID: A unique identifier assigned to each detected obstacle or island.
- CentroidX: The X-coordinate (cartesian) of the object’s center in image space.
- CentroidY: The Y-coordinate (cartesian) of the object’s center in image space.
- CentroidLongitude: The geographic longitude of the object’s centroid.
- CentroidLatitude: The geographic latitude of the object’s centroid.
- Area: The surface area of the object in pixels or grid cells.
- BBoxX: The X-coordinate of the top-left corner of the object’s bounding box.
- BBoxY: The Y-coordinate of the top-left corner of the object’s bounding box.
- BBoxWidth: The horizontal size of the bounding box in pixels.
- BBoxHeight: The vertical size of the bounding box in pixels.
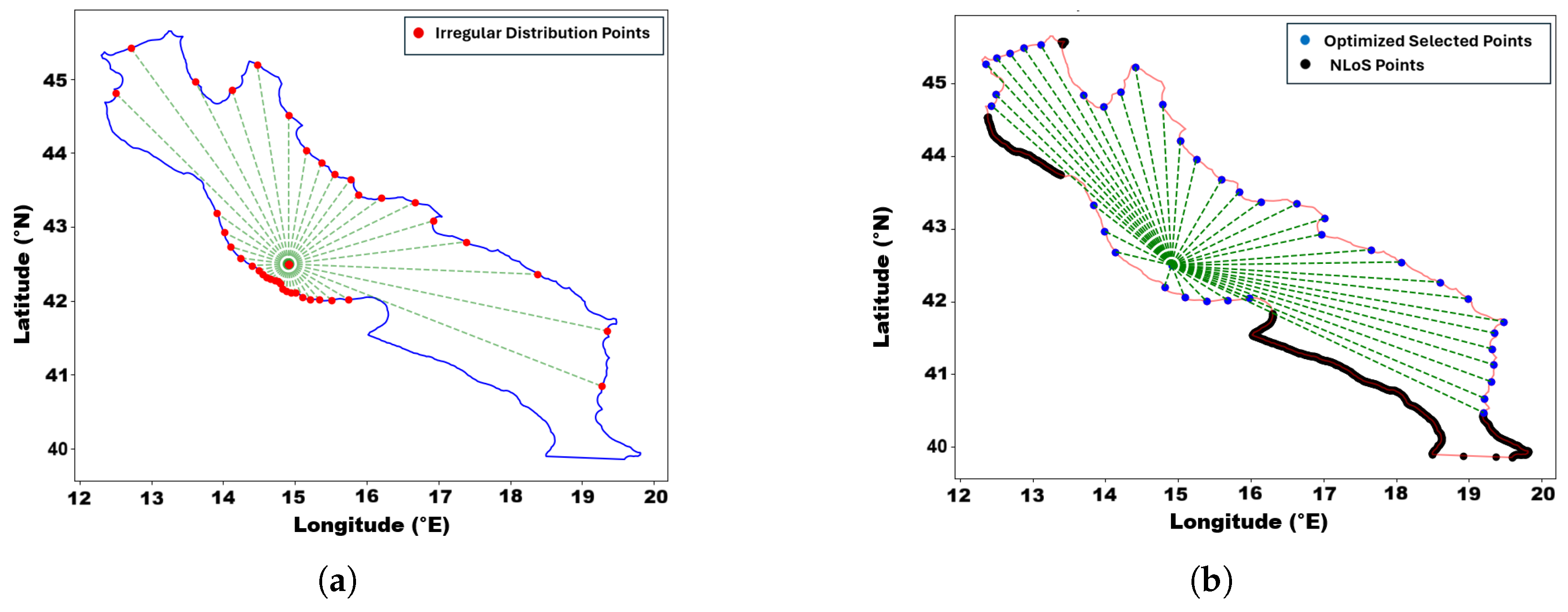
3.3.4. Radial Sampling Strategy
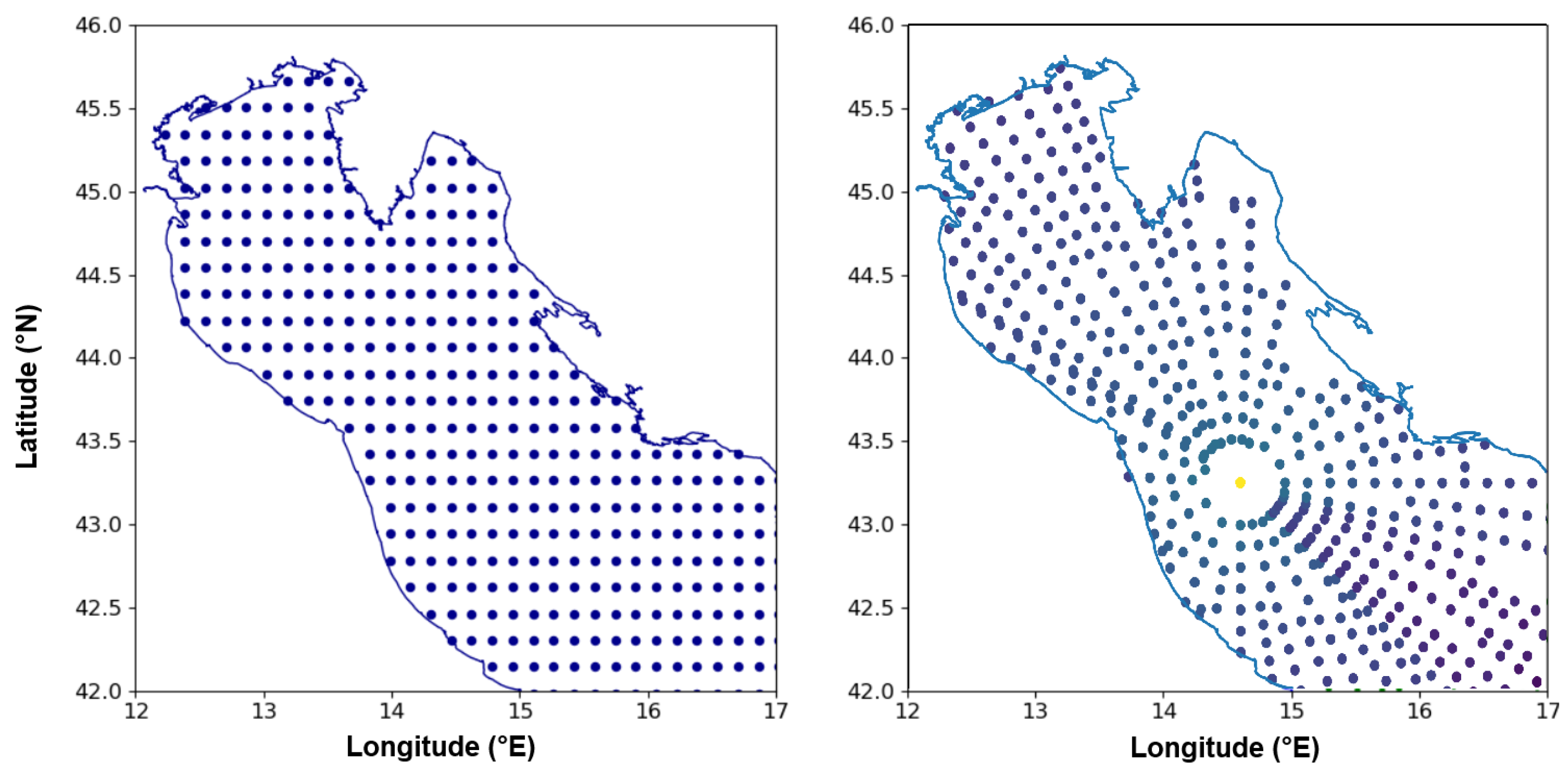
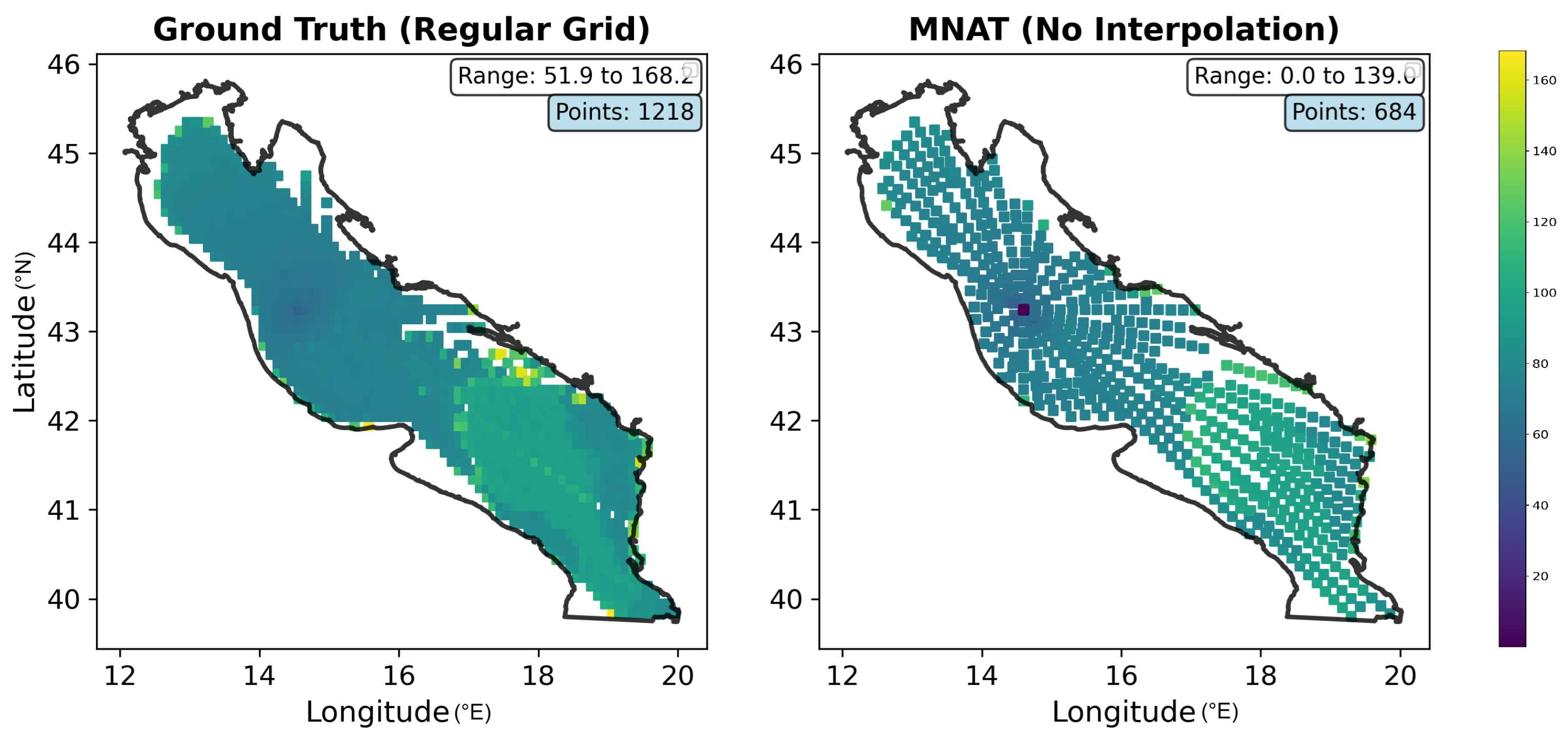
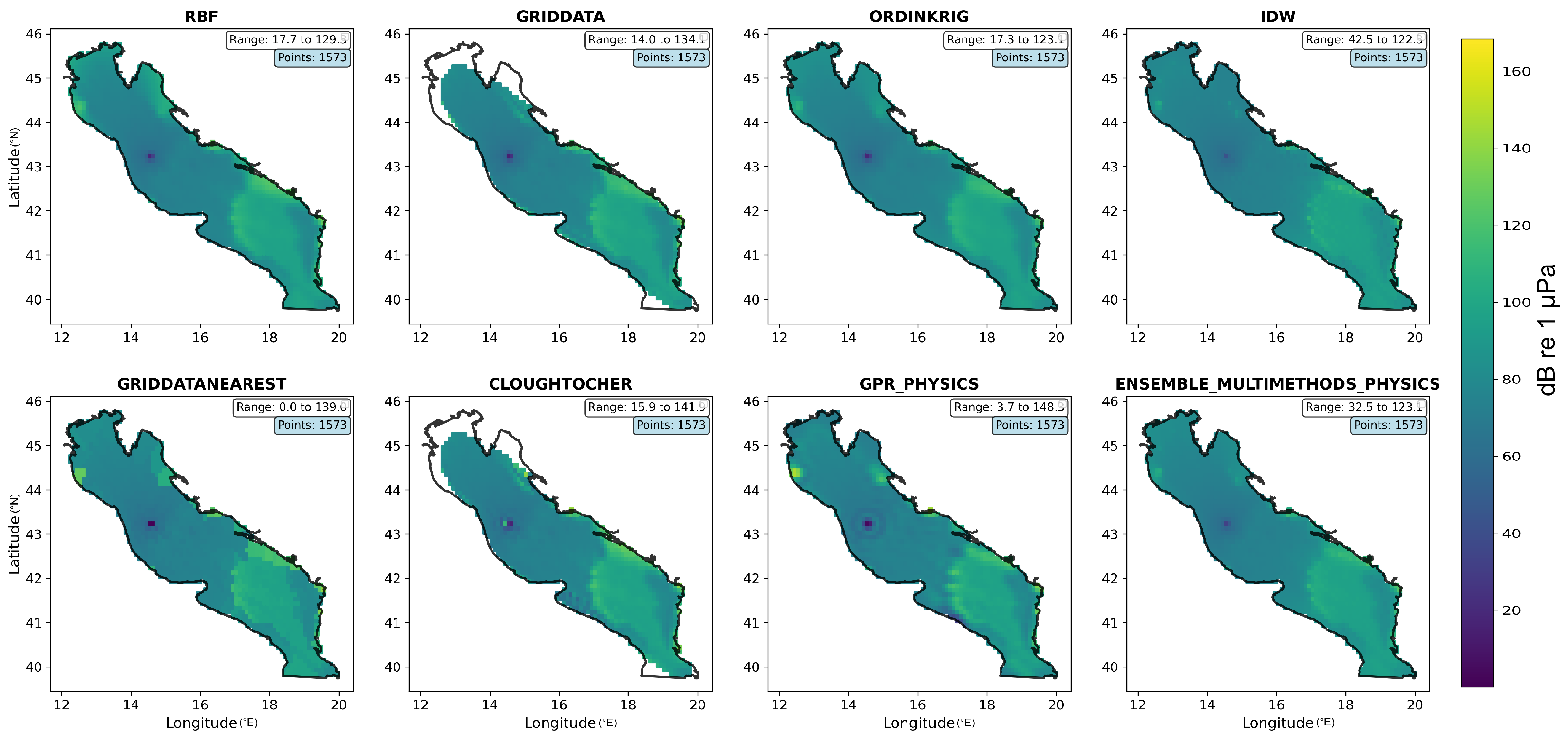
3.3.5. Grid Data Imputation
- Datagrid (Nearest neighbor): Ref. [54] utilizes the closest known point without regard to surrounding variability.
- Datagrid (Linear): Ref. [55] estimates between neighboring data points in a triangle.
- CloughTocher: Ref. [56] a piecewise cubic interpolation method on triangulated irregular networks that produces smooth and continuous surfaces.
- RBF: Ref. [57] uses radial basis functions centered on data points in constructing a smooth surface.
- Inverse Distance Weighting (IDW): Ref. [58] a deterministic method in which unknowns are approximated by a weighted average of nearby observations, where the weights are inversely related to distance.
- Ordinary kriging: Ref. [59] a geostatistical technique that utilizes variograms to account for autocorrelation while making minimum-variance, unbiased predictions.
- Gaussian Process Regression (GPR)-Physics: Ref. [60] an advanced interpolation technique that models spatial correlations in oceanographic data using Gaussian process regression. It automatically learns the best parameters (such as measurement noise levels and spatial correlation length scales) from the training data. The technique uses a WhiteKernel, which explicitly models the noise in GPR to find and remove it, and uses the RBF kernel to make the interpolation smooth and continuous [61]. In addition to interpolated values, GPR-Physics also provides uncertainty estimates (standard deviations) for every grid point during prediction. This distinguishes GPR-Physics from other interpolation techniques by measuring prediction confidence while preserving physics-aware spatial modeling.
- Ensemble MultiMethods Physics: the goal of this physics-based ensemble approach is to produce more reliable results than any one method could by combining IDW (60%), ordinary kriging (20%), and RBF (20%) interpolation techniques. Furthermore, it uses the Euclidean distance to determine the closest interpolated value for each grid point. Then, compute a weighted average in which IDW is used for local accuracy and other methods are used for global spatial correlation. In the integration of physics step, it makes use of real geographic coordinates (latitude/longitude) and takes spatial relationships between points into account.
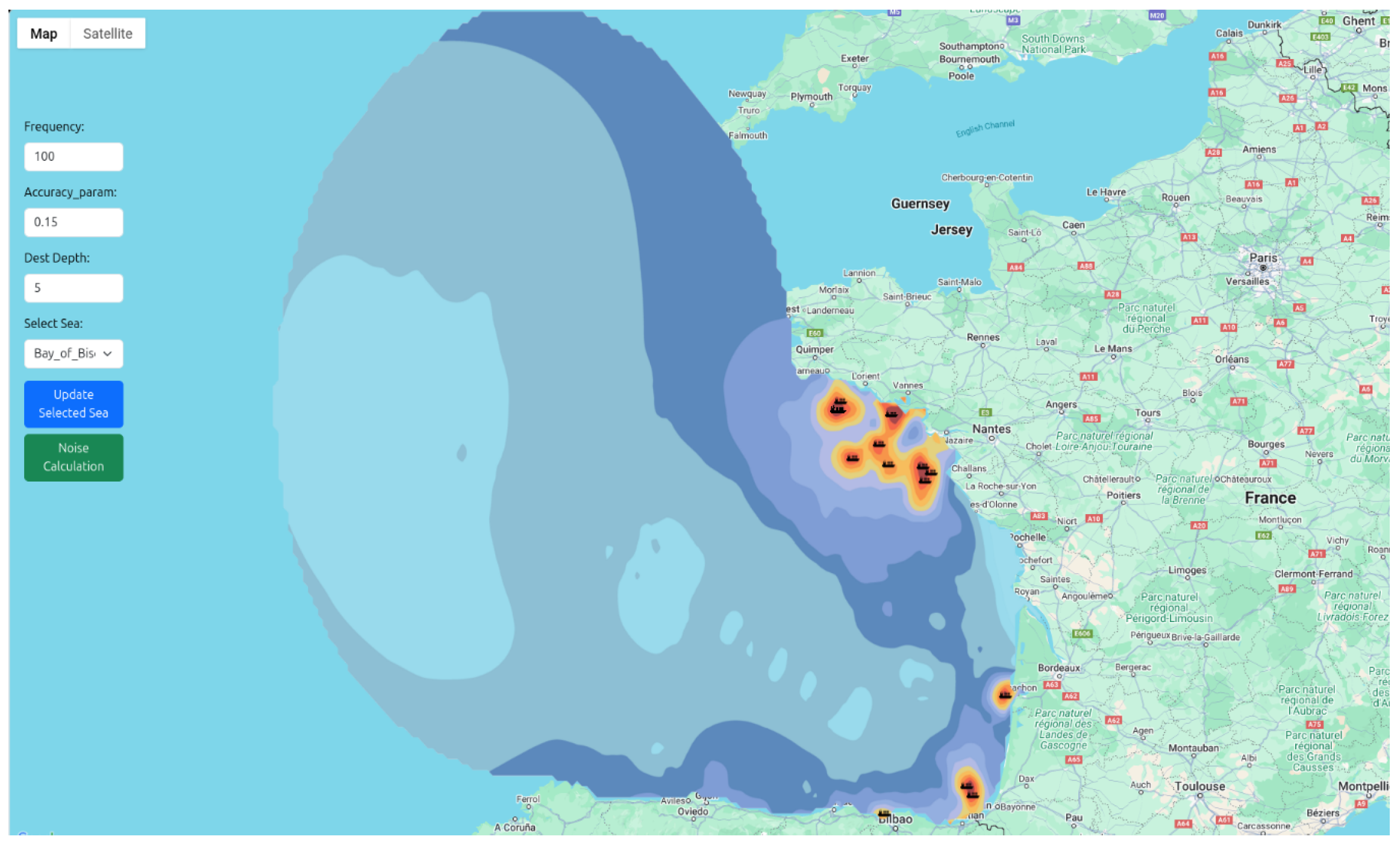
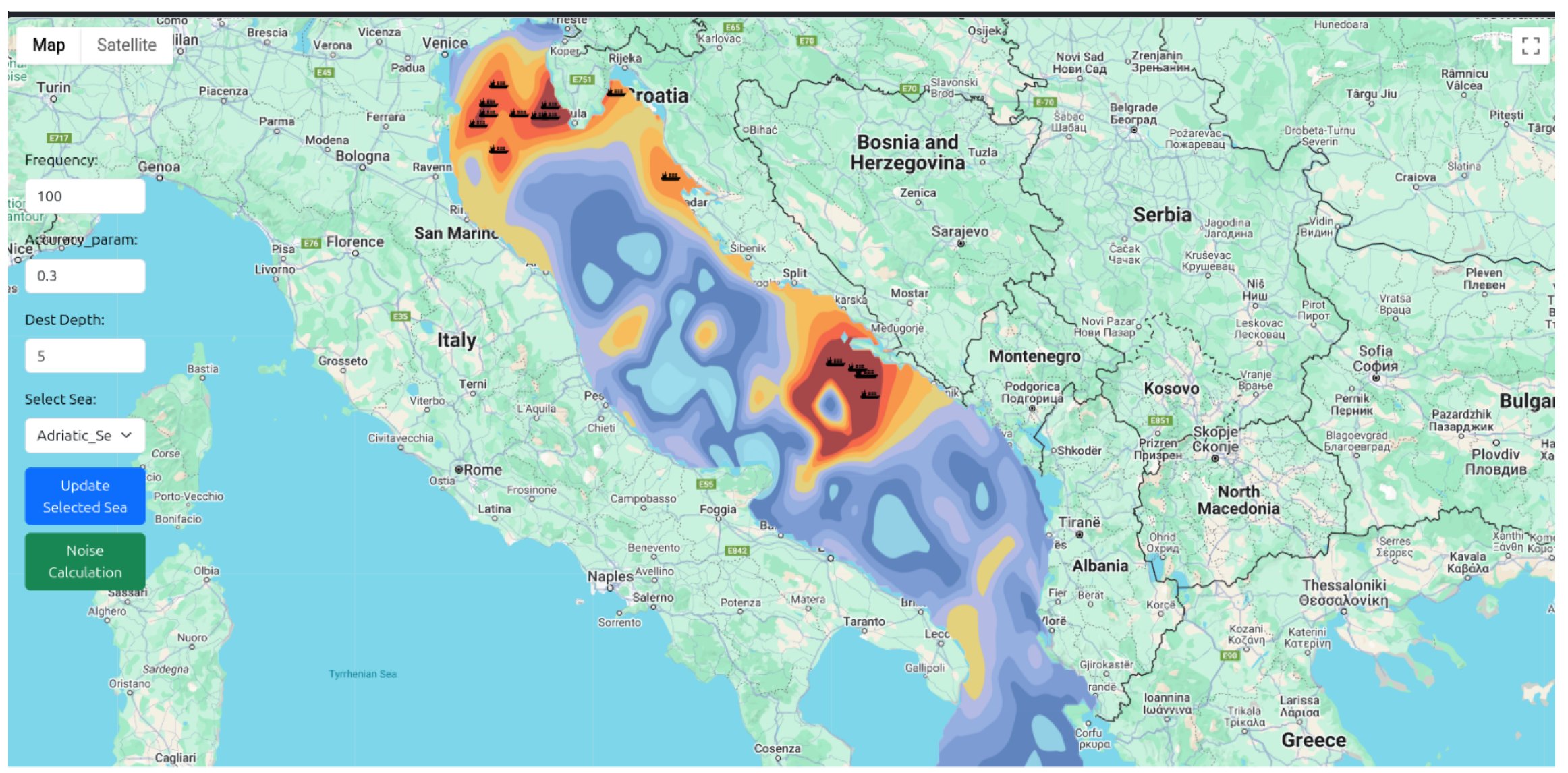
3.3.6. Google Maps Integration for Noise Mapping
4. Use Cases
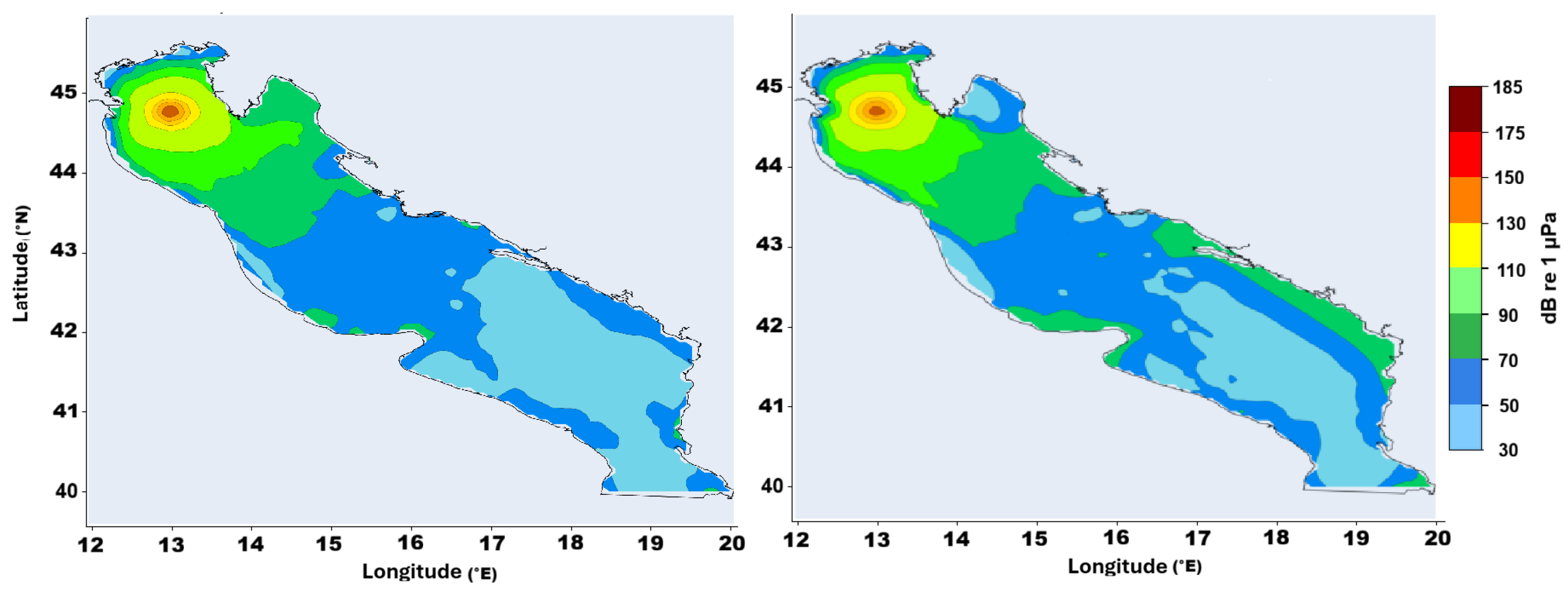
4.1. Vessel Noise Propagation
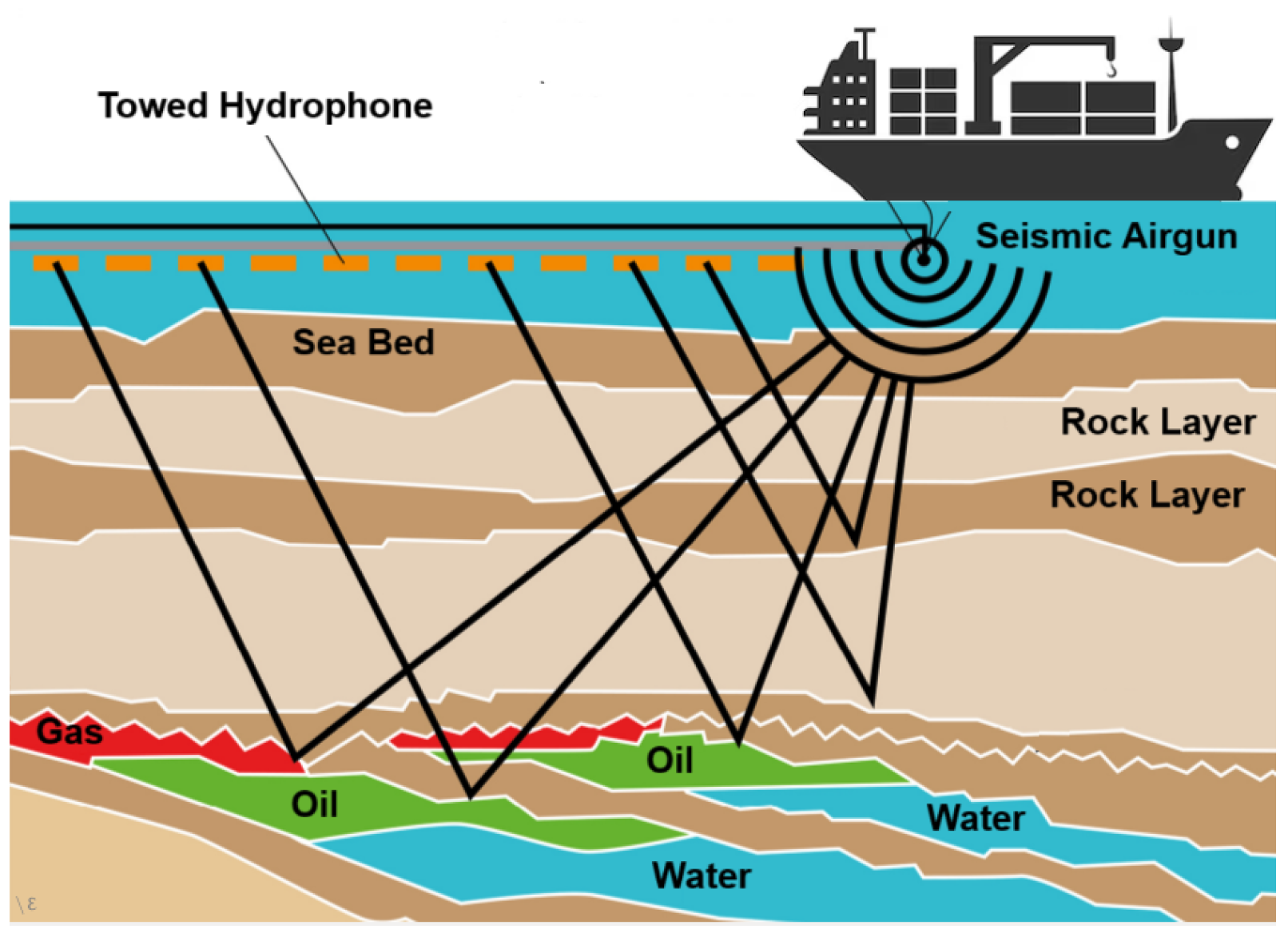
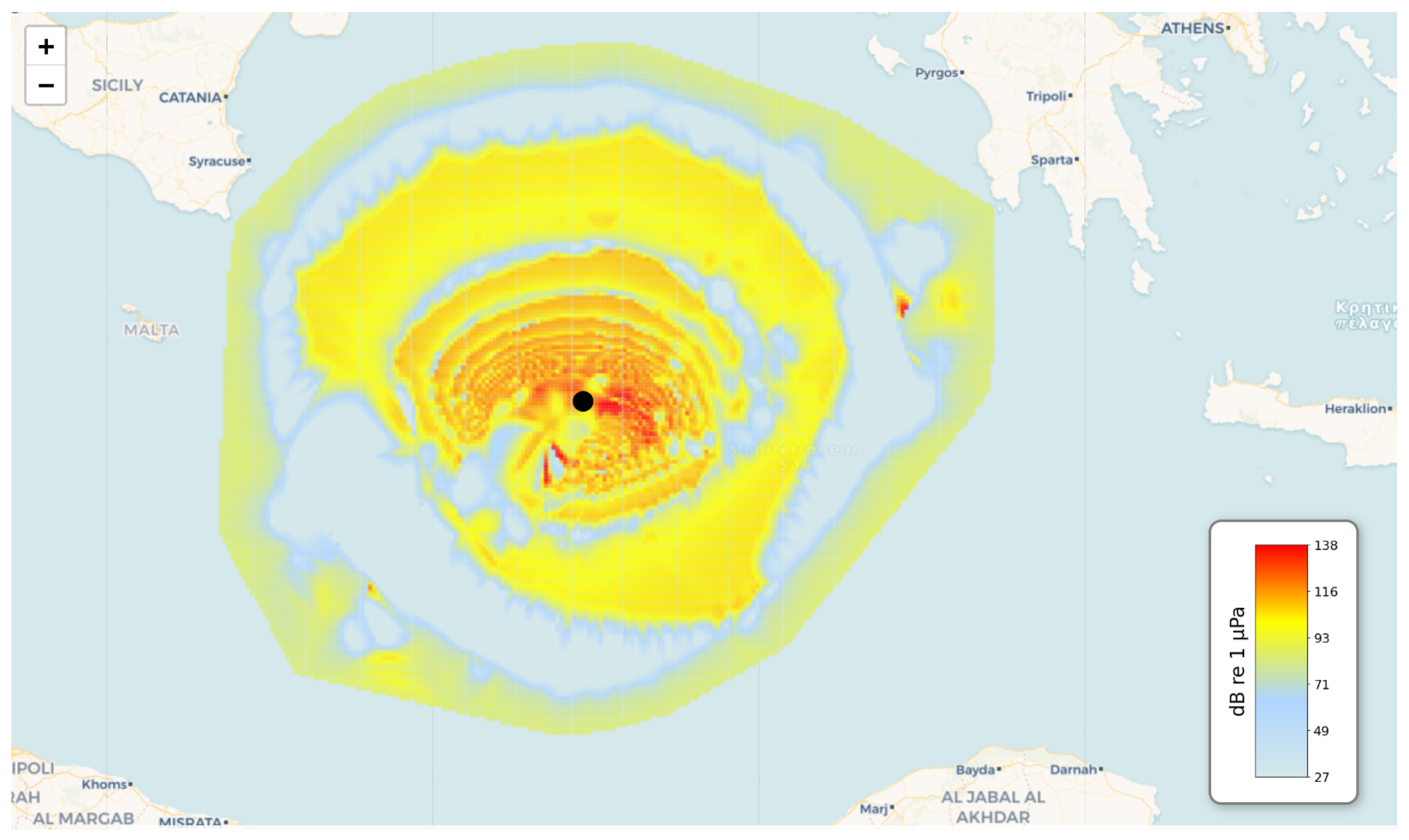
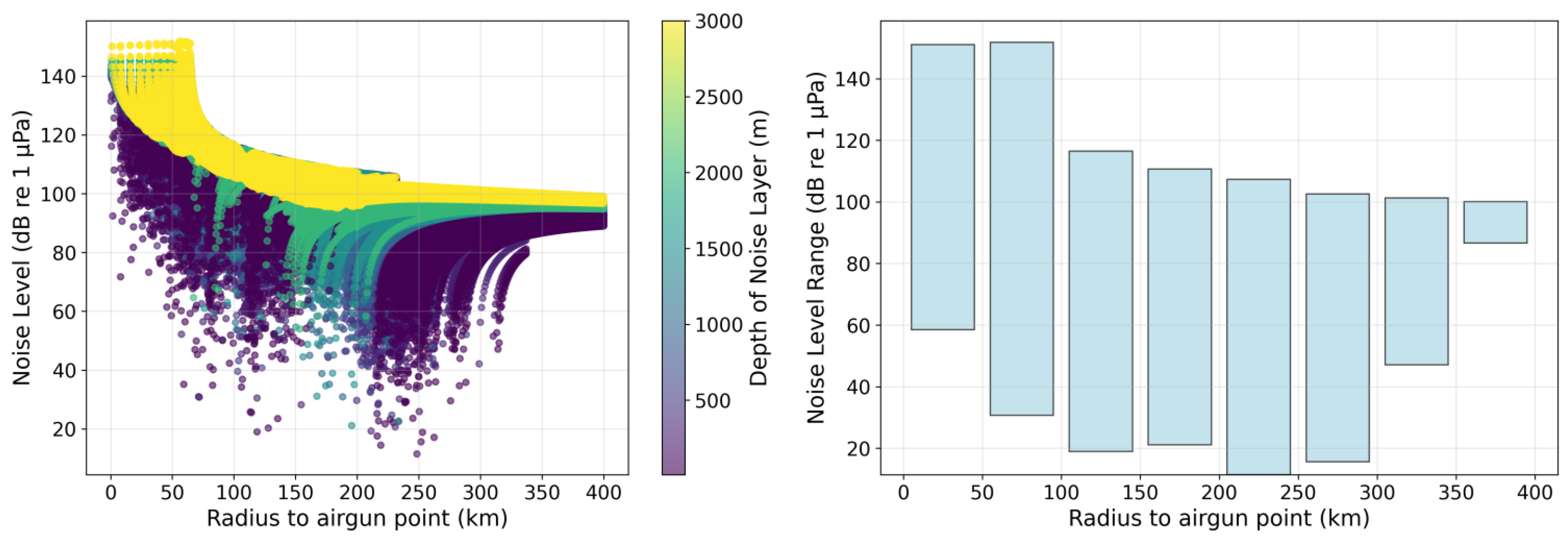
4.2. Airgun Noise Emission
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AIS | Automatic Identification System |
| API | Application Programming Interface |
| AT | Acoustic Toolbox |
| COG | Course Over Ground |
| GEBCO | General Bathymetric Chart of the Oceans |
| GIS | Geographic Information System |
| GPS | Global Positioning System |
| GMM | Gaussian Mixture Model |
| GNN | Graph Neural Network |
| GPR | Gaussian Process Regression |
| HSC | High Speed Craft |
| IDW | Inverse Distance Weighting |
| ITU | International Telecommunication Union |
| LAT | Latitude |
| LON | Longitude |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| MLP | Multilayer Perceptron |
| MNAT | Marine Noise Analysis Tool |
| MMSI | Maritime Mobile Service Identity |
| NB | Naïve Bayes |
| OASES | Ocean Acoustics and Seismic Exploration Synthesis |
| Probability Density Function | |
| PE | Parabolic Equation |
| RAM | Range-Dependent Acoustic Model |
| RBF | Radial Basis Function |
| RMSE | Root Mean Squared Error |
| SL | Source Level |
| SQL | Structured Query Language |
| SOG | Speed Over Ground |
| SR | Stacking Regressor |
| SSP | Sound Speed Profile |
| SVM | Support Vector Machine |
| WOSS | World Ocean Simulation System |
References
- Markus, T.; Sánchez, P.P.S. Managing and Regulating Underwater Noise Pollution. In Handbook on Marine Environment Protection: Science, Impacts and Sustainable Management; Salomon, M., Markus, T., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 971–995. [Google Scholar] [CrossRef]
- Küsel, E.T.; Siderius, M. Comparison of Propagation Models for the Characterization of Sound Pressure Fields. IEEE J. Ocean. Eng. 2019, 44, 598–610. [Google Scholar] [CrossRef]
- Collins, M.D. A split-step Padé solution for the parabolic equation method. J. Acoust. Soc. Am. 1993, 93, 1736–1742. [Google Scholar] [CrossRef]
- Porter, M.B. The BELLHOP Manual and User’s Guide: Preliminary Draft; Technical Report; Beam/ray tracing model for ocean acoustics; Naval Research Laboratory: Washington, DC, USA, 1992. [Google Scholar]
- Zhang, L.; Meng, C. Modeling of Radiated Noise Passing Characteristic for Ship in Different Marine Environments. In Proceedings of the 2018 3rd International Conference on Modelling, Simulation and Applied Mathematics (MSAM 2018), Shanghai, China, 22–23 July 2018; Available online: https://api.semanticscholar.org/CorpusID:160002924 (accessed on 21 October 2025). [CrossRef]
- Neenan, S.T.V.; White, P.R.; Leighton, T.G.; Shaw, P.J. Modeling vessel noise emissions through the accumulation and propagation of Automatic Identification System data. In Proceedings of the Fourth International Conference on the Effects of Noise on Aquatic Life, Dublin, Ireland, 10–16 July 2016. [Google Scholar] [CrossRef]
- Racca, R.; Ainslie, M.A.; Bosschers, J.; Hermans, M.; Lloyd, T.; MacGillivray, A.O.; Pace, F.; Schuster, M.; Sertlek, Ö.; Wood, M.A. NAVISON Final Report: Calculation and analysis of shipping sound maps for all European seas from 2016 to 2050. J. Acoust. Soc. Am. 2024. [Google Scholar]
- Hartstra, I.; Salomons, E.M.; Colin, M.; Prior, M.K. Environment dependent transition frequencies for RAM and Bellhop. In Proceedings of the UACE 2019, Hersonissos, Greece, 30 June–5 July 2019; Available online: https://api.semanticscholar.org/CorpusID:199119962 (accessed on 21 October 2025).
- Larayedh, R.; Cornuelle, B.D.; Krokos, G.; Hoteit, I. Numerical investigation of shipping noise in the Red Sea. Sci. Rep. 2024, 14, 5851. [Google Scholar] [CrossRef]
- Durofchalk, N.C.; Doran, A.K.; Torres, J.R. Modeling sea surface noise in the presence of seamounts and ocean fronts using Nx2D and 3-D methods. J. Acoust. Soc. Am. 2023, 154, A355. [Google Scholar] [CrossRef]
- Laws, N. A Parabolic Equation Analysis of the Underwater Noise Radiated by Impact Pile Driving. Master’s Thesis, Portland State University, Portland, OR, USA, 2013. [Google Scholar] [CrossRef]
- Guelton, S.; Clorennec, D.; Pardo, E.; Brunet, P.; Folégot, T. Quonops©, la Prévision Opérationnelle en Acoustique Sous-Marine sur Grille de Calcul. 2013. Available online: https://api.semanticscholar.org/CorpusID:185456164 (accessed on 21 October 2025).
- Meng, C.; Xia, C.; Li, X.Y. Reconstruction and Evaluation of Ship Radiated Noise Signal in Ocean Channel. In Proceedings of the 2020 4th Annual International Conference on Data Science and Business Analytics (ICDSBA), Changsha, China, 5–6 September 2020; pp. 312–316. [Google Scholar] [CrossRef]
- Prokopovich, V.; Shafranyuk, A.V. Underwater radiated noise model of marine object. J. Phys. Conf. Ser. 2020, 1536, 012005. [Google Scholar] [CrossRef]
- Huang, I.L.; Lee, M.C.; Nieh, C.Y.; Huang, J.C. Ship Classification Based on AIS Data and Machine Learning Methods. Electronics 2023, 13, 98. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Zhang, H. Ship Classification in High-Resolution SAR Images Using Deep Learning of Small Datasets. Sensors 2018, 18, 2929. [Google Scholar] [CrossRef]
- Luo, P.; Gao, J.; Wang, G.; Han, Y. Research on Ship Classification Method Based on AIS Data. In Proceedings of the Chinese Conference on Computer Supported Cooperative Work and Social Computing, Shenzhen, China, 7–9 November 2020. [Google Scholar] [CrossRef]
- Li, T.; Xu, H.; Zeng, W. Ship Classification Method for Massive AIS Trajectories Based on GNN. J. Phys. Conf. Ser. 2021, 2025, 012024. [Google Scholar] [CrossRef]
- Baeg, S.; Hammond, T.A. Ship Type Classification Based on The Ship Navigating Trajectory and Machine Learning. In Proceedings of the ACM IUI Workshops, Sydney, NSW, Australia, 27–31 March 2023; pp. 179–189. Available online: https://hdl.handle.net/1969.1/199814 (accessed on 21 October 2025).
- University of Washington. Ocean Noise Explorer (ONE). 2024. Available online: https://ocean-noise-explorer.readthedocs.io/en/latest/ (accessed on 21 October 2025).
- Cmst Web Team. Centre for Marine Science and Technology (CSMT)-Download AcTUP V2.2L Software. Online. 2009. Available online: https://api.semanticscholar.org/CorpusID:231077324 (accessed on 21 October 2025).
- Blue OASIS Software. 2024. Available online: https://blueoasis.pt/services/acoustics/ (accessed on 21 October 2025).
- ImageSoft. ImageSoft Tool. 2024. Available online: https://imagesoft.fi/ (accessed on 21 October 2025).
- Skylight. Skylight Tool. 2024. Available online: https://www.skylight.global/platform/ (accessed on 21 October 2025).
- Das, A. Indian Ocean Region (IOR) Mapping Platform. 2024. Available online: https://maritimeresearchcenter.com (accessed on 21 October 2025).
- Andrew, R.; Miksis-Olds, J.L.; Dugan, P.J.; Martin, S.B.; Klinck, H.; Mellinger, D.K.; Mann, D.A.; Ponirakis, D.; Boebel, O. Ocean Sound Analysis Software for Making Ambient Noise Trends Accessible (MANTA). Front. Mar. Sci. 2021, 8, 703650. [Google Scholar] [CrossRef]
- dBSea. dBSea, Underwater Noise Prediction and Visualisation Software. 2024. Available online: https://www.dbsea.co.uk/ (accessed on 21 October 2025).
- Park, M.H.; Yeo, S.; Choi, J.H.; Lee, W.J. Review of noise and vibration reduction technologies in marine machinery: Operational insights and engineering experience. Appl. Ocean. Res. 2024, 152, 104195. [Google Scholar] [CrossRef]
- Stream AIS. Websocket API Documentation. 2014. Available online: https://aisstream.io/ (accessed on 21 October 2025).
- Casari, P.; Tapparello, C.; Guerra, F.; Favaro, F.; Calabrese, I.; Toso, G.; Azad, S.; Masiero, R.; Zorzi, M. Open source suites for underwater networking: WOSS and DESERT underwater. IEEE Netw. 2014, 28, 38–46. [Google Scholar] [CrossRef]
- World Ocean Atlas (WOA). 2025. Available online: http://www.nodc.noaa.gov (accessed on 21 October 2025).
- General Bathymetric Chart of the Oceans. GEBCO. 2025. Available online: www.gebco.net (accessed on 21 October 2025).
- National Geophysical Data Center. Deck41, Seafloor Surficial Sediment Descriptions. 2025. Available online: https://www.ncei.noaa.gov/access/metadata/landing-page/bin/iso?id=gov.noaa.ngdc.mgg.geology:G02094 (accessed on 21 October 2025).
- International Telecommunication Union. Technical Characteristics for an Automatic Identification System Using Time Division Multiple Access in the VHF Maritime Mobile Frequency Band, 2014. Recommendation ITU-R M.1371-5. Available online: https://www.itu.int/rec/R-REC-M.1371-5-201402-I (accessed on 21 October 2025).
- Gandhi, I.; Pandey, M. Hybrid Ensemble of classifiers using voting. In Proceedings of the 2015 International Conference on Green Computing and Internet of Things (ICGCIoT), Greater Noida, India, 8–10 October 2015; pp. 399–404. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Machine Learning. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. arXiv 2016. [Google Scholar] [CrossRef]
- Hearst, M.; Dumais, S.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Rokach, L.; Maimon, O. Decision Trees. In Data Mining and Knowledge Discovery Handbook; Maimon, O., Rokach, L., Eds.; Springer: Boston, MA, USA, 2005; pp. 165–192. [Google Scholar] [CrossRef]
- Mucherino, A.; Papajorgji, P.J.; Pardalos, P.M. k-Nearest Neighbor Classification. In Data Mining in Agriculture; Springer: New York, NY, USA, 2009; pp. 83–106. [Google Scholar] [CrossRef]
- Anand, M.V.; KiranBala, B.; Srividhya, S.R.; Kavitha, C.; Younus, M.; Rahman, M.H.; Kumar Reddy, M.P. Gaussian Naïve Bayes Algorithm: A Reliable Technique Involved in the Assortment of the Segregation in Cancer. Mob. Inf. Syst. 2022, 2022, 2436946. [Google Scholar] [CrossRef]
- Nassara, E.I.G.; Grall-Maës, E.; Kharouf, M. Linear Discriminant Analysis for Large-Scale Data: Application on Text and Image Data. In Proceedings of the 2016 15th IEEE International Conference on Machine Learning and Applications (ICMLA), Anaheim, CA, USA, 18–20 December 2016; pp. 961–964. [Google Scholar] [CrossRef]
- Biggs, F.; Zantedeschi, V.; Guedj, B. On Margins and Generalisation for Voting Classifierse. 2022. Available online: https://arxiv.org/pdf/2206.04607 (accessed on 21 October 2025).
- Parsons, M.J.G.; Erbe, C.; Meekan, M.G.; Parsons, S.K. A Review and Meta-Analysis of Underwater Noise Radiated by Small (<25 m Length) Vessels. J. Mar. Sci. Eng. 2021, 9, 827. [Google Scholar] [CrossRef]
- Lloyd, T.; Daniel, J.; Bosschers, J.; Schuster, M. ‘PIANO’: A physics-based semi-empirical source level model for fleet-scale ship URN prediction. In Proceedings of the Eighth International Symposium on Marine Propulsors Smp’24, Berlin, Germany, 17–20 March 2024. [Google Scholar] [CrossRef]
- Veirs, S.; Veirs, V.; Wood, J.D. Ship noise extends to frequencies used for echolocation by endangered killer whales. PeerJ 2016, 4, e1657. [Google Scholar] [CrossRef] [PubMed]
- Last, P.; Bahlke, C.; Hering-Bertram, M.; Linsen, L. Comprehensive Analysis of Automatic Identification System (AIS) Data in Regard to Vessel Movement Prediction. J. Navig. 2014, 67, 791–809. [Google Scholar] [CrossRef]
- Nguyen, D.; Fablet, R. A Transformer Network with Sparse Augmented Data Representation and Cross Entropy Loss for AIS-Based Vessel Trajectory Prediction. IEEE Access 2021, 12, 21596–21609. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30, Available online: https://proceedings.neurips.cc/paper_files/paper/2017/file/6449f44a102fde848669bdd9eb6b76fa-Paper.pdf (accessed on 21 October 2025).
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Advances in Neural Information Processing Systems; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31, Available online: https://proceedings.neurips.cc/paper_files/paper/2018/file/14491b756b3a51daac41c24863285549-Paper.pdf (accessed on 21 October 2025).
- McDonald, G.C. Ridge regression. WIREs Comput. Stat. 2009, 1, 93–100. [Google Scholar] [CrossRef]
- Reynolds, D. Gaussian Mixture Models. In Encyclopedia of Biometrics; Li, S.Z., Jain, A., Eds.; Springer: Boston, MA, USA, 2009; pp. 659–663. [Google Scholar] [CrossRef]
- Cometti, D.S.; Mazuelas, S.; Sacco, G.; Melazzi, N.B.; Bartoletti, S. Location-Aided Iterative Beam Search via Learning-based Generative Models. In Proceedings of the 2025 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 8–12 June 2025; pp. 1906–1911. [Google Scholar] [CrossRef]
- Huang, H.; Cui, C.; Cheng, L.; Liu, Q.; Wang, J. Grid interpolation algorithm based on nearest neighbor fast search. Earth Sci. Inf. 2012, 5, 181–187. [Google Scholar] [CrossRef]
- Amidror, I. Scattered data interpolation methods for electronic imaging systems: A survey. J. Electron. Imaging 2002, 11, 157–176. [Google Scholar] [CrossRef]
- Worsey, A.; Farin, G. Ann-dimensional Clough-Tocher interpolant. Constr. Approx. 1987, 3, 99–110. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y.; Zhao, N.; Guo, B.; Mou, N. Least Squares Compactly Supported Radial Basis Function for Digital Terrain Model Interpolation from Airborne Lidar Point Clouds. Remote Sens. 2018, 10, 587. [Google Scholar] [CrossRef]
- Benmoshe, N. A Simple Solution for the Inverse Distance Weighting Interpolation (IDW) Clustering Problem. Sci 2025, 7, 30. [Google Scholar] [CrossRef]
- Raid, I.; Kusnezowa, T.; Seewig, J. Application of ordinary kriging for interpolation of micro-structured technical surfaces. Meas. Sci. Technol. 2013, 24, 095201. [Google Scholar] [CrossRef]
- Chang, C.; Zeng, T. A hybrid data-driven-physics-constrained Gaussian process regression framework with deep kernel for uncertainty quantification. J. Comput. Phys. 2023, 486, 112129. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. White noise kernel. In Gaussian Processes for Machine Learning; Springer International Publishing: Berlin/Heidelberg, Germany, 2006; Available online: https://gaussianprocess.org/gpml/ (accessed on 21 October 2025).
- Lu, G.Y.; Wong, D.W. An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci. 2008, 34, 1044–1055. [Google Scholar] [CrossRef]
- Turner, S.; Zykov, M.; MacGillivray, A. Preliminary Acoustic Level Measurements of Airgun Sources from Conoco Phillips’ 2006 Seismic Survey in Alaskan Chukchi Sea; JASCO Research Ltd.: Victoria, BC, Canada, 2006. [Google Scholar]
- Keen, K.A.; Thayre, B.J.; Hildebrand, J.A.; Wiggins, S.M. Seismic airgun sound propagation in Arctic Ocean waveguides. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2018, 141, 24–32. Available online: https://api.semanticscholar.org/CorpusID:53056420 (accessed on 21 October 2025). [CrossRef]
- Kaifu, K.; Segawa, S.; Tsuchiya, K. Behavioral Responses to Underwater Sound in the Small Benthic Octopus Octopus ocellatus. J. Mar. Acoust. Soc. Jpn. 2007, 34, 266–273. [Google Scholar] [CrossRef]
- Blackwell, S.B.; Nations, C.S.; McDonald, T.L.; Thode, A.M.; Mathias, D.; Kim, K.H.; Greene, C.R., Jr.; Macrander, A.M. Effects of Airgun Sounds on Bowhead Whale Calling Rates: Evidence for Two Behavioral Thresholds. PLoS ONE 2015, 10, e0125720. [Google Scholar] [CrossRef] [PubMed]




| Feature | dBSea | MANTA | AcTUP | MNAT (Proposed) |
|---|---|---|---|---|
| Scalability | Scenario-limited, solver-dependent. | Processes large soundscape archives, but in only batch mode. | Allows batch runs of multiple acoustic toolbox methods; research-grade, MATLAB-dependent. | Designed for basin- and sea-level simulations with real-time multi-vessel handling; use goes beyond research contexts. |
| Speed | Advanced solvers (e.g., PE) can be slow. | Batch postprocessing can be slow. | Moderate; solver-dependent, not optimized for real-time. | Standard models may be slow, but machine learning used in parallel accelerates their performance. |
| Usability | Requires acoustic expertise and manual tuning. | GUI with calibration support, but requires technical knowledge. | Menu-driven MATLAB interface; automated acoustic tool integration. | Web-based geographical GUI; automated AIS preprocessing and ML-aided vessel classification. |
| Innovation gap | Validated propagation models for scenario accuracy. | Standardized noise datasets for comparability. | Unifies acoustic tool codes in one interface with batch capability. | Integrates preprocessed real-time AIS data, estimates source noise levels close to reality, leverages machine learning to accelerate processing, and offers a scalable web-based simulation with interactive visualization. |
| Attribute | Type | Description |
|---|---|---|
| PositionData table | ||
| UserID | Integer | Unique vessel identifier |
| Cog | Float | Course over ground in degrees |
| Latitude | Float | Vessel’s latitude coordinate |
| Longitude | Float | Vessel’s longitude coordinate |
| MessageID | Integer | AIS message type identifier |
| NavigationalStatus | Integer | Vessel’s operational status (e.g., underway, anchored, moored) |
| RateOfTurn | Float | Rate of turn in degrees per minute |
| Sog | Float | Speed over ground in knots |
| Timestamp | Integer | Unix timestamp of the position report |
| TrueHeading | Integer | Vessel’s true heading in degrees |
| UpdatedTime | DateTime | Database update timestamp |
| ShipStaticData table | ||
| UserID | Integer | Unique vessel identifier (primary key) |
| DimensionA | Integer | Distance from reference point to bow |
| DimensionB | Integer | Distance from reference point to stern |
| DimensionC | Integer | Distance from reference point to port side |
| DimensionD | Integer | Distance from reference point to starboard |
| ImoNumber | Integer | International Maritime Organization number |
| MaximumStaticDraught | Float | Maximum static draught in meters |
| MessageID | Integer | AIS message type identifier |
| Type | Integer | Ship-type classification |
| UpdatedTime | DateTime | Database update timestamp |
| Precision | Recall | F1-Score | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | Cargo | Fishing | Tanker | Cargo | Fishing | Tanker | Cargo | Fishing | Tanker | Accuracy |
| Voting Classifier | 0.90 | 0.94 | 0.89 | 0.92 | 0.99 | 0.82 | 0.91 | 0.97 | 0.86 | 0.91 |
| Random Forest | 0.90 | 0.95 | 0.90 | 0.93 | 0.99 | 0.83 | 0.91 | 0.97 | 0.87 | 0.91 |
| XGBoost | 0.91 | 0.95 | 0.89 | 0.92 | 0.99 | 0.84 | 0.91 | 0.97 | 0.86 | 0.91 |
| SVM | 0.84 | 0.93 | 0.70 | 0.78 | 0.99 | 0.74 | 0.81 | 0.96 | 0.72 | 0.81 |
| Decision Tree | 0.86 | 0.94 | 0.82 | 0.88 | 0.94 | 0.79 | 0.87 | 0.94 | 0.80 | 0.87 |
| KNN | 0.81 | 0.94 | 0.73 | 0.83 | 0.99 | 0.68 | 0.82 | 0.96 | 0.70 | 0.81 |
| Gaussian NB | 0.66 | 0.91 | 0.58 | 0.84 | 0.95 | 0.30 | 0.74 | 0.93 | 0.40 | 0.70 |
| Logistic Regression | 0.76 | 0.91 | 0.59 | 0.71 | 0.99 | 0.62 | 0.74 | 0.95 | 0.61 | 0.74 |
| LDA | 0.72 | 0.94 | 0.80 | 0.91 | 0.95 | 0.43 | 0.80 | 0.94 | 0.56 | 0.78 |
| Model | MAE (dB) | RMSE (dB) | (Ratio) |
|---|---|---|---|
| Stacking Regressor | 2.6 | 3.2 | 0.98 |
| XGBoost | 2.7 | 3.4 | 0.98 |
| CatBoost | 2.9 | 3.6 | 0.98 |
| Random Forest | 3.4 | 4.3 | 0.97 |
| LightGBM | 3.4 | 4.3 | 0.97 |
| Extra Trees | 3.4 | 4.3 | 0.97 |
| Gradient Boosting | 3.6 | 4.5 | 0.97 |
| Voting Regressor | 4.0 | 5.0 | 0.96 |
| KNN | 6.4 | 8.0 | 0.92 |
| Rank | Vessel | Position | Closest Cluster | Score |
|---|---|---|---|---|
| 1 | v8 | (45.17, 12.78) | C0 | 96.3 |
| 2 | v5 | (44.86, 12.97) | C0 | 94.9 |
| 3 | v12 | (44.87, 13.02) | C0 | 94.9 |
| 4 | v2 | (40.75, 18.68) | C3 | 93.8 |
| 5 | v1 | (40.54, 18.89) | C3 | 92.1 |
| 6 | v10 | (45.45, 13.35) | C0 | 91.3 |
| 7 | v4 | (44.74, 13.17) | C0 | 91.2 |
| 8 | v13 | (44.68, 12.88) | C0 | 91.0 |
| 9 | v14 | (44.67, 13.04) | C0 | 90.9 |
| 10 | v9 | (44.62, 12.72) | C0 | 88.8 |
| 11 | v3 | (43.24, 14.59) | C2 | 85.5 |
| 12 | v11 | (44.31, 12.64) | C0 | 82.6 |
| 13 | v7 | (43.81, 15.00) | C1 | 74.3 |
| 14 | v6 | (42.08, 16.00) | C2 | 63.5 |
| Pick sequence | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Global rank | 1 | 4 | 11 | 13 | 12 | 10 | 9 | 8 | 14 | 5 | 7 | 6 | 3 | 2 |
| Vessel | v8 | v2 | v3 | v7 | v11 | v9 | v14 | v13 | v6 | v1 | v4 | v10 | v12 | v5 |
| Cluster | C0 | C3 | C2 | C1 | C0 | C0 | C0 | C0 | C2 | C3 | C0 | C0 | C0 | C0 |
| Method | Parameter | Value |
|---|---|---|
| RBF | Function | cubic |
| Epsilon | 9.7088 | |
| IDW | Power | 4.9987 |
| GPR-Physics | White Kernel noise level | 0.01 |
| RBF Kernel length scale | 0.1 | |
| Alpha | ||
| Restarts optimizer | 15 | |
| Kriging | Variogram model | Exponential |
| Nugget | 0.0015 | |
| Sill | 4.0368 | |
| Range | 8.6882 | |
| Griddata (Nearest) | Fill value | NaN |
| Griddata (Linear) | Fill value | NaN |
| Clough-Tocher | Triangulation method | Convex hull |
| Interpolation order | Linear | |
| Boundary handling | Extrapolate | |
| Fill value | NaN | |
| Ensemble MultiMethods Physics | IDW Weight | 60% |
| Other Methods Weight | 40% | |
| Distance Metric | Euclidean | |
| Matching Strategy | Nearest Neighbor | |
| Spatial Resolution | Grid-based |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanhatalab, M.R.; Casari, P. MNAT: A Simulation Tool for Underwater Radiated Noise. J. Mar. Sci. Eng. 2025, 13, 2045. https://doi.org/10.3390/jmse13112045
Tanhatalab MR, Casari P. MNAT: A Simulation Tool for Underwater Radiated Noise. Journal of Marine Science and Engineering. 2025; 13(11):2045. https://doi.org/10.3390/jmse13112045
Chicago/Turabian StyleTanhatalab, Mohammad Rasoul, and Paolo Casari. 2025. "MNAT: A Simulation Tool for Underwater Radiated Noise" Journal of Marine Science and Engineering 13, no. 11: 2045. https://doi.org/10.3390/jmse13112045
APA StyleTanhatalab, M. R., & Casari, P. (2025). MNAT: A Simulation Tool for Underwater Radiated Noise. Journal of Marine Science and Engineering, 13(11), 2045. https://doi.org/10.3390/jmse13112045








