Coupled Aero–Hydrodynamic Analysis in Floating Offshore Wind Turbines: A Review of Numerical and Experimental Methodologies
Abstract
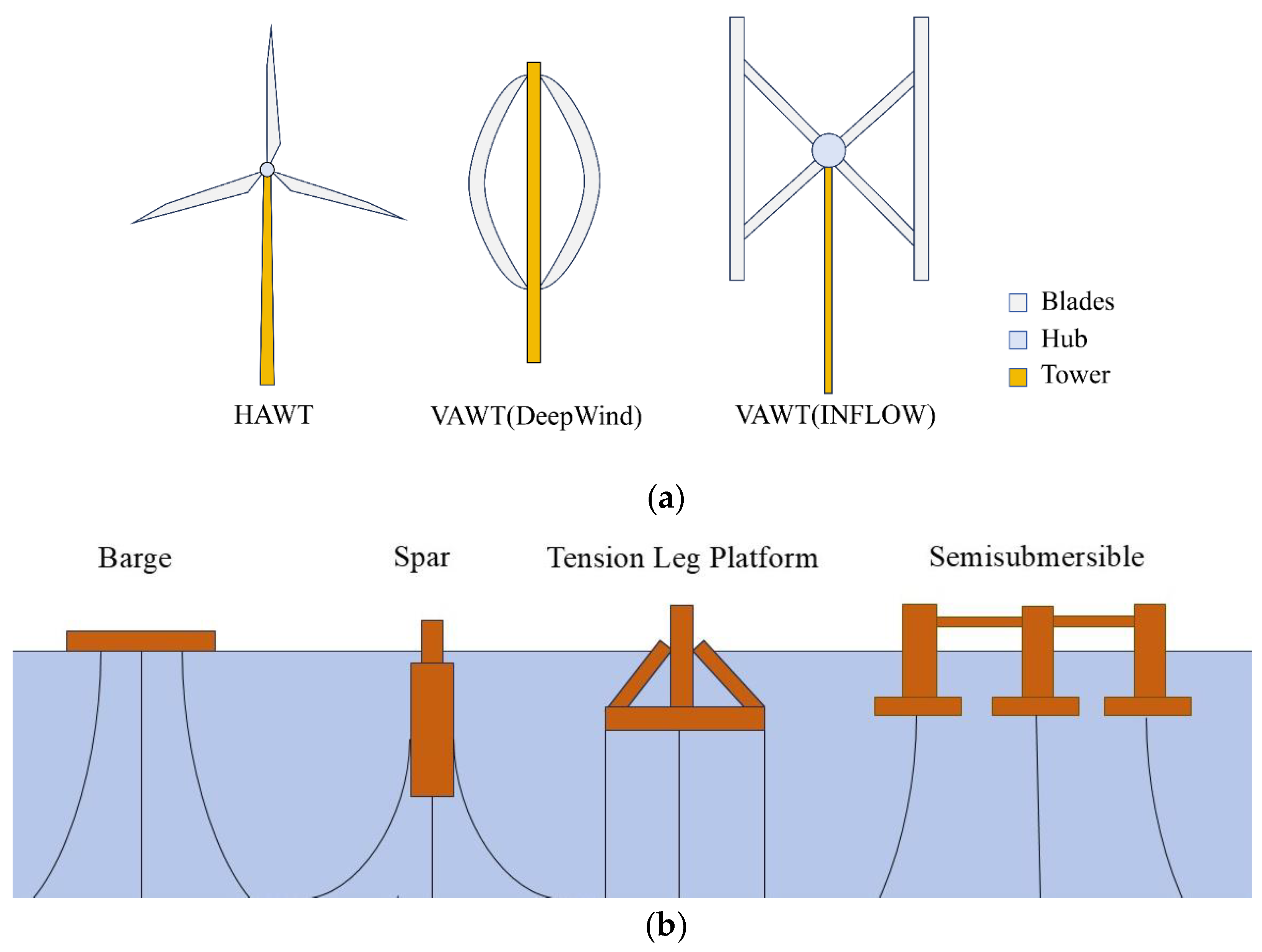
1. Introduction
2. Numerical Simulation Methods
2.1. Aerodynamics
2.2. Hydrodynamics
3. Uncoupled Analysis
3.1. Aerodynamics Analysis
3.1.1. Power Output
3.1.2. Aeroelasticity
3.1.3. TSR (Tip Speed Ratio)
3.1.4. Other Aspects
3.2. Hydrodynamics Analysis
3.2.1. DeepCwind Semisubmersible Platforms
3.2.2. Other Semisubmersible Platforms
3.3. Summary
4. Partially Coupled Analysis
4.1. Aerodynamics Analysis
4.1.1. Thrust and Power
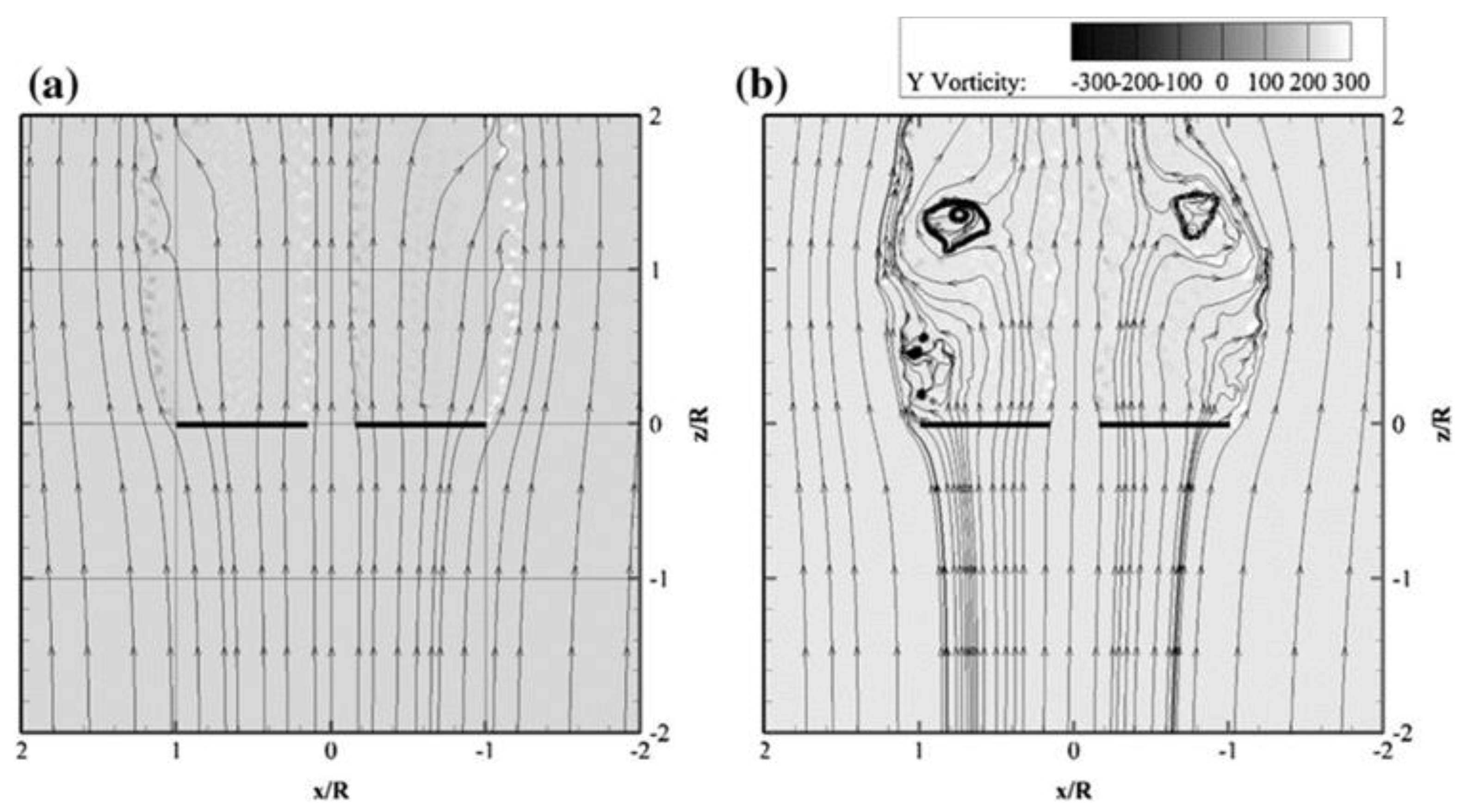
4.1.2. Wake and Vortices
4.1.3. Effect of Aeroelasticity and TSR on Aerodynamic Performance
4.1.4. Effect of Coupled Motion on Aerodynamic Performance
4.2. Hydrodynamics Analysis
4.2.1. CFD
4.2.2. FAST (OpenFAST)
4.2.3. ANSYS-AQWA
4.3. Summary
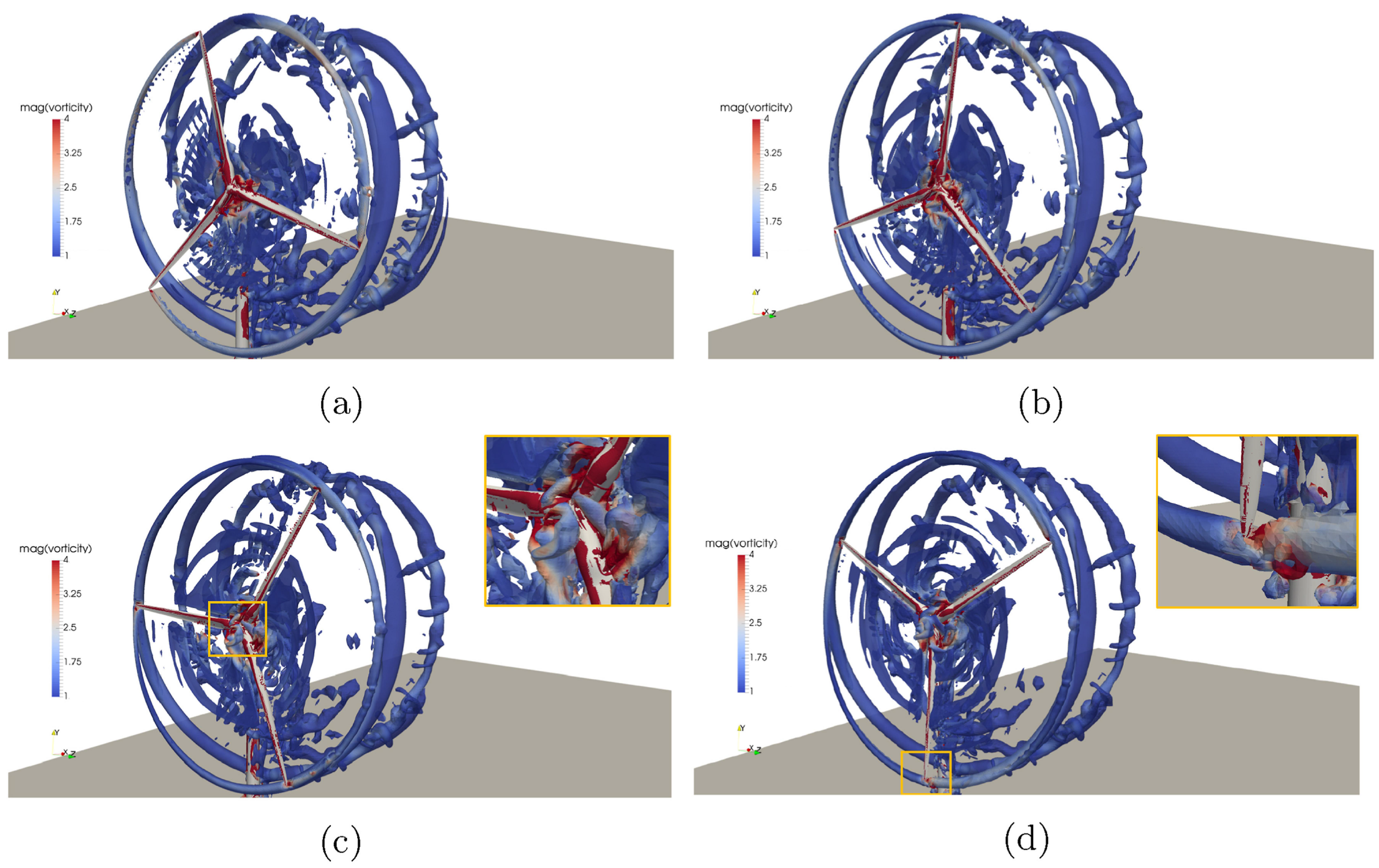
5. Fully Coupled Analysis
5.1. Simulation Analysis
5.1.1. CFD
5.1.2. FAST (OpenFAST)
5.1.3. F2A
5.2. Summary
6. Physical Model Tests
6.1. Wave Basin Tests
6.1.1. DeepCwind Project
6.1.2. Other Aspects
6.2. Wind Tunnel Tests
6.2.1. UNAFLOW Project
6.2.2. Optimization of Scaled Wind Turbine Models
6.3. Real-Time Hybrid Tests (RTHT)
6.3.1. RTHT Based on Numerical Wind Tunnel
6.3.2. RTHT Based on Numerical Wave Basin
6.4. Summary
7. Conclusions and Challenges
7.1. Conclusions
7.2. Future Trends and Challenges
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature:
| ADM | Actuator disc model |
| ALM | Actuator line model |
| BEM | Blade element momentum |
| CFD | Computational fluid dynamics |
| CSD | Computational Structural Dynamics |
| COG | Central of Gravity |
| DTU | Technical University of Denmark |
| DFBI | Dynamic Fluid–Body Interaction |
| DOF | Degree of Freedom |
| DES | Detached eddy simulation |
| DWM | Dynamic Wake Meandering |
| EOG | Extreme operating gust |
| FAST | Fatigue, Aerodynamics, Structure and Turbulence |
| FVM | Free vortex method |
| FOWT | Floating offshore wind turbine |
| FEA | Finite Element Method |
| GDW | Generalized dynamic wake |
| HAWT | Horizontal-axis wind turbine |
| IDDES | Improved delayed detached eddy simulation |
| IEA | International Energy Agency |
| LES | Large eddy simulation |
| ME | Morison equation |
| NREL | National Renewable Energy Laboratory |
| NTNU | Norwegian University of Science and Technology |
| N-S | Navier–Stokes |
| OC3 | Offshore Code Comparison Collaboration |
| OC4 | Offshore Code Comparison Collaboration Continuation |
| OC5 | Offshore Code Comparison Collaboration Continued with Correlation |
| OC6 | Offshore Code Comparison Collaboration, Continued, with Correlation, and unCertainty |
| PF | Potential flow |
| PSD | Power spectral density |
| RANS | Reynolds averaged Navier–Stokes |
| RAO | Response amplitude operator |
| RSM | Reynolds Stress Model |
| RTHT | Real-time hybrid tests |
| SIL | Software-in-the-loop |
| TSR | Tip speed ratio |
| TLP | Tension leg platform |
| TWS | Turbulent wake state |
| UDF | User-defined function |
| VAWT | Vertical-axis wind turbine |
| VLM | Vortex lattice method |
| VOF | Volume of fluid |
| VRS | Vortex ring state |
References
- Esteban, M.D.; Diez, J.J.; López, J.S.; Negro, V. Why offshore wind energy? Renew. Energy 2011, 36, 444–450. [Google Scholar] [CrossRef]
- Lauria, A.; Loprieno, P.; Francone, A.; Leone, E.; Tomasicchio, G. Recent advances in understanding the dynamic characterization of floating offshore wind turbines. Ocean Eng. 2024, 307, 118189. [Google Scholar] [CrossRef]
- Joyce, L.; Feng, Z. Global Wind Report 2024; Global Wind Energy Council: Incheon, Republic of Korea, 2024. [Google Scholar]
- Subbulakshmi, A.; Verma, M.; Keerthana, M.; Sasmal, S.; Harikrishna, P.; Kapuria, S. Recent advances in experimental and numerical methods for dynamic analysis of floating offshore wind turbines—An integrated review. Renew. Sustain. Energy Rev. 2022, 164, 112525. [Google Scholar] [CrossRef]
- Heronemus, W.E. Pollution-free energy from offshore winds. In Proceedings of the 8th Annual Conference and Exposition, Marine Technology Society, Washington, DC, USA, 11–13 September 1972. [Google Scholar]
- Zhao, Z.; Wang, D.; Wang, T.; Shen, W.; Liu, H.; Chen, M. A review: Approaches for aerodynamic performance improvement of lift-type vertical axis wind turbine. Sustain. Energy Technol. Assess. 2022, 49, 101789. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009. [Google Scholar]
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Natarajan, A.; Hansen, M. Description of the DTU 10 MW Reference Wind Turbine; DTU Wind Energy Report-I-0092; DTU Research Database: Roskilde, Denmark, 2013. [Google Scholar]
- Gaertner, E.; Rinker, J.; Sethuraman, L.; Zahle, F.; Anderson, B.; Barter, G.; Abbas, N.; Meng, F.; Bortolotti, P.; Skrzypinski, W. Definition of the IEA 15-Megawatt Offshore Reference Wind Turbine; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2020. [Google Scholar]
- Zahle, F.; Barlas, T.; Lonbaek, K.; Bortolotti, P.; Zalkind, D.; Wang, L.; Labuschagne, C.; Sethuraman, L.; Barter, G. Definition of the IEA Wind 22-Megawatt Offshore Reference Wind Turbine; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2024. [Google Scholar]
- Robertson, A.; Jonkman, J.; Masciola, M.; Song, H.; Goupee, A.; Coulling, A.; Luan, C. Definition of the Semisubmersible Floating System for Phase II of OC4; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2014. [Google Scholar]
- Robertson, A.N.; Wendt, F.; Jonkman, J.M.; Popko, W.; Dagher, H.; Gueydon, S.; Qvist, J.; Vittori, F.; Azcona, J.; Uzunoglu, E.; et al. OC5 Project Phase II: Validation of Global Loads of the DeepCwind Floating Semisubmersible Wind Turbine. In Proceedings of the 14th Deep Sea Offshore Wind R and D Conference (EERA DeepWind), Trondheim, Norway, 18–20 January 2017; pp. 38–57. [Google Scholar]
- Zhang, Y.; Kim, B. A Fully Coupled Computational Fluid Dynamics Method for Analysis of Semi-Submersible Floating Offshore Wind Turbines Under Wind-Wave Excitation Conditions Based on OC5 Data. Appl. Sci. 2018, 8, 2314. [Google Scholar] [CrossRef]
- Yu, W.; Müller, K.; Lemmer, F.; Bredmose, H.; Borg, M.; Sanchez, G.; Landbo, T. Public definition of the two LIFES50+ 10 MW floater concepts. LIFES50+ Deliv. 2017, 4, 15. [Google Scholar]
- Allen, C.; Viscelli, A.; Dagher, H.; Goupee, A.; Gaertner, E.; Abbas, N.; Hall, M.; Barter, G. Definition of the UMaine VolturnUS-S Reference Platform Developed for the IEA Wind 15-Megawatt Offshore Reference Wind Turbine; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2020. [Google Scholar]
- Chen, P.; Chen, J.H.; Hu, Z.Q. Review of Experimental-Numerical Methodologies and Challenges for Floating Offshore Wind Turbines. J. Mar. Sci. Appl. 2020, 19, 339–361. [Google Scholar] [CrossRef]
- Otter, A.; Murphy, J.; Pakrashi, V.; Robertson, A.; Desmond, C. A review of modelling techniques for floating offshore wind turbines. Wind. Energy 2021, 25, 831–857. [Google Scholar] [CrossRef]
- Glauert, H. An Aerodynamic Theory of the Airscrew; H.M. Stationery Office: London, UK, 1922. [Google Scholar]
- Peters, D.A.; He, C.J. Correlation of measured induced velocities with a finite-state wake model. J. Am. Helicopter Soc. 1991, 36, 59–70. [Google Scholar] [CrossRef]
- Suzuki, A. Application of Dynamic Inflow Theory to Wind Turbine Rotors; Department of Mechanical Engineering, University of Utah: Salt Lake City, UT, USA, 2000. [Google Scholar]
- Katz, J.; Plotkin, A. Low-Speed Aerodynamics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Hess, J.L. Calculation of Potential Flow About Arbitrary Three-Dimensional Lifting Bodies; McDonnell Douglas Report, MDC J5679-01; DTIC: Pretoria, South Africa, 1972. [Google Scholar]
- Leishman, J.G.; Bhagwat, M.J.; Bagai, A. Free-Vortex Filament Methods for the Analysis of Helicopter Rotor Wakes. J. Aircr. 2002, 39, 759–775. [Google Scholar] [CrossRef]
- Dumitrescu, H.; Cardos, V. Predictions of unsteady HAWT aerodynamics by lifting line theory. Math. Comput. Model. 2001, 33, 469–481. [Google Scholar] [CrossRef]
- Sørensen, J.N.; Myken, A. Unsteady actuator disc model for horizontal axis wind turbines. J. Wind Eng. Ind. Aerodyn. 1992, 39, 139–149. [Google Scholar] [CrossRef]
- Sorensen, J.N.; Shen, W.Z. Numerical modeling of wind turbine wakes. J. Fluids Eng. 2002, 124, 393–399. [Google Scholar] [CrossRef]
- Boorsma, K.; Schepers, G.; Aagard Madsen, H.; Pirrung, G.; Sørensen, N.; Bangga, G.; Imiela, M.; Grinderslev, C.; Meyer Forsting, A.; Shen, W.Z.; et al. Progress in the validation of rotor aerodynamic codes using field data. Wind Energy Sci. 2023, 8, 211–230. [Google Scholar] [CrossRef]
- Sharma, A.; Brazell, M.J.; Vijayakumar, G.; Ananthan, S.; Cheung, L.; deVelder, N.; de Frahan, M.T.H.; Matula, N.; Mullowney, P.; Rood, J.; et al. ExaWind: Open-source CFD for hybrid-RANS/LES geometry-resolved wind turbine simulations in atmospheric flows. Wind Energy 2024, 27, 225–257. [Google Scholar] [CrossRef]
- Morison, J.; Johnson, J.W.; Schaaf, S.A. The force exerted by surface waves on piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Bai, C.J.; Wang, W.C. Review of computational and experimental approaches to analysis of aerodynamic performance in horizontal-axis wind turbines (HAWTs). Renew. Sustain. Energy Rev. 2016, 63, 506–519. [Google Scholar] [CrossRef]
- Chavan, D.S.; Gaikwad, S.; Singh, A.; Himanshu; Parashar, D.; Saahil, V.; Sankpal, J.; Karandikar, P.B.; IEEE. Impact of vertical wind shear on wind turbine performance. In Proceedings of the IEEE International Conference on Circuit, Power and Computing Technologies (ICCPCT), Kollam, India, 20–21 April 2017; pp. 1–6. [Google Scholar]
- Xu, B.F.; Feng, J.H.; Wang, T.G.; Yuan, Y.; Zhao, Z.Z.; Zhong, W. Trailing-Edge Flap Control for Mitigating Rotor Power Fluctuations of a Large-Scale Offshore Floating Wind Turbine under the Turbulent Wind Condition. Entropy 2018, 20, 12. [Google Scholar] [CrossRef]
- Wisatesajja, W.; Roynarin, W.; Intholo, D. Analysis of Influence of Tilt Angle on Variable-Speed Fixed-Pitch Floating Offshore Wind Turbines for Optimizing Power Coefficient Using Experimental and CFD Models. Int. J. Renew. Energy Dev. 2021, 10, 201–212. [Google Scholar] [CrossRef]
- Zhang, Z.; Han, Z.; Zhou, D.; Bao, Y.; Zhu, H.; Zhao, Y. Numerical Investigation of Aerodynamic and Wake Characteristics of a Twin-Rotor Floating Wind Turbine: Under Different Wind Directions. In Proceedings of the The 33rd International Ocean and Polar Engineering Conference, Ottawa, ON, Canada, 19–23 June 2023; p. ISOPE-I-23-051. [Google Scholar]
- Sayed, M.; Lutz, T.; Krämer, E.; Shayegan, S.; Wüchner, R. Aeroelastic analysis of 10 MW wind turbine using CFD-CSD explicit FSI-coupling approach. J. Fluids Struct. 2019, 87, 354–377. [Google Scholar] [CrossRef]
- Li, Z.; Wen, B.; Dong, X.; Peng, Z.; Qu, Y.; Zhang, W. Aerodynamic and aeroelastic characteristics of flexible wind turbine blades under periodic unsteady inflows. J. Wind Eng. Ind. Aerodyn. 2020, 197, 104057. [Google Scholar] [CrossRef]
- Zhu, R.S.; Zhao, H.L.; Peng, J.Y.; Li, J.P.; Wang, S.Q.; Zhao, H. A numerical investigation of fluid-structure coupling of 3 MW wind turbine blades. Int. J. Green Energy 2016, 13, 241–247. [Google Scholar] [CrossRef]
- Rinker, J.; Gaertner, E.; Zahle, F.; Skrzypinski, W.; Abbas, N.; Bredmose, H.; Barter, G.; Dykes, K. Comparison of loads from HAWC2 and OpenFAST for the IEA Wind 15 MW Reference Wind Turbine. J. Phys. Conf. Ser. 2020, 1618, 052052. [Google Scholar] [CrossRef]
- Wang, L.; Quant, R.; Kolios, A. Fluid structure interaction modelling of horizontal-axis wind turbine blades based on CFD and FEA. J. Wind Eng. Ind. Aerodyn. 2016, 158, 11–25. [Google Scholar] [CrossRef]
- Giahi, M.H.; Dehkordi, A.J. Investigating the influence of dimensional scaling on aerodynamic Characteristics of wind turbine using CFD simulation. Renew. Energy 2016, 97, 162–168. [Google Scholar] [CrossRef]
- Pinto, M.L.; Franzini, G.R.; Simos, A.N. A CFD analysis of NREL’s 5 MW wind turbine in full and model scales. J. Ocean Eng. Mar. Energy 2020, 6, 211–220. [Google Scholar] [CrossRef]
- Kim, H.; Lee, S.; Lee, S. Influence of blade-tower interaction in upwind-type horizontal axis wind turbines on aerodynamics. J. Mech. Sci. Technol. 2011, 25, 1351–1360. [Google Scholar] [CrossRef]
- Tran, T.T.; Ryu, G.J.; Kim, Y.H.; Kim, D.H. CFD-based design load analysis of 5 MW offshore wind turbine. AIP Conf. Proc. 2012, 1493, 533–545. [Google Scholar]
- Oggiano, L. CFD simulations on the NTNU wind turbine rotor and comparison with experiments. In Proceedings of the 3rd Renewable Energy Research Conference (RERC), Sffe, Oslo, Norway, 16–18 June 2014; pp. 111–116. [Google Scholar]
- Kono, T.; Nebucho, S.; Kogaki, T.; Kiwata, T.; Kimura, S.; Komatsu, N. Numerical Analysis of the Effects of Rotating Wind Turbine Blades on the Aerodynamic Forces Acting on Tower. Energies 2017, 10, 121. [Google Scholar] [CrossRef]
- Sivalingam, K.; Wala, A.A.S.; Davies, P.; Day, S.; IEEE. CFD Validation of Scaled Floating Offshore Wind Turbine Rotor. In Proceedings of the 2nd International Conference on Green Energy and Applications (ICGEA), Singapore, 24–26 March 2018; pp. 176–182. [Google Scholar]
- Popescu, F.; Mahu, R.; Rusu, E.; Ion, I.V. A Robust and Efficient Computational Fluid Dynamics Approach for the Prediction of Horizontal-Axis Wind Turbine Performance. J. Mar. Sci. Eng. 2022, 10, 1243. [Google Scholar] [CrossRef]
- Zhong, J.; Li, J. Aerodynamic performance prediction of NREL phase VI blade adopting biplane airfoil. Energy 2020, 206, 118182. [Google Scholar] [CrossRef]
- Zhang, J.W.; Wang, J.W.; Yan, S.J. The effect of yaw speed and delay time on power generation and stress of a wind turbine. Int. J. Green Energy 2023, 20, 153–165. [Google Scholar] [CrossRef]
- Benitz, M.A.; Schmidt, D.P.; Lackner, M.A.; Stewart, G.M.; Jonkman, J.; Robertson, A.; Asme. Comparison of Hydrodynamic Load Predictions Between Reduced Order Engineering Models and Computational Fluid Dynamics for the OC4-DeepCwind Semi-Submersible. In Proceedings of the 2014 33rd ASME International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; p. V09BT09A006. [Google Scholar]
- Tran, T.T.; Kim, D.-H. The coupled dynamic response computation for a semi-submersible platform of floating offshore wind turbine. J. Wind Eng. Ind. Aerodyn. 2015, 147, 104–119. [Google Scholar] [CrossRef]
- Kim, H.; Jeon, G.-Y.; Choung, J.; Yoon, S.-W. Study on Mooring System Design of Floating Offshore Wind Turbine in Jeju Offshore Area. Int. J. Ocean Syst. Eng. 2013, 3, 209–217. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, H.-C. Verification and Validation of Computational Fluid Dynamic Simulations of a FOWT Semi-Submersible Under Bichromatic and Random Waves. J. Offshore Mech. Arct. Eng. 2023, 145, 062001. [Google Scholar] [CrossRef]
- Zeng, F.X.; Zhang, N.C.; Huang, G.X.; Gu, Q.; He, M. Dynamic response of floating offshore wind turbines under freak waves with large crest and deep trough. Energy 2023, 278, 127679. [Google Scholar] [CrossRef]
- Bruinsma, N.; Paulsen, B.T.; Jacobsen, N.G. Validation and application of a fully nonlinear numerical wave tank for simulating floating offshore wind turbines. Ocean Eng. 2018, 147, 647–658. [Google Scholar] [CrossRef]
- Burmester, S.; Vaz, G.; el Moctar, O. Towards credible CFD simulations for floating offshore wind turbines. Ocean Eng. 2020, 209, 107237. [Google Scholar] [CrossRef]
- Wisudawan, A.; Jaksic, V.; Pakrashi, V.; Murphy, J. Variability of Kinetic Response Estimates of Froude Scaled DeepCwind Semisubmersible Platforms Subjected to Wave Loading. J. Offshore Mech. Arct. Eng. 2023, 146, 022002. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, H.-C.; Koop, A.; Vaz, G. Hydrodynamic response of a FOWT semi-submersible under regular waves using CFD: Verification and validation. Ocean Eng. 2022, 258, 111742. [Google Scholar] [CrossRef]
- Wang, L.; Robertson, A.; Jonkman, J.; Yu, Y.H. OC6 phase I: Improvements to the OpenFAST predictions of nonlinear, low-frequency responses of a floating offshore wind turbine platform. Renew. Energy 2022, 187, 282–301. [Google Scholar] [CrossRef]
- Wang, L.; Robertson, A.; Jonkman, J.; Yu, Y.-H.; Koop, A.; Borràs Nadal, A.; Li, H.; Bachynski-Polić, E.; Pinguet, R.; Shi, W.; et al. OC6 Phase Ib: Validation of the CFD predictions of difference-frequency wave excitation on a FOWT semisubmersible. Ocean Eng. 2021, 241, 110026. [Google Scholar] [CrossRef]
- Meng, H.; Liu, Y.; Tian, D.; Long, K.; Li, B.; Su, Y.; Sun, K. Parametric study of catenary mooring system on floating wind turbine foundation dynamic response. J. Renew. Sustain. Energy 2024, 16, 023301. [Google Scholar] [CrossRef]
- Saleh, S.; Akers, R.; Koo, B.; Yau, H.; Lopez, T.; Thiagarajan, K. Comparison of Fatigue Characteristics of Polyester and Nylon Mooring Lines for Shallow Water Floating Offshore Wind Turbines. In Proceedings of the 5th International Offshore Wind Technical Conference, Exeter, UK, 18–19 December 2023; p. V001T001A016. [Google Scholar]
- Zhong, W.J.; Zhang, X.M.; Wan, D.C. Hydrodynamic characteristics of a 15 MW semi-submersible floating offshore wind turbine in freak waves. Ocean Eng. 2023, 283, 115094. [Google Scholar] [CrossRef]
- Liu, Z.; Fan, Y.; Wang, W.; Qian, G. Numerical study of a proposed semi-submersible floating platform with different numbers of offset columns based on the DeepCwind prototype for improving the wave-resistance ability. Appl. Sci. 2019, 9, 1255. [Google Scholar] [CrossRef]
- Johannesen, I.P.; Ransley, E.; Hann, M.; Cheng, S.; Greaves, D. Passive motion reduction of semisubmersible floating offshore wind turbine foundations. In Proceedings of the Trends in Renewable Energies Offshore, Lisbon, Portugal, 8–10 November 2022; pp. 501–508. [Google Scholar]
- Califano, A.; Berthelsen, P.A.; Da Fonseca, N.M.D. Effect of body motion on the wave loads computed with CFD on the INO-WINDMOOR floater. J. Phys. Conf. Ser. 2023, 2626, 012034. [Google Scholar] [CrossRef]
- Barooni, M.; Ashuri, T.; Sogut, D.V.; Wood, S.; Taleghani, S.G. Floating Offshore Wind Turbines: Current Status and Future Prospects. Energies 2023, 16, 2. [Google Scholar] [CrossRef]
- Tran, T.; Kim, D.; Song, J. Computational Fluid Dynamic Analysis of a Floating Offshore Wind Turbine Experiencing Platform Pitching Motion. Energies 2014, 7, 5011–5026. [Google Scholar] [CrossRef]
- Tran, T.-T.; Kim, D.-H.; Hieu Nguyen, B. Aerodynamic Interference Effect of Huge Wind Turbine Blades with Periodic Surge Motions Using Overset Grid-Based Computational Fluid Dynamics Approach. J. Sol. Energy Eng. 2015, 137, 061003. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.H. The aerodynamic interference effects of a floating offshore wind turbine experiencing platform pitching and yawing motions. J. Mech. Sci. Technol. 2015, 29, 549–561. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.-H. A CFD study into the influence of unsteady aerodynamic interference on wind turbine surge motion. Renew. Energy 2016, 90, 204–228. [Google Scholar] [CrossRef]
- Micallef, D.; Sant, T. Loading effects on floating offshore horizontal axis wind turbines in surge motion. Renew. Energy 2015, 83, 737–748. [Google Scholar] [CrossRef]
- Sivalingam, K.; Bahuguni, A.; Gullman-Strand, J.; Davies, P.; Tan NGUYEN, V. Effects of platform pitching motion on Floating Offshore Wind Turbine (FOWT) rotor. In Proceedings of the Offshore Technology Conference, OnePetro, Houston, TX, USA, 4–7 May 2015; p. OTC-25962. [Google Scholar]
- Sivalingam, K.; Martin, S.; Singapore Wala, A. Numerical Validation of Floating Offshore Wind Turbine Scaled Rotors for Surge Motion. Energies 2018, 11, 2578. [Google Scholar] [CrossRef]
- Wu, C.H.K.; Nguyen, V.T. Aerodynamic simulations of offshore floating wind turbine in platform-induced pitching motion. Wind Energy 2017, 20, 835–858. [Google Scholar] [CrossRef]
- Leble, V.; Barakos, G. 10-MW Wind Turbine Performance Under Pitching and Yawing Motion. J. Sol. Energy Eng. 2017, 139, 041003. [Google Scholar] [CrossRef]
- Wen, B.R.; Tian, X.L.; Dong, X.J.; Peng, Z.K.; Zhang, W.M. Influences of surge motion on the power and thrust characteristics of an offshore floating wind turbine. Energy 2017, 141, 2054–2068. [Google Scholar] [CrossRef]
- Cormier, M.; Caboni, M.; Lutz, T.; Boorsma, K.; Kramer, E. Numerical analysis of unsteady aerodynamics of floating offshore wind turbines. J. Phys. Conf. Ser. 2018, 1037, 072048. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, Q.; Incecik, A.; Peyrard, C. Aeroelastic analysis of a floating offshore wind turbine in platform-induced surge motion using a fully coupled CFD-MBD method. Wind Energy 2019, 22, 1–20. [Google Scholar] [CrossRef]
- Corniglion, R.; Harris, J.; Peyrard, C.; Capaldo, M. Comparison of the free vortex wake and actuator line methods to study the loads of a wind turbine in imposed surge motion. J. Phys. Conf. Ser. 2020, 1618, 052045. [Google Scholar] [CrossRef]
- Lienard, C.; Boisard, R.; Daudin, C. Aerodynamic Behavior of a Floating Offshore Wind Turbine. AIAA J. 2020, 58, 3835–3847. [Google Scholar] [CrossRef]
- Fang, Y.; Duan, L.; Han, Z.L.; Zhao, Y.S.; Yang, H. Numerical analysis of aerodynamic performance of a floating offshore wind turbine under pitch motion. Energy 2020, 192, 116621. [Google Scholar] [CrossRef]
- Feng, X.H.; Lin, Y.G.; Zhang, G.H.; Li, D.Y.; Liu, H.W.; Wang, B. Influence of Combined Motion of Pitch and Surge with Phase Difference on Aerodynamic Performance of Floating Offshore Wind Turbine. J. Mar. Sci. Eng. 2021, 9, 699. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, X.; Mei, Y.; Ye, Z.; Guo, X. Effect of coupled platform pitch-surge motions on the aerodynamic characters of a horizontal floating offshore wind turbine. Renew. Energy 2022, 196, 278–297. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, X.; Kang, S. Effect of the Coupled Pitch–Yaw Motion on the Unsteady Aerodynamic Performance and Structural Response of a Floating Offshore Wind Turbine. Processes 2021, 9, 290. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, X.; Guo, Y.; Kang, S. Numerical analysis of unsteady aerodynamic performance of floating offshore wind turbine under platform surge and pitch motions. Renew. Energy 2021, 163, 1849–1870. [Google Scholar] [CrossRef]
- Kyle, R.; Lee, Y.C.; Früh, W.-G. Propeller and vortex ring state for floating offshore wind turbines during surge. Renew. Energy 2020, 155, 645–657. [Google Scholar] [CrossRef]
- Jeon, M.; Lee, S.; Lee, S. Unsteady aerodynamics of offshore floating wind turbines in platform pitching motion using vortex lattice method. Renew. Energy 2014, 65, 207–212. [Google Scholar] [CrossRef]
- Kyle, R.; Fruh, W.G. The transitional states of a floating wind turbine during high levels of surge. Renew. Energy 2022, 200, 1469–1489. [Google Scholar] [CrossRef]
- Fu, S.F.; Li, Z.; Zhu, W.J.; Han, X.X.; Liang, X.L.; Yang, H.; Shen, W.Z. Study on aerodynamic performance and wake characteristics of a floating offshore wind turbine under pitch motion. Renew. Energy 2023, 205, 317–325. [Google Scholar] [CrossRef]
- Sun, Q.H.; Li, G.; Duan, L.; He, Z.Y. The coupling of tower-shadow effect and surge motion intensifies aerodynamic load variability in downwind floating offshore wind turbines. Energy 2023, 282, 128788. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Song, Y.; Shen, C.; Chen, N.Z. Aerodynamic and structural analysis for blades of a 15 MW floating offshore wind turbine. Ocean Eng. 2023, 287, 115785. [Google Scholar] [CrossRef]
- Huijs, F.; de Bruijn, R.; Savenije, F. Concept design verification of a semi-submersible floating wind turbine using coupled simulations. In Proceedings of the EERA 11th Deep Sea Offshore Wind R and D Conference (DeepWind), Trondheim, Norway, 22–24 January 2014; pp. 2–12. [Google Scholar]
- Zhao, W.; Wan, D. Numerical study of interactions between phase II of OC4 wind turbine and its semi-submersible floating support system. J. Ocean Wind Energy 2015, 2, 45–53. [Google Scholar]
- Zheng, K.; Shi, W.; Ren, N. Dynamic response of a semi-submersible floating offshore wind turbine under flooded column damage. In Proceedings of the 2018 7th International Conference on Energy, Environment and Sustainable Development (ICEESD 2018), Shenzhen, China, 30–31 March 2018; Atlantis Press: Amsterdam, The Netherlands, 2018; pp. 1569–1575. [Google Scholar]
- Hussein, K.R.; Duncan, D. Sequentially Coupled Analysis for a Semi-Submersible Floating Offshore Wind Turbine. In Proceedings of the 5th International Offshore Wind Technical Conference, Exeter, UK, 18–19 December 2023; p. V001T001A024. [Google Scholar]
- Shi, W.; Zhang, L.X.; Ning, D.Z.; Jiang, Z.Y.; Michailides, C.; Karimirad, M.; Asme. A comparative study on the dynamic response of three semisubmersible floating offshore wind turbines. In Proceedings of the 38th ASME International Conference on Ocean, Offshore and Arctic Engineering, Univ Strathclyde, Glasgow, Scotland, UK, 9–14 June 2019; p. V010T009A074. [Google Scholar]
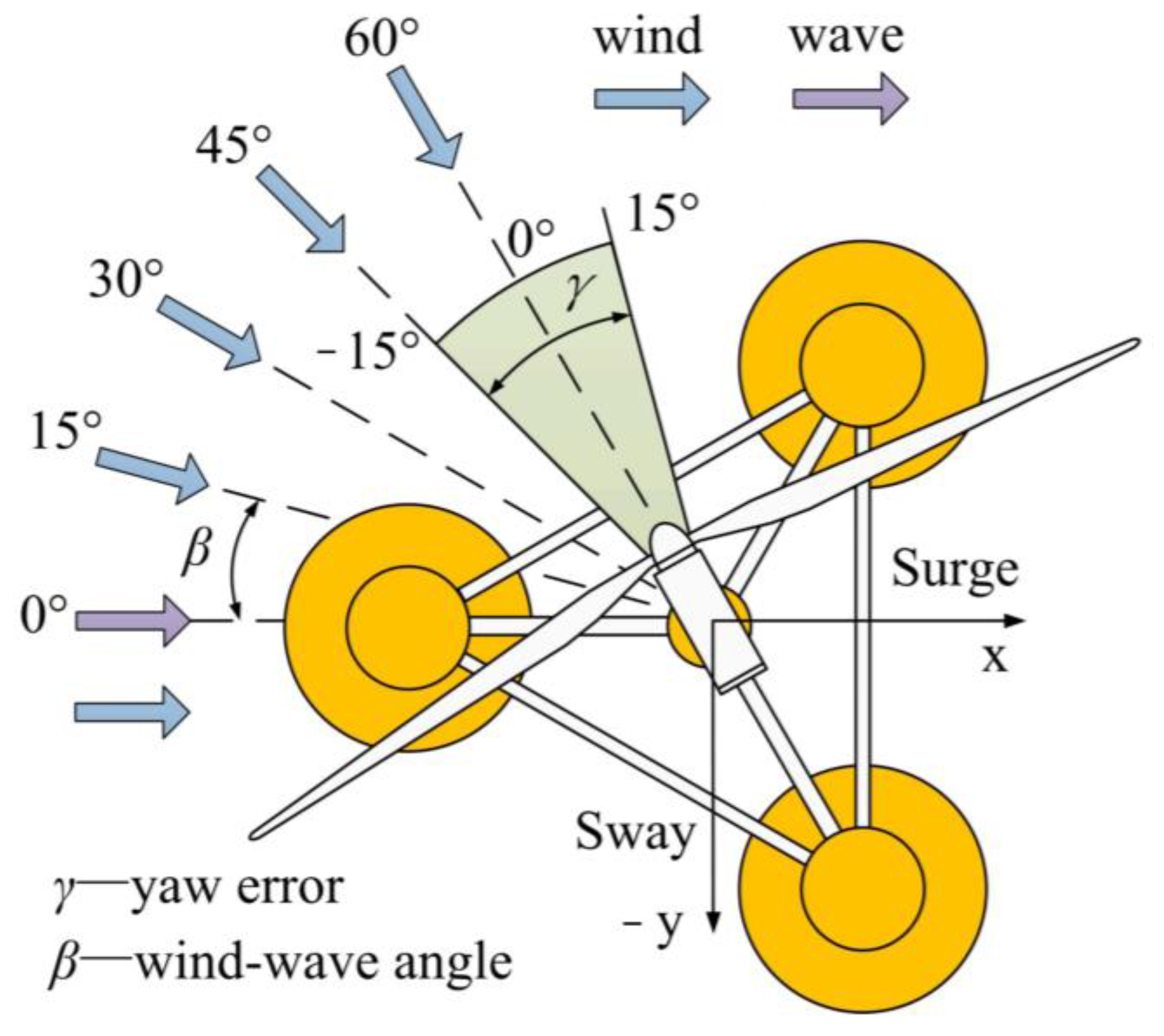
- Li, X.H.; Zhu, C.C.; Fan, Z.X.; Chen, X.; Tan, J.J. Effects of the yaw error and the wind-wave misalignment on the dynamic characteristics of the floating offshore wind turbine. Ocean Eng. 2020, 199, 106960. [Google Scholar] [CrossRef]
- Zhang, B.-J.; Yu, G.; She, W.-X. Offshore Wind Turbine Coupled Motion in Regular Waves. Mar. Technol. Soc. J. 2020, 54, 5–16. [Google Scholar] [CrossRef]
- Xu, X.S.; Wang, F.; Gaidai, O.; Naess, A.; Xing, Y.H.; Wang, J.L. Bivariate statistics of floating offshore wind turbine dynamic response under operational conditions. Ocean Eng. 2022, 257, 111657. [Google Scholar] [CrossRef]
- Huo, F.L.; Zhao, Y.P.; Zhang, J.X.; Zhang, M.; Yuan, Z.M. Study on wave slamming characteristics of a typical floating wind turbine under freak waves. Ocean Eng. 2023, 269, 113464. [Google Scholar] [CrossRef]
- NREL. FAST n.d. Available online: https://www.nrel.gov/wind/nwtc/fast.html (accessed on 29 October 2024).
- Liu, Y.; Xiao, Q.; Incecik, A.; Peyrard, C.; Wan, D. Establishing a fully coupled CFD analysis tool for floating offshore wind turbines. Renew. Energy 2017, 112, 280–301. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, Q. Development of a fully coupled aero-hydro-mooring-elastic tool for floating offshore wind turbines. J. Hydrodyn. 2019, 31, 21–33. [Google Scholar] [CrossRef]
- Cheng, P.; Huang, Y.; Wan, D. A numerical model for fully coupled aero-hydrodynamic analysis of floating offshore wind turbine. Ocean Eng. 2019, 173, 183–196. [Google Scholar] [CrossRef]
- Xu, S.; Wang, N.; Wan, D.; Strijhak, S. Large Eddy Simulations for Floating Wind Turbine Under Complex Atmospheric Inflow. In Proceedings of the 32nd International Ocean and Polar Engineering Conference, Shanghai, China, 5–10 June 2022; p. ISOPE-I-22-028. [Google Scholar]
- Zhou, Y.; Xiao, Q.; Liu, Y.C.; Incecik, A.; Peyrard, C.; Wan, D.C.; Li, S.W.; Amer Soc Mech, E. A CFD study for floating offshore wind turbine aerodynamics in turbulent wind field. In Proceedings of the 2021 3rd ASME International Offshore Wind Technical Conference, Virtual, 16–17 February 2021; p. V001T001A005. [Google Scholar]
- Zhou, Y.; Xiao, Q.; Liu, Y.C.; Incecik, A.; Peyrard, C.; Wan, D.C.; Pan, G.; Li, S.W. Exploring inflow wind condition on floating offshore wind turbine aerodynamic characterisation and platform motion prediction using blade resolved CFD simulation. Renew. Energy 2022, 182, 1060–1079. [Google Scholar] [CrossRef]
- Zhou, Y.; Xiao, Q.; Peyrard, C.; Pan, G. Assessing focused wave applicability on a coupled aero-hydro-mooring FOWT system using CFD approach. Ocean Eng. 2021, 240, 109987. [Google Scholar] [CrossRef]
- Shi, W.; Jiang, J.; Sun, K.; Ju, Q. Aerodynamic performance of semi-submersible floating wind turbine under pitch motion. Sustain. Energy Technol. Assess. 2021, 48, 101556. [Google Scholar] [CrossRef]
- Alkhabbaz, A.; Hamza, H.; Daabo, A.M.; Yang, H.-S.; Yoon, M.; Koprulu, A.; Lee, Y.-H. The aero-hydrodynamic interference impact on the NREL 5-MW floating wind turbine experiencing surge motion. Ocean Eng. 2024, 295, 116970. [Google Scholar] [CrossRef]
- Yang, H.-S.; Alkhabbaz, A.; Tongphong, W.; Lee, Y.-H. Cross-comparison analysis of environmental load components in extreme conditions for pontoon-connected semi-submersible FOWT using CFD and potential-based tools. Ocean Eng. 2024, 304, 117248. [Google Scholar] [CrossRef]
- Hall, M.; Goupee, A. Validation of a lumped-mass mooring line model with DeepCwind semisubmersible model test data. Ocean Eng. 2015, 104, 590–603. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.H. Fully coupled aero-hydrodynamic analysis of a semi-submersible FOWT using a dynamic fluid body interaction approach. Renew. Energy 2016, 92, 244–261. [Google Scholar] [CrossRef]
- Bae, Y.H.; Kim, M.H.; Kim, H.C. Performance changes of a floating offshore wind turbine with broken mooring line. Renew. Energy 2017, 101, 364–375. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Yoshida, S.; Yamamoto, H.; Toyofuku, A.; He, G.H.; Yang, S.H. Response Characteristics of the DeepCwind Floating Wind Turbine Moored by a Single-Point Mooring System. Appl. Sci. 2018, 8, 2306. [Google Scholar] [CrossRef]
- Yang, R.Y.; Chuang, T.C.; Zhao, C.Y.; Johanning, L. Dynamic Response of an Offshore Floating Wind Turbine at Accidental Limit States-Mooring Failure Event. Appl. Sci. 2022, 12, 1525. [Google Scholar] [CrossRef]
- Niranjan, R.; Ramisetti, S.B. Dynamic Response of 15 MW Floating Wind Turbine with Non-Redundant and Redundant Mooring Systems Under Extreme and Accidental Conditions. J. Offshore Mech. Arct. Eng. 2023, 145, 062002. [Google Scholar] [CrossRef]
- Yang, Y.; Bashir, M.; Michailides, C.; Li, C.; Wang, J. Development and application of an aero-hydro-servo-elastic coupling framework for analysis of floating offshore wind turbines. Renew. Energy 2020, 161, 606–625. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, C.Y.; Pan, W.C.; Li, Y.J.; Wang, X.K. Design and Fully Coupled Dynamic Response Analysis of a New Floating Offshore Wind Platform. J. Mar. Sci. Eng. 2023, 11, 1368. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, H.; Li, C.B. Fully Coupled Dynamic Analysis of the OO-STAR Floating Wind Turbine in Different Water Depths. In Proceedings of the 32nd International Ocean and Polar Engineering Conference, Shanghai, China, 5–10 June 2022; p. ISOPE-I-22-032. [Google Scholar]
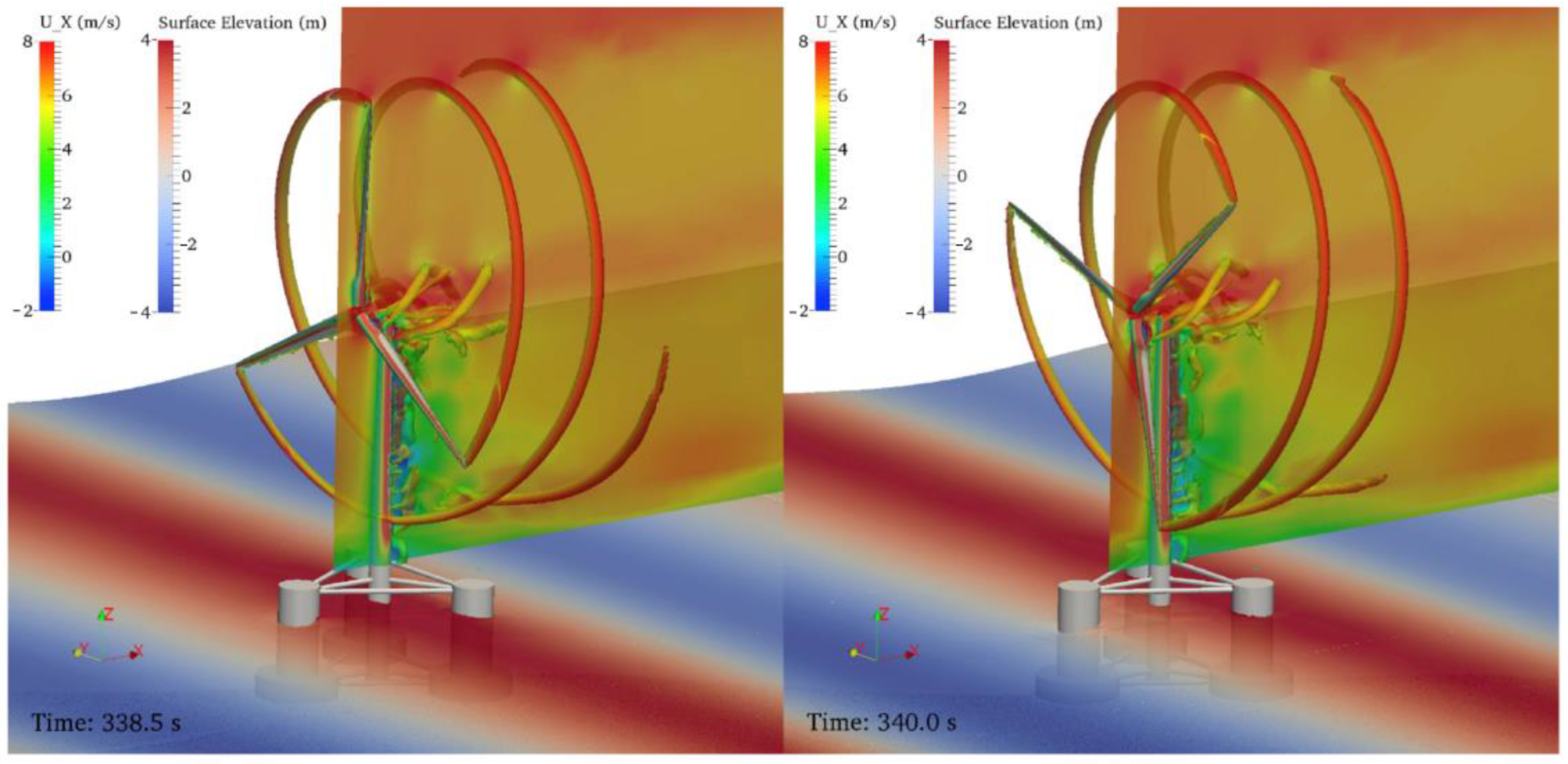
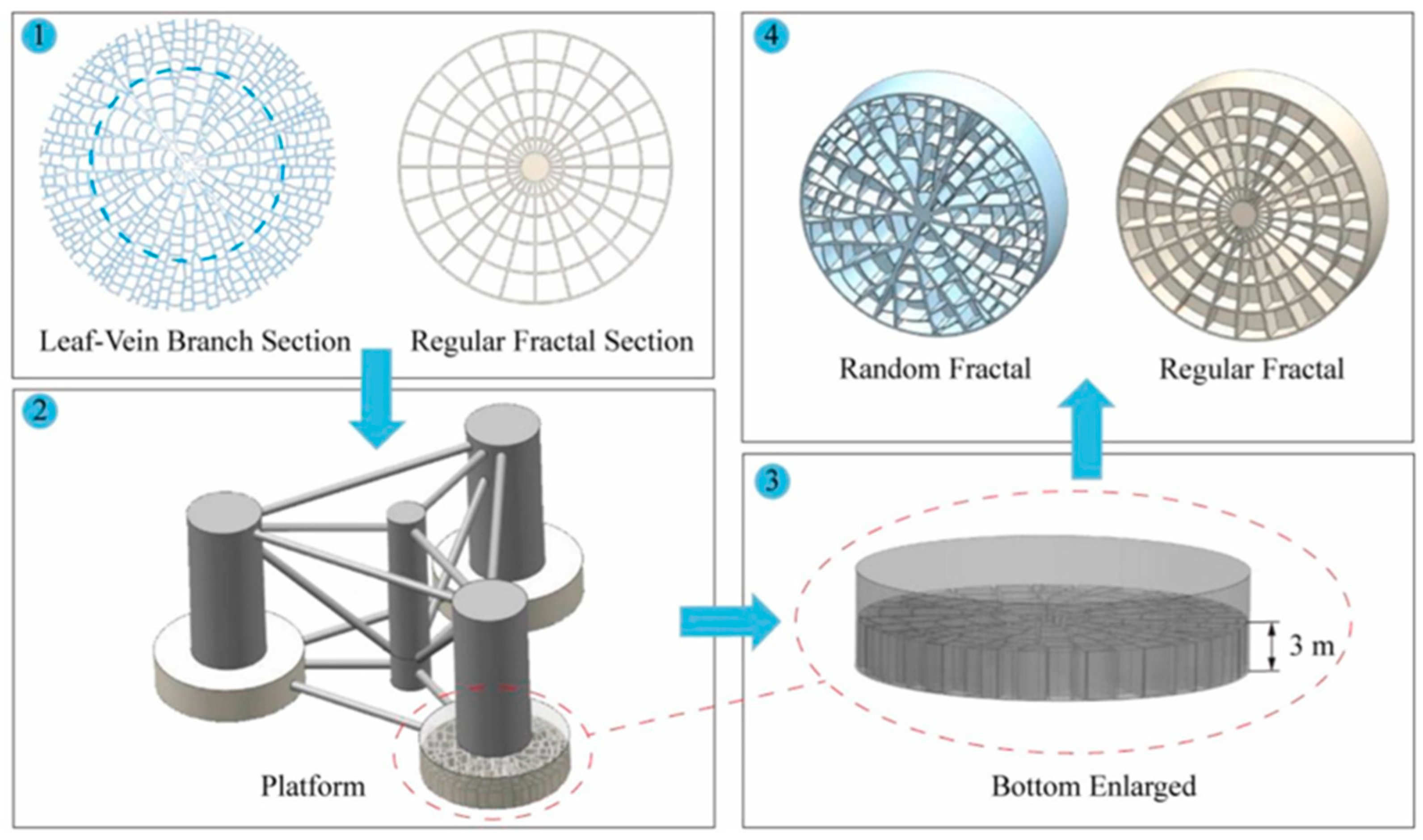
- Huang, H.D.; Liu, Q.S.; Yue, M.N.; Miao, W.P.; Wang, P.L.; Li, C. Fully coupled aero-hydrodynamic analysis of a biomimetic fractal semi-submersible floating offshore wind turbine under wind-wave excitation conditions. Renew. Energy 2023, 203, 280–300. [Google Scholar] [CrossRef]
- Berdugo-Parada, I.; Servan-Camas, B.; Garcia-Espinosa, J. Numerical Framework for the Coupled Analysis of Floating Offshore Multi-Wind Turbines. J. Mar. Sci. Eng. 2024, 12, 85. [Google Scholar] [CrossRef]
- Yang, Y.; Bashir, M.; Li, C.; Wang, J. Investigation on mooring breakage effects of a 5 MW barge-type floating offshore wind turbine using F2A. Ocean Eng. 2021, 233, 108887. [Google Scholar] [CrossRef]
- Yang, Y.; Bashir, M.; Michailides, C.; Mei, X.; Wang, J.; Li, C. Coupled analysis of a 10 MW multi-body floating offshore wind turbine subjected to tendon failures. Renew. Energy 2021, 176, 89–105. [Google Scholar] [CrossRef]
- Zou, Q.; Lu, Z.Y.; Shen, Y.J. Short-term prediction of hydrodynamic response of a novel semi-submersible FOWT platform under wind, current and wave loads. Ocean Eng. 2023, 278, 114471. [Google Scholar] [CrossRef]
- Li, J.H.; Shi, W.; Zhang, L.X.; Michailides, C.; Li, X. Wind-Wave Coupling Effect on the Dynamic Response of a Combined Wind-Wave Energy Converter. J. Mar. Sci. Eng. 2021, 9, 1101. [Google Scholar] [CrossRef]
- Chen, M.S.; Xiao, P.P.; Zhou, H.; Li, C.B.; Zhang, X.X. Fully Coupled Analysis of an Integrated Floating Wind-Wave Power Generation Platform in Operational Sea-States. Front. Energy Res. 2022, 10, 931057. [Google Scholar] [CrossRef]
- Goupee, A.J.; Koo, B.; Lambrakos, K.; Kimball, R. Model tests for three floating wind turbine concepts. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2012; p. OTC-23470. [Google Scholar]
- Goupee, A.J.; Fowler, M.J.; Kimball, R.W.; Helder, J.; de Ridder, E.-J. Additional wind/wave basin testing of the DeepCwind semi-submersible with a performance-matched wind turbine. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; p. V09BT09A026. [Google Scholar]
- Helder, J.A.; Pietersma, M. UMaine—DeepCwind/OC4 Semi Floating Wind Turbine Repeat Tests; MARIN Report No. 27005-1-OB; U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 2013. [Google Scholar]
- Wendt, F.F.; Robertson, A.N.; Jonkman, J.M. FAST model calibration and validation of the OC5-DeepCwind floating offshore wind system against wave tank test data. Int. J. Offshore Polar Eng. 2019, 29, 15–23. [Google Scholar] [CrossRef]
- Robertson, A.N.; Bachynski, E.E.; Gueydon, S.; Wendt, F.; Schünemann, P.; Jonkman, J. Assessment of experimental uncertainty for a floating wind semisubmersible under hydrodynamic loading. In Proceedings of the ASME 2018 37th International Conference on Ocean Offshore Mechanics and Arctic Engineering, Madrid, Spain, 17–22 June 2018; p. V010T009A076. [Google Scholar]
- Gueydon, S.; Alfen, R.V. MARINET 2 OC6 Model Tests: A Series of Tests Focusing on the Hydrodynamics of the OC5 Semisubmersible; MARIN Report No. 29305-01; National Renewable Energy Laboratory: Golden, CO, USA, 2018. [Google Scholar]
- Robertson, A.N.; Wendt, F.; Jonkman, J.M.; Popko, W.; Borg, M.; Bredmose, H.; Schlutter, F.; Qvist, J.; Bergua, R.; Harries, R. OC5 Project Phase Ib: Validation of hydrodynamic loading on a fixed, flexible cylinder for offshore wind applications. Energy Procedia 2016, 94, 82–101. [Google Scholar] [CrossRef]
- Robertson, A.N.; Gueydon, S.; Bachynski, E.; Wang, L.; Jonkman, J.; Alarcon, D.; Amet, E.; Beardsell, A.; Bonnet, P.; Boudet, B. OC6 Phase I: Investigating the underprediction of low-frequency hydrodynamic loads and responses of a floating wind turbine. J. Phys. Conf. Ser. 2020, 1618, 032033. [Google Scholar] [CrossRef]
- Robertson, A.; Bachynski, E.E.; Gueydon, S.; Wendt, F.; Schünemann, P. Total experimental uncertainty in hydrodynamic testing of a semisubmersible wind turbine, considering numerical propagation of systematic uncertainty. Ocean Eng. 2020, 195, 106605. [Google Scholar] [CrossRef]
- Robertson, A.; Mucha, P.; Wendt, F.; Jonkman, J. OC6 Phase Ia Definition Document: Validation of Nonlinear Hydrodynamic Loading on the DeepCwind Semisubmersible; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2022. [Google Scholar]
- Roddier, D.; Cermelli, C.; Aubault, A.; Weinstein, A. WindFloat: A floating foundation for offshore wind turbines. J. Renew. Sustain. Energy 2010, 2, 033104. [Google Scholar] [CrossRef]
- Huijs, F.; de Ridder, E.-J.; Savenije, F. Comparison of Model Tests and Coupled Simulations for a Semi-Submersible Floating Wind Turbine. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; p. V09AT09A012. [Google Scholar]
- de Ridder, E.-J.; Otto, W.; Zondervan, G.-J.; Huijs, F.; Vaz, G. Development of a Scaled-Down Floating Wind Turbine for Offshore Basin Testing. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; p. V09AT09A027. [Google Scholar]
- Guo, J.; Liu, M.; Fang, Z.; Xiao, L.; Chen, W.; Pan, X. Motion and mooring load responses of a novel 12 MW semi-submersible floating wind turbine: An experimental study. J. Offshore Mech. Arct. Eng. 2024, 146, 062001. [Google Scholar] [CrossRef]
- Viselli, A.M.; Goupee, A.J.; Dagher, H.J. Model Test of a 1:8-Scale Floating Wind Turbine Offshore in the Gulf of Maine1. J. Offshore Mech. Arct. Eng. 2015, 137, 041901. [Google Scholar] [CrossRef]
- Fowler, M.L.; Lenfest, E.; Viselli, A.; Goupee, A.J.; Kimball, R.W.; Zalkind, D.; Wright, A.; Bergua, R.; Wang, L.; Robertson, A. 1:70-Scale Model Testing of the Reference OpenSource Controller (ROSCO) on the IEA-Wind 15 MW Reference Wind Turbine Including Floating Feedback. In Proceedings of the The 33rd International Ocean and Polar Engineering Conference, Ottawa, ON, Canada, 19–23 June 2023; p. ISOPE-I-23-074. [Google Scholar]
- Tosdevin, T.; Jin, S.; Simmonds, D.; Hann, M.; Greaves, D. On the use of constrained focused waves for characteristic load prediction. In Proceedings of the Trends in Renewable Energies Offshore, Lisbon, Portugal, 8–10 November 2022; pp. 609–617. [Google Scholar]
- Bayati, I.; Belloli, M.; Bernini, L.; Zasso, A. A Formulation for the Unsteady Aerodynamics of Floating Wind Turbines, with Focus on the Global System Dynamics. In Proceedings of the ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017; p. V010T009A055. [Google Scholar]
- Bayati, I.; Belloli, M.; Facchinetti, A.; Giappino, S. Wind tunnel tests on floating offshore wind turbines: A proposal for hardware-in-the-loop approach to validate numerical codes. Wind Eng. 2013, 37, 557–568. [Google Scholar] [CrossRef]
- Bayati, I.; Belloli, M.; Ferrari, D.; Fossati, F.; Giberti, H. Design of a 6-DoF robotic platform for wind tunnel tests of floating wind turbines. Energy Procedia 2014, 53, 313–323. [Google Scholar] [CrossRef]
- Bayati, I.; Belloli, M.; Bernini, L.; Zasso, A. Wind tunnel validation of AeroDyn within LIFES50+ project: Imposed Surge and Pitch tests. J. Phys. Conf. Ser. 2016, 753, 092001. [Google Scholar] [CrossRef]
- Bayati, I.; Belloli, M.; Bernini, L.; Zasso, A. Wind Tunnel Wake Measurements of Floating Offshore Wind Turbines. In Proceedings of the 14th Deep Sea Offshore Wind R and D Conference (EERA DeepWind), Trondheim, Norway, 18–20 January 2017; pp. 214–222. [Google Scholar]
- Bergua, R.; Robertson, A.; Jonkman, J.; Branlard, E.; Fontanella, A.; Belloli, M.; Schito, P.; Zasso, A.; Persico, G.; Sanvito, A. OC6 project Phase III: Validation of the aerodynamic loading on a wind turbine rotor undergoing large motion caused by a floating support structure. Wind Energy Sci. Discuss. 2022, 8, 465–485. [Google Scholar] [CrossRef]
- Rockel, S.; Camp, E.; Schmidt, J.; Peinke, J.; Cal, R.B.; Hölling, M. Experimental study on influence of pitch motion on the wake of a floating wind turbine model. Energies 2014, 7, 1954–1985. [Google Scholar] [CrossRef]
- Hu, H.; Khosravi, M.; Sarkar, P. An experimental investigation on the aeromechanic performance and wake characteristics of a wind turbine model subjected to pitch motions. In Proceedings of the 34th Wind Energy Symposium, San Diego, CA, USA, 4–8 January 2016; p. 1997. [Google Scholar]
- Messmer, T.; Peinke, J.; Hölling, M. Wind tunnel investigation on the recovery and dynamics of the wake of a floating offshore wind turbine subjected to low inflow turbulence. J. Phys. Conf. Ser. 2024, 2767, 092083. [Google Scholar] [CrossRef]
- Cao, Q.; Xiao, L.; Cheng, Z.; Liu, M.; Wen, B. Operational and extreme responses of a new concept of 10 MW semi-submersible wind turbine in intermediate water depth: An experimental study. Ocean Eng. 2020, 217, 108003. [Google Scholar] [CrossRef]
- Wang, X.; Cai, C.; Zhou, T.; Yang, Y.; Chen, Y.; Wang, T.; Hou, C.; Zhou, S. A new similarity criterion and design method for wind tunnel model tests of floating offshore wind turbines. Energy Convers. Manag. 2023, 277, 116560. [Google Scholar] [CrossRef]
- Luo, T.X.; Wu, G.X.; Zhang, P.; Zhang, H.R. A new similarity criterion for wind tunnel testing of floating wind turbines achieving dynamic aerodynamic characteristics similarity. Energy Convers. Manag. 2024, 301, 118015. [Google Scholar] [CrossRef]
- Hall, M.; Moreno, J.; Thiagarajan, K. Performance specifications for real-time hybrid testing of 1: 50-scale floating wind turbine models. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; p. V09BT09A047. [Google Scholar]
- Azcona, J.; Bouchotrouch, F.; González, M.; Garciandía, J.; Munduate, X.; Kelberlau, F.; Nygaard, T.A. Aerodynamic thrust modelling in wave tank tests of offshore floating wind turbines using a ducted fan. J. Phys. Conf. Ser. 2014, 524, 012089. [Google Scholar] [CrossRef]
- Matoug, C.; Augier, B.; Paillard, B.; Maurice, G.; Sicot, C.; Barre, S. An hybrid approach for the comparison of VAWT and HAWT performances for floating offshore wind turbines. J. Phys. Conf. Ser. 2020, 1618, 032026. [Google Scholar] [CrossRef]
- Pires, O.; Azcona-Armendáriz, J.; Casanovas, C.; Castelló, I. Hybrid Testing System Development for Single Point Mooring Lines FOWT’s. J. Phys. Conf. Ser. 2024, 2875, 012042. [Google Scholar] [CrossRef]
- Sauder, T.; Chabaud, V.; Thys, M.; Bachynski, E.E.; Sæther, L.O. Real-time hybrid model testing of a braceless semi-submersible wind turbine: Part I—The hybrid approach. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Busan, Republic of Korea, 19–24 June 2016; p. V006T009A039. [Google Scholar]
- Bachynski, E.E.; Thys, M.; Sauder, T.; Chabaud, V.; Sæther, L.O. Real-time hybrid model testing of a braceless semi-submersible wind turbine: Part II—Experimental results. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Busan, Republic of Korea, 19–24 June 2016; p. V006T009A040. [Google Scholar]
- Berthelsen, P.A.; Bachynski, E.E.; Karimirad, M.; Thys, M. Real-time hybrid model tests of a braceless semi-submersible wind turbine: Part III—Calibration of a numerical model. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Busan, Republic of Korea, 19–24 June 2016; p. V006T009A047. [Google Scholar]
- Karimirad, M.; Bachynski, E.E.; Berthelsen, P.A.; Ormberg, H. Comparison of Real-Time Hybrid Model Testing of a Braceless Semi-Submersible Wind Turbine and Numerical Simulations. In Proceedings of the ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017; p. V010T009A061. [Google Scholar]
- Hall, M.; Goupee, A.J. Validation of a hybrid modeling approach to floating wind turbine basin testing. Wind Energy 2018, 21, 391–408. [Google Scholar] [CrossRef]
- Urbán, A.M.; Guanche, R. Wind turbine aerodynamics scale-modeling for floating offshore wind platform testing. J. Wind Eng. Ind. Aerodyn. 2019, 186, 49–57. [Google Scholar] [CrossRef]
- Otter, A.; Murphy, J.; Desmond, C.J. Emulating aerodynamic forces and moments for hybrid testing of floating wind turbine models. J. Phys. Conf. Ser. 2020, 1618, 032022. [Google Scholar] [CrossRef]
- Ha, Y.J.; Ahn, H.; Park, S.; Park, J.Y.; Kim, K.H. Development of hybrid model test technique for performance evaluation of a 10 MW class floating offshore wind turbine considering asymmetrical thrust. Ocean Eng. 2023, 272, 113783. [Google Scholar] [CrossRef]
- Bayati, I.; Belloli, M.; Facchinetti, A. Wind Tunnel 2-DoF Hybrid/HIL Tests on the OC5 Floating Offshore Wind Turbine. In Proceedings of the ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25 June 2017; p. V010T009A076. [Google Scholar]
- Ambrosini, S.; Bayati, I.; Facchinetti, A.; Belloli, M. Methodological and Technical Aspects of a Two-Degrees-of-Freedom Hardware-In-the-Loop Setup for Wind Tunnel Tests of Floating Systems. J. Dyn. Syst. Meas. Control 2020, 142, 061002. [Google Scholar] [CrossRef]
- Bayati, I.; Facchinetti, A.; Fontanella, A.; Giberti, H.; Belloli, M. A wind tunnel/HIL setup for integrated tests of Floating Offshore Wind Turbines. J. Phys. Conf. Ser. 2018, 1037, 052025. [Google Scholar] [CrossRef]
- Belloli, M.; Bayati, I.; Facchinetti, A.; Fontanella, A.; Giberti, H.; La Mura, F.; Taruffi, F.; Zasso, A. A hybrid methodology for wind tunnel testing of floating offshore wind turbines. Ocean Eng. 2020, 210, 107592. [Google Scholar] [CrossRef]
- Thys, M.; Fontanella, A.; Taruffi, F.; Belloli, M.; Berthelsen, P.A. Hybrid Model Tests for Floating Offshore Wind Turbines. In Proceedings of the ASME 2019 2nd International Offshore Wind Technical Conference, St. Julian’s, Malta, 3–6 November 2019; p. V001T001A023. [Google Scholar]
- Fontanella, A.; Facchinetti, A.; Belloli, M. Wind tunnel hardware-in-the-loop experiments about the global response of a 15 MW floating wind turbine. J. Phys. Conf. Ser. 2023, 2626, 012059. [Google Scholar] [CrossRef]


| Platform | Location | Project Name | Details of Wind Turbines | Year |
|---|---|---|---|---|
| Semisubmersible | Portugal | WindFloat Atlantic Phase 1 | 2 MW | 2011 |
| WindFloat Atlantic Phase 2 | 3 × 8.3 MW | 2019 | ||
| Japan | Fukushima Forward Phase 1 | 2 MW | 2013 | |
| Fukushima Forward Phase 2 | 7 MW | 2015 | ||
| IDEOL Kitakyushu Demo | 3 MW | 2018 | ||
| France | Floatgen | 2 MW | 2018 | |
| Eolink | 3 × 5 MW | 2024 | ||
| UK | Kincardine Phase 1 | 2 MW | 2018 | |
| Kincardine Phase 2 | 5 × 9.5 MW | 2021 | ||
| Spain | W2Power | 2 MW | 2019 | |
| Republic of Korea | Ulsan Demo | 0.75 MW | 2020 | |
| China | Three Gorges Leading | 5.5 MW | 2021 | |
| Fuyao | 6.2 MW | 2022 | ||
| Guanlan | 7.25 MW | 2023 | ||
| Ireland | AFLOWT | 6 MW | 2022 | |
| Norway | Flagship | 11 MW | 2024 | |
| Spar | Norway | Hywind | 2.3 MW | 2009 |
| Tetraspar Demonstration | 3.6 MW | 2021 | ||
| Hywind Tampen | 11 × 8.6 MW | 2023 | ||
| Japan | Kabashima | 2 MW | 2013 | |
| Fukushima Forward Phase 3 | 5 MW | 2016 | ||
| Sakiyama | 2 MW | 2016 | ||
| UK | Hywind Pilot Plant | 6 MW | 2017 | |
| Tension Leg Platform | Spain | Pivot Buoy | 0.22 MW | 2021 |
| France | Provence Grand Large | 3 × 8.4 MW | 2024 | |
| Barge | Spain | DemoSATH | 2 MW | 2023 |
| Wind Turbine and Wind Speed (WS) | Platform Motion | Tool/Method | Aim/Conclusion/Focus of Study | Ref. |
|---|---|---|---|---|
| NREL 5 MW WS = 11 m/s | Pitch (Amplitude 4°; Frequency 0.1 Hz) | STAR-CCM+/CFD | Comparison of CFD simulation results with previous studies | Tran et al. [68] & |
| Surge (Amplitude 4–16 m; Frequency 0.127–0.770 rad/s) | Variations in wake intensity under surge motion of the platform and blade–wake interaction. | Tran et al. [69] & | ||
| Pitch and Yaw (Amplitude 1°and 4°; Frequency 0.1 Hz) | Effect of pitch and yaw motion on thrust and power at the same amplitude and frequency. | Tran et al. [70] & | ||
| Surge (Amplitude 4–16 m; Frequency 0.127–0.770 rad/s) | Influence of platform motion and tower interference. Impact of blade–wake interaction. | Tran et al. [71] & | ||
| NREL 5 MW WS = 11.4 m/s | Surge (Amplitude 1.02 m; Period 9 s) | FLUENT/CFD | Comparison of BEM, GDW, and ADM methods at different TSRs. | Micallef et al. [72] -- |
| NREL 5 MW WS = 8 m/s | Pitch (Amplitude 1.29°; Period 10 s) | FLUENT/CFD | Comparison between CFD and BEM methods, accurate capture of wind turbine wake rotation by CFD. | Sivalingam et al. [73] & |
| NREL 5 MW WS = 11.4 m/s and 13.2 m/s | Surge (Amplitude 0.0238–0.0952 m; Frequency 0.18 Hz–0.89 Hz) | Effect of surge motion on thrust and power. Blade wake under high amplitude and high frequency. | Sivalingam et al. [74] & | |
| NREL 5 MW WS = 8 m/s and 11.2 m/s | Pitch (Amplitude 0.85°; Period 10 s) | OpenFOAM/CFD | Differences in results between CFD and BEM under large platform motions. | Wu et al. [75] & |
| NREL Phase VI WS = 7 m/s DTU 10 MW WS = 11 m/s | Pitch (Amplitude 3°and 5°; Period 8.8s) Yaw (Amplitude 3°; Period 8.8 s) | HMB3/CFD | Influence of different pitch amplitudes on blade vortices and wake. | Leble et al. [76] & |
| NREL 5 MW WS = 11.4 m/s | Surge (Amplitude 0–2.5 m; Frequency 0–3 Hz) | FVM | Influence of different tip speeds on thrust and power. | Wen et al. [77] -- |
| DTU 10 MW WS = 4 m/s | Surge (Amplitude 0.008–0.035 m; Frequency 1–2 Hz) | Finite-Volume Flow solver/FVM and BEM | Influence of the amplitude and frequency of surge motion on thrust and power. | Cormier et al. [78] & |
| NREL 5 MW WS = 11.4 m/s | Surge (Amplitude 2 m; Period 12 s) | OpenFOAM/ CFD | Impact of blade flexibility on output power. | Liu et al. [79] -- |
| NREL 5 MW WS = 11.4 m/s | Surge (Amplitude 8 m and 16 m; Frequency 0.1 Hz) | ALM and FVM | Limited predictive capability of ALM and FVM methods for dynamic stall phenomena. | Corniglion et al. [80] -- |
| NREL 5 MW WS = 11.4 m/s | Pitch (Frequency 0.1 Hz; Amplitude 4° and 8°) Surge (Frequency 0.1 Hz; Amplitude 4° and 8°) | ELSA Software/CFD | Effects of surge motion and pitch motion on wind turbines are similar. | Lienard et al. [81] & |
| NREL 5 MW (1:50) WS = 1.61 m/s | Pitch (Amplitude 1.5°–3°; Period 0.375 s–3 s) | STAR-CCM+/CFD | Influence of the frequency and amplitude of surge motion on thrust and power. | Fang et al. [82] * |
| NREL 5 MW WS = 11.4 m/s | Pitch (Frequency 0.1–0.2 Hz; Amplitude 1°–4°) Surge (Frequency 0.1–0.2 Hz; Amplitude 1–4 m) Coupled surge and pitch motions | STAR-CCM+/CFD | Pitch motion has a greater impact on power than surge motion. Impact of the coupled pitch and surge motion on performances. | Feng et al. [83] & |
| NREL 5 MW WS = 11.4 m/s | Pitch (Frequency 0.1 and 0.2 Hz; Amplitude 2° and 4°;) Surge (Frequency 0.1 and 0.2 Hz; Amplitude 1 and 2 m;) Coupled surge and pitch motions | -- | Comparison of power and thrust fluctuations when the pitch and surge motions are coupled at different frequencies and compared to coupling at the same frequency. | Guo et al. [84] & |
| NREL 5 MW WS = 11.4 m/s | Pitch (Amplitude 4° Frequency 0.1 and 0.2 Hz) Yaw (Amplitude 4°; Frequency 0.1 and 0.2 Hz) Coupled yaw and pitch motions | FLUENT/CFD | Effect of the frequency and amplitude of platform motions on thrust and power, with greater impact of pitch motion than yaw motion. Effect of the coupled motion of pitch and yaw on thrust and power | Chen et al. [85] & |
| Pitch (Frequency 0.1 and 0.2 Hz; Amplitude 1°–4°;) Surge (Frequency 0.1 and 0.2 Hz; Amplitude 1 and 2 m;) Coupled surge and pitch motions | Effect of the frequency and amplitude of platform motions on thrust and power. Effect of the coupled surge and pitch motion on performances. | Chen et al. [86] & | ||
| NREL 5 MW WS = 7 m/s and 11.4 m/s | Surge (Amplitude 9.4 m; Period 8.1 s) | OpenFOAM/ CFD | Influence of surge motion on thrust and power. Interaction between blades and vortices. | Kyle et al. [87] & |
| Platform Model | Tool/Method | Environmental Conditions | Platform Motion | Ref. |
|---|---|---|---|---|
| GustoMSC Tri-Floater (NREL 5 MW) | ANSYS-AQWA PHATAS/PF and BEM | Steady Wind/Regular Wave and Irregular Wave WS = 11.4 m/s and H = 4.5 m T = 7.5 s–10 s WS = 14 m/s and H = 6.5 m T = 9–12 s WS = 25 m/s and H = 9.4 m T = 11 s–14 s | Sway Surge Heave | Huijs et al. [93] |
| OC4 DeepCwind | OpenFOAM/CFD | Steady Wind/Regular Wave WS = 5 m/s and H = 9.7 m T = 3.66 s WS = 7 m/s and H = 9.7 m T = 3.66 s WS = 11.4 m/s and H = 9.7 m T = 3.66 s | Pitch Heave | Zhao et al. [94] |
| OC4 DeepCwind | ANSYS-AQWA/PF | Steady Wind/Regular Wave and Irregular Wave WS = 11.4 m/s and H = 3 m T = 10 s | Six DOF motions | Zheng et al. [95] |
| VolturnUS-S | ANSYS-AQWA/PF | Turbulent wind/Irregular Wave WS = 4–47.5 m/s and H = 1.1–10.7 m T = 8.52–14.2 s | Surge Pitch Heave | Raed et al. [96] |
| V-shaped Semi OC4 DeepCwind Bracessless Semi | ANSYS-AQWA/PF | Steady Wind/Regular Wave and Irregular Wave WS = 8 m/s and H = 3 m T = 10 s WS = 49 m/s and H = 14.1 m T = 13.3 s | Surge Pitch Heave | Shi et al. [97] |
| OC4 DeepCwind | FAST/BEM | Steady Wind/Regular Wave WS = 11.4 m/s and H = 4.5 m T = 11 s | Six DOF motions | Li et al. [98] |
| OC4 DeepCwind | STAR-CCM+/CFD | Steady Wind/Regular Wave WS = 5 m/s and H = 9.7 m T = 3.66 s WS = 8 m/s and H = 11.3 m T = 5.49 s WS = 11 m/s and H = 13.6 m T = 9.14 s | Heave Pitch | Zhang et al. [99] |
| OC5 DeepCwind | OpenFAST/BEM | Elizabeth Actual Environment | Pitch | Xu et al. [100] |
| Platform Model | Wind Turbine Model | Tool/Method | Environmental Conditions | Platform Motion | Ref. |
|---|---|---|---|---|---|
| OC4 DeepCwind | NREL 5 MW | OpenFOAM/CFD | Steady Wind/Regular Wave WS = 7.32 m/s and H = 3.79 s T = 12.1 s WS = 11 m/s and H = 3.79 s T = 12.1 s | Pitch Surge Heave | Liu et al. [103] |
| Steady Wind/Regular Wave WS = 11.4 m/s and H = 3.79 m T = 12.1 s | Pitch Surge | Liu et al. [104] | |||
| OC4 DeepCwind | Steady Wind/Regular Wave WS = 11.4 m/s and H = 3.66 m T = 9.7 s WS = 11.4 m/s and H = 7.58 m T = 12.1 s | Pitch Surge Heave | Cheng et al. [105] | ||
| OC4 DeepCwind | Steady Wind and Turbulent wind/ Iregular Wave WS = 11.4 m/s and H = 7.58 m T = 12.1 s | Six DOF motions | Xu et al. [106] | ||
| OC4 DeepCwind | Turbulent Wind/Regular Wave Mann Turbulence WS = 11.4 m/s and H = 7.58 m T = 12.1 s | Pitch Surge | Zhou et al. [107] | ||
| Zhou et al. [108] | |||||
| Steady Wind/Irregular Waves and Focused Waves WS = 11.4 m/s and H = 1.94–5.13 m T = 15.0 s–16.8 s | Pitch Surge | Zhou et al. [109] | |||
| OC4 DeepCwind | STAR-CCM+/CFD | Steady Wind/Regular Wave WS = 6 m/s and H = 7.58 m T = 12.1 s–14.3 s WS = 11.4 m/s and H = 7.58 m T = 12.1 s–14.3 s | Pitch | Shi et al. [110] | |
| OC4 DeepCwind | Steady Wind/Regular Wave WS = 11.4 m/s and H = 7.58 m T = 12.1 s | Surge | Ali et al. [111] | ||
| OC5 DeepCwind | Steady Wind/Regular Wave WS = 11.4 m/s and H = 7.58 m T = 12.1 s | Pitch Surge Heave | Zhang et al. [13] | ||
| OC5 DeepCwind | Steady Wind/Regular Wave WS = 40.28 m/s and H = 16.68 m T = 13.1 s | Pitch Surge Heave Yaw | Yang et al. [112] | ||
| MARIN DeepCwind | FAST/BEM | Steady Wind/Regular Wave WS = 11.4 m/s and H = 1.92 m–11.122 m T = 7.5 s–20 s Irregular Waves WS = 11.4 m/s and H = 10.5 m T = 14.3 s | Pitch Surge Heave | Hall et al. [113] | |
| OC4 DeepCwind | Steady Wind/Regular Wave WS = 11 m/s and H = 7.58 m T = 12.1 s | Six DOF motions | Tran et al. [114] | ||
| OC4 DeepCwind | Steady Wind/Irregular Waves WS = 15 m/s and H = 7.1 m T = 12.1 s | Six DOF motions | Bae et al. [115] | ||
| OC4 DeepCwind | Steady Wind/Regular Wave and Irregular Wave WS = 8 m/s and PSD = 1 m2/Hz for 0.05–0.25 Hz | Six DOF motions | Liu et al. [116] | ||
| OC4 DeepCwind | FAST/BEM | Steady Wind/Regular Wave and Irregular Wave WS = 60 m/s and H = 9.1 m T = 12.7 s | Heave | Yang et al. [117] | |
| VolturnUS-S | IEA 15 MW | FAST/BEM | Turbulent wind/Irregular Wave WS = 12 m/s and H = 1.84 m T = 7.44 s WS = 47.5 m/s and H = 10.7 m T = 14.2 s | Surge Sway Pitch Yaw | Niranjan et al. [118] |
| OC3 Hywind | NREL 5 MW | FAST and AQWA/ BEM and PF | Steady Wind and Turbulent wind/ Regular Wave WS = 4 m/s–25 m/s and H = 1.6 m–4.0 m T = 3.4 s–8.8 s | Pitch Surge Heave | Yang et al. [119] |
| V-shaped Semi Triangle-shaped Semi | FAST and AQWA/ BEM and PF | Steady Wind/Irregular Waves WS = 55 m/s and H = 10.1 m T = 17 s | Six DOF motions | Shen et al. [120] | |
| OO-Star | DTU 10 MW | FAST and AQWA/ BEM and PF | Turbulent wind/Irregular Wave WS = 11.4 m/s and H = 6.97 m T = 10.4 s | Pitch Surge Heave | Chen et al. [121] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Men, X.; Jiao, B.; Lin, H.; Sun, H.; Lin, X.-M. Coupled Aero–Hydrodynamic Analysis in Floating Offshore Wind Turbines: A Review of Numerical and Experimental Methodologies. J. Mar. Sci. Eng. 2024, 12, 2205. https://doi.org/10.3390/jmse12122205
He J, Men X, Jiao B, Lin H, Sun H, Lin X-M. Coupled Aero–Hydrodynamic Analysis in Floating Offshore Wind Turbines: A Review of Numerical and Experimental Methodologies. Journal of Marine Science and Engineering. 2024; 12(12):2205. https://doi.org/10.3390/jmse12122205
Chicago/Turabian StyleHe, Jinlong, Xuran Men, Bo Jiao, Haihua Lin, Hongyuan Sun, and Xue-Mei Lin. 2024. "Coupled Aero–Hydrodynamic Analysis in Floating Offshore Wind Turbines: A Review of Numerical and Experimental Methodologies" Journal of Marine Science and Engineering 12, no. 12: 2205. https://doi.org/10.3390/jmse12122205
APA StyleHe, J., Men, X., Jiao, B., Lin, H., Sun, H., & Lin, X.-M. (2024). Coupled Aero–Hydrodynamic Analysis in Floating Offshore Wind Turbines: A Review of Numerical and Experimental Methodologies. Journal of Marine Science and Engineering, 12(12), 2205. https://doi.org/10.3390/jmse12122205








