Optimal Route Generation and Route-Following Control for Autonomous Vessel
Abstract
1. Introduction
2. Related Work
2.1. Route Generation
2.2. Route-Following Control
3. Dynamic Vessel Model
3.1. Coordinate Systems
3.2. Vessel Equation of Motion
- (1)
- Roll, pitch, and heave motions of the vessel are negligible.
- (2)
- The shape of the vessel is symmetrical in the plane.
- (3)
- The origin of the body-fixed coordinate system is located at the center of the vessel.
3.2.1. Forward Speed Model
3.2.2. Maneuvering Model
3.2.3. Vessel Model Used in This Study
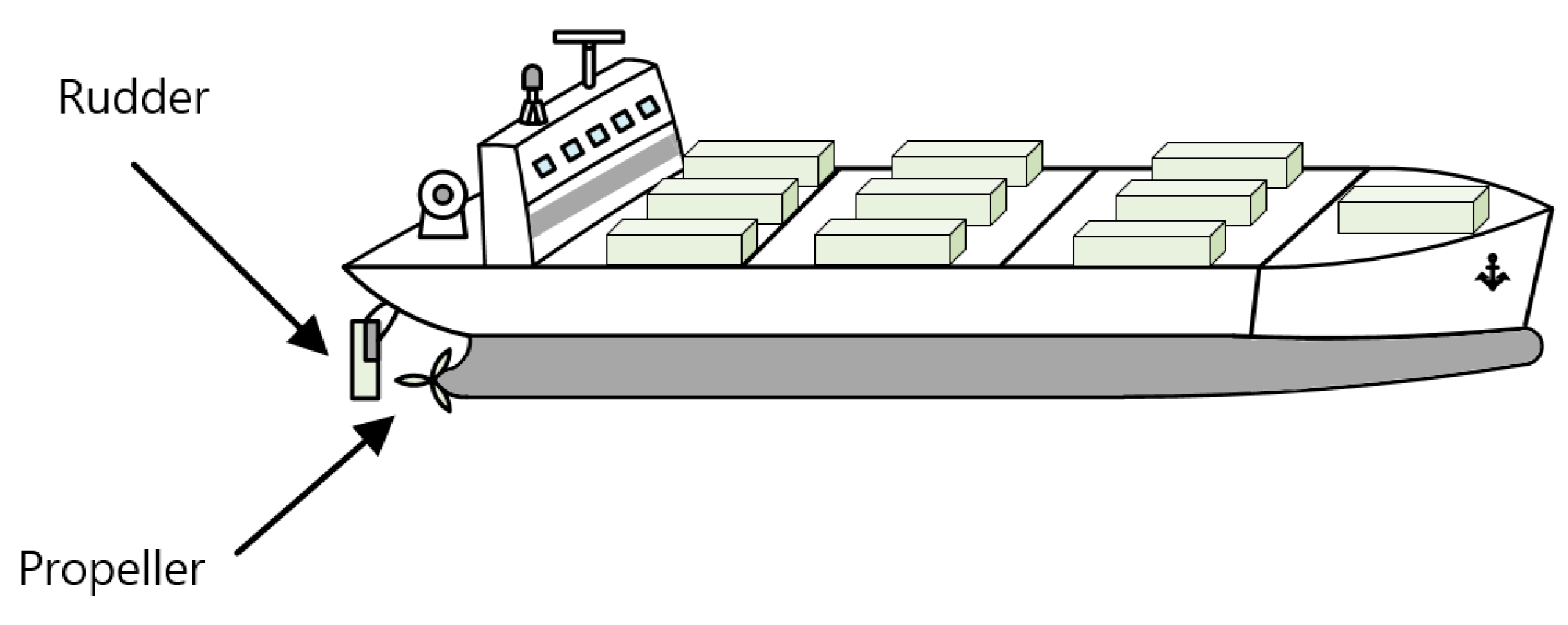
3.3. Specifications of the Vessel
4. Optimal Route Generation
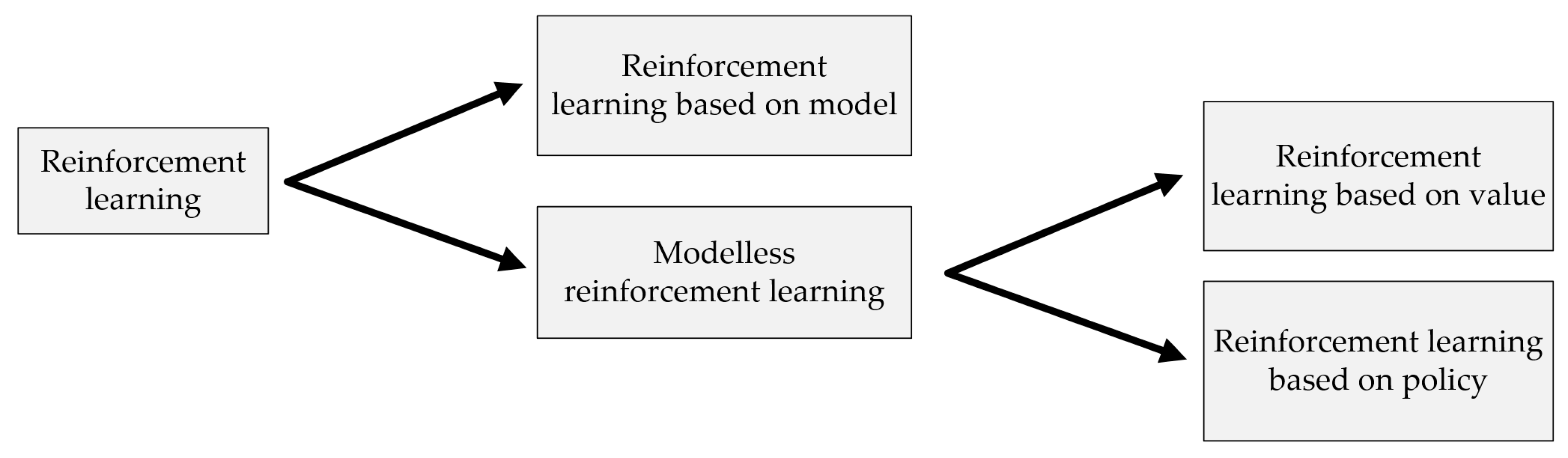
4.1. Reinforcement-Learning Algorithm
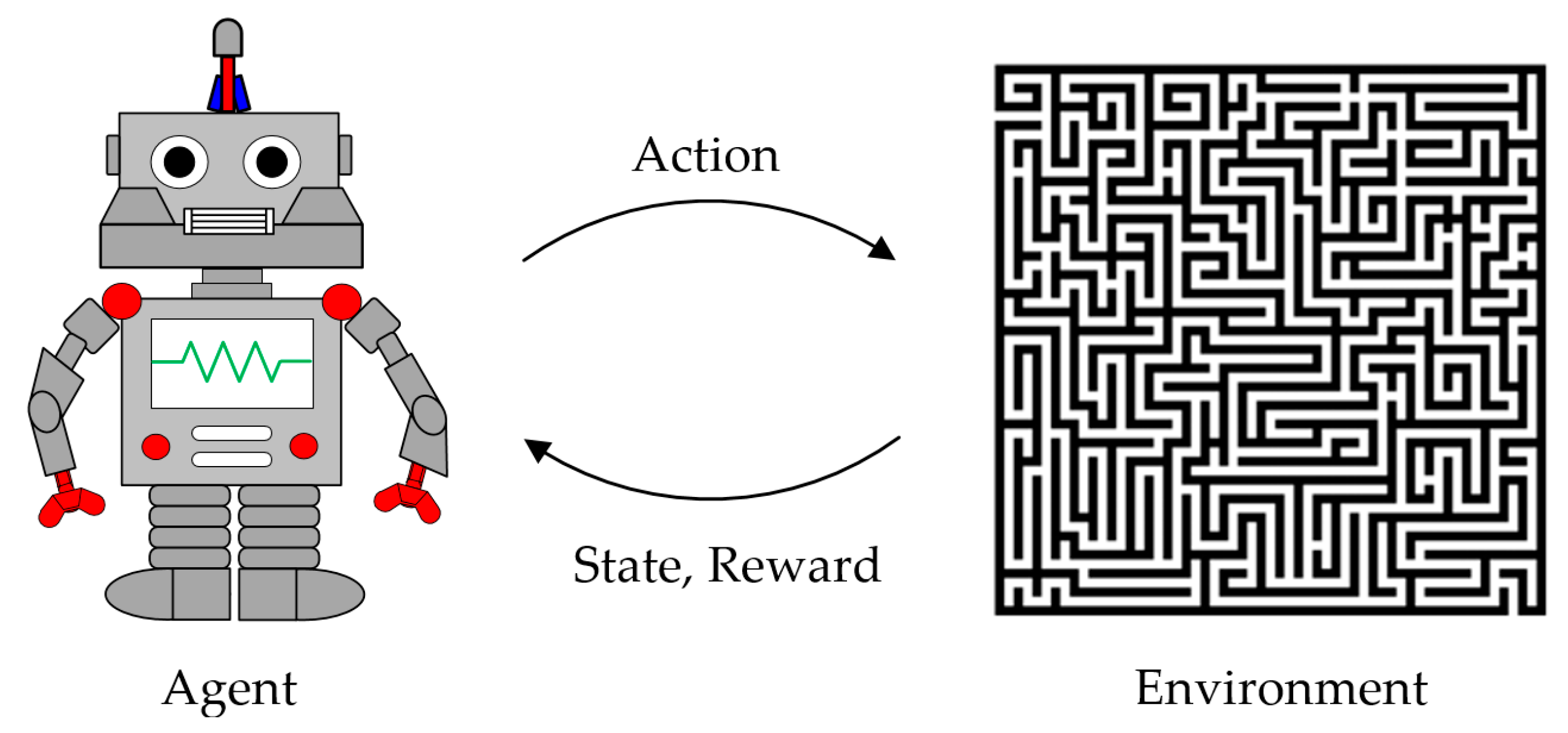
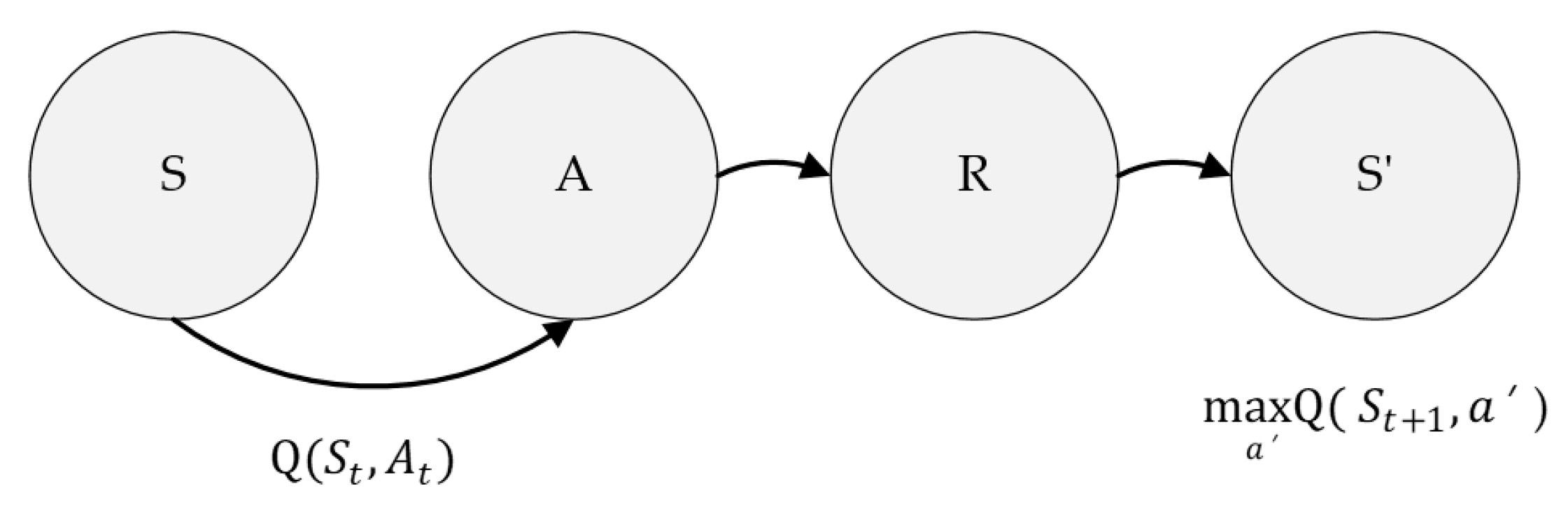
4.1.1. Definition of Reinforcement Learning
- (1)
- The agent observes the current state .
- (2)
- The agent uses to perform a suitable action and provides it to the environment.
- (3)
- The environment communicates the next state and reward for the action to the agent.
- (4)
- The agent performs the next action according to the reward received from the environment.
- (5)
- By repeating the above processes, the agent continuously implements actions to obtain the maximum reward.
4.1.2. Selection of Reinforcement-Learning Algorithm
4.2. Considerations for Optimal Route Generation
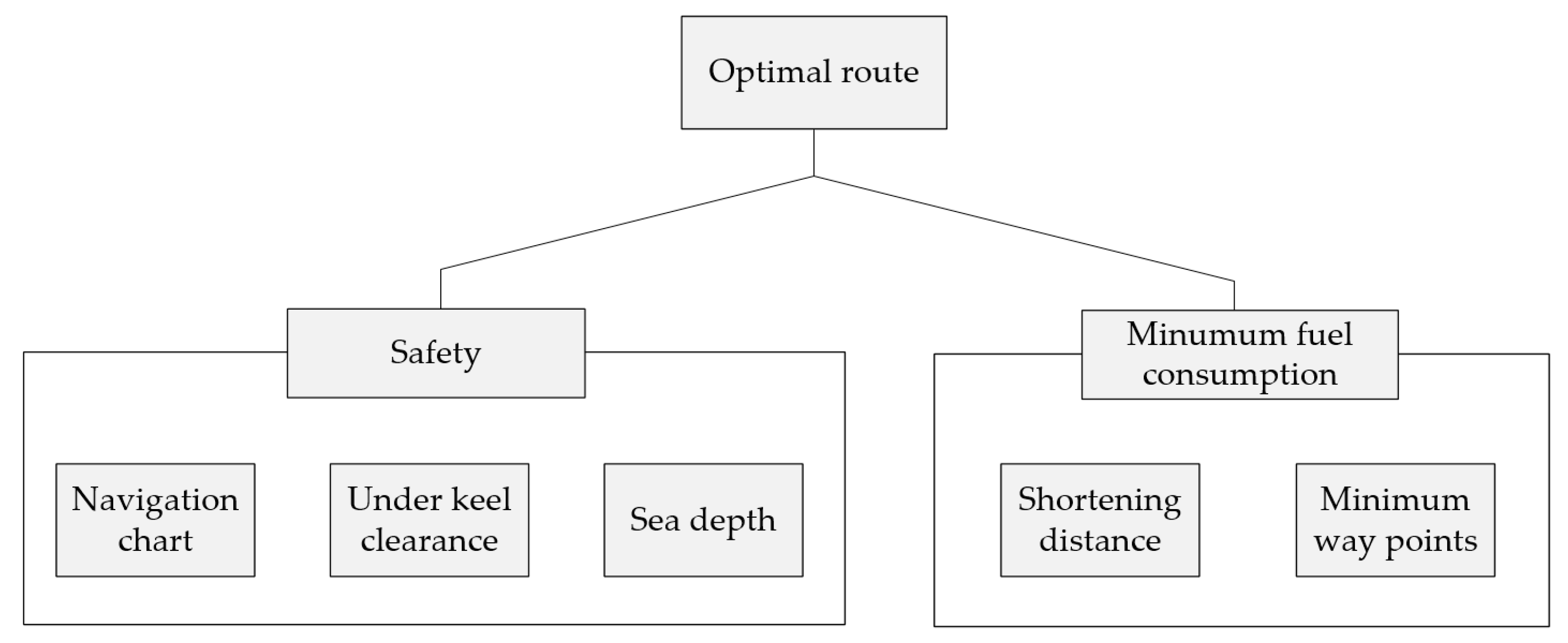
4.2.1. Definition of the Optimal Route
4.2.2. Data Used to Satisfy Safety Requirements
4.2.3. Algorithm Used to Satisfy Minimum Fuel Consumption
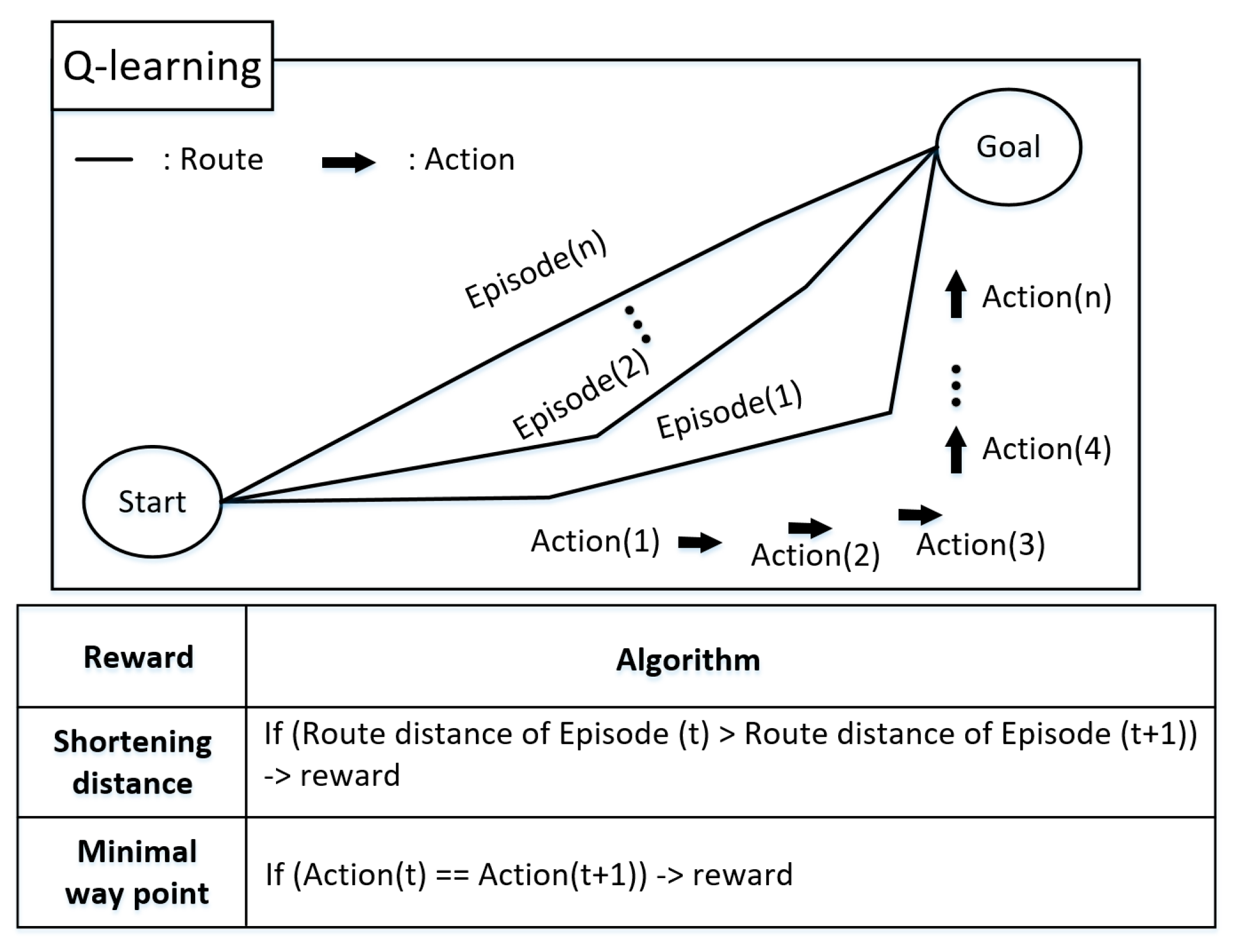
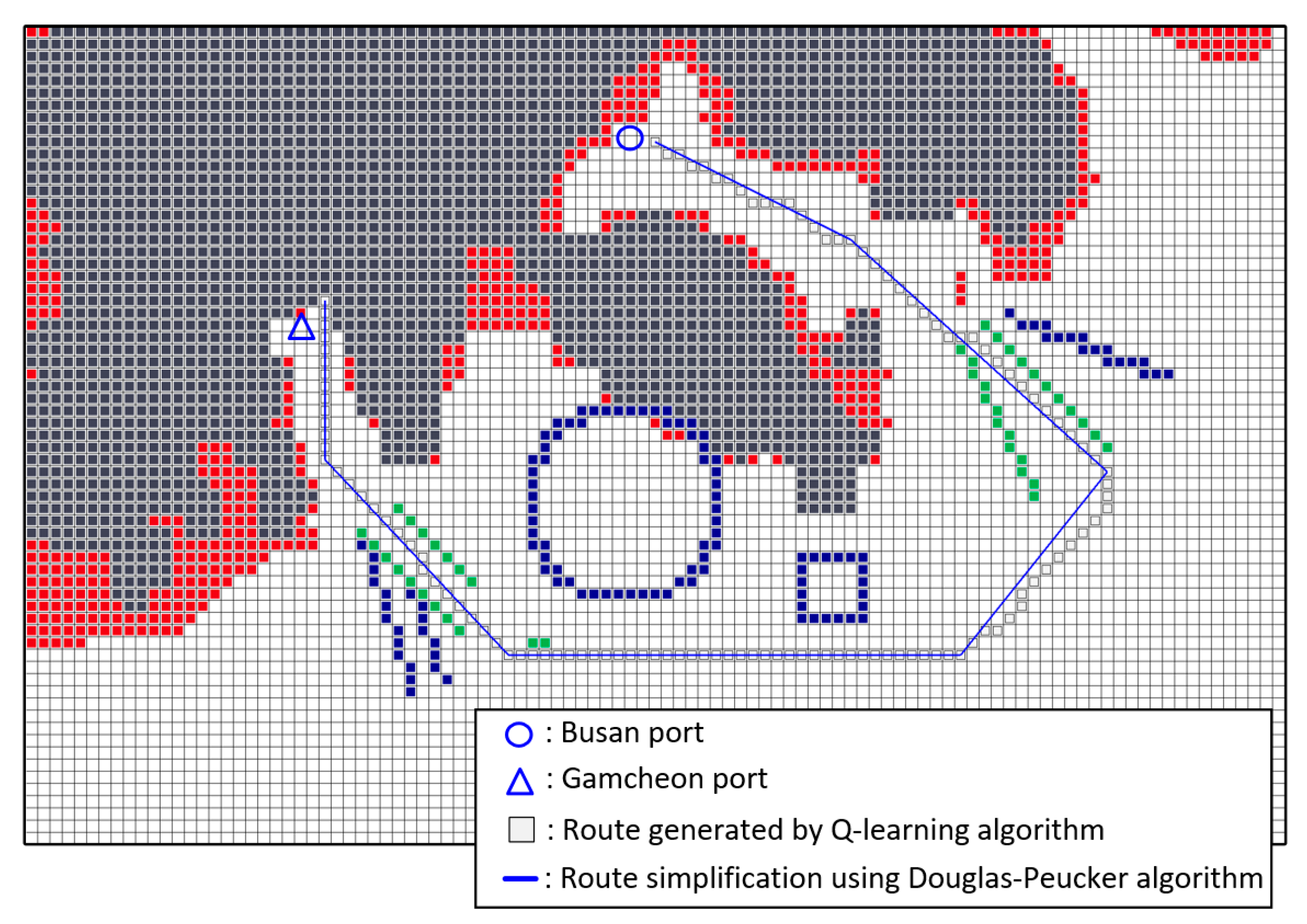
4.3. Generation of the Optimal Route Using a Q-Learning Algorithm
4.3.1. Environment Settings for Training the Q-Learning Algorithm
4.3.2. Simulation Condition
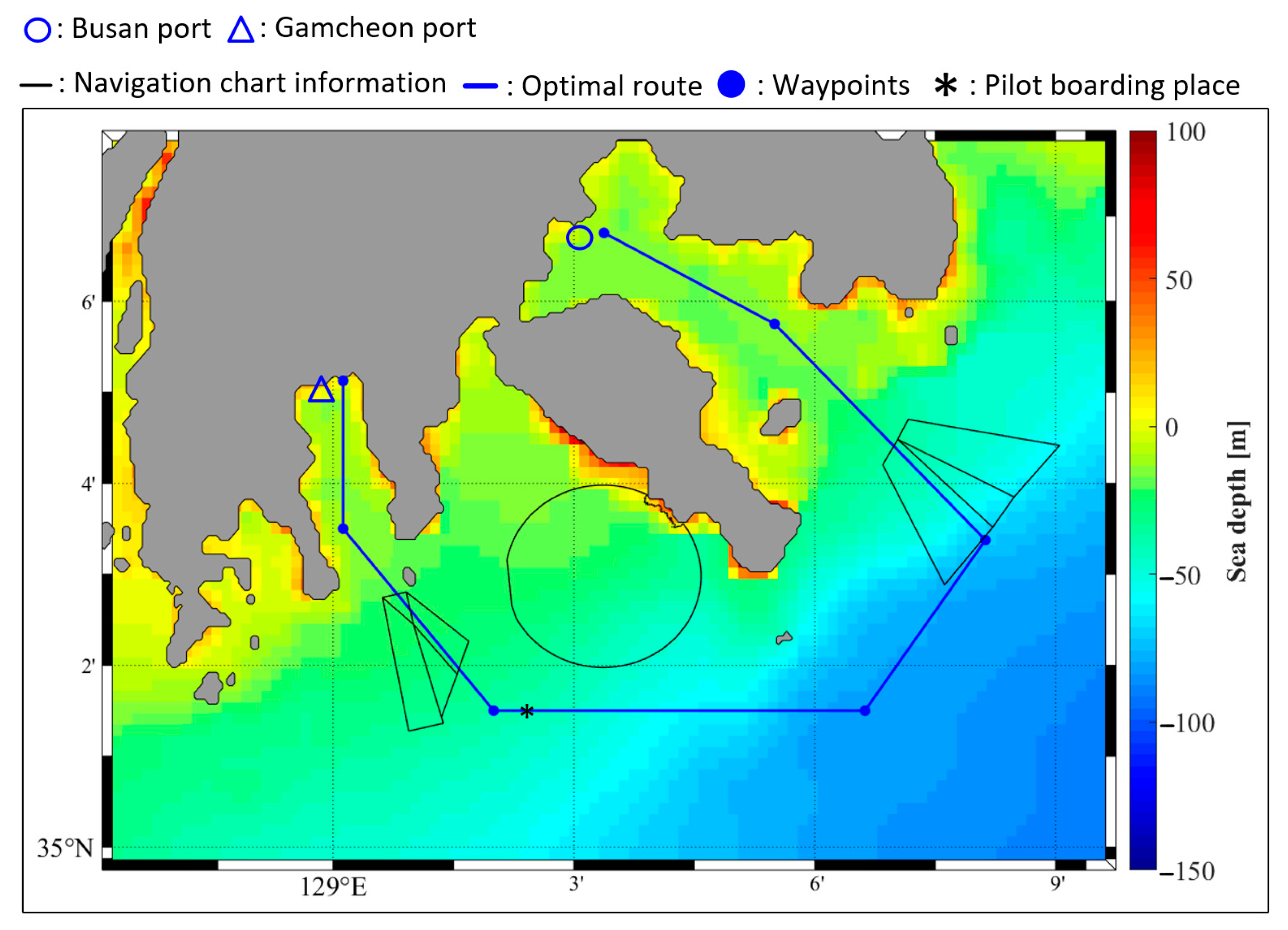
4.3.3. Simulation Results
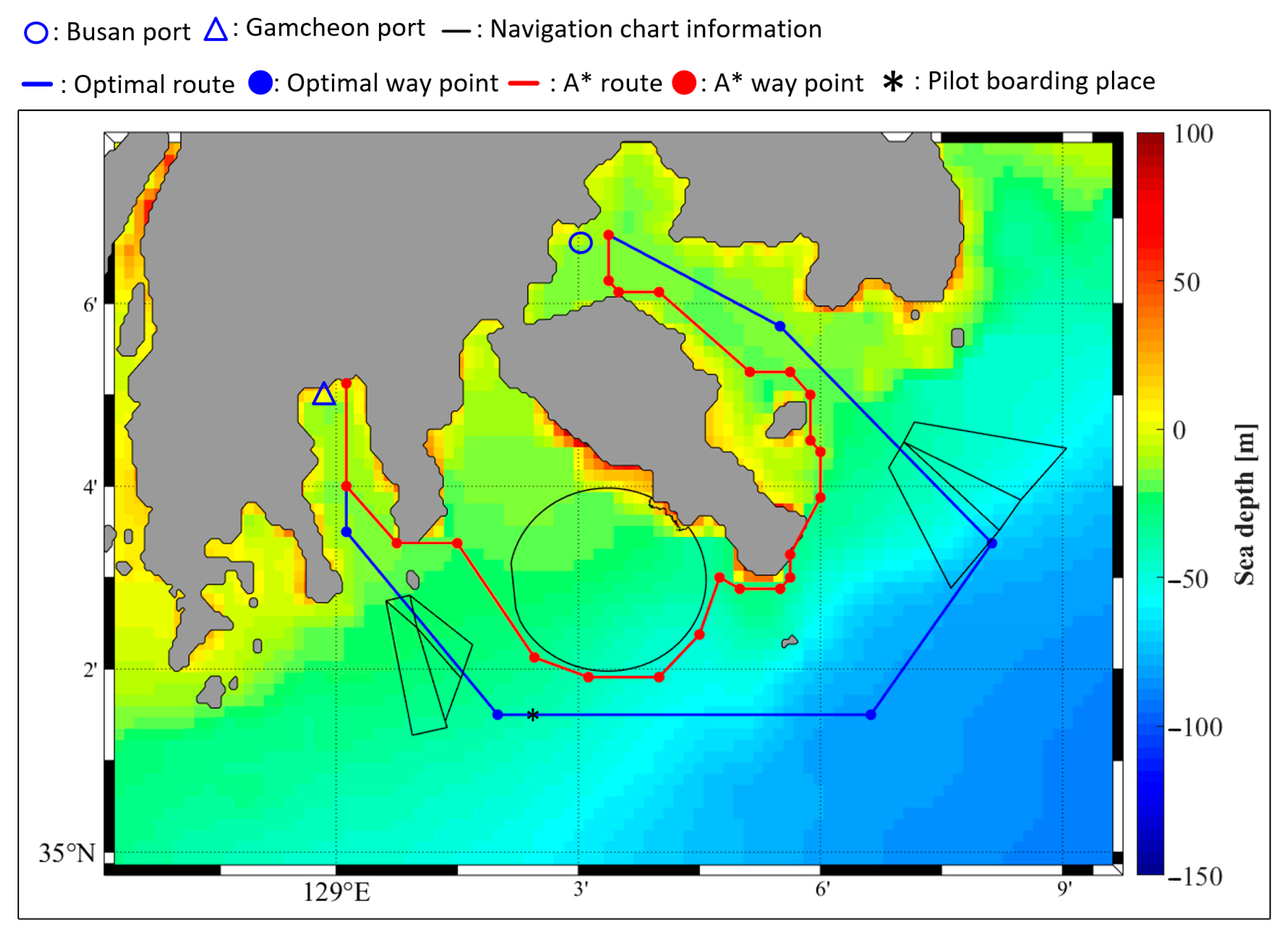
4.4. Comparison with Algorithm
5. Route-Following Control
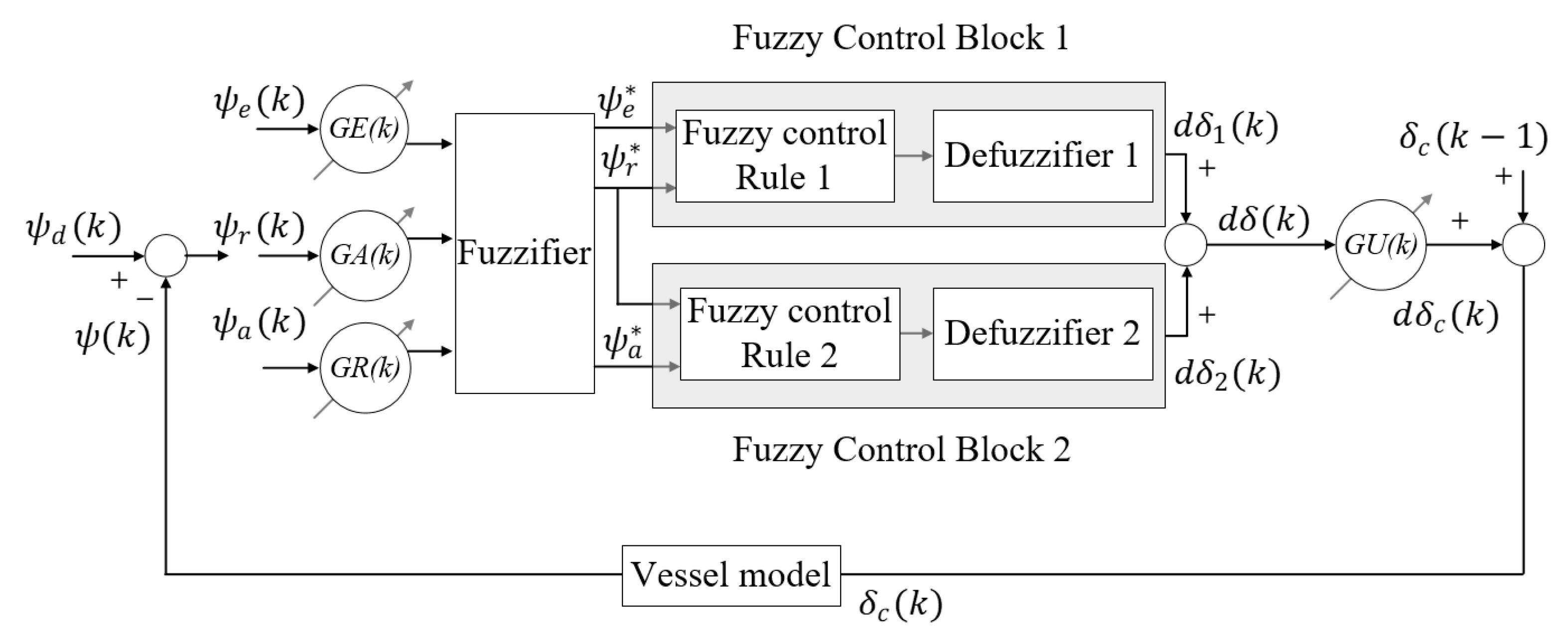
5.1. Design of the Velocity-Type Fuzzy PID Controller
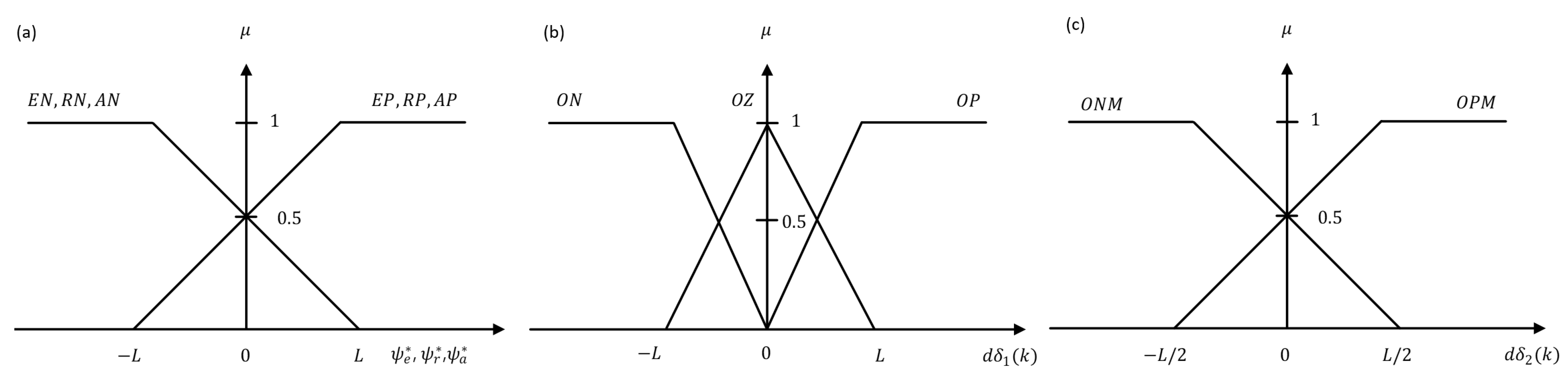
5.1.1. Fuzzification Algorithm
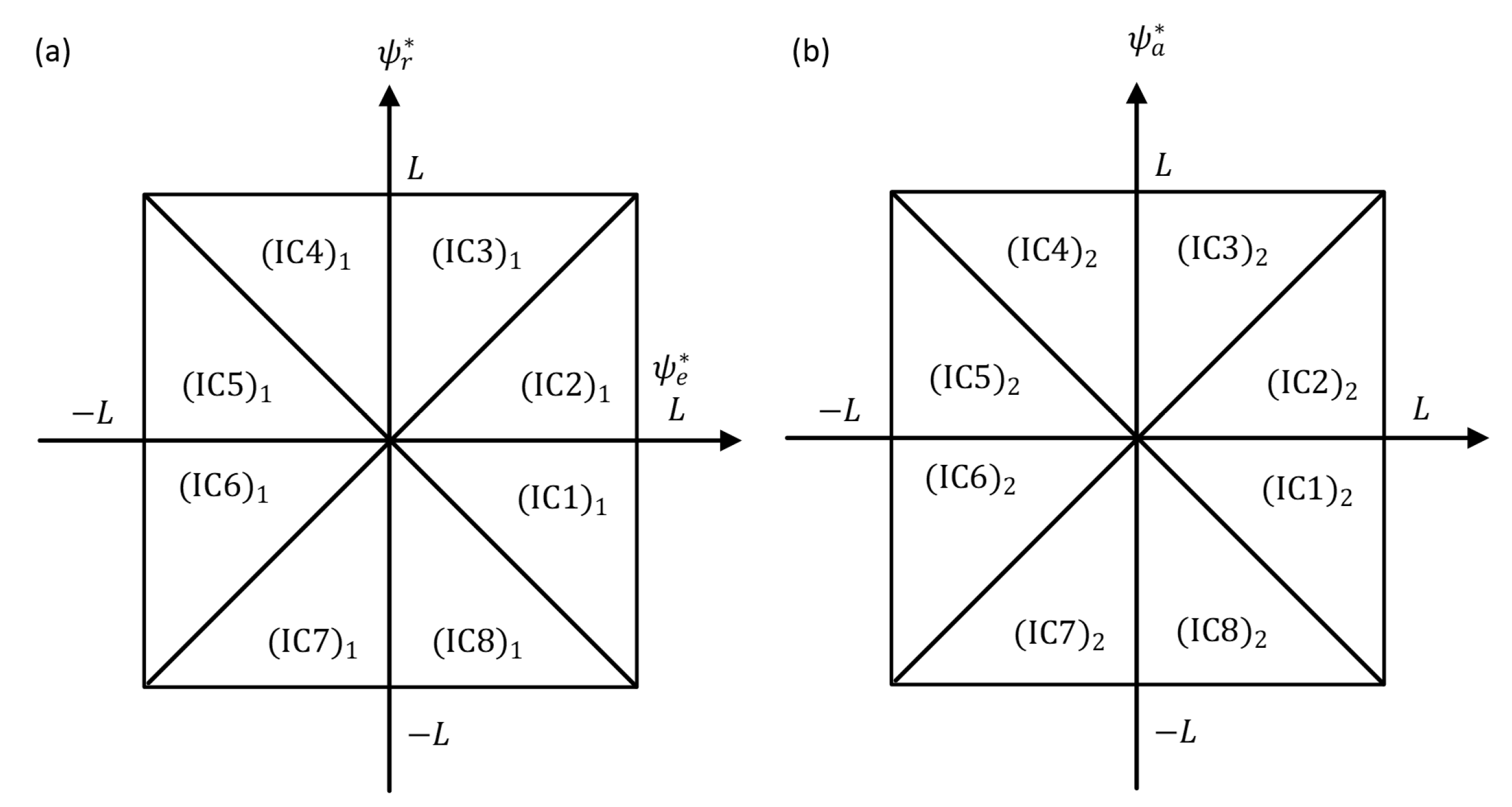
5.1.2. Fuzzy Control Rule
5.1.3. Defuzzification Algorithm
5.2. Performance Verification of Velocity-Type Fuzzy PID Controller
5.2.1. Simulation Condition
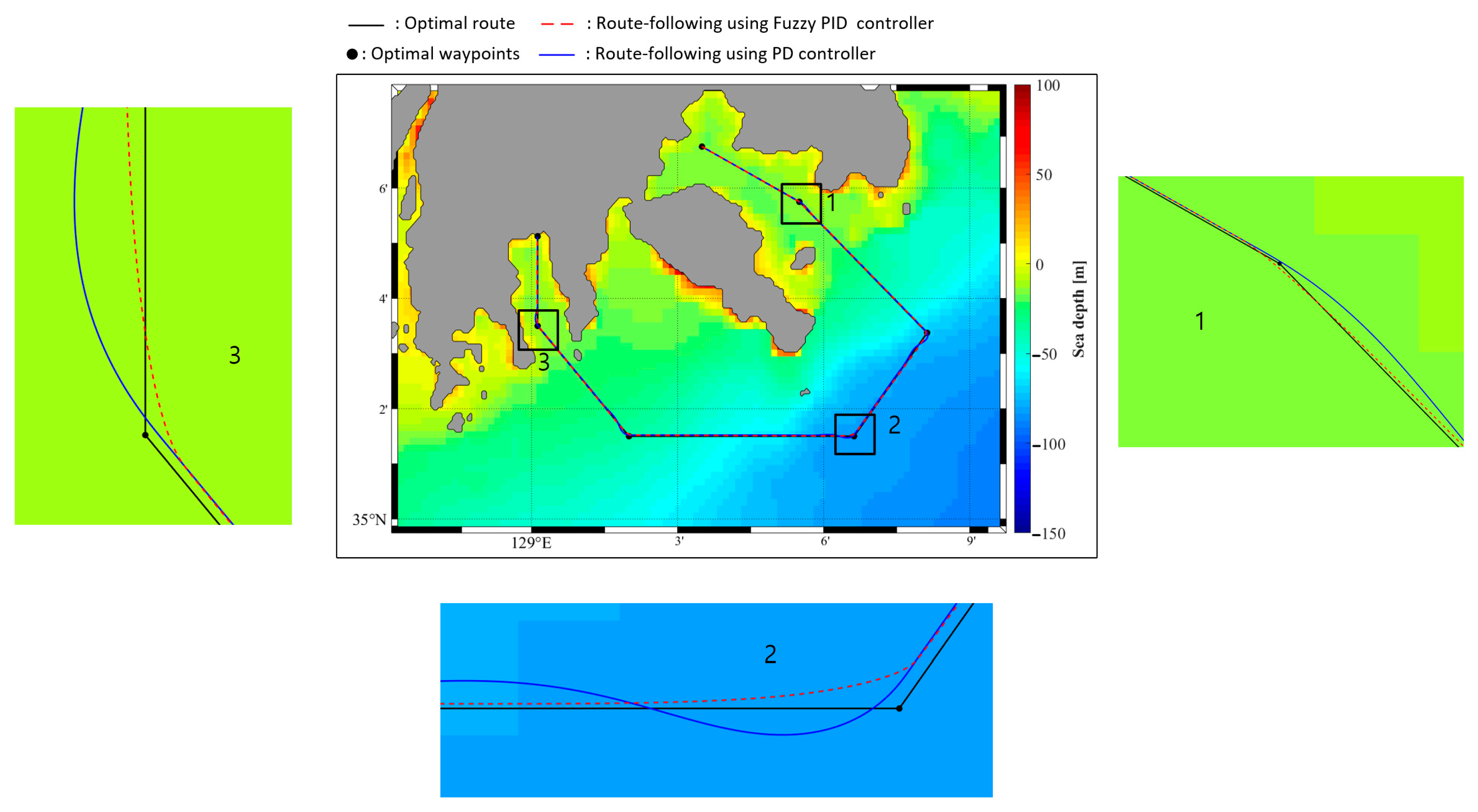
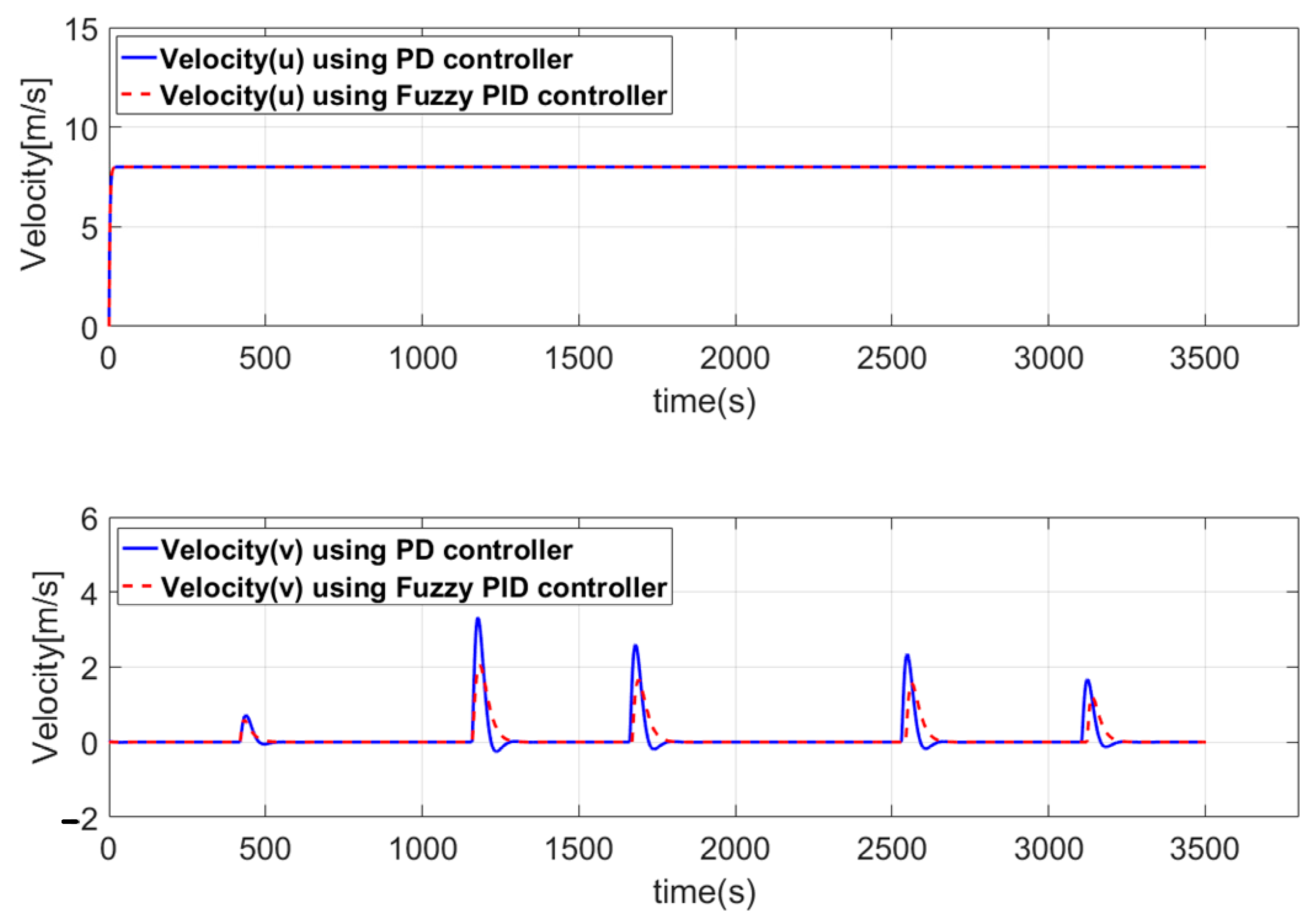
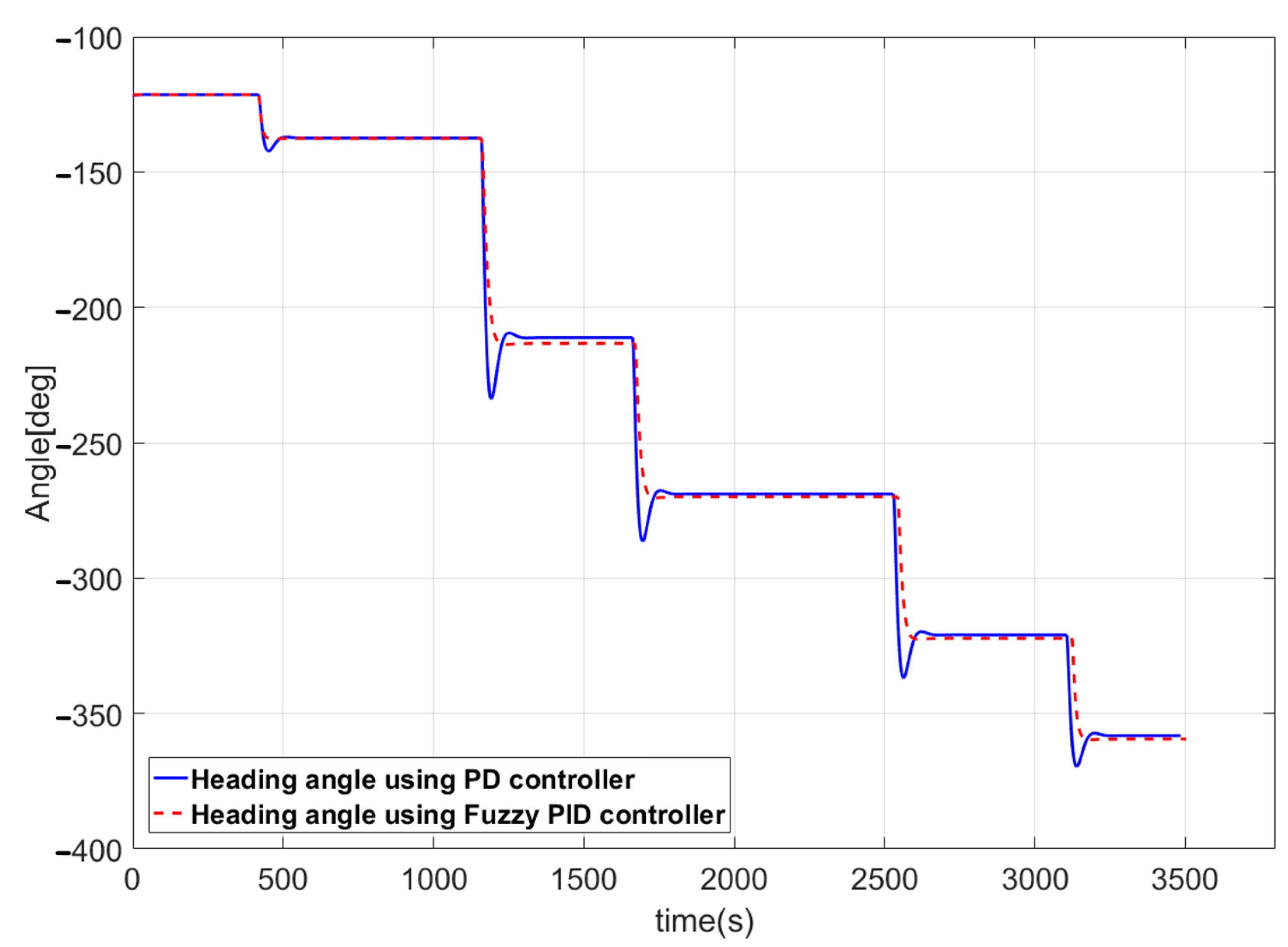
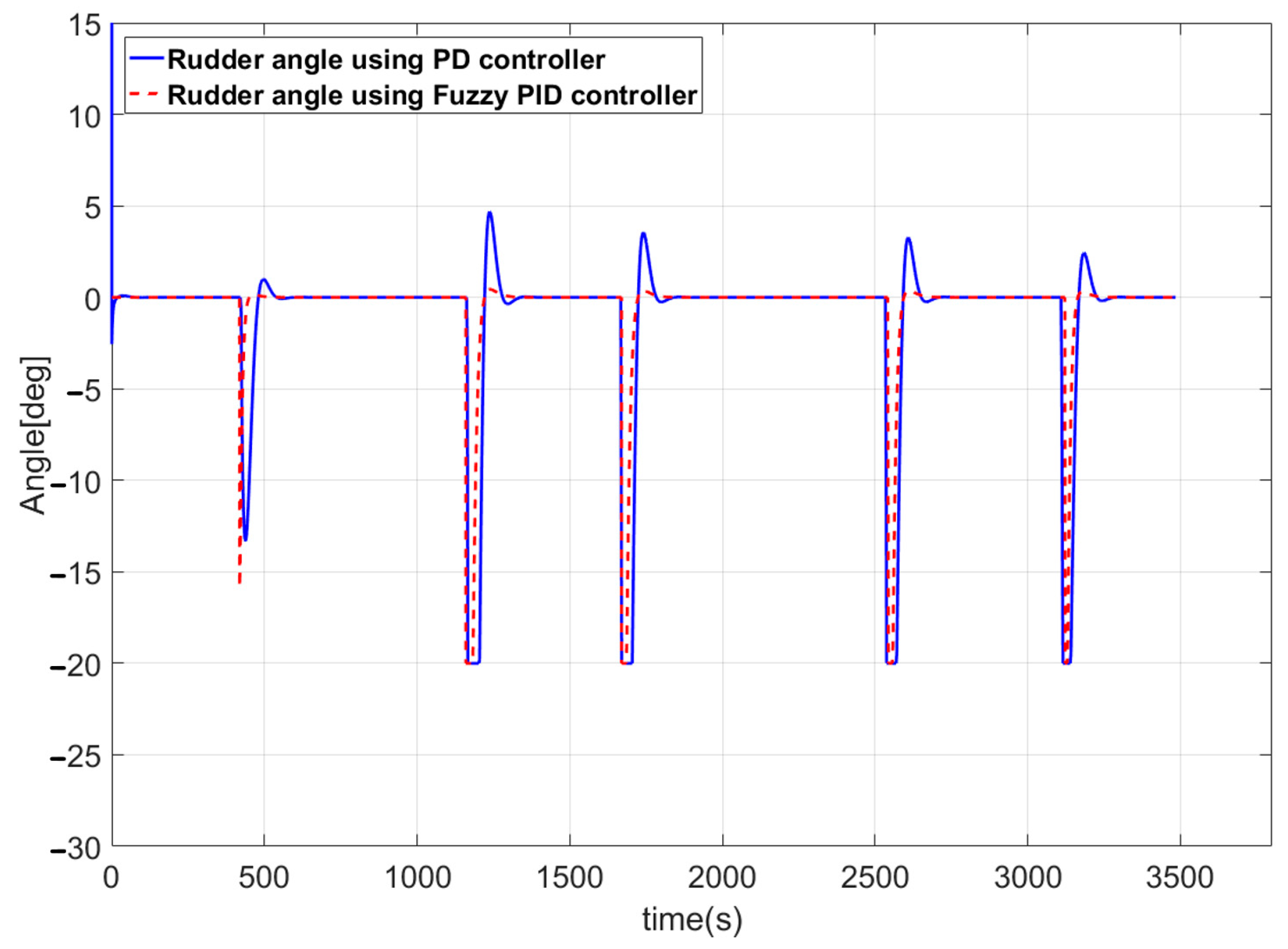
5.2.2. Simulation Results for the Route-Following Control
6. Estimation of Environmental Disturbances Using a Fuzzy Disturbance Estimator
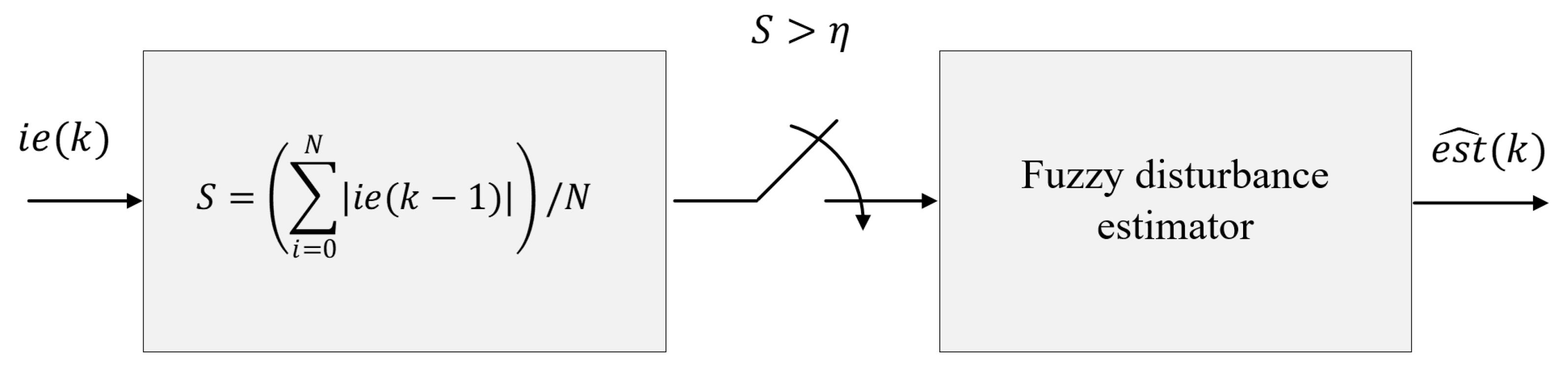
6.1. Method for Determining the Existence of Environmental Disturbances
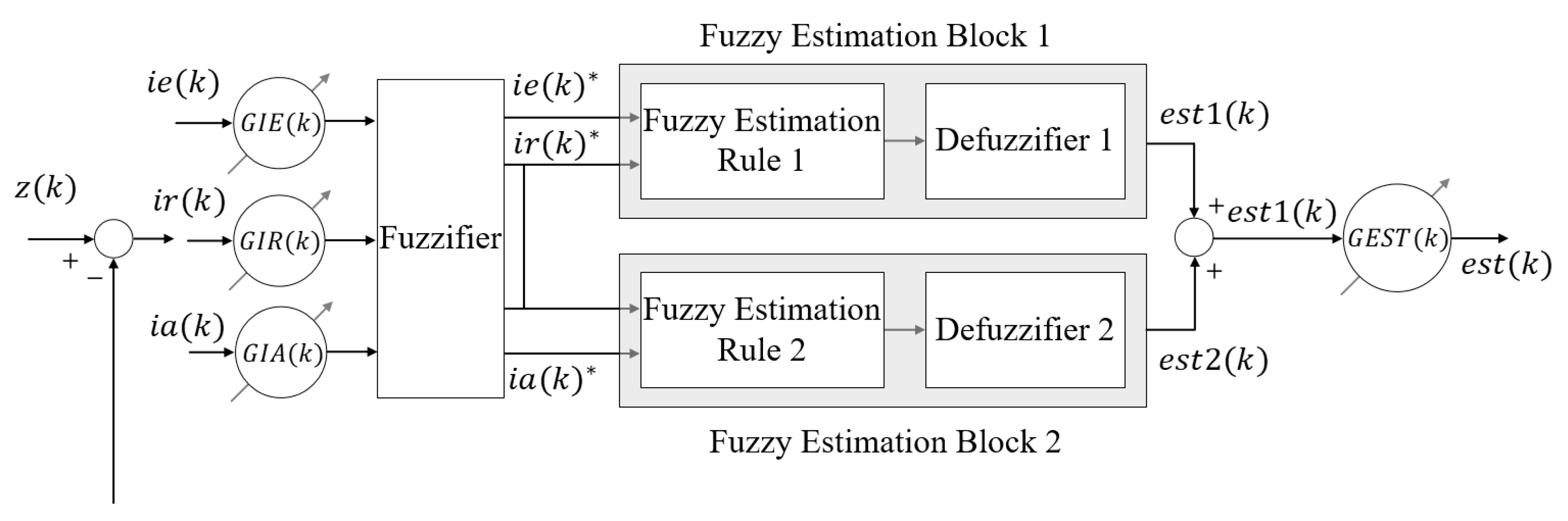
6.2. Design of the Fuzzy Disturbance Estimator
6.3. Route-Following Control System to Eliminate the Effects of Environmental Disturbance
6.4. Simulation of Route-Following Control
6.4.1. Simulation Conditions
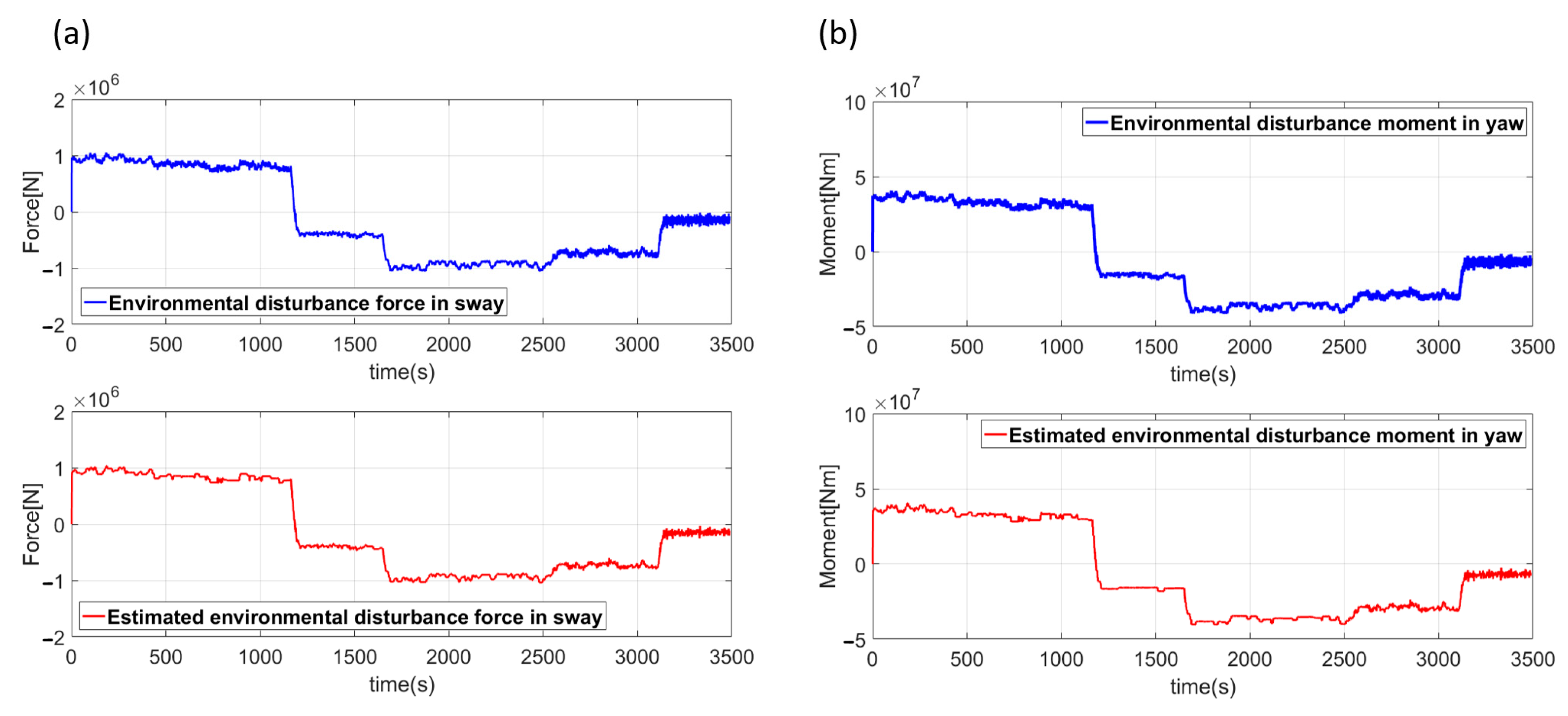
6.4.2. Simulation of Environmental Disturbance Estimation
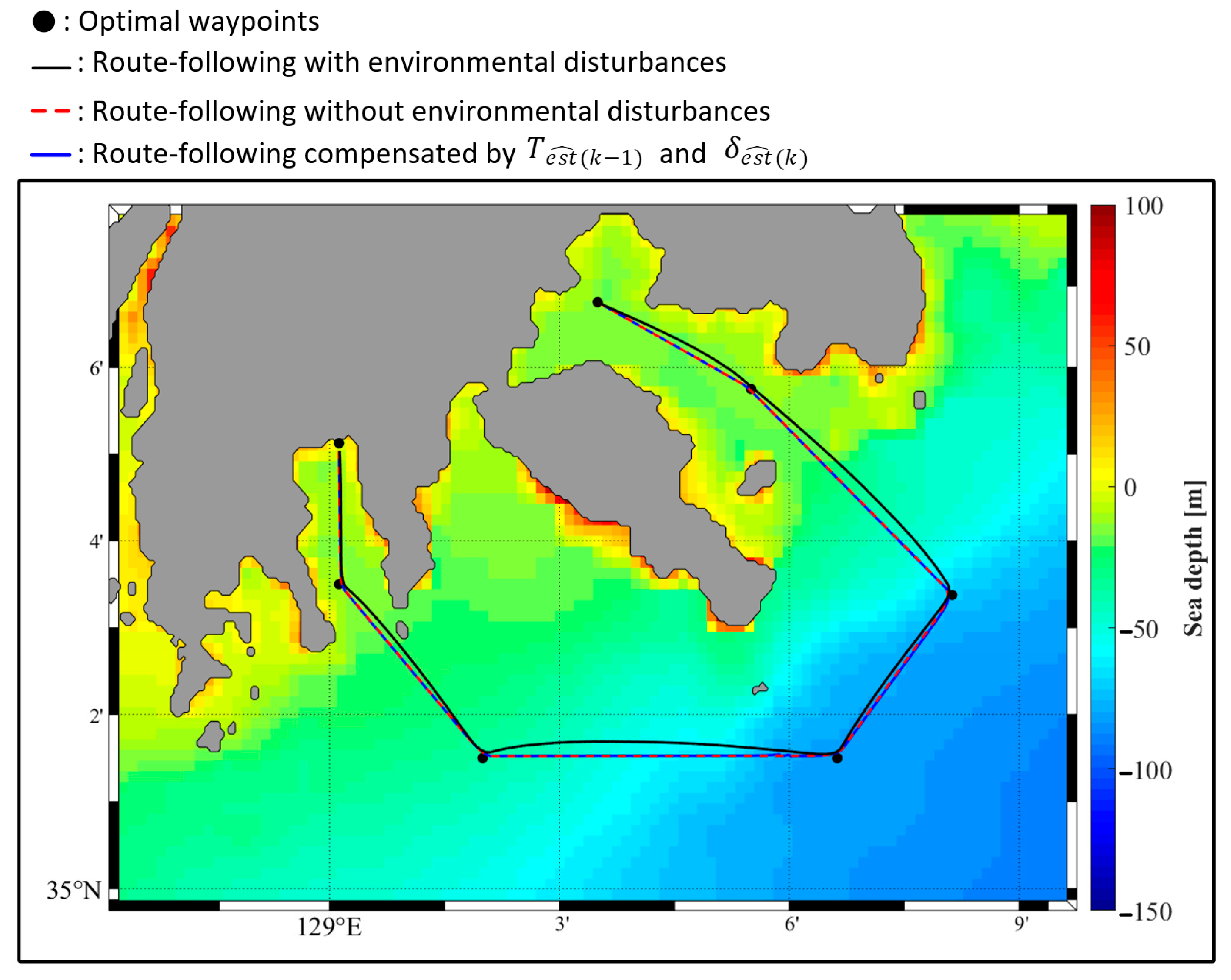
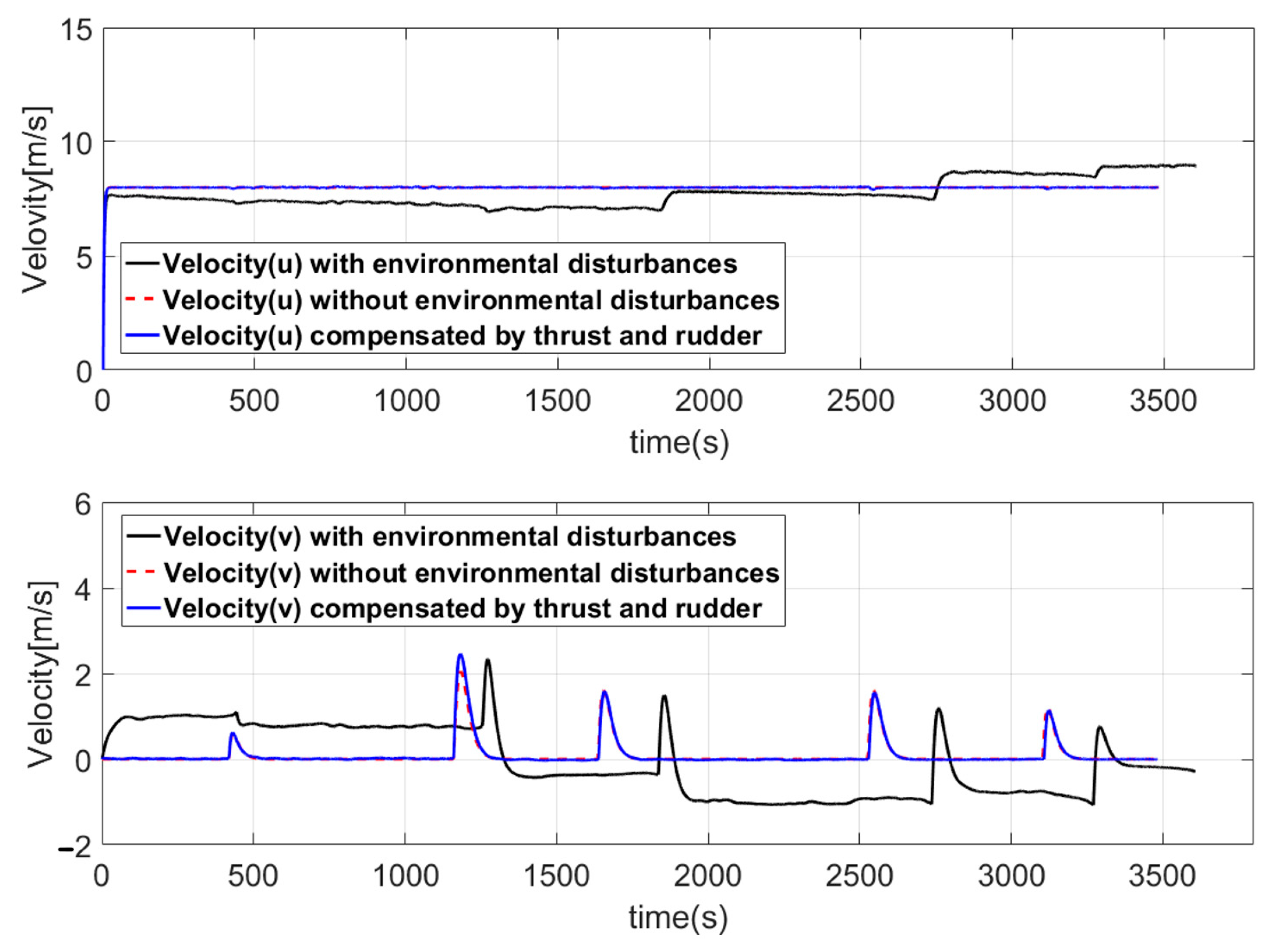
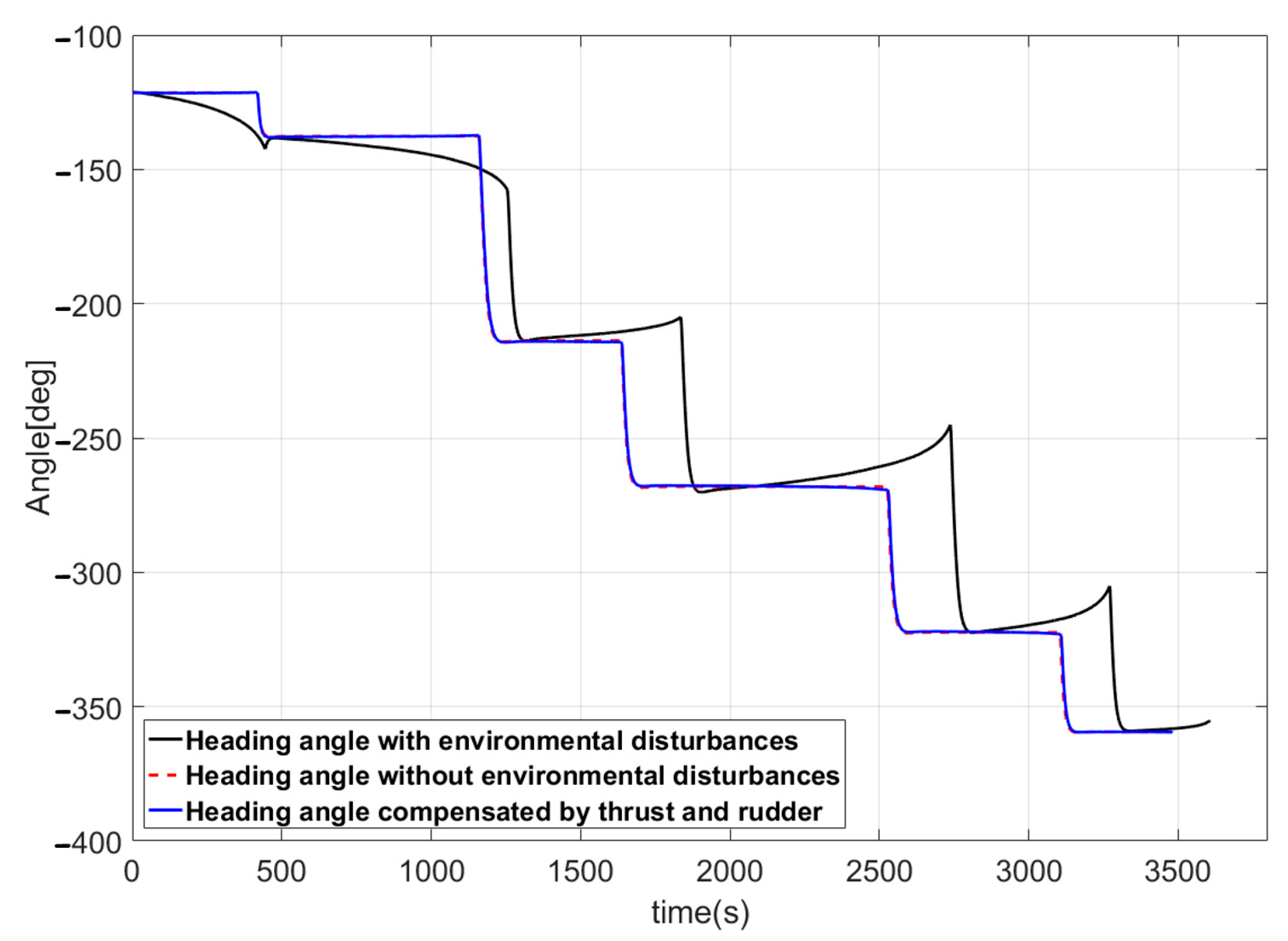
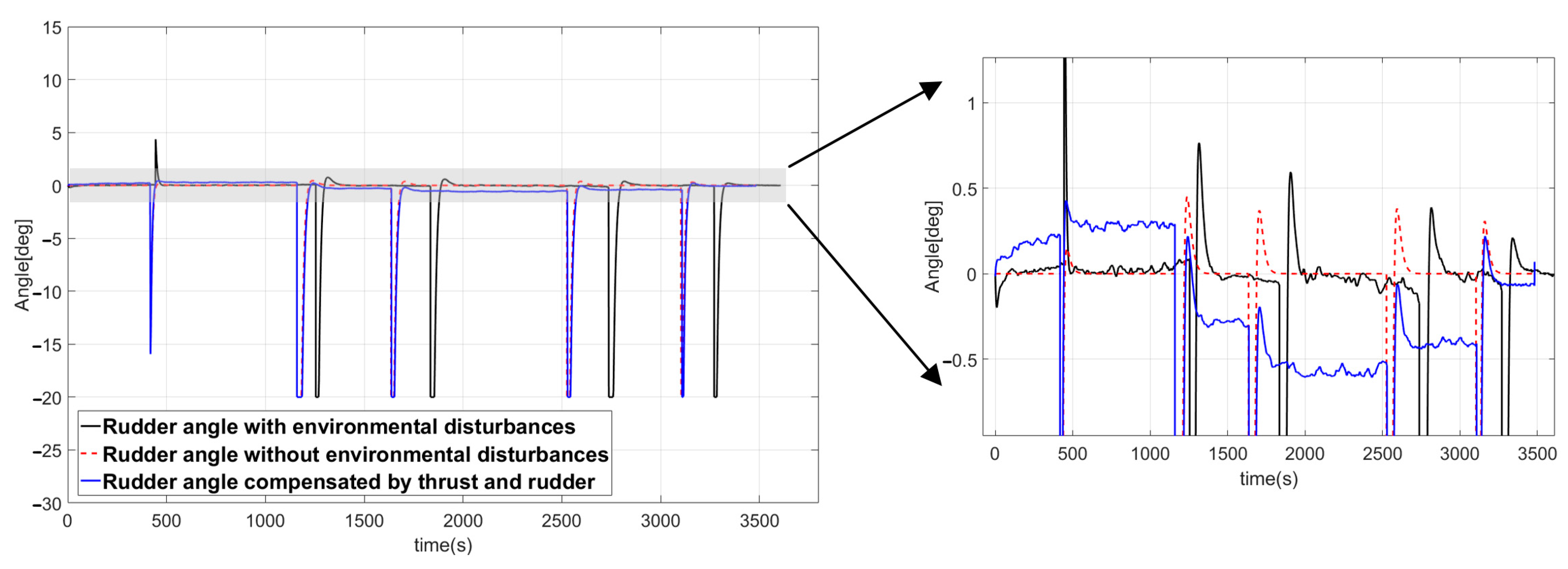
6.4.3. Simulation of Route-Following Control
7. Conclusions
- (1)
- To generate an optimal route, reinforcement learning based on Q-learning algorithms was introduced. The optimal route was generated in a manner that ensured vessel safety and minimized fuel consumption. To ensure safety, under-keel clearance, navigation charts, and sea depth were considered; shortening distance and minimum number of waypoints were considered to minimize fuel consumption. The optimal route from Busan port to Gamcheon port was determined using a traffic separation scheme, restricted area, anchorage, and pilot boarding place. The results of the simulation using the Q-learning algorithm confirmed that the optimal route could be generated while satisfying the requirements.
- (2)
- For the optimal route generated using the Q-learning algorithm, a route-following control method that can accurately follow the route is required. Conventionally, a PD controller is used to control the vessel, but such a controller has limitations including fast course alterations, rough rudder angle changes, and route deviation related to large overshoot. To resolve these problems, a velocity-type fuzzy PID controller was introduced. Use of the velocity-type fuzzy PID controller did not result in large overshoot; thus, the vessel did not deviate from the designated route. Additionally, because the changes in rudder angle were smooth, the vessel energy efficiency increased.
- (3)
- Despite the use of a velocity-type fuzzy PID controller, the application of environmental disturbances (ocean current, waves, and wind) to the vessel prevented accurate route-following control. To resolve this problem, a control method capable of following the route without deviation, regardless of environmental disturbances, was proposed. First, the presence or absence of environmental disturbance was determined based on the characteristics of the Kalman filter innovation process; when environmental disturbance was present, the magnitude of the disturbance was estimated using the fuzzy disturbance estimator. Conversion of the magnitude of the estimated environmental disturbance into thrust and rudder angle actually controlling the vessel allowed the designated route to be accurately followed, even in the presence of such environmental disturbances.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Statheros, T.; Howells, G.; Maier, K. Autonomous ship collision avoidance navigation concepts, technologies and techniques. J. Navig. 2008, 61, 129–142. [Google Scholar] [CrossRef]
- Chun, D.H.; Roh, M.I.; Lee, H.W.; Ha, J.; Yu, D. Deep reinforcement learning-based collision avoidance for an autonomous ship. Ocean Eng. 2021, 234, 109216. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, X.; Zheng, Y.; Du, Y. An autonomous path planning model for unmanned ships based on deep reinforcement learning. Sensors 2020, 20, 426. [Google Scholar] [CrossRef]
- Batakden, B.M.; Leikanger, P.; Wide, P. Towards autonomous maritime operations. In Proceedings of the IEEE International Conference on Nomputational Intelligence and Virtual Environments for Measurement Systems and Applications, Annecy, France, 26–28 June 2017; pp. 1–6. [Google Scholar]
- MUNIN. MUNIN Results. 2016. Available online: http://www.unmanned-ship.org/munin/about/munin-results-2 (accessed on 5 January 2016).
- Chang, C.H.; Kontovas, C.; Yu, Q.; Yang, Z. Risk assessment of the operations of maritime autonomous surface ships. Reliab. Eng. Syst. Saf. 2021, 207, 107324. [Google Scholar] [CrossRef]
- Goerlandt, F. Maritime autonomous surface ships from a risk governance perspective: Interpretation and implications. Saf. Sci. 2020, 128, 104758. [Google Scholar] [CrossRef]
- Lewantowica, Z.H. Architectures and GPS/INS integration: Impact on mission accomplish. IEEE Aerosp. Electron. Syst. Mag. 1992, 7, 16–20. [Google Scholar] [CrossRef]
- Vik, B.; Fossen, T.I. A Nonlinear observer for integration of GPS and inertial navigation systems. Mic J. 2000, 21, 192–208. [Google Scholar] [CrossRef]
- Lie, C.; Mao, Q.; Chu, X.; Xie, S. An improved A-star algorithm considering water current, traffic separation and berthing for vessel path planning. Appl. Sci. 2019, 9, 1057. [Google Scholar] [CrossRef]
- Wang, H.; Mao, W.; Eriksson, A. A three-dimensional Dijkstra’s algorithm for multi-objective ship voyage optimization. Ocean Eng. 2019, 186, 106131. [Google Scholar] [CrossRef]
- Roland, S.B. An intelligent integrated ship guidance system. IFAC Proc. Vol. 1992, 25, 13–25. [Google Scholar]
- Fang, M.C.; Lin, Y.H.; Wang, B.J. Applying the PD controller on the roll reduction and track keeping for the ship advancing in waves. Ocean Eng. 2012, 54, 13–25. [Google Scholar] [CrossRef]
- Heidar, A.; Li, M.H.; Chen, G. New design and stability analysis of fuzzy proportional-derivative control systems. IEEE Trans. Fuzzy Syst. 1994, 2, 245–254. [Google Scholar]
- Cho, K.H.; Kim, C.W.; Lim, J.T. On stability analysis of nonlinear plants with fuzzy logic controllers. In Proceedings of the Korean Institute of Intelligent Systems Conference, Taejon, Republic of Korea, 1 June 1993; pp. 1094–1097. [Google Scholar]
- Nam, S.K.; Yoo, W.S. Fuzzy PID control with accelerated reasoning for DC servo motors. Eng. Appl. Artif. Intell. 1994, 7, 559–569. [Google Scholar] [CrossRef]
- He, S.; Tan, S.; Xu, F.; Wang, P. Fuzzy self-tuning of PID controllers. Fuzzy Sets Syst. 1993, 56, 37–46. [Google Scholar] [CrossRef]
- Ju, J.; Zhang, C.; Liu, Y. Vibration suppression of a flexible-joint robot based on parameter identification and fuzzy PID controller. Algorithms 2018, 11, 189. [Google Scholar] [CrossRef]
- Huang, H.; Yang, X.Y.; Deng, X.L.; Qiao, Z.H. A parameter auto-tuning method of fuzzy PID controller. Fuzzy Inf. Eng. 2009, 2, 1193–1200. [Google Scholar]
- Li, Z.; Sun, J. Disturbance compensating model predictive control with application to ship heading control. IEEE Trans. Control Syst. Technol. 2011, 20, 257–265. [Google Scholar] [CrossRef]
- Zhang, H.L.; Wei, Y.; Hu, X. Anti-disturbance control for dynamic positioning system of ships with disturbances. Appl. Math. Comput. 2021, 396, 125929. [Google Scholar] [CrossRef]
- Siswantoro, J.; Prabuwono, A.S.; Abdullah, A. A linear model based on Kalman filter for improving neural network classification performance. Expert Syst. Appl. 2016, 49, 112–122. [Google Scholar] [CrossRef]
- Wierenga, R.D. An evaluation of a pilot model based on Kalman filtering and optimal control. IEEE Trans. Man-Mach. Syst. 1969, 10, 109–117. [Google Scholar] [CrossRef]
- Soule, A.; Salamatain, K.; Nucci, A.; Taft, N. Traffic matrix tracking using Kalman filter. ACM Sigmatrics Perform. Eval. Rev. 2005, 33, 24–31. [Google Scholar] [CrossRef]
- Zhen, Y.; Harlim, J. Adaptive error covariance estimation methods for ensemble Kalman filters. J. Comput. Phys. 2015, 294, 619–638. [Google Scholar] [CrossRef]
- Chen, C.; Chen, X.Q.; Ma, F.; Zeng, X.J.; Wang, J. A knowledge-free path planning approach for smart ships based on reinforcement learning. Ocean Eng. 2019, 189, 106299. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, X.; Du, Y.; Zheng, Y.; Cao, Z. Path planning of coastal ships based on optimized DQN reward function. Jmse 2021, 9, 210. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, X.; Zheng, Y.; Du, Y. An autonomous path planning model for unmanned ships based on deep reinforcement learning. Sensors 2020, 20, 426. [Google Scholar] [CrossRef]
- Shen, H.; Hashimoto, H.; Matsuda, A.; Taniguchi, Y.; Terada, D.; Guo, C. Automatic collision avoidance of multiple ships based on deep Q-learning. Appl. Ocean Res. 2019, 86, 268–288. [Google Scholar] [CrossRef]
- Zhao, L.; Roh, M.I. COLREGs-compliant multiship collision avoidance based on deep reinforcement learning. Ocean Eng. 2019, 191, 106436. [Google Scholar] [CrossRef]
- Li, L.; Wu, D.; Huang, Y.; Yuan, Z.M. A path planning strategy unified with a COLREGS collision avoidance function based on deep reinforcement learning and artificial potential field. Appl. Ocean Res. 2021, 113, 102759. [Google Scholar] [CrossRef]
- Zhao, L.; Roh, M.I.; Lee, S.J. Control method for path following and collision avoidance of autonomous ship based on deep reinforcement learning. J. Mar. Sci. Technol. 2019, 27, 1. [Google Scholar]
- Nan, G.; Dan, W.; Zhouhua, P.; Jun, W.; Qing, L.H. Advances in line-of-sight guidance for path following of autonomous marine vehicles: An overview. IEEE Trans. Syst. Man Cybern. 2023, 53, 12–28. [Google Scholar]
- Lili, W.; Yixin, S.; Huajun, Z.; Binghua, S.; Mahmoud, S.A. An improved integral light-of sight guidance law for path following of unmanned surface vehicles. Ocean Eng. 2020, 205, 107302. [Google Scholar]
- Zhang, Q.; Ding, Z.; Zhang, M. Adaptive self-regulation PID control of course-keeping for ships. Pol. Marit. Res. 2020, 27, 39–45. [Google Scholar] [CrossRef]
- Wang, L.; Wu, Q.; Liu, J.; Li, S.; Negenborn, R.R. State-of-the-art research on motion control of maritime autonomous surface ships. J. Mar. Sci. Eng. 2019, 7, 438. [Google Scholar] [CrossRef]
- Le, T.T. Ship heading control system using neural network. J. Mar. Sci. Technol. 2021, 26, 963–972. [Google Scholar] [CrossRef]
- Wang, L.; Xu, H.; Zou, U. Regular unknown input functional observers for 2-D singular systems. Int. J. Control Autom. Syst. 2013, 11, 911–918. [Google Scholar] [CrossRef]
- Lee, M.K. Unknown input estimation of the linear systems using integral observer. J. Korean Inst. Illum. Electr. Install. Eng. 2008, 22, 101–106. [Google Scholar]
- Youssef, T.; Chadli, M.; Karimi, H.R.; Wang, R. Actuator and sensor faults estimation based on proportional integral observer for TS fuzzy model. J. Frankl. Inst. 2017, 354, 2524–2542. [Google Scholar] [CrossRef]
- Witczak, M.; Kornicz, J.; Jozefowicz, R. Design of unknown input observers for non-linear stochastic systems and their application to robust fault diagnosis. Control Cybern. 2013, 42, 227–256. [Google Scholar]
- Lee, K.K.; Ha, W.S.; Back, J.H. Overview of disturbance observation techniques for linear and nonlinear systems. J. Inst. Control Robot. Syst. 2016, 22, 332–338. [Google Scholar] [CrossRef]
- Kwak, G.; Park, S. State space disturbance observer considering sliding mode and robustness improvement for mismatched disturbance. J. Inst. Control Robot. Syst. 2021, 27, 639–645. [Google Scholar] [CrossRef]
- Zhao, Z.; Cao, D.; Yang, J.; Wang, H. High-order sliding mode observer-based trajectory tracking control for a quadrotor UAV with uncertain dynamics. Nonlinear Dyn. 2020, 102, 2583–2596. [Google Scholar] [CrossRef]
- Kim, M.K.; Park, D.H.; Oh, Y.W.; Kim, J.H.; Choi, J.K. Towfish attitude control: A consideration of towing point, center of gravity, and towing speed. J. Mar. Sci. Eng. 2021, 9, 641. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Willy & Sons LTD: Sussex, UK, 2011. [Google Scholar]
- Blanke, M. Ship Propulsion Losses Related to Automated Steering and Prime Mover Control. Ph.D. Thesis, The Technical University of Denmark, Kongens Lyngby, Denmark, 1981. [Google Scholar]
- Davidson, K.S.M.; Schiff, L.I. Turning and Course Keeping Qualities Transactions of SNAME; Report number T1946-1/SNAME; Marine and Transport Technology: Delft, The Netherlands, 1946. [Google Scholar]
- Fossen, T.I. Marine Control System; Marine Cybermetics: Trondheim, Norway, 2002. [Google Scholar]
- Kim, M.K.; Yang, H.; Kim, J.H. Improvement of ship’s DP system performance using control increment of velocity type fuzzy PID controller. J. Korean Soc. Mar. Eng. 2019, 43, 40–47. [Google Scholar]
- Dayan, P.; Niv, Y. Reinforcement learning: The good, the bad and the ugly. Curr. Opin. Neurobiol. 2008, 18, 185–196. [Google Scholar] [CrossRef]
- Bae, H.; Kim, G.; Kim, J.; Qian, D.; Lee, S. Multi-robot path planning method using reinforcement learning. Appl. Sci. 2019, 9, 3057. [Google Scholar] [CrossRef]
- Maoudj, A.; Hentout, A. Optimal path planning approach based on Q-learning algorithm for mobile robots. Appl. Soft Comput. 2020, 97, 106796. [Google Scholar] [CrossRef]
- Yan, C.; Xiang, X. A path planning algorithm for UAV based on improved Q-learning. In Proceedings of the 2018 2th International Conference on Robotics and Automation Science 2018, Wuhan, China, 23–25 June 2018; pp. 1–5. [Google Scholar]
- Lee, W.; Yoo, W.; Choi, G.H.; Ham, S.H.; Kim, T.W. Determination of optimal ship route in coastal sea considering sea state and under keel clearance. J. Soc. Nav. Archit. Korea 2019, 56, 480–487. [Google Scholar] [CrossRef]
- Kim, J.H.; Oh, S.J. A fuzzy PID controller for nonlinear and uncertain systems. Soft Comput. 2000, 4, 123–129. [Google Scholar] [CrossRef]
- Long, Z.; Yuan, Y.; Long, W. Designing fuzzy controllers with variable universes of discourse using input-output data. Eng. Appl. Artif. Intell. 2014, 36, 215–221. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, Y.; Li, S.; Zhou, Y. Fuzzy controller design of micro-unmanned helicopter relying on improved genetic optimization algorithm. Aerosp. Sci. Technol. 2020, 98, 105685. [Google Scholar] [CrossRef]
- Zhu, Z.; Liu, Y.; He, Y.; Wu, W.; Wang, H.; Huang, C.; Ye, B. Fuzzy PID control of the three-degree-of-freedom parallel mechanism based on genetic algorithm. Appl. Sci. 2022, 12, 11128. [Google Scholar] [CrossRef]
- Sumar, R.R.; Coelho, A.A.R.; Coelho, L.D.S. Computational intelligence approach to PID controller design using the universal model. Inf. Sci. 2010, 180, 3980–3991. [Google Scholar] [CrossRef]
- Kim, Y.H.; Ahn, S.C.; Kwon, W.H. Computational complexity of general fuzzy logic control and its simplification for a loop controller. Fuzzy Sets Syst. 2000, 111, 215–224. [Google Scholar] [CrossRef]
- Peters, L.; Guo, S.; Camposano, R. A novel analog fizzy controller for intelligent sensors. Fuzzy Sets Syst. 1995, 70, 235–247. [Google Scholar] [CrossRef]
- Dumitrescu, C.; Ciotirnae, P.; Vizitiu, C. Fuzzy logic for intelligent control system using soft computing applications. Sensors 2021, 21, 2617. [Google Scholar] [CrossRef] [PubMed]
- Kwak, S.; Choi, B.J. Deffuzzification scheme and its numerical example for fuzzy logic based control system. J. Korea Inst. Intell. Syst. 2018, 28, 350–354. [Google Scholar]
- Kim, J.H.; Ha, Y.S.; Lim, J.K.; Seo, S.K. A suggestion of fuzzy estimation technique for uncertainty estimation of linear time invariant system based on Kalman filter. J. Korea Soc. Mar. Eng. 2012, 36, 919–926. [Google Scholar] [CrossRef]
- Kim, D.; Lee, S.M.; Jung, S.; Koo, J.; Myung, H. Particle swarm optimization-based receding horizon formation control of multi-agent surface vehicle. Adv. Robot. Res. 2018, 2, 161–182. [Google Scholar]
- Chen, X.; Zhou, L.; Zhou, M.; Shao, A.; Ren, K.; Chen, Q.; Gu, G.; Wan, M. Infrared ocean image simulation algorithm based on pierson-moskowitz spectrum and bidirectional reflectance distribution function. Photonics 2022, 9, 166. [Google Scholar] [CrossRef]
- Berge, S.P.; Ohtsu, K.; Fossen, T.I. Nonlinear control of ships minimizing the position tracking errors. Model. Identif. Control 1999, 20, 177–189. [Google Scholar] [CrossRef]
- Isherwood, R.W. Wind resistance of merchant ships. RINA Trans. 1972, 115, 327–338. [Google Scholar]
- Kim, M.K. A Study on Generation of Optimal Route and Route following Control for Autonomous Vessel. Ph.D. Dissertation, Korea Maritime & Ocean University, Busan, Republic of Korea, February 2023. [Google Scholar]

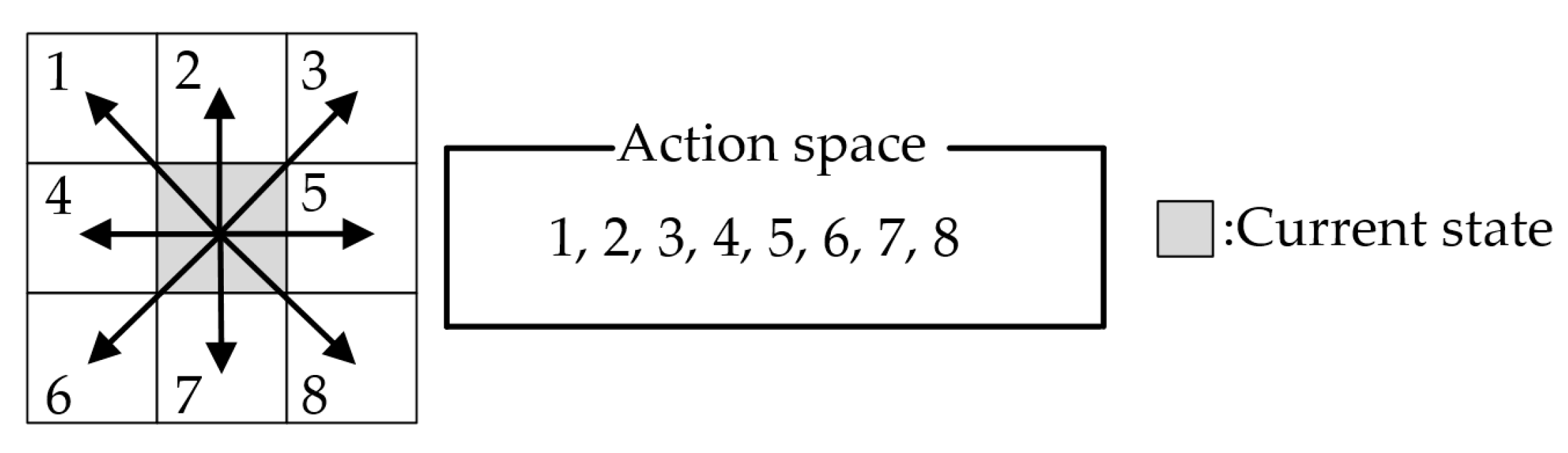


| Hydrodynamic Coefficients | Definition |
|---|---|
| Added mass in surge | |
| Drag force coefficient in surge | |
| Thrust deduction number | |
| Propeller thrust | |
| Resistance related to rudder deflection | |
| Flow velocity past the rudder | |
| Excessive drag force related to combined sway-yaw motion | |
| Excessive drag force in yaw | |
| Loss term or added resistance | |
| External force related to winds and waves |
| Parameter | Length/Volume | Parameter | Length/Volume |
|---|---|---|---|
| Information | |
|---|---|
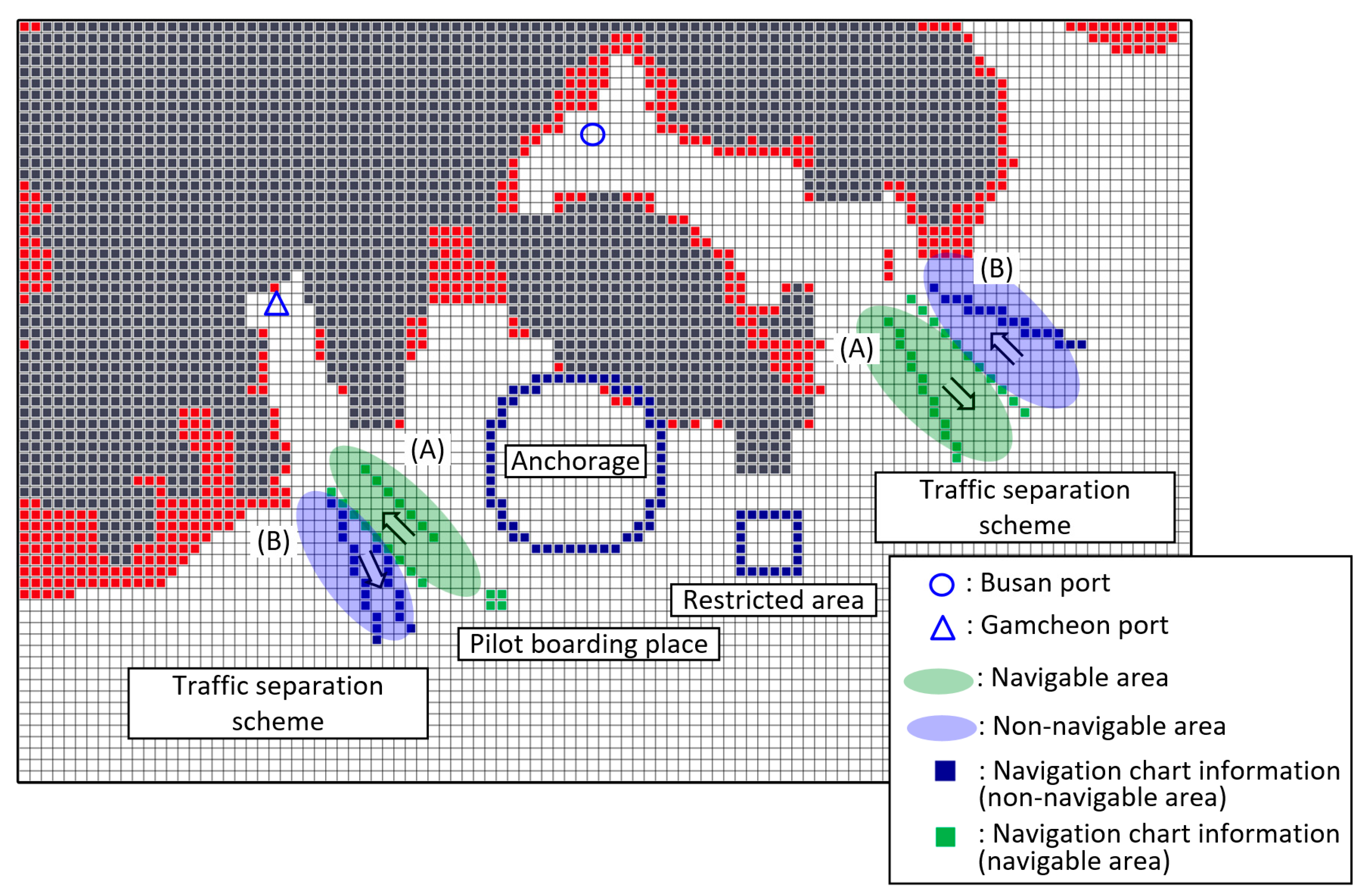
| 1 | Restricted area |
| 2 | Pilot boarding place |
| 3 | Anchorage |
| 4 | Traffic separation scheme (Busan port) |
| 5 | Traffic separation scheme (Gamcheon port) |
| Parameter Values | |
| 0.2 | |
| 0.01 | |
| 0.9 | |
| Rewards | |
| Land | End learning |
| Sea depth < | End learning |
| Traffic separation scheme (A), pilot boarding place | 20 |
| Traffic separation scheme (B), anchorage, restricted area | −20 |
| Arrival at the port of entry | 10 |
| Shortening distance algorithm | 100 |
| Minimum waypoint algorithm | 20 |
| Fuzzy Control Block 1 |
| Fuzzy Control Block 2 |
| Conditions for Environmental Disturbances | |
|---|---|
| 15 | |
| −5 | |
| 0.3 | |
| 10 | |
| 1 | |
| −5 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.-K.; Kim, J.-H.; Yang, H. Optimal Route Generation and Route-Following Control for Autonomous Vessel. J. Mar. Sci. Eng. 2023, 11, 970. https://doi.org/10.3390/jmse11050970
Kim M-K, Kim J-H, Yang H. Optimal Route Generation and Route-Following Control for Autonomous Vessel. Journal of Marine Science and Engineering. 2023; 11(5):970. https://doi.org/10.3390/jmse11050970
Chicago/Turabian StyleKim, Min-Kyu, Jong-Hwa Kim, and Hyun Yang. 2023. "Optimal Route Generation and Route-Following Control for Autonomous Vessel" Journal of Marine Science and Engineering 11, no. 5: 970. https://doi.org/10.3390/jmse11050970
APA StyleKim, M.-K., Kim, J.-H., & Yang, H. (2023). Optimal Route Generation and Route-Following Control for Autonomous Vessel. Journal of Marine Science and Engineering, 11(5), 970. https://doi.org/10.3390/jmse11050970







