Improving Computational Efficiency in WEC Design: Spectral-Domain Modelling in Techno-Economic Optimization
Abstract
1. Introduction
2. The ISWEC Concept
2.1. Time-Domain Model
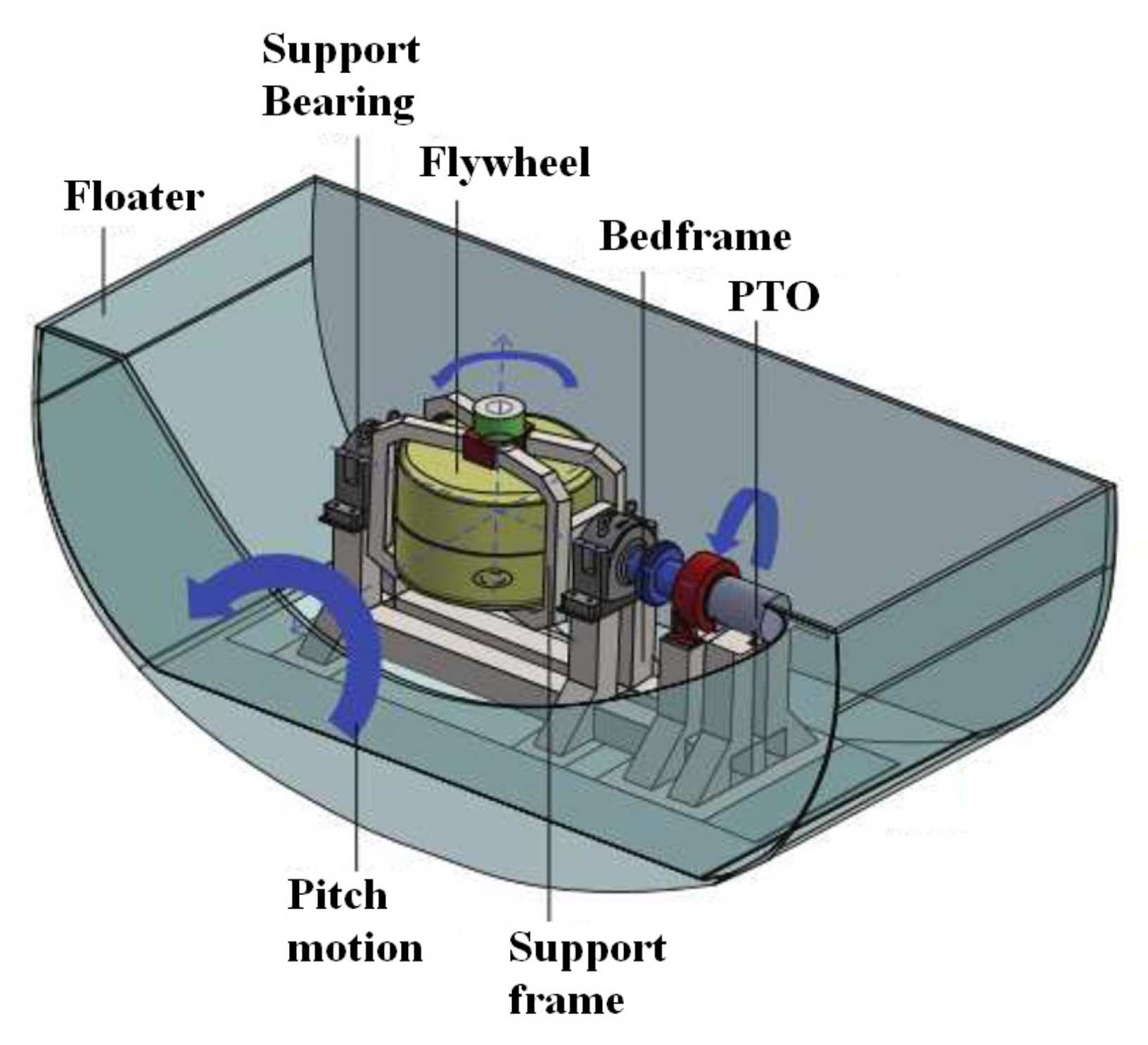
2.1.1. Floater and Gyroscope System
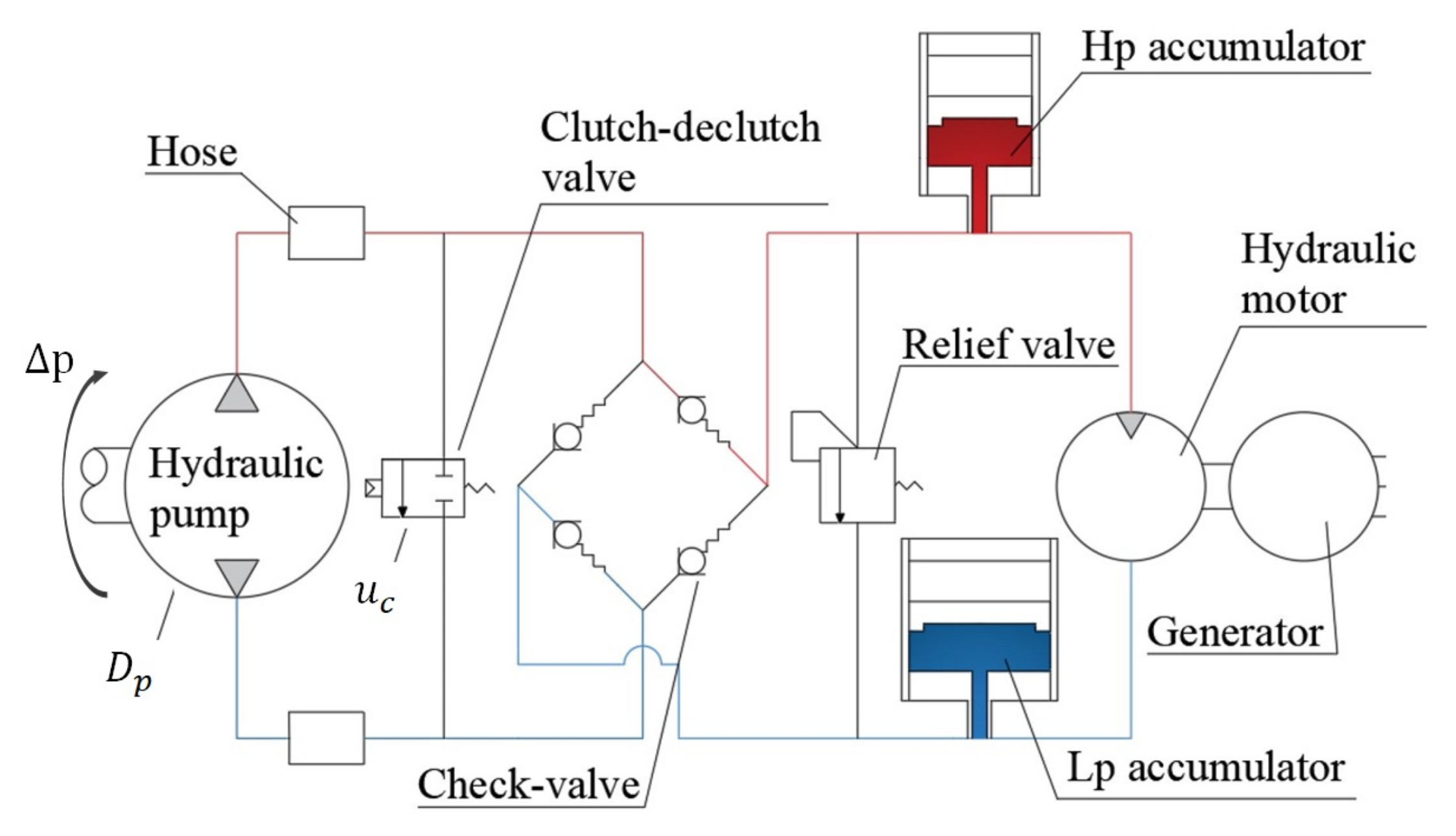
2.1.2. Hydraulic PTO
2.2. Spectral-Domain Model
2.2.1. Floater and Gyroscope Equations
2.2.2. Hydraulic PTO Equation
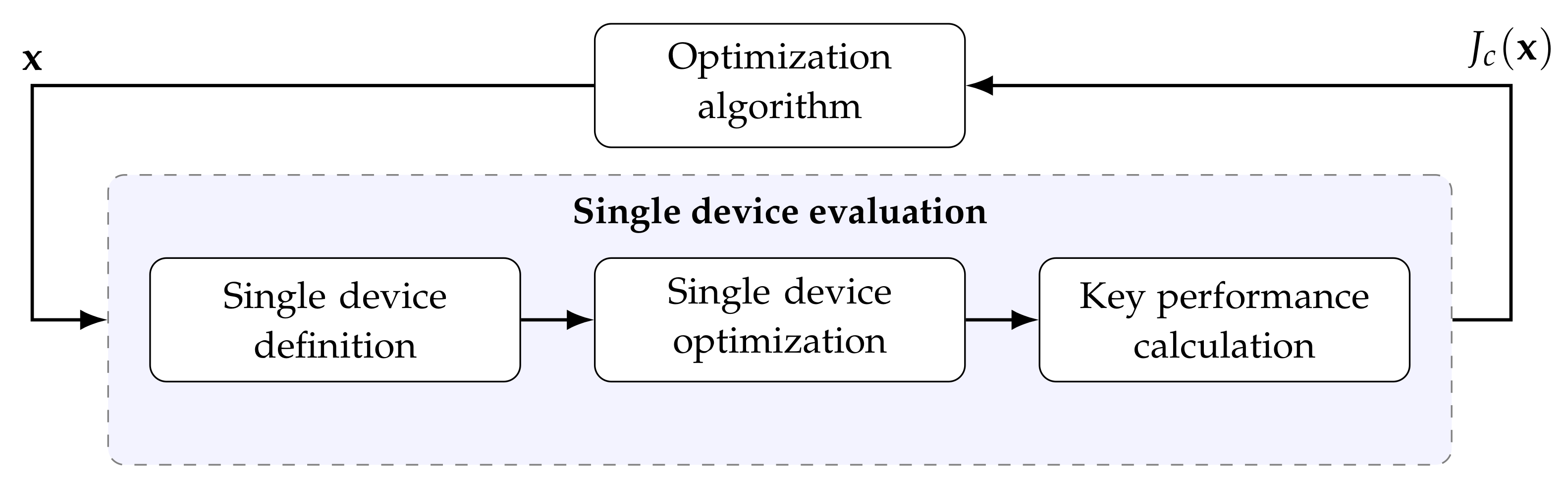
3. Design Tool Architecture
- Single device definition;
- Single device optimization;
- Key performance calculation.
3.1. Device Parametrization and Assumptions
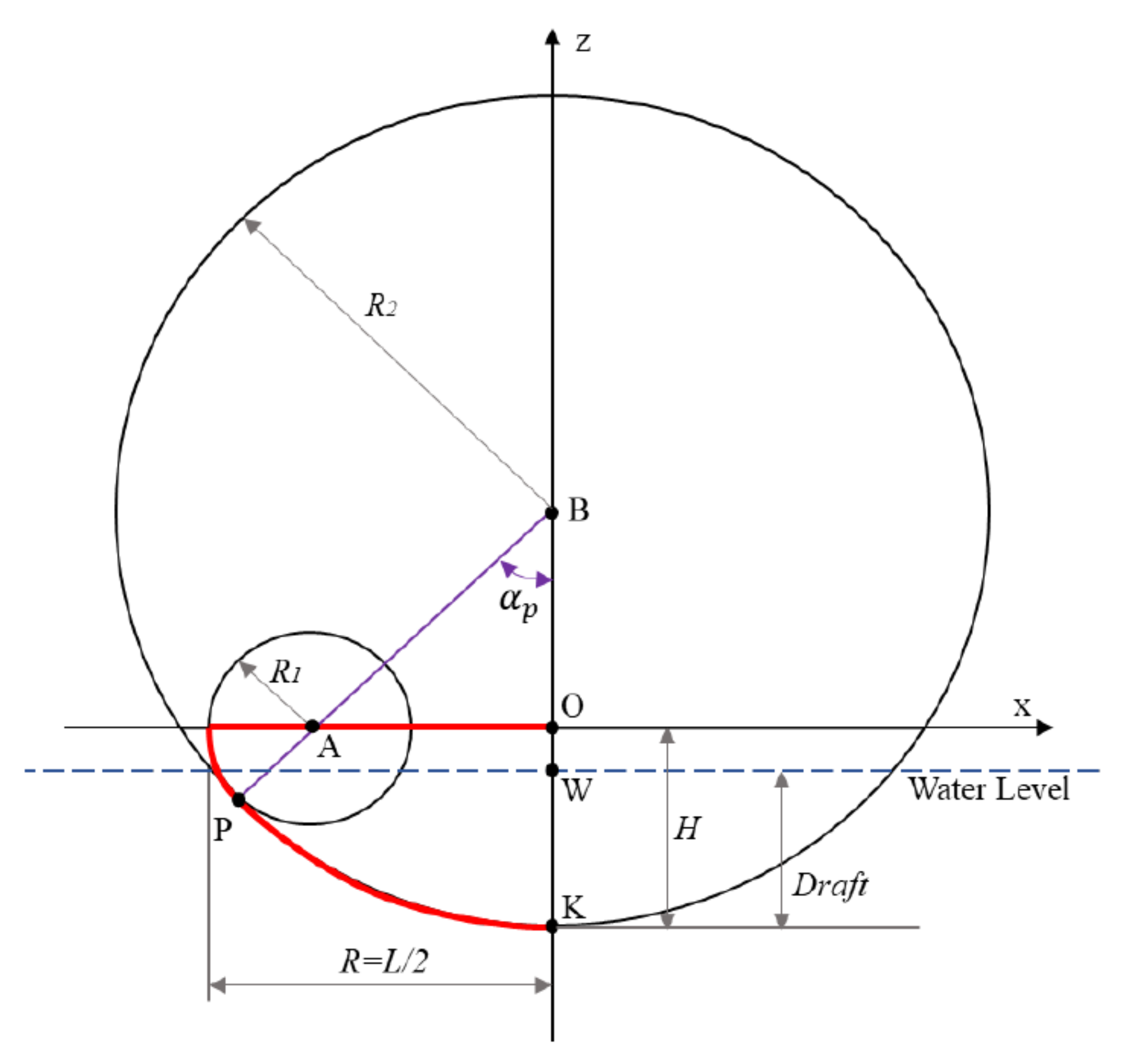
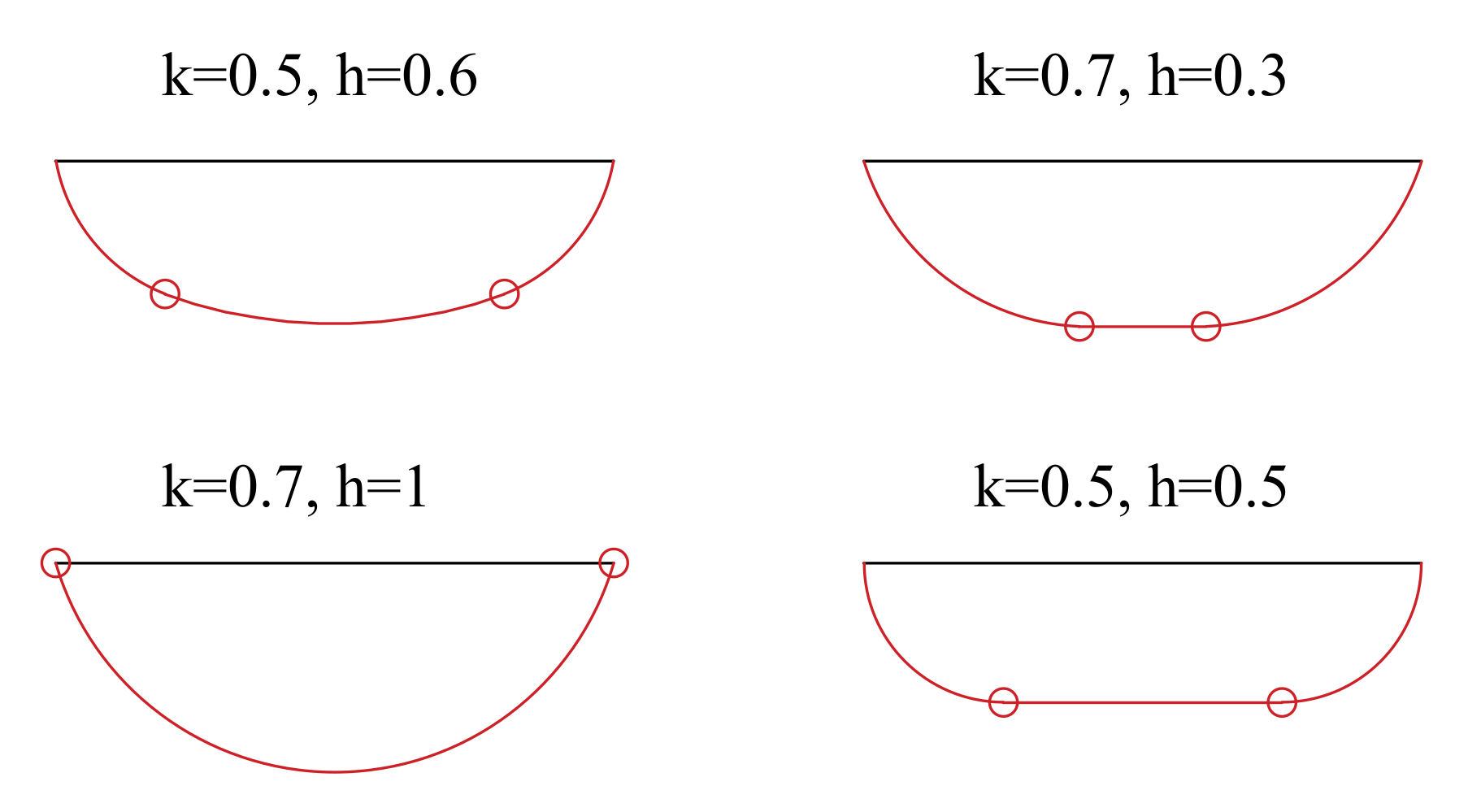
3.1.1. Floater Geometry and Parameters
- : length of the floater;
- : hull width factor. It defines the width of the hull W as a function of the gyroscope unit dimension and the number of gyroscopic units ;
- : bow/stern circumference ratio;
- : height ratio;
- : maximum pitching angle, defined as the maximum pitch rotation to avoid the deck to be submerged. It defines the hull draft D function of the floater semi-length R and the floater height H;
- : ballast filling ratio, which is defined as the ratio of ballast located in aft/fore ballast tanks over the total ballast (: all the ballast is stored in aft/fore ballast tanks; : all the ballast is stored in the bottom ballast tank).
3.1.2. Gyroscope Parameters
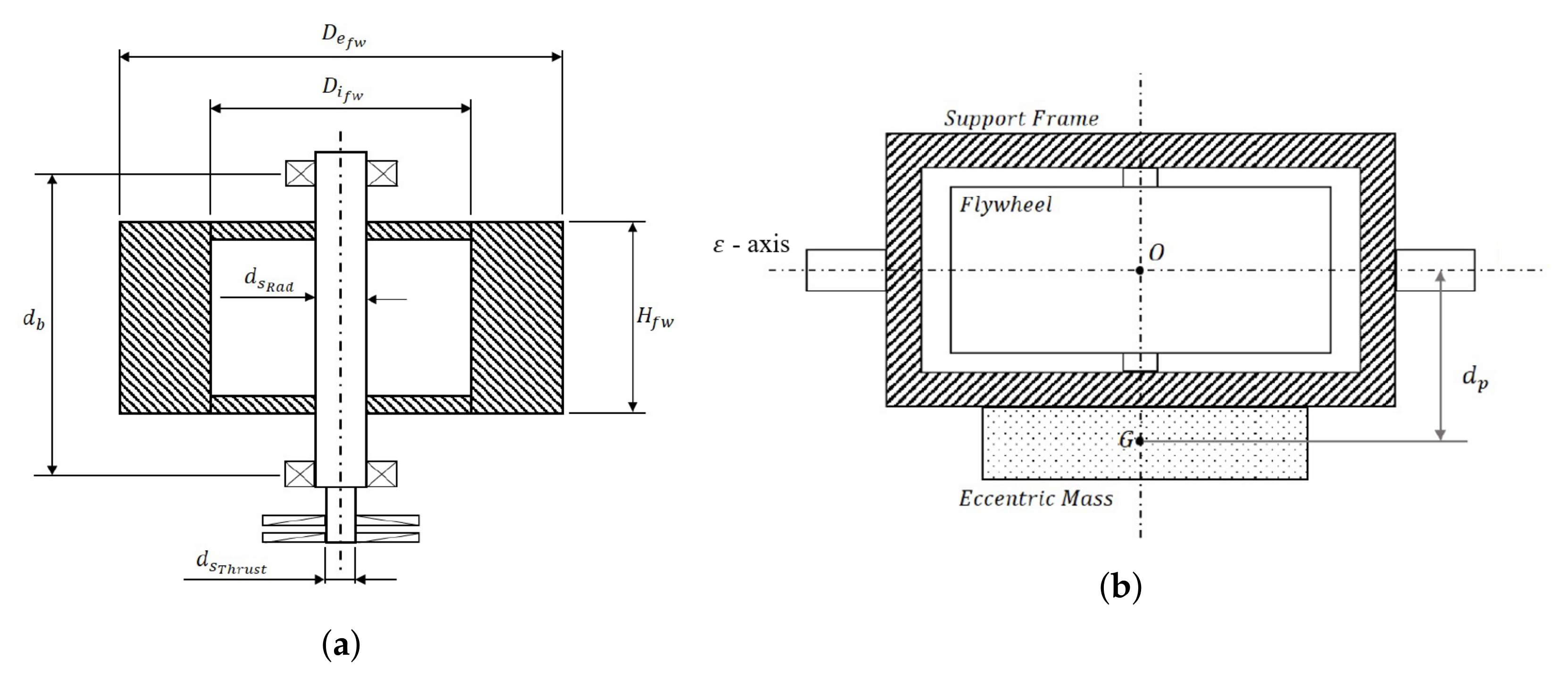
- J: the flywheel inertia about its vertical rotational axis. J determines the angular momentum of the gyroscope, and it is used to derive its dimensions;
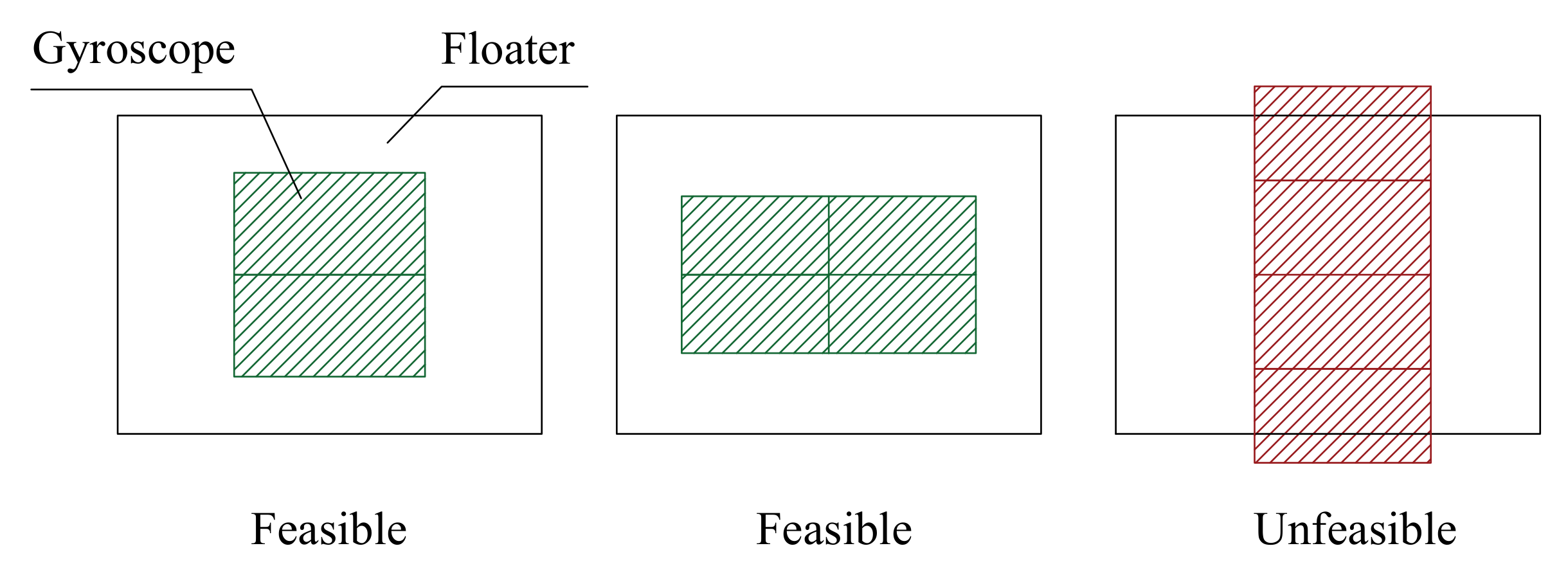
- : the number of gyroscopic units inside the hull. The realization of one single gyroscope with a high inertia J can result in high loads and costs. Moreover, the device will be not balanced on the roll axis since the precession motion of one single gyroscope affects the equilibrium around the -axis of the floater.
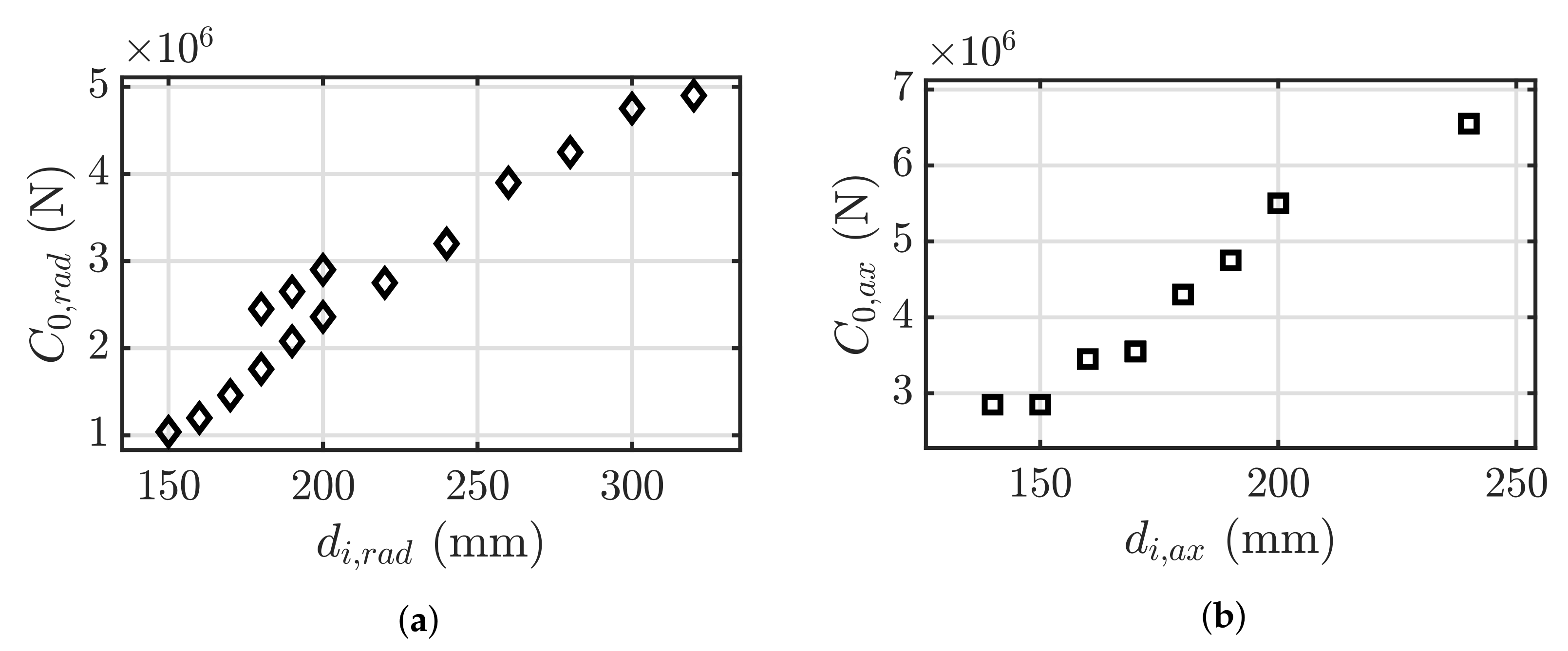
3.1.3. Flywheel Bearings
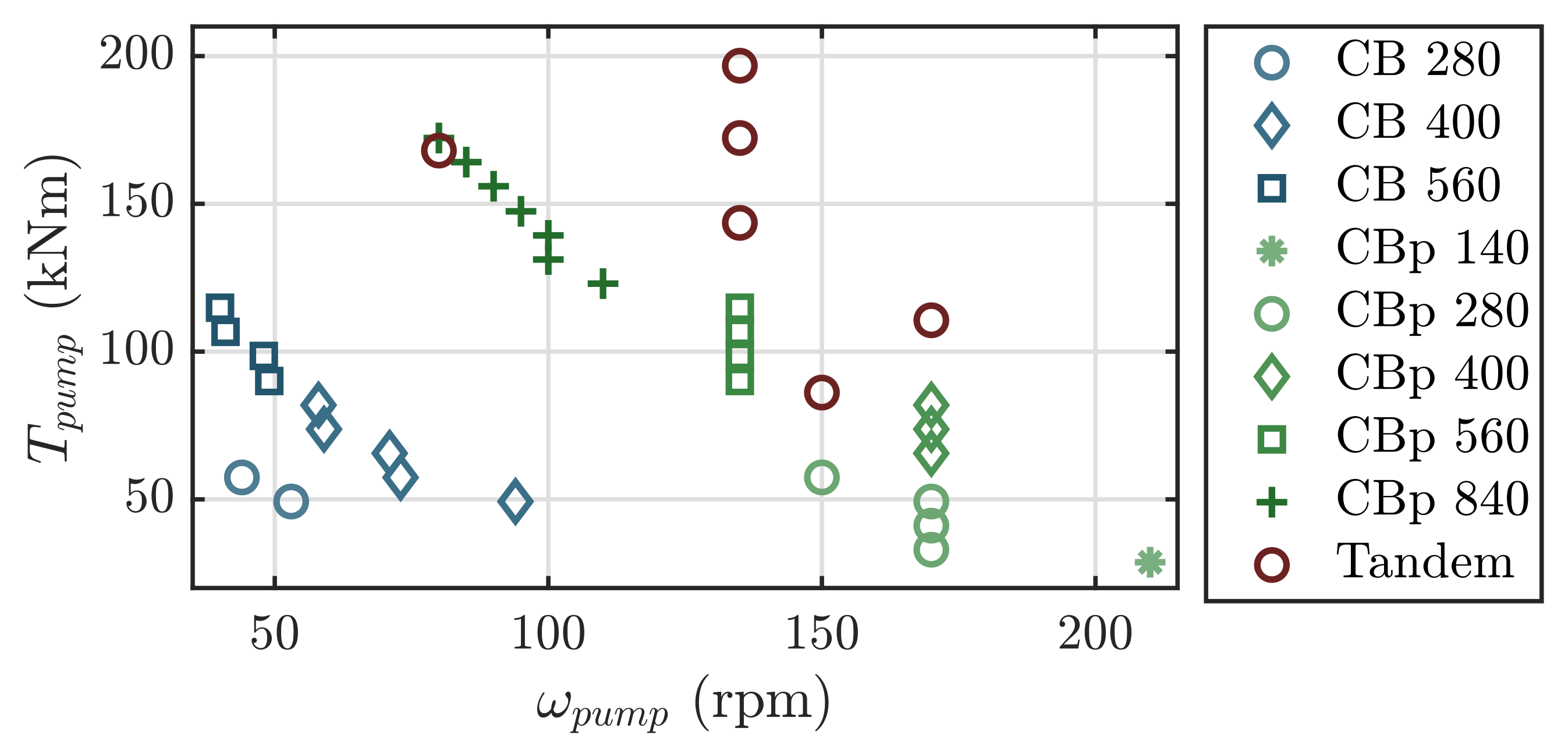
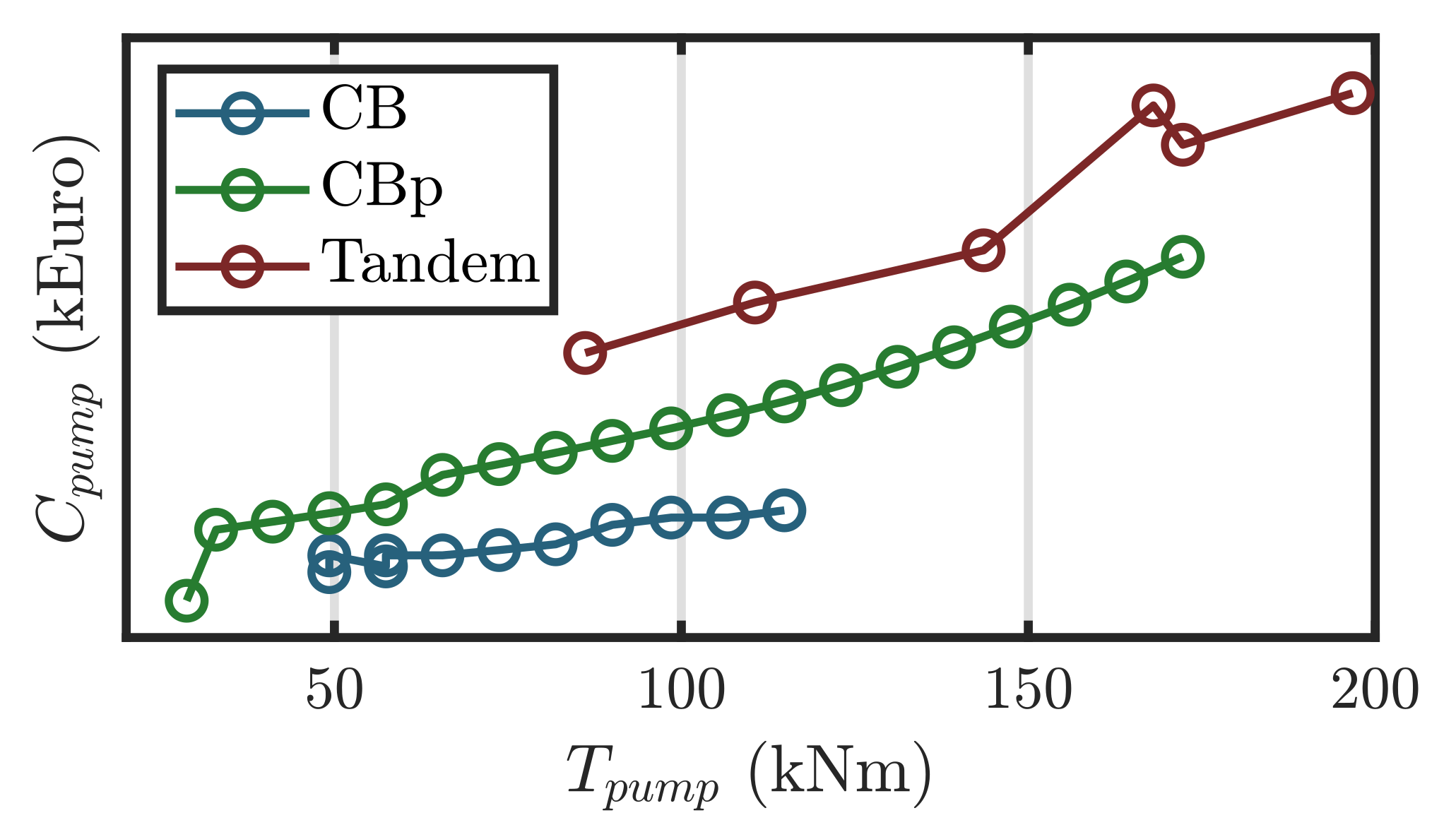
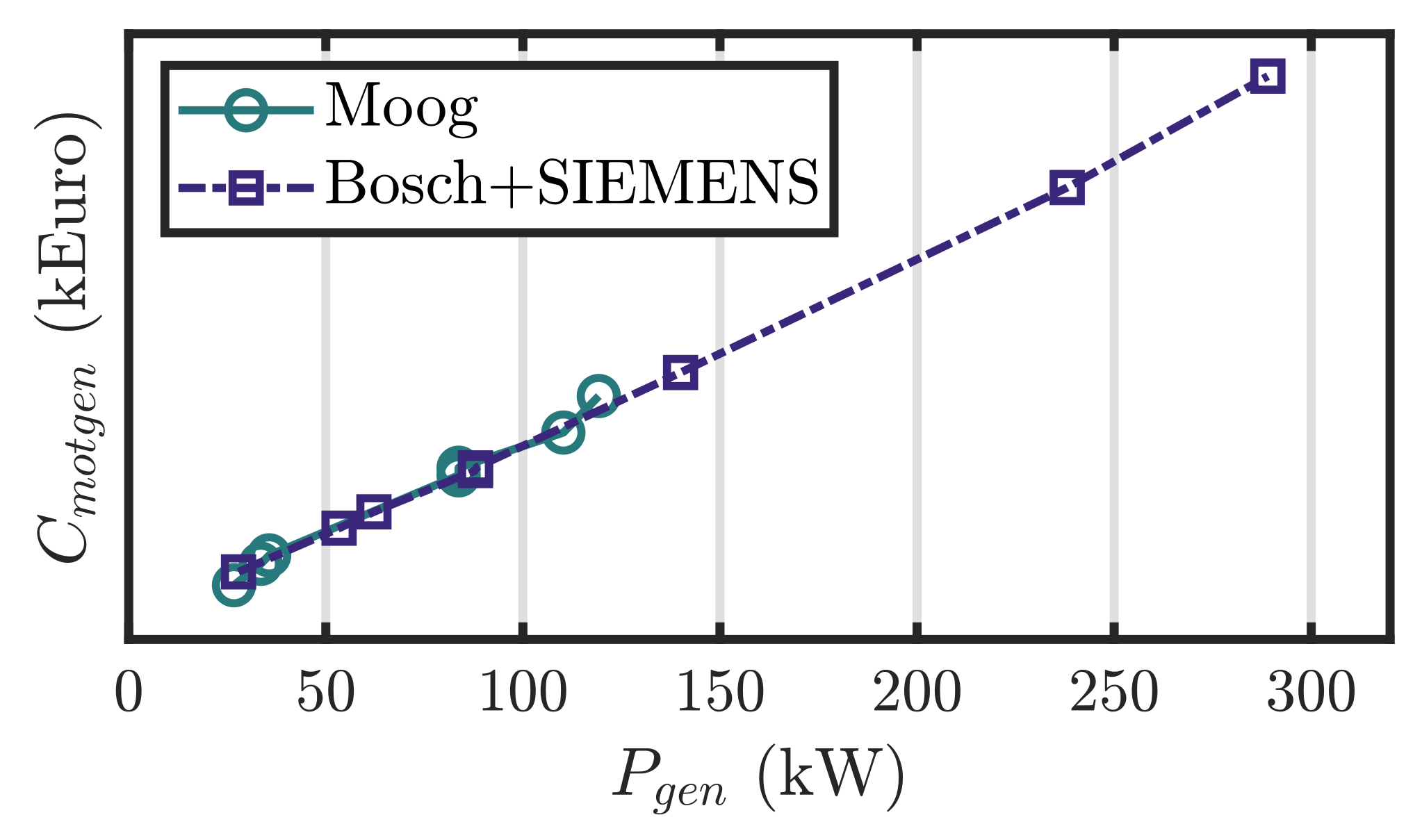
3.1.4. Hydraulic PTO Parameters
3.1.5. Device Cost Estimation
3.2. Single Device Optimization
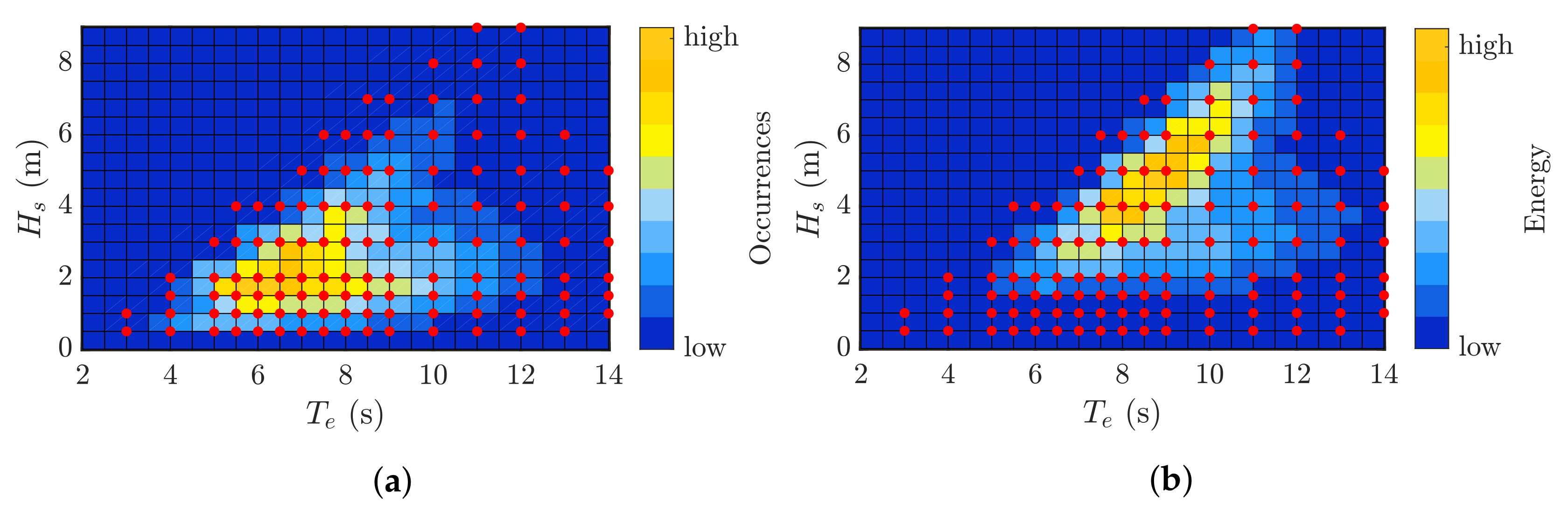
3.2.1. Sea States Definition
3.2.2. Control Tuning
3.3. Key Performance Indicators
- AEP: annual energy production (MWh/y). With AEP, we refer to the ISWEC production, computed through the net power produced by the system for each wave considered and with the annual occurence distribution associated to the sea site of interest:where is the total number of waves, is the average net power extracted with the wave, and is the annual occurrence associated with the wave. The coefficient converts the annual productivity into MWh/y.
- CoE: cost of energy (Euro/MWh). In this work, the CoE is defined as the ratio between the device cost and the AEP multiplied by the lifetime of the device, fixed to 25 years:
3.4. Optimization Algorithm
4. Optimization Results
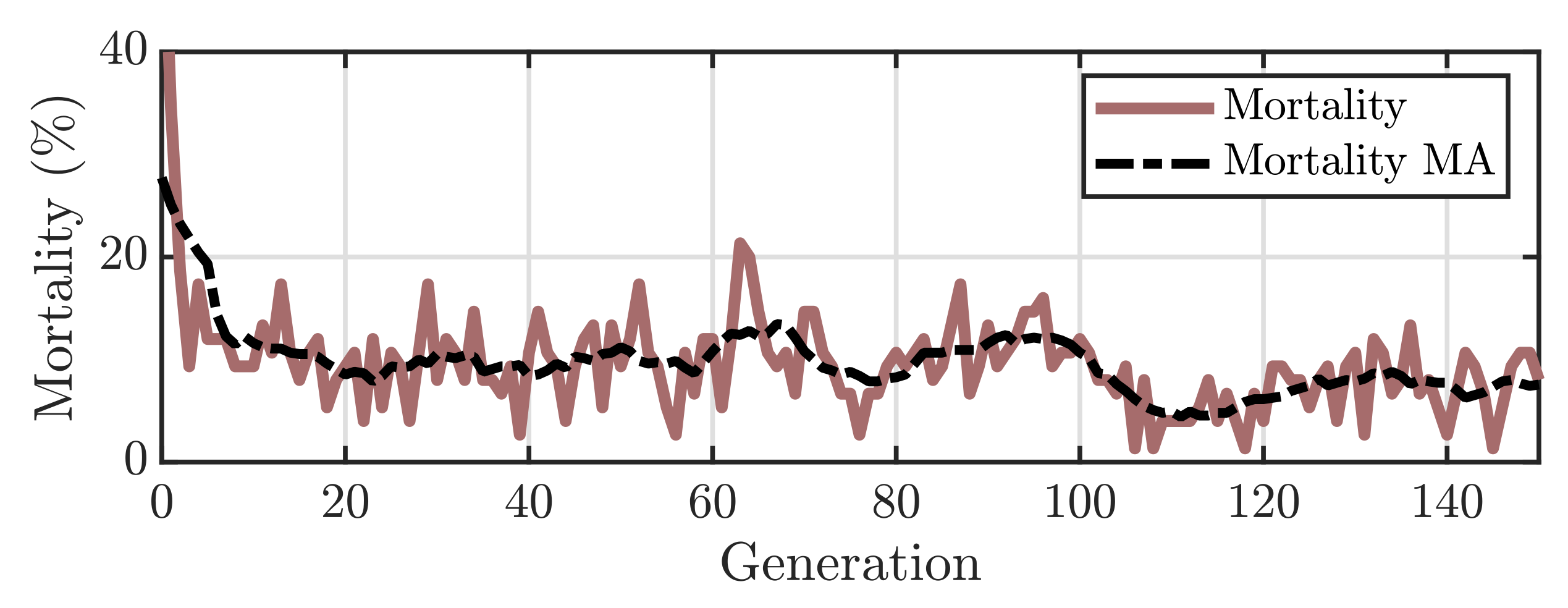
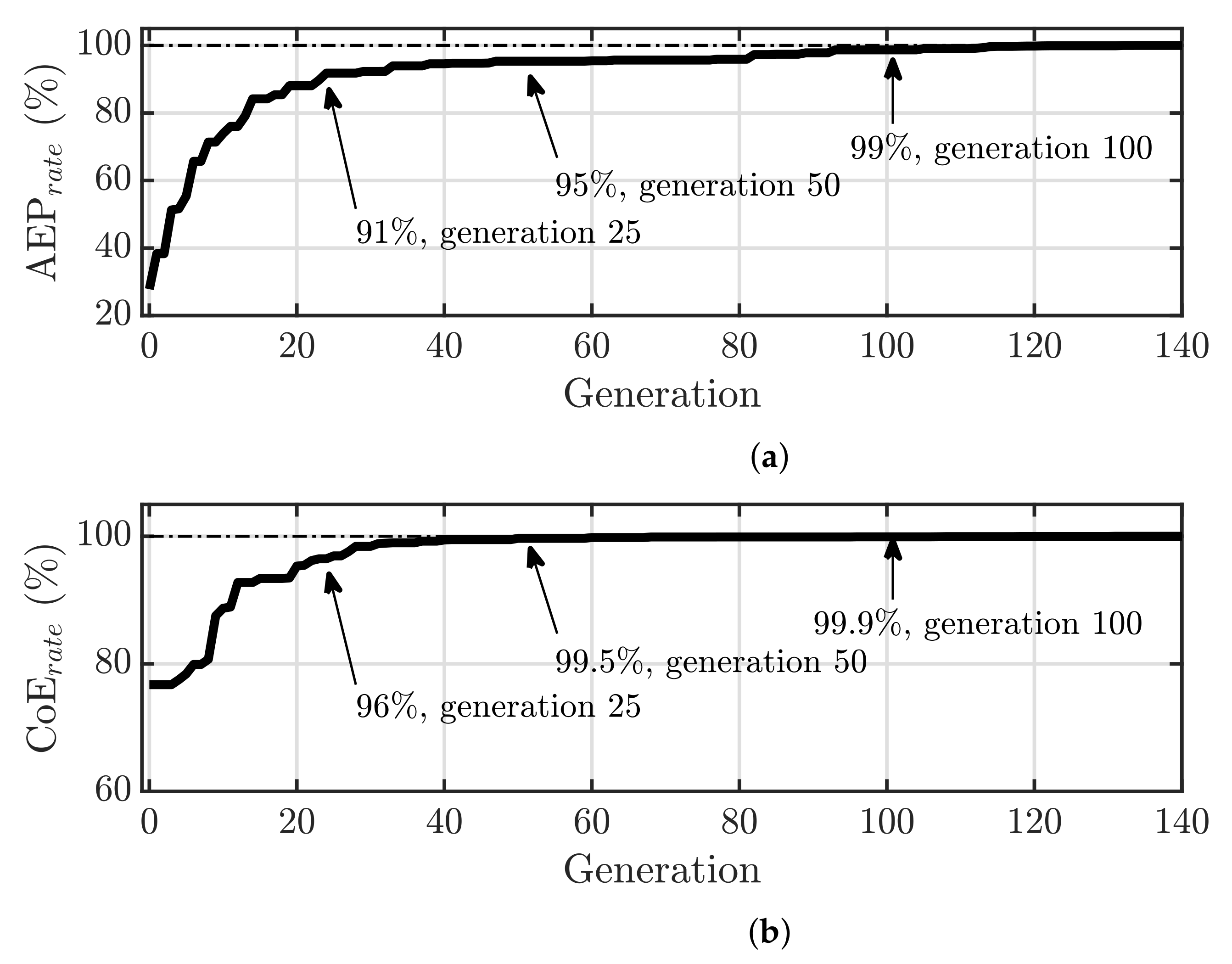
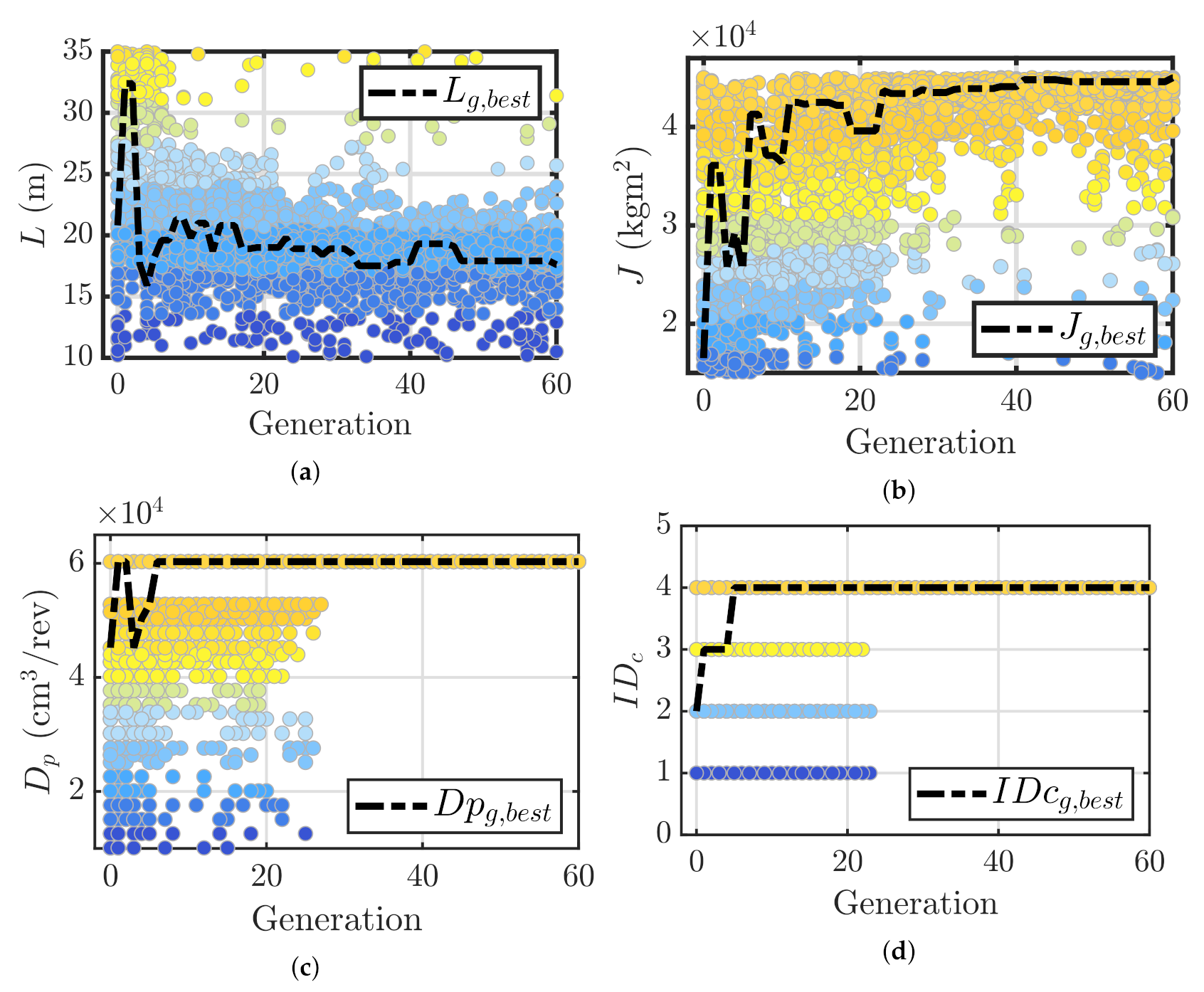
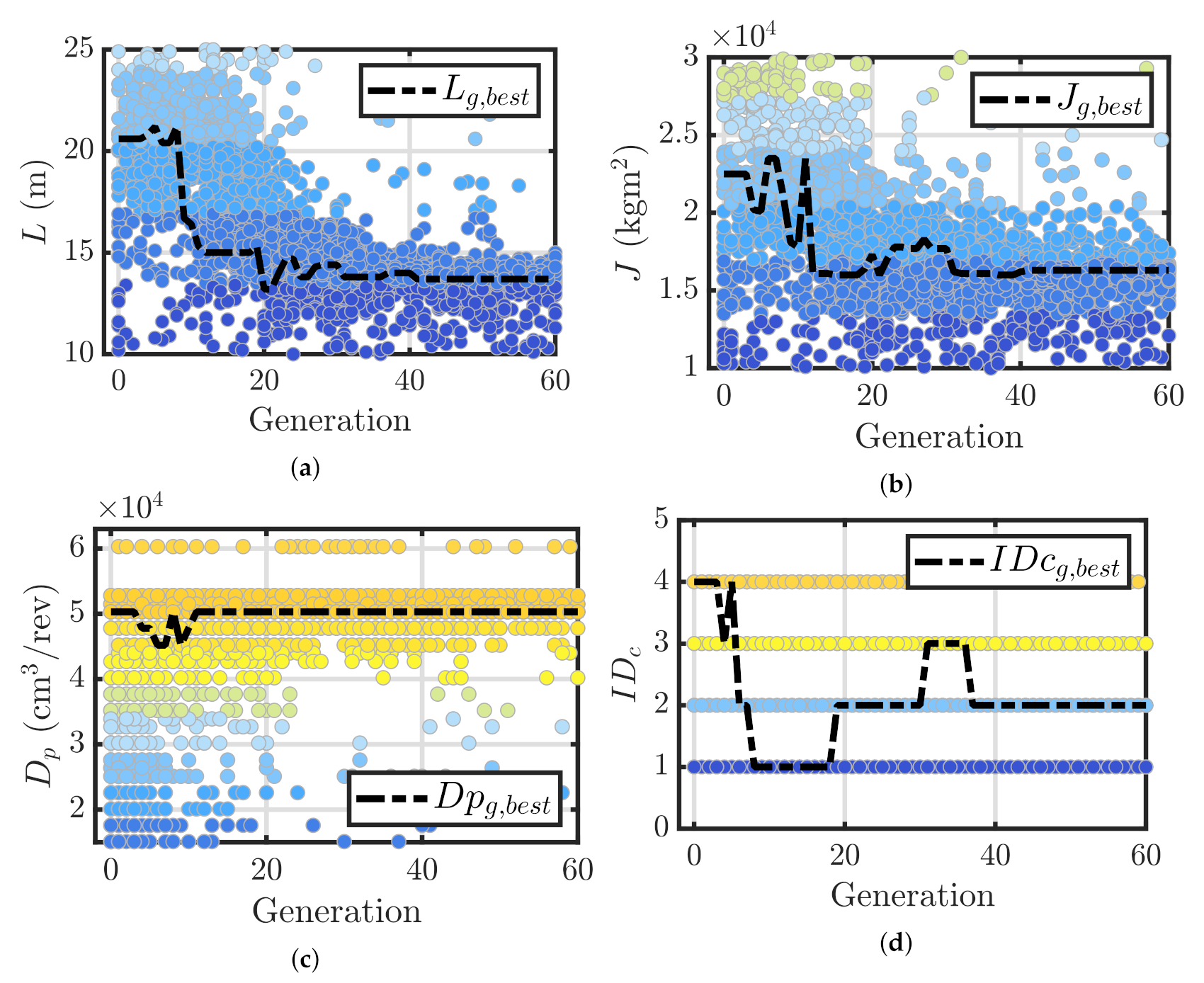
4.1. Convergence Analysis
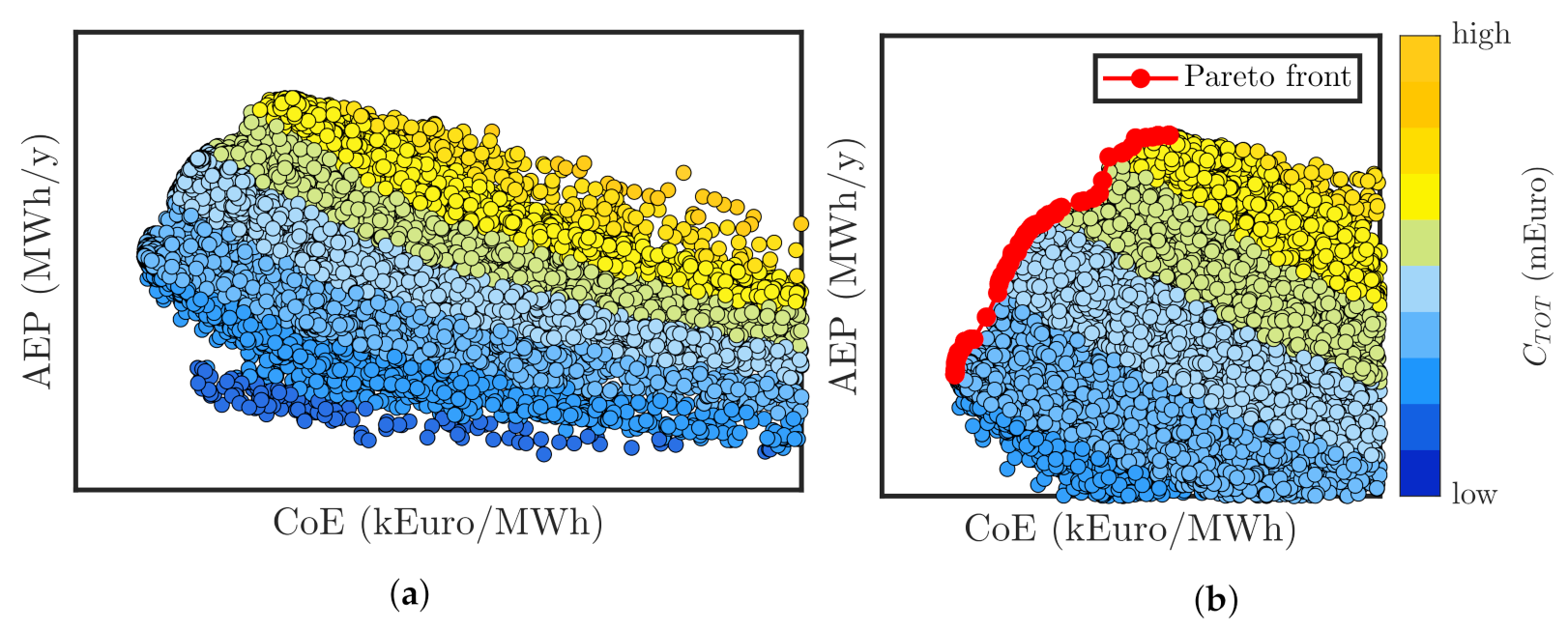
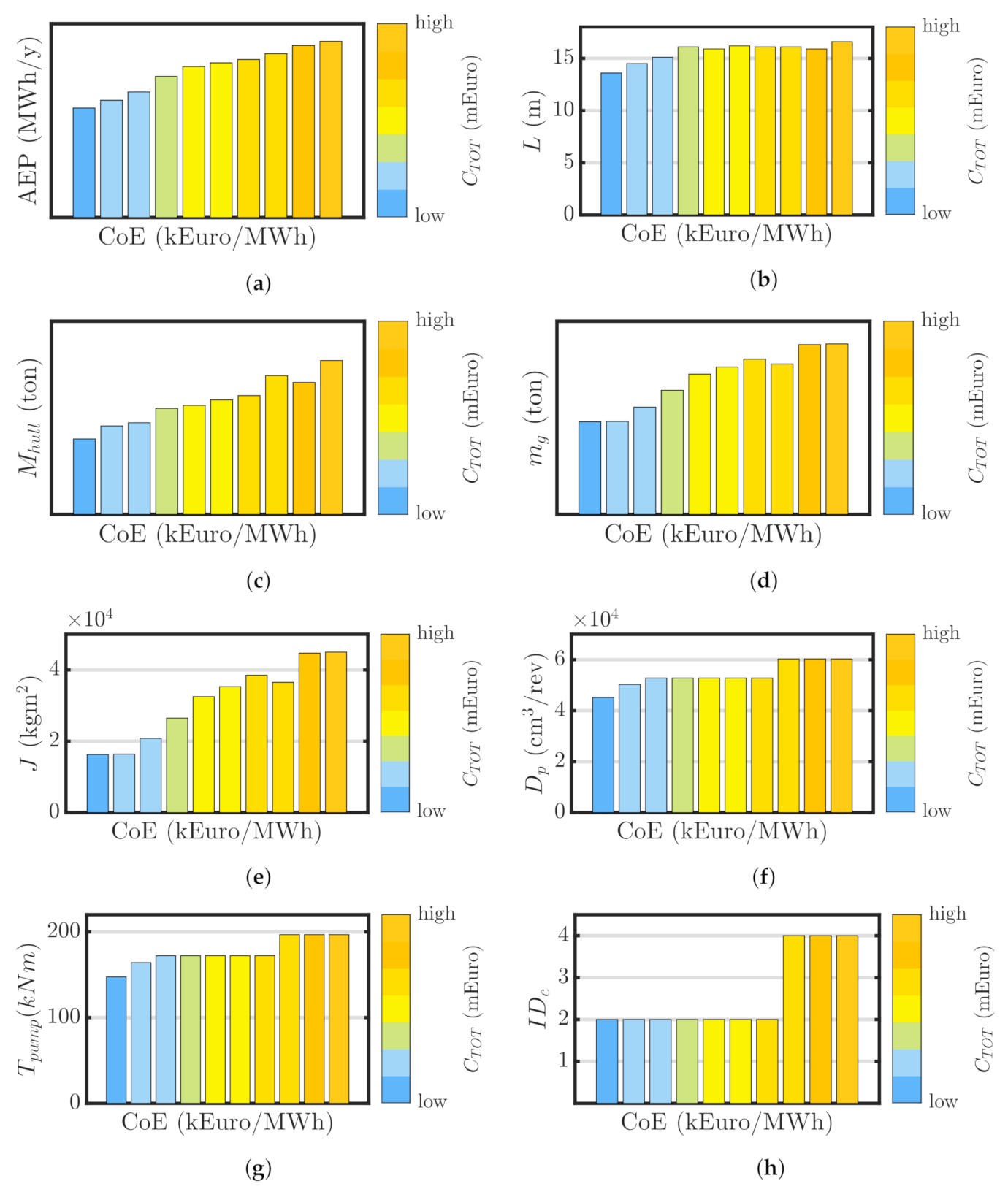
4.2. Optimization Output and Techno-Economic Trends
4.3. Optimal Devices
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| WEC | Wave Energy Converter |
| PTO | Power Take-Off |
| GA | Genetic Algorithm |
| NSGA-II | Non-dominated Sorting Genetic Algorihm II |
| HPTO | Hydraulic PTO |
| TDM | Time-Domain Model |
| SDM | Spectral-Domain Model |
| AEP | Annual Energy Production |
| CoE | Cost of Energy |
| MA | Moving Average |
| 1 |
References
- Salter, S.H.; Taylor, J.R.; Caldwell, N.J. Power conversion mechanisms for wave energy. Proc. Inst. Mech. Eng. Part J. Eng. Marit. Environ. 2002, 216, 1–27. [Google Scholar] [CrossRef]
- Cruz, J. Ocean Wave Energy; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Trueworthy, A.; Dupont, B. The wave energy converter design process: Methods applied in industry and shortcomings of current practices. J. Mar. Sci. Eng. 2020, 8, 932. [Google Scholar] [CrossRef]
- Sirigu, S.A.; Foglietta, L.; Giorgi, G.; Bonfanti, M.; Cervelli, G.; Bracco, G.; Mattiazzo, G. Techno-Economic optimisation for a wave energy converter via genetic algorithm. J. Mar. Sci. Eng. 2020, 8, 482. [Google Scholar] [CrossRef]
- Carapellese, F.; Sirigu, S.A.; Giorgi, G.; Bonfanti, M.; Mattiazzo, G. Multiobjective optimisation approaches applied to a wave energy converter design. In Proceedings of the European Wave and Tidal Energy Conference, European Wave and Tidal Energy Conference Series, Plymouth, UK, 5–9 September 2021; pp. 2114-1–2114-8. [Google Scholar]
- Giorcelli, F.; Sirigu, S.A.; Pasta, E.; Gioia, D.G.; Bonfanti, M.; Mattiazzo, G. Wave Energy Converter Optimal Design Under Parameter Uncertainty. In Proceedings of the ASME 2022 41th International Conference on Ocean, Offshore and Artic Engineering, Hamburg, Germany, 5–10 June 2022. in press. [Google Scholar]
- Babarit, A.; Clément, A.H.; Gilloteaux, J.C. Optimization and Time-Domain Simulation of the SEAREV Wave Energy Converter. In Proceedings of the ASME 2005 24th International Conference on Offshore Mechanics and Arctic Engineering, Halkidiki, Greece, 12–17 June 2005. [Google Scholar] [CrossRef]
- Babarit, A.; Clement, A.H. Shape optimisation of the SEAREV wave energy converter. In Proceedings of the World Renewable Energy Congress IX, Florence, Italy, 19–25 August 2006. [Google Scholar]
- Teixeira-Duarte, F.; Clemente, D.; Giannini, G.; Rosa-Santos, P.; Taveira-Pinto, F. Review on layout optimization strategies of offshore parks for wave energy converters. Renew. Sustain. Energy Rev. 2022, 163, 112513. [Google Scholar] [CrossRef]
- Li, L.; Gao, Z.; Yuan, Z.M. On the sensitivity and uncertainty of wave energy conversion with an artificial neural-network-based controller. Ocean. Eng. 2019, 183, 282–293. [Google Scholar] [CrossRef]
- Neshat, M.; Mirjalili, S.; Sergiienko, N.Y.; Esmaeilzadeh, S.; Amini, E.; Heydari, A.; Garcia, D.A. Layout optimisation of offshore wave energy converters using a novel multi-swarm cooperative algorithm with backtracking strategy: A case study from coasts of Australia. Energy 2022, 239, 122463. [Google Scholar] [CrossRef]
- Zhu, K.; Shi, H.; Han, M.; Cao, F. Layout study of wave energy converter arrays by an artificial neural network and adaptive genetic algorithm. Ocean Eng. 2022, 260, 112072. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, Q.; Kang, Y.; Yu, F. Hydrodynamic interactions among wave energy converter array and a hierarchical genetic algorithm for layout optimization. Ocean Eng. 2022, 256, 111521. [Google Scholar] [CrossRef]
- He, Z.; Ning, D.; Gou, Y.; Zhou, Z. Wave energy converter optimization based on differential evolution algorithm. Energy 2022, 246, 123433. [Google Scholar] [CrossRef]
- Garcia-Teruel, A.; Forehand, D.I. Manufacturability considerations in design optimisation of wave energy converters. Renew. Energy 2022, 187, 857–873. [Google Scholar] [CrossRef]
- Garcia-Teruel, A.; DuPont, B.; Forehand, D.I. Hull geometry optimisation of wave energy converters: On the choice of the optimisation algorithm and the geometry definition. Appl. Energy 2020, 280, 115952. [Google Scholar] [CrossRef]
- Giannini, G.; Rosa-Santos, P.; Ramos, V.; Taveira-Pinto, F. Wave energy converters design combining hydrodynamic performance and structural assessment. Energy 2022, 249, 123641. [Google Scholar] [CrossRef]
- Pedersen, H.C.; Hansen, R.H.; Hansen, A.H.; Andersen, T.O.; Bech, M.M. Design of full scale wave simulator for testing Power Take off systems for wave energy converters. Int. J. Mar. Energy 2016, 13, 130–156. [Google Scholar] [CrossRef]
- Hansen, R.H.; Andersen, T.O.; Pedersen, H.C. Model Based Design of Efficient Power Take-Off Systems for Wave Energy Converters. In Proceedings of the 12th Scandinavian International Conference on Fluis Power, Tampere, Finland, 18–20 May 2011; pp. 1–15. [Google Scholar]
- Wave Star. Unlimited Clean Energy with the Wavestar Machine. Available online: http://wavestarenergy.com/ (accessed on 30 November 2020).
- Liu, C.H.; Yang, Q.J.; Bao, G. Performance investigation of a two-raft-type wave energy converter with hydraulic power take-off unit. Appl. Ocean. Res. 2017, 62, 139–155. [Google Scholar] [CrossRef]
- Zheng, S.M.; Zhang, Y.H.; Zhang, Y.L.; Sheng, W.A. Numerical study on the dynamics of a two-raft wave energy conversion device. J. Fluids Struct. 2015, 58, 271–290. [Google Scholar] [CrossRef]
- Liu, C.; Yang, Q.; Bao, G. Influence of hydraulic power take-off unit parameters on power capture ability of a two-raft-type wave energy converter. Ocean. Eng. 2018, 150, 69–80. [Google Scholar] [CrossRef]
- Gaspar, J.F.; Calvário, M.; Kamarlouei, M.; Soares, C.G. Design tradeoffs of an oil-hydraulic power take-off for wave energy converters. Renew. Energy 2018, 129, 245–259. [Google Scholar] [CrossRef]
- Jusoh, M.A.; Ibrahim, M.Z.; Daud, M.Z.; Yusop, Z.M.; Albani, A.; Rahman, S.J.; Mohad, S. Parameters estimation of hydraulic power take-off system for wave energy conversion system using genetic algorithm. IOP Conf. Ser. Earth Environ. Sci. 2020, 463, 012129. [Google Scholar] [CrossRef]
- Siemens Digital Industries. Siemens Simcenter Amesim. 2020. Available online: https://www.plm.automation.siemens.com/global/en/products.html (accessed on 5 November 2020).
- Calvário, M.; Gaspar, J.F.; Kamarlouei, M.; Hallak, T.S.; Guedes Soares, C. Oil-hydraulic power take-off concept for an oscillating wave surge converter. Renew. Energy 2020, 159, 1297–1309. [Google Scholar] [CrossRef]
- Sarkar, D.; Doherty, K.; Dias, F. The modular concept of the Oscillating Wave Surge Converter. Renew. Energy 2016, 85, 484–497. [Google Scholar] [CrossRef]
- Sarkar, D.; Contal, E.; Vayatis, N.; Dias, F. Prediction and optimization of wave energy converter arrays using a machine learning approach. Renew. Energy 2016, 97, 504–517. [Google Scholar] [CrossRef]
- MOREnergy Lab. ISWEC. 2022. Available online: http://www.morenergylab.polito.it/iswec/ (accessed on 22 August 2022).
- Pozzi, N.; Bonetto, A.; Bonfanti, M.; Bracco, G.; Dafnakis, P.; Giorcelli, E.; Passione, B.; Sirigu, S.; Mattiazzo, G. PeWEC: Preliminary design of a full-scale plant for the mediterranean sea. In Proceedings of the NAV International Conference on Ship and Shipping Research, Trieste, Italy, 20–22 June 2018. Number 221499. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Sirigu, S.; Bonfanti, M.; Carapellese, F.; Bracco, G. Stochastic modelling via statistical linearization of a wave energy converter. In Proceedings of the European Wave and Tidal Energy Conference, Plymouth, UK, 5–9 September 2021; pp. 2132-1–2132-9. [Google Scholar]
- Bonfanti, M.; Sirigu, S.; Mattiazzo, G. ISWEC approaching the spectral-domain: Modelling and numerical experiments. In Proceedings of the International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME 2021), Flic En Flac, Mauritius, 7–8 October 2021. [Google Scholar] [CrossRef]
- Bonfanti, M.; Bracco, G. Non-linear Frequency Domain Modelling of a Wave Energy Harvester. In The International Conference of IFToMM ITALY; Springer: Cham, Switzerland, 2022; Volume 122 MMS, pp. 874–881. [Google Scholar] [CrossRef]
- Silva, L.S.; Sergiienko, N.Y.; Pesce, C.P.; Ding, B.; Cazzolato, B.; Morishita, H.M. Stochastic analysis of nonlinear wave energy converters via statistical linearization. Appl. Ocean. Res. 2020, 95, 102023. [Google Scholar] [CrossRef]
- Pozzi, N.; Bonfanti, M.; Mattiazzo, G. Mathematical Modeling and Scaling of the Friction Losses of a Mechanical Gyroscope. Int. J. Appl. Mech. 2018, 10, 1850024. [Google Scholar] [CrossRef]
- Sirigu, S.A.; Gallizio, F.; Giorgi, G.; Bonfanti, M.; Giovanni, B.; Mattiazzo, G. Numerical and experimental identification of the aerodynamic power losses of the ISWEC. J. Mar. Sci. Eng. 2020, 8, 49. [Google Scholar] [CrossRef]
- Sirigu, S.; Bonfanti, M.; Dafnakis, P.; Bracco, G.; Mattiazzo, G.; Brizzolara, S. Pitch Resonance Tuning Tanks: A novel technology for more efficient wave energy harvesting. In Proceedings of the OCEANS 2018 MTS/IEEE, Charleston, SC, USA, 22–25 October 2018. [Google Scholar] [CrossRef]
- Sirigu, S.A.; Bracco, G.; Bonfanti, M.; Dafnakis, P.; Mattiazzo, G. On-board sea state estimation method validation based on measured floater motion. IFAC-PapersOnLine 2018, 51, 68–73. [Google Scholar] [CrossRef]
- Bonfanti, M.; Hillis, A.; Sirigu, S.A.; Dafnakis, P.; Bracco, G.; Mattiazzo, G.; Plummer, A. Real-time wave excitation forces estimation: An application on the ISWEC device. J. Mar. Sci. Eng. 2020, 8, 825. [Google Scholar] [CrossRef]
- Bonfanti, M.; Sirigu, S.A.; Giorgi, G.; Dafnakis, P.; Bracco, G.; Mattiazzo, G. A passive control strategy applied to the iswec device: Numerical modelling and experimental tests. Int. J. Mech. Control. 2020, 21, 143–154. [Google Scholar]
- Giorgi, G.; Sirigu, S.; Bonfanti, M.; Bracco, G.; Mattiazzo, G. Fast nonlinear Froude–Krylov force calculation for prismatic floating platforms: A wave energy conversion application case. J. Ocean. Eng. Mar. Energy 2021, 7, 439–457. [Google Scholar] [CrossRef]
- Genuardi, L.; Bracco, G.; Sirigu, S.A.; Bonfanti, M.; Paduano, B.; Dafnakis, P.; Mattiazzo, G. An application of model predictive control logic to inertial sea wave energy converter. In IFToMM World Congress on Mechanism and Machine Science; Springer: Cham, Switzerland, 2019; Volume 73, pp. 3561–3571. [Google Scholar] [CrossRef]
- Niosi, F.; Parrinello, L.; Paduano, B.; Pasta, E.; Carapellese, F.; Bracco, G. On the Influence of Mooring in Wave Energy Converters Productivity: The PeWEC case. In Proceedings of the 2021 International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Flic En Flac, Mauritius, 7–8 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Anerdi, C.; Paduano, B.; Casalone, P.; Mattiazzo, G.; Giordano, L. Design of a Reinforced Concrete Wave Energy Converter in Extreme Wave Conditions. In Proceedings of the I4SDG Workshop 2021, Online, 25–26 November 2021; Quaglia, G., Gasparetto, A., Petuya, V., Carbone, G., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 70–77. [Google Scholar]
- Hatecke, H. The impulse response fitting and ship motions. Ship Technol. Res. 2015, 62, 97–106. [Google Scholar] [CrossRef]
- Temarel, P. Loads on ships and offshore structures. In Proceedings of the 26th International Conference on Offshore Mechanics and Arctic Engineering (OMAE 2007), San Diego, CA, USA, 10–15 June 2007; p. 10. [Google Scholar] [CrossRef]
- Peña-Sanchez, Y.; Faedo, N.; Penalba, M.; Giorgi, G.; Merigaud, A.; Windt, C.; Garc, D.; Wang, L.; Ringwood, J.V. Finite-Order hydrodynamic Approximation by Moment-Matching (FOAMM ) toolbox for wave energy applications. In Proceedings of the 13th European Wave and Tidal Energy Conference, Napoli, Italy, 1–6 September 2019. [Google Scholar]
- Babarit, A.; Guglielmi, M.; Clément, A.H. Declutching control of a wave energy converter. Ocean. Eng. 2009, 36, 1015–1024. [Google Scholar] [CrossRef]
- Wu, J.; Yao, Y.; Zhou, L.; Göteman, M. Latching and declutching control of the solo duck wave-energy converter with different load types. Energies 2017, 10, 70. [Google Scholar] [CrossRef]
- Folley, M.; Whittaker, T. Preliminary cross-Validation of wave energy converter array interactions. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering-OMAE. American Society of Mechanical Engineers Digital Collection, Nantes, France, 9–14 June 2013; Volume 8. [Google Scholar] [CrossRef]
- Babarit, A.; Hals, J.; Kurniawan, A.; Muliawan, M.; Moan, T.; Krokstad, J. The NumWEC Project: Numerical Esitmation of Energy Delivery from a Selection of Wave Energy Converters; Technical Report December; Norwegian University of Science and Technology: Trondheim, Norway, 2011. [Google Scholar] [CrossRef]
- Folley, M. Chapter 4 - Spectral-Domain Models. In Numerical Modelling of Wave Energy Converters; Academic Press: Cambridge, MA, USA, 2016; pp. 67–80. ISBN 9780128032107. [Google Scholar] [CrossRef]
- Roberts, J.; Spanos, P. Random Vibration and Statistical Linearization by Roberts JB, Spanos PD; John Wiley & Sons: New York, NY, USA, 1990. [Google Scholar]
- Da Silva, L.S.; Morishita, H.M.; Pesce, C.P.; Gonçalves, R.T. Nonlinear analysis of a heaving point absorber in frequency domain via statistical linearization. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Glasgow, Scotland, UK, 9–14 June 2019; Volume 9. [Google Scholar] [CrossRef]
- Gudmestad, O.T.; Connor, J.J. Linearization methods and the influence of current on the nonlinear hydrodynamic drag force. Appl. Ocean. Res. 1983, 5, 184–194. [Google Scholar] [CrossRef]
- Spanos, P.D.; Arena, F.; Richichi, A.; Malara, G. Efficient dynamic analysis of a nonlinear wave energy harvester model. J. Offshore Mech. Arct. Eng. 2016, 138, 1–8. [Google Scholar] [CrossRef]
- Spanos, P.D.; Strati, F.M.; Malara, G.; Arena, F. Stochastic dynamic analysis of U-OWC wave energy converters. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Trondheim, Norway, 25–30 June 2017; Volume 10. [Google Scholar] [CrossRef]
- Bain, L.J.; Engelhardt, M. Introduction to Probability and Mathematical Statistics; Classic Series; Brooks/Cole Cengage Learning: Boston, MA, USA, 1993; Volume 49, p. 673. [Google Scholar] [CrossRef]
- Rexroth, B. Hägglunds Drive Systems and Solutions. 2020. Available online: https://dc-us.resource.bosch.com/media/us (accessed on 22 January 2021).
- Hansen, R.H.; Kramer, M.M.; Vidal, E. Discrete displacement hydraulic power take-off system for the wavestar wave energy converter. Energies 2013, 6, 4001–4044. [Google Scholar] [CrossRef]
- Hansen, R.H. Aalborg Universitet Design and Control of the PowerTake-Off System for a Wave Energy Converter with Multiple Absorbers Hansen, Rico Hjerm Publication Date. Ph.D. Thesis, Aalborg Universitet, Aalborg, Denmark, 2013. [Google Scholar]
- Garcia-Teruel, A.; Forehand, D.I.; Jeffrey, H. Wave Energy Converter hull design for manufacturability and reduced LCOE. In Proceedings of the 7th International Conference on Ocean Energy (ICOE), Cherbourg, Normandy, France, 12–14 June 2018; pp. 1–9. [Google Scholar]
- Fontana, M.; Casalone, P.; Sirigu, S.A.; Giorgi, G.; Bracco, G.; Mattiazzo, G. Viscous damping identification for a wave energy converter using CFD-URANS simulations. J. Mar. Sci. Eng. 2020, 8, 355. [Google Scholar] [CrossRef]
- Bracco, G.; Giorcelli, E.; Giorgi, G.; Mattiazzo, G.; Passione, B.; Raffero, M.; Vissio, G. Performance assessment of the full scale ISWEC system. In Proceedings of the IEEE International Conference on Industrial Technology, Seville, Spain, 17–19 March 2015; Volume 2015-June, pp. 2499–2505. [Google Scholar] [CrossRef]
- SKF. Cuscinetti Super-Precision. 2015. Available online: https://www.skf.com/binaries/pub44/Images/0901d196803e9f7d-13383_1-IT_tcm_44-129877.pdf (accessed on 26 January 2020).
- Moog. Electro-Hydrostatic Actuation System. 2020. Available online: https://www.moog.com/content/sites/global/en/products.html (accessed on 5 February 2021).
- Rexroth, B. Fixed Motor. 2020. Available online: https://www.boschrexroth.com/it/xc/products/product-groups/industrial-hydraulics/motors/axial-piston-motors/fixed-motors (accessed on 5 February 2021).
- SIEMENS. 1PH8 Servomotors (Synchronous). Available online: https://mall.industry.siemens.com/mall/it/it/Catalog/Products/10045151 (accessed on 5 February 2021).
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Eake, K.; Euring, J.A.; Gicnapp, A.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the joint North Sea wave project (JONSWAP). Deut. Hydrogr. Z. 1973, 8, 1–95. [Google Scholar]
- Ruellan, M.; Benahmed, H.; Multon, B.; Josset, C.; Babarit, A.; Clement, A. Design methodology for a SEAREV wave energy converter. IEEE Trans. Energy Convers. 2010, 25, 760–767. [Google Scholar] [CrossRef]
- Garcia-Rosa, P.B.; Bacelli, G.; Ringwood, J.V. Control-informed geometric optimization of wave energy converters: The impact of device motion and force constraints. Energies 2015, 8, 13672–13687. [Google Scholar] [CrossRef]
- Giorgi, G.; Ringwood, J.V. Parametric motion detection for an oscillating water column spar buoy. In Proceedings of the Advances in Renewable Energies Offshore - Proceedings of the 3rd International Conference on Renewable Energies Offshore, RENEW, Lisbon, Portugal, 8–10 October 2018; pp. 505–512. [Google Scholar]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence properties of the Nelder-Mead simplex method in low dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Sirigu, S.A.; Vissio, G.; Bracco, G.; Giorcelli, E.; Passione, B.; Raffero, M.; Mattiazzo, G. ISWEC design tool. Int. J. Mar. Energy 2016, 15, 201–213. [Google Scholar] [CrossRef]
- Ambühl, S.; Kramer, M.; Sørensen, J.D. Reliability-based structural optimization of wave energy converters. Energies 2014, 7, 8178–8200. [Google Scholar] [CrossRef]
- De Andres, A.; Maillet, J.; Todalshaug, J.H.; Möller, P.; Bould, D.; Jeffrey, H. Techno-economic related metrics for a wave energy converters feasibility assessment. Sustainability 2016, 8, 1109. [Google Scholar] [CrossRef]
- Driscoll, F.R.; Weber, J.W.; Jenne, D.S. Methodology to Calculate the ACE and HPQ Metrics Used in the Wave Energy Prize; Technical Report; NREL/TP-5000-70592; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2018. [Google Scholar] [CrossRef][Green Version]
- Joines, J.A.; Houck, C.R. On the use of non-stationary penalty functions to solve nonlinear constrained optimization problems with GA’s. In Proceedings of the IEEE Conference on Evolutionary Computation—Proceedings, IEEE, Walt Disney World Dolphin Hotel, Orlando, FL, USA, 27–29 June 1994; Number 2/-. pp. 579–584. [Google Scholar] [CrossRef]
- Homaifar, A.; Qi, C.X.; Lai, S.H. Constrained optimization via genetic algorithms. Simulation 1994, 62, 242–254. [Google Scholar] [CrossRef]
- Sivanandam, S.N.; Deepa, S.N. Introduction to Genetic Algorithms; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–442. [Google Scholar] [CrossRef]
- Horst, R.; Panos, P. Handbook of Global Optimization Volume 2; Springer: Berlin, Germany, 2002; Volume 53, pp. 1689–1699. [Google Scholar] [CrossRef]
- Arora, J. Introduction to Optimum Design; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar] [CrossRef]



| Hull | ||||
|---|---|---|---|---|
| Design Parameter | Symbol | Unit | LB | UB |
| Hull length | L | m | 10 | 45 |
| Hull width factor | − | 1 | 4 | |
| Bow/stern circ. ratio | − | 0.5 | 1 | |
| Height ratio | − | 0.5 | 1 | |
| Maximum pitch angle | deg | 10 | 20 | |
| Ballast filling ratio | − | 0.35 | 1 | |
| Gyroscope | ||||
| Design Parameter | Symbol | Unit | LB | UB |
| Flywheel inertia | J | kgm2 | 10,000 | 45,000 |
| Gyroscope units | − | 2 | 4 | |
| Pendulum mass | kg | 500 | 8000 | |
| Bearings id | − | 1 | 15 | |
| Hydraulic PTO | ||||
| Design Parameter | Symbol | Unit | LB | UB |
| Pump id | − | 1 | 36 | |
| Hydraulic control id | − | 1 | 4 | |
| Declutching Control | Pump Switching * | |
|---|---|---|
| 1 | no | no |
| 2 | yes | no |
| 3 | no | yes |
| 4 | yes | yes |
| Set Label | Description | AEP Weight () | CoE Weight () |
|---|---|---|---|
| 1 | AEP-driven | 1 | 0 |
| 2 | AEP-weighed-CoE-weighed | 0.75 | 0.25 |
| 3 | AEP-weighed-CoE-weighed | 0.5 | 0.5 |
| 4 | AEP-weighed-CoE-weighed | 0.25 | 0.75 |
| 5 | CoE-driven | 0 | 1 |
| Name | Symbol | Value |
|---|---|---|
| Population size | 75 | |
| Maximum generations | 150 | |
| Maximum stall generations | 50 | |
| Convergence threshold | 10 | |
| Elitism percentage | 5% |
| Performance | Symbol | Delta AEP-CoE-Optimum |
|---|---|---|
| Delta Annual energy production | AEP | −37.4% |
| Delta Cost of energy | CoE | −14.9% |
| Delta Device cost | −52.3% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonfanti, M.; Giorgi, G. Improving Computational Efficiency in WEC Design: Spectral-Domain Modelling in Techno-Economic Optimization. J. Mar. Sci. Eng. 2022, 10, 1468. https://doi.org/10.3390/jmse10101468
Bonfanti M, Giorgi G. Improving Computational Efficiency in WEC Design: Spectral-Domain Modelling in Techno-Economic Optimization. Journal of Marine Science and Engineering. 2022; 10(10):1468. https://doi.org/10.3390/jmse10101468
Chicago/Turabian StyleBonfanti, Mauro, and Giuseppe Giorgi. 2022. "Improving Computational Efficiency in WEC Design: Spectral-Domain Modelling in Techno-Economic Optimization" Journal of Marine Science and Engineering 10, no. 10: 1468. https://doi.org/10.3390/jmse10101468
APA StyleBonfanti, M., & Giorgi, G. (2022). Improving Computational Efficiency in WEC Design: Spectral-Domain Modelling in Techno-Economic Optimization. Journal of Marine Science and Engineering, 10(10), 1468. https://doi.org/10.3390/jmse10101468







